Determination of Vickers Hardness in D2 Steel and TiNbN Coating Using Convolutional Neural Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Architectures of Neural Networks
2.2.2. Implementation of the CNN (Convolutional Neural Network)
- Representative image of the indentation footprint: An image that exemplifies the indentation footprint used in the study is selected;
- Image cropping and cleaning: The image is cropped to isolate the indentation footprint, and cleaning techniques are applied to remove noise and enhance its quality;
- Data augmentation: A data augmentation technique is employed to increase the diversity of the training set. This involves applying random transformations, such as rotations, scaling, or contrast adjustments, to the existing images, thereby generating new training samples;
- Dataset division: The dataset is divided into three subsets—an training set, a validation set, and a final test set;
- YOLO adaptation for training: The YOLO neural network architecture is adapted and configured specifically for the detection of corners in indentation footprints. This involves addressing transfer learning, where the pre-trained weights of the neurons used for detecting the 80 classes in the COCO dataset are fine-tuned to detect a single class, which, in this case, is corners. This allows for more efficient training with a smaller training dataset;
- Training set labeling using LabelImg: The LabelImg tool is used to manually label the corners of the indentation footprints in the training set. The coordinates of the corners are marked and annotated on each image;
- Conversion from XML to YOLO format: The corner annotations in XML format are converted to a YOLO-compatible label format, which is typically a plain text file with a specific format;
- Corner detection: A convolutional neural network (CNN) is employed to detect the corners in the processed indentation footprints. The CNN learns to identify relevant features that indicate the presence of a corner in an image, which are obtained through the convolutions that enrich the feature map;
- Corner prediction: Once the corners are detected, predictions are made to determine the precise coordinates of the corners in the image, including object probabilities, confidence probabilities, and coordinate probabilities;
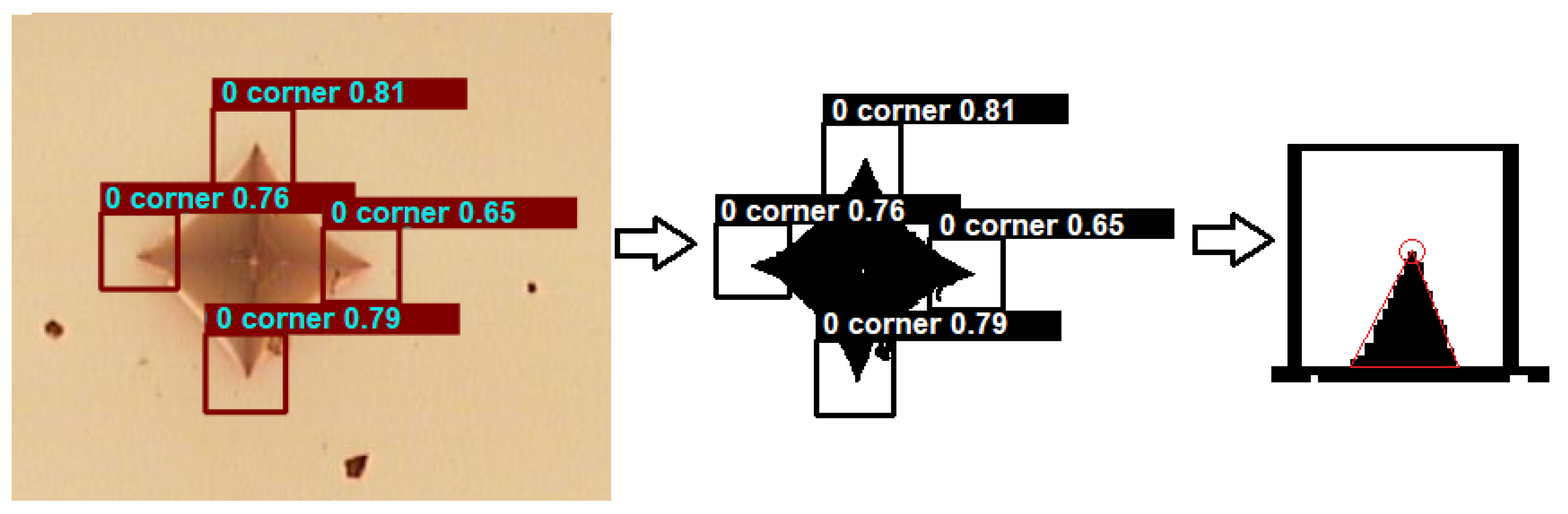
- Euclidean distance scanning algorithm: An algorithm based on Euclidean distance scanning is applied to identify the corresponding corners that form the main diagonals of the indentation footprint. This allows for the measurement and calculation of the lengths of the main diagonals;
- Drawing of the main diagonals: The main diagonals are drawn on the indentation footprint image to provide a clear and accurate visualization of the indentation geometry;
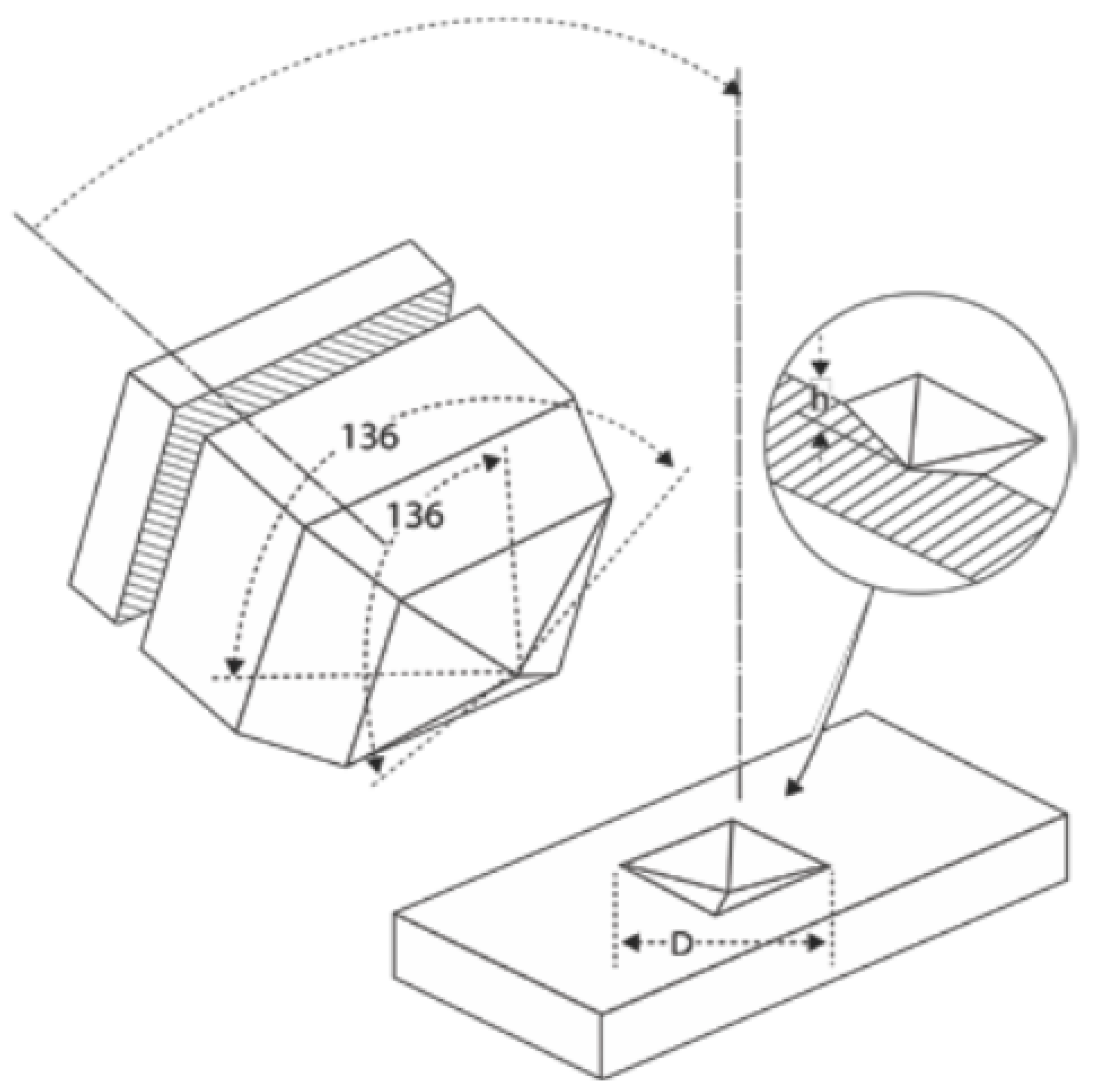
- Conversion from pixels to micrometers: The pixel coordinates of the corners and the lengths of the diagonals are converted to micrometer units to obtain more precise and meaningful measurements, taking into account the scale at which the image was captured;
- Input values into the Vickers hardness equation: The obtained values are used to calculate the Vickers hardness using the specific equation for this type of hardness test;
- Determination of Vickers hardness value: Finally, the corresponding Vickers hardness value of the analyzed indentation footprint is determined, providing information about the material’s hardness.
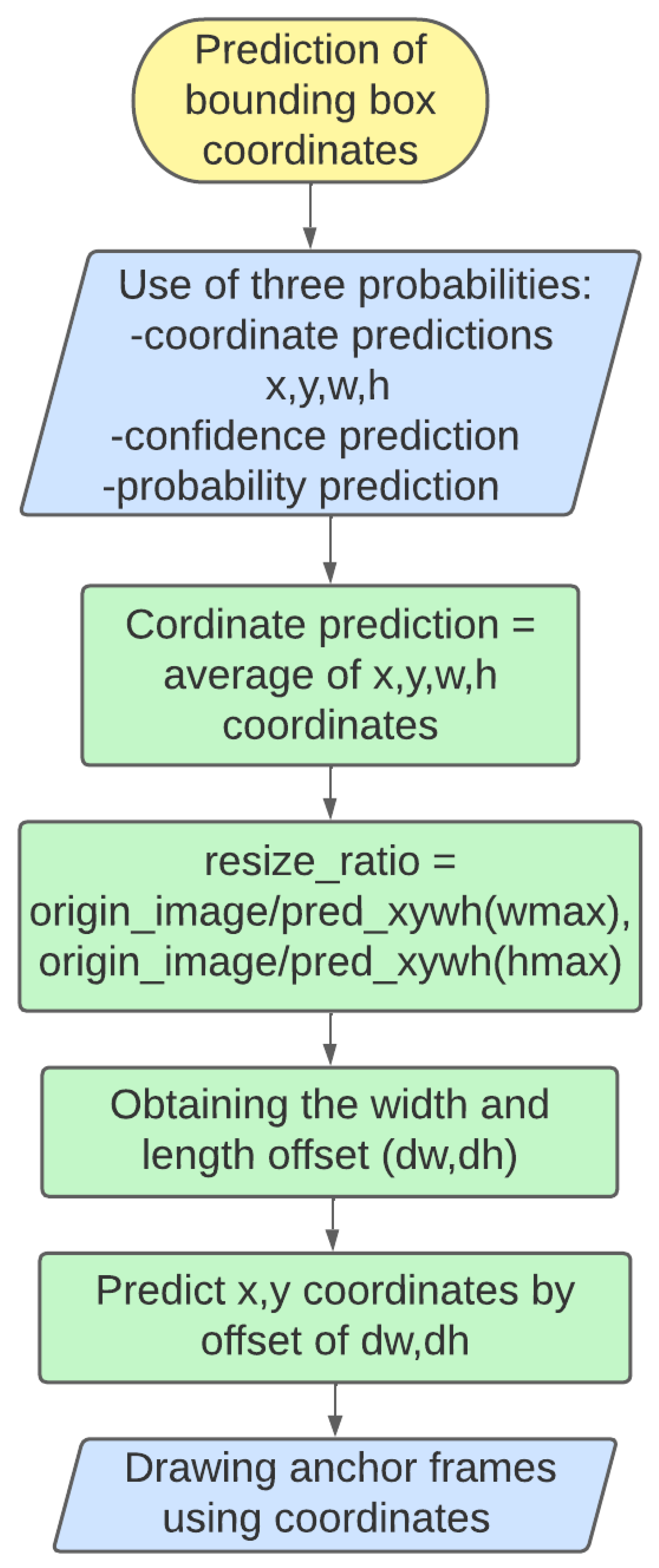
- Use of three probabilities: During the prediction of bounding boxes, three distinct probabilities are used. The first is the coordinate prediction , which represents the average of the predicted coordinates for each bounding box. The second is the confidence prediction, indicating how confident the model is that the object is present in the bounding box. The third is the probability prediction, assigning a probability to each object class within the bounding box;
- Computation of the resizing factor: The resizing factor is calculated using the size of the original image and the maximum width and height values of the predicted bounding boxes. The resizing factor is obtained by dividing the size of the original image by the values and . This factor is used to adjust the predict coordinates to the scale of the original image;
- Obtaining the width and height offset : The width and height offsets of the bounding boxes are computed using the resizing factor. These offsets represent the difference between the actual size of the bounding boxes and the size predicted by the model;
- Prediction of the x and y coordinates through the offset : The predicted x and y coordinates are adjusted by considering the previously calculated width and height offsets. This is carried out by adding or subtracting the values of and to the predicted coordinates, depending on the position of the bounding box with respect to the original image;
- Drawing the bounding boxes using the coordinates: Finally, the bounding boxes are drawn using the predicted coordinates and the resizing factor. These bounding boxes represent the delimited regions where the model has identified the presence of objects of interest.
3. Results
3.1. Identifier Using Transfer Learning
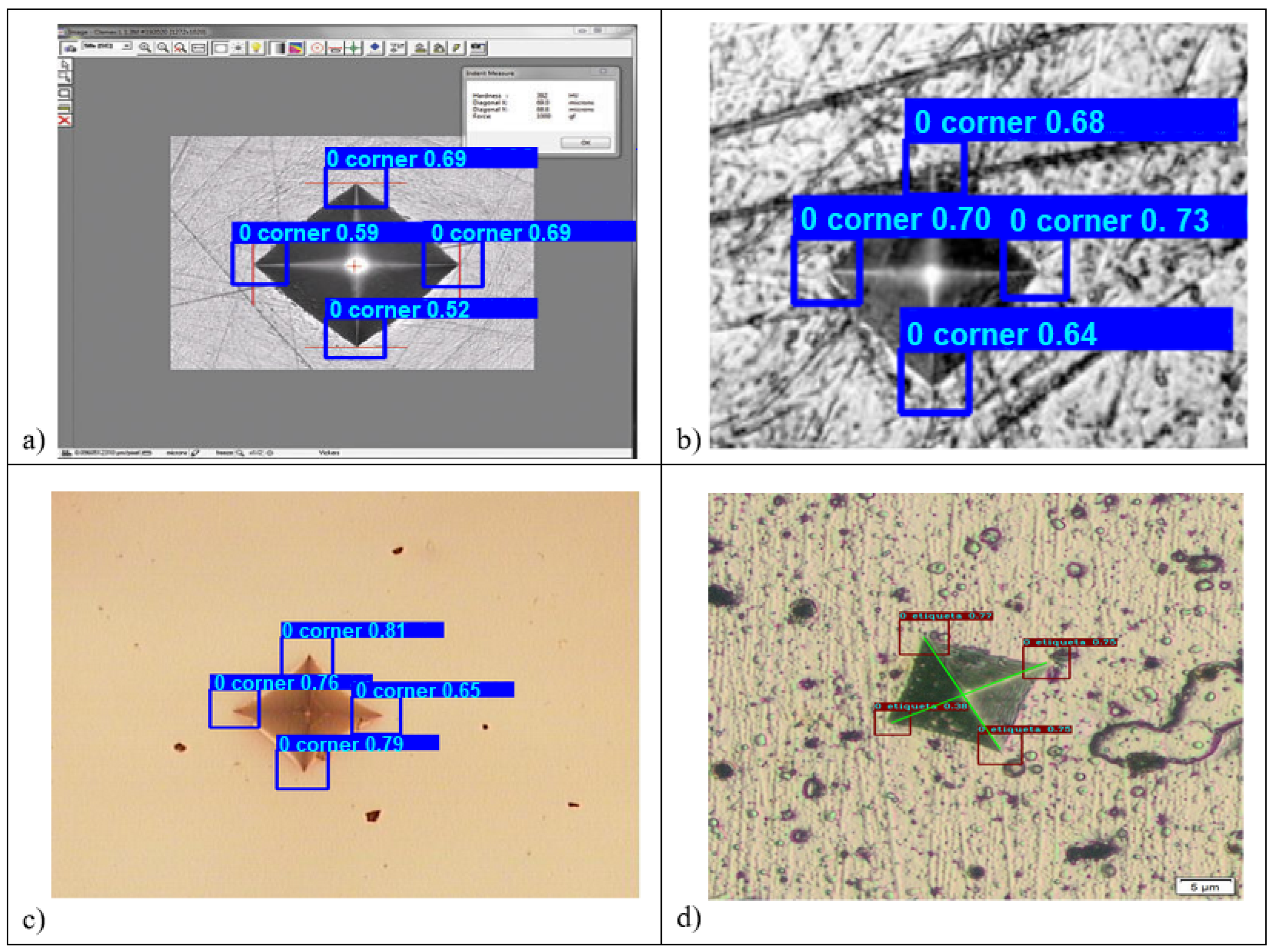
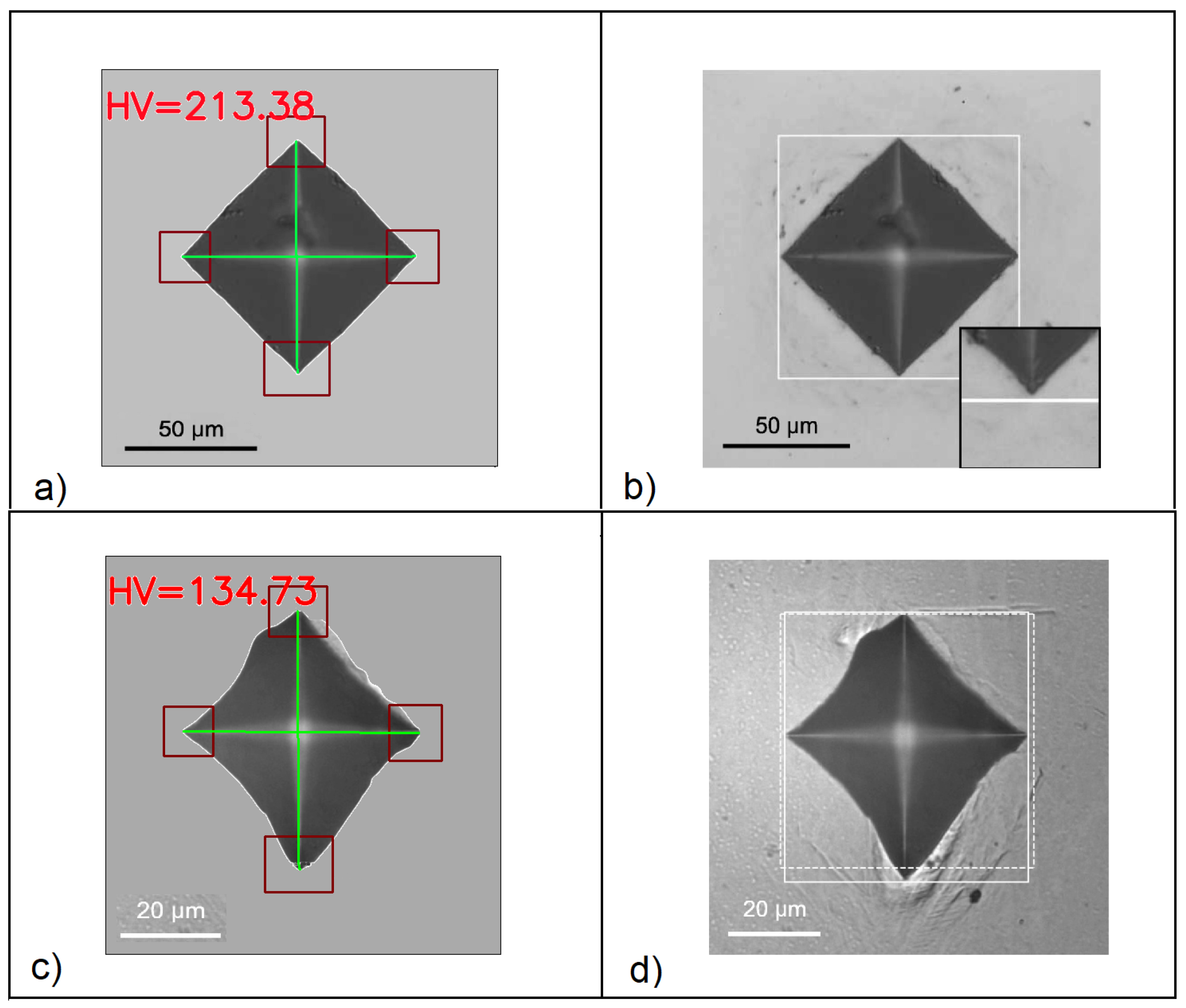
3.2. Corner Identification on Final Test Images
3.3. Corner Identification on Other Images
3.4. Drawing of Main Diagonals
3.5. Comparison between the Tanaka Method and the One Developed
3.6. Comparison between the Manual Measurement and the One Developed
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Castillo Gutiérrez, D.E.; Angarita Moncaleano, I.I.; Rodríguez Baracaldo, R. Microstructural and mechanical characterization of dual phase steels (ferrite-martensite), obtained by thermomechanical processes. Ingeniare Rev. Chil. Ing. 2018, 26, 430–439. [Google Scholar] [CrossRef]
- Arenas, W.; Martínez, O. Roughness and hardness optimization of 12L-14 steel using the response surface methodology. Ing. Ind. 2019, 37, 125–151. [Google Scholar] [CrossRef]
- Ageev, E.; Khardikov, S. Processing of Graphic Information in the Study of the Microhardness ofthe Sintered Sample of Chromium-containing Waste. In Proceedings of the CEUR Workshop, Pescaia, Italy, 16–19 June 2019; pp. 252–255. [Google Scholar] [CrossRef]
- Koch, M.; Ebersbach, U. Experimental study of chromium PVD coatings on brass substrates for the watch industry. Surf. Eng. 1997, 13, 157–164. [Google Scholar] [CrossRef]
- ASTM E384-99; Standard Test Method for Microindentation Hardness of Materials. ASTM International: West Conshohocken, PA, USA, 2017; pp. 1–40. [CrossRef]
- ASTM E92-17; Standard Test Methods for Vickers Hardness and Knoop Hardness of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2017; pp. 1–27. [CrossRef]
- Buehler. Pruebas de Dureza Vickers. Available online: https://www.buehler.com/es/blog/pruebas-de-dureza-vickers/ (accessed on 23 June 2023).
- Tanaka, Y.; Seino, Y.; Hattori, K. Automated Vickers hardness measurement using convolutional neural networks. Int. J. Adv. Manuf. Technol. 2020, 109, 1345–1355. [Google Scholar] [CrossRef]
- Dominguez-Nicolas, S.M.; Wiederhold, P. Indentation image analysis for vickers hardness testing. In Proceedings of the 2018 15th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE 2018), Mexico City, Mexico, 5–7 September 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Sugimoto, T.; Kawaguchi, T. Development of an automatic Vickers hardness testing system using image processing technology. IEEE Trans. Ind. Electron. 1997, 44, 696–702. [Google Scholar] [CrossRef]
- Polanco, J.D.; Jacanamejoy-Jamioy, C.; Mambuscay, C.L.; Piamba, J.F.; Forero, M.G. Automatic Method for Vickers Hardness Estimation by Image Processing. J. Imaging 2023, 9, 8. [Google Scholar] [CrossRef] [PubMed]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Satat, G.; Tancik, M.; Gupta, O.; Heshmat, B.; Raskar, R. Object classification through scattering media with deep learning on time resolved measurement. Opt. Express 2017, 25, 17466–17479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salazar Guerrero, J.E. Implementación de un Prototipo de Sistema Autónomo de Visión Artificial para la Detección de Objetos en Vídeo Utilizando Técnicas de Aprendizaje Profundo. 2019. Available online: http://repositorio.espe.edu.ec/handle/21000/20995 (accessed on 23 June 2023).
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D.D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef] [Green Version]
- Hussain, M.; Bird, J.J.; Faria, D.R. A Study on CNN Transfer Learning for Image Classification; Springer: Berlin/Heidelberg, Germany, 2019; Volume 840, pp. 191–202. [Google Scholar] [CrossRef]
- Jalilian, E.; Uhl, A. Deep Learning Based Automated Vickers Hardness Measurement. In Proceedings of the Computer Analysis of Images and Patterns, Virtual Event, 28–30 September 2021; Tsapatsoulis, N., Panayides, A., Theocharides, T., Lanitis, A., Pattichis, C., Vento, M., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 3–13. [Google Scholar] [CrossRef]
- Li, Z.; Yin, F. Automated measurement of Vickers hardness using image segmentation with neural networks. Measurement 2021, 186, 110200. [Google Scholar] [CrossRef]
- Cheng, W.S.; Chen, G.Y.; Shih, X.Y.; Elsisi, M.; Tsai, M.H.; Dai, H.J. Vickers Hardness Value Test via Multi-Task Learning Convolutional Neural Networks and Image Augmentation. Appl. Sci. 2022, 12, 10820. [Google Scholar] [CrossRef]
- Gonzalez-Carmona, J.M.; Mambuscay, C.L.; Ortega-Portilla, C.; Hurtado-Macias, A.; Piamba, J.F. TiNbN Hard Coating Deposited at Varied Substrate Temperature by Cathodic Arc: Tribological Performance under Simulated Cutting Conditions. Materials 2023, 16, 4531. [Google Scholar] [CrossRef] [PubMed]
- Redmon, J.; Divvala, S.K.; Girshick, R.B.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Zhao, L.; Li, S. Object Detection Algorithm Based on Improved YOLOv3. Electronics 2020, 9, 537. [Google Scholar] [CrossRef] [Green Version]
- Ammar, A.; Koubaa, A.; Ahmed, M.; Saad, A.; Benjdira, B. Vehicle Detection from Aerial Images Using Deep Learning: A Comparative Study. Electronics 2021, 10, 820. [Google Scholar] [CrossRef]
- Otomo, H.; Zhang, R.; Chen, H. Improved phase-field-based lattice Boltzmann models with a filtered collision operator. Int. J. Mod. Phys. 2018, 30, 1941009. [Google Scholar] [CrossRef] [Green Version]
- Gai, W.; Liu, Y.; Zhang, J.; Jing, G. An improved Tiny YOLOv3 for real-time object detection. Syst. Sci. Control. Eng. 2021, 9, 314–321. [Google Scholar] [CrossRef]
- Tan, L.; Huangfu, T.; Wu, L.; Chen, W. Comparison of RetinaNet, SSD, and YOLO v3 for real-time pill identification. BMC Med. Inform. Decis. Mak. 2021, 21, 324. [Google Scholar] [CrossRef] [PubMed]
- ZwickRoell. Durómetro ZHVμ. Available online: https://www.zwickroell.com/es/productos/equipos-de-ensayos-de-dureza/durometros-vickers/zhvm/ (accessed on 15 May 2022).
- Lloyd Instruments. Microhardness Testing—Minimizing Common Problems. AZoM. Available online: https://www.azom.com/article.aspx?ArticleID=10807 (accessed on 15 May 2022).
- Ebatco. Microindentation. Available online: https://www.ebatco.com/laboratory-services/mechanical/microindentation/ (accessed on 10 May 2022).












| Ts (°C) | Ti (at%) | Nb (at%) | N (at%) | Thickness (m) |
|---|---|---|---|---|
| 200 | 57.86 ± 7.28 | 0.21 ± 0.01 | 41.93 ± 7.27 | 4.68 ± 0.03 |
| 400 | 51.06 ± 0.57 | 0.18 ± 0.02 | 48.76 ± 0.58 | 6.80 ± 0.12 |
| 600 | 44.72 ± 3.09 | 0.15 ± 0.02 | 55.12 ± 3.08 | 5.93 ± 0.04 |
| Load (N) | Steel (HV) | Quenched (HV) | Tempered (HV) | TiNbN-200 (HV) | TiNbN-400 (HV) | TiNbN-600 (HV) |
|---|---|---|---|---|---|---|
| 1 | 576.25 ± 87.19 | 2106.27 ± 82.41 | 1935.61 ± 111.47 | 1701.23 ± 107.64 | ||
| 2 | 650.93 ± 39.38 | 1581.30 ± 41.66 | 1537.44 ± 135.49 | 1435.31 ± 12.20 | ||
| 3 | 596.64 ± 14.37 | 1476.44 ± 214.36 | 1290.03 ± 3.83 | 1331.98 ± 70.11 | ||
| 4.9 | 157.44 ± 2.97 | 542.86 ± 10.93 | ||||
| 5 | 578.89 ± 24.17 | 1303.58 ± 173.80 | 1044.25 ± 41.49 | 1024.40 ± 21.92 | ||
| 9.8 | 243.78 ± 5.04 | 796.16 ± 9.61 | 639.54 ± 17.10 | |||
| 10 | 533.82 ± 3.69 | 1009.21 ± 14.53 | 846.24 ± 49.16 | 844.35 ± 49.02 |
| Architecture | BFLOP (%) | Accuracy | Time(ms) |
|---|---|---|---|
| Darknet-19 | 7.29 | 91.8 | 5.84 |
| ResNet-101 | 19.7 | 93.7 | 18.86 |
| ResNet-152 | 29.4 | 93.8 | 27.02 |
| Darknet-53 | 18.7 | 93.8 | 12.82 |
| Parameters | Value |
|---|---|
| Data transfer | True |
| COCO dataset | False |
| Training epochs | 100 |
| Batch | 4 |
| lr | 1 × 10 a 1 × 10 |
| Neurons | 2535 |
| Threshold IoU | 0.5 |
| Diagonal Length (m) | Vickers Hardness (HV) | |||||
|---|---|---|---|---|---|---|
| Load (N) | Manual | Tanaka | Purpose Methode | Manual | Tanaka | Purpose Methode |
| 9.807 | 93.7 | 93.6 | 93.3 | 211.4 | 211.6 | 213.38 |
| 1.961 | 54.6 | 54.3 | 52.4 | 124.8 | 126.2 | 134.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buitrago Diaz, J.C.; Ortega-Portilla, C.; Mambuscay, C.L.; Piamba, J.F.; Forero, M.G. Determination of Vickers Hardness in D2 Steel and TiNbN Coating Using Convolutional Neural Networks. Metals 2023, 13, 1391. https://doi.org/10.3390/met13081391
Buitrago Diaz JC, Ortega-Portilla C, Mambuscay CL, Piamba JF, Forero MG. Determination of Vickers Hardness in D2 Steel and TiNbN Coating Using Convolutional Neural Networks. Metals. 2023; 13(8):1391. https://doi.org/10.3390/met13081391
Chicago/Turabian StyleBuitrago Diaz, Juan C., Carolina Ortega-Portilla, Claudia L. Mambuscay, Jeferson Fernando Piamba, and Manuel G. Forero. 2023. "Determination of Vickers Hardness in D2 Steel and TiNbN Coating Using Convolutional Neural Networks" Metals 13, no. 8: 1391. https://doi.org/10.3390/met13081391
APA StyleBuitrago Diaz, J. C., Ortega-Portilla, C., Mambuscay, C. L., Piamba, J. F., & Forero, M. G. (2023). Determination of Vickers Hardness in D2 Steel and TiNbN Coating Using Convolutional Neural Networks. Metals, 13(8), 1391. https://doi.org/10.3390/met13081391







