Indentation of Commercial Pure Titanium Processed by Cold Rolling
Abstract
:1. Introduction
2. Experimental
2.1. Materials and Processing Methods
2.2. Microindentation Tests
3. Results and Discussion
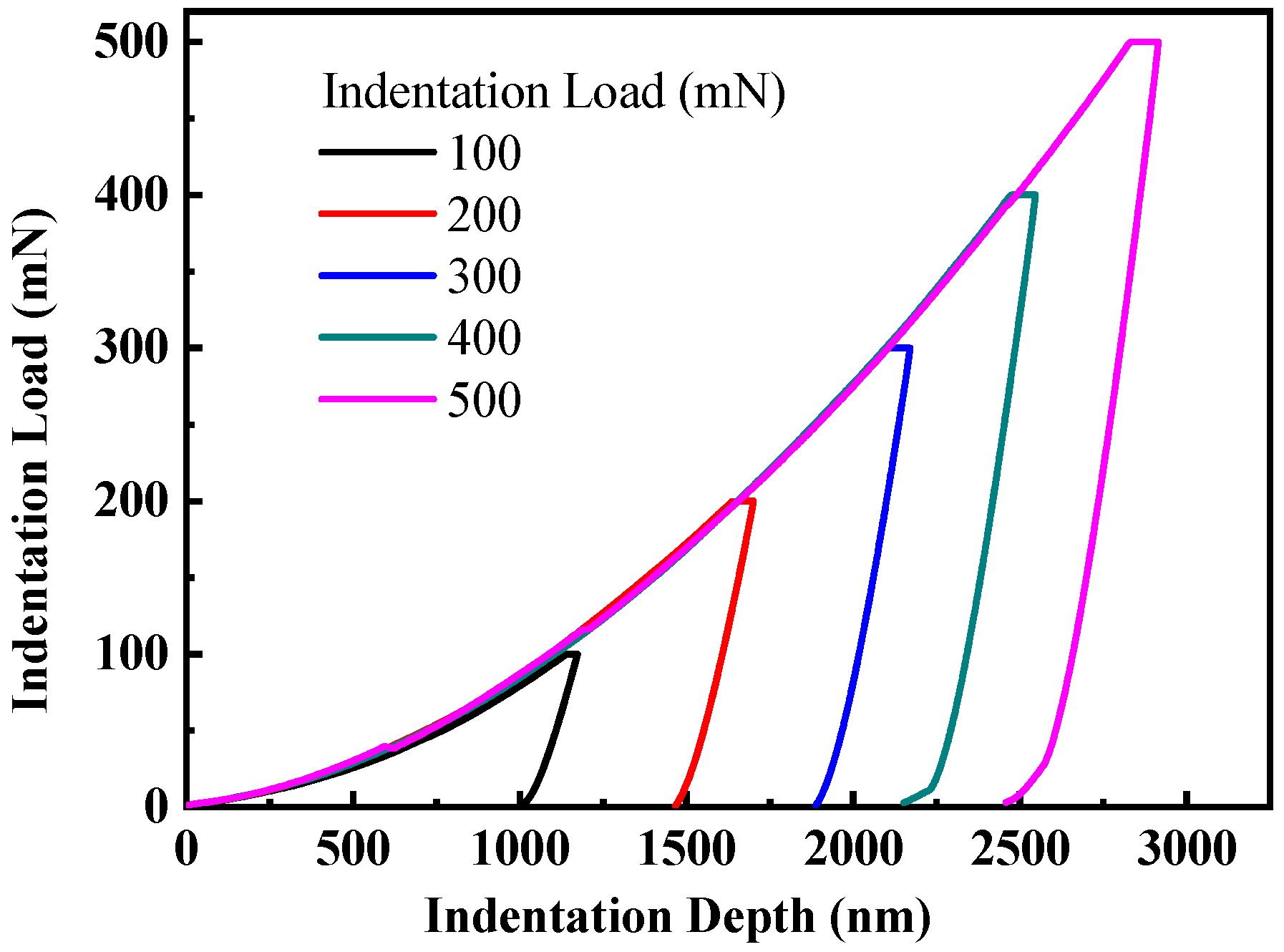
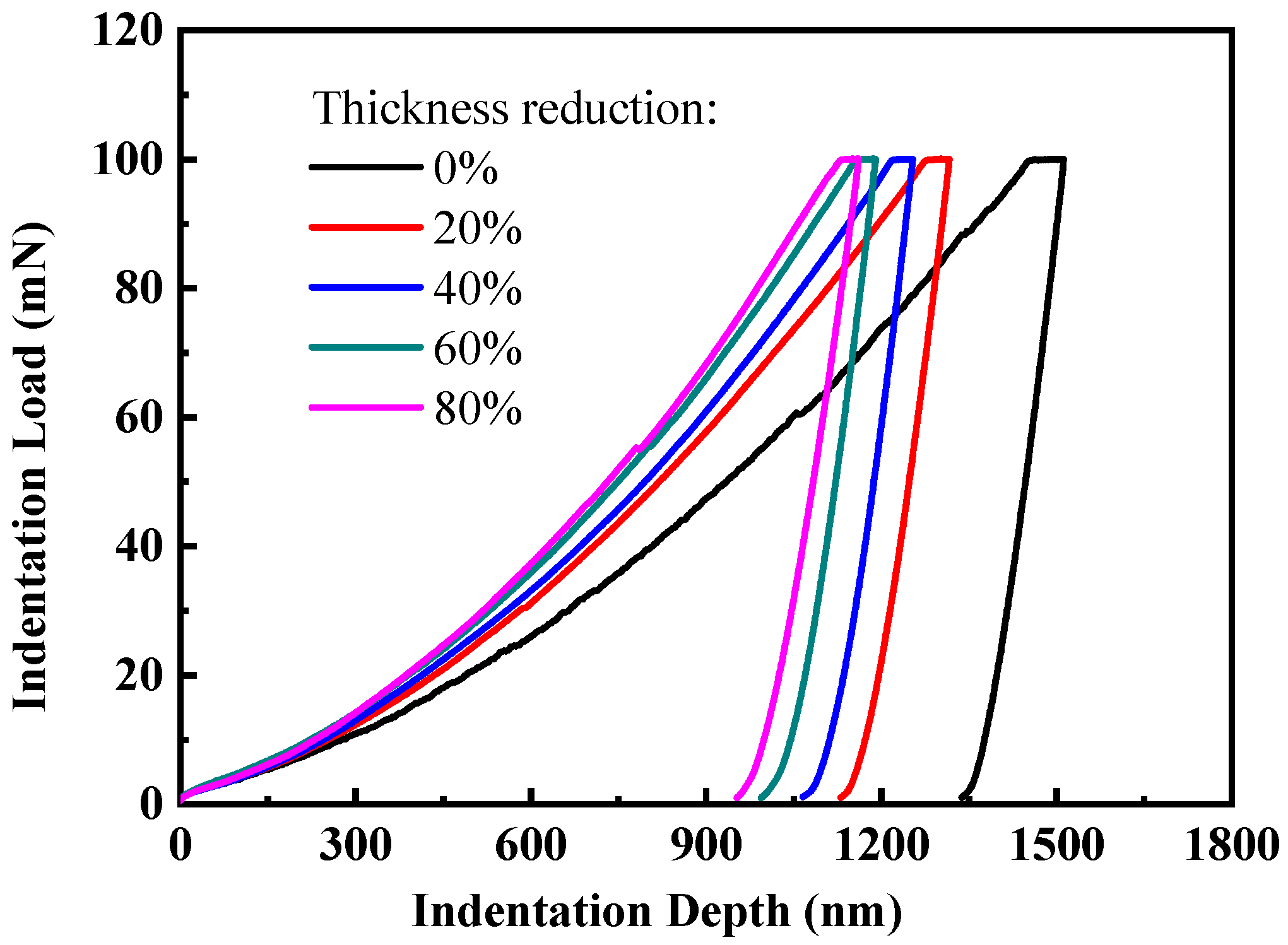
3.1. Indentation Deformation of the Cold-Rolled CP-Ti
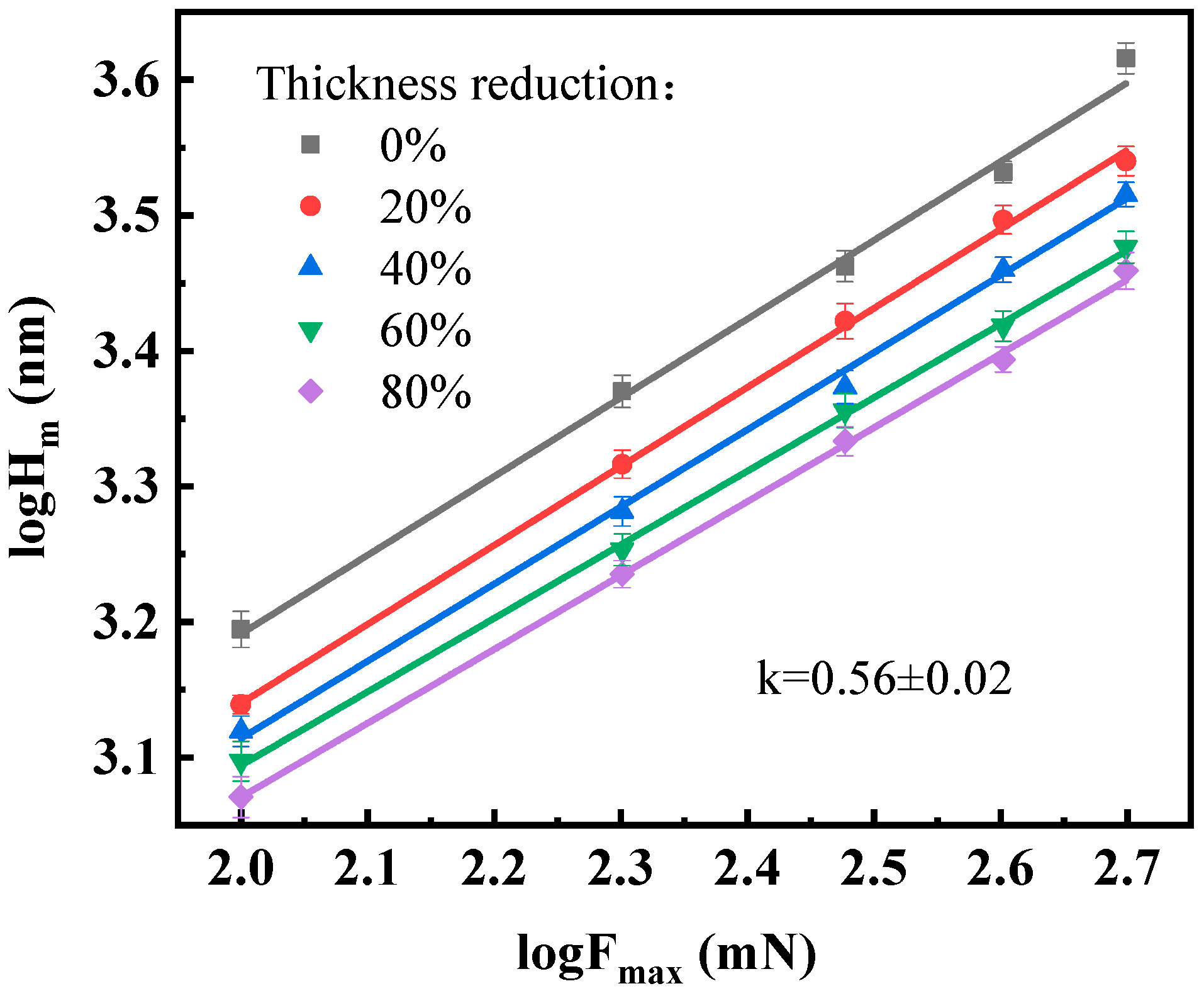
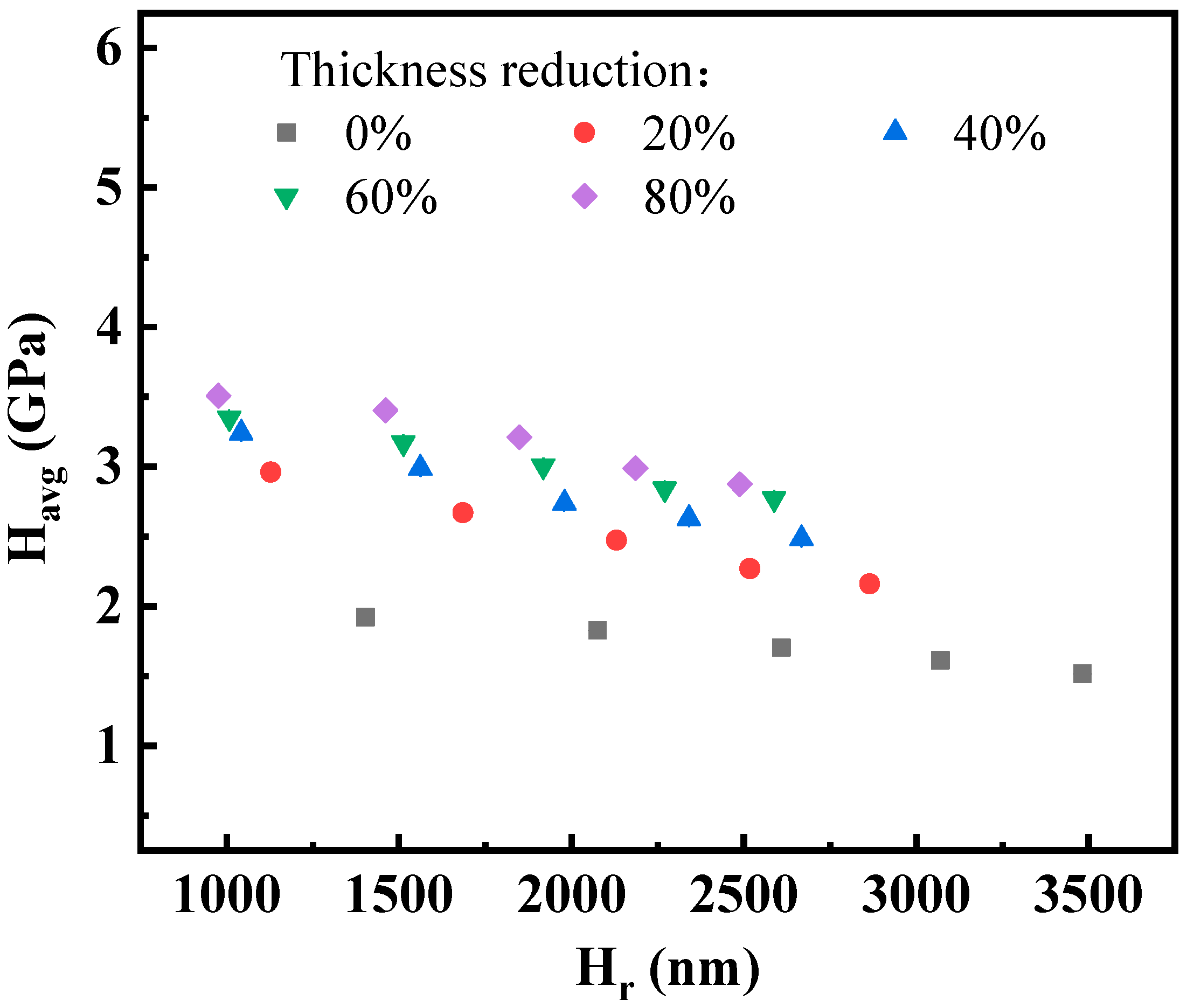
3.2. Vickers Hardness of the Cold-Rolled CP-Ti
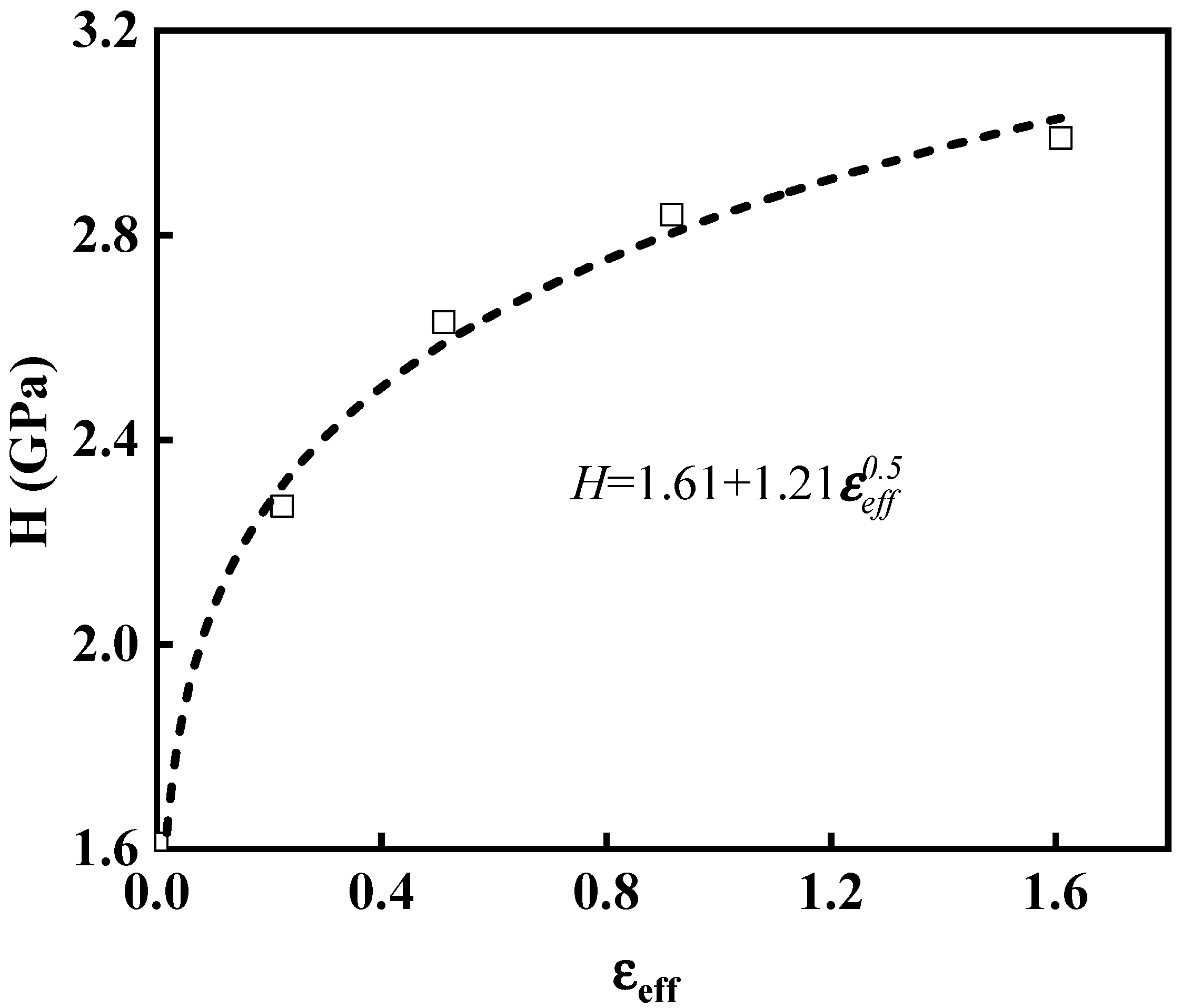
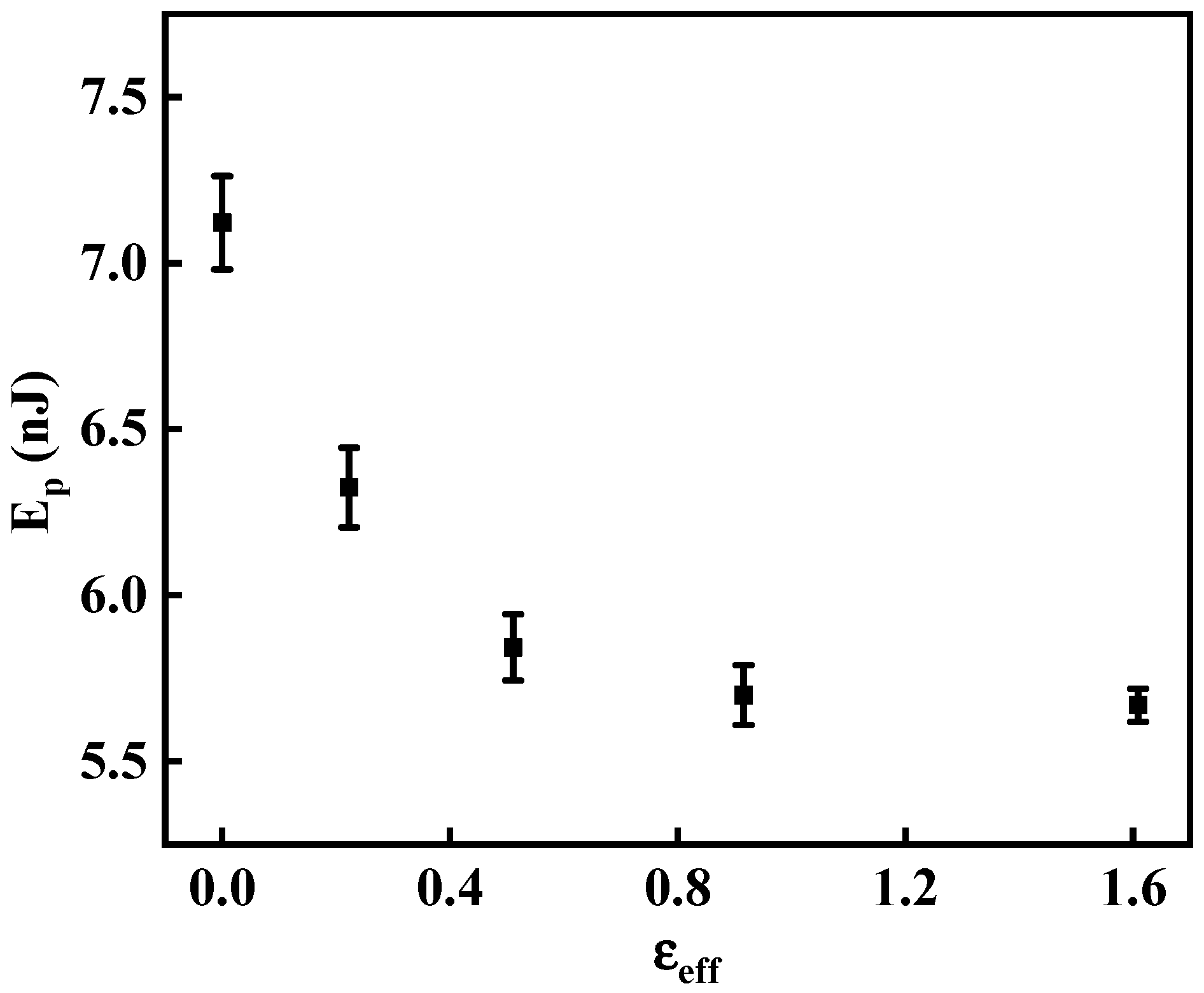
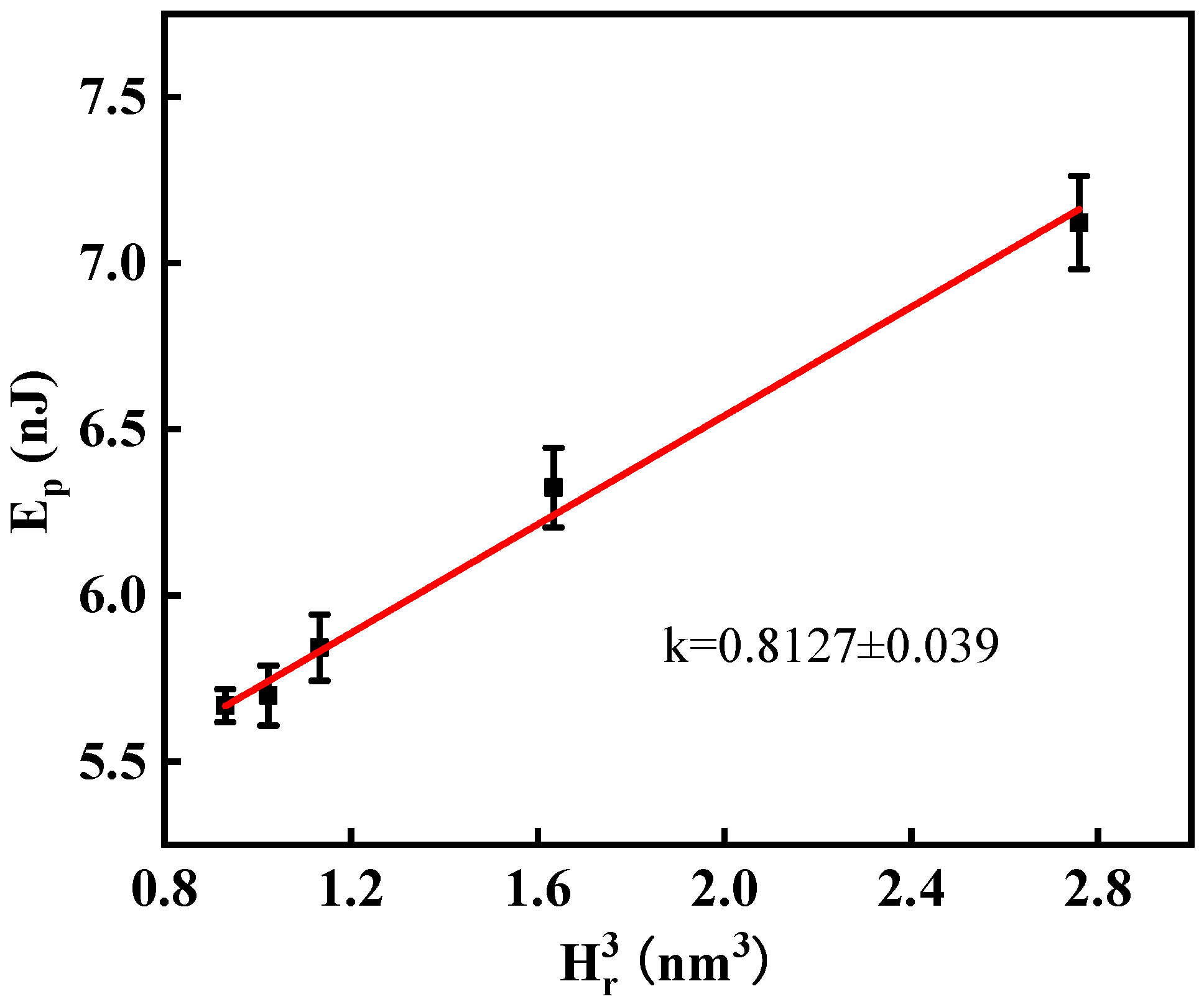
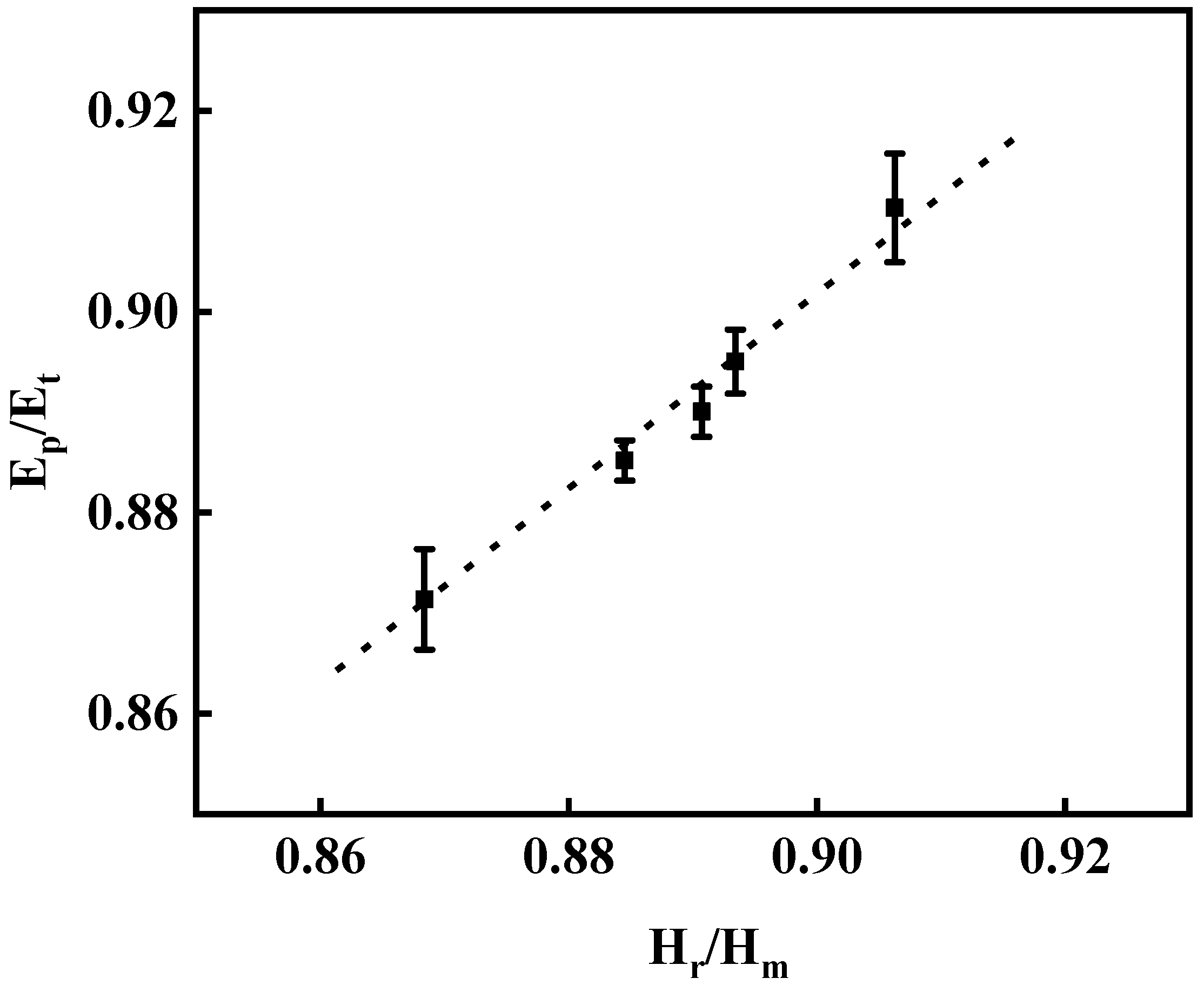
3.3. Energy Dissipation of the Cold-Rolled CP-Ti
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Liu, K.; Chen, T.; Xu, C.; Chen, C.; Yan, D.S.; Dippel, A.C.; Sun, J.; Ding, X.D. Inverse gradient nanostructure through gradient cold rolling demonstrated with superelasticity improvement in Ti-50.3Ni shape memory alloy. J. Mater. Sci. Technol. 2024, 185, 233–244. [Google Scholar] [CrossRef]
- Hussain, G.; Shehbaz, T.; Alkahtani, M.; Khaliq, U.A.; Wei, H. Nanomechanical, mechanical and microstructural characterization of electron beam welded Al2219-T6 tempered aerospace grade alloy: A comprehensive study. Heliyon 2024, 10, e23835. [Google Scholar] [CrossRef]
- Fattahi, M.; Hsu, C.-Y.; Ali, A.O.; Mahmoud, Z.H.; Dang, N.P.; Kianfar, E. Severe plastic deformation: Nanostructured materials, metal-based and polymer-based nanocomposites: A review. Heliyon 2023, 9, e22559. [Google Scholar] [CrossRef]
- George, V.; Mohammadreza, Y. Review of Nanoindentation Size Effect: Experiments and Atomistic Simulation. Crystals 2017, 7, 321. [Google Scholar]
- Bond, T.; Badmos, A.; Ahmed, R.A.; Obayemi, J.D.; Salifu, A.; Rahbar, N.; Soboyejo, W.O. Indentation size effects in aluminum and titanium alloys. Mater. Sci. Eng. A 2022, 839, 142542. [Google Scholar] [CrossRef]
- Stegall, D.E.; Mamun, M.A.; Crawford, B.; Elmustafa, A. Indentation size effect in FCC metals: An examination of experimental techniques and the bilinear behavior. J. Mater. Res. 2012, 27, 1543–1552. [Google Scholar] [CrossRef]
- Zong, Z.; Soboyejo, W. Indentation size effects in face centered cubic single crystal thin films. Mater. Sci. Eng. A 2005, 404, 281–290. [Google Scholar] [CrossRef]
- Pharr, G.M.; Herbert, E.G.; Gao, Y. The Indentation Size Effect: A Critical Examination of Experimental Observations and Mechanistic Interpretations. Annu. Rev. Mater. Res. 2010, 40, 271–292. [Google Scholar] [CrossRef]
- Hayes, J.; Keyte, R.; Prangnell, P. Effect of grain size on tensile behaviour of a submicron grained Al–3 wt-%Mg alloy produced by severe deformation. Mater. Sci. Technol. 2000, 16, 1259–1263. [Google Scholar] [CrossRef]
- Zhang, Z.; Hosoda, S.; Kim, I.S.; Watanabe, Y. Grain refining performance for Al and Al–Si alloy casts by addition of equal-channel angular pressed Al–5 mass% Ti alloy. Mater. Sci. Eng. A 2006, 425, 55–63. [Google Scholar] [CrossRef]
- Jun, T.S.; Sernicola, G.; Dunne, F.P.; Britton, T.B. Local deformation mechanisms of two-phase Ti alloy. Mater. Sci. Eng. A 2016, 649, 39–47. [Google Scholar] [CrossRef]
- Jawed, S.F.; Rabadia, C.D.; Khan, M.A.; Khan, S.J. Effect of Alloying Elements on the Compressive Mechanical Properties of Biomedical Titanium Alloys: A Systematic Review. ACS Omega 2022, 7, 29526–29542. [Google Scholar] [CrossRef]
- Meng, Q.; Bai, C.; Xu, D. Flow behavior and processing map for hot deformation of ATI425 titanium alloy. J. Mater. Sci. Technol. 2018, 34, 105–114. [Google Scholar] [CrossRef]
- Cao, F.; Liu, R.; Kong, S.; Guo, N.; Xu, P.; Xu, G. Microstructural evolution, high temperature tensile deformation behavior, and deformation mechanism in an Mg–Zn–Y–Ca–Zr alloy processed by multidirectional forging and hot rolling. J. Mater. Res. Technol. 2023, 27, 6729–6743. [Google Scholar] [CrossRef]
- Thakur, S.K.; Harish, L.; Das, A.K.; Rath, S.; Jha, B.K. Hot deformation behavior and processing map of Nb-V-Ti micro-alloyed steel. Mater. Today Proc. 2020, 28, 1973–1979. [Google Scholar] [CrossRef]
- Li, B.; He, W.; Chen, Z.; Huang, H.; Liu, Q. Evolution of interface and collaborative deformation between Ti and steel during hot roll bonding. Mater. Charact. 2020, 164, 110354. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, X.; Liu, X.; Qiang, M.; Yue, X.; Chen, W. Analysis of Microstructure, Texture Evolution, and the Mechanism of Grain Refinement of Commercially Pure Titanium During Cold Rolling: Experiment and Simulation. Adv. Eng. Mater. 2023. [Google Scholar] [CrossRef]
- Chen, W.; Liu, G.; Gao, Y.; He, W.; Chen, Z.; Jiang, B. Fabrication of dual-gradient microstructure and their effects on the mechanical properties of commercial pure Ti. J. Mater. Res. Technol. 2023, 24, 3309–3322. [Google Scholar] [CrossRef]
- Lee, M.-S.; Lee, J.-R.; Jeon, J.B.; Won, J.W.; Hyun, Y.-T.; Jun, T.-S. In-situ study of anisotropic strain-hardening and grain boundary mediated deformation in commercially pure titanium. J. Mater. Res. Technol. 2023, 24, 5389–5403. [Google Scholar] [CrossRef]
- Majchrowicz, K.; Sotniczuk, A.; Adamczyk-Cieślak, B.; Chromiński, W.; Jóźwik, P.; Pakieła, Z.; Garbacz, H. The influence of microstructure and texture on the hardening by annealing effect in cold-rolled titanium. J. Alloys Compd. 2023, 948, 169791. [Google Scholar] [CrossRef]
- Behera, A.; Gupta, R.; Yasin, G.; Nguyen, T.A.; Al, E. Mechanical and Tribological Properties Evaluation of Plasma-Sprayed Shape Memory Alloy Coating. J. Alloys Compd. 2021, 863, 158599. [Google Scholar]
- Rominiyi, A.; Mashinini, P.M. Nanoindentation study of mechanical and wear properties of spark plasma sintered Ti-6Ni-xTiCN composites. Ceram. Int. 2023, 49, 2194–2203. [Google Scholar] [CrossRef]
- Yapici, G.G.; Karaman, I.; Maier, H.J. Mechanical flow anisotropy in severely deformed pure titanium. Mater. Sci. Eng. A 2006, 434, 294–302. [Google Scholar] [CrossRef]
- Jiang, L.; Guo, L.F.; Kai, M.X.; Jie, Z.M.; Wei, Y.Z. Micromechanical Study of the Forged Ti-1023 Titanium Alloy by Micro-Indentation. Key Eng. Mater. 2018, 765, 160–165. [Google Scholar]
- Ellard, J.J.M.; Mathabathe, M.N.; Siyasiya, C.; Bolokang, A.S. Vacuum melting of compressed powders and hot rolling of the as-cast Ti-48Al-2Nb-0.7Cr-0.3Si intermetallic alloy: Mechanical properties and microstructural analysis. J. Manuf. Process. 2023, 101, 1214–1223. [Google Scholar] [CrossRef]
- Mahadule, D.; Demiral, M.; Mulki, H.; Khatirkar, R.K. Experiments and Crystal Plasticity Finite Element Simulations of Texture Development during Cold Rolling in a Ti-15V-3Cr-3Sn-3Al Alloy. Crystals 2023, 13, 137. [Google Scholar] [CrossRef]
- Arohi, A.C.; Shekhar, S.; Sen, I. Effect of thermomechanical processing on microstructure evolution and mechanical properties of metastable β Ti–5Al–5V–5Mo–3Cr alloy. Mater. Chem. Phys. 2024, 314, 128809. [Google Scholar] [CrossRef]
- Yang, F.; Du, W.; Okazaki, K. Effect of cold rolling on the indentation deformation of AA6061 aluminum alloy. J. Mater. Res. 2011, 20, 1172–1179. [Google Scholar] [CrossRef]
- Chen, R.; Yang, F.; Okazaki, K.; Imam, M.A.; Feng, C.R.; Pao, P. Indentation of titanium processed by equal channel angular pressing. J. Phys. D Appl. Phys. 2008, 41, 105407. [Google Scholar] [CrossRef]
- Yang, F.; Peng, L.; Okazaki, K. Microindentation of aluminum. Metall. Mater. Trans. A 2004, 35, 3323–3328. [Google Scholar] [CrossRef]
- Chen, R.; Yang, F.; Imam, M.A.; Feng, C.R.; Pao, P. Microindentation of titanium: Dependence of plastic energy on the indentation depth and time-dependent plastic deformation. J. Mater. Res. 2011, 23, 1068–1075. [Google Scholar] [CrossRef]
- Alcalá, J.; Pike, L.M.; Giovannoni, J.J. Identification of Plastome Variants useful for Cytoplasmic Selection and Cultivar Identification in Onion. J. Am. Soc. Hortic. Sci. 1999, 124, 122–127. [Google Scholar] [CrossRef]
- Pintaude, G. Hardness as an indicator of material strength: A critical review. Crit. Rev. Solid State Mater. Sci. 2023, 48, 623–641. [Google Scholar] [CrossRef]
- Zhou, D.; Du, W.; Wen, X.; Qiao, J.; Liang, W.; Yang, F. Local Deformation and Texture of Cold-Rolled AA6061 Aluminum Alloy. Materials 2018, 11, 1866. [Google Scholar] [CrossRef] [PubMed]
- Pugno, N.M. A general shape/size-effect law for nanoindentation. Acta Mater. 2007, 55, 1947–1953. [Google Scholar] [CrossRef]
- Mencik, J.; Swain, M.V. Micro-indentation Test with Pointed Indenters. Metals Forum 1994, 18, 277–288. [Google Scholar]
- Cheng, Y.; Cheng, C. Scaling, Dimensional Analysis, and Indentation Measurements. Mater. Sci. Eng. R 2004, 44, 91–149. [Google Scholar] [CrossRef]




| C | Fe | H | N | O | Ti |
| 0.08 | 0.3 | 0.0015 | 0.05 | 0.3 | Bal. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, D.; Yu, J.; Dong, Y.; Qin, Y.; Hao, X. Indentation of Commercial Pure Titanium Processed by Cold Rolling. Metals 2024, 14, 327. https://doi.org/10.3390/met14030327
Zhou D, Yu J, Dong Y, Qin Y, Hao X. Indentation of Commercial Pure Titanium Processed by Cold Rolling. Metals. 2024; 14(3):327. https://doi.org/10.3390/met14030327
Chicago/Turabian StyleZhou, Diaoyu, Jiasheng Yu, Yiwei Dong, Yalu Qin, and Xinwei Hao. 2024. "Indentation of Commercial Pure Titanium Processed by Cold Rolling" Metals 14, no. 3: 327. https://doi.org/10.3390/met14030327
APA StyleZhou, D., Yu, J., Dong, Y., Qin, Y., & Hao, X. (2024). Indentation of Commercial Pure Titanium Processed by Cold Rolling. Metals, 14(3), 327. https://doi.org/10.3390/met14030327





