Morphological and Dimensional Evolution of Nanosized Amorphous Silicon Nitride in α-Fe: Diffusional and Elastic Effects
Abstract
:1. Introduction
2. Materials and Methods
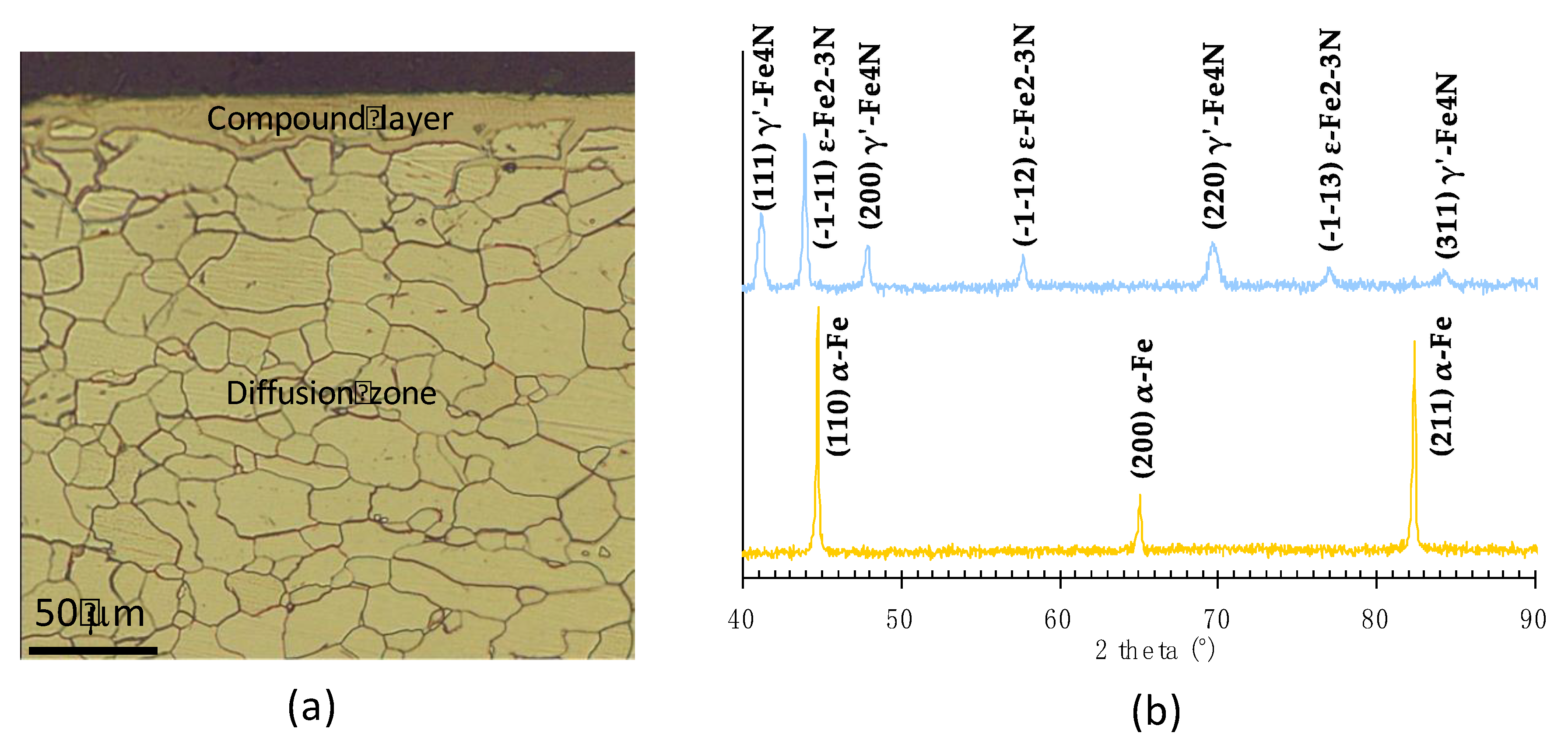
2.1. Processing and Nitriding
2.2. Sample Characterisation
3. Modelling
3.1. Methodology
3.2. Mass Transport Equation
3.3. Mechanical Governing Equation and Time Derivative of Variables
3.4. Numerical Methodology and Discretisation
3.5. Modelling Validation
3.5.1. Analytical Kinetic Solutions
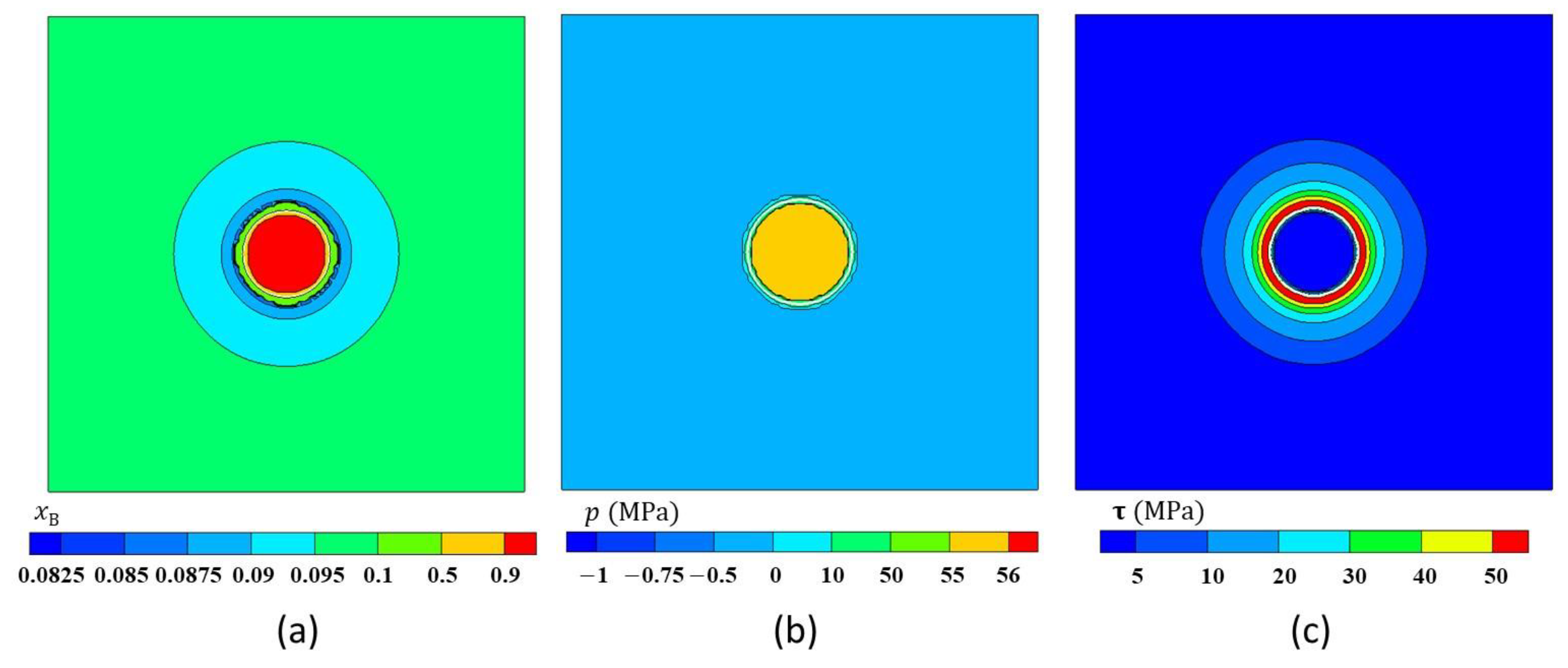
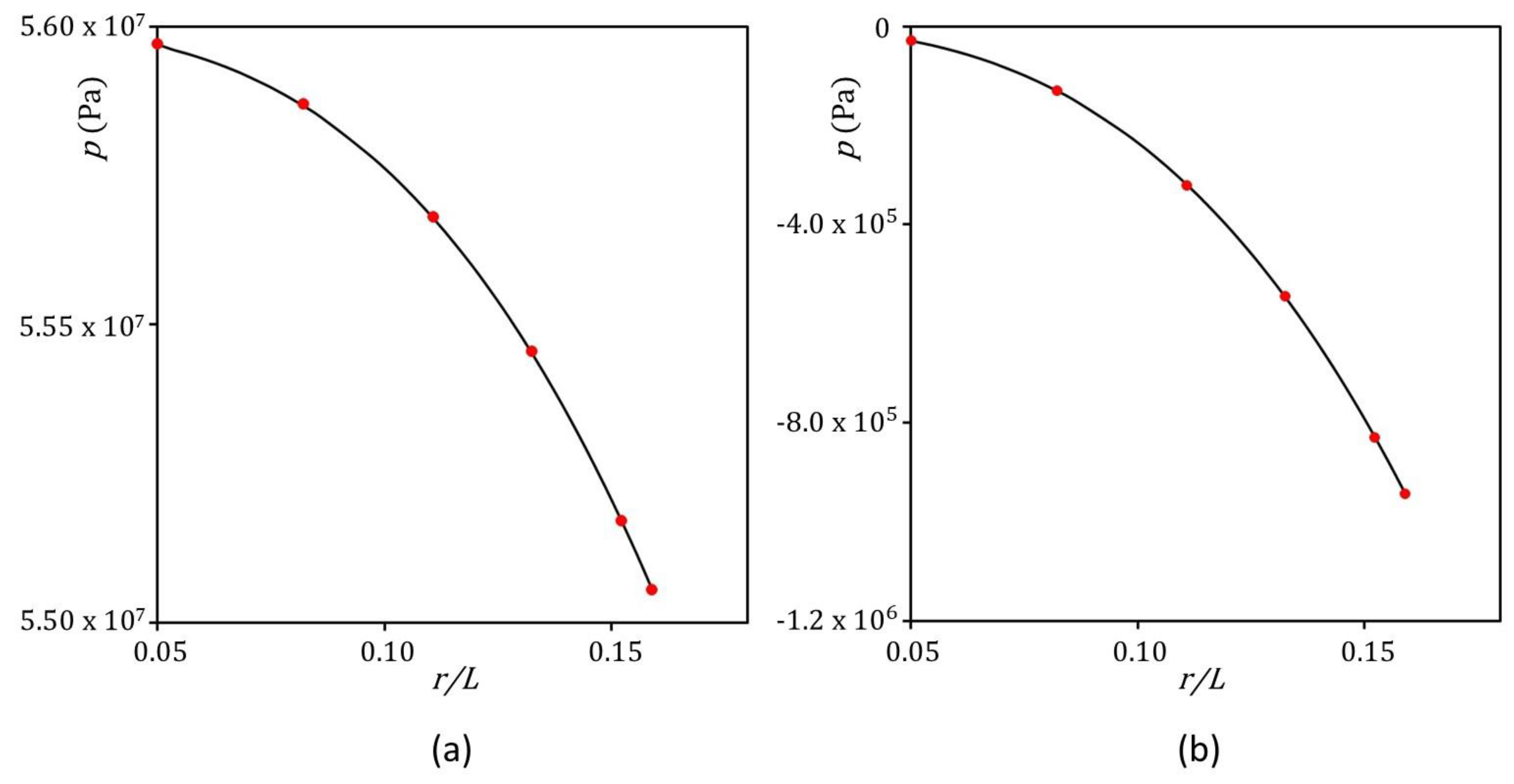
3.5.2. Simulation Results
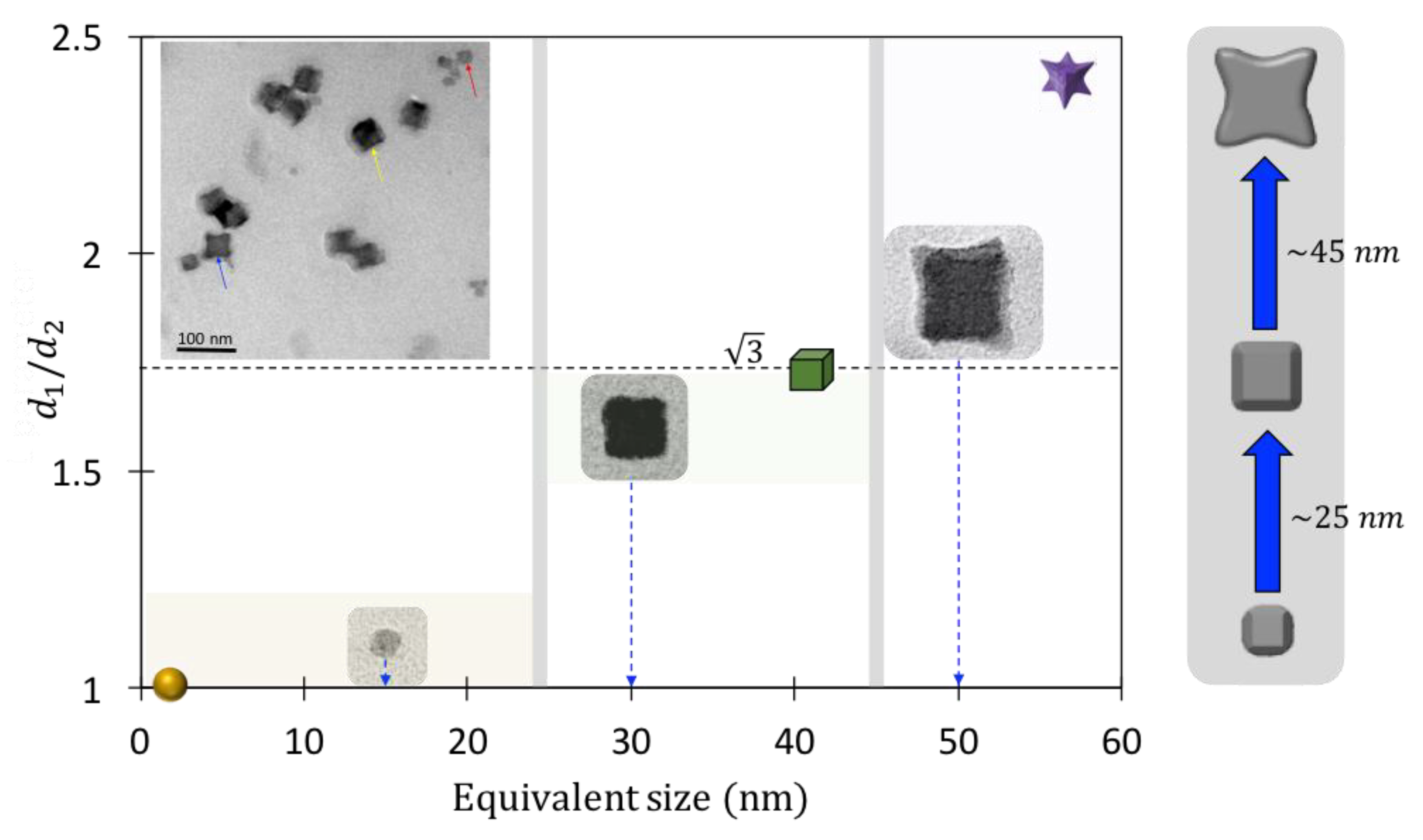
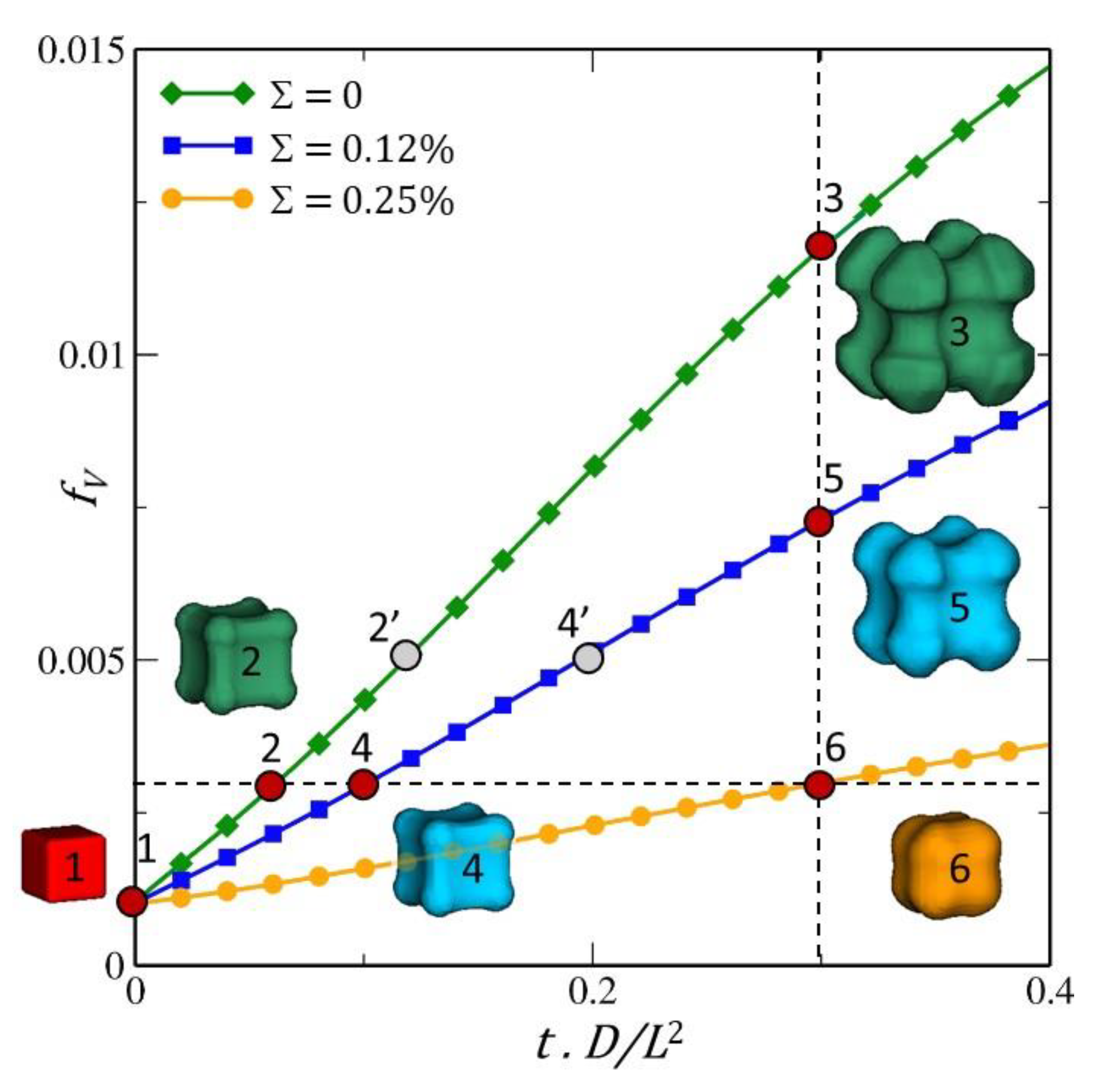
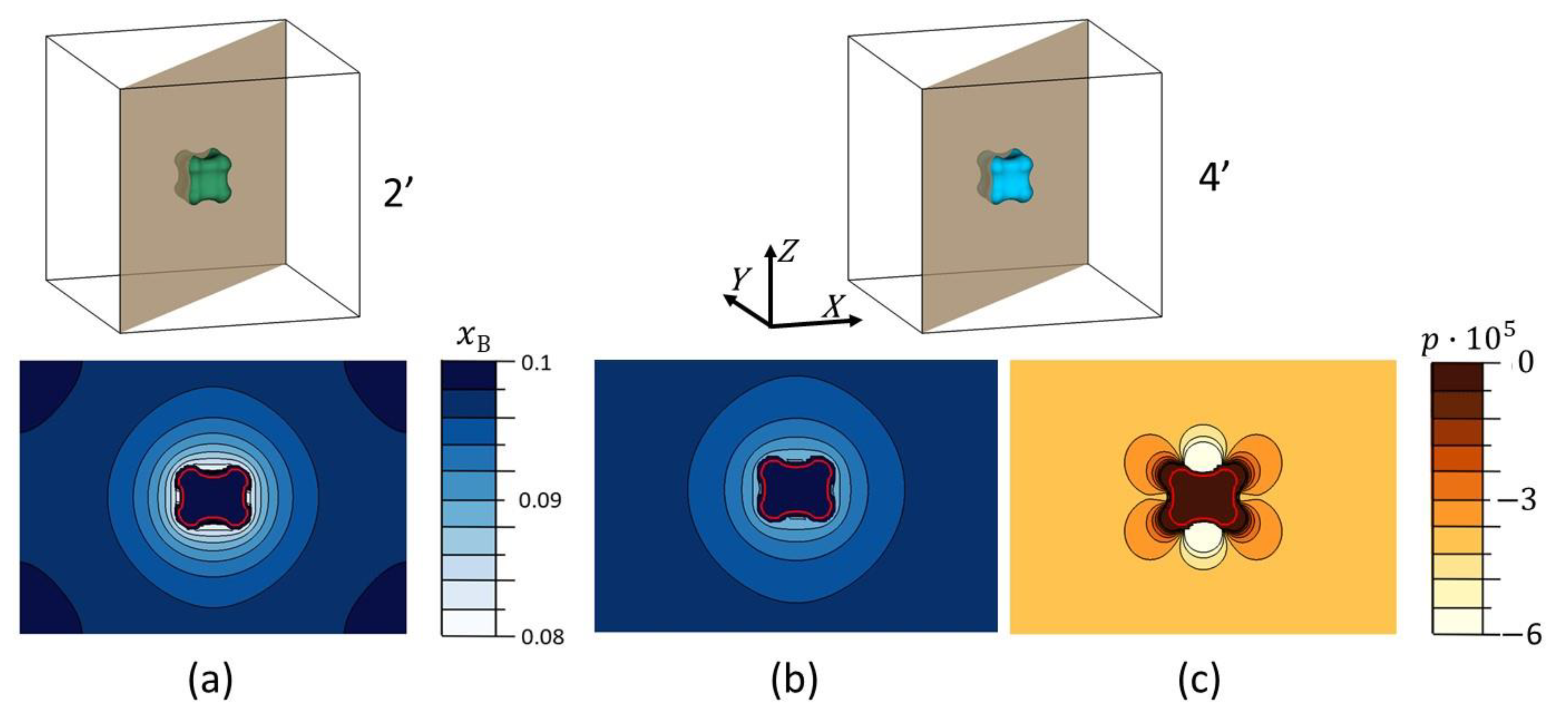
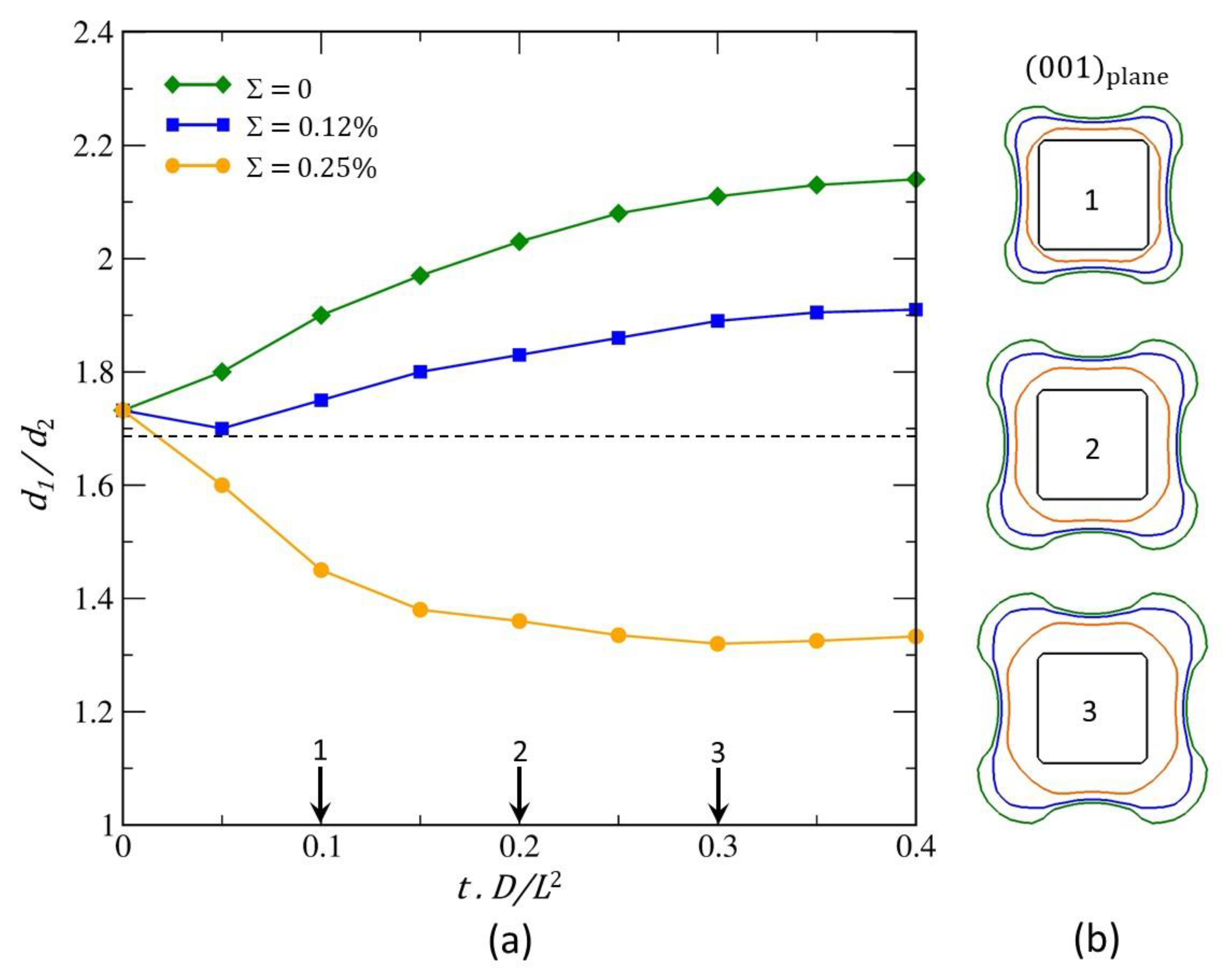
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mittemeijer, E.; Biglari, M.; Böttger, A.; Van der Pers, N.; Sloof, W.; Tichelaar, F. Precipitation of amorphous Si3N4 in α-Fe. Scripta Mater. 1999, 41, 625–630. [Google Scholar] [CrossRef]
- Meka, S.R.; Jung, K.S.; Bischoff, E.; Mittemeijer, E.J. Unusual precipitation of amorphous silicon nitride upon nitriding Fe–2at.%Si alloy. Philos. Mag. 2012, 92, 1435–1455. [Google Scholar] [CrossRef]
- Meka, S.R.; Bischoff, E.; Rheingans, B.; Mittemeijer, E.J. Octapod-shaped, nanosized, amorphous precipitates in a crystalline ferrite matrix. Philos. Mag. Lett. 2013, 93, 238–245. [Google Scholar] [CrossRef]
- Van Landeghem, H.P.; Gouné, M.; Epicier, T.; Redjaïmia, A. Unexpected low-temperature crystallization of amorphous silicon nitride into α-Si3N4 in a ferritic Fe–Si matrix. Scr. Mater. 2013, 68, 187–190. [Google Scholar] [CrossRef]
- Van Landeghem, H.P.; Gouné, M.; Bordère, S.; Danoix, F.; Redjaïmia, A. Competitive precipitation of amorphous and crystalline silicon nitride in ferrite: Interaction between structure, morphology, and stress relaxation. Acta Mater. 2015, 93, 218–234. [Google Scholar] [CrossRef]
- Van Landeghem, H.P.; Gouné, M.; Redjaïmia, A. Investigation of a Ferrite/Silicon Nitride Composite Concept Aimed at Automotive Applications. Steel Res. Int. 2012, 83, 590–593. [Google Scholar] [CrossRef]
- Van Landeghem, H.P. Métallurgie à L’azote: Nanoprecipitation Amorphe et Cristalline de Nitrure de Silicium Dans le Système Fe-Si-N. Ph.D. Thesis, Université de Lorraine, Lorraine, France, 2012. [Google Scholar]
- Böhm, H.J.; Rasool, A. Effects of particle shape on the thermoelastoplastic behavior of particle reinforced composites. Int. J. Solid Struct. 2016, 87, 90–101. [Google Scholar] [CrossRef]
- Makineni, S.K.; Sugathan, S.; Meher, S.; Banerjee, R.; Bhattacharya, S.; Kumar, S.; Chattopadhyay, K. Enhancing elevated temperature strength of copper containing aluminium alloys by forming L12 Al3Zr precipitates and nucleating θ″ precipitates on them. Sci. Rep. 2017, 7, 11154. [Google Scholar] [CrossRef]
- Jokisaari, A.M.; Naghavi, S.S.; Wolverton, C.; Voorhees, P.W.; Heinonen, O.G. Predicting the morphologies of γ′ precipitates in cobalt-based superalloys. Acta Mater. 2017, 141, 273–284. [Google Scholar] [CrossRef]
- Miyazaki, T.; Imamura, H.; Kozakai, T. The formation of γ′ precipitate doublets in NiAl alloys and their energetic stability. Mater. Sci. Eng. 1982, 54, 9–15. [Google Scholar] [CrossRef]
- Doi, M.; Miyazaki, T.; Wakatsuki, T. The effect of elastic interaction energy on the morphology of γ′ precipitates in nickel-based alloys. Mater. Sci. Eng. 1984, 67, 247–253. [Google Scholar] [CrossRef]
- Dhanish, S.; Daniel, B.S.S. Elastic Field Evolution in Al–X (X = Sc, Zr, Er) Alloy during Heat Treatment, Insights from 3D-Multiphase Field Study. J. Eng. Mater. Technol. 2024, 146, 606–626. [Google Scholar] [CrossRef]
- Hazote, A.; Grosdidier, T.; Denis, S. γ′ precipitate splitting in Nickel-based superalloys: A 3D finite element analysis. Scripta Mater. 1996, 34, 601–608. [Google Scholar] [CrossRef]
- Chen, K.X.; Korzhavyi, P.A.; Demange, G.; Zapolsky, H.; Patte, R.; Boisse, J. Morphological instability of iron-rich precipitates in Cu–Fe–Co alloys. Acta Mater. 2019, 163, 55–67. [Google Scholar] [CrossRef]
- Lebbad, H.; Appolaire, B.; Le Bouar, Y.; Finel, A. Insights into the selection mechanism of Widmanstätten growth by phase-field calculations. Acta Mater. 2021, 217, 117148. [Google Scholar] [CrossRef]
- Le Bouar, Y.; Finel, A.; Appolaire, B.; Cottura, M. Phase field models for modeling microstructure evolution in single-crystal Ni-base superalloys. In Nickel Base Single Crystals Across Length Scales; Elsevier: Amsterdam, The Netherlands, 2022; pp. 379–399. [Google Scholar] [CrossRef]
- Gennari, G.; Jefferson-Loveday, R.; Pickering, S.J. A phase-change model for diffusion-driven mass transfer problems in incompressible two-phase flows. Chem. Eng. Sci. 2022, 259, 117791. [Google Scholar] [CrossRef]
- Schulz, A.; Wecker, C.; Inguva, V.; Lopatin, A.S.; Kenig, E.Y. A PLIC-based method for species mass transfer at free fluid interfaces. Chem. Eng. Sci. 2022, 251, 117357. [Google Scholar] [CrossRef]
- Zanutto, C.P.; Paladino, E.E.; Evrard, F.; van Wachem, B.; Denner, F. Modeling of interfacial mass transfer based on a single-field formulation and an algebraic VOF method considering non-isothermal systems and large volume changes. Chem. Eng. Sci. 2022, 247, 116855. [Google Scholar] [CrossRef]
- Bordère, S.; Glockner, S. Numerical modelling of diffusion-controlled phase transformation using the Darken method: Application to the dissolution/precipitation processes in materials. Comput. Mater. Sci. 2021, 186, 109944. [Google Scholar] [CrossRef]
- Zhao, Y. Understanding and design of metallic alloys guided by phase-field simulations. npj Comput. Mater. 2023, 9, 94. [Google Scholar] [CrossRef]
- Yamanaka, A. Phase-field modelling and simulation of solid state phase transformations in steel. ISIJ. Inter. 2023, 63, 395–406. [Google Scholar] [CrossRef]
- Cheng, T.-L.; Wen, Y.-H. Phase-field model of precipitation processes with coherency loss. NPJ Comput. Mater. 2021, 7, 36. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows Volume 2: Computational Methods for Inviscid and Viscous Flows, 1st ed.; John Wiley & Sons: Chichester, UK, 1990; pp. 536–552. [Google Scholar]
- Alabi-Babalola, O.; Zhong, J.; Moggridge, G.D.; D’Agostino, G. Rationalizing the use of mutual diffusion prediction models in non-ideal binary mixtures. Chem. Eng. Sci. 2024, 291, 119930. [Google Scholar] [CrossRef]
- Sridhar, S. A Commentary on “Diffusion, Mobility and Their Interrelation through Free Energy in Binary Metallic Systems” L.S. Darken: Trans. AIME, 1948, vol. 175, p. 184ff. Metall. Mater. Trans. A 2010, 41, 543–562. [Google Scholar] [CrossRef]
- Herrnring, J.; Sundman, B.; Klusemann, B. Diffusion-driven microstructure evolution in OpenCalphad. Comput. Mater. Sci. 2020, 175, 109236. [Google Scholar] [CrossRef]
- Bordère, S.; Caltagirone, J.-P. A unifying model for fluid flow and elastic solid deformation: A novel approach for fluid–structure interaction. J. Fluids. Struct. 2014, 51, 344–353. [Google Scholar] [CrossRef]
- Bordère, S.; Caltagirone, J.-P. A multi-physics and multi-time scale approach for modeling fluid–solid interaction and heat transfer. Comput. Struct. 2016, 164, 38–52. [Google Scholar] [CrossRef]
- Notus CFD Code. Available online: https://notus-cfd.org (accessed on 2 January 2016).
- Glockner, S.; Jost, A.M.D.; Erriguible, A. Advanced petascale simulations of the scaling up of mixing limited flow processes for materials synthesis. Chem. Eng. J. 2022, 431, 133647. [Google Scholar] [CrossRef]
- Zener, C. Theory of Growth of Spherical Precipitates from Solid Solution. J. Appl. Phys. 1949, 20, 950–953. [Google Scholar] [CrossRef]
- Li, J.C.-M. Physical chemistry of some microstructural phenomena. Met. Trans. A 1978, 9, 1353–1380. [Google Scholar] [CrossRef]
- Scherer, G.W. Relaxation in Glass and Composites, 1st ed.; Wiley: New York, NY, USA, 1986; 331p. [Google Scholar]
- Kazemi-Lari, M.A.; Shaw, J.A.; Wineman, A.S.; Shimkunas, B.; Jian, Z.; Hegyi, B.; Hegyi, B.; Izu, L.; Chen-Izu, Y. A viscoelastic Eshelby inclusion model and analysis of the Cell-in-Gel system. Int. J. Eng. Sci. 2021, 165, 103489. [Google Scholar] [CrossRef] [PubMed]
- Ammar, K.; Appolaire, B.; Cailletaud, G.; Feyel, F.; Forest, S. Finite element formulation of a phase field model based on the concept of generalized stresses. Comput. Mater. Sci. 2009, 45, 800–805. [Google Scholar] [CrossRef]
- Laraia, V.J.; Johnson, W.C. Growth of a coherent precipitate from a supersaturated solution. J. Mater. Res. 1988, 3, 257–266. [Google Scholar] [CrossRef]
- Martinavicius, A.; Van Landeghem, H.P.; Danoix, R.; Redjaïmia, A.; Gouné, M.; Danoix, F. Mechanism of Si3N4 precipitation in nitrided Fe-Si alloys: A novel example of particle-stimulated-nucleation. Mater. Lett. 2017, 189, 25–27. [Google Scholar] [CrossRef]
- Voorhess, P.W.; Mc Fadden, G.B.; Johnsson, W.C. On the morphological development of second-phase particles in elastically-stressed solid. Acta Metal. Mater. 1992, 40, 2979–2992. [Google Scholar] [CrossRef]
- Souissi, M.; Numakura, H. Elastic properties of Fe-C and Fe-N martensites. ISIJ Int. 2015, 55, 1512–1521. [Google Scholar] [CrossRef]
- Wang, Y.; Khachaturyan, A.G. Shape instability during precipitate growth in coherent solids. Acta Metall. Mater. 1995, 43, 1837–1857. [Google Scholar] [CrossRef]
- Uchiyama, K.; O’Handley, R.C. Lattice strain in sputterdeposited Fe–N–Si films: Effects of interstitial mobility. IEEE Trans. Magn. 1999, 35, 2024–2028. [Google Scholar] [CrossRef]








| (s−1) | ω | κ | ||||
|---|---|---|---|---|---|---|
| Without stress | 1.0 | 0.08 | 0.01 | 1.0 × 10−6 | 0.021739 | 0.1151359 |
| With stress | 1.0 | 0.08 | 0.01 | 1.0 × 10−6 | 0.01663 | 0.0994093 |
| Symbol | α-Phase | β-Phase | |
|---|---|---|---|
| Initial molar fraction | 0.1 | 1 | |
| Equilibrium molar fraction | 0.08 | 1 | |
| Young’s modulus (GPa) | EY | 178 | 320 |
| Poisson coefficient | ν | 0.30 | 0.26 |
| Compressibility coefficient (Pa−1) | |||
| First Lamé’s coefficient (GPa) | 68 | 130 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bordère, S.; Van Landeghem, H.-P.; Redjaïmia, A.; Gouné, M. Morphological and Dimensional Evolution of Nanosized Amorphous Silicon Nitride in α-Fe: Diffusional and Elastic Effects. Metals 2024, 14, 442. https://doi.org/10.3390/met14040442
Bordère S, Van Landeghem H-P, Redjaïmia A, Gouné M. Morphological and Dimensional Evolution of Nanosized Amorphous Silicon Nitride in α-Fe: Diffusional and Elastic Effects. Metals. 2024; 14(4):442. https://doi.org/10.3390/met14040442
Chicago/Turabian StyleBordère, Sylvie, Hugo-Paul Van Landeghem, Abdelkrim Redjaïmia, and Mohamed Gouné. 2024. "Morphological and Dimensional Evolution of Nanosized Amorphous Silicon Nitride in α-Fe: Diffusional and Elastic Effects" Metals 14, no. 4: 442. https://doi.org/10.3390/met14040442






