Twinning–Detwinning-Dominated Cyclic Deformation Behavior of a High-Strength Mg-Al-Sn-Zn Alloy during Loading Reversals: Experiment and Modeling
Abstract
1. Introduction
2. Materials and Methods
3. Crystal Plasticity Modeling
3.1. The EVPSC-TDT Model
3.2. Modeling Details and Parameter Calibration
4. Results and Discussion
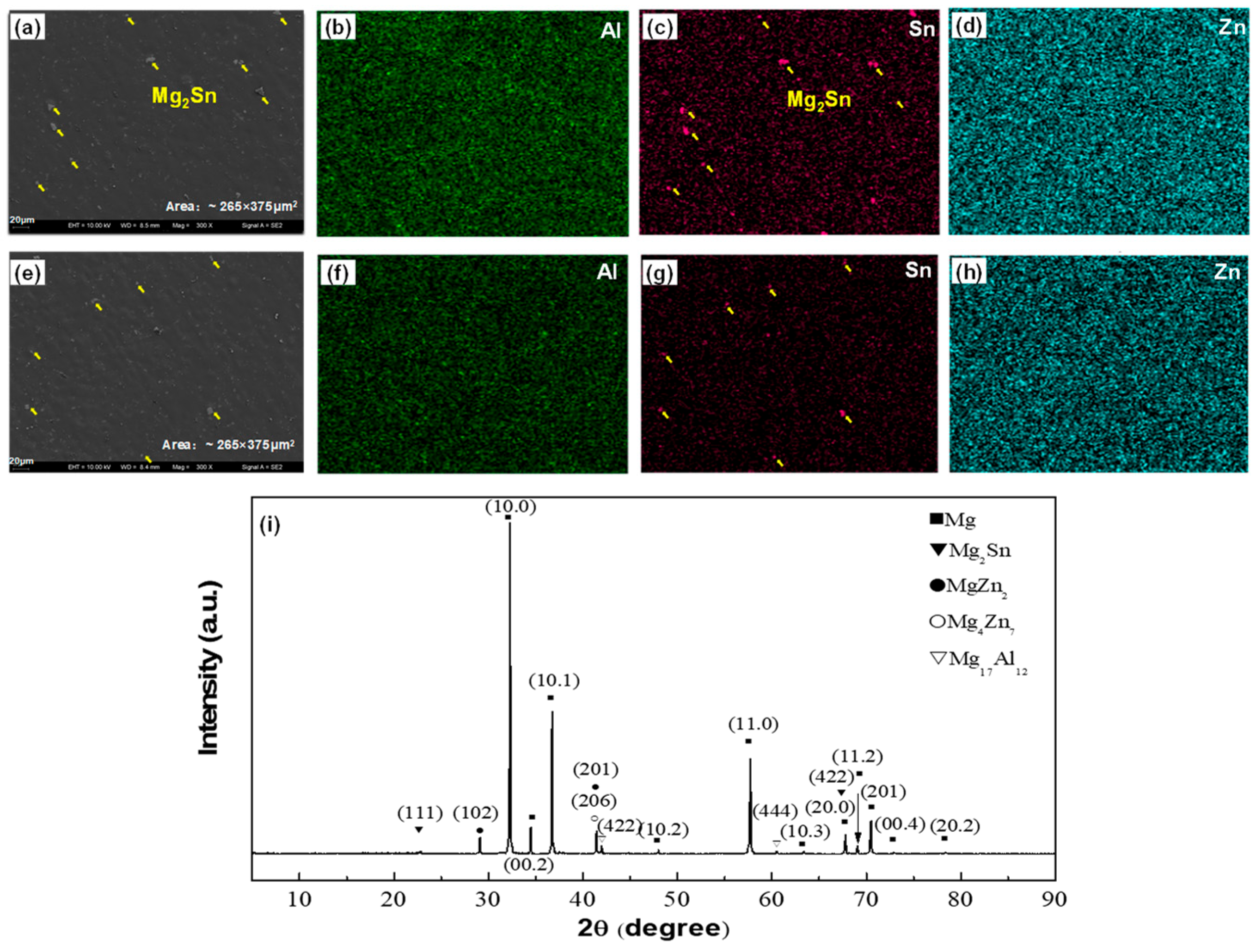
4.1. Initial Microstructure and Crystallographic Texture
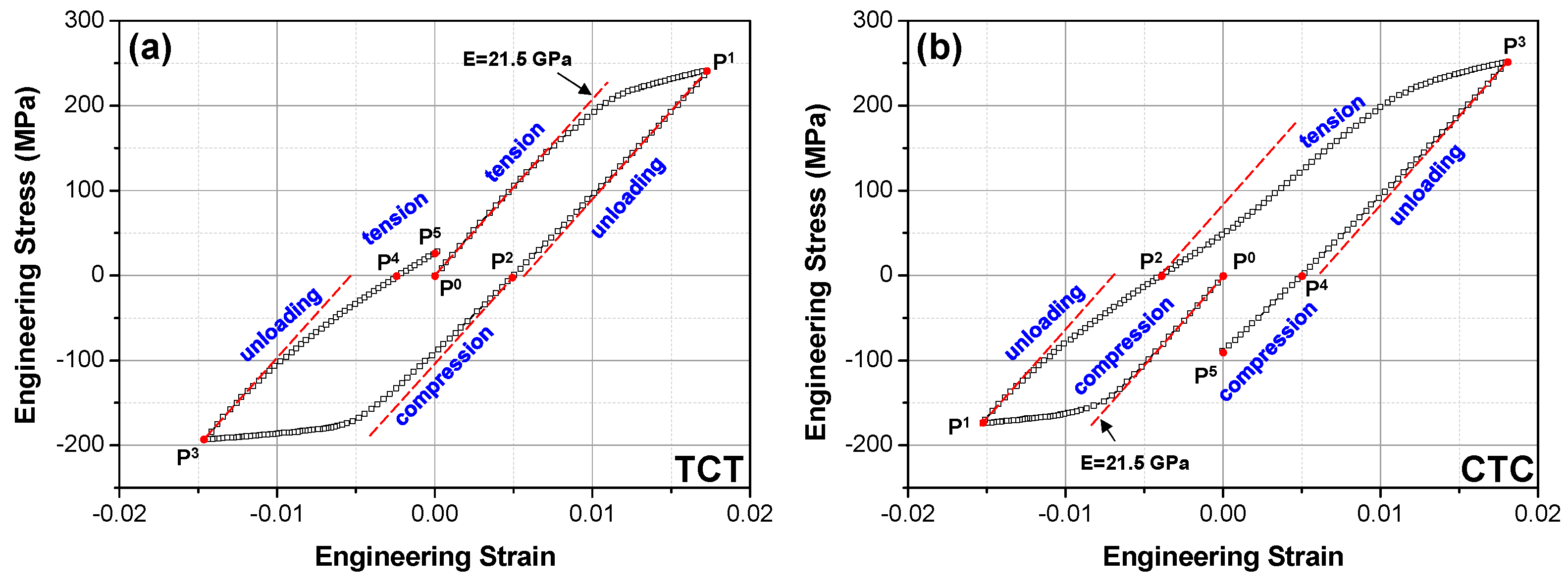
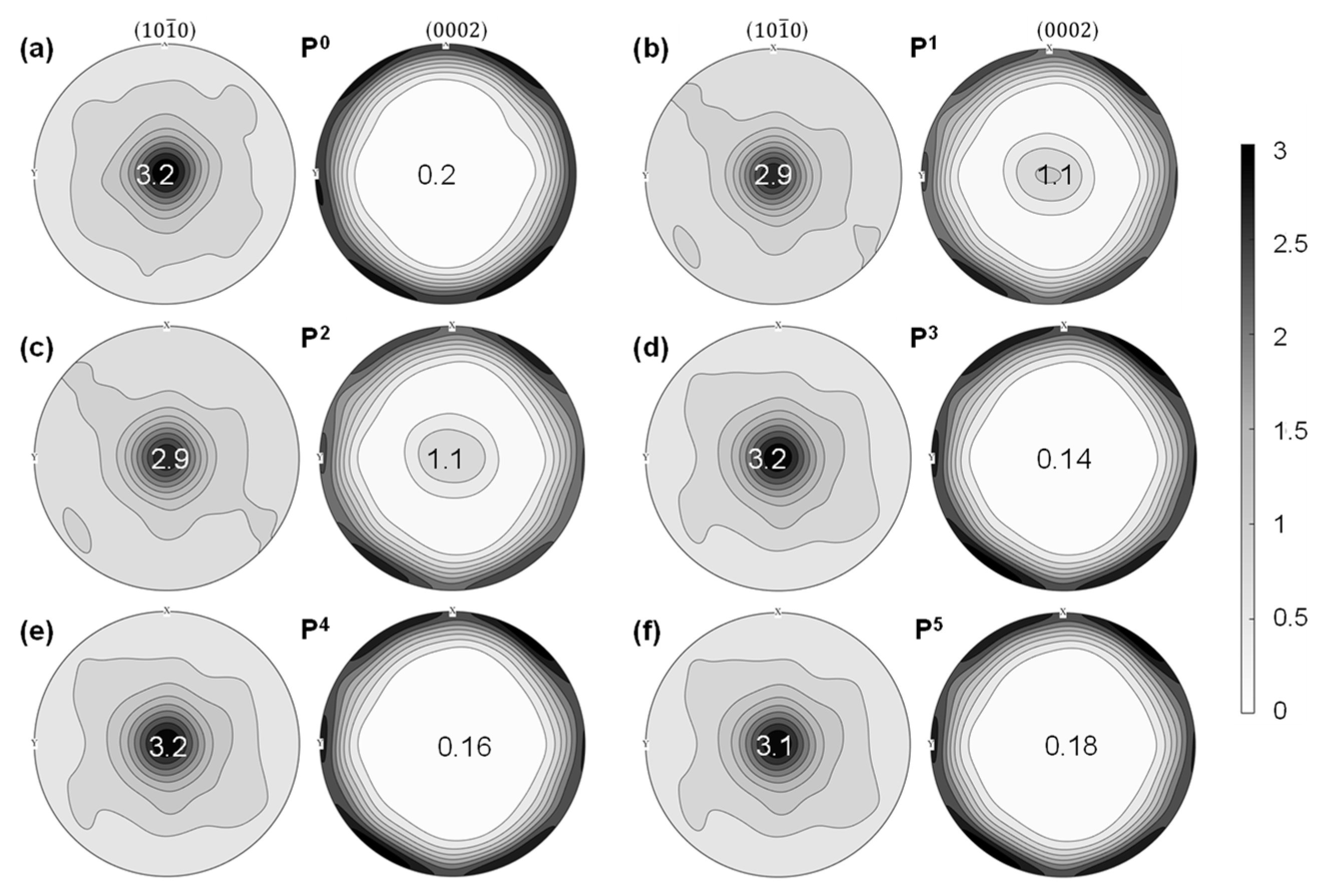
4.2. Stress–Strain Behavior and Deformed Microstructures
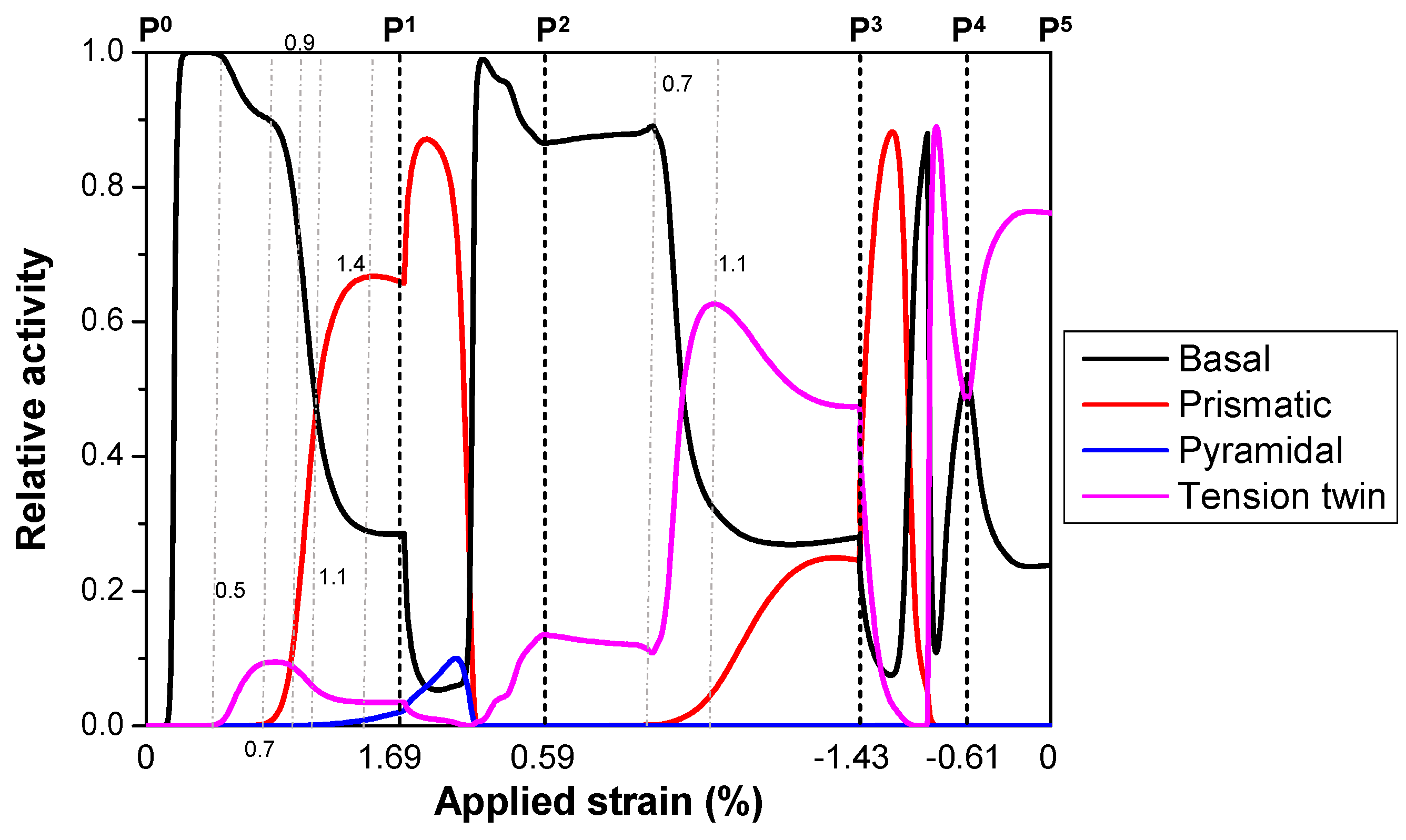
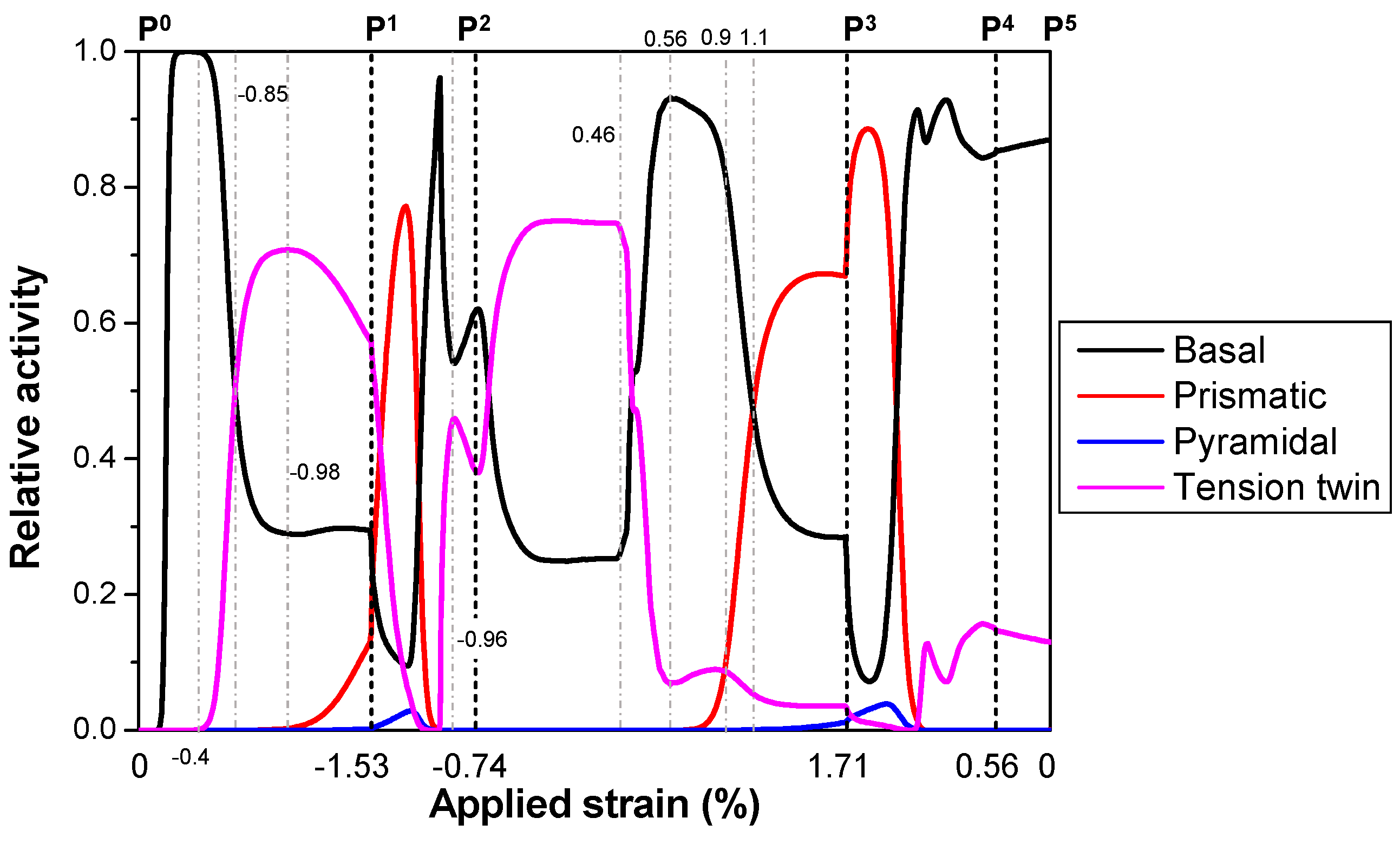
4.3. Evolution of Slip and Twinning Activities during Cyclic Deformation
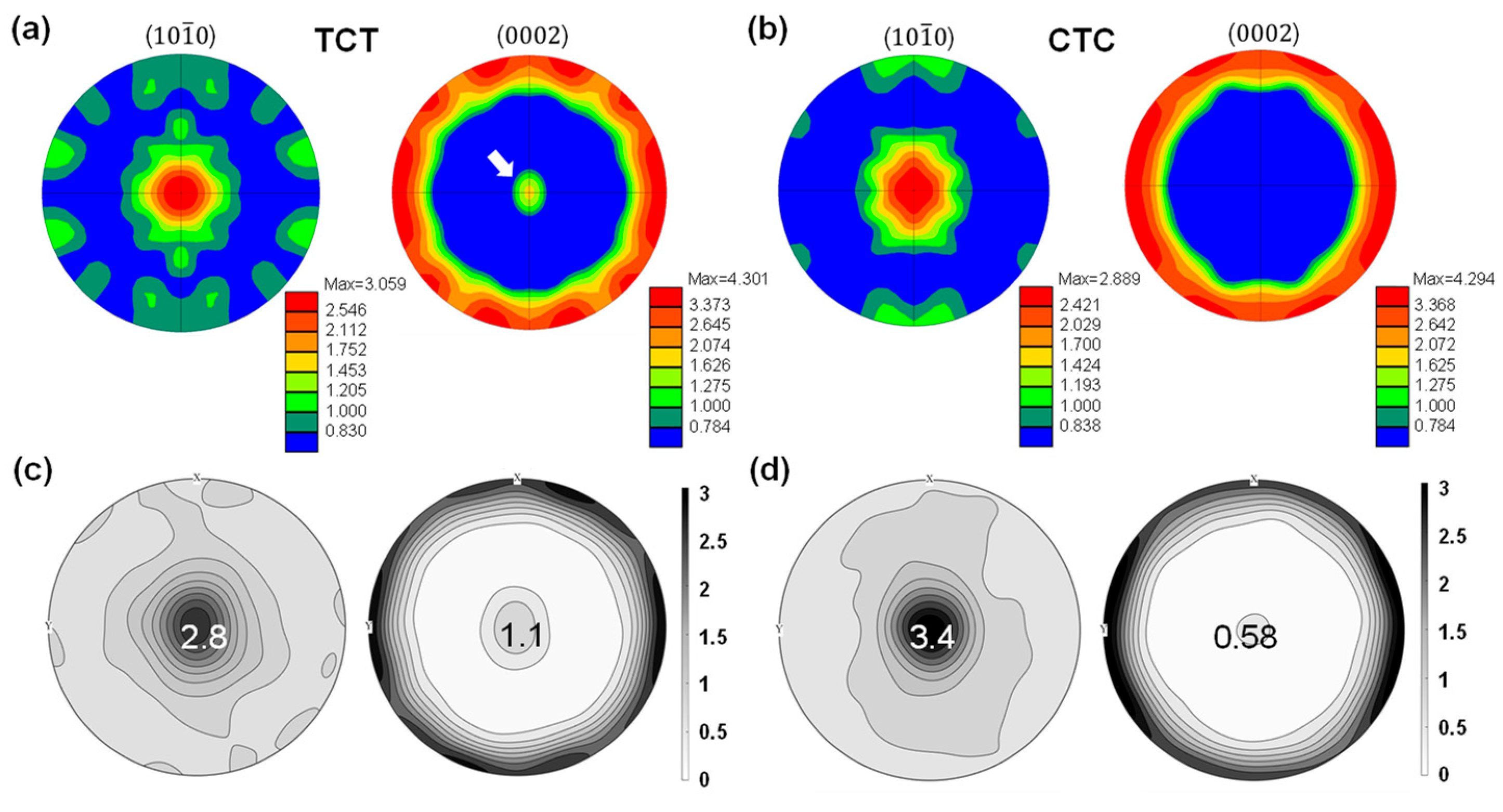
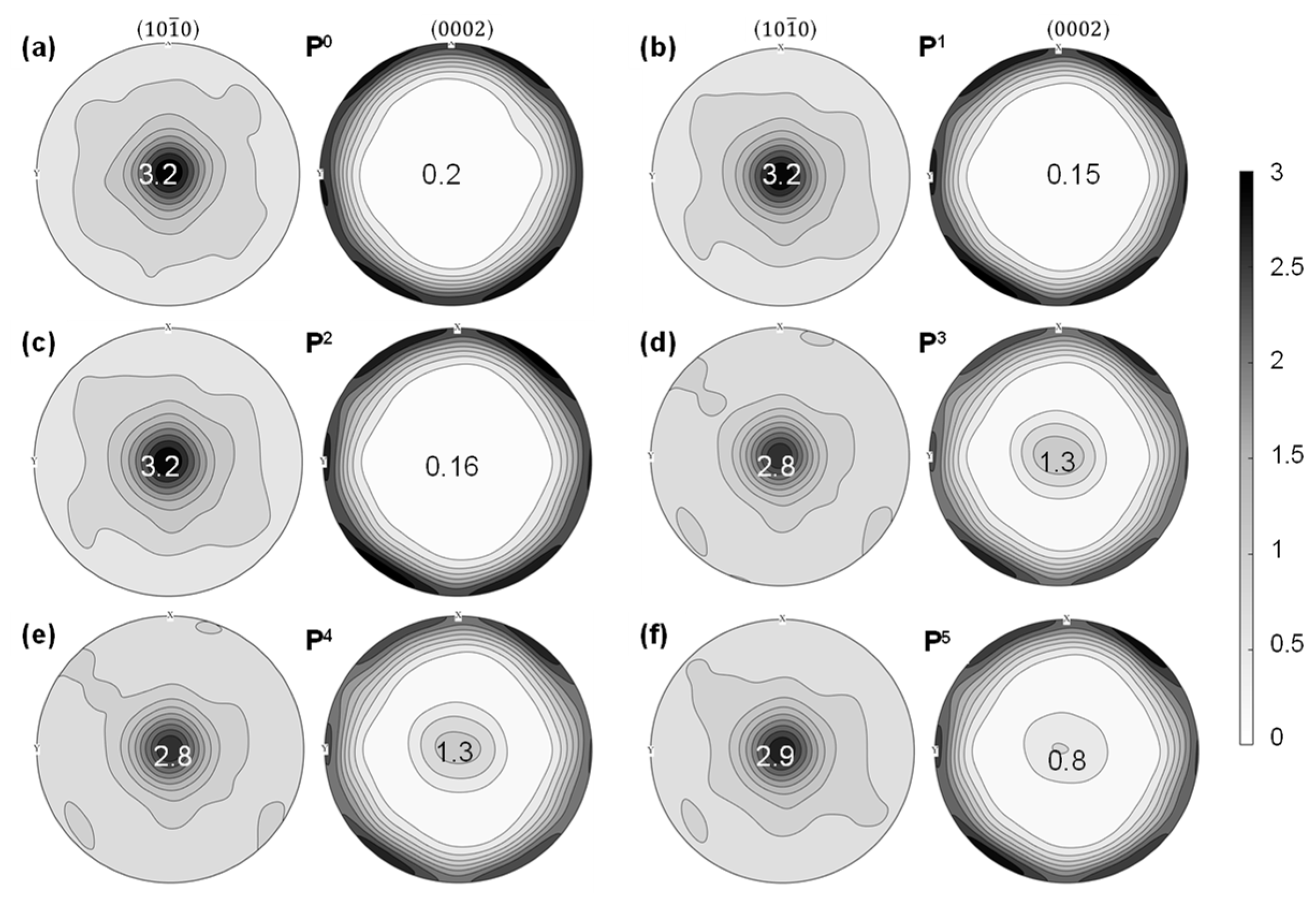
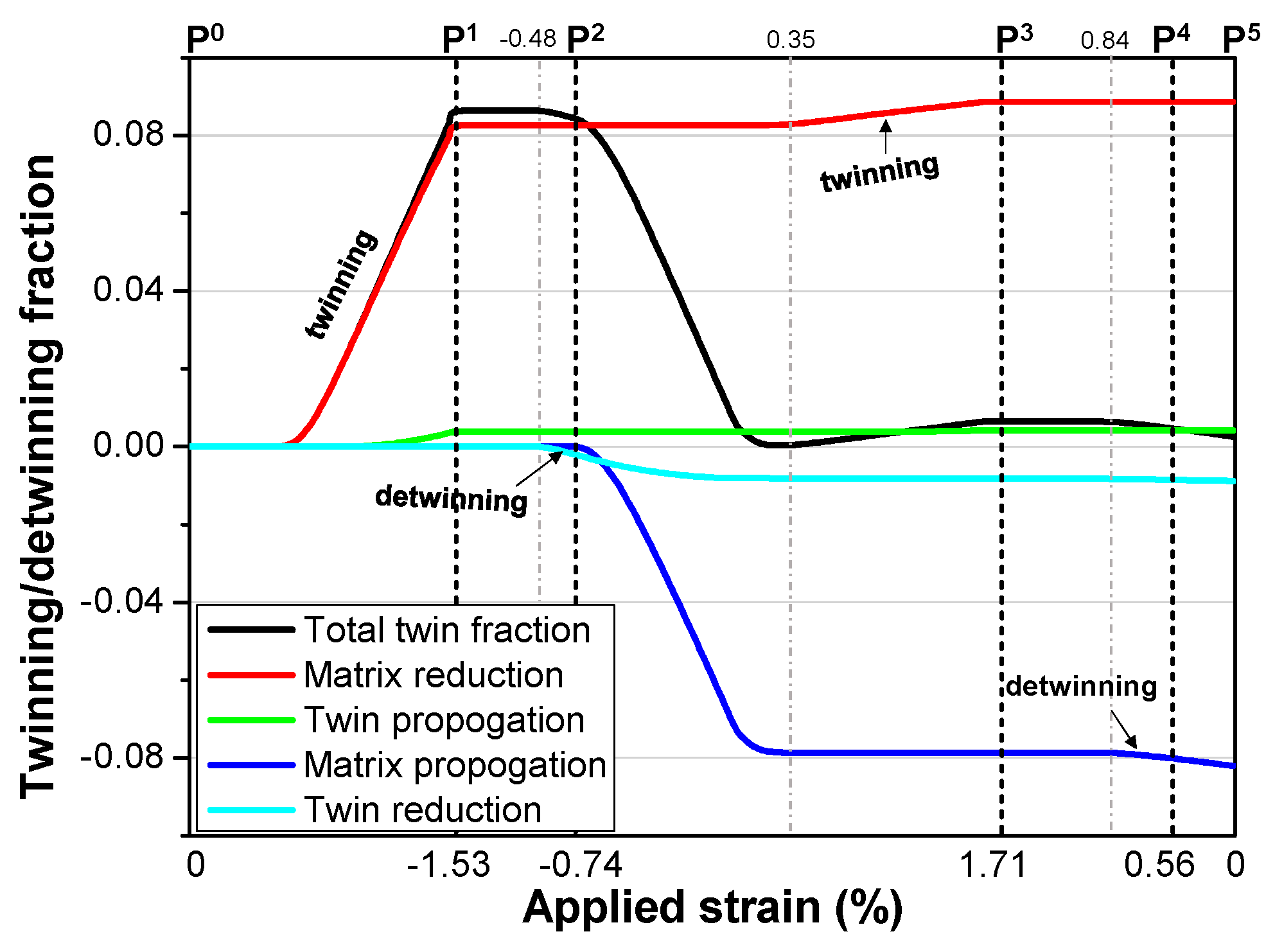
4.4. Twinning–Detwinning Behavior and Evolution of Textures
5. Conclusions
- (1)
- The as-aged alloy shows an equi-axis grain morphology, featuring an average grain size of 19.8 µm and a weakened basal texture. In contrast to conventional wrought alloys, this alloy displays reduced yielding asymmetry, with a tensile YS of 215 MPa and a compressive YS of 160 MPa. Its remarkable strength is attributed to the presence of Mg2Sn particles and Mg17Al12 precipitates.
- (2)
- The alloy exhibits pronounced anelastic behavior during unloading and reverse loading phases, owing to the reversal movements of basal <a> slip and detwinning activity. Notably, the deviation from elastic behavior is more prominent during compressive unloading and subsequent reverse tensile loading, facilitated by pre-existing twins formed during the initial compressive loading. After the loading cycles, the area fractions of residual twins are determined to be 7.51% and 0.93% in the TCT and CTC cases, respectively.
- (3)
- While the EVPSC-TDT model accurately predicts the overall stress–strain behavior during both loading cycles, it underestimates detwinning activity during compression unloading and the early stages of reverse tensile loading due to the model’s lack of consideration for back stresses. Initially, basal <a> slip governs plastic deformation in both loading cycles, succeeded by tension twinning after a strain of 0.85% in the CTC case and prismatic <a> slip after a strain of 1.1% in the TCT case. Basal <a> slip contributes over 85% of the anelastic plastic deformation during the tensile unloading process, while maximum tension twinning activity reaches 46% and 89% in the CTC and TCT cases, respectively, during compressive unloading.
- (4)
- The EVPSC-TDT model accurately predicts the deformed textures of the alloy after both loading cycles. It is observed that twinning and detwinning are primarily influenced by stresses in the matrix, allowing simultaneous occurrence during reverse loading due to distinct stress states among different grains. Variations in the fractions of residual twins between the two cases are attributed to differing unloading and reverse loading sequences.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.J.; Xu, D.K.; Wu, R.Z.; Chen, X.B.; Peng, Q.M.; Jin, L.; Xin, Y.C.; Zhang, Z.Q.; Liu, Y.; Chen, X.H.; et al. What Is Going on in Magnesium Alloys? J. Mater. Sci. Technol. 2018, 34, 245–247. [Google Scholar] [CrossRef]
- Jin, Z.-Z.; Zha, M.; Wang, S.-Q.; Wang, S.-C.; Wang, C.; Jia, H.-L.; Wang, H.-Y. Alloying Design and Microstructural Control Strategies towards Developing Mg Alloys with Enhanced Ductility. J. Magnes. Alloys 2022, 10, 1191–1206. [Google Scholar] [CrossRef]
- Nie, J.-F. Precipitation and Hardening in Magnesium Alloys. Met. Mater. Trans. A 2012, 43, 3891–3939. [Google Scholar] [CrossRef]
- Homma, T.; Kunito, N.; Kamado, S. Fabrication of Extraordinary High-Strength Magnesium Alloy by Hot Extrusion. Scr. Mater. 2009, 61, 644–647. [Google Scholar] [CrossRef]
- Wu, Z.; Ahmad, R.; Yin, B.; Sandlöbes, S.; Curtin, W.A. Mechanistic Origin and Prediction of Enhanced Ductility in Magnesium Alloys. Science 2018, 359, 447–452. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Kang, R.; Li, J.; Xie, H.; Zeng, Z.; Huang, Q.; Yang, C.; Ren, Y.; Qin, G. Mechanistic Investigation of a Low-Alloy Mg–Ca-Based Extrusion Alloy with High Strength–Ductility Synergy. Acta Mater. 2020, 186, 278–290. [Google Scholar] [CrossRef]
- Jiang, B.; Dong, Z.; Zhang, A.; Song, J.; Pan, F. Recent Advances in Micro-Alloyed Wrought Magnesium Alloys: Theory and Design. Trans. Nonferrous Met. Soc. China 2022, 32, 1741–1780. [Google Scholar] [CrossRef]
- Sabat, R.K.; Brahme, A.P.; Mishra, R.K.; Inal, K.; Suwas, S. Ductility Enhancement in Mg-0.2%Ce Alloys. Acta Mater. 2018, 161, 246–257. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, P.; Luo, A.A.; She, J.; Tang, A.; Pan, F. Dynamic Precipitation and Enhanced Mechanical Properties of ZK60 Magnesium Alloy Achieved by Low Temperature Extrusion. Mater. Sci. Eng. A 2022, 829, 142143. [Google Scholar] [CrossRef]
- Dong, X.; Fu, J.; Wang, J.; Yang, Y. Microstructure and Tensile Properties of As-Cast and as-Aged Mg–6Al–4Zn Alloys with Sn Addition. Mater. Des. 2013, 51, 567–574. [Google Scholar] [CrossRef]
- Yan, T.; Pei, D.; Cheng, M.; Liang, Z.; Li, X.; Wang, X. Development of Mg–6Al–4Sn–1Zn Alloy Sheets with Ultra-High Strength by Combining Extrusion and High-Speed Rolling. J. Mater. Res. Technol. 2024, 29, 1487–1497. [Google Scholar] [CrossRef]
- Ma, C.-Y.; Xia, N.; Wang, C.; Li, M.-X.; Hua, Z.-M.; Ren, M.-W.; Wang, H.-Y. A Novel Mg-5Al-2Zn-2Sn Alloy with High Strength-Ductility Synergy Fabricated via Simple Hot Rolling and Annealing Treatment. J. Alloys Compd. 2021, 869, 159308. [Google Scholar] [CrossRef]
- Park, S.H.; Jung, J.-G.; Yoon, J.; You, B.S. Influence of Sn Addition on the Microstructure and Mechanical Properties of Extruded Mg–8Al–2Zn Alloy. Mater. Sci. Eng. A 2015, 626, 128–135. [Google Scholar] [CrossRef]
- Wang, H.; Rong, J.; Liu, G.; Zha, M.; Wang, C.; Luo, D.; Jiang, Q. Effects of Zn on the Microstructure and Tensile Properties of As-Extruded Mg-8Al-2Sn Alloy. Mater. Sci. Eng. A 2017, 698, 249–255. [Google Scholar] [CrossRef]
- Wang, L.; Huang, G.; Quan, Q.; Bassani, P.; Mostaed, E.; Vedani, M.; Pan, F. The Effect of Twinning and Detwinning on the Mechanical Property of AZ31 Extruded Magnesium Alloy during Strain-Path Changes. Mater. Des. 2014, 63, 177–184. [Google Scholar] [CrossRef]
- Song, B.; Guo, N.; Liu, T.; Yang, Q. Improvement of Formability and Mechanical Properties of Magnesium Alloys via Pre-Twinning: A Review. Mater. Des. 2014, 62, 352–360. [Google Scholar] [CrossRef]
- Hu, J.; Nie, X.; Fu, S.; Liu, Z.; Gao, H. Effects of Pre-Compression Modes on Mechanical Properties and Fatigue Behaviors of Rolled ZK60 Magnesium Alloy. Int. J. Fatigue 2024, 183, 108235. [Google Scholar] [CrossRef]
- Drozdenko, D.; Bohlen, J.; Yi, S.; Minárik, P.; Chmelík, F.; Dobroň, P. Investigating a Twinning–Detwinning Process in Wrought Mg Alloys by the Acoustic Emission Technique. Acta Mater. 2016, 110, 103–113. [Google Scholar] [CrossRef]
- Zhang, H.; Jérusalem, A.; Salvati, E.; Papadaki, C.; Fong, K.S.; Song, X.; Korsunsky, A.M. Multi-Scale Mechanisms of Twinning-Detwinning in Magnesium Alloy AZ31B Simulated by Crystal Plasticity Modeling and Validated via in Situ Synchrotron XRD and in Situ SEM-EBSD. Int. J. Plast. 2019, 119, 43–56. [Google Scholar] [CrossRef]
- Wu, L.; Jain, A.; Brown, D.W.; Stoica, G.M.; Agnew, S.R.; Clausen, B.; Fielden, D.E.; Liaw, P.K. Twinning–Detwinning Behavior during the Strain-Controlled Low-Cycle Fatigue Testing of a Wrought Magnesium Alloy, ZK60A. Acta Mater. 2008, 56, 688–695. [Google Scholar] [CrossRef]
- Zhu, Y.; Hou, D.; Li, Q. Quasi In-Situ EBSD Analysis of Twinning-Detwinning and Slip Behaviors in Textured AZ31 Magnesium Alloy Subjected to Compressive-Tensile Loading. J. Magnes. Alloys 2022, 10, 956–964. [Google Scholar] [CrossRef]
- Lou, X.Y.; Li, M.; Boger, R.K.; Agnew, S.R.; Wagoner, R.H. Hardening Evolution of AZ31B Mg Sheet. Int. J. Plast. 2007, 23, 44–86. [Google Scholar] [CrossRef]
- Bong, H.J.; Lee, J.; Lee, M.-G. Modeling Crystal Plasticity with an Enhanced Twinning–Detwinning Model to Simulate Cyclic Behavior of AZ31B Magnesium Alloy at Various Temperatures. Int. J. Plast. 2022, 150, 103190. [Google Scholar] [CrossRef]
- Guo, X.; Cheng, Y.; Xin, Y.; Wu, W.; Ma, C.; An, K.; Liaw, P.K.; Wu, P.; Liu, Q. Crystal Plasticity Modeling of Low-Cycle Fatigue Behavior of an Mg-3Al-1Zn Alloy Based on a Model, Including Twinning and Detwinning Mechanisms. J. Mech. Phys. Solids 2022, 168, 105030. [Google Scholar] [CrossRef]
- Li, H.; Yu, C.; Kang, G. Crystal Plasticity Modeling of the Multiaxial Ratchetting of Extruded AZ31 Mg Alloy. Int. J. Plast. 2022, 152, 103242. [Google Scholar] [CrossRef]
- Wang, H.; Lee, S.Y.; Wang, H.; Woo, W.; Huang, E.-W.; Jain, J.; An, K. On Plastic Anisotropy and Deformation History-Driven Anelasticity of an Extruded Magnesium Alloy. Scr. Mater. 2020, 176, 36–41. [Google Scholar] [CrossRef]
- Han, L.; Yu, Y.; Wei, D.; Wang, X.; Zhao, G.; Wang, G. The Synergistic and Interactive Effects of Slip Systems and Dynamic Recrystallization on the Weakening Basal Texture of Mg-Y-Nd-Zr-Gd Magnesium Alloy. Mater. Des. 2024, 237, 112583. [Google Scholar] [CrossRef]
- Wang, S.; Gao, F.-H.; Lv, B.-J.; Cui, N.; Guo, F. Effects of 0.5 Wt.% Nd Addition on the Microstructure and Mechanical Properties of As-Extruded and Aged Mg-6Al-3Sn-2Zn Alloys. J. Mater. Eng. Perform 2023, 32, 2635–2645. [Google Scholar] [CrossRef]
- Park, S.H.; Jung, J.-G.; Kim, Y.M.; You, B.S. A New High-Strength Extruded Mg-8Al-4Sn-2Zn Alloy. Mater. Lett. 2015, 139, 35–38. [Google Scholar] [CrossRef]
- ASTM E606/E606M-21; Standard Test Method for Strain-Controlled Fatigue Testing. ASTM Standards: West Conshohocken, PA, USA, 2021.
- Wang, H.; Wu, P.D.; Wang, J.; Tomé, C.N. A Crystal Plasticity Model for Hexagonal Close Packed (HCP) Crystals Including Twinning and de-Twinning Mechanisms. Int. J. Plast. 2013, 49, 36–52. [Google Scholar] [CrossRef]
- Barnett, M.R. Twinning and the Ductility of Magnesium Alloys: Part I: “Tension” Twins. Mater. Sci. Eng. A 2007, 464, 1–7. [Google Scholar] [CrossRef]
- Lebensohn, R.A.; Tomé, C.N. A Self-Consistent Anisotropic Approach for the Simulation of Plastic Deformation and Texture Development of Polycrystals: Application to Zirconium Alloys. Acta Metall. Mater. 1993, 41, 2611–2624. [Google Scholar] [CrossRef]
- Wang, H.; Raeisinia, B.; Wu, P.D.; Agnew, S.R.; Tomé, C.N. Evaluation of Self-Consistent Polycrystal Plasticity Models for Magnesium Alloy AZ31B Sheet. Int. J. Solids Struct. 2010, 47, 2905–2917. [Google Scholar] [CrossRef]
- Wang, H.; Lee, S.Y.; Gharghouri, M.A.; Wu, P.D.; Yoon, S.G. Deformation Behavior of Mg-8.5wt.%Al Alloy under Reverse Loading Investigated by in-Situ Neutron Diffraction and Elastic Viscoplastic Self-Consistent Modeling. Acta Mater. 2016, 107, 404–414. [Google Scholar] [CrossRef]
- Qiao, H.; Agnew, S.R.; Wu, P.D. Modeling Twinning and Detwinning Behavior of Mg Alloy ZK60A during Monotonic and Cyclic Loading. Int. J. Plast. 2015, 65, 61–84. [Google Scholar] [CrossRef]
- Fang, Z.; Guo, T.; Wang, Y.; Li, Z. Dynamic Strength Differential and Bauschinger Effects in an Extruded AZ80 Magnesium Alloy. J. Mater. Res. Technol. 2024, 30, 5990–6002. [Google Scholar] [CrossRef]
- Xie, D.; Lyu, Z.; Li, Y.; Liaw, P.K.; Chew, H.B.; Ren, Y.; Chen, Y.; An, K.; Gao, Y. In Situ Monitoring of Dislocation, Twinning, and Detwinning Modes in an Extruded Magnesium Alloy under Cyclic Loading Conditions. Mater. Sci. Eng. A 2021, 806, 140860. [Google Scholar] [CrossRef]
- Lee, S.Y.; Wang, H.; Gharghouri, M.A.; Nayyeri, G.; Woo, W.; Shin, E.; Wu, P.D.; Poole, W.J.; Wu, W.K. An Deformation Behavior of Solid-Solution-Strengthened Mg–9 Wt.% Al Alloy: In Situ Neutron Diffraction and Elastic–Viscoplastic Self-Consistent Modeling. Acta Mater. 2014, 73, 139–148. [Google Scholar] [CrossRef]
- Wang, H.; Wu, P.D.; Wang, J. Modeling Inelastic Behavior of Magnesium Alloys during Cyclic Loading–Unloading. Int. J. Plast. 2013, 47, 49–64. [Google Scholar] [CrossRef]
- Lee, S.Y.; Gharghouri, M.A. Pseudoelastic Behavior of Magnesium Alloy during Twinning-Dominated Cyclic Deformation. Mater. Sci. Eng. A 2013, 572, 98–102. [Google Scholar] [CrossRef]
- Muránsky, O.; Carr, D.G.; Šittner, P.; Oliver, E.C. In Situ Neutron Diffraction Investigation of Deformation Twinning and Pseudoelastic-like Behaviour of Extruded AZ31 Magnesium Alloy. Int. J. Plast. 2009, 25, 1107–1127. [Google Scholar] [CrossRef]
- Hama, T.; Takuda, H. Crystal-Plasticity Finite-Element Analysis of Inelastic Behavior during Unloading in a Magnesium Alloy Sheet. Int. J. Plast. 2011, 27, 1072–1092. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, K.; Wang, H.; Jiang, Y.; Sun, X.; Liu, C.; Yu, Q.; Jiang, Y.; Wu, P.; Wang, H. On the Cyclic Torsion Behavior of Extruded AZ61A Magnesium Alloy Tube. Int. J. Fatigue 2023, 174, 107704. [Google Scholar] [CrossRef]
- Suh, B.-C.; Kim, J.H.; Bae, J.H.; Hwang, J.H.; Shim, M.-S.; Kim, N.J. Effect of Sn Addition on the Microstructure and Deformation Behavior of Mg-3Al Alloy. Acta Mater. 2017, 124, 268–279. [Google Scholar] [CrossRef]




| Al | Sn | Zn | Nd | Ce | Mg | |
|---|---|---|---|---|---|---|
| Nominal | 6.00 | 4.00 | 2.00 | 0.50 | 0.50 | Bal. |
| Region 1 | 5.50 | 3.96 | 2.20 | 0.63 | 0.40 | Bal. |
| Region 2 | 5.46 | 4.03 | 2.22 | — | 0.41 | Bal. |
| A | B | |||||
|---|---|---|---|---|---|---|
| Basal <a> | 38 | 30 | 300 | 0 | - | - |
| Prismatic <a> | 105 | 45 | 300 | 0 | - | - |
| Pyramidal <c+a> | 120 | 90 | 1000 | 0 | - | - |
| Tension twin | 66 | 0 | 0 | 0 | 0.6 | 0.7 |
| 𝜿 = 0.35 | 𝜿 = 0.55 | 𝜿 = 0.75 | EBSD | |
|---|---|---|---|---|
| TCT | 3.83% | 5.72% | 7.17% | 7.51% |
| CTC | 0.24% | 0.26% | 0.36% | 0.93% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Yu, Y.; Lv, B.; Song, M.; Xie, X. Twinning–Detwinning-Dominated Cyclic Deformation Behavior of a High-Strength Mg-Al-Sn-Zn Alloy during Loading Reversals: Experiment and Modeling. Metals 2024, 14, 635. https://doi.org/10.3390/met14060635
Wang H, Yu Y, Lv B, Song M, Xie X. Twinning–Detwinning-Dominated Cyclic Deformation Behavior of a High-Strength Mg-Al-Sn-Zn Alloy during Loading Reversals: Experiment and Modeling. Metals. 2024; 14(6):635. https://doi.org/10.3390/met14060635
Chicago/Turabian StyleWang, Huai, Yongze Yu, Binjiang Lv, Ming Song, and Xuefang Xie. 2024. "Twinning–Detwinning-Dominated Cyclic Deformation Behavior of a High-Strength Mg-Al-Sn-Zn Alloy during Loading Reversals: Experiment and Modeling" Metals 14, no. 6: 635. https://doi.org/10.3390/met14060635
APA StyleWang, H., Yu, Y., Lv, B., Song, M., & Xie, X. (2024). Twinning–Detwinning-Dominated Cyclic Deformation Behavior of a High-Strength Mg-Al-Sn-Zn Alloy during Loading Reversals: Experiment and Modeling. Metals, 14(6), 635. https://doi.org/10.3390/met14060635







