Fracture Model of Al–Cu Alloys with Gradient Crystals Based on Crystal Plasticity
Abstract
:1. Introduction
2. Methods and Materials
2.1. Crystal Plasticity Finite Element Model
2.2. Cohesive Model
2.3. Finite Element Modeling and Materials
3. Results
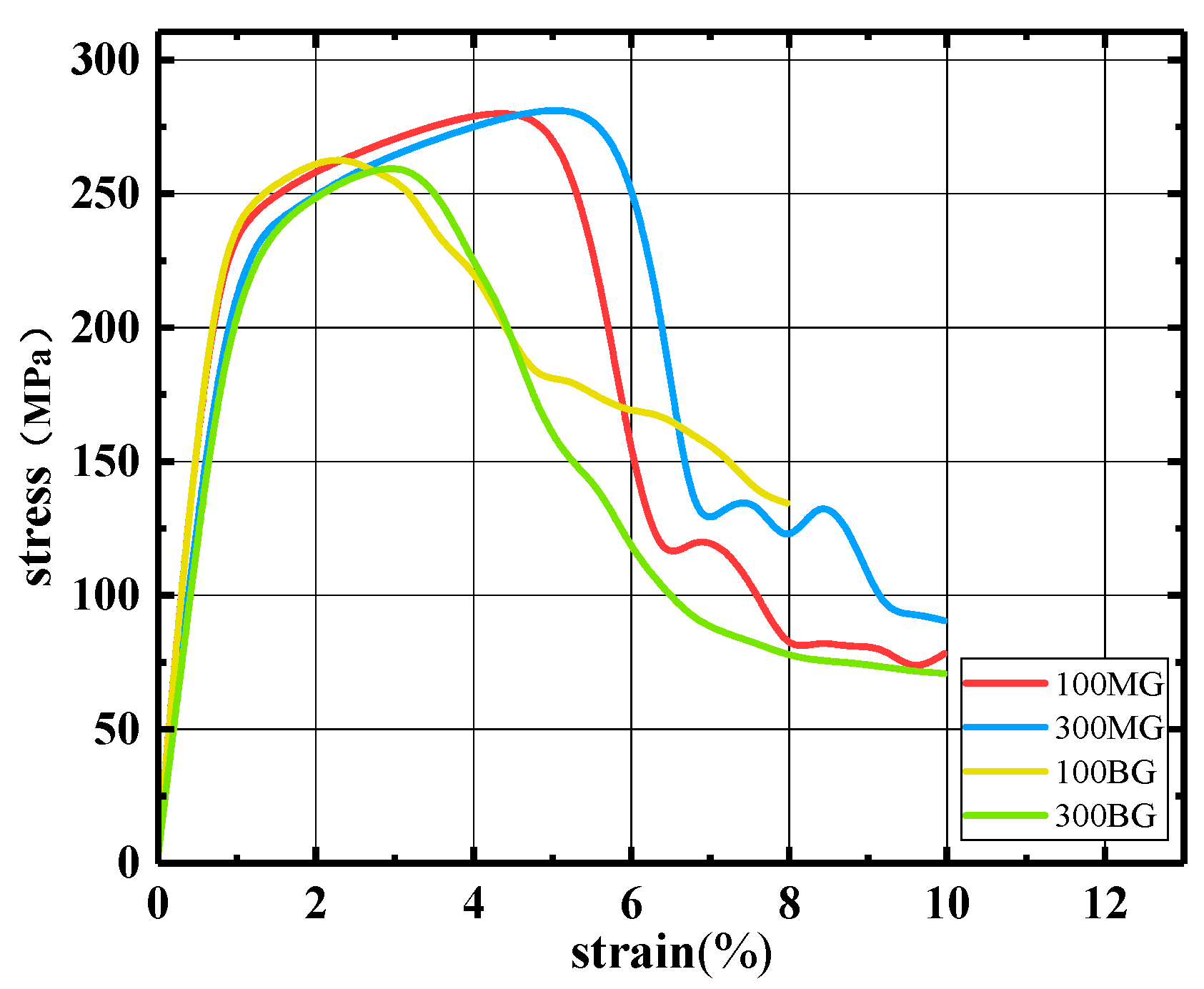
3.1. Stress–Strain Curves of Different Graded Crystals
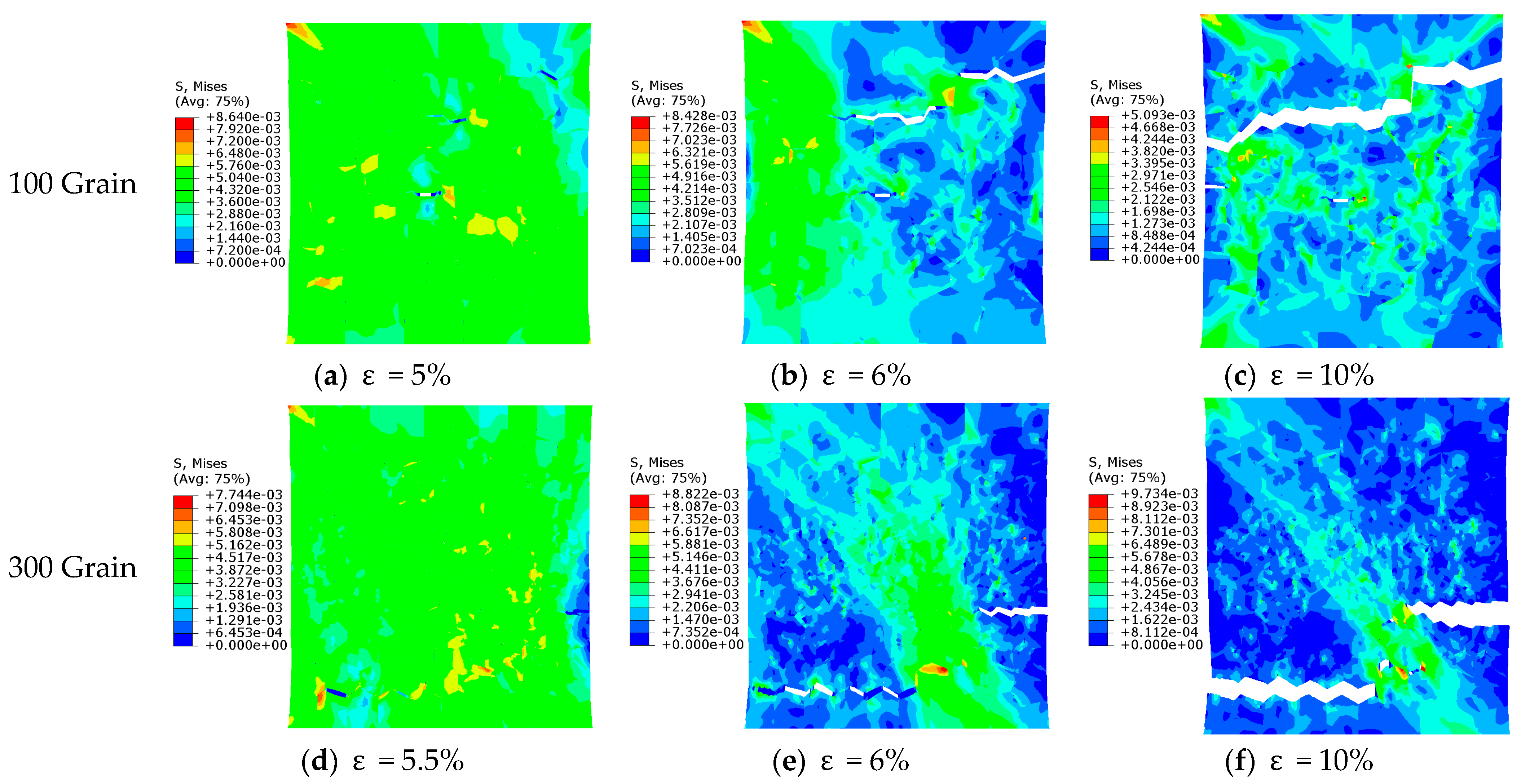
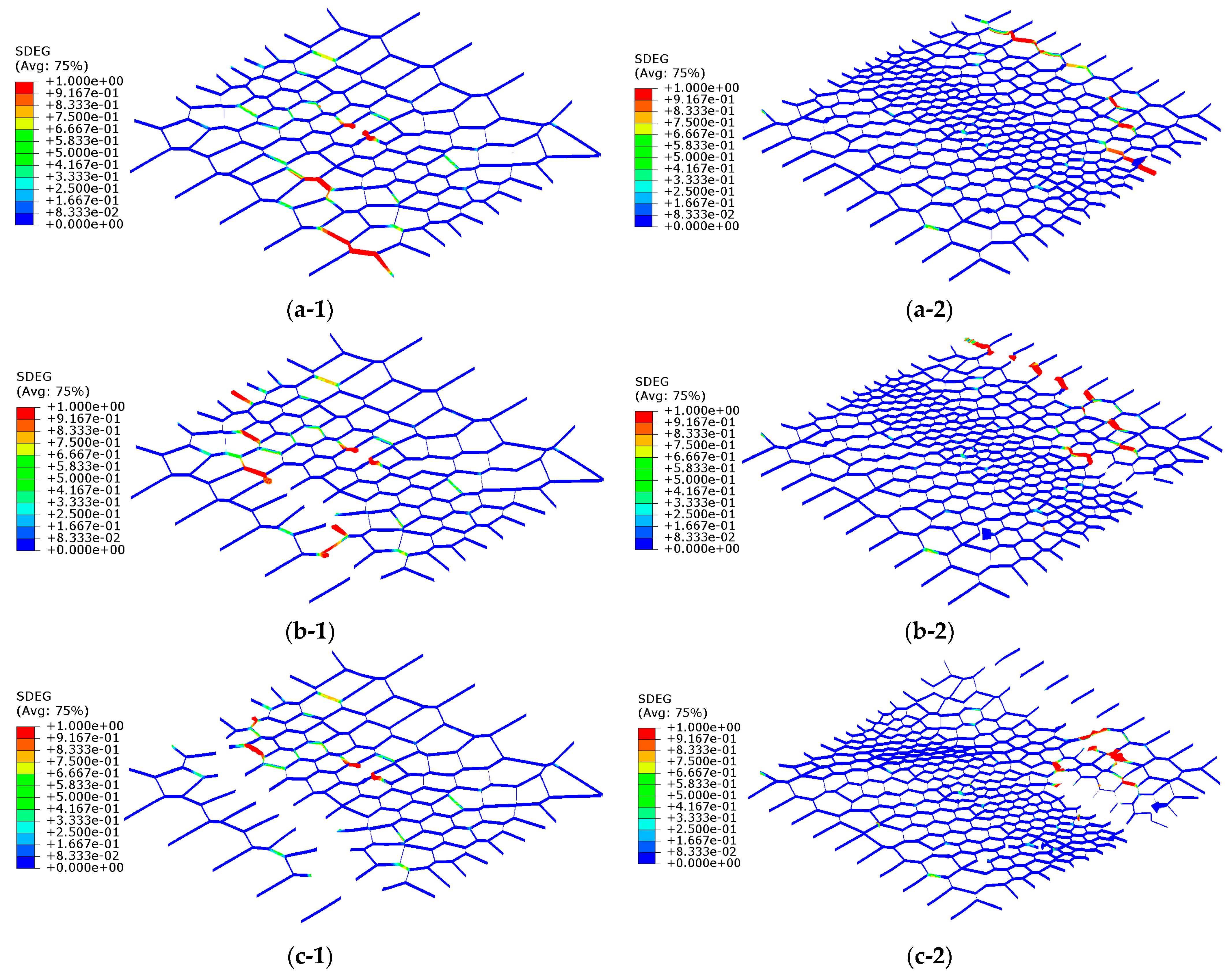
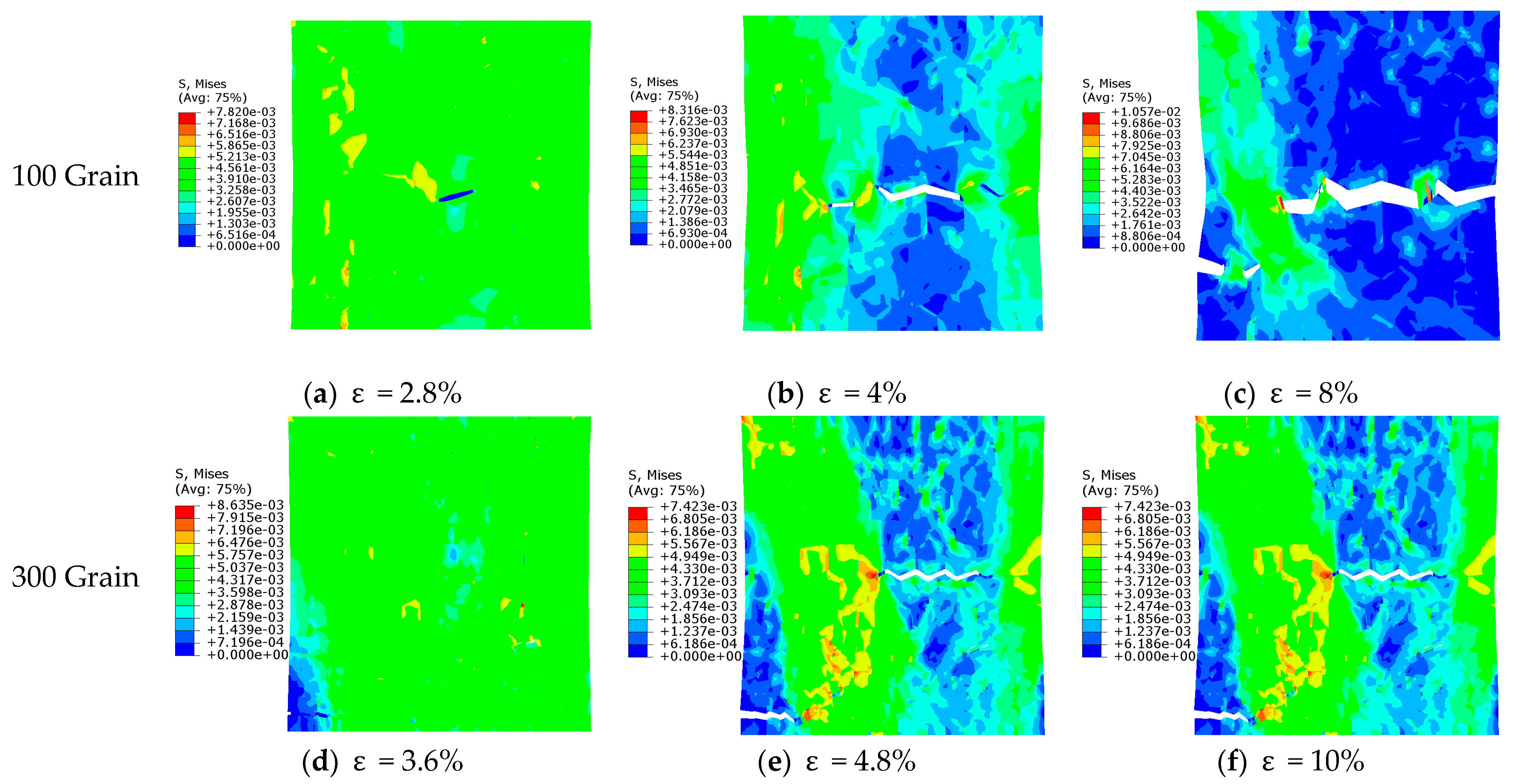
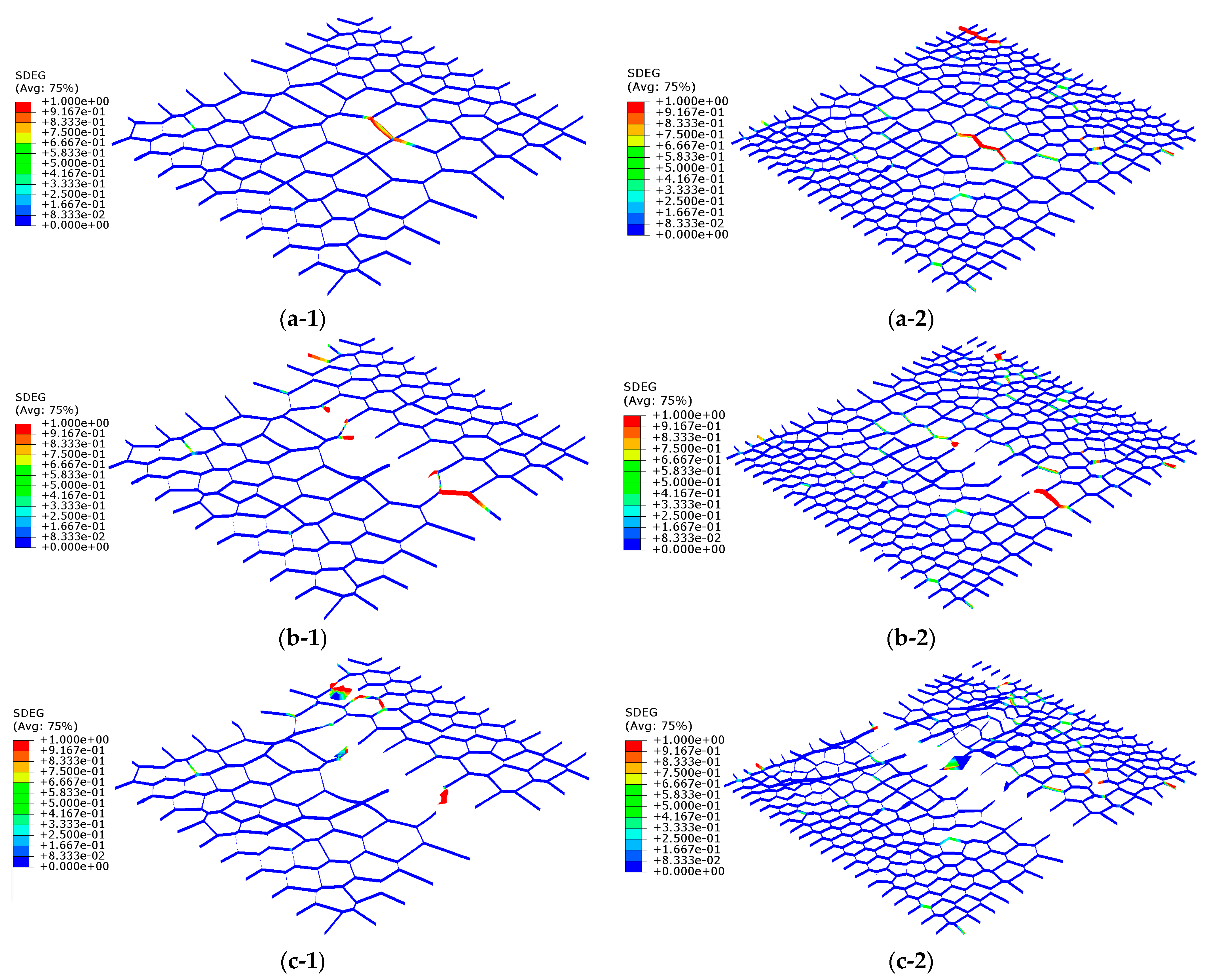
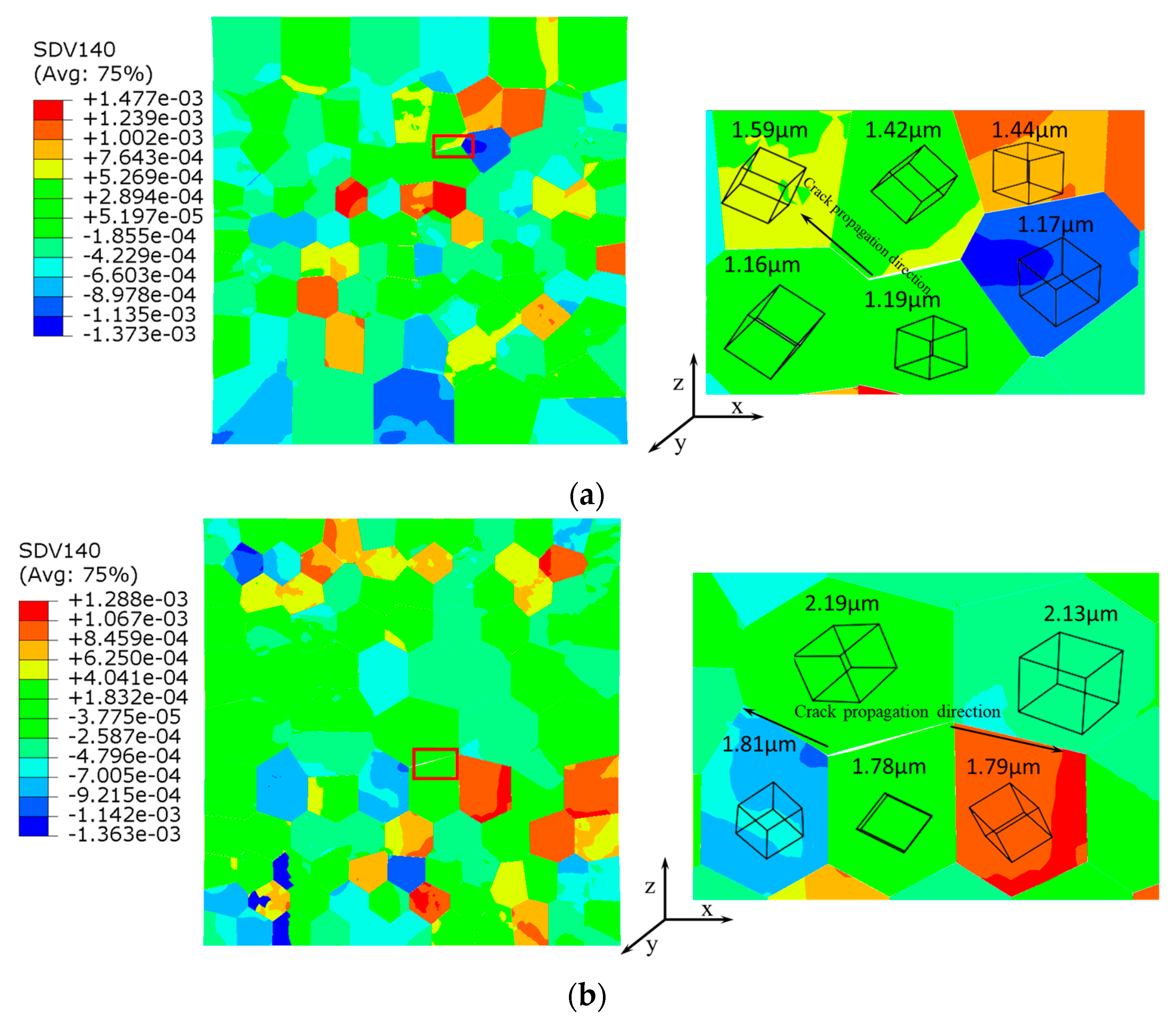
3.2. The Results of MG Crystals
3.3. The Results of BG Crystals
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, X.; Ma, X.; Moering, J.; Zhou, H.; Wang, W.; Gong, Y.; Tao, J.; Zhu, Y.; Zhu, X. Influence of gradient structure volume fraction on the mechanical properties of pure copper. Mater. Sci. Eng. A 2015, 645, 280–285. [Google Scholar] [CrossRef]
- Yin, Z.; Yang, X.; Ma, X.; Moering, J.; Yang, J.; Gong, Y.; Zhu, Y.; Zhu, X. Strength and ductility of gradient structured copper obtained by surface mechanical attrition treatment. Mater. Des. 2016, 105, 89–95. [Google Scholar] [CrossRef]
- Wu, X.L.; Yang, M.X.; Yuan, F.P.; Chen, L.; Zhu, Y.T. Combining gradient structure and TRIP effect to produce austenite stainless steel with high strength and ductility. Acta Mater. 2016, 112, 337–346. [Google Scholar] [CrossRef]
- Tan, X.; Kok, Y.; Tan, Y.J.; Descoins, M.; Mangelinck, D.; Tor, S.B.; Leong, K.F.; Chua, C.K. Graded microstructure and mechanical properties of additive manufactured Ti–6Al–4V via electron beam melting. Acta Mater. 2015, 97, 1–16. [Google Scholar] [CrossRef]
- Chen, W.; You, Z.S.; Tao, N.R.; Jin, Z.H.; Lu, L. Mechanically-Induced grain coarsening in gradient nano-Grained copper. Acta Mater. 2017, 125, 255–264. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, Y. Heterogeneous materials: A new class of materials with unprecedented mechanical properties. Mater. Res. Lett. 2017, 5, 527–532. [Google Scholar] [CrossRef]
- Wang, C.; Ding, L.; Shi, S.; Liu, J.; Zhou, W.; Liu, Q.; Fu, X.; Jia, Z. Origin mechanism of heterostructure nanograins with gradient grain size suppressing strain localization. Mater. Sci. Eng. A 2023, 885, 145584. [Google Scholar] [CrossRef]
- Korchuganov, A.; Kryzhevich, D.; Zolnikov, K. Fracture of Fe 95 Ni 5Alloys with Gradient-Grained Structure under Uniaxial Tension. Metals 2023, 13, 1308. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, R.; Yang, Y.; Guo, J.; Su, Y.; Ding, H.; Fu, H. Effects of grain size and precipitated phases on mechanical properties in TiAl gradient materials. Mater. Sci. Eng. A 2018, 731, 634–641. [Google Scholar] [CrossRef]
- An, X.; Bao, W.; Zhang, Z.; Jiang, Z.; Yuan, S.; You, Z.; Zhang, Y. Gradient Enhanced Strain Hardening and Tensile Deformability in a Gradient-Nanostructured Ni Alloy. Nanomaterials 2021, 11, 2437. [Google Scholar] [CrossRef]
- Hasan, M.; Liu, Y.; An, X.; Gu, J.; Song, M.; Cao, Y.; Li, Y.; Zhu, Y.; Liao, X. Simultaneously enhancing strength and ductility of a high-entropy alloy via gradient hierarchical microstructures. Int. J. Plast. 2019, 123, 178–195. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, G.; Wang, W.; Wang, X.; Li, Q.; Wei, Y. Optimal stress and deformation partition in gradient materials for better strength and tensile ductility: A numerical investigation. Sci. Rep. 2017, 7, 10954. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.H.; Park, H.K.; Jung, J.; Hwang, K.J.; Kim, H.S. Microstructural tailoring in reverse gradient-structured copper sheet using single-roll angular-rolling and subsequent annealing. Mater. Sci. Eng. A 2019, 764, 138258. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, X.; Xu, D.; Lu, L.; Gao, H.; Zhu, T. Gradient plasticity in gradient nano-grained metals. Extrem. Mech. Lett. 2016, 8, 213–219. [Google Scholar] [CrossRef]
- Fang, Q.; Li, L.; Li, J.; Wu, H. Strengthening mechanism of gradient nanostructured body-centred cubic iron film: From inverse Hall-Petch to classic Hall-Petch. Comput. Mater. Sci. 2018, 152, 236–242. [Google Scholar] [CrossRef]
- Li, L.; Fang, Q.; Li, J.; Wu, H. Origin of strengthening-softening trade-off in gradient nanostructured body-centred cubic alloys. J. Alloys Compd. 2019, 775, 270–280. [Google Scholar] [CrossRef]
- Jin, H.; Zhou, J.; Chen, Y. Grain size gradient and length scale effect on mechanical behaviors of surface nanocrystalline metals. Mater. Sci. Eng. A 2018, 725, 1–7. [Google Scholar] [CrossRef]
- Zhao, J.; Lu, X.; Yuan, F.; Kan, Q.; Qu, S.; Kang, G.; Zhang, X. Multiple mechanism based constitutive modeling of gradient nanograined material. Int. J. Plast. 2020, 125, 314–330. [Google Scholar] [CrossRef]
- He, C.Y.; Yang, X.F.; Chen, H.; Zhang, Y.; Yuan, G.J.; Jia, Y.F.; Zhang, X.C. Size-dependent deformation mechanisms in copper gradient nano-grained structure: A molecular dynamics simulation. Mater. Today Commun. 2022, 31, 145584. [Google Scholar] [CrossRef]
- Liu, L.Y.; Yang, Q.S.; Liu, X.; Nian, X.C. Crystal Cracking of Grain-Gradient Aluminum by a Combined CPFEM-CZM Method. Eng. Fract. Mech. 2020, 242, 107507. [Google Scholar] [CrossRef]
- Xu, L.; Huang, Z.; Shen, Q.; Chen, F. Atomistic Simulations of Plasticity Heterogeneity in Gradient Nano-Grained FCC Metals. Mater. Des. 2022, 221, 110929. [Google Scholar] [CrossRef]
- Omid, S.; Hamidreza, A. Strain-Gradient Crystal Plasticity Finite Element Modeling of Slip Band Formation in α-Zirconium. Crystals 2021, 11, 1382. [Google Scholar] [CrossRef]
- Huang, Y. A User-Material Subroutine Incorporating Single Crystal Plasticity in the ABAQUS Finite Element Program; Harvard University: Cambridge, UK, 1991. [Google Scholar]
- Roters, F.; Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Reuber, C.; Wong, S.L.; Maiti, T.; Ebrahimi, A.; Hochrainer, T.; Fabritius, H.-O. DAMASK–The Düsseldorf Advanced MaterialSimulation Kit for modeling multi-physics crystal plasticity, thermal, and damagephenomena from the single crystal up to the component scale. Comput. Sci. 2019, 158, 420–478. [Google Scholar]
- Kreyca, J.F. State Parameter Based Modelling of Stress-Straincurves in Aluminium Alloys. Ph.D. Thesis, Vienna University of Technology, Vienna, Austria, 2017. [Google Scholar]
- Li, J.; Yi, M.; Wu, H.; Fang, Q.; Liu, Y.; Liu, B.; Zhou, K.; Liaw, P.K. Fine-grain-embedded dislocation-cellstructures for high strength and ductility in additively manufactured steels. Mater. Sci. Eng. A 2020, 790, 139736. [Google Scholar] [CrossRef]
- Hunter, A.; Preston, D.L. Analytic model of dislocation density evolution in fcc polycrystals accounting for dislocation generation storage and dynamic recovery mechanisms. Int. J. Plast. 2022, 151, 103178. [Google Scholar] [CrossRef]
- Rohith, P.; Sainath, G.; Srinivasan, V.S. Effect of size temperature and strain rate on dislocation density and deformation mechanisms in Cu nanowires. Phys. B Condens. Matter 2019, 561, 136–140. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J.R. Constitutive Analysis of Elastic-Plastic Crystals at Arbitrary Strain. J. Mech. Phys. Solids 1972, 151, 401–413. [Google Scholar] [CrossRef]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part I—Theoretical. Proc. R. Soc. Lond. 1934, 145, 362–387. [Google Scholar]
- Shanthraj, P.; Zikry, M. Dislocation density evolution and interactions in crystalline materials. Acta Mater. 2011, 59, 7695–7702. [Google Scholar] [CrossRef]
- Zheng, Z.; Fei, S.; Liao-Liang, K.A. dislocation density-based crystal plasticity damage model for rolling contact fatigue of gradient grained structures. Int. J. Fatigue 2024, 179, 108038. [Google Scholar] [CrossRef]
- Wu, Q.; Zikry, M.A. Dynamic fracture predictions of microstructural mechanisms and characteristics in martensitic steels. Eng. Fract. Mech. 2015, 145, 54–66. [Google Scholar] [CrossRef]
- Hatem, T.M.; Zikry, M.A. Dislocation density crystalline plasticity modeling of lath martensitic microstructures in steel alloys. Philos. Mag. 2009, 89, 3087–3109. [Google Scholar] [CrossRef]
- Khanikar, P.; Liu, Y.; Zikry, M.A. Experimental and computational investigation of the dynamic behavior of Al–Cu–Li alloys. Mater. Sci. Eng. A 2014, 604, 67–77. [Google Scholar] [CrossRef]
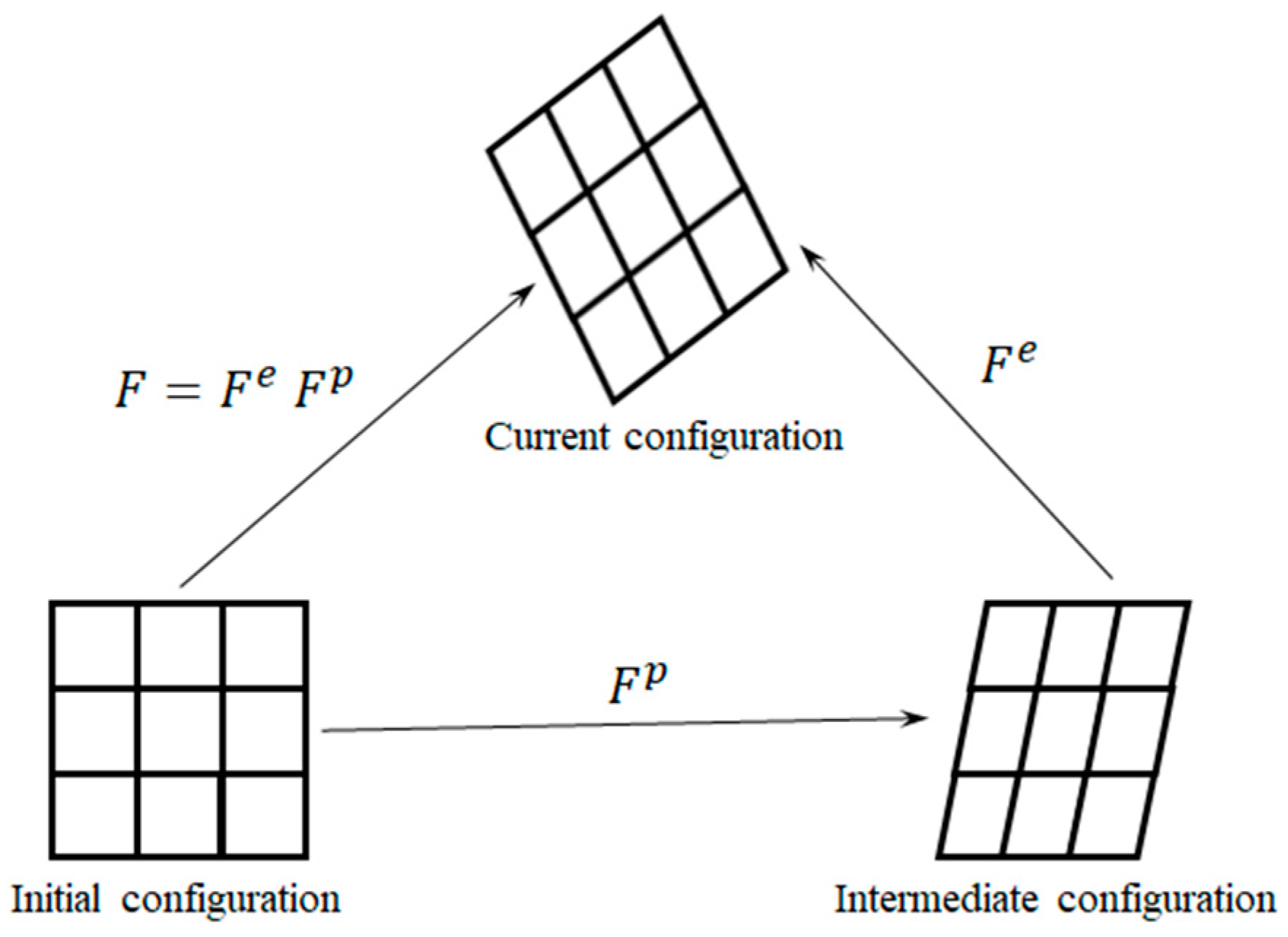
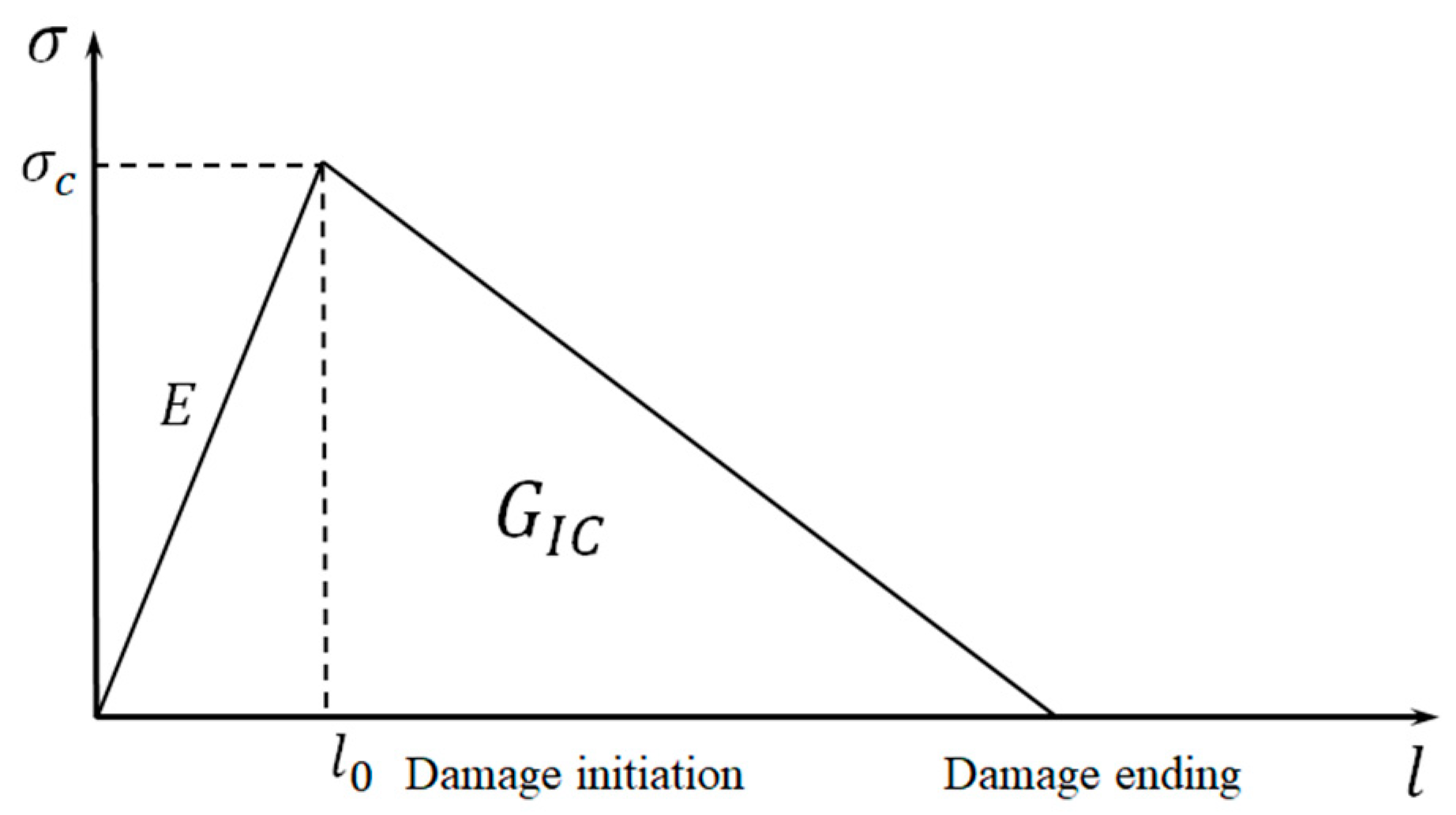

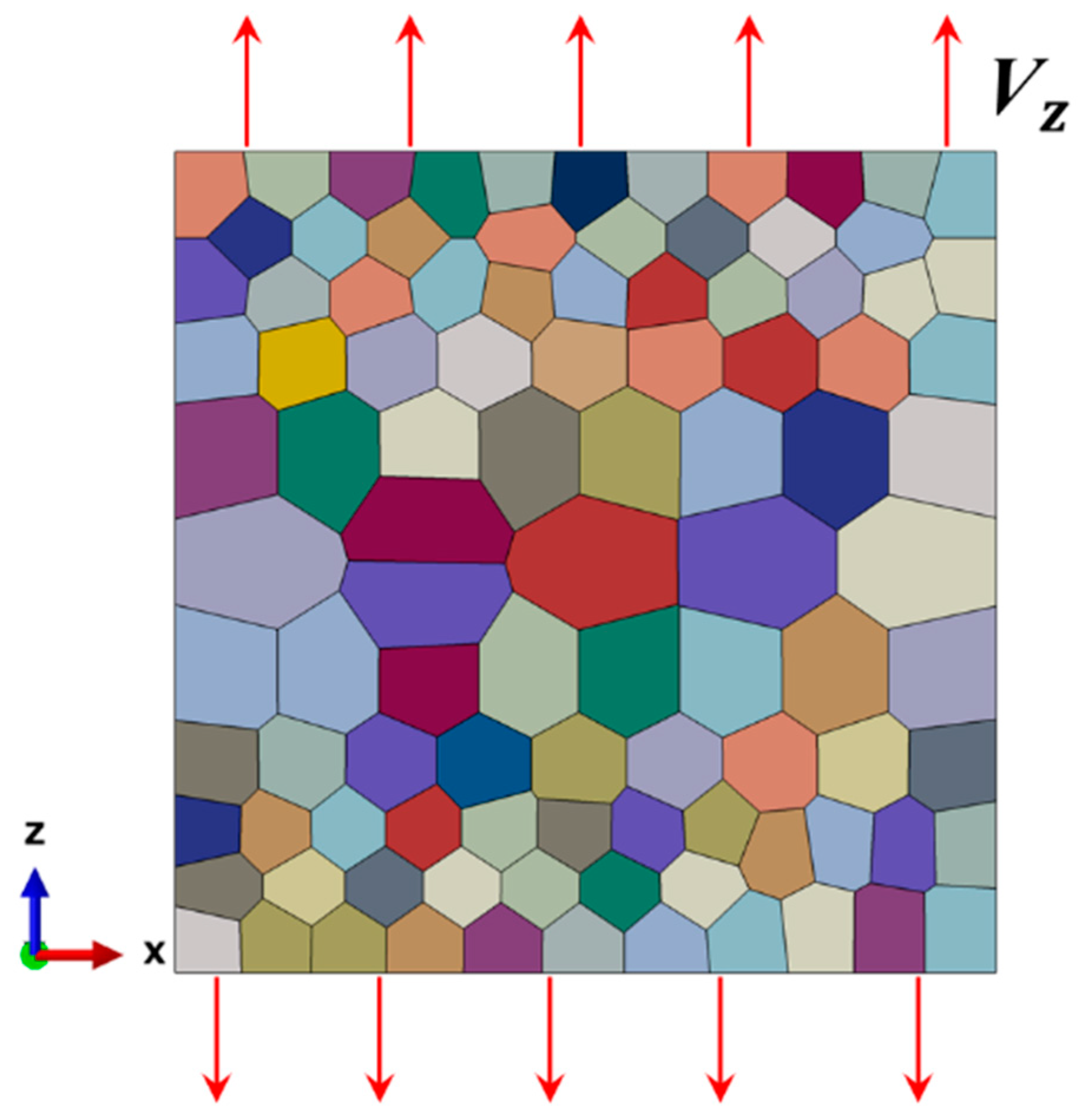
| Deformation gradient | |
| , | Elastic and plastic deformation gradients |
| Velocity gradient | |
| , | Elastic and plastic velocity gradients |
| Shear strain rate | |
| , | Slip direction and normal direction of slip plane |
| Burgers vector | |
| Reference shear stress | |
| , | Movable and immovable dislocation density |
| Ration of activation enthalpy | |
| Boltzmann constant | |
| , , , , | Dislocation evolution correlation coefficient |
| Saturation value for immobile dislocation density | |
| Breaking energy | |
| , , | cohesive element stiffness |
| , , | n, s, t direction displacement |
| , , | n, s, t directional stress |
| , , | n, s, t direction strain |
| , | critical stress and critical strain |
| Parameters | GIC [J/mm] | C1 [MPa] | C2 | C3 | [MPa] | ||
|---|---|---|---|---|---|---|---|
| Value | 35 | 69,000 | 69,000 | 69,000 | 345 | 345 | 345 |
| Parameters | Value | Dimensionless |
|---|---|---|
| E [GPa] | 69 | 1 |
| 0.34 | 0.34 | |
| 35 | 5.07246 × 10−4 | |
| 2.7 | 1 | |
| Cp [J/kgK] | 902 | 0.0103416 |
| [k/K] | 2500 | 8.53242 |
| 0.001 | 1.97814 × 10−13 | |
| |b| [m] | 3 × 1010 | 0.0003 |
| 1 | ||
| 104 | ||
| 0.01 | ||
| [K] | 293 | 1 |
| 0.025 | 0.025 | |
| 0.5 | 0.5 | |
| 0.9 | 0.9 | |
| 2.76 × 10−5 | 2.76 × 10−5 | |
| 6.69 × 104 | 6.69 × 104 | |
| 5.53 × 104 | 5.53 × 104 | |
| 0.0127 | 0.0127 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, M.; Yao, J.; Huang, C. Fracture Model of Al–Cu Alloys with Gradient Crystals Based on Crystal Plasticity. Metals 2024, 14, 694. https://doi.org/10.3390/met14060694
Xiao M, Yao J, Huang C. Fracture Model of Al–Cu Alloys with Gradient Crystals Based on Crystal Plasticity. Metals. 2024; 14(6):694. https://doi.org/10.3390/met14060694
Chicago/Turabian StyleXiao, Mao, Ji Yao, and Chunyang Huang. 2024. "Fracture Model of Al–Cu Alloys with Gradient Crystals Based on Crystal Plasticity" Metals 14, no. 6: 694. https://doi.org/10.3390/met14060694






