Mechanisms of Low-Temperature Dislocation Motion in High-Entropy Al_0.5CoCrCuFeNi Alloy

Abstract

An analysis of the processes of plastic deformation and acoustic relaxation in a high-entropy alloy, Al_0.5CoCrCuFeNi, was carried out. The following were established: dominant dislocation defects; types of barriers that prevent the movement of dislocations; mechanisms of thermally activated movement of various elements of dislocation lines through barriers at room and low temperatures. Based on modern dislocation theory, quantitative estimates were obtained for the most important characteristics of dislocations and their interaction with barriers.

1. Introduction

At the beginning of the 21st century, two articles [1] appeared in which a new strategy for the development of new multicomponent metal alloys was proposed. These alloys are called high-entropy alloys (HEAs), since they have an increased entropy of mixing. Their structure consists of different major elements in the range of 5–35 atomic percent and they typically contain a single phase, instead of the many metallic phases formed in the structure of traditional alloys. Due to their structural features, HEAs have many improved mechanical properties: increased strength and ductility, high fracture toughness at both high and low temperatures, good wear resistance, increased resistance to corrosion, and oxidation [2,3,4,5,6,7]. In this regard, many articles have appeared in the literature studying the mechanical properties of HEAs using active deformation methods ata wide range of both high and low temperatures [8,9,10]. At the same time, the number of studies of HEAs with small deformations in the elastic region is clearly not enough. Obviously, this delays the establishment of the physical mechanisms responsible for the plastic deformation of HEAs. It is known that one of the main methods for studying deformations in the elastic region is the method of mechanical resonance spectroscopy. This makes it possible to excite cyclic elastic deformation in samples with an amplitude of ~10⁻⁷, caused by short segments of dislocation strings (dislocation relaxers), which oscillate with amplitudes on the order of the lattice parameter. Previously, we used this method at temperatures T < 300 K to measure the acoustic properties (features such as temperature dependences of internal friction and dynamic Young’s modulus) and mechanical properties (under uniaxial compression and tension) in one of the typical Al_0.5CoCrCuFeNi HEAs with an fcc lattice [11,12].

In this publication, we will take a closer look at the relationship between these properties and the features of the dynamics and kinetics of elementary dislocation processes in this alloy. We will also discuss the possibility of using the fundamental principles of modern dislocation theory to interpret these properties. We use data from two different experimental methods with different intensities of influence on the dislocation structure in the studied alloy samples:

• Method of resonant mechanical spectroscopy—excitation in samples of cyclic elastic deformation with an amplitude of ${\epsilon }_0$~10⁻⁷, caused by short segments of dislocation strings (dislocation relaxers), which oscillate with amplitudes on the order of the lattice parameter;
• Method of active deformation—when used, significant plastic deformations of $\epsilon$~3 × 10⁻¹ are achieved, caused by the translational movement of extended dislocations over macroscopic distances.

2. Materials and Methods of Research

The production method and characteristics of the alloy are described in [10,11,12]. The original cast ingots of the Al_0.5CoCrCuFeNi alloy were obtained by electric arc melting. The alloy was studied in 2 structural states: (I)—initial cast; (II)—after high-temperature annealing in vacuum at 975 °C for 6 h. Data on the microstructure of the alloy [10] showed that state (I) has a dendritic structure and consists of two fcc lattices with the parameters a₁ = (3.596 ± 1·10⁻³)Å (for dendritic regions) and a₂ = (3.625 ± 3·10⁻³)Å (for interdendritic regions), with noticeable differences in the elemental chemical composition. It has been shown [13] that the distribution of elements included in the alloy is non-uniform at the nanoscale. In the microstructure of the alloy, regions are observed in the form of stripes 15–20 nm wide, with significantly different concentrations of various elements; such regions form a three-dimensional irregular lattice in the microstructure. Significantstructural distortions are observed near the lattice nodes. The distance between these inhomogeneities is equal to ~20 nm. In addition, clusters of several atoms of one of the constituent elements of the alloy are observed. Several adjacent atoms of an element with a relatively large atomic radius create local distortions of the crystal lattice. The characteristic distance between clusters is several nanometers. In state (II), the alloy has a dendritic structure, which consists of two fcc phases with traces of bcc phases (type B2). Averaged lattice parameters in this case for fcc phases: a₁ = (3.5882 ± 6·10⁻⁴)Å (for dendritic regions) and a₂ = (3.620 ± 2·10⁻³)Å (for interdendritic regions); that for the bcc phase: a = (2.870 ± 1·10⁻³)Å. The samples for acoustic measurements had the shape of a thin plate with dimensions 3 × 20 × 0.3 mm³. Uniaxial compression of the samples (4 × 2 × 2 mm³) with a strain rate of 3 × 10⁻⁴ s⁻¹ was carried out at an ambient temperature of 300 K and cryogenic temperatures obtained using liquid and gaseous nitrogen and helium.

3. Experimental Results

3.1. Acoustic Properties

The temperature dependences of internal friction $Q_{\exp }^{-1}\left(T\right)$ and dynamic Young’s modulus $E_{\exp }\left(T\right)$ were studied in [12] using the method of mechanical resonance spectroscopy. The technique for measuring acoustic absorption (internal friction) and dynamic Young’s modulus in these experiments is described in [14].

As the temperature decreases, $E_{\exp }\left(T\right)$ for state (I) increases monotonically and $Q_{\exp }^{-1}\left(T\right)$ decreases monotonically, while the temperature dependences $Q_{\exp }^{-1}\left(T\right)$ and $E_{\exp }\left(T\right)$ do not show any significant features such as relaxation resonances.

The transition to state (II) leads to the appearance of a relaxation resonance—an acoustic absorption peak and a corresponding step in the temperature dependence of the dynamic modulus (Figure 1).

To interpret the acoustic relaxation resonances observed in the experiments [12], it is necessary to carry out initial processing of the measurement results of $E_{\exp }\left(T\right)$ and $Q_{\exp }^{-1}\left(T\right)$ identify based on these temperature dependences the resonant contributions $E_R\left(T\right)$ and $Q_R^{-1}\left(T\right)$ of individual subsystems of relaxers against the background of the contributions $E_{BG}\left(T\right)$ and $Q_{BG}^{-1}\left(T\right)$ of other relaxation processes.

In general, the dynamic modulus of elasticity depends on both temperature $T$ and frequency $\omega$. However, our measurements were performed at a fixed value of the sample oscillation frequency ${\omega }_r=2\pi f_r$. It has been established [14] that the dependence $E_{\exp }\left(T,\omega \right)$ recorded in experiments can be divided into resonant $E_R\left(T,\omega \right)$ and background $E_{BG}\left(T,\omega \right)$ components:

$$E_{\exp }\left(T,\omega \right)=E_0\left(\omega \right)-E_{BG}\left(T,\omega \right)-E_R\left(T,\omega \right)$$

(1)

where $E_0\left(\omega \right)$ is the limit value of the module at $T\to 0$. For most crystalline materials, the value $E_0$ is close to the value of the static modulus of elasticity of a dislocation-free crystal.

According to [15], for many crystalline materials the background component $E_{BG}\left(T,\omega \right)$ in the region of low temperatures $T<300 \mathrm{K}$ and frequencies $\omega \le {10}^7{ \mathrm{s}}^{-1}$ is determined primarily by the interaction of elastic vibrations with thermal phonons. For the Einstein model of the phonon spectrum with a characteristic temperature ${\Theta }_E$, the softening of the elastic modulus by phonons is described by the equation

$$\frac{E_{BG}\left(T,\omega \right)}{E_0\left(\omega \right)}=\beta \cdot T\exp \left(-\frac{T_{\eta }}{T}\right),$$

(2)

where the coefficient $\beta$ depends on the material under study and the vibration mode under study, and the characteristic temperature $T_{\eta }$ in most cases for materials with simple phonon spectra is of the order of the Einstein ${\Theta }_E$ or Debye ${\Theta }_D$ temperatures: $T_{\eta }\le {\Theta }_E=h{\nu }_E\approx \frac{3}{4}{\Theta }_D$ (h—Planck constant), since in real crystals the frequencies of acoustic phonons are lower than the Einstein frequency ${\nu }_E$ [16]. In the simplest case ${\Theta }_E=\frac{3}{4}{\Theta }_D$.

In the temperature range T ≤ 10 K, together with phonon contribution (2), one can also distinguish a relatively weak electronic contribution in $E_{BG}\left(T,\omega \right)$ [14], but it does not play a significant role in the analysis of dynamic elastic moduli in the temperature range $T<{\Theta }_D$.

Then,

$$E_{\exp }\left(T,\omega \right)=E_0\left(\omega \right)\cdot \eta \left(T\right)-E_R\left(T,\omega \right), \eta \left(T\right)=1-\beta T\exp \left(-T_{\eta }/T\right)$$

(3)

It has been shown [11] that (3) well describes the $E_{\exp }\left(T,\omega \right)$ of the alloy under study in the absence of relaxation resonances, when $E_R\left(T,\omega \right)\equiv 0$ (state I). Its use for approximating the results obtained when studying state (II) is illustrated in Figure 1a (solid line), and the corresponding parameter values are given in

Table 1. Parameters of background $E_{BG}\left(T,\omega \right)·\omega =2\pi f_r$ and $Q_{BG}^{-1}\left(T\right)$ for the HEA Al_0.5CoCrCuFeNi in state (II).

$\mathit{\omega }=2\mathit{\pi }{\mathit{f}}_{\mathit{r}}$	${\mathit{E}}_0$	$\mathit{\beta }$	${\mathit{T}}_{\mathit{\eta }}$	${\mathit{E}}_{\mathit{R}0}$	A1	A2	${\mathit{U}}_{\mathit{B}\mathit{G}}$
3.34·103 s−1	236 GPa	3.5·10−4 K−1	160 K	0.33 GPa	6·10−5	0.3	0.16 eV

. When transitioning from state (I) to state (II), the parameter $E_0$ increases, but the characteristic temperature $T_{\eta }$ and coefficient $\beta$ remain unchanged.

The temperature dependence of the resonant component of the Young’s modulus for state (II) is shown in Figure 1a. Its graph has the shape of a step with a height characteristic of relaxation resonances $E_{R0}=E_R\left(T\gg T_p,\omega \right)$ (Table 1).

$$E_R\left(T,\omega \right)=E_0\left(\omega \right)\cdot \eta \left(T\right)-E_{\exp }\left(T,\omega \right)$$

(4)

The experimentally observed dependence $Q_{\exp }^{-1}\left(T,\omega \right)$ consists of the sum of resonant $Q_R^{-1}\left(T,\omega \right)$ and background $Q_{BG}^{-1}\left(T,\omega \right)$ absorption. The interpretation of the internal friction peaks recorded in the experiment comes down to a comparison with the theory of the difference value:

$$Q_R^{-1}\left(T,\omega \right)=Q_{\exp }^{-1}\left(T,\omega \right)-Q_{BG}^{-1}\left(T,\omega \right)$$

(5)

We consider [14] the $Q_{BG}^{-1}\left(T\right)$ to be partially caused by thermally activated dislocation relaxation with an activation energy of $U_{BG}$, which differs significantly from the activation energy of the studied resonance absorption. For the description of $Q_{BG}^{-1}\left(T\right)$, we use the following relation [17]:

$$Q_{BG}^{-1}\left(T\right)=A_1+A_2\exp (-\frac{U_{BG}}{k_{B}T})$$

(6)

where $A_1$, $A_2$ and $U_{BG}$ are fitting parameters. The coefficient $A_1$ characterizes the contributions to the absorption of the phonon, electronic and magnetic subsystems of the metal, which weakly depend on the temperature near resonance.

Relationship (6) well describes the temperature dependence of the acoustic absorption background for state (II)—solid line in Figure 1b $A_1$, $A_2$ and $U_{BG}$ are given in Table 1.

The temperature dependence $Q_R^{-1}\left(T,\omega \right)$ of the alloy under study in state (II), after subtracting the background $Q_{BG}^{-1}\left(T\right)$, is shown in Figure 1b. Analysis of the temperature dependence of the derivative $\frac{\partial }{\partial T}{Q}_R^{-1}\left(T,\omega \right)$ makes it possible to clarify the peak temperature $T_p$, obtain the values of the coordinates of the inflection points $T^{(-)}$ and $T^{(+)}$ on the graph of $Q_R^{-1}\left(T,\omega \right)$ (see Figure 1b), and also estimate the value of the ratio

$$K=\frac{\max \frac{\partial }{\partial T}{Q}_R^{-1}\left(T,\omega \right)}{\left|\min \frac{\partial }{\partial T}{Q}_R^{-1}\left(T,\omega \right)\right|}$$

(7)

The registration in experiments of the characteristics of acoustic relaxation resonance $T_p$, $T^{(-)}$, $T^{(+)}$, $\max Q_R^{-1}$, $E_{R0}$ and $K$ (see

Table 2. Characteristics of the main absorption peak (a) and its satellite (b) in state (II).

(a)
$T_p$	$T^{(-)}$	$T^{(+)}$	$\max Q^{-1}$	$\max \frac{\partial }{\partial T}{\overline{Q}}^{-1}$	$\min \frac{\partial }{\partial T}{\overline{Q}}^{-1}$	$K$
228 K	213 K	242 K	1.5·10−4	7.6·10−6 K−1	−9.1·10−6 K−1	0.83
(b)
$T_{ps}$	$T_s^{(-)}$	$T_s^{(+)}$	$\max Q_s^{-1}$	$\max \frac{\partial }{\partial T}{\overline{Q}}_s^{-1}$	$\min \frac{\partial }{\partial T}{\overline{Q}}_s^{-1}$	$K_s$
190 K	182.6 K	202.0 K	2.64·10−5	3.1·10−6 K−1	−2.5·10−6 K−1	1.24

) allows us to formulate a microscopic model of the relaxer and obtain estimates for its parameters [14,18].

However, the resonant component of acoustic relaxation in state (II) is not limited only to the contributions of relaxers responsible for the appearance of the peak $T_p=228 \mathrm{K}$. Figure 1b shows that the resonant component $Q_R^{-1}\left(T,\omega \right)$ contains another relaxation resonance, localized on the left slope of the peak $T_p=228 \mathrm{K}$—a satellite $T_{ps}=190 \mathrm{K}$. Its characteristics were obtained after a detailed analysis of the main peak.

3.2. Mechanical Properties

Mechanical tests of the alloy were carried out in the temperature range 0.5 K < T < 300 K. The technique for studying mechanical properties by the method of active deformation at a constant rate is described in [11].

The experimental results for structural state (I) are shown in Figure 2 with a series of compression deformation diagrams $\tau \left(\epsilon ;T\right)$ for the coordinates “shear stress τ—strain ε” at a given strain rate $\dot{\epsilon }$ = 4·10⁻⁴ s⁻¹.

It was previously established that the plastic deformation of the alloy under study is determined by the conservative movement of complete dislocations in the {111}<110> slip system, which is typical of fcc crystals.

The deformation diagrams in Figure 2 at $\epsilon <0.1$ have a three-stage shape, typical of metallic polycrystals, in which the lattice symmetry of individual grains allows the existence of easy slip systems. The uniaxial compressive or tensile deformation of such materials begins from the elastic stage, according to Hooke’s law:$\tau \left(\epsilon \right)=E\epsilon$ and $\frac{d\tau \left(\epsilon \right)}{d\epsilon }=E$. The second stage is the beginning of plastic deformation in grains that are most favorably oriented with respect to the direction of the deforming stress, with the gradual involvement of other grains in this regime and a decrease in the derivative $\frac{d\tau \left(\epsilon \right)}{d\epsilon }<E$. The third stage is the plastic deformation of all grains in a stationary mode with a steady-state value of $\frac{d\tau \left(\epsilon \right)}{d\epsilon }=const\ll E$; this is called the “stage of linear strain hardening”.

Analysis of the change in the derivative $\frac{d\tau \left(\epsilon \right)}{d\epsilon }$ at the initial stages of the deformation diagram showed (inset in Figure 2) that the transition from the second to the third stage occurs at ε ≈ 0.02 = 2%; therefore, for this HEA we will consider stress of ${\tau }_2\left(T,\dot{\epsilon }\right)=\tau \left(\epsilon =0.02;T,\dot{\epsilon }\right)$ as the yield stress. Figure 3a shows the values, ${\tau }_2\left(T\right)={\tau }_2\left(T,\dot{\epsilon }=4\cdot {10}^{-4} s^{-1}\right)$, obtained from the strain diagrams in Figure 2.

During the process of active deformation at a given temperature, the stress increment $\Delta {\tau }_2\left(T\right)$ was also recorded with the strain rate $\stackrel{.}{\epsilon }$ increasing by 4.4 times from 4 × 10⁻⁴ s⁻¹ to 1.8 × 10⁻³ s⁻¹. At deformation $\epsilon =0.02$, the strain rate sensitivity $\gamma \left(T\right)$ of the conditional yield strength ${\tau }_2$ and the activation volume $V\left(T\right)$ of the plastic deformation process were determined (Figure 3):

$$\gamma \left(T\right)=\frac{\Delta {\tau }_2\left(T\right)}{\Delta \ln \dot{\epsilon }}, V\left(T\right)=kT\frac{\Delta \ln \dot{\epsilon }}{\Delta {\tau }_2\left(T\right)}=\frac{kT}{\gamma \left(T\right)}, A=-T\left[\frac{\Delta {\tau }_2\left(T\right)}{\Delta T}\right]{\left[\frac{\Delta {\tau }_2\left(T\right)}{\Delta \ln \dot{\epsilon }}\right]}_T^{-1},$$

(8)

where k is Boltzmann’s constant.

4. Low-Temperature Dislocation Processes in HEA Al_0.5CoCrCuFeNi

The alloy under study in states (I) and (II) has the morphology of a polycrystalline with an fcc lattice. Therefore, it is natural to assume that the features of the initial stage of plastic deformation and acoustic relaxation resonances in this alloy are due to the dynamics and kinetics of dislocation processes similar to low-temperature dislocation processes in polycrystals of monatomic materials with an fcc structure [14,19,20,21,22,23,24,25,26,27]. Differences in the atomic structure and morphology of grain boundaries in HEAs and simple metals must be taken into account only when interpreting experimental results obtained under conditions of sufficiently high temperatures, when their acoustic and mechanical properties are significantly influenced by the processes of thermally activated diffusion transformation of grain boundaries of polycrystals, in particular, the absorption and generation of dislocations that determine plastic deformation.

The interpretation of the laws of dislocation plasticity and the influence of dislocations on the acoustic properties of metals is based on the idea of the presence of easy slip planes in their structure and the specificity of the nucleation and movement of dislocations in these planes [28,29]. Currently, experimental methods for observing such processes have been developed, as well as theoretical descriptions of the results of these experiments based on concepts of the dynamics and kinetics of thermally activated and quantum motion of dislocations in easy slip planes through various barriers, taking into account their inhibition not only by barriers but also by quasiparticles—conductivity electrons and phonons [12,14,18].

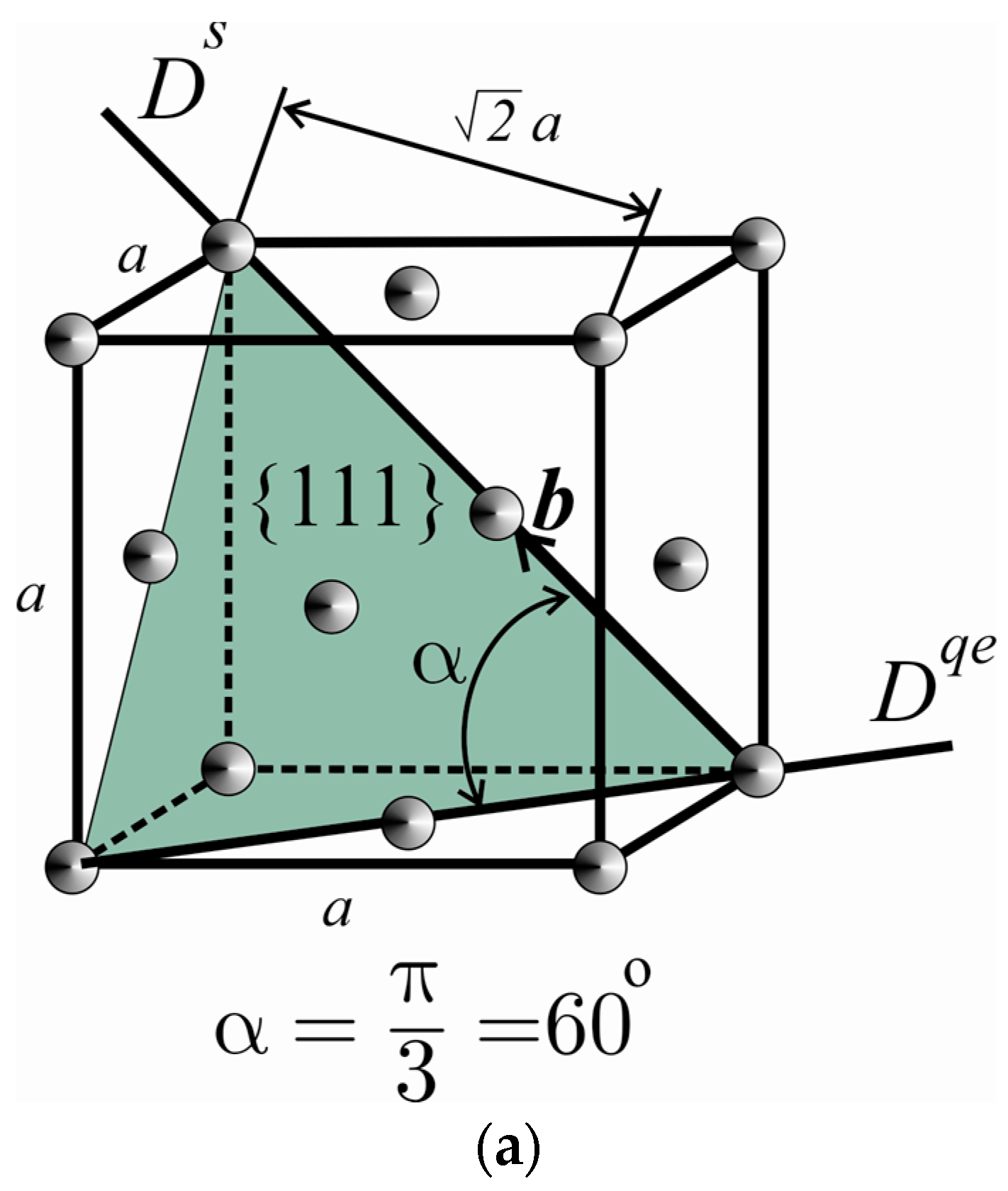
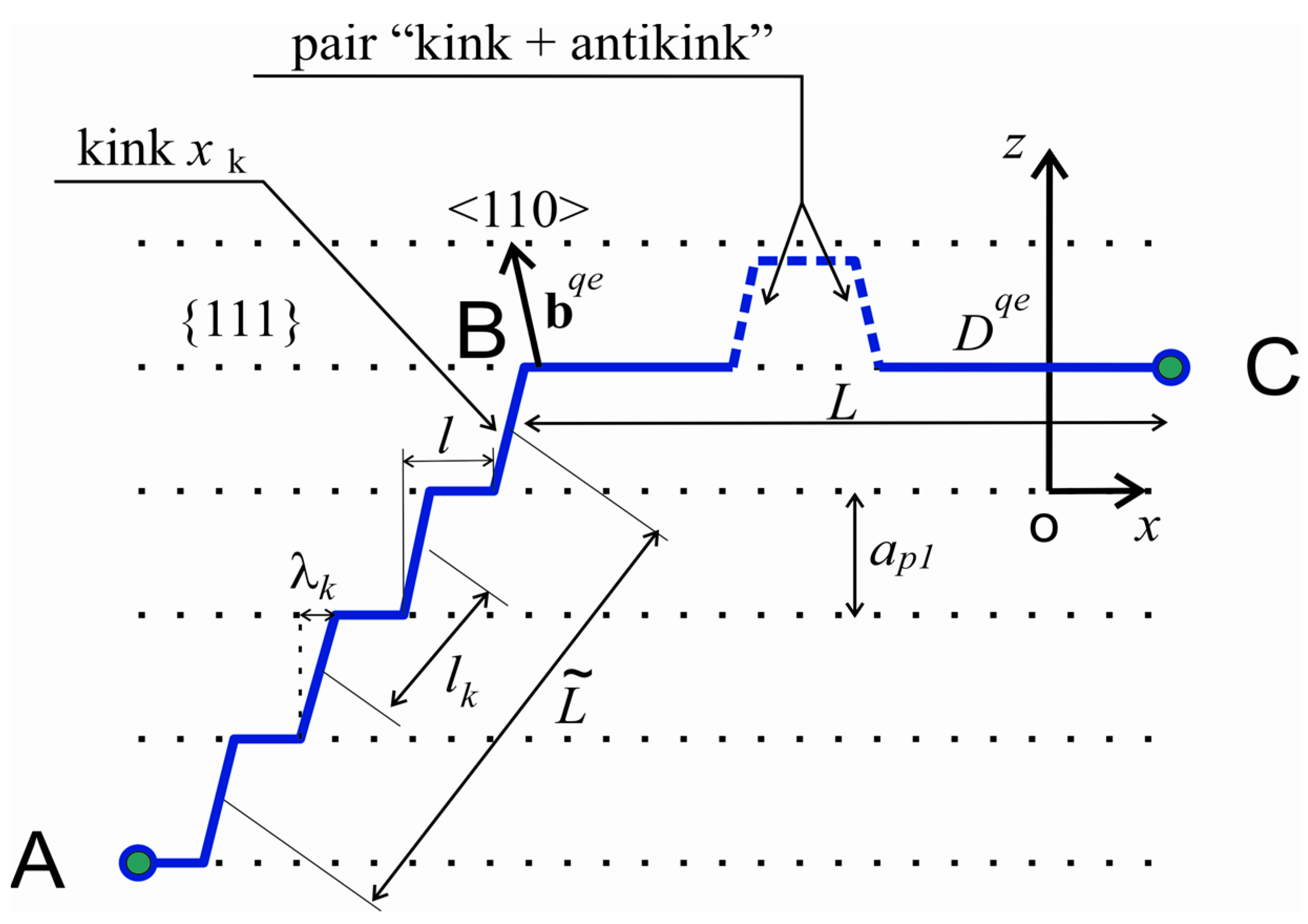
4.1. Models of Dislocation Relaxers

Let us use the algorithm [14,18] for analyzing mechanical spectroscopy data, which allows us to establish the microscopic mechanism of relaxation resonances and obtain estimates for the parameters of elementary relaxers based on an analysis of the temperature dependences $Q_{\exp }^{-1}(T)$ and $E_{\exp }\left(T\right)$ obtained in experiments at one fixed value of the sample oscillation frequency ${\omega }_r=2\pi f_r$.

Since the bulk of the samples of the studied alloy, both in state (I) and state (II), consist of a material with an fcc lattice, it is natural to assume that the observed acoustic relaxation resonances in this alloy are determined by mechanisms that are similar to the resonances in metals with an fcc structure. Such resonances are interpreted as a consequence of the interaction of elastic vibrations of the sample with a system of dislocation relaxers, since they are observed only after preliminary plastic deformation of the samples. On the temperature dependence of internal friction, they correspond to Bordoni peaks in the range 20 K < T < 100 K [21,22,23,24] and Hasiguti peaks in the range 100 K < T < 200 K [30]. The positions of these peaks T_p($\omega$) on the temperature axis depend on the vibration frequency $\omega$ and differ for different metals.

In fcc crystals at the initial stage of deformation, dislocation plastic sliding predominantly occurs along close-packed <110> directions and {111} planes (Figure 4). In the {111}<110> slip system, there are two types of rectilinear dislocations with the Burgers vector b whose lines $D^{qe}$ and $D^s$ are oriented along the directions $ox$ of dense packing. But for $D^{qe}$, the vector $b^{qe}$ has a quasi-edge (close to the edge) orientation, and for $D^s$ the vector ${\mathbf{b}}^s$ has a purely s screw orientation: the angle between the vector $b^{qe}$ and the unit $\tau$ of the dislocation line has the value $\alpha ={60}^{°}$, and the angle between ${\mathbf{b}}^s$ and $\tau$ is equal to zero, while $\left|b^{qe}\right|=\left|b^s\right|=\left|b\right|=\frac{\sqrt{3}}{2}=a_0$; $a_0$ is the distance between the nearest nodes.

To move lines in the transverse direction, the movements of rectilinear dislocation lines in the transverse direction oz are controlled by the first kind of Peierls lattice potential relief with period $a_{p1}$, but the height of the barriers for this relief and the corresponding Peierls critical stress values ${\tau }_{p1}^s$ and ${\tau }_{p1}^{qe}$ for pure screw dislocations are significantly greater than those for quasi-edge (${\tau }_{p1}^s\gg {\tau }_{p1}^{qe}$).

When such dislocations nucleate and move in real materials with structural defects on the surface and in the bulk, the formation of only straight configurations of dislocation lines is unlikely [31]. At the early stages of plastic deformation, a set of curved dislocation segments is formed (see Figure 5) with ABC configurations between the attachment points, which consist of shorter fragments AB and BC with significantly different crystal geometric and dynamic properties. Straight-line segments of the dislocation line BC with a length $L$ are oriented along the directions of dense packing and are located in the valleys of the Peierls relief, and fragments AB with a length $\tilde{L}$ consist of chains of kinks connecting short straight-line segments of dislocation lines in neighboring valleys of the relief. The self-energy of an individual kink also has a periodic component if its center $x_k$ moves along the direction of close packing parallel to the axis $ox$: this is called the secondary Peierls relief. The period of this relief is equal to the minimum distance between nodes $a_{p2}=a_0$ and the height of the barriers; the values of critical stresses ${\tau }_{p2}^s$ and ${\tau }_{p2}^{qe}$ are different for $D^{qe}$ and $D^s$ dislocations (${\tau }_{p2}^s\ll {\tau }_{p2}^{qe}$). The ABC segment has the properties of a two-mode dislocation relaxer, which consists of fragments $L$ and $\tilde{L}$. The significant difference in the crystal geometric and energy characteristics of the fragments also determines the difference in the dynamic and relaxation properties of these components $L$ and $\tilde{L}$ of the relaxer during its interaction with the elastic vibrations of the sample.

It is known that the elementary relaxers for the Bordoni and Hasiguti peaks are fragments of dislocation lines in easy slip systems {111}〈110〉 of fcc metals, which are excited by elastic vibrations [27,30]. In the proposed model of a two-mode dislocation relaxer, the role of such fragments is played by its components BC (length L) and AB (length $\tilde{L}$). It is assumed that their ends A, B and C are fixed by local defects in the lattice structure, which prevent the movement of the dislocation line in the slip plane.

Bordoni peaks were interpreted by Seeger [25,26,27] as being a result of the thermally activated nucleation of paired kinks on straight segments of dislocation lines L located in the valleys of the Peierls relief (Figure 6a).

For Hasiguti peaks, Koiwa and Hasiguti [30] considered the thermally activated detachment of a dislocation line segment $L=l_1+l_2$ from an individual point defect (impurity atom, vacancy, radiation defect, etc.) as an elementary relaxation process (Figure 6b). It has been established that vibrations of a chain of geometric kinks on a segment of a dislocation line with fixed ends are described by the equation of vibrations of a segment of a dislocation string [29,31].

4.2. Thermal Activation and Statistical Analysis of the Dislocation Contribution to Acoustic Relaxation

A separate elementary statistically independent process of thermally activated excitation of a dislocation relaxer is characterized by a relaxation time, which depends on temperature according to the Arrhenius law:

$$\theta \left(T\right)={\theta }_0\exp \left(\frac{U_0}{k_{B}T}\right),$$

(9)

where $U_0$ (activation energy) and ${\theta }_0$ (effective period of attempts) are determined by the crystal geometric and energy characteristics of a particular relaxer in a particular crystal. The ${\theta }_0$ has a weak power-law dependence on temperature which can be neglected against the background of the exponential dependence of the second factor at low temperatures kT<<$U_0$.

The temperature–frequency dependence of internal friction, caused by a system of relaxers with the same values of parameters $U_0$ and ${\theta }_0$, is described by the equation

$$Q_R^{-1}\left(T,\omega \right)=C_r{\Delta }_{0}F\left(\omega \theta \right),$$

(10)

where ${\Delta }_0$ and $C_r$ are, respectively, the effective specific contribution of an individual relaxer and its concentration, and $F\left(\omega \theta \right)$ is a positive definite function with a sharp maximum at $\omega \theta \simeq 1$. The form of the function $F\left(\omega \theta \right)$ and the position of its maximum on the temperature axis $T_p\left(\omega \right)$ depend on the nature of the relaxers. Most of them belong to the class of Debye relaxers, for which thermal activation occurs simultaneously in the forward and reverse directions with respect to the exciting voltage; the Seeger relaxation meets this criterion and is a special case of the Debye relaxation. But in the Koiwa–Hasiguti process, thermal activation stimulates the excitation of relaxers only in the forward direction, and their return to the initial unexcited state occurs under the action of the linear tension force of the dislocation segments. This results in two different expressions for the function $F\left(\omega \theta \right)$ [18,30]:

$$F^D\left(x\right)=\frac{x}{1+x^2}, F^{K-H}\left(x\right)=\frac{x^2}{2\left(1+x^2\right)}\left[1-\exp \left(-\frac{2\pi }{x}\right)\right], x=\omega \theta$$

(11)

For relaxation processes of both types, the function $F^{D,K-H}\left(x\right)$ vanishes at $x\to 0$ and $x\to \infty$, but has a sharp maximum at $x_m^D=1$ and $x_m^{K-H}=2.67$, respectively. If the value of the oscillation frequency $\omega$ is fixed, then for a system of identical relaxers with parameters $U_0$ and ${\theta }_0$ internal friction $Q_R^{-1}\left(T,\omega \right)$ on the temperature axis has a sharp maximum (peak) at temperature $T_p^{D,K-H}\left(\omega \right)$:

$$T_p^{D,K-H}\left(\omega \right)=\frac{U_0}{k_B{\alpha }^{D,K-H}}; {\alpha }_D=-\ln \omega {\theta }_0, {\alpha }_{K-H}=-\ln \frac{\omega {\theta }_0}{2.67}\approx 1-\ln \omega {\theta }_0$$

(12)

The estimates for parameters $U_0$, ${\theta }_0$, $C_r{\Delta }_0$ were obtained:

• for Seeger relaxers,

$$U_0\sim 0.1\mathrm{eV}, {\theta }_0\sim {10}^{-11}°\mathrm{s} \mathrm{and} C_r{\Delta }_0\sim {10}^{-1}{\rho }_L{L}^3,$$

(13)

where $L$ is the length of a straight dislocation segment in the Peierls relief valley, and ${\rho }_L$ is the number of such segments per unit volume;

• for Koiwa–Hasiguti relaxers,

$$U_0\sim \left(0.3÷0.5\right)\mathrm{eV}, {\theta }_0\sim {10}^{-13}°\mathrm{s} \mathrm{and} C_r{\Delta }_0\sim {10}^{-1}{\rho }_L{L}^3,$$

(14)

where $L$ and ${\rho }_L$ are, respectively, the length and volume density of dislocation segments breaking away from an individual point defect.

The action of the relaxation process is accompanied by a decrease in the dynamic modulus of elasticity by the amount $E_R\left(T,\omega \right)=E_R\left(\omega \theta \right)$. In this case $E_R\left(\omega \theta \to \infty \right)=0$, and a decrease in ωθ lead to a monotonic increase in $E_R(T,\omega )$ to $E_{R0}=E_R\left(\omega \theta \to 0\right)$.

Let us note two differences between the Debye and Koiwa–Hasiguti processes:

• In [14], it is shown that these processes correspond to different values of the ratio of the peak height $\max Q_R^{-1}\left(\omega \theta \right)$ to the step height $E_{R0}=E_R\left(\omega \theta \to 0\right)-E_R\left(\omega \theta \to \infty \right)$ on the temperature–frequency dependences of the contributions of these relaxation processes to the internal friction and dynamic elasticity of materials:

  $${\left[\frac{E_0}{E_{R0}}\cdot \max Q_R^{-1}\right]}^D=0.5, {\left[\frac{E_0}{E_{R0}}\cdot \max Q_R^{-1}\right]}^{K-H}\approx 0.13$$

  (15)
• In [18], it was established that the parameter K determined by relation (7) does not depend on temperature and U₀, and its frequency dependence is described by monotonic functions $K=K_{D,K-H}\left(\omega {\theta }_0\right)$, while

  $$K_D\left(\omega {\theta }_0\right)>1.2, K_{K-H}\left(\omega {\theta }_0\right)<1.2, \omega {\theta }_0<{10}^{-3}$$

  (16)

Relations (9)–(16) describe the acoustic relaxation resonance in an ideal crystal, caused by a system of similar dislocation relaxers with the same values for the parameters of an individual relaxer $U_0$, ${\theta }_0$ and ${\Delta }_0$. In real HEAs, there is a complex system of random structural defects or inhomogeneities and the internal stress fields they create. Therefore, the parameters of the same type of relaxers $U_0$, ${\theta }_0$ and ${\Delta }_0$ acquire random additives in different areas of the sample, which leads to a statistical broadening of peaks and steps in the dependence graphs of $Q_R^{-1}\left(T,\omega \right)$ and $E_R\left(T,\omega \right)$; it also leads to a shift in the temperature $T_p\left(\omega \right)$ of their localization. In HEAs, random inhomogeneities are associated not only with the chaotic distribution of defects but also with distortions of unit cells in the crystal lattice by random configurations of alloy components and differences in their atomic radii [32].

Following [14,18], we will consider $U_0$, ${\theta }_0$ and ${\Delta }_0$ as random variables with their corresponding distribution patterns. But at low temperatures $k_{B}T\ll U_0$, it is enough to take into account only statistical deviations in the activation energy $U$ from $U_0$ and with exponential accuracy we can neglect the scatter of parameters ${\theta }_0$ and ${\Delta }_0$. In this case, the contribution of relaxers to internal friction $\langle Q_R^{-1}\left(T,\omega \right)\rangle$ and the dynamic modulus of elasticity $\langle E_R\left(T,\omega \right)\rangle$ will be determined by averaging the initial equations for the dependencies $Q_R^{-1}\left(T,\omega \right)$ and $E_R\left(T,\omega \right)$ with a quasi-Gaussian distribution function $P\left(U;U_0,D\right)$ for the activation energy, in which the role of parameters is played by activation energy $U_0$ and its dispersion characteristics $D$ [12,14,18].

After averaging, relation (10) takes the following form:

$$\langle Q_R^{-1}\rangle =Q_R^{-1}\left(T,\omega ;{\theta }_0,U_0,D\right)=C_r{\Delta }_0{\displaystyle \underset{0}{\overset{\infty }{\int }}dUP\left(U;U_0,D\right)F^{D,K-H}\left(\omega \theta \right)},$$

(17)

The statistical spread of the activation energy does not affect the form of functions $K_{D,K-H}\left(\omega {\theta }_0\right)$ and preserves (16), which allows us to establish a physical model of a dislocation relaxer.

The statistical spread of the activation energy leads to a decrease in the height of the internal friction peak $\max \langle Q_R^{-1}\rangle <\max Q_R^{-1}$ and an increase in its width; it also increases the width of the step on the temperature dependence of the module $\langle E_R\left(T,\omega \right)\rangle$, but it maintains its height $E_{R0}$. Therefore, at a small value of the parameter $D\ll U_0$, relation (15) is approximately preserved and can be used to select a relaxer model.

4.3. Dislocation Mechanism of the Internal Friction Peak $T_p=228 \mathrm{K}$ (Analogue of the HasigutiPeak)

Comparing the resonance parameters (Table 2) near temperature $T_p=228 \mathrm{K}$ with relations (15) and (16), we come to the conclusion that they correspond to the Koiwa–Hasiguti process, i.e., thermally activated separation of the dislocation segments from point defects:

$$K=0.83<1.2,\hspace{1em}\hspace{1em}\frac{E_0}{E_{R0}}\cdot \max Q_R^{-1}\approx 0.1$$

In the present alloy, the role of point defects can be played by nanoclusters of several atoms of one of the chemical elements of the alloy, as in (3), or traditional point defects of the crystal structure—vacancies and interstitial atoms. Therefore, for a theoretical description of resonance, we use (17), assuming that $F\left(\omega \theta \right)=F^{K-H}\left(\omega \theta \right)$, and in the future we will omit the index “K-H”. In [14], relations were obtained that allow one to estimate the values of the parameters $U_0$, ${\theta }_0$, ${\Delta }_0$ and $D$ if we use the experimentally recorded values of the resonance characteristics $T_P$, $T^{(-)}$, $T^{(+)}$, $\max Q_R^{-1}$, $E_{R0}$ and $K$ (see Table 2):

$${\left(\alpha -1\right)}^{1.43}=\frac{10}{K-0,7}, \omega {\theta }_0=\exp \left(1-\alpha \right);$$

$$C_r{\Delta }_0=2.5\max Q_R^{-1}\cdot \exp \left(\frac{7\sqrt{2}\alpha D}{56\sqrt{2}D+20U_0}\right)$$

(18)

$$U_0=8k_B{\alpha }^2\cdot \left(2T_p-T^{(-)}-T^{(+)}\right), D=\frac{20k_B\alpha }{11\sqrt{2}}\cdot \left(9T^{(+)}+10T^{(-)}-19T_p\right)$$

(19)

Substituting the values of the resonance characteristics from Table 2 into (18) and (19),we obtain estimates for the relaxer parameters $U_0$, ${\Delta }_0$ and ${\theta }_0$ (

Table 3. Parameters of dislocation relaxers for the peak of internal friction $T_p$ and its satellite $T_{ps}$.

${\mathit{\theta }}_0$	${\mathit{U}}_0$	$\mathit{D}$	${\mathit{C}}_{\mathit{r}}{\mathbf{\Delta }}_0$	${\mathit{\theta }}_0^{\mathit{s}}$	${\mathit{U}}_0^{\mathit{s}}$	${\mathit{D}}^{\mathit{s}}$	${\mathit{C}}_{\mathit{r}}^{\mathit{s}}{\mathbf{\Delta }}_0^{\mathit{s}}$
2 × 10−13 s	0.43 eV	0.01 eV	4 × 10−4	4 × 10−11 s	0.07 eV	0.01 eV	1 × 10−4

), which allows us to calculate the theoretical profile $\langle Q_R^{-1}\rangle$ of the internal friction peak (dashed line in Figure 1).

The obtained values of activation energy $U_0$ ≈ 0.4 eV and the effective oscillation period ${\theta }_0$ ≈ 10⁻¹³ s are typical for Koiwa–Hasiguti relaxers in simple metals with an fcc structure. A small value of $D\sim {10}^{-2}{U}_0$ indicates the absence of significant structural distortions in state (II), which is due to long-term annealing, which was used to form this structural state.

Using (14) and assuming $C_r\approx {\rho }_L$ we obtain an estimate ${\Delta }_0\sim {10}^{-1}{L}^3$ for the contribution of one relaxer to internal friction and the decreasing of the elastic modulus. Let us assume that the role of local centers of pinning of dislocation segments is played by small atomic clusters with a distance between them of the order of several nanometers: they are recorded in state (II) using electron microscopy methods [13]. Then, when estimating the length $L$, we can take twice the distance between clusters $L$~10 nm, and the data given in Table 2 correspond to the volume density of relaxers $C_r={\rho }_L\sim 4\cdot {10}^{21}$ m⁻³. For the dislocation density ${\Lambda }_d=l{\rho }_L$ (total length of dislocation segments per unit volume), which effectively interacts with elastic vibrations of the sample, we obtain the estimate ${\Lambda }_d\sim 4\cdot {10}^{13}$ m⁻².

4.4. Dislocation Mechanism of Internal Friction Peak $T_{ps}=190 \mathrm{K}$ (Analogue of Bordoni Peak)

A satellite peak with a maximum at $T_{ps}=190 \mathrm{K}$ is observed on the low-temperature branch of the main peak $T_p=228 \mathrm{K}$. To isolate it and perform the subsequent analysis, it is necessary to subtract the contribution of theoretical dependence $\langle Q_R^{-1}\rangle$ from the experimentally observed relaxation $Q_{\exp }^{-1}\left(T\right)$ for the values of the relaxation parameters $U_0$, ${\theta }_0$ and ${\Delta }_0$ corresponding to the main peak (Table 3). The results of this procedure are shown in the inset in Figure 1b.

Using the statistical and thermal activation analysis described above, we come to the conclusion that the peak $T_{ps}=190 \mathrm{K}$ is due to Seeger relaxation, and the estimates for its parameters are given in Table 3.

We will carry out a theoretical description of the movement of a dislocation line in the first kind of Peierls relief in the case of a sinusoidal relief, when the linear energy density $W\left(z_d\right)$ of an element of a dislocation line has the following form:

$$W\left(z_d\right)=\Gamma +W_0{\sin }^2\frac{\pi z_d}{a_p}-b\sigma z_d, W_0=\frac{b{a}_p}{\pi }{\tau }_{p1}$$

(20)

where $\Gamma$ is the energy per unit length of a dislocation in the continuum approximation (linear tension); $W_0$ and ${\tau }_{p1}$—magnitude of barriers and critical stress for Peierls relief of the first type; $\tau ={\tau }_{xz}$—shear stress component in the slip plane; $z_d$—coordinate of the dislocation line element along the axis $oz$ (Figure 5).

The equation of motion of a string with linear mass density $M$ in potential (20) has soliton solutions in the form of kinks, and their characteristics are related to the parameters of the potential and dislocation using the following relationships [14]:

$${\lambda }_k=a_p\sqrt{\frac{2\Gamma }{\pi b{a}_p{\tau }_{p1}}}, m_k=\frac{2a_{p}M}{\pi }\sqrt{\frac{2b{a}_p{\tau }_{p1}}{\pi \Gamma }},$$

$${\epsilon }_k=m_k{c}_t^2, {\theta }_{p1}=\frac{\pi {\lambda }_k}{c_t}, c_t=\sqrt{\frac{\Gamma }{M}}.$$

(21)

where ${\lambda }_k$, $m_k$, ${\epsilon }_k$ are the width, mass and energy of the kink, respectively; ${\theta }_{p1}$ is the period of natural oscillations of a rectilinear segment in the relief valley and $c_t$ is the characteristic value of the speed of transverse sound vibrations in the crystal.

The average time for the thermallyactivated nucleation of kink–antikink pairs on a straight segment of a dislocation line (Figure 6a) is described by the Arrhenius law (9) with activation energy $U \approx 2{\epsilon }_k$ and attempt period ${\theta }_0$ ≈ ${\theta }_{p1}$. The interaction of elastic vibrations $\tau \ll {\tau }_{p1}$ with such a process is one of the mechanisms of relaxation resonance [21]. If the sample contains the volume density ${\rho }_L$ of straight dislocation segments with length $L$, then their contribution to the dynamic modulus of elasticity and vibration decrement is described, without taking into account the statistical scatter of parameters, by Equations (9)–(12), in which

$$U=U_0\simeq 2{\epsilon }_k, {\theta }_0\approx {\theta }_{p1},$$

(22)

We assume that the discussed resonance $T_{ps}=190 \mathrm{K}$ in the studied HEA is caused by the Seeger process; therefore, according to (13),

$$C_r{\Delta }_0={\left(C_r{\Delta }_0\right)}_L\approx {10}^{-1}{L}^3{\rho }_L.$$

(23)

The comparison of the values of parameters $U_0^s$ and ${\theta }_0^s$ obtained as a result of the analysis of experimental data (see Table 3) with the equations of the theory, seen in (20)–(23), does not lead to contradictions and allows us to obtain estimates for the characteristics of dislocations responsible for resonance.

From (21) and (22), the next relations are as follows:

$$U_0=2c_t^2{m}_k, \frac{U_0}{{\theta }_{p1}}=\frac{4c_{t}b{a}_p}{{\pi }^2}{\tau }_{p1},$$

$$U_0{\theta }_{p1}=\frac{8a_p^2}{\pi }\sqrt{\Gamma M}=\frac{8a_p^2}{\pi c_t}\Gamma =\frac{8c_t{a}_p^2}{\pi }M$$

(24)

The parameters necessary for further assessments of the studied HEA have the following values [12,19]:

$$b=a_0=2.54\cdot {10}^{-10} \mathrm{m}, a_p=\frac{\sqrt{3}}{2}{a}_0\approx 0.87a_0\approx 2.2\cdot {10}^{-10} \mathrm{m};$$

$$\rho =7.98\cdot {10}^3 \frac{\mathrm{kg}}{{\mathrm{m}}^3},$$

$$G=\frac{E}{2\left(1+\nu \right)}=0.94\cdot {10}^{11} \mathrm{Pa}, c_t=\sqrt{\frac{G}{\rho }}\approx 3.4\cdot {10}^3 \frac{\mathrm{m}}{\mathrm{s}}$$

(25)

where $G$ is the shear modulus, Poisson’s ratio $\nu \approx 0.22$ [33] and $\rho$ is the density. The resulting estimate $c_t=\sqrt{\frac{G}{\rho }}\approx 3.4\cdot {10}^3 \frac{\mathrm{m}}{\mathrm{s}}$ is in good agreement with the data [33].

Substituting the values of the activation energy $U_0=U_0^s\approx 11.2\cdot {10}^{-21}$ J, the period of attempts ${\theta }_0^s\simeq 4\cdot {10}^{-11}$ s and ${\left(C_r{\Delta }_0\right)}_L\le 1\cdot {10}^{-4}$ for resonance $T_{ps}=190 \mathrm{K}$ leads to the following estimates for the parameters of the dislocation model under consideration:

$$m_k\approx 5·{10}^{-3}{m}_a\approx 5·{10}^{-28} \mathrm{kg}, {\lambda }_k\approx 40a_0\approx 1·{10}^{-8} \mathrm{m}$$

$${\tau }_{p1}\approx 3.6\cdot {10}^6 \mathrm{Pa}\approx 4\cdot {10}^{-5}G,$$

$$M\approx 1.1\cdot {10}^{-15} \frac{\mathrm{kg}}{\mathrm{m}}\approx 2.1\rho b^2, \Gamma \approx 12.4\cdot {10}^{-9} \frac{\mathrm{J}}{\mathrm{m}}\approx 2.1G{b}^2, {\rho }_L{L}^3\le {10}^{-3};$$

(26)

where the mass $m_k$ and width ${\lambda }_k$ of the kink are compared with the average mass $m_a$ of an atom of the studied alloy, the minimum interatomic distance $a_0$ and the Peierls critical stress ${\tau }_{p1}$ with the shear modulus $G$.

The good correspondence of the estimates for parameters $\Gamma$ and $M$ with their estimates of $\Gamma \approx G{b}^2$ and $M\approx \rho b^2$ in the continuum theory of dislocations is a serious argument in favor of the adequacy of the proposed model of the relaxation process $T_{ps}=190 \mathrm{K}$ for the experimentally recorded resonance properties.

4.5. Dislocation Processes of Low-Temperature Plastic Deformation

In the previous sections, an analogy was established and described between elementary dislocation processes that determine the low-temperature acoustic resonances of simple polycrystalline metals with an fcc atomic structure and the HEA Al_0.5CoCrCuFeNi, namely the thermal excitation of components of two-mode dislocation relaxers in an easy slip system {111}〈110〉. It is assumed that such two-mode relaxers (Figure 6) are formed in polycrystal grains during the preparation and primary processing of samples. It is natural to assume that in order to interpret the results of low-temperature mechanical tests of the HEA Al_0.5CoCrCuFeNi within the framework of dislocation concepts, the use of this analogy will also be appropriate and effective.

In modern physics of low-temperature plasticity [34], one of the central tasks is to elucidate the relative role of Peierls relief and local barriers (impurity and intrinsic interstitial atoms, vacancies and a number of other violations of the atomic structure with dimensions of atomic scales) in the processes of the movement of dislocations. When studying this problem, the ultimate goal is to interpret the yield stresses and the initial stages of plastic deformation.

During the low-temperature deformation of pure bcc metals in the stationary easy slip mode, it was established [35] that the kinetics of deformation are determined by the movement of dislocations in the {110} plane of the bcc structure through Peierls barriers according to the mechanism of nucleation and expansion of pair kinks as a result of the action of thermal or quantum fluctuations (a scheme of such a process is shown in Figure 6a). This mechanism corresponds to a large value of the yield stress $\approx {10}^{-3}G$ and its sharp increase with decreasing temperature, and the dependence shows a characteristic feature during the transition from small to large values of deforming stress, due to a change in the law of interaction of kinks. Impurity interstitial atoms at concentrations above 0.7at.% have a noticeable effect on the magnitude and temperature dependence of the yield stress of these metals [36].

In simple fcc metals, the Peierls barriers in the easy slip plane {111} are negligible, the yield stress is $\le {10}^{-5}G$ and the main obstacles to dislocation glide are local barriers created by substitutional impurities, which are overcome by dislocation strings due to thermal or quantum fluctuations (a diagram of such a process is shown in Figure 6b). Substitutional impurities in fcc metals are relatively weak barriers to dislocations; therefore, this mechanism corresponds to a less sharp increase in the yield strength when cooling samples than in the case of pure bcc metals.

At high concentrations of impurities (1 at.% and higher), the yield strength of simple fcc metals increases more sharply upon cooling and can acquire a characteristic low-temperature anomaly, namely a maximum in the dependence of the conditional yield strength, which arises due to the transition from a purely fluctuational to a fluctuation–inertial mechanism of dislocation motion through impurity barriers (unzipping effect) [34,37]. In this case, the ${\tau }_{0.2}$ decreases with decreasing temperature since some of the local obstacles are overcome by dislocations without activation. The condition for the inertial movement of dislocations is a high effective stress ${\tau }^{*}\left(T\right)=\tau -{\tau }_i$ ($\tau$—deformation stress, ${\tau }_i={\tau }_i\left(\epsilon ;T\right)$—long-range internal stress) and a low coefficient of dynamic friction of dislocations.

To describe the kinetics of plastic deformation during the purely thermally activated stationary motion of dislocations through a system of similar local obstacles, the Arrhenius relation is used, which determines the exponential dependence of the strain rate $\dot{\epsilon }$ on the deforming stress $\tau$ and temperature $T$:

$$\dot{\epsilon }={\dot{\epsilon }}_0\exp \left[-\frac{H\left({\tau }^{*}\right)}{kT}\right], {\tau }^{*}=\tau -{\tau }_i\left(\epsilon ;T\right);$$

(27)

where ${\dot{\epsilon }}_0$ is the pre-exponential factor, proportional to the frequency ${\theta }_0^{-1}$ of attempts to overcome obstacles and the volume density of elementary independent structural units, the activation of which determines the kinetics of the process (Figure 6), and $H\left({\tau }^{*}\right)$ is the effective energy (enthalpy) of activation. It is assumed that the power-law dependence ${\dot{\epsilon }}_0$ on stress and temperature in a purely thermally activated mode of dislocation motion is insignificant against the background of the exponential dependence of the second factor in (27). This dependence should be taken into account only when transitioning to the thermoinertial mode of dislocation motion, taking into account the unzipping effect.

The dependence $H\left({\tau }^{*}\right)$ is determined by the force law of interaction of a dislocation with the center of pinning (obstacle), as well as the statistics of the distribution of obstacles along the dislocation. In most cases [37],

$$H\left({\tau }^{*}\right)=H_0{\left[1-{\left(\frac{{\tau }^{*}}{{\tau }_c}\right)}^p\right]}^q,$$

(28)

where $H_0$ is the energy parameter of the dislocation–barrier interaction (enthalpy of activation at ${\tau }^{*}$= 0); $0\le p\le 1$ and $1\le q\le 2$ are parameters depending on the distribution of obstacles along the dislocation and the shape of the potential barrier created by the obstacle, where q depends on the shape of the barrier and p depends on the properties of the barrier and the statistics of the distribution of barriers.

It is obvious that (27) can only be used at the stage of well-developed plastic deformation of the material at $\frac{d\tau \left(\epsilon ;T,\dot{\epsilon }\right)}{d\dot{\epsilon }}\ll E$, when the rate of plastic deformation significantly exceeds the rate of elastic deformation. From (27) and (28), it follows that

$$\tau (\epsilon ;T,\dot{\epsilon })={\tau }_i\left(\epsilon ;T\right)+{\tau }_c{\left[1-{\left(\frac{T}{T_0}\right)}^{1/q}\right]}^{1/p},{\tau }^{*}\left(T\right)={\tau }_c{\left[1-{\left(\frac{T}{T_0}\right)}^{1/q}\right]}^{1/p},$$

(29)

$$\begin{gathered} {\left(\frac{\partial {\tau }^{*}}{\partial \ln \dot{\epsilon }}\right)}_T=\frac{{\tau }_c}{pqA}{\left(\frac{T}{T_0}\right)}^{1/q}{\left[1-{\left(\frac{T}{T_0}\right)}^{1/q}\right]}^{(1-p)/p}, T_0=\frac{H_0}{kA}, \\ A=\ln \left(\frac{{\dot{\epsilon }}_0}{\dot{\epsilon }}\right) \end{gathered}$$

(30)

According to (29) and (30), the stress ${\tau }^{*}\left(T,\dot{\epsilon }\right)$ decreases monotonically with increasing temperature, and the value ${\left(\frac{\partial {\tau }^{*}}{\partial \ln \dot{\epsilon }}\right)}_T$ reaches a maximum at $T_m=p^q{T}_0$ and becomes zero at T = 0 K and T = $T_0$.

It was shown [35] that additional features in the temperature dependences of the plasticity characteristics of metals can appear when the temperature dependences $E\left(T\right)=E_0\eta \left(T\right)$ of the elastic modulus are taken into account in (29) and (30) (see Section 3.1). In this case, the temperature dependence of the parameters τ_c, τ_i and $H_0$ will be determined by $\eta \left(T\right)$:

$${\tau }_c\left(T\right)={\tau }_{c0}\eta \left(T\right), {\tau }_i\left(T\right)={\tau }_{i0}\eta \left(T\right), H_0\left(T\right)=H_{00}\eta \left(T\right)$$

(31)

4.6. Low-Temperature Plasticity of the Present Alloy

The strong temperature dependence ${\tau }_2\left(T\right)$ (Figure 3) indicates the thermally activated nature of plastic deformation, while both Peierls barriers and local barriers can be controlling obstacles to the movement of dislocations.

The elementary act of plastic deformation in the first case is the thermally activated nucleation of a paired kink on a dislocation segment $L$ in the Peierls relief (Figure 6a); in the second case, it is the thermally activated overcoming of a local barrier by a dislocation segment $L=l_1+l_2$ (Figure 6b). As a result of the analysis of low-temperature acoustic resonances in the studied HEA, it was established that the Peierls stress ${\tau }_{p1}\approx 4\cdot {10}^6 \mathrm{Pa}$ for dislocations in the easy slip system is significantly less than the low temperature values of the yield strength ${\tau }_{0.2},{\tau }_2\approx \left(2÷3\right)\cdot {10}^8 \mathrm{Pa}\approx 50\cdot {\tau }_{p1}$. Consequently, the Peierls relief cannot have a significant effect on the kinetics of the low-temperature plastic deformation of this material; it can only be controlled by a sufficiently high volume of the density of local barriers.

The role of structural inhomogeneities that determine the thermally activated plastic deformation of HEAs can be played by clusters of atoms of one of the constituent elements of the alloy. Several adjacent atoms of an element with a relatively large atomic radius create local distortions of the crystal lattice and are a significant obstacle to dislocations. Such clusters were experimentally observed in [13] and the characteristic distance between them is several nanometers, i.e., for them, $L\approx 10 \mathrm{nm}$ (see Section 4.3).

To check the adequacy of the results of an experimental study of the alloy (Figure 3) for the assumption of the controlling influence of these local defects on the kinetics of its plastic deformation at low temperatures, we use the relations obtained from (29) and (30) with values $\epsilon =0.02$, $\dot{\epsilon }=4\cdot {10}^{-4}{ \mathrm{s}}^{-1}$ and ${\tau }_i\left(\epsilon =0.02;T\right)={\tau }_{i2}\left(T\right)$:

$${\tau }_2\left(T\right)={\tau }_{i2}\left(T\right)+{\tau }_c{\left[1-{\left(\frac{T}{T_0}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$q$}\right.}\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$p$}\right.},$$

$$\gamma \left(T\right)=\frac{{\tau }_c}{pqA}{\left(\frac{T}{T_0}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$q$}\right.}{\left[1-{\left(\frac{T}{T_0}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$q$}\right.}\right]}^{\frac{1-p}{p}}.$$

(32)

Parameter $A$ (Figure 3b) was obtained using experimental dependences ${\tau }_2\left(T\right)$, $\gamma \left(T\right)$ and relation (30).

The absence of deviations $A$ from the average value $\overline{A}\approx 19$ with temperature changes justifies the neglect of the weak temperature dependence of the parameter $\stackrel{.}{\epsilon }$ in (27) and it is one of the criteria for the applicability of relations (29)–(32) for describing the low-temperature thermally activated deformation of metals. Approximations (31) and (32) of the experimental data are shown with solid lines in Figure 3, and parameters ${\tau }_{ic}$, ${\tau }_c$, $p$, $q$, $T_0$ are given in

Table 4. Parameters of the dislocation theory of plasticity for the HEA Al_0.5CoCrCuFeNi in state (I).

$\mathit{p}$	$\mathit{q}$	${\mathit{\tau }}_{\mathit{i}2}$, MPa	${\mathit{\tau }}_{\mathit{c}}$, MPa	${\mathit{H}}_0$, eV	${\mathit{T}}_0$, K	$\mathit{A}$
0.6	1.1	170	104	0.65	400	19

.

The agreement between the analytical and experimental points in Figure 4 confirms the adequacy of the theoretical model used and allows us to speak about a single mechanism that controls thermally activated plasticity in the alloy under study in the studied temperature range at ε ≈ 2%. The activation energy in the absence of applied stress $H_0$ ≈ 0.5–1 eV is typical for processes in metals associated with the thermally activated movement of dislocations through local barriers [34].

The model parameters and algorithm [35] given in Table 4 for thermal activation analysis of the experimental results make it possible to obtain estimates for the parameters of local barriers and the distances between them in slip planes. When dislocations move through a network of randomly located local obstacles, various physical situations can occur, among which two limiting cases stand out. These cases correspond to the Mott–Labusch statistics [38], in which p = 1, and the Friedel statistics [28], in which p = 2/3. In our case, p ≈ 0.6, which better corresponds to the Friedel statistics. Therefore,

$$L\left({\tau }^{*}\right)={\left(\frac{2\Gamma S_0}{b{\tau }^{*}}\right)}^{1/3},$$

(33)

where S₀ is the average area per local obstacle. The stress of activation-free detachment of a dislocation from a barrier is determined by the condition

$$f_m=b{\tau }_{c}L\left({\tau }_c\right).$$

(34)

Using (33) and (34), we obtain an expression for the value of S₀, which allows us to estimate the density of local obstacles that control the movement of the dislocation

$$S_0=\frac{f_m^3}{2b^2\Gamma {\tau }_c^2}.$$

(35)

The value of q ≈ 1 indicates that the force barrier has steep slopes and its shape is close to rectangular in the range of values ${\tau }^{*}$ that were achieved in our experiments. Therefore, the width w of the force barrier will weakly depend on ${\tau }^{*}$, and for the value of the maximum force the following estimate will be true: $f_m=H_0/w$. Using this estimate and expression (35), we obtain the following:

$$S_0=\frac{H_0^3}{2b^2{w}^3\Gamma {\tau }_c^2}=\frac{H_0^3}{2b^5\Gamma {\tau }_c^2}{\left(\frac{b}{w}\right)}^3.$$

(36)

Using (36) and the values $H_0$ and ${\tau }_c$ from Table 1, we obtainthe estimate S₀ = 1.7∙10⁻¹⁷(b/w)³, m². Taking w~b, we obtain an upper estimate for the value S₀ = 261b², which corresponds to the distance between local obstacles in the sliding plane l = (S₀)^1/2 = 16b = 4.1 nm and $L=2l\approx 10 \mathrm{nm}$.

5. Conclusions

The analysis and physical interpretation, based on modern dislocation theory, of the results of a comprehensive experimental study [11,12] of the processes of plastic deformation and acoustic relaxation in the HEA Al_0.5CoCrCuFeNi made it possible to establish the following:

• The most important types of dislocation defects in the lattice structure of the alloy;
• The types of barriers that prevent the movement of dislocation lines (strings);
• Adequate mechanisms of thermallyactivated movement of various elements of dislocation strings through barriers under conditions of moderate and deep cooling;
• Quantitative estimates for the most important characteristics of dislocations and their interaction with barriers.