Machine-Learning-Assisted Design of Novel TiZrNbVAl Refractory High-Entropy Alloys with Enhanced Ductility
Abstract
:1. Introduction
2. Alloy Design and Experimental Methods
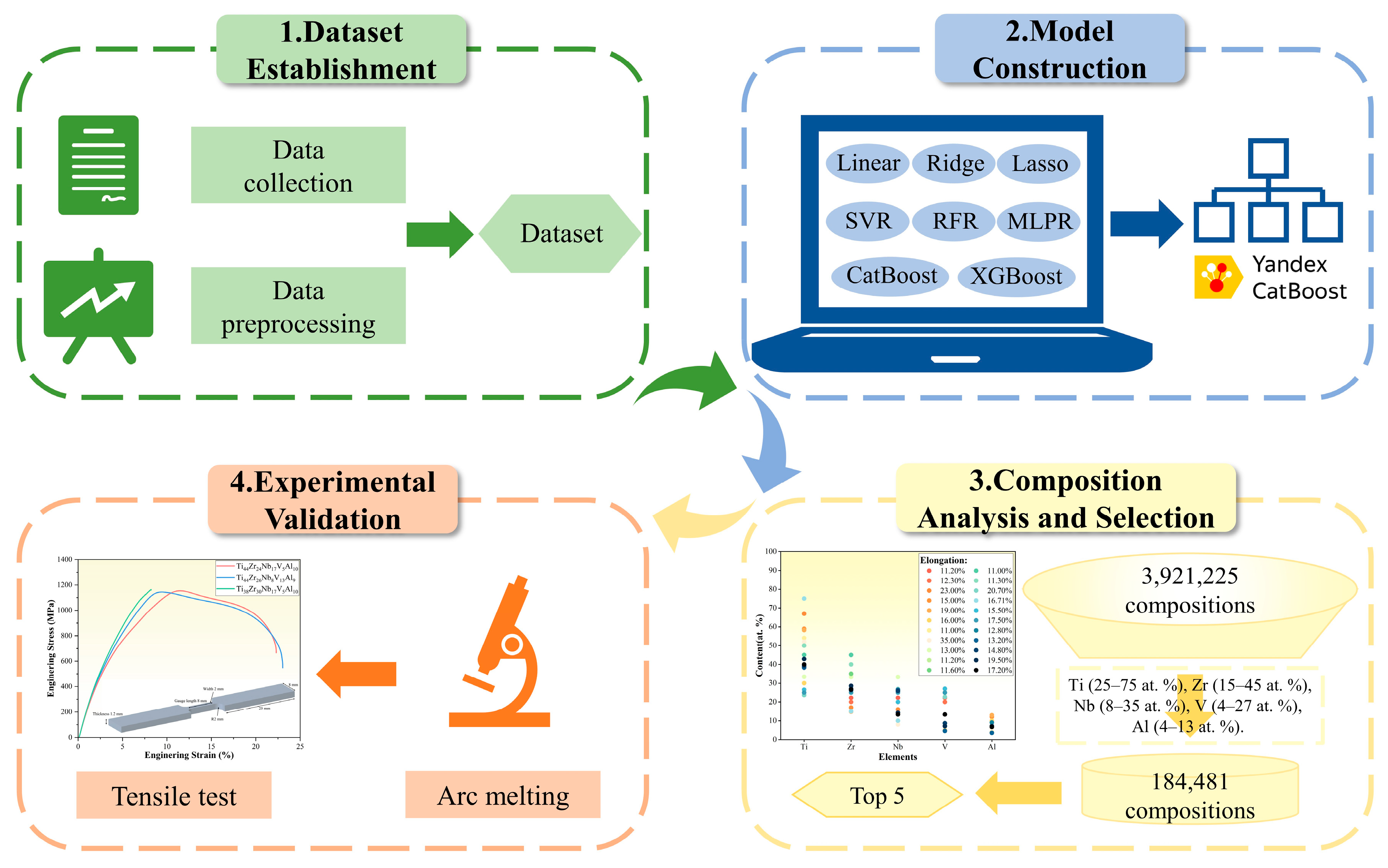
2.1. Dataset Establishment
- Average atomic size:where ci and ri are the atomic percentage and atomic radius of the ith element, respectively.
- Standard deviation on the atomic size:
- Average melting point of the contained elements:where Ti is the melting temperature of the ith element.
- Standard deviation on the melting point:
- Mixing enthalpy:where Hij and cj are the binary mixture enthalpy of the ith and jth elements and the atomic percentage of the jth element, respectively.
- Standard deviation on the mixing enthalpy:
- Mixing entropy:where kb is the Boltzmann constant (kb ≈ 1.380649 × 10−23 J/K).
- Pauling electronegativity:where is electronegativity of the ith element.
- Standard deviation on the Pauling electronegativity:
- Average VEC:where VECi is the number of valence electrons of the ith element.
- Standard deviation on the VEC:
2.2. Model Construction
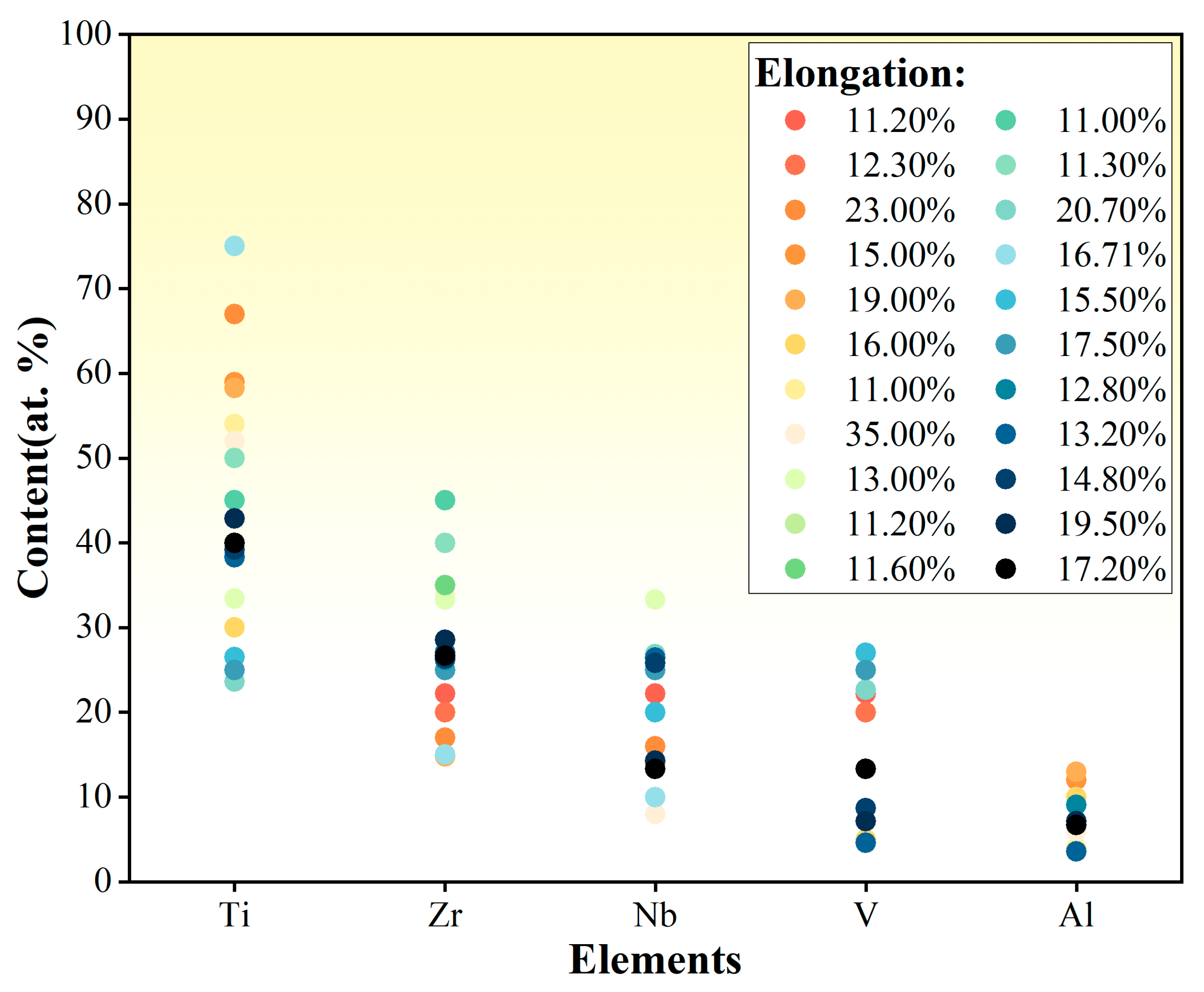
2.3. Composition Analysis and Selection
2.4. Experimental Validation
3. Results
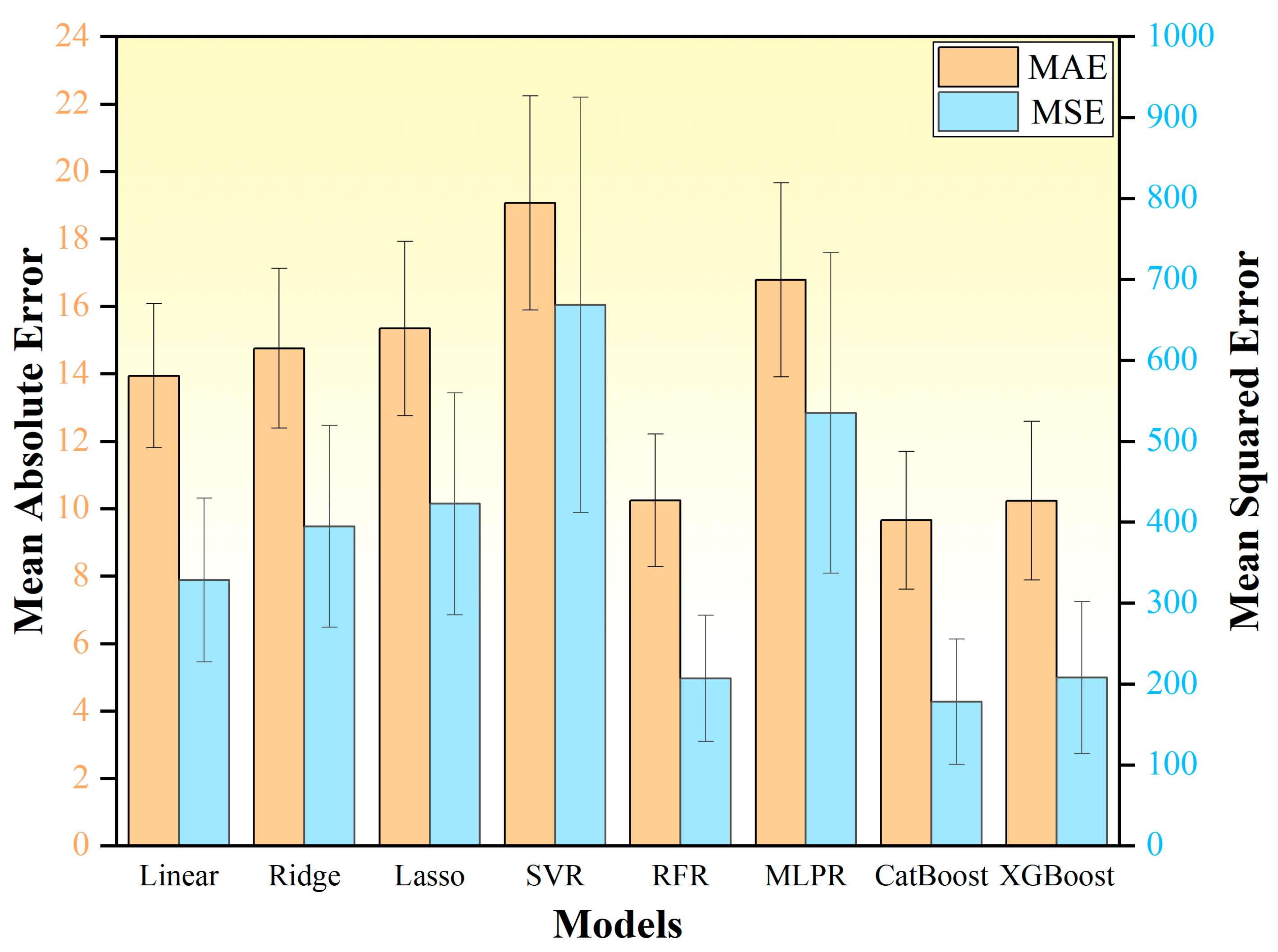
3.1. Machine Learning Results
3.2. Experimental Validation
4. Discussion
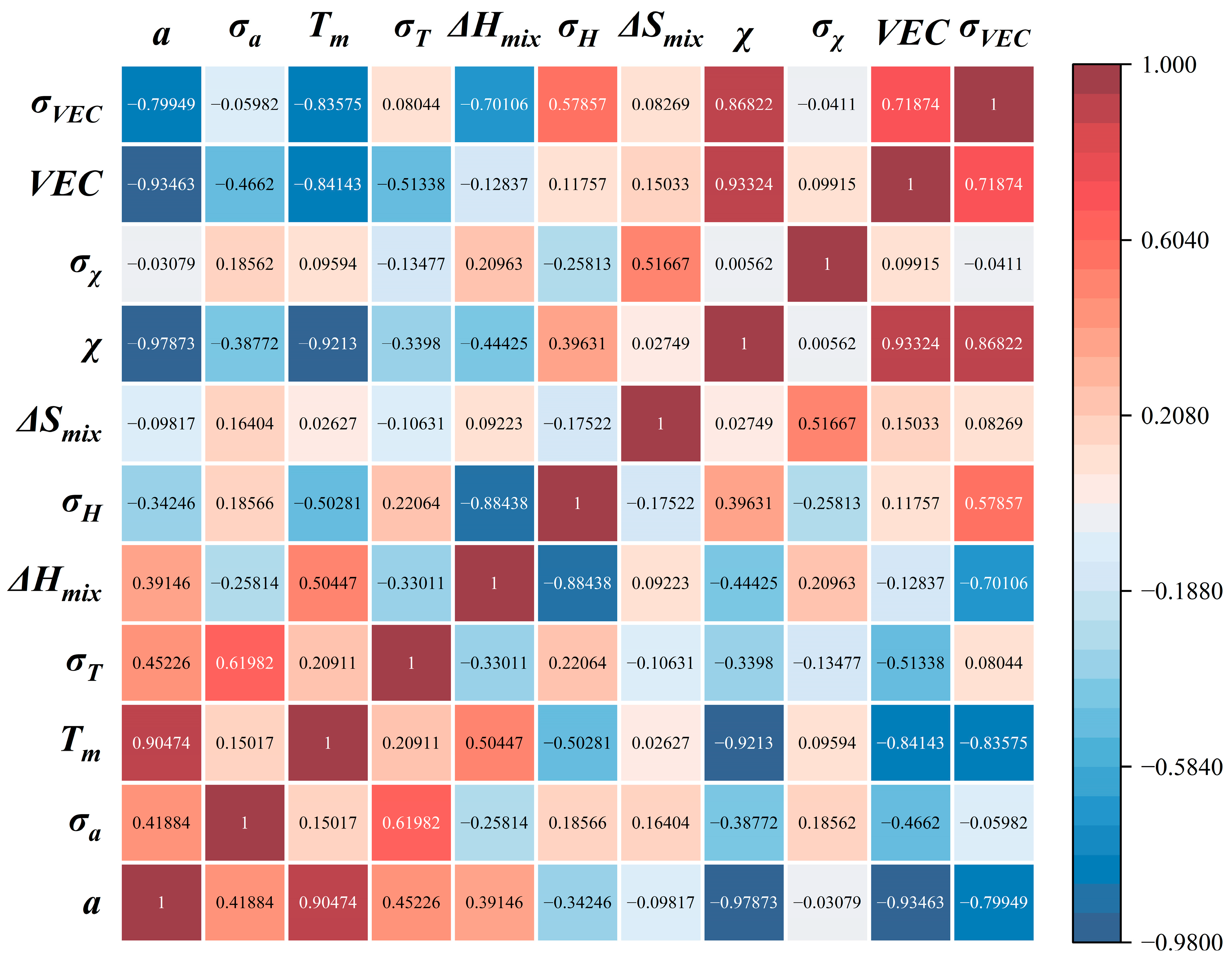
4.1. Influence of Thermodynamic Parameters
4.2. Density and Phase Analysis
5. Conclusions
- By using Pearson correlation plots to select features, the risk of overfitting due to excessive feature variables was reduced. A CatBoost ML model was chosen based on a comparison with MAE and MSE, and it performed better with limited data in the dataset. The goodness of fit (R2) for this ML model was 0.8016, with an error rate of 9.47%.
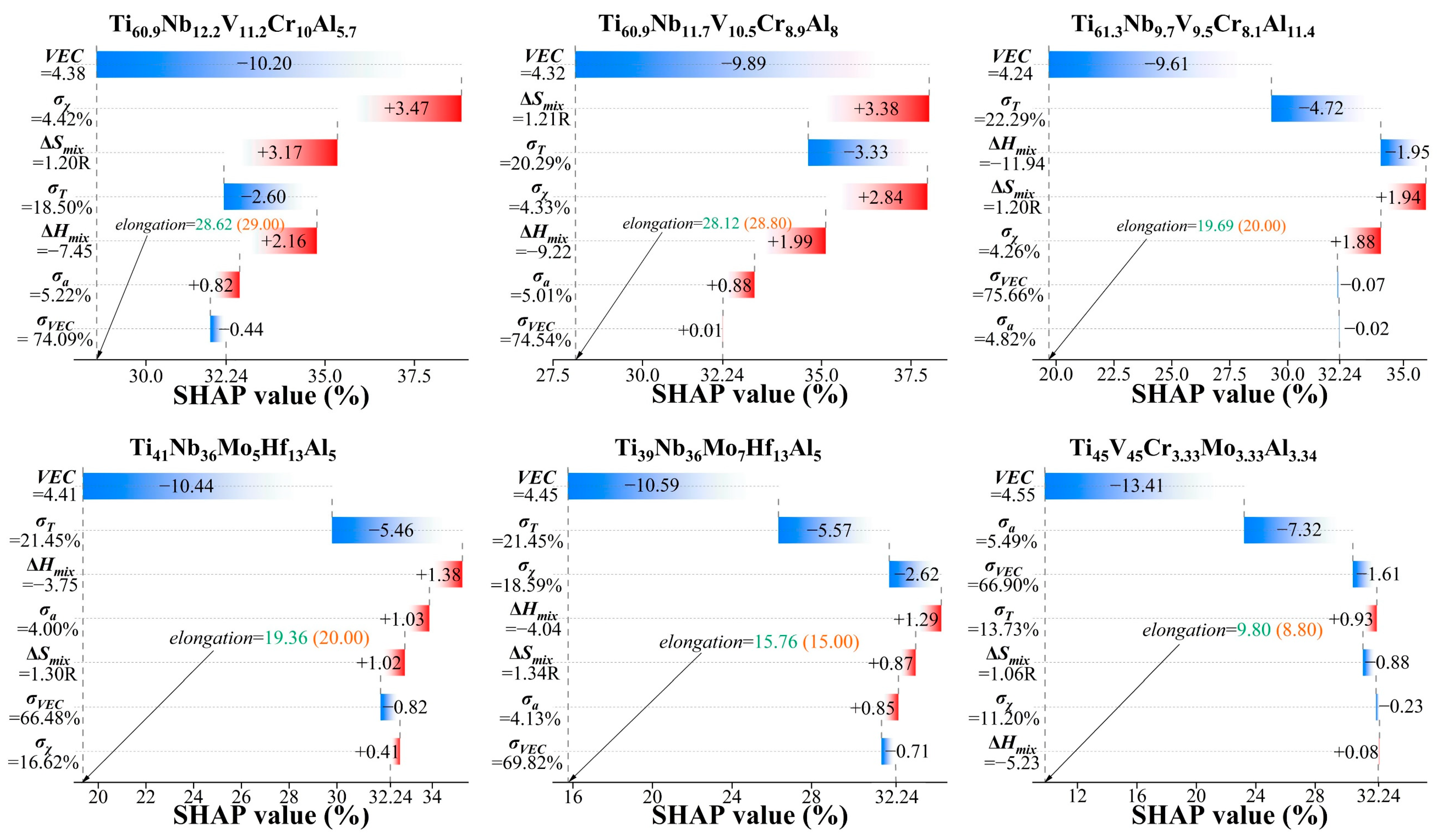
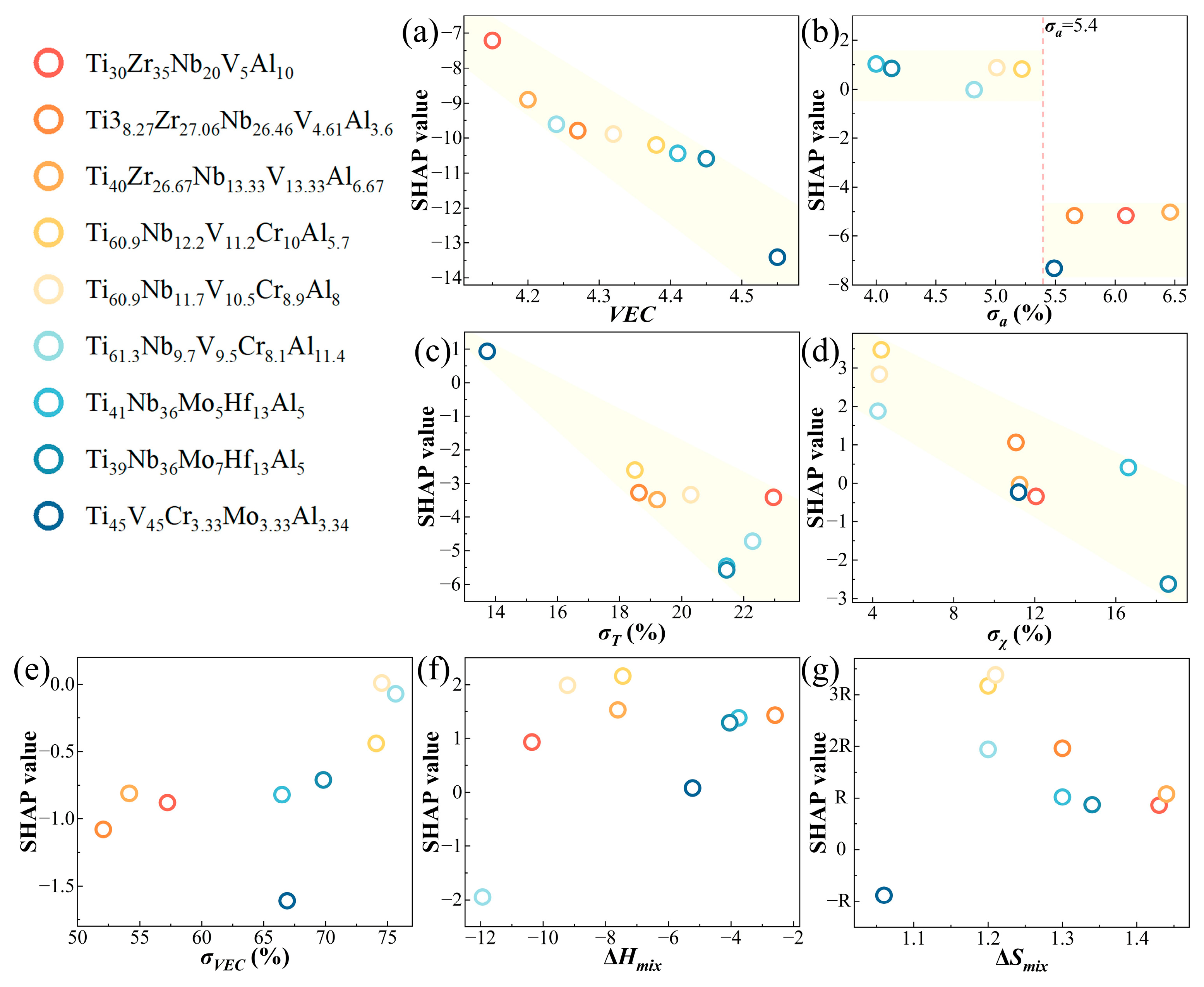
- According to the SHAP plots, the effect of VEC on the elongation of RHEAs was most pronounced, with a decrease in VEC leading to an enhancement in alloy ductility. The thermodynamic parameters σT and σχ exhibited a negative correlation with ductility. Generally, higher ductility was observed when σa was less than 5.4%. Balancing the relationships among these features should be considered for simultaneously improving the strength and toughness of RHEAs.
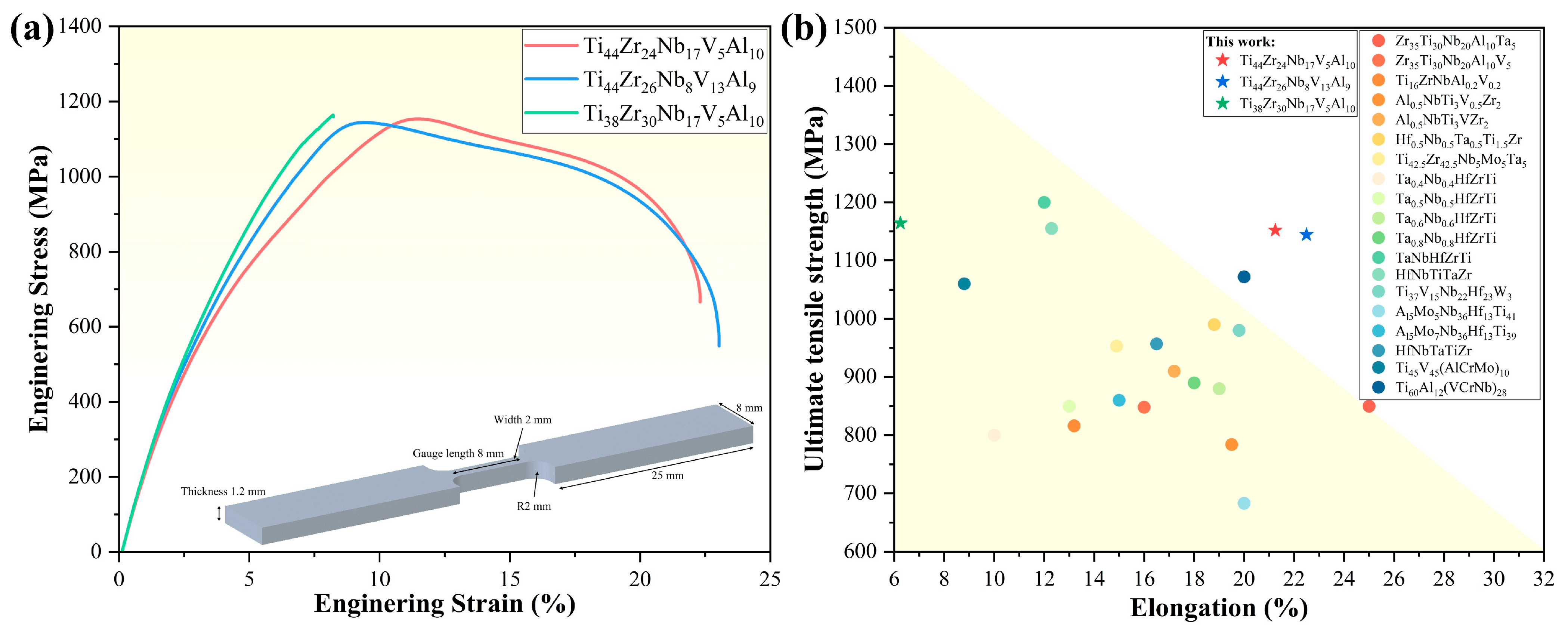
- According to the predictions of the ML model, high-strength and high-toughness Ti44Zr24Nb17V5Al10 and Ti44Zr26Nb8V13Al9 RHEAs were discovered, with their ultimate tensile strengths both being around 1180 MPa and average fracture elongations of 21.25% and 22.5%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hao, J.; Zhang, Y.; Wang, Q.; Ma, Y.; Sun, L.; Zhang, Z. Enhanced plasticity in a Zr-rich refractory high-entropy alloy via electron irradiation. J. Nucl. Mater. 2024, 590, 154876. [Google Scholar] [CrossRef]
- Moschetti, M.; Burr, P.; Obbard, E.; Kruzic, J.J.; Hosemann, P.; Gludovatz, B. Design considerations for high entropy alloys in advanced nuclear applications. J. Nucl. Mater. 2022, 567, 153814. [Google Scholar] [CrossRef]
- Sadeghilaridjani, M.; Ayyagari, A.; Muskeri, S.; Hasannaeimi, V.; Salloom, R.; Chen, W.Y.; Mukherjee, S. Ion irradiation response and mechanical behavior of reduced activity high entropy alloy. J. Nucl. Mater. 2020, 529, 151955. [Google Scholar] [CrossRef]
- Fan, X.J.; Qu, R.T.; Zhang, Z.F. Remarkably high fracture toughness of HfNbTaTiZr refractory high-entropy alloy. J. Mater. Sci. Technol. 2022, 123, 70–77. [Google Scholar] [CrossRef]
- Wei, S.; Kim, S.J.; Kang, J.; Zhang, Y.; Zhang, Y.; Furuhara, T.; Park, E.S.; Tasan, C.C. Natural-mixing guided design of refractory high-entropy alloys with as-cast tensile ductility. Nat. Mater. 2020, 19, 1175–1181. [Google Scholar] [CrossRef]
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef]
- Tian, Y.; Zhou, W.; Tan, Q.; Wu, M.; Qiao, S.; Zhu, G.; Dong, A.; Shu, D.; Sun, B. A review of refractory high-entropy alloys. Trans. Nonferrous Met. Soc. China (Engl. Ed.) 2022, 32, 3487–3515. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, Z.; Huang, H.; He, T.; Yan, H.; Zhang, Y.; Lu, Y.; Wang, T.; Li, T. Microstructures, mechanical properties, and irradiation tolerance of the Ti–Zr–Nb–V–Mo refractory high-entropy alloys. Intermetallics 2023, 157, 107873. [Google Scholar] [CrossRef]
- Yang, L.; Ge, H.; Zhang, J.; Xiong, T.; Jin, Q.; Zhou, Y.; Shao, X.; Zhang, B.; Zhu, Z.; Zheng, S.; et al. High He-ion irradiation resistance of CrMnFeCoNi high-entropy alloy revealed by comparison study with Ni and 304SS. J. Mater. Sci. Technol. 2019, 35, 300–305. [Google Scholar] [CrossRef]
- Stepanov, N.D.; Yurchenko, N.Y.; Skibin, D.V.; Tikhonovsky, M.A.; Salishchev, G.A. Structure and mechanical properties of the AlCrxNbTiV (x = 0, 0.5, 1, 1.5) high entropy alloys. J. Alloys Compd. 2015, 652, 266–280. [Google Scholar] [CrossRef]
- Yurchenko, N.; Panina, E.; Salishchev, G.; Stepanov, N. Structure and mechanical properties of near-eutectic refractory Al-Cr-Nb-Ti-Zr high entropy alloys. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1014, 012058. [Google Scholar] [CrossRef]
- He, J.Y.; Liu, W.H.; Wang, H.; Wu, Y.; Liu, X.J.; Nieh, T.G.; Lu, Z.P. Effects of Al addition on structural evolution and tensile properties of the FeCoNiCrMn high-entropy alloy system. Acta Mater. 2014, 62, 105–113. [Google Scholar] [CrossRef]
- Zhang, Y.; Bu, Z.; Yao, T.; Yang, L.; Li, W.; Li, J. Novel BCC Ti-Al-Nb-Zr medium-entropy alloys with ultrahigh specific strength and ductility. J. Alloys Compd. 2023, 936, 107873. [Google Scholar] [CrossRef]
- Senkov, O.N.; Miracle, D.B.; Chaput, K.J.; Couzinie, J.P. Development and exploration of refractory high entropy alloys—A review. J. Mater. Res. 2018, 33, 3092–3128. [Google Scholar] [CrossRef]
- Lai, W.; Liu, H.; Yu, X.; Yi, Y.; Li, W.; Zhou, S.; Cui, S.; Wang, X. A design of TiZr-rich body-centered cubic structured multi-principal element alloys with outstanding tensile strength and ductility. Mater. Sci. Eng. A 2021, 813, 141135. [Google Scholar] [CrossRef]
- Sheikh, S.; Shafeie, S.; Hu, Q.; Ahlström, J.; Persson, C.; Veselý, J.; Zýka, J.; Klement, U.; Guo, S. Alloy design for intrinsically ductile refractory high-entropy alloys. J. Appl. Phys. 2016, 120, 164902. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Qian, M.; Shi, Z.; Song, T.; Huang, L.; Zou, J. Compositional design of strong and ductile (tensile) Ti-Zr-Nb-Ta medium entropy alloys (MEAs) using the atomic mismatch approach. Mater. Sci. Eng. A 2019, 742, 762–772. [Google Scholar] [CrossRef]
- Huang, H.; Wu, Y.; He, J.; Wang, H.; Liu, X.; An, K.; Wu, W.; Lu, Z. Phase-Transformation Ductilization of Brittle High-Entropy Alloys via Metastability Engineering. Adv. Mater. 2017, 29, 1701678. [Google Scholar] [CrossRef]
- Wang, X.; An, Z.; Cai, J.; Jiang, C.; Su, H.; Luo, X.; Li, Z.; Wu, S.; Yang, L.; Long, H.; et al. Design of novel AlCoFeNiV high-entropy alloys with high-strength and high-ductility. Mater. Charact. 2023, 203, 113059. [Google Scholar] [CrossRef]
- Ye, Y.F.; Wang, Q.; Lu, J.; Liu, C.T.; Yang, Y. High-entropy alloy: Challenges and prospects. Mater. Today 2016, 19, 349–362. [Google Scholar] [CrossRef]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Li, T.; Wang, S.; Fan, W.; Lu, Y.; Wang, T.; Li, T.; Liaw, P.K. CALPHAD-aided design for superior thermal stability and mechanical behavior in a TiZrHfNb refractory high-entropy alloy. Acta Mater. 2023, 246, 118728. [Google Scholar] [CrossRef]
- Lee, C.; Song, G.; Gao, M.C.; Ouyang, L.; An, K.; Fensin, S.J.; Liaw, P.K. Effects of Zr addition on lattice strains and electronic structures of NbTaTiV high-entropy alloy. Mater. Sci. Eng. A 2022, 831, 142293. [Google Scholar] [CrossRef]
- Lu, W.; Xiao, R.; Yang, J.; Li, H.; Zhang, W. Data mining-aided materials discovery and optimization. J. Mater. 2017, 3, 191–201. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, T.; Ju, W.; Shi, S. Materials discovery and design using machine learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Taylor, C.D.; Tossey, B.M. High temperature oxidation of corrosion resistant alloys from machine learning. NPJ Mater. Degrad. 2021, 5, 38. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, M.; Cavin, J.; Flores, K.; Mishra, R. A Fast and Robust Method for Predicting the Phase Stability of Refractory Complex Concentrated Alloys using Pairwise Mixing Enthalpy. Acta Mater. 2022, 241, 118389. [Google Scholar] [CrossRef]
- Catal, A.A.; Bedir, E.; Yilmaz, R.; Swider, M.A.; Lee, C.; El-Atwani, O.; Maier, H.J.; Ozdemir, H.C.; Canadinc, D. Machine learning assisted design of novel refractory high entropy alloys with enhanced mechanical properties. Comput. Mater. Sci. 2024, 231, 112612. [Google Scholar] [CrossRef]
- Mustafi, L.; Nguyen, V.T.; Lu, S.L.; Song, T.; Murdoch, B.J.; Fabijanic, D.M.; Qian, M. Microstructure, tensile properties and deformation behaviour of a promising bio-applicable new Ti35Zr15Nb25Ta25 medium entropy alloy (MEA). Mater. Sci. Eng. A 2021, 824, 141805. [Google Scholar] [CrossRef]
- Mei, W.; Zhang, G.; Yu, K. Predicting elastic properties of refractory high-entropy alloys via machine-learning approach. Comput. Mater. Sci. 2023, 226, 112249. [Google Scholar] [CrossRef]
- Vazquez, G.; Singh, P.; Sauceda, D.; Couperthwaite, R.; Britt, N.; Youssef, K.; Johnson, D.D.; Arróyave, R. Efficient machine-learning model for fast assessment of elastic properties of high-entropy alloys. Acta Mater. 2022, 232, 117924. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, Y.; He, Q.; Ding, Z.; Li, F.; Yang, Y. Machine learning guided appraisal and exploration of phase design for high entropy alloys. NPJ Comput. Mater. 2019, 5, 128. [Google Scholar] [CrossRef]
- Chen, L.; Jarlöv, A.; Seet, H.L.; Nai, M.L.S.; Li, Y.; Zhou, K. Exploration of V–Cr–Fe–Co–Ni high-entropy alloys with high yield strength: A combination of machine learning and molecular dynamics simulation. Comput. Mater. Sci. 2023, 217, 111888. [Google Scholar] [CrossRef]
- Huang, T.D.; Wu, S.Y.; Jiang, H.; Lu, Y.P.; Wang, T.M.; Li, T.J. Effect of Ti content on microstructure and properties of TixZrVNb refractory high-entropy alloys. Int. J. Miner. Metall. Mater. 2020, 27, 1318–1325. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, Y.; Zhang, Z.; Liu, L.; Sun, L. Two novel Zr-rich refractory high-entropy alloys with excellent tensile mechanical properties. Intermetallics 2023, 157, 107872. [Google Scholar] [CrossRef]
- Yao, T.T.; Zhang, Y.G.; Yang, L.; Bu, Z.Q.; Li, J.F. A metastable Ti–Zr–Nb–Al multi-principal-element alloy with high tensile strength and ductility. Mater. Sci. Eng. A 2022, 851, 143646. [Google Scholar] [CrossRef]
- Hu, S.; Li, T.; Su, Z.; Liu, D. Research on suitable strength, elastic modulus and abrasion resistance of Ti–Zr–Nb medium entropy alloys (MEAs) for implant adaptation. Intermetallics 2022, 140, 107401. [Google Scholar] [CrossRef]
- Wang, J.; Bai, S.; Tang, Y.; Li, S.; Liu, X.; Jia, J.; Ye, Y.; Zhu, L. Effect of the valence electron concentration on the yield strength of Ti–Zr–Nb–V high-entropy alloys. J. Alloys Compd. 2021, 868, 159190. [Google Scholar] [CrossRef]
- Calderon-Moreno, J.M.; Vasilescu, C.; Drob, S.I.; Ivanescu, S.; Osiceanu, P.; Drob, P.; Popa, M.; Preda, S.; Vasilescu, E. Microstructural and mechanical properties, surface and electrochemical characterisation of a new Ti-Zr-Nb alloy for implant applications. J. Alloys Compd. 2014, 612, 398–410. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, X.G.; Jiang, Z.Q.; Chen, M.; Sun, M.; Zhang, X.F. Phase transition and mechanical performance evolution in TiVZr-Nbx alloys. J. Alloys Compd. 2023, 937, 168458. [Google Scholar] [CrossRef]
- Wang, H.; Chen, W.; Fu, Z.; Chu, C.; Tian, Z.; Jiang, Z.; Wen, H. Lightweight Ti-Zr-Nb-Al-V refractory high-entropy alloys with superior strength-ductility synergy and corrosion resistance. Int. J. Refract Met. Hard. Mater. 2023, 116, 106331. [Google Scholar] [CrossRef]
- Wang, T.; Jiang, W.; Wang, X.; Jiang, B.; Rong, C.; Wang, Y.; Yang, J.; Zhu, D. Microstructure and properties of Al0.5NbTi3VxZr2 refractory high entropy alloys combined with high strength and ductility. J. Mater. Res. Technol. 2023, 24, 1733–1743. [Google Scholar] [CrossRef]
- Yurchenko, N.; Panina, E.; Tojibaev, A.; Novikov, V.; Salishchev, G.; Zherebtsov, S.; Stepanov, N. Effect of B2 ordering on the tensile mechanical properties of refractory AlxNb40Ti40V20−x medium-entropy alloys. J. Alloys Compd. 2023, 937, 168465. [Google Scholar] [CrossRef]
- Yuan, Y.; Wu, Y.; Yang, Z.; Liang, X.; Lei, Z.; Huang, H.; Wang, H.; Liu, X.; An, K.; Wu, W.; et al. Formation, structure and properties of biocompatible TiZrHfNbTa high-entropy alloys. Mater. Res. Lett. 2019, 7, 225–231. [Google Scholar] [CrossRef]
- Zýka, J.; Málek, J.; Veselý, J.; Lukáč, F.; Čížek, J.; Kuriplach, J.; Melikhova, O. Microstructure and room temperature mechanical properties of different 3 and 4 element medium entropy alloys from HfNbTaTiZr system. Entropy 2019, 21, 114. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Hou, J.; Wang, X.; Qiao, J.; Wu, Y. Excellent room-temperature tensile ductility in as-cast Ti37V15Nb22Hf23W3 refractory high entropy alloys. Intermetallics 2022, 151, 107735. [Google Scholar] [CrossRef]
- Huang, R.; Wang, W.; Li, T.; Zhang, L.; Amar, A.; Chen, X.; Ren, Z.; Lu, Y. A novel AlMoNbHfTi refractory high-entropy alloy with superior ductility. J. Alloys Compd. 2023, 940, 168821. [Google Scholar] [CrossRef]
- Di, Y.; Wang, M.; Zhang, L.; Yan, H.; Zhang, Y.; Lu, Y. A novel Ti45V45(AlCrMo)10 lightweight medium-entropy alloy with outstanding mechanical properties. Mater. Lett. 2023, 339, 134089. [Google Scholar] [CrossRef]
- Liao, Y.C.; Ye, W.T.; Chen, P.S.; Tsai, P.H.; Jang, J.S.C.; Hsieh, K.C.; Chen, C.Y.; Huang, J.C.; Wu, H.J.; Lo, Y.C.; et al. Effect of Al concentration on the microstructural and mechanical properties of lightweight Ti60Alx(VCrNb)40-x medium-entropy alloys. Intermetallics 2021, 135, 107213. [Google Scholar] [CrossRef]
- Jas, K.; Dodagoudar, G.R. Explainable machine learning model for liquefaction potential assessment of soils using XGBoost-SHAP. Soil Dyn. Earthq. Eng. 2023, 165, 107662. [Google Scholar] [CrossRef]
- Guo, S.; Ng, C.; Lu, J.; Liu, C.T. Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 2011, 109, 103505. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y. Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys. 2012, 132, 233–238. [Google Scholar] [CrossRef]
- Ren, M.X.; Li, B.S.; Fu, H.Z. Formation condition of solid solution type high-entropy alloy. Trans. Nonferrous Met. Soc. China (Engl. Ed.) 2013, 23, 991–995. [Google Scholar] [CrossRef]
- Zhang, W.; Liaw, P.K.; Zhang, Y. Science and technology in high-entropy alloys. Sci. China Mater. 2018, 61, 2–22. [Google Scholar] [CrossRef]
- Tan, Y.; Li, J.; Tang, Z.; Wang, J.; Kou, H. Design of high-entropy alloys with a single solid-solution phase: Average properties vs. their variances. J. Alloys Compd. 2018, 742, 430–441. [Google Scholar] [CrossRef]





| Alloy | Elongation | σa | σT | ΔHmix | ΔSmix | σχ | VEC | σVEC |
|---|---|---|---|---|---|---|---|---|
| Ti44Zr24Nb17V5Al10 | 24.42% | 5.48% | 22.81% | −10.20 | 1.39 R | 10.61% | 4.12 | 55.28% |
| Ti45Zr26Nb8V12Al9 | 24.00% | 6.26% | 19.90% | −10.54 | 1.38 R | 11.00% | 4.11 | 52.72% |
| Ti44Zr26Nb8V13Al9 | 23.89% | 6.36% | 19.89% | −10.56 | 1.40 R | 11.06% | 4.12 | 53.44% |
| Ti38Zr30Nb17V5Al10 | 23.89% | 5.82% | 22.67% | −10.48 | 1.41 R | 11.42% | 4.12 | 55.28% |
| Ti42Zr30Nb9V10Al9 | 23.88% | 6.27% | 20.14% | −10.56 | 1.39 R | 11.41% | 4.10 | 51.96% |
| Alloy | Elongation | σa | σT | ΔHmix | ΔSmix | σχ | VEC | σVEC | References |
|---|---|---|---|---|---|---|---|---|---|
| Ti30Zr35Nb20V5Al10 | 16.00% | 6.09% | 22.97% | −10.36 | 1.43 R | 12.06% | 4.15 | 57.23% | [13] |
| Ti38.27Zr27.06Nb26.46V4.61Al3.6 | 13.20% | 5.66% | 18.63% | −2.59 | 1.3 R | 11.07% | 4.27 | 52.08% | [41] |
| Ti40Zr26.67Nb13.33V13.33Al6.67 | 17.20% | 6.46% | 19.21% | −7.61 | 1.44 R | 11.25% | 4.20 | 54.16% | [42] |
| Ti60.9Nb12.2V11.2Cr10Al5.7 | 29.00% | 5.22% | 18.50% | −7.45 | 1.20 R | 4.42% | 4.38 | 74.09% | [49] |
| Ti60.9Nb11.7V10.5Cr8.9Al8 | 28.80% | 5.01% | 20.29% | −9.22 | 1.21 R | 4.33% | 4.32 | 74.54% | [49] |
| Ti61.3Nb9.7V9.5Cr8.1Al11.4 | 20.00% | 4.82% | 22.29% | −11.94 | 1.20 R | 4.26% | 4.24 | 75.66% | [49] |
| Ti41Nb36Mo5Hf13Al5 | 20.00% | 4.00% | 21.45% | −3.75 | 1.30 R | 16.62% | 4.41 | 66.48% | [47] |
| Ti39Nb36Mo7Hf13Al5 | 15.00% | 4.13% | 21.45% | −4.04 | 1.34 R | 18.59% | 4.45 | 69.82% | [47] |
| Ti45V45Cr3.33Mo3.33Al3.34 | 8.80% | 5.49% | 13.73% | −5.23 | 1.06 R | 11.20% | 4.55 | 66.90% | [48] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Wei, Z.; Zhao, J.; Jia, Y.; Cao, S.; Wang, D.; Lei, Y. Machine-Learning-Assisted Design of Novel TiZrNbVAl Refractory High-Entropy Alloys with Enhanced Ductility. Metals 2024, 14, 894. https://doi.org/10.3390/met14080894
Zhao X, Wei Z, Zhao J, Jia Y, Cao S, Wang D, Lei Y. Machine-Learning-Assisted Design of Novel TiZrNbVAl Refractory High-Entropy Alloys with Enhanced Ductility. Metals. 2024; 14(8):894. https://doi.org/10.3390/met14080894
Chicago/Turabian StyleZhao, Xinyi, Zihang Wei, Junfeng Zhao, Yandong Jia, Shuo Cao, Dan Wang, and Yucheng Lei. 2024. "Machine-Learning-Assisted Design of Novel TiZrNbVAl Refractory High-Entropy Alloys with Enhanced Ductility" Metals 14, no. 8: 894. https://doi.org/10.3390/met14080894
APA StyleZhao, X., Wei, Z., Zhao, J., Jia, Y., Cao, S., Wang, D., & Lei, Y. (2024). Machine-Learning-Assisted Design of Novel TiZrNbVAl Refractory High-Entropy Alloys with Enhanced Ductility. Metals, 14(8), 894. https://doi.org/10.3390/met14080894







