Thermomechanical Behavior and Experimental Study of Additive Manufactured Superalloy/Titanium Alloy Horizontal Multi-Material Structures
Abstract
:1. Introduction
2. Finite Element Model
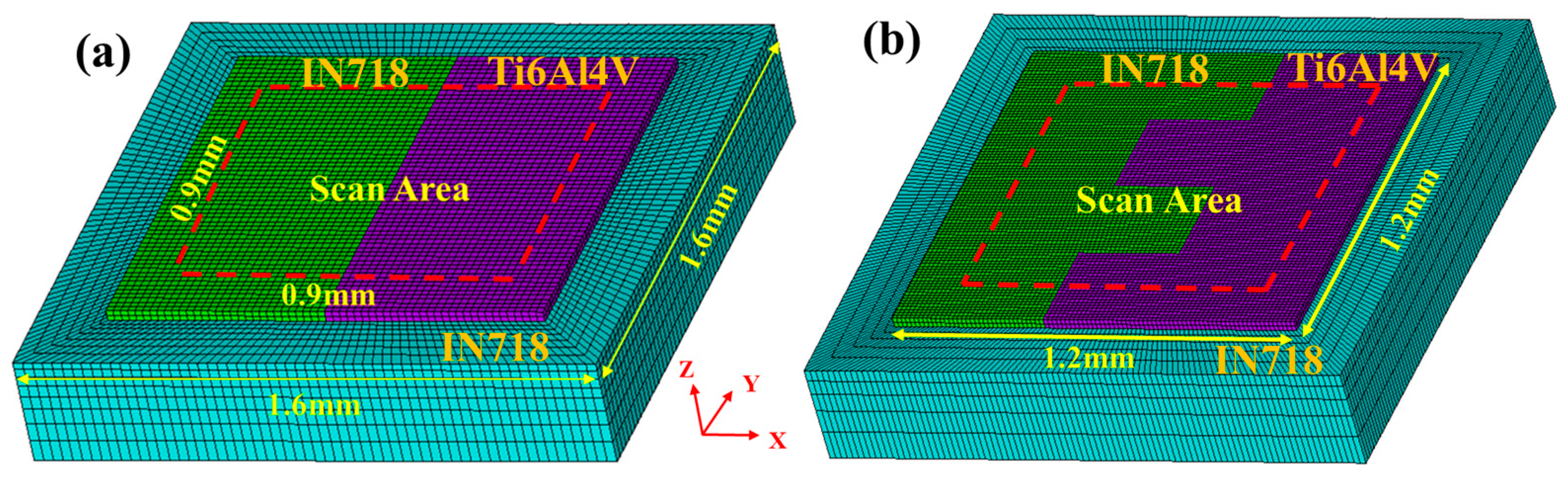
2.1. Establishment of Finite Element Model and Assumptions
2.2. Temperature Field Control Equations
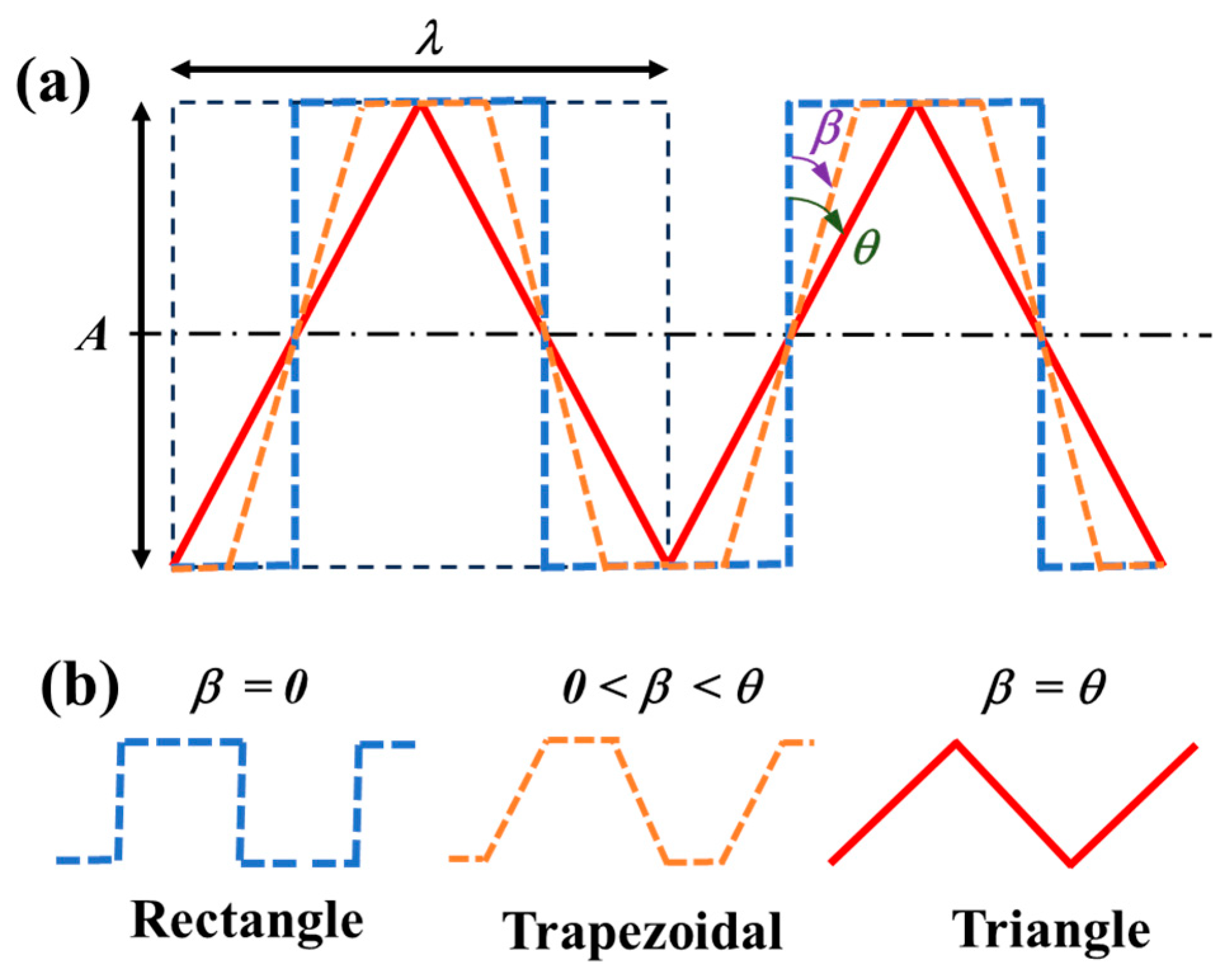
2.3. Heat Source Modelling
2.4. Stress Field Governing Equations
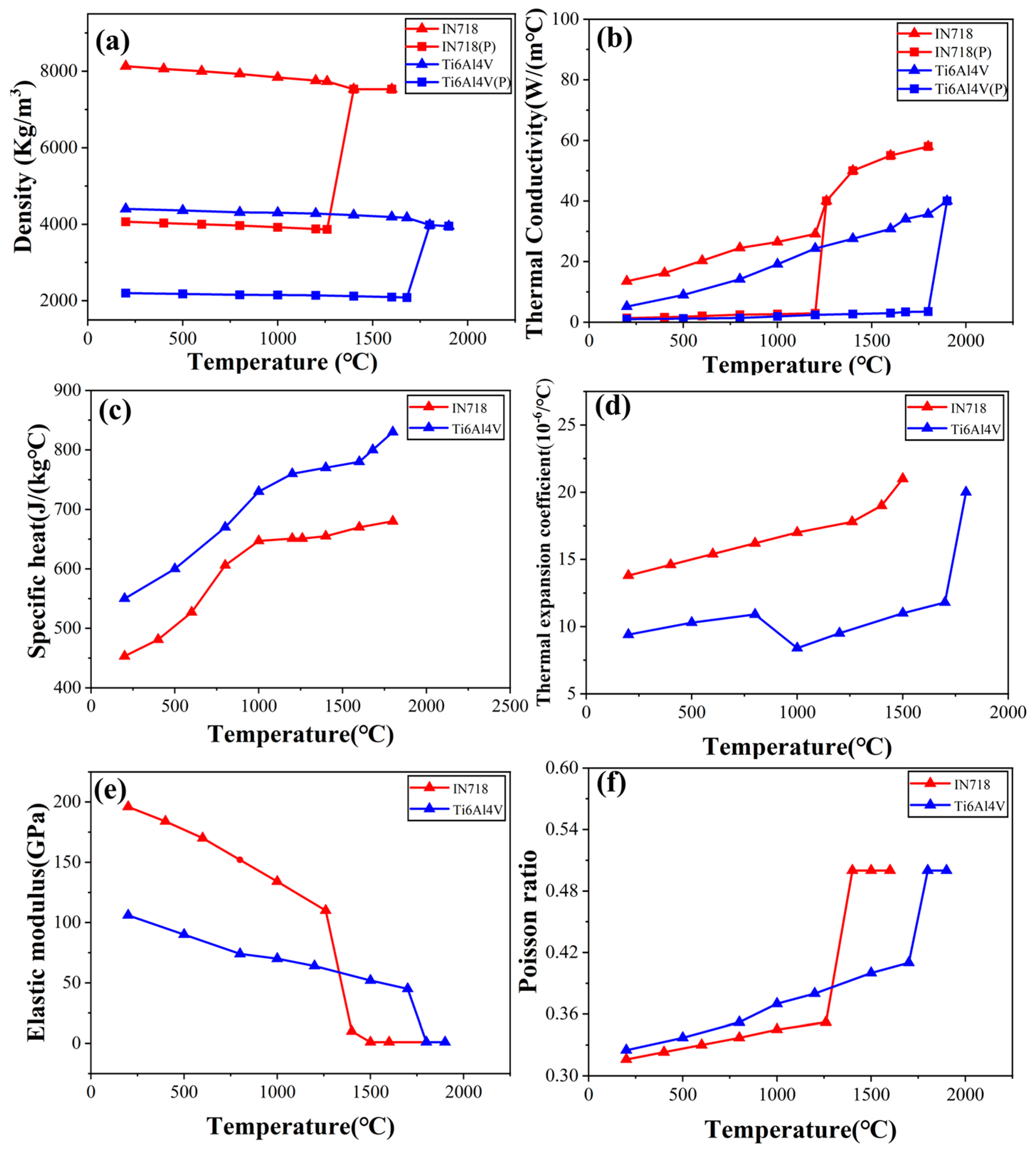
2.5. Material Properties
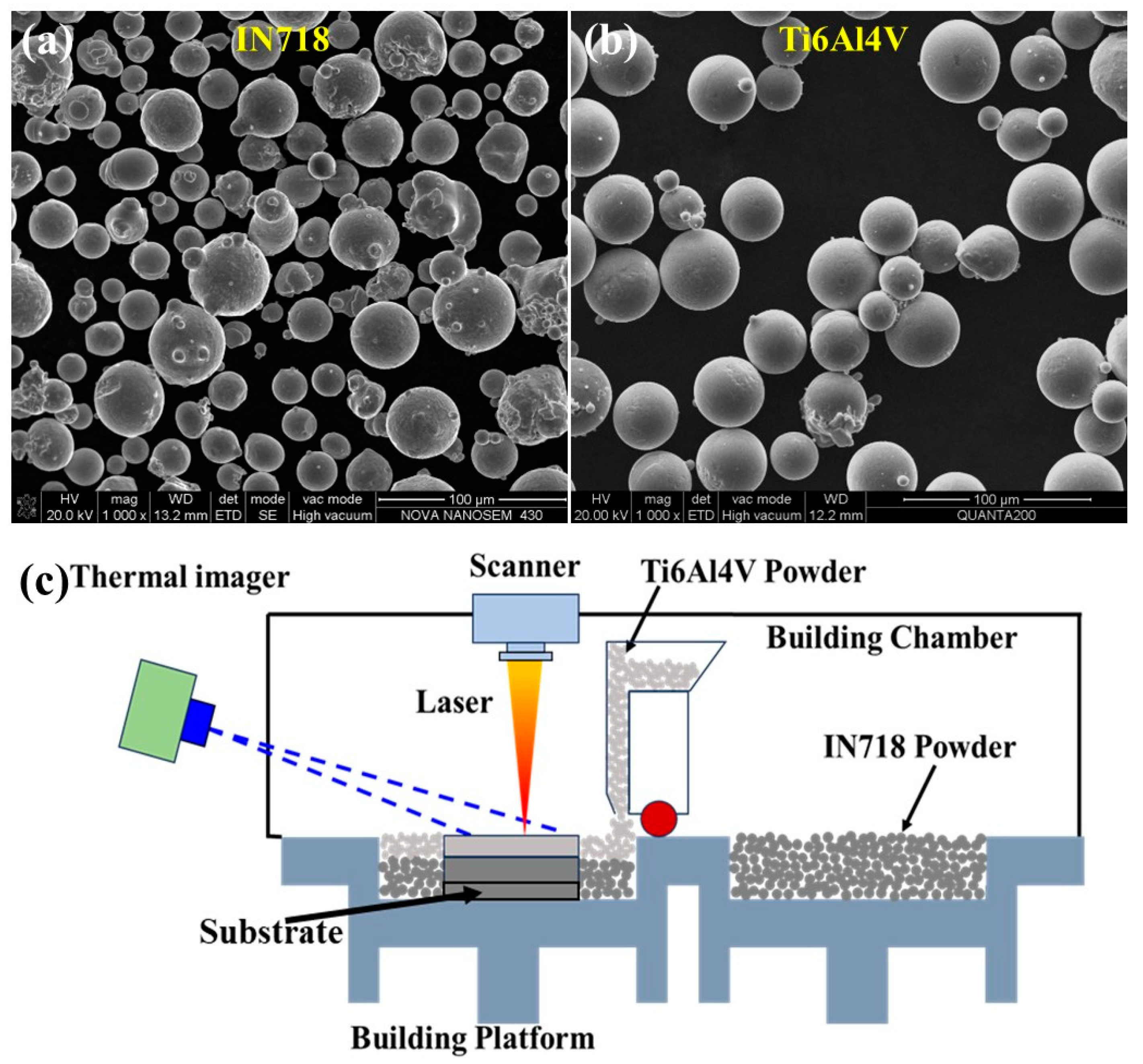
3. Experimental
4. Results and Discussion
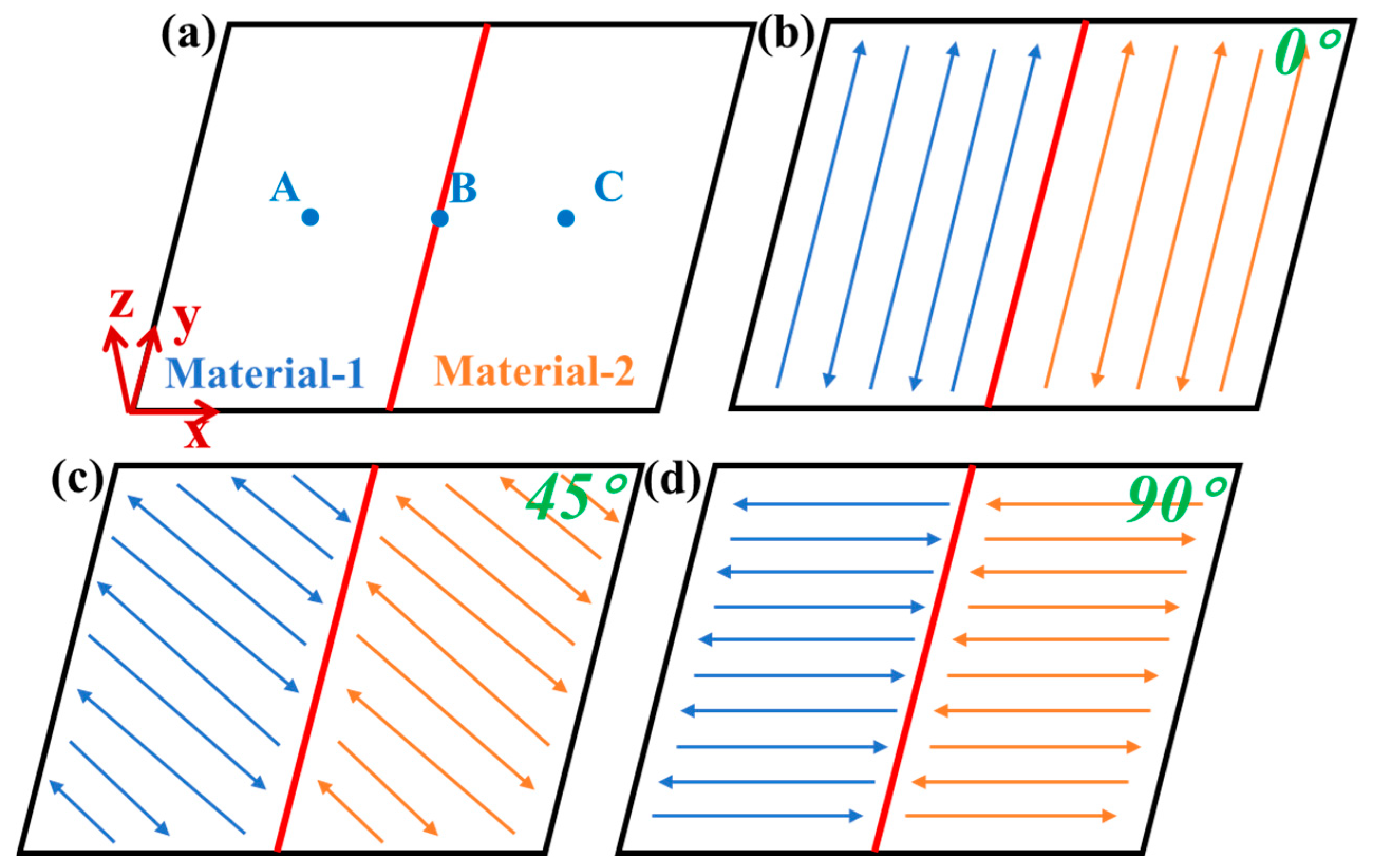
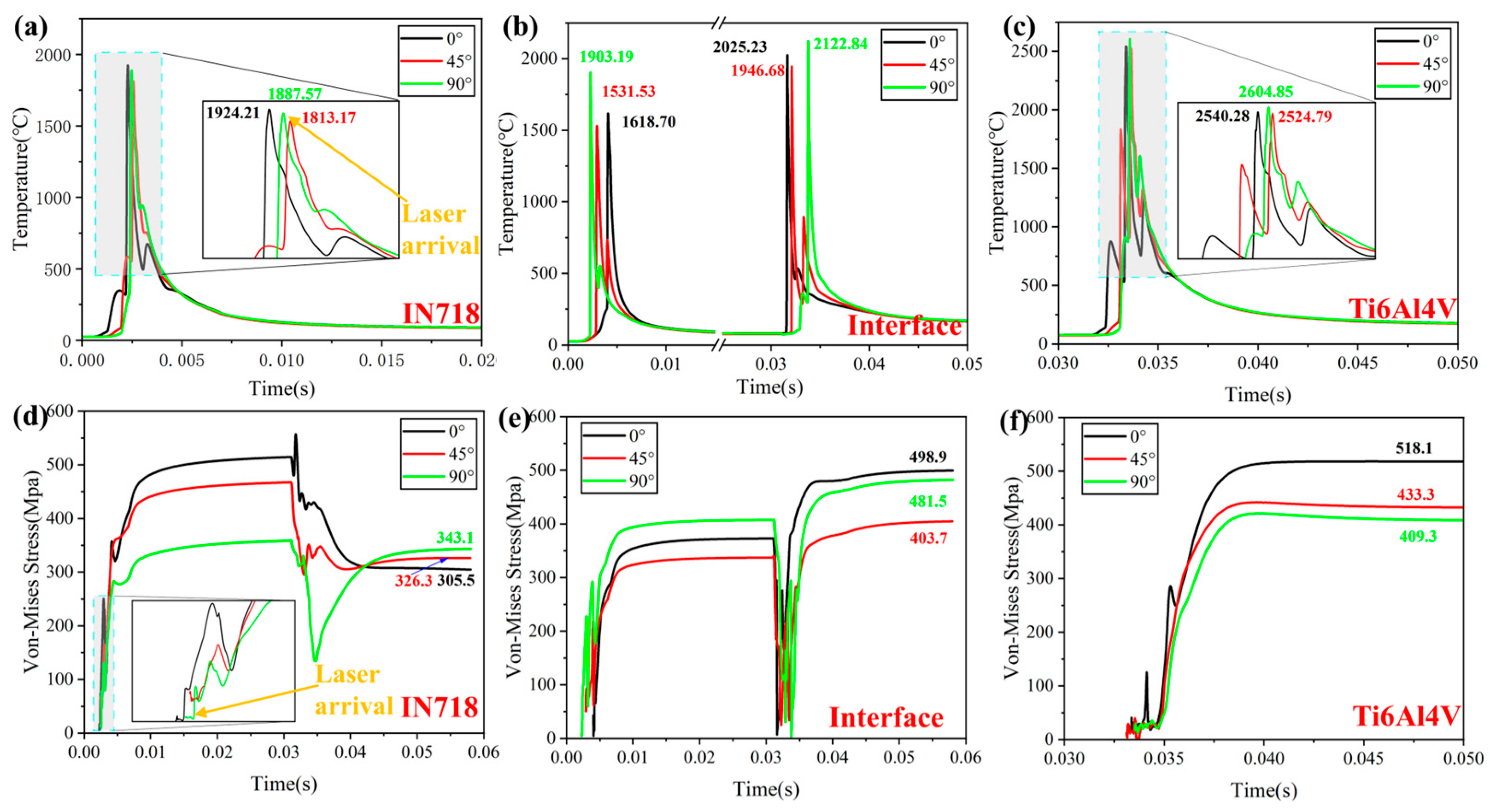
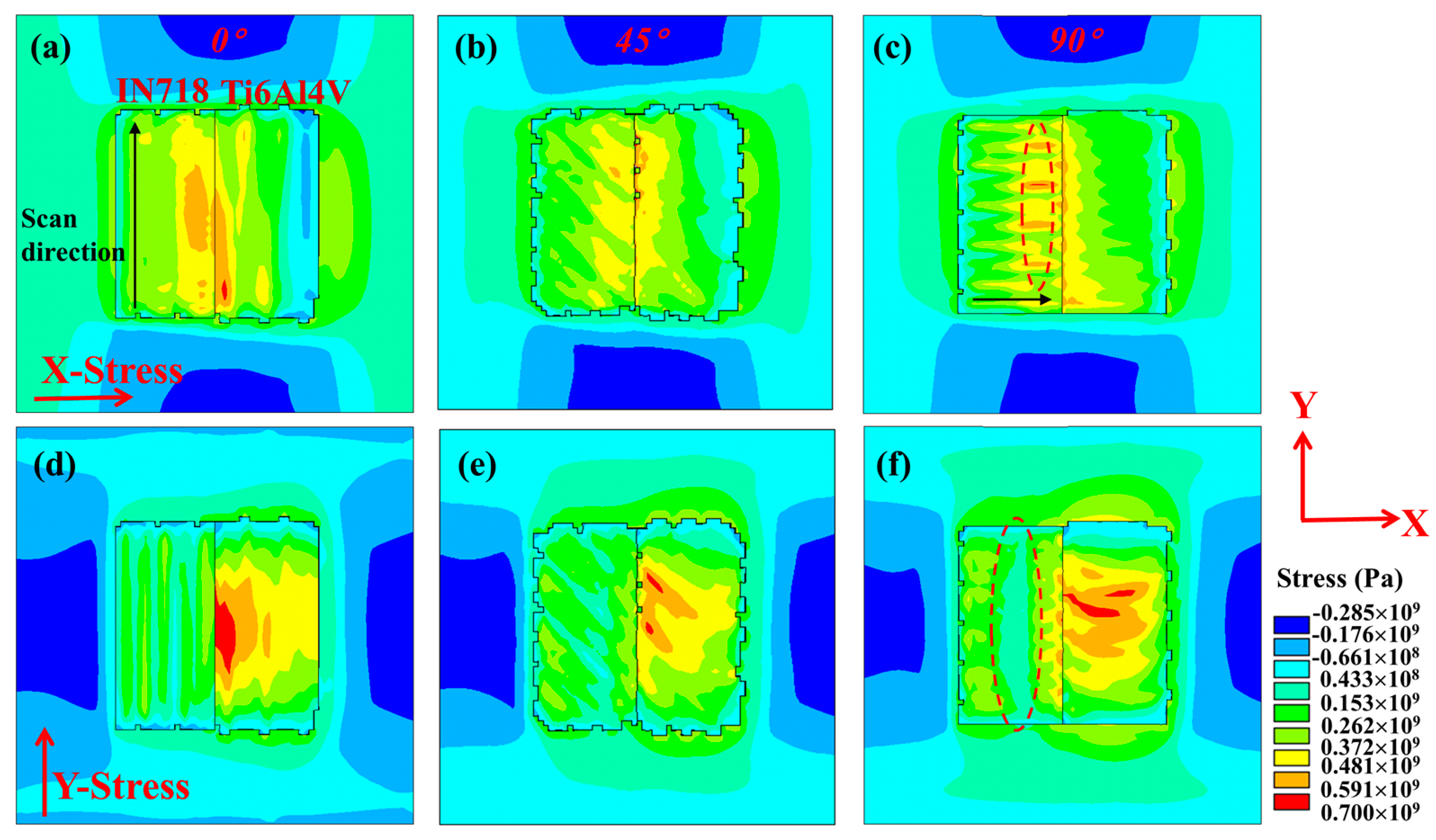
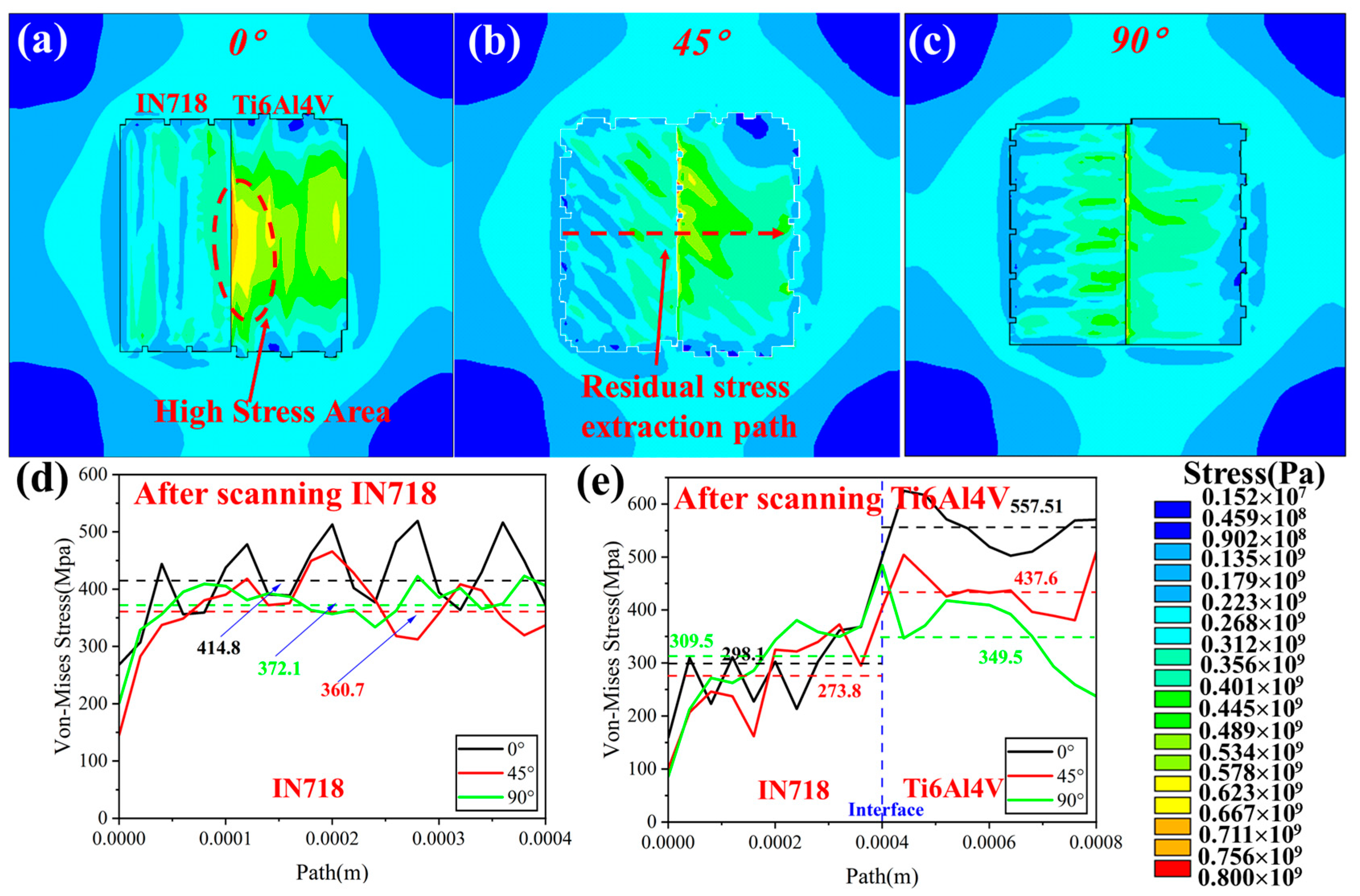
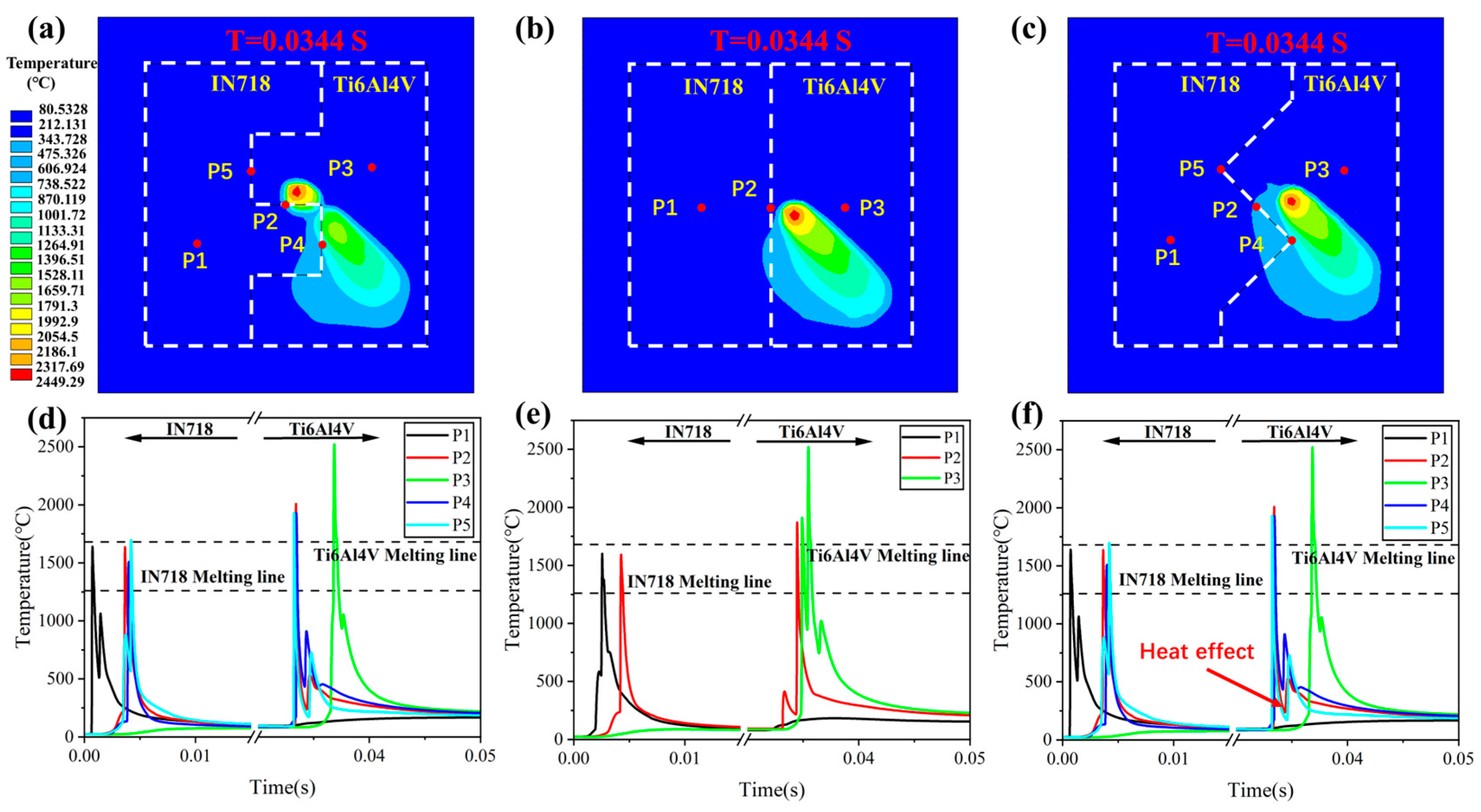
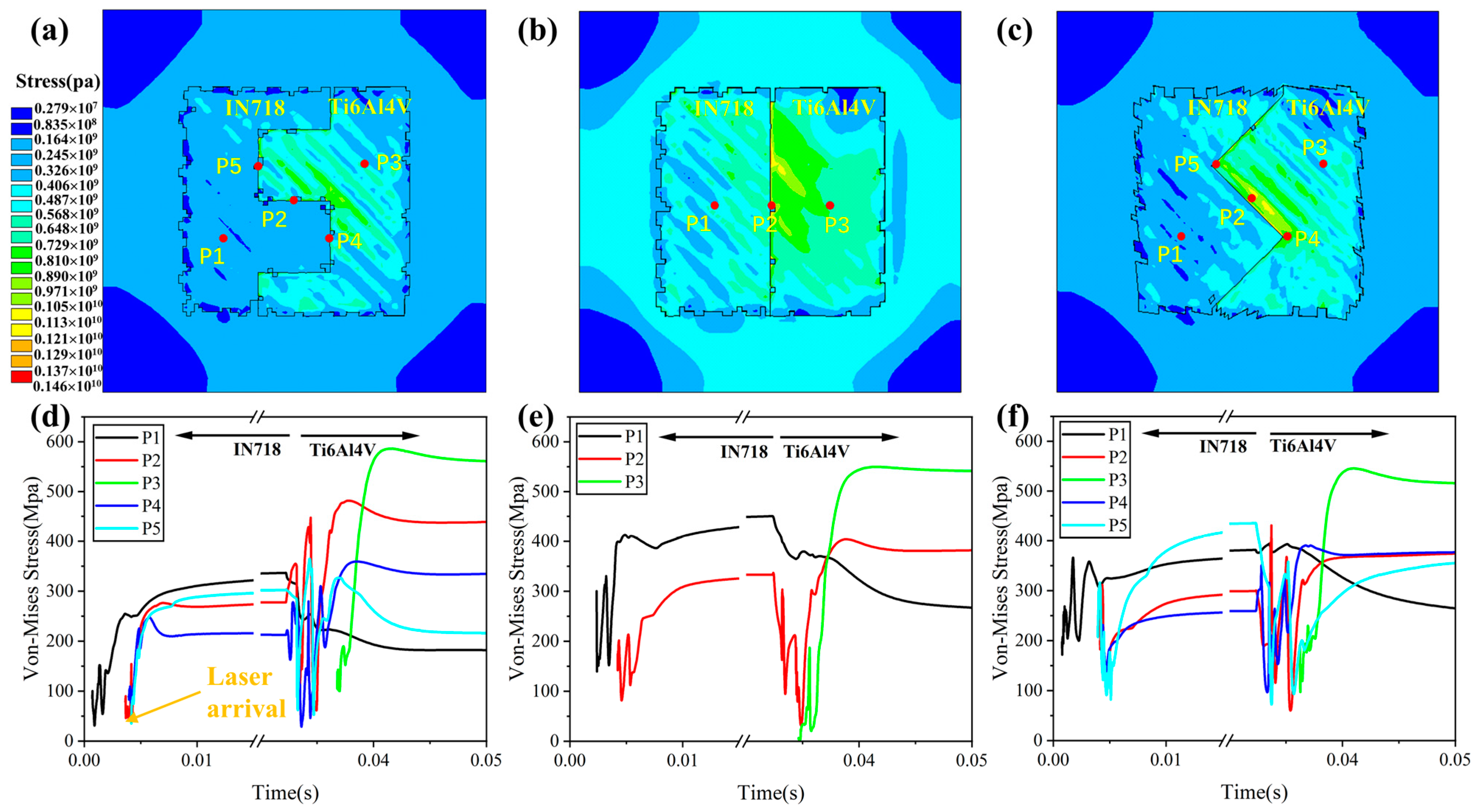
4.1. Effect of Scanning Strategy on Thermomechanical Behavior
4.2. Effect of Forming Sequence on Thermomechanical Behavior
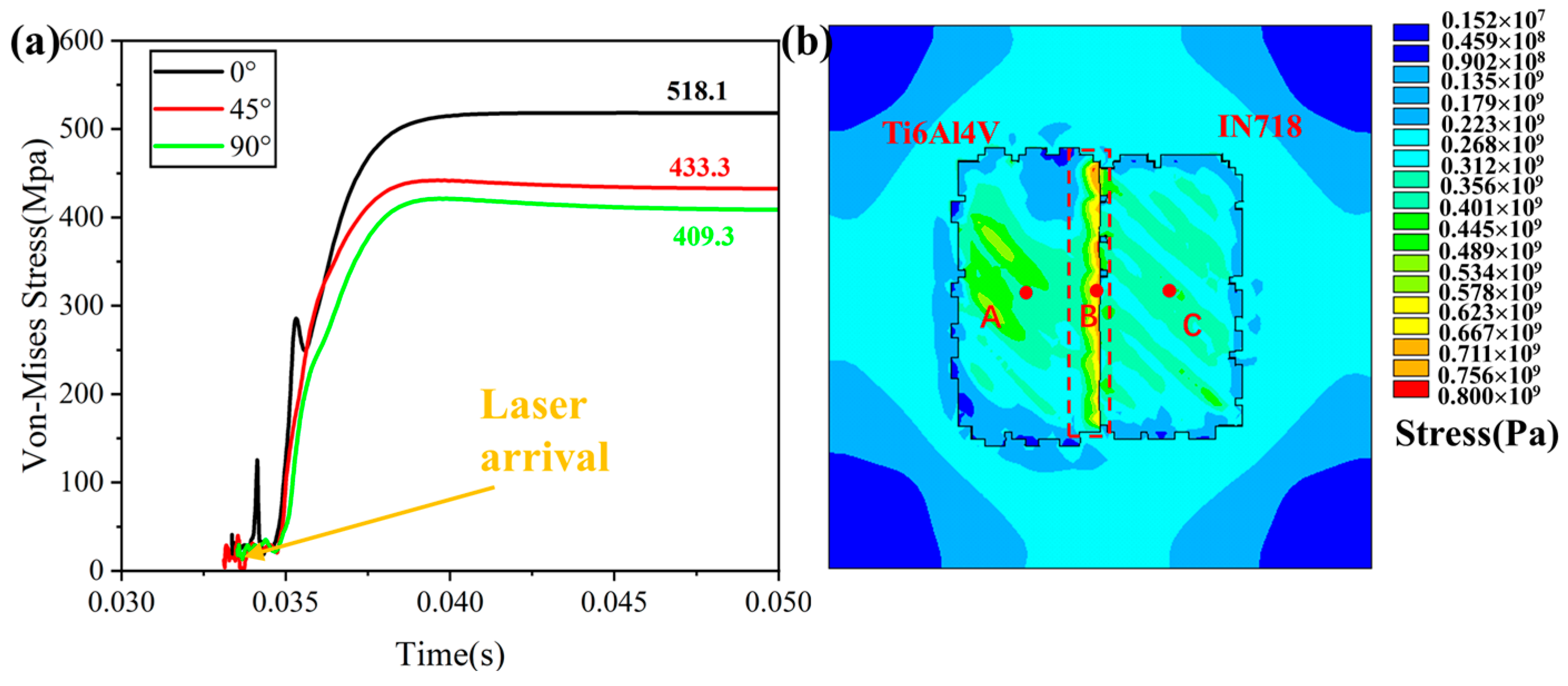
4.3. Effect of Interfacial Structure on Thermomechanical Behavior
5. Experimental Results
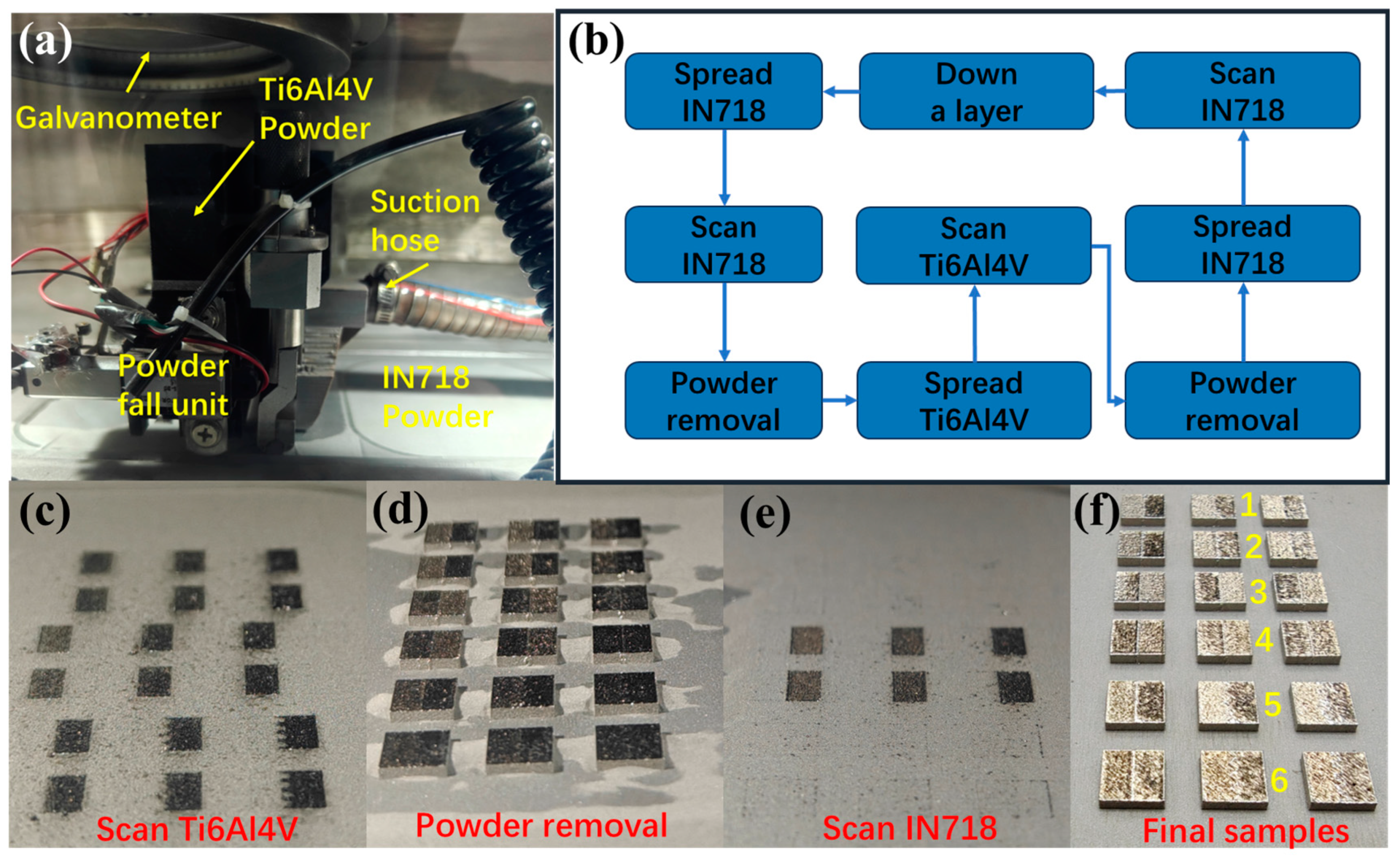
5.1. Experimental Process
5.2. Analysis of Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sam, M.; Jojith, R.; Radhika, N. Progression in Manufacturing of Functionally Graded Materials and Impact of Thermal Treatment—A Critical Review. J. Manuf. Process. 2021, 68, 1339–1377. [Google Scholar] [CrossRef]
- Wang, D.; Liu, L.; Deng, G.; Deng, C.; Bai, Y.; Yang, Y.; Wu, W.; Chen, J.; Liu, Y.; Wang, Y.; et al. Recent Progress on Additive Manufacturing of Multi-Material Structures with Laser Powder Bed Fusion. Virtual Phys. Prototyp. 2022, 17, 329–365. [Google Scholar] [CrossRef]
- Wei, C.; Li, L. Recent Progress and Scientific Challenges in Multi-Material Additive Manufacturing via Laser-Based Powder Bed Fusion. Virtual Phys. Prototyp. 2021, 16, 347–371. [Google Scholar] [CrossRef]
- Ansari, M.; Jabari, E.; Toyserkani, E. Opportunities and Challenges in Additive Manufacturing of Functionally Graded Metallic Materials via Powder-Fed Laser Directed Energy Deposition: A Review. J. Mater. Process. Technol. 2021, 294, 117117. [Google Scholar] [CrossRef]
- Hosseini, E.; Popovich, V.A. A Review of Mechanical Properties of Additively Manufactured Inconel 718. Addit. Manuf. 2019, 30, 100877. [Google Scholar] [CrossRef]
- Karim, A.N.M.; Ikram, M.; Emrul Kays, H.M.; Abdesselam, M.; Ginta, T.L. Assessment of Machining Cost for End-Milling of Ti-6Al-4V Titanium Alloy through RSM-Based Parametric Model. Adv. Mater. Res. 2014, 903, 83–89. [Google Scholar] [CrossRef]
- Jin, B.; Wang, Q.; Zhao, L.; Pan, A.; Ding, X.; Gao, W.; Song, Y.; Zhang, X. A Review of Additive Manufacturing Techniques and Post-Processing for High-Temperature Titanium Alloys. Metals 2023, 13, 1327. [Google Scholar] [CrossRef]
- Soni, N.; Renna, G.; Leo, P. Advancements in Metal Processing Additive Technologies: Selective Laser Melting (SLM). Metals 2024, 14, 1081. [Google Scholar] [CrossRef]
- Razavykia, A.; Brusa, E.; Delprete, C.; Yavari, R. An Overview of Additive Manufacturing Technologies—A Review to Technical Synthesis in Numerical Study of Selective Laser Melting. Materials 2020, 13, 3895. [Google Scholar] [CrossRef]
- Yang, Y.; Jiang, R.; Han, C.; Chen, J.; Li, H.; Wang, Y.; Tang, J.; Zhou, H.; Hu, W.; Zheng, B.; et al. Frontiers in Laser Additive Manufacturing Technology. Addit. Manuf. Front. 2024, 3, 200160. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, F.; Huang, Z.; Jia, M.; Chen, G.; Ye, Y.; Lin, Y.; Liu, W.; Chen, B.; Shen, Q.; et al. Additive Manufacturing of Functionally Graded Materials: A Review. Mater. Sci. Eng. A 2019, 764, 138209. [Google Scholar] [CrossRef]
- Xie, D.; Lv, F.; Yang, Y.; Shen, L.; Tian, Z.; Shuai, C.; Chen, B.; Zhao, J. A Review on Distortion and Residual Stress in Additive Manufacturing. Chin. J. Mech. Eng. Addit. Manuf. Front. 2022, 1, 100039. [Google Scholar] [CrossRef]
- Shah, K.; Haq, I.U.; Shah, S.A.; Khan, F.U.; Khan, M.T.; Khan, S. Experimental Study of Direct Laser Deposition of Ti-6Al-4V and Inconel 718 by Using Pulsed Parameters. Sci. World J. 2014, 2014, 841549. [Google Scholar] [CrossRef]
- Willy, H.J.; Li, X.; Tan, Y.H.; Chen, Z.; Cagirici, M.; Borayek, R.; Herng, T.S.; Ong, C.Y.A.; Li, C.; Ding, J. Overview of Finite Elements Simulation of Temperature Profile to Estimate Properties of Materials 3D-Printed by Laser Powder-Bed Fusion. Chin. Phys. B 2020, 29, 48101. [Google Scholar] [CrossRef]
- Chen, C.; Gu, D.; Dai, D.; Du, L.; Wang, R.; Ma, C.; Xia, M. Laser Additive Manufacturing of Layered TiB2/Ti6Al4V Multi-Material Parts: Understanding Thermal Behavior Evolution. Opt. Laser Technol. 2019, 119, 105666. [Google Scholar] [CrossRef]
- Huang, G.; Lin, K.; Gu, D.; Wang, R.; Liu, H.; Shi, K. The Influence of Building Parameters on Residual Stress, Interfacial Structure, and Cracking Control of Laser Powder Bed Fusion Processed Ti6Al4V/AlMgScZr Multi-Material Parts. J. Mater. Process. Technol. 2024, 330, 118479. [Google Scholar] [CrossRef]
- Mao, S.; Yang, B.; Liu, G.; Liu, G.; Zhang, Z. Temperature Distribution and Residual Stress Evolution at the Interface of CuCrZr/316 L Multi-Material by Laser Powder Bed Fusion. Opt. Laser Technol. 2023, 163, 109355. [Google Scholar] [CrossRef]
- Roberts, I.A.; Wang, C.J.; Esterlein, R.; Stanford, M.; Mynors, D.J. A Three-Dimensional Finite Element Analysis of the Temperature Field during Laser Melting of Metal Powders in Additive Layer Manufacturing. Int. J. Mach. Tools Manuf. 2009, 49, 916–923. [Google Scholar] [CrossRef]
- Wang, X.; Liu, M.; Li, Z.; Yao, B.; Wang, B.; Wang, N. Finite Element Simulation and Experimental Study of Selective Laser Melted 40Cr Steel Forming Process. Opt. Laser Technol. 2024, 169, 110080. [Google Scholar] [CrossRef]
- Roy, S.; Juha, M.; Shephard, M.S.; Maniatty, A.M. Heat Transfer Model and Finite Element Formulation for Simulation of Selective Laser Melting. Comput. Mech. 2018, 62, 273–284. [Google Scholar] [CrossRef]
- Luo, C.; Qiu, J.; Yan, Y.; Yang, J.; Uher, C.; Tang, X. Finite Element Analysis of Temperature and Stress Fields during the Selective Laser Melting Process of Thermoelectric SnTe. J. Mater. Process. Technol. 2018, 261, 74–85. [Google Scholar] [CrossRef]
- Mishra, A.K.; Aggarwal, A.; Kumar, A.; Sinha, N. Identification of a Suitable Volumetric Heat Source for Modelling of Selective Laser Melting of Ti6Al4V Powder Using Numerical and Experimental Validation Approach. Int. J. Adv. Manuf. Technol. 2018, 99, 2257–2270. [Google Scholar] [CrossRef]
- Hussein, A.; Hao, L.; Yan, C.; Everson, R. Finite Element Simulation of the Temperature and Stress Fields in Single Layers Built Without-Support in Selective Laser Melting. Mater. Des. 2013, 52, 638–647. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, W.; Xu, Y.; Lu, Z.; Li, D. The Thermal-Mechanical Behavior of WTaMoNb High-Entropy Alloy via Selective Laser Melting (SLM): Experiment and Simulation. Int. J. Adv. Manuf. Technol. 2018, 96, 461–474. [Google Scholar] [CrossRef]
- Zhang, Y.; Guillemot, G.; Bernacki, M.; Bellet, M. Macroscopic Thermal Finite Element Modeling of Additive Metal Manufacturing by Selective Laser Melting Process. Comput. Methods Appl. Mech. Eng. 2018, 331, 514–535. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, P.; Liu, Z.; Feng, Z.; Wang, C.; Guo, Y. Thermofluid Field of Molten Pool and Its Effects during Selective Laser Melting (SLM) of Inconel 718 Alloy. Addit. Manuf. 2018, 21, 567–578. [Google Scholar] [CrossRef]
- Gao, S.; Tan, Z.; Lan, L.; Lu, G.; He, B. Experimental Investigation and Numerical Simulation of Residual Stress and Distortion of Ti6Al4V Components Manufactured Using Selective Laser Melting. J. Mater. Eng. Perform. 2022, 31, 8113–8123. [Google Scholar] [CrossRef]
- Kubra Karayagiz Alaa Elwany, G.T.B.F.L.J.J.M.I.K.; Arróyave, R. Numerical and Experimental Analysis of Heat Distribution in the Laser Powder Bed Fusion of Ti-6Al-4V. IISE Trans. 2019, 51, 136–152. [Google Scholar] [CrossRef]
- Nigito, E.; Diemer, F.; Husson, S.; Ou, S.F.; Tsai, M.H.; Rézaï-Aria, F. Microstructure of NiTi superelastic alloy manufactured by selective laser melting. Mater. Lett. 2022, 324, 132665. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Wang, D. A Study on the Residual Stress during Selective Laser Melting (SLM) of Metallic Powder. Int. J. Adv. Manuf. Technol. 2016, 87, 647–656. [Google Scholar] [CrossRef]
- Yadroitsava, I.; Grewar, S.; Hattingh, D.; Yadroitsev, I. Residual Stress in SLM Ti6Al4V Alloy Specimens. In Proceedings of the Materials Science Forum, Graz, Austria, 10–14 May 2015; Volume 828, pp. 305–310. [Google Scholar]
- Liu, B.; Li, B.-Q.; Li, Z.; Bai, P.; Wang, Y.; Kuai, Z. Numerical Investigation on Heat Transfer of Multi-Laser Processing during Selective Laser Melting of AlSi10Mg. Results Phys. 2019, 12, 454–459. [Google Scholar] [CrossRef]
- Dunlop, J.W.C.; Weinkamer, R.; Fratzl, P. Artful Interfaces within Biological Materials. Mater. Today 2011, 14, 70–78. [Google Scholar] [CrossRef]
- Li, Y.; Ortiz, C.; Boyce, M.C. A Generalized Mechanical Model for Suture Interfaces of Arbitrary Geometry. J. Mech. Phys. Solids 2013, 61, 1144–1167. [Google Scholar] [CrossRef]
- Liu, L.; Wang, D.; Wang, T.; Han, C.; Li, Y.; Tan, H.; Zhou, W.; Yan, X.; Lei, L.; Yang, Y. Laser Additive Manufacturing of Multimaterials with Hierarchical Interlocking Interface via a Flexible Scraper-Based Method. Int. J. Mach. Tools Manuf. 2025, 205, 104236. [Google Scholar] [CrossRef]
- Zou, F.; Yao, S.; Dong, Y.; Zheng, X.; Xie, M.; Yang, L.; Wang, D. Research on Multiscale Numerical Simulation Method for SLM Melting Process. Metals 2024, 14, 825. [Google Scholar] [CrossRef]




| Parametric | IN718 | Ti6Al4V |
|---|---|---|
| Absorption rate | 0.3 [26] | 0.4 [27] |
| Porosity | 0.5 | 0.5 |
| Thermal conductivity (W/m·°C) | 100 | 100 |
| Melting point (°C) | 1260 | 1680 |
| Scanning speed (mm/s) | 900 | 900 |
| Laser power (W) | 160 | 190 |
| Layer thickness (μm) | 30 | |
| Scanning pitch (μm) | 80 | |
| Spot diameter (μm) | 80 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Wang, T.; Liu, L.; Li, Y.; Han, C.; Tan, H.; Zhou, W.; Yang, Y.; Wang, D. Thermomechanical Behavior and Experimental Study of Additive Manufactured Superalloy/Titanium Alloy Horizontal Multi-Material Structures. Metals 2025, 15, 454. https://doi.org/10.3390/met15040454
Huang Y, Wang T, Liu L, Li Y, Han C, Tan H, Zhou W, Yang Y, Wang D. Thermomechanical Behavior and Experimental Study of Additive Manufactured Superalloy/Titanium Alloy Horizontal Multi-Material Structures. Metals. 2025; 15(4):454. https://doi.org/10.3390/met15040454
Chicago/Turabian StyleHuang, Yanlu, Tianyu Wang, Linqing Liu, Yang Li, Changjun Han, Hua Tan, Wei Zhou, Yongqiang Yang, and Di Wang. 2025. "Thermomechanical Behavior and Experimental Study of Additive Manufactured Superalloy/Titanium Alloy Horizontal Multi-Material Structures" Metals 15, no. 4: 454. https://doi.org/10.3390/met15040454
APA StyleHuang, Y., Wang, T., Liu, L., Li, Y., Han, C., Tan, H., Zhou, W., Yang, Y., & Wang, D. (2025). Thermomechanical Behavior and Experimental Study of Additive Manufactured Superalloy/Titanium Alloy Horizontal Multi-Material Structures. Metals, 15(4), 454. https://doi.org/10.3390/met15040454







