High-Throughput Screening of Rare-Earth-Lean Intermetallic 1-13-X Compounds for Good Hard-Magnetic Properties
Abstract
:1. Introduction
2. Theoretical Approach
2.1. Screening with TB-LMTO-ASA
2.2. Calculation of the Magnetocrystalline Anisotropy Energy
2.3. Phase Stability
2.4. Structure Models
2.5. Structural Relaxation with VASP
3. Results and Discussion
3.1. Crystal Structures
3.2. Results of the Screening
3.3. Comparison to ThMn Compounds
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| NdFe | NdFeN | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| H | K | L | 2 | I/rel. | H | K | L | 2 | I/rel. | |
| 1 | 1 | 2 | 25.421 | 6.56 | 2 | 0 | 0 | 24.722 | 6.36 | |
| 2 | 0 | 0 | 25.424 | 3.20 | 1 | 1 | 2 | 25.188 | 6.14 | |
| 2 | 1 | 1 | 29.906 | 0.00 | 2 | 1 | 1 | 29.177 | 0.07 | |
| 2 | 0 | 2 | 31.267 | 20.62 | 2 | 0 | 2 | 30.785 | 23.46 | |
| 0 | 0 | 4 | 36.255 | 5.65 | 2 | 2 | 0 | 35.245 | 14.70 | |
| 2 | 2 | 0 | 36.263 | 11.29 | 0 | 0 | 4 | 36.584 | 7.05 | |
| 2 | 1 | 3 | 39.642 | 0.00 | 2 | 1 | 3 | 39.230 | 0.14 | |
| 1 | 1 | 4 | 40.714 | 27.01 | 3 | 1 | 0 | 39.568 | 38.96 | |
| 2 | 2 | 2 | 40.720 | 27.13 | 2 | 2 | 2 | 39.876 | 29.24 | |
| 3 | 1 | 0 | 40.721 | 27.06 | 1 | 1 | 4 | 40.786 | 31.35 | |
| 2 | 0 | 4 | 44.802 | 50.24 | 3 | 1 | 2 | 43.812 | 100.00 | |
| 3 | 1 | 2 | 44.807 | 100.00 | 2 | 0 | 4 | 44.657 | 55.56 | |
| 3 | 2 | 1 | 47.689 | 0.00 | 3 | 2 | 1 | 46.385 | 0.01 | |
| 2 | 2 | 4 | 52.215 | 0.23 | 4 | 0 | 0 | 50.700 | 0.01 | |
| 4 | 0 | 0 | 52.221 | 0.09 | 2 | 2 | 4 | 51.708 | 0.08 | |
| 2 | 1 | 5 | 54.800 | 52.35 | 4 | 1 | 1 | 53.262 | 63.36 | |
| 3 | 2 | 3 | 54.806 | 52.28 | 3 | 2 | 3 | 53.751 | 63.47 | |
| 4 | 1 | 1 | 54.808 | 52.34 | 3 | 3 | 0 | 54.016 | 8.71 | |
| 0 | 0 | 6 | 55.640 | 4.63 | 4 | 0 | 2 | 54.259 | 4.10 | |
| 3 | 1 | 4 | 55.647 | 4.42 | 2 | 1 | 5 | 54.719 | 60.42 | |
| 4 | 0 | 2 | 55.652 | 2.27 | 3 | 1 | 4 | 54.981 | 3.35 | |
| 3 | 3 | 0 | 55.653 | 9.36 | 0 | 0 | 6 | 56.171 | 5.37 | |
| 1 | 1 | 6 | 58.938 | 11.56 | 4 | 2 | 0 | 57.199 | 17.86 | |
| 3 | 3 | 2 | 58.949 | 11.63 | 3 | 3 | 2 | 57.432 | 11.60 | |
| 4 | 2 | 0 | 58.950 | 11.49 | 1 | 1 | 6 | 59.277 | 12.83 |
References
- Coey, J.M.D. Hard Magnetic Materials: A Perspective. IEEE. Trans. Magn. 2011, 47, 4671–4681. [Google Scholar] [CrossRef]
- Gutfleisch, O.; Willard, M.A.; Brück, E.; Chen, C.H.; Sankar, S.G.; Liu, J.P. Magnetic materials and devices for the 21st century: Stronger, lighter, and more energy efficient. Adv. Mater. 2011, 23, 821–842. [Google Scholar] [CrossRef]
- Kuz’min, M.D.; Skokov, K.P.; Jian, H.; Radulov, I.; Gutfleisch, O. Towards high-performance permanent magnets without rare earths. J. Phys. Condens. Matter 2014, 26, 064205. [Google Scholar]
- Felser, C.; Wollmann, L.; Chadov, S.; Fecher, G.H.; Parkin, S.S.P. Basics and prospective of magnetic Heusler compounds. Appl. Mater. 2015, 3, 041518. [Google Scholar] [CrossRef]
- Fujieda, S.; Fujita, A.; Fukamichi, K. Large magnetocaloric effect in La(FexSi1-x)13 itinerant-electron metamagnetic compounds. Appl. Phys. Lett. 2002, 81, 1276. [Google Scholar] [CrossRef]
- Löwe, K.; Liu, J.; Skokov, K.; Moore, J.D.; Sepehri-Amin, H.; Hono, K.; Katter, M.; Gutfleisch, O. The effect of the thermal decomposition reaction on the mechanical and magnetocaloric properties of La(Fe,Si,Co)13. Acta Mater. 2012, 60, 4268–4276. [Google Scholar] [CrossRef]
- Skokov, K.P.; Karpenkov, A.Y.; Karpenkov, D.Y.; Gutfleisch, O. Heat exchangers made of polymer-bonded La(Fe,Si)13. J. Appl. Phys. 2014, 115, 17A941. [Google Scholar] [CrossRef]
- Skokov, K.P.; Müller, K.-H.; Moore, J.D.; Liu, J.; Karpenkov, A.Y.; Krautz, M.; Gutfleisch, O. Influence of thermal hysteresis and field cycling on the magnetocaloric effect in LaFe11.6Si1.4. J. Alloys Compd. 2013, 552, 310–317. [Google Scholar] [CrossRef]
- Krautz, M.; Skokov, K.; Gottschall, T.; Teixeira, C.S.; Waske, A.; Liu, J.; Schultz, L.; Gutfleisch, O. Systematic investigation of Mn substituted La(Fe,Si)13 alloys and their hydrides for room-temperature magnetocaloric application. J. Alloys Compd. 2014, 598, 27–32. [Google Scholar] [CrossRef]
- Shen, Y.; Turgut, Z.; Horwath, J.; Yang, M. Bulk nanocomposite LaCo5/LaCo13 magnets. J. Appl. Phys. 2011, 109, 07A765. [Google Scholar] [CrossRef]
- Pani, M.; Manfrinetti, P.; Provino, A.; Yuan, F.; Mozharivskyj, Y.; Morozkin, A.V.; Knotko, A.V.; Garshev, A.V.; Yapaskurt, V.O.; Isnard, O. New tetragonal derivatives of cubic NaZn13-type structures:RNi6Si6 compounds, crystal structure and magnetic ordering (R=Y,La,Ce,Sm,Gd-Yb). J. Solid State Chem. 2014, 210, 45–52. [Google Scholar] [CrossRef]
- Michor, H.; El-Hagary, M.; Mea, M.D.; Pieper, M.W.; Reissner, M.; Hilscher, G.; Khmelevskyi, S.; Mohn, P.; Schneider, G.; Giester, G.; et al. Itinerant electron metamagnetism in LaCo9Si4. Phys. Rev. B 2004, 69, 081404. [Google Scholar] [CrossRef]
- Körner, W.; Krugel, G.; Elsässer, C. Theoretical screening of intermetallic ThMn12-type phases for new hard-magnetic compounds with low rare earth content. Sci. Rep. 2016, 6, 24686. [Google Scholar]
- Körner, W.; Krugel, G.; Urban, D.F.; Elsässer, C. Screening of rare-earth-lean intermetallic 1-11 and 1-11-X compounds of YNi9In2-type for hard-magnetic applications. Scr. Mater. 2018, 154, 295. [Google Scholar]
- Hirayama, Y.; Takahashi, Y.K.; Hirosawa, S.; Hono, K. NdFe12Nx hard-magnetic compound with high magnetization and anisotropy field. Scr. Mater. 2015, 95, 70–72. [Google Scholar] [CrossRef]
- Miyake, T.; Terakura, K.; Harashima, Y.; Kino, H.; Ishibashi, S. First-Principles Study of Magnetocrystalline Anisotropy and Magnetization in NdFe12, NdFe11Ti, and NdFe11TiN. J. Phys. Soc. Jpn. 2014, 83, 043702. [Google Scholar] [CrossRef]
- Harashima, Y.; Terakura, K.; Kino, H.; Ishibashi, S.; Miyake, T. First-Principles Study of Structural and Magnetic Properties of R(Fe,Ti)12 and R(Fe,Ti)12N (R = Nd, Sm, Y). JPS Conf. Proc. 2015, 5, 011021. [Google Scholar]
- Andersen, O.K. Linear methods in band theory. Phys. Rev. B 1975, 12, 3060. [Google Scholar] [CrossRef]
- Hummler, K.; Fähnle, M. Ab initio calculation of local magnetic moments and the crystal field in scrR2Fe14B (scrR = Gd, Tb, Dy, Ho, and Er). Phys. Rev. B 1992, 45, 3161. [Google Scholar] [CrossRef]
- Fähnle, M.; Hummler, K.; Liebs, M.; Beuerle, T. Ab initio electron theory for hard-magnetic rare-earth- transition-metal intermetallics. Appl. Phys. A 1993, 57, 67–76. [Google Scholar] [CrossRef]
- Drebov, N.; Martinez-Limia, A.; Kunz, L.; Gola, A.; Shigematsu, T.; Eckl, T.; Gumbsch, P.; Elsässer, C. Ab initio screening methodology applied to the search for new permanent magnetic materials. New J. Phys. 2013, 15, 125023. [Google Scholar] [CrossRef]
- Brooks, M.S.S.; Nordström, L.; Johannson, B. 3d-5d band magnetism in rare earth-transition metal intermetallics: Total and partial magnetic moments of the RFe2 (R = Gd-Yb) Laves phase compounds. J. Phys. Condens. Matter 1991, 3, 2357. [Google Scholar] [CrossRef]
- Koelling, D.D.; Harmon, B.N. A technique for relativistic spin-polarised calculations. J. Phys. C Solid State Phys. 1977, 10, 3107. [Google Scholar] [CrossRef]
- Von Barth, U.; Hedin, L. A local exchange-correlation potential for the spin polarized case. J. Phys. C Solid State Phys. 1972, 5, 1629. [Google Scholar]
- Moruzzi, V.L.; Janak, J.F.; Williams, A.R. Calculated Electronic Properties of Metals; Pergamon: New York, NY, USA, 1978. [Google Scholar]
- Beuerle, T.; Fähnle, M. Ab initio calculation of magnetic moments and hyperfine fields in Y2Fe17Z3 (Z = H, C, N). Phys. Stat. Solidi B 1992, 174, 257–272. [Google Scholar] [CrossRef]
- Richter, M.; Oppeneer, P.M.; Eschrig, H.; Johansson, B. Calculated crystal-field parameters of SmCo5. Phys. Rev. B 1992, 46, 13919. [Google Scholar] [CrossRef]
- Richter, M. Band structure theory of magnetism in 3d-4f compounds. J. Phys. D Appl. Phys. 1998, 31, 1017–1048. [Google Scholar] [CrossRef]
- Stevens, K.W.H. Matrix Elements and Operator Equivalents Connected with the Magnetic Properties of Rare Earth Ions. Proc. Phys. Soc. 1952, A65, 209–215. [Google Scholar] [CrossRef]
- Cadieu, F.J.; Hegde, H.; Navarathna, A.; Rani, R.; Chen, K. High-energy product ThMn12 Sm-Fe-T and Sm-Fe permanent magnets synthesized as oriented sputtered films. Appl. Phys. Lett. 1991, 59, 875. [Google Scholar] [CrossRef]
- Ohashi, K.; Yokoyama, T.; Osugi, R.; Tawara, Y. The magnetic and structural properties of R-Ti-Fe Ternary compounds. IEEE Trans. Magn. 1987, 23, 3101–3103. [Google Scholar] [CrossRef]
- Akayama, M.; Fujii, H.; Yamamoto, K.; Tatami, K. Physical properties of nitrogenated RFe11Ti intermetallic compounds (R = Ce, Pr and Nd) with ThMn12-type structure. J. Magn. Magn. Mater. 1994, 130, 99. [Google Scholar] [CrossRef]
- Sato, T.; Ohsuna, T.; Yano, M.; Kato, A.; Kaneko, Y. Permanent magnetic properties of NdFe12Nx sputtered films epitaxially grown on V buffer layer. J. Appl. Phys. 2017, 122, 053903. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- For Details on PAW Potentials Provided with VASP. Available online: http://cms.mpi.univie.ac.at/vasp/vasp/PAW_potentials.html (accessed on 9 August 2019).
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Kraus, W.; Nolze, G. POWDER CELL—A program for the representation and manipulation of crystal structures and calculation of the resulting X-ray powder patterns. J. Appl. Cryst. 1996, 29, 301–303. [Google Scholar] [CrossRef]
- Buschow, K.H.J. Chapter Rare Earth Magnets: Materials (Table I). In Concise Encyclopedia of Magnetic and Superconducting Materials, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Herbst, J.F. R2Fe14B materials: Intrinsic properties and technological aspects. Rev. Mod. Phys. 1991, 63, 819–898. [Google Scholar] [CrossRef]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Butcher, T.; Körner, W.; Krugel, G.; Elsässer, C. Dependence of magnetisation and magnetocrystalline anisotropy on site distribution of alloying elements in RE-TM phases with ThMn12 structure. J. Magn. Magn. Mater. 2017, 441, 1–5. [Google Scholar] [CrossRef]
- Coey, J.M.D. Novel Permanent Magnetic Materials. Phys. Scr. 1991, 39, 21. [Google Scholar] [CrossRef]
- Skomski, R.; Kuz’min, M.D.; Coey, J.M.D. Crystal field in nitrogenated rare-earth intermetallics. J. Appl. Phys. 1993, 73, 6934–6936. [Google Scholar] [CrossRef]
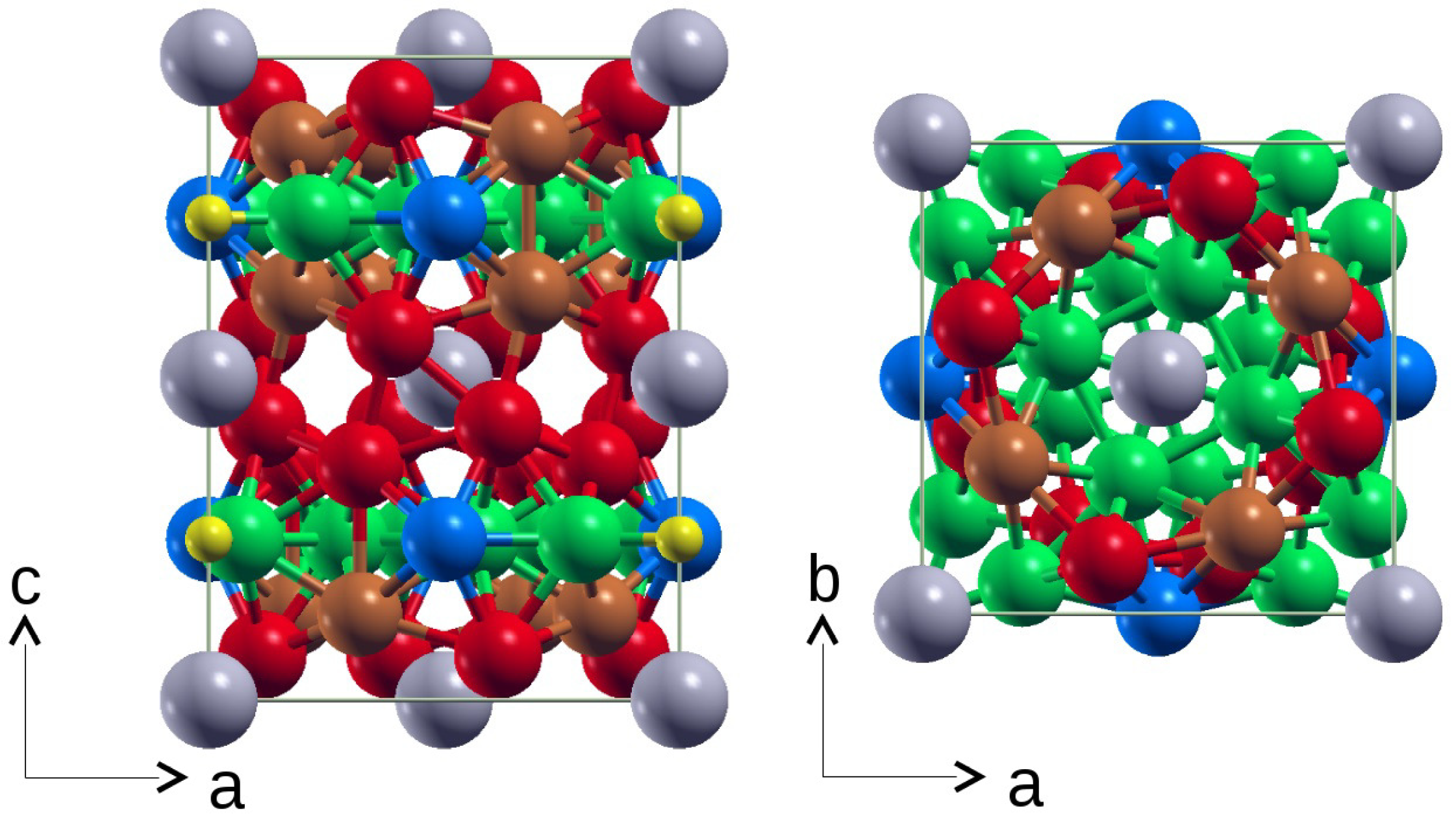

| Wyckoff Position Representative Site | (16k) | (16l) | (16l) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x | y | z | x | y | z | x | y | z | |||
| LaCoSi | 0.070 | 0.201 | 0 | 0.627 | 0.127 | 0.180 | 0.170 | 0.670 | 0.121 | ||
| NdFe | 0.064 | 0.203 | 0 | 0.617 | 0.117 | 0.180 | 0.180 | 0.680 | 0.117 | ||
| NdFeN | 0.067 | 0.211 | 0 | 0.615 | 0.115 | 0.180 | 0.179 | 0.679 | 0.116 |
| System | (BH) | M | K | H | |
|---|---|---|---|---|---|
| (kJ/m) | (T) | (MJ/m) | (T) | (eV/atom) | |
| NdFeB | 617 | 1.96 | 0 | 0 | −0.25 |
| NdFeC | 611 | 1.95 | −10 | −16 | −0.20 |
| NdFeN | 660 | 2.02 | −19 | −23 | −0.44 |
| NdCoN | 327 | 1.42 | −13 | −29 | −0.34 |
| SmFeB | 526 | 1.81 | 2 | 3 | −0.26 |
| SmFeC | 521 | 1.80 | 19 | 26 | −0.22 |
| SmFeN | 566 | 1.87 | 34 | 45 | −0.45 |
| SmCoN | 262 | 1.27 | 24 | 48 | −0.35 |
| SmFeTiN | 406 | 1.59 | 34 | 54 | −0.54 |
| SmFeVN | 411 | 1.60 | 36 | 57 | −0.52 |
| SmFeCoN | 551 | 1.85 | 33 | 45 | −0.44 |
| SmFeNiN | 506 | 1.77 | 34 | 48 | −0.43 |
| SmFeCuN | 481 | 1.73 | 33 | 48 | −0.41 |
| SmFeZnN | 459 | 1.68 | 34 | 50 | −0.46 |
| SmFeGaN | 434 | 1.64 | 34 | 53 | −0.56 |
| SmFeAlN | 418 | 1.61 | 36 | 56 | −0.56 |
| SmFeSiN | 410 | 1.59 | 36 | 57 | −0.63 |
| SmFePN | 423 | 1.62 | 37 | 57 | −0.65 |
| NdFeB | 556 (516 ) | 1.87 (1.86 ) | 19 (4.9 ) | 26 (6.7 ) | −0.02 |
| SmCo | 174 (219 ) | 1.04 (1.07 ) | 69 (17.2 ) | 162 (40.4 ) | 0.06 |
| SmFeN | 459 (472 ) | 1.69 (1.54 ) | 27 (8.6 ) | 40 (14.0 ) | −0.82 |
| (MJ/m) | NdFeN | NdFeN | SmFeN | SmFeN |
|---|---|---|---|---|
| (1-12-X) | 47 | 42 | −71 | −63 |
| * (1-13-X) | −26 | −19 | 49 | 34 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krugel, G.; Körner, W.; Urban, D.F.; Gutfleisch, O.; Elsässer, C. High-Throughput Screening of Rare-Earth-Lean Intermetallic 1-13-X Compounds for Good Hard-Magnetic Properties. Metals 2019, 9, 1096. https://doi.org/10.3390/met9101096
Krugel G, Körner W, Urban DF, Gutfleisch O, Elsässer C. High-Throughput Screening of Rare-Earth-Lean Intermetallic 1-13-X Compounds for Good Hard-Magnetic Properties. Metals. 2019; 9(10):1096. https://doi.org/10.3390/met9101096
Chicago/Turabian StyleKrugel, Georg, Wolfgang Körner, Daniel F. Urban, Oliver Gutfleisch, and Christian Elsässer. 2019. "High-Throughput Screening of Rare-Earth-Lean Intermetallic 1-13-X Compounds for Good Hard-Magnetic Properties" Metals 9, no. 10: 1096. https://doi.org/10.3390/met9101096
APA StyleKrugel, G., Körner, W., Urban, D. F., Gutfleisch, O., & Elsässer, C. (2019). High-Throughput Screening of Rare-Earth-Lean Intermetallic 1-13-X Compounds for Good Hard-Magnetic Properties. Metals, 9(10), 1096. https://doi.org/10.3390/met9101096





