Evaluation of Heat Sources for the Simulation of the Temperature Distribution in Gas Metal Arc Welded Joints
Abstract
1. Introduction
2. Material
3. Methods
3.1. Thermal Analysis
- Constant initial temperature (CIT), as explained in Section 3.2;
- Constant volumetric heat flux (CVHF), as explained in Section 3.3;
- Goldak’s heat source distribution (GHSD), as explained in Section 3.4.
3.2. Constant Initial Temperature
3.3. Constant Volumetric Heat Flux
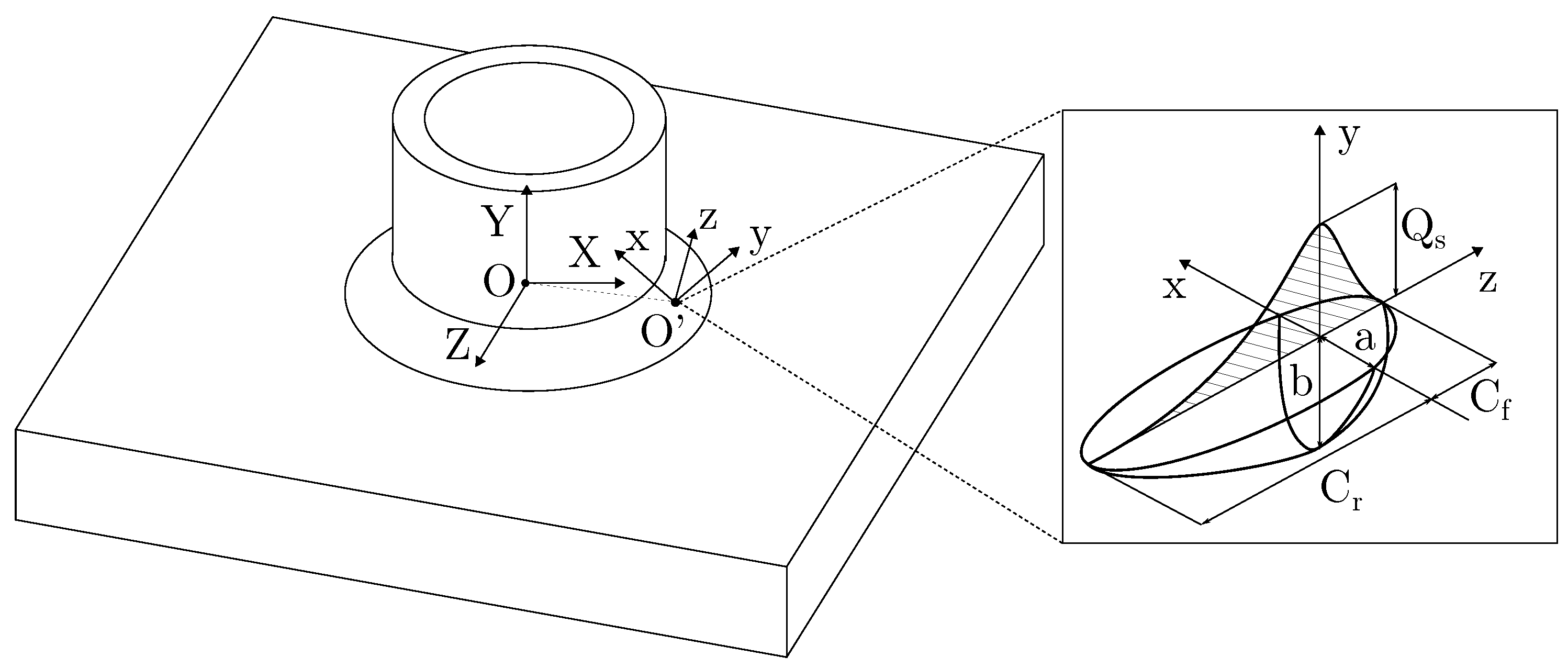
3.4. Goldak’s Heat Source Distribution
3.5. Weld Pool Shape
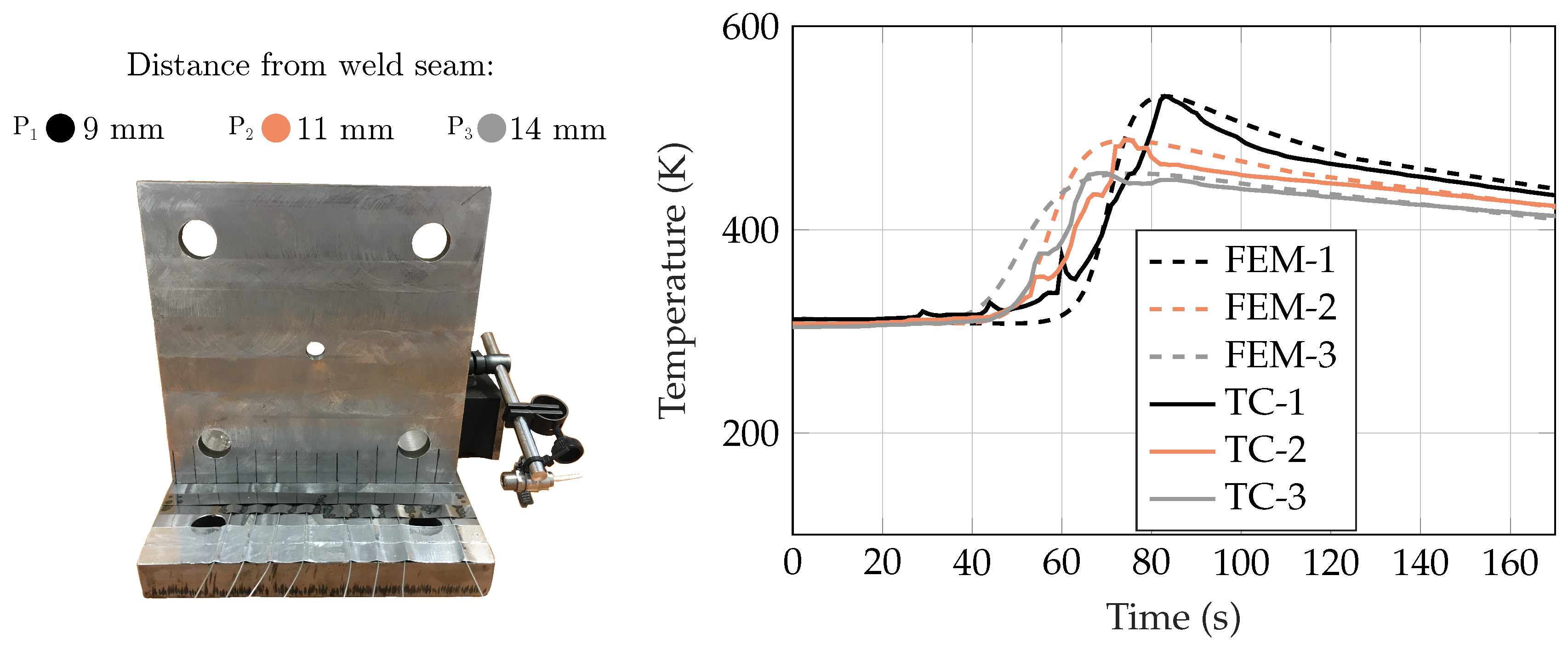
3.6. Experimental Set-Up
4. Results and Discussion
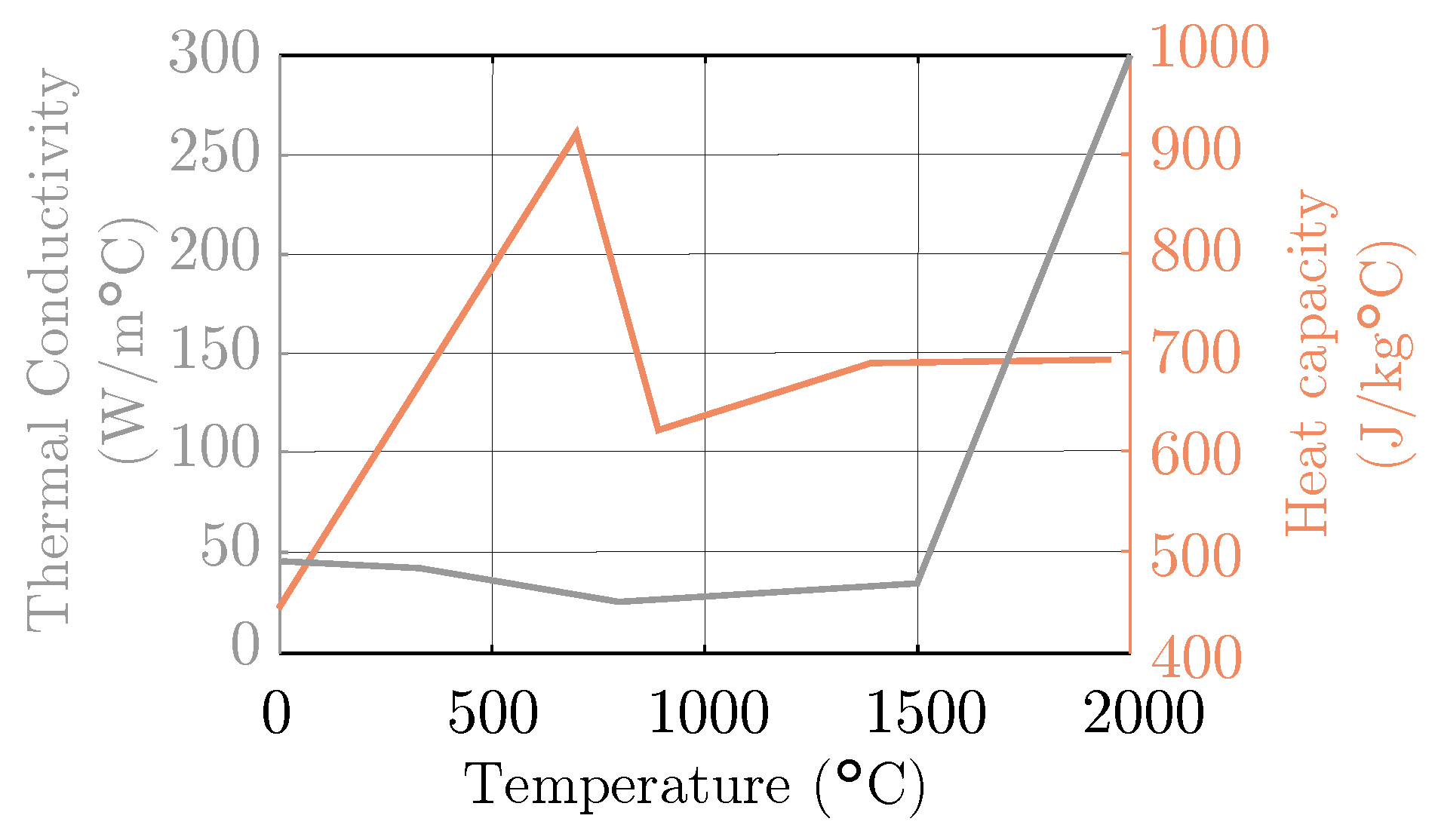
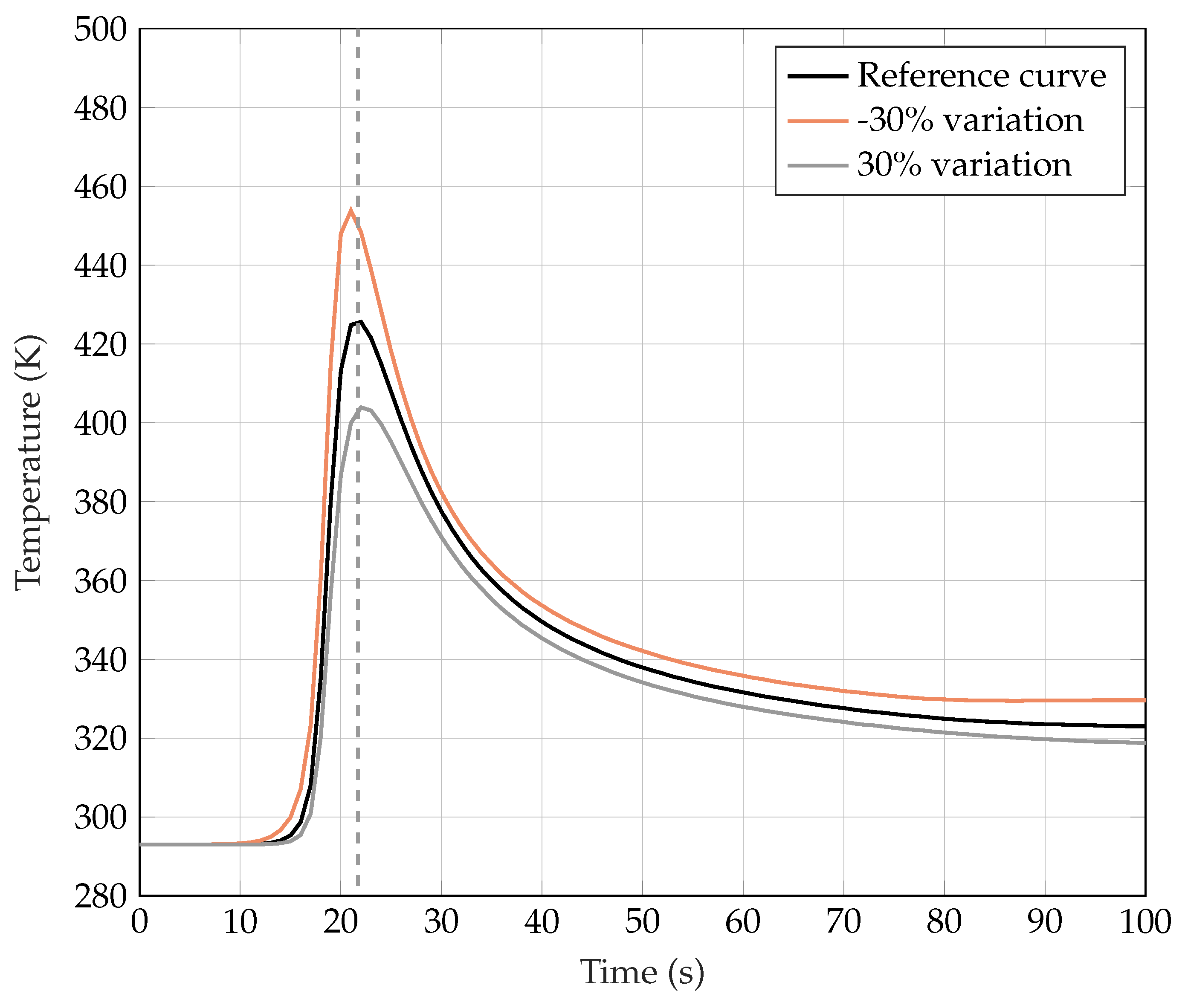
4.1. Sensitivity Analysis
- Thermal Conductivity, k (W m−1 K−1);
- Heat Capacity, c (J kg−1 K−1);
- Convection, h (W m−2 K−1);
- Emissivity, .
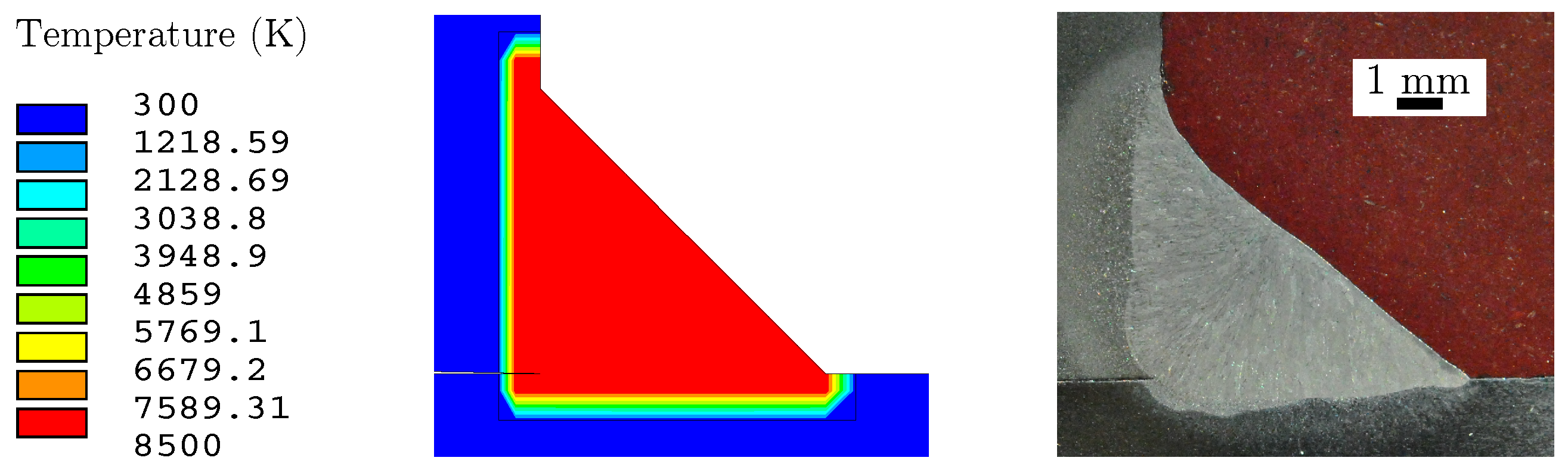
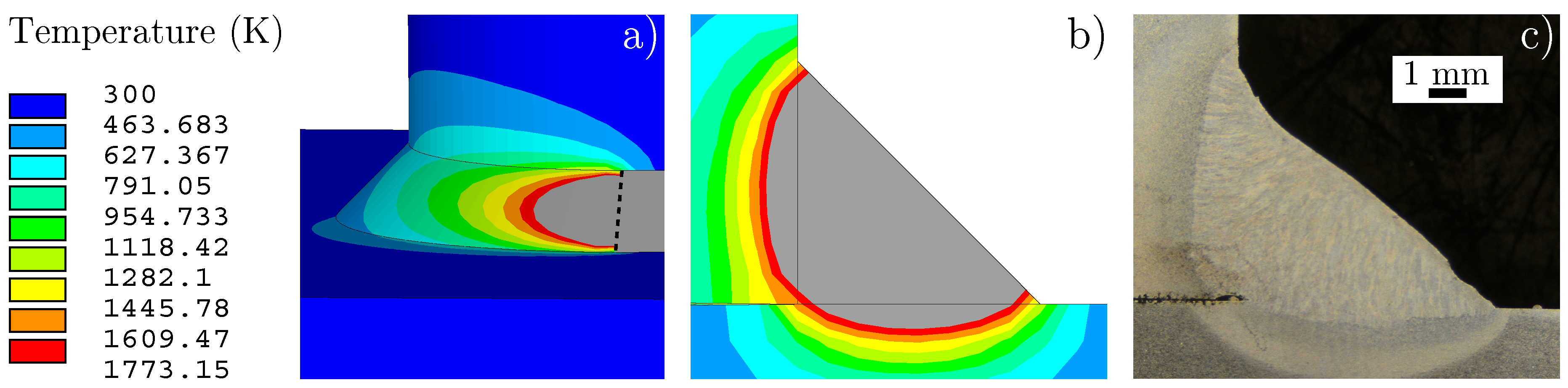
4.2. Results
Numerical Results
4.3. Comparison with Experimental Temperature Measurements
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Frija, M.; Hassine, T.; Fathallah, R.; Bouraoui, C.; Dogui, A. Finite element modelling of shot peening process: Prediction of the compressive residual stresses, the plastic deformations and the surface integrity. Mater. Sci. Eng. A 2006, 426, 173–180. [Google Scholar] [CrossRef]
- Macdonald, K.A. (Ed.) Fracture and Fatigue of Welded Joints and Structures; Woodhead Publishing: Sawston, Cambridge, UK, 2011; ISBN 9781845695132. [Google Scholar]
- Li, C.; Liu, Z.; Fang, X.; Guo, Y. Residual Stress in Metal Additive Manufacturing. Procedia CIRP 2018, 71, 348–353. [Google Scholar] [CrossRef]
- Bartolozzi, R.; Frendo, F. Stiffness and strength aspects in the design of automotive coil springs for McPherson front suspensions: A case study. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2011, 225, 1377–1391. [Google Scholar] [CrossRef]
- Elber, W. The Significance of Fatigue Crack Closure. In Damage Tolerance in Aircraft Structures; ASTM International: Philadelphia, PA, USA, 1971; pp. 230–243. [Google Scholar] [CrossRef]
- Deng, D. FEM prediction of welding residual stress and distortion in carbon steel considering phase transformation effects. Mater. Des. 2009, 30, 359–366. [Google Scholar] [CrossRef]
- Kik, T.; Górka, J. Numerical Simulations of Laser and Hybrid S700MC T-Joint Welding. Materials 2019, 12, 516. [Google Scholar] [CrossRef] [PubMed]
- Asserin, O.; Loredo, A.; Petelet, M.; Iooss, B. Global sensitivity analysis in welding simulations – what are the material data you really need? Finite Elem. Anal. Des. 2011, 47, 1004–1016. [Google Scholar] [CrossRef]
- Sajek, A. Application of FEM simulation method in area of the dynamics of cooling AHSS steel with a complex hybrid welding process. Weld. World 2019, 63, 1065–1073. [Google Scholar] [CrossRef]
- Gery, D.; Long, H.; Maropoulos, P. Effects of welding speed, energy input and heat source distribution on temperature variations in butt joint welding. J. Mater. Process. Technol. 2005, 167, 393–401. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. A new finite element model for welding heat sources. Metall. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Moravec, J.; Kik, T.; Novakova, I. Application of numerical simulations on X10CRWMOVNB9-2 steel multilayer welding. MM Sci. J. 2016, 2016, 1190–1193. [Google Scholar] [CrossRef]
- Zubairuddin, M.; Albert, S.K.; Mahadevan, S.; Vasudevan, M.; Chaudhari, V.; Suri, V.K. Experimental and finite element analysis of residual stress and distortion in GTA welding of modified 9Cr-1Mo steel. J. Mech. Sci. Technol. 2014, 28, 5095–5105. [Google Scholar] [CrossRef]
- Flint, T.; Francis, J.; Smith, M.; Balakrishnan, J. Extension of the double-ellipsoidal heat source model to narrow-groove and keyhole weld configurations. J. Mater. Process. Technol. 2017, 246, 123–135. [Google Scholar] [CrossRef]
- Cho, J.; Lee, B.; Moon, Y.; Tyne, C.V. Investigation of residual stress and post weld heat treatment of multi-pass welds by finite element method and experiments. J. Mater. Process. Technol. 2004, 155–156, 1690–1695. [Google Scholar] [CrossRef]
- Bhatti, A.A.; Barsoum, Z.; Murakawa, H.; Barsoum, I. Influence of thermo-mechanical material properties of different steel grades on welding residual stresses and angular distortion. Mater. Des. (1980–2015) 2015, 65, 878–889. [Google Scholar] [CrossRef]
- Frendo, F.; Bertini, L. Fatigue resistance of pipe-to-plate welded joint under in-phase and out-of-phase combined bending and torsion. Int. J. Fatigue 2015, 79, 46–53. [Google Scholar] [CrossRef]
- Bertini, L.; Cera, A.; Frendo, F. Experimental investigation of the fatigue resistance of pipe-to-plate welded connections under bending, torsion and mixed mode loading. Int. J. Fatigue 2014, 68, 178–185. [Google Scholar] [CrossRef]
- Bertini, L.; Frendo, F.; Marulo, G. Effects of plate stiffness on the fatigue resistance and failure location of pipe-to-plate welded joints under bending. Int. J. Fatigue 2016, 90, 78–86. [Google Scholar] [CrossRef]
- Zhu, J.; Khurshid, M.; Barsoum, Z. Accuracy of computational welding mechanics methods for estimation of angular distortion and residual stresses. Weld. World 2019. [Google Scholar] [CrossRef]
- Teng, T.L.; Chang, P.H.; Tseng, W.C. Effect of welding sequences on residual stresses. Comput. Struct. 2003, 81, 273–286. [Google Scholar] [CrossRef]
- Technical Office for Utilization of Steel. Data on Some Currently Used Steels (Données Physiques sur Quelques Aciers D’utilisation Courante); OTUA: Neuilly, France, 1975. [Google Scholar]
- Guen, E.L.; Carin, M.; Fabbro, R.; Coste, F.; Masson, P.L. 3D heat transfer model of hybrid laser Nd:Yag-MAG welding of S355 steel and experimental validation. Int. J. Heat Mass Transf. 2011, 54, 1313–1322. [Google Scholar] [CrossRef]
- Barsoum, Z.; Lundbäck, A. Simplified FE welding simulation of fillet welds—3D effects on the formation residual stresses. Eng. Fail. Anal. 2009, 16, 2281–2289. [Google Scholar] [CrossRef]
- Wikander, L.; Karlsson, L.; Nasstrom, M.; Webster, P. Finite element simulation and measurement of welding residual stresses. Model. Simul. Mater. Sci. Eng. 1994, 2, 845–864. [Google Scholar] [CrossRef]
- Frank, P.; Incropera, D.P.D. Introduction to Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 1986. [Google Scholar]
- Parkitny, R.; Winczek, J. Analytical solution of temporary temperature field in half-infinite body caused by moving tilted volumetric heat source. Int. J. Heat Mass Transf. 2013, 60, 469–479. [Google Scholar] [CrossRef]
- Bayock, F.N.; Kah, P.; Layus, P.; Karkhin, V. Numerical and Experimental Investigation of the Heat Input Effect on the Mechanical Properties and Microstructure of Dissimilar Weld Joints of 690-MPa QT and TMCP Steel. Metals 2019, 9, 355. [Google Scholar] [CrossRef]
- Winczek, J.; Gawronska, E.; Gucwa, M.; Sczygiol, N. Theoretical and Experimental Investigation of Temperature and Phase Transformation During SAW Overlaying. Appl. Sci. 2019, 9, 1472. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H.; Liang, W. Numerical and experimental investigations on welding residual stress in multi-pass butt-welded austenitic stainless steel pipe. Comput. Mater. Sci. 2008, 42, 234–244. [Google Scholar] [CrossRef]
- Sun, J.; Klassen, J.; Nitschke-Pagel, T.; Dilger, K. Effects of heat source geometric parameters and arc efficiency on welding temperature field, residual stress, and distortion in thin-plate full-penetration welds. Int. J. Adv. Manuf. Technol. 2018, 99, 497–515. [Google Scholar] [CrossRef]
- Cunat, P.J. The Welding of Stainless Steels. In Materials and Applications Series, Volume 3; Euro Inox: Luxembourg, 2007; ISBN 978-2-87997-180-3. [Google Scholar]
- Bowditch, W.A.B.K.E. Welding Technology Fundamentals; Goodheart-Willcox Co.: Tinley Park, IL, USA, 1997. [Google Scholar]
- Cai, X.; Dong, B.; Lin, S.; Murphy, A.B.; Fan, C.; Yang, C. Heat Source Characteristics of Ternary-Gas-Shielded Tandem Narrow-Gap GMAW. Materials 2019, 12, 1397. [Google Scholar] [CrossRef]




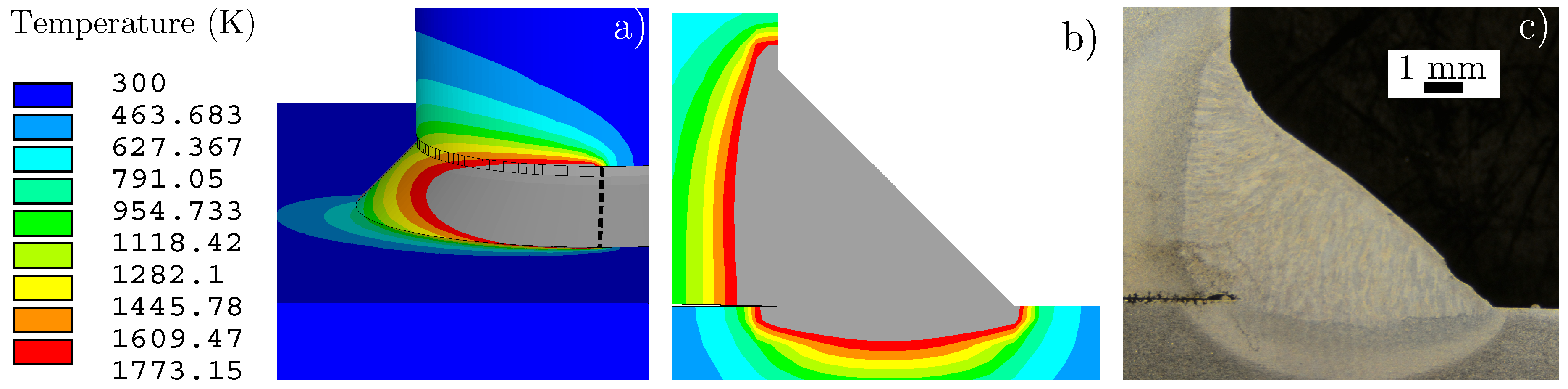




| Welding Current (I) | Arc Voltage (U) | Welding Time | Welding Speed | |||
| 211 | 25 | 75 | ||||
| Filler material | Welding wire diameter | Shielding gas | Gas flowrate | |||
| G3/4 Si1 | mm | 82% Ar 18% CO | m3 h−1 | |||
| Filler material composition | ||||||
| C% | Si% | Mn% | Cu% | |||
| 0.065–0.08 | 0.90–1.00 | 1.60–1.70 | max. 0.30 | |||
| Base material composition | ||||||
| C% | Si% | Mn% | P% | S% | N% | Cu% |
| 0.24 | 0.55 | 1.6 | 0.035 | 0.035 | 0.012 | 0.55 |
| Global Input Parameters | |||
|---|---|---|---|
| Arc Efficiency () | Arc Voltage () | Welding Current () | Heat Source Volume () |
| 0.75 | 25 | 211 | |
| Goldak’s heat source distribution (GHSD) input parameters | |||
| a | b | ||
| Parameters fine-tuned with GHSD model as reference | |||
| Constant volumetric heat flux (CVHF) input parameters | CIT input parameters | ||
| 36 | 7900 | ||
| Parameters fine-tuned with experimental results as reference | |||
| 40 | 8500 | ||
| d | d | d | d | ||||
| TC-1 | 8 | TC-2 | 10 | TC-3 | 12 | TC-4 | 14 |
| d | d | d | d | ||||
| TC-5 | 10 | TC-6 | 13 | TC-7 | 16 | TC-8 | 19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiocca, A.; Frendo, F.; Bertini, L. Evaluation of Heat Sources for the Simulation of the Temperature Distribution in Gas Metal Arc Welded Joints. Metals 2019, 9, 1142. https://doi.org/10.3390/met9111142
Chiocca A, Frendo F, Bertini L. Evaluation of Heat Sources for the Simulation of the Temperature Distribution in Gas Metal Arc Welded Joints. Metals. 2019; 9(11):1142. https://doi.org/10.3390/met9111142
Chicago/Turabian StyleChiocca, Andrea, Francesco Frendo, and Leonardo Bertini. 2019. "Evaluation of Heat Sources for the Simulation of the Temperature Distribution in Gas Metal Arc Welded Joints" Metals 9, no. 11: 1142. https://doi.org/10.3390/met9111142
APA StyleChiocca, A., Frendo, F., & Bertini, L. (2019). Evaluation of Heat Sources for the Simulation of the Temperature Distribution in Gas Metal Arc Welded Joints. Metals, 9(11), 1142. https://doi.org/10.3390/met9111142






