Prediction of Joint Shear Deformation Index of RC Beam–Column Joints
Abstract
:1. Introduction
2. Description of Test Program
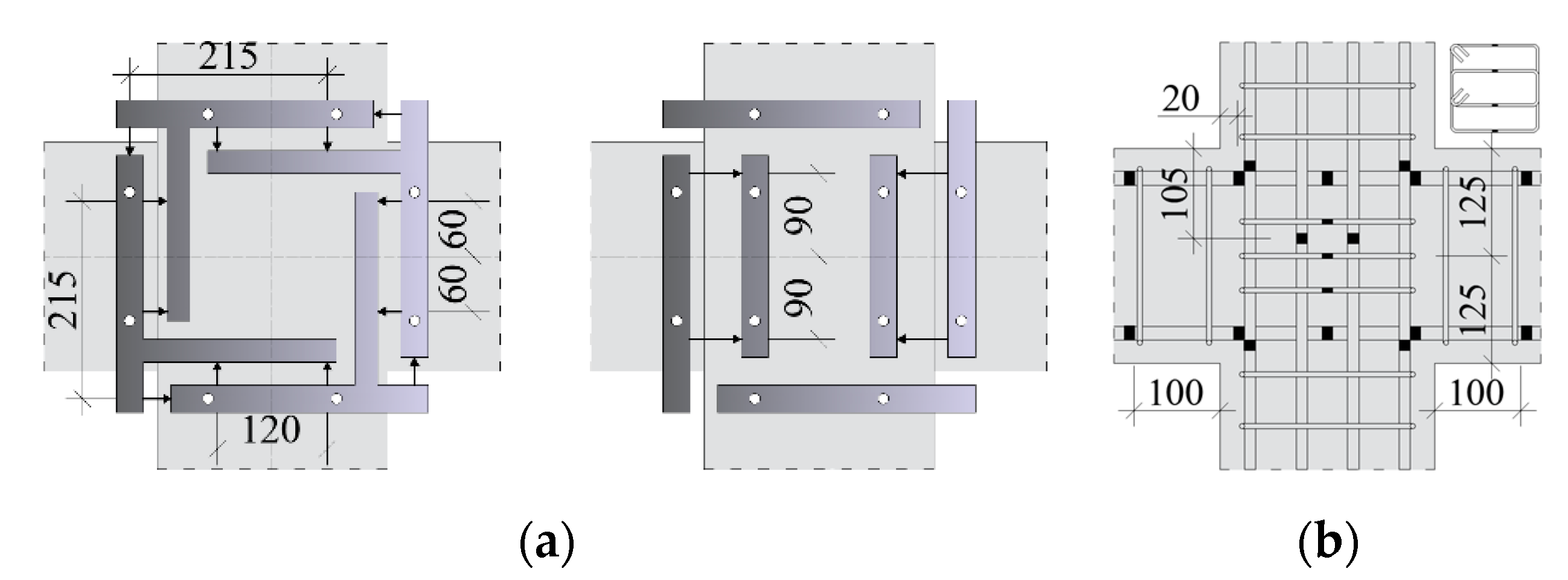
2.1. Test Specimens
2.2. Material Properties
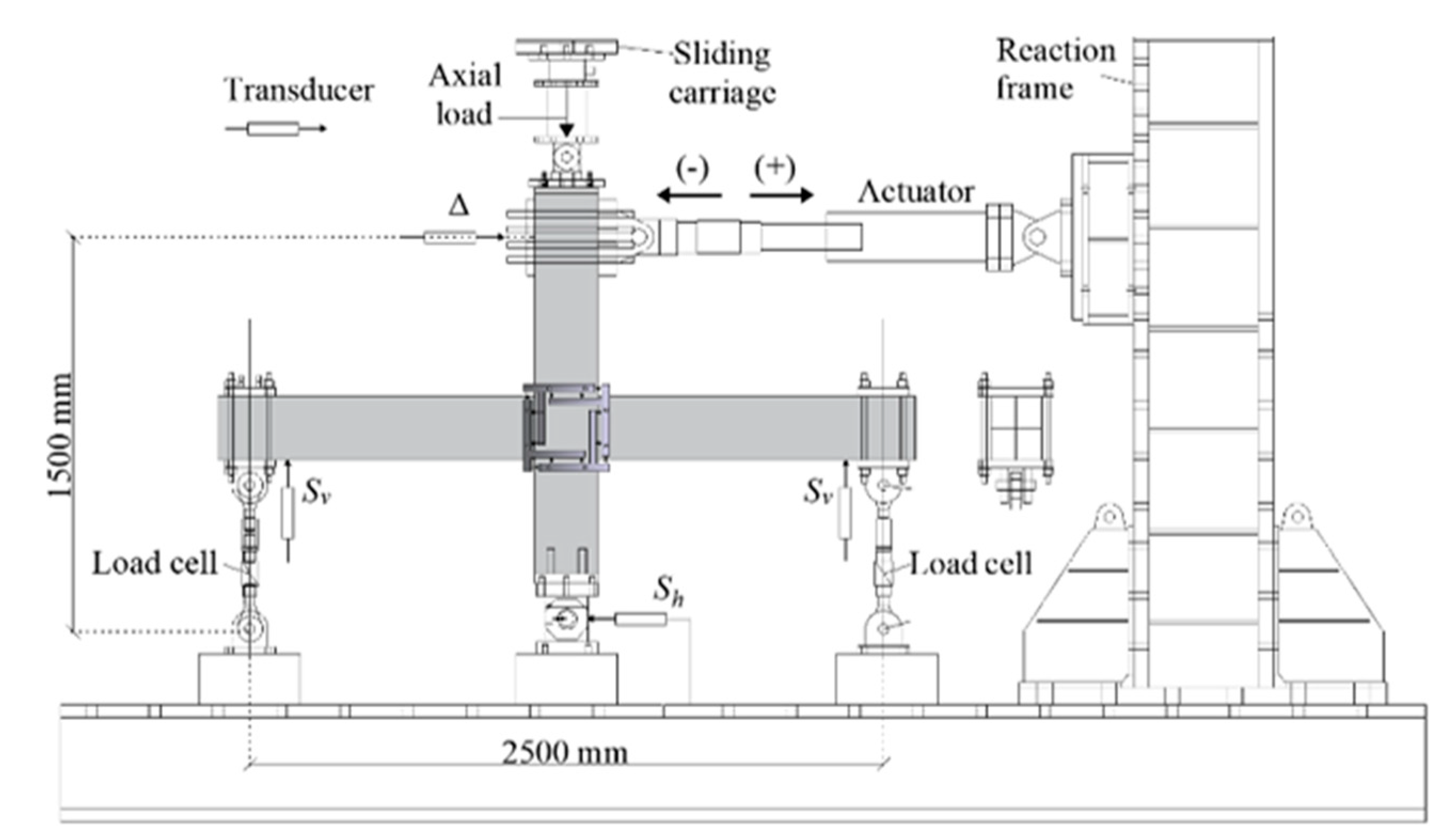
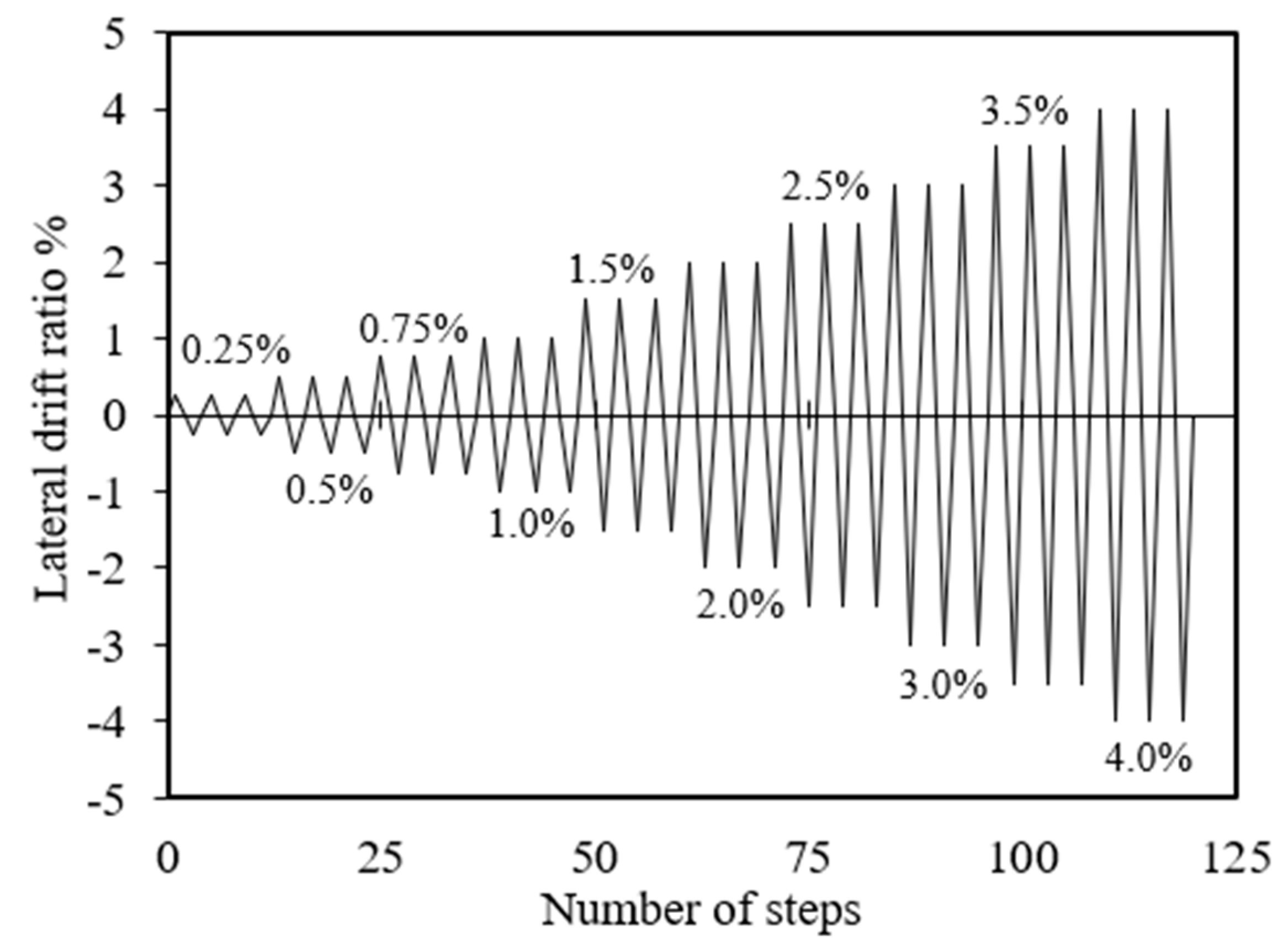
2.3. Test Setup and Loading History
2.4. Instrumentation
3. Test Results
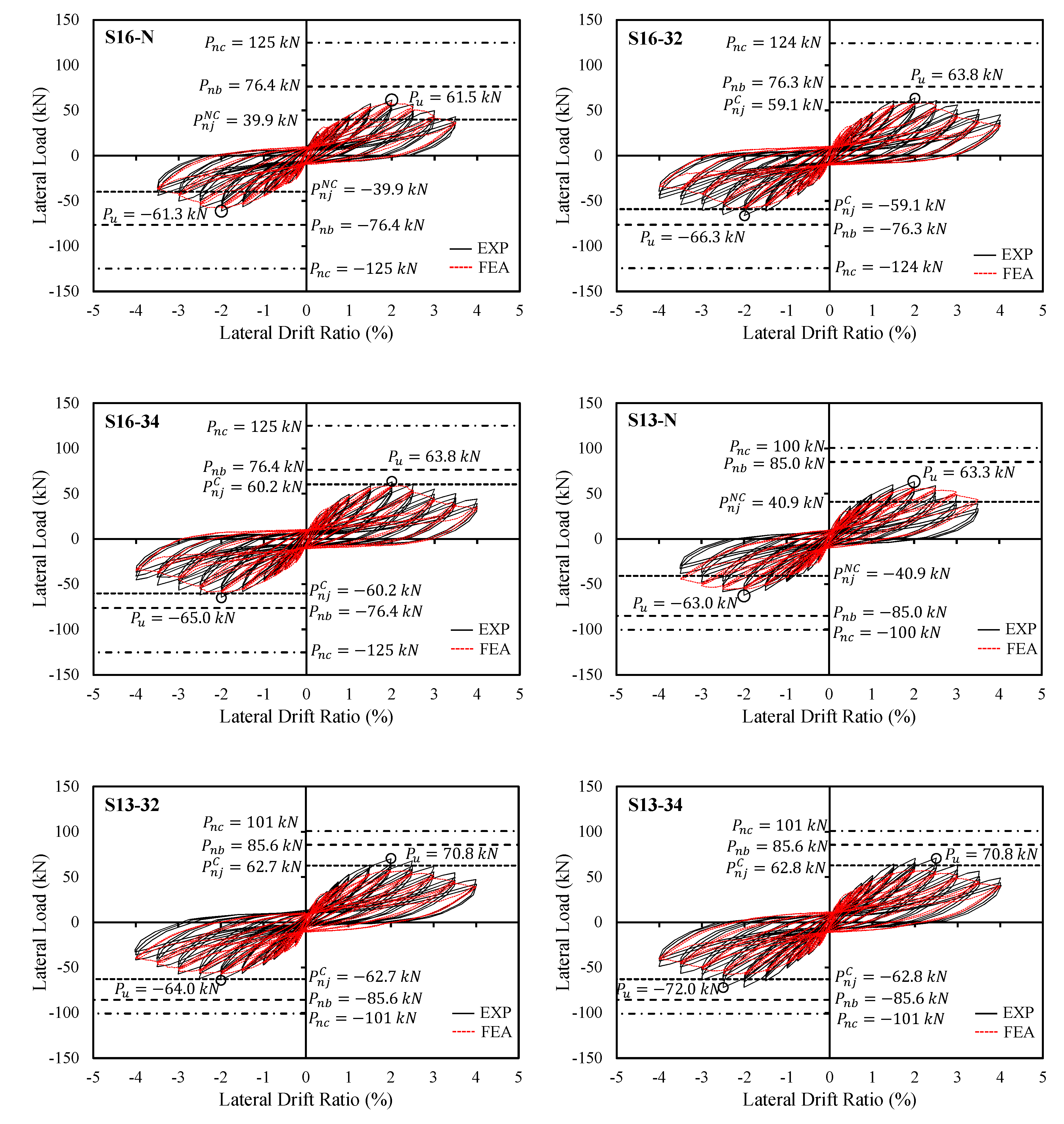
3.1. Lateral Load–Drift Ratio Relationships and Failure Modes
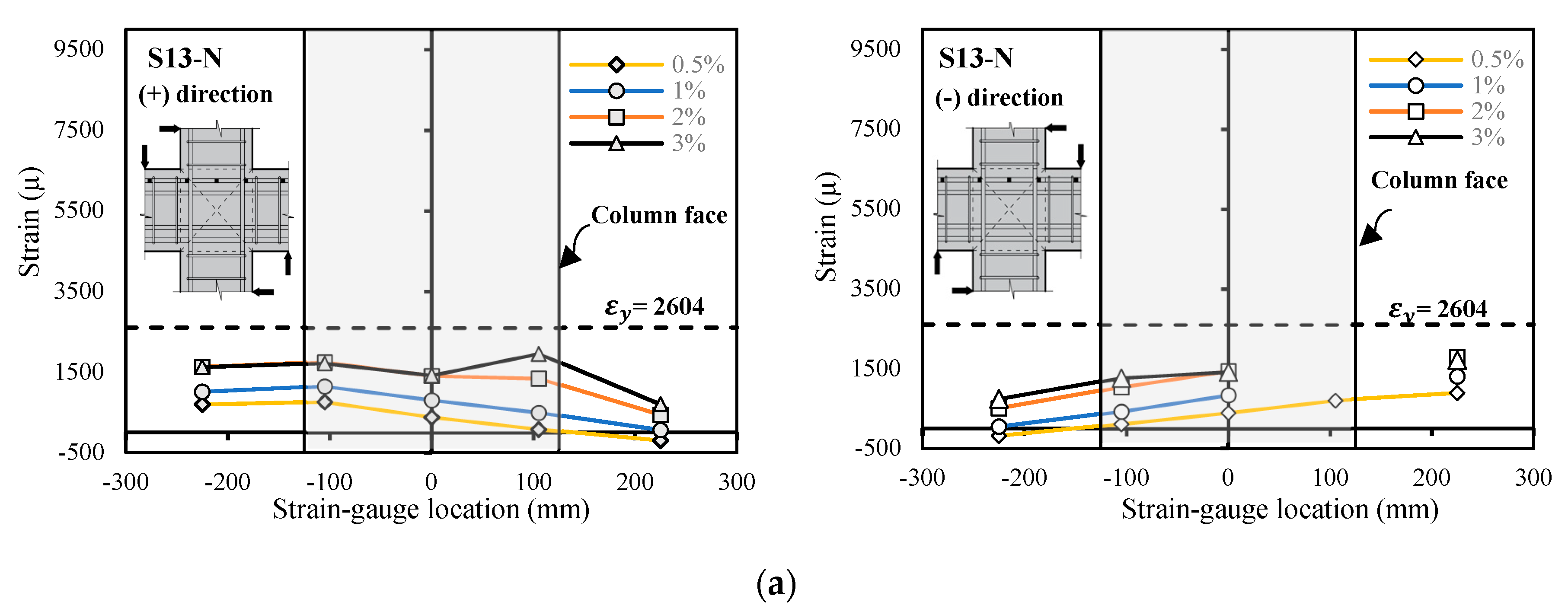
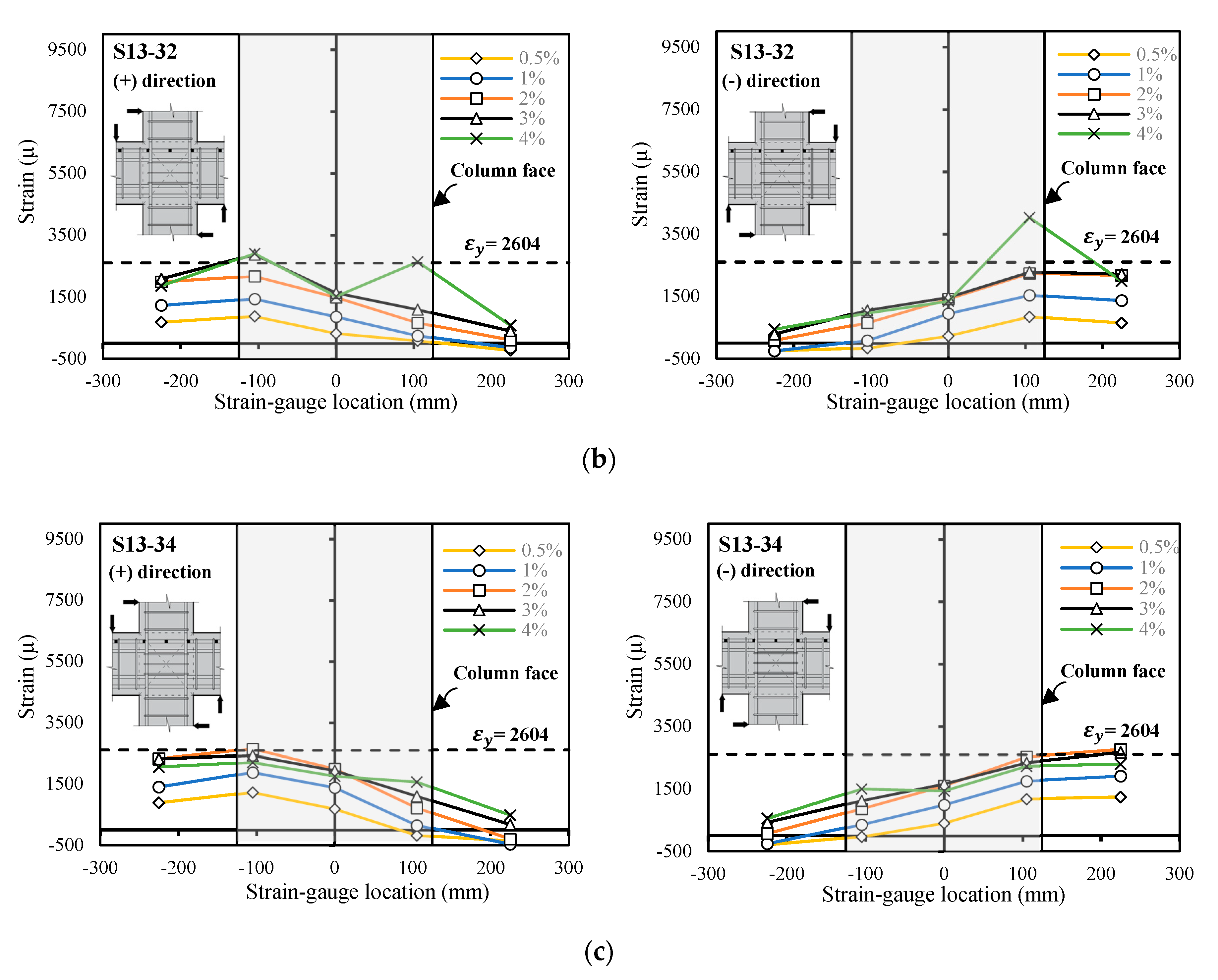
3.2. Strains of Beam Reinforcement
- At the peak strength of the specimens (), the strains in flexural beam bars measured at the beam end (i.e., the joint face) were lower than the yield strains ( = 2604 μ) or equal to the yield strains. In the subsequent loading, the strains at the beam end did not increase. This indicates that the specimens failed owing to joint shear.
- The amount of shear damage in the joint significantly decreased when the moderate amount of joint shear reinforcement was provided. Thus, the beam reinforcement strains at the beam end increased (compare the strains in Figure 10a–c). This indicates that the joint shear reinforcement successfully reduced the joint shear damage and increased the maximum lateral loads.
- The beam reinforcement at the column right face under positive loading was subjected to compressive stress at the beginning of the test. However, above , the bond deterioration of the beam-reinforcing bar passing through the joint occurred. Consequently, the transition of the compressive stress in the beam bar on the compression side at the beam end section to the tensile stress occurred (Figure 10a–c). The concrete took this compressive stress in the beam bar on the compression side, and the height of the compressive zone for the concrete may have increased, resulting in a smaller moment of the lever arm. Therefore, the moment in the beam section at the column face may have decreased. This phenomenon may have caused lateral strength degradation and stiffness degradation in all the test specimens (Figure 8). Our experiments are consistent with previous findings in the literature (Hakuto et al. [5] and Shiohara [12]).
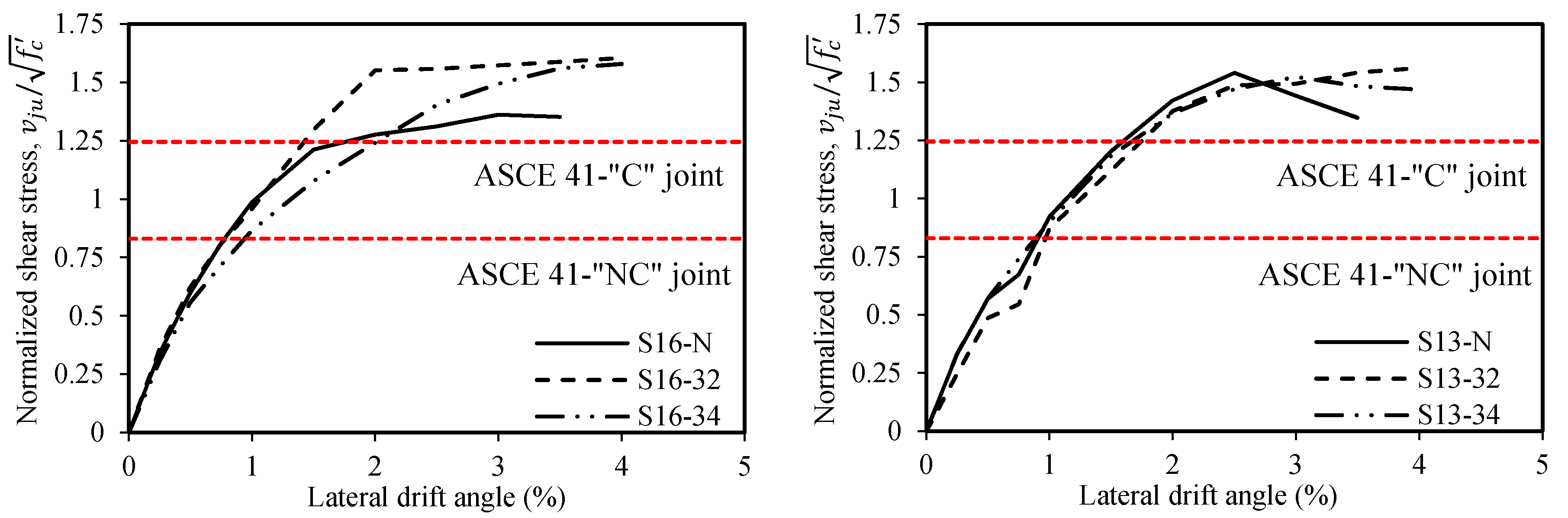
3.3. Joint Shear Stress
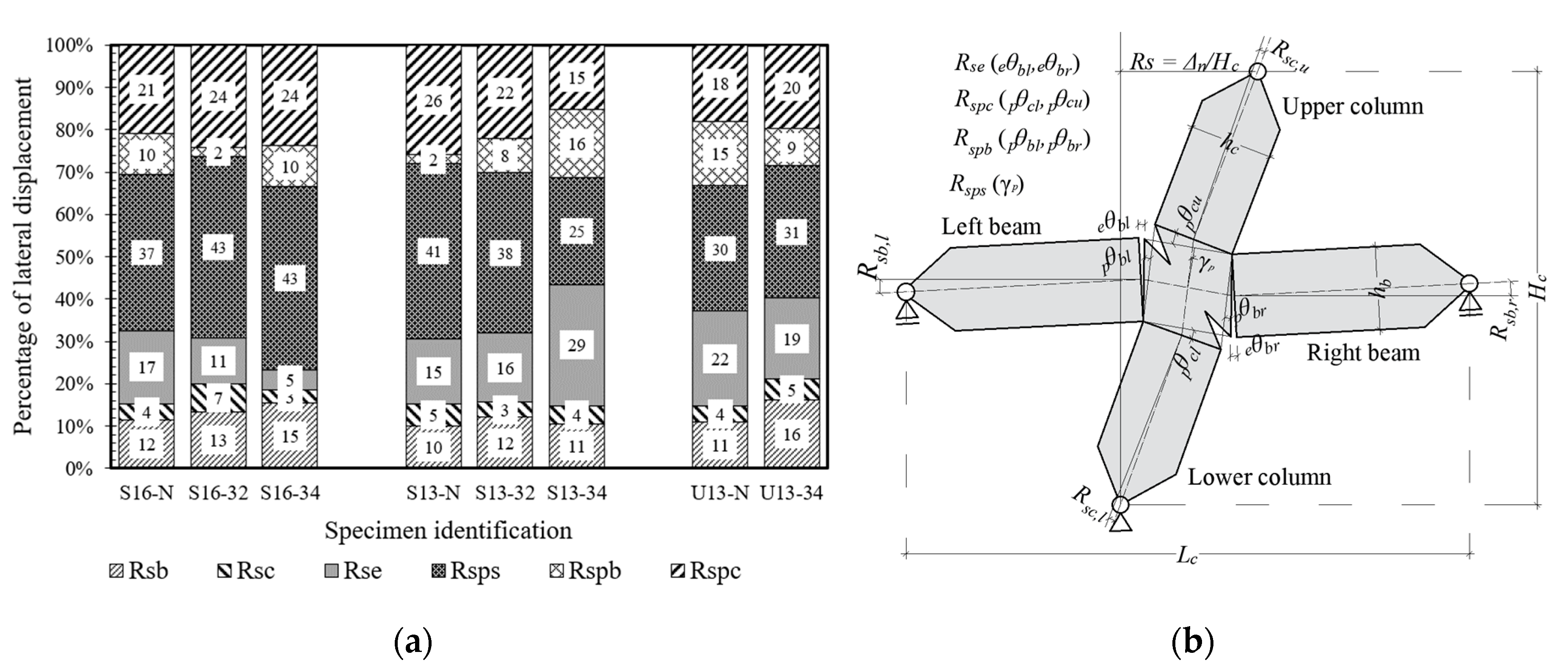
3.4. Decomposition of Lateral Drift
4. Analytical Studies of Interior Beam–Column Joints
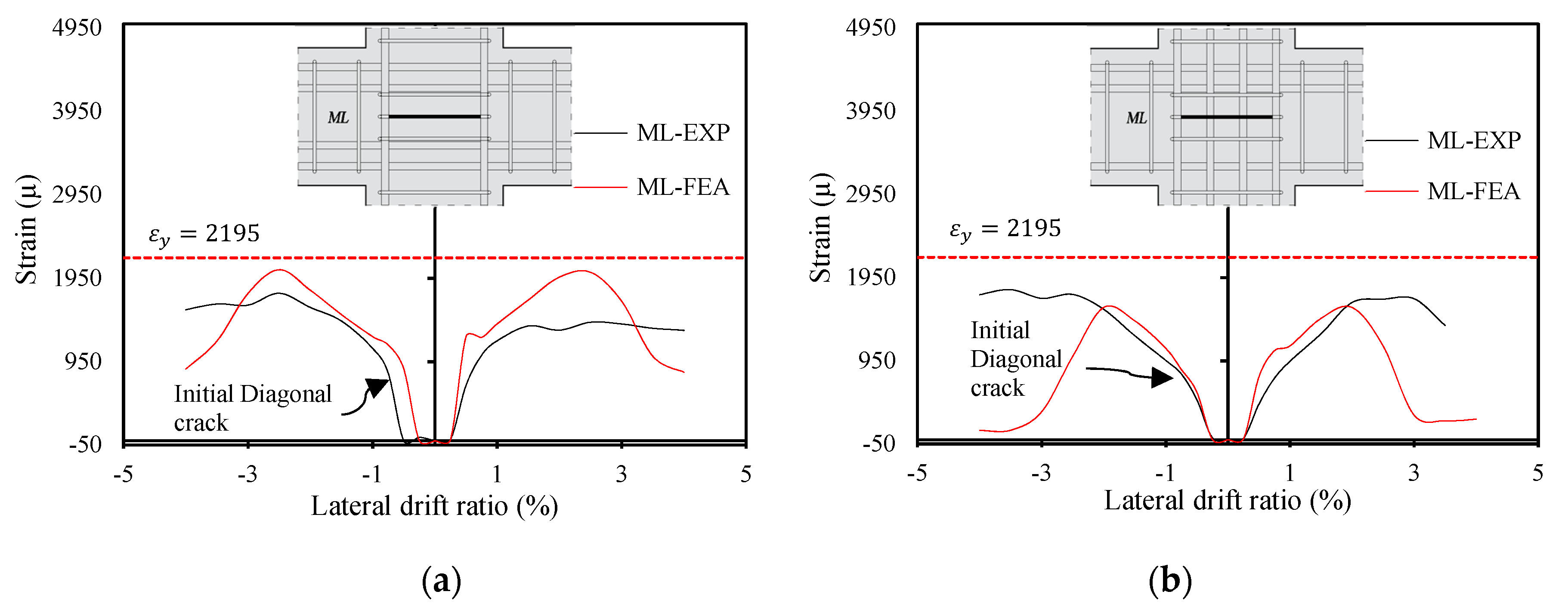
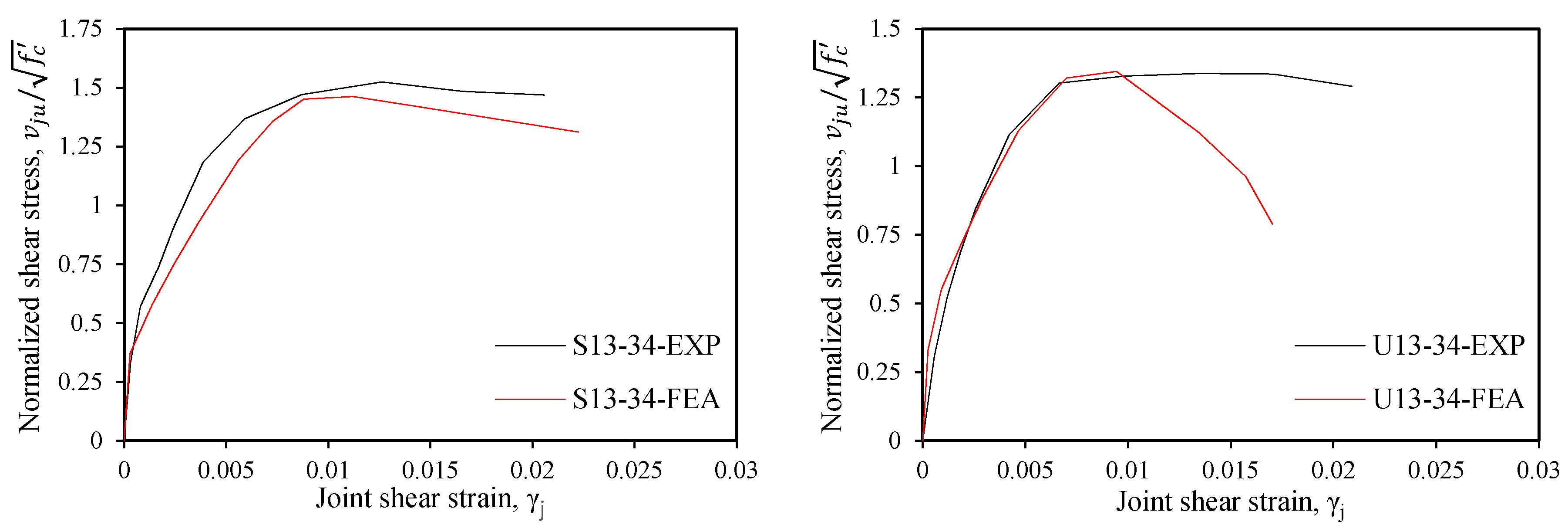
4.1. Finite-Element Modeling and Verification
4.2. Parametric Studies
4.3. Shear Stress and Shear Deformation of Interior Joints
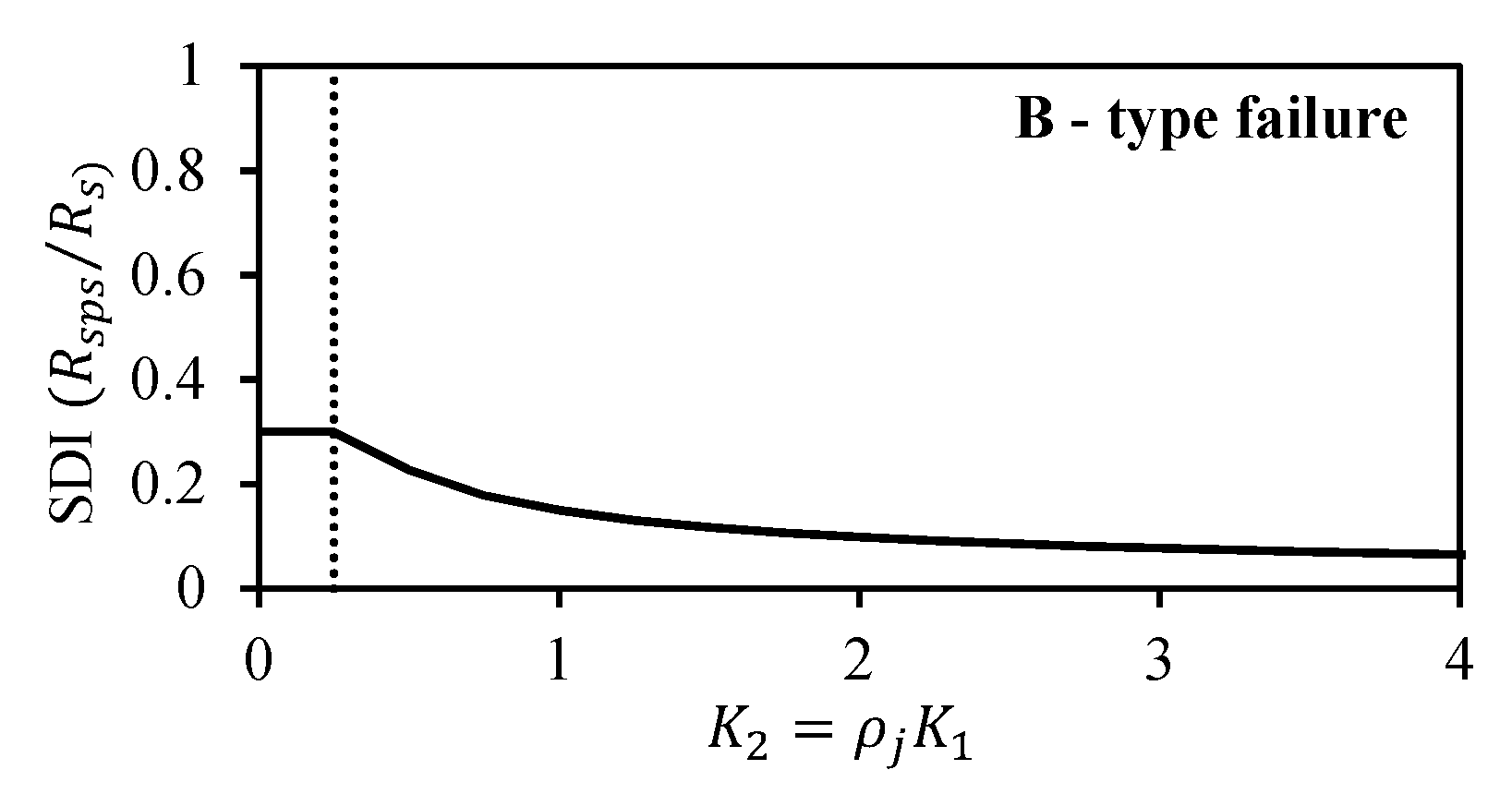
- .
- .
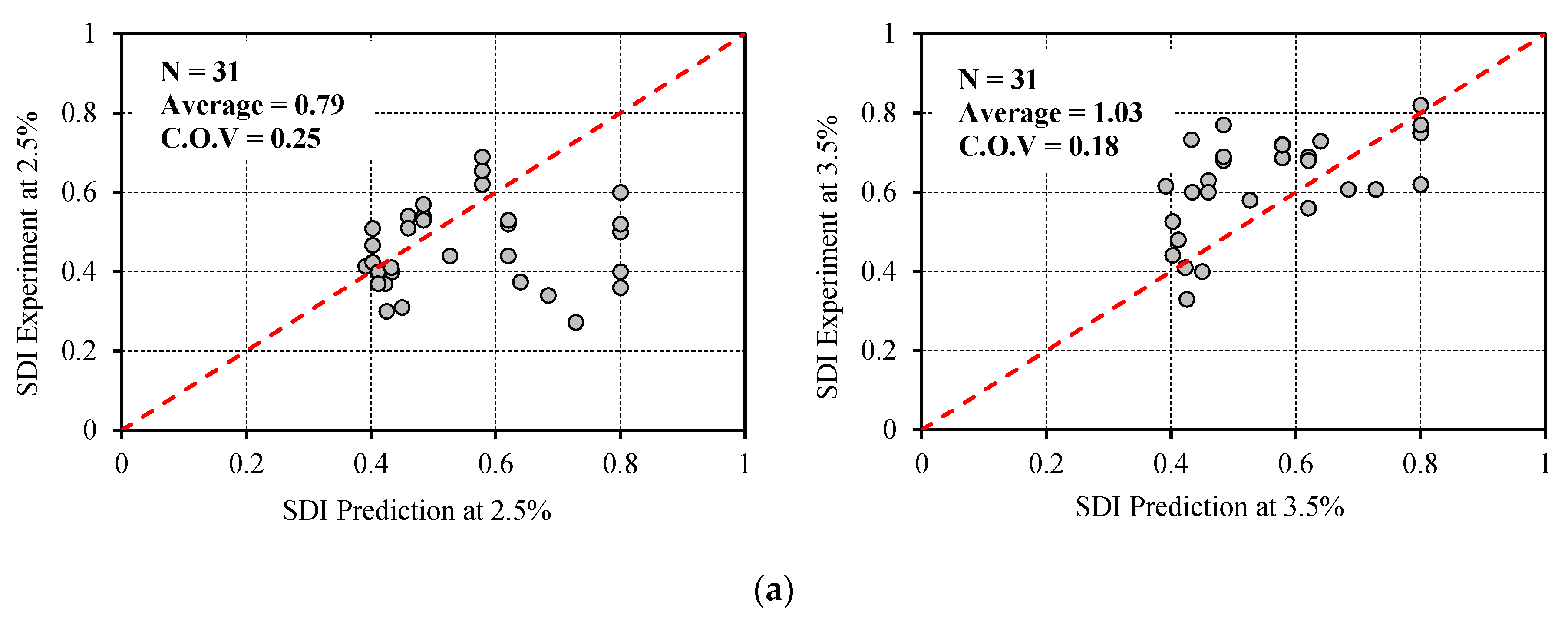
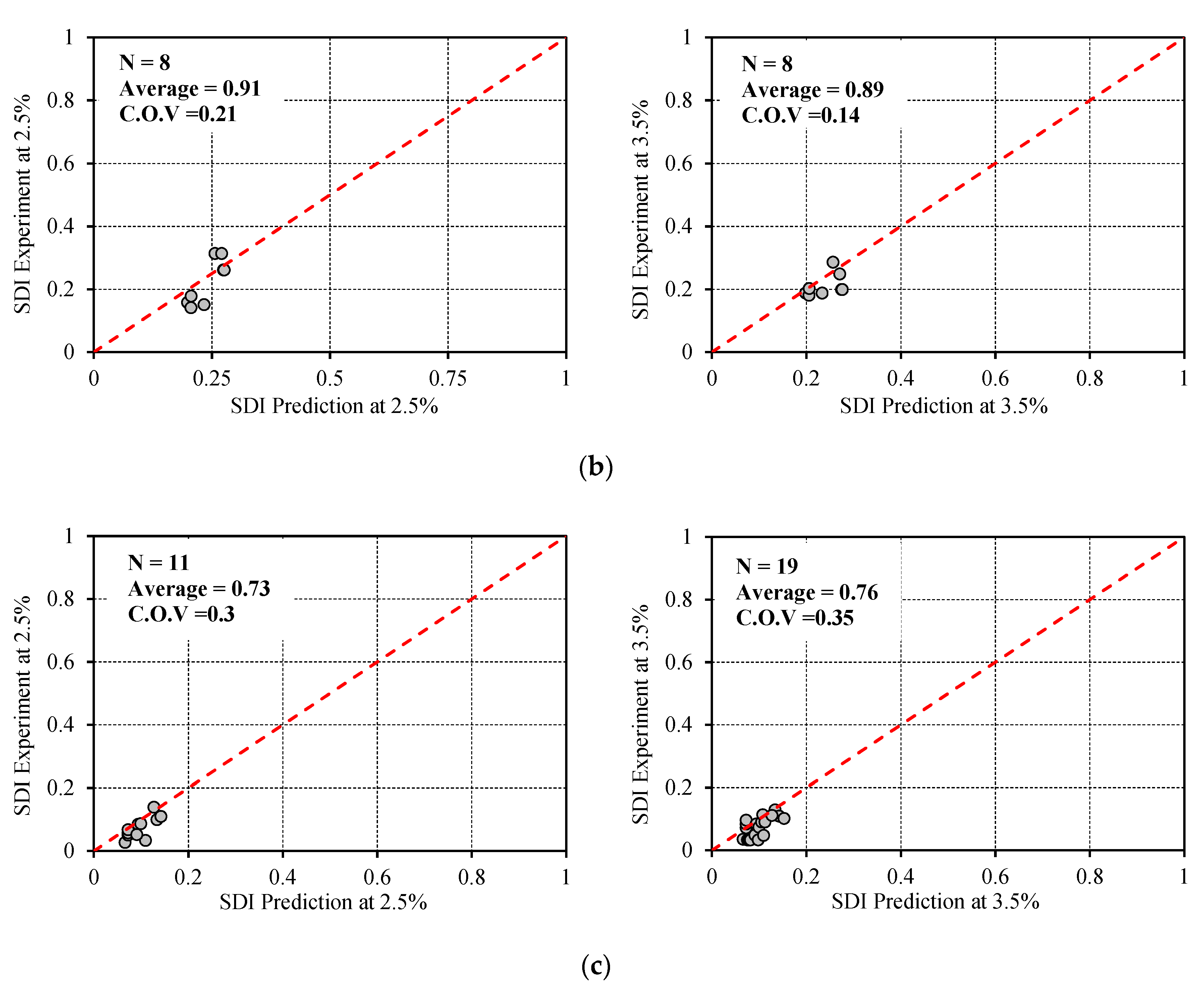
4.4. Verification of Proposed Equations
5. Conclusions
- With regard to the strength and stiffness, the performance of the test specimens was satisfactory up to = 2.0% (lateral drift ratio), beyond which the strength and stiffness generally degraded. The maximum loads occurred at = 2.0–2.5%, after which concrete cracking and spalling became severe at = 3.5–4.0%. Among the eight specimens, S13-N exhibited the worst performance. This was mainly due to the absence of joint shear reinforcement and the smaller flexural strength ratio.
- Experimental and finite-element investigations indicated that throughout the lateral loading, the joint shear stress increased, while the width of the diagonal shear cracks on the joint core surfaces increased. The maximum joint shear stress values exceeded the limits of for and for suggested by ASCE 41. The joint shear deformation contributed approximately 40% of the total lateral drift at the maximum shear stress , and the corresponding lateral drift ratio was approximately 3.0–3.5%. This indicates that the “joint shear” is a useful index for the beam–column joints with high shear stress levels of but is unsuitable for defining the shear failure of beam–column joints with medium or low shear stress levels of and .
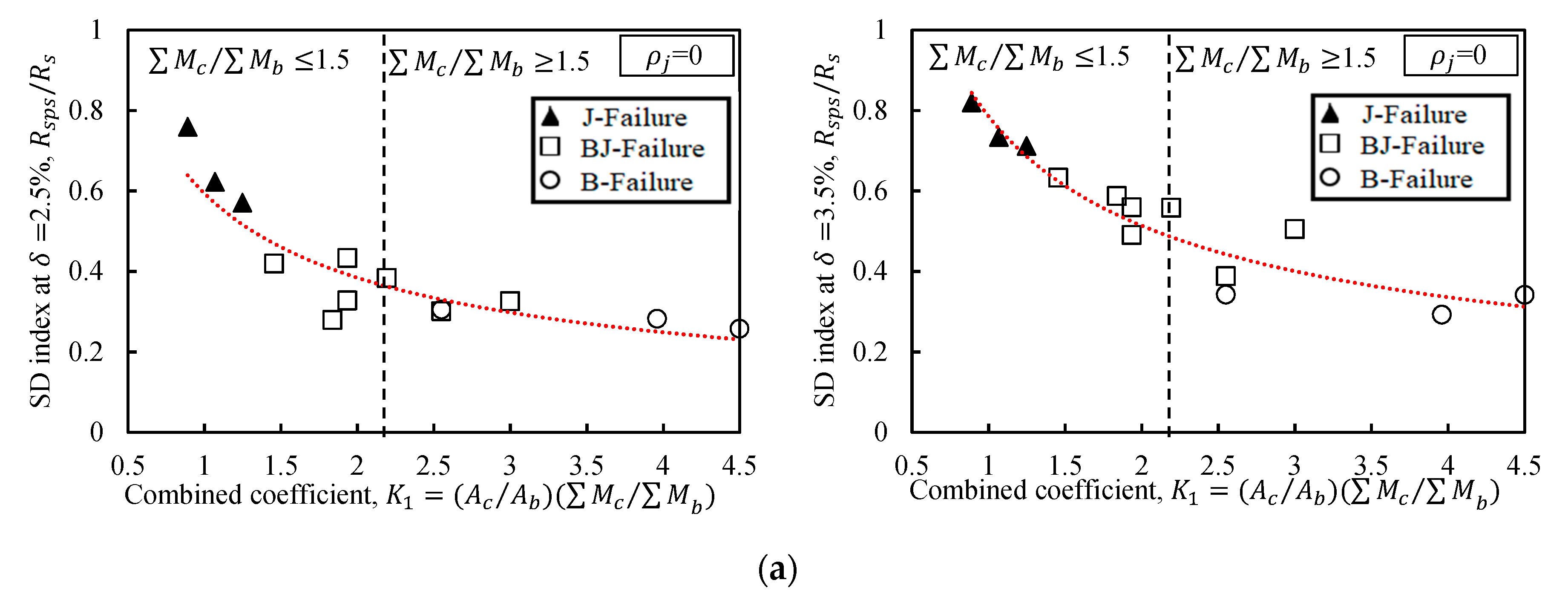
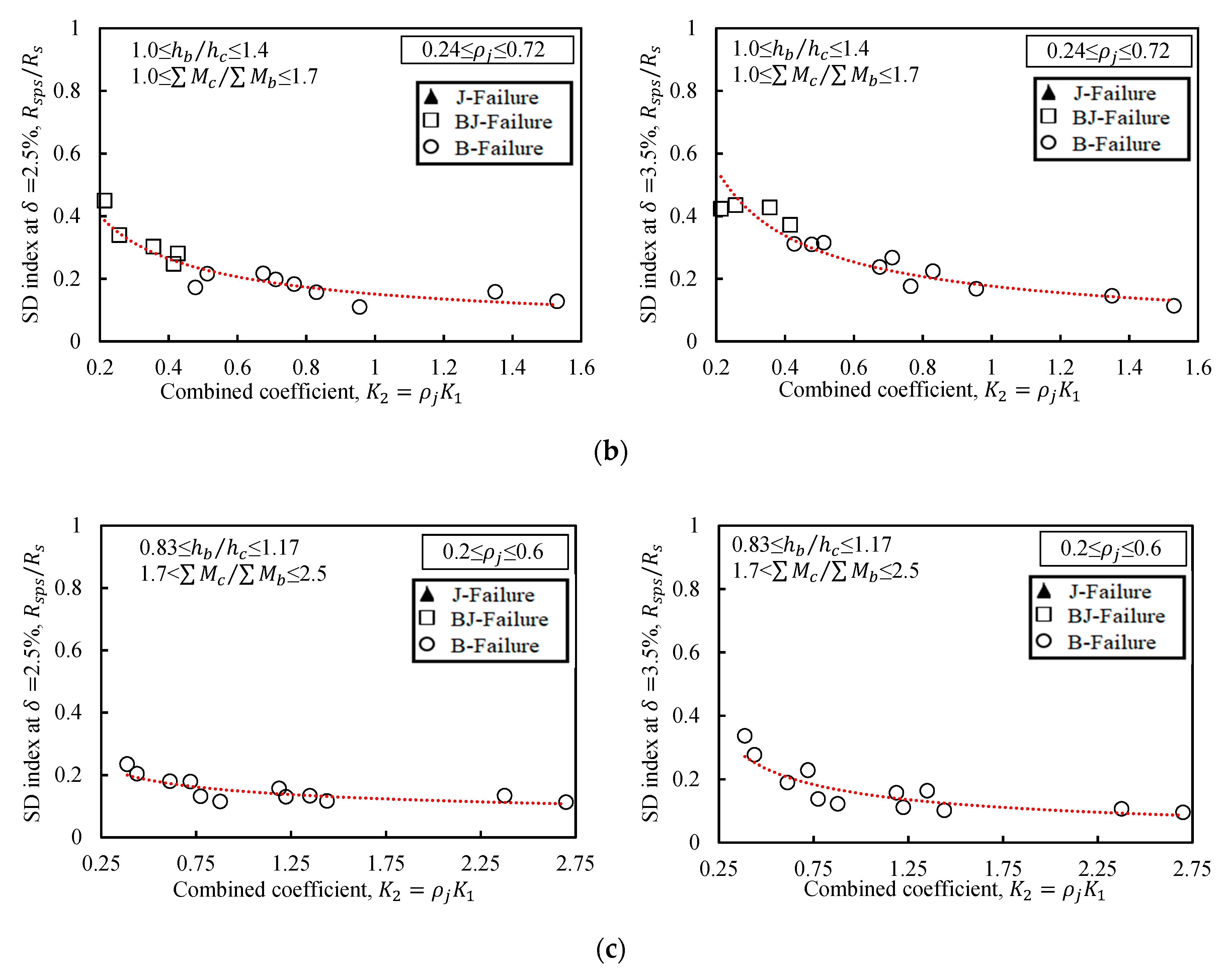
- Using the results of parametric studies (39 specimens), the shear stress of the interior joints was investigated considering the design variables , , and . The maximum shear stress varied between 0.85 and 1.65. However, joint failure did not occur in some specimens, even if was relatively large. This is because the increase in the proposed coefficient K0, together with the joint shear reinforcement shifts the failure plane to a beam flexural hinge yield mechanism.
- The shear deformation of interior joints was examined with consideration of the design variables , and . The contribution of the joint shear deformation to the total deformation ranged from 10.0% to 80.0% depending on the values of the proposed coefficients and . The joints with smaller values of and performed poorly, exhibiting wide inclined cracks and deformations that accounted for up to 80% of the overall lateral deformation ( = 2.5% and = 3.5%). Larger values of and yielded smaller deformation of the joint region.
- The design based on limiting the joint shear stress can be used for safety. However, it should be supplemented with consideration of the corresponding joint shear deformation to define the joint failure clearly. According to the results, three simple equations were proposed for predicting the joint deformation contribution to the total story drift of beam–column joints under critical structural deformations. The equations were able to predict SDI values with reasonable agreement with the experimental data. Compared with previously proposed models and theories, our method does not require complex nonlinear numerical analyses of the structure or sub-assemblage.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Current Design Methods
Appendix A.1. Flexural Yielding of Beam or Column

Appendix A.2. Shear Strength of Beam–Column Joint
Appendix A.3. Bond Strength of Beam Reinforcement
Appendix A.4. Strength Predictions for Test Specimens
| Specimen | Column Yielding | Beam Yielding | Joint Shear Failure | Failure Mode | Anchorage Length | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Conforming | Nonconforming | ||||||||||||
| S16-N | 78.0 | 125 | 51.6 | 51.6 | 76.4 | - | - | 247.93 | 39.9 | 39.9 | J | 250 | 0.78 |
| S16-32 | 77.7 | 124 | 51.5 | 51.5 | 76.3 | 367 | 59.1 | - | - | 59.1 | J | 250 | 0.78 |
| S16-34 | 78.2 | 125 | 51.6 | 51.6 | 76.4 | 375 | 60.2 | - | - | 60.2 | J | 250 | 0.78 |
| S13-N | 62.8 | 100 | 57.4 | 57.4 | 85.0 | - | - | 254 | 40.9 | 40.9 | J | 250 | 0.96 |
| S13-32 | 63.0 | 101 | 57.8 | 57.8 | 85.6 | 389 | 62.7 | - | - | 62.7 | J | 250 | 0.96 |
| S13-34 | 63.1 | 101 | 57.8 | 57.8 | 85.6 | 391 | 62.8 | - | - | 62.8 | J | 250 | 0.96 |
| U13-N | 79.9 | 128 | 56.9 | 42.1 | 73.3 | - | - | 264 | 42.4 | 42.4 | J | 250 | 0.96 |
| U13-34 | 79.9 | 128 | 56.9 | 42.1 | 73.3 | 396 | 63.6 | - | - | 63.6 | BJ | 250 | 0.96 |
Appendix B. Constitutive Model for Nonlinear Fe Analysis of Test Specimens
Appendix B.1.Constitutive Law for Concrete
Appendix B.1.1. Tensile Behavior
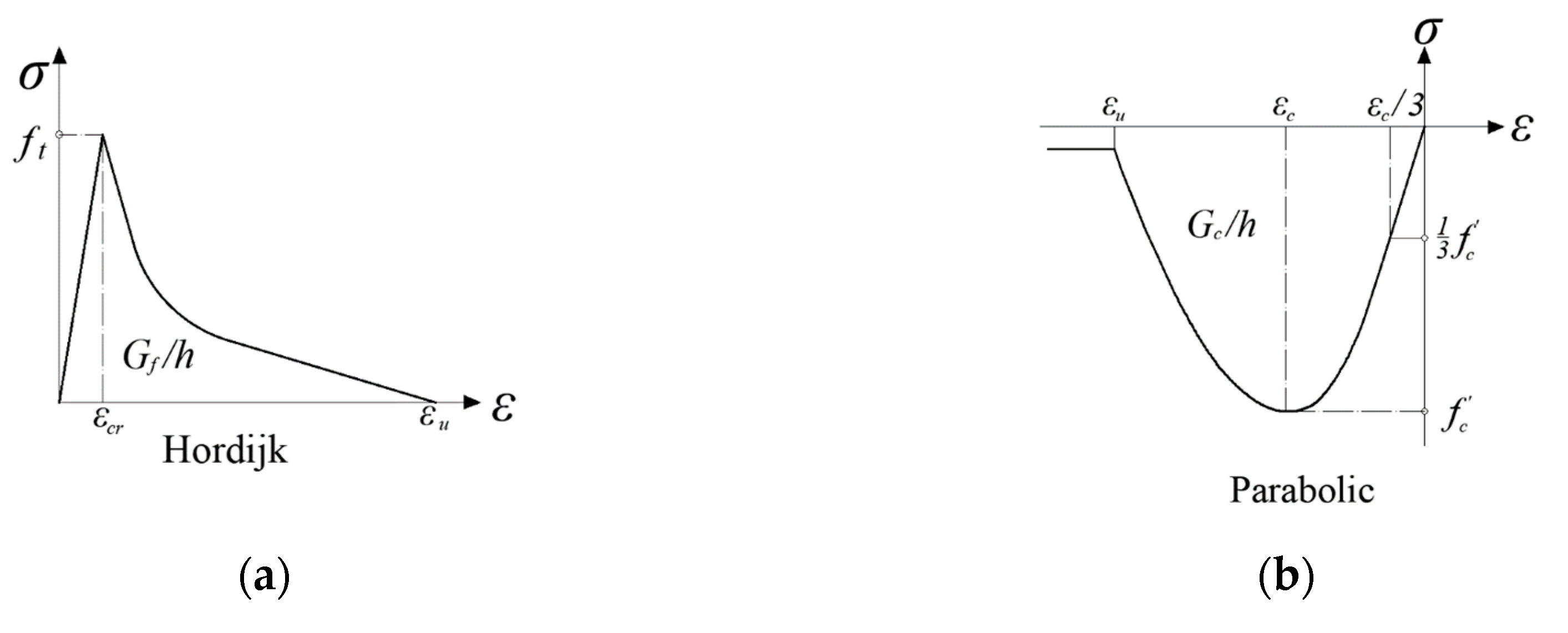
Appendix B.1.2. Compressive Behavior
Appendix B.2. Constitutive Law for Reinforcement

Bond–Slip Law
Appendix B.3. Geometry Modeling

Appendix C. Analysis Variables of Parametric Study
| Specimens | Geometric Properties | Top Rebar of Beam | Bottom Rebar of Beam | Joint Hoop Ratio | Joint Aspect Ratio | Area Ratio | Strength Ratio | Failure Mode | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | |||||||||||||||
| L | H | hc | bc | hb | bb | db | As | fy | db | As | fy | ρj, (%) | FE Prediction | |||||
| Group 1 | M1 | 6000 | 3000 | 600 | 600 | 500 | 400 | 22 | 1548 | 431 | 19 | 1146 | 431 | - | 0.83 | 1.8 | 2.5 | B |
| M2 | 0.3 | 0.83 | 1.8 | 2.5 | B | |||||||||||||
| M3 | 0.6 | 0.83 | 1.8 | 2.5 | B | |||||||||||||
| M4 | 25 | 2026 | - | 0.83 | 1.8 | 2.2 | B | |||||||||||
| M5 | 0.3 | 0.83 | 1.8 | 2.2 | B | |||||||||||||
| M6 | 0.6 | 0.83 | 1.8 | 2.2 | B | |||||||||||||
| M7 | 600 | 400 | 22 | 1548 | - | 1.0 | 1.5 | 2.0 | BJ | |||||||||
| M8 | 0.24 | 1.0 | 1.5 | 2.0 | B | |||||||||||||
| M9 | 0.48 | 1.0 | 1.5 | 2.0 | B | |||||||||||||
| M10 | 25 | 2026 | - | 1.0 | 1.5 | 1.7 | BJ | |||||||||||
| M11 | 0.24 | 1.0 | 1.5 | 1.7 | B | |||||||||||||
| M12 | 0.48 | 1.0 | 1.5 | 1.7 | B | |||||||||||||
| M13 | 700 | 400 | 22 | 1548 | - | 1.17 | 1.29 | 1.7 | BJ | |||||||||
| M14 | 0.2 | 1.17 | 1.29 | 1.7 | B | |||||||||||||
| M15 | 0.4 | 1.17 | 1.29 | 1.7 | B | |||||||||||||
| M16 | 25 | 2026 | - | 1.17 | 1.29 | 1.5 | BJ | |||||||||||
| M17 | 0.2 | 1.17 | 1.29 | 1.5 | B | |||||||||||||
| M18 | 0.4 | 1.17 | 1.29 | 1.5 | B | |||||||||||||
| Group 2 | M19 | 6000 | 3000 | 500 | 500 | 500 | 400 | 22 | 1548 | - | 1.0 | 1.25 | 1.7 | B | ||||
| M20 | 0.36 | 1.0 | 1.25 | 1.7 | B | |||||||||||||
| M21 | 0.72 | 1.0 | 1.25 | 1.7 | B | |||||||||||||
| M22 | 25 | 2026 | - | 1.0 | 1.25 | 1.5 | BJ | |||||||||||
| M23 | 0.36 | 1.0 | 1.25 | 1.5 | B | |||||||||||||
| M24 | 0.72 | 1.0 | 1.25 | 1.5 | B | |||||||||||||
| M25 | 600 | 400 | 22 | 1548 | - | 1.2 | 1.04 | 1.4 | BJ | |||||||||
| M26 | 0.29 | 1.2 | 1.04 | 1.4 | BJ | |||||||||||||
| M27 | 0.57 | 1.2 | 1.04 | 1.4 | B | |||||||||||||
| M28 | 25 | 2026 | - | 1.2 | 1.04 | 1.2 | J | |||||||||||
| M29 | 0.29 | 1.2 | 1.04 | 1.2 | BJ | |||||||||||||
| M30 | 0.57 | 1.2 | 1.04 | 1.2 | B | |||||||||||||
| M31 | 700 | 400 | 22 | 1548 | - | 1.4 | 0.89 | 1.2 | J | |||||||||
| M32 | 0.24 | 1.4 | 0.89 | 1.2 | BJ | |||||||||||||
| M33 | 0.48 | 1.4 | 0.89 | 1.2 | B | |||||||||||||
| M34 | 25 | 2026 | - | 1.4 | 0.89 | 1.0 | J | |||||||||||
| M35 | 0.24 | 1.4 | 0.89 | 1.0 | BJ | |||||||||||||
| M36 | 0.48 | 1.4 | 0.89 | 1.0 | B | |||||||||||||
| M37 | 550 | 550 | 600 | 400 | 25 | 2026 | - | 1.1 | 1.26 | 1.46 | BJ | |||||||
| M38 | 0.26 | 1.1 | 1.26 | 1.46 | B | |||||||||||||
| M39 | 0.52 | 1.1 | 1.26 | 1.46 | B | |||||||||||||
Appendix D. Summary of Beam–Column Connection Tests
| Research Team | Specimens | Joint Hoop Ratio | Joint Aspect Ratio | Area Ratio | Strength Ratio | Mechanical Reinforcement Ratio | SDI at 2.5% | SDI at 3.5% | Failure Mode |
|---|---|---|---|---|---|---|---|---|---|
| ρj, (%) | Test Result | ||||||||
| Fuji and Morita (1991) [17] | A1 | 0.52 | 1.14 | 1.21 | 1.24 | 0.50 | 0.62 | 0.69 | J |
| A2 | 0.52 | 1.14 | 1.21 | 2.02 | 0.19 | 0.41 | 0.62 | J | |
| A3 | 0.52 | 1.14 | 1.21 | 1.24 | 0.50 | 0.65 | 0.72 | J | |
| A4 | 0.69 | 1.14 | 1.21 | 1.24 | 0.50 | 0.69 | 0.72 | J | |
| Joh et al. (1991 [16]) | HL | 1.27 | 1.17 | 1.29 | 2.41 | 0.09 | 0.03 | 0.04 | B |
| MH | 0.55 | 1.17 | 1.29 | 2.41 | 0.09 | 0.03 | 0.05 | B | |
| B9 | 1.1 | 1.17 | 1.29 | 2.41 | 0.10 | 0.05 | 0.07 | B | |
| B10 | 1.1 | 1.17 | 1.29 | 2.41 | 0.10 | 0.06 | 0.09 | B | |
| B11 | 1.1 | 1.17 | 1.29 | 2.41 | 0.10 | 0.07 | 0.10 | B | |
| Noguchi and Kashiwazaki (1992) [38] | J1 | 0.66 | 1.00 | 1.50 | 1.53 | 0.24 | 0.40 | 0.48 | BJ |
| J3 | 0.66 | 1.00 | 1.50 | 1.48 | 0.17 | 0.37 | 0.41 | J | |
| J4 | 0.66 | 1.00 | 1.50 | 1.53 | 0.24 | 0.37 | 0.48 | BJ | |
| J5 | 0.66 | 1.00 | 1.50 | 1.37 | 0.26 | 0.31 | 0.40 | J | |
| J6 | 0.66 | 1.00 | 1.50 | 1.47 | 0.27 | 0.30 | 0.33 | J | |
| Oka and Shiohara (1992) [39] | J1 | 0.46 | 1.00 | 1.25 | 1.72 | 0.15 | 0.40 | 0.60 | BJ |
| J7 | 0.46 | 1.00 | 1.25 | 2.12 | 0.13 | 0.10 | 0.13 | B | |
| J10 | 0.46 | 1.00 | 1.25 | 1.35 | 0.34 | 0.44 | 0.58 | J | |
| Kimamura et al. (2000) [18] | No.1 | 0.15 | 1.00 | 1.39 | 1.7 | 0.24 | 0.47 | 0.53 | J |
| No.2 | 0.31 | 1.00 | 1.39 | 1.7 | 0.24 | 0.51 | 0.44 | J | |
| No.3 | 0.62 | 1.00 | 1.39 | 1.7 | 0.24 | 0.42 | 0.44 | J | |
| No.4 | 0.31 | 1.00 | 1.39 | 2.56 | 0.16 | 0.11 | 0.11 | B | |
| No.5 | 0.62 | 1.00 | 1.39 | 2.56 | 0.16 | 0.08 | 0.08 | B | |
| Li and Leong (2014) [40] | NS1 | 0.71 | 1.11 | 1.08 | 2.11 | 0.07 | N/A | 0.09 | B |
| AS1 | 0.71 | 1.11 | 1.08 | 3.59 | 0.07 | N/A | 0.03 | B | |
| NS2 | 0.48 | 1.11 | 1.08 | 1.86 | 0.03 | N/A | 0.10 | B | |
| AS2 | 0.48 | 1.11 | 1.08 | 3.9 | 0.03 | N/A | 0.03 | B | |
| NS3 | 0.71 | 1.11 | 1.08 | 2.35 | 0.07 | N/A | 0.09 | B | |
| AS3 | 0.71 | 1.11 | 1.08 | 3.83 | 0.07 | N/A | 0.03 | B | |
| NS4 | 0.57 | 1.11 | 1.08 | 2.82 | 0.03 | N/A | 0.11 | B | |
| AS4 | 0.57 | 1.11 | 1.08 | 5.15 | 0.03 | N/A | 0.03 | B | |
| Hwang et al. (2014) [41] | C1-400 | 1.34 | 0.91 | 1.57 | 1.67 | 0.31 | 0.18 | 0.20 | BJ |
| C2-600 | 1.34 | 0.91 | 1.57 | 1.68 | 0.27 | 0.14 | 0.18 | BJ | |
| C3-600 | 1.34 | 0.91 | 1.41 | 1.22 | 0.27 | 0.15 | 0.19 | BJ | |
| C4-600 | 1.34 | 0.91 | 1.57 | 1.88 | 0.27 | 0.16 | 0.19 | BJ | |
| Melo et al. (2014) [42] | IPA-1 | 0 | 1.67 | 0.60 | 0.94 | 0.06 | 0.60 | 0.82 | J |
| IPA-2 | 0 | 1.67 | 0.60 | 0.99 | 0.04 | 0.40 | 0.75 | J | |
| IPB | 0 | 1.67 | 0.60 | 0.96 | 0.06 | 0.50 | 0.62 | J | |
| IPE | 0 | 1.67 | 0.60 | 1.23 | 0.06 | 0.36 | 0.75 | J | |
| ID | 0 | 1.67 | 0.60 | 0.88 | 0.07 | 0.52 | 0.77 | J | |
| Alaee and Li (2017) [43] | IN80 | 0.71 | 1.11 | 1.08 | 1.71 | 0.05 | 0.14 | 0.11 | B |
| IH80 | 0.57 | 1.11 | 1.08 | 2.18 | 0.06 | 0.26 | 0.20 | BJ | |
| IH80A | 0.57 | 1.11 | 1.08 | 3.75 | 0.06 | 0.05 | 0.05 | B | |
| IN100 | 0.71 | 1.11 | 1.08 | 1.72 | 0.04 | 0.26 | 0.20 | BJ | |
| IH100 | 0.71 | 1.11 | 1.08 | 2.19 | 0.05 | 0.31 | 0.29 | BJ | |
| IH60 | 0.57 | 1.11 | 1.08 | 2.29 | 0.06 | 0.31 | 0.25 | BJ | |
| IH60A | 0.57 | 1.11 | 1.08 | 3.23 | 0.06 | 0.09 | 0.07 | B | |
| Yang and Zhao (2018) [44] | CL1 | 1.17 | 1.25 | 0.91 | 1.23 | 0.13 | 0.27 | 0.61 | BJ |
| CL2 | 1.54 | 1.25 | 1.07 | 1.24 | 0.19 | 0.37 | 0.73 | BJ | |
| CL3 | 1.60 | 0.89 | 1.58 | 1.37 | 0.23 | 0.41 | 0.73 | BJ | |
| CL4 | 1.54 | 1.25 | 1.07 | 1.14 | 0.16 | 0.34 | 0.61 | BJ |
References
- Kitayama, K.; Otani, S.; Aoyama, H. Development of Design Criteria for RC Interior Beam-Column Joints. ACI Struct. J. 1991, SP-123, 97–123. [Google Scholar]
- Bonacci, J.; Pantazopoulou, S. Parametric investigation of joint mechanics. ACI Struct. J. 1993, 90, 61–71. [Google Scholar] [CrossRef]
- Shiohara, H.; Kobayashi, F.; Sato, Y.; Kusuhara, F. Earthquake response of multi-story reinforced concrete plane frame structures and seismic design of beam-column joints. J. Struct. Constr. Eng. 2017, 82, 1437–1447. [Google Scholar] [CrossRef]
- Nagae, T.; Ghannoum, W.M.; Kwon, J.; Tahara, K.; Fukuyama, K.; Matsumori, T.; Shiohara, H.; Kabeyasawa, T.; Kono, S.; Nishiyama, M.; et al. Design implications of large-scale shake-table test on four-story reinforced concrete building. ACI Struct. J. 2015, 112, 135–146. [Google Scholar] [CrossRef]
- Hakuto, S.; Park, R.; Tanaka, H. Effect of deterioration of bond of beam bars passing through interior beam-column joints on flexural strength and ductility. ACI Struct. J. 1999, 96, 858–864. [Google Scholar] [CrossRef]
- Paulay, T.; Park, R.; Priestley, M.J.N. Reinforced Concrete Beam-Column Joints Under Seismic Actions. ACI Struct. J. 1978, 75, 585–593. [Google Scholar]
- Ichinose, T. Interaction Between Bond at Beam Bars and Shear Reinforcement in R/C Interior Joints. ACI Struct. J. 1991, 123, 379–400. [Google Scholar]
- British Standards Institution. Eurocode 8: Design of Structures for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Buildings; British Standards Institution: London, UK, 2005. [Google Scholar]
- Standards New Zealand. Concrete Structures Standard—The Design of Concrete Structures; NZ S3101-12006; Standards New Zealand: Wellington, New Zealand, 2017; Volume 1, ISBN 1-86975-043-8. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI318-14) and Commentary (318R-14); American Concrete Institute: Farmington Hills, MI, USA, 2014; p. 443. [Google Scholar]
- Otani, S. The architectural institute of Japan proposal of ultimate strength design requirements for RC buildings with emphasis on beam-column joints. ACI Struct. J. 1991, SP-123, 125–144. [Google Scholar]
- Shiohara, H. New model for shear failure of RC interior beam-column connections. J. Struct. Eng. 2001, 127, 152–160. [Google Scholar] [CrossRef]
- Shiohara, H. Reinforced concrete beam-column joints: An overlooked failure mechanism. ACI Struct. J. 2012, 109, 65–74. [Google Scholar]
- Shiohara, H.; Kusuhara, F. Joint Shear? or Column-to-Beam Strength Ratio? Which is a key parameter for seismic design of RC Beam-column joints—Test Series on Interior Joints. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; pp. 1–9. [Google Scholar]
- American Society of Civil Engineers. Seismic Evaluation and Retrofit of Existing Structures ASCE/SEI 41-13; American Society of Civil Engineers: Reston, VA, USA, 2014; p. 554. [Google Scholar]
- Joh, O.; Goto, Y.; Shibata, T. Influence of Transverse Joint and Beam Reinforcement and Relocation of Plastic Hinge Region on Beam Column Joint Stiffness Deterioration. ACI Struct. J. 1991, 123, 187–224. [Google Scholar] [CrossRef]
- Fuji, S.; Morita, S. Comparison between Interior and Exterior R/C Beam-Column Joint Behavior, Design of Beam-Column Joints for Seismic Resistance. ACI Struct. J. 1991, 132, 145–166. [Google Scholar]
- Kamimura, T.; Takeda, S.; Tochio, M. Influence of joint reinforcement on strength and deformation of interior beam-column subassemblages. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; p. 2267. [Google Scholar]
- Kim, J.; LaFave, J.M. Key influence parameters for the joint shear behaviour of reinforced concrete (RC) beam-column connections. Eng. Struct. 2008, 29, 2523–2539. [Google Scholar] [CrossRef]
- Hwang, S.J.; Lee, H.J.; Liao, T.F.; Wang, K.C.; Tsai, H.H. Role of hoops on shear strength of reinforced concrete beam-column joints. ACI Struct. J. 2005, 102, 445–453. [Google Scholar] [CrossRef]
- Hwang, S.J.; Lee, H.J. Analytical model for predicting shear strengths of interior reinforced concrete beam-column joints for seismic resistance. ACI Struct. J. 2000, 97, 35–44. [Google Scholar] [CrossRef]
- Hwang, S.J.; Tsai, R.J.; Lam, W.K.; Moehle, J.P. Simplification of softened strut-and-tie model for strength prediction of discontinuity regions. ACI Struct. J. 2017, 114, 1239–1248. [Google Scholar] [CrossRef]
- Hong, S.G.; Lee, S.G.; Kang, T.H.K. Deformation-based strut-and-tie model for interior joints of frames subject to load reversal. ACI Struct. J. 2011, 108, 423–433. [Google Scholar] [CrossRef]
- Hwang, H.J.; Eom, T.S.; Park, H.G. Shear strength degradation model for performance-based design of interior beam-column joints. ACI Struct. J. 2017, 114, 1143–1154. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Park, J.; Kim, C. Deformations of reinforced-concrete beam-column joint assemblies. Mag. Concr. Res. 2020, 72, 649–669. [Google Scholar] [CrossRef]
- Tajiri, S.; Fukuyama, H.; Suwada, H.; Kusuhara, F.; Shiohara, H. Energy Dissipation of RC Interior Beam-column Connection Confined by Lateral Reinforcements, Axial Force, and Column Longitudinal Reinforcements. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Park, R. Ductility evaluation from laboratory and analytical testing. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo, Japan, 2–9 August 1988; pp. 605–616. [Google Scholar]
- ACI Committee 374. Commentary on Acceptance Criteria for Moment Frames Based on Structural Testing; (ACI 374.1-05); American Concrete Institute: Farmington Hills, MI, USA, 2002. [Google Scholar]
- Kusuhara, F.; Shiohara, H. New instrumentation for damage and stress in reinforced concrete beam-column joint. In Proceedings of the 8th U.S. National Conference on Earthquake Engineering, San Francisco, CA, USA, 18–22 April 2006; Volume 7, pp. 4006–4015. [Google Scholar]
- Joint ACI-ASCE Committee 352. Recommendations for Design of Beam-Column Connections in Monolithic Reinforced Concrete Structures; (ACI 352R-02); American Concrete Institute: Farmington Hills, MI, USA, 2002. [Google Scholar]
- DIANA Version 10.3; Computer software; TNO Building and Construction Research: Delft, The Netherlands, 2019.
- Design of Concrete Structures: CEB-FIP Model-Code 1990; Thomas Telford Service Ltd.: London, UK, 1990.
- Deaton, J.B. Nonlinear Finite Element Analysis of Reinforced Concrete Exterior Beam-Column Joints with Nonseismic Detailing. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2013; pp. 1–315. [Google Scholar]
- Hordijk, D.A. Local Approach to Fatigue of Concrete. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1991. [Google Scholar]
- Nakamura, H.; Higai, T. Compressive fracture energy and fracture zone length of Concrete, Modelling of inelastic behavior of RC structures under seismic loads edited by Shing, P., Tanabe, T. ASCE 1999, 10, 471–487. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. Compression response of cracked reinforced concrete. J. Struct. Eng. 1993, 119, 3590–3610. [Google Scholar] [CrossRef]
- Selby, R.G.; Vecchio, F.J.; Collins, M.P. Analysis of reinforced concrete members subject to shear and axial compression. ACI Struct. J. 1996, 93, 306–315. [Google Scholar]
- Noguchi, H.; Kashiwazaki, T. Experimental studies on shear performances of RC interior column-beam joints with high-strength materials. In Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 19–24 July 1992. [Google Scholar]
- Oka, J.; Shiohara, H. Tests of high-strength concrete interior beam-column-joint subassemblages. In Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 19–24 July 1992. [Google Scholar]
- Li, B.; Leong, C.L. Experimental and numerical investigations of the seismic behavior of high-strength concrete beam-column joints with column axial load. J. Struct. Eng. 2015, 141, 04014220. [Google Scholar] [CrossRef]
- Hwang, H.J.; Park, H.G.; Choi WSChung, L.; Kim, J.K. Cyclic loading test for beam-column connections with 600 MPa (87 ksi) beam flexural bars. ACI Struct. J. 2014, 111, 913–924. [Google Scholar] [CrossRef]
- Melo, J.; Varum, H.; Rossetto, T. Cyclic behavior of interior beam-column joints reinforced with plain bars. Earthq. Eng. Struct. Dyn. 2015, 44, 1351–1371. [Google Scholar] [CrossRef]
- Alaee, P.; Li, B. High-strength concrete interior beam-column joints with high-yield-strength steel reinforcements. J. Struct. Eng. 2017, 143, 04017038. [Google Scholar] [CrossRef]
- Yang, H.; Zhao, W.; Zhu, Z.; Fu, J. Seismic behavior comparison of reinforced concrete interior beam-column joints based on different loading methods. Eng. Struct. 2018, 116, 31–45. [Google Scholar] [CrossRef]

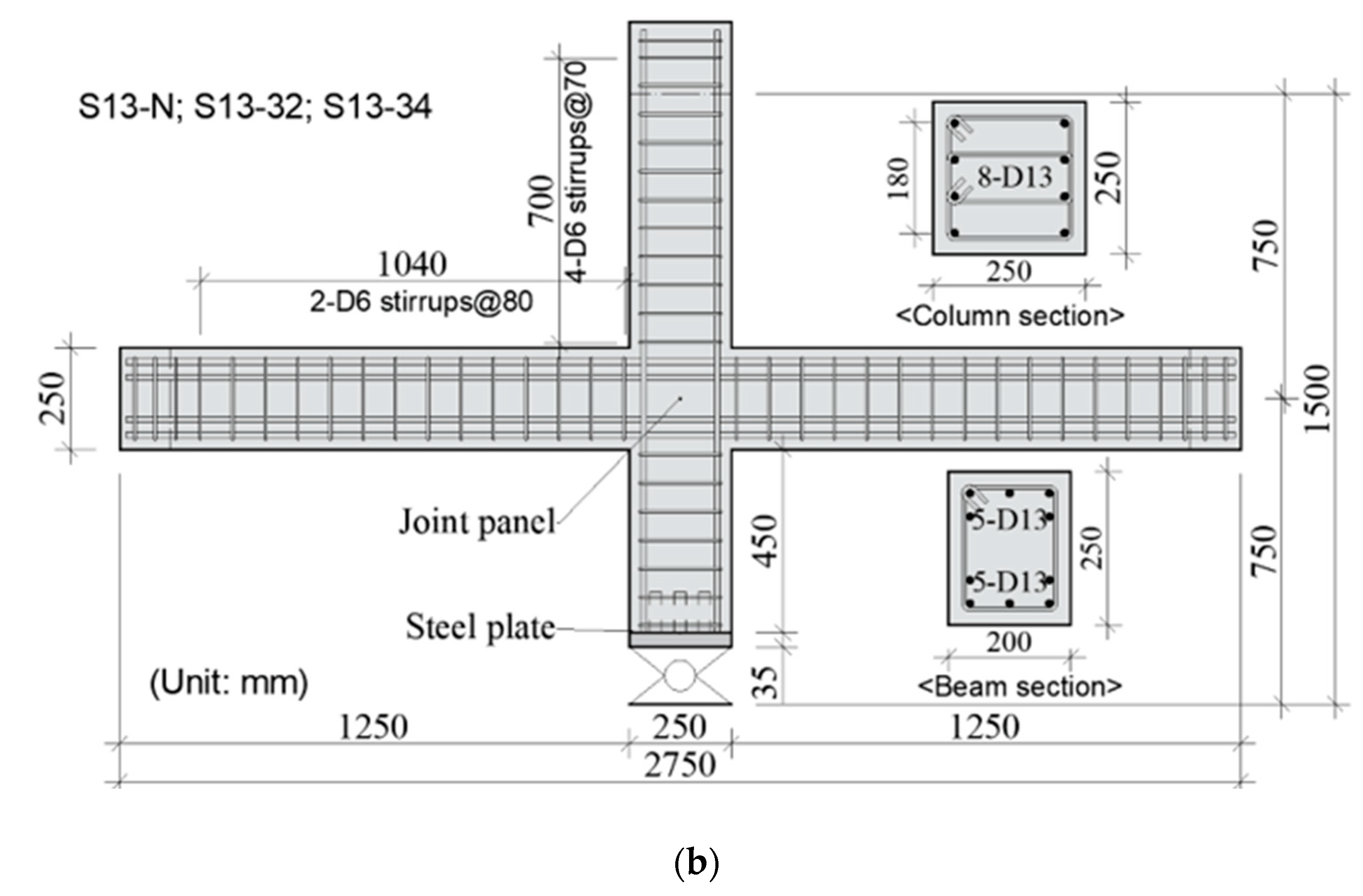
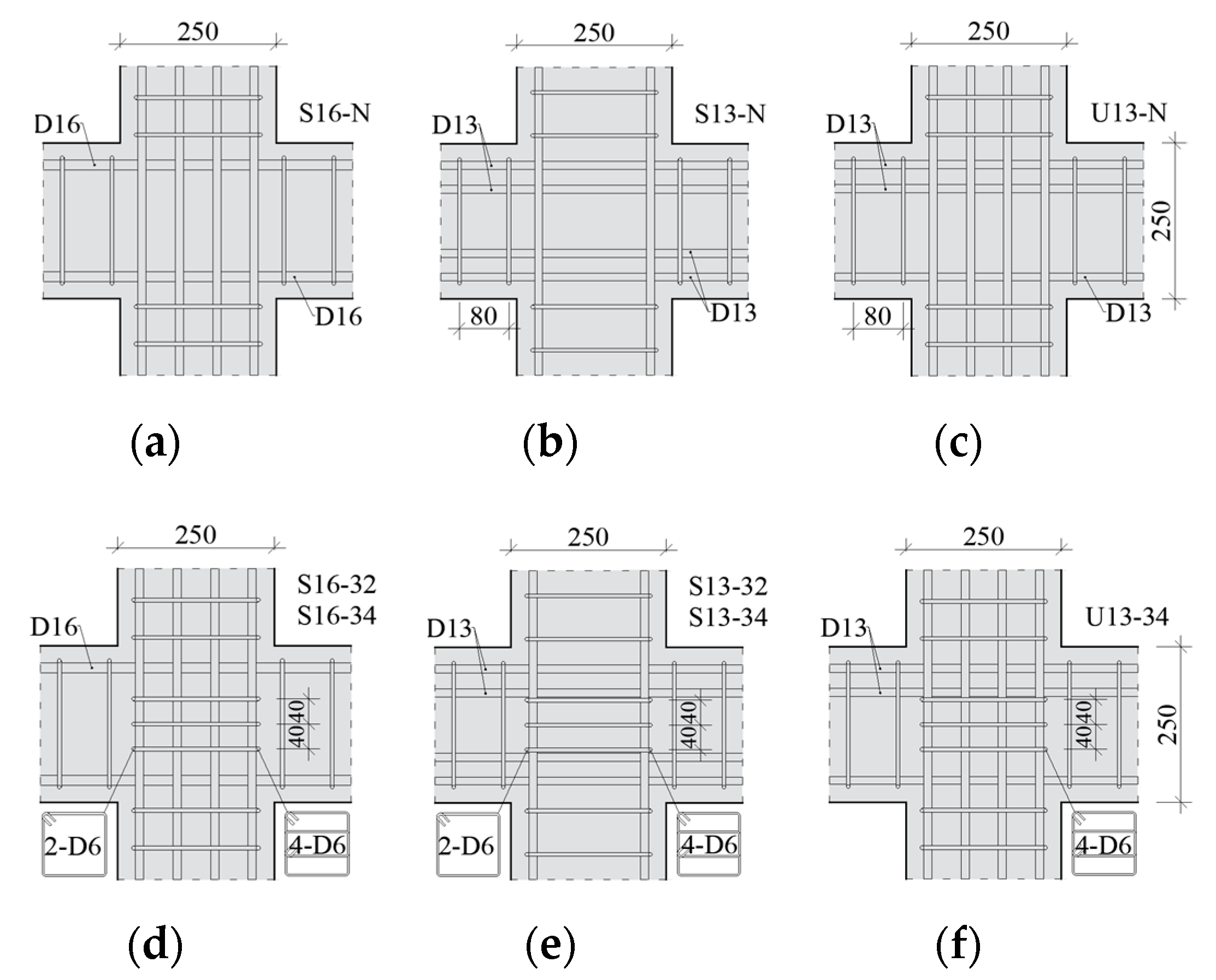








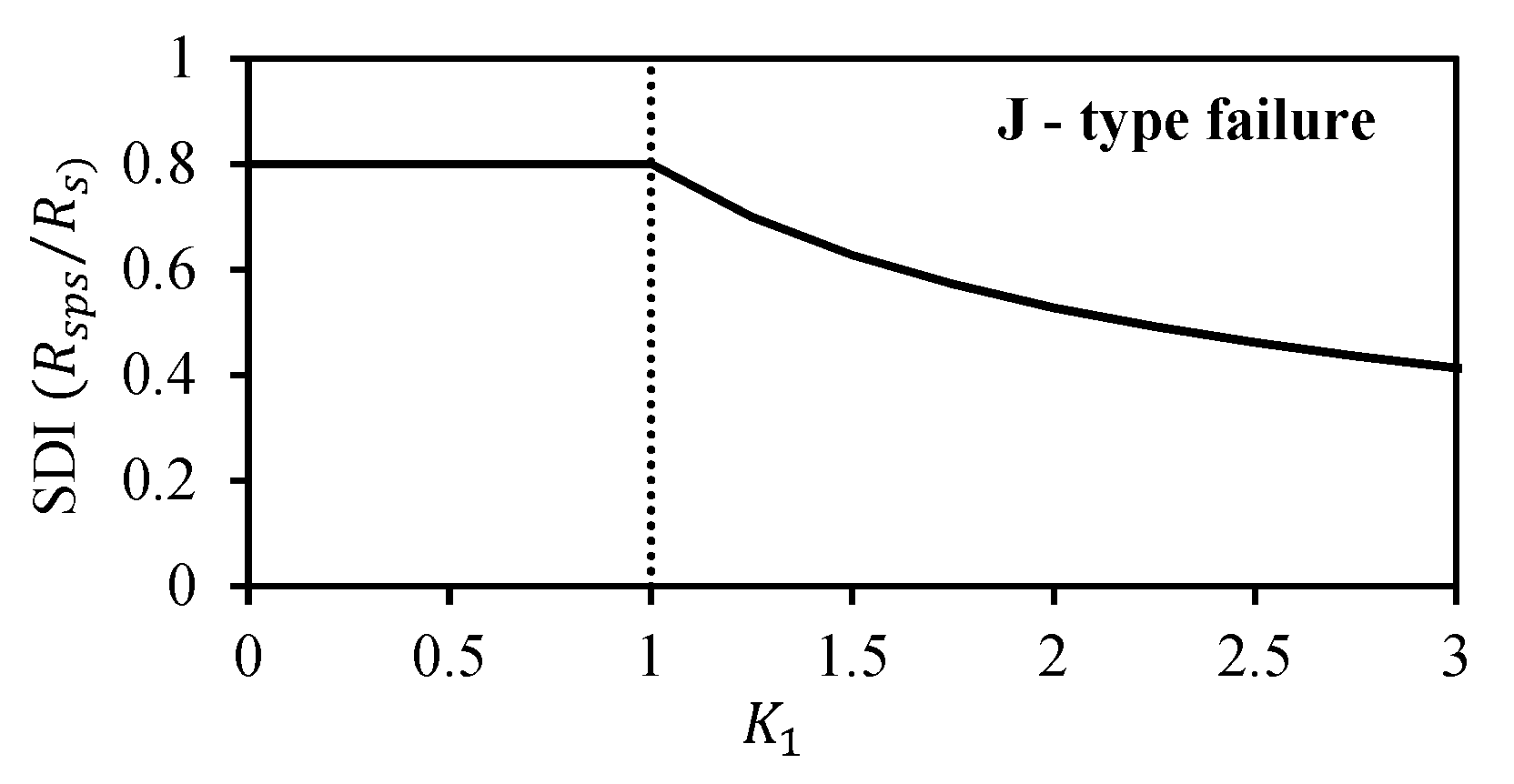
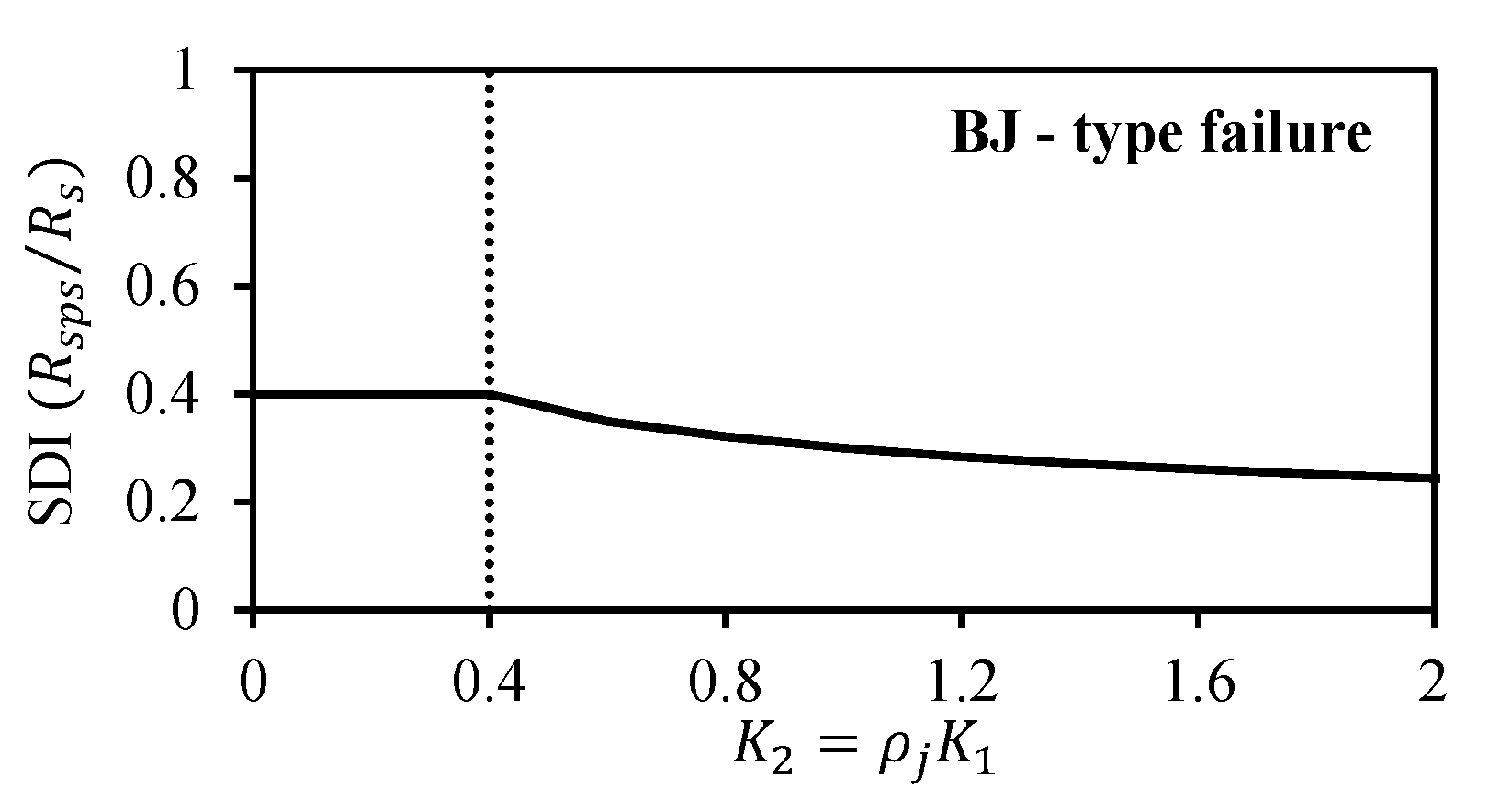
| Specimens | S16-N | S16-32 | S16-34 | S13-N | S13-32 | S13-34 | U13-N | U13-34 | |
|---|---|---|---|---|---|---|---|---|---|
| Concrete Strength, (MPa) | 28.2 | 27.5 | 28.6 | 29.7 | 30.9 | 31.1 | 32.1 | 31.9 | |
| Axial Load Ratio, () | 0.07 | 0.08 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | |
| Beam | Width × Depth in mm | 200 × 250 | 200 × 250 | 200 × 250 | |||||
| Top Rebar, % | 1.35 | 1.44 | 1.44 | ||||||
| Bottom Rebar, % | 1.35 | 1.44 | 0.88 | ||||||
| Column | Width × Depth in mm | 250 × 250 | 250 × 250 | 250 × 250 | |||||
| Reinforcing Bar Ratio (%) | 2.43 | 1.62 | 2.43 | ||||||
| Joint | Hoop Ratio (%) | - | 0.36 | 0.72 | - | 0.36 | 0.72 | - | 0.72 |
| Flexural Strength Ratio | 1.5 | 1.5 | 1.5 | 1.1 | 1.1 | 1.1 | 1.6 | 1.6 | |
| Joint Demand Ratio () | 0.82 | 0.76 | 0.91 | ||||||
| Anchorage Length Ratio ( | 15.6 | 19.2 | 19.2 | ||||||
| Diameter | Grade | ||||
|---|---|---|---|---|---|
| D6 | SD345 | 363 | 1998 | 542 | 182 |
| D13 | SD390 | 498 | 2602 | 669 | 192 |
| D16 | 440 | 2449 | 618 | 180 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gombosuren, D.; Maki, T. Prediction of Joint Shear Deformation Index of RC Beam–Column Joints. Buildings 2020, 10, 176. https://doi.org/10.3390/buildings10100176
Gombosuren D, Maki T. Prediction of Joint Shear Deformation Index of RC Beam–Column Joints. Buildings. 2020; 10(10):176. https://doi.org/10.3390/buildings10100176
Chicago/Turabian StyleGombosuren, Dagvabazar, and Takeshi Maki. 2020. "Prediction of Joint Shear Deformation Index of RC Beam–Column Joints" Buildings 10, no. 10: 176. https://doi.org/10.3390/buildings10100176
APA StyleGombosuren, D., & Maki, T. (2020). Prediction of Joint Shear Deformation Index of RC Beam–Column Joints. Buildings, 10(10), 176. https://doi.org/10.3390/buildings10100176




