Seismic Vulnerability of Masonry Lighthouses: A Study of the Bengut Lighthouse, Dellys, Boumerdès, Algeria
Abstract
:1. Introduction
- Manuals of preservation for the lighthouses drawn up by the International Association of Lighthouses Authorities (IALA) and Association Internationale de Signalisation Maritime (AISM) [5].
- Catalogues of the lighthouses, semaphores, and beacons within the Mediterranean region.
2. Seismic Vulnerability of Masonry Buildings: A Brief Overview
- Quality of walls and texture: the overall in-plane and out-of-plane behavior is strictly related to the properties and arrangement of the different constituents, which are extremely variable, especially in ancient constructions.
- Proper structural organization, to enhance the spatial behavior and allow the distribution of actions among all supporting elements: this is mainly related to the presence of effective connections between orthogonal walls, and between masonry walls and horizontal diaphragms to ensure the “box-like” behavior during an earthquake.
- Rigidity and resistance of floor diaphragms for effectively guaranteeing the redistribution of seismic actions, reducing out-of-plane vibrations of walls and increasing structural redundancy.
3. Lighthouses in Algeria
Seismic Vulnerability of Lighthouses from the 19th and 20th in Algeria
- Geometry of towers: as already mentioned, the tower generally has high compressive vertical stresses due to gravity loads. Under seismic loading, the slenderness can cause significant flexural loads and lateral drifts, easily leading to local damage or global collapses. The presence of adjoining structures can also influence the tower seismic vulnerability: the possible interaction reduces the slenderness of the tower but, at the same time, provides stress concentrations at the contact zone between tower and the confining structures [36].
- Geographical position: they are in zones of medium–strong seismicity (Figure 2).
- Degradation due to age: the lighthouses dating from the French colonial era are sometimes more than 150 years old (the first one was built in 1861, the last one in 1954 [37]).
4. The Lighthouse at Cap Bengut
- Geometric irregularity in plan (Figure 4a): the square tower is contiguous to a rectangular building.
- Volumetric imbalance in elevation (Figure 4b): the total height of the tower equals three times the building height, with no seismic joints between them.
- Bad connection between external walls in the corners, because of the poor effectiveness between chaining stone and walls.
5. Seismic Vulnerability Analysis of the Bengut Lighthouse
5.1. Identification of Collapse Mechanisms
5.2. Numerical Analyses
- By following the classification table of RPA2003, the Bengut Lighthouse is classified as a building of great importance (group 1B).
- It is in a high seismic hazard region (zone III), in which PGA is 0.3 g.
- The soil classification is “hard rock”—S12.
- A behavior factor R = 2 is assigned, by assuming the lowest class for existing URM buildings.
- The quality factor “Q” of the structure defined by the Algerian code RPA 2003 depends on: redundancy in plan, regularity both in plan and elevation, quality control and execution of materials, and is Q = 1.35 for the building group 1B.
- For the site of Bengut Lighthouse, the RPA03 response spectrum plotted in Figure 5 is adopted (the highest acceleration value is 0.483 g = 4.83 m/s).
5.2.1. Preliminary Modal Analysis
5.2.2. Pushover Analysis
6. Proposal of Retrofitting Solutions for the Bengut Lighthouse
6.1. A Literature Review of Seismic Repair and Retrofitting for Masonry Structures
6.2. Suggestions for Seismic Retrofitting Techniques
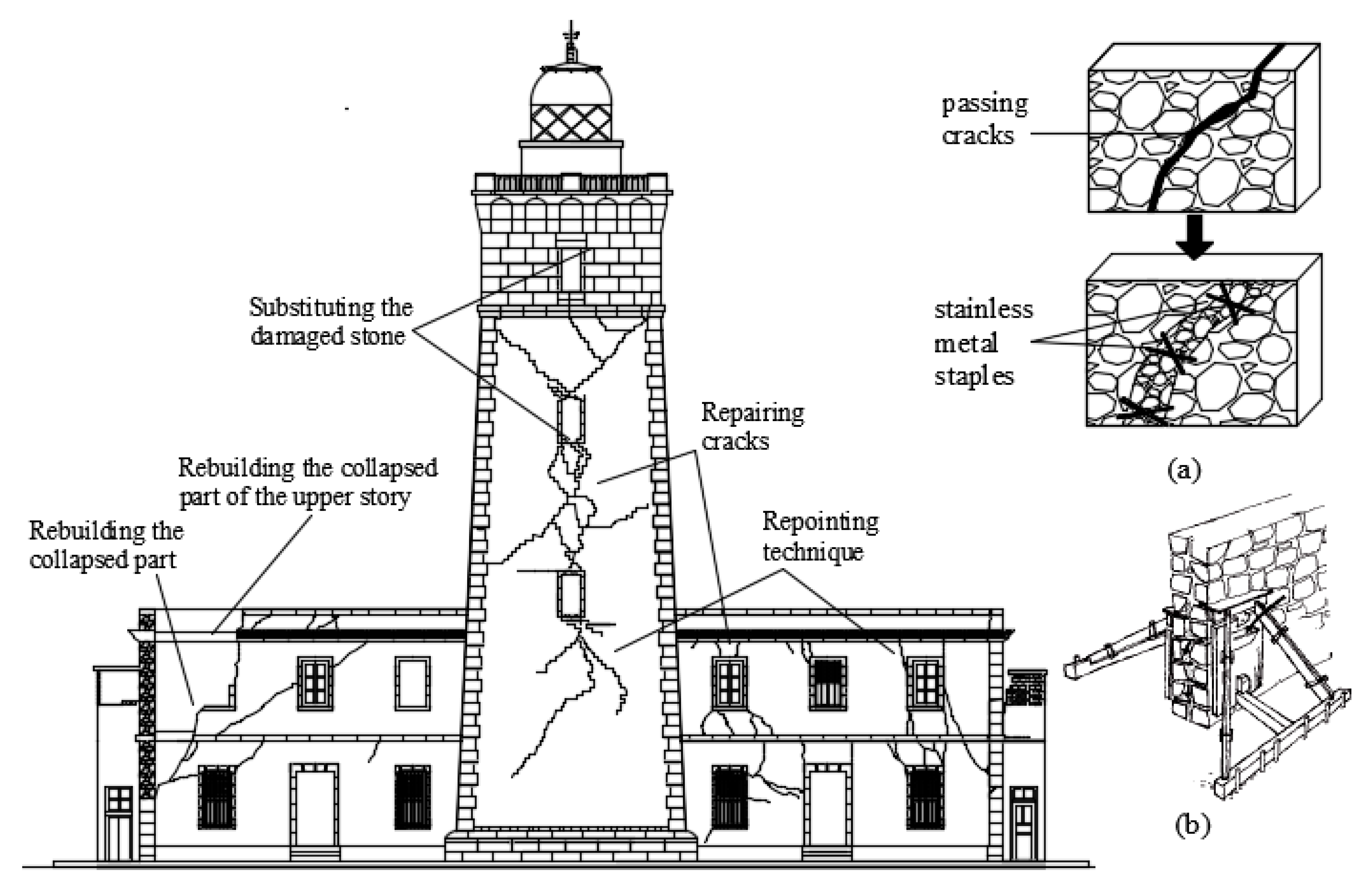
- The collapsed part of the north-east façade shall be reconstructed by using materials with mechanical characteristics similar to the original ones. The objective of this intervention is only to restore the restore the original bearing capacity of the damaged parts.
- The partial collapse of the roof has caused severe degradation to the whole structure because of water infiltration, humidity and corrosion of the steel IPE beams, and is a very urgent intervention to be taken. Therefore, the collapsed part of the floor will be rebuilt using bricks similar to the original ones and the steel IPE beams detached from the collapsed wall will be replaced with new ones and anchored to the supporting walls.
- The masonry on both sides of passing cracks will be disassembled, restoring the gaps using stones of the same original material, stainless metal staples, and oblique mortar injections (Figure 12a). This technique is known “indenting” (“cuci e scuci” in Italy).
- The mortar joints damaged by superficial cracks or infested by plant roots plants will be cleaned with compressed air and stripped to a depth of 3 cm, then moistened, and finally a liquid mortar will be introduced under pressure till the complete filling of vacuum (Figure 12b). The compatibility of the repointing mortars with the existent ones is a fundamental condition to assure the proper effectiveness of this intervention.
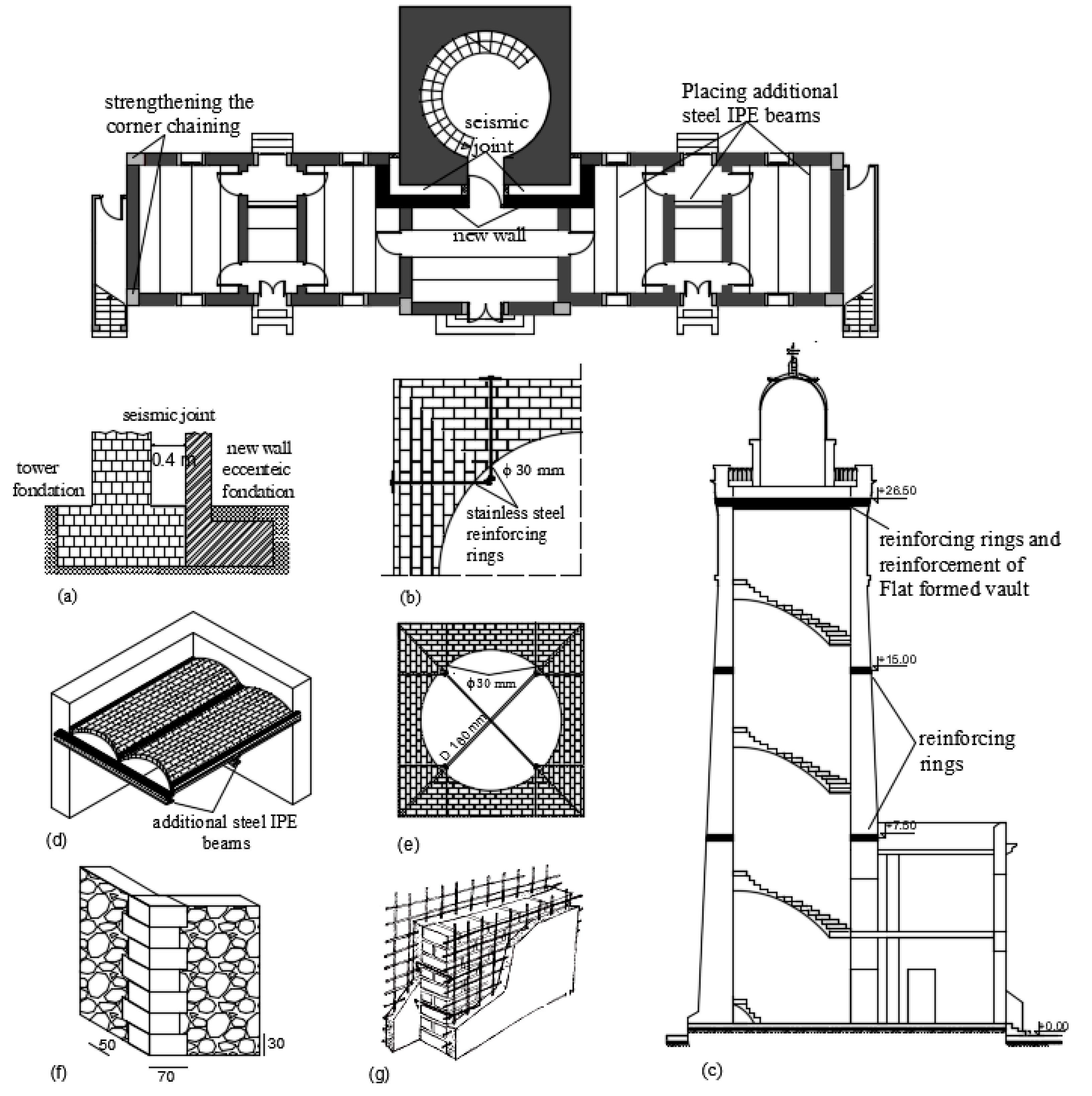
- The most important provision to be taken consists of creating a seismic joint between the tower and the rest of the main building walls. According to RPA recommendations, if two neighboring structures have a steep difference in height, they should be separated by a seismic joint whose minimum displacement dmin satisfies the following condition:
- A second important intervention to improve the structural behavior of the tower is the reinforcing of the four tower sides. This technique consists of inserting a series of horizontal stainless steel reinforcing rings all along the height of the tower Figure 13b, to confine the masonry, improve the connection between the orthogonal walls at the corners and assure the box-like behavior of the tower under seismic loads [18].
- The structural reinforcement of the floors is another important provision. The interventions will be applied both on the brick vault of the building and on the flat formed vault of the tower. Additional steel IPE beams will be screwed on the bottom part of the vaulted floor and will be anchored to the walls in a perpendicularly direction to the original IPE beams (Figure 13d) [57]; a diaphragm solution is proposed for the flat formed vault at the height of 26.50 m, consisting of a structure of steel elements and tie rods (Figure 13e) anchored in the exterior of the tower [18].
- For guaranteeing the box-like behavior of the main building, the suggested intervention is the improvement of corner chaining, since the actual connection between the blocks in the external orthogonal walls is insufficient. The corner stone blocks will be dismantled and substituted with new ones of same nature and dimensions (50 cm × 70 cm × 30 cm), as shown in Figure 13f.
- An additional intervention is proposed for guaranteeing the structural stability of interior walls and increasing their tensile strength, shear strength, and ductility. This technique has been largely applied in Italy. It consists first in jacketing the existing wall on both faces with wire meshes joined together by transversal steel ties, then in the application of a thick mortar layer on both faces. Overall, the thickness of the wall will be increased from 40 cm to 50 cm (Figure 13g) [56,57,60].
6.3. Seismic Re-Evaluation
- The principal modes of the tower are similar to those of the original configuration, but with a strong increase in the participating masses. The 1st mode is translational along the direction X, the 2nd translational along the direction Y, and they have a comparable participating mass over 70%. The 3rd mode has very small mass participation and is a local mode. The mass participation is increased by approximately 30.57% and 25.43% in the 1st and 2nd mode, respectively.
- Also, the main building, in the new configuration, has much higher values of the translational participating masses (over 90%). The 1st mode is translational along Y, the 2nd is a local mode with a very small mass participation and the 3rd is translational along X. The mass participation is increased by 50.01% in the X direction and 42.96% in Y direction.
7. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bartolomei, C. The Architecture of Italian Lighthouse; Alinea Edition: Firenze, Italy, 2005. [Google Scholar]
- Jonatan, C. Les phares antiques, entre défense et aide à la navigation. Exemples en Méditerranée Occidentale. Defensive Archit. Mediterr. XV XVIII Centuries 2015, 2, 65–70. [Google Scholar]
- CCLV. Les Phares de la Méditerranée; Chasse-Marée: Paris, France, 2009. [Google Scholar]
- ONSM. Etat de Signalisation Maritime: Phares et Balises; L’Office National de Signalisation Maritime: Alger, Algérie, 1979. [Google Scholar]
- AISM-IALA. IALA Lighthouse Conservation Manual, 1st ed.; AISM-IALA: Ile de France, France, 2006. [Google Scholar]
- MED-PHARES. Catalogo dei Fari e Semafori Delle Coste Tirreniche e Ioniche Italiane. Agenzia Conservatoria delle Coste, 2016. Available online: http://www.enpicbcmed.eu/communication/med-phares-project-looking-staff-0 (accessed on 20 November 2020).
- MED-PHARES. Catalogue des Phares et Sémaphores de Méditerranée Française. Conservatoire du Littoral, 2016. Available online: http://docplayer.fr/26356491-Catalogue-des-phares-et-semaphores-de-mediterranee-francaise.html (accessed on 20 November 2020).
- MED-PHARES. Catalogue des Phares et Sémaphores du Liban. Société pour la Protection de la Nature du Liban, 2016. Available online: http://www.sardegnaambiente.it/documenti/23_508_20171219171801.pdf (accessed on 20 November 2020).
- MED-PHARES. Catalogue des Phares de la Tunisie; Agence de Protection et d’Aménagement du Littoral: Tunis, Tunisia, 2016. [Google Scholar]
- Pelà, L. New trends and challenges in large-scale and urban assessment of seismic risk in historical centres. Int. J. Archit. Herit. 2018, 12, 1051–1054. [Google Scholar] [CrossRef] [Green Version]
- Polese, M.; Di Ludovico, M.; Gaetani d’Aragona, M.; Prota, A.; Manfredi, G. Regional vulnerability and risk assessment accounting for local building typologies. Int. J. Disaster Risk Reduct. 2020, 43. [Google Scholar] [CrossRef]
- Uva, G.; Sanjust, C.A.; Casolo, S.; Mezzina, M. ANTAEUS project for the regional vulnerability assessment of the current building stock in historical centers. Int. J. Archit. Herit. 2016, 10, 20–43. [Google Scholar] [CrossRef]
- Lourenço, P.B. Experimental and Numerical Issues in the Modeling of the Mechanical Behaviour of Masonry. In Structural Analysis of Historical Constructions II; Roca, P., González, J.L., Oñate, E., Lourenço Barcelona, P.B., Eds.; CIMNE: Barcelona, Spain, 1998; pp. 57–91. [Google Scholar]
- Uva, G.; Salerno, G. Towards a multiscale analysis of periodic masonry brickwork: A FEM algorithm with damage and friction. Int. J. Solids Struct. 2006, 43, 3739–3769. [Google Scholar] [CrossRef]
- Menon, A.; Magenes, G. Out-of-Plane Seismic Response of Unreinforced Masonry: Definition of Seismic Input; Research Report; IUSS Press/European School for Advanced Studies in Reduction of Seismic Risk: Pavia, Italy, 2008. [Google Scholar]
- Casolo, S.; Uva, G. Nonlinear analysis of out-of-plane masonry façades: Full dynamic versus pushover methods by rigid body and spring model. Earthq. Eng. Struct. Dyn. 2013, 42, 499–521. [Google Scholar] [CrossRef]
- Casolo, S. A numerical study on the cumulative out-of-plane damage to church masonry façades due to a sequence of strong ground motions. Earthq. Eng. Struct. Dyn. 2017, 46, 2717–2737. [Google Scholar] [CrossRef]
- Modena, C.; Valluzzi, M.R.; Folli, R.T.; Binda, L. Design choices and intervention techniques for repairing and strengthening of the Monza cathedral bell-tower. Constr. Build. Mater. 2002, 16, 385–395. [Google Scholar] [CrossRef]
- Casolo, S. Significant ground motion parameters for evaluation of the seismic performance of slender masonry towers. J. Earthq. Eng. 2001, 5, 187–204. [Google Scholar] [CrossRef]
- Casolo, S.; Diana, V.; Uva, G. Influence of soil deformability on the seismic response of a masonry tower. Bull. Earthq. Eng. 2017, 15, 1991–2014. [Google Scholar] [CrossRef]
- Casolo, S.; Milani, G.; Uva, G.; Alessandri, C. Comparative seismic vulnerability analysis on ten masonry towers in the coastal Po Valley in Italy. Eng. Struct. 2013, 49, 465–490. [Google Scholar] [CrossRef]
- Torelli, G.; D’Ayala, D.; Betti, M.; Bartoli, G. Analytical and Numerical Seismic Assessment of Heritage Masonry Towers. Bull. Earthq. Eng. 2020, 18, 969–1008. [Google Scholar] [CrossRef] [Green Version]
- Sangiorgio, V.; Pantoja, J.C.; Varum, H.; Uva, G.; Fatiguso, F. Structural degradation assessment of RC buildings: Calibration and comparison of semeiotic-based methodology for decision support system. J. Perform. Constr. Facil. 2019, 33. [Google Scholar] [CrossRef]
- Ruggieri, S.; Perrone, D.; Leone, M.; Uva, G.; Aiello, M.A. A prioritization RVS methodology for the seismic risk assessment of RC school buildings. Int. J. Disaster Risk Reduct. 2020, 51, 101807. [Google Scholar] [CrossRef]
- Sangiorgio, V.; Uva, G.; Adam, J.M. Integrated seismic vulnerability assessment of historical masonry churches including architectural and artistic assets based on macro-element approach. Int. J. Archit. Herit. 2020. [Google Scholar] [CrossRef]
- Ruggieri, S.; Tosto, C.; Rosati, G.; Uva, G.; Ferro, G.A. Seismic Vulnerability Analysis of Masonry Churches in Piemonte after 2003 Valle Scrivia Earthquake: Post-event Screening and Situation 17 Years Later. Int. J. Archit. Herit. 2020. [Google Scholar] [CrossRef]
- De Matteis, G.; Corlito, V.; Guadagnuolo, M.; Tafuro, A. Seismic vulnerability assessment and retrofitting strategies of italian masonry churches of the Alife-Aiazzo diocese in Caserta. Int. J. Archit. Herit. 2020, 14, 1180–1195. [Google Scholar] [CrossRef]
- Aiello, M.A.; Ciampoli, P.L.; Fiore, A.; Perrone, D.; Uva, G. Influence of infilled frames on seismic vulnerability assessment of recurrent building typologies. Ing. Sismica 2017, 34, 58–80. [Google Scholar]
- Lieussou, A. Etude sur les Ports d’Algérie; DGM Edition: Paris, France, 1857. [Google Scholar]
- Léon, R. Les Phares; The Navy Anchor: Paris, France, 1867. [Google Scholar]
- CRAAG. Les Séismes en Algérie de 1365 à 1992, CRAAG Report; Centre de Recherche en Astronomie Astrophysique et Géophysique: Bouzareah Alger, Algérie, 1994. [Google Scholar]
- Hamadach, M.; José, A.; Yelles, K.; Chauche, A. The Algiers, Algeria earthquake (M6.8) of 21 May 2003. Preliminary report. Seismol. Res. Lett. 2004, 75, 360–367. [Google Scholar] [CrossRef]
- Djeddi, M. Seism Tectonics and Seismology the North of Algeria, Department of Geophysics; University of Boumerdès: Boumerdès, Algeria, 2005. [Google Scholar]
- RPA99. Règles Parasismiques Algérienne; Centre National de Recherche Appliquée en Génie Parasismique, CGS: Alger, Algérie, 2003. [Google Scholar]
- Farsi, M.; Lazzali, F.; Ait-Méziane, Y. Stone Masonry Apartment Building. In World Housing Encyclopedia Report; EERI: Oakland, CA, USA, 2003. [Google Scholar]
- Bartoli, G.; Betti, M.; Vignoli, A.M. A numerical study on seismic risk assessment of historic masonry towers: A case study in San Gimignano. Bull. Earthq. Eng. 2016, 14, 1475–1518. [Google Scholar] [CrossRef]
- Zebar, Z.; Balhi, M. Les phares d’Algérie; Vigies de la côte; Kasbah édition: Alger, Algérie, 2015. [Google Scholar]
- Visbecq, M.A. Dellys: Petite Monographie Locale; L. Chaix Fils &C.: Alger, Algérie, 1925. [Google Scholar]
- S.T.A Data. 3Muri: Seismic Calculation of Masonry Structures According to the Italian Technical Codes for Constructions; S.T.A Data: Turin, Italy, 2016. [Google Scholar]
- Italian NTC 2018. New Technical Standards for Constructions; DM 17/01/2018; Ministero delle Infrastrutture e dei Trasporti, Istituto Poligrafico e Zecca dello Stato: Rome, Italy, 2018. (In Italian) [Google Scholar]
- Campione, G. Structural analysis, retrofitting design, and in situ control of permanently damaged long-span timber beams of a historical building in the south of Italy. Pract. Period. Struct. Des. Constr. 2020, 25. [Google Scholar] [CrossRef]
- Jaafari, C.; Mohammadi, J. Floor vibration control as a serviceability requirement in design standards and practices: Review. Pract. Period. Struct. Des. Constr. 2018, 23. [Google Scholar] [CrossRef]
- Bergamo, O.; Campione, G. Experimental investigation for degradation analysis of an RC italian viaduct and retrofitting design. Pract. Period. Struct. Des. Constr. 2020, 25. [Google Scholar] [CrossRef]
- Elias, S.; Matsagar, V. Seismic vulnerability of a non-linear building with distributed multiple tuned vibration absorbers. Struct. Infrastruct. Eng. 2019, 15, 1103–1118. [Google Scholar] [CrossRef]
- Abdessemed, F.A.; Misseri, A.; Rovero, G.L. Effects of the Boumerdès earthquake of May 21st, 2003 on the Great Mosque of Dellys (Algeria) and Solutions of the Restoration Project. In Proceedings of the Vienna Congress on Recent Advances in Earthquake Engineering and Structural Dynamics, Vienna, Austria, 28–30 August 2013. [Google Scholar]
- NIKER EU Project. Deliverable 3.1—Report Inventory of Earthquake-Induced Failure Mechanisms Related to Construction Types, Structural Elements, and Materials, Annex 1: Damage Abacus. Politecnico di Milano: 2010. Available online: http://www.niker.eu/assets/Files/Download (accessed on 20 November 2020).
- NIKER EU Project. Instructions for the Application of the Technical Building Code (NTC, 2008); Ministero delle Infrastrutture e dei Trasporti Istituto Poligrafico e Zecca dello Stato: Rome, Italy, 2009. (In Italian) [Google Scholar]
- Penna, A. A Macro-Element Procedure for the non-Linear Dynamic Analysis of Masonry Buildings. Ph.D Thesis, Politecnico di Milano, Milan, Italy, 2002. [Google Scholar]
- Lagomarsino, S.; Penna, A.; Galasco, A.; Cattari, S. TreMuri program: SeismicAnalyses of 3D Masonry Buildings, Release 2.0; University of Genoa: Genova, Italy, 2012. [Google Scholar]
- Gambarotta, L.; Lagomarsino, S. On Dynamic Response of Masonry Panels. In National Conference “Masonry Mechanics between Theory and Practice”; Ed. Pitagora: Messina, Italy, 1996. [Google Scholar]
- Darwish, M.; Rashwan, M. Structural dynamic characteristics of ancient Egyptian obelisks and their responses to earthquake loads. Pract. Period. Struct. Des. Constr. 2018, 23. [Google Scholar] [CrossRef]
- Avci, O.; Al-Smadi, Y.M. Unreinforced masonry façade assessment of a historic building for excessive displacements due to a nearby subway construction. Pract. Period. Struct. Des. Constr. 2019, 24. [Google Scholar] [CrossRef]
- EN 1996-1:2005. Eurocode 6: Design of Masonry Structure; CEN, European Committee of Standardisation: Brussels, Belgium, 2005. [Google Scholar]
- EN 1998. Eurocode 8: Design of Structures for Earthquake Resistance; CEN, European Committee of Standardisation: Brussels, Belgium, 1999. [Google Scholar]
- NPS; USCG; DDLRMP; USLS. Historic Lighthouse Preservation, 1997. Available online: https://www.nps.gov/maritime/nhlpa/handbook.htm (accessed on 20 November 2020).
- Penazzi, D.; Valluzzi, M.R.; Saisi, A.; Binda, L.; Modena, C. Repair and Strengthening of Historic Masonry Buildings in Seismic Areas. In Proc. Int. Millennium Congress ‘More than Two Thousand Years in the History of Architecture Safeguarding the Structure of Our Architectural Heritage; UNESCO: Bethlehem, Palestine, 2001. [Google Scholar]
- Chuang, S.W.; Zhuge, Y. Seismic Retrofitting of Unreinforced Masonry Buildings-A Literature Review. Aust. J. Struct. Eng. 2005, 6, 25–36. [Google Scholar] [CrossRef]
- Brandois, P.; Babics, F. Manuel de Sensibilisation à la Restauration de la Maçonnerie; Ministère de la Culture et de la Communication: Paris, France, 2006. [Google Scholar]
- Navarro, J.L.G. Diagnostic et Traitement des Pathologies Structurelles du Bâtiment; Institut National du Patrimoine tunisie: Kairouan, Tunisia, 2006. [Google Scholar]
- Díaz, G.C. La réhabilitation des éléments structuraux de l’architecture traditionnelle méditerranéenne. Méthode RehabiMed: Les Techniques de Réhabilitation; Renforcer les Structures 2007, 8, 297–308. [Google Scholar]
- Vicente, R.; Rodrigues, H.; Varum, H.; Silva, J.A.R. Evaluation of strengthening techniques of traditional masonry buildings: Case Study of a four-building aggregate. J. Perform. Constr. Facil. 2011, 25, 202–216. Available online: www.nps.gov (accessed on 20 November 2020). [CrossRef] [Green Version]
- D’Ayala, D. Seismic Retrofit of Earthquake Damaged Masonry Housing; K4D Helpdesk Report: Brighton, UK, 2016. [Google Scholar]
- Croci, G. The conservation and structural restoration of architectural heritage. In Computational Mechanics Publications; WIT Press: Southampton, UK, 1998. [Google Scholar]
- ICOMOS. Recommendations for the Analysis, Conservation and Structural Restoration of Architectural Heritage. In Proceedings of the ICOMOS 14th General Assembly, Victoria Falls, Zimbabwe, 27–31 October 2003. [Google Scholar]
- D’Ayala, D. Conservation Principles and Performance-Based Strengthening of Heritage Buildings in Post-Event Reconstruction; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Laefer, D.; Baronio, G.; Anzani, A.; Binda, L. Measurement of Grout Injection Efficacy for Stone Masonry walls. In Proceedings of the Seventh North American Masonry Conference, The Masonry Society, Boulder, Colorado, 2–5 June 1996; pp. 484–496. [Google Scholar]
















| In-plan shape | Quadrangular (11) | Circular (08) | Octagonal (05) |
 |  |  | |
| Height | 10–20 m (16) | 20–30 m (07) | 30–40 m (01) |
 |  |  | |
| Position of the tower | At the center of building (09) | Attached to the building (10) | Independent (05) |
 |  |  |
| Structural Element | Geometrical Scheme | Description |
|---|---|---|
| Walls of the main building |  | Walls made of rubble stone. Thickness of exterior walls: 50 cm, chaining at angles. Thickness of interior walls: 40 cm. |
| Walls of the tower |  | Walls build of cut stone masonry. |
| Floors |  | Vaulted ceilings. Flat formed arches made from cut stone. |
| Damage Abacus | Illustration | Description |
|---|---|---|
| Global overturning of the façade |  | Separation of the north-west façade from the lateral walls in proximity of the corner, because of the insufficient connection between orthogonal walls and between walls and floors. |
| Partial overturning with diagonal rotation axis |  | Vertical overturning of the north-east façade, with corner expulsion. This out-of-plane mechanism, with provides local failures of the upper part of the walls and collapse, is due to the stress concentrations that occur at the intersection of transverse walls and to the presence of large openings. |
| Shear mechanism in the façade plane |  | Cracks in the façades:
|
| Overturning of the tower top |  | Vertical, horizontal, and diagonal thin cracks in the four sides of the tower, due to long-term compressive actions and seismic bending actions. |
| Shear cracks of the internal walls |  | Diagonal and vertical cracks in the inner partition walls. |
| Floor damage |  | Cracks in the vaults. Partial expulsion of the upper story and detachment of steel IPN beams from side walls. |
| Rubble Stone | Cut Soft Stone | Block Stone | ||||
|---|---|---|---|---|---|---|
| Min–Max | Average | Min–Max | Average | Min–Max | Average | |
| E (N/mm2) | 690–1050 | 870 | 900–1260 | 1080 | 2400–3200 | 2800 |
| G (N/mm2) | 230–350 | 290 | 300–420 | 360 | 780–940 | 860 |
| W (kN/m3) | 19 | 16 | 22 | |||
| Mode | T (s) | mx (kg) | Mx (%) | my (kg) | My (%) | mz (kg) | Mz (%) |
|---|---|---|---|---|---|---|---|
| 1 | 1.22975 | 1,281,492 | 42.28 | 2 | 0.00 | 0 | 0.00 |
| 2 | 1.21589 | 2 | 0.00 | 1,449,487 | 47.82 | 1 | 0.00 |
| 3 | 0.79637 | 20,245 | 0.67 | 0 | 0.00 | 0 | 0.00 |
| 4 | 0.43207 | 31,977 | 1.05 | 3 | 0.00 | 0 | 0.00 |
| 5 | 0.37531 | 2 | 0.00 | 1,245,551 | 41.09 | 22 | 0.00 |
| 6 | 0.34775 | 1,033,403 | 34.09 | 4 | 0.00 | 0 | 0.00 |
| 7 | 0.31534 | 258,212 | 8.52 | 1 | 0.00 | 0 | 0.00 |
| 8 | 0.28018 | 87,862 | 2.90 | 0 | 0.00 | 4 | 0.00 |
| 9 | 0.25022 | 0 | 0.00 | 213,320 | 7.04 | 0 | 0.00 |
| 10 | 0.23033 | 153,386 | 5.06 | 0 | 0.00 | 1,668,540 | 0.00 |
| 11 | 0.20577 | 0 | 0.00 | 610 | 0.02 | - | 55.05 |
| 12 | 0.20502 | 20,023 | 0.66 | 0 | 0.00 | - | 0.00 |
| Σ | - | - | 95.23 | - | 95.97 | - | 55.05 |
| - | 1st Mode | 2nd Mode | 3rd Mode |
|---|---|---|---|
| Original structure | T(s): 1.22 | T(s): 1.21 | T(s): 1.79 |
| Mx (%): 42.28 | Mx (%): 0.00 | Mx (%): 0.67 | |
| My (%): 0.00 | My (%): 47.82 | My (%): 0.00 | |
| Mz (%): 0.00 | Mz (%): 0.00 | Mz (%): 0.00 | |
| Tower | T(s): 1.35 | T(s): 1.34 | T(s): 1.90 |
| Mx (%): 72.85 | Mx (%): 0.04 | Mx (%): 0.04 | |
| My (%): 0.04 | My (%): 73.25 | My (%): 0.00 | |
| Mz (%): 0.00 | Mz (%): 0.00 | Mz (%): 0.00 | |
| Main building | T(s): 0.43 | T(s): 0.33 | T(s): 0.30 |
| Mx (%): 0.00 | Mx (%): 1.78 | Mx (%): 92.29 | |
| My (%): 90.78 | My (%): 0.00 | My (%): 0.00 | |
| Mz (%): 0.01 | Mz (%): 0.00 | Mz (%): 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amari, K.; Abdessemed Foufa, A.; Cheikh Zouaoui, M.; Uva, G. Seismic Vulnerability of Masonry Lighthouses: A Study of the Bengut Lighthouse, Dellys, Boumerdès, Algeria. Buildings 2020, 10, 247. https://doi.org/10.3390/buildings10120247
Amari K, Abdessemed Foufa A, Cheikh Zouaoui M, Uva G. Seismic Vulnerability of Masonry Lighthouses: A Study of the Bengut Lighthouse, Dellys, Boumerdès, Algeria. Buildings. 2020; 10(12):247. https://doi.org/10.3390/buildings10120247
Chicago/Turabian StyleAmari, Karima, Amina Abdessemed Foufa, Mustapha Cheikh Zouaoui, and Giuseppina Uva. 2020. "Seismic Vulnerability of Masonry Lighthouses: A Study of the Bengut Lighthouse, Dellys, Boumerdès, Algeria" Buildings 10, no. 12: 247. https://doi.org/10.3390/buildings10120247
APA StyleAmari, K., Abdessemed Foufa, A., Cheikh Zouaoui, M., & Uva, G. (2020). Seismic Vulnerability of Masonry Lighthouses: A Study of the Bengut Lighthouse, Dellys, Boumerdès, Algeria. Buildings, 10(12), 247. https://doi.org/10.3390/buildings10120247






