Effect of the Particle Size on TDA Shear Strength Parameters in Triaxial Tests
Abstract
:1. Introduction
2. Materials and Methods
3. Large-Scale Triaxial Apparatus
4. Testing Scheme
4.1. Sample Preparation Stage
4.2. Saturation Stage
4.3. Consolidation Stage
4.4. Shearing Stage
4.5. Corrections
5. Results
5.1. Consistency and Repeatability of the Tests
5.2. Stress-Strain Curves
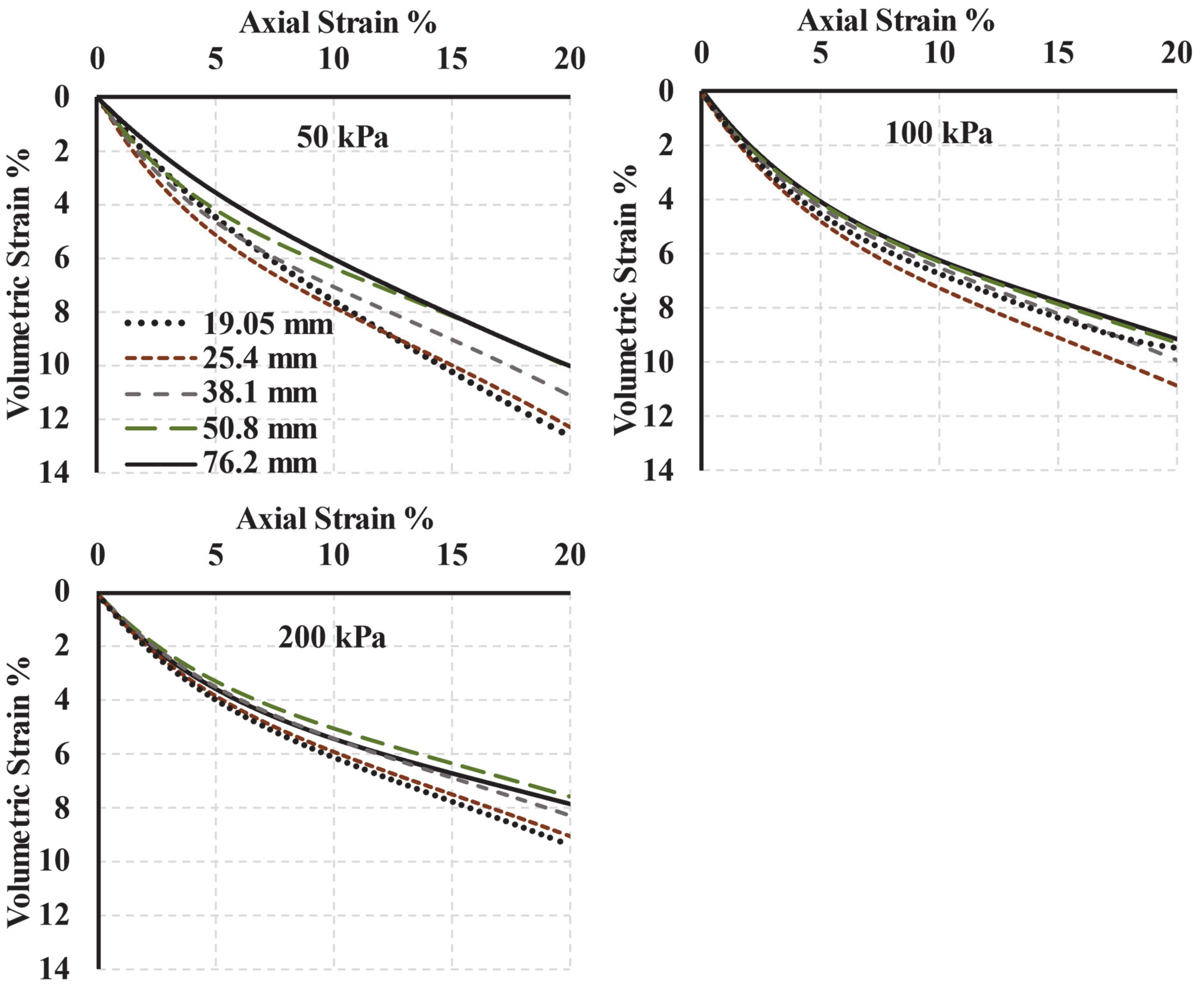
5.3. Volumetric Strain
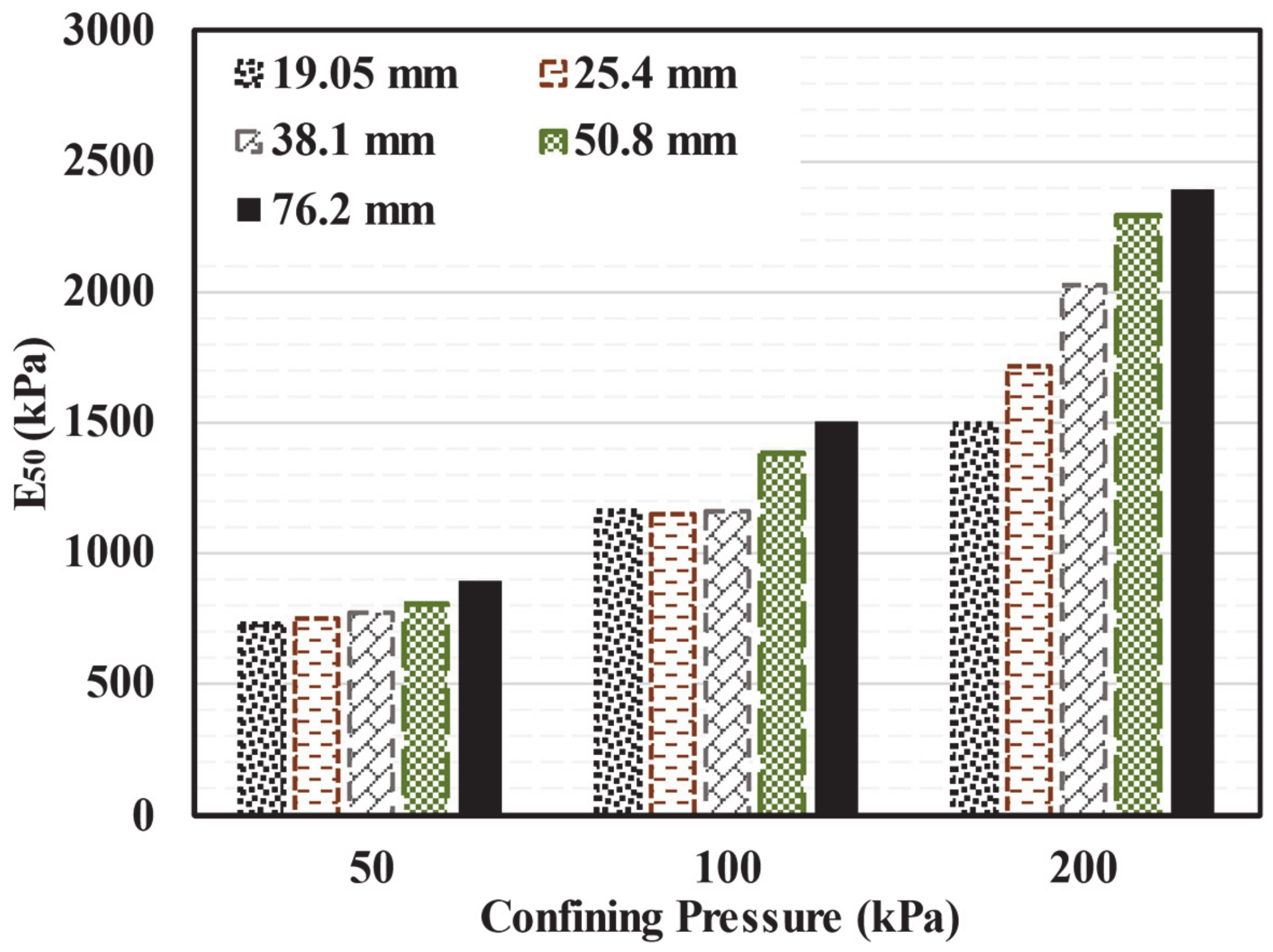
5.4. Stiffness
5.5. Stiffness Degradation of TDA
6. Conclusions
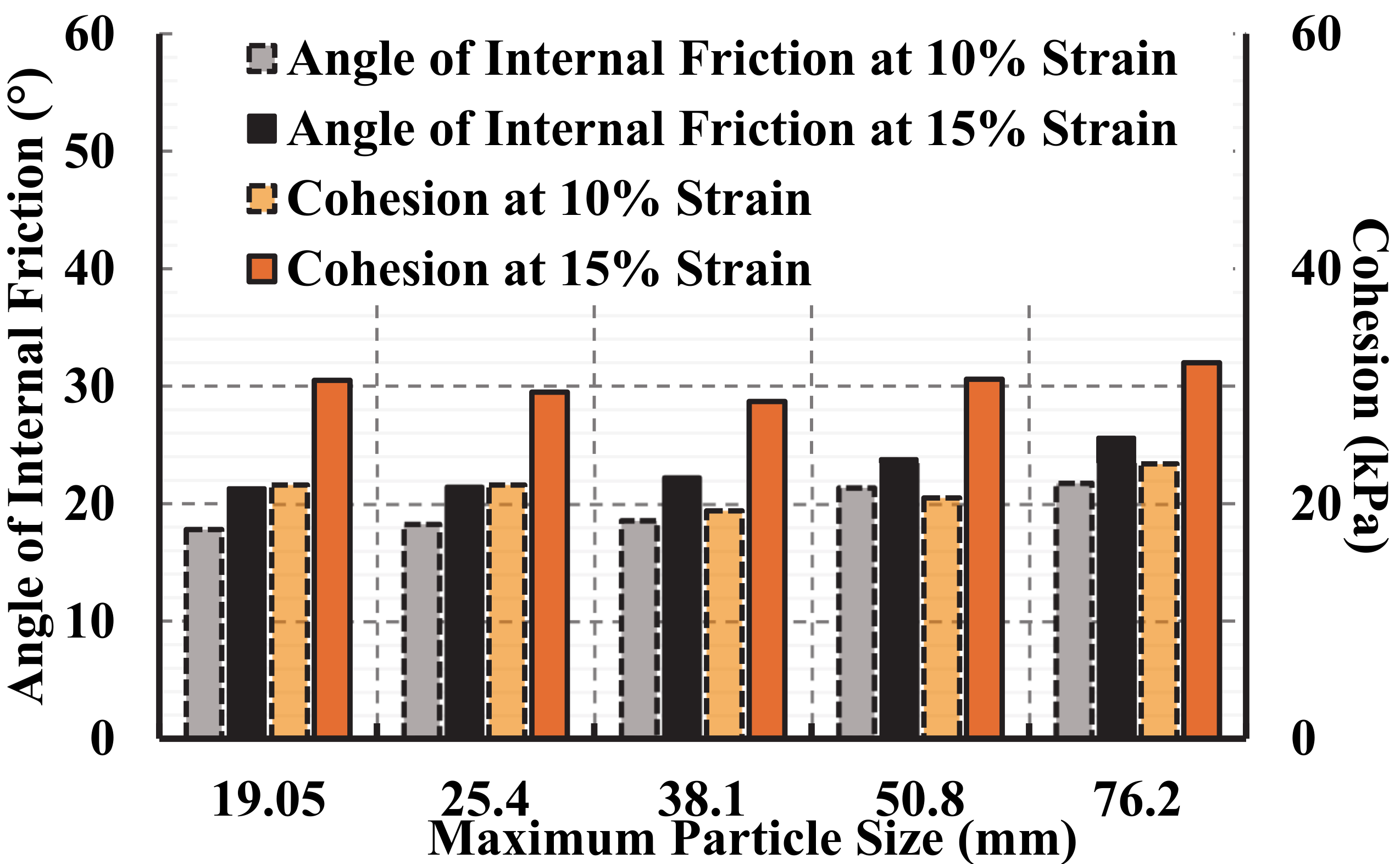
- The effective angle of internal friction of TDA increases by increasing the maximum particle size.
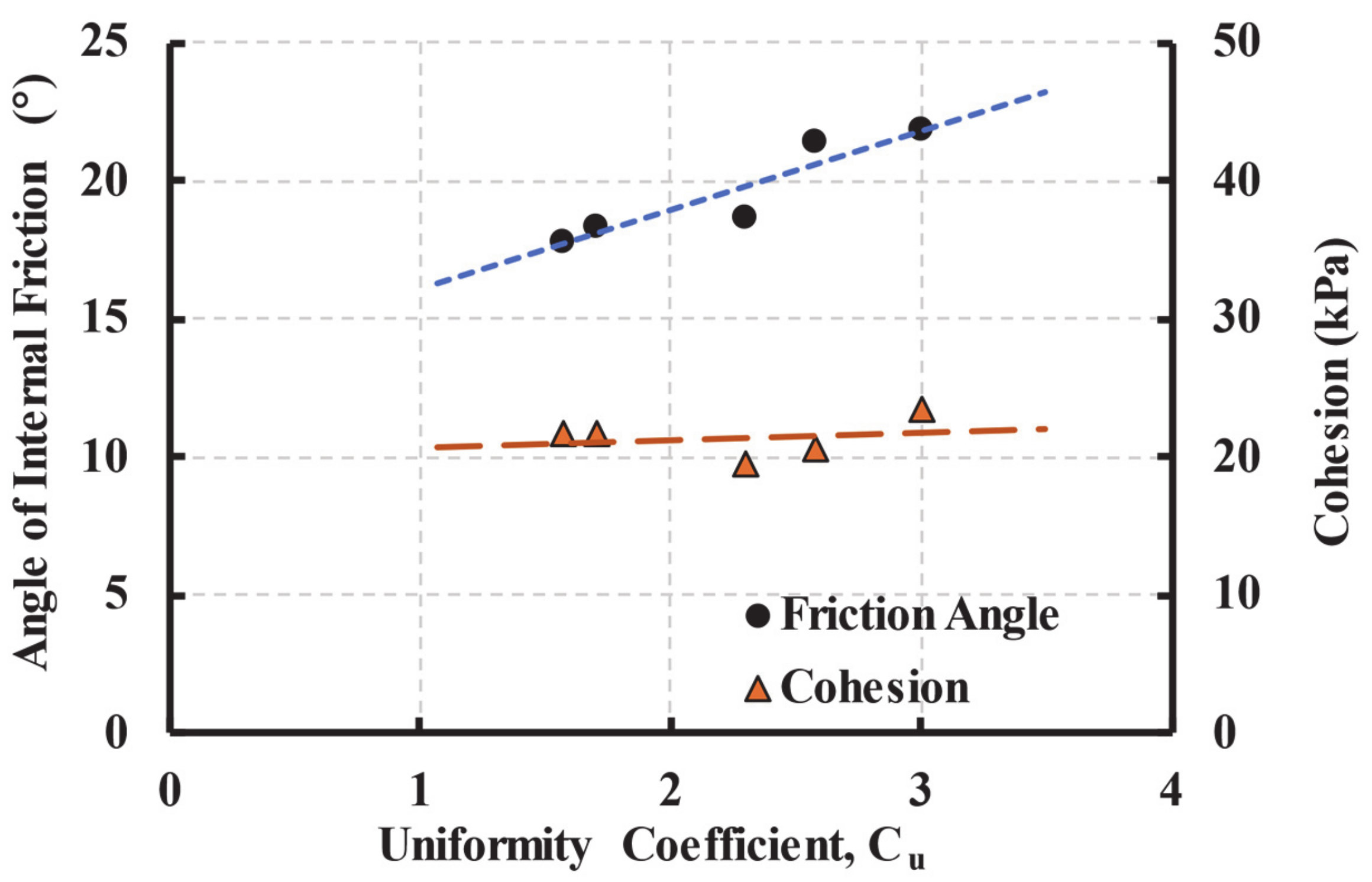
- The effective angle of internal friction was also found to increase as the coefficient of uniformity increases.
- The cohesion of TDA did not show a defined correlation with the particle size as the cohesion exhibited a slight decrease followed by an increase by increasing the particle size. i.e., the interlocking cohesion of TDA is not significantly affected by the particle size (the difference was less than 3.3 kPa at most). The same conclusion was reported by El Naggar et al. [6] from direct shear tests on TDA.
- The secant elastic modulus of TDA increases by increasing the maximum particle size (Dmax) or the confining pressure.
- At all strains, the overall stiffness of all specimens increases as the confining pressure increase.
- Upon reaching a strain level near 0.02%, in the small strain zone, the stress-strain behaviour becomes noticeably nonlinear, and the secant modulus, Esec, begins to degrade nonlinearly with the increasing strain up to a strain level of about 0.3%.
- The onset of the large strain behaviour zone occurs at a strain level of about 0.3%. At a strain level of about 1%, in the large strain zone, the secant modulus of TDA becomes relatively small and loses 50 to 80% of its threshold.
- At higher strain levels, 5% and more, under confining pressures of 100 and 200 kPa, the TDA loses approximately 90% of its stiffness.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ahmed, I.; Lovell, C. Rubber soils as lightweight geomaterial. Transp. Res. Board 1993, 1422, 61–70. [Google Scholar]
- Ahn, I.S.; Cheng, L.; Fox, P.; Wright, J. Material properties of large-size tire derived aggregate for civil engineering applications. J. Mater. Civ. Eng. 2015, 27, 04014258. [Google Scholar] [CrossRef]
- Bosscher, P.J.; Edil, T.B.; Kuraoka, S. Design of Highway Embankments Using Tire Chips. J. Geotech. Geoenvironmental Eng. 1997, 123, 295–304. [Google Scholar] [CrossRef]
- Cecich, V.; Gonzales, L.; Hoisaeter, A.; Williams, J.; Reddy, K. Use of Shredded Tires as Lightweight Backfill Material for Retaining Structures. Waste Manag. Res. 1996, 14, 433–451. [Google Scholar] [CrossRef]
- El Naggar, H.; Soleimani, P.; Fakhroo, A. Strength and Stiffness Properties of Green Lightweight Fill Mixtures. Geotech. Geol. Eng. 2016, 34, 867–876. [Google Scholar] [CrossRef]
- El Naggar, H.; Zahran, K.; Moussa, A. Effect of the Particle Size on the TDA Shear Strength and Stiffness Parameters in Large-Scale Direct Shear Tests. Geotechnics 2021, 1, 1. [Google Scholar] [CrossRef]
- El Naggar, H.; Ashari, M.; Mahgoub, A. Development of an Empirical Hyperbolic Material Model for TDA Using Large Scale Triaxial Testing. Int. J. Geotech. Eng. (Minor Revis.) 2021. [Google Scholar]
- Humphrey, D.N.; Sandford, T.C.; Cribbs, M.M.; Manion, W.P. Shear strength and compressibility of tire chips for use as retaining wall backfill. Transp. Res. Rec. 1993, 1422, 29–35. [Google Scholar]
- Humphrey, D.N.; Eaton, R.A. Field Performance of Tire Chips as Subgrade Insulation for Rural Roads. In Proceedings of the Transportation Research Board Conference Proceedings, Minneapolis, MN, USA, 25–29 June 1995. [Google Scholar]
- Humphrey, D.N.; Manion, W.P. Properties of tire chips for lightweight fill. In Grouting, Soil Improvement and Geosynthetics; ASCE: Reston, VA, USA, 1992; pp. 1344–1355. [Google Scholar]
- Humphrey, D.N.; Nickles, W.L. Tire chips as subgrade insulation and lightweight fill. In Proceedings of the 18th Annual Meeting of the Asphalt Recycling and Reclaiming Association, Annapolis, MD, USA, 1994; pp. 83–105. [Google Scholar]
- Lee, H.J.; Roh, H.S. The use of recycled tire chips to minimize dynamic earth pressure during compaction of backfill. Constr. Build. Mater. 2007, 21, 1016–1026. [Google Scholar] [CrossRef]
- Lee, J.H.; Salgado, R.; Bernal, A.; Lovell, C.W. Shredded Tires and Rubber-Sand as Lightweight Backfill. J. Geotech. Geoenvironmental Eng. 1999, 125, 132–141. [Google Scholar] [CrossRef]
- Shahrokhi-Shahraki, R.; Kwon, P.S.; Park, J.; O’Kelly, B.C.; Rezania, S. BTEX and heavy metals removal using pulverized waste tires in engineered fill materials. Chemosphere 2020, 242, 125281. [Google Scholar] [CrossRef]
- Sparkes, J.; El Naggar, H.; Valsangkar, A. Compressibility and Shear Strength Properties of Tire-Derived Aggregate Mixed with Lightweight Aggregate. J. Pipeline Syst. Eng. Pr. 2019, 10, 04018031. [Google Scholar] [CrossRef]
- Soltani, A.; Taheri, A.; Deng, A.; O’Kelly, B.C. Improved Geotechnical Behavior of an Expansive Soil Amended with Tire-Derived Aggregates Having Different Gradations. Minerals 2020, 10, 923. [Google Scholar] [CrossRef]
- Zahran, K.; El Naggar, H. Effect of Sample Size on TDA Shear Strength Parameters in Direct Shear Tests. Transp. Res. Rec. J. Transp. Res. Board 2020, 2674, 1110–1119. [Google Scholar] [CrossRef]
- Mahgoub, A.; El Naggar, H. Using TDA as an Engineered Stress-Reduction Fill over Preexisting Buried Pipes. J. Pipeline Syst. Eng. Pr. 2019, 10, 04018034. [Google Scholar] [CrossRef]
- Mahgoub, A.; El Naggar, H. Innovative Application of Tire-Derived Aggregate around Corrugated Steel Plate Culverts. J. Pipeline Syst. Eng. Pr. 2020, 11, 04020025. [Google Scholar] [CrossRef]
- Mahgoub, A.; El Naggar, H. Coupled TDA-Geocell Stress-Bridging System for Buried Corrugated Metal Pipes. J. Geotech. Geoenvironmental Eng. 2020, 146, 04020052. [Google Scholar] [CrossRef]
- Mahgoub, A.; El Naggar, H. Using TDA Underneath Shallow Foundations: Field Tests and Numerical Modelling. J. Comput. Geotech. 2020. (In Production) [Google Scholar] [CrossRef]
- Gabryś, K.; Sas, W.; Soból, E.; Głuchowski, A. Application of bender elements technique in testing of anthropogenic soil—Recycled concrete aggregate and its mixture with rubber chips. Appl. Sci. 2017, 7, 741. [Google Scholar] [CrossRef] [Green Version]
- Sas, W.; Głuchowski, A.; Szymański, A. The geotechnical properties of recycled concrete aggregate with addition of rubber chips during cyclic loading. Int. J. GEOMATE 2017, 12, 25–32. [Google Scholar] [CrossRef]
- Moussa, A.; El Naggar, H. Dynamic Characterization of Tire Derived Aggregates. J. Mater. Civ. Eng. 2021, 33, 04020471. [Google Scholar] [CrossRef]
- Moussa, A.; El Naggar, H. Numerical Evaluation of Buried Wave Barriers Performance. Int. J. Geosynth. Ground Eng. 2020, 6, 1–13. [Google Scholar] [CrossRef]
- Kirkpatric, W.M. Effects of Grain Size and Grading on the Shearing Behaviour of Granular Materials. In Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering, Montreal, QC, Canada, 8–15 September 1965; Volume I, pp. 273–277. [Google Scholar]
- Islam, M.N.; Siddika, A.; Hossain, M.B.; Rahman, A.; Asad, M.A. Effect of particle size on the shear strength behaviour of sands. Aust. Geomech. J. 2011, 46, 85–95. [Google Scholar]
- Kim, D.; Ha, S. Effects of Particle Size on the Shear Behavior of Coarse Grained Soils Reinforced with Geogrid. Materials 2014, 7, 963–979. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.-J.; Zhang, H.-P.; Tang, S.-C.; Liang, Y. Effects of Particle Size Distribution on Shear Strength of Accumulation Soil. J. Geotech. Geoenvironmental Eng. 2013, 139, 1994–1997. [Google Scholar] [CrossRef]
- Vangla, P.; Latha, G.M. Influence of Particle Size on the Friction and Interfacial Shear Strength of Sands of Similar Morphology. Int. J. Geosynth. Ground Eng. 2015, 1, 1–12. [Google Scholar] [CrossRef] [Green Version]
- ASTM D6270-08. Standard Practice for Use of Scrap Tires in Civil Engineering Applications; ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]
- ASTM C136/C136M-14. Standard Test Method for Sieve Analysis of Fine and Coarse Aggregates; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Holtz, R.; Kovacs, W. An Introduction to Geotechnical Engineering; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1981; ISBN 0-13-484394-0. [Google Scholar]
- ASTM D7181-11. Method for Consolidated Drained Triaxial Compression Test for Soils; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- Baldi, G.; Hueckel, T.; Pellegrini, R. Thermal volume changes of the mineral–water system in low-porosity clay soils. Can. Geotech. J. 1988, 25, 807–825. [Google Scholar] [CrossRef]
- Lade, P.V. Triaxial Testing of Soils; Wiley, Blackwell: New York, NY, USA, 2016. [Google Scholar]
- Moo-Young, H.; Sellasie, K.; Zeroka, D.; Sabnis, G. Physical and Chemical Properties of Recycled Tire Shreds for Use in Construction. J. Environ. Eng. 2003, 129, 921–929. [Google Scholar] [CrossRef]
- La Rochelle, P.; Leroueil, S.; Trak, B.; Blais-Leroux, L.; Tavenas, F. Observational approach to membrane and area corrections in triaxial tests. Adv. Triaxial Test. Soil Rock STP 1988, 977, 715–731. [Google Scholar]
- Garga, V.K.; Zhang, H. Volume changes in undrained triaxial tests on sands. Can. Geotech. J. 1997, 34, 762–772. [Google Scholar] [CrossRef]
- Chaney, R.; Demars, K.; Masad, E.; Taha, R.; Ho, C.; Papagiannakis, T. Engineering Properties of Tire/Soil Mixtures as a Lightweight Fill Material. Geotech. Test. J. 1996, 19, 297–304. [Google Scholar] [CrossRef]
- Youwai, S.; Bergado, D.T. Strength and deformation characteristics of shredded rubber tire sand mixtures. Can. Geotech. J. 2003, 40, 254–264. [Google Scholar] [CrossRef]
- Zornberg, J.G.; Cabral, A.R.; Viratjandr, C. Behaviour of tire shred sand mixtures. Can. Geotech. J. 2004, 41, 227–241. [Google Scholar] [CrossRef]
- Yi, Y.; Meles, D.; Nassiri, S.; Bayat, A. On the compressibility of tire-derived aggregate: Comparison of results from laboratory and field tests. Can. Geotech. J. 2015, 52, 442–458. [Google Scholar] [CrossRef]
- Meles, D.; Bayat, A.; Shafiee, M.H.; Nassiri, S.; Gül, M. Investigation of tire derived aggregate as a fill material for highway embankment. Int. J. Geotech. Eng. 2013, 8, 182–190. [Google Scholar] [CrossRef]
- Atkinson, J.; Sallfors, G. Experimental determination of stress-strain-time characteristics in laboratory and in situ tests. In Proceedings of the 10th European Conference on Soil Mechanics and Foundation Engineering, Florence, Italy, 26–30 May 1991; Volume 3, pp. 915–956. [Google Scholar]

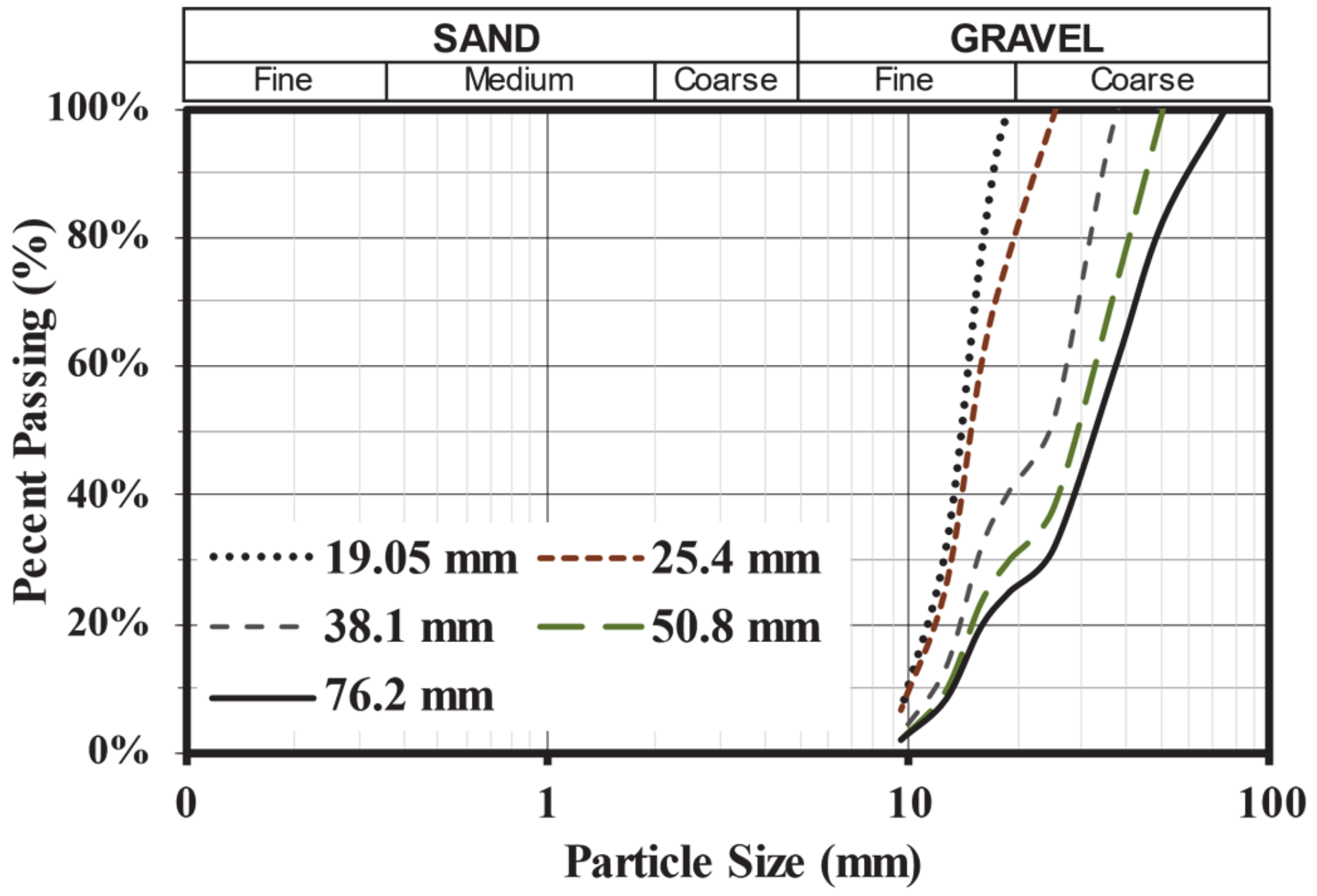


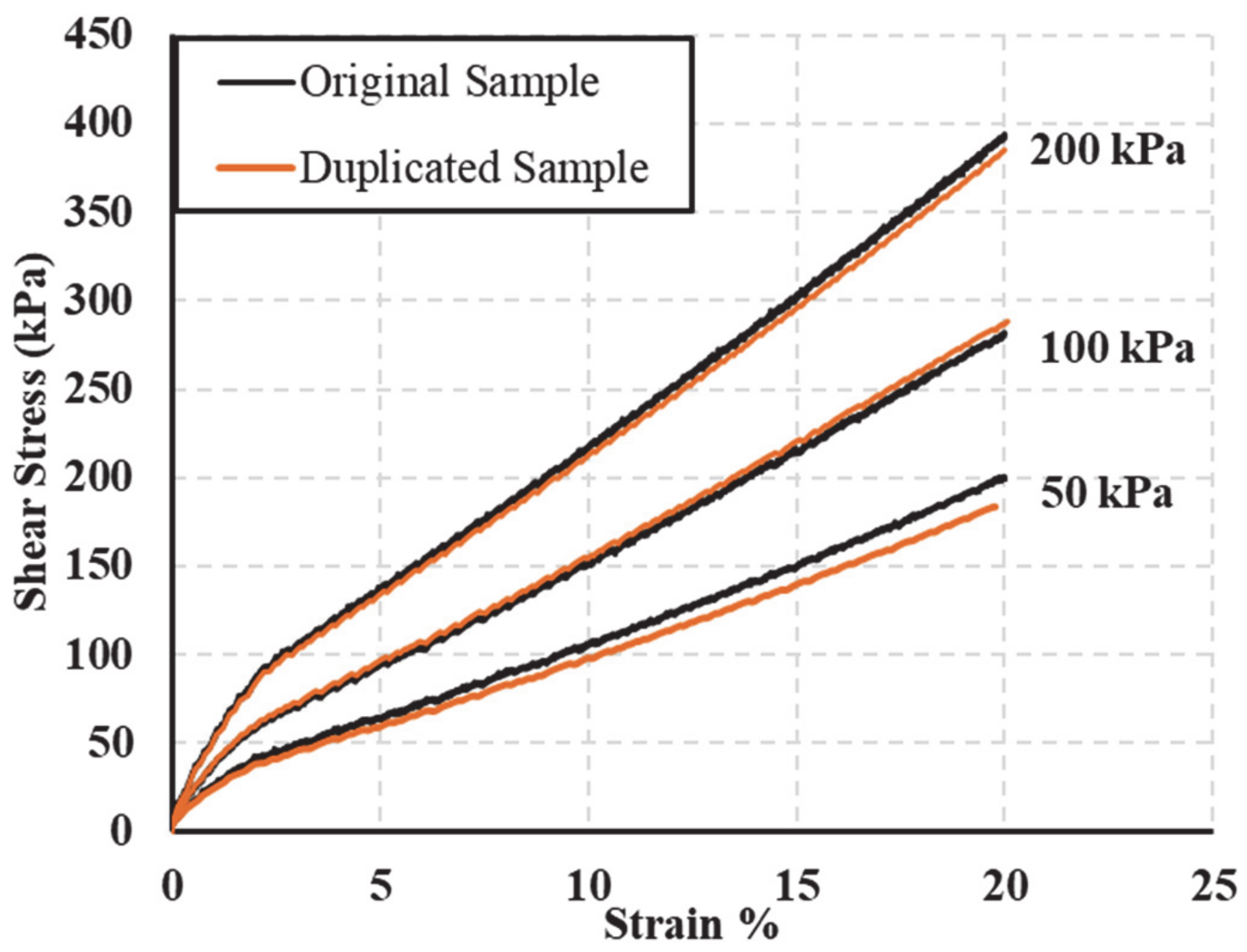
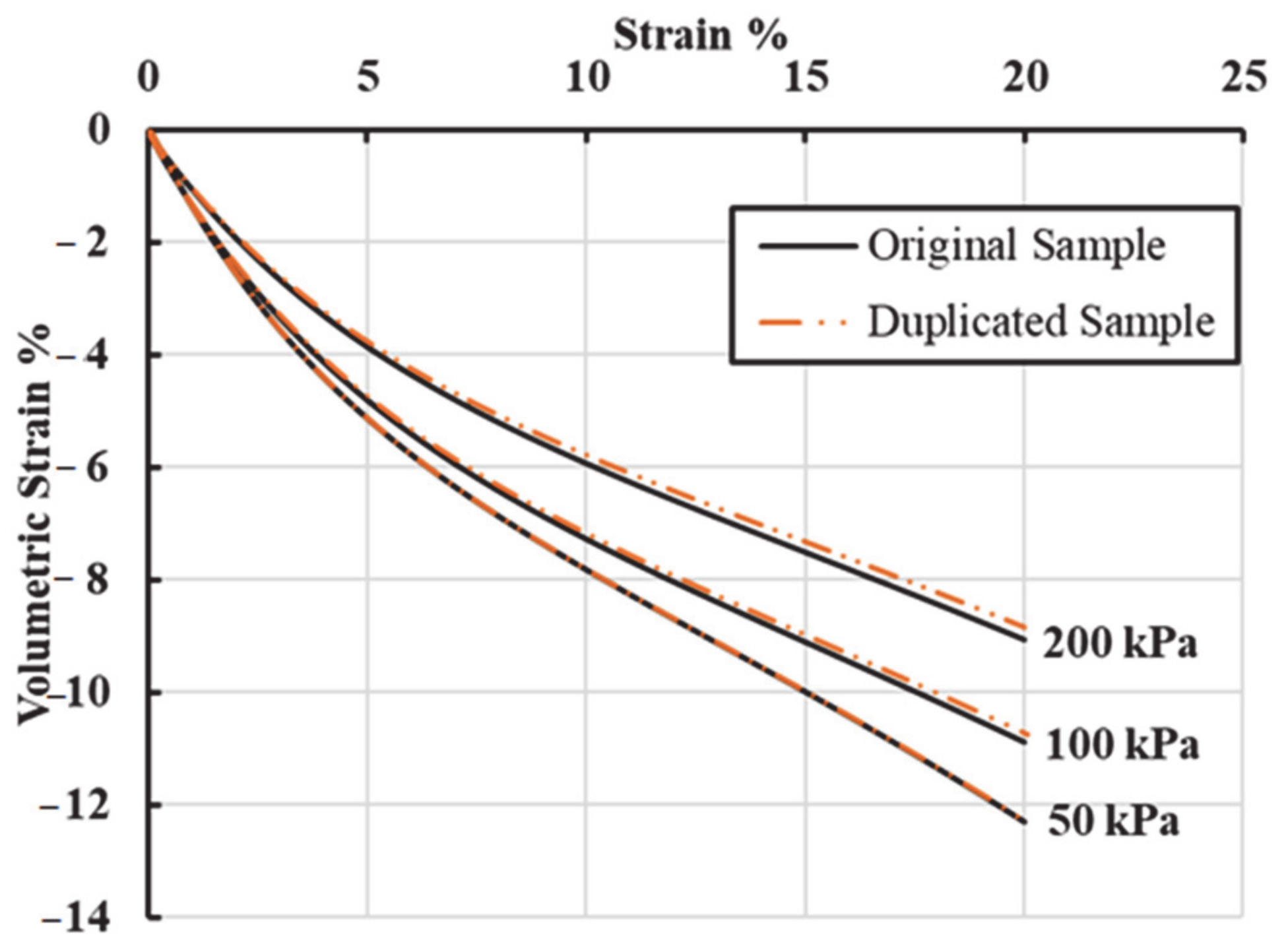
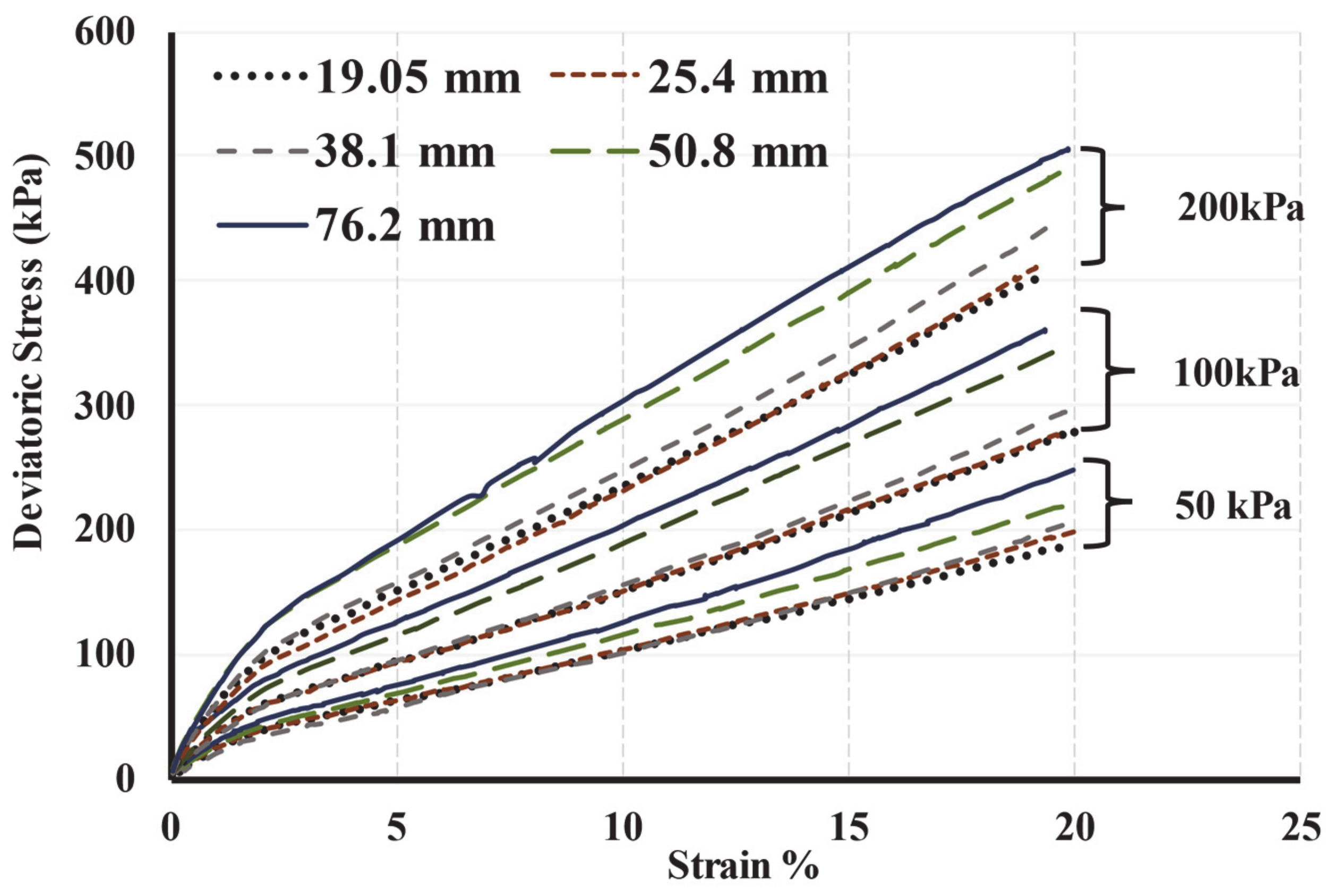


| Characteristics | Sample#1 | Sample #2 | Sample #3 | Sample #4 | Sample #5 |
|---|---|---|---|---|---|
| D10 (mm) | 9.8 | 10 | 12 | 13.1 | 13.2 |
| D30 (mm) | 12.4 | 13.2 | 16 | 19 | 25 |
| D50 (mm) | 14 | 16 | 25 | 29.5 | 33 |
| D60 (mm) | 15.5 | 17 | 27.5 | 33 | 39 |
| Dmax (mm) | 19.05 | 25.4 | 38.1 | 50.8 | 76.2 |
| Size Range (mm) | 9.5–19.05 | 9.5–25.4 | 9.5–38.1 | 9.5–50.8 | 9.5–76.2 |
| Cu | 1.58 | 1.70 | 2.29 | 2.52 | 2.95 |
| Cc | 1.01 | 1.02 | 0.78 | 0.84 | 1.21 |
| USCS Classification | Poorly graded | Poorly graded | Poorly graded | Poorly graded | Poorly graded |
| Study | Area Correction Equation | Deformation Shape |
|---|---|---|
| La Rochelle et al. [38] | Right Circular Cylinder | |
| La Rochelle et al. [38] | parabolic | |
| Garga and Zhang [39] | parabolic |
| Sample (Dmax) | Strain 10% | Strain 15% | ||
|---|---|---|---|---|
| Angle of Internal Friction, φ′ (°) | Cohesion, c′ (kPa) | Angle of Internal Friction, φ′ (°) | Cohesion, c′ (kPa) | |
| 19.05 mm | 17.8 | 21.6 | 21.3 | 30.5 |
| 25.4 mm | 18.3 | 21.6 | 21.5 | 29.5 |
| 38.1 mm | 18.6 | 19.4 | 22.3 | 28.7 |
| 50.8 mm | 21.4 | 20.5 | 23.8 | 30.6 |
| 76.2 mm | 21.8 | 23.4 | 25.6 | 32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Naggar, H.; Zahran, K. Effect of the Particle Size on TDA Shear Strength Parameters in Triaxial Tests. Buildings 2021, 11, 76. https://doi.org/10.3390/buildings11020076
El Naggar H, Zahran K. Effect of the Particle Size on TDA Shear Strength Parameters in Triaxial Tests. Buildings. 2021; 11(2):76. https://doi.org/10.3390/buildings11020076
Chicago/Turabian StyleEl Naggar, Hany, and Khaled Zahran. 2021. "Effect of the Particle Size on TDA Shear Strength Parameters in Triaxial Tests" Buildings 11, no. 2: 76. https://doi.org/10.3390/buildings11020076
APA StyleEl Naggar, H., & Zahran, K. (2021). Effect of the Particle Size on TDA Shear Strength Parameters in Triaxial Tests. Buildings, 11(2), 76. https://doi.org/10.3390/buildings11020076







