Fractal Dimension Calculation and Visual Attention Simulation: Assessing the Visual Character of an Architectural Façade
Abstract
1. Introduction
2. Fractal Dimension and Visual Attention
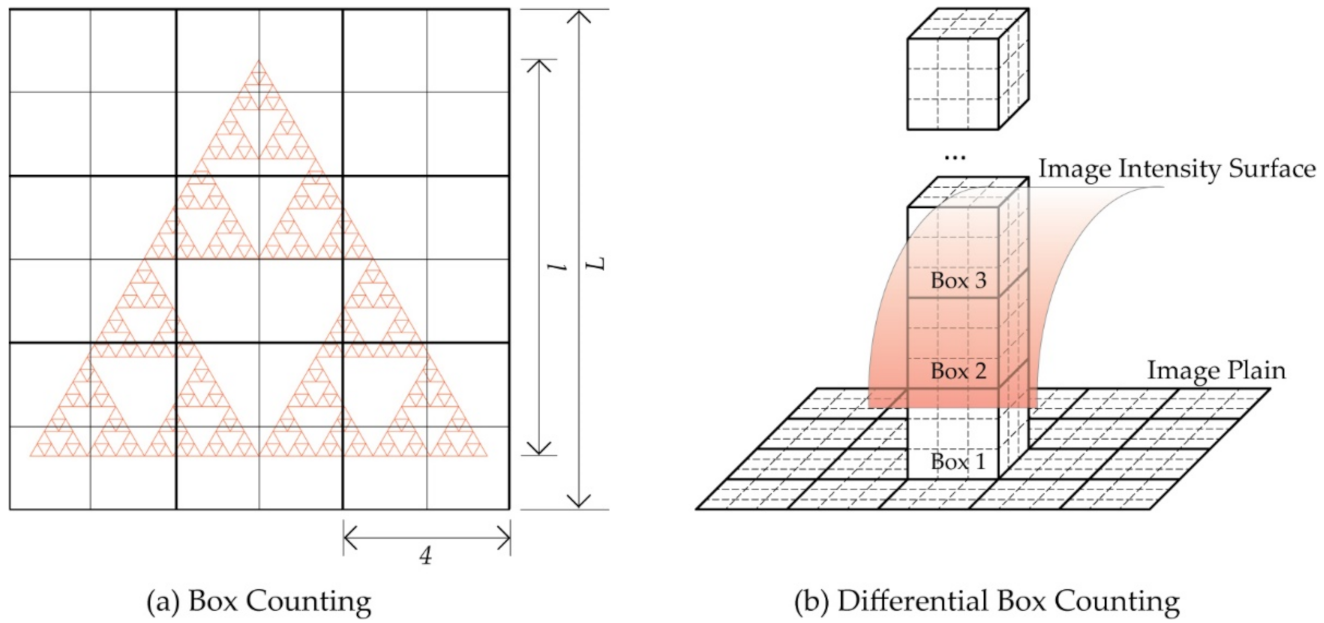
2.1. Fractal Dimension Calculation
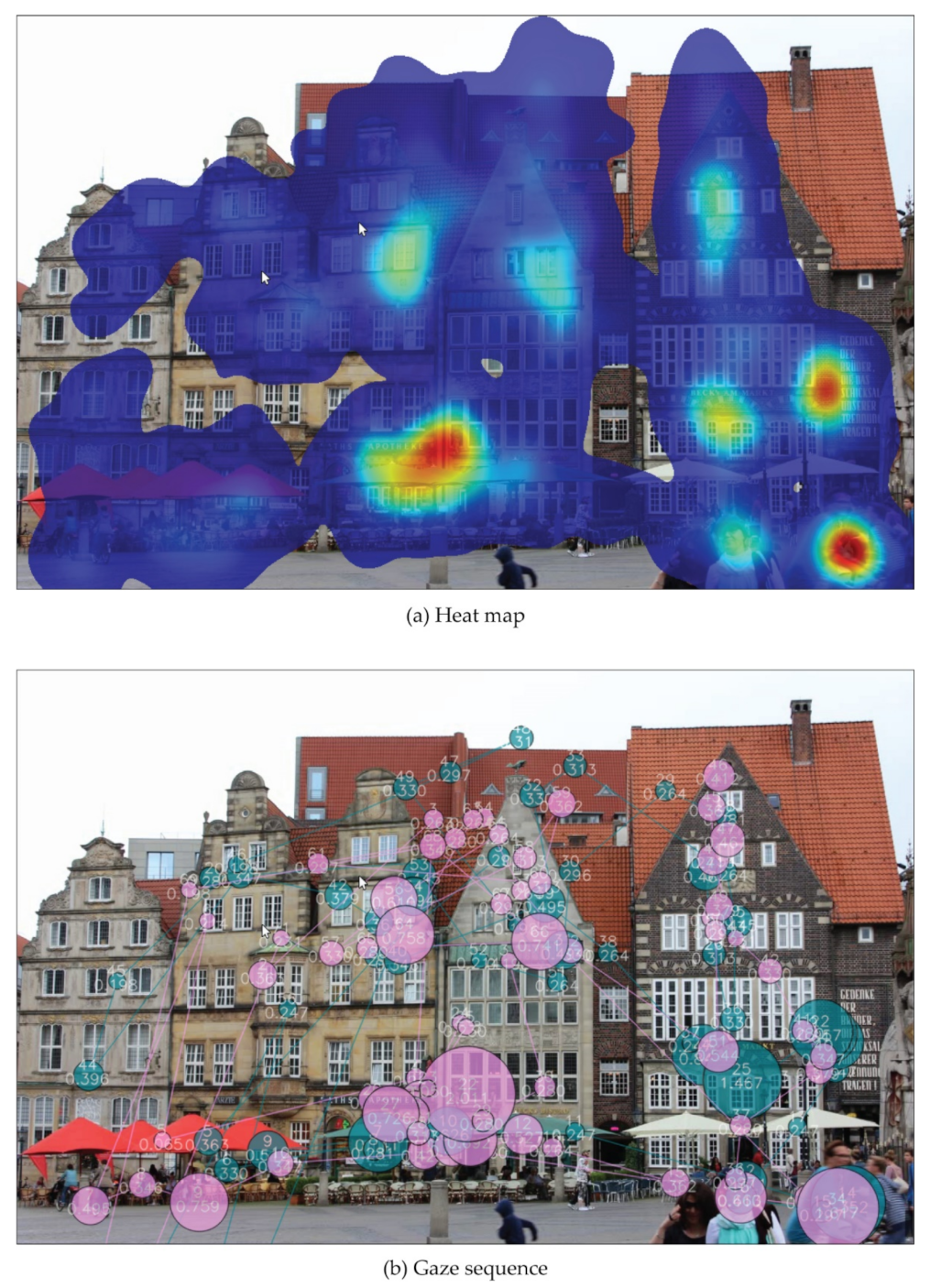
2.2. Visual Attention Simulation
3. Methodology
3.1. Two Computational Applications (ImageJ+FracLac and VAS)
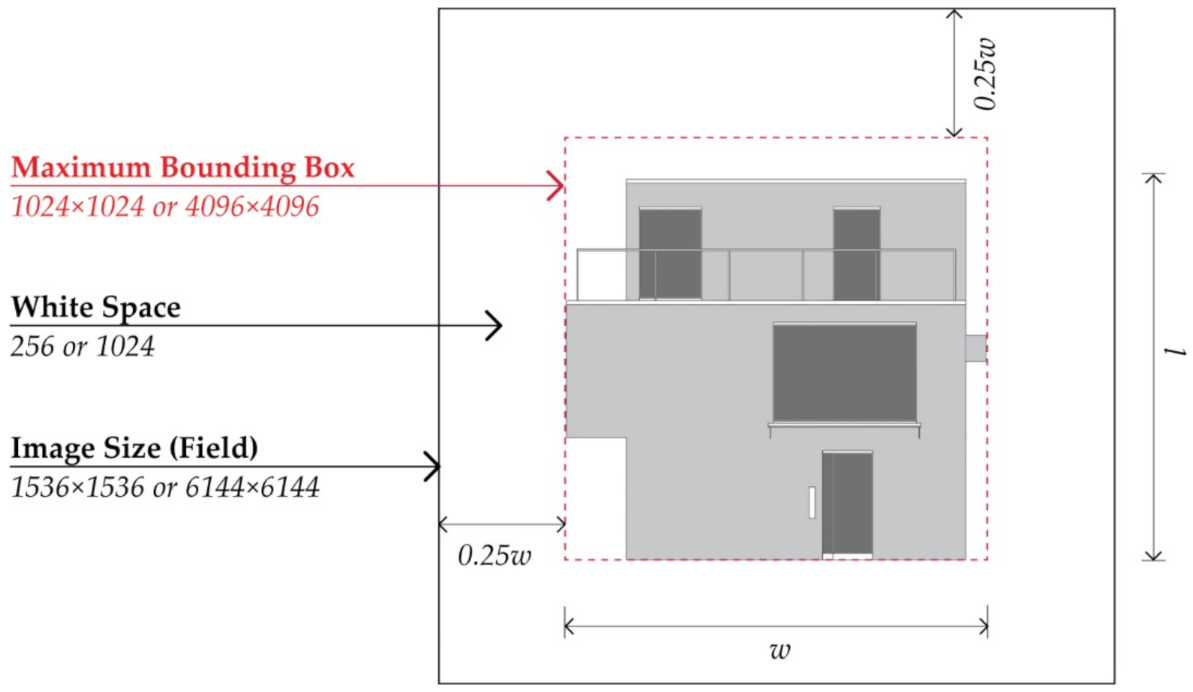
3.2. Image Processing
4. Results
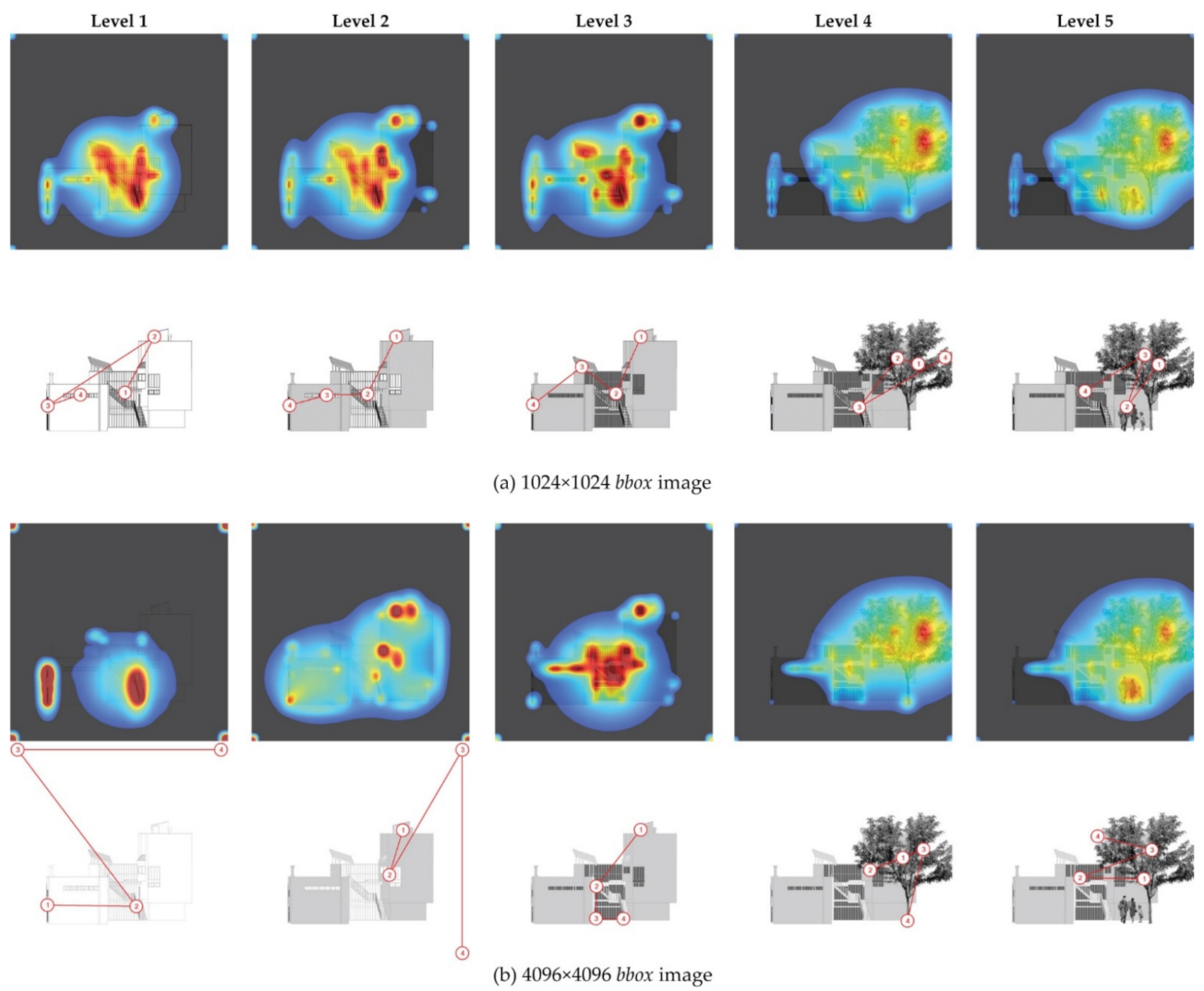
4.1. Fractal Dimension
4.2. Visual Attention
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stamps, A.E., III. Physical determinants of preferences for residential facades. Environ. Behav. 1999, 31, 723–751. [Google Scholar] [CrossRef]
- Stevens, S.S. On the psychophysical law. Psychol. Rev. 1957, 64, 153–181. [Google Scholar] [CrossRef]
- Dehaene, S. The neural basis of the Weber–Fechner law: A logarithmic mental number line. Trends Cogn. Sci. 2003, 7, 145–147. [Google Scholar] [CrossRef]
- Hollander, J.B.; Anderson, E.C. The impact of urban façade quality on affective feelings. Archnet-IJAR Int. J. Archit. Res. 2020, 14, 219–232. [Google Scholar] [CrossRef]
- Simpson, J.; Freeth, M.; Simpson, K.J.; Thwaites, K. Visual engagement with urban street edges: Insights using mobile eye-tracking. J. Urban Int. Res. Placemaking Urban Sustain. 2019, 12, 259–278. [Google Scholar] [CrossRef]
- Gehl, J.; Kaefer, L.J.; Reigstad, S. Close encounters with buildings. Urban Des. Int. 2006, 11, 29–47. [Google Scholar] [CrossRef]
- Kusenbach, M. Street phenomenology: The go-along as ethnographic research tool. Ethnography 2003, 4, 455–485. [Google Scholar] [CrossRef]
- Heffernan, E.; Heffernan, T.; Pan, W. The relationship between the quality of active frontages and public perceptions of public spaces. Urban Des. Int. 2014, 19, 92–102. [Google Scholar] [CrossRef]
- Lee, J.H.; Ostwald, M.J. Creative decision-making processes in parametric design. Buildings 2020, 10, 242. [Google Scholar] [CrossRef]
- Olewnik, A.T.; Lewis, K. On validating engineering design decision support tools. Concurrent Eng. 2005, 13, 111–122. [Google Scholar] [CrossRef]
- Carrasco, M. Visual attention: The past 25 years. Vision Res. 2011, 51, 1484–1525. [Google Scholar] [CrossRef]
- De la Fuente Suárez, L.A. Subjective experience and visual attention to a historic building: A real-world eye-tracking study. Front. Archit. Res. 2020, 9, 774–804. [Google Scholar] [CrossRef]
- Hollander, J.B.; Sussman, A.; Purdy Levering, A.; Foster-Karim, C. Using eye-tracking to understand human responses to traditional neighborhood designs. Plann. Pract. Res. 2020, 35, 485–509. [Google Scholar] [CrossRef]
- Suurenbroek, F.; Spanjar, G. Exploring eye-tracking technology: Assessing how the design of densified built environments can promote inhabitants’ well-being. In Urban Experience and Design: Contemporary Perspectives on Improving the Public Realm; Hollander, J.B., Sussman, A., Eds.; Routledge: New York, NY, USA, 2021; pp. 91–103. [Google Scholar]
- Lisińska-Kuśnierz, M.; Krupa, M. Suitability of eye tracking in assessing the visual perception of architecture—A case study concerning selected projects located in cologne. Buildings 2020, 10, 20. [Google Scholar] [CrossRef]
- Luck, R. Participatory design in architectural practice: Changing practices in future making in uncertain times. Des. Stud. 2018, 59, 139–157. [Google Scholar] [CrossRef]
- Hocking, V.T.; Brown, V.A.; Harris, J.A. Tackling wicked problems through collective design. Intell. Build. Int. 2016, 8, 24–36. [Google Scholar] [CrossRef]
- Nasar, J.L. Urban design aesthetics: The evaluative qualities of building exteriors. Environ. Behav. 1994, 26, 377–401. [Google Scholar] [CrossRef]
- Forsythe, A.; Nadal, M.; Sheehy, N.; Cela-Conde, C.J.; Sawey, M.; Sawey, M. Predicting beauty: Fractal dimension and visual complexity in art. Br. J. Psychol. 2011, 102, 49–70. [Google Scholar] [CrossRef]
- Ostwald, M.J.; Vaughan, J. The Fractal Dimension of Architecture; Birkhäuser: Cham, Switzerland, 2016. [Google Scholar]
- Pickover, C.A. Keys to Infinity; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Hagerhall, C.M.; Purcell, T.; Taylor, R. Fractal dimension of landscape silhouette outlines as a predictor of landscape preference. J. Environ. Psychol. 2004, 24, 247–255. [Google Scholar] [CrossRef]
- Katona, V. Relief method: The analysis of architectonic façades by fractal geometry. Buildings 2021, 11, 16. [Google Scholar] [CrossRef]
- Friedenberg, J. Visual Attention and Consciousness; Psychology Press: New York, NY, USA; London, UK, 2013. [Google Scholar]
- Hollander, J.B.; Purdy, A.; Wiley, A.; Foster, V.; Jacob, R.J.K.; Taylor, H.A.; Brunyé, T.T. Seeing the city: Using eye-tracking technology to explore cognitive responses to the built environment. J. Urban. Int. Res. Placemaking Urban Sustain. 2018, 12, 156–171. [Google Scholar] [CrossRef]
- Salingaros, N.A.; Sussman, A. biometric pilot-studies reveal the arrangement and shape of windows on a traditional façade to be implicitly “engaging”, whereas contemporary façades are not. Urban Sci. 2020, 4, 26. [Google Scholar] [CrossRef]
- Milliken, P.; Hollander, J.B.; Sussman, A.; Situ, M. Identifying biophilic design elements in streetscapes: A study of visual attention and sense of place. In Urban Experience and Design: Contemporary Perspectives on Improving the Public Realm; Hollander, J.B., Sussman, A., Eds.; Routledge: New York, NY, USA, 2021; pp. 75–90. [Google Scholar]
- 3M. How Does VAS Work and What is First-Glace Vision? Available online: https://vas.3m.com/support (accessed on 8 February 2021).
- Bovill, C. Fractal Geometry in Architecture and Design; Birkhäuser: Boston, MA, USA, 1996. [Google Scholar]
- Sarkar, N.; Chaudhuri, B.B. An efficient differential box-counting approach to compute fractal dimension of image. IEEE Trans. Syst. Man Cybern. 1994, 24, 115–120. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Batty, M.; Longley, P.A. Fractal Cities: A Geometry of Form and Function; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Burkle-Elizondo, G.; Valdez-Cepeda, R.D. Do the mesoamerican artistic and architectural works have fractal dimension? In Emergent Nature: Patterns, Growth and Scaling in the Sciences; World Scientific: Singapore, 2001; pp. 431–432. [Google Scholar]
- Oleschko, K.; Brambila, R.; Brambila, F.; Parrot, J.F.; López, P. Fractal analysis of teotihuacan, mexico. J. Archaeolog. Sci. 2000, 27, 1007–1016. [Google Scholar] [CrossRef]
- Çagdaş, G.; Gözübüyük, G.; Ediz, Ö. Fractal based generative design for harmony between old and new. In Generative Art 2005, Proceedings of the 8th GENERATIVE ART CONFERENCE(GA2005), Milan, Italy, 15–17 December 2005; Domus Argenia: Milan, Italy, 2005; pp. 150–159. [Google Scholar]
- Ostwald, M.J.; Ediz, Ö. Measuring form, ornament and materiality in sinan’s kiliç ali paşa mosque: An analysis using fractal dimensions. Nexus. Netw. J. 2015, 17, 5–22. [Google Scholar] [CrossRef]
- Samper, A.; Herrera, B. The fractal pattern of the french gothic cathedrals. Nexus. Netw. J. 2014, 16, 251–271. [Google Scholar] [CrossRef]
- Panigrahy, C.; Seal, A.; Mahato, N.K.; Bhattacharjee, D. Differential box counting methods for estimating fractal dimension of gray-scale images: A survey. Chaos Solitons Fractals 2019, 126, 178–202. [Google Scholar] [CrossRef]
- Liu, Y.U.; Chen, L.; Wang, H.; Jiang, L.; Zhang, Y.; Zhao, J.; Wang, D.; Zhao, Y.; Song, Y. An improved differential box-counting method to estimate fractal dimensions of gray-level images. J. Visual. Commun. Image. Represent. 2014, 25, 1102–1111. [Google Scholar] [CrossRef]
- Foroutan-pour, K.; Dutilleul, P.; Smith, D.L. Advances in the implementation of the box-counting method of fractal dimension estimation. Appl. Math. Comput. 1999, 105, 195–210. [Google Scholar] [CrossRef]
- Koch, H.P. The concept of fractals in the pharmaceutical sciences. Pharmazie 1993, 48, 643–659. [Google Scholar] [PubMed]
- Cooper, J.; Oskrochi, R. Fractal analysis of street vistas: A potential tool for assessing levels of visual variety in everyday street scenes. Environ. Plann B Plann. Des. 2008, 35, 349–363. [Google Scholar] [CrossRef]
- Karperien, A. Fraclac for Imagej. Available online: http://rsb.info.nih.gov/ij/plugins/fraclac/FLHelp/Introduction.htm (accessed on 15 February 2021).
- Taylor, R. Science in culture. Nature 2001, 410, 1038. [Google Scholar] [CrossRef]
- Aks, D.J.; Sprott, J.C. Quantifying aesthetic preference for chaotic patterns. Empirical. Stud. Arts 1996, 14, 1–16. [Google Scholar] [CrossRef]
- Sussman, A.; Hollander, J.B. Cognitive Architecture: Designing for How We Respond to the Built Environment; Routledge: New York, NY, USA, 2015. [Google Scholar]
- McMains, S.A.; Kastner, S. Visual Attention. In Encyclopedia of Neuroscience; Binder, M.D., Hirokawa, N., Windhorst, U., Eds.; Springer: Berlin, Germany, 2009; pp. 4296–4302. [Google Scholar] [CrossRef]
- Anderson, C.H.; Van Essen, D.C.; Olshausen, B.A. CHAPTER 3–Directed visual attention and the dynamic control of information flow. In Neurobiology of Attention; Itti, L., Rees, G., Tsotsos, J.K., Eds.; Academic Press: Burlington, VT, USA, 2005; pp. 11–17. [Google Scholar] [CrossRef]
- Treisman, A. Features and objects in visual processing. Sci. Am. 1986, 255, 114B–125. [Google Scholar] [CrossRef]
- Treisman, A.M.; Gelade, G. A feature-integration theory of attention. Cognitive. Psychol. 1980, 12, 97–136. [Google Scholar] [CrossRef]
- Rensink, R.A. The management of visual attention in graphic displays. In Human Attention in Digital Environments; Roda, C., Ed.; Cambridge University Press: Cambridge, UK, 2011; pp. 63–92. [Google Scholar] [CrossRef]
- Rensink, R.A. Commentary: Changes. In Progress in Brain Research; Hyona, J., Munoz, D.P., Heide, W., Radach, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2002; Volume 140, pp. 197–207. [Google Scholar]
- Rensink, R.A. The dynamic representation of scenes. Visual Cognition 2000, 7, 17–42. [Google Scholar] [CrossRef]
- Yanulevskaya, V.; Uijlings, J.; Geusebroek, J.M.; Sebe, N.; Smeulders, A. A proto-object-based computational model for visual saliency. J. Vision 2013, 13, 27. [Google Scholar] [CrossRef][Green Version]
- Zhang, L.M.; Zhang, R.X.; Jeng, T.S.; Zeng, Z.Y. Cityscape protection using VR and eye tracking technology. J. Visual Commun. Image Represent. 2019, 64, 102639. [Google Scholar] [CrossRef]
- Mohammadpour, A.; Karan, E.; Asadi, S.; Rothrock, L. Measuring end-user satisfaction in the design of building projects using eye-tracking technology. In Computing in Civil Engineering 2015; American Society of Civil Engineers (ASCE): Austin, TX, USA, 2015; pp. 564–571. [Google Scholar]
- Tang, M. Analysis of signage using eye-tracking technology. Interdisciplin. J. Signage Wayfinding 2020, 4. [Google Scholar] [CrossRef]
- Niebur, E.; Koch, C. Computational architectures for attention. In The Attentive Brain; Parasuraman, R., Ed.; The MIT Press: Cambridge, MA, USA, 1998; pp. 163–186. [Google Scholar]
- Massaro, D.; Savazzi, F.; Di Dio, C.; Freedberg, D.; Gallese, V.; Gilli, G.; Marchetti, A. When art moves the eyes: A behavioral and eye-tracking study. PLoS ONE 2012, 7, e37285. [Google Scholar] [CrossRef] [PubMed]
- Quian Quiroga, R.; Pedreira, C. How do we see art: An eye-tracker study. Front. Hum. Neurosci. 2011, 5, 98. [Google Scholar] [CrossRef] [PubMed]
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinf. 2017, 18, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Salingaros, N.A. Life and complexity in architecture from a thermodynamic analogy. Phys. Essays 1997, 10, 165–173. [Google Scholar] [CrossRef]
- Mayrhofer-Reinhartshuber, M.; Ahammer, H. Pyramidal fractal dimension for high resolution images. Chaos Interdisciplin. J. Nonlinear Sci. 2016, 26, 073109. [Google Scholar] [CrossRef]
- Coburn, A.; Kardan, O.; Kotabe, H.; Steinberg, J.; Hout, M.C.; Robbins, A.; MacDonald, J.; Hayn-Leichsenring, G.; Berman, M.G. Psychological responses to natural patterns in architecture. J. Environ. Psychol. 2019, 62, 133–145. [Google Scholar] [CrossRef]
- Alexander, C. The Nature of Order: An Essay on the Art of Building and the Nature of the Universe; Center for Environmental Structure: Berkeley, CA, USA, 2004; Volume 1–4. [Google Scholar]
- Nayak, S.R.; Mishra, J.; Khandual, A.; Palai, G. Fractal dimension of RGB color images. Optik 2018, 162, 196–205. [Google Scholar] [CrossRef]




| Variable | Optimal Setting | Variable | Optimal Setting |
|---|---|---|---|
| Scaling coefficient | 1.4142:1 | Maximum grid size | 0.25l |
| Grid position | Four corners * | Minimum grid size | 10 pixels |
| Façade Design | Image Size (bbox Size) | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|---|
| Spiller House | 1024 × 1024 | 1.5366 | 1.5333 | 1.5489 | 1.7251 | 1.7431 |
| 4096 × 4096 | 1.5241 | 1.5245 | 1.6140 | 1.7678 | 1.7803 | |
| Juicy House | 1024 × 1024 | 1.3076 | 1.3063 | 1.5255 | 1.6597 | 1.6859 |
| 4096 × 4096 | 1.2856 | 1.2856 | 1.6033 | 1.7266 | 1.7357 |
| Façade Design | Image Size (bbox Size) | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
|---|---|---|---|---|---|---|
| Spiller House | 1024 × 1024 | 1.4331 | 1.4160 | 1.3865 | 1.5410 | 1.5524 |
| 4096 × 4096 | 1.4567 | 1.4465 | 1.4391 | 1.5478 | 1.5527 | |
| Juicy House | 1024 × 1024 | 1.2462 | 1.2308 | 1.2090 | 1.4120 | 1.4306 |
| 4096 × 4096 | 1.2723 | 1.2683 | 1.2653 | 1.4271 | 1.4375 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.H.; Ostwald, M.J. Fractal Dimension Calculation and Visual Attention Simulation: Assessing the Visual Character of an Architectural Façade. Buildings 2021, 11, 163. https://doi.org/10.3390/buildings11040163
Lee JH, Ostwald MJ. Fractal Dimension Calculation and Visual Attention Simulation: Assessing the Visual Character of an Architectural Façade. Buildings. 2021; 11(4):163. https://doi.org/10.3390/buildings11040163
Chicago/Turabian StyleLee, Ju Hyun, and Michael J. Ostwald. 2021. "Fractal Dimension Calculation and Visual Attention Simulation: Assessing the Visual Character of an Architectural Façade" Buildings 11, no. 4: 163. https://doi.org/10.3390/buildings11040163
APA StyleLee, J. H., & Ostwald, M. J. (2021). Fractal Dimension Calculation and Visual Attention Simulation: Assessing the Visual Character of an Architectural Façade. Buildings, 11(4), 163. https://doi.org/10.3390/buildings11040163








