A Spiral Single-Layer Reticulated Shell Structure: Imperfection and Damage Tolerance Analysis and Stability Capacity Formulation for Conceptual Design
Abstract
:1. Introduction
2. A Modified Structure Design of Single-Layer Reticulated Shell Structure
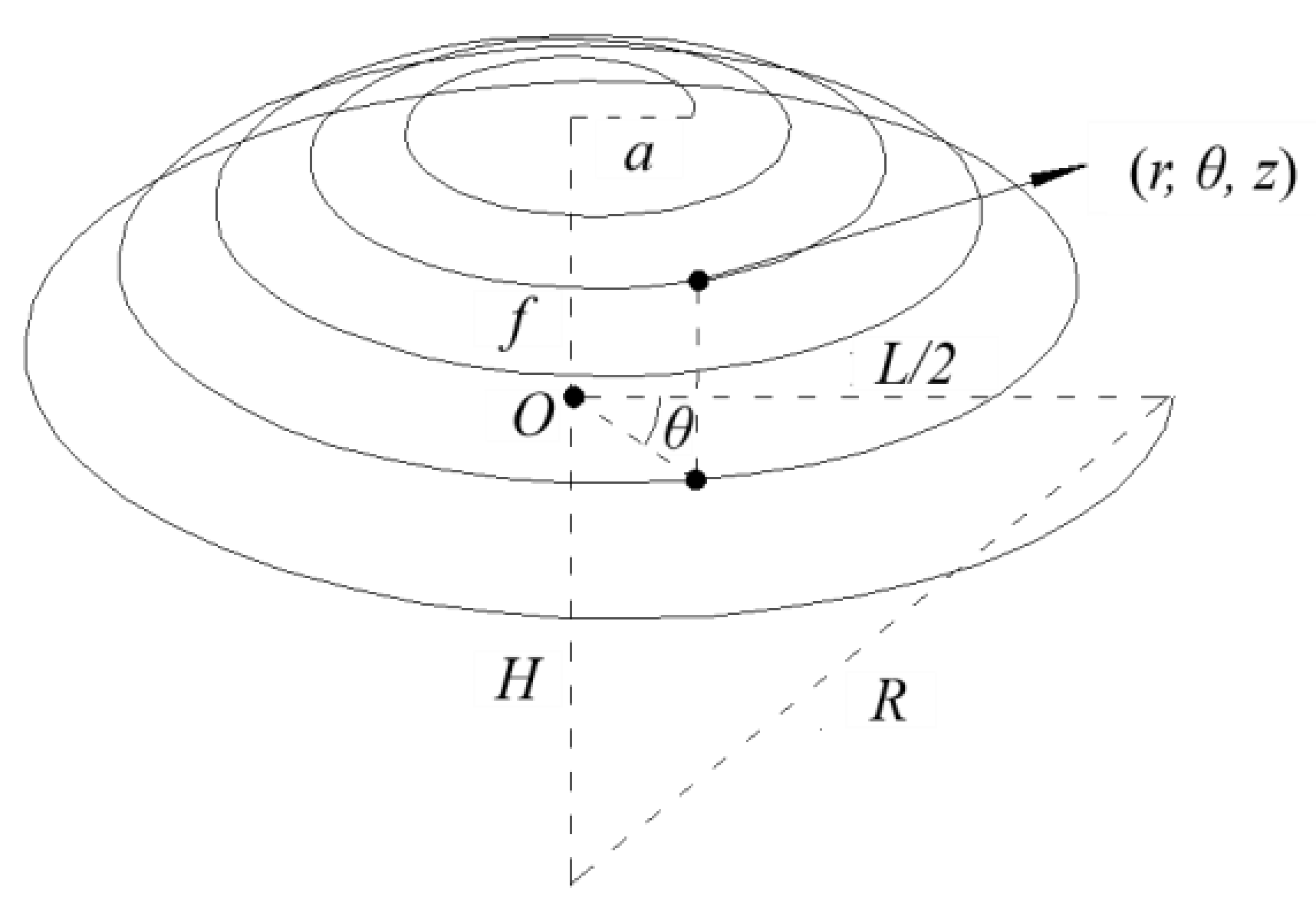
2.1. Mathematical Model of the Modified Structure
2.2. The Geometric Model of the Modified Structure
3. Engineering Design of the Modified Structure
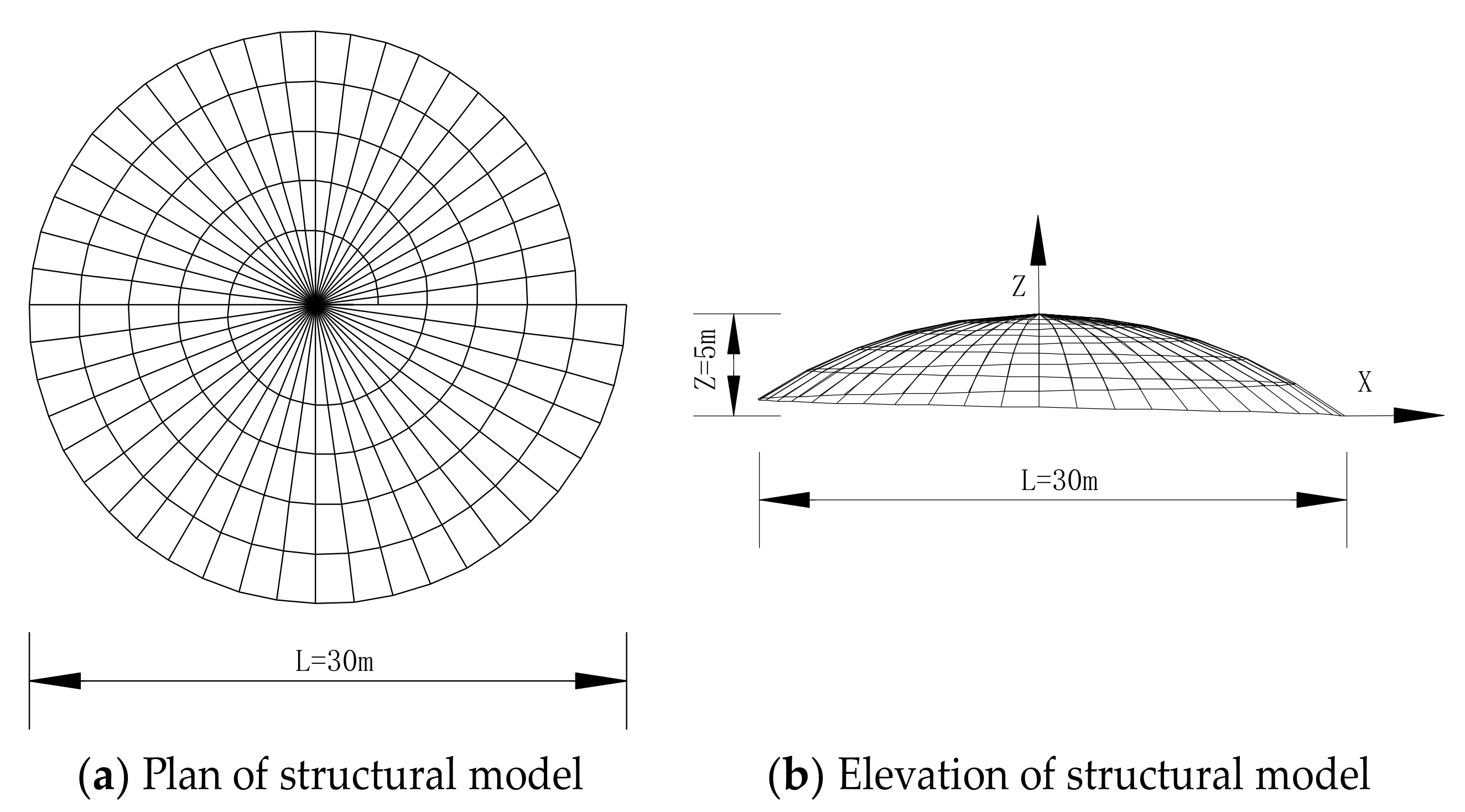
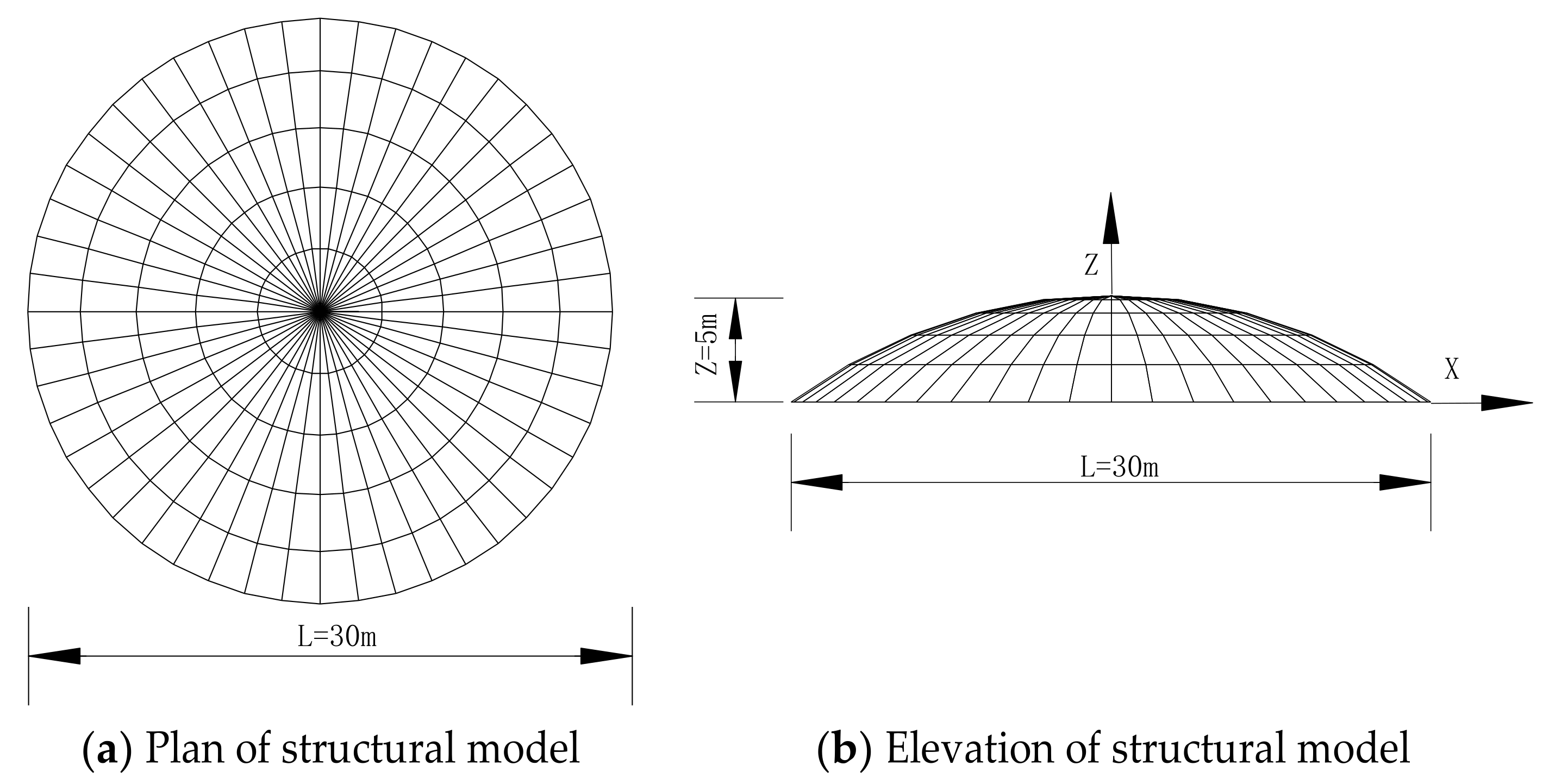
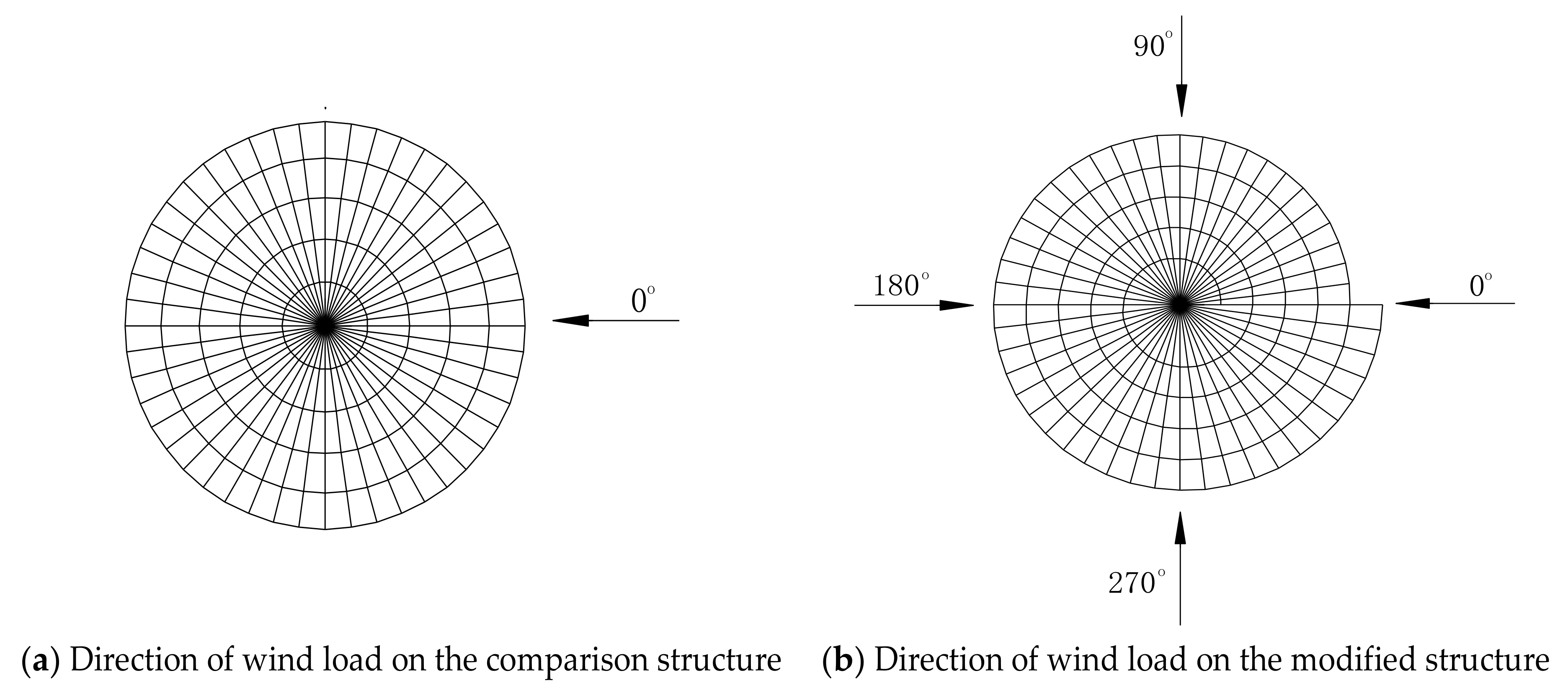
3.1. Finite Element Models
3.2. Design Calculation of the Modified Structure
3.2.1. Support Reactions
3.2.2. Structural Displacement
3.2.3. Equivalent Stress
4. Structural Imperfection and Damage Tolerance Analysis
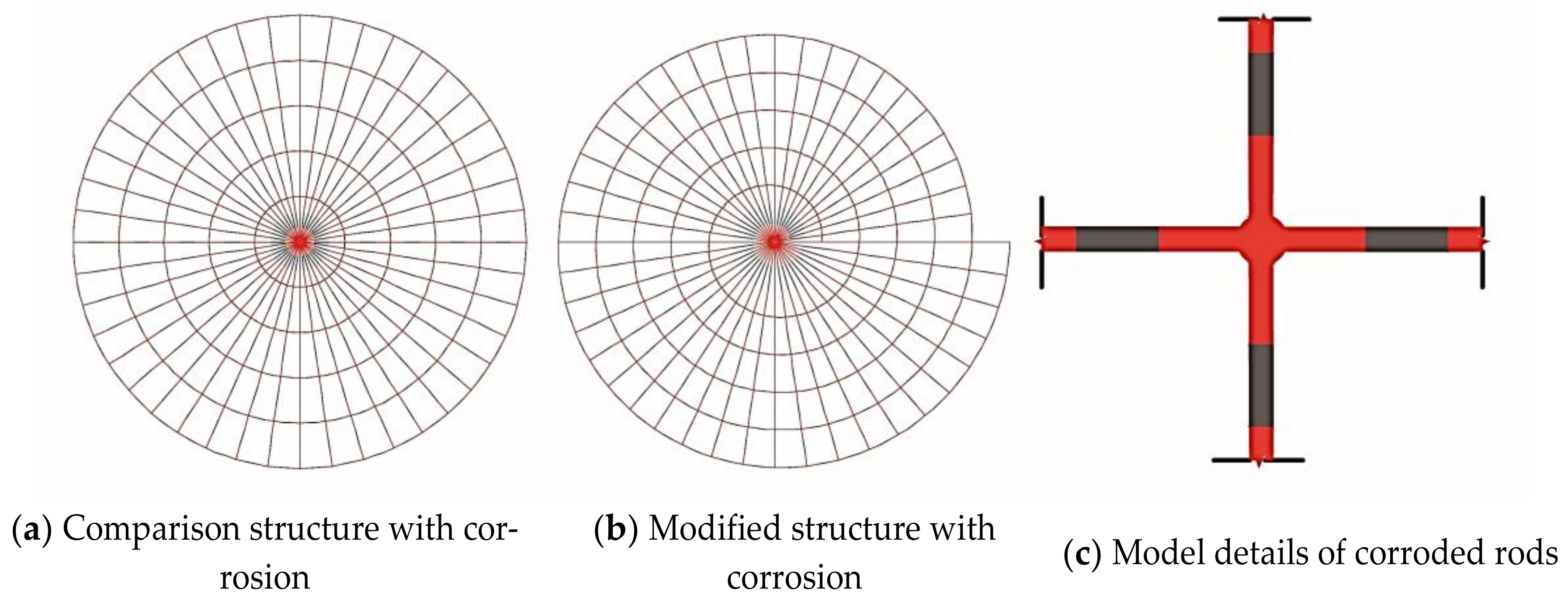
4.1. Description of the Calculation Example
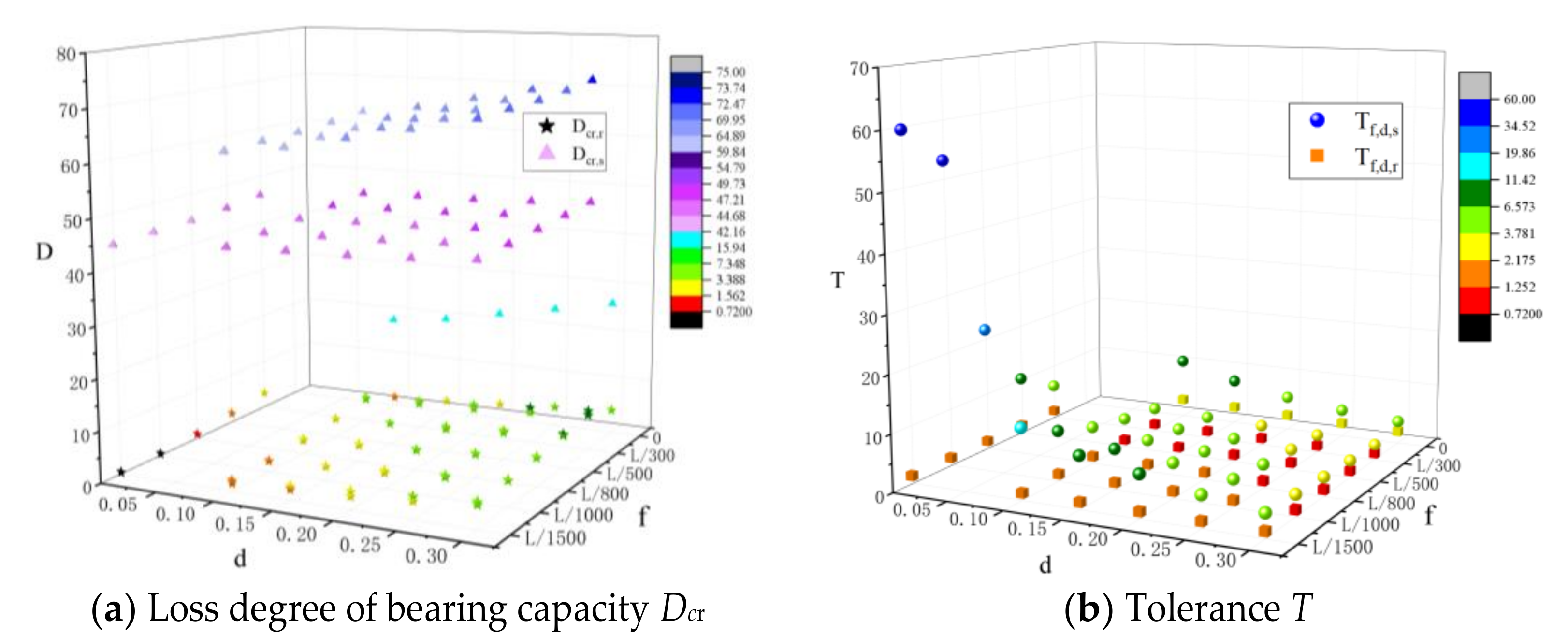
4.2. Tolerance to Node Imperfection
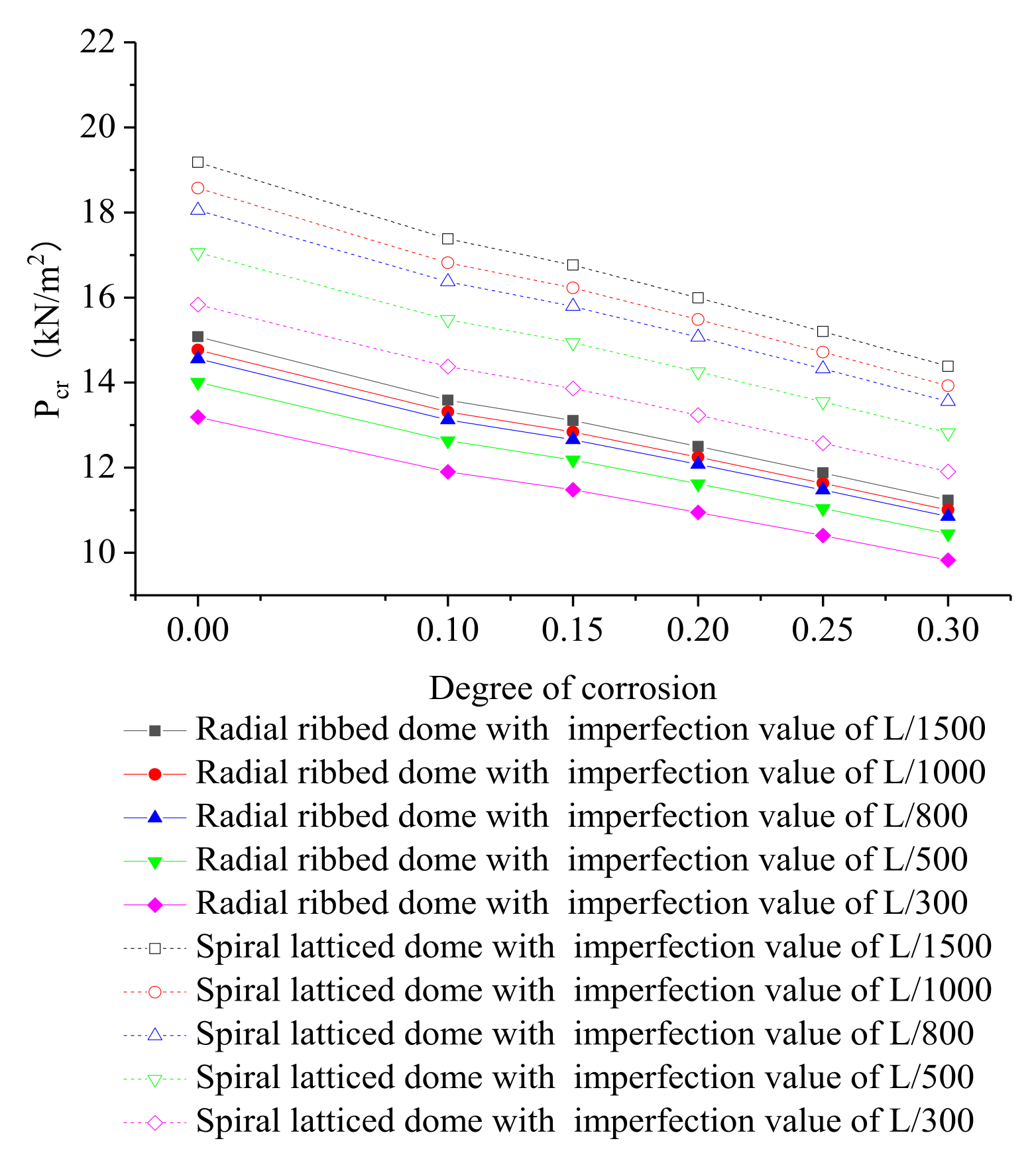
4.3. Tolerance to Damage
5. Formulation of the Stable Bearing Capacity of the Modified Structure
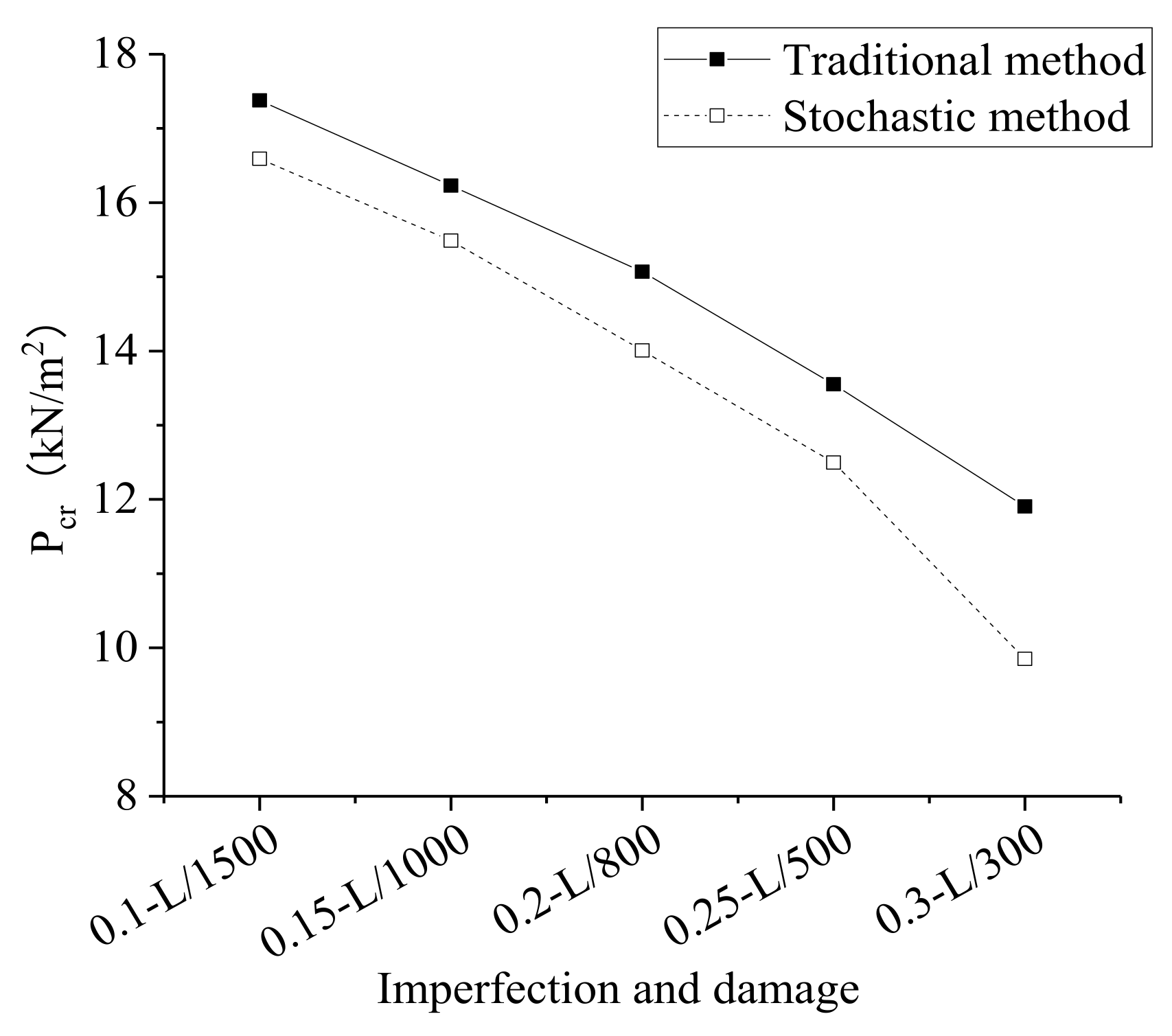
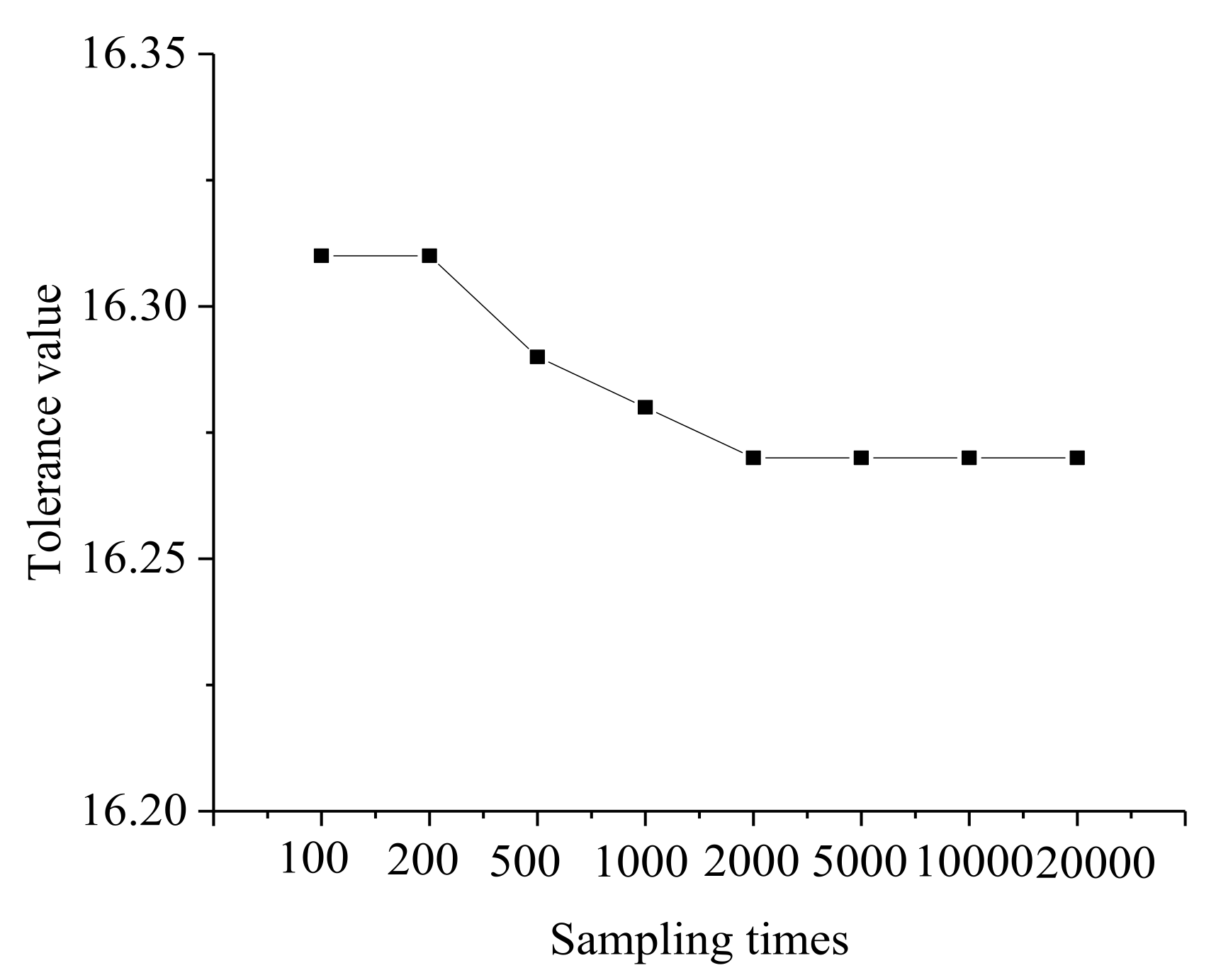
5.1. Algorithm
5.2. Numerical Models
5.3. Formula for Stable Bearing Capacity of the Modified Structure
6. Conclusions
- (1)
- The spiral structure is more stable than the traditional structure and has better corrosion and damage tolerance.
- (2)
- The spiral line of the new design can successfully convert the vertical wind pressure (wind suction) into the plane reaction force of the structural support, therefore, it has better wind resistance.
- (3)
- The unified stable bearing capacity formula of the modified structure allows engineers to consider its structural performance when choosing a model with high accuracy and to thus make more effective model selection decisions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ke, C. Struct. concepts of public buildings in Japan. ArchiCreation 2002, 7, 18–27. [Google Scholar] [CrossRef]
- Dong, S. Continuous analysis method of reticulated spherical shell. J. Build. Struct. 1988, 9, 1–14. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, H.; Wang, X.; Song, C.; Gao, X. Structural design of large-spanl single-layer reticulated shell with bidirectional spirals in Tianjin Yujiapu, Tianjin. Spat. Struct. 2015, 21, 29–33. [Google Scholar] [CrossRef]
- Connor, J.J.; Logcher, R.D.; Chan, S.C. Nonlinear analysis of elastic framed structures. J. Struct. Div. 1968, 94, 1525–1548. [Google Scholar] [CrossRef]
- Riks, E. An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Struct. 1979, 15, 529–551. [Google Scholar] [CrossRef]
- Crisfield, M.A. An arc-length method including line searches and accelerations. Int. J. Numer. Methods Ieng. 1983, 19, 1269–1289. [Google Scholar] [CrossRef]
- Bathe, K.J.; Dvorkin, E.N. On the automatic solution of nonlinear finite element equations. Comput. Struct. 1983, 17, 871–879. [Google Scholar] [CrossRef] [Green Version]
- Szilard, R. Critical load and post-buckling analysis by FEM using energy balancing technique. Comput. Struct. 1985, 20, 277–286. [Google Scholar] [CrossRef]
- Greco, G.; Pantano, M.F.; Mazzolai, B.; Pugno, N.M. Imaging and mechanical characterization of different junctions in spider orb webs. Sci. Rep. 2019, 9, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Batoz, J.L.; Dhatt, G. Incremental displacement algorithms for nonlinear problems. Int. J. Numer. Methods Eng. 1979, 14, 1262–1267. [Google Scholar] [CrossRef]
- Cranford, S.W.; Tarakanova, A.; Pugno, N.M.; Buehler, M.J. Nonlinear material behaviour of spider silk yields robust webs. Nature 2012, 482, 72–76. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forde, B.W.R.; Stiemer, S.F. Improved arc length orthogonality methods for nonlinear finite element analysis. Comput. Struct. 1987, 27, 625–630. [Google Scholar] [CrossRef]
- Li, Y.; Shen, Z. Tracking strategy and program realization of extreme point instability and branch point instability in stability analysis. China Civil Eng. J. 1998, 3, 65–71. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical Specification for Space Frame Structures; JGJ7-2010; China Architecture and Building Press: Beijing, China, 2010.
- Ansys® Academic Research Mechanical, Release 18.1. Available online: https://www.ansys.com/academic/terms-and-conditions.
- Ministry of Construction of the People’s Republic of China. Load Code for the Design of Building Structures; GB 50009-2012; China Architecture and Building Press: Beijing, China, 2012.
- Tang, H. Research on Geometry, Static Property and Stability of 800 Meters Super-Span Dome Lotus-Shaped Reticulated Mega-Structure. M.S. Thesis, ChongQing University, Chongqing, China, 2017. [Google Scholar]
- Liu, H.; Zhang, W.; Yuan, H. Struct. stability analysis of single-layer reticulated shells with stochastic imperfections. Eng. Struct. 2016, 124, 473–479. [Google Scholar] [CrossRef]
- Dong, S.; Zhan, W. Non-linear stability critical loads of single-layer and double-layer and reticulated spherical shallow shells based on continuum analyogy method. Eng. Mech. 2004, 21, 6. [Google Scholar] [CrossRef]
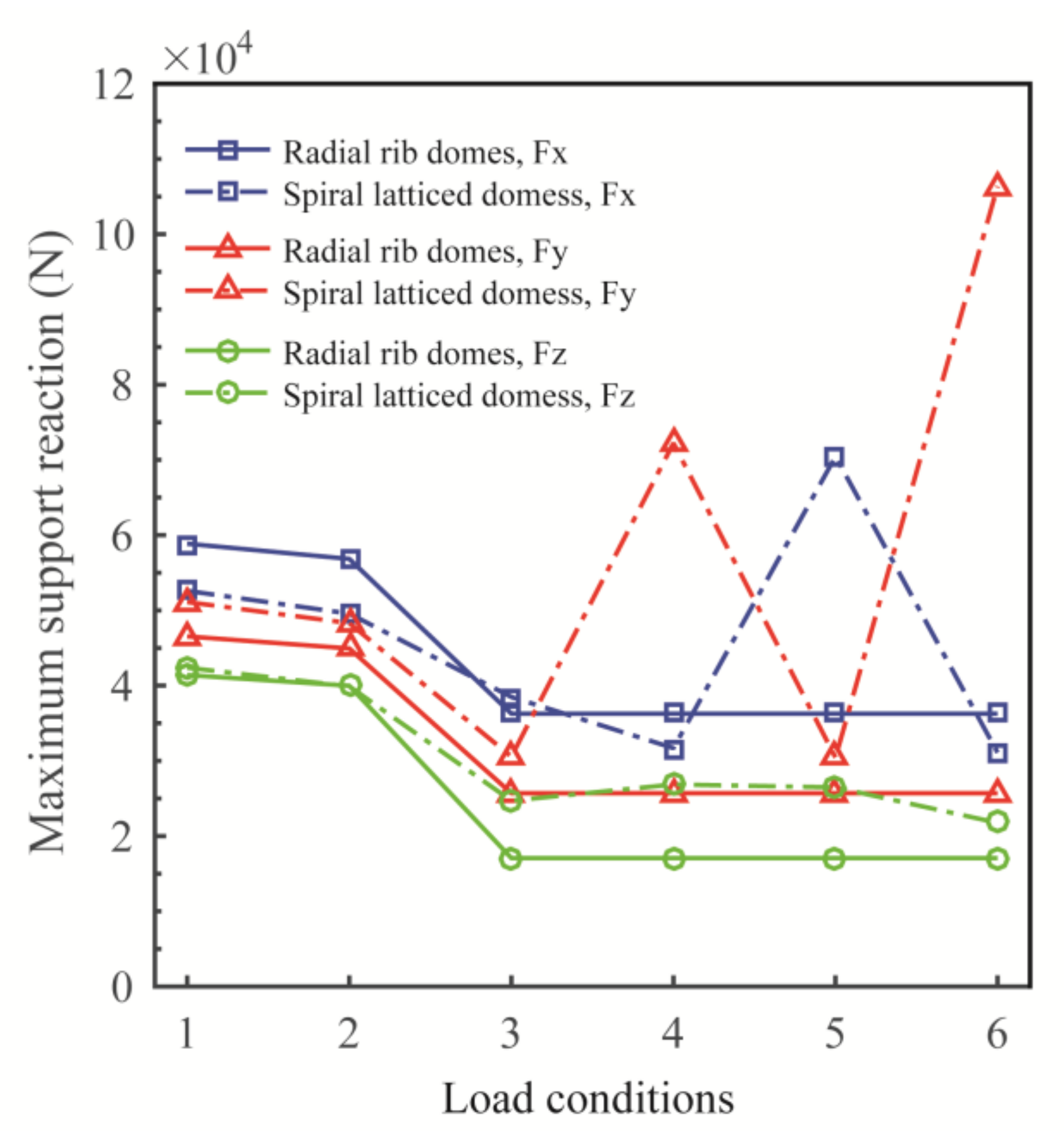
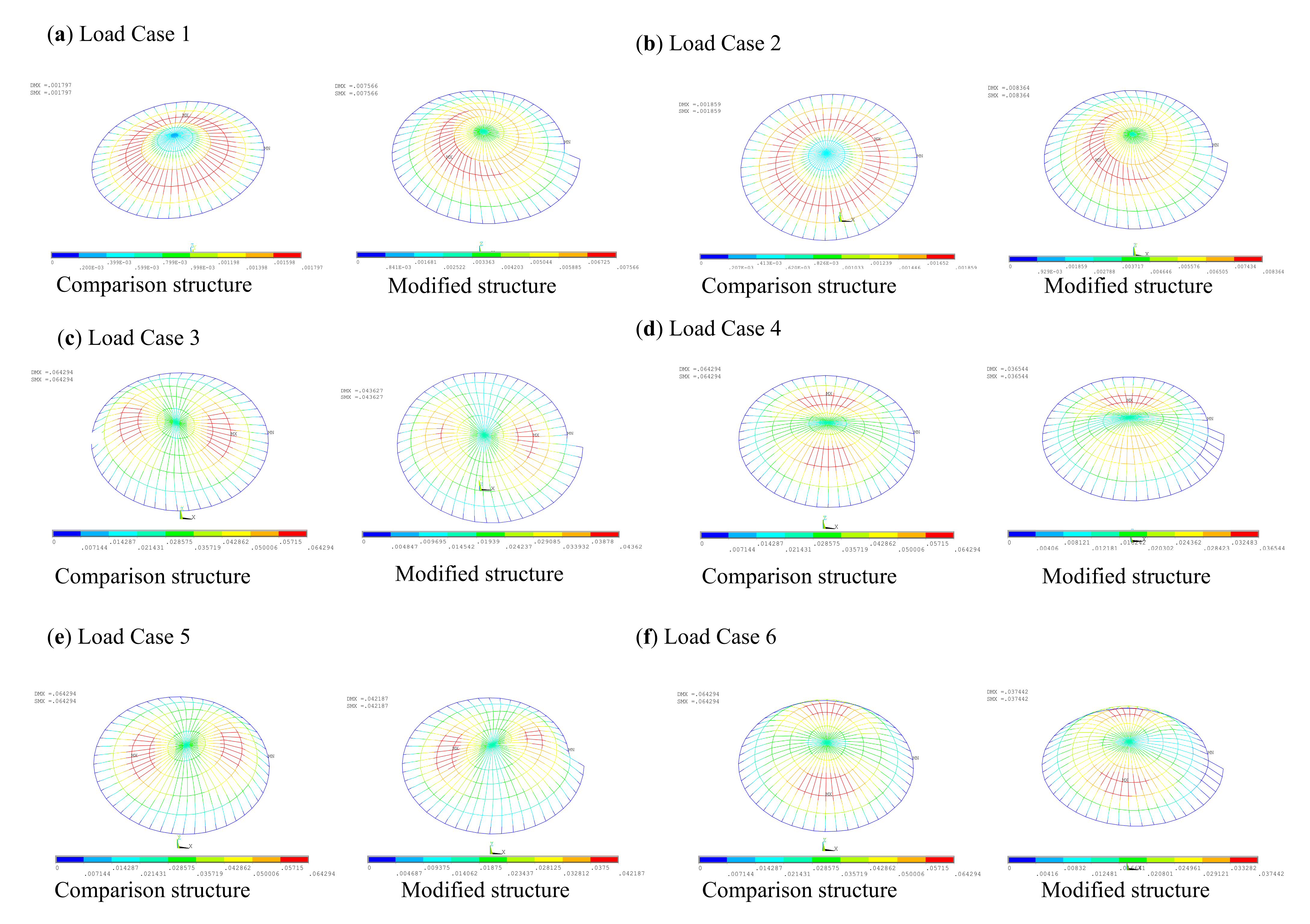


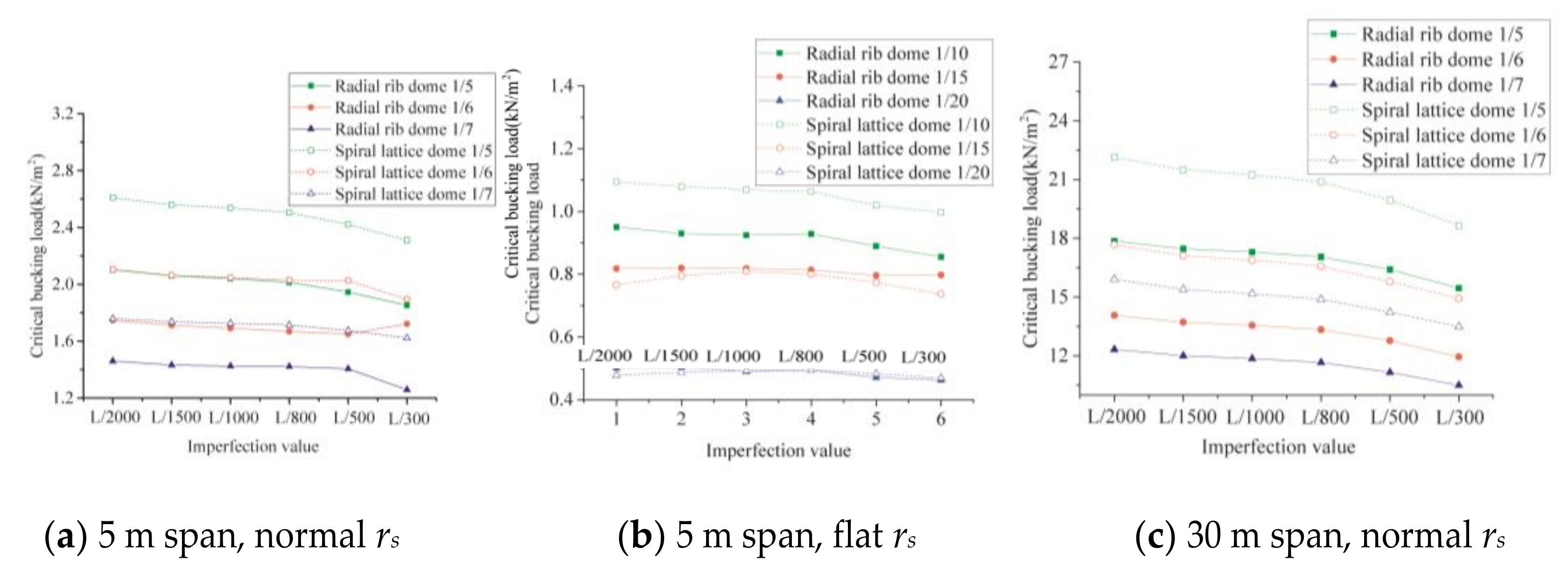
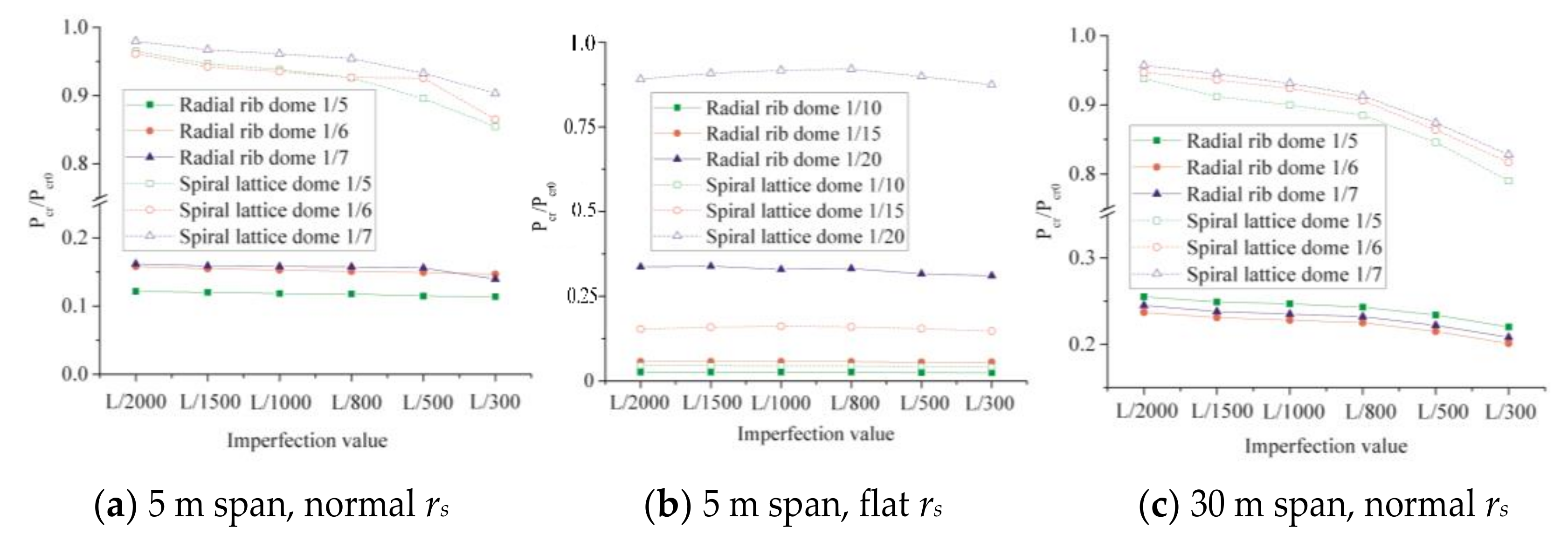
| rs | Maximum Radius rmax (m) | Height/Rise f or Z (m) |
|---|---|---|
| 1/5 | 15 | 6 |
| 1/6 | 15 | 5 |
| 1/7 | 15 | 30/7 |
| Load Case | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| rG | 1.35 | 1.3 | 1.3 | 1.3 | 1.3 | 1.3 |
| rQ | 1.5 × 0.7 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| Example Group No. | 1 | 2 | 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| rs | 1/5 | 1/6 | 1/7 | 1/10 | 1/15 | 1/20 | 1/5 | 1/6 | 1/7 |
| rmax (m) | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 | 2.5 | 15 | 15 | 15 |
| f (m) | 1 | 5/6 | 5/7 | 1/2 | 1/3 | 1/4 | 6 | 5 | 30/7 |
| Example Group No. | 1 | 2 | 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| rs | 1/5 | 1/6 | 1/7 | 1/10 | 1/15 | 1/20 | 1/5 | 1/6 | 1/7 |
| Modified Structure Pcr0 (kN/m2) | 2.703 | 2.190 | 1.796 | 2.999 | 0.626 | 0.067 | 23.591 | 18.278 | 16.289 |
| Comparison Structure Pcr0 (kN/m2) | 13.962 | 11.044 | 9.014 | 23.591 | 18.278 | 16.289 | 59.099 | 52.361 | 45.338 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Li, F.; Yuan, H.; Ai, D.; Xu, C. A Spiral Single-Layer Reticulated Shell Structure: Imperfection and Damage Tolerance Analysis and Stability Capacity Formulation for Conceptual Design. Buildings 2021, 11, 280. https://doi.org/10.3390/buildings11070280
Liu H, Li F, Yuan H, Ai D, Xu C. A Spiral Single-Layer Reticulated Shell Structure: Imperfection and Damage Tolerance Analysis and Stability Capacity Formulation for Conceptual Design. Buildings. 2021; 11(7):280. https://doi.org/10.3390/buildings11070280
Chicago/Turabian StyleLiu, Huijuan, Fukun Li, Hao Yuan, Desheng Ai, and Chunli Xu. 2021. "A Spiral Single-Layer Reticulated Shell Structure: Imperfection and Damage Tolerance Analysis and Stability Capacity Formulation for Conceptual Design" Buildings 11, no. 7: 280. https://doi.org/10.3390/buildings11070280
APA StyleLiu, H., Li, F., Yuan, H., Ai, D., & Xu, C. (2021). A Spiral Single-Layer Reticulated Shell Structure: Imperfection and Damage Tolerance Analysis and Stability Capacity Formulation for Conceptual Design. Buildings, 11(7), 280. https://doi.org/10.3390/buildings11070280





