Structural Efficiency of Hollow Reinforced Concrete Beams Subjected to Partial Uniformly Distributed Loading
Abstract
:1. Introduction
1.1. Experimental Studies
1.2. Numerical Studies
1.3. Significance of the Study
2. Geometric Configurations of the Numerical Models
3. Mechanical Properties of the Concrete and Steel Materials
4. Numerical Analysis Approach
4.1. Assumptions
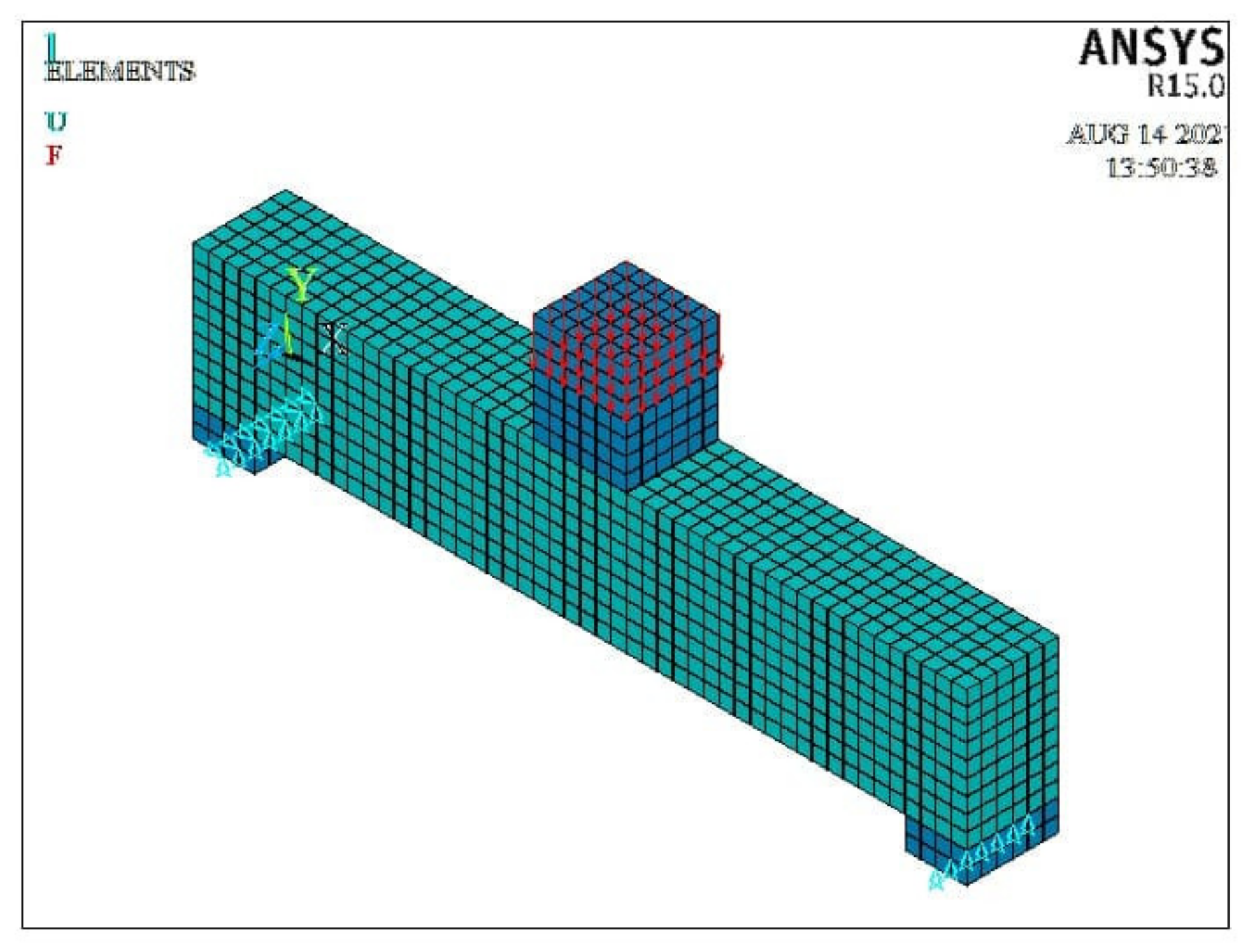
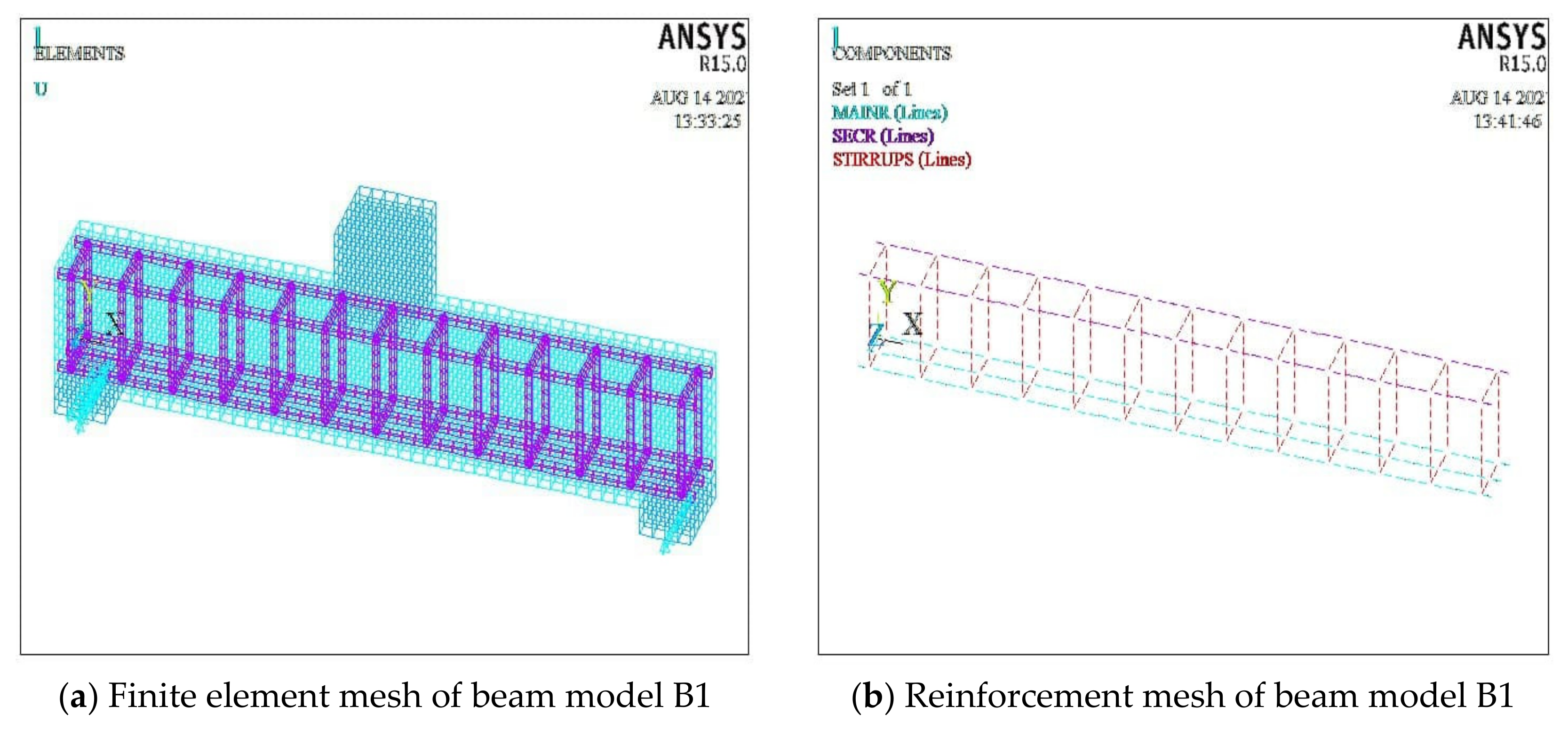
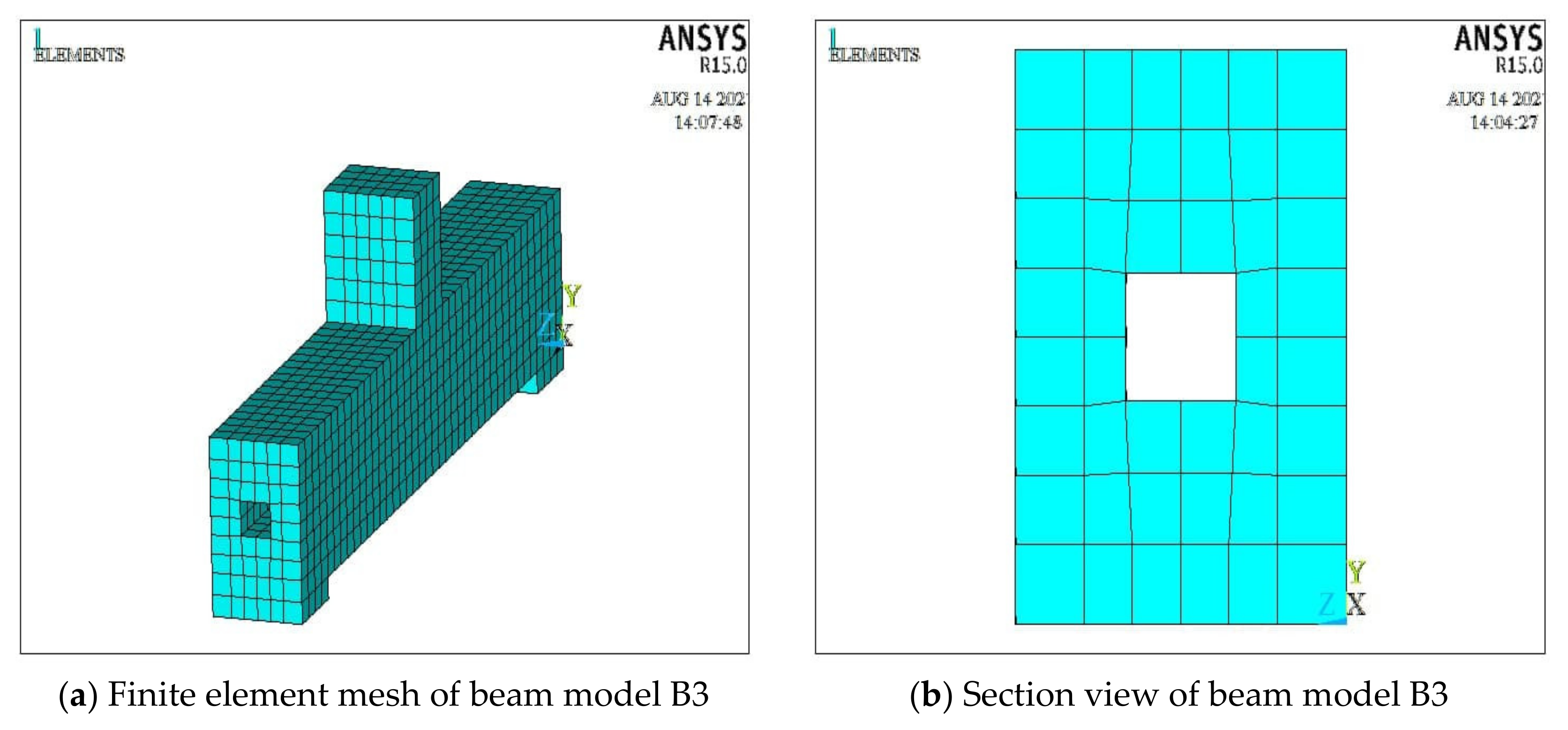
4.2. Numerical Modelling Using Finite Element Software ANSYS
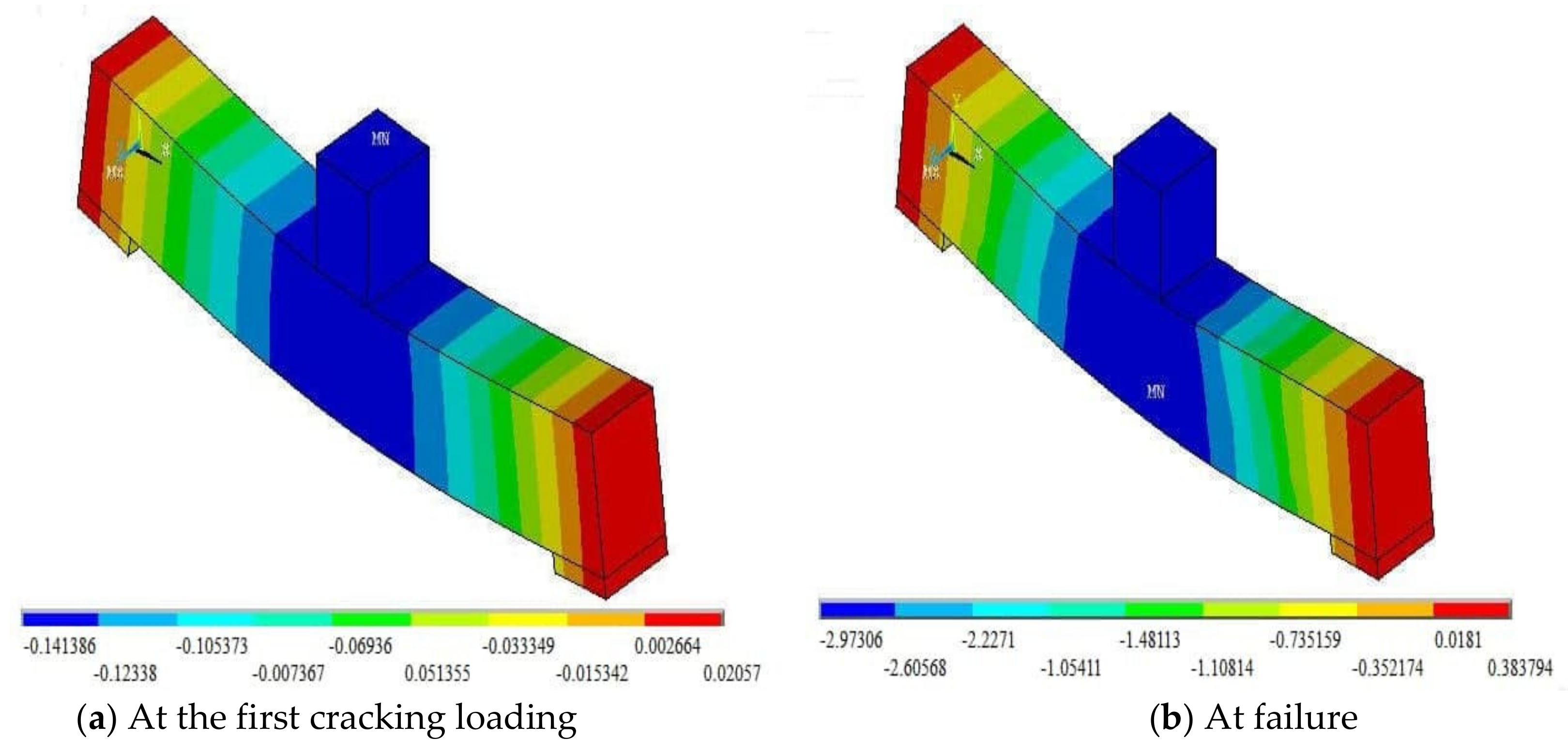
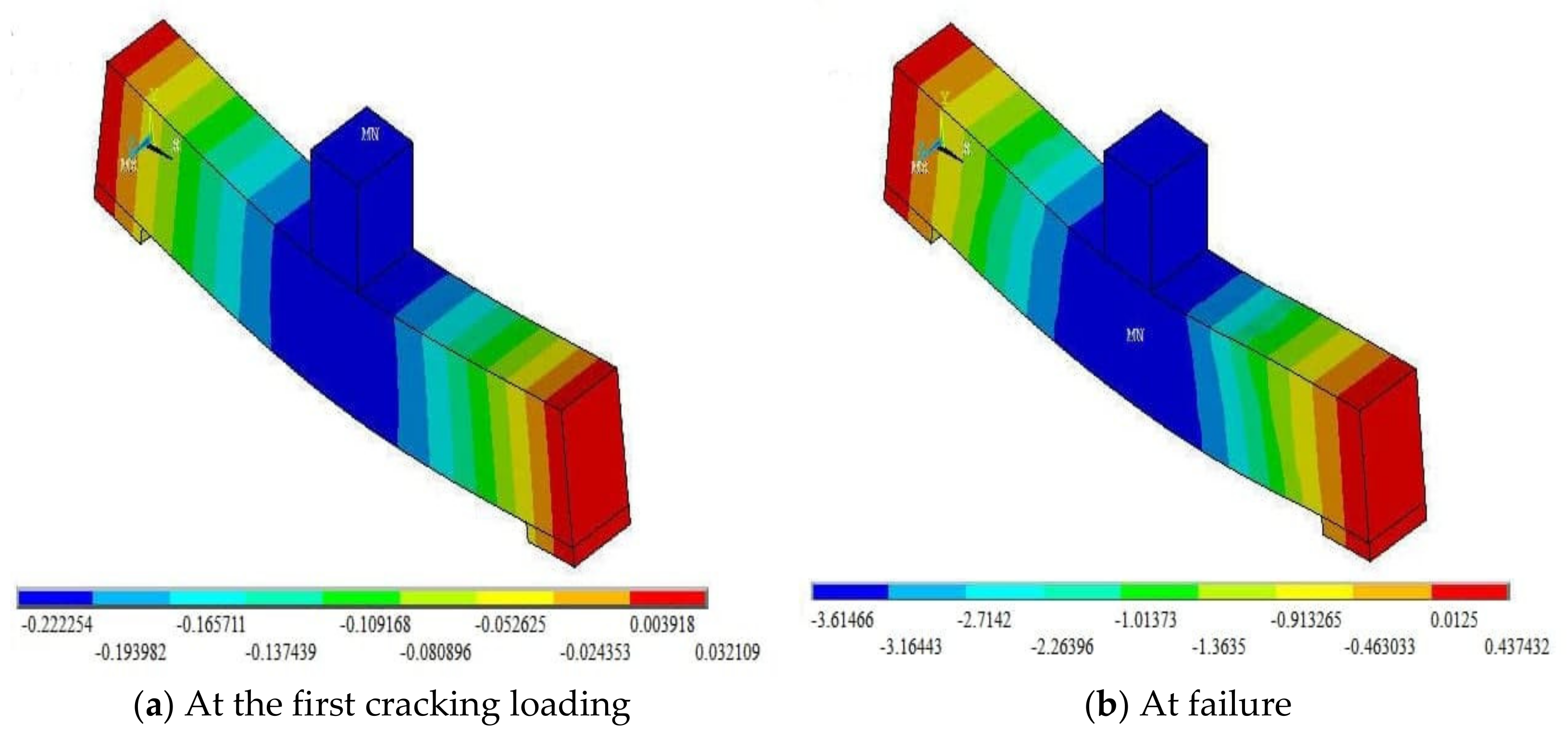
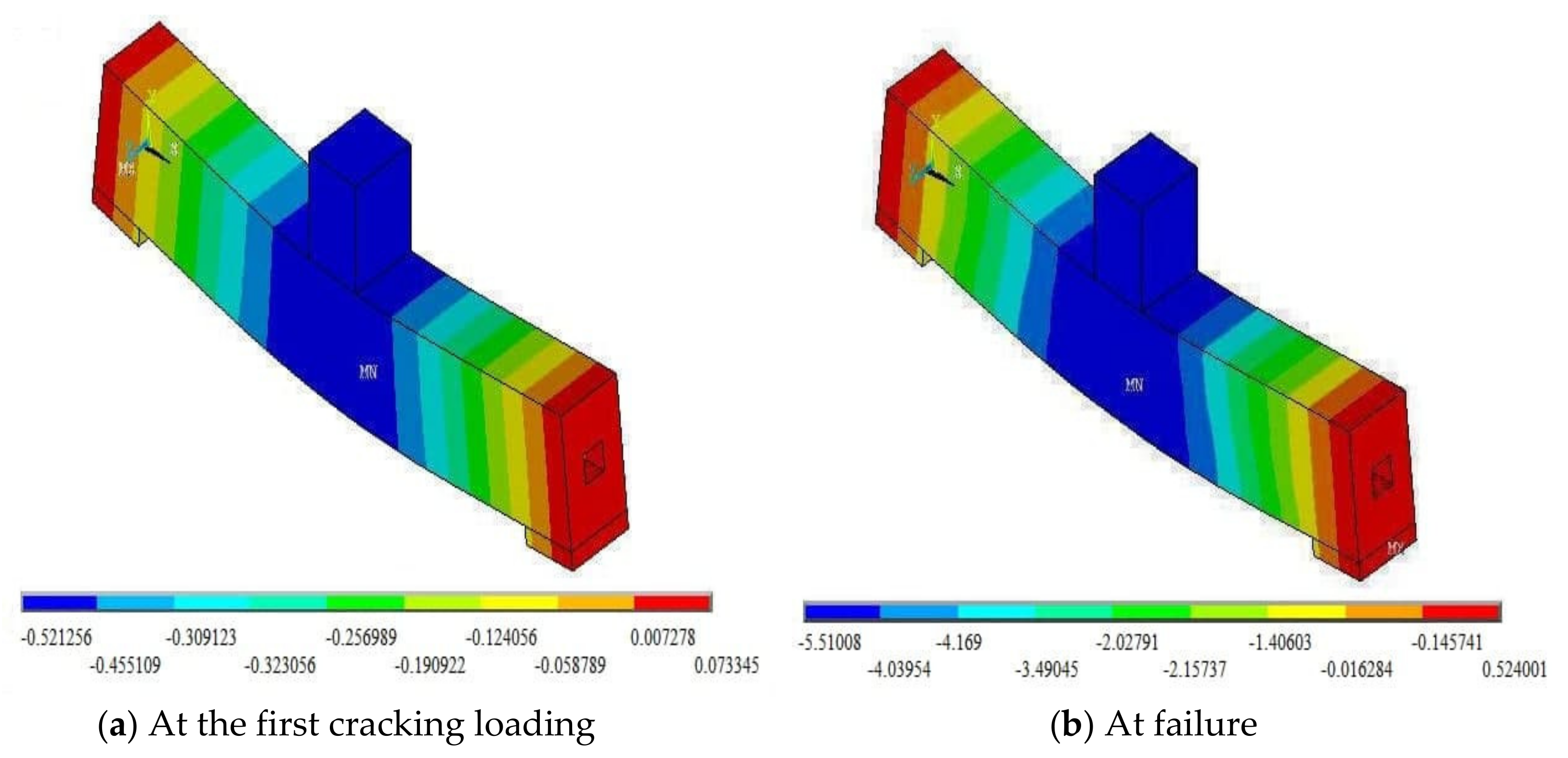
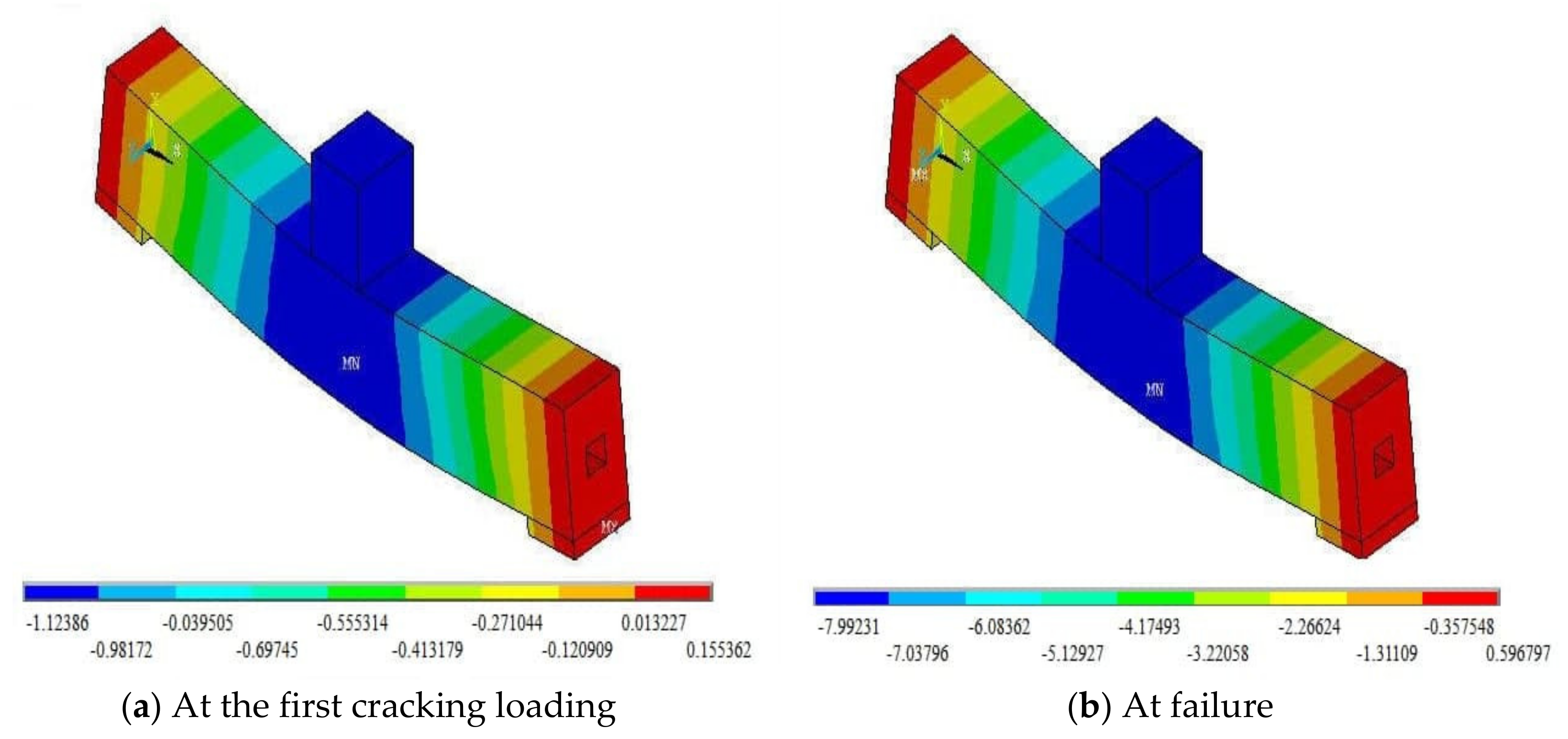
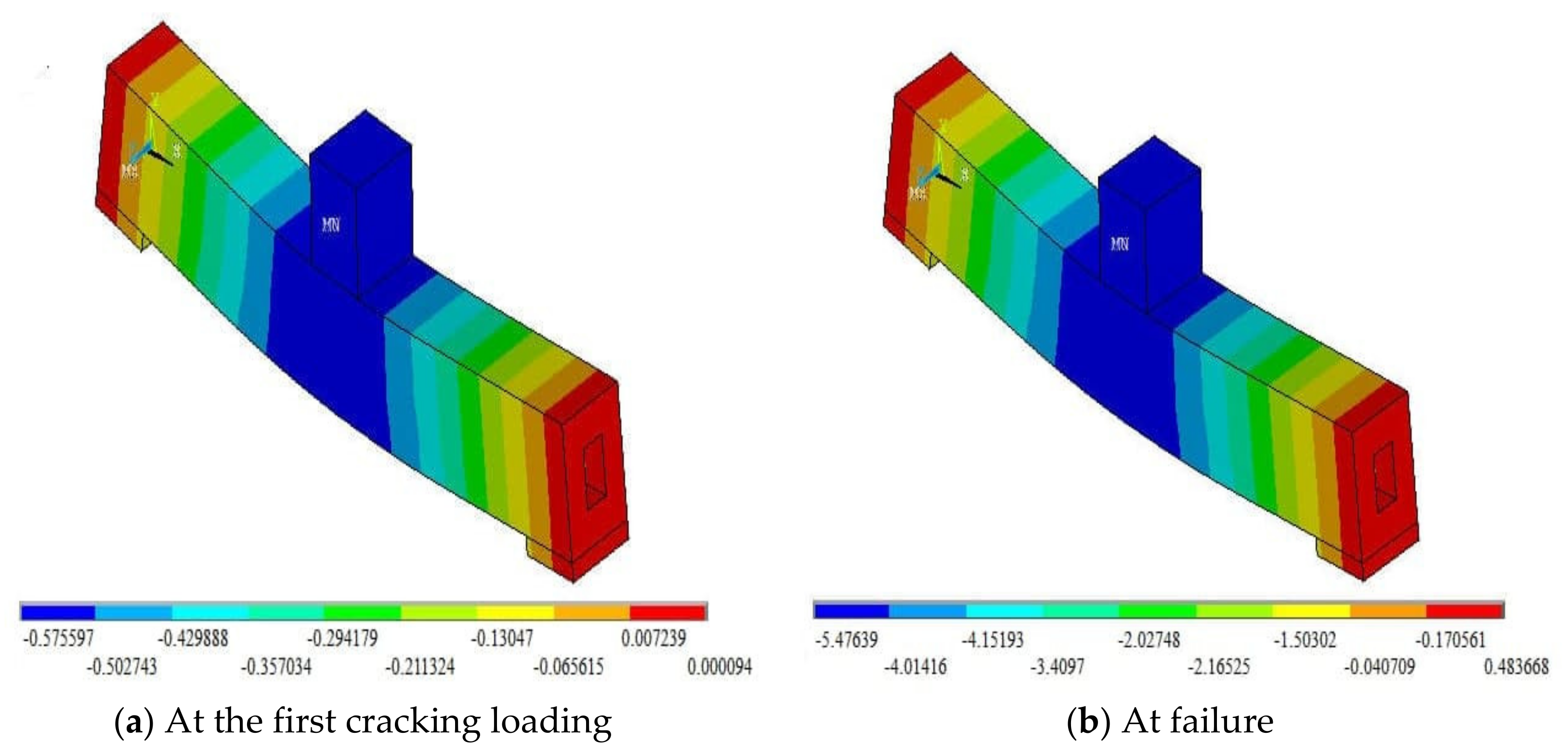
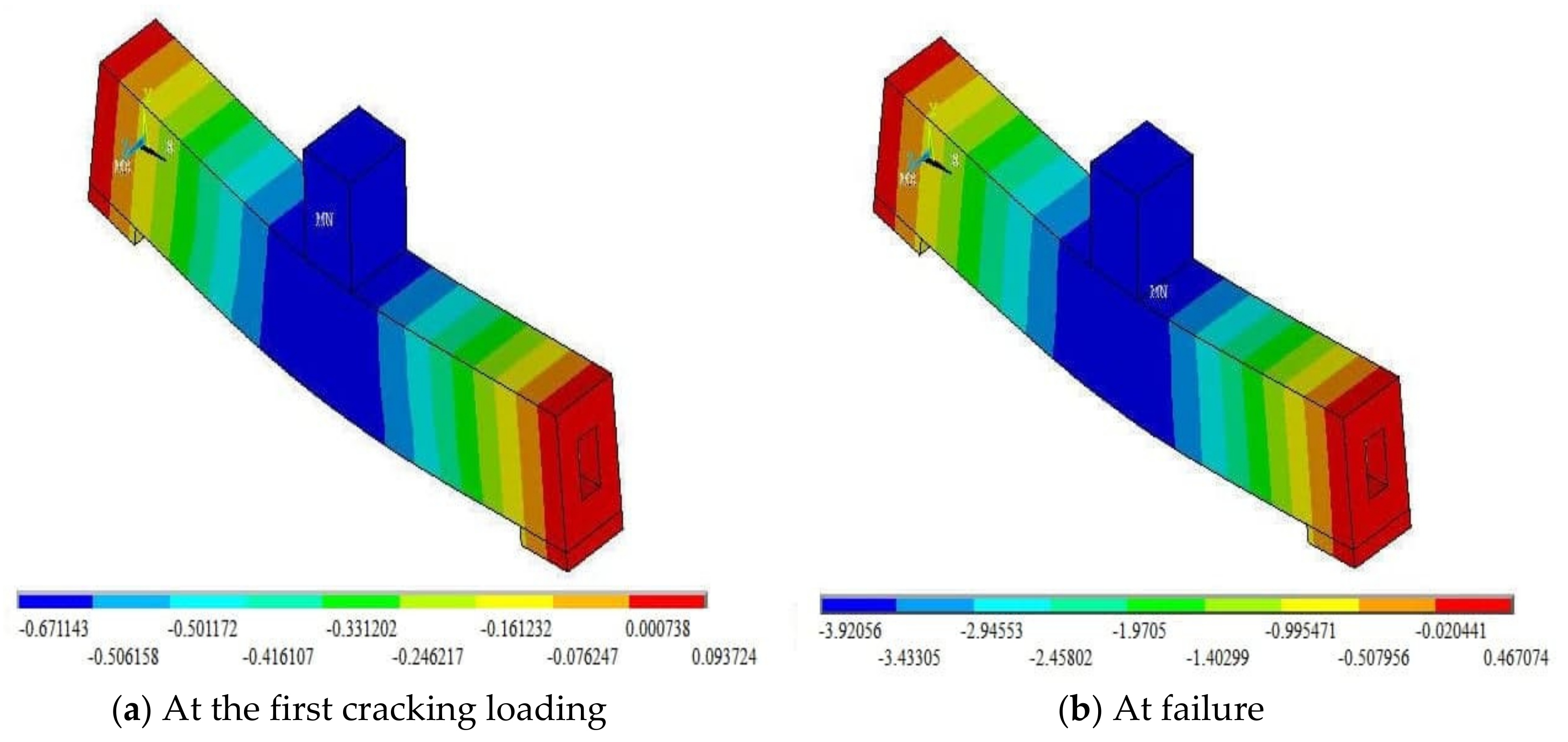
5. Numerical Analysis Results and Discussion
6. Conclusions
- The load causing the first crack relied on different influencing factors and was mainly affected by the increase in the vertical shear reinforcement ratio along the length, which would enhance the ductility and stiffness of concrete.
- All beam models sustained compound failures due to the propagations of shear and flexural cracks.
- The trends of the load-deflection curves varied for the beam models due to the composite actions between concrete and steel reinforcements, causing increases in the equivalent modulus of elasticity and moment of inertia of the beam members, both being the stiffness parameters.
- The presence of the hollow cores located in the central regions of the reinforced concrete beam models could be considered in the design to reduce the self-weight of RC beams and allow the service utilities to pass through them. The losses in the load capacity due to the presence of the openings could be compensated and enhanced by increasing the vertical shear reinforcement ratio.
- The numerical results using finite element method showed excellent agreements with the corresponding experimental results. Therefore, this numerical method could be used to explore and predict the remaining strengths of the RC beams by considering the indicated parameters in this study.
- The statistical analyses on the mean and standard deviation values of the ductility indices (DIs) for the experimental and numerical deflections at the first cracking load and ultimate load indicated the closely obtained results and confirmed the accuracy of the current numerical simulations.
- The current study provided the opportunity to develop a further insight on the effects of multilayer steel reinforcements on the load capacity of RC beams, repairing RC beams by using carbon fibre reinforced polymers (CFRPs) to resist the effect of dynamic loading, and utilising the benefit of openings in vertical and transverse directions. The current strategy of simulating RC beams with longitudinal hollow cores could be used as a starting point for analysis and design recommendations for dimensions and locations of hollow cores in RC beams.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Al-Balhawi, A. Dynamic Responses of Tall Reinforced Concrete Buildings Subjected to Wind Loading. Ph.D. Thesis, Glasgow Caledonian University, Glasgow, UK, 2018. [Google Scholar]
- Abbass, A.; Abid, S.; Özakça, M. Experimental investigation on the effect of steel fibers on the flexural behavior and ductility of high-strength concrete hollow beams. Adv. Civ. Eng. 2019, 2019, 8390345. [Google Scholar] [CrossRef]
- Katzer, J. Strength performance comparison of mortars made with waste fine aggregate and ceramic fume. Constr. Build. Mater. 2013, 47, 1–6. [Google Scholar] [CrossRef]
- Abid, S.R.; Nahhab, A.H.; Al-Aayedi, H.K.; Nuhair, A.M. Expansion and strength properties of concrete containing contaminated recycled concrete aggregate. Case Stud. Constr. Mater. 2018, 9, e00201. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, Z.; Zhu, C.; Feng, C.; Liu, J. Experiment on the bonding performance of the lightweight aggregate and normal weight concrete composite beams. Case Stud. Constr. Mater. 2021, 15, e00565. [Google Scholar] [CrossRef]
- Horňáková, M.; Lehner, P. Relationship of surface and bulk resistivity in the case of mechanically damaged fibre reinforced red ceramic waste aggregate concrete. Materials 2020, 13, 5501. [Google Scholar] [CrossRef] [PubMed]
- Omar, A.T.; Hassan, A.A.A. Behaviour of expanded slate semi-lightweight SCC beams with improved cracking performance and shear capacity. Structures 2021, 32, 1577–1588. [Google Scholar] [CrossRef]
- Hassan, R.F.; Jaber, M.H.; Al-Salim, N.H.; Hussein, H.H. Experimental research on torsional strength of synthetic/steel fiberreinforced hollow concrete beam. Eng. Struct. 2020, 220, 110948. [Google Scholar] [CrossRef]
- Al-Nuaimi, A.S.; Al-Jabri, K.S.; Hago, A. Comparison between solid and hollow reinforced concrete beams. Mater. Struct. 2008, 41, 269–286. [Google Scholar] [CrossRef]
- Hassan, N.Z.; Ismael, H.M.; Salman, A.M. Study behavior of hollow reinforced concrete beams. Int. J. Curr. Eng. Technol. 2018, 6, 1640–1651. [Google Scholar] [CrossRef]
- Balaji, G.; Vetturayasudharsanan, R. Experimental investigation on flexural behaviour of RC hollow beams. Mater. Today Proc. 2020, 21, 509–516. [Google Scholar] [CrossRef]
- Hemzah, S.A.; Alyhya, W.S.; Hassan, S.A. Experimental investigation for structural behaviour of self-compacting reinforced concrete hollow beams with in-place circular openings strengthened with CFRP laminates. Structures 2020, 24, 99–106. [Google Scholar] [CrossRef]
- Mansur, M.A. Effect of openings on the behaviour and strength of R/C beams in shear. Cem. Concr. Compos. 1998, 6, 477–486. [Google Scholar] [CrossRef]
- Abdalla, H.A.; Torkey, A.M.; Haggag, H.A.; Abu-Amira, A.F. Design against cracking at openings in reinforced concrete beams strengthened with composite sheets. Compos. Struct. 2003, 2, 197–204. [Google Scholar] [CrossRef]
- Amiri, J.V.; Bygie, M.H. Effect of small circular opening on the shear and flexural behavior and ultimate strength of reinforced concrete beams using normal and high strength concrete. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Yang, K.H.; Eun, H.C.; Chung, H.S. The influence of web openings on the structural behavior of reinforced high-strength concrete deep beams. Eng. Struct. 2006, 13, 1825–1834. [Google Scholar] [CrossRef]
- Aykaç, S.; Yilmaz, M.C. Behaviour and strength of RC beams with regular triangular or circular web openings. J. Fac. Eng. Archit. Gazi Univ. 2011, 3, 711–718. [Google Scholar]
- Ahmed, A.; Fayyadh, M.M.; Naganathan, S.; Nasharuddin, K. Reinforced concrete beams with web openings: A state of the art review. Mater. Des. 2012, 40, 90–102. [Google Scholar] [CrossRef]
- Mahmoud, A.M. Strengthening of concrete beams having shear zone openings using orthotropic CFRP modeling. Ain Shams Eng. J. 2012, 3, 177–190. [Google Scholar] [CrossRef] [Green Version]
- Aykac, B.; Aykac, S.; Kalkan, I.; Dundar, B.; Can, H. Flexural behavior and strength of reinforced concrete beams with multiple transverse openings. ACI Struct. J. 2014, 2, 267–277. [Google Scholar]
- Jabbar, S.; Hejazi, F.; Mahmod, H.M. Effect of an opening on reinforced concrete hollow beam web under torsional, flexural, and cyclic loadings. Lat. Am. J. Solids Struct. 2016, 8, 1576–1595. [Google Scholar] [CrossRef] [Green Version]
- Nie, X.F.; Zhang, S.S.; Teng, J.G.; Chen, G.M. Experimental study on RC T-section beams with an FRP-strengthened web opening. Compos. Struct. 2018, 185, 273–285. [Google Scholar] [CrossRef]
- Majeed, Q.G.; Ahmed, Q.W.; Mohammed, A.H.; Sammen, S.S. Experimental study of reinforced concrete beams with elliptical opening under flexural loading. IOP Conf. Ser. Mater. Sci. Eng. 2020, 1, 1–10. [Google Scholar] [CrossRef]
- Jabbar, D.N.; Al-Rifaie, A.; Hussein, A.M.; Shubbar, A.A.; Nasr, M.S.; Al-Khafaji, Z.S. Shear behaviour of reinforced concrete beams with small web openings. Mater. Today Proc. 2021, 5, 2713–2716. [Google Scholar] [CrossRef]
- Salih, R.; Abbas, N.; Zhou, F. Experimental and Numerical investigations on the cyclic load behavior of beams with rectangular web openings strengthened using FRP sheets. Structures 2021, 33, 655–677. [Google Scholar] [CrossRef]
- Altun, F.; Haktanir, T.; Ari, K. Experimental investigation of steel fiber reinforced concrete box beams under bending. Mater. Struct. 2006, 4, 491–499. [Google Scholar] [CrossRef]
- Alshimmeri, A.J.H.; Al-Maliki, H.N.G. Structural behavior of reinforced concrete hollow beams under partial uniformly distributed load. J. Eng. 2014, 7, 130–145. [Google Scholar]
- Al-Gasham, T.S.S. Reinforced concrete moderate deep beams with embedded PVC pipes. Wasit J. Eng. Sci. 2015, 1, 19–29. [Google Scholar] [CrossRef]
- Murugesan, A.; Narayanan, A. Influence of a longitudinal circular hole on flexural strength of reinforced concrete beams. Pract. Period. Struct. Des. Constr. 2017, 22, 04016021. [Google Scholar] [CrossRef]
- Murugesan, A.; Narayanan, A. Deflection of reinforced concrete beams with longitudinal circular hole. Pract. Period. Struct. Des. Constr. 2018, 23, 04017034. [Google Scholar] [CrossRef]
- Al-Khuzaie, H.M.A.; Atea, R.S. Investigation of torsional behavior and capacity of reactive powder concrete (RPC) of hollow T-beam. J. Mater. Res. Technol. 2019, 1, 199–207. [Google Scholar] [CrossRef]
- Abbass, A.A.; Abid, S.R.; Arna’ot, F.H.; Al-Ameri, R.A.; Ozakca, M. Flexural response of hollow high strength concrete beams considering different size reductions. Structures 2020, 23, 69–86. [Google Scholar] [CrossRef]
- Hassan, S.A. Structural Behaviour of Self-Compacted Concrete Box Girders with In-Place Openings. Master’s Thesis, University of Kerbala, Kerbala, Iraq, 2020. [Google Scholar]
- Hassan, S.A.; Hemzah, S.A.; Alyhya, W.S. Experimental investigation of the structural behaviours of self-compacted reinforced concrete hollow beams with inplace circular openings. IOP Conf. Ser. Mater. Sci. Eng. 2020, 671, 1–10. [Google Scholar] [CrossRef]
- El-Kassas, A.I.; Hassan, H.M.; Arab, M.A.E.S. Effect of longitudinal opening on the structural behavior of reinforced high-strength self-compacted concrete deep beams. Case Stud. Constr. Mater. 2020, 12, e00348. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Madhavi, T.C. Behaviour of self compacting concrete with hybrid fibers in hollow beams. Mater. Today Proc. 2021, 46, 3212–3219. [Google Scholar] [CrossRef]
- Al-Nuaimi, A.S.; Bhatt, P. 2D idealisation of hollow reinforced concrete beams subjected to combined torsion, bending and shear. J. Eng. Res. 2005, 1, 53–68. [Google Scholar] [CrossRef] [Green Version]
- Hauhnar, L.; Rajkumar, R.; Umamaheswari, N. Behavior of reinforced concrete beams with circular opening in the flexural zone strengthened by steel pipes. Int. J. Civ. Eng. Technol. 2017, 5, 303–309. [Google Scholar]
- Elamary, A.S.; Sharaky, I.A.; Alqurashi, M. Flexural behaviour of hollow concrete beams under three points loading: Experimental and numerical study. Structures 2021, 32, 1543–1552. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS Fluent User’s Guide; ANSYS: Canonsburg, PA, USA, 2015. [Google Scholar]
- American Concrete Institute (ACI). ACI-318 Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar] [CrossRef]
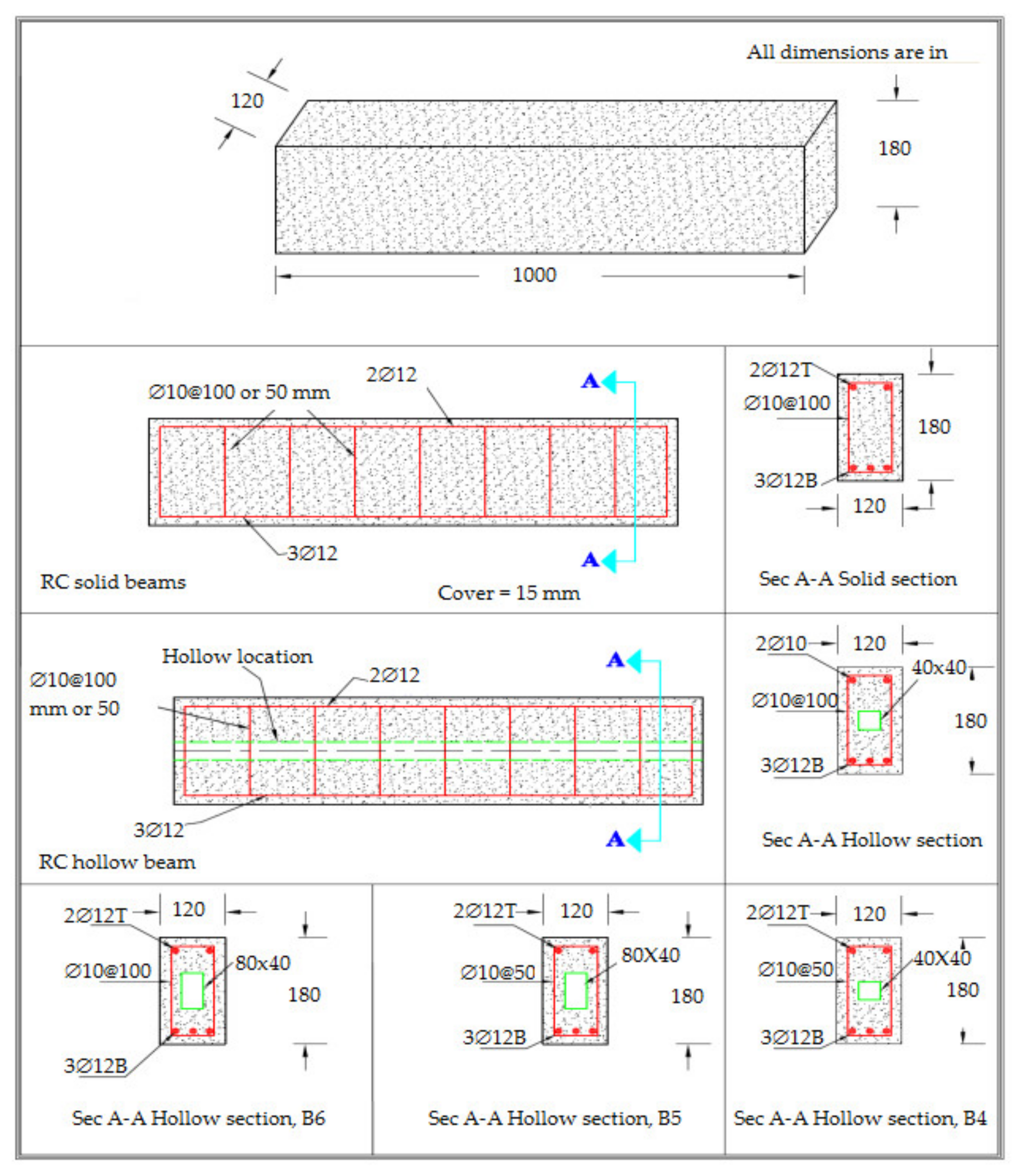
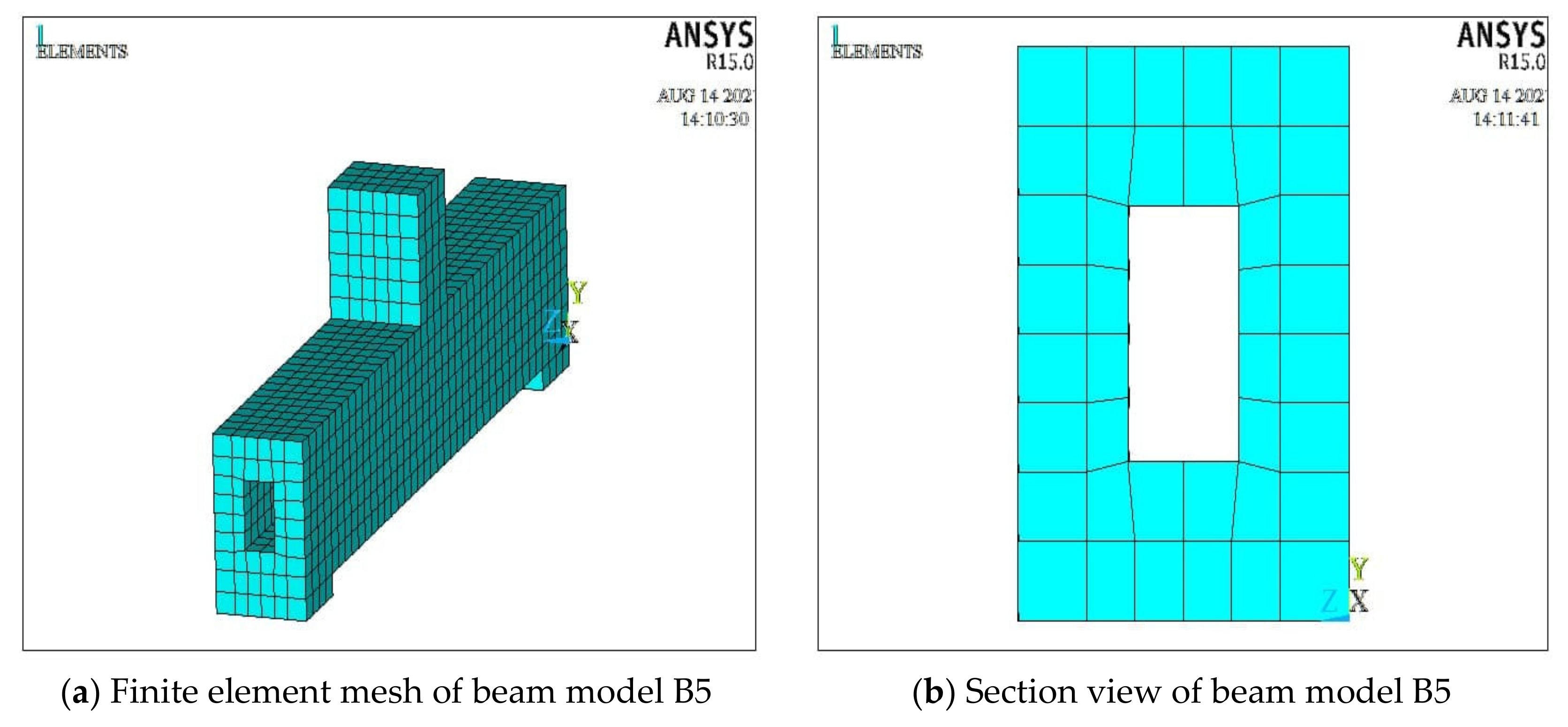
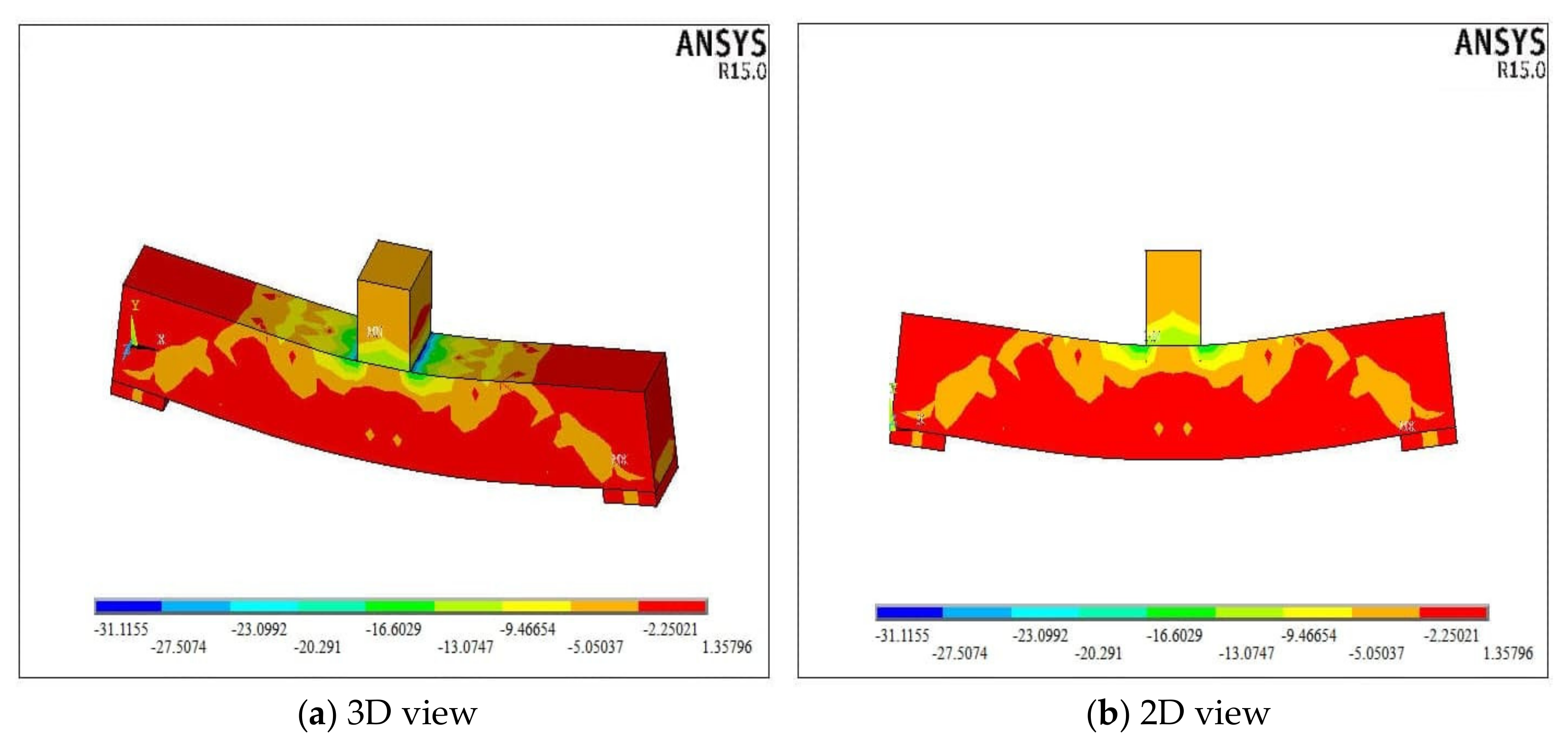
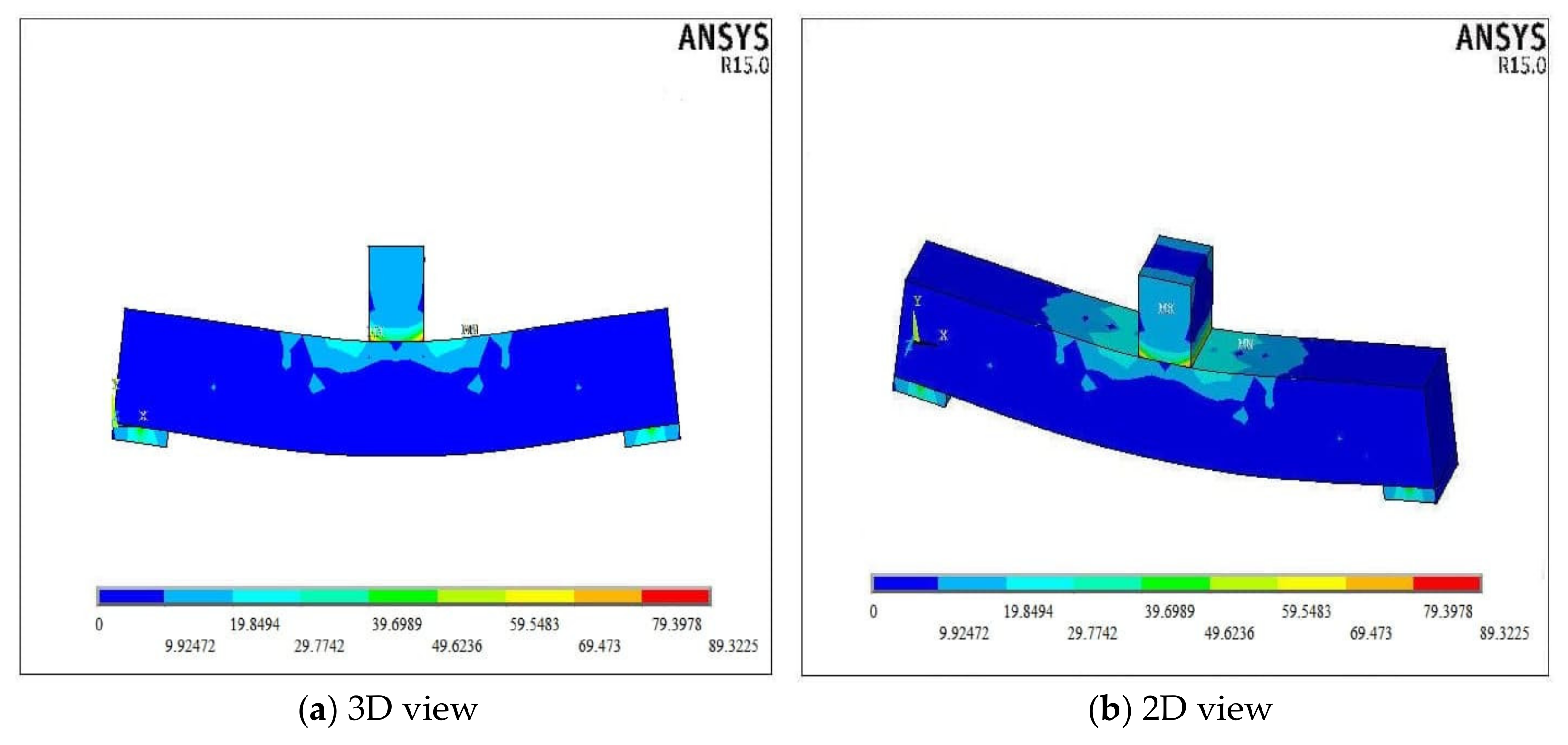
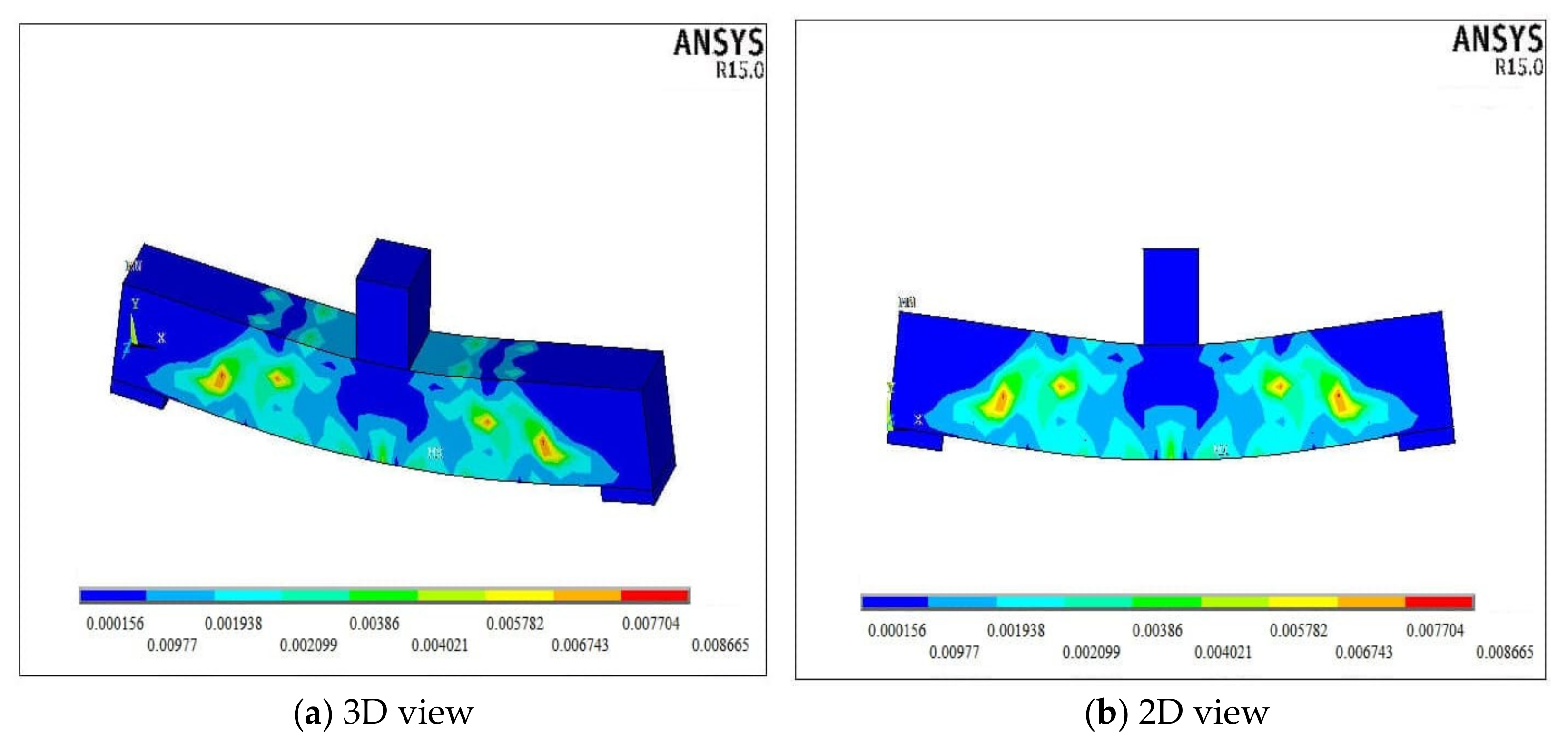



| Model | As | As′ | Diameter/Spacing of Stirrups (mm) | Section Type | Hollow Size (mm) | Hollow Ratio (%) |
|---|---|---|---|---|---|---|
| B1 | 3∅12 | 2∅12 | ∅10/100 | S | ||
| B2 | ∅10/50 | S | ||||
| B3 | ∅10/100 | H | 40 × 40 | 7.4 | ||
| B4 | ∅10/50 | H | 40 × 40 | 7.4 | ||
| B5 | ∅10/50 | H | 80 × 40 | 14.8 | ||
| B6 | ∅10/100 | H | 80 × 40 | 14.8 |
| fc′ (MPa) | ft (MPa) | fr (MPa) | Ec (GPa) | vc |
|---|---|---|---|---|
| 28.52 | 3.16 | 3.74 | 25.105 | 0.15 |
| Rebar Diameter ∅ (mm) | fy (MPa) | fu (MPa) | Es (GPa) | Vs |
|---|---|---|---|---|
| 10 | 421 | 520 | 205 | 0.30 |
| 12 | 480 | 570 |
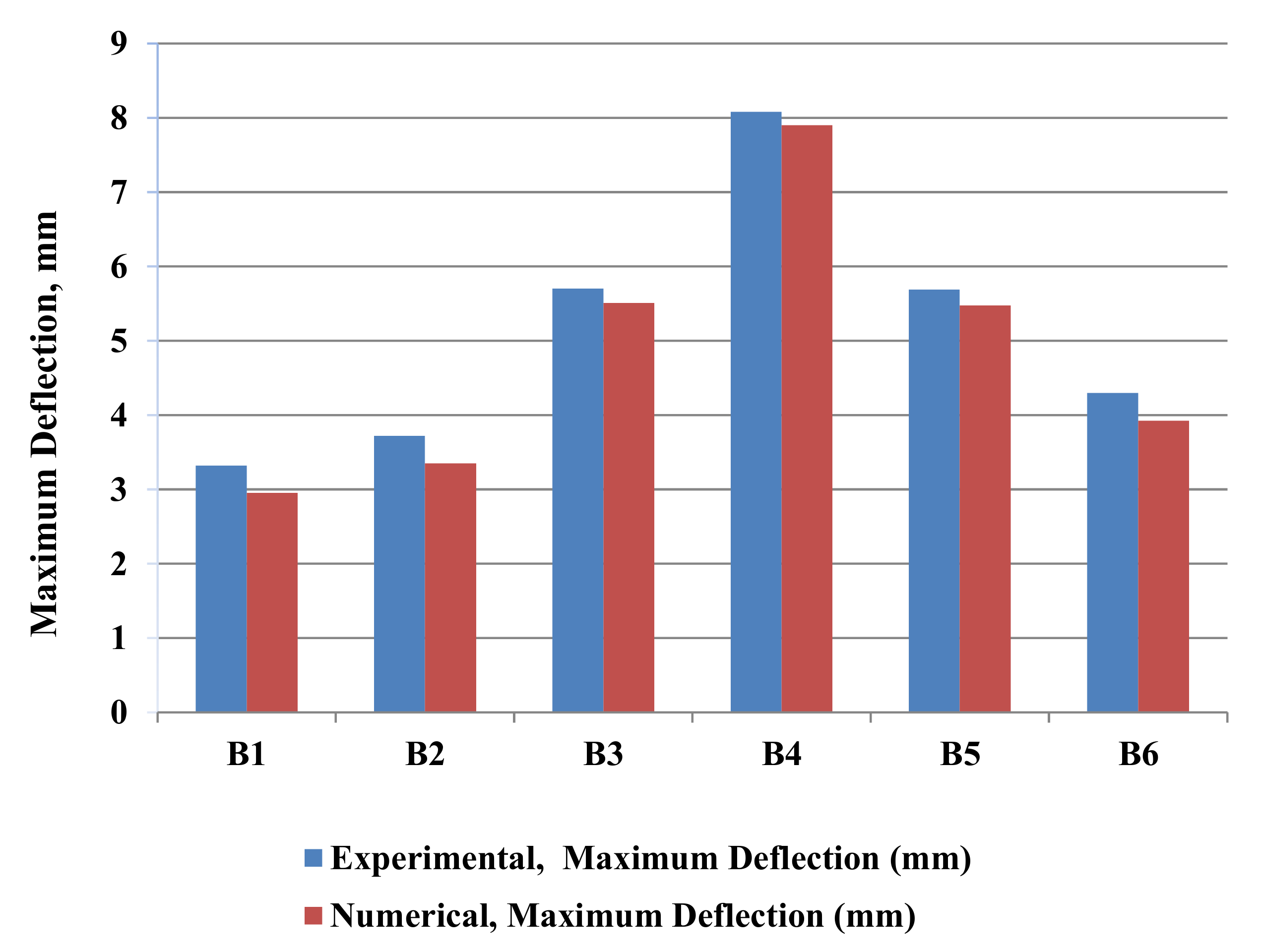
| Beam Model | Experimental Loads (kN) | Experimental Deflections (mm) | Numerical Deflection (mm) | Numerical/Experimental Deflection Ratio | ||||
|---|---|---|---|---|---|---|---|---|
| First | Failure | First | Failure | First | Failure | First | Failure | |
| B1 | 5 | 60 | 0.30 | 3.32 | 0.29 | 3.21 | 0.97 | 0.97 |
| B2 | 10 | 87.5 | 0.35 | 3.72 | 0.32 | 3.35 | 0.91 | 0.90 |
| B3 | 4 | 40 | 0.44 | 5.70 | 0.42 | 5.51 | 0.95 | 0.97 |
| B4 | 5 | 55 | 0.38 | 8.08 | 0.37 | 7.99 | 0.97 | 0.99 |
| B5 | 3 | 35 | 0.60 | 5.69 | 0.59 | 5.46 | 0.98 | 0.96 |
| B6 | 2.5 | 25 | 0.86 | 4.30 | 0.82 | 3.92 | 0.95 | 0.91 |
| Mean | 0.96 | 0.95 | ||||||
| STD | 0.02 | 0.03 | ||||||
| Beam Model | Experimental Deflection (mm) | Ductility Index, DI | Numerical Deflection (mm) | Ductility Index, DI | Numerical/Experimental DI | ||
|---|---|---|---|---|---|---|---|
| First | Failure | Exp. | First | Failure | Num. | ||
| B1 | 0.30 | 3.32 | 11.07 | 0.29 | 3.21 | 11.07 | 1.00 |
| B2 | 0.35 | 3.72 | 10.63 | 0.32 | 3.35 | 10.47 | 0.98 |
| B3 | 0.44 | 5.70 | 12.95 | 0.42 | 5.51 | 13.11 | 1.01 |
| B4 | 0.38 | 8.08 | 21.26 | 0.37 | 7.99 | 21.60 | 1.02 |
| B5 | 0.60 | 5.69 | 9.48 | 0.59 | 5.46 | 9.25 | 0.98 |
| B6 | 0.86 | 4.30 | 5.00 | 0.82 | 3.92 | 4.78 | 0.96 |
| Mean | 0.99 | ||||||
| STD | 0.02 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Maliki, H.N.G.; Al-Balhawi, A.; Alshimmeri, A.J.H.; Zhang, B. Structural Efficiency of Hollow Reinforced Concrete Beams Subjected to Partial Uniformly Distributed Loading. Buildings 2021, 11, 391. https://doi.org/10.3390/buildings11090391
Al-Maliki HNG, Al-Balhawi A, Alshimmeri AJH, Zhang B. Structural Efficiency of Hollow Reinforced Concrete Beams Subjected to Partial Uniformly Distributed Loading. Buildings. 2021; 11(9):391. https://doi.org/10.3390/buildings11090391
Chicago/Turabian StyleAl-Maliki, Hadi Naser Ghadhban, Ali Al-Balhawi, Ahmad Jabbar Hussain Alshimmeri, and Binsheng Zhang. 2021. "Structural Efficiency of Hollow Reinforced Concrete Beams Subjected to Partial Uniformly Distributed Loading" Buildings 11, no. 9: 391. https://doi.org/10.3390/buildings11090391
APA StyleAl-Maliki, H. N. G., Al-Balhawi, A., Alshimmeri, A. J. H., & Zhang, B. (2021). Structural Efficiency of Hollow Reinforced Concrete Beams Subjected to Partial Uniformly Distributed Loading. Buildings, 11(9), 391. https://doi.org/10.3390/buildings11090391









