The Behaviour of Load-Carrying Members from Cordwood
Abstract
:1. Introduction
2. Materials and Methods
2.1. Analytical Method for the Design of Cordwood
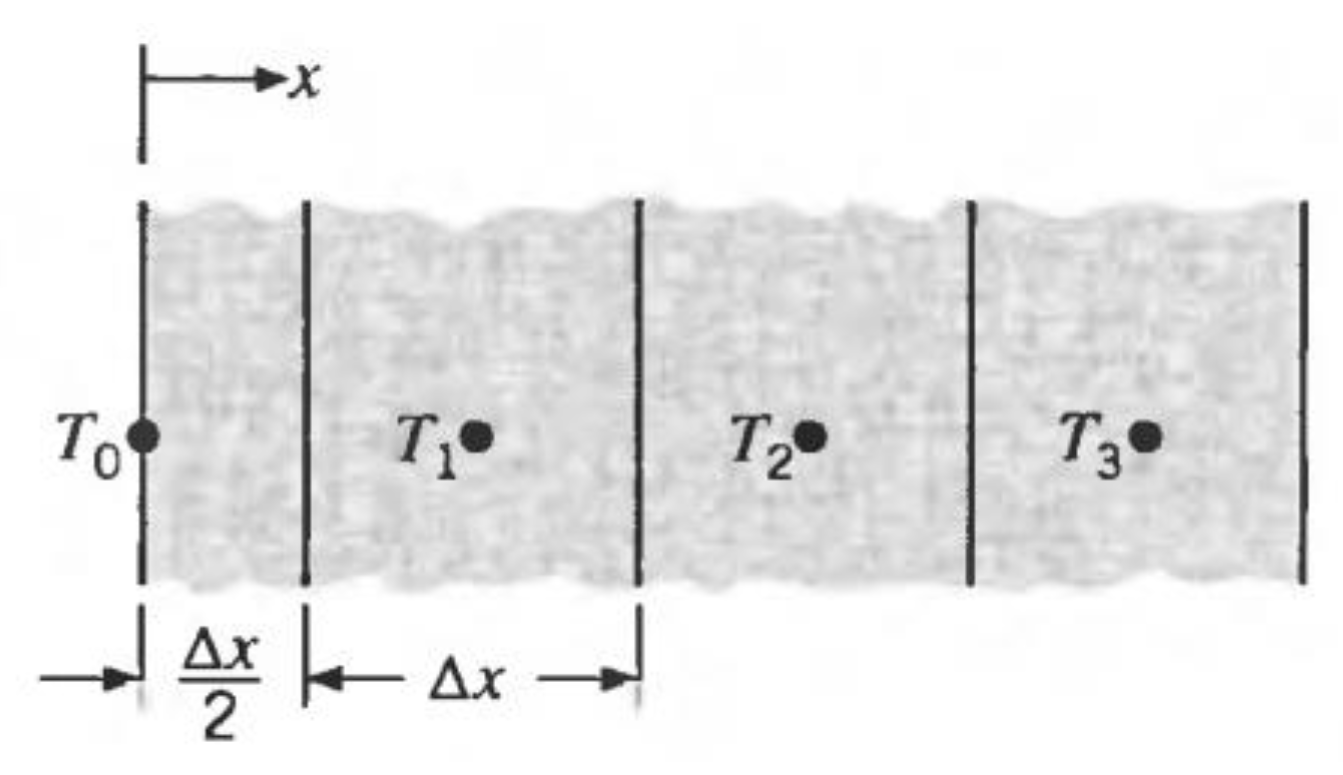
2.2. Analytical Method for the Design of Cordwood in Case of Fire Action
2.3. Developing Comparison Criteria for Cordwood
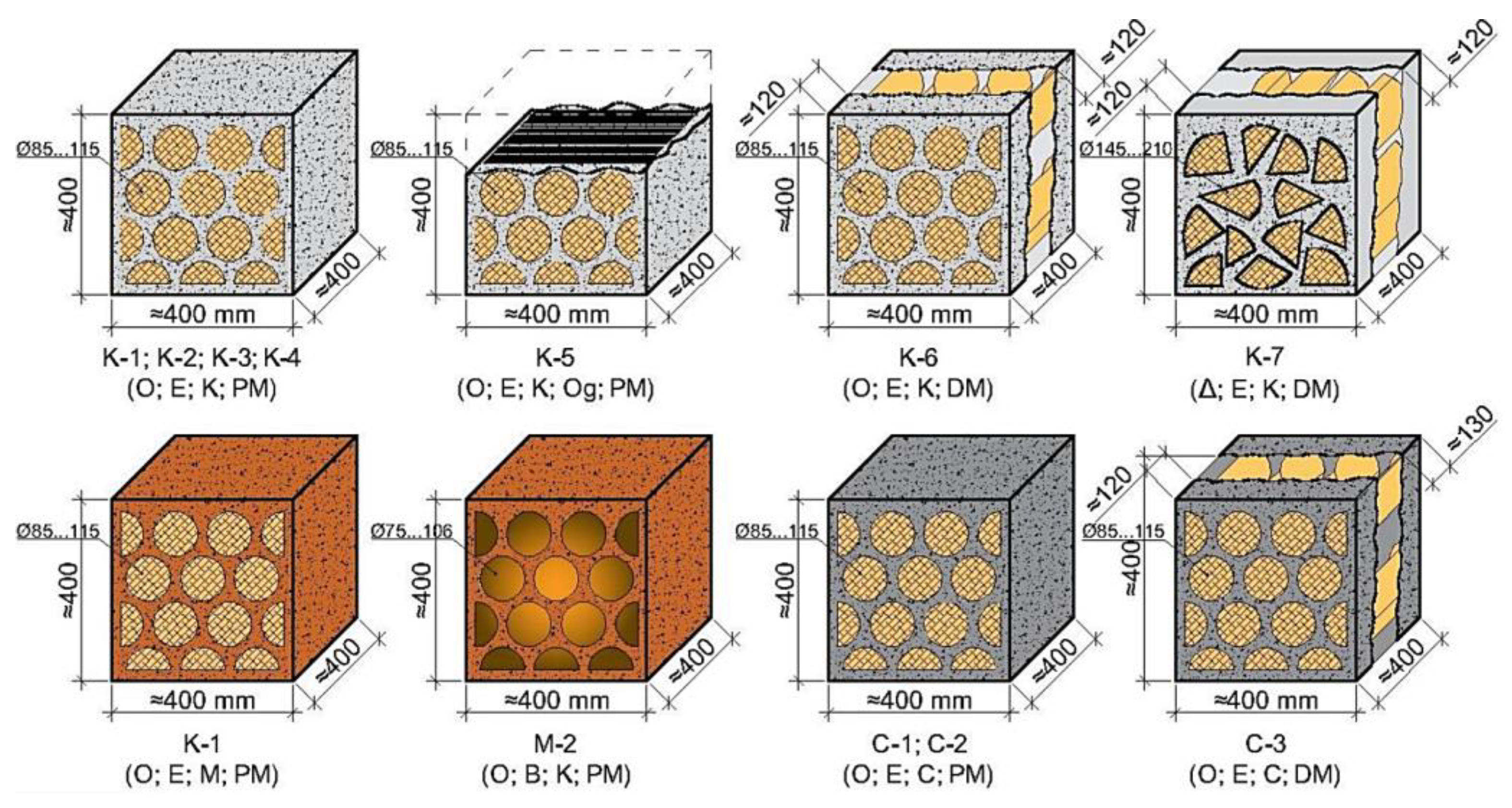
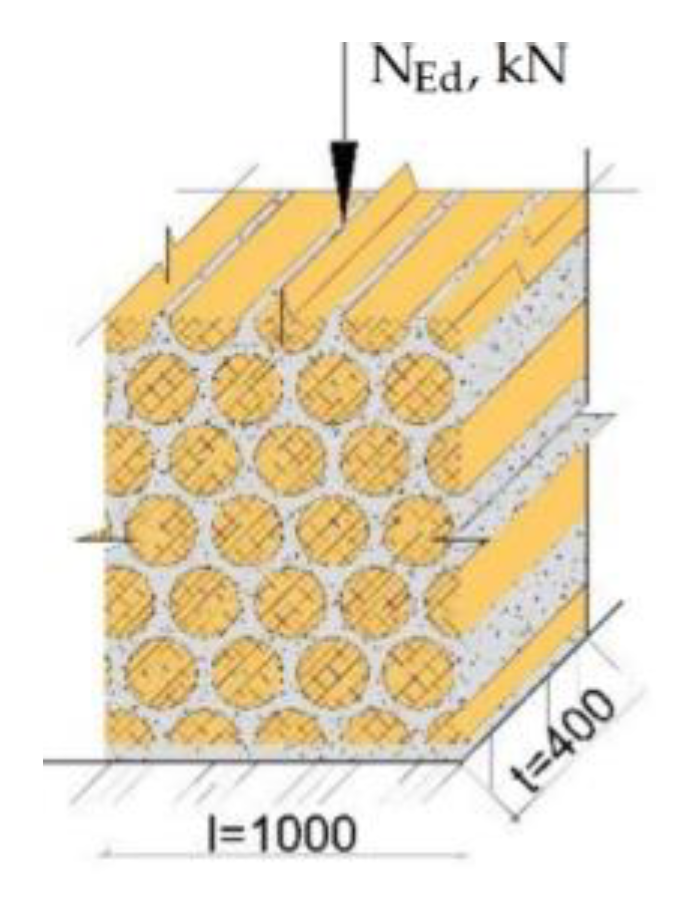
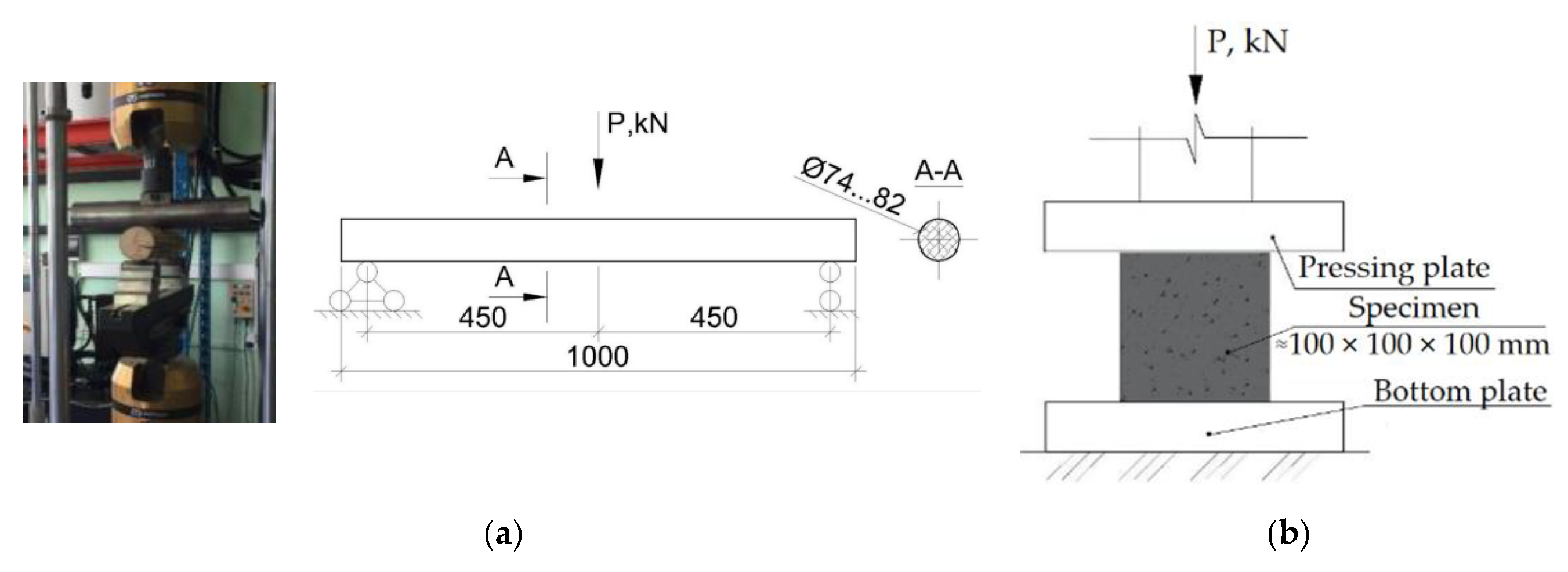
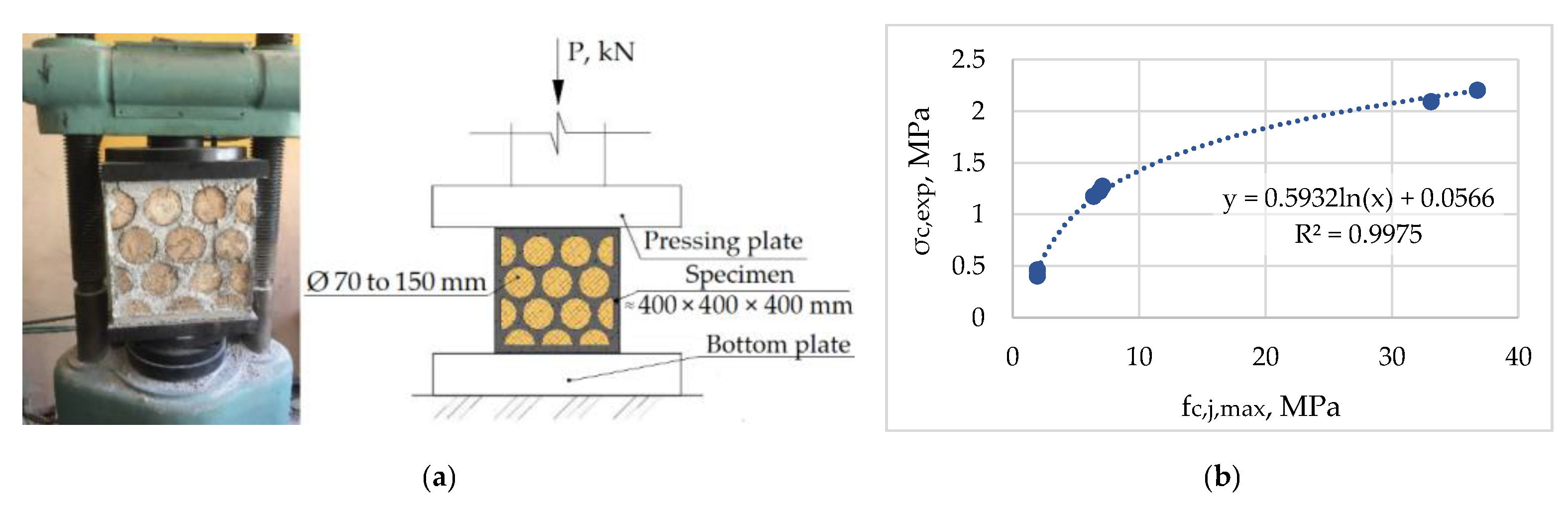
2.4. Description of Laboratory Experiment
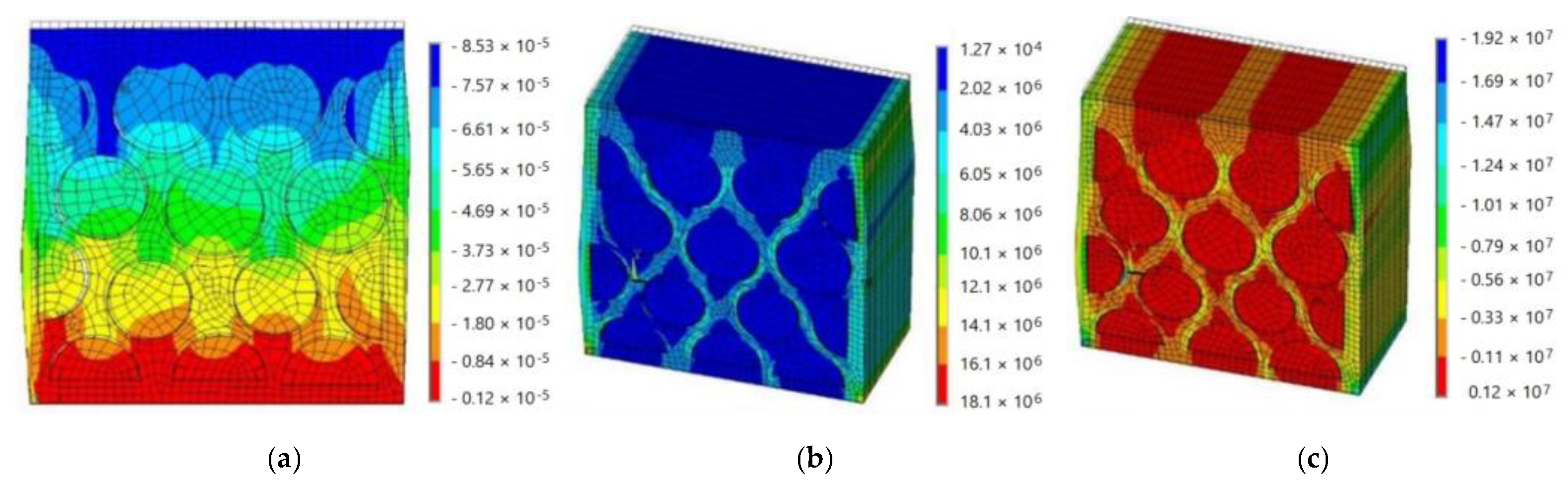
2.5. FEM Modelling of Cordwood Specimens
3. Results
3.1. The Numerical Realisation of the Developed Analytical Method for the Design of Cordwood
3.2. The Numerical Realisation of Developed Analytical Method for the Design of Cordwood in Case of Fire Action
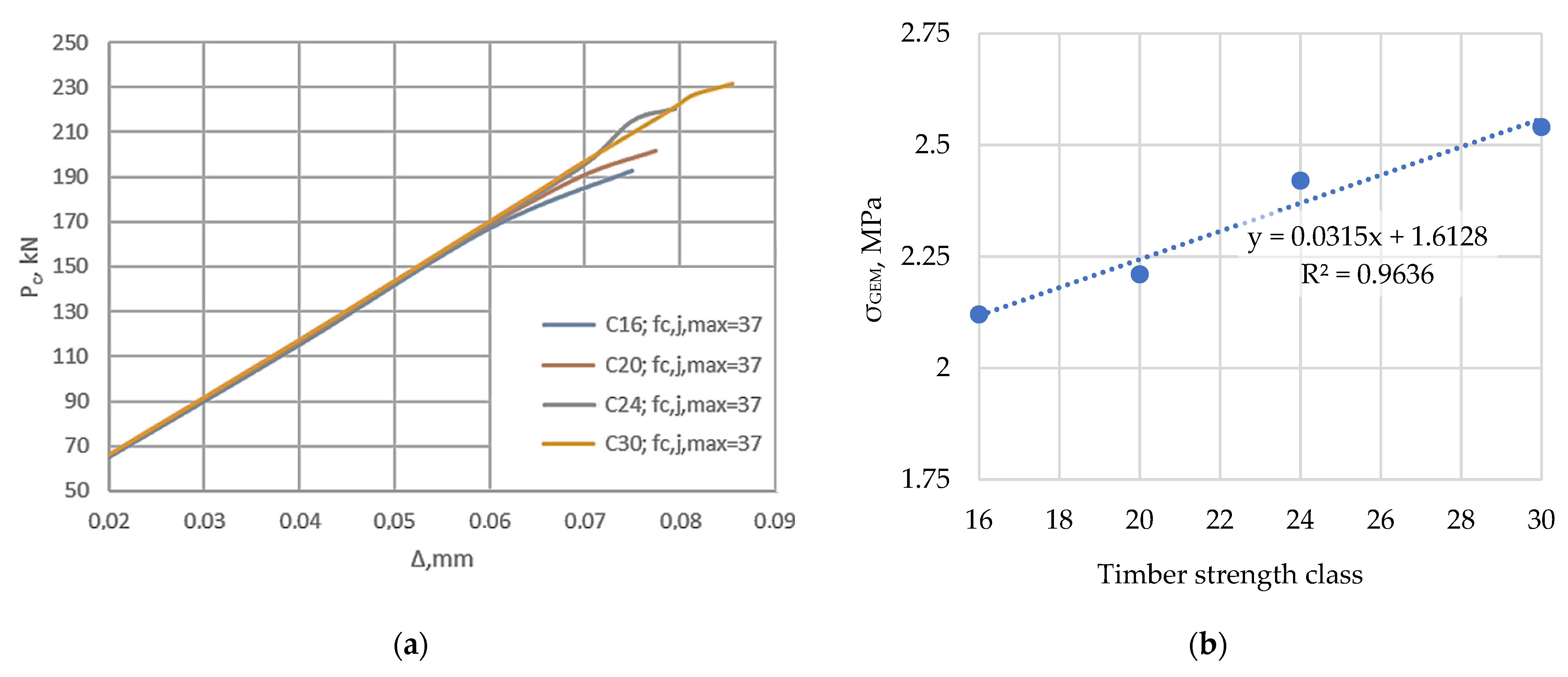
3.3. Results of the Laboratory Experiment
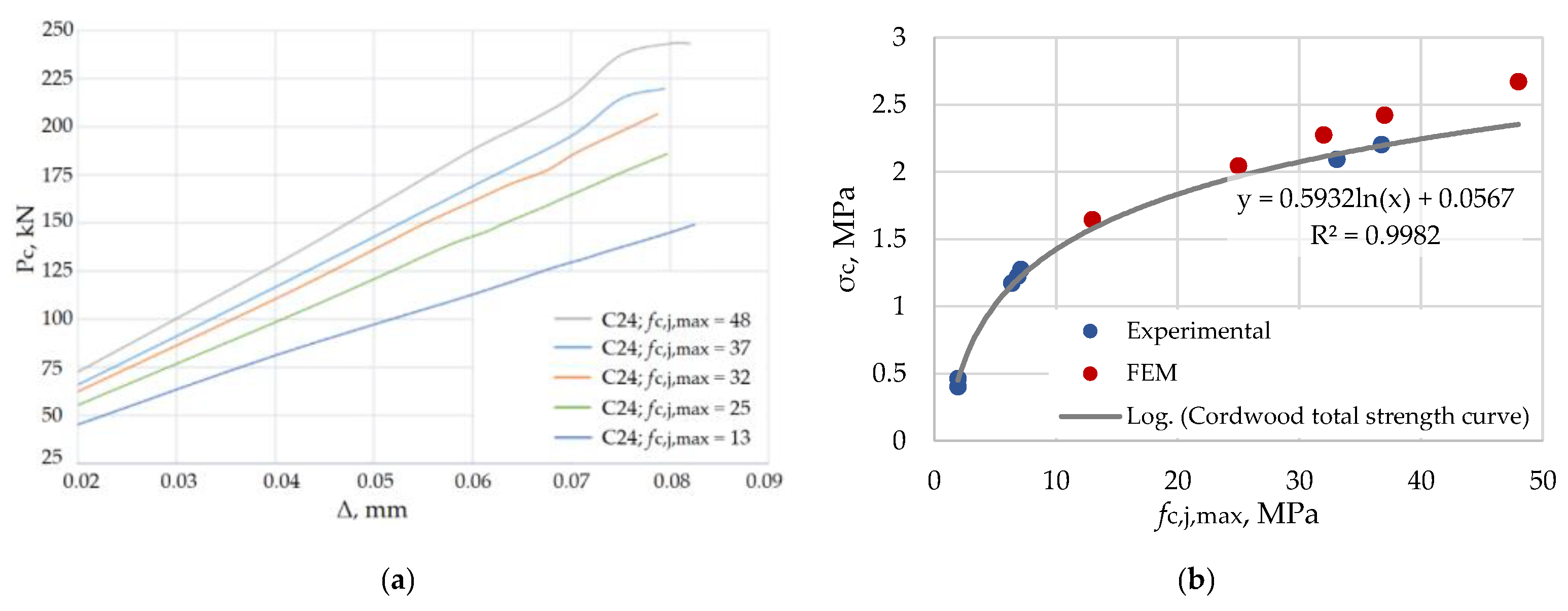
3.4. Results of FEM Modelling
4. Conclusions
- The most rational and economical cordwood solution involves using a low- or medium-high-strength mortar (up to 10 MPa). The use of higher strength mortar does not significantly increase the strength of cordwood. It was proven experimentally that the use of mortars with compressive strengths of 36.76, 7.12 and 1.94 MPa for producing cordwood specimens enables obtaining a compression strength of cordwood of 2.14, 1.22 and 0.43 MPa, respectively. The increase in the wood billets’ strength class did not significantly influence the compressive strength of cordwood. Therefore, increasing the strength class of wood billets from C16 to C30 increased the compressive strength of cordwood to 21% only when the lime mortar with a compressive strength of 7.12 MPa was used. By using a cordwood wall with a thickness of 40 cm, which corresponds to the most commonly used cordwood wall thickness, it is possible to obtain load-bearing walls for two-storey buildings that provide very high fire resistance—R180, in the case of double-sided fire resistance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Švajlenka, J.; Kozlovská, M. Factors Influencing the Sustainability of Wood-Based Constructions’ Use from the Perspective of Users. Sustainability 2021, 13, 12950. [Google Scholar] [CrossRef]
- Roy, R. Cordwood Building: A Comprehensive Guide to the State of the Art—Fully Revised Second Edition; Fully Revised 2nd Edition; New Society Publishers: La Vergne, TN, USA, 2016; ISBN 9780865718289. [Google Scholar]
- Morin, B.; Ahmadi, M.; Rector, L.; Allen, G. Development of an Integrated Duty Cycle Test Method to Assess Cordwood Stove Performance. J. Air Waste Manag. Assoc. 2022, 72, 629–646. [Google Scholar] [CrossRef] [PubMed]
- Buka-Vaivade, K.; Serdjuks, D.; Pakrastins, L. Cost Factor Analysis for Timber–Concrete Composite with a Lightweight Plywood Rib Floor Panel. Buildings 2022, 12, 761. [Google Scholar] [CrossRef]
- Sultana, R.; Rashedi, A.; Khanam, T.; Jeong, B.; Hosseinzadeh-Bandbafha, H.; Hussain, M. Life Cycle Environmental Sustainability and Energy Assessment of Timber Wall Construction: A Comprehensive Overview. Sustainability 2022, 14, 4161. [Google Scholar] [CrossRef]
- Poranek, N.; Łaźniewska-Piekarczyk, B.; Czajkowski, A.; Pikoń, K. MSWIBA Formation and Geopolymerisation to Meet the United Nations Sustainable Development Goals (SDGs) and Climate Mitigation. Buildings 2022, 12, 1083. [Google Scholar] [CrossRef]
- Gravit, M.; Serdjuks, D.; Bardin, A.; Prusakov, V.; Buka-Vaivade, K. Fire Design Methods for Structures with Timber Framework. Mag. Civ. Eng. 2019, 85, 92–106. [Google Scholar] [CrossRef]
- Nicholls, D.; Miles, T. Cordwood Energy Systems for Community Heating in Alaska—An Overview; General Technical Report PNW-GTR-783; U.S. Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 2009; Volume 783, 17p. [CrossRef]
- Nanni, A.; Venturi, M.; Paiter, L. Permaculture MESMIS—A Methodology to Evaluate Ecological Well-Being on Permaculture Farms. Int. Res. J. Biol. Sci. 2021, 10, 47–57. [Google Scholar]
- Morel, K.; Léger, F.; Ferguson, R. Permaculture. Encycl. Ecol. 2018, 4, 559–567. [Google Scholar]
- Szewczyk, J. Cordwood Heritage; Bialystok Technical University: Bialystok, Poland, 2007; p. 128. ISBN 978995528. [Google Scholar]
- McCann, R.; Thomas, B. Permaculture; Utah State University: Logan, UT, USA, 2013. [Google Scholar]
- Flatau, R.; Flatau, B. Cordwood and Community. Back Home Magazine, Jan/Feb 2010. 41–43.
- Hagman, O. A Technology in Permanent Transition: 200 Years of Cordwood Building with Consumers as Producers. ICON 2012, 18, 142–156. [Google Scholar]
- Mouterde, R.; Morel, J.-C.; Martinet, V.; Sallet, F. The Mechanical Performance of Cordwood. Biosyst. Eng. 2011, 108, 237–243. [Google Scholar] [CrossRef]
- Yanfeng, T.; Ping, W.-J. The Research of Development Framework for Workflow Based on Cordwood Structure. In Proceedings of the 2013 6th International Conference on Intelligent Networks and Intelligent Systems (ICINIS), Shenyang, China, 1–3 November 2013; pp. 17–20. [Google Scholar] [CrossRef]
- Gravit, M.; Shabunina, D.; Antonov, S.; Danilov, A. Thermal Characteristics of Fireproof Plaster Compositions in Exposure to Various Regimes of Fire. Buildings 2022, 12, 630. [Google Scholar] [CrossRef]
- Gravit, M.; Simonenko, Y.; Larionov, A. Method Single Burning Item (SBI) for Fire Hazard of Wood Constructions. E3S Web Conf. 2019, 91, 02049. [Google Scholar] [CrossRef]
- Korolkov, D.; Gravit, M.; Aleksandrovskiy, M. Estimation of the Residual Resource of Wooden Structures by Changing Geometric Parameters of the Cross-Section. E3S Web Conf. 2021, 244, 04010. [Google Scholar] [CrossRef]
- Gaile, L.; Pakrastins, L.; Ratnika, L. Structural Health Monitoring by Merging Dynamic Response Data. Mag. Civ. Eng. 2022, 111, 11111. [Google Scholar] [CrossRef]
- Gaile, L.; Ratnika, L.; Pakrastins, L. RC Medium-Rise Building Damage Sensitivity with SSI Effect. Materials 2022, 15, 1653. [Google Scholar] [CrossRef] [PubMed]
- Brics, A. Behaviours Analysis of Load-Carrying Members of Cordwood Houses; Riga Technical University: Riga, Latvia, 2019. [Google Scholar]
- EN 1996-1-1:2005+A1:2012; Eurocode 6—Design of Masonry Structures—Part 1-1: General Rules for Reinforced and Unreinforced Masonry Structures. iTeh Inc.: Newark, DE, USA, 2005. Available online: https://standards.iteh.ai/catalog/standards/cen/502c057e-25f1-4228-a10a-635c4aa9efd4/en-1996-1-1-2005a1-2012 (accessed on 25 August 2022).
- EN 1995-1-2:2004; Eurocode 5: Design of Timber Structures—Part 1-2: General— Structural Fire Design. iTeh Inc.: Newark, DE, USA, 2004. Available online: https://standards.iteh.ai/catalog/standards/cen/7c5128eb-3949-494d-abe5-f1832864cb15/en-1995-1-2-2004 (accessed on 2 September 2022).
- EN 1992-1-2:2004/A1:2019; Eurocode 2: Design of Concrete Structures—Part 1-2: General Rules—Structural Fire Design. iTeh Inc.: Newark, DE, USA, 2019. Available online: https://standards.iteh.ai/catalog/standards/cen/651bc53c-16d5-4983-bc4f-be403472ee95/en-1992-1-2-2004-a1-2019 (accessed on 2 September 2022).
- Incropera, F.P.; Incropera, F.P. (Eds.) Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley: Hoboken, NJ, USA, 2007; ISBN 9780471457282. [Google Scholar]
- Harrington, J.; Jacobson, M.; Short, C. Handbook on Structural Timber Design to Eurocode 5 (IS EN 1995-1-1) Rules Including Strength Capacity Tables for Structural Elements; COFORD: Dublin, Ireland, 2006; ISBN 9781902696522. [Google Scholar]
- EN 1991-1-2:2002/AC:2013; Eurocode 1: Actions on Structures—Part 1-2: General Actions—Actions on Structures Exposed to Fire. iTeh Inc.: Newark, DE, USA, 2002. Available online: https://standards.iteh.ai/catalog/standards/cen/6499fb76-e1b3-4837-98a9-ff338860a4f9/en-1991-1-2-2002-ac-2013 (accessed on 2 September 2022).
- EN 1996-1-2:2005; Eurocode 6—Design of Masonry Structures—Part 1-2: General Rules—Structural Fire Design. iTeh Inc.: Newark, DE, USA, 2005. Available online: https://standards.iteh.ai/catalog/standards/cen/ab1c6dc8-e5f0-4c77-ae93-521b41d4b81a/en-1996-1-2-2005 (accessed on 2 September 2022).
- EN 338:2016; Structural Timber—Strength Classes. iTeh Inc.: Newark, DE, USA, 2016. Available online: https://standards.iteh.ai/catalog/standards/cen/492c108d-268a-4cbd-9b59-3f31792887c5/en-338-2016 (accessed on 25 August 2022).

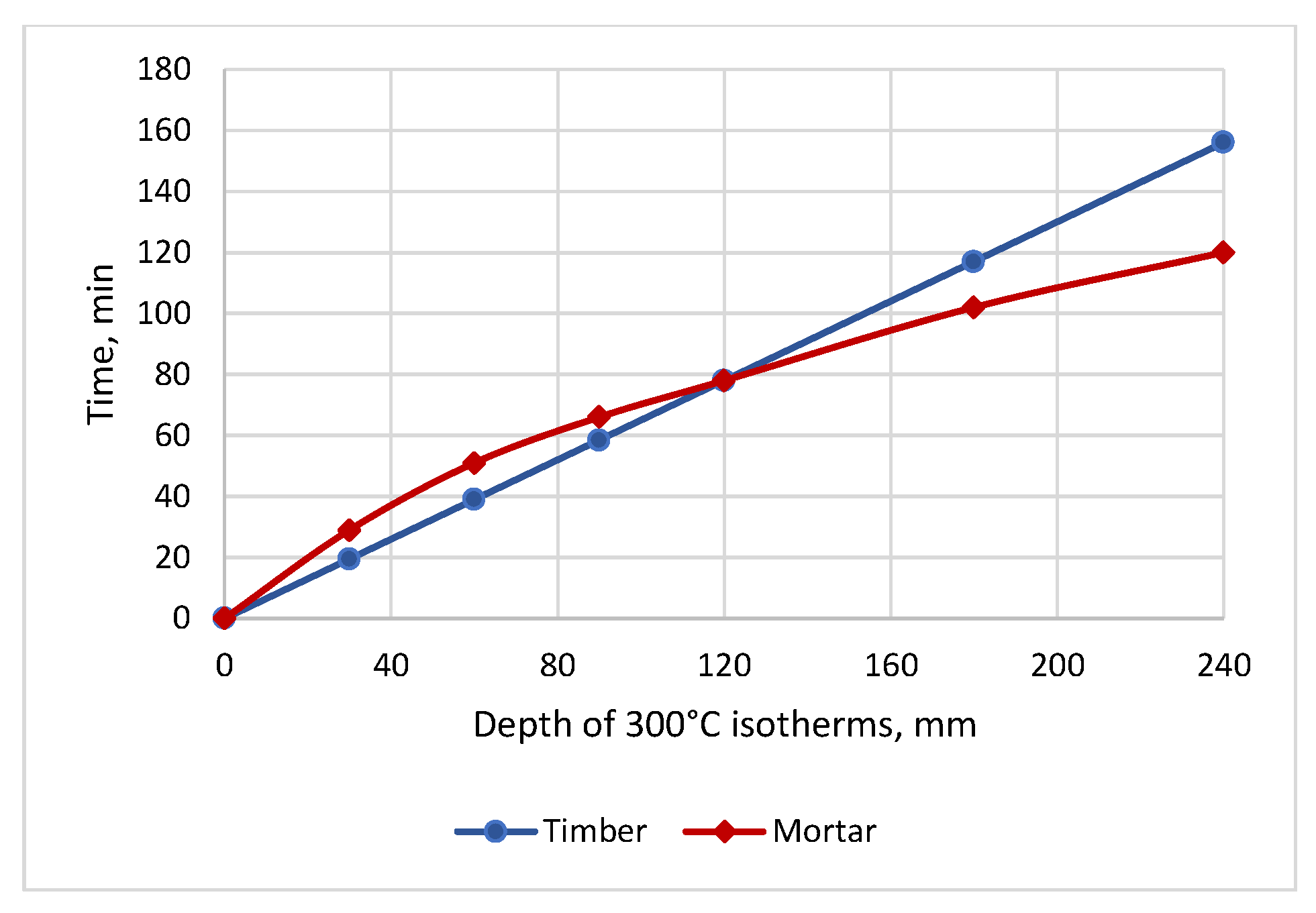




| Time t, min | Charring Depth dchar,0, mm | Depth of 300 °C Isotherms in Mortar, mm | Reduction in Wall Cross-Section, mm |
|---|---|---|---|
| 30 | 19.5 | 29 | 36 |
| 60 | 39.0 | 51 | 57 |
| 90 | 58.5 | 66 | 73 |
| 120 | 78 | 78 | 85 |
| 180 | 117 | 102 | 124 |
| 240 | 156 | 120 | 163 |
| Time t, min | Charring Depth dchar,0 | Depth of 300 °C Isotherms in Mortar, mm/Reduction in Wall Cross-Section, mm | ||
|---|---|---|---|---|
| b = 200 mm | b = 300 mm | b ≥ 400 mm wall | ||
| 30 | 19.5 | 29/72 | 29/72 | 29/72 |
| 60 | 39.0 | 51/116 | 51/116 | 51/116 |
| 90 | 58.5 | 69/152 | 66/146 | 66/146 |
| 120 | 78 | -/- | 81/176 | 78/170 |
| 180 | 117 | -/- | 116/248 | 105/248 |
| 240 | 156 | -/- | -/- | 123/326 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brics, A.; Serdjuks, D.; Gravit, M.; Buka-Vaivade, K.; Goremikins, V.; Vatin, N.I.; Podkoritovs, A. The Behaviour of Load-Carrying Members from Cordwood. Buildings 2022, 12, 1702. https://doi.org/10.3390/buildings12101702
Brics A, Serdjuks D, Gravit M, Buka-Vaivade K, Goremikins V, Vatin NI, Podkoritovs A. The Behaviour of Load-Carrying Members from Cordwood. Buildings. 2022; 12(10):1702. https://doi.org/10.3390/buildings12101702
Chicago/Turabian StyleBrics, Arvis, Dmitrijs Serdjuks, Marina Gravit, Karina Buka-Vaivade, Vadims Goremikins, Nikolai Ivanovich Vatin, and Andrejs Podkoritovs. 2022. "The Behaviour of Load-Carrying Members from Cordwood" Buildings 12, no. 10: 1702. https://doi.org/10.3390/buildings12101702
APA StyleBrics, A., Serdjuks, D., Gravit, M., Buka-Vaivade, K., Goremikins, V., Vatin, N. I., & Podkoritovs, A. (2022). The Behaviour of Load-Carrying Members from Cordwood. Buildings, 12(10), 1702. https://doi.org/10.3390/buildings12101702









