A Novel Safety Risk Assessment Based on Fuzzy Set Theory and Decision Methods in High-Rise Buildings
Abstract
:1. Introduction
2. Literature Review
2.1. Managerial Factors
2.2. Individual Factors
2.3. Environmental Factors
2.4. Multi-Criteria Decision-Making Methods
2.4.1. Best–Worst Method
- Compatibility of data in BWM
2.4.2. Fuzzy VIKOR Method
- Determining the positive and negative ideal for each criterion in the form of (j = 1, 2, 3, …, n);
- 2.
- If and , the normal fuzzy subtractions are obtained via the following equations:
- 3.
- Calculating the weighted fuzzy summation and the maximum fuzzy performance is obtained using the equations below:
- 4.
- The values are calculated using the equations below:
- 5.
- Defuzzification of the quantities above using the median to the second weight and their conversion to the absolute values;
- 6.
- Arranging the absolute values in descending order and ranking the options;
- 7.
- Determining the compromise solution in terms of the optimal quantity if the two conditions below are established.
- Alternative and if only Condition 2 is not satisfied.
- Alternatives , ,…., A(H), if Condition 1 is not satisfied, A(H) is the last alternative with which Condition 1 is not satisfied i.e.,for maximum H [48].
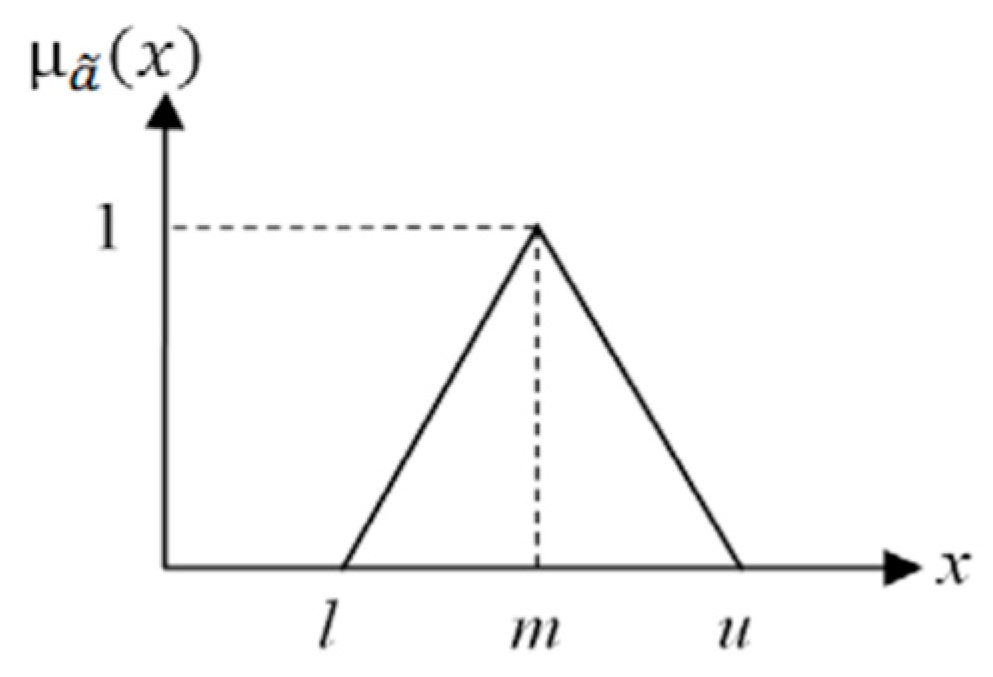
2.4.3. Fuzzy Sets
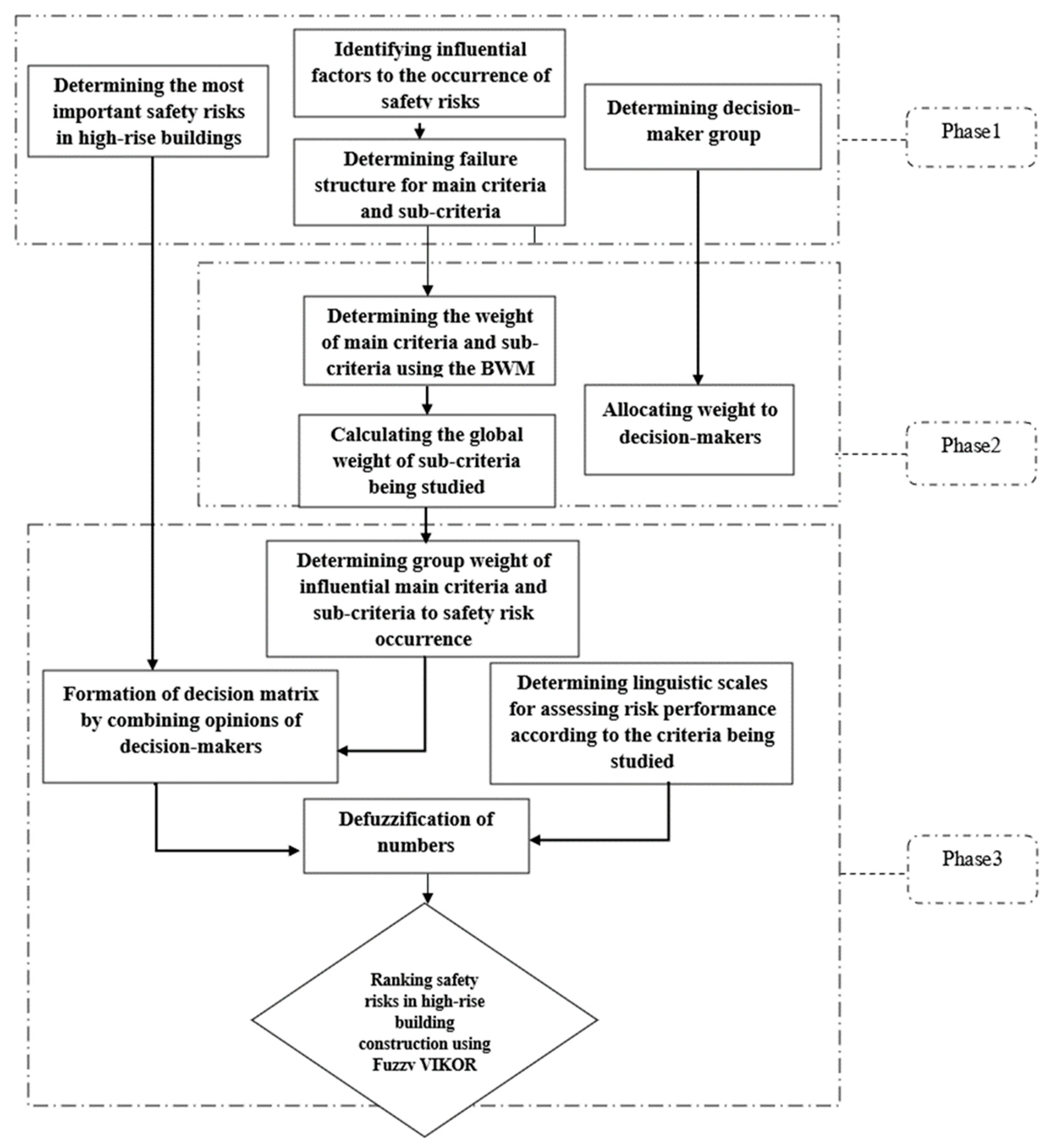
3. Materials and Methods
4. Case Study
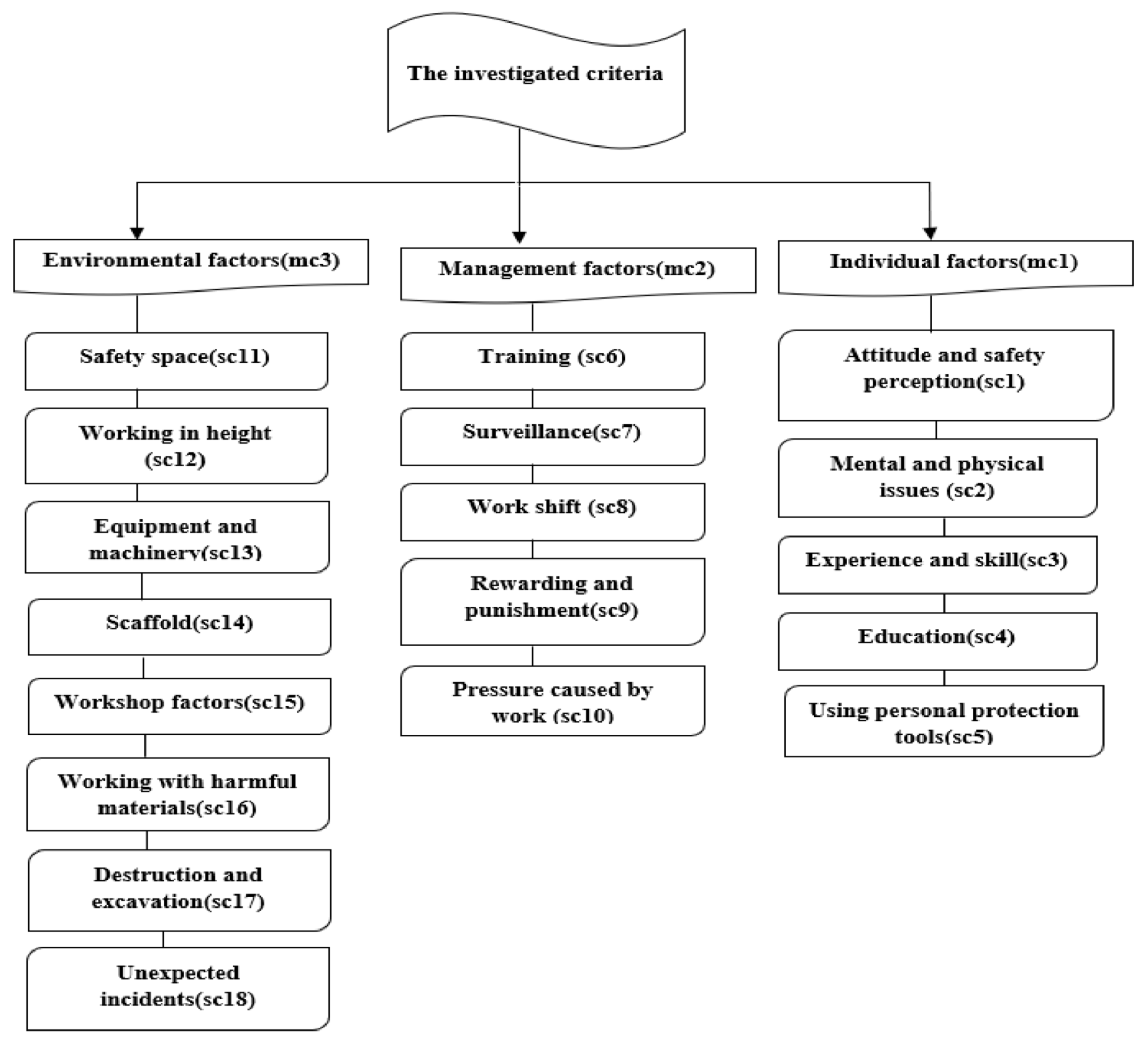
4.1. The Investigated Criteria
4.2. The Weight of the Investigated Criteria
4.3. The Decision Matrix Formation
4.4. Ranking the Options
5. The Sensitivity Analysis of the Results
Analysis and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Ning, Y.; Chen, W.T. Critical success factors for safety management of high-rise building construction projects in China. Adv. Civ. Eng. 2018, 2018, 1516354. [Google Scholar] [CrossRef]
- Li, Q.; Wang, S.; Zhang, Z.; Qian, H.; Pei, J. AHP_FCE-based high-rise building construction risk assessment. IOP Conf. Ser. Mater. Sci. Eng. 2020, 780, 072035. [Google Scholar] [CrossRef]
- Manzoor, B.; Othman, I.; Manzoor, M. Evaluating the critical safety factors causing accidents in high-rise building projects. Ain Shams Eng. J. 2021, 12, 2485–2492. [Google Scholar] [CrossRef]
- Ardeshir, A.; Maknoon, R.; Rekab Eslami Zadeh, M.; Jahantab, Z. Assessing the safety risks affecting the health of individuals in high-rise projects with a fuzzy approach. Occup. Health Iran 2014, 11, 82–95. [Google Scholar]
- Taylan, O.; Bafail, A.O.; Abdulaal, R.M.; Kabli, M.R. Construction projects selection and risk assessment by fuzzy AHP and fuzzy TOPSIS methodologies. Appl. Soft Comput. 2014, 17, 105–116. [Google Scholar] [CrossRef]
- Sofwan, N.M.; Zaini, A.A.; Mahayuddin, S.A. Preliminary study on the identification of safety risks factors in the high-rise building construction. J. Teknol. 2016, 78, 3–5. [Google Scholar] [CrossRef] [Green Version]
- Manzoor, B.; Othman, I.; Pomares, J.C.; Chong, H.Y. A Research Framework of Mitigating Construction Accidents in High-Rise Building Projects via Integrating Building Information Modeling with Emerging Digital Technologies. Appl. Sci. 2021, 11, 8359. [Google Scholar] [CrossRef]
- Debnath, J.; Animesh, B.; Preshobh, S.; Krishna, N.; Subhashis, S. Fuzzy inference model for assessing occupational risks in construction sites. Int. J. Ind. Ergon. 2016, 55, 114–128. [Google Scholar] [CrossRef]
- Sanni, M.S.A.; Mahmoud, A.S.; Hassanain, M.A.; Salami, B.A. A risk assessment approach for enhancing construction safety performance. Saf. Sci. 2020, 121, 15–29. [Google Scholar] [CrossRef]
- Hatefi, S.M.; Jolanta, T. An integrated fuzzy DEMATEL-fuzzy ANP model for evaluating construction projects by considering interrelationships among risk factors. J. Civ. Eng. Manag. 2019, 25, 114–131. [Google Scholar] [CrossRef] [Green Version]
- Aghaei, P.; Asadollahfardi, G.; Katabi, A. Safety risk assessment in shopping center construction projects using Fuzzy Fault Tree Analysis method. Qual. Quant. 2022, 56, 43–59. [Google Scholar] [CrossRef]
- Zaini, A.; Nurzawani, M.; Sofwan, D. Modelling risk factors and challenges with the implementation of risk management in high-rise building construction. Malays. Constr. Res. 2022, 32, 59–70. [Google Scholar]
- Murali, K.; Deraman, R. Analysis of Critical Management Factors for Managing Safety and Health of High-Rise Building Construction Projects. Recent Trends Civ. Eng. Built Environ. 2021, 2, 17–30. [Google Scholar] [CrossRef]
- Newaz, M.T.; Ershadi, M.; Jefferies, M.; Davis, P. Assessing safety management factors to develop a research agenda for the construction industry. Saf. Sci. 2021, 142, 105396. [Google Scholar] [CrossRef]
- Gholamnia, R.; Ebrahimian, M.; Gendeshmin, S.B.; Saeedi, R.; Firooznia, S. Effective factors on the occurrence of falling from height accidents in construction projects by using DEMATEL method. In Congress of the International Ergonomics Association; Springer: Cham, Switzerland, 2018; Volume 819, pp. 293–305. [Google Scholar]
- Mohammadi, A.; Tavakolan, M. Identifying safety archetypes of construction workers using system dynamics and content analysis. Saf. Sci. 2020, 129, 104831. [Google Scholar] [CrossRef]
- Martinez, J.G.; Gheisari, M.; Alarcón, L.F. UAV integration in current construction safety planning and monitoring processes: Case study of a high-rise building construction project in Chile. J. Manag. Eng. 2020, 36, 05020005. [Google Scholar] [CrossRef]
- Ardeshir, A.; Mohajeri, M. Assessment of safety culture among job positions in high-rise construction: A hybrid fuzzy multi criteria decision-making (FMCDM) approach. Int. J. Inj. Control. Saf. Promot. 2018, 25, 195–206. [Google Scholar] [CrossRef] [PubMed]
- Loosemore, M.; Malouf, N. Safety training and positive safety attitude formation in the Australian construction industry. Saf. Sci. 2019, 113, 233–243. [Google Scholar] [CrossRef]
- Alkaissy, M.; Arashpour, M.; Ashuri, B.; Bai, Y.; Hosseini, R. Safety management in construction: 20 years of risk modeling. Saf. Sci. 2020, 129, 104805. [Google Scholar] [CrossRef]
- Asilian-Mahabadi, H.; Khosravi, Y.; Hassanzadeh-Rangi, N.; Hajizadeh, E.; Behzadan, A.H. Factors affecting unsafe behavior in construction projects: Development and validation of a new questionnaire. Int. J. Occup. Saf. Ergon. 2018, 26, 219–226. [Google Scholar] [CrossRef]
- Cangan, G.S. Analysis of Construction Site Safety by using ANN and Fuzzy Logic. Int. J. Mod. Trends Sci. Technol. 2019, 2455–3778. Available online: http://www.ijmtst.com/vol5issue11.html (accessed on 11 November 2019).
- He, C.; McCabe, B.; Jia, G. Effect of leader-member exchange on construction worker safety behavior: Safety climate and psychological capital as the mediators. Saf. Sci. 2021, 142, 105401. [Google Scholar] [CrossRef]
- Wang, H.; Jieh-Haur, C.; Achmad, M.; Masoud, G. Exploring empirical rules for construction accident prevention based on unsafe behaviors. Sustainability 2022, 14, 4058. [Google Scholar] [CrossRef]
- Wong, T.K.M.; Man, S.S.; Chan, A.H. Critical factors for the use or non-use of personal protective equipment amongst construction workers. Saf. Sci. 2020, 126, 104663. [Google Scholar] [CrossRef]
- Bruno, L.T.; Low, C.T.; Idiake, J. Compliance with the use of personal protective equipment (PPE) on construction sites in Johor, Malaysia. Int. J. Real Estate Stud. 2020, 14, 123–138. [Google Scholar]
- Bussier, M.J.P.; Chong, H.Y. Relationship between safety measures and human error in the construction industry: Working at heights. Int. J. Occup. Saf. Ergon. 2022, 28, 162–173. [Google Scholar] [CrossRef]
- Kim, J.; Don, S.; Jin, D.; Gwang, H. Priority of accident cause based on tower crane type for the realization of sustainable management at Korean construction sites. Sustainability 2020, 13, 242. [Google Scholar] [CrossRef]
- Bedi, J.K.; Rahman, A.; Din, Z. Heavy Machinery Operators: Necessary Competencies to Reduce Construction Accidents. IOP Conf. Ser. Earth Environ. Sci. 2021, 641, 012007. [Google Scholar] [CrossRef]
- Ildarabadi, P.; Mehrdost, A.R.; Alamatian, J. A new solution for evaluating the conditions of high-rise buildings in Mashhad with HSE approach (Case study of construction projects). Ferdowsi Civ. Eng. 2020, 33, 21–38. [Google Scholar]
- Błazik, B.; Ewa, R.G.; Piotr, W. The probability of a scaffolding failure on a construction site. Eng. Fail. Anal. 2022, 131, 105864. [Google Scholar] [CrossRef]
- Koulinas, G.K.; Marhavilas, P.K.; Demesouka, O.E.; Vavatsikos, A.P.; Koulouriotis, D.E. Risk analysis and assessment in the worksites using the fuzzy-analytical hierarchy process and a quantitative technique–A case study for the Greek construction sector. Saf. Sci. 2019, 112, 96–104. [Google Scholar] [CrossRef]
- Ilbahar, E.; Karaşan, A.; Cebi, S.; Kahraman, C. A novel approach to risk assessment for occupational health and safety using Pythagorean fuzzy AHP & fuzzy inference system. Saf. Sci. 2018, 103, 124–136. [Google Scholar] [CrossRef]
- Ardeshir, A.; Maknoon, R.; Rekab Islami Zadeh, M.; Jahantab, Z. HSE risks assessment in urban high-rise construction using Fuzzy Approach. Health Saf. Work. 2015, 5, 1–12. [Google Scholar]
- Grill, M.; Nielsen, K. Promoting and impeding safety–A qualitative study into direct and indirect safety leadership practices of constructions site managers. Saf. Sci. 2019, 114, 148–159. [Google Scholar] [CrossRef]
- Cyma-Wejchenig, M.; Tarnas, J.; Marciniak, K.; Stemplewski, R. The influence of proprioceptive training with the use of virtual reality on postural stability of workers working at height. Sensors 2020, 20, 3731. [Google Scholar] [CrossRef] [PubMed]
- Mandal, S.; Singh, K.; Behera, R.K.; Sahu, S.K.; Raj, N.; Maiti, J. Human error identification and risk prioritization in overhead crane operations using HTA, SHERPA and fuzzy VIKOR method. Expert Syst. Appl. 2015, 42, 7195–7206. [Google Scholar] [CrossRef]
- Mohandes, S.R.; Durdyev, S.; Sadeghi, H.; Mahdiyar, A.; Hosseini, M.R.; Banihashemi, S.; Martek, I. Towards enhancement in reliability and safety of construction projects: Developing a hybrid multi-dimensional fuzzy-based approach. Eng. Constr. Archit. Manag. 2022. ahead-of-print. [Google Scholar] [CrossRef]
- Othman, I.; Majid, R.; Mohamad, H.; Shafiq, N.; Napiah, M. Variety of accident causes in construction industry. MATEC Web Conf. 2018, 203, 9. [Google Scholar] [CrossRef] [Green Version]
- Hoła, A.; Hoła, B.; Szóstak, M. Analysis of the causes and consequences of falls from scaffolding using the Polish construction industry as an example. IOP Conf. Ser. Mater. Sci. Eng. 2017, 251, 012050. [Google Scholar] [CrossRef]
- Rey-Merchán, M.D.C.; Gómez-de-Gabriel, J.M.; Fernández-Madrigal, J.A.; López-Arquillos, A. Improving the prevention of fall from height on construction sites through the combination of technologies. Int. J. Occup. Saf. Ergon. 2020, 28, 590–599. [Google Scholar] [CrossRef]
- Mohajeri, M.; Ardeshir, A.; Banki, M.T.; Malekitabar, H. Discovering causality patterns of unsafe behavior leading to fall hazards on construction sites. Int. J. Constr. Manag. 2020, 22, 3034–3044. [Google Scholar] [CrossRef]
- Yılmaz, F.; Ozcan, M.S. A Risk Analysis and Ranking Application for Lifting Vehicles Used in Construction Sites with Inte-grated AHP and Fine-Kinney Approach. Adv. Sci. Technol. Res. J. 2019, 13, 152–161. [Google Scholar] [CrossRef]
- Mohandes, S.R.; Sadeghi, H.; Mahdiyar, A.; Durdyev, S.; Banaitis, A.; Yahya, K.; Ismail, S. Assessing construction labours’ safety level: A fuzzy MCDM approach. J. Civ. Eng. Manag. 2020, 26, 175–188. [Google Scholar] [CrossRef] [Green Version]
- Chung, W.W.S.; Tariq, S.; Mohandes, S.R.; Zayed, T. IoT-based application for construction site safety monitoring. Int. J. Constr. Manag. 2020, 1–17. [Google Scholar] [CrossRef]
- Elsebaei, M.; Elnawawy, O.; Othman, A.A.E.; Badawy, M. Causes and impacts of site accidents in the Egyptian construction industry. Int. J. Constr. Manag. 2020, 22, 2659–2670. [Google Scholar] [CrossRef]
- Guo, S.; He, J.; Li, J.; Tang, B. Exploring the impact of unsafe behaviors on building construction accidents using a Bayesian network. Int. J. Environ. Res. Public Health 2020, 17, 221. [Google Scholar] [CrossRef] [PubMed]
- Opricovic, S. Fuzzy VIKOR with an application to water resources planning. Expert Syst. Appl. 2011, 38, 12983–12990. [Google Scholar] [CrossRef]
- Kaya, İ.; Cengiz, K. A comparison of fuzzy multicriteria decision making methods for intelligent building assessment. J. Civ. Eng. Manag. 2014, 20, 59–69. [Google Scholar] [CrossRef] [Green Version]
- Yeganeh, A.; Moein, Y.H.; Razavian, S.B.; Behzadian, K.; Shariatmadar, H. Applying a new systematic fuzzy FMEA technique for risk management in light steel frame systems. J. Asian Archit. Build. Eng. 2022, 21, 2481–2502. [Google Scholar] [CrossRef]
- Li, H.X.; Hussein, M.A.; Zhen, L.; Ziad, A. Risk identification and assessment of modular construction utilizing fuzzy analytic hierarchy process (AHP) and simulation. Can. J. Civ. Eng. 2013, 40, 1184–1195. [Google Scholar] [CrossRef]
- Kamranfar, S.; Azimi, Y.; Gheibi, M.; Amir, M.; Fathollahi, F.; Hajiaghaei, M.K. Analyzing green construction development barriers by a hybrid decision-making method based on DEMATEL and the ANP. Buildings 2022, 12, 1641. [Google Scholar] [CrossRef]
- Shahsavar, M.M.; Akrami, M.; Kian, Z.; Gheibi, M.; Amir, M.; Fathollahi, F.; Hajiaghaei, M.K.; Behzadian, K. Bio-recovery of municipal plastic waste management based on an integrated decision-making framework. J. Ind. Eng. Chem. 2022, 108, 215–234. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multicriteria decision-making method: Some properties and a linear model. Omega 2016, 64, 126–130. [Google Scholar] [CrossRef]
- Zeng, J.; An, M.; Smith, N.J. Application of a fuzzy based decision-making methodology to construction project risk assessment. Int. J. Proj. Manag. 2007, 25, 589–600. [Google Scholar] [CrossRef]
- Wu, Z.; Ahmad, J.; Xu, J. A group decision making framework based on fuzzy VIKOR approach for machine tool selection with linguistic information. Appl. Soft Comput. 2016, 42, 314–324. [Google Scholar] [CrossRef]
- Deng, H. Multicriteria analysis with fuzzy pairwise comparison. Int. J. Approx. Reason. 1999, 21, 215–231. [Google Scholar] [CrossRef]
| Reference | The Investigated Criteria | Ranking | Weight | The Method Used | Sub-Criteria | Research Field | ||
|---|---|---|---|---|---|---|---|---|
| Individual Factors | Management Factors | Environmental Factors | ||||||
| Present study | ✓ | ✓ | ✓ | ✓ | ✓ | BWM, and Fuzzy VIKOR | Safety attitude and perception, experience and skill, training, surveillance, …. | Weighting influential factors in safety risk occurrences and prioritizing these risks in high-rise construction buildings |
| [1] | ✓ | ✓ | semi-structured interviews and a questionnaire | Management measures, Management measures, safety environment worker safety quality | Critical Success Factors for Safety Management of High-Rise Building Construction Projects in China | |||
| [2] | ✓ | AHP, FCE | Safety signs, personal protection equipment, falling from a height, scaffold break down, working conditions, and personal factors | Identifying influential factors to safety accidents in high-rise projects | ||||
| [4] | ✓ | Interview, fuzzy numbers | Accident severity, effect, and probability of occurrence | Safety risk assessment and risk prioritization in high-rise building projects | ||||
| [5] | ✓ | ✓ | FAHP, TOPSIS | Time, cost, quality, safety | assess the overall risks of construction projects | |||
| [6] | ✓ | working environment, exposure to hazardous condition, work at high elevation, inadequate safety protection and temporary structures | Preliminary study on the identification of safety risks factors in the high-rise building construction | |||||
| [7] | Interview, NVivo 11 software, and zoom software | Integration of drone, RFID, GPS, and BIM for assessing safety accidents in high-rise building projects | ||||||
| [13] | ✓ | ✓ | Questionnaire | Safety education and training of workers, safety incentive or reward system, suitable supervision, safety environment | Analysis of Critical Management Factors for High Rise Building Construction Projects | |||
| [15] | ✓ | ✓ | ✓ | DEMATEL | Determining the most important factors in falling from a height | |||
| [17] | ✓ | Safety monitoring | safety planning and monitoring processes of a high-rise building construction project in Chile | |||||
| [18] | ✓ | ✓ | ✓ | ✓ | FTOPSIS, FDMATEL, FANP | Safety culture, safety attitude, monitoring, training | Assessment of safety culture among job positions in high-rise construction | |
| [21] | ✓ | Questionnaire | Safety motivations and prohibitions, safety attitudes and beliefs, client safety climate, contractor competency, safety supervision and management, safety behaviors, contract management, social climate, psychological unsafety | Factors affecting unsafe behavior in construction projects | ||||
| [22] | Fuzzy logic, ANN | HSE | identifying the causes for accidents and implementing solutions | |||||
| [26] | Questionnaire | Safety helmet, eye protectors, ear protectors, mark and respirator, protective gloves, safety belts, safety footwear, protective clothing | Using personal protective equipment in construction projects, Malaysia | |||||
| [28] | ✓ | Questionnaire | Psychological distress | the relationship between safety measures and human error with the objective of identifying the impact of psychological distress among workers working at heights within the construction industry | ||||
| [32] | ✓ | FAHP, PRAT | Accident risks physical risks environmental risks | Risk analysis and assessment in the Greek construction sector | ||||
| [33] | ✓ | ✓ | ✓ | Fuzzy Pythagoras, AHP, Fine Kinney | Risk occurrence probability, number of repetitions, risk severity | Health and occupational safety risk assessment in excavation process at a construction site | ||
| [34] | Checklist, Fuzzy AHP | Sanitation, safety, environmental risks | HSE risks in high-rise buildings in Tehran | |||||
| [35] | Interview | Direct management, indirect management | Qualitative study, safety leading methods in construction projects | |||||
| [36] | Excel software | Effect of training workers working at height by virtual reality | ||||||
| [37] | ✓ | Fuzzy FMEA, Fuzzy VIKOR | Risk occurrence, severity, and detection probability | Crane evaluation | ||||
| [38] | ✓ | ✓ | FAHP, TOPSIS | Probability, severity, exposure, detectability, worsening factor | Rating of safety risks in green high-rise construction | |||
| [39] | ✓ | ✓ | Fault of person, accidents, injury, ancestry and social environment | Investigating reasons behind accidents | ||||
| [40] | ✓ | ✓ | Pareto-Lorenz | Technical causes, organizational causes, and human causes | Investigating the reasons be-hind falling from a height | |||
| [41] | GPS, BIM, RFID, BLE | Monitoring approaches | Preventing individuals from falling from a height, using a monitoring system | |||||
| [42] | ✓ | Questionnaire | Demographic Cognitive Psychological | Causes of workers’ unsafe behaviors | ||||
| [43] | ✓ | ✓ | AHP | Risk analyses of lifting equipment | Elevator risks | |||
| [44] | ✓ | ✓ | FBWM, IVFTOPSIS | Severity and probability | Worker’s safety risks assessment | |||
| [45] | Questionnaire, AHP, IoT | Safety monitoring | Safety monitoring | |||||
| [46] | ✓ | ✓ | ✓ | Questionnaire, Microsoft Excel | Economic impact, social impact | Identifying reasons behind construction accidents in Egypt | ||
| Criteria Number | |||||||
|---|---|---|---|---|---|---|---|
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | Scale |
| 0.1667 | 0.1667 | 0.1667 | 0.1667 | 0.1667 | 0.1667 | 0.1667 | 3 |
| 0.2683 | 0.2577 | 0.2527 | 0.2206 | 0.1898 | 0.1529 | 0.1112 | 4 |
| 0.2960 | 0.2844 | 0.2716 | 0.2546 | 0.2306 | 0.1994 | 0.1354 | 5 |
| 0.3262 | 0.3221 | 0.3144 | 0.3044 | 0.2643 | 0.1990 | 0.1330 | 6 |
| 0.3403 | 0.3251 | 0.3144 | 0.3029 | 0.2819 | 0.2457 | 0.1294 | 7 |
| 0.3657 | 0.3620 | 0.3408 | 0.3154 | 0.2958 | 0.2521 | 0.1309 | 8 |
| 0.3662 | 0.3620 | 0.3517 | 0.3333 | 0.3062 | 0.2681 | 0.1359 | 9 |
| Participants Evaluation Criterion | Sub-Criterion | Participation Percentage |
|---|---|---|
| Education level | BSc | 20% |
| MSc | 50% | |
| PhD | 30% | |
| Work experience | 5 to 10 years | 20% |
| 10 to 20 years | 30% | |
| 20 years and over | 50% | |
| Organizational position | Senior manager | 20% |
| Intermediate manager | 20% | |
| Operational manager | 60% | |
| Which of the project stakeholder you are? | Customer | 10% |
| Contractor | 50% | |
| Consultant | 20% | |
| Project manager | 20% | |
| Major | Civil engineering | 40% |
| Architectural engineering | 30% | |
| Electrical equipment engineering | 10% | |
| Mechanical equipment engineering | 0% | |
| Industrial engineering | 0% | |
| Project management | 20% |
| Abbreviations | The Main Identified Risks |
|---|---|
| A1 | The severe damages caused by working with the manual tools |
| A2 | Excavations, buildings adjacent to excavations, and issues related to deep excavation |
| A3 | Fire |
| A4 | Electrocution |
| A5 | Falls from height (fall) |
| A6 | Damages caused by working with machinery and equipment |
| Preference of the Best Criterion over Others | ||||
|---|---|---|---|---|
| MC3 | MC2 | MC1 | Best Criterion | Decision Maker |
| 7 | 1 | 2 | MC2 | DM1 |
| 1 | 8 | 5 | MC3 | DM2 |
| 1 | 6 | 3 | MC3 | DM3 |
| 8 | 1 | 8 | MC2 | DM4 |
| 9 | 1 | 2 | MC2 | DM5 |
| 9 | 1 | 3 | MC2 | DM6 |
| 7 | 1 | 7 | MC2 | DM7 |
| 5 | 8 | 1 | MC1 | DM8 |
| 9 | 1 | 3 | MC2 | DM9 |
| 9 | 1 | 2 | MC2 | DM10 |
| Preference of Other Criteria over the Worst Criterion | ||||
| 8 | MC2 | MC1 | Worst Criterion | Decision-Maker |
| 1 | 9 | 2 | MC3 | DM1 |
| 5 | 2 | 1 | MC1 | DM2 |
| 8 | 1 | 2 | MC2 | DM3 |
| 1 | 5 | 2 | MC3 | DM4 |
| 1 | 9 | 2 | MC3 | DM5 |
| 1 | 9 | 3 | MC3 | DM6 |
| 3 | 5 | 1 | MC1 | DM7 |
| 3 | 1 | 3 | MC2 | DM8 |
| 1 | 7 | 2 | MC3 | DM9 |
| 1 | 9 | 2 | MC3 | DM10 |
| MC3 | MC2 | MC1 | threshold | Decision-Maker |
| 0.0000 | 0.0476 | 0.0714 | 0.1359 | DM1 |
| 0.0000 | 0.55 | 0.0000 | DM2 | |
| 0.0333 | 0.0000 | 0.0000 | DM3 | |
| 0.0000 | 0.0535 | 0.1428 | DM4 | |
| 0.0000 | 0.0000 | 0.0694 | DM5 | |
| 0.0000 | 0.0000 | 0.0000 | DM6 | |
| 0.3333 | 0.0476 | 0.0000 | DM7 | |
| 0.125 | 0.0000 | 0.0892 | DM8 | |
| 0.0000 | 0.0277 | 0.0555 | DM9 | |
| 0.0000 | 0.0000 | 0.0694 | DM10 | |
| Preference of the Best Criterion over Others | ||||||
|---|---|---|---|---|---|---|
| SC5 | SC4 | SC3 | SC2 | SC1 | Best Criterion | Decision Maker |
| 1 | 2 | 8 | 9 | 8 | SC5 | DM1 |
| 1 | 8 | 6 | 4 | 7 | SC5 | DM2 |
| 1 | 2 | 4 | 2 | 8 | SC5 | DM3 |
| 6 | 5 | 4 | 7 | 1 | SC1 | DM4 |
| 5 | 1 | 4 | 9 | 6 | SC4 | DM5 |
| 6 | 9 | 1 | 5 | 4 | SC3 | DM6 |
| 4 | 7 | 3 | 3 | 1 | CS1 | DM7 |
| 4 | 3 | 6 | 9 | 1 | SC1 | DM8 |
| 6 | 8 | 3 | 5 | 1 | CS1 | DM9 |
| 1 | 2 | 8 | 9 | 6 | CS5 | DM10 |
| Preference of Other Criteria over the Worst Criterion | ||||||
| SC5 | SC4 | SC3 | SC2 | SC1 | Worst Criterion | Decision Maker |
| 9 | 2 | 5 | 1 | 3 | CS2 | DM1 |
| 8 | 1 | 4 | 3 | 4 | SC4 | DM2 |
| 5 | 3 | 4 | 3 | 1 | SC1 | DM3 |
| 2 | 2 | 3 | 1 | 7 | SC2 | DM4 |
| 5 | 7 | 5 | 1 | 4 | SC2 | DM5 |
| 6 | 1 | 9 | 7 | 5 | SC4 | DM6 |
| 3 | 1 | 3 | 2 | 1 | SC4 | DM7 |
| 6 | 4 | 6 | 1 | 9 | SC2 | DM8 |
| 5 | 1 | 5 | 2 | 8 | SC4 | DM9 |
| 9 | 2 | 33 | 1 | 4 | SC2 | DM10 |
| SC5 | SC4 | SC3 | SC2 | SC1 | threshold | Decision Maker |
| 0.000 | 0.0892 | 0.4305 | 0.000 | 0.2083 | 0.3062 | DM1 |
| 0.000 | 0.000 | 0.2857 | 0.0714 | 0.3571 | DM2 | |
| 0.0535 | 0.0535 | 0.1428 | 0.0357 | 0.0000 | DM3 | |
| 0.119 | 0.0714 | 0.1190 | 0.000 | 0.000 | DM4 | |
| 0.222 | 0.0277 | 0.1527 | 0.0000 | 0.2083 | DM5 | |
| 0.375 | 0.000 | 0.0000 | 0.3611 | 0.1527 | DM6 | |
| 0.119 | 0.000 | 0.0476 | 0.142 | 0.142 | DM7 | |
| 0.2083 | 0.0416 | 0.375 | 0.0000 | 0.000 | DM8 | |
| 0.3928 | 0.000 | 0.125 | 0.0357 | 0.000 | DM9 | |
| 0.000 | 0.0694 | 0.2083 | 0.0000 | 0.2083 | DM10 | |
| Preference of the Best Criterion over Others | ||||||
|---|---|---|---|---|---|---|
| SC10 | SC9 | SC8 | SC7 | SC6 | Best Criterion | Decision Maker |
| 3 | 7 | 4 | 1 | 9 | SC7 | DM1 |
| 8 | 2 | 9 | 1 | 5 | SC7 | DM2 |
| 2 | 7 | 2 | 6 | 1 | SC6 | DM3 |
| 3 | 2 | 7 | 1 | 5 | SC7 | DM4 |
| 2 | 2 | 9 | 2 | 1 | SC6 | DM5 |
| 4 | 4 | 9 | 1 | 7 | SC7 | DM6 |
| 2 | 7 | 2 | 4 | 1 | CS6 | DM7 |
| 5 | 1 | 3 | 8 | 7 | SC9 | DM8 |
| 4 | 7 | 2 | 1 | 2 | CS7 | DM9 |
| 3 | 2 | 4 | 1 | 9 | CS7 | DM10 |
| Preference of Other Criteria over the Worst Criterion | ||||||
| SC10 | SC9 | SC8 | SC7 | SC6 | Worst Criterion | Decision Maker |
| 3 | 5 | 8 | 9 | 1 | CS6 | DM1 |
| 4 | 4 | 1 | 6 | 6 | SC8 | DM2 |
| 3 | 1 | 2 | 4 | 4 | SC9 | DM3 |
| 2 | 3 | 1 | 6 | 5 | SC8 | DM4 |
| 2 | 2 | 1 | 4 | 9 | SC8 | DM5 |
| 3 | 2 | 1 | 9 | 6 | SC8 | DM6 |
| 2 | 1 | 2 | 8 | 9 | SC9 | DM7 |
| 6 | 9 | 9 | 1 | 2 | SC7 | DM8 |
| 1 | 1 | 2 | 7 | 4 | SC9 | DM9 |
| 3 | 4 | 3 | 9 | 1 | SC6 | DM10 |
| SC10 | SC9 | SC8 | SC7 | SC6 | threshold | Decision Maker |
| 0.000 | 0.361 | 0.319 | 0.000 | 0.000 | 0.3062 | DM1 |
| 0.319 | 0.138 | 0.000 | 0.041 | 0.291 | DM2 | |
| 0.0238 | 0.000 | 0.0714 | 0.404 | 0.071 | DM3 | |
| 0.0238 | 0.0238 | 0.000 | 0.023 | 0.428 | DM4 | |
| 0.0694 | 0.0694 | 0.000 | 0.013 | 0.000 | DM5 | |
| 0.0416 | 0.138 | 0.0000 | 0.000 | 0.458 | DM6 | |
| 0.0714 | 0.000 | 0.0714 | 0.595 | 0.047 | DM7 | |
| 0.392 | 0.0178 | 0.339 | 0.0000 | 0.107 | DM8 | |
| 0.0714 | 0.000 | 0.0714 | 0.000 | 0.023 | DM9 | |
| 0.000 | 0.0138 | 0.0416 | 0.0000 | 0.000 | DM10 | |
| Preference of the Best Criterion over Others | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| SC18 | SC17 | SC16 | SC15 | SC14 | SC13 | SC12 | SC11 | Best Criterion | Decision Maker |
| 5 | 6 | 9 | 6 | 3 | 6 | 5 | 1 | SC11 | DM1 |
| 5 | 6 | 4 | 5 | 7 | 5 | 6 | 1 | SC11 | DM2 |
| 4 | 5 | 2 | 7 | 5 | 2 | 7 | 1 | SC13 | DM3 |
| 9 | 5 | 4 | 6 | 5 | 1 | 5 | 6 | SC13 | DM4 |
| 8 | 6 | 5 | 3 | 4 | 6 | 1 | 6 | SC12 | DM5 |
| 6 | 1 | 7 | 5 | 9 | 6 | 6 | 8 | SC17 | DM6 |
| 4 | 5 | 2 | 3 | 9 | 8 | 4 | 1 | CS11 | DM7 |
| 6 | 7 | 5 | 8 | 7 | 6 | 7 | 1 | SC11 | DM8 |
| 3 | 6 | 7 | 3 | 5 | 1 | 5 | 6 | CS13 | DM9 |
| 4 | 5 | 9 | 5 | 4 | 5 | 6 | 1 | CS11 | DM10 |
| Preference of Other Criteria over the Worst Criterion | |||||||||
| SC18 | SC17 | SC16 | SC15 | SC14 | SC13 | SC12 | SC11 | Worst Criterion | Decision Maker |
| 3 | 3 | 1 | 6 | 6 | 6 | 8 | 9 | CS16 | DM1 |
| 7 | 3 | 2 | 5 | 1 | 4 | 3 | 7 | SC14 | DM2 |
| 3 | 4 | 3 | 1 | 4 | 3 | 4 | 5 | SC15 | DM3 |
| 1 | 6 | 2 | 4 | 6 | 6 | 7 | 5 | SC18 | DM4 |
| 1 | 4 | 2 | 6 | 7 | 4 | 9 | 4 | SC18 | DM5 |
| 8 | 9 | 6 | 4 | 1 | 4 | 5 | 4 | SC14 | DM6 |
| 4 | 5 | 2 | 3 | 1 | 6 | 4 | 6 | SC14 | DM7 |
| 5 | 4 | 3 | 1 | 4 | 8 | 4 | 9 | SC15 | DM8 |
| 1 | 3 | 1 | 4 | 4 | 7 | 4 | 3 | SC16 | DM9 |
| 2 | 5 | 1 | 4 | 6 | 5 | 4 | 9 | SC16 | DM10 |
| SC18 | SC17 | SC16 | SC15 | SC14 | SC13 | SC12 | SC11 | threshold | Decision Maker |
| 0.0833 | 0.125 | 0.000 | 0.375 | 0.125 | 0.375 | 0.4305 | 0.000 | 0.3620 | DM1 |
| 0.6666 | 0.2619 | 0.0238 | 0.4285 | 0.000 | 0.3093 | 0.2619 | 0.000 | DM2 | |
| 0.119 | 0.3095 | 0.0238 | 0.000 | 0.3095 | 0.0238 | 0.5 | 0.0476 | DM3 | |
| 0.000 | 0.2916 | 0.0138 | 0.2083 | 0.2916 | 0.0416 | 0.3611 | 0.2916 | DM4 | |
| 0.000 | 0.2857 | 0.0357 | 0.1785 | 0.3571 | 0.2857 | 0.0178 | 0.2857 | DM5 | |
| 0.541 | 0.000 | 0.4583 | 0.1527 | 0.000 | 0.2083 | 0.2916 | 0.3194 | DM6 | |
| 0.0972 | 0.2222 | 0.0694 | 0.000 | 0.000 | 0.5416 | 0.0972 | 0.0416 | DM7 | |
| 0.3928 | 0.3571 | 0.125 | 0.000 | 0.3571 | 0.7142 | 0.3571 | 0.0178 | DM8 | |
| 0.0952 | 0.2619 | 0.000 | 0.119 | 0.3095 | 0.000 | 0.3095 | 0.2619 | DM9 | |
| 0.0138 | 0.2222 | 0.000 | 0.1527 | 0.2083 | 0.2222 | 0.2083 | 0.000 | DM10 | |
| Preference of the Best Criterion over Others | ||||
|---|---|---|---|---|
| MC3 | MC2 | MC1 | Best Criterion | Decision Maker |
| 7 | 1 | 2 | MC2 | DM1 |
| 1 | 3 | 5 | MC3 | DM2 |
| 1 | 6 | 3 | MC3 | DM3 |
| 8 | 1 | 4 | MC2 | DM4 |
| 9 | 1 | 2 | MC2 | DM5 |
| 9 | 1 | 3 | MC2 | DM6 |
| 2 | 1 | 7 | MC2 | DM7 |
| 5 | 8 | 1 | MC1 | DM8 |
| 9 | 1 | 3 | MC2 | DM9 |
| 9 | 1 | 2 | MC2 | DM10 |
| Preference of Other Criteria over the Worst Criterion | ||||
| MC3 | MC2 | MC1 | Worst Criterion | Decision Maker |
| 1 | 9 | 2 | MC3 | DM1 |
| 5 | 2 | 1 | MC1 | DM2 |
| 8 | 1 | 2 | MC2 | DM3 |
| 1 | 5 | 2 | MC3 | DM4 |
| 1 | 9 | 2 | MC3 | DM5 |
| 1 | 9 | 3 | MC3 | DM6 |
| 3 | 5 | 1 | MC1 | DM7 |
| 3 | 1 | 3 | MC2 | DM8 |
| 1 | 7 | 2 | MC3 | DM9 |
| 1 | 9 | 2 | MC3 | DM10 |
| MC3 | MC2 | MC1 | threshold | Decision Maker |
| 0.0000 | 0.0476 | 0.0714 | 0.1359 | DM1 |
| 0.0000 | 0.05 | 0.0000 | DM2 | |
| 0.0333 | 0.0000 | 0.0000 | DM3 | |
| 0.0000 | 0.0535 | 0.0357 | DM4 | |
| 0.0000 | 0.0000 | 0.0694 | DM5 | |
| 0.0000 | 0.0000 | 0.0000 | DM6 | |
| 0.0238 | 0.0476 | 0.0000 | DM7 | |
| 0.125 | 0.0000 | 0.0892 | DM8 | |
| 0.0000 | 0.0277 | 0.0555 | DM9 | |
| 0.0000 | 0.0000 | 0.0694 | DM10 | |
| Preference of the Best Criterion over Others | ||||||
|---|---|---|---|---|---|---|
| SC5 | SC4 | SC3 | SC2 | SC1 | Best Criterion | Decision Maker |
| 1 | 2 | 4 | 9 | 8 | SC5 | DM1 |
| 1 | 8 | 6 | 4 | 7 | SC5 | DM2 |
| 1 | 2 | 4 | 2 | 8 | SC5 | DM3 |
| 6 | 5 | 4 | 7 | 1 | SC1 | DM4 |
| 5 | 1 | 4 | 9 | 6 | SC4 | DM5 |
| 4 | 9 | 1 | 5 | 4 | SC3 | DM6 |
| 4 | 7 | 3 | 3 | 1 | CS1 | DM7 |
| 4 | 3 | 4 | 9 | 1 | SC1 | DM8 |
| 6 | 8 | 3 | 5 | 1 | CS1 | DM9 |
| 1 | 2 | 8 | 9 | 6 | CS5 | DM10 |
| Preference of Other Criteria over the Worst Criterion | ||||||
| SC5 | SC4 | SC3 | SC2 | SC1 | Worst Criterion | Decision Maker |
| 9 | 2 | 5 | 1 | 3 | CS2 | DM1 |
| 8 | 1 | 4 | 3 | 2 | SC4 | DM2 |
| 5 | 3 | 4 | 3 | 1 | SC1 | DM3 |
| 2 | 2 | 3 | 1 | 7 | SC2 | DM4 |
| 5 | 7 | 5 | 1 | 4 | SC2 | DM5 |
| 6 | 1 | 9 | 2 | 5 | SC4 | DM6 |
| 3 | 1 | 3 | 2 | 1 | SC4 | DM7 |
| 6 | 4 | 6 | 1 | 9 | SC2 | DM8 |
| 3 | 1 | 5 | 2 | 8 | SC4 | DM9 |
| 9 | 2 | 33 | 1 | 4 | SC2 | DM10 |
| SC5 | SC4 | SC3 | SC2 | SC1 | threshold | Decision Maker |
| 0.000 | 0.0892 | 0.1527 | 0.000 | 0.2083 | 0.3062 | DM1 |
| 0.000 | 0.000 | 0.2857 | 0.0714 | 0.1071 | DM2 | |
| 0.0535 | 0.0535 | 0.1428 | 0.0357 | 0.0000 | DM3 | |
| 0.119 | 0.0714 | 0.1190 | 0.000 | 0.000 | DM4 | |
| 0.222 | 0.0277 | 0.1527 | 0.0000 | 0.2083 | DM5 | |
| 0.2083 | 0.000 | 0.0000 | 0.0138 | 0.1527 | DM6 | |
| 0.119 | 0.000 | 0.0476 | 0.142 | 0.142 | DM7 | |
| 0.2083 | 0.0416 | 0.208 | 0.0000 | 0.000 | DM8 | |
| 0.1785 | 0.000 | 0.125 | 0.0357 | 0.000 | DM9 | |
| 0.000 | 0.0694 | 0.2083 | 0.0000 | 0.2083 | DM10 | |
| Preference of the Best Criterion over Others | ||||||
|---|---|---|---|---|---|---|
| SC10 | SC9 | SC8 | SC7 | SC6 | Best Criterion | Decision Maker |
| 3 | 3 | 4 | 1 | 9 | SC7 | DM1 |
| 2 | 2 | 9 | 1 | 5 | SC7 | DM2 |
| 2 | 7 | 2 | 3 | 1 | SC6 | DM3 |
| 3 | 2 | 7 | 1 | 3 | SC7 | DM4 |
| 2 | 2 | 9 | 2 | 1 | SC6 | DM5 |
| 4 | 4 | 9 | 1 | 7 | SC7 | DM6 |
| 2 | 7 | 2 | 2 | 1 | CS6 | DM7 |
| 5 | 1 | 3 | 8 | 7 | SC9 | DM8 |
| 4 | 7 | 2 | 1 | 2 | CS7 | DM9 |
| 3 | 2 | 4 | 1 | 9 | CS7 | DM10 |
| Preference of Other Criteria over the Worst Criterion | ||||||
| SC10 | SC9 | SC8 | SC7 | SC6 | Worst Criterion | Decision Maker |
| 3 | 5 | 3 | 9 | 1 | CS6 | DM1 |
| 4 | 4 | 1 | 6 | 6 | SC8 | DM2 |
| 3 | 1 | 2 | 4 | 4 | SC9 | DM3 |
| 2 | 3 | 1 | 6 | 5 | SC8 | DM4 |
| 2 | 2 | 1 | 4 | 9 | SC8 | DM5 |
| 3 | 2 | 1 | 9 | 4 | SC8 | DM6 |
| 2 | 1 | 2 | 8 | 9 | SC9 | DM7 |
| 3 | 9 | 3 | 1 | 2 | SC7 | DM8 |
| 1 | 1 | 2 | 7 | 4 | SC9 | DM9 |
| 3 | 4 | 3 | 9 | 1 | SC6 | DM10 |
| SC10 | SC9 | SC8 | SC7 | SC6 | threshold | Decision Maker |
| 0.000 | 0.0833 | 0.0416 | 0.000 | 0.000 | 0.3062 | DM1 |
| 0.0138 | 0.138 | 0.000 | 0.041 | 0.291 | DM2 | |
| 0.0238 | 0.000 | 0.0714 | 0.119 | 0.071 | DM3 | |
| 0.0238 | 0.0238 | 0.000 | 0.023 | 0.190 | DM4 | |
| 0.0694 | 0.0694 | 0.000 | 0.013 | 0.000 | DM5 | |
| 0.0416 | 0.138 | 0.0000 | 0.000 | 0.263 | DM6 | |
| 0.0714 | 0.000 | 0.0714 | 0.214 | 0.047 | DM7 | |
| 0.125 | 0.0178 | 0.0178 | 0.0000 | 0.107 | DM8 | |
| 0.0714 | 0.000 | 0.0714 | 0.000 | 0.023 | DM9 | |
| 0.000 | 0.0138 | 0.0416 | 0.0000 | 0.000 | DM10 | |
| Preference of the Best Criterion over Others | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| SC18 | SC17 | SC16 | SC15 | SC14 | SC13 | SC12 | SC11 | Best Criterion | Decision Maker |
| 5 | 6 | 9 | 5 | 3 | 6 | 5 | 1 | SC11 | DM1 |
| 5 | 6 | 4 | 5 | 7 | 5 | 6 | 1 | SC11 | DM2 |
| 4 | 5 | 2 | 7 | 5 | 2 | 4 | 1 | SC13 | DM3 |
| 9 | 5 | 4 | 6 | 5 | 1 | 5 | 6 | SC13 | DM4 |
| 8 | 6 | 5 | 3 | 4 | 6 | 1 | 6 | SC12 | DM5 |
| 6 | 1 | 7 | 5 | 9 | 6 | 6 | 8 | SC17 | DM6 |
| 4 | 5 | 2 | 3 | 9 | 8 | 4 | 1 | CS11 | DM7 |
| 6 | 7 | 5 | 8 | 7 | 6 | 7 | 1 | SC11 | DM8 |
| 3 | 6 | 7 | 3 | 5 | 1 | 5 | 6 | CS13 | DM9 |
| 4 | 5 | 9 | 5 | 4 | 5 | 6 | 1 | CS11 | DM10 |
| Preference of Other Criteria over the Worst Criterion | |||||||||
| SC18 | SC17 | SC16 | SC15 | SC14 | SC13 | SC12 | SC11 | Worst Criterion | Decision Maker |
| 3 | 3 | 1 | 6 | 6 | 3 | 4 | 9 | CS16 | DM1 |
| 2 | 3 | 2 | 3 | 1 | 4 | 3 | 7 | SC14 | DM2 |
| 3 | 4 | 3 | 1 | 4 | 3 | 4 | 5 | SC15 | DM3 |
| 1 | 6 | 2 | 4 | 6 | 6 | 7 | 5 | SC18 | DM4 |
| 1 | 4 | 2 | 6 | 7 | 4 | 9 | 4 | SC18 | DM5 |
| 3 | 9 | 3 | 4 | 1 | 4 | 5 | 4 | SC14 | DM6 |
| 4 | 5 | 2 | 3 | 1 | 4 | 4 | 6 | SC14 | DM7 |
| 3 | 4 | 3 | 1 | 4 | 4 | 4 | 9 | SC15 | DM8 |
| 1 | 3 | 1 | 4 | 4 | 7 | 4 | 3 | SC16 | DM9 |
| 2 | 5 | 1 | 4 | 6 | 5 | 4 | 9 | SC16 | DM10 |
| SC18 | SC17 | SC16 | SC15 | SC14 | SC13 | SC12 | SC11 | threshold | Decision Maker |
| 0.0833 | 0.125 | 0.000 | 0.2916 | 0.125 | 0.125 | 0.1527 | 0.000 | 0.3620 | DM1 |
| 0.0714 | 0.2619 | 0.0238 | 0.1904 | 0.000 | 0.3093 | 0.2619 | 0.000 | DM2 | |
| 0.119 | 0.3095 | 0.0238 | 0.000 | 0.3095 | 0.0238 | 0.2142 | 0.0476 | DM3 | |
| 0.000 | 0.2916 | 0.0138 | 0.2083 | 0.2916 | 0.0416 | 0.3611 | 0.2916 | DM4 | |
| 0.000 | 0.2857 | 0.0357 | 0.1785 | 0.3571 | 0.2857 | 0.0178 | 0.2857 | DM5 | |
| 0.125 | 0.000 | 0.1666 | 0.1527 | 0.000 | 0.2083 | 0.2916 | 0.3194 | DM6 | |
| 0.0972 | 0.2222 | 0.0694 | 0.000 | 0.000 | 0.3194 | 0.0972 | 0.0416 | DM7 | |
| 0.1785 | 0.3571 | 0.125 | 0.000 | 0.3571 | 0.2857 | 0.3571 | 0.0178 | DM8 | |
| 0.0952 | 0.2619 | 0.000 | 0.119 | 0.3095 | 0.000 | 0.3095 | 0.2619 | DM9 | |
| 0.0138 | 0.2222 | 0.000 | 0.1527 | 0.2083 | 0.2222 | 0.2083 | 0.000 | DM10 | |
| Main Criteria | ||||||||
|---|---|---|---|---|---|---|---|---|
| MC3 | MC2 | MC1 | ||||||
| 0.2822 | 0.4384 | 0.2794 | Group average | |||||
| Sub-criteria CS1 to CS5 | ||||||||
| SC5 | SC4 | SC3 | SC2 | SC1 | ||||
| 0.2899 | 0.1017 | 0.2170 | 0.0878 | 0.3036 | Group average | |||
| Sub-criteria CS6 to CS10 | ||||||||
| SC10 | SC9 | SC8 | SC7 | SC6 | ||||
| 0.0646 | 0.049 | 0.0670 | 0.4005 | 0.4189 | Group average | |||
| Sub-criteria CS11 to CS18 | ||||||||
| SC18 | SC17 | SC16 | SC15 | SC14 | SC13 | SC12 | SC11 | |
| 0.0870 | 0.1144 | 0.0807 | 0.1002 | 0.1139 | 0.1372 | 0.1423 | 0.2243 | Group average |
| Rank | Global Weights | Local Weights | Sub-Criteria | Main Criteria Weights | Main Criteria |
|---|---|---|---|---|---|
| 3 | 0.0848 | 0.3036 | SC1 | 0.2794 | MC1 |
| 16 | 0.0245 | 0.0878 | SC2 | ||
| 6 | 0.0606 | 0.2170 | SC3 | ||
| 12 | 0.0284 | 0.1017 | SC4 | ||
| 4 | 0.0810 | 0.2899 | SC5 | ||
| 1 | 0.1836 | 0.4189 | SC6 | 0.4384 | MC2 |
| 2 | 0.1755 | 0.4005 | SC7 | ||
| 11 | 0.0293 | 0.0670 | SC8 | ||
| 18 | 0.0214 | .0490 | SC9 | ||
| 13 | 0.0283 | 0.0646 | SC10 | ||
| 5 | 0.0633 | 0.2243 | SC11 | 0.2822 | MC3 |
| 7 | 0.0401 | 0.1423 | SC12 | ||
| 8 | 0.0387 | 0.1372 | SC13 | ||
| 10 | 0.0321 | 0.1139 | SC14 | ||
| 14 | 0.0282 | 0.1002 | SC15 | ||
| 17 | 0.0228 | 0.0807 | SC16 | ||
| 9 | 0.0323 | 0.1144 | SC17 | ||
| 15 | 0.0245 | 0.0870 | SC18 |
| TFN | Abbreviation | Linguistic Variable |
|---|---|---|
| (0.9, 1, 1) | VG | Very Good |
| (0.7, 0.9, 1) | G | Good |
| (0.5, 0.7, 0.9) | MG | Medium Good |
| (0.3, 0.5, 0.7) | F | Fair |
| (0.1, 0.3, 0.5) | MP | Medium Poor |
| (0, 0.1, 0.3) | P | Poor |
| (0, 0, 0.1) | VP | Very Poor |
| SC18(-) | SC16(-) | SC15(-) | SC14(-) | SC13(-) | SC12(-) | SC11(+) | SC10(-) | SC9(+) | SC8(-) | SC7(+) | SC6(+) | SC5(+) | SC4(+) | SC3(+) | SC2(-) | SC1(+) | Criteria |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.02455 | 0.0228 | 0.02827 | 0.0321 | 0.0387 | 0.0401 | 0.0633 | 0.02832 | 0.0214 | 0.0293 | 0.1755 | 0.1836 | 0.081 | 0.0284 | 0.0606 | 0.02453 | 0.0848 | Weights Alternatives |
| (0.433, 0.633, 0.5) | (0, 0.066, 0.233) | (0.433, 0.633, 0.833) | (0.9, 1, 1) | (0.3, 0.5, 0.7) | (0.9, 1, 1) | (0.3, 0.5, 0.7) | (0.433, 0.633, 0.5) | (0.033, 0.166, 0.366) | (0.233, 0.433, 0.633) | (0.633, 0.5, 0.9) | (0.1, 0.2, 0.366) | (0.7, 0.866, 0.966) | (0, 0.1, 0.3) | (0.633, 0.8, 0.9) | (0.13, 0.3, 0.5) | (0.333, 0.5, 0.666) | A1 |
| (0.566, 0.766, 0.933) | (0, 0, 0.1) | (0.3, 0.5, 0.7) | (0.1, 0.3, 0.5) | (0.9, 1, 1) | (0.066, 0.233, 0.433) | (0.3, 0.5, 0.7) | (0.1, 0.3, 0.5) | (0, 0.1, 0.3) | (0.1, 0.3, 0.5) | (0.7, 0.9, 1) | (0.7, 0.9, 1) | (0, 0, 0.1) | (0.1, 0.3, 0.5) | (0.566, 0.766, 0.933) | (0, 0.1, 0.3) | (0.633, 0.833, 0.966) | A2 |
| (0.1, 0.3, 0.5) | (0.1, 0.3, 0.5) | (0.433, 0.633, 0.833) | (0, 0, 0.1) | (0.1, 0.3, 0.5) | (0, 0, 0.1) | (0.1, 0.3, 0.5) | (0.233, 0.433, 0.633) | (0.1, 0.3, 0.5) | (0.033, 0.166, 0.366) | (0.233, 0.433, 0.633) | (0.133, 0.266, 0.433) | (0.13, 0.3, 0.5) | (0, 0.1, 0.3) | (0.366, 0.566, 0.766) | (0.13, 0.3, 0.5) | (0.266, 0.433, 0.366) | A3 |
| (0.033, 0.133, 0.3) | (0, 0, 0.1) | (0.3, 0.5, 0.7) | (0, 0, 0.1) | (0, 0.033, 0.166) | (0.366, 0.566, 0.766) | (0.1, 0.3, 0.5) | (0.233, 0.433, 0.633) | (0, 0, 0.1) | (0.1, 0.3, 0.5) | (0.166, 0.366, 0.566) | (0.366, 0.566, 0.766) | (0.7, 0.9, 1) | (0, 0.1, 0.3) | (0.3, 0.5, 0.7) | (0.033, 0.166, 0.366) | (0.7, 0.9, 1) | A4 |
| (0, 0, 0.1) | (0, 0.033, 0.166) | (0.166, 0.366, 0.566) | (0.166, 0.366, 0.566) | (0.566, 0.733, 0.866) | (0.7, 0.9, 1) | (0.5, 0.7, 0.9) | (0.766, 0.933, 1) | (0.1, 0.3, 0.5) | (0.3, 0.5, 0.7) | (0.766, 0.933, 1) | (0.766, 0.933, 1) | (0.766, 0.933, 1) | (0, 0.1, 0.3) | (0.766, 0.933, 1) | (0.3, 0.5, 0.7) | (0.766, 0.933, 1) | A5 |
| (0.1, 0.3, 0.5) | (0, 0.1, 0.3) | (0.1, 0.3, 0.5) | (0.1, 0.3, 0.5) | (0.9, 1, 1) | (0.233, 0.433, 0.633) | (0.5, 0.7, 0.9) | (0.5, 0.7, 0.866) | (0, 0.1, 0.3) | (0.5, 0.7, 0.866) | (0.633, 0.833, 0.966) | (0.633, 0.833, 0.966) | (0.1, 0.3, 0.5) | (0.5, 0.7, 0.9) | (0.7, 0.866, 0.966) | (0.1, 0.3, 0.5) | (0.1, 0.3, 0.5) | A6 |
| Decision Matrix for Illustrative Example | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SC18(-) | SC17(-) | SC16(-) | SC15(-) | SC14(-) | SC13(-) | SC12(-) | SC11(+) | SC10(-) | SC9(+) | SC8(-) | SC7(+) | SC6(+) | SC5(+) | SC4(+) | SC3(+) | SC2(-) | SC1(+) | Criteria | |
| 0.02455 | 0.0323 | 0.0228 | 0.02827 | 0.0321 | 0.0387 | 0.0401 | 0.0633 | 0.02832 | 0.0214 | 0.0293 | 0.1755 | 0.1836 | 0.081 | 0.0284 | 0.0606 | 0.02453 | 0.0848 | Weights Criteria | |
| (0, 0, 0.1) | (0, 0.1, 0.3) | (0, 0, 0.1) | (0.1, 0.3, 0.5) | (0, 0, 0.1) | (0, 0.033, 0.166) | (0, 0, 0.1) | (0.5, 0.7, 0.9) | (0.1, 0.3, 0.5) | (0.1, 0.3, 0.5) | (0.033, 0.166, 0.366) | (0.766, 0.933, 1) | (0.766, 0.933, 1) | (0.766, 0.933, 1) | (0.5, 0.7, 0.9) | (0.766, 0.933, 1) | (0, 0.1, 0.3) | (0.766, 0.933, 1) | F+ | |
| (0.566, 0.766, 0.933) | (0.9, 1, 1) | (0.1, 0.3, 0.5) | (0.433, 0.633, 0.833) | (0.9, 1, 1) | (0.9, 1, 1) | (0.9, 1, 1) | (0.1, 0.3, 0.5) | (0.766, 0.933, 1) | (0, 0, 0.1) | (0.5, 0.7, 0.866) | (0.166, 0.366, 0.566) | (0.1, 0.2, 0.366) | (0, 0, 0.1) | (0, 0.1, 0.3) | (0.3, 0.5, 0.7) | (0.3, 0.5, 0.7) | (0.1, 0.3, 0.5) | F- | |
| (0.356, 0.678, 0.535) | (0, 0.4, 0.7) | (−0.2, 0.132, 0.466) | (−0.091, 0.454, 1) | (0.8, 1, 1) | (0.134, 0.467, 0.7) | (0.8, 1, 1) | (−0.25, 0.25, 0.75) | (−0.074, 0.37, 0.44) | (−0.532, 0.268, 0.934) | (−0.159, 0.320, 0.720) | (−0.16, 0.519, 0.44) | (0.444, 0.814, 1) | (−0.2, 0.067, 0.3) | (0.222, 0.666, 1) | (−0.191, 0.19, 0.524) | (−0.242, 0.285, 0.714) | (0.111, 0.481, 0.741) | A1 | |
| (0.499, 0.821, 1) | (0.6, 0.9, 1) | (−0.2, 0, 0.2) | (−0.272, 0.272, 0.818) | (0, 0.3, 0.5) | (0.734, 0.967, 1) | (−0.034, 0.233, 0.433) | (−0.25, 0.25, 0.75) | (−0.444, 0, 0.444) | (−0.4, 0.4, 1) | (−0.319, 0.16, 0.56) | (−0.28, 0.039, 0.359) | (−0.26, 0.036, 0.333) | (0.666, 0.933, 1) | (0, 0.444, 0.888) | (−0.238, 0.238, 0.62) | (−0.428, 0, 0.428) | (−0.222, 0.111, 0.407) | A2 | |
| (0, 0.321, 0.535) | (0.2, 0.6, 0.866) | (0, 0.6, 1) | (−0.091, 0.454, 1) | (−0.1, 0, 0.1) | (−0.066, 0.267, 0.5) | (−0.1, 0, 0.1) | (0, 0.5, 1) | (−0.296, 0.147, 0.592) | (−0.8, 0, 0.8) | (−0.399, 0, 0.399) | (0.159, 0.599, 0.919) | (0.37, 0.741, 0.963) | (0.266, 0.633, 0.87) | (0.222, 0.666, 1) | (0, 0.524, 0.905) | (−0.242, 0.285, 0.714) | (0.444, 0.555, 0.815) | A3 | |
| (−0.071, 0.142, 0.321) | (−0.267, 0.033, 0.3) | (−0.2, 0, 0.2) | (−0.272, 0.272, 0.818) | (−0.1, 0, 0.1) | (−0.166, 0, 0.166) | (0.266, 0.566, 0.766) | (0, 0.5, 1) | (−0.296, 0.147, 0.592) | (0, 0.6, 1) | (−0.319, 0.16, 0.56) | (0.239, 0.679, 1) | (0, 0.407, 0.704) | (−0.234, 0.033, 0.3) | (0.222, 0.666, 1) | (0.094, 0.618, 0.1) | (−0.381, 0.094, 0.522) | (−0.26, 0.036, 0.333) | A4 | |
| (−0.107, 0, 0.107) | (−0.3, 0, 0.3) | (−0.2, 0.066, 0.332) | (−0.455, 0.09, 0.635) | (0.066, 0.366, 0.566) | (0.4, 0.7, 0.866) | (0.6, 0.9, 0.1) | (−0.5, 0, 0.5) | (0.295, 0.703, 1) | (−0.8, 0, 0.8) | (−0.079, 0.4, 0.8) | (−0.28, 0, 0.28) | (−0.26, 0, 0.26) | (−0.234, 0, 0.234) | (0.222, 0.666, 1) | (−0.334, 0, 0.334) | (0, 0.571, 0.1) | (−0.26, 0, 0.26) | A5 | |
| (0, 0.321, 0.535) | (0.4, 0.8, 0.1) | (−0.2, 0.2, 0.6) | (−0.545, 0, 0.545) | (0, 0.3, 0.5) | (0.734, 0.967, 1) | (0.133, 0.433, 0.633) | (−0.5, 0, 0.5) | (0, 0.444, 0.851) | (−0.4, 0.4, 1) | (0.16, 0.641, 1) | (−0.239, 0.119, 0.44) | (−0.222, 0.111, 0.407) | (0.266, 0.633, 0.9) | (−0.444,0,0.444) | (−0.285, 0.095, 0.428) | (−0.285, 0.285, 0.714) | (0.295, 0.703, 1) | A6 | |
| (0.008, 0.016, 0.013) | (0, 0.012, 0.022) | (−0.004, 0.003, 0.01) | (−0.002, 0.012, 0.028) | (0.025, 0.032, 0.032) | (0.005, 0.018, 0.027) | (0.032, 0.04, 0.04) | (−0.015, 0.015, 0.047) | (−0.002, 0.01, 0.012) | (−0.011, 0.005, 0.019) | (−0.004, 0.009, 0.021) | (−0.028, 0.091, 0.077) | (0.081, 0.149, 0.183) | (−0.016, 0.005, 0.024) | (0.006, 0.018, 0.028) | (−0.011, 0.011, 0.031) | (−0.005, 0.006, 0.017) | (0.009, 0.04, 0.06) | A1 | |
| (0.012, 0.02, 0.024) | (0.019, 0.029, 0.032) | (−0.004, 0, 0.004) | (−0.007, 0.007, 0.023) | (0, 0.009, 0.016) | (0.028, 0.037, 0.038) | (−0.001, 0.009, 0.017) | (−0.015, 0.015, 0.047) | (−0.012, 0, 0.012) | (−0.008, 0.008, 0.021) | (−0.009, 0.004, 0.016) | (−0.042, 0.021, 0.077) | (−0.047, 0.006, 0.061) | (0.053, 0.075, 0.081) | (0, 0.012, 0.025) | (−0.014, 0.014, 0.037) | (−0.01, 0, 0.01) | (−0.018, 0.009, 0.034) | A2 | |
| (0, 0.007, 0.013) | (0.006, 0.019, 0.027) | (0, 0.013, 0.022) | (−0.002, 0.012, 0.028) | (−0.003, 0, 0.003) | (−0.002, 0.01, 0.019) | (−0.004, 0, 0.004) | (0, 0.031, 0.063) | (−0.008, 0.004, 0.016) | (−0.017, 0, 0.017) | (−0.011, 0, 0.011) | (0.027, 0.104, 0.161) | (0.067, 0.136, 0.176) | (0.021, 0.051, 0.07) | (0.006, 0.018, 0.028) | (0, 0.031, 0.054) | (−0.005, 0.006, 0.017) | (0.037, 0.047, 0.069) | A3 | |
| (−0.001, 0.003, 0.007) | (−0.008, 0.001, 0.009) | (−0.004, 0, 0.004) | (−0.007, 0.007, 0.023) | (−0.003, 0, 0.003) | (−0.006, 0, 0.006) | (0.01, 0.022, 0.03) | (0, 0.031, 0.063) | (−0.008, 0.004, 0.016) | (0, 0.012, 0.021) | (−0.009, 0.004, 0.016) | (0.041, 0.119, 0.175) | (0, 0.074, 0.129) | (−0.018, 0.002, 0.024) | (0.006, 0.018, 0.028) | (0.005, 0.037, 0.06) | (−0.009, 0.002, 0.012) | (−0.022, 0.003, 0.028) | A4 | |
| (−0.002, 0, 0.002) | (−0.009, 0, 0.009) | (−0.004, 0.001, 0.007) | (−0.012, 0.002, 0.017) | (0.002, 0.011, 0.018) | (0.015, 0.027, 0.033) | (0.024, 0.036, 0.04) | (−0.031, 0, 0.031) | (0.008, 0.019, 0.028) | (−0.017, 0, 0.017) | (−0.002, 0.011, 0.023) | (−0.049, 0.006, 0.063) | (−0.047, 0, 0.047) | (−0.018, 0, 0.018) | (0.006, 0.018, 0.028) | (−0.02, 0, 0.02) | (0, 0.014, 0.024) | (−0.022, 0, 0.022) | A5 | |
| (0, 0.007, 0.013) | (0.012, 0.025, 0.032) | (−0.004, 0.004, 0.013) | (−0.015, 0, 0.015) | (0, 0.009, 0.016) | (0.028, 0.037, 0.038) | (0.005, 0.017, 0.025) | (−0.031, 0, 0.031) | (0, 0.012, 0.024) | (−0.008, 0.008, 0.021) | (0.004, 0.081, 0.029) | (−0.049, 0, 0.049) | (−0.04, 0.02, 0.074) | (0.021, 0.051, 0.072) | (−0.012, 0, 0.012) | (−0.017, 0.005, 0.025) | (−0.006, 0.006, 0.017) | (0.025, 0.059, 0.084) | A6 | |
| A1 | (0.068, 0.492, 0.691) | (0.081, 0.149, 0.183) | (−0.209, 0.243, 0.571) |
| A2 | (−0.082, 0.254, 0.563) | (0.666, 0.933, 1) | (0.551, 0.51, 0.917) |
| A3 | (0.112, 0.489, 0.798) | (0.067, 0.136, 0.176) | (−0.191, 0.235, 0628) |
| A4 | (−0.033, 0.339, 0.654) | (0.041, 0.119, 0.175) | (−0.279, 0.141, 546) |
| A5 | (−0.171, 0.165, 0.474) | (0.024, 0.036, 0.04) | (−0.374, 0, 0.374) |
| A6 | (−0.087, 0.342, 0.591) | (0.025, 0.059, 0.084) | (−0.223, 0.112, 0.463) |
| (−0.087, 0.342, 0.591) | |||
| (0.024, 0.036, 0.04) | |||
| −0.087 | 0.024 | ||
| 0.798 | 0.183 |
| Rankings (with Respect to) | Parameters | Alternatives | ||||
|---|---|---|---|---|---|---|
| 6 | 6 | 5 | 0.4127 | 0.1405 | 0.4357 | A1 |
| 3 | 3 | 2 | 0.088 | 0.071 | 0.2472 | A2 |
| 5 | 5 | 6 | 0.395 | 0.1287 | 0.472 | A3 |
| 4 | 4 | 4 | 0.266 | 0.1135 | 0.3247 | A4 |
| 1 | 1 | 1 | −0.028 | 0.034 | 0.1582 | A5 |
| 2 | 2 | 3 | 0.084 | 0.0567 | 0.297 | A6 |
| Changes V | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 4 | 5 | 4 | 3 | 3 | 3 | 3 | 3 | 4 | 4 |
| A2 | 5 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 3 | 5 |
| A3 | 3 | 4 | 5 | 4 | 4 | 4 | 4 | 4 | 5 | 2 |
| A4 | 6 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 3 |
| A5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| A6 | 2 | 3 | 3 | 5 | 5 | 5 | 5 | 5 | 6 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ansari, R.; Dehghani, P.; Mahdikhani, M.; Jeong, J. A Novel Safety Risk Assessment Based on Fuzzy Set Theory and Decision Methods in High-Rise Buildings. Buildings 2022, 12, 2126. https://doi.org/10.3390/buildings12122126
Ansari R, Dehghani P, Mahdikhani M, Jeong J. A Novel Safety Risk Assessment Based on Fuzzy Set Theory and Decision Methods in High-Rise Buildings. Buildings. 2022; 12(12):2126. https://doi.org/10.3390/buildings12122126
Chicago/Turabian StyleAnsari, Ramin, Parisa Dehghani, Mahdi Mahdikhani, and Jaewook Jeong. 2022. "A Novel Safety Risk Assessment Based on Fuzzy Set Theory and Decision Methods in High-Rise Buildings" Buildings 12, no. 12: 2126. https://doi.org/10.3390/buildings12122126
APA StyleAnsari, R., Dehghani, P., Mahdikhani, M., & Jeong, J. (2022). A Novel Safety Risk Assessment Based on Fuzzy Set Theory and Decision Methods in High-Rise Buildings. Buildings, 12(12), 2126. https://doi.org/10.3390/buildings12122126










