Research on Vibration Control of Power Transmission Lines-TMDI Based on Colliding Bodies Optimization
Abstract
:1. Introduction
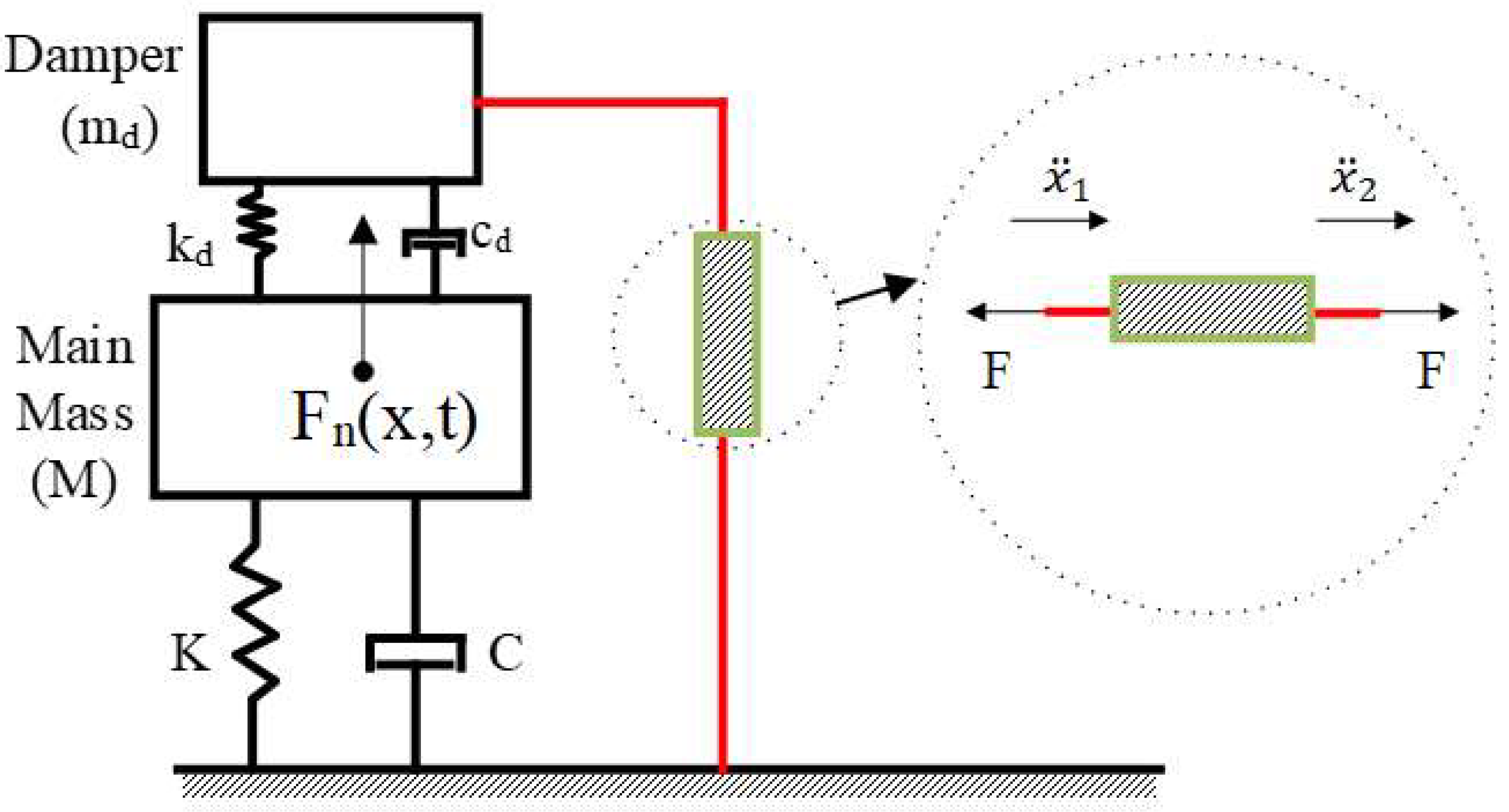
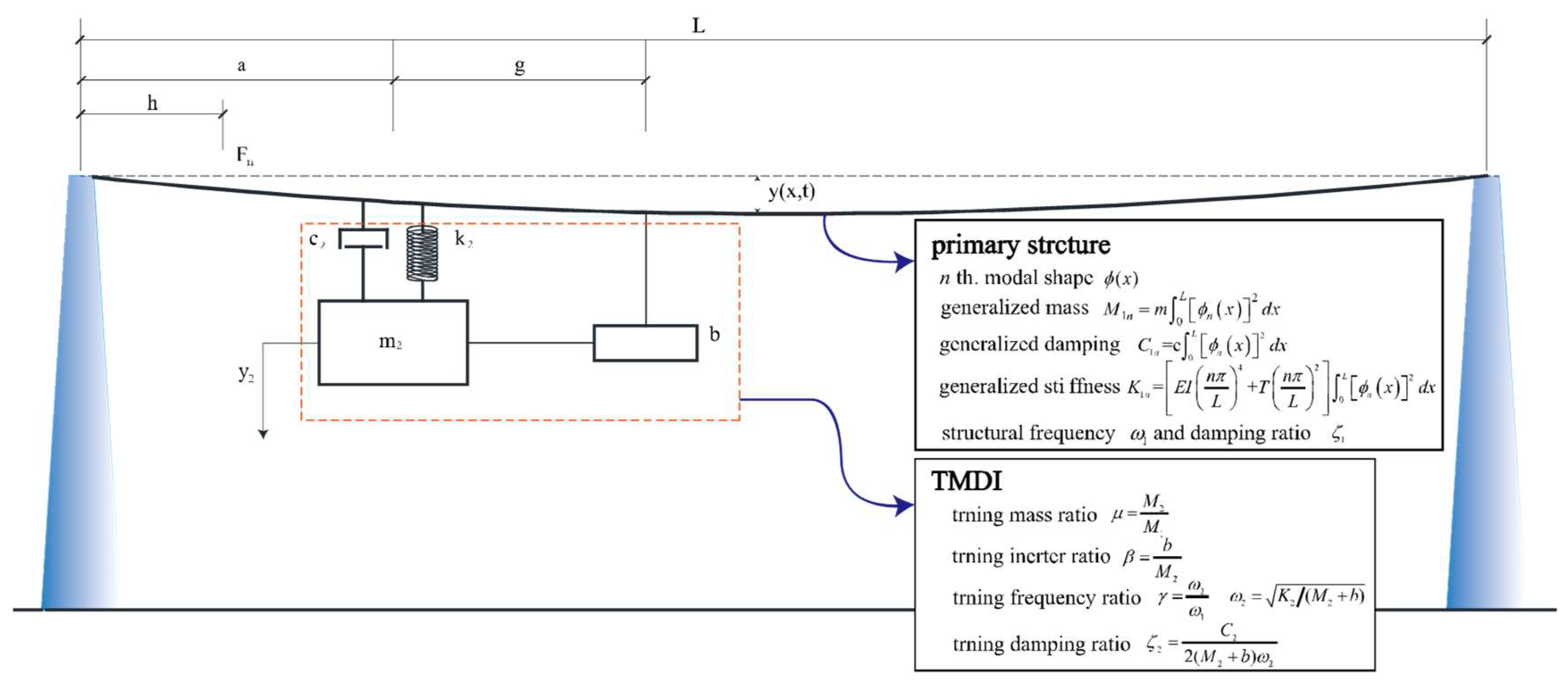
2. Control Equations for Combined Transmission of the Wire-TMDI Systems
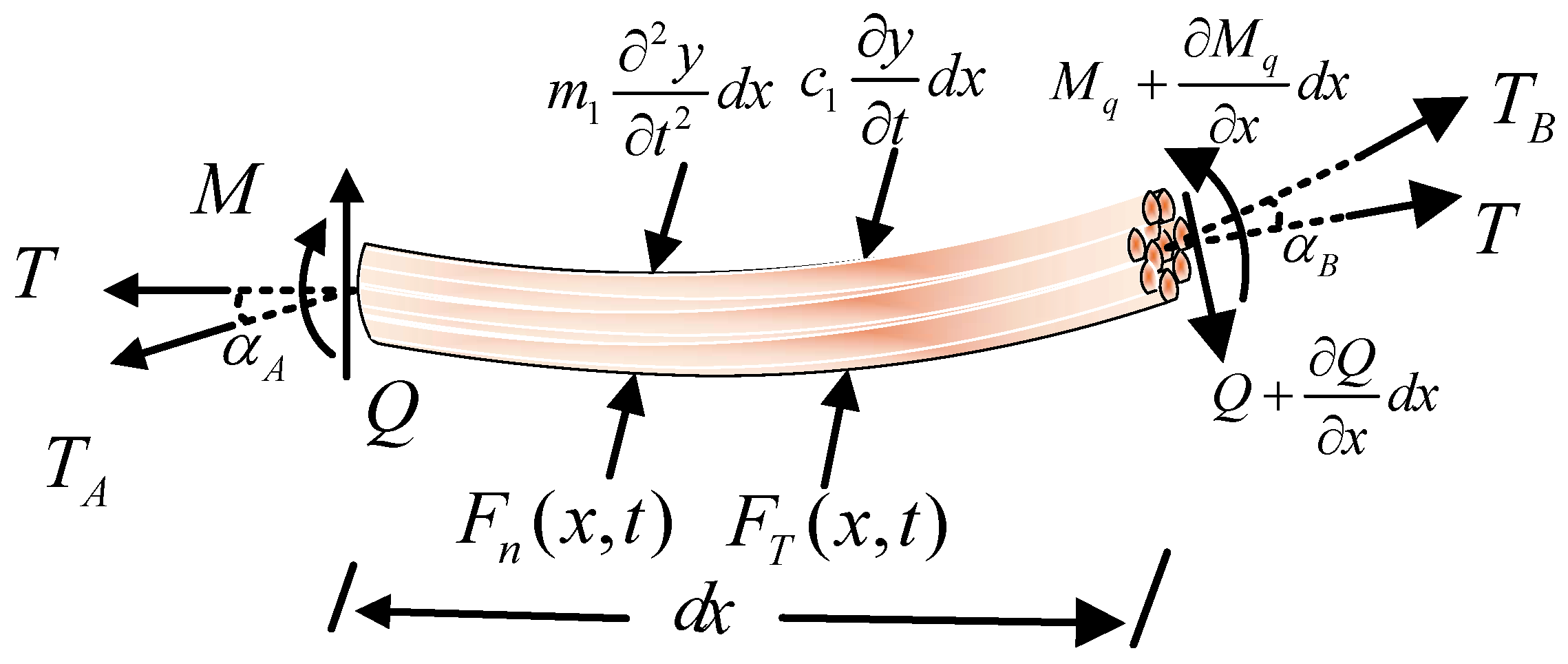
2.1. Movement in the PLANE of Transmission Wire
2.2. Approximate Series Solution of the Equations of Motion
3. Solution Method Based on CBO
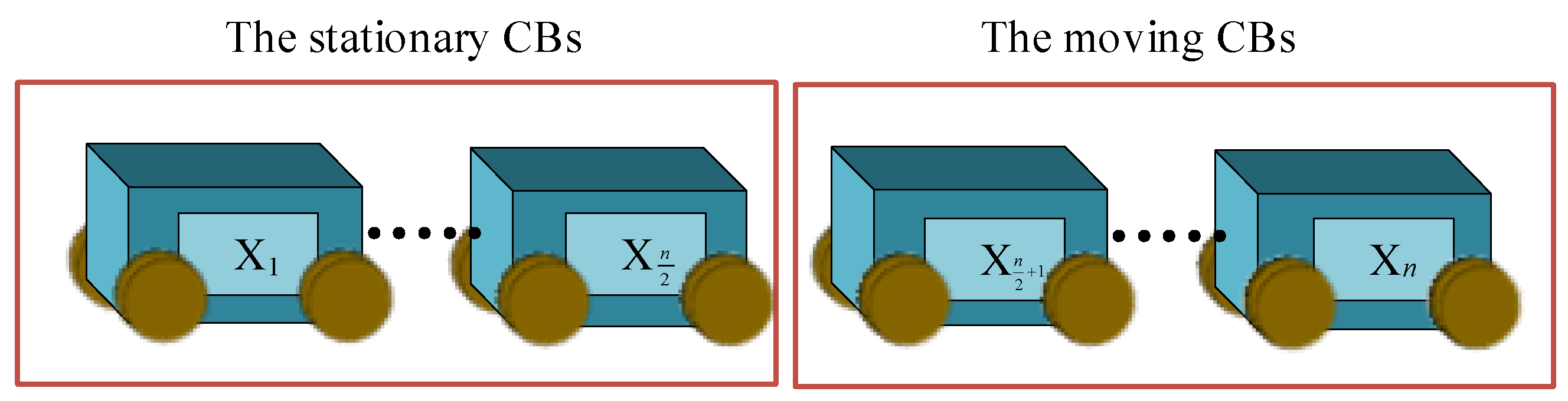
3.1. The Optimization Process of CBO
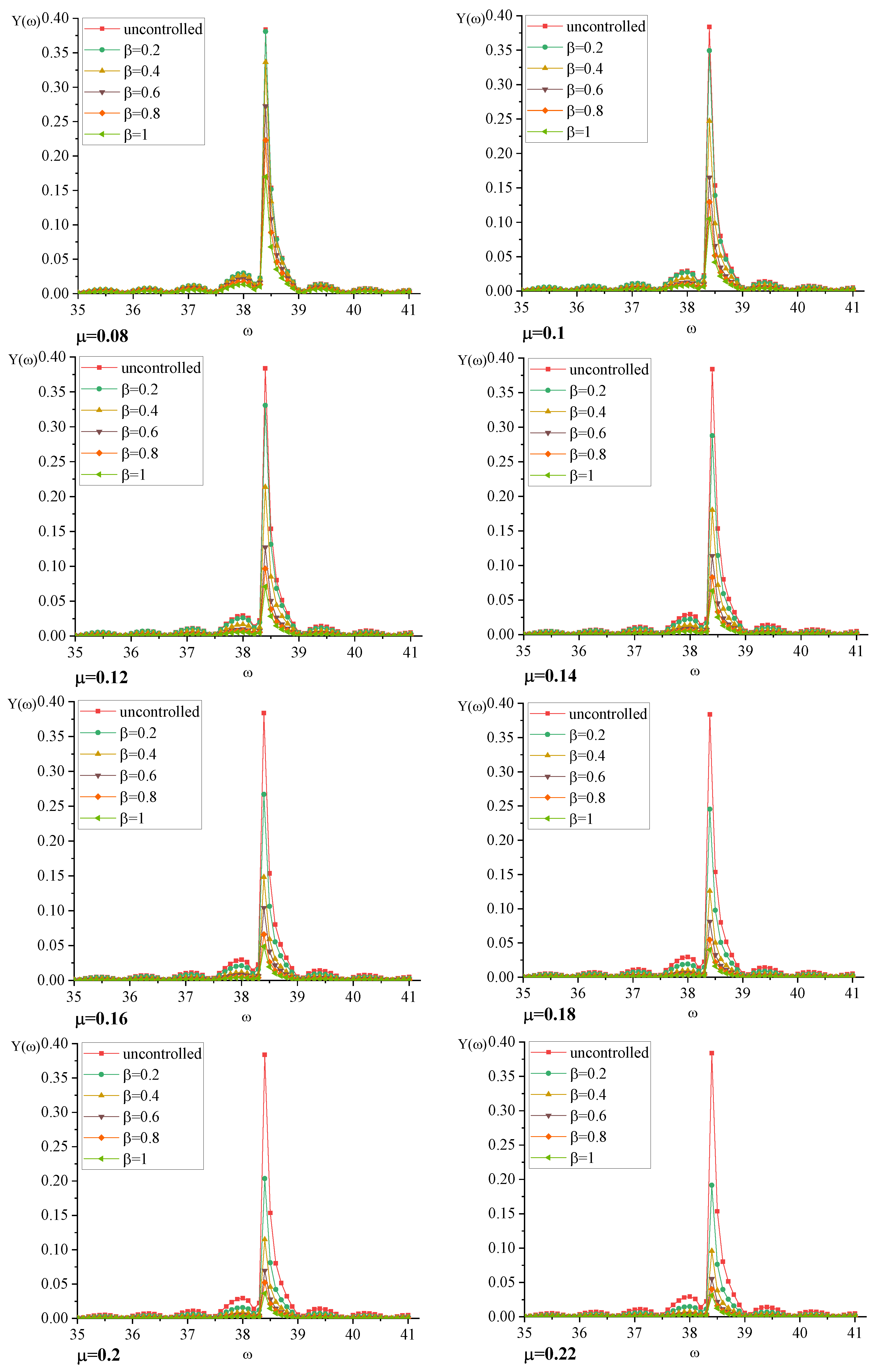
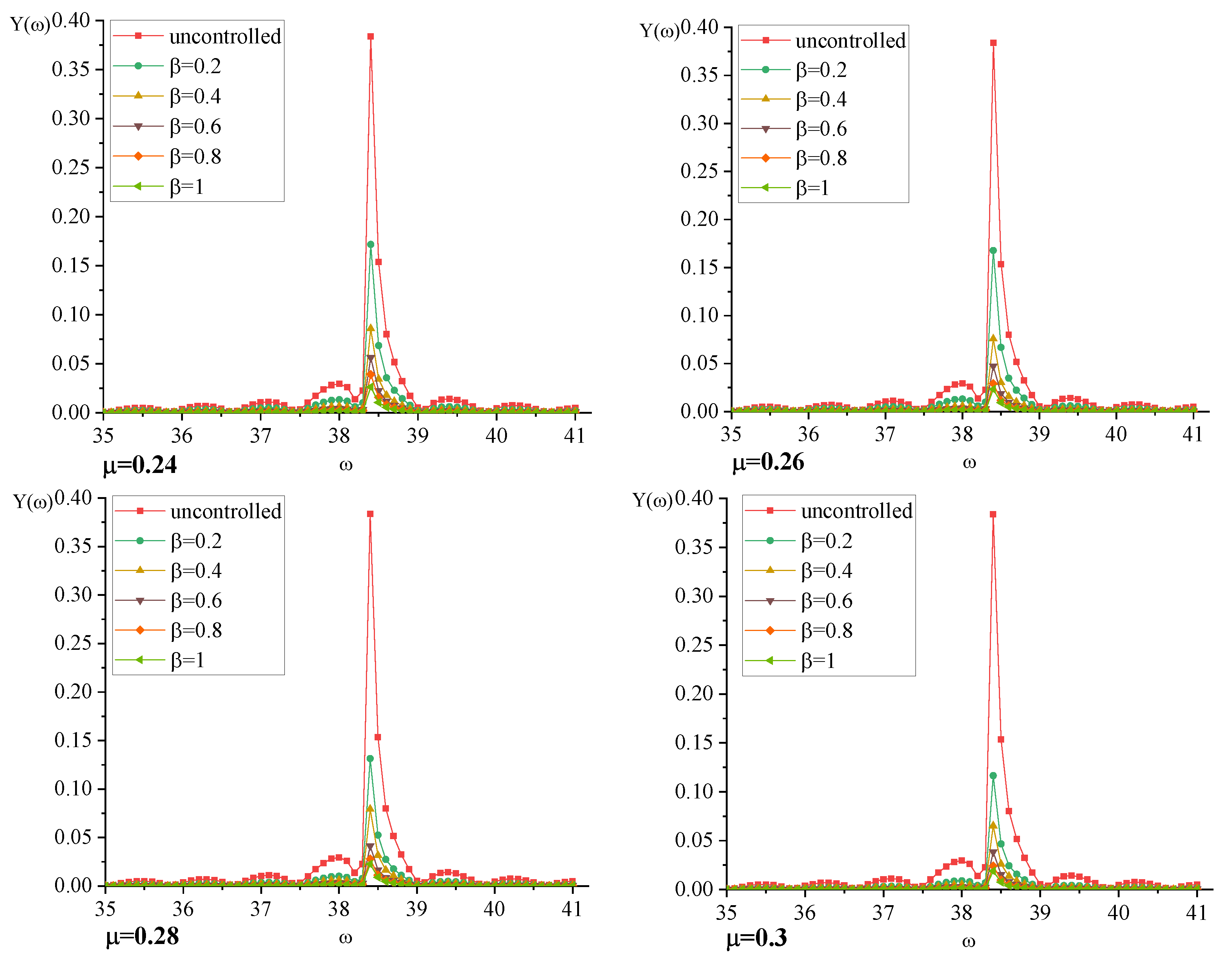
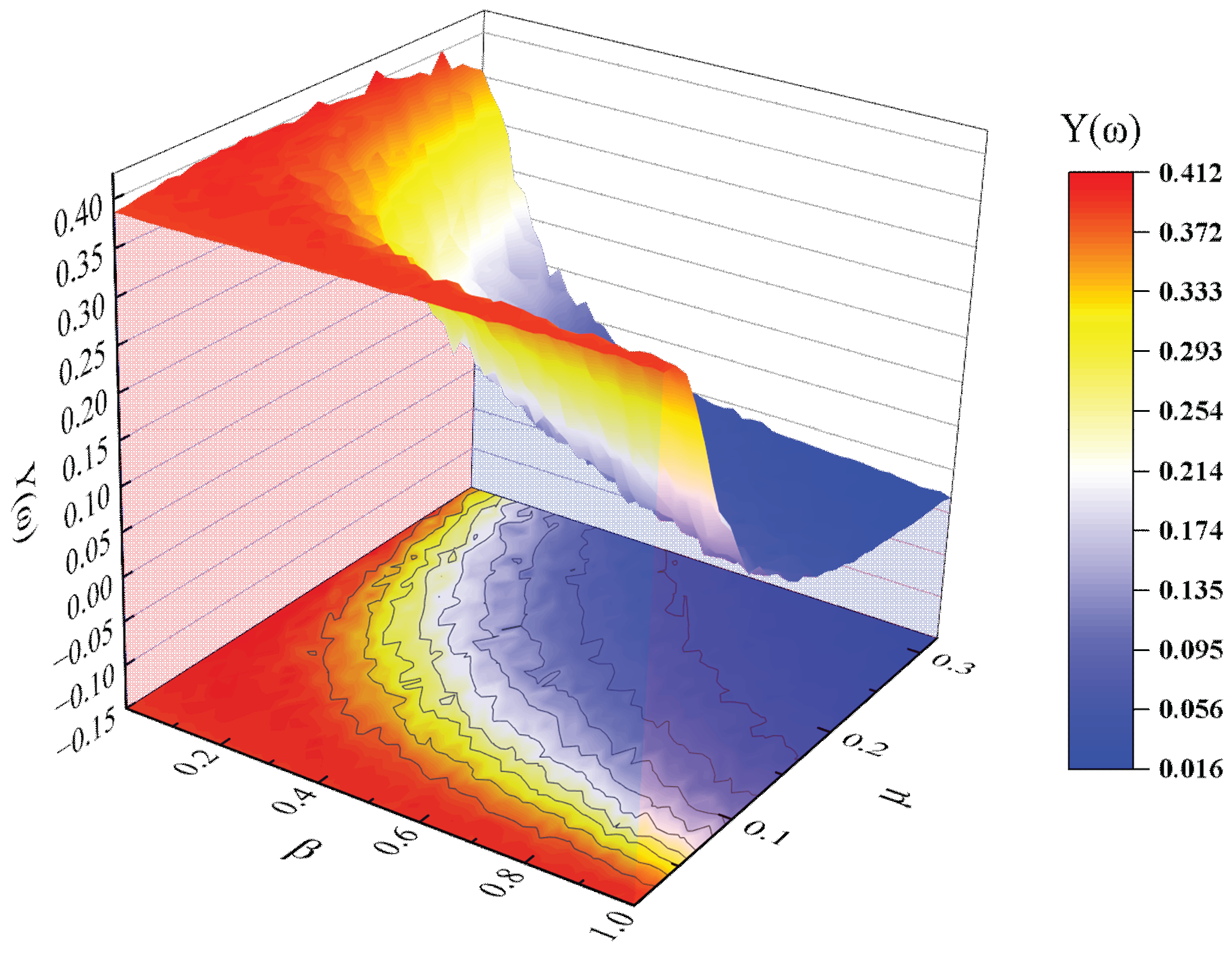
3.2. Numerical Analysis
3.3. TMDI Validity Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deyi, K. Research of Transmission Line Aeolian Vibration Based on Dynamic Method. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2009. [Google Scholar]
- Housner, G.W.; Bergman, L.A.; Caughey, T.K.; Chassiakos, A.G.; Claus, R.O.; Masri, S.F.; Skelton, R.E.; Soong, T.T.; Spencer, B.F.; Yao JT, P. Structural control: Past, present, and future. J. Eng. Mech. 1997, 123, 897–971. [Google Scholar] [CrossRef]
- Yao, J.T.P. Concept of structural control. J. Struct. Div. 1972, 98, 1567–1574. [Google Scholar] [CrossRef]
- Jinping, O. Structure Vibration Control; Science Press: Beijing, China, 2003. [Google Scholar]
- Crewe, A. Passive energy dissipation systems in structural engineering. Struct. Saf. 1998, 20, 197–198. [Google Scholar] [CrossRef]
- Feldmann, D. Aeolian vibrations: Possible effects of nonlinear behaviour of Stockbridge dampers. In Proceedings of the International Conference on Overhead Line Design & Construction: Theory & Practice, London, UK, 28–30 November 1988. [Google Scholar]
- Hou, J.; Wu, X.; Sun, Z. Research and progress of breeze vibration of anti-vibration hammer-transmission line system. J. Hefei Univ. Technol. (Nat. Sci. Ed.) 2011, 34, 743–747. [Google Scholar]
- Zhang, H. Examples of overhead transmission line breeze vibration hazards and the importance of field vibration measurement. Electr. Constr. 1997, 8, 4. [Google Scholar]
- Zhang, M.; Wu, T.; Øiseth, O. Vortex-induced vibration control of a flexible circular cylinder using a nonlinear energy sink. Wind. Eng. Ind. Aerodyn. 2022, 229, 105163. [Google Scholar] [CrossRef]
- Frahm, H. Device for Damping Vibrations of Bodies. U.S. Patent 9,899,58A, 18 April 1911. [Google Scholar]
- Huang, B.; Tang, J.X. Wind vibration control of self-supporting high-voltage transmission towers with large spans. Spec. Struct. 1997, 3, 49–52. [Google Scholar]
- Hu, S. Research on Wind Vibration Response and Vibration Control of Large-Span Transmission Lines. Ph.D. Thesis, Tongji University, Shanghai, China, 1999. [Google Scholar]
- Deng, H.; Zhu, S.; Chen, Y.; Wang, Z. Research on wind vibration control of large span transmission tower system. J. Build. Struct. 2003, 24, 60–64. [Google Scholar]
- Qu, C. Application of bidirectional TMD in the study of wind vibration control of transmission lines. Hydropower Energy Sci. 2012, 30, 195–199. [Google Scholar]
- Bisegna, P.; Caruso, G. Closed-form formulas for the optimal pole-based design of tuned mass dampers. J. Sound Vib. 2012, 331, 2291–2314. [Google Scholar] [CrossRef]
- Greco, R.; Marano, G.C. Optimum design of tuned mass dampers by displacement and energy perspectives. Soil Dyn. Earthq. Eng. 2013, 49, 243–253. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, F. Tuned mass damper for self-excited vibration control: Optimization involving nonlinear aeroelastic effect. J. Wind. Eng. Ind. Aerodyn. 2022, 220, 104836. [Google Scholar] [CrossRef]
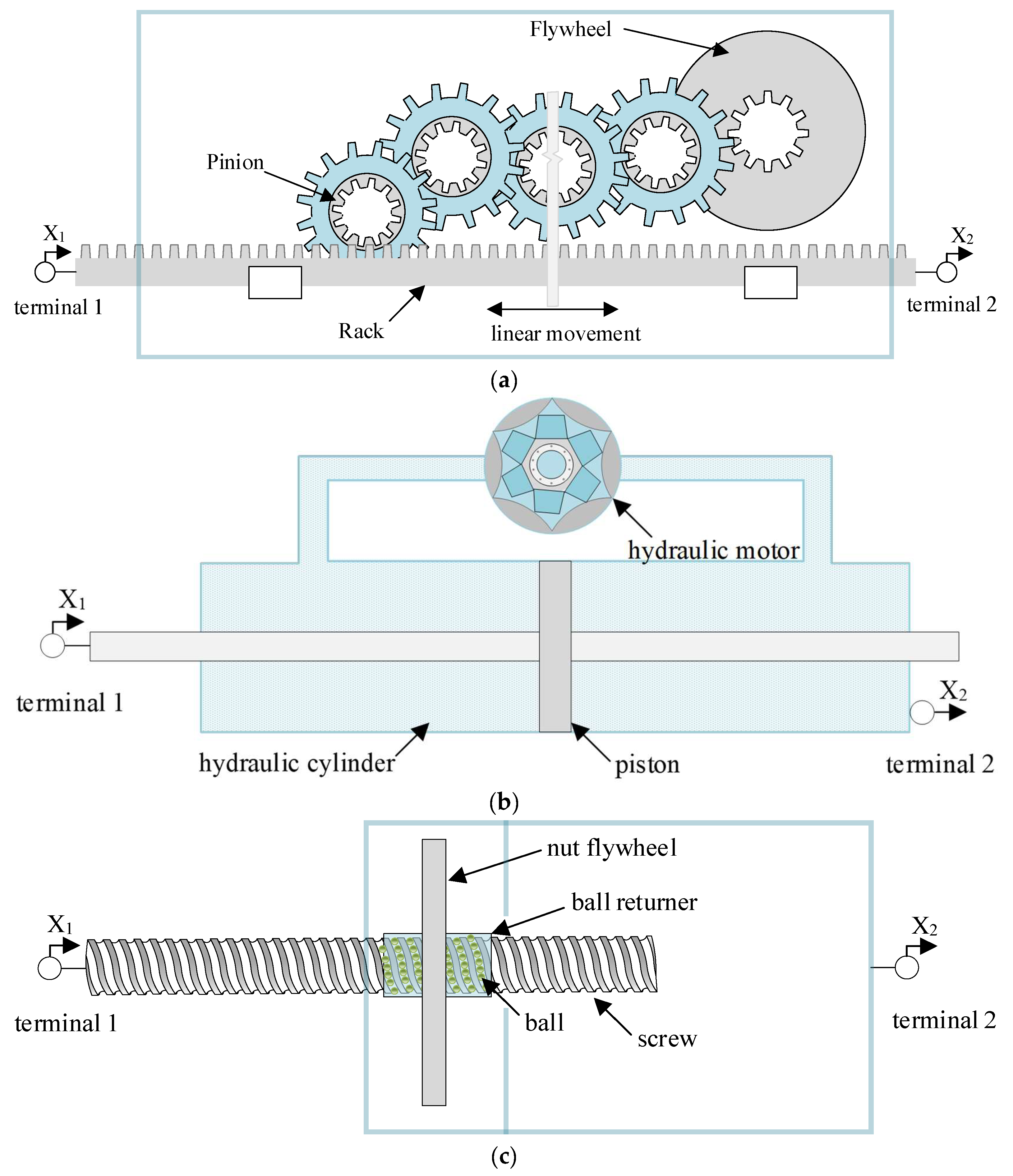
- Smith, M.C. Synthesis of mechanical networks: The inerter. IEEE Trans. Autom. Control 2002, 47, 1648–1662. [Google Scholar] [CrossRef] [Green Version]
- Ormondroyd, J.; Den Hartog, J.P. The theory of the dynamic vibration absorber. Trans. ASME 1928, 50, 9–22. [Google Scholar]
- Marian, L.; Giaralis, A. Optimal design of inverter devices combined with TMDs for vibration control of buildings exposed to stochastic seismic excitations. In Proceedings of the 11th International Conference on Structural Safety and Reliability, New York, NY, USA, 16–20 June 2013. [Google Scholar]
- Marian, L.; Giaralis, A. Optimal design of a novel tuned mass-damper–inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probabilistic Eng. Mech. 2014, 38, 156–164. [Google Scholar] [CrossRef]
- Evangelou, S.; Limebeer DJ, N.; Sharp, R.S.; Smith, M.C. Steering compensation for high-performance motorcycles. In Proceedings of the 43rd IEEE Conference on Decision and Control, Atlantis, Paradise Island, Bahamas, 14–17 December 2004. [Google Scholar]
- Papageorgiou, C.; Smith, M.C. Laboratory experimental testing of inerters. In Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference, Seville, Spain, 12–15 December 2005. [Google Scholar]
- Long, C.; Hao, R.E.N.; Ruo-chen, W. Simulations and Tests for Mechanical Properties of a Hydraulic Inerter. J. Vib. Shock. 2014, 33, 87–92. [Google Scholar]
- De Domenico, D.; Ricciardi, G. Optimal design and seismic performance of tuned mass damper inerter (TMDI) for structures with nonlinear base isolation systems. Earthq. Eng. Struct. Dyn. 2018, 47, 2539–2560. [Google Scholar]
- De Domenico, D.; Ricciardi, G. An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthq. Eng. Struct. Dyn. 2018, 47, 1169–1192. [Google Scholar] [CrossRef]
- Pietrosanti, D.; De Angelis, M.; Basili, M. Optimal design and performance evaluation of systems with Tuned Mass Damper Inerter (TMDI). Earthq. Eng. Struct. Dyn. 2017, 46, 1138–1367. [Google Scholar] [CrossRef]
- Giaralis, A.; Petrini, F. Wind-Induced Vibration Mitigation in Tall Buildings Using the Tuned Mass-Damper-Inerter. J. Struct. Eng. 2017, 143, 04017127. [Google Scholar] [CrossRef]
- Giaralis, A.; Petrini, F. Optimum design of the tuned mass-damper-inerter for serviceability limit state performance in wind-excited tall buildings. Procedia Eng. 2017, 199, 1773–1778. [Google Scholar] [CrossRef]
- Dai, J.; Xu, Z.D.; Gai, P.P. Tuned mass-damper-inerter control of wind-induced vibration of flexible structures based on inerter location. Eng. Struct. 2019, 199, 109585. [Google Scholar] [CrossRef]
- Zhang, Z.; Fitzgerald, B. Tuned mass-damper-inerter (TMDI) for suppressing edgewise vibrations of wind turbine blades. Eng. Struct. 2020, 221, 110928. [Google Scholar] [CrossRef]
- Lee, L.; Allen, D. Vibration frequency and lock-in bandwidth of tensioned, flexible cylinders experiencing vortex shedding. J. Fluids Struct. 2010, 26, 602–610. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Mechanical Vibrations; Courier Corporation: North Chelmsford, MA, USA, 1985. [Google Scholar]
- Dong, F.; Sun, F.; Yin, W.; Chu, M.; Wang, B.; Chao, Z.; Yao, Z.; Gong, Q.; Jin, H. Two-stage design method for damping high-frequency TMD of steel plate sandwich. Adv. Build. Steel Struct. 2021, 23, 85–93+100. [Google Scholar]
- Li, Y.; Li, S.; Chen, Z. Optimization and performance evaluation of variable inertial mass-tuned mass dampers. J. Vib. Eng. 2020, 33, 21–28. [Google Scholar]
- Luo, H.; Zhang, R.; Shen, H.; Weng, D. Parameter optimization of tandem viscous mass dampers based on fixed-point theory. Struct. Eng. 2017, 33, 41–46. [Google Scholar]
- Ikago, K.; Saito, K.; Inoue, N. Seismic control of single-degree-of-freedom structure using tuned viscous mass damper. Earthq. Eng. Struct. Dyn. 2012, 41, 453–474. [Google Scholar]
- Barredo, E.; Blanco, A.; Colín, J.; Penagos, V.M.; Abúndez, A.; Vela, L.G.; Mayén, J. Closed-form solutions for the optimal design of inerter-based dynamic vibration absorbers. Int. J. Mech. Sci. 2018, 144, 41–53. [Google Scholar] [CrossRef]
- Hadi, M.N.; Arfiadi, Y. Optimum design of absorber for MDOF structures. Optimum design of absorber for MDOF structures. Univ. Wollongong 1998, 11, 124. [Google Scholar]
- Febbo, M.; Vera, S.A. Optimization of a two degree of freedom system acting as a dynamic vibration absorber. J. Vib. Acoust. 2008, 130, 011013. [Google Scholar] [CrossRef]
- Bozer, A.; Özsarıyıldız, S.S. Free parameter search of multiple tuned mass dampers by using artificial bee colony algorithm. Struct. Control Health Monit. 2018, 25, e2066. [Google Scholar] [CrossRef]
- Kaveh, A. Colliding bodies optimization. In Advances in Metaheuristic Algorithms for Optimal Design of Structures; Springer: Cham, Switzerland, 2014; pp. 195–232. [Google Scholar]
- Kong, D.; Li, L.; Long, X.; Liang, Z. Finite element analysis of breeze vibration of ultra-high voltage overhead transmission lines. Vib. Shock. 2007, 26, 4. [Google Scholar]
- Tolman, R.C. The Principles of Statistical Mechanics; Clarendon Press: Oxford, UK, 1979. [Google Scholar]
- Kaveh, A.; Fahimi Farzam, M.; Hojat Jalali, H.; Maroofiazar, R. Robust optimum design of a tuned mass damper inerter. Acta Mech. 2020, 231, 3871–3896. [Google Scholar] [CrossRef]
- Kaveh, A.; Mahdavi, V.R. Colliding bodies optimization: A novel meta-heuristic method. Comput. Struct. 2014, 139, 18–27. [Google Scholar] [CrossRef]
- Fahimi Farzam, M.; Kaveh, A. Optimum design of tuned mass dampers using colliding bodies optimization in frequency domain. Iran. J. Sci. Technol. Trans. Civ. Eng. 2020, 44, 787–802. [Google Scholar] [CrossRef]
- Jiancheng, M. Breeze Vibration of Large Span Transmission Lines. Master’s Thesis, Huazhong University of Technology, Wuhan, China, 1996. [Google Scholar]
- Zhang, Z.; Zhou, L.; Qi, Y.; Liu, S. Factors influencing the strength of breeze vibration of large span conductors. Vibration. Test. Diagn. 2021, 4, 710–714. [Google Scholar]




| Parameters | Numerical Value | Parameters | Numerical Value | |
|---|---|---|---|---|
| Structure Number of roots/diameter (mm) | Aluminum | 48/2.85 | Outer diameter (mm) | 23.76 |
| Steel | 7/2.22 | Calculation of pull-off force (N) | 83,410 | |
| Calculated area | Aluminum | 306.21 | Modulus of elasticity (N/mm2) | 65,000 |
| Steel | 27.1 | Mass per unit length (kg/km) | 1058 | |
| Total | 333.31 | Length of test section (m) | 30.84 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Li, S.; Wu, C.; Zhong, Y.; Bian, Y. Research on Vibration Control of Power Transmission Lines-TMDI Based on Colliding Bodies Optimization. Buildings 2022, 12, 2200. https://doi.org/10.3390/buildings12122200
Liu X, Li S, Wu C, Zhong Y, Bian Y. Research on Vibration Control of Power Transmission Lines-TMDI Based on Colliding Bodies Optimization. Buildings. 2022; 12(12):2200. https://doi.org/10.3390/buildings12122200
Chicago/Turabian StyleLiu, Xinpeng, Siyuan Li, Chaoyue Wu, Yongli Zhong, and Yongfei Bian. 2022. "Research on Vibration Control of Power Transmission Lines-TMDI Based on Colliding Bodies Optimization" Buildings 12, no. 12: 2200. https://doi.org/10.3390/buildings12122200
APA StyleLiu, X., Li, S., Wu, C., Zhong, Y., & Bian, Y. (2022). Research on Vibration Control of Power Transmission Lines-TMDI Based on Colliding Bodies Optimization. Buildings, 12(12), 2200. https://doi.org/10.3390/buildings12122200







