Development of a Water Supplement System for a Tuned Liquid Damper under Excitation
Abstract
:1. Introduction
- (1)
- A TLD with a stable replenishment sub-tank (TLD-SRS) is proposed. The dynamic liquid pressure in the TLD is obtained with the speed potential function. Based on studies on TLCDs and TLCDAs, the relationship between the dimensionless size of the sub-tank and the maximum wave height and the dynamic liquid pressure are obtained. Thus, the TLD-SRS system with passive automatic liquid replenishment in a sub-tank is designed, using a floating ball.
- (2)
- The wave height and dynamic liquid pressure in the main tank under different wind loads are obtained. A large-scale TLD shaking table experiment is conducted to study the sloshing wave height of the liquid. The roof acceleration of 1-, 10- and 50-year return periods (YRP) for along-wind loads and a 10-year return period for across-wind loads are used as the excitation load. The time history of the wave height is obtained via video recognition. The dynamic liquid pressure and the flow speed in the connecting pipe is obtained via sloshing mode decomposition.
- (3)
- The overshoot of the TLD with a regular floating ball replenishment device and the TLD-SRS system during the wind loads are compared. The peak accelerations of the structure with TLDs are compared considering the overshoot of liquid supplementation.
- (4)
- An analysis of the effect of the diameter of the connecting pipe of the TLD-SRS system on the overshoot and damping efficiency is conducted.
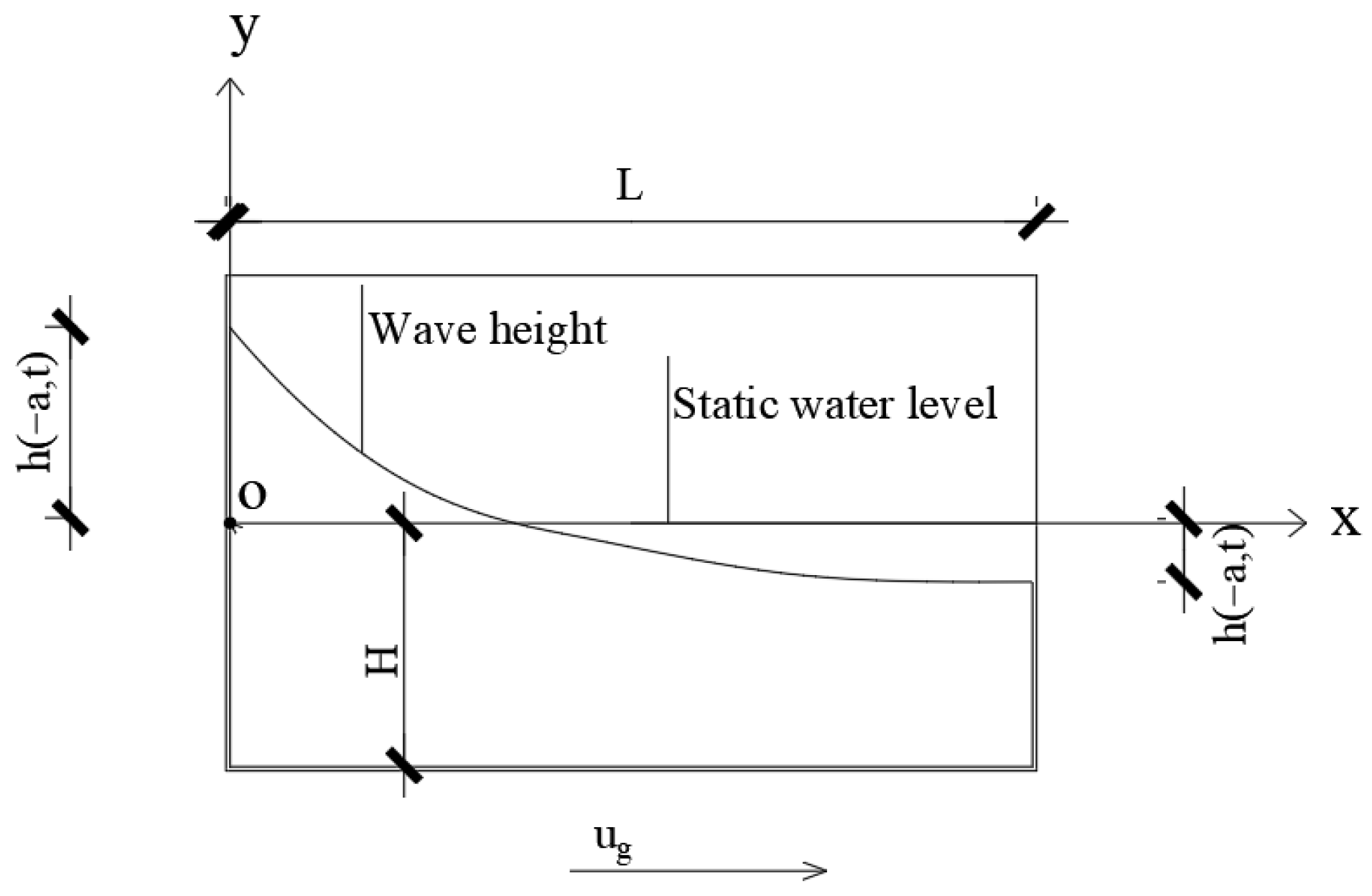
2. Proposed TLD with Stable Recharge Sub-Tank System
2.1. System Description
2.2. Design of the TLS-SRS
2.3. Design of the Connecting Pipe
3. Analysis of the TLD-SRS System Based on an Experiment
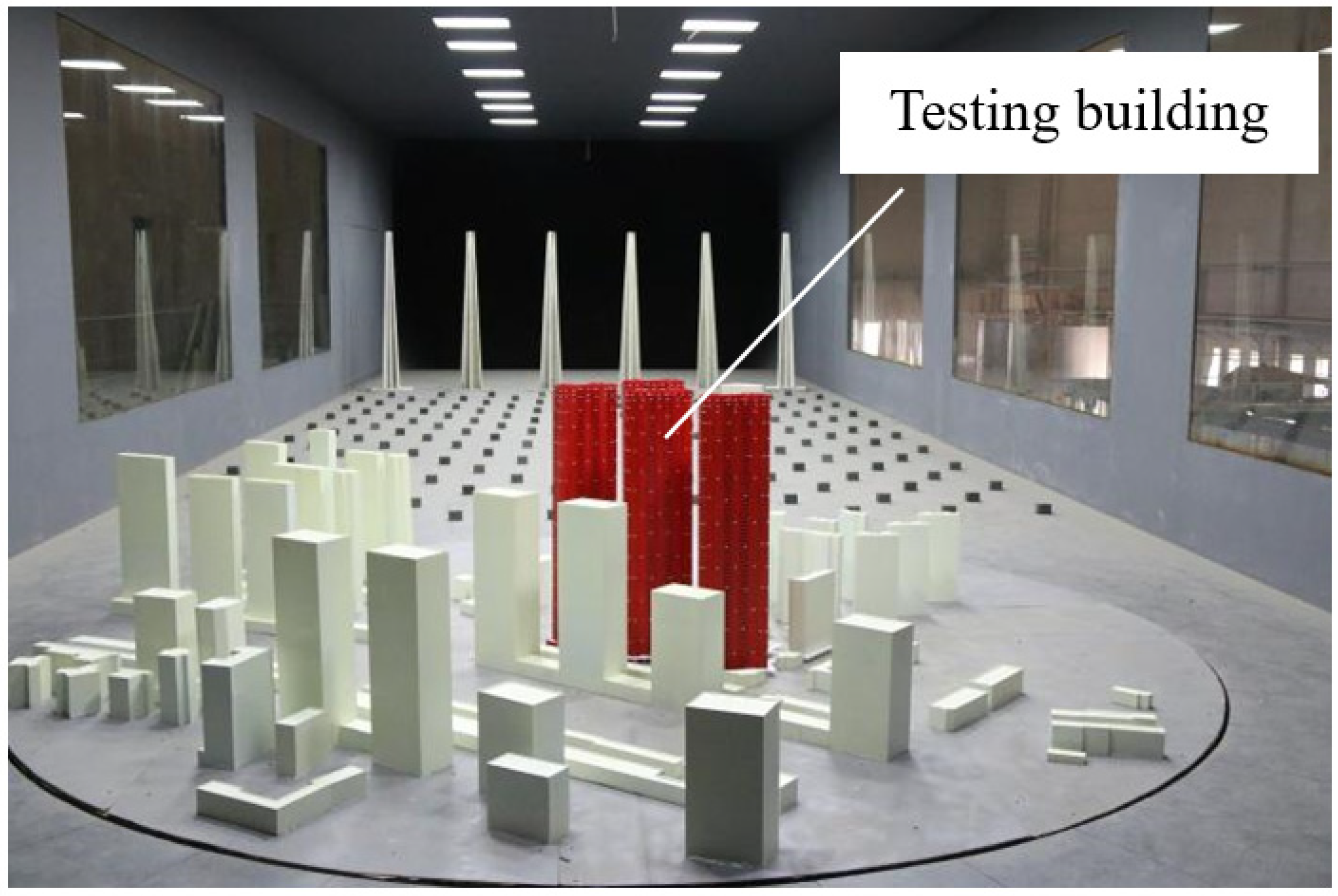
3.1. Tall Building Information
3.2. Wind Tunnel Experiment
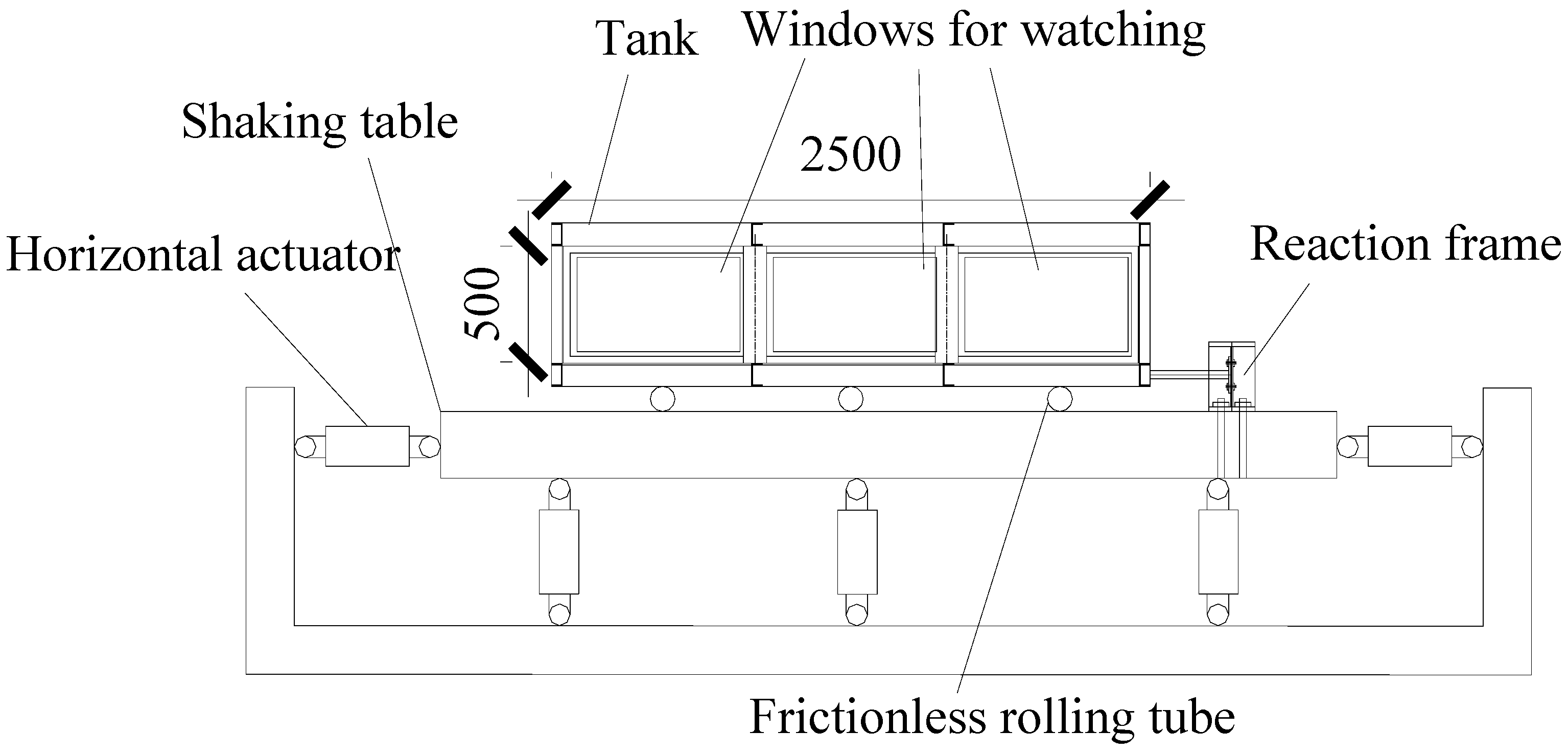
3.3. Shaking Table Experiment of TLD
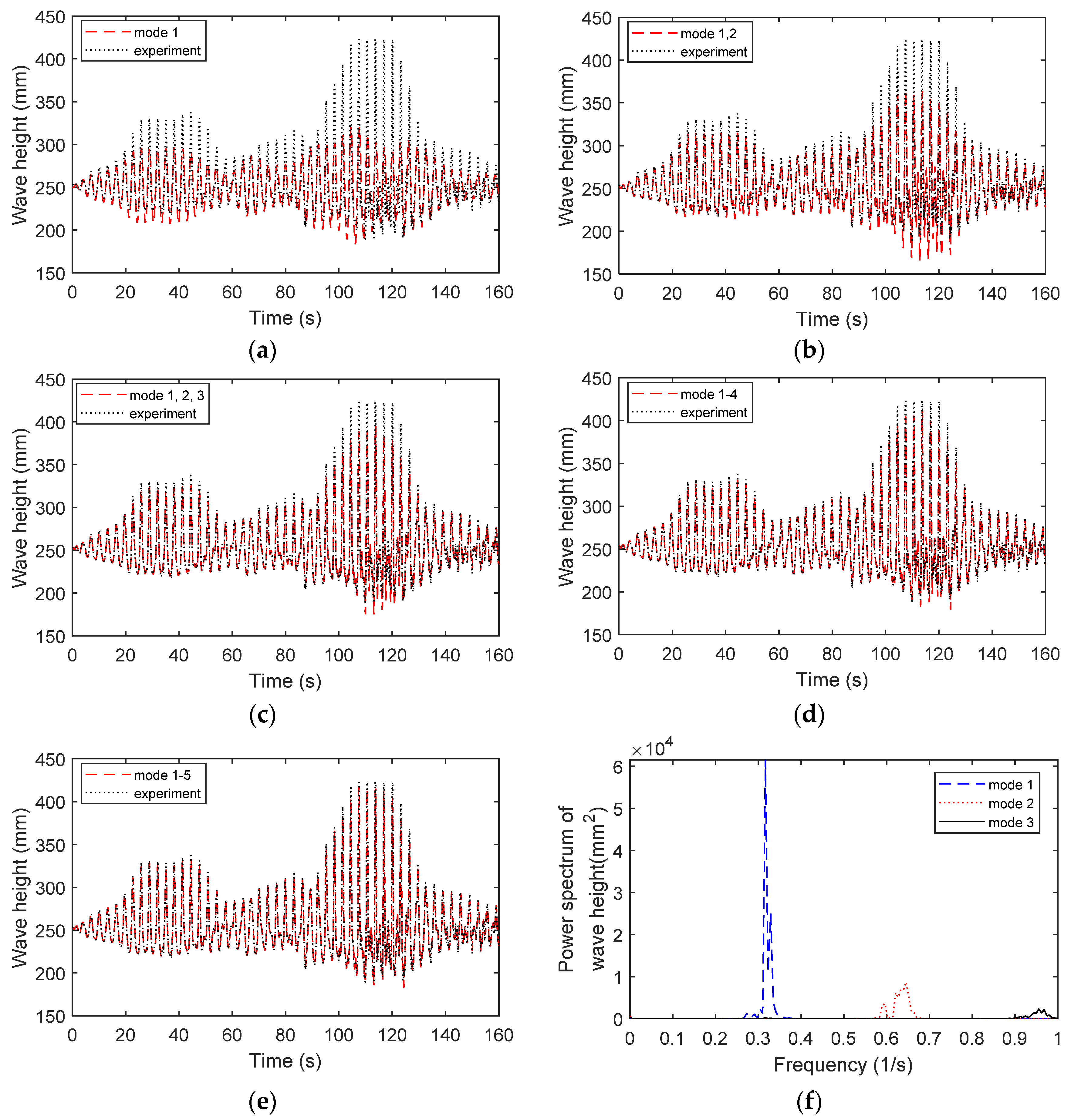
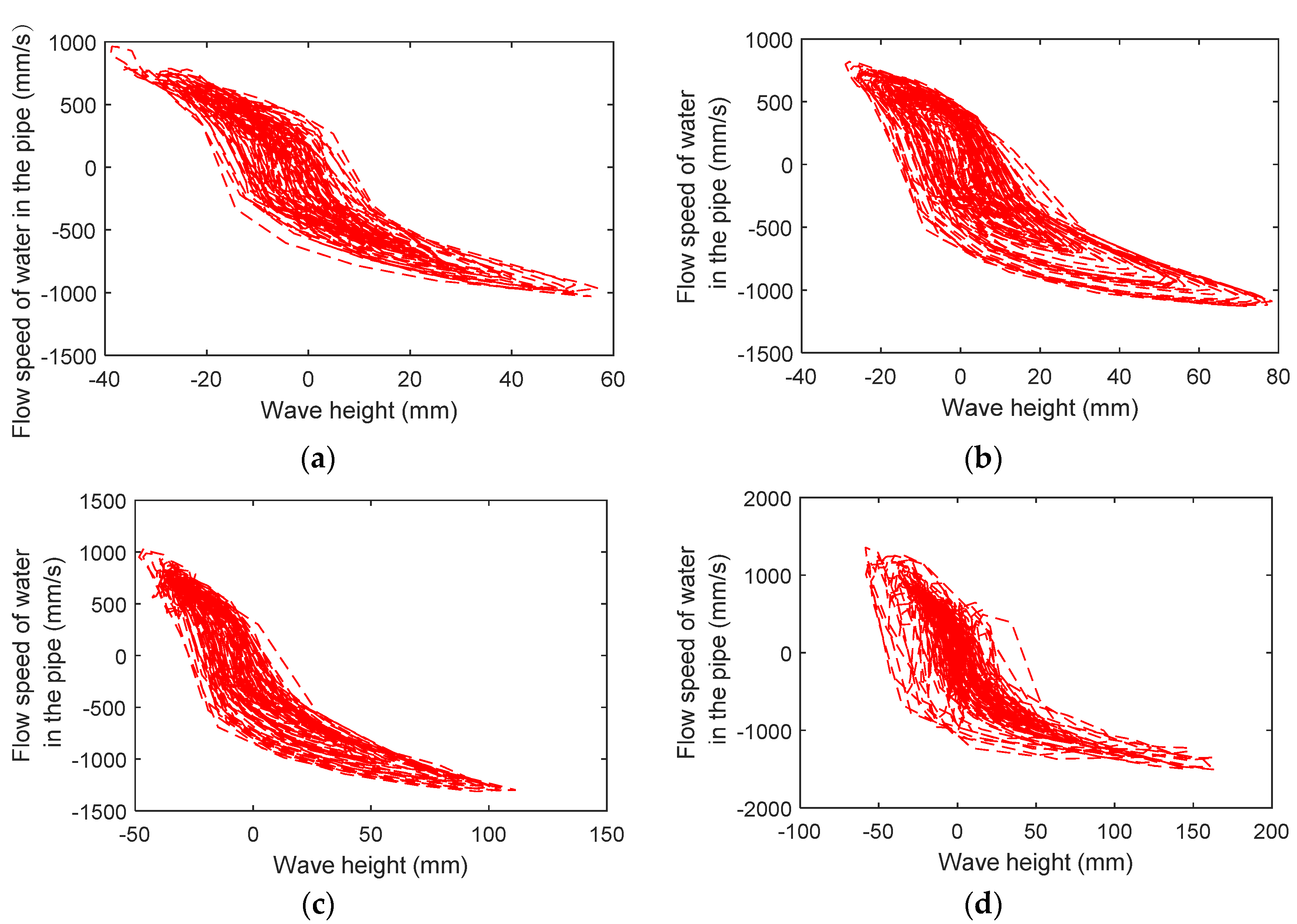
3.4. Sloshing Mode Analysis
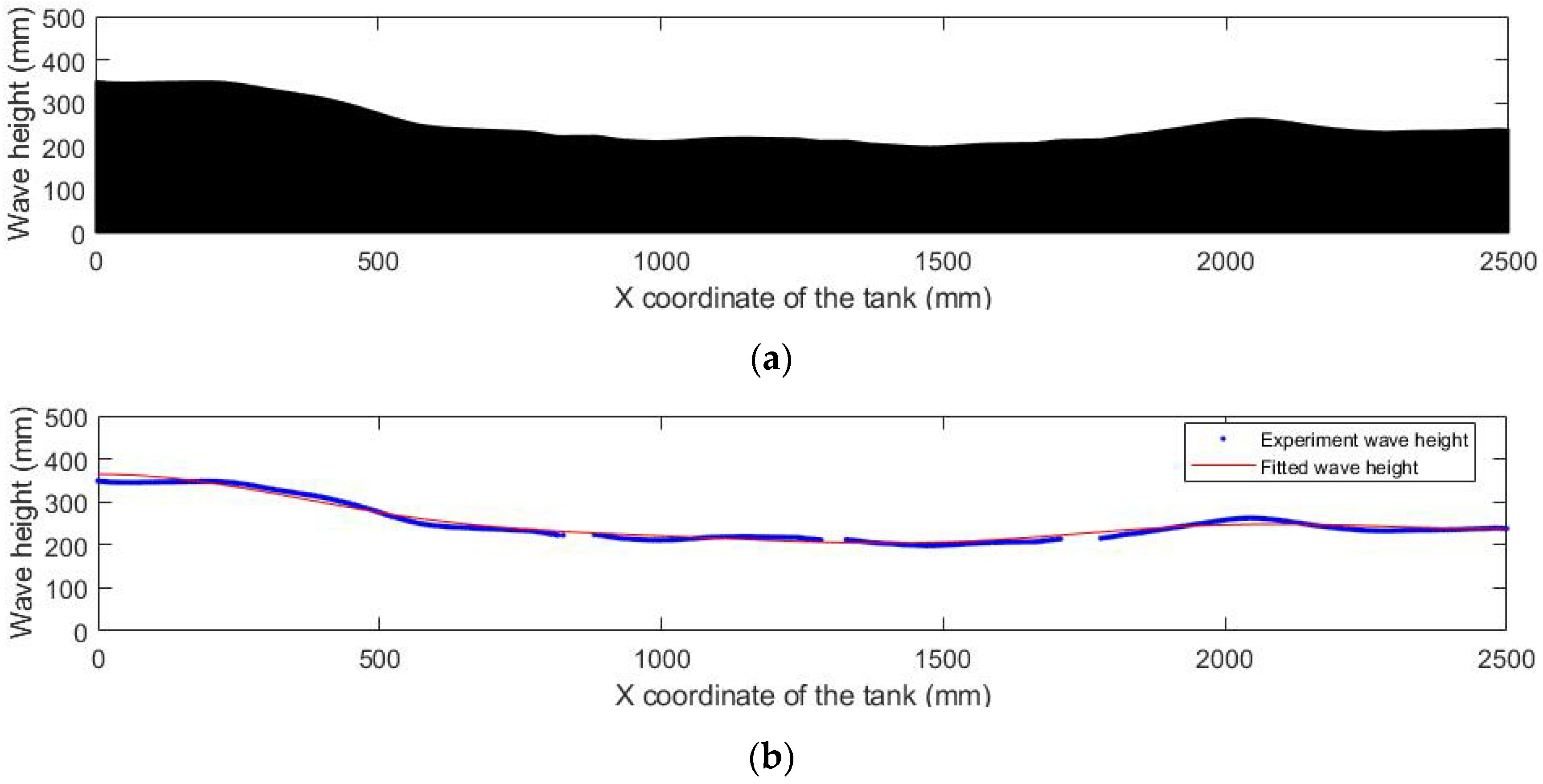
3.5. Solution of Liquid Dynamics Based on Wave Height Recognition
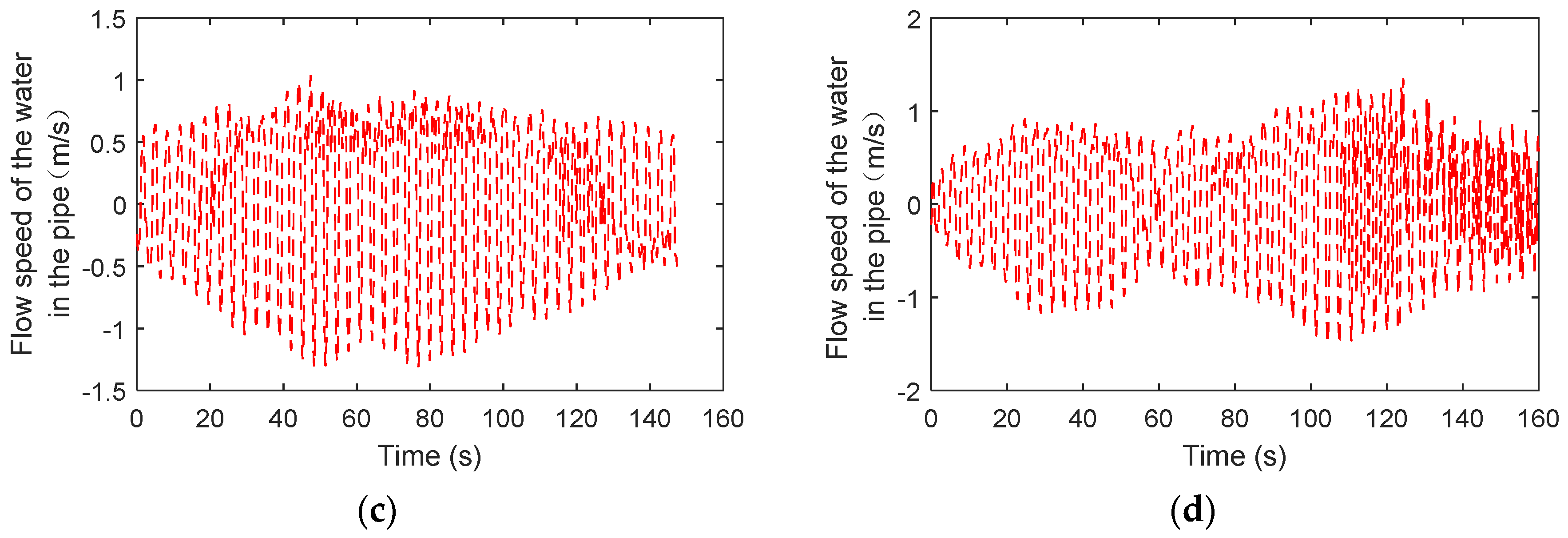
3.6. Liquid Flow between the Main Tank and Sub-Tank
4. Overshoot of Liquid Supplementation
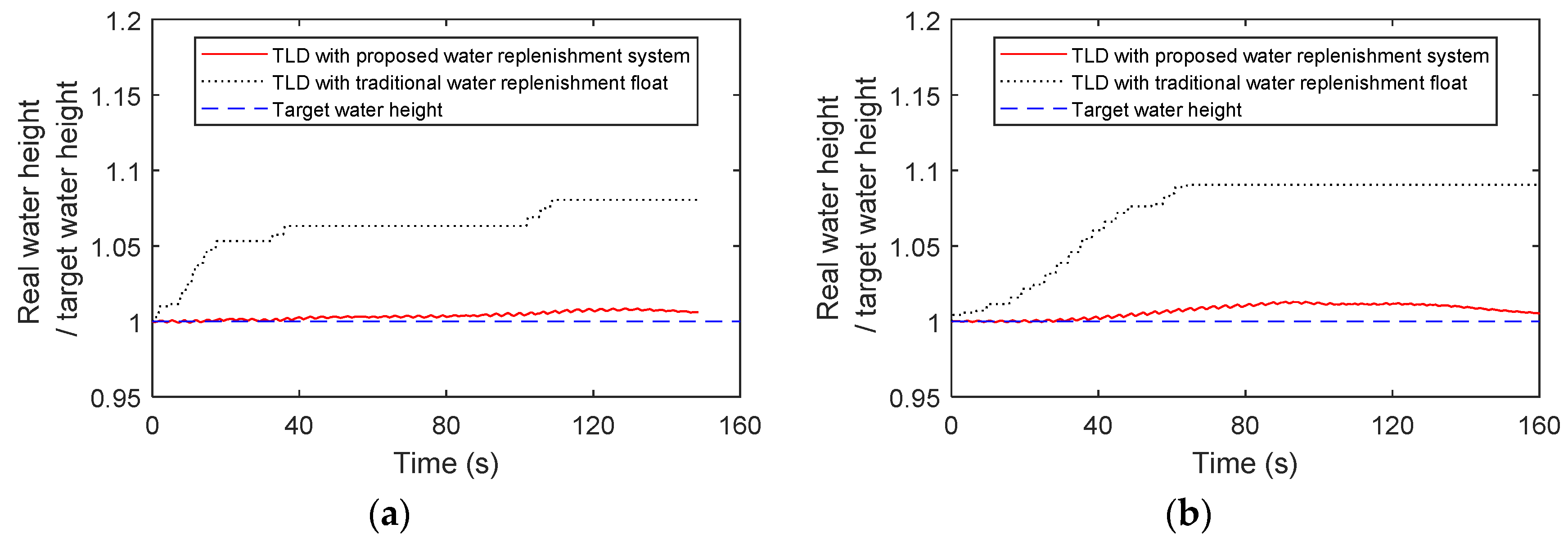
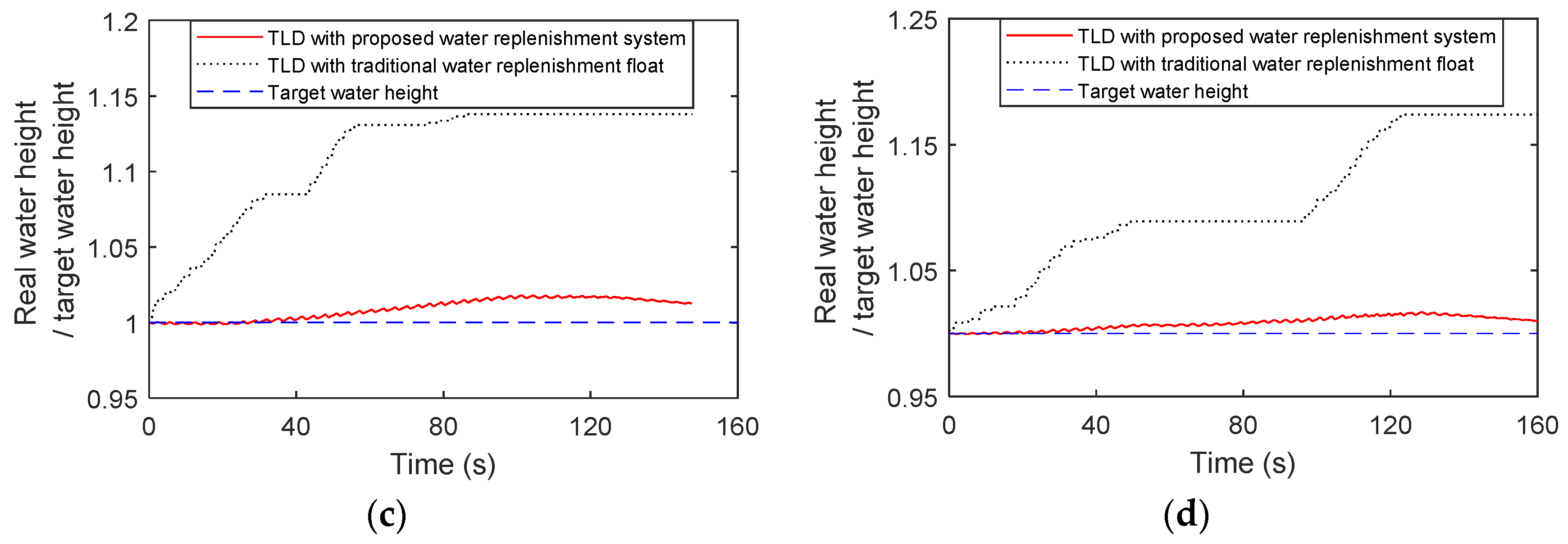
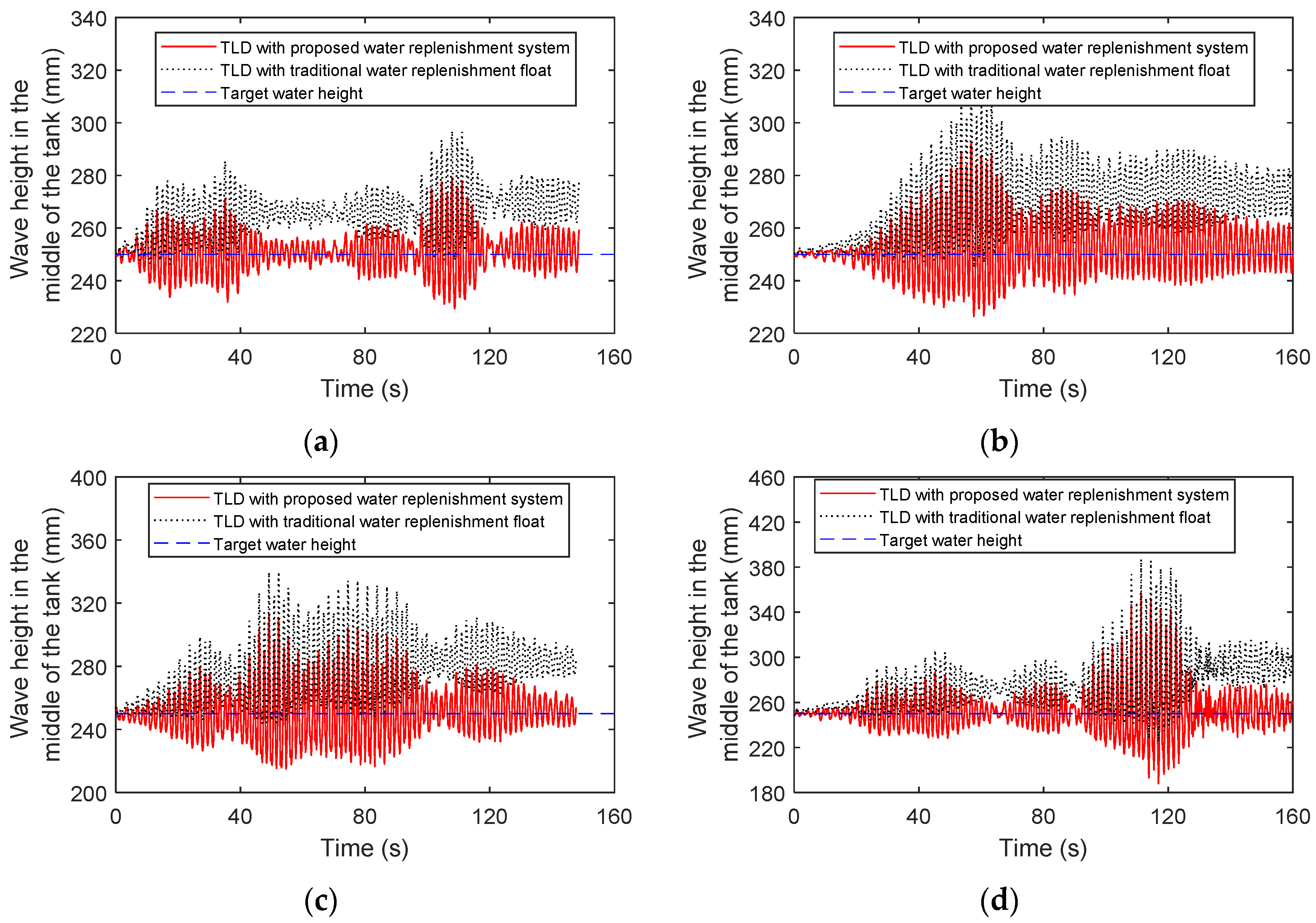
4.1. Overshoot of the Regular Liquid Replenishment Device
4.2. Overcompensation of the Proposed Liquid Replenishment
4.3. Damping Effect Considering Overcompensation
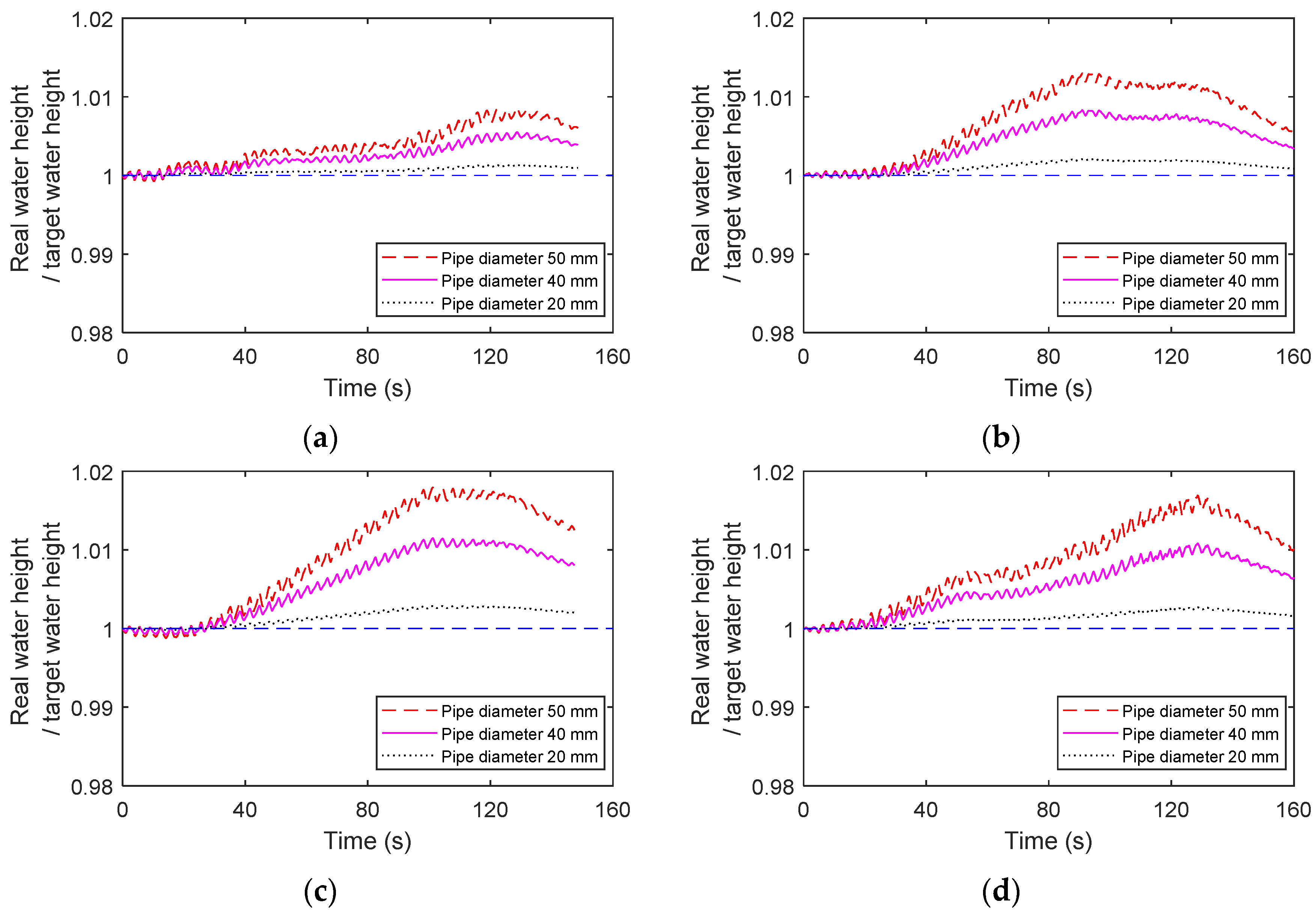
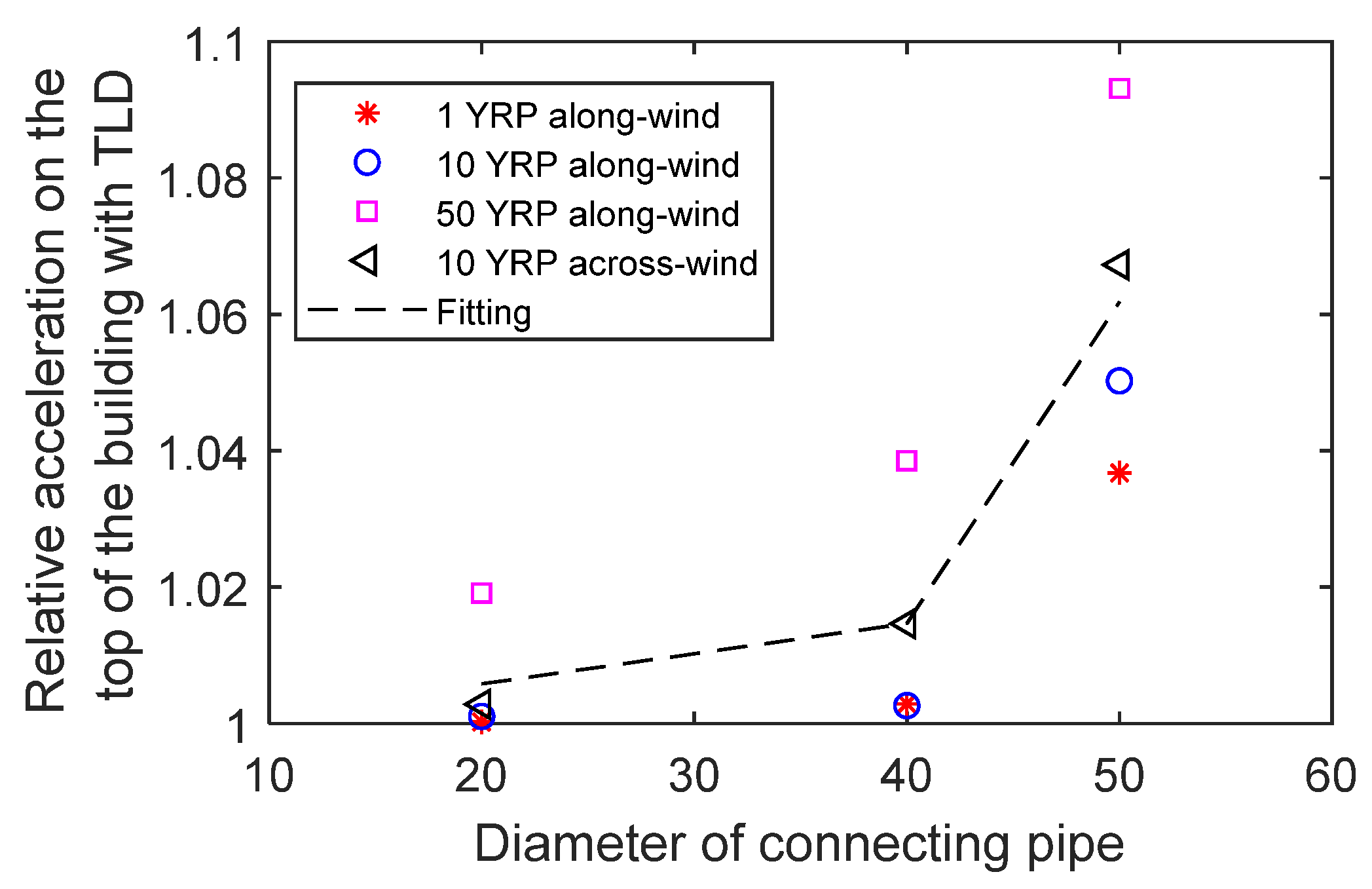
4.4. Overshoot with Different Pipe Dimensions
5. Conclusions
- (1)
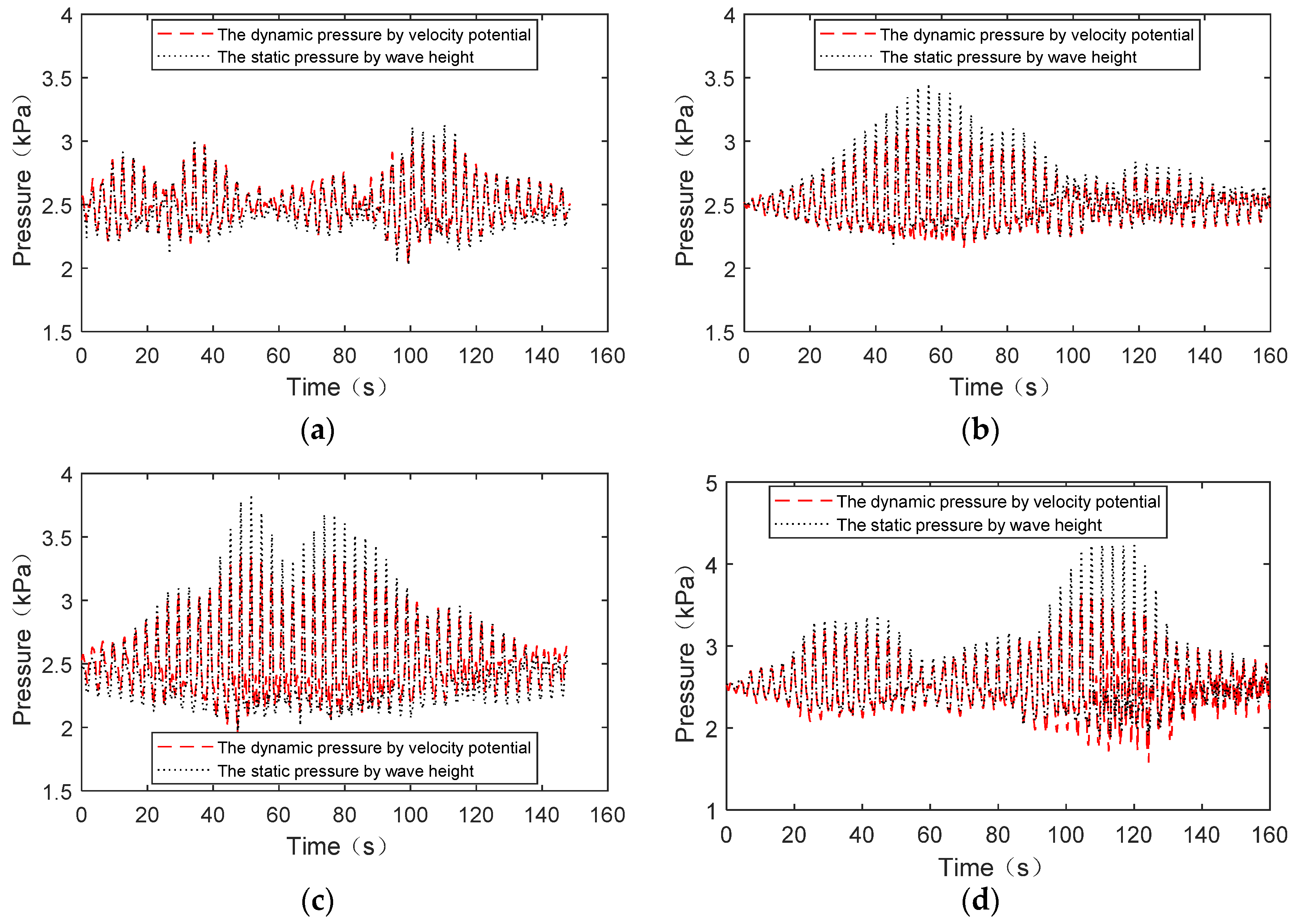
- A shaking table experiment of TLDs is conducted to capture the sloshing wave height time history with wind loads. By obtaining the velocity potential from the wave height, dynamic pressure, static pressure, wave height of each mode and the flow velocity in the connecting pipe of the TLD-SRS system are presented. The dynamic liquid pressure is different from the static liquid pressure, and the former determines the flow velocity in the connecting pipe during the shaking process.
- (2)
- The sloshing liquid wave height obtained from the experiment can be decomposed in the first three or five orders of sloshing modes. The root-mean-square error between the wave height represented by the first five order modes and the actual wave height is less than 4%, and the root-mean-square error between the TLD swaying wave height represented by the first three order modes and the actual wave height is less than 8%. The liquid sloshing in a TLD is mainly determined by the first five sloshing modes.
- (3)
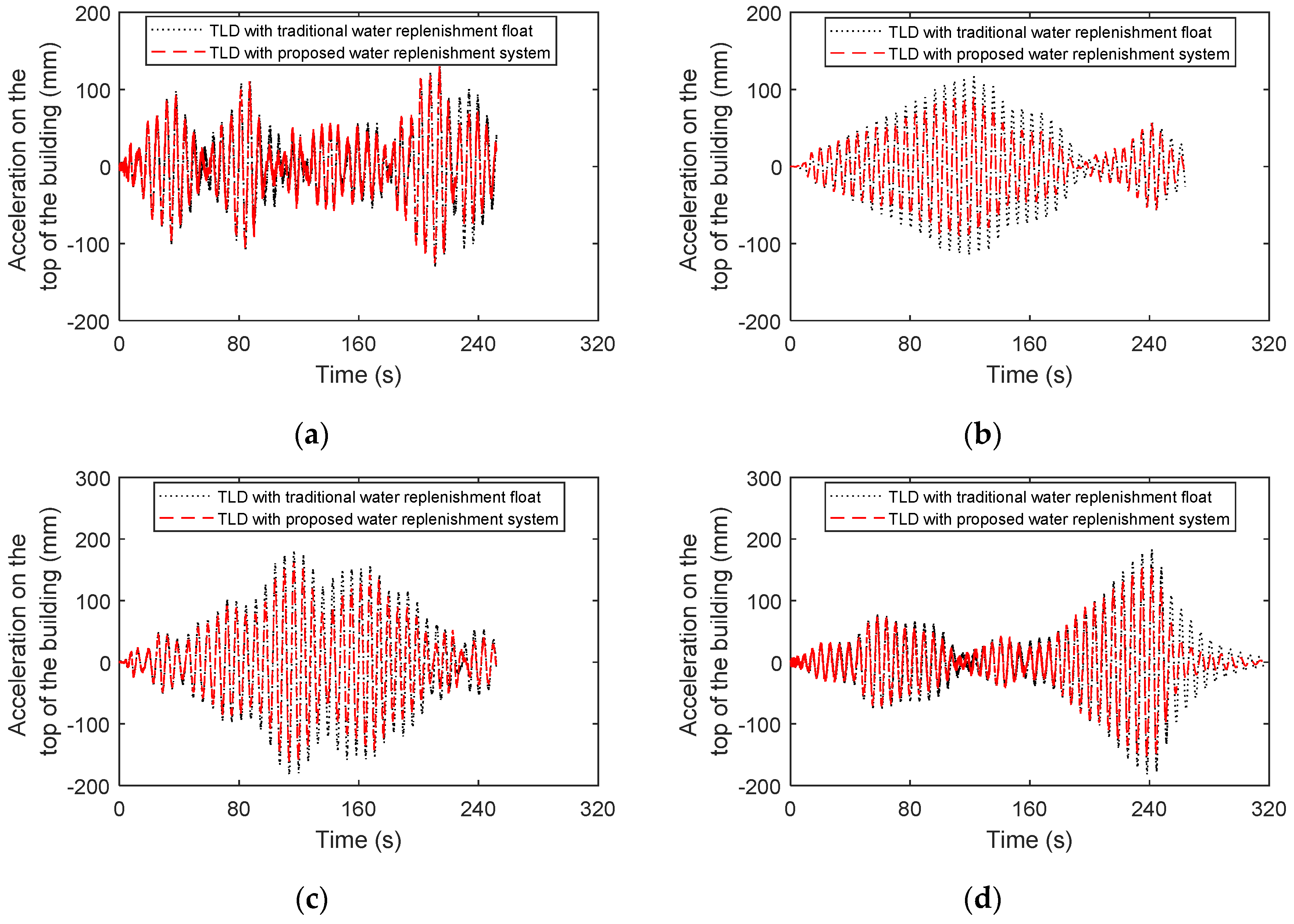
- The overshoot of liquid supplementation by the TLD-SRS system and by the regular floating ball liquid replenishment device are compared with wind loads. During the liquid sloshing in the TLD, the water in the sub-tank of the TLD-SRS almost remains without sloshing to avoid misactivation, and the regular replenishment device may be frequently misactivated. The TLD-SRS can reduce the maximum overshoot by 15% (using the regular floating ball liquid replenishment device) to 2%.
- (4)
- The TLD-SRS system can significantly improve the damping effect of the TLD considering the overshoot during sloshing. The RMS acceleration on the top of the building reduces it by 17~36% with the TLD keeping at an optimal liquid level, by 14~33% with the TLD-SRS system and by 10~22% with the TLD installed with a regular supplement device with different wind loads.
- (5)
- As the diameter of the connecting pipe in the TLD-SRS becomes smaller, the overshoot of the TLD also becomes smaller, considering the liquid sloshing under wind loads. When the diameter of the connecting pipe is 50 mm, the acceleration of the structure can already reach below 1.08 times of the optimal control acceleration, which is recommended in most situations. When there is a higher control requirement, it is a good choice to use a connecting pipe of 40 mm diameter, and the relative acceleration can reduce to 1.02.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sharma, A.; Mittal, H.; Gairola, A. Mitigation of wind load on tall buildings through aerodynamic modifications: Review. J. Build. Eng. 2018, 18, 180–194. [Google Scholar] [CrossRef]
- Jafari, M.; Alipour, A. Methodologies to mitigate wind-induced vibration of tall buildings: A state-of-the-art review. J. Build. Eng. 2021, 33, 101582. [Google Scholar] [CrossRef]
- Yue, Y.; Li, C.; Jia, K.; Zhang, Y.; Tian, J. Optimization of the Seismic Performance of a Steel-Concrete Wind Turbine Tower with the Tuned Mass Damper. Buildings 2022, 12, 1474. [Google Scholar] [CrossRef]
- Huang, H.C. Efficiency of the motion amplification device with viscous dampers and its application in high-rise buildings. Earthq. Eng. Eng. Vib. 2009, 8, 521–536. [Google Scholar] [CrossRef]
- Sato, D.; Chang, T.; Chen, Y. Effects of Different Frequency Sensitivity Models of a Viscoelastic Damper on Wind-Induced Response of High-Rise Buildings. Buildings 2022, 12, 2182. [Google Scholar] [CrossRef]
- Takewaki, I.; Murakami, S.; Yoshitomi, S.; Tsuji, M. Fundamental mechanism of earthquake response reduction in building structures with inertial dampers. Struct. Control Health Monit. 2012, 19, 590–608. [Google Scholar] [CrossRef]
- Bian, Y.; Liu, X.; Sun, Y.; Zhong, Y. Optimized Design of a Tuned Mass Damper Inerter (TMDI) Applied to Circular Section Members of Transmission Towers. Buildings 2022, 12, 1154. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, Y.; Zhang, C.; Li, S.; Tan, P. Performance-Based Compositive Passive Control Analysis of Multi-Tower Building with Chassis: Optimization of Kelvin-Voigt Dampers. Buildings 2022, 12, 137. [Google Scholar] [CrossRef]
- Ashasi-Sorkhabi, A.; Malekghasemi, H.; Ghaemmaghami, A.; Mercan, O. Experimental investigations of tuned liquid damper-structure interactions in resonance considering multiple parameters. J. Sound Vib. 2017, 388, 141–153. [Google Scholar] [CrossRef]
- Ishikawa, S.; Kondou, T.; Matsuzaki, K.; Yamamura, S. Analysis of nonlinear shallow water waves in a tank by concentrated mass model. J. Sound Vib. 2016, 371, 171–182. [Google Scholar] [CrossRef]
- An, Y.; Wang, Z.; Ou, G.; Pan, S.; Ou, J. Vibration Mitigation of Suspension Bridge Suspender Cables Using a Ring-Shaped Tuned Liquid Damper. J. Bridge Eng. 2019, 24, 4019020. [Google Scholar] [CrossRef]
- Hemmati, A.; Oterkus, E.; Barltrop, N. Fragility reduction of offshore wind turbines using tuned liquid column dampers. Soil Dyn. Earthq. Eng. 2019, 125, 105705. [Google Scholar] [CrossRef]
- Konar, T.; Ghosh, A.D. Bimodal vibration control of seismically excited structures by the liquid column vibration absorber. J. Vib. Control 2012, 19, 385–394. [Google Scholar] [CrossRef]
- Smith, M.J.; Kobine, J.J.; Davidson, F.A. Free and forced motion in an asymmetric liquid-column oscillator. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 905–922. [Google Scholar] [CrossRef]
- Fei, Z.; Jinting, W.; Feng, J.; Liqiao, L. Control performance comparison between tuned liquid damper and tuned liquid column damper using real-time hybrid simulation. Earthq. Eng. Eng. Vib. 2019, 18, 695–701. [Google Scholar] [CrossRef]
- Zhang, Z. Understanding and exploiting the nonlinear behavior of tuned liquid dampers (TLDs) for structural vibration control by means of a nonlinear reduced-order model (ROM). Eng. Struct. 2022, 251, 113524. [Google Scholar] [CrossRef]
- Rimal, H.; Pradhan, P.; Gautam, D.; Rupakhety, R. Seismic Fragility of Aging Elevated Water Tank with Smooth Bars Considering Soil Structure Interaction. Buildings 2023, 13, 4. [Google Scholar] [CrossRef]
- Konar, T.; Ghosh, A.D. Flow Damping Devices in Tuned Liquid Damper for Structural Vibration Control: A Review. Arch. Comput. Methods Eng. 2021, 28, 2195–2207. [Google Scholar] [CrossRef]
- Jin, L.; Li, B.; Lin, S.; Li, G. Optimal Design Formula for Tuned Mass Damper Based on an Analytical Solution of Interaction between Soil and Structure with Rigid Foundation Subjected to Plane SH-Waves. Buildings 2023, 13, 17. [Google Scholar] [CrossRef]
- Ocak, A.; Bekdaş, G.; Nigdeli, S.M.; Kim, S.; Geem, Z.W. Optimization of Tuned Liquid Damper Including Different Liquids for Lateral Displacement Control of Single and Multi-Story Structures. Buildings 2022, 12, 377. [Google Scholar] [CrossRef]
- Roy, A.; Zhang, Z.; Ghosh, A.D.; Basu, B. On the nonlinear performance of a tuned sloshing damper under small amplitude excitation. J. Vib. Control 2019, 25, 2695–2705. [Google Scholar] [CrossRef]
- Tait, M.J.; Isyumov, N.; El, D.A.A. Performance of Tuned Liquid Dampers. J. Eng. Mech. 2008, 134, 417–427. [Google Scholar] [CrossRef]
- Roy, A.; Ghosh, A.D.; Chatterjee, S. Influence of tuning of passive TLD on the seismic vibration control of elevated water tanks under various tank-full conditions. Struct. Control Health Monit. 2017, 24, e1924. [Google Scholar] [CrossRef]
- Konar, T.; Ghosh, A. A review on various configurations of the passive tuned liquid damper. J. Vib. Control 2022, 160766109. [Google Scholar] [CrossRef]
- Kickert, W.J.M.; Van Nauta Lemke, H.R. Application of a fuzzy controller in a warm water plant. Automatica 1976, 12, 301–308. [Google Scholar] [CrossRef]
- Erschler, J.; Roubellat, F.; Vernhes, J.P. Automation of a hydroelectric power station using variable-structure control systems. Automatica 1974, 10, 31–36. [Google Scholar] [CrossRef]
- Kumar, B.; Rajita, G.; Mandal, N. A Review on Capacitive-Type Sensor for Measurement of Height of Liquid Level. Meas. Control 2014, 47, 219–224. [Google Scholar] [CrossRef]
- Chamorro-Atalaya, O.; Arce-Santillan, D.; Morales-Romero, G.; Quispe-Andía, A.; Trinidad-Loli, N.; Auqui-Ramos, E.; León-Velarde, C.; Gutiérrez-Zubieta, E. Level Transducer Circuit Implemented by Ultrasonic Sensor and Controlled with Arduino Nano for its Application in a Water Tank of a Fire System. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 464–471. [Google Scholar] [CrossRef]
- Kodathala, V.; Kumar, K.; Vunnam, R.C.; Raju, C. Water Level Management Using Ultrasonic Sensor (Automation). Int. J. Comput. Sci. Eng. 2018, 6, 799–804. [Google Scholar] [CrossRef]
- Getu, B.; Attia, H. Automatic water level sensor and controller system. In Proceedings of the 2016 5th International Conference on Electronic Devices, 6–8 December 2016, Ras Al Khaimah, United Arab Emirates, 6–8 December 2016; pp. 1–4. [Google Scholar]
- Xu, J.; Hang, C.; Liu, C. Parallel structure and tuning of a fuzzy PID controller. Automatica 2000, 36, 673–684. [Google Scholar] [CrossRef]
- Ribeiro, J.M.S.; Santos, M.F.; Carmo, M.J.; Silva, M.F. Comparison of PID controller tuning methods: Analytical/classical techniques versus optimization algorithms. In Proceedings of the 2017 18th International Carpathian Control Conference (ICCC), Sinaia, Romania, 28–31 May 2017; pp. 533–538. [Google Scholar]
- Roy, P.; Kar, B.; Roy, B.K. Fractional Order PI-PD Control of Liquid Level in Coupled Two Tank System and its Experimental Validation. Asian J. Control 2017, 19, 1699–1709. [Google Scholar] [CrossRef]
- Sundaravadivu, K.; Arun, B.; Saravanan, K. Design of Fractional Order PID controller for liquid level control of spherical tank. In Proceedings of the 2011 IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 25–27 November 2011; pp. 291–295. [Google Scholar]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
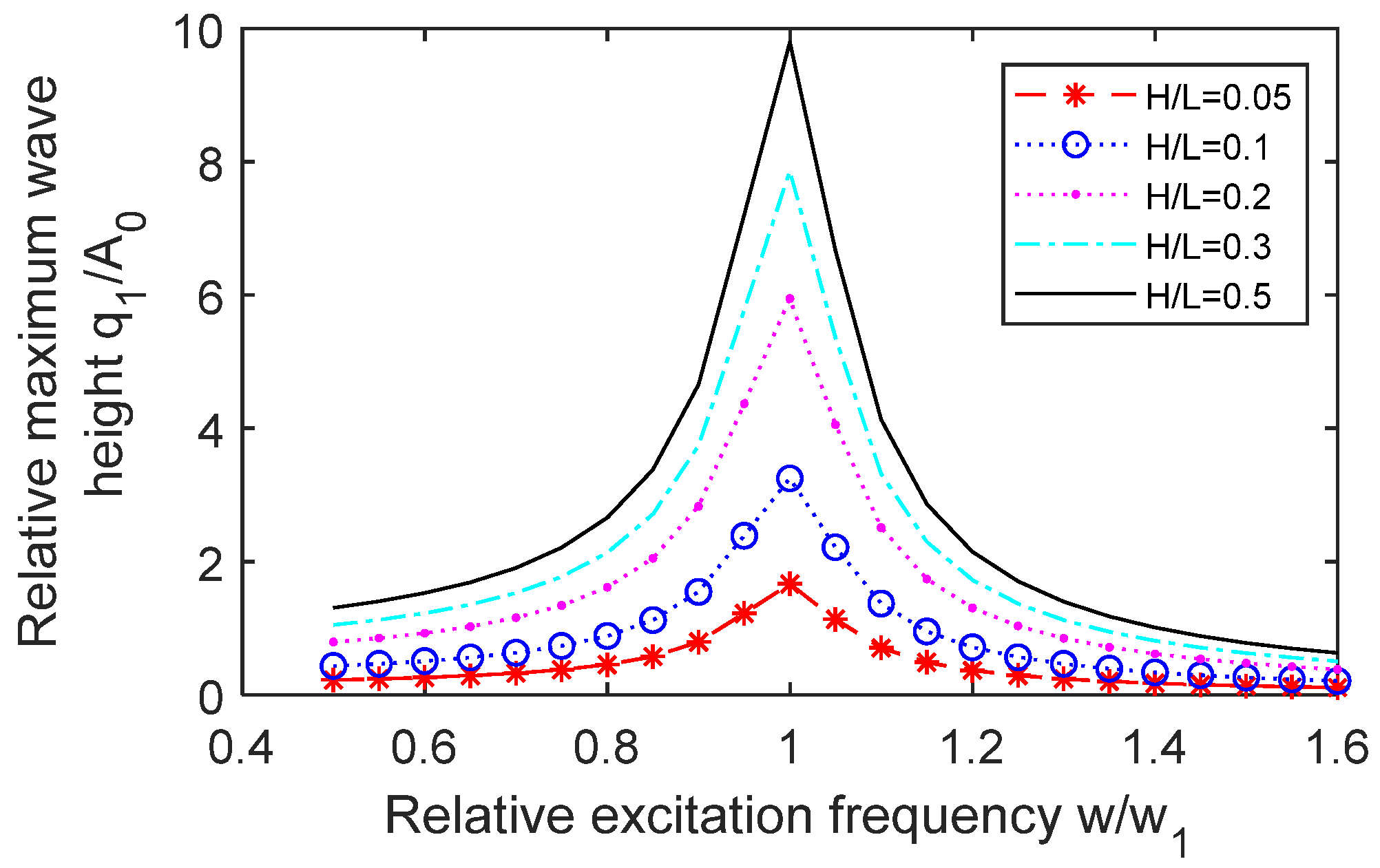
- Love, J.S.; Tait, M.J. Frequency domain prediction of peak nonlinear wave heights of structure-TLD systems. Eng. Struct. 2019, 194, 1–10. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Pilipchuk, V.N.; Ikeda, T. Recent Advances in Liquid Sloshing Dynamics. Appl. Mech. Rev. 2001, 54, 133–199. [Google Scholar] [CrossRef]
- Love, J.S.; Tait, M.J. Nonlinear simulation of a tuned liquid damper with damping screens using a modal expansion technique. J. Fluid. Struct. 2010, 26, 1058–1077. [Google Scholar] [CrossRef]
- Ibrahim, R.A. Liquid Sloshing Dynamics Theory and Applications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kareem, A.; Yalla, S.; Mccullough, M. Sloshing-Slamming Dynamics–S2–Analogy for Tuned Liquid Dampers. In Vibro-Impact Dynamics of Ocean Systems and Related Problems; Ibrahim, R.A., Babitsky, V.I., Okuma, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 123–133. ISBN 978-3-642-00629-6. [Google Scholar]
- Konar, T.; Ghosh, A. Development of a novel tuned liquid damper with floating base for converting deep tanks into effective vibration control devices. Adv. Struct. Eng. 2021, 24, 401–407. [Google Scholar] [CrossRef]
- Espinoza, G.; Carrillo, C.; Suazo, A. Analysis of a tuned liquid column damper in non-linear structures subjected to seismic excitations. Lat. Am. J. Solids Stru. 2018, 15. [Google Scholar] [CrossRef]
- Dziedziech, K.; Staszewski, W.; Ghosh, A.; Basu, B.; Uhl, T. Characterisation of instantaneous dynamic parameters in vibration analysis of tuned liquid column dampers. Nonlinear Dynam. 2017, 90, 717–731. [Google Scholar] [CrossRef]
- Chakraborty, S.; Debbarma, R.; Marano, G.C. Performance of tuned liquid column dampers considering maximum liquid motion in seismic vibration control of structures. J. Sound Vib. 2012, 331, 1519–1531. [Google Scholar] [CrossRef]
- Das, A.; Maity, D.; Bhattacharyya, S.K. Characterization of liquid sloshing in U-shaped containers as dampers in high-rise buildings. Ocean Eng. 2020, 210, 107462. [Google Scholar] [CrossRef]
- Ghosh, A.; Saha, P.; Basu, B. Study of a Tank-Pipe Damper System for Seismic Vibration Control of Structures. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisboa, Portugal, 24–28 September 2012. [Google Scholar]
- Di Matteo, A.; Lo Iacono, F.; Navarra, G.; Pirrotta, A. Innovative modeling of Tuned Liquid Column Damper motion. Commun. Nonlinear Sci. 2015, 23, 229–244. [Google Scholar] [CrossRef]
- Tait, M.J. Modelling and preliminary design of a structure-TLD system. Eng. Struct. 2008, 30, 2644–2655. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J. A supplementary, exact solution of an equivalent mechanical model for a sloshing fluid in a rectangular tank. J. Fluid. Struct. 2012, 31, 147–151. [Google Scholar] [CrossRef]
- Pereira, T.S.; de Carvalho, T.P.; Mendes, T.A.; Formiga, K.T. Evaluation of Water Level in Flowing Channels Using Ultrasonic Sensors. Sustainability 2022, 14, 5512. [Google Scholar] [CrossRef]
- Shin, Y.; Kim, J. Multipoint Wave Measurement in Tuned Liquid Damper Using Laser Doppler Vibrometer and Stepwise Rotating Galvanometer Scanner. Sensors 2021, 21, 8211. [Google Scholar] [CrossRef] [PubMed]










| Test ID (TS-) | Excitation Conditions | Excitation Displacement Amplitude ug0 (mm) | Excitation Acceleration Amplitude üg0 (mm s−2) |
|---|---|---|---|
| 1 | 1 YRP along-wind | 8 | 50 |
| 2 | 10 YRP along-wind | 16 | 65 |
| 3 | 50 YRP along-wind | 30 | 120 |
| 4 | 10 YRP across-wind | 29 | 150 |
| Load Case | Experiment | Mode 1 | Mode 1, 2 | Mode 1–3 | Mode 1–4 | Mode 1–5 | |
|---|---|---|---|---|---|---|---|
| 1 YRP along-wind | RMS of wave height | 17.36 | 15.90 | 16.74 | 16.81 | 16.91 | 17.16 |
| Fitted/Experimental | 100% | 92% | 96% | 97% | 97% | 99% | |
| 10 YRP along-wind | RMS of wave height | 20.43 | 15.75 | 18.82 | 19.22 | 19.50 | 19.73 |
| Fitted/Experimental | 100% | 77% | 92% | 94% | 95% | 97% | |
| 50 YRP along-wind | RMS of wave height | 32.02 | 25.69 | 29.28 | 30.22 | 30.63 | 31.25 |
| Fitted/Experimental | 100% | 80% | 91% | 94% | 96% | 98% | |
| 10 YRP across-wind | RMS of wave height | 36.06 | 26.34 | 31.77 | 33.06 | 33.93 | 34.62 |
| Fitted/Experimental | 100% | 73% | 88% | 92% | 94% | 96% | |
| Excitation Conditions | TLD with Regular Supplement Device | TLD with TLD-SRS System |
|---|---|---|
| 1 YRP along-wind | 8.05% | 0.75% |
| 10 YRP along-wind | 9.06% | 1.12% |
| 50 YRP along-wind | 13.80% | 1.70% |
| 10 YRP across-wind | 17.40% | 1.58% |
| Without TLD | With TLD Keeping at Optimal Liquid Level | With TLD Installed with Regular Supplement Device | With TLD-SRS System | ||
|---|---|---|---|---|---|
| 1 YRP along-wind | Maximum | 130 | 83 | 117 | 90 |
| Maximum/without TLD | 100% | 64% | 90% | 69% | |
| RMS | 53 | 34 | 46 | 36 | |
| RMS/without TLD | 100% | 65% | 86% | 67% | |
| 10 YRP along-wind | Maximum | 157 | 130 | 138 | 134 |
| Maximum/without TLD | 100% | 83% | 88% | 86% | |
| RMS | 54 | 36 | 45 | 40 | |
| RMS/without TLD | 100% | 67% | 84% | 75% | |
| 50 YRP along-wind | Maximum | 223 | 166 | 181 | 161 |
| Maximum/without TLD | 100% | 74% | 81% | 72% | |
| RMS | 93 | 62 | 72 | 59 | |
| RMS/without TLD | 100% | 67% | 78% | 64% | |
| 10 YRP across-wind | Maximum | 226 | 153 | 184 | 161 |
| Maximum/without TLD | 100% | 68% | 81% | 71% | |
| RMS | 65 | 47 | 52 | 44 | |
| RMS/without TLD | 100% | 72% | 80% | 67% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, C.; Wu, Z.; Chen, K.; Tang, Y.; Yan, Y. Development of a Water Supplement System for a Tuned Liquid Damper under Excitation. Buildings 2023, 13, 1115. https://doi.org/10.3390/buildings13051115
Xiao C, Wu Z, Chen K, Tang Y, Yan Y. Development of a Water Supplement System for a Tuned Liquid Damper under Excitation. Buildings. 2023; 13(5):1115. https://doi.org/10.3390/buildings13051115
Chicago/Turabian StyleXiao, Congzhen, Zhenhong Wu, Kai Chen, Yi Tang, and Yalin Yan. 2023. "Development of a Water Supplement System for a Tuned Liquid Damper under Excitation" Buildings 13, no. 5: 1115. https://doi.org/10.3390/buildings13051115
APA StyleXiao, C., Wu, Z., Chen, K., Tang, Y., & Yan, Y. (2023). Development of a Water Supplement System for a Tuned Liquid Damper under Excitation. Buildings, 13(5), 1115. https://doi.org/10.3390/buildings13051115






