Quantitative Investigation of Body Part Selection for Data-Driven Personal Overall Thermal Preference Prediction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Questionnaire
2.3. Measurement of Skin Temperature
2.4. Procedure
2.5. Machine Learning Algorithms
2.6. Evaluation Metrics
2.7. Selection of Body Part Combination
3. Results
3.1. Thermal Experience
3.2. Thermal Preference
3.3. Prediction of Overall Thermal Preference
3.3.1. The Best Combination
3.3.2. The Fewest Combination
3.3.3. The Common Combinations
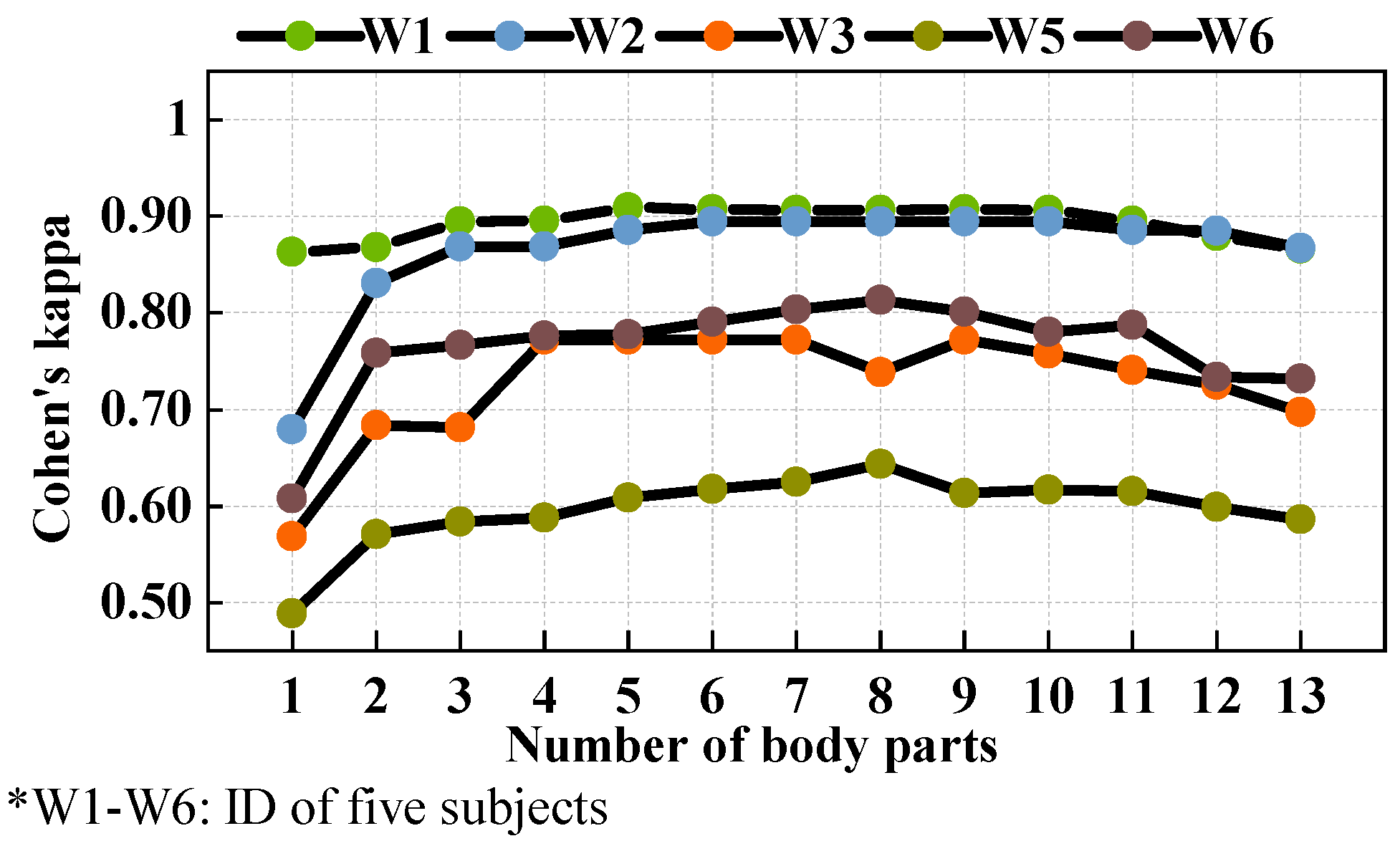
3.4. Model Validation
4. Discussion
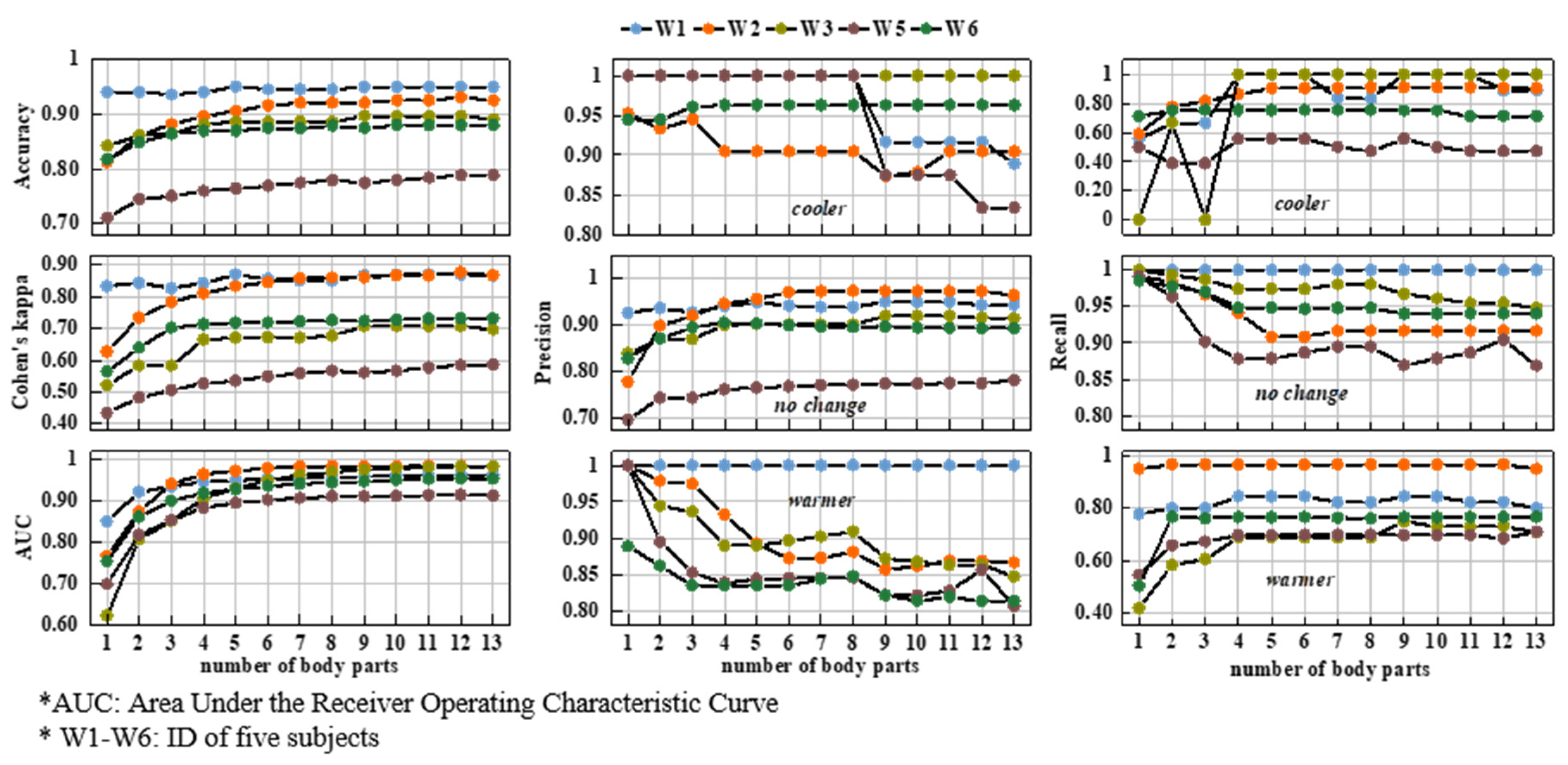
4.1. The Prediction Power of Different Combinations
4.2. Comparison of the Best Combination, Fewest Combination, and Common Combinations
4.3. Limitations and Future Studies
5. Conclusions
- This study proposed three combinations: the BC, FC, and CCs. The BC consisted of eight, six, six, eight, and six body parts for subjects W1, W2, W3, W5, and W6, respectively, while the FC consisted of two, three, four, three, and four. From 26 commonly used combinations, one combination with four body parts and three combinations with five body parts were selected as the CCs.
- This study compared the effects of the three combination strategies. In the first stage, the BC performed the best and the FC performed slightly worse than the CCs. In the second stage, the validation of these models using another 14 subjects, the BC and CCs showed nearly equal prediction power. Among the four CCs, “Common A” and “Common B” had better comprehensive performances than “Common C” or “Common D”.
- Overall, a CC strategy is recommended. The validation of the five BCs, five FCs, and four CCs certified their prediction power. Their accuracy, Cohen’s kappa, and AUC were 0.91 ± 0.07, 0.75 ± 0.16, and 0.87 ± 0.09, respectively. The four CCs had an advantage in terms of the prediction power and the minimal number of local body parts used.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A



Appendix B
| Subject ID | M6 | M7 | M8 | M9 | M10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Questionnaires | 161 | 156 | 150 | 154 | 153 | ||||||||||
| Percentage of votes | cooler | no change | warmer | cooler | no change | warmer | cooler | no change | warmer | cooler | no change | warmer | cooler | no change | warmer |
| Overall | 49.38 | 48.75 | 1.88 | 17.50 | 80.63 | 1.88 | 2.50 | 91.88 | 5.63 | 0.63 | 95.00 | 4.38 | 1.25 | 98.13 | 0.63 |
| Head | 20.78 | 75.32 | 3.90 | 13.64 | 81.82 | 4.55 | 11.69 | 78.57 | 9.74 | 10.39 | 83.77 | 5.84 | 9.09 | 88.96 | 1.95 |
| Face | 18.71 | 75.48 | 5.81 | 16.77 | 79.35 | 3.87 | 16.77 | 79.35 | 3.87 | 16.77 | 79.35 | 3.87 | 17.42 | 78.71 | 3.87 |
| Nape | 14.57 | 83.44 | 1.99 | 14.57 | 83.44 | 1.99 | 14.57 | 82.78 | 2.65 | 14.57 | 83.44 | 1.99 | 13.91 | 86.09 | 0 |
| Chest | 24.84 | 64.33 | 10.83 | 24.20 | 64.33 | 11.46 | 24.20 | 64.33 | 11.46 | 23.57 | 65.61 | 10.83 | 23.57 | 66.24 | 10.19 |
| Back | 38.61 | 60.76 | 0.63 | 5.70 | 92.41 | 1.90 | 3.80 | 94.30 | 1.90 | 2.53 | 96.20 | 1.27 | 10.76 | 87.97 | 1.27 |
| Upper arm | 16.77 | 81.94 | 1.29 | 15.48 | 83.87 | 0.65 | 12.90 | 85.16 | 1.94 | 7.10 | 92.90 | 0 | 5.16 | 94.84 | 0 |
| Lower arm | 12.67 | 83.33 | 4.00 | 4.00 | 87.33 | 8.67 | 3.33 | 88.00 | 8.67 | 2.67 | 96.00 | 1.33 | 4.67 | 94.00 | 1.33 |
| Wrist | 12.99 | 83.77 | 3.25 | 13.64 | 75.32 | 11.04 | 10.39 | 79.22 | 10.39 | 10.39 | 85.71 | 3.90 | 9.09 | 87.01 | 3.90 |
| Hand | 47.06 | 52.29 | 0.65 | 49.67 | 43.79 | 6.54 | 43.14 | 52.94 | 3.92 | 41.83 | 56.86 | 1.31 | 41.18 | 57.52 | 1.31 |
| Leg | 27.15 | 58.28 | 14.57 | 12.58 | 62.25 | 25.17 | 7.95 | 68.21 | 23.84 | 1.99 | 96.69 | 1.32 | 3.31 | 96.03 | 0.66 |
| Calf | 16.56 | 82.12 | 1.32 | 5.30 | 94.04 | 0.66 | 0.66 | 86.09 | 13.25 | 0 | 100 | 0 | 1.32 | 98.01 | 0.66 |
| Ankle | 57.42 | 41.29 | 1.29 | 20 | 65.16 | 14.84 | 12.26 | 67.74 | 20 | 5.81 | 90.32 | 3.87 | 10.97 | 89.03 | 0 |
| Foot | 22.88 | 65.36 | 11.76 | 7.19 | 64.05 | 28.76 | 7.19 | 66.01 | 26.80 | 3.27 | 85.62 | 11.11 | 3.92 | 82.35 | 13.73 |
| Subject ID | M11 | M12 | M13 | M14 | |||||||||||
| Questionnaires | 151 | 151 | 155 | 153 | |||||||||||
| Percentage of votes | cooler | no change | warmer | cooler | no change | warmer | cooler | no change | warmer | cooler | no change | warmer | |||
| Overall | 14.38 | 85.63 | 0 | 6.25 | 91.88 | 1.88 | 2.50 | 95.00 | 2.50 | 31.88 | 66.25 | 1.88 | |||
| Head | 12.34 | 87.01 | 0.65 | 12.34 | 79.87 | 7.79 | 9.09 | 68.83 | 22.08 | 9.09 | 85.71 | 5.19 | |||
| Face | 16.77 | 81.29 | 1.94 | 16.13 | 81.94 | 1.94 | 16.13 | 81.94 | 1.94 | 16.13 | 81.94 | 1.94 | |||
| Nape | 13.91 | 86.09 | 0 | 13.91 | 86.09 | 0 | 13.91 | 86.09 | 0 | 13.91 | 85.43 | 0.66 | |||
| Chest | 23.57 | 65.61 | 10.83 | 22.29 | 64.97 | 12.74 | 22.29 | 66.24 | 11.46 | 23.57 | 66.24 | 10.19 | |||
| Back | 7.59 | 91.77 | 0.63 | 7.59 | 91.77 | 0.63 | 2.53 | 97.47 | 0 | 3.80 | 96.20 | 0 | |||
| Upper arm | 15.48 | 83.87 | 0.65 | 14.84 | 84.52 | 0.65 | 5.81 | 93.55 | 0.65 | 14.84 | 81.94 | 3.23 | |||
| Lower arm | 2.00 | 92.67 | 5.33 | 2.00 | 92.67 | 5.33 | 2.00 | 97.33 | 0.67 | 6.00 | 92.67 | 1.33 | |||
| Wrist | 8.44 | 90.26 | 1.30 | 7.79 | 92.21 | 0 | 7.14 | 92.21 | 0.65 | 7.14 | 92.21 | 0.65 | |||
| Hand | 41.83 | 50.33 | 7.84 | 40.52 | 53.59 | 5.88 | 42.48 | 50.98 | 6.54 | 44.44 | 48.37 | 7.19 | |||
| Leg | 16.56 | 72.19 | 11.26 | 13.91 | 74.83 | 11.26 | 3.97 | 94.04 | 1.99 | 3.31 | 95.36 | 1.32 | |||
| Calf | 4.64 | 94.70 | 0.66 | 0 | 84.77 | 15.23 | 0 | 99.34 | 0.66 | 7.28 | 86.09 | 6.62 | |||
| Ankle | 16.13 | 60.65 | 23.23 | 12.26 | 54.19 | 33.55 | 6.45 | 82.58 | 10.97 | 20.65 | 78.06 | 1.29 | |||
| Foot | 9.15 | 77.12 | 13.73 | 8.50 | 78.43 | 13.07 | 9.15 | 84.97 | 5.88 | 13.07 | 74.51 | 12.42 | |||
Appendix C
| Combination | Body Parts | |
|---|---|---|
| 4 | Common A | Face, back, upper arm, calf |
| 5 | Common B | Face, back, upper arm, wrist, calf |
| Common C | Face, back, upper arm, leg, ankle | |
| Common D | Face, back, lower arm, leg, ankle | |
| 6 | Common 6.1 | Head, face, chest, upper arm, hand, ankle |
| Common 6.2 | Face, nape, chest, upper arm, hand, ankle | |
| Common 6.3 | Face, chest, back, upper arm, leg, ankle | |
| Common 6.4 | Face, chest, back, lower arm, leg, ankle | |
| Common 6.5 | Face, chest, back, lower arm, calf, ankle | |
| Common 6.6 | Face, chest, upper arm, lower arm, hand, ankle | |
| Common 6.7 | Face, chest, lower arm, wrist, hand, ankle | |
| Common 6.8 | Face, chest, lower arm, wrist, leg, ankle | |
| 7 | Common 7.1 | Head, face, chest, upper arm, lower arm, hand, ankle |
| Common 7.2 | Head, nape, back, upper arm, hand, leg, foot | |
| Common 7.3 | Face, nape, chest, lower arm, hand, leg, ankle | |
| Common 7.4 | Face, nape, back, lower arm, wrist, leg, ankle | |
| Common 7.5 | Face, chest, lower arm, hand, leg, ankle, foot | |
| 8 | Common 8.1 | Head, face, chest, upper arm, hand, leg, calf, ankle |
| Common 8.2 | Head, face, chest, upper arm, hand, leg, ankle, foot | |
| Common 8.3 | Face, chest, back, upper arm, hand, leg, ankle, foot | |
| Common 8.4 | Face, chest, back, lower arm, hand, leg, calf, ankle | |
| 9 | Common 9.1 | Face, nape, chest, back, upper arm, hand, leg, ankle, foot |
| Common 9.2 | Face, nape, chest, upper arm, lower arm, hand, leg, ankle, foot | |
| Common 9.3 | Face, nape, chest, upper arm, hand, leg, calf, ankle, foot | |
| Common 9.4 | Face, chest, upper arm, lower arm, wrist, hand, leg, ankle, foot | |
| 13 | Common 13.1 | Head, face, chest, upper arm, lower arm, wrist, hand, leg, ankle, foot |
Appendix D
| Combination | Accuracy | Cohen’s Kappa | AUC | Precision | Recall | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cooler | No Change | Warmer | Cooler | No Change | Warmer | |||||
| 4 | Common A | 0.87 ± 0.06 | 0.71 ± 0.13 | 0.91 ± 0.04 | 0.86 ± 0.10 | 0.89 ± 0.09 | 0.84 ± 0.21 | 0.75 ± 0.18 | 0.93 ± 0.05 | 0.81 ± 0.22 |
| 5 | Common B | 0.88 ± 0.07 | 0.74 ± 0.13 | 0.93 ± 0.02 | 0.85 ± 0.10 | 0.90 ± 0.09 | 0.86 ± 0.18 | 0.79 ± 0.14 | 0.93 ± 0.05 | 0.80 ± 0.26 |
| Common C | 0.88 ± 0.06 | 0.73 ± 0.13 | 0.94 ± 0.02 | 0.86 ± 0.07 | 0.90 ± 0.07 | 0.92 ± 0.07 | 0.78 ± 0.12 | 0.92 ± 0.05 | 0.72 ± 0.27 | |
| Common D | 0.88 ± 0.07 | 0.74 ± 0.13 | 0.94 ± 0.03 | 0.87 ± 0.06 | 0.90 ± 0.08 | 0.90 ± 0.06 | 0.77 ± 0.12 | 0.93 ± 0.05 | 0.82 ± 0.23 | |
| 6 | Common 6.1 | 0.88 ± 0.07 | 0.73 ± 0.14 | 0.95 ± 0.03 | 0.88 ± 0.10 | 0.88 ± 0.08 | 0.90 ± 0.11 | 0.75 ± 0.09 | 0.94 ± 0.04 | 0.69 ± 0.28 |
| Common 6.2 | 0.88 ± 0.07 | 0.73 ± 0.13 | 0.95 ± 0.03 | 0.91 ± 0.07 | 0.87 ± 0.07 | 0.82 ± 0.21 | 0.73 ± 0.09 | 0.96 ± 0.05 | 0.63 ± 0.23 | |
| Common 6.3 | 0.88 ± 0.07 | 0.74 ± 0.12 | 0.95 ± 0.02 | 0.87 ± 0.07 | 0.90 ± 0.07 | 0.91 ± 0.13 | 0.78 ± 0.11 | 0.92 ± 0.07 | 0.82 ± 0.16 | |
| Common 6.4 | 0.88 ± 0.07 | 0.74 ± 0.13 | 0.95 ± 0.02 | 0.87 ± 0.08 | 0.90 ± 0.08 | 0.90 ± 0.14 | 0.78 ± 0.11 | 0.92 ± 0.07 | 0.79 ± 0.19 | |
| Common 6.5 | 0.88 ± 0.07 | 0.73 ± 0.13 | 0.94 ± 0.03 | 0.84 ± 0.10 | 0.90 ± 0.08 | 0.88 ± 0.19 | 0.79 ± 0.11 | 0.91 ± 0.07 | 0.79 ± 0.19 | |
| Common 6.6 | 0.88 ± 0.06 | 0.73 ± 0.13 | 0.95 ± 0.03 | 0.90 ± 0.09 | 0.88 ± 0.07 | 0.89 ± 0.13 | 0.74 ± 0.08 | 0.95 ± 0.04 | 0.56 ± 0.35 | |
| Common 6.7 | 0.89 ± 0.07 | 0.75 ± 0.13 | 0.94 ± 0.03 | 0.90 ± 0.09 | 0.89 ± 0.08 | 0.91 ± 0.12 | 0.75 ± 0.09 | 0.95 ± 0.04 | 0.78 ± 0.22 | |
| Common 6.8 | 0.88 ± 0.07 | 0.73 ± 0.13 | 0.95 ± 0.03 | 0.85 ± 0.09 | 0.90 ± 0.07 | 0.87 ± 0.15 | 0.80 ± 0.10 | 0.91 ± 0.07 | 0.59 ± 0.36 | |
| 7 | Common 7.1 | 0.88 ± 0.07 | 0.73 ± 0.13 | 0.95 ± 0.03 | 0.91 ± 0.07 | 0.88 ± 0.08 | 0.82 ± 0.12 | 0.73 ± 0.08 | 0.96 ± 0.03 | 0.63 ± 0.40 |
| Common 7.2 | 0.88 ± 0.07 | 0.72 ± 0.13 | 0.94 ± 0.02 | 0.88 ± 0.11 | 0.88 ± 0.08 | 0.93 ± 0.07 | 0.75 ± 0.13 | 0.94 ± 0.06 | 0.57 ± 0.34 | |
| Common 7.3 | 0.88 ± 0.06 | 0.74 ± 0.12 | 0.95 ± 0.03 | 0.86 ± 0.08 | 0.90 ± 0.07 | 0.85 ± 0.14 | 0.79 ± 0.12 | 0.92 ± 0.07 | 0.62 ± 0.23 | |
| Common 7.4 | 0.88 ± 0.07 | 0.73 ± 0.13 | 0.95 ± 0.03 | 0.86 ± 0.08 | 0.90 ± 0.08 | 0.92 ± 0.08 | 0.79 ± 0.12 | 0.93 ± 0.06 | 0.60 ± 0.24 | |
| Common 7.5 | 0.89 ± 0.07 | 0.75 ± 0.13 | 0.95 ± 0.03 | 0.88 ± 0.07 | 0.91 ± 0.07 | 0.89 ± 0.14 | 0.80 ± 0.11 | 0.92 ± 0.07 | 0.66 ± 0.23 | |
| 8 | Common 8.1 | 0.88 ± 0.05 | 0.73 ± 0.11 | 0.95 ± 0.03 | 0.88 ± 0.07 | 0.90 ± 0.07 | 0.89 ± 0.12 | 0.77 ± 0.11 | 0.94 ± 0.04 | 0.61 ± 0.39 |
| Common 8.2 | 0.89 ± 0.06 | 0.74 ± 0.12 | 0.95 ± 0.03 | 0.89 ± 0.07 | 0.90 ± 0.08 | 0.89 ± 0.12 | 0.79 ± 0.12 | 0.94 ± 0.04 | 0.55 ± 0.34 | |
| Common 8.3 | 0.89 ± 0.07 | 0.76 ± 0.14 | 0.96 ± 0.02 | 0.88 ± 0.08 | 0.90 ± 0.08 | 0.93 ± 0.08 | 0.81 ± 0.12 | 0.93 ± 0.06 | 0.79 ± 0.19 | |
| Common 8.4 | 0.89 ± 0.06 | 0.74 ± 0.12 | 0.95 ± 0.03 | 0.88 ± 0.07 | 0.90 ± 0.07 | 0.90 ± 0.14 | 0.77 ± 0.13 | 0.94 ± 0.05 | 0.78 ± 0.18 | |
| 9 | Common 9.1 | 0.89 ± 0.07 | 0.75 ± 0.13 | 0.96 ± 0.03 | 0.86 ± 0.08 | 0.90 ± 0.08 | 0.92 ± 0.11 | 0.81 ± 0.12 | 0.93 ± 0.06 | 0.73 ± 0.25 |
| Common 9.2 | 0.89 ± 0.06 | 0.75 ± 0.11 | 0.96 ± 0.03 | 0.88 ± 0.07 | 0.90 ± 0.07 | 0.88 ± 0.10 | 0.80 ± 0.12 | 0.94 ± 0.04 | 0.72 ± 0.24 | |
| Common 9.3 | 0.88 ± 0.06 | 0.74 ± 0.12 | 0.95 ± 0.03 | 0.86 ± 0.08 | 0.90 ± 0.08 | 0.92 ± 0.11 | 0.79 ± 0.12 | 0.93 ± 0.05 | 0.71 ± 0.23 | |
| Common 9.4 | 0.89 ± 0.06 | 0.75 ± 0.11 | 0.96 ± 0.03 | 0.87 ± 0.07 | 0.90 ± 0.07 | 0.85 ± 0.14 | 0.79 ± 0.11 | 0.93 ± 0.05 | 0.79 ± 0.19 | |
| 13 | Common 13.1 | 0.89 ± 0.06 | 0.75 ± 0.12 | 0.96 ± 0.03 | 0.87 ± 0.08 | 0.90 ± 0.07 | 0.92 ± 0.07 | 0.79 ± 0.10 | 0.93 ± 0.05 | 0.80 ± 0.21 |
Appendix E

References
- Yao, R.; Li, B.; Steemers, K. Energy policy and standard for built environment in China. Renew. Energy 2005, 30, 1973–1988. [Google Scholar] [CrossRef]
- Yong, C.; Yiping, W.; Li, Z. Performance analysis on a building-integrated solar heating and cooling panel. Renew. Energy 2015, 74, 627–632. [Google Scholar] [CrossRef]
- Chenari, B.; Dias Carrilho, J.; Gameiro da Silva, M. Towards sustainable, energy-efficient and healthy ventilation strategies in buildings: A review. Renew. Sustain. Energy Rev. 2016, 59, 1426–1447. [Google Scholar] [CrossRef]
- Lan, L.; Tang, J.Y.; Wargocki, P.; Wyon, D.P.; Lian, Z. Cognitive performance was reduced by higher air temperature even when thermal comfort was maintained over the 24–28 degrees C range. Indoor Air 2022, 32, e12916. [Google Scholar] [CrossRef] [PubMed]
- Kükrer, E.; Eskin, N. Effect of design and operational strategies on thermal comfort and productivity in a multipurpose school building. J. Build. Eng. 2021, 44, 102697. [Google Scholar] [CrossRef]
- Criteria for the Indoor Environment Including Thermal, Indoor Air Quality, Light and Noise; EN15251:2007; European Committee for Standardization: Brussels, Belgium, 2007.
- ASHRAE. Thermal Environmental Conditions for Human Occupancy; ANSI/ASHRAE Standard 55-2013; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2013. [Google Scholar]
- ISO. Ergonomics of the Thermal Environment—Analytical Determination and Interpretation of Thermal Comfort Using Calculation of the PMV and PPD Indices and Local Thermal Comfort Criteria; ISO: Geneva, Switzerland, 2006. [Google Scholar]
- Fanger, P.O. Thermal Comfort. Analysis and Applications in Environmental Engineering; Danish Technical Press: Copenhagen, Denmark, 1970. [Google Scholar]
- De Dear, R.J.; Brager, G.S. Developing an Adaptive Model of Thermal Comfort and Preference. In Proceedings of the ASHRAE Transactions, Toronto, ON, Canada, 27 June–1 July 1998; pp. 145–167. [Google Scholar]
- Nicol, J.F.; Humphreys, M.A. Adaptive thermal comfort and sustainable thermal standards for buildings. Energy Build. 2002, 34, 563–572. [Google Scholar] [CrossRef]
- Zaki, S.A.; Damiati, S.A.; Rijal, H.B.; Hagishima, A.; Razak, A.A. Adaptive thermal comfort in university classrooms in Malaysia and Japan. Build. Environ. 2017, 122, 294–306. [Google Scholar] [CrossRef]
- Khalid, W.; Zaki, S.A.; Rijal, H.B.; Yakub, F. Investigation of comfort temperature and thermal adaptation for patients and visitors in Malaysian hospitals. Energy Build. 2019, 183, 484–499. [Google Scholar] [CrossRef]
- Jiao, Y.; Yu, H.; Yu, Y.; Wang, Z.; Wei, Q. Adaptive thermal comfort models for homes for older people in Shanghai, China. Energy Build. 2020, 215, 109918. [Google Scholar] [CrossRef]
- Beshir, M.Y.; Ramsey, J.D. Comparison between male and female subjective estimates of thermal effects and sensations. Appl. Ergon. 1981, 12, 29–33. [Google Scholar] [CrossRef]
- Wang, Z.; de Dear, R.; Luo, M.; Lin, B.; He, Y.; Ghahramani, A.; Zhu, Y. Individual difference in thermal comfort: A literature review. Build. Environ. 2018, 138, 181–193. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, H.; He, Y.; Luo, M.; Li, Z.; Hong, T.; Lin, B. Revisiting individual and group differences in thermal comfort based on ASHRAE database. Energy Build. 2020, 219, 110017. [Google Scholar] [CrossRef]
- Arens, E.; Humphreys, M.A.; de Dear, R.; Zhang, H. Are ‘class A’ temperature requirements realistic or desirable? Build. Environ. 2010, 45, 4–10. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Schiavon, S.; Brager, G. Personal comfort models—A new paradigm in thermal comfort for occupant-centric environmental control. Build. Environ. 2018, 132, 114–124. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Lian, Z.; Zhao, B. A neural network evaluation model for individual thermal comfort. Energy Build. 2007, 39, 1115–1122. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhao, Y.; Wang, F.; Wang, J.; Jiang, Y.; Zhang, F. A data-driven method to describe the personalized dynamic thermal comfort in ordinary office environment: From model to application. Build. Environ. 2014, 72, 309–318. [Google Scholar] [CrossRef]
- Auffenberg, F.; Stein, S.; Rogers, A. A personalised thermal comfort model using a Bayesian network. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Aryal, A.; Becerik-Gerber, B. A comparative study of predicting individual thermal sensation and satisfaction using wrist-worn temperature sensor, thermal camera and ambient temperature sensor. Build. Environ. 2019, 160, 106223. [Google Scholar] [CrossRef]
- Liu, S.; Schiavon, S.; Das, H.P.; Jin, M.; Spanos, C.J. Personal thermal comfort models with wearable sensors. Build. Environ. 2019, 162, 106281. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.-H.; Yeom, D. Study of data-driven thermal sensation prediction model as a function of local body skin temperatures in a built environment. Build. Environ. 2017, 121, 130–147. [Google Scholar] [CrossRef]
- Dai, C.; Zhang, H.; Arens, E.; Lian, Z. Machine learning approaches to predict thermal demands using skin temperatures: Steady-state conditions. Build. Environ. 2017, 114, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Chaudhuri, T.; Zhai, D.; Soh, Y.C.; Li, H.; Xie, L. Thermal comfort prediction using normalized skin temperature in a uniform built environment. Energy Build. 2018, 159, 426–440. [Google Scholar] [CrossRef]
- Kim, J.; Zhou, Y.; Schiavon, S.; Raftery, P.; Brager, G. Personal comfort models: Predicting individuals’ thermal preference using occupant heating and cooling behavior and machine learning. Build. Environ. 2018, 129, 96–106. [Google Scholar] [CrossRef] [Green Version]
- Du, C.; Li, B.; Liu, H.; Ji, Y.; Yao, R.; Yu, W. Quantification of personal thermal comfort with localized airflow system based on sensitivity analysis and classification tree model. Energy Build. 2019, 194, 1–11. [Google Scholar] [CrossRef]
- Katić, K.; Li, R.; Zeiler, W. Machine learning algorithms applied to a prediction of personal overall thermal comfort using skin temperatures and occupants’ heating behavior. Appl. Ergon. 2020, 85, 103078. [Google Scholar] [CrossRef] [PubMed]
- Salehi, B.; Ghanbaran, A.H.; Maerefat, M. Intelligent models to predict the indoor thermal sensation and thermal demand in steady state based on occupants’ skin temperature. Build. Environ. 2020, 169, 106579. [Google Scholar] [CrossRef]
- Liu, W.; Tian, X.; Yang, D.; Deng, Y. Evaluation of individual thermal sensation at raised indoor temperatures based on skin temperature. Build. Environ. 2021, 188, 107486. [Google Scholar] [CrossRef]
- Pigliautile, I.; Casaccia, S.; Morresi, N.; Arnesano, M.; Pisello, A.L.; Revel, G.M. Assessing occupants’ personal attributes in relation to human perception of environmental comfort: Measurement procedure and data analysis. Build. Environ. 2020, 177, 106901. [Google Scholar] [CrossRef]
- Morresi, N.; Casaccia, S.; Sorcinelli, M.; Arnesano, M.; Uriarte, A.; Torrens-Galdiz, J.I.; Revel, G.M. Sensing Physiological and Environmental Quantities to Measure Human Thermal Comfort Through Machine Learning Techniques. IEEE Sens. J. 2021, 21, 12322–12337. [Google Scholar] [CrossRef]
- Xie, J.; Li, H.; Li, C.; Zhang, J.; Luo, M. Review on occupant-centric thermal comfort sensing, predicting, and controlling. Energy Build. 2020, 226, 110392. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, H.; Luo, M.; Wang, Z.; Zhang, H.; Jiao, Y. Predicting older people’s thermal sensation in building environment through a machine learning approach: Modelling, interpretation, and application. Build. Environ. 2019, 161, 106231. [Google Scholar] [CrossRef] [Green Version]
- Tejedor, B.; Casals, M.; Gangolells, M.; Macarulla, M.; Forcada, N. Human comfort modelling for elderly people by infrared thermography: Evaluating the thermoregulation system responses in an indoor environment during winter. Build. Environ. 2020, 186, 107354. [Google Scholar] [CrossRef]
- Li, X.; Chen, Q. Development of a novel method to detect clothing level and facial skin temperature for controlling HVAC systems. Energy Build. 2021, 239, 110859. [Google Scholar] [CrossRef]
- Chaudhuri, T.; Zhai, D.; Soh, Y.C.; Li, H.; Xie, L. Random forest based thermal comfort prediction from gender-specific physiological parameters using wearable sensing technology. Energy Build. 2018, 166, 391–406. [Google Scholar] [CrossRef]
- Jia, M.; Choi, J.-H.; Liu, H.; Susman, G. Development of facial-skin temperature driven thermal comfort and sensation modeling for a futuristic application. Build. Environ. 2022, 207, 108479. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, Y.L.; Luo, M.H.; Zhang, L.; Zhang, Q.; Zhang, X. Thermal comfort under radiant asymmetries of floor cooling system in 2 h and 8 h exposure durations. Energy Build. 2019, 188, 98–110. [Google Scholar] [CrossRef] [Green Version]
- Pellerin, N.; Deschuyteneer, A.; Candas, V. Local thermal unpleasantness and discomfort prediction in the vicinity of thermoneutrality. Eur. J. Appl. Physiol. 2004, 92, 717–720. [Google Scholar] [CrossRef]
- Zhang, H.; Arens, E.; Huizenga, C.; Han, T. Thermal sensation and comfort models for non-uniform and transient environments, part III: Whole-body sensation and comfort. Build. Environ. 2010, 45, 399–410. [Google Scholar] [CrossRef] [Green Version]
- Ergonomics of the Physical Environment—Subjective Judgement Scales for Assessing Physical Environments; ISO 10551:2019; ISO: Geneva, Switzerland, 2019.
- Schweiker, M.; André, M.; Al-Atrash, F.; Al-Khatri, H.; Alprianti, R.R.; Alsaad, H.; Amin, R.; Ampatzi, E.; Arsano, A.Y.; Azar, E.; et al. Evaluating assumptions of scales for subjective assessment of thermal environments—Do laypersons perceive them the way, we researchers believe? Energy Build. 2020, 211, 109761. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 21 December 2021).
- Luo, M.; Xie, J.; Yan, Y.; Ke, Z.; Yu, P.; Wang, Z.; Zhang, J. Comparing machine learning algorithms in predicting thermal sensation using ASHRAE Comfort Database II. Energy Build. 2020, 210, 109776. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Zhang, H. Human Thermal Sensation and Comfort in Transient and Non-Uniform Thermal Environments; University of California: Berkeley, CA, USA, 2003. [Google Scholar]
- Jin, Q.; Li, X.; Duanmu, L.; Shu, H.; Sun, Y.; Ding, Q. Predictive model of local and overall thermal sensations for non-uniform environments. Build. Environ. 2012, 51, 330–344. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, R. Effect of local exposure on human responses. Build. Environ. 2007, 42, 2737–2745. [Google Scholar] [CrossRef]
- Shan, C.; Hu, J.; Wu, J.; Zhang, A.; Ding, G.; Xu, L.X. Towards non-intrusive and high accuracy prediction of personal thermal comfort using a few sensitive physiological parameters. Energy Build. 2020, 207, 109594. [Google Scholar] [CrossRef]












| ID | Sex | Age | Height (m) | Weight (kg) | BMI (kg/m2) | Questionnaires of Subjects | Participation Period |
|---|---|---|---|---|---|---|---|
| W1 | Male | 31 | 1.70 | 63 | 21.8 | 203 | 17 December 2020–19 January 2021 |
| W2 | Male | 26 | 1.79 | 63 | 19.7 | 203 | 17 December 2020–14 January 2021 |
| W3 | Male | 24 | 1.74 | 57 | 18.8 | 203 | 22 December 2020–27 January 2021 |
| W5 | Female | 22 | 1.61 | 48 | 18.5 | 204 | 15 January 2021–4 February 2021 |
| W6 | Male | 23 | 1.74 | 80 | 26.4 | 192 | 21 December 2020–7 February 2021 |
| M1 | Female | 23 | 1.60 | 52 | 20.3 | 160 | 19 September 2021–28 September 2021 |
| M2 | Male | 22 | 1.80 | 72 | 22.2 | 154 | 19 September 2021–28 September 2021 |
| M3 | Female | 25 | 1.62 | 65 | 24.8 | 155 | 19 September 2021–29 September 2021 |
| M4 | Female | 24 | 1.68 | 55 | 19.5 | 151 | 19 September 2021–28 September 2021 |
| M5 | Male | 23 | 1.76 | 76 | 24.5 | 160 | 19 September 2021–29 September 2021 |
| M6 | Female | 22 | 1.63 | 51 | 19.2 | 161 | 19 September 2021–29 September 2021 |
| M7 | Male | 22 | 1.78 | 66 | 20.8 | 156 | 19 September 2021–29 September 2021 |
| M8 | Female | 22 | 1.60 | 48 | 18.8 | 150 | 19 September 2021–30 September 2021 |
| M9 | Female | 21 | 1.74 | 68 | 22.5 | 154 | 19 September 2021–2 October 2021 |
| M10 | Male | 22 | 1.75 | 70 | 22.9 | 153 | 19 September 2021–1 October 2021 |
| M11 | Male | 22 | 1.75 | 60 | 19.6 | 151 | 19 September 2021–30 September 2021 |
| M12 | Male | 25 | 1.76 | 75 | 24.2 | 151 | 19 September 2021–2 October |
| M13 | Male | 23 | 1.70 | 66 | 22.8 | 155 | 19 September 2021–1 October |
| M14 | Female | 21 | 1.66 | 50 | 18.1 | 153 | 19 September 2021–1 October |
| Subject ID | M1 | M2 | M3 | M4 | M5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Questionnaires | 160 | 154 | 155 | 151 | 160 | ||||||||||
| Percent of votes | cooler | no change | warmer | cooler | no change | warmer | cooler | no change | warmer | cooler | no change | warmer | cooler | no change | warmer |
| Overall | 27.50 | 71.25 | 1.25 | 5.63 | 93.13 | 1.25 | 15.00 | 83.75 | 1.25 | 23.13 | 76.25 | 0.63 | 35.63 | 64.38 | 0 |
| Head | 17.53 | 78.57 | 3.90 | 14.94 | 84.42 | 0.65 | 16.88 | 82.47 | 0.65 | 16.88 | 82.47 | 0.65 | 18.83 | 81.17 | 0 |
| Face | 17.42 | 78.71 | 3.87 | 18.06 | 77.42 | 4.52 | 18.06 | 77.42 | 4.52 | 17.42 | 78.71 | 3.87 | 18.71 | 77.42 | 3.87 |
| Nape | 13.91 | 84.77 | 1.32 | 14.57 | 85.43 | 0 | 14.57 | 85.43 | 0 | 14.57 | 85.43 | 0 | 14.57 | 85.43 | 0 |
| Chest | 24.84 | 64.33 | 10.83 | 24.84 | 64.97 | 10.19 | 24.84 | 64.97 | 10.19 | 24.84 | 63.69 | 11.46 | 24.84 | 63.69 | 11.46 |
| Back | 40.51 | 58.23 | 1.27 | 22.15 | 77.85 | 0 | 17.72 | 82.28 | 0 | 37.34 | 62.66 | 0 | 32.28 | 67.72 | 0 |
| Upper arm | 15.48 | 81.94 | 2.58 | 16.77 | 83.23 | 0 | 17.42 | 82.58 | 0 | 17.42 | 82.58 | 0 | 15.48 | 84.52 | 0 |
| Lower arm | 12.67 | 78.67 | 8.67 | 9.33 | 90 | 0.67 | 8.67 | 90.67 | 0.67 | 10 | 88.67 | 1.33 | 12.00 | 86.00 | 2.00 |
| Wrist | 11.04 | 86.36 | 2.60 | 5.19 | 92.21 | 2.60 | 4.55 | 94.16 | 1.30 | 5.84 | 92.21 | 1.95 | 9.09 | 88.96 | 1.95 |
| Hand | 54.90 | 37.25 | 7.84 | 46.41 | 53.59 | 0 | 47.71 | 52.29 | 0 | 43.79 | 54.90 | 1.31 | 47.06 | 49.67 | 3.27 |
| Leg | 19.87 | 72.19 | 7.95 | 7.28 | 92.72 | 0 | 7.95 | 92.05 | 0 | 7.28 | 92.05 | 0.66 | 25.17 | 62.25 | 12.58 |
| Calf | 9.27 | 87.42 | 3.31 | 5.30 | 94.04 | 0.66 | 5.96 | 94.04 | 0 | 3.31 | 96.69 | 0 | 15.89 | 82.12 | 1.99 |
| Ankle | 49.68 | 49.03 | 1.29 | 36.13 | 63.23 | 0.65 | 54.19 | 45.81 | 0 | 41.94 | 51.61 | 6.45 | 65.16 | 34.84 | 0 |
| Foot | 22.22 | 57.52 | 20.26 | 10.46 | 88.24 | 1.31 | 16.34 | 82.35 | 1.31 | 19.61 | 74.51 | 5.88 | 18.95 | 75.16 | 5.88 |
| ID | W1 | W2 | W3 | W5 | W6 |
|---|---|---|---|---|---|
| S | 9 | 9 | 8 | 4 | 7 |
| N | 4 | 3 | 4 | 3 | 2 |
| Combination Type | Details of Body Parts | Accuracy | Cohen’s Kappa | AUC |
|---|---|---|---|---|
| Common A | Face, back, upper arm, calf | 0.87 ± 0.06 | 0.71 ± 0.11 | 0.91 ± 0.04 |
| Common B | Face, back, upper arm, wrist, calf | 0.88 ± 0.06 | 0.74 ± 0.11 | 0.93 ± 0.02 |
| Common C | Face, back, upper arm, leg, ankle | 0.88 ± 0.06 | 0.73 ± 0.11 | 0.94 ± 0.02 |
| Common D | Face, back, lower arm, leg, ankle | 0.88 ± 0.06 | 0.74 ± 0.12 | 0.94 ± 0.02 |
| ID | Common A | Common B | Common C | Common D | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | Cohen’s Kappa | AUC | Accuracy | Cohen’s Kappa | AUC | Accuracy | Cohen’s Kappa | AUC | Accuracy | Cohen’s Kappa | AUC | |
| M1 | 0.87 | 0.70 | 0.80 | 0.87 | 0.69 | 0.80 | 0.90 | 0.77 | 0.82 | 0.88 | 0.65 | 0.80 |
| M2 | 0.91 | 0.70 | 0.89 | 0.92 | 0.72 | 0.88 | 0.92 | 0.75 | 0.88 | 0.92 | 0.66 | 0.89 |
| M3 | 0.99 | 0.96 | 1.00 | 0.99 | 0.98 | 1.00 | 0.99 | 0.96 | 1.00 | 0.99 | 0.96 | 1.00 |
| M4 | 0.97 | 0.83 | 0.83 | 0.96 | 0.83 | 0.84 | 0.97 | 0.83 | 0.83 | 0.95 | 0.87 | 0.84 |
| M5 | 0.98 | 0.95 | 0.99 | 0.97 | 0.95 | 0.99 | 0.97 | 0.94 | 0.98 | 0.96 | 0.94 | 0.98 |
| M6 | 0.85 | 0.72 | 0.90 | 0.84 | 0.72 | 0.92 | 0.85 | 0.69 | 0.91 | 0.86 | 0.71 | 0.90 |
| M7 | 0.97 | 0.91 | 0.74 | 0.97 | 0.91 | 0.72 | 0.97 | 0.91 | 0.71 | 0.99 | 0.93 | 0.94 |
| M8 | 0.99 | 0.96 | 1.00 | 0.99 | 0.96 | 1.00 | 0.99 | 0.96 | 1.00 | 0.99 | 0.96 | 1.00 |
| M9 | 0.95 | 0.82 | 0.92 | 0.94 | 0.66 | 0.88 | 0.95 | 0.72 | 0.88 | 0.92 | 0.67 | 0.89 |
| M10 | 0.92 | 0.88 | 0.97 | 0.92 | 0.82 | 0.97 | 0.92 | 0.86 | 0.97 | 0.85 | 0.75 | 0.88 |
| M11 | 0.84 | 0.55 | 0.92 | 0.87 | 0.61 | 0.93 | 0.86 | 0.50 | 0.92 | 0.81 | 0.53 | 0.94 |
| M12 | 0.94 | 0.65 | 0.93 | 0.91 | 0.65 | 0.93 | 0.93 | 0.56 | 0.69 | 0.91 | 0.47 | 0.82 |
| M13 | 0.85 | 0.72 | 0.78 | 0.88 | 0.72 | 0.78 | 0.88 | 0.73 | 0.90 | 0.88 | 0.75 | 0.83 |
| M14 | 0.80 | 0.58 | 0.92 | 0.80 | 0.64 | 0.92 | 0.81 | 0.65 | 0.91 | 0.80 | 0.65 | 0.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Yu, H.; Tang, Y.; Luo, M.; Su, Z.; Li, C. Quantitative Investigation of Body Part Selection for Data-Driven Personal Overall Thermal Preference Prediction. Buildings 2022, 12, 170. https://doi.org/10.3390/buildings12020170
Zhang K, Yu H, Tang Y, Luo M, Su Z, Li C. Quantitative Investigation of Body Part Selection for Data-Driven Personal Overall Thermal Preference Prediction. Buildings. 2022; 12(2):170. https://doi.org/10.3390/buildings12020170
Chicago/Turabian StyleZhang, Kege, Hang Yu, Yin Tang, Maohui Luo, Zixiong Su, and Chaoen Li. 2022. "Quantitative Investigation of Body Part Selection for Data-Driven Personal Overall Thermal Preference Prediction" Buildings 12, no. 2: 170. https://doi.org/10.3390/buildings12020170
APA StyleZhang, K., Yu, H., Tang, Y., Luo, M., Su, Z., & Li, C. (2022). Quantitative Investigation of Body Part Selection for Data-Driven Personal Overall Thermal Preference Prediction. Buildings, 12(2), 170. https://doi.org/10.3390/buildings12020170








