Impacts of Courtyard Envelope Design on Energy Performance in the Hot Summer–Cold Winter Region of China

Abstract

This paper aims to investigate the effects of courtyard envelope design on the energy performance of office buildings in the hot summer–cold winter region of China. Two types of courtyard buildings were simulated with 200 energy models by changing the following variables: window–wall ratio (south, north, east, and west walls), window U-value, wall U-value, solar heat gain coefficient, and orientation. The treed Gaussian process (TGP) sensitivity analysis method was employed to quantify the contributions of parameters related to courtyard design that result in the changes of annual cooling, heating, lighting, and total energy consumption. The results show that the courtyard envelope design has a significant effect on the energy consumption in this case study. The most influential factor affecting annual cooling energy consumption and the annual total energy consumption is the orientation, which is responsible for 37% and 81%, respectively, in two layouts to annual cooling energy use. The corresponding proportion increased to 45% and 86% in terms of the total energy consumption. The most influential factor influencing annual heating energy use is the window U-value, which explained nearly 60% of the changes to the heating energy use. The effect of the solar heat gain coefficient in two kinds of layouts is as high as 82% and 79% for lighting energy use in this case study. Due to the different courtyard forms, the magnitude of the effect of the parameters on energy consumption and the main trend of the effect is slightly different.

1. Introduction

With the increase in environmental and energy problems, the world of sustainable development faces more and more challenges, particularly in the building energy efficiency field. Courtyards as the typical and traditional building form have been distributed around many different places of the world [1]. The oldest Chinese courtyard building could be traced back to 5000 years ago [2]. According to the historic experiment, courtyard spaces are often regarded as microclimate modifiers, which can improve the thermal comfort of both outdoor and indoor spaces. As passive design strategies in houses or public buildings [3], courtyards can mitigate the urban heat island effects and reduce the energy demand as well as increase the natural light and ventilation [4]. Meanwhile, courtyards have some social and cultural benefits due to the safe and private spaces to activate lots of activities such as gardening, conversing, working, and playing.

This research focuses on the impact of courtyard design on the energy consumption of office buildings in the hot summer–cold winter region of China. Courtyards offer considerable potential for saving energy, which depends on the design characters such as courtyard shape, size, envelope, vegetation, and orientation. According to previous studies, the amount of solar radiation has an important effect on the energy performance of courtyard buildings. Therefore, one of the most important goals of courtyard design is to reduce solar heat gain during the hot seasons and increase daylight as well as sunlight in cold seasons [5].

Many studies have been conducted to examine the influence of courtyard design on energy consumption. Previous studies suggested that the energy performance of courtyard buildings has obvious distinctions in different climates and microclimates. Aldawoud [6] evaluated the energy performance of courtyard buildings in four different cities located in cold, temperate, hot–humid, and hot–dry climatic regions, respectively. Their results showed that the courtyard is more energy efficient in hot–dry and hot–humid climates compared to temperate and cold climates. Taleghani et al. [7] indicated the effects of courtyard spaces on heating energy demand to dwellings in the Netherlands by 2050. Results showed that climate change affected the heating energy demand as well as thermal comfort and courtyards, which can improve energy efficiency from May to October. Fatemeh Biabani Moghadam Baboli et al. [8] examined the design characteristics of thirty-four courtyard houses in the moderate climate of Iran. Results suggested that courtyards can adapt to the moderate and humid climatic region besides the hot and arid climatic region. Regarding the climatic factors, the orientation and ventilation have a significant effect on the thermal and energy performance of courtyard buildings. Taleghani et al. [9] studied the thermal performance of courtyards with different orientations in the Netherlands and pointed out that they were the least and most comfortable indoor environments in North–South and East–West orientations, respectively.

In other studies, the effects of courtyard configurations on energy consumption have been investigated to optimize courtyard form design. Aldawoud et al. [10] compared the energy performance between courtyard and atrium and found out that courtyards are more energy efficient compared to the atrium in low-rise buildings. Muhaisen et al. [11] explored the effect of proportions of the courtyard on energy demand and proved that deep courtyard forms were preferable to reducing the cooling and heating loads. Moreover, Muhaisen [12] pointed out that courtyard proportions have critical effects on the shading of the courtyard internal envelope. Martinelli et al. [13] examined the influence of height/width proportions of the courtyard on thermal comfort. Results showed that this factor can affect solar access to adjust the indoor thermal comfort and also suggested that the optimum height/width proportions were 4:5 to 5:5 in warmer climates and 3:5 to 4:5 in colder climates. Manioğlu et al. [14] examined reducing heating and cooling loads by varying the proportion of the courtyard. The results showed that the width/length ratio has a significant effect on energy demand and also indicated that the influence of the proportion on energy performance in winter was more efficient than in summer in the hot–dry region of Turkey. Kubota et al. [15] examined the vernacular passive cooling strategies such as night ventilation, roof or ceiling insulation, window or wall shading, and courtyard or forced ventilation in a hot–humid climate Malaysia. The results showed that the small courtyard can enhance ventilation and release heat at night. Yaşa et al. [5] pointed out that an optimum courtyard ratio is a form that allows minimum radiation during summer and maximum radiation during winter.

In another study strand, the material, construction, facing, and shading of courtyard walls that affect the energy performance were discussed. Aldawoud [6] pointed out that the decrease in courtyard glazing U-value and the window-to-wall ratio were beneficial to reduce the energy consumption. Taleghani et al. [9] suggested that roof and courtyard greening was the most effective strategy to mitigate heat gain. Cantón et al. [16] assessed the effect of geometry and shade of the courtyard on the energy and thermal conditions in a school building. The results indicated that the efficient shading of the courtyard has enormous effects on the energy conditions of classrooms in Mendoza, Argentina, which is a semi-dry area characterized by cold winters and hot summers. Vaisman et al. [17] examined courtyard design on the energy performance and natural light in houses in the cold climate of Toronto. The main results showed that internal courtyards can improve the illuminance hours from 9% to 20% and the window-to-wall ratio played an important role in influencing the energy load but does not affect the hours of daylight inside the house. Ghaffarianhoseini et al. [18] evaluated unshaded courtyard variables such as orientations, height, the albedo of the wall enclosure, and the use of vegetation on the thermal performance of courtyards in the hot and humid climate of Kuala Lumpur, Malaysia. As a result, the study showed that proper location and orientation as well as increasing the height and albedo of wall enclosures and abundant vegetation of the courtyard can improve the courtyard thermal comfort and provide cooling well in summer. Sadafi et al. [19] explored the effects of the internal courtyard on the indoor thermal performance of its surrounding spaces of terrace housing in tropical climate regions. Results showed that suitable shading devices and materials of courtyard walls can relieve the negative influence of solar radiation. Berkovic et al. [20] pointed out that the contribution of wind to the thermal comfort of the courtyard was much smaller than the shade, and the courtyard orientation has a decisive effect on the amount of shade. Farzaneh et al. [21] examined the impact of courtyard design variants including geometrical properties and orientation on the shading performance of traditional courtyard houses in the hot–arid climate of Iran. The results showed that the courtyard’s design variants have a considerable influence on the shading performance of courtyards, and decreasing the length-to-width ratio was a benefit to obtain more shading, and they also found out that square-shaped courtyards performed better than rectangular shapes and increasing the rotation angle from the north direction can decrease the shading area. Al-Masri et al. [22] evaluated the design parameters such as the number of floors, glazing type, wall thickness, insulation type, and thickness on the performance of a courtyard building in the hot–arid climate of Dubai. Results showed that the courtyard form can provide more usable daylight than the conventional form during both winter and summer.

Previous studies mainly concentrated on the influence of climatic, geometrical, and physical factors of a courtyard on the energy performance, which had two obvious deficiencies. On the one hand, the received solar radiation by courtyard walls is considered to be the predominant factor affecting the thermal and energy performance of the building. Similarly, the efficient courtyard walls as the heat exchange boundary can ensure adequate solar radiation accessibility in winter as well as prevent the solar heat gain in summer, which can maintain good thermal comfort in the surrounding building. However, the effects of courtyard walls or internal envelopes on energy performance have been rarely studied. In particular, the key design variables of the courtyard envelope for improving energy efficiency are not clear. On the other hand, in regard to the interaction of different factors and the complexity of their effects on the performance of courtyard buildings, it is necessary to explore the effects of courtyard design parameters using the multi-parameter analysis method. However, most of the previous studies analyzed the design parameters only considering a single parameter.

As a multi-parameter analysis method, global sensitivity analysis has been widely applied in various models of parameter analysis and optimization [23]. In the field of building energy performance, this method was used to compare the relative importance of various parameters [24,25,26,27,28,29,30]. However, the study of courtyard buildings using the global sensitivity analysis method is still in its infancy. Therefore, the global sensitivity analysis method was employed in this study to explore the effects of multi-parameters on the energy performance of courtyard buildings.

This research aims to explore the relationship between courtyard envelope design and energy performance and identify the key parameters that should be paid more attention to in the early architectural design and renovation stages. The meta-model sensitivity analysis method has been utilized to explore the influence of each design parameter on the energy performance with the change of all parameters. Moreover, the ranking of the sensitivity index of parameters and the momentous variable will be recognized to determine primary factors in courtyard design. The annual cooling, heating, lighting, and total energy consumption of the 400 office courtyard buildings have been calculated, which are located in Wuhan (30° N, 114° E), which is a typical city of the hot summer–cold winter region of China. In order to evaluate the energy use, two kinds of courtyard forms are chosen with various orientations, and envelope designs have been simulated by computer simulation tools. This study can provide a theoretical basis for the low energy and sustainable design of courtyard buildings.

2. Materials and Methods

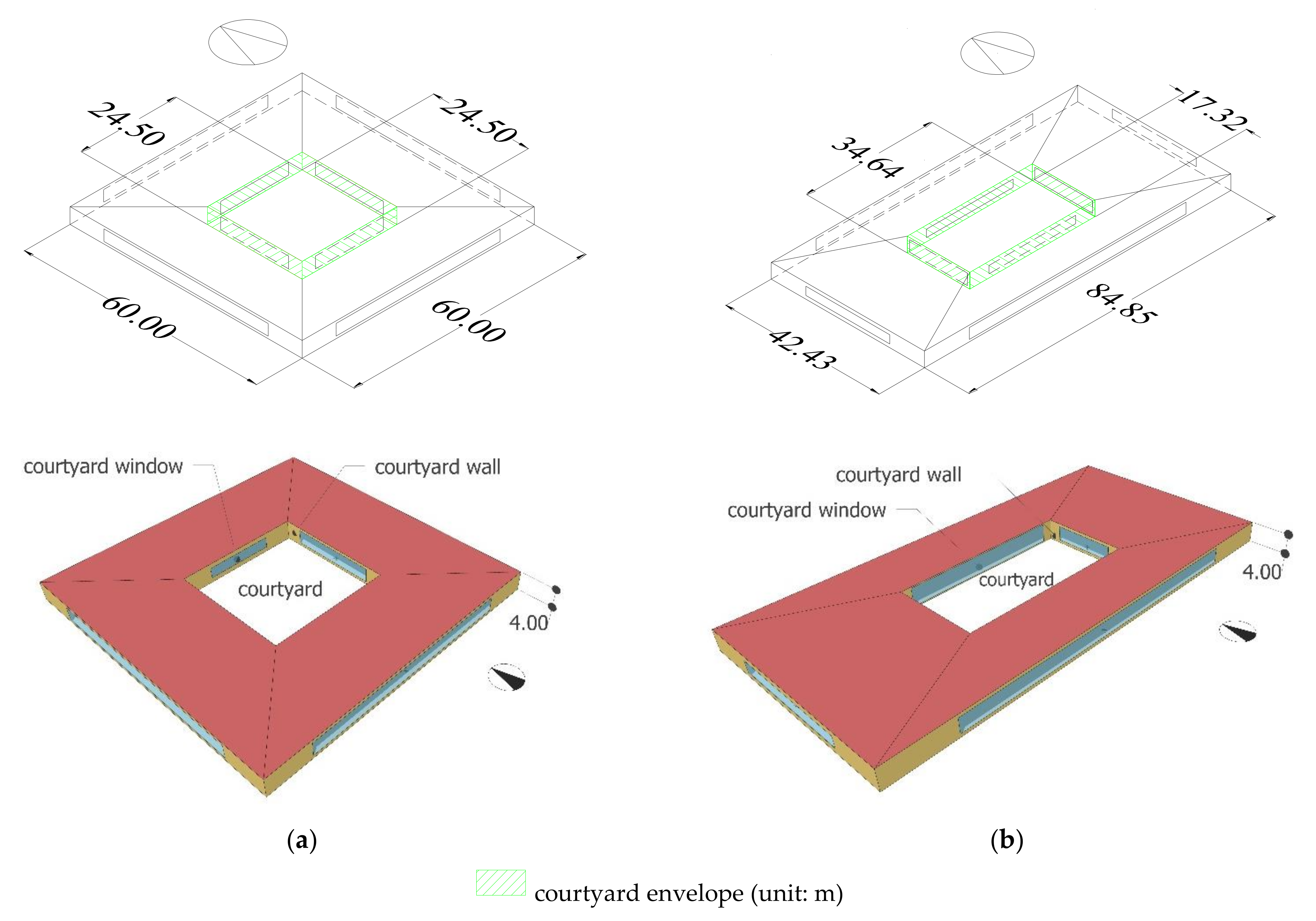
2.1. Geometric Model

The difference between the atrium and courtyard is that the atrium has a skylight, while the courtyard has no skylight. The object of this paper is courtyard buildings. Considering that the research object is the middle floor of the building, which only contacts the upper and lower floors and does not directly contact the ground, the influence of the ground area and ground reflection on the case building heat load is not considered. Therefore, this study takes the courtyard wall as the basic research object. To distinguish the courtyard wall from the building external wall, this paper refers to the external wall surrounding the courtyard as the courtyard envelope. Two standard layer buildings with central closed courtyards were used as study cases to represent square and rectangle shape, which were named case A (square) and case B (rectangle), respectively (see Figure 1). Both of the two cases have the same building and courtyard area, which is 3000 m² and 600 m², respectively. The height of the two cases is 4 m. The ratio of length to width (L/W) is the main difference between case A and case B. For case A, both the building and courtyard have the same L/W ratio, which is equal to 1. In addition, the ratio of window to wall for all the external walls is 0.5, which can avoid the impact of the window or wall areas in a different direction on energy consumption. For case B, the L/W ratio of both the building and courtyard is 2, the ratio of window to wall in the north and south walls is 0.5, and that in the east and west walls is 0.3.

2.2. Energy Models and Parameter Settings

The courtyard building energy models are created and calculated by using the dynamic energy simulation software EnergyPlus (8.1, Department of Energy and Lawrence Berkeley National Laboratory, Berkeley, CA, USA). We select ASHRAEClearSky for solar modeling in the calculation of the solar radiation in the winter design days and ASHRAETau for solar modeling in the summer design days. Each model is divided into four zones with the same area: namely, north, south, east, and west. The standard layout of the upper and lower floors is set to adiabatic, and all the external envelopes can have indoor and outdoor heat transfer. Each thermal zone is equipped with two natural lighting controllers with a height of 0.8 m. When the indoor natural light is less than 500 lux, the artificial lighting is automatically activated. Meteorological parameters are derived from the EnergyPlus website using the typical weather data of Wuhan, China. The HVAC (Heating Ventilation and Air Conditioning) system uses fan coils plus a fresh air system. Internal heat gains and hourly schedules for these gains are based on the “Public building energy efficiency design standards” (GB50189-2015) [31]. The output of the model is the cooling, heating, lighting, and total energy consumption per unit of building area (unit: kWh·m⁻²). Both heating and cooling in this building are provided by a heat pump system. Hence, all the energy in this building is supplied from grid electricity.

On the one hand, the impact of solar radiation on the building is mainly achieved through the outer envelope structure. On the other hand, the courtyard increases the impact of solar radiation. Therefore, this paper chooses eight design parameters: the building orientation, the heat transfer coefficient of the external window, the heat transfer coefficient of the external wall, the solar heat coefficient, and the window wall ratio in four dimensions (i.e., north, south, west, and east) of the courtyard as the design parameters. The range of each parameter is selected according to the “Design Standard” in China (GB50189-2015) [31], and the specific parameters are set in

Table 1. Input parameters for energy model.

Parameters	Abbreviation	Range	Unit
East window–wall ratio	EWW	0.1–0.8
West window–wall ratio	WWW	0.1–0.8
South window–wall ratio	SWW	0.1–0.8
North window–wall ratio	NWW	0.1–0.8
Window U-value	GU	1.0–2.5	W·m−2·K−1
Wall U-value	WU	0.15–0.35	W·m−2·K−1
Solar heat gain coefficient	SG	0.25–0.5
Orientation	OT	0–180	°

. In addition, when the building faces 0°, the direction is north and south, from 0° to 180°, and the building changes clockwise.

2.3. Methods

2.3.1. Sensitivity Analysis

Sensitivity analysis is a method of studying how the uncertainty associated with the input parameters of the model affects the output of the model [23], i.e., the effect of uncertain parameter input on model output uncertainty. There are two types of sensitivity analysis, i.e., local sensitivity and global sensitivity analysis. The global sensitivity includes regression-based methods, screening methods, variance-based methods, and meta-model methods [29,32,33]. With the capability to analyze the complex nonlinear models, the meta-model method was employed in this study [34]. The treed Gaussian process (TGP) is a combination of Gaussian processes and decision trees, which is suitable for nonparametric and non-static regression models [35]. TGP sensitivity analysis is a mixture of TGP and Sobol sensitivity methods [35], which is characterized by:

(1)

A little calculation: It can calculate by creating a model with a small amount of energy consumption.

(2)

Practical: It is suitable for nonlinear, dynamic regression, and other complex models.

(3)

Quantitative analysis: The effect of parameters on model output can be quantified.

(4)

Interval estimation: The impact of the parameters on the model output is an interval rather than just a point value, which is more reliable.

TGP sensitivity analysis has two sensitivity indicators, namely the first-order effect and total effect. The larger the indices, the more important the parameter. The calculation formulae for two sensitivity indicators calculation follow [35]:

$${\mathrm{S}}_{\mathrm{i}}=\frac{\mathrm{V}\left(\mathrm{E}\left({\mathrm{Y}|\mathrm{X}}_{\mathrm{i}}\right)\right)}{\mathrm{V}\left(\mathrm{Y}\right)}$$

(1)

$${\mathrm{T}}_{\mathrm{i}}=1-\frac{\mathrm{V}\left(\mathrm{E}\left({\mathrm{Y}|\mathrm{X}}_{~\mathrm{i}}\right)\right)}{\mathrm{V}\left(\mathrm{Y}\right)}$$

(2)

where S_i is the first-order effect, Y is the response, X_i is the i-th input variable, and X_~i are the entire variables except for the i-th variable. The above calculation suggested that the ranges for both first-order and total effects are between 0 and 1. The first-order effect Si represents the main effect contributions of the i-th input factor to the variance of the response. Compared to the first-order effect, the total effect considers not only the independent influence of the i-th input factor but also all high-order interaction effects among input variables. The difference between the two indicators is the interaction effects between the i-th input and all the remaining input variables.

TGP sensitivity analysis follows two steps. First, based on the 400 group design parameters and energy consumption data, the machine learning model can be established by TGP. Second, the Sobol method is used to analyze the results of the model and to calculate the contribution of changes of each parameter to changes in energy consumption. In addition, to facilitate the comparison of the sensitivity of different parameters and to avoid the interference of the unit, the parameters and model outputs are standardized. In the following main effect trend graph, the parameter value is from small to large in the interval [−0.5,0.5], the output result (effect) mean is 0, and the interval is 1. R tgp package is used to conduct the meta-model sensitivity analysis.

2.3.2. Calculation Procedure

The sensitivity analysis can be divided into three steps as below.

(1)

Sampling and combination of design parameters

The sampling and combination of design parameters are generated by using R language programming. The Latin-hypercube sampling (LHS), which is widely used in simulation experiments, has the advantages of better uniformity in spatial distribution and avoiding repeated sampling [29]. Therefore, LHS was employed in this study to sample the design parameters uniformly. The number of samples is determined by the particular analytical method. In the meta-model analysis, the sampling is usually based on the principle that the sampling number is at least 10 times the parameters. There are 8 parameters considered in this study. Therefore, at least 80 times samples are required. To achieve better convergence of the model, 200 times are sampled for each case, and then 400 models can be built in total for this study.

(2)

Construction and calculation of energy model of building

Firstly, SketchUp software is used to build the geometry model, which is then imported into the EnergyPlus to set up parameters and conduct calculations. The above process can generate a new model as the basic energy model. After that, R language is adopted to rewrite the basic energy consumption model where the parameters of the sample data are placed to create 400 dynamic energy consumption models. Finally, the models are calculated by using the EnergyPlus software to obtain output data such as cooling, heating, lighting, and total energy consumption.

(3)

Sensitivity analysis

R language is used to collect energy consumption data. Consequently, TGP is used to analyze the sensitivity of each parameter.

3. Results

This paper explores the influence of design parameters on energy consumption from two case buildings reported in the previous section. The following diagrams presented in the form of probability density curve and bar chart show the result of energy consumption, while the results of the sensitivity analysis are demonstrated in a set of three charts: namely, the main effect, the first-order effect, and the total-order effect.

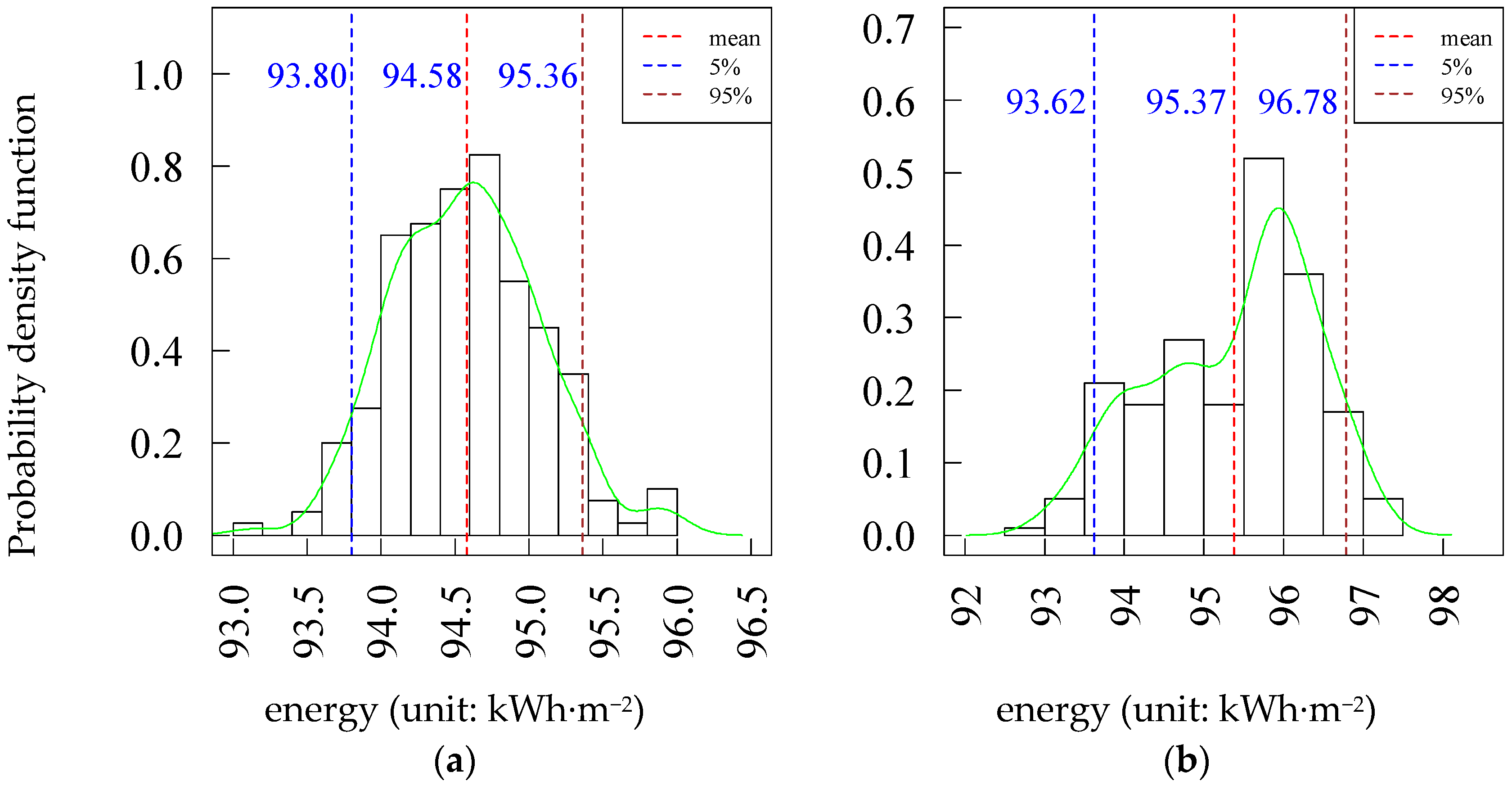
3.1. Cooling Energy Use

It can be observed from Figure 2 that the distribution of cooling energy use in case A is similar to the normal distribution. The cooling energy use is a left-skewed distribution. The mean of energy distribution is 36.18 kWh·m⁻² and 36.24 kWh·m⁻² in case A and case B, respectively. From the 90% cooling energy consumption, case B energy consumption is slightly higher than that of case A. In addition, the range of main energy consumption in case B (34.56–37.82 kWh·m⁻²) is much larger than that of case A (35.38–37.06 kWh·m⁻²). This suggests that under the influence of multiple parameters, the cooling energy consumption distribution of case A is more concentrated than that of case B.

Figure 3 shows the results of sensitivity analysis for the two case buildings. The three subplots represent mean main effects, first-order effect, and total effect for the corresponding variables. Figure 3a shows the change of output as a function of input variables. As can be seen from this figure, there exist linear relationships between annual cooling energy use and the inputs except for the orientation (OT). In the linear relationship, an increase in each variable would lead to a rise in cooling energy use except for the window U-value (GU). In the nonlinear relationship, when the number of the orientation (OT) becomes larger (from 0° to 180°), the cooling energy use has four extremes: the maximum datum appearing at about 30° and 120° and the minimum value appearing at about 60° and 150° in case A, while there is one peak at about 80° in case B.

Figure 3b illustrates the first-order effect on cooling energy use. The two dominant factors influencing cooling energy use are the orientation (OT) and solar heat gain coefficient (SG) in case A, while the orientation (OT) is the most important factor affecting cooling energy in case B. The orientation (OT) accounts for 30–40% of the variations of the output in case A, and this proportion rises to about 80% in case B. The next important variable is the solar heat gain coefficient (SG) affecting nearly 30% of the cooling energy use in case A, and it falls to about 10% in case B. The remaining factors only made a minor contribution to the uncertainty in cooling energy use. Even if the wall and windows area of each internal envelope is uniform, the shaded and sunlit areas of the internal envelope are different as the orientation becomes changed. Accordingly, different orientation of the courtyard building results in the change of heat gain and loss. When the area of each internal envelope is different, the influence of the orientation on cooling energy can be reinforced. Hence, the first effective measure for reducing cooling energy in these cases is to find the optimal orientation in every condition.

Figure 3c illustrates the total order effect on the cooling energy use. The influential factors to the cooling energy use are the same in the first-order effect and total effects for both case A and case B. However, the interactions between the variables are not the same in different cases. The total effects for most variables are greater than the first-order effects in case A, while the interactions between the variables are not significant in case B.

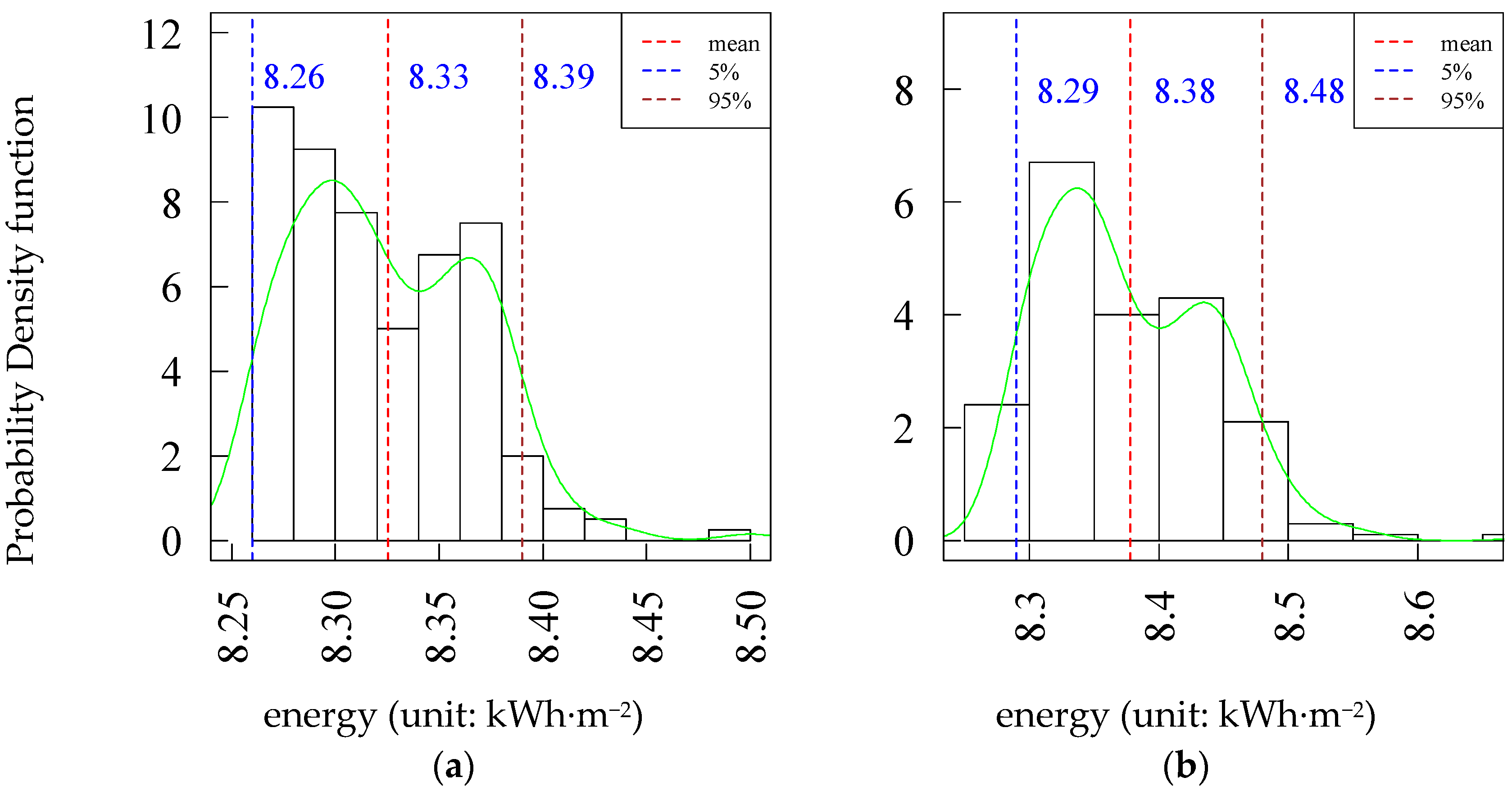
3.2. Heating Energy Use

It can be observed from Figure 4 that the distribution of the heating energy consumption in case A is similar to that in case B. Meanwhile, the distribution patterns are high in the middle and low on both sides. However, from the 90% range of the energy data, the heating energy consumption range in case A is 15.87–17.08 kWh·m⁻², and for case B, it is 16.54–17.79 kWh·m⁻². This suggests that the square courtyard (CR = 1:1) is more suitable than the strip form (CR = 1:2) from the viewpoint of saving heating energy consumption. In terms of the difference between 95% and 5% energy consumption, the fluctuations of the two cases are similar: for example, 1.21 in case A and 1.25 in case B. It is indicated that the influences of the eight parameters of different courtyard buildings on heating energy consumption are similar.

Figure 5a shows the change of the heating energy use due to the mean of the main effects of eight variables. With an increase in the orientation (OT), the pattern of influence of the heating energy use has three extreme points for both cases. When the orientation (OT) is about 45° and 135°, the heating energy reached a peak, and the smallest number is about 90°. This point is quite different with regard to the influence of orientation (OT) on cooling energy. It is worth noting that the influence of the same parameter on different kinds of energy use is different, which may have the opposite effect. Hence, the design strategy should be selected carefully according to the focus of energy saving. Similarly, all these changes are almost linear or monotonic except for the change of output caused by the orientation (OT). Increasing the window U-value (GU) would result in an evident rise in annual heating energy, and the solar heat gain coefficient (SG) has a contrary effect.

Figure 5b,c show the first-order and total effects of sensitivity indices for all eight input factors, which affect annual cooling energy. The window U-value (GU) is a dominant factor to be responsible for around 60% of the variance of the output in both cases. Therefore, it is very important to install low U-value windows to reduce the heating energy use in these buildings. The next important variable is the solar heat gain coefficient (SG), which accounts for nearly 20% of the total variations of the output. The remaining factors have minor influences on heating energy in both cases. In addition, the interactions between the variables are not significant in the two cases on heating energy.

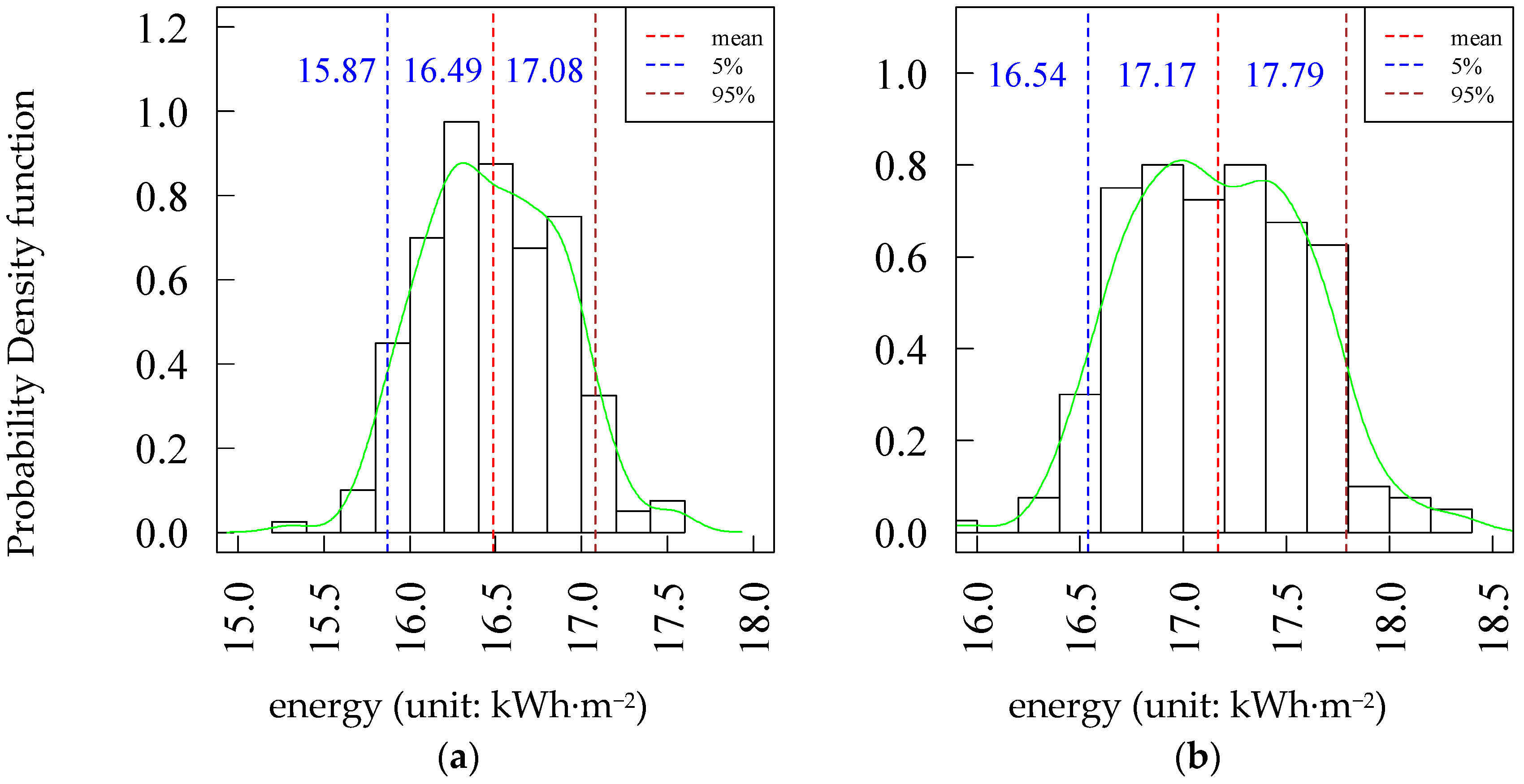
3.3. Lighting Energy Use

It can be observed from Figure 6 that the distribution of lighting energy consumption shows obvious primary and secondary peaks with a right-skewed distribution. In case A, the values of 8.26–8.39 kWh·m⁻² cover almost most of the lighting energy consumption, while case B, the values range from 8.29 to 8.48 kWh·m⁻². The mean of lighting energy consumption of case B is greater than that of case A, and the energy consumption data of case B are more spread compared with case A. It is worth noting that the possibility of high lighting energy in case B is larger than that in case A. If not handled properly, it may cause high energy consumption.

Figure 7a shows the change of the lighting energy use due to all eight variables. As can be seen from Figure 7a, there are linear or monotonic relationships between annual lighting energy and all the input factors except for the orientation (OT). The trend that the lighting energy is changed with the increase in the solar heat gain coefficient (SG) is nearly one peak value of the symmetric curve. The increase in the solar heat gain coefficient (SG) would decrease lighting energy rapidly. As is shown in Figure 7a, the lighting energy use would decrease dramatically when the east window–wall ratio (EWW) changes from −0.4 to −0.2 (that equals the actual data 0.1–0.3). After that, the speed of decrease in lighting energy use becomes slow with an increase in the east window–wall ratio (EWW) (from 0.3 to 0.8).

Figure 7b,c show the first-order and total effects of sensitivity indices for all eight input factors affecting lighting energy use. The solar heat gain coefficient (SG) is a dominant factor in these two cases accounting for around 80% of the total variations of the output, which is markedly higher than any other factors in terms of both the first-order and total effects of sensitivity index. Note that the east window–wall ratio (EWW) is the most important variable in the four ratios of window to wall on lighting energy. However, the impacts of all four window-to-wall ratios are very weak on lighting energy. As a result of the limitations of the area and self-shading of the courtyard, the change of all the window-to-wall ratios does not cause a significant difference in lighting energy. Therefore, the reduction of the solar heat gain coefficient (SG) is more efficient than the increase in the window-to-wall ratios of the courtyard using natural lighting to reduce the artificial lighting in these two cases. In addition, natural lighting not only can reduce the lighting energy but also affect the change of cooling and heating energy. Hence, the optimization of part of the parameters should consider the impact of a variety of types of energy consumption.

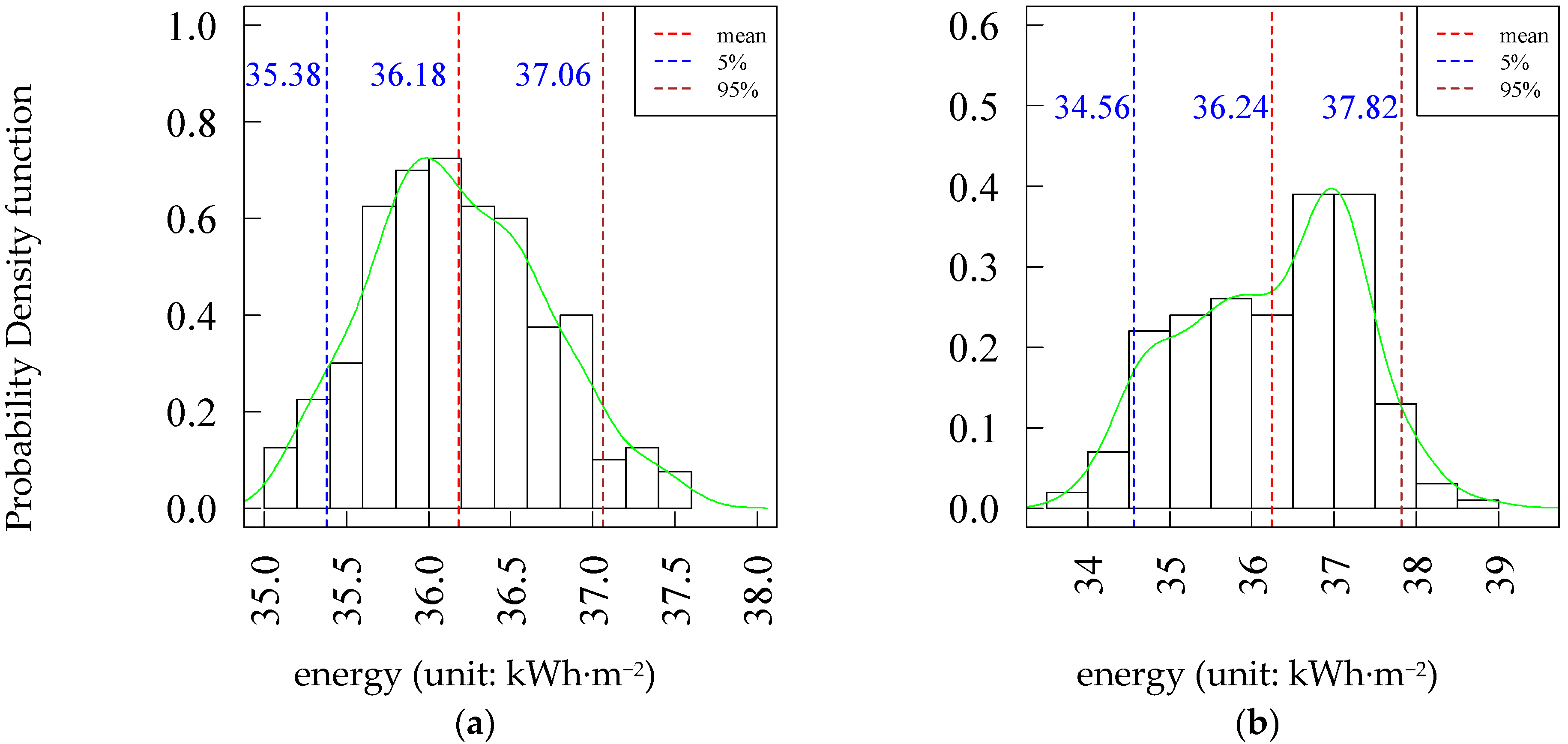
3.4. Total Energy Use

As can be seen from Figure 8, the distribution of total energy consumption of the two cases is significantly different. The distribution pattern of case B shows an obvious left-skewed, and case A’s distribution is more concentrated than case B. The total energy consumption of case A is concentrated from 93.80 to 95.36 kWh·m⁻², while case B is between 93.80 and 95.36 kWh·m⁻². It is worth noting that the energy of case A is more likely to be less than that of case B.

Figure 9a shows the results of sensitivity analysis of the mean main effect of input variables on annual total energy for both cases. The relationship between the orientation (OT) and total energy is nonlinear, which is similar to the pattern of influence on cooling energy. The relationships between the remaining input parameters (except for the building orientation) and the total energy use are approximately linear, as shown in Figure 9a. The total energy use in these two buildings would increase with these input parameters, including the wall U-value, window U-value, solar heat gain coefficients of windows, and window–wall ratios.

As can be seen from Figure 9b,c, the only dominant factor is the orientation (OT), which can, respectively, explain around 45% and 80% of the variation of total energy in cases A and B. In addition, the difference of sensitivity analyses results between these two cases is that case A’s interactions among variables are more significant than those in case B. Without considering other factors and external shading, orientation has the greatest impact on energy consumption compared to window–wall ratio, window U-value, wall U-value, and solar heat gain coefficient. Therefore, choosing the appropriate orientation is a very important energy-saving measure. In addition, the effect of each parameter on total energy in the different forms of courtyard building is not the same.

4. Discussion

(1)

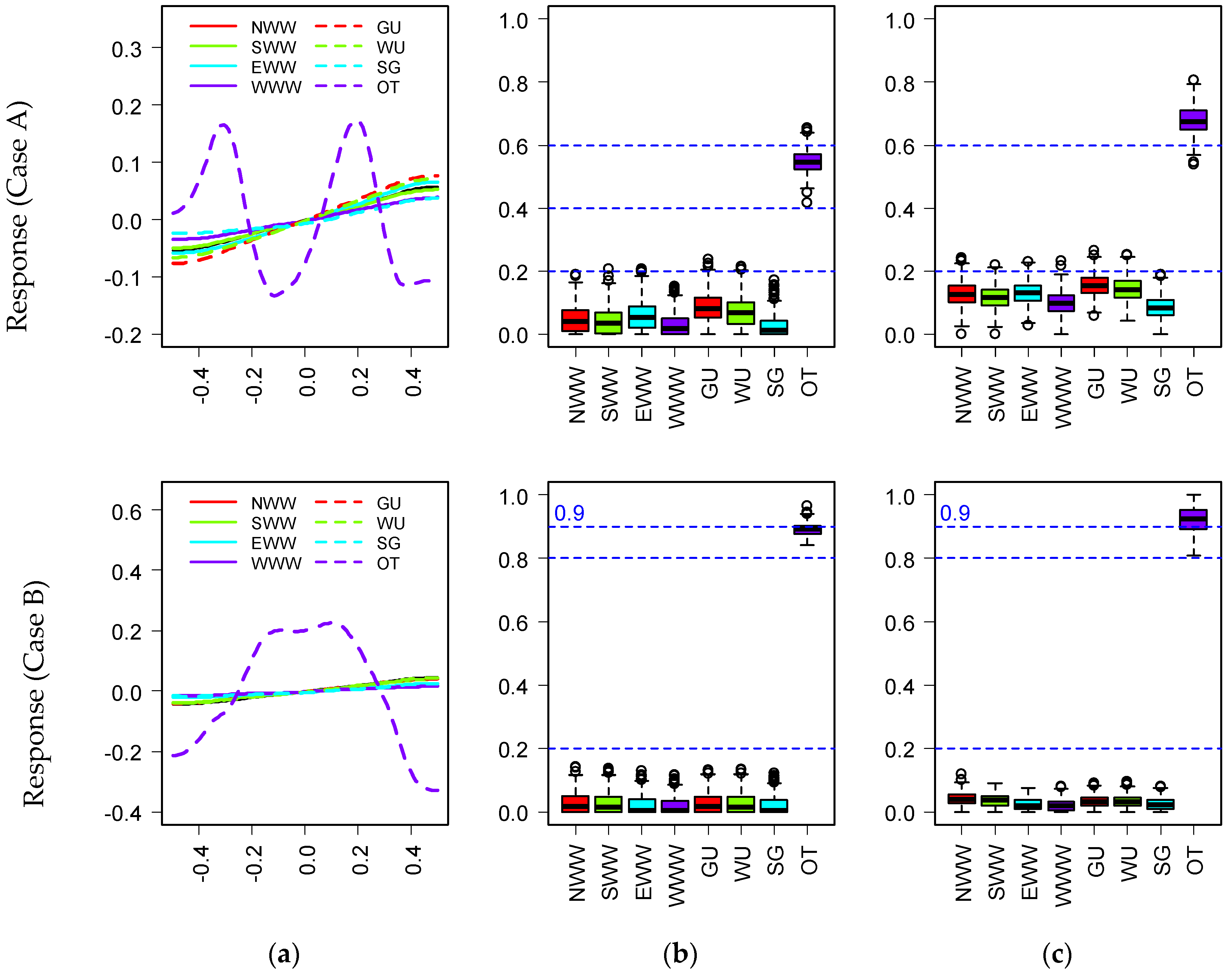
The annual cooling energy use is about two times the heating energy use and about four times the lighting energy use. Therefore, the most important parameter affecting cooling energy use is also the key parameter influencing total energy. In addition, due to the probability density of energy use, both the single energy (cooling, heating, and lighting energy) use and total energy in case B are higher than that in case A.

(2)

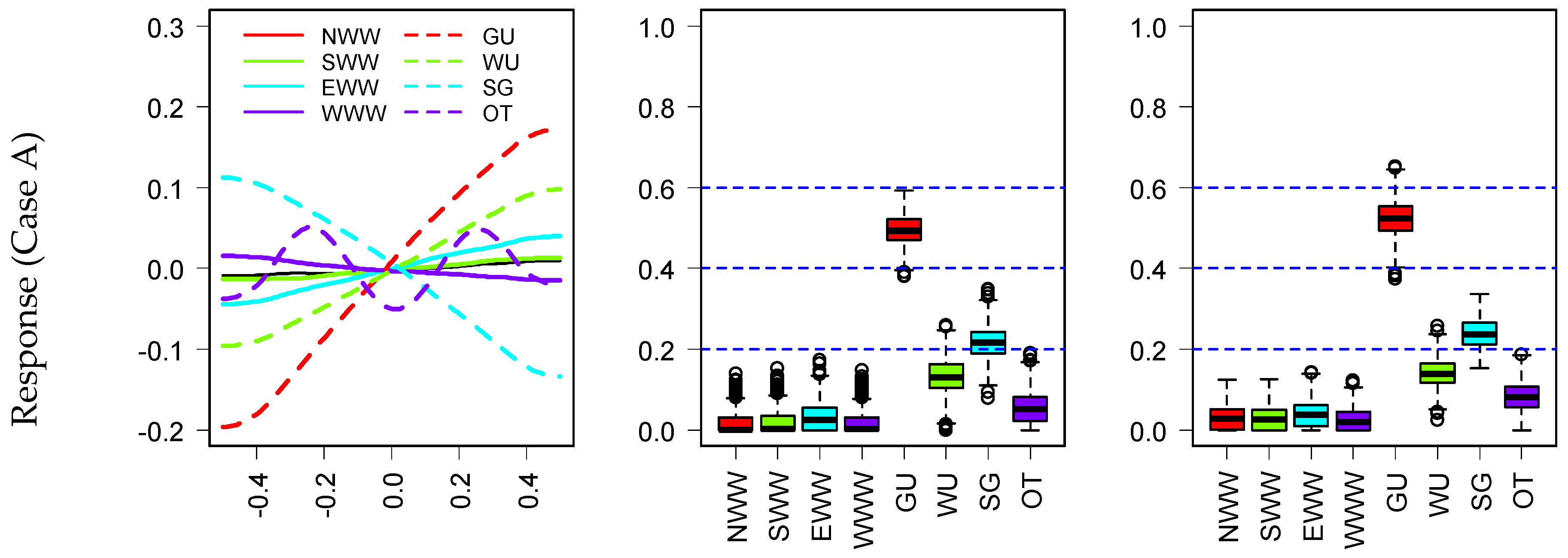
In case A, the influence pattern of the orientation (OT) on the cooling, heating, lighting, and total energy use has a significant symmetry, the reason of which is that the area of the courtyard walls and windows in four directions is equal. This leads to the same solar radiation absorbed in the symmetrical orientation.

(3)

The impact of the identical parameter on different kinds of energy use is different, and the key parameters affecting the different kinds of energy use are not the same. Hence, the targeted energy-saving strategy should be proposed based on the specific relationship between input parameters and particular energy use.

The ranking and mean of the main effects of eight input variables on various kinds of energy use are listed in

Table 2. Mean of the main effect and ranking for two cases.

Parameters	Cooling Energy (Ranking)		Heating Energy (Ranking)		Lighting Energy (Ranking)		Total Energy (Ranking)
	Case A	Case B	Case A	Case B	Case A	Case B	Case A	Case B
NWW	0.0447(5)	0.0274(4)	0.0193(7)	0.0211(7)	0.0188(6)	0.0185(6)	0.0623(3)	0.0355(2)
SWW	0.0301(6)	0.0226(7)	0.0191(8)	0.0219(6)	0.0194(5)	0.0189(5)	0.0404(5)	0.0278(5)
EWW	0.0268(7)	0.0241(6)	0.0389(4)	0.0262(5)	0.1028(2)	0.1114(2)	0.0609(4)	0.0288(4)
WWW	0.0507(4)	0.0255(5)	0.0198(6)	0.0191(8)	0.0186(7)	0.0181(7)	0.0321(6)	0.0221(6)
GU	0.0545(3)	0.0313(3)	0.5913(1)	0.5956(1)	0.0195(4)	0.0196(4)	0.1190(2)	0.0354(3)
WU	0.0177(8)	0.019(8)	0.0312(5)	0.0307(4)	0.0184(8)	0.0180(8)	0.0251(8)	0.0204(8)
SG	0.2793(2)	0.0886(2)	0.1890(2)	0.1818(2)	0.8229(1)	0.7858(1)	0.0269(7)	0.0217(7)
OT	0.3673(1)	0.8111(1)	0.0635(3)	0.0615(3)	0.0377(3)	0.0498(3)	0.4513(1)	0.8564(1)

.

(1)

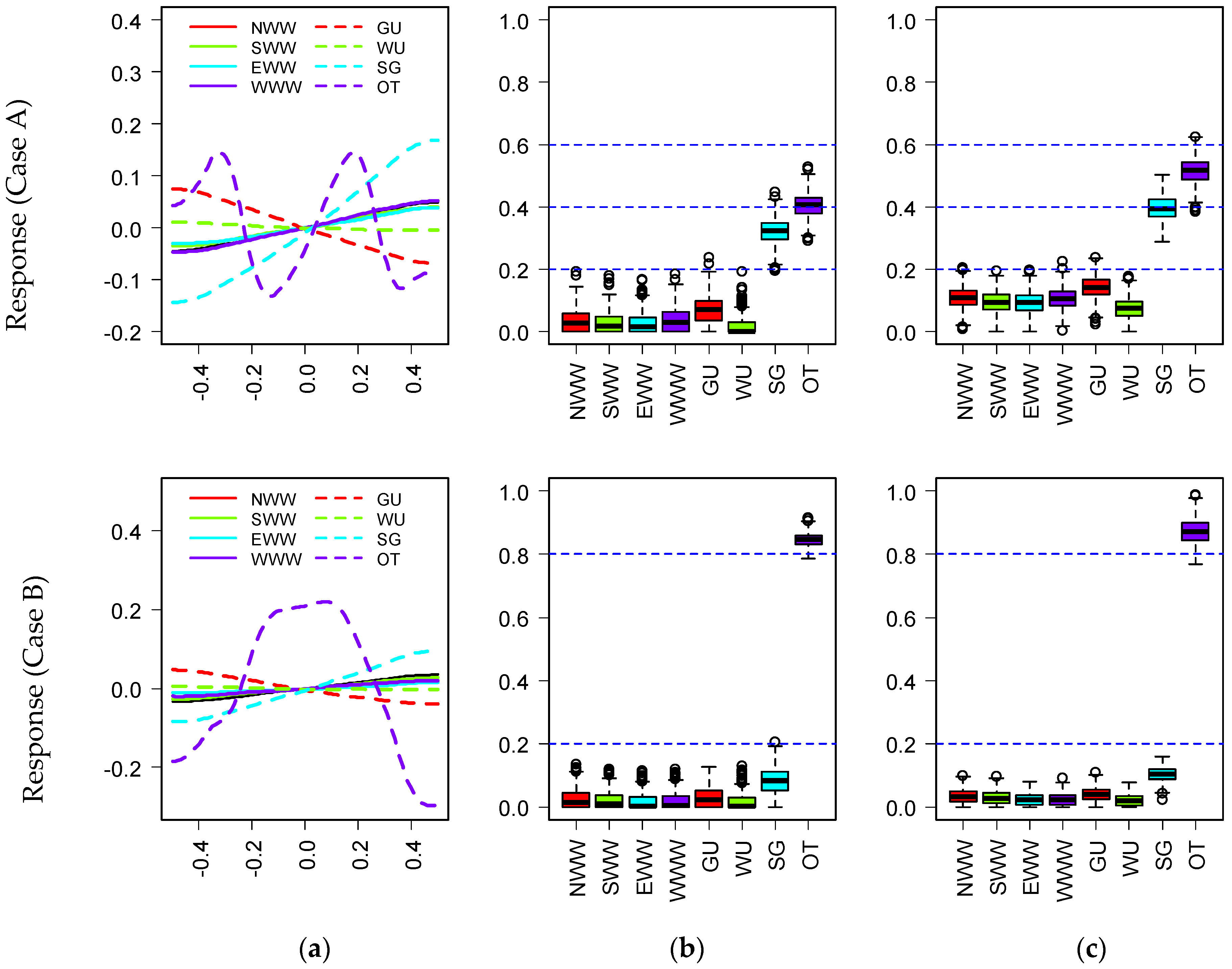
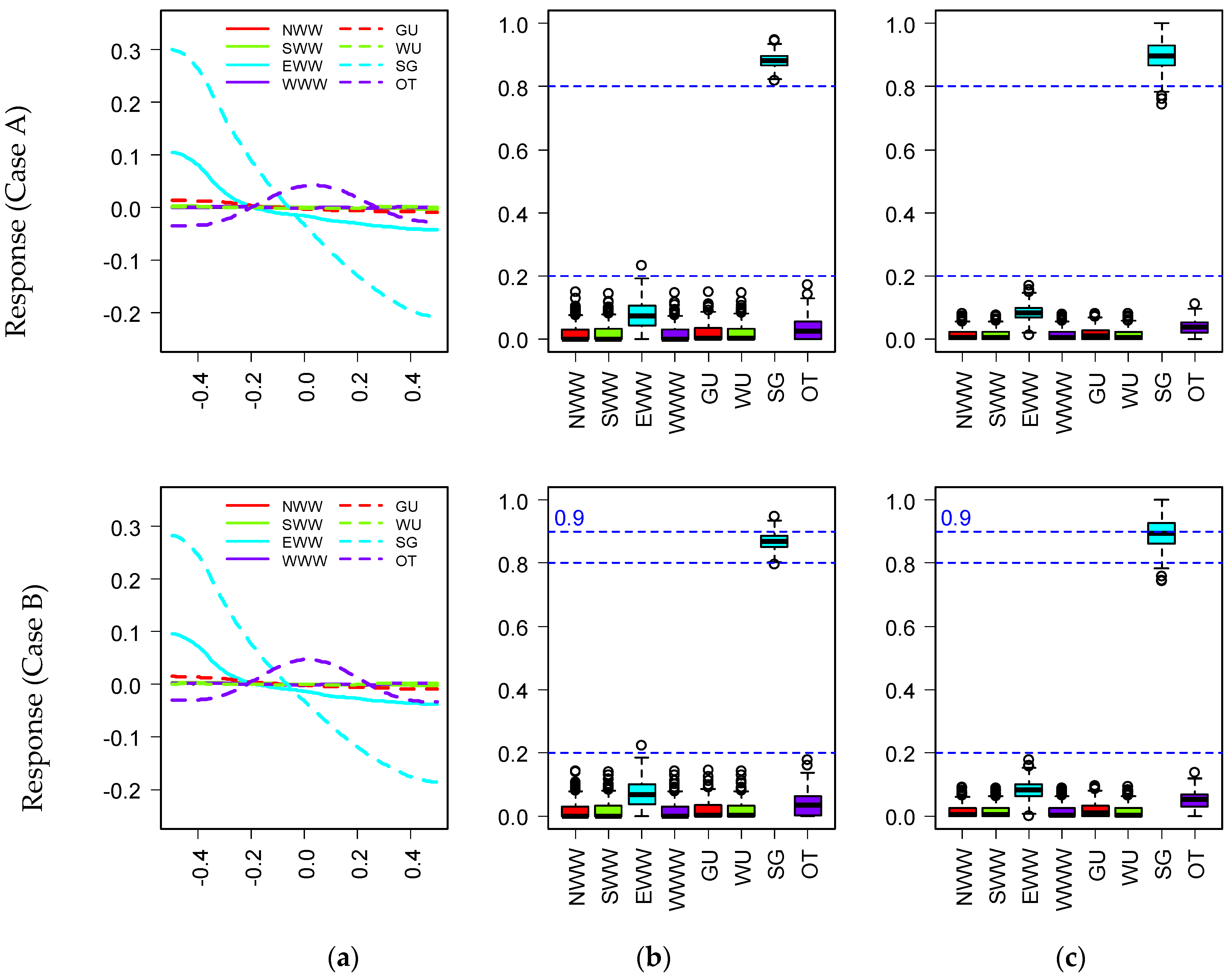
For each kind of energy consumption, the order of eight parameters is similar, and the most influential parameter is the same in both cases. However, the influence of identical parameters in these two cases is different due to the different courtyard forms. For example, orientation is the most important parameter that is influencing cooling energy and total energy use in both cases. As a result of the change of courtyard form (case A and B), the orientation accounts for 37% and 81% of the variance of cooling energy in the two cases. The same statement is also true that the orientation in two cases is responsible for 45% and 86% of the variance of total energy use, respectively.

(2)

The rank of parameters affecting total energy use is strongly correlated with the key variables and the proportion of every kind of energy use. As a result of the large proportion of cooling and heating energy use, the orientation and the window U-value are the most significant factors in cooling and heating energy respectively that also have important impacts on total energy. However, some parameters play a major role in heating or cooling energy but are not significant on total energy. For example, the solar heat gain coefficient is the most important parameter affecting lighting energy, which is the second most important parameter affecting cooling and heating energy. However, the solar heat gain coefficient only contributes a small proportion of variations of total energy due to the combined effects for cooling, heating, and lighting energy. The solar heat gain coefficient is positively correlated with cooling energy and negatively correlated with other kinds of energy use. The cooling energy and total energy use would increase slowly due to the increase in the solar heat gain coefficient, although the increase in this factor would result in the reduction of heating energy and lighting energy use. In addition, some parameters have no major impact on individual energy use (cooling, heating, and lighting energy), but they play an important role in total energy use. For example, the north window–wall ratio has a slight impact on individual energy use, which is one of the first three important factors in total energy use.

(3)

The wall U-value, commonly considered as a dominant factor in practice, has little impact on each kind of energy except for heating energy. The reason is that the range and the maximum value of the wall U-value are small. Hence, after the value of the WU decreases to a certain number, the subsequent decrease has little influence on the energy efficiency of the building.

5. Conclusions

The meta-modeling sensitivity analysis was conducted to identify key variables affecting building cooling, heating, lighting, and total energy in two courtyard office buildings in Wuhan, China. The following conclusions can be drawn:

(1)

For annual cooling energy, the dominant variable is the orientation (OT) that has more effects on case B than case A. Meanwhile, the relationships between inputs and outputs are approximately monotonous except for the orientation in both cases. The cooling, heating, lighting, and total energy have a periodic change when the orientation changes from 0° to 180°, while the changes of other parameters only lead to a monotonic increase or decrease in energy use. The window U-value (GU) is the key factor, which accounts for 60% of the change in the heating energy in these cases. The solar heat gain coefficient (SG) is the most significant parameter affecting lighting energy. The most influential parameter affecting total energy is the same as those for cooling energy.

(2)

The ranks of the influence of input parameters are nearly the same on the four outputs in both cases. This indicates that the influence of key factors (the orientation, etc.) should be given more attention in a variety of courtyard buildings.

(3)

By comparing case A and case B, the energy consumption and the effect of each parameter are related to the courtyard form. Hence, the suitable energy-saving measure would be changed due to the different courtyard forms.