Stochastic Buffeting Analysis of Uncertain Long-Span Bridge Deck with an Optimized Method
Abstract
:1. Introduction
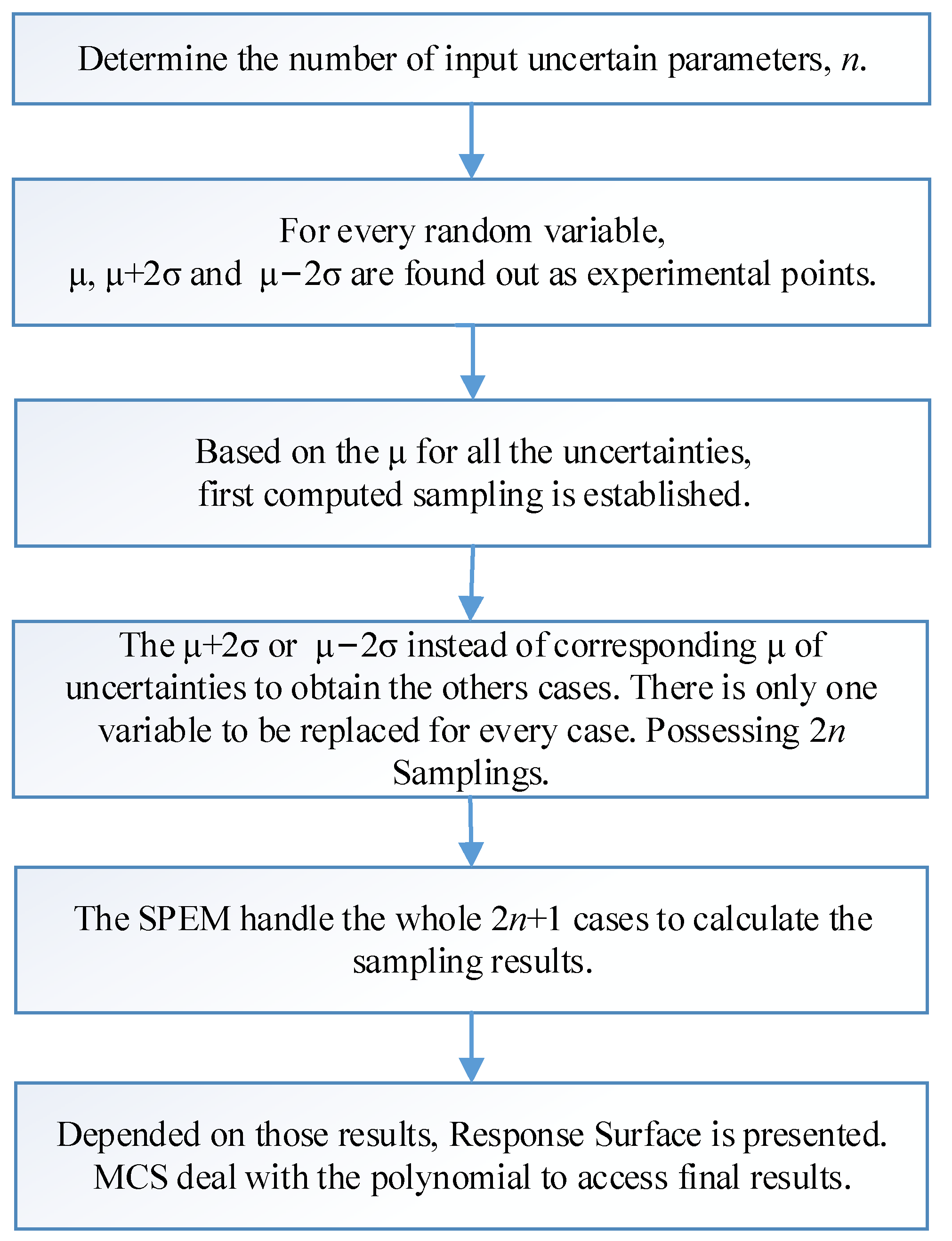
2. Theoretical Formulas
3. Features and Parameters for the Case Study
4. Comparison of Buffeting Response for Deck
5. Case Study
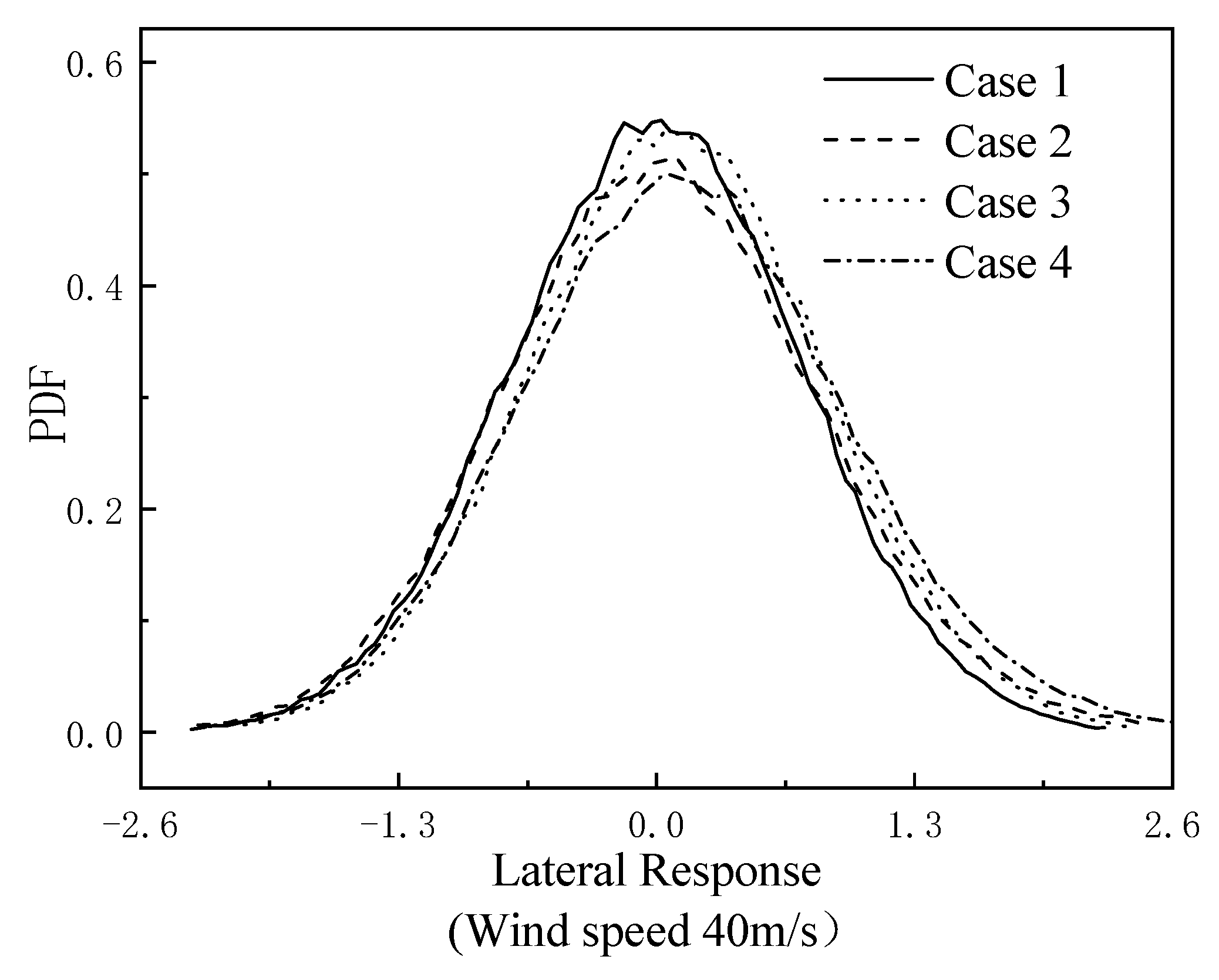
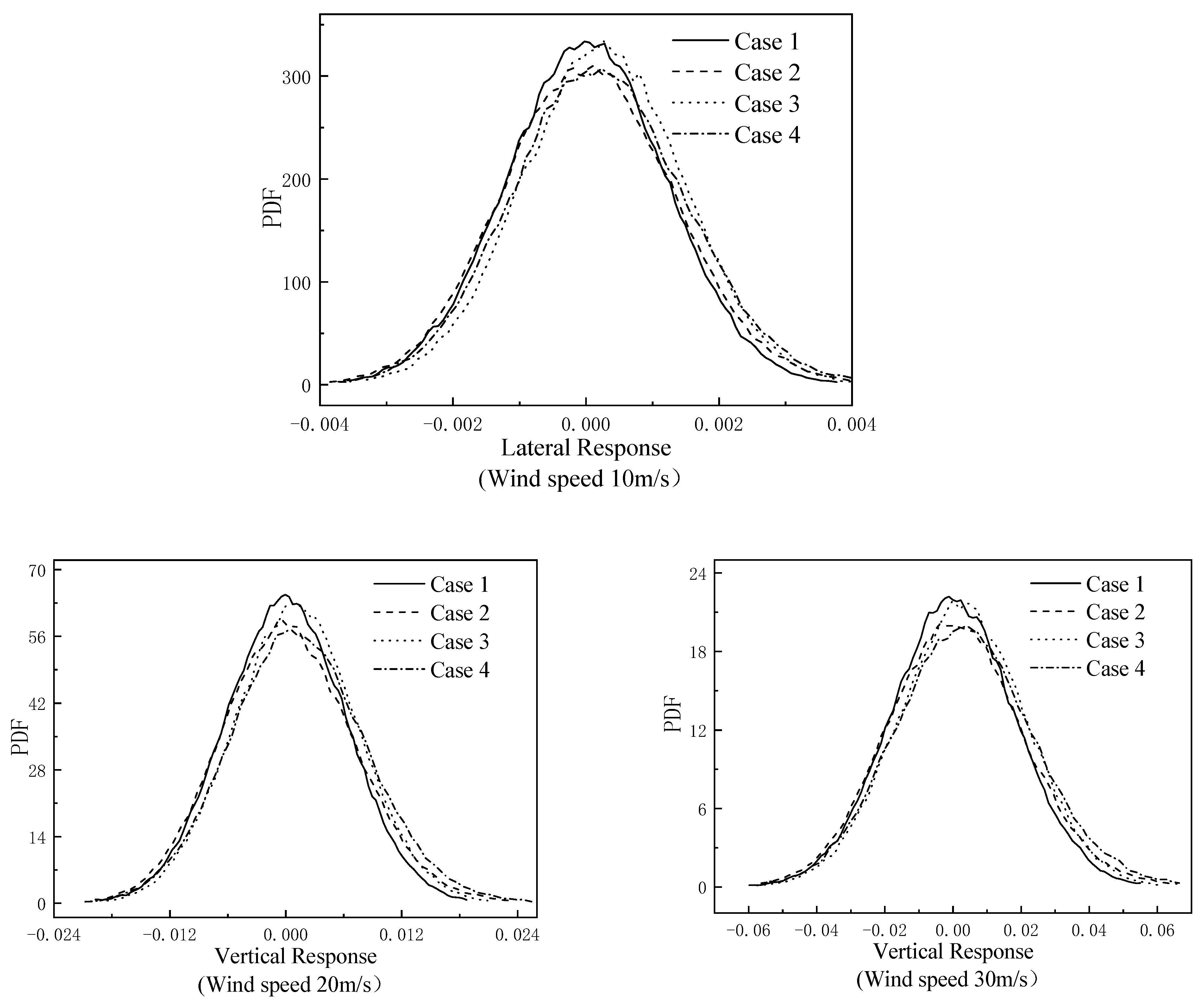
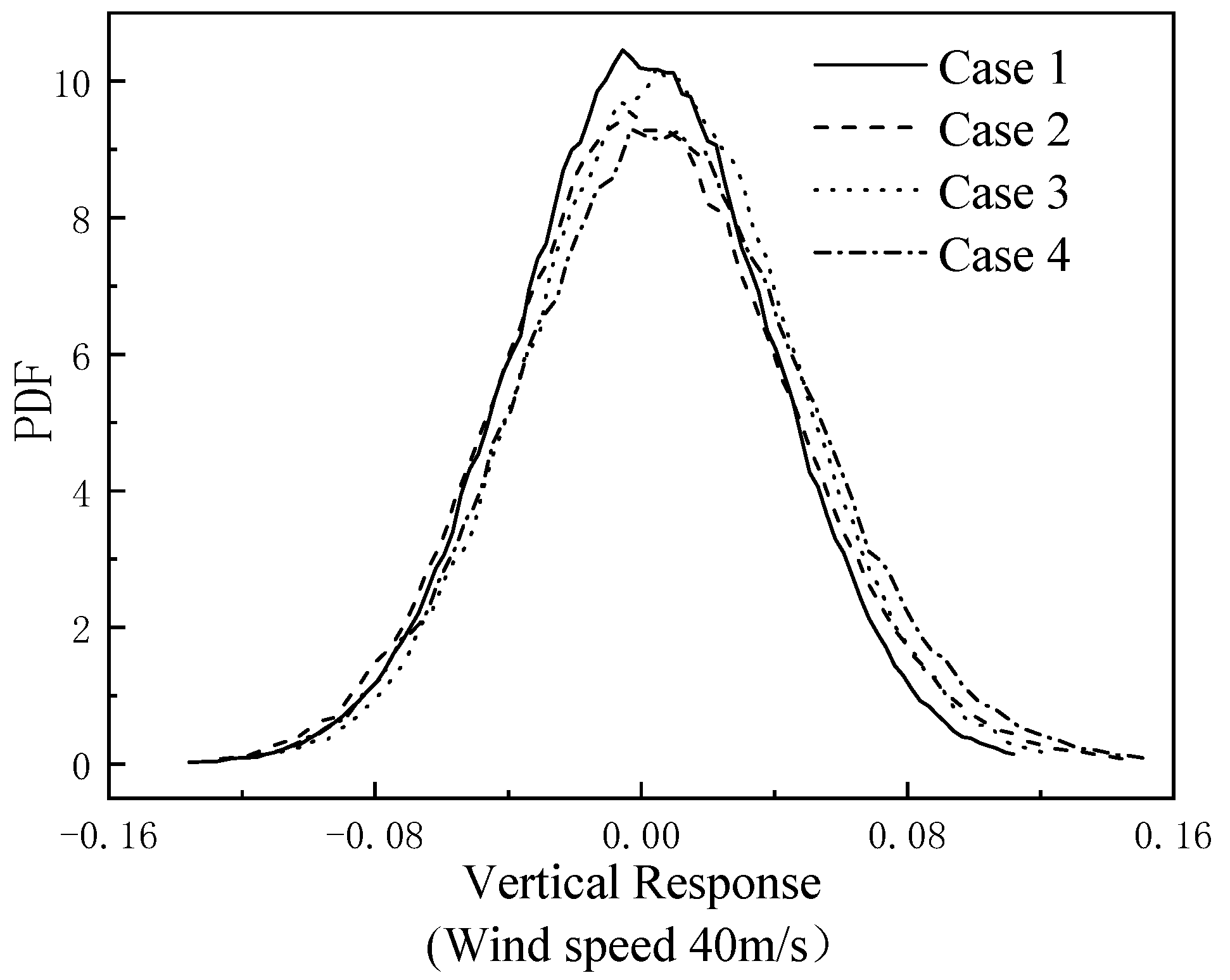
5.1. The Interaction between Structural Uncertainties and Uncertain Wind Speed
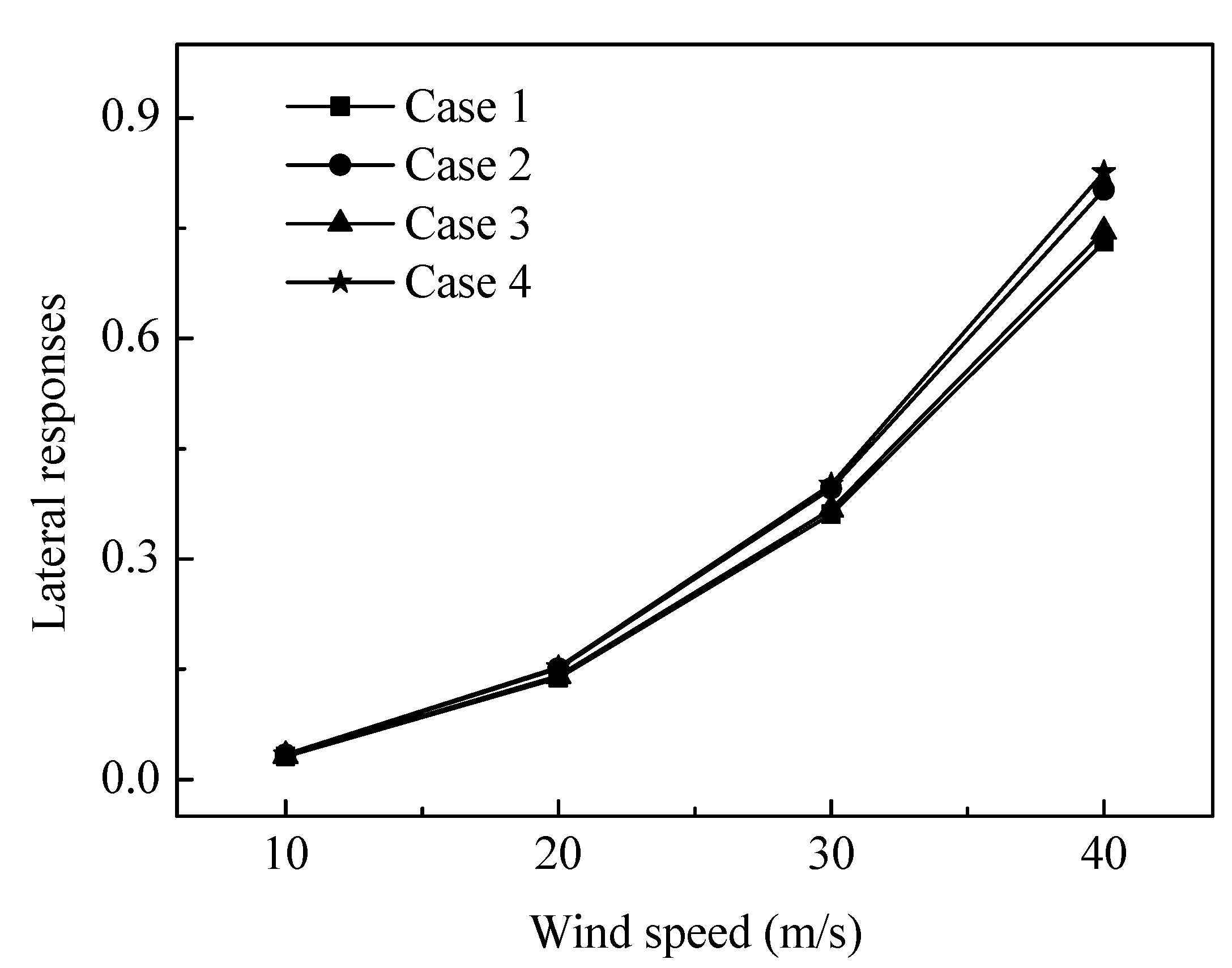
5.2. The Effect of Different Wind Speed on Structural Responses
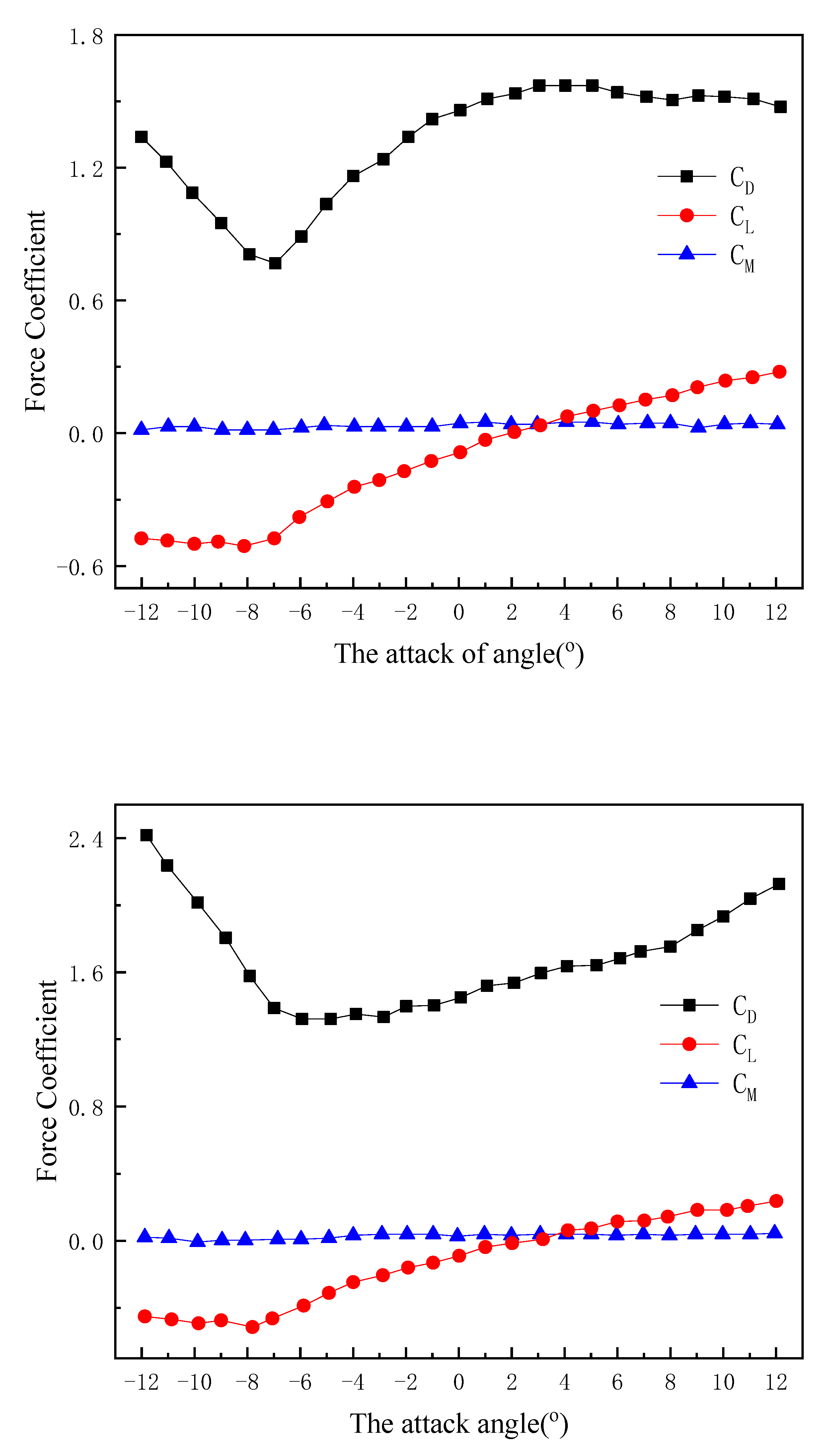
5.3. The Effect of Different Attack Angle on Structural Responses
6. Conclusions
- (1)
- The comparison between SPEM-RSM and MSC is significantly satisfactory. The efficiency of SPEM-RSM increases as much as 34.01 times. The errors between two methods of buffeting analysis responses in the verification are less than 1%.
- (2)
- The combined effect of the uncertainties of structural parameters and wind speed cause the slight asymmetrical distribution of the random vibration of the uncertain structure.
- (3)
- The response is more sensitive to the effect of uncertain wind speed than structural uncertainties. The effect of uncertain wind speed increases with the wind speed, but the effect of structural uncertainties has no disciplinary rule with different wind speed.
- (4)
- The random buffeting vibration is significantly sensitive to the varying attack angle. For this case, a positive angle makes the structure appear to be in the most dangerous state.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Kareem, A. Advanced analysis of coupled buffeting response of bridges: A complex modal decomposition approach. Probabilistic Eng. Mech. 2002, 17, 201–213. [Google Scholar] [CrossRef]
- Davenport, A.G.; King, J.P.C. Influence of topography on the dynamic wind loading of long span bridges. J. Wind Eng. Ind. Aerodyn. 1990, 36, 1373–1382. [Google Scholar] [CrossRef]
- Ge, Y.J.; Ke, S.T.; Xu, L. Study of random characteristics of fluctuating wind loads on ultra-large cooling towers in full construction process. Wind Struct. 2018, 26, 191–204. [Google Scholar]
- Li, Y.; Chen, X.; Wu, C.; Wang, D. Aerostatic and buffeting response characteristics of catwalk in a long-span suspension bridge. Wind Struct. 2014, 19, 665–686. [Google Scholar] [CrossRef]
- Scanlan, R.H. Action of flexible bridges under wind-2: Buffeting theory. J. Sound Vib. 1978, 60, 201–211. [Google Scholar] [CrossRef]
- Xu, Y.L.; Zhu, L.D.; Xiang, H.F. Buffeting response of long suspension bridges to skew winds. Wind Struct. Int. J. 2003, 6, 179–196. [Google Scholar] [CrossRef]
- Zhu, L.D.; Xu, Y.L. Buffeting response of long-span cable-supported bridges under skew winds. Part 1: Theory. J. Sound Vib. 2005, 281, 647–673. [Google Scholar] [CrossRef]
- Lombardo, F.T. Treatment of Uncertainty for Windstorm Risk Assessment. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2019, 5, 1–2. [Google Scholar] [CrossRef] [Green Version]
- Lystad, T.M.; Fenerci, A.; Øiseth, O. Long-term extreme buffeting response of cable-supported bridges with uncertain turbulence parameters. Eng. Struct. 2021, 236, 112126. [Google Scholar] [CrossRef]
- Shen, Z.; Li, J.; Li, R.; Gao, G. Nonuniform wind characteristics and buffeting response of a composite cable-stayed bridge in a trumpet-shaped mountain pass. J. Wind Eng. Ind. Aerodyn. 2021, 217, 104730. [Google Scholar] [CrossRef]
- Cui, W.; Zhao, L.; Ge, Y. Non-Gaussian turbulence induced buffeting responses of long-span bridges based on state augmentation method. Eng. Struct. 2022, 254, 113774. [Google Scholar] [CrossRef]
- Xu, Z.; Dai, G.; Zhang, L.; Chen, Y.F.; Flay, R.G.J.; Rao, H. Effect of non-Gaussian turbulence on extreme buffeting response of a high-speed railway sea-crossing bridge. J. Wind Eng. Ind. Aerodyn. 2022, 224, 104981. [Google Scholar] [CrossRef]
- Kareem, A.; Sun, W.J. Dynamic response of structures with uncertain damping. Eng. Struct. 1990, 12, 2–8. [Google Scholar] [CrossRef]
- Marano, G.C.; Morrone, E.; Quaranta, G. Analysis of randomly vibrating structures under hybrid uncertainty. Eng. Struct. 2009, 31, 2677–2686. [Google Scholar] [CrossRef]
- Huang, M.F.; Chan, C.M.; Lou, W.J. Optimal performance-based design of wind sensitive tall buildings considering uncertainties. Comput. Struct. 2012, 98–99, 7–16. [Google Scholar] [CrossRef]
- Ge, Y.J.; Xiang, H.F.; Tanaka, H. Application of a reliability analysis model to bridge flutter under extreme winds. J. Wind Eng. Ind. Aerodyn. 2000, 86, 155–167. [Google Scholar] [CrossRef]
- Canor, T.; Caracoglia, L.; Denoël, V. Application of random eigenvalue analysis to assess bridge flutter probability. J. Wind Eng. Ind. Aerodyn. 2015, 140, 79–86. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Chen, X. Assessing probabilistic wind load effects via a multivariate extreme wind speed model: A unified framework to consider directionality and uncertainty. J. Wind Eng. Ind. Aerodyn. 2015, 147, 30–42. [Google Scholar] [CrossRef] [Green Version]
- Bruno, L.; Corbetta, A. Uncertainties in crowd dynamic loading of footbridges: A novel multi-scale model of pedestrian traffic. Eng. Struct. 2017, 147, 545–566. [Google Scholar] [CrossRef]
- Bruno, L.; Fransos, D. Probabilistic evaluation of the aerodynamic properties of a bridge deck. J. Wind Eng. Ind. Aerodyn. 2011, 99, 718–728. [Google Scholar] [CrossRef]
- Solari, G.; Piccardo, G. Probabilistic 3-D turbulence modeling for gust buffeting of structures. Probabilistic Eng. Mech. 2001, 16, 73–86. [Google Scholar] [CrossRef]
- Caracoglia, L. Influence of uncertainty in selected aerodynamic and structural parameters on the buffeting response of long-span bridges. J. Wind Eng. Ind. Aerodyn. 2008, 96, 327–344. [Google Scholar] [CrossRef]
- Zhou, Q.; Zheng, S.; Chen, Z.; Yang, F.; Liu, J. Vortex-induced Vibration Reliability Analysis in Cable-stayed Bridges: Wind and Aerodynamic Uncertainties. Struct. Eng. Int. 2019, 31, 51–59. [Google Scholar] [CrossRef]
- Liu, S.; Cai, C.S.; Han, Y.; Li, C. Reliability analysis on flutter of the long-span Aizhai bridge. Wind Struct. 2018, 27, 175–186. [Google Scholar] [CrossRef]
- Kusano, I.; Baldomir, A.; Jurado, J.Á.; Hernández, S. Probabilistic optimization of the main cable and bridge deck of long-span suspension bridges under flutter constraint. J. Wind Eng. Ind. Aerodyn. 2015, 146, 59–70. [Google Scholar] [CrossRef]
- Kusano, I.; Montoya, M.C.; Baldomir, A.; Nieto, F.; Jurado, J.Á.; Hernández, S. Reliability based design optimization for bridge girder shape and plate thicknesses of long-span suspension bridges considering aeroelastic constraint. J. Wind Eng. Ind. Aerodyn. 2020, 202, 104176. [Google Scholar] [CrossRef]
- Tmla, B.; Af, B.; Oi, B. Buffeting response of long-span bridges considering uncertain turbulence parameters using the environmental contour method. Eng. Struct. 2020, 213, 110575. [Google Scholar]
- Zhang, M.; Xu, F. Tuned mass damper for self-excited vibration control: Optimization involving nonlinear aeroelastic effect. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104836. [Google Scholar] [CrossRef]
- Zhu, S.; Li, Y.; Togbenou, K.; Xiang, T. An advanced algorithm to study the effect of uncertainties on the stochastic performance of high-pier bridge under earthquake. Soil Dyn. Earthq. Eng. 2019, 126, 105805. [Google Scholar] [CrossRef]
- Zhu, S.; Xiang, T.; Li, Y. An advanced pseudo excitation method and application in analyzing stochastic wind-induced response of slender bridge tower. Adv. Struct. Eng. 2019, 22, 2021–2032. [Google Scholar] [CrossRef]
- Lin, J.H.; Zhang, Y.H.; Li, Q.S.; Williams, F.W. Seismic spatial effects for long-span bridges, using the pseudo excitation method. Eng. Struct. 2004, 26, 1207–1216. [Google Scholar] [CrossRef]
- Lin, J.H.; Zhang, Y.H.; Zhao, Y. Pseudo Excitation Method and Its Application in Seismic Design and Disaster Mitigation of Long-Span Structures. In Earth and Space 2010; Song, G., Malla, R.B., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2010; pp. 2941–2948. [Google Scholar]
- Lin, J.H.; Zhang, Y.H.; Zhao, Y. Pseudo Excitation Method and Some Recent Developments. Procedia Eng. 2011, 14, 2453–2458. [Google Scholar] [CrossRef] [Green Version]
- Kiureghian, A.D. The geometry of random vibrations and solutions by FORM and SORM. Probabilistic Eng. Mech. 2000, 15, 81–90. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, G. Random buckling bearing capacity of super-large cooling towers considering stochastic material properties and wind loads. Probabilistic Eng. Mech. 2013, 33, 18–25. [Google Scholar] [CrossRef]
- Davenport, A.G.; Hill-Carroll, P. Damping in tall building: Its variability and treatment in design. Build. Motion Wind 1986, 10, 2–57. [Google Scholar]
- Melchers, R.E. Structural Reliability Analysis and Prediction; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Alduse, B.P.; Jung, S.; Vanli, O.A.; Kwon, S.-D. Effect of uncertainties in wind speed and direction on the fatigue damage of long-span bridges. Eng. Struct. 2015, 100, 468–478. [Google Scholar] [CrossRef]
- Davenport, A.G. Past, present and future of wind engineering. J. Wind Eng. Ind. Aerodyn. 2002, 90, 1371–1380. [Google Scholar] [CrossRef]




| Mode Features | Natural Frequencies (Hz) |
|---|---|
| First symmetrical Lateral bending | 0.0580 |
| First asymmetrical Lateral bending | 0.1524 |
| First asymmetrical vertical bending | 0.0950 |
| First symmetrical vertical bending | 0.1438 |
| First symmetrical torsion | 0.3013 |
| First asymmetrical torsion | 0.3569 |
| Parameter | Distribution | COV | Refs. |
|---|---|---|---|
| Elastic Modulus | Normal | 0.1 | [37] |
| Wind Speed | Type I Extreme Value | 0161 | [35] |
| Damping Ratio | Log-normal | 0.4 | [36,38] |
| Uncertain Structural Parameters | Uncertain Wind Speed | |
|---|---|---|
| Case 1 | Not involved | Not involved |
| Case 2 | Not involved | Involved |
| Case 3 | Involved | Not involved |
| Case 4 | Involved | Involved |
| Lateral Displacement | Vertical Displacement | |
|---|---|---|
| Case 1 | 0.03130 | 0.00120 |
| Case 2 | 0.03338 | 0.00130 |
| Case 3 | 0.03205 | 0.00122 |
| Case 4 | 0.03414 | 0.00132 |
| Angle | Lateral Response | Vertical Response |
|---|---|---|
| −5° | 0.88068 | 0.04711 |
| −3° | 0.88068 | 0.04685 |
| 0° | 0.82631 | 0.04434 |
| +3° | 0.70252 | 0.04086 |
| +5° | 0.58219 | 0.03939 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, S.; Li, Y.; Yang, Y.; Ju, N. Stochastic Buffeting Analysis of Uncertain Long-Span Bridge Deck with an Optimized Method. Buildings 2022, 12, 632. https://doi.org/10.3390/buildings12050632
Zhu S, Li Y, Yang Y, Ju N. Stochastic Buffeting Analysis of Uncertain Long-Span Bridge Deck with an Optimized Method. Buildings. 2022; 12(5):632. https://doi.org/10.3390/buildings12050632
Chicago/Turabian StyleZhu, Siyu, Yongle Li, Yuyun Yang, and Nengpan Ju. 2022. "Stochastic Buffeting Analysis of Uncertain Long-Span Bridge Deck with an Optimized Method" Buildings 12, no. 5: 632. https://doi.org/10.3390/buildings12050632
APA StyleZhu, S., Li, Y., Yang, Y., & Ju, N. (2022). Stochastic Buffeting Analysis of Uncertain Long-Span Bridge Deck with an Optimized Method. Buildings, 12(5), 632. https://doi.org/10.3390/buildings12050632






