Compressive Strength Prediction of Fly Ash Concrete Using Machine Learning Techniques
Abstract
:1. Introduction
2. Methodology
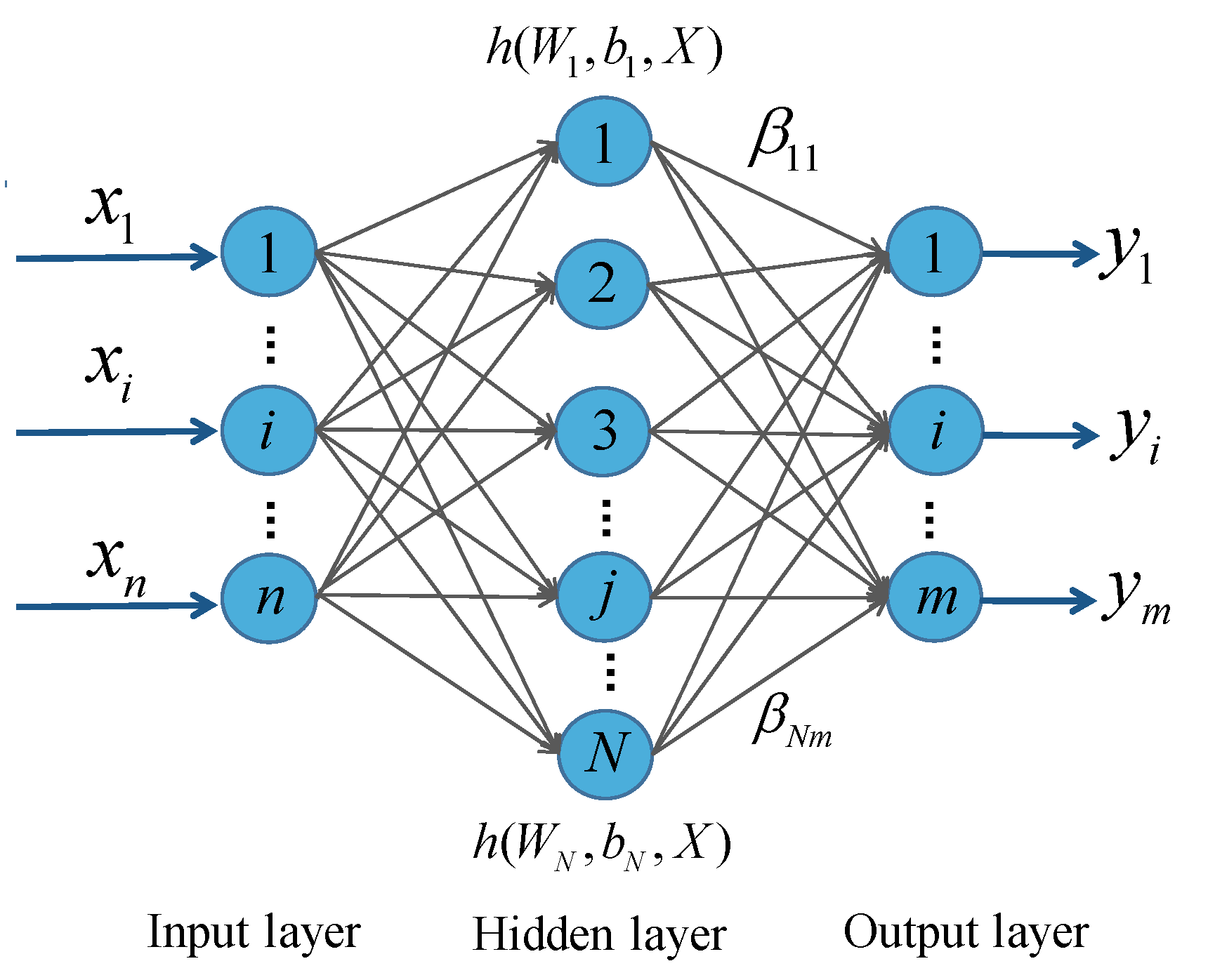
2.1. Extreme Learning Machine
2.2. Random Forest
2.3. Support Vector Regression Model
2.4. Grid Search Optimization Algorithm
3. Materials and Dataset Description
3.1. Input and Output Variables
3.2. Evaluation Metrics
4. Model Performance
5. Sensitivity Analysis of Input Variables
6. Conclusions
- (1)
- The proposed hybrid model could effectively capture the complicated nonlinear correlations between the eight input variables and the output compressive strength of the fly ash concrete.
- (2)
- The prediction performance of the SVR-GS model was better than that of the other three machine learning models with a higher prediction accuracy and smaller error, and is recommended for the pre-estimation of the compressive strength of fly ash concrete before laboratory compression experiments.
- (3)
- Concerning the eight input variables, age was the most important, followed by W/C, water, cement, fine aggregate, and fly ash. Coarse aggregate and superplasticizer were less important for compressive strength. Moreover, age, cement, fly ash, and superplasticizer all played a positive role in the compressive strength and their increase led to an increase in the compressive strength, while water and W/C were negative for the compressive strength of fly ash concrete.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, Y.; Lin, R.-S.; Wang, X.-Y. Compressive Strength Estimation and CO2 Reduction Design of Fly Ash Composite Concrete. Buildings 2022, 12, 139. [Google Scholar] [CrossRef]
- Ahmad, W.; Ahmad, A.; Ostrowski, K.A.; Aslam, F.; Joyklad, P.; Zajdel, P. Application of Advanced Machine Learning Approaches to Predict the Compressive Strength of Concrete Containing Supplementary Cementitious Materials. Materials 2021, 14, 5762. [Google Scholar] [CrossRef] [PubMed]
- Taji, I.; Ghorbani, S.; de Brito, J.; Tam, V.W.Y.; Sharifi, S.; Davoodi, A.; Tavakkolizadeh, M. Application of statistical analysis to evaluate the corrosion resistance of steel rebars embedded in concrete with marble and granite waste dust. J. Clean. Prod. 2019, 210, 837–846. [Google Scholar] [CrossRef]
- Vieira, G.L.; Schiavon, J.Z.; Borges, P.M.; da Silva, S.R.; de Oliveira Andrade, J.J. Influence of recycled aggregate replacement and fly ash content in performance of pervious concrete mixtures. J. Clean. Prod. 2020, 271, 122665. [Google Scholar] [CrossRef]
- Li, Y.; Qiao, C.; Ni, W. Green concrete with ground granulated blast-furnace slag activated by desulfurization gypsum and electric arc furnace reducing slag. J. Clean. Prod. 2020, 269, 122212. [Google Scholar] [CrossRef]
- Shubbar, A.A.; Jafer, H.; Dulaimi, A.; Hashim, K.; Atherton, W.; Sadique, M. The development of a low carbon binder produced from the ternary blending of cement, ground granulated blast furnace slag and high calcium fly ash: An experimental and statistical approach. Constr. Build. Mater. 2018, 187, 1051–1060. [Google Scholar] [CrossRef]
- Juenger, M.C.G.; Snellings, R.; Bernal, S.A. Supplementary cementitious materials: New sources, characterization, and performance insights. Cem. Concr. Res 2019, 122, 257–273. [Google Scholar] [CrossRef]
- Diaz-Loya, I.; Juenger, M.; Seraj, S.; Minkara, R. Extending supplementary cementitious material resources: Reclaimed and remediated fly ash and natural pozzolans. Cem. Concr. Compos. 2019, 101, 44–51. [Google Scholar] [CrossRef]
- Barkhordari, M.S.; Armaghani, D.J.; Mohammed, A.S.; Ulrikh, D.V. Data-Driven Compressive Strength Prediction of Fly Ash Concrete Using Ensemble Learner Algorithms. Buildings 2022, 12, 132. [Google Scholar] [CrossRef]
- Moradi, M.J.; Khaleghi, M.; Salimi, J.; Farhangi, V.; Ramezanianpour, A.M. Predicting the compressive strength of concrete containing metakaolin with different properties using ANN. Measurement 2021, 183, 109790. [Google Scholar] [CrossRef]
- Tang, F.; Wu, Y.; Zhou, Y. Hybridizing Grid Search and Support Vector Regression to Predict the Compressive Strength of Fly Ash Concrete. Adv. Civ. Eng. 2022, 2022, 3601914. [Google Scholar] [CrossRef]
- Ahmad, A.; Ahmad, W.; Aslam, F.; Joyklad, P. Compressive strength prediction of fly ash-based geopolymer concrete via advanced machine learning techniques. Case Stud. Constr. Mater. 2022, 16, e00840. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y. Hybrid machine learning model and Shapley additive explanations for compressive strength of sustainable concrete. Constr. Build. Mater. 2022, 330, 127298. [Google Scholar] [CrossRef]
- Sonebi, M.; Cevik, A.; Grünewald, S.; Walraven, J. Modelling the fresh properties of self-compacting concrete using support vector machine approach. Constr. Build. Mater. 2016, 106, 55–64. [Google Scholar] [CrossRef]
- Yan, K.; Shi, C. Prediction of elastic modulus of normal and high strength concrete by support vector machine. Constr. Build. Mater. 2010, 24, 1479–1485. [Google Scholar] [CrossRef]
- Ahmad, A.; Chaiyasarn, K.; Farooq, F.; Ahmad, W.; Suparp, S.; Aslam, F. Compressive Strength Prediction via Gene Expression Programming (GEP) and Artificial Neural Network (ANN) for Concrete Containing RCA. Buildings 2021, 11, 324. [Google Scholar] [CrossRef]
- Han, B.; Wu, Y.; Liu, L. Prediction and uncertainty quantification of compressive strength of high-strength concrete using optimized machine learning algorithms. Struct Concr. 2022, 1–14. [Google Scholar] [CrossRef]
- Han, Q.; Gui, C.; Xu, J.; Lacidogna, G. A generalized method to predict the compressive strength of high-performance concrete by improved random forest algorithm. Constr. Build. Mater. 2019, 226, 734–742. [Google Scholar] [CrossRef]
- Saha, P.; Debnath, P.; Thomas, P. Prediction of fresh and hardened properties of self-compacting concrete using support vector regression approach. Neural Comput. Appl. 2020, 32, 7995–8010. [Google Scholar] [CrossRef]
- Farooq, F.; Nasir Amin, M.; Khan, K.; Rehan Sadiq, M.; Faisal Javed, M.; Aslam, F.; Alyousef, R. A Comparative Study of Random Forest and Genetic Engineering Programming for the Prediction of Compressive Strength of High Strength Concrete (HSC). Appl. Sci. 2020, 10, 7330. [Google Scholar] [CrossRef]
- Al-Shamiri, A.K.; Kim, J.H.; Yuan, T.-F.; Yoon, Y.S. Modeling the compressive strength of high-strength concrete: An extreme learning approach. Constr. Build. Mater. 2019, 208, 204–219. [Google Scholar] [CrossRef]
- Chen, H.; Li, X.; Wu, Y.; Zuo, L.; Lu, M.; Zhou, Y. Compressive Strength Prediction of High-Strength Concrete Using Long Short-Term Memory and Machine Learning Algorithms. Buildings 2022, 12, 302. [Google Scholar] [CrossRef]
- Ling, H.; Qian, C.; Kang, W.; Liang, C.; Chen, H. Combination of Support Vector Machine and K-Fold cross validation to predict compressive strength of concrete in marine environment. Constr. Build. Mater. 2019, 206, 355–363. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, Y. Prediction and feature analysis of punching shear strength of two-way reinforced concrete slabs using optimized machine learning algorithm and Shapley additive explanations. Mech. Adv. Mater. Struct. 2022, 1–11. [Google Scholar] [CrossRef]
- Ghorbani, B.; Arulrajah, A.; Narsilio, G.; Horpibulsuk, S. Experimental investigation and modelling the deformation properties of demolition wastes subjected to freeze–thaw cycles using ANN and SVR. Constr. Build. Mater. 2020, 258, 119688. [Google Scholar] [CrossRef]
- Zhang, W.; Khan, A.; Huyan, J.; Zhong, J.; Peng, T.; Cheng, H. Predicting Marshall parameters of flexible pavement using support vector machine and genetic programming. Constr. Build. Mater. 2021, 306, 124924. [Google Scholar] [CrossRef]
- Wu, Y.; Li, S. Damage degree evaluation of masonry using optimized SVM-based acoustic emission monitoring and rate process theory. Measurement 2022, 190, 110729. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. Training v-Support Vector Regression: Theory and Algorithms. Neural Comput. 2002, 14, 1959–1977. [Google Scholar] [CrossRef]
- Lichman, M. UCI Machine Learning Repository; University of California, School of Information and Computer Science: Irvine, CA, USA, 2013; Available online: http://archive.ics.uci.edu/ml. (accessed on 27 November 2020).
- Jueyendah, S.; Lezgy-Nazargah, M.; Eskandari-Naddaf, H.; Emamian, S.A. Predicting the mechanical properties of cement mortar using the support vector machine approach. Constr. Build. Mater. 2021, 291, 123396. [Google Scholar] [CrossRef]
- Farooq, F.; Ahmed, W.; Akbar, A.; Aslam, F.; Alyousef, R. Predictive modeling for sustainable high-performance concrete from industrial wastes: A comparison and optimization of models using ensemble learners. J. Clean. Prod. 2021, 292, 126032. [Google Scholar] [CrossRef]
- Aslam, F.; Farooq, F.; Amin, M.N.; Khan, K.; Waheed, A.; Akbar, A.; Javed, M.F.; Alyousef, R.; Alabdulijabbar, H. Applications of Gene Expression Programming for Estimating Compressive Strength of High-Strength Concrete. Adv. Civ. Eng. 2020, 2020, 8850535. [Google Scholar] [CrossRef]
- Mangalathu, S.; Hwang, S.-H.; Jeon, J.-S. Failure mode and effects analysis of RC members based on machine-learning-based SHapley Additive exPlanations (SHAP) approach. Eng. Struct. 2020, 219, 110927. [Google Scholar] [CrossRef]
- Lyngdoh, G.A.; Zaki, M.; Krishnan, N.M.A.; Das, S. Prediction of concrete strengths enabled by missing data imputation and interpretable machine learning. Cem. Concr. Compos. 2022, 128, 104414. [Google Scholar] [CrossRef]
- Mangalathu, S.; Shin, H.; Choi, E.; Jeon, J.-S. Explainable machine learning models for punching shear strength estimation of flat slabs without transverse reinforcement. J. Build. Eng. 2021, 39, 102300. [Google Scholar] [CrossRef]














| Variable | Unit | Max | Min | Average | Standard Deviation | Kurtosis | Skewness |
|---|---|---|---|---|---|---|---|
| Cement | kg/m3 | 540 | 247 | 361 | 85.33 | −0.50 | 0.82 |
| Fly ash | kg/m3 | 142 | 0 | 28 | 48.26 | −0.44 | 1.2 |
| Water | kg/m3 | 228 | 140 | 184 | 19.13 | 0.29 | −0.38 |
| Superplasticizer | kg/m3 | 28 | 0 | 4 | 5.94 | 3.52 | 1.77 |
| Coarse aggregate | kg/m3 | 1125 | 801 | 997 | 77.12 | −0.19 | −0.26 |
| Fine aggregate | kg/m3 | 900 | 594 | 776 | 79.77 | −0.07 | −0.67 |
| Age | day | 365 | 1 | 53 | 75.91 | 7.01 | 2.62 |
| W/C | - | 0.70 | 0.27 | 0.53 | 0.11 | −0.04 | −0.92 |
| Strength | MPa | 80 | 6 | 36 | 14.97 | −0.13 | 0.45 |
| Evaluation Metrics | Equation |
|---|---|
| R | |
| MAE | |
| MSE | |
| RMSE | |
| MAPE |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Li, H.; Zhou, Y. Compressive Strength Prediction of Fly Ash Concrete Using Machine Learning Techniques. Buildings 2022, 12, 690. https://doi.org/10.3390/buildings12050690
Jiang Y, Li H, Zhou Y. Compressive Strength Prediction of Fly Ash Concrete Using Machine Learning Techniques. Buildings. 2022; 12(5):690. https://doi.org/10.3390/buildings12050690
Chicago/Turabian StyleJiang, Yimin, Hangyu Li, and Yisong Zhou. 2022. "Compressive Strength Prediction of Fly Ash Concrete Using Machine Learning Techniques" Buildings 12, no. 5: 690. https://doi.org/10.3390/buildings12050690
APA StyleJiang, Y., Li, H., & Zhou, Y. (2022). Compressive Strength Prediction of Fly Ash Concrete Using Machine Learning Techniques. Buildings, 12(5), 690. https://doi.org/10.3390/buildings12050690





