Shaking Table Seismic Experimental Investigation of Lightweight Rigid Bodies
Abstract
:1. Introduction
2. Rigid Body Motion
3. Test Setup
3.1. The Adopted Specimens
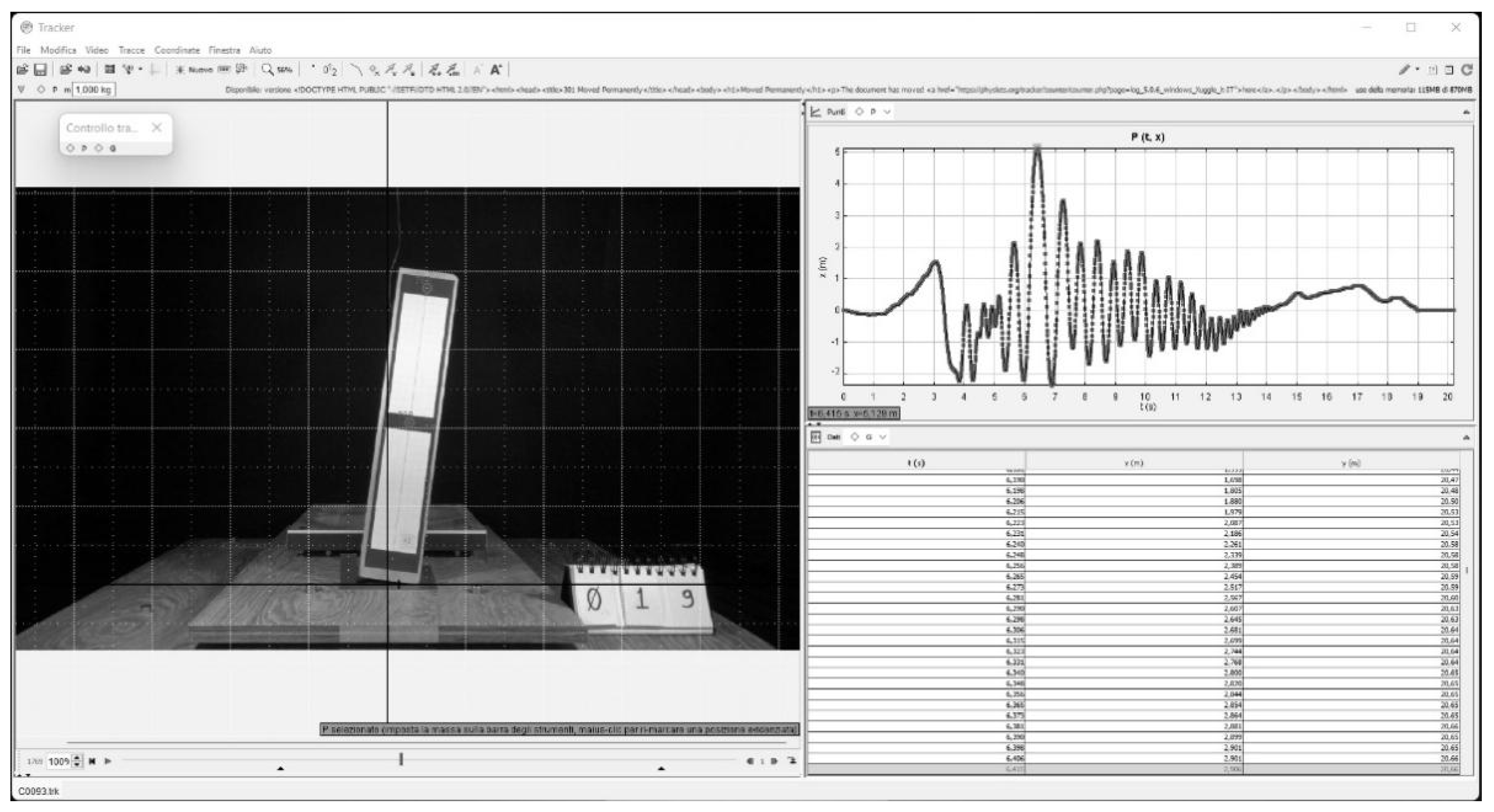
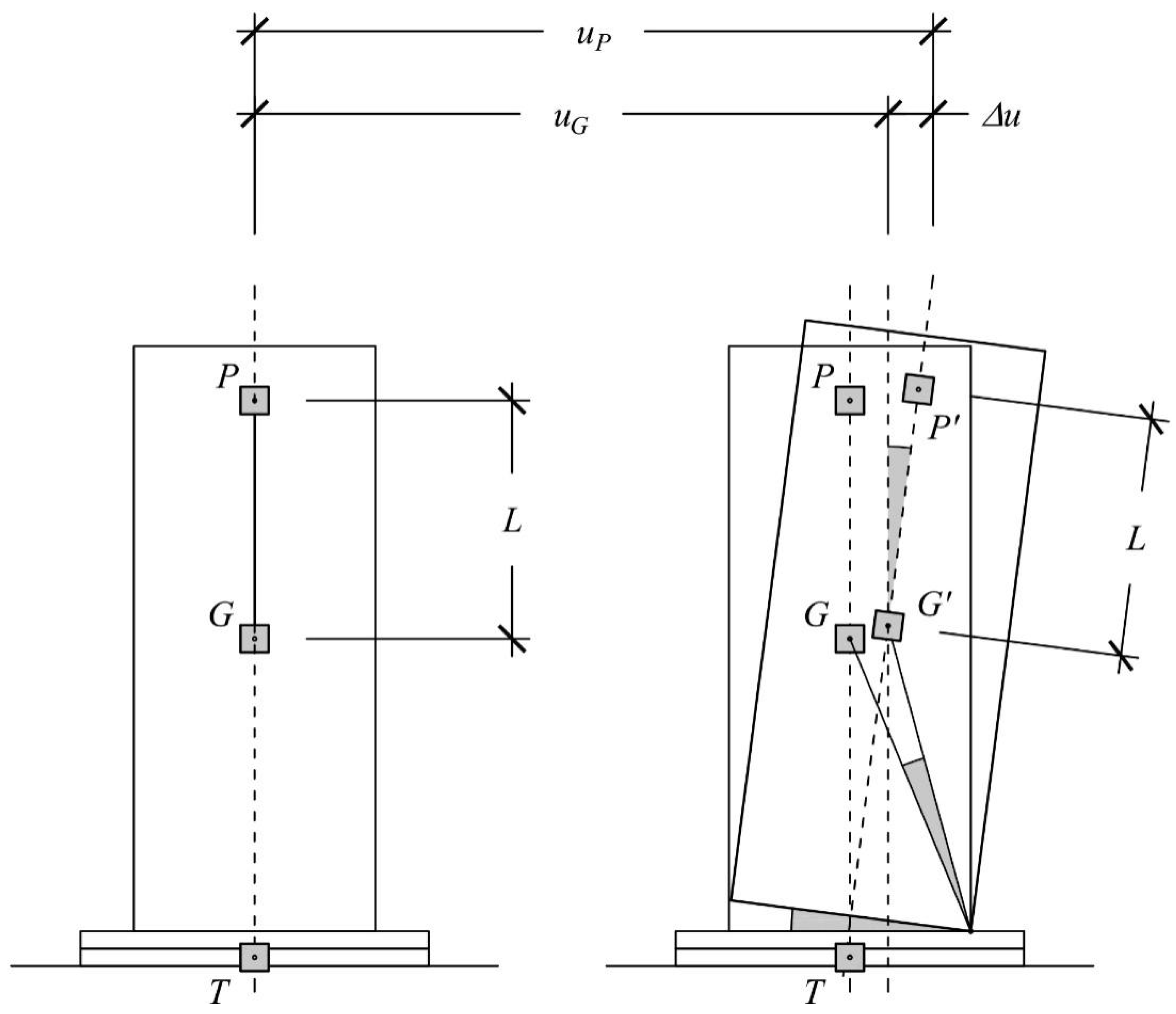
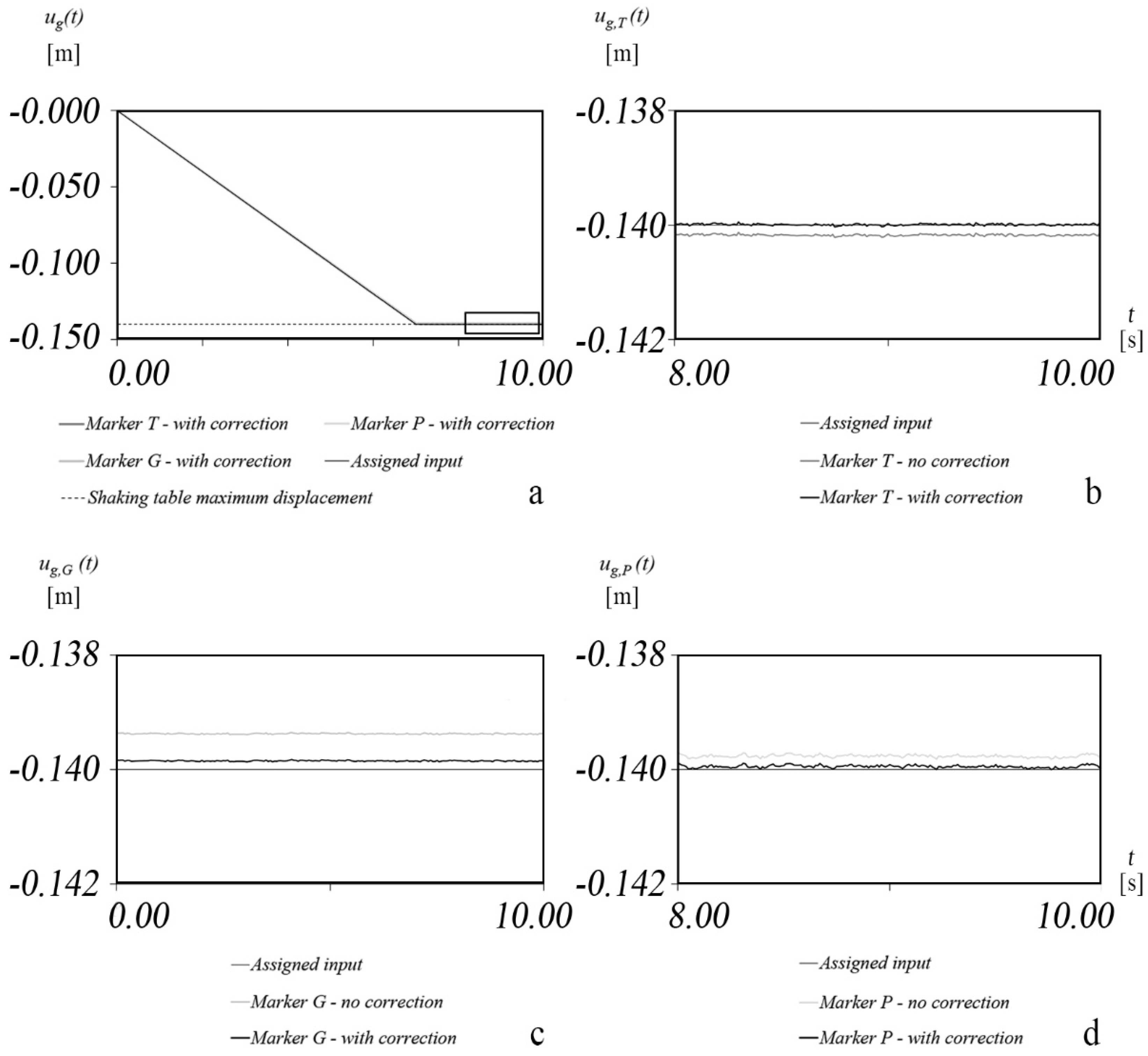
3.2. Instrumentation and Testing Protocol
4. Experimental Campaign
- Uniformly accelerated motion to identify the uplift acceleration of the blocks;
- Free rocking oscillations, which aim at experimentally identifying the restitution coefficient;
- Application of pulses with different intensities and angular frequencies, to reconstruct stability maps;
- Ground motions associated to natural accelerograms with increasing PGA.
4.1. Uniformly Accelerated Motion
4.2. Free Vibrations
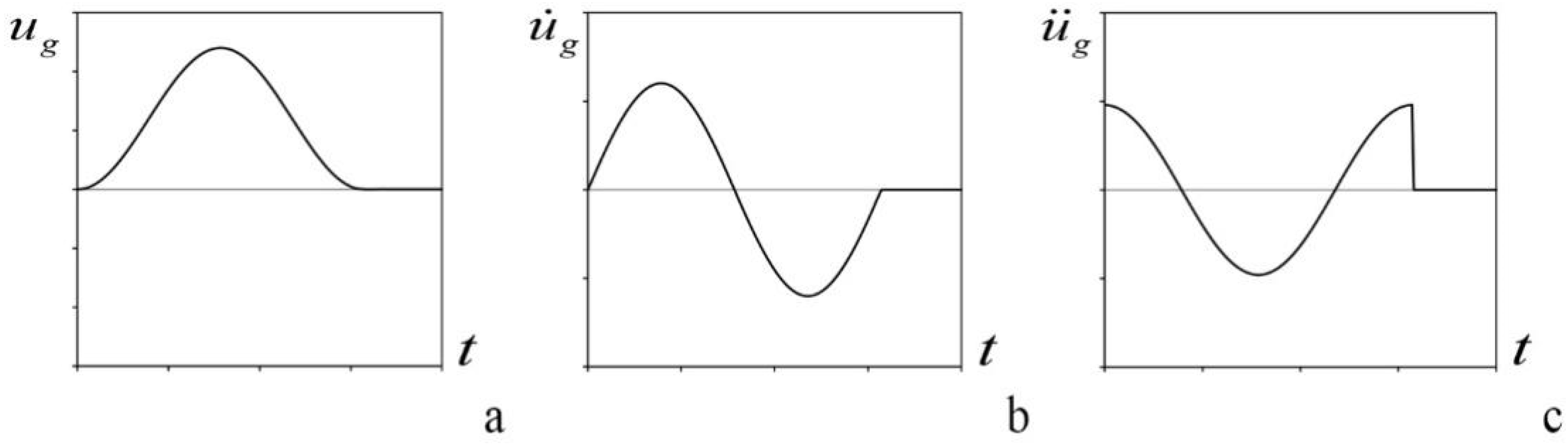
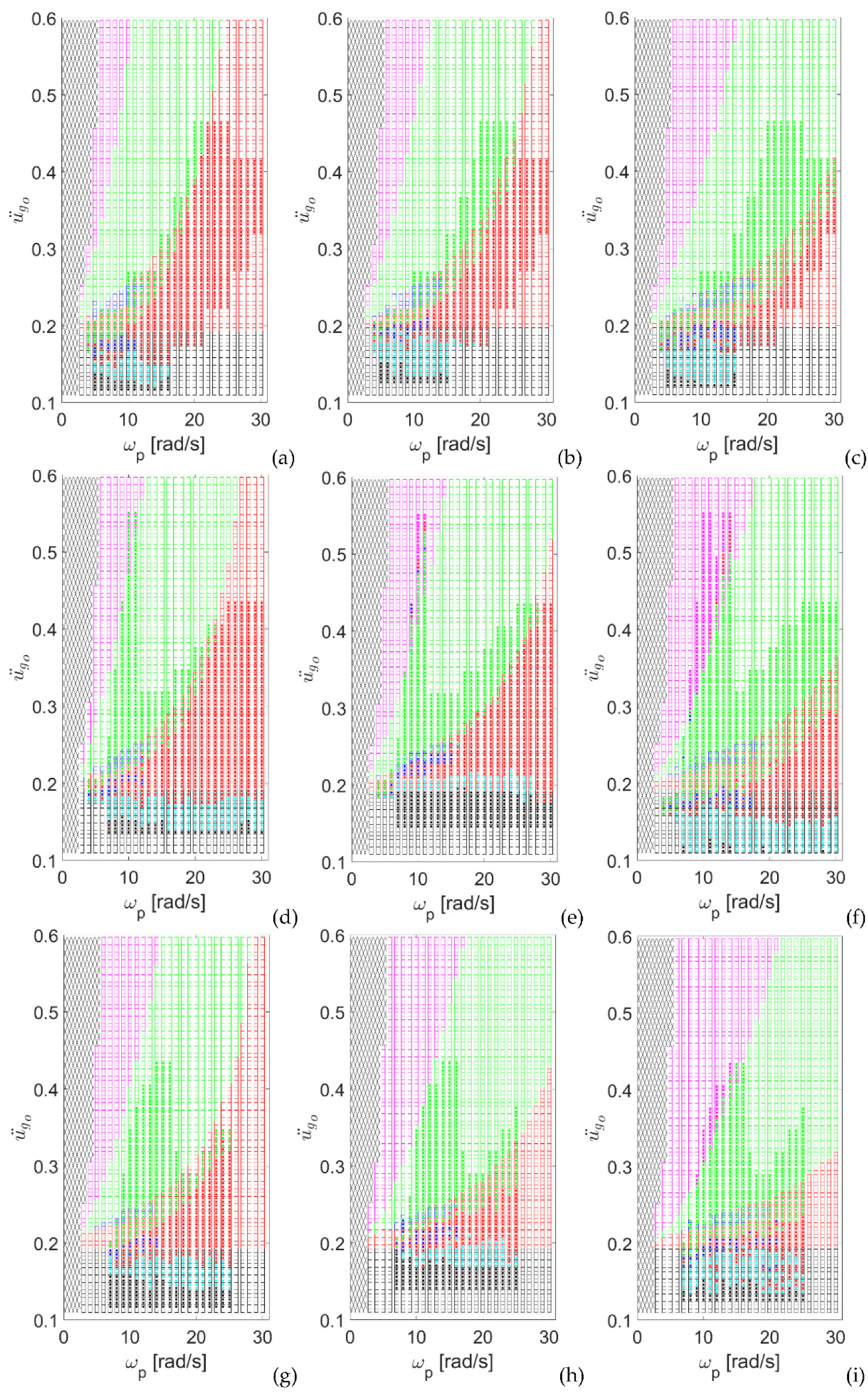
4.3. Stability Spectra
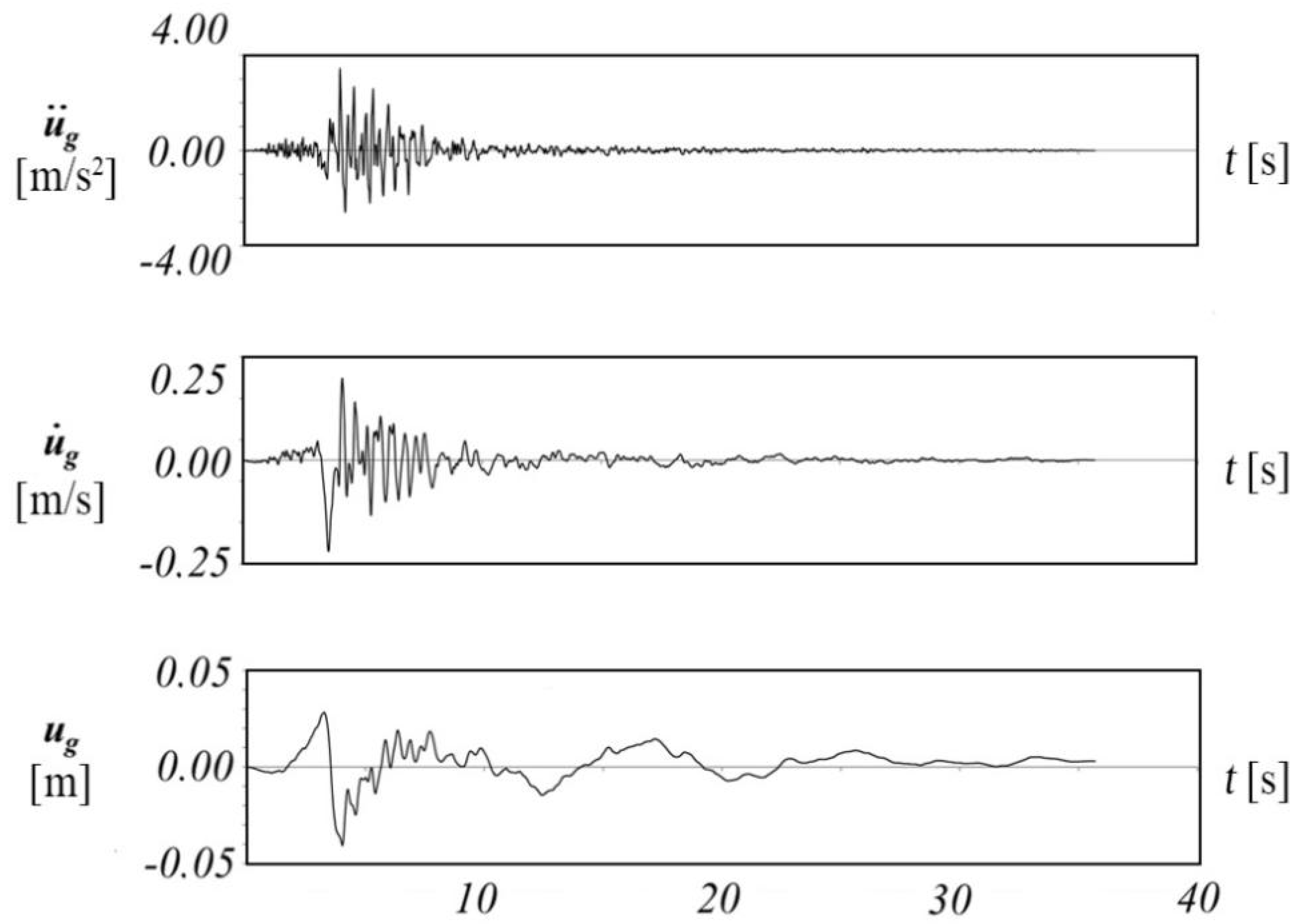
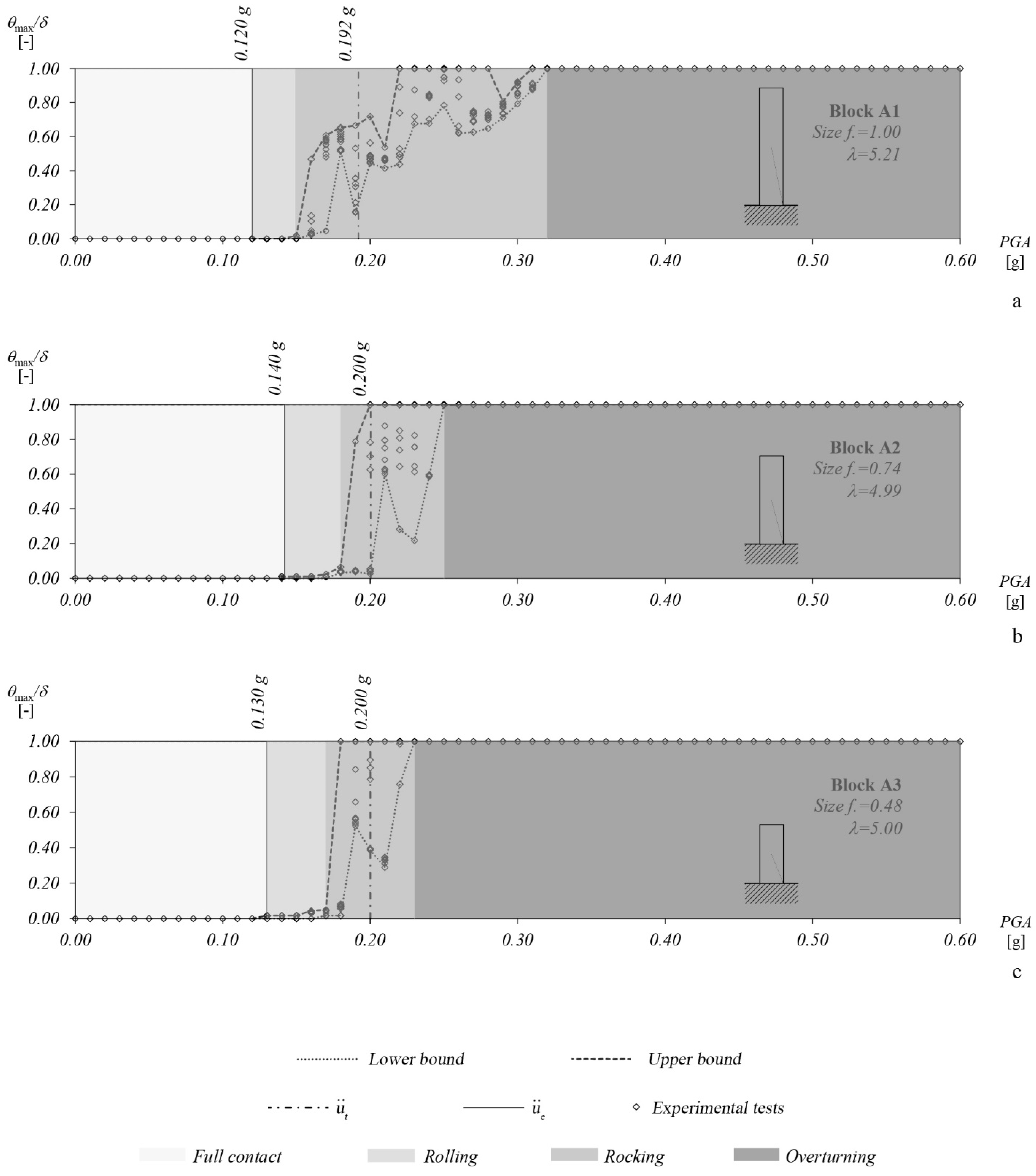
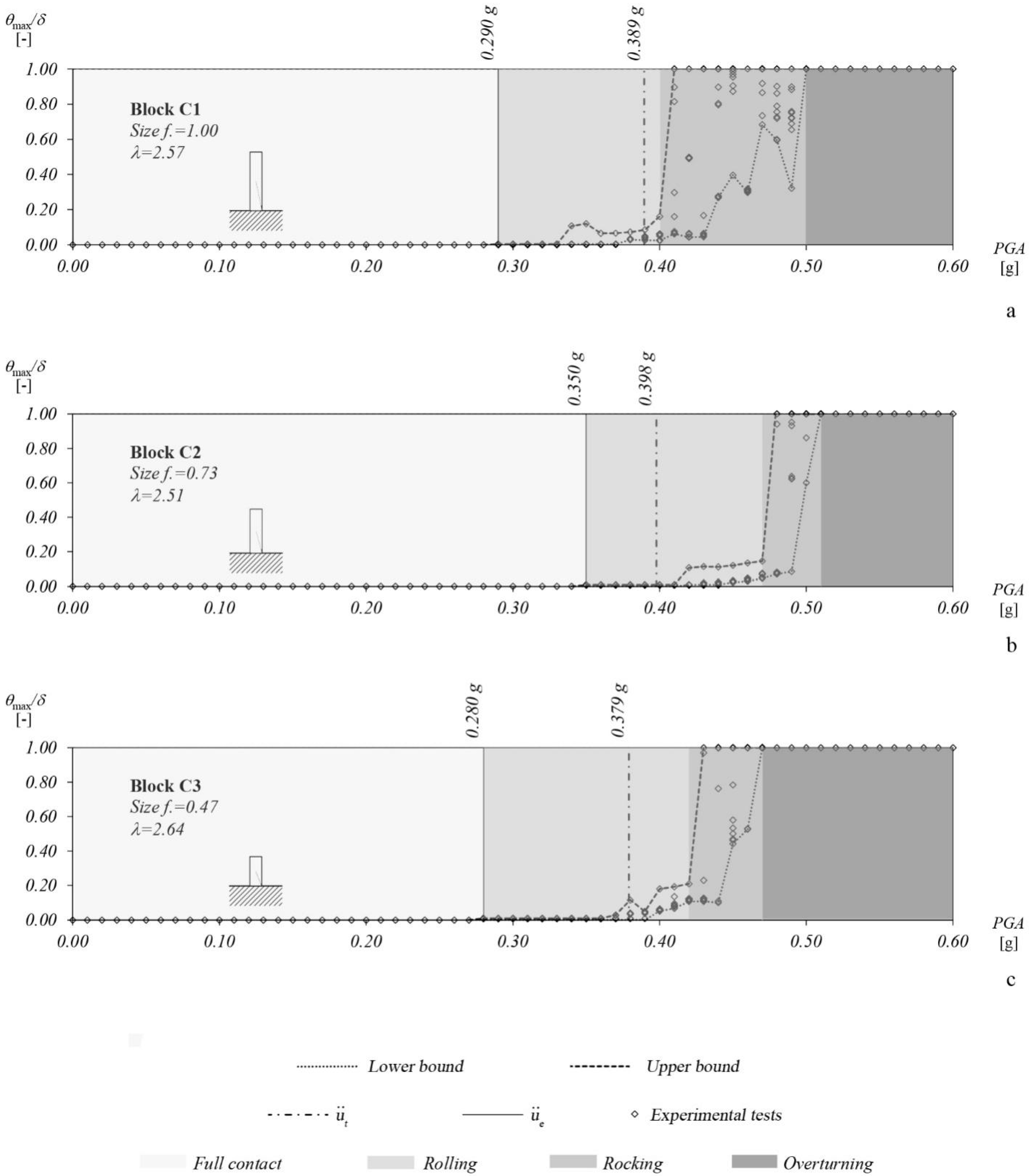
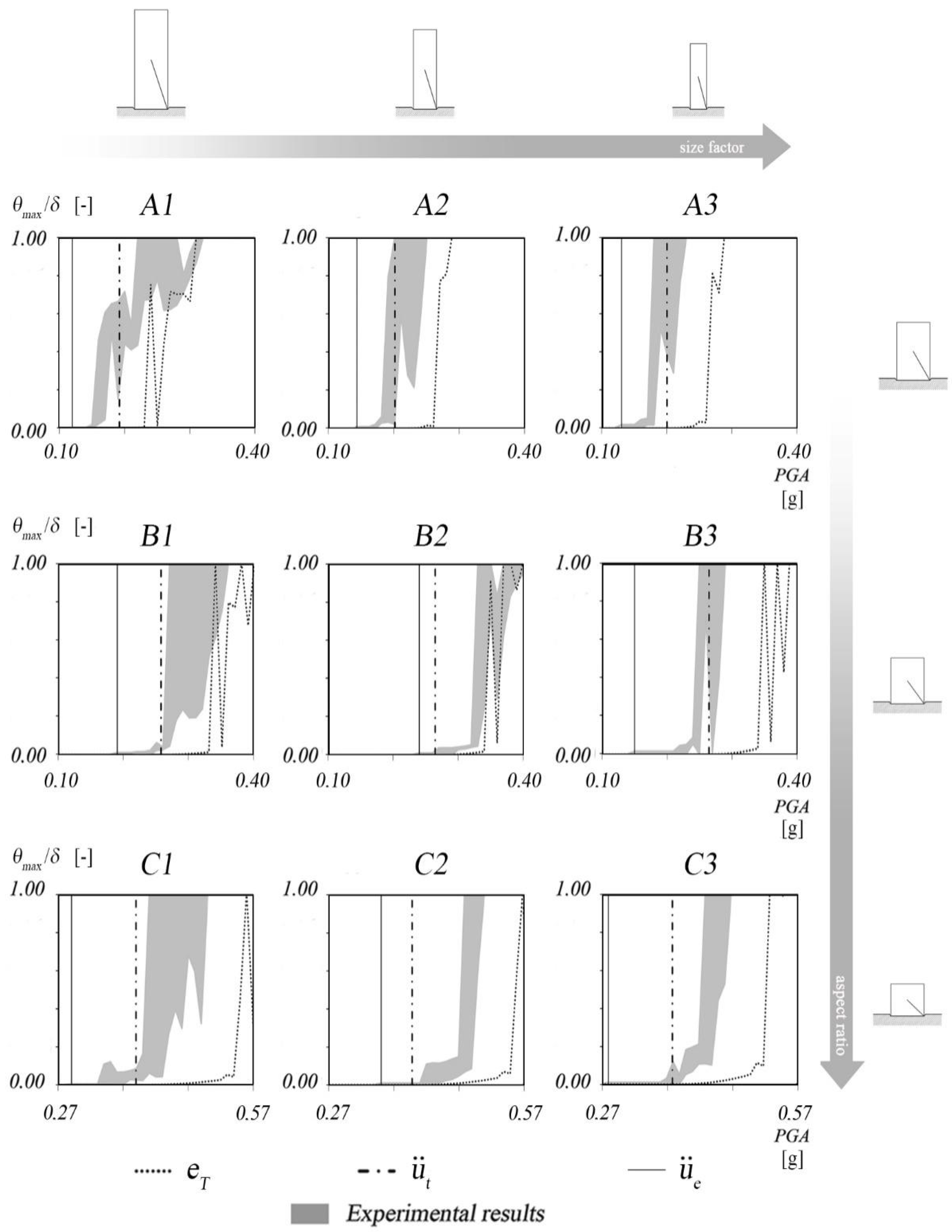
4.4. Earthquake Motions
- full contact, for all the duration of the ground motion the incipient rocking condition is not achieved;
- rolling, encountered for low values of the PGA, the block oscillates but does not rock and the response variability is limited (conventionally assuming );
- rocking, for higher values of the PGA, the block rocks and occasionally can overturn;
- overturning is associated to a band that starts when the block always overturns.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Uzdin, A.M.; Doronin, F.A.; Davydova, G.V.; Avidon, G.E.; Karlina, E.A. Performance analysis of seismic-insulating elements with negative stiffness. Soil Mech. Found. Eng. 2009, 46, 15–21. [Google Scholar] [CrossRef]
- Makris, N.; Vassiliou, M.F. Planar rocking response and stability analysis of an array of free-standing columns capped with a freely supported rigid beam. Earthq. Eng. Struct. D 2013, 42, 431–449. [Google Scholar] [CrossRef]
- Oliveto, G.; Caliò, I.; Greco, A. Large displacement behaviour of a structural model with foundation uplift under impulsive and earthquake excitations. Earthq. Eng. Struct. D 2003, 32, 369–393. [Google Scholar] [CrossRef]
- Konstantinidis, D.; Makris, N. Seismic response analysis of multidrum classical columns. Earthq. Eng. Struct. D 2005, 34, 1243–1270. [Google Scholar] [CrossRef]
- Psycharis, I.N.; Lemos, J.V.; Papastamatiou, D.Y.; Zambas, C.; Papantonopoulos, C. Numerical study of the seismic behaviour of a part of the Parthenon Pronaos. Earthq. Eng. Struct. D 2003, 32, 2063–2084. [Google Scholar] [CrossRef]
- Caddemi, S.; Caliò, I.; Cannizzaro, F.; Marletta, M.; Pantò, B. Seismic Vulnerability of the Concordia Temple. Adv. Mater. Res. 2010, 133–134, 759–764. [Google Scholar] [CrossRef]
- Caliò, I.; Marletta, M. Passive control of the seismic rocking response of art objects. Eng. Struct. 2003, 25, 1009–1018. [Google Scholar] [CrossRef]
- Contento, A.; Di Egidio, A. Investigations into the benefits of base isolation for non-symmetric rigid blocks. Earthq. Eng. Struct. D 2009, 38, 849–866. [Google Scholar] [CrossRef]
- Dar, A.; Konstantinidis, D.; El-Dakhakhni, W.W. Evaluation of ASCE 43-05 seismic design criteria for rocking objects in nuclear facilities. J. Struct. Eng. 2016, 142, 04016110. [Google Scholar] [CrossRef]
- Cocuzza Avellino, G.; Cannizzaro, F.; Di Martino, A.; Valenti, R.; Paternò, E.; Caliò, I.; Impollonia, N. Numerical and Experimental Response of Free-Standing Art Objects Subjected to Ground Motion. Int. J. Archit. Herit. 2021. [Google Scholar] [CrossRef]
- Housner, G.W. The behavior of inverted pendulum structures during earthquakes. Bull. Seismol. Soc. Am. 1963, 53, 403–417. [Google Scholar] [CrossRef]
- Di Egidio, A.; Contento, A. Seismic response of a non-symmetric rigid block on a constrained oscillating base. Eng. Struct. 2010, 32, 3028–3039. [Google Scholar] [CrossRef]
- Kalliontzis, D.; Sritharan, S.; Schultz, A. Improved Coefficient of Restitution Estimation for Free Rocking Members. J. Struct. Eng. 2016, 142, 06016002. [Google Scholar] [CrossRef]
- Augusti, G.; Sinopoli, A. Modelling the dynamics of large block structures. Meccanica 1992, 27, 195–211. [Google Scholar] [CrossRef]
- Zulli, D.; Contento, A.; Di Egidio, A. Three-dimensional model of rigid block with a rectangular base subject to pulse-type excitation. Int. J. Nonlinear Mech. 2012, 47, 679–687. [Google Scholar] [CrossRef]
- Lipscombe, P.R.; Pellegrino, S. Free rocking of prismatic blocks. J. Eng. Mech. 1993, 119, 1387–1410. [Google Scholar] [CrossRef] [Green Version]
- Tocci, C. Dinamica delle Strutture a Blocchi Sovrapposti. Le Colonne Isolate. Ph.D. Thesis, History of Science and Constructive Techniques, Faculty of Architecture, University of Rome “La Sapienza”, Rome, Italy, 1996. [Google Scholar]
- Casapulla, C.; Giresini, L.; Lourenço, P.B. Rocking and kinematic approaches for rigid block analysis of masonry walls: State of the art and recent developments. Buildings 2017, 7, 69. [Google Scholar] [CrossRef] [Green Version]
- Al Abadi, H.; Paton-Cole, V.; Gad, E.; Lam, N.; Patel, V. Rocking Behavior of Irregular Free-Standing Objects Subjected to Earthquake Motion. J. Earthq. Eng. 2019, 23, 793–809. [Google Scholar] [CrossRef]
- Kounadis, A.N. On the overturning instability of a rectangular rigid block under ground excitation. Open Mech. J. 2010, 4, 43–57. [Google Scholar] [CrossRef]
- Wittich, C.E. Seismic Response of Freestanding Structural Systems: Shake Table Tests and Model Validation. Doctor’s Dissertation, University of California, San Diego, San Diego, CA, USA, 2016. [Google Scholar]
- ElGawady, M.A.; Ma, Q.; Butterworth, J.; Ingham, J.M. Probabilistic analysis of rocking blocks. In Proceedings of the Technical Conference NZ Society for Earthquake Engineering, Napier, New Zealand, 10–12 March 2006; Brabhaharan, P., Ed.; Remembering Napier 1931, Building on 75 years of Earthquake Engineering in New Zealand. Paper Number 17. pp. 1–8. [Google Scholar]
- Yim, C.S.; Chopra, A.K.; Penzien, J. Rocking response of rigid blocks to earthquakes. Earthq. Eng. Struct. D 1980, 8, 565–587. [Google Scholar] [CrossRef]
- Al Shawa, O.; De Felice, G.; Mauro, A.; Sorrentino, L. Out-of-plane seismic behavior of rocking masonry walls. Earthq. Eng. Struct. D 2012, 41, 949–968. [Google Scholar] [CrossRef]
- Bachmann, J.A.; Blöchlinger, P.; Wellauer, M.; Vassiliou, M.F.; Stojadinović, B. Experimental investigation of the seismic response of a column rocking and rolling on a concave base. In Proceedings of the ECCOMAS Congress 2016 VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete Island, Greece, 5–10 June 2016. [Google Scholar] [CrossRef] [Green Version]
- Bachmann, J.A.; Vassiliou, M.F.; Stojadinovic, B. Rolling and rocking of rigid uplifting structures. Earthq. Eng. Struct. D 2019, 48, 1556–1574. [Google Scholar] [CrossRef]
- ElGawady, M.A.; Ma, Q.; Butterworth, J.; Ingham, J.M. The effect of interface material on the dynamic behavior of free rocking blocks. In Proceedings of the 8th U.S. National Conference on Earthquake Engineering, San Francisco, CA, USA, 18–22 April 2006. Paper No. 589. [Google Scholar]
- Kalliontzis, D.; Sritharan, S. Characterizing Dynamic Decay of Motion of Free-standing Rocking Members. Earthq. Spectra 2018, 34, 843–866. [Google Scholar] [CrossRef]
- Spanos, P.D.; Di Matteo, A.; Pirrotta, A.; Di Paola, M. Nonlinear rocking of rigid blocks on flexible foundation: Analysis and experiments. Procedia Eng. 2017, 199, 284–289. [Google Scholar] [CrossRef] [Green Version]
- Vassiliou, M.F.; Cengiz, C.; Dietz, M.; Dihoru, L.; Broccardo, M.; Mylonakis, G.; Sextos, A.; Stojadinovic, B. Data set from shake table tests of free-standing rocking bodies. Earthq. Spectra 2021, 37, 2971–2987. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.; Norman, J.; Mylonakis, G. Fractal like overturning maps for stacked rocking blocks with numerical and experimental validation. Soil Dyn. Earthq. Eng. 2019, 125, 105659. [Google Scholar] [CrossRef]
- Bachmann, J.A. Development of Self-Centering Systems with Geometry-Controlled Stiffness for Earthquake Hazard Mitigation. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2018. [Google Scholar]
- Aslam, M.; Salise, D.T.; Godden, W.G. Earthquake rocking response of rigid bodies. J. Struct. Div.-ASCE 1980, 106, 377–392. [Google Scholar] [CrossRef]
- Drosos, V.; Anastasopoulos, I. Shaking table testing of multidrum columns and portals. Earthq. Eng. Struct. D 2014, 43, 1703–1723. [Google Scholar] [CrossRef]
- ElGawady, M.A.; Ma, Q.; Butterworth, J.W.; Ingham, J. Effects of interface material on the performance of free rocking blocks. Earthq. Eng. Struct. D 2011, 40, 375–392. [Google Scholar] [CrossRef]
- Ma, Q.T.M. The Mechanics of Rocking Structures Subjected to Ground Motion. Ph.D. Thesis, ResearchSpace, Auckland, New Zealand, 2010. [Google Scholar]
- Mouzakis, H.P.; Psycharis, I.N.; Papastamatiou, D.Y.; Carydis, P.G.; Papantonopoulos, C.; Zambas, C. Experimental investigation of the earthquake response of a model of a marble classical column. Earthq. Eng. Struct. D 2002, 31, 1681–1698. [Google Scholar] [CrossRef]
- Pena, F.; Prieto, F.; Lourenço, P.B.; Campos Costa, A.; Lemos, J.V. On the dynamics of rocking motion of single rigid-block structures. Earthq. Eng. Struct. D 2007, 36, 2383–2399. [Google Scholar] [CrossRef] [Green Version]
- Priestley, M.J.N.; Evison, R.J.; Carr, A.J. Seismic response of structures free to rock on their foundations. Bull. N. Z. Soc. Earthq. Eng. 1978, 11, 141–150. [Google Scholar] [CrossRef]
- Lin, H.; Yim, C.S. Nonlinear rocking motion. I: Chaos under noisy periodic excitations. J. Eng. Mech. 1996, 122, 719–727. [Google Scholar] [CrossRef]
- Jeong, M.Y.; Lee, H.; Kim, J.H.; Yang, I.Y. Chaotic Behavior on Rocking Vibration of Rigid Body Block Structure under Two-dimensional Sinusoidal Excitation (In the Case of No Sliding). KSME Int. J. 2003, 17, 1249–1260. [Google Scholar] [CrossRef]
- Bachmann, J.A.; Strand, M.; Vassiliou, M.F.; Broccardo, M.; Stojadinović, B. Is rocking motion predictable? Earthq. Eng. Struct. D 2017, 47, 535–552. [Google Scholar] [CrossRef]
- Scislo, L.; Guinchard, M. Non-invasive measurements of ultra-lightweight composite materials using laser Dopple vibrometry system. In Proceedings of the 26th International Conference on Sound and Vibration, Montreal, QC, Canada, 7–11 July 2019. [Google Scholar]
- Cocuzza Avellino, G.; Cannizzaro, F.; Impollonia, N. Dataset of the Experimental Campaign Presented in the Paper Entitled “Shaking Table Seismic Experimental Investigation of Lightweight Rigid Bodies”, Zenodo: Geneva, Switzerland, 2022. [CrossRef]
- Cocuzza Avellino, G. Rigid Body Seismic Vulnerability and Protection by Means of Low-Cost Rolling Ball System Isolator: Numerical and Experimental Analyses. Ph.D. Thesis, University of Catania, Catania, Italy, 2020. [Google Scholar]
- Brown, D.; Wolfgang, C. Simulating what you see: Combining computer modeling with video analysis. In Proceedings of the MPTL 16—HSCI 2011, Ljubljana, Slovenia, 15–17 September 2011. [Google Scholar]
- Centrotecnica srl. Lo.F.Hi.S. User Manual; Centrotecnica srl: Masate, Italy, 2018. [Google Scholar]
- Seismosoft “SeismoSignal—A Computer Program for Signal Processing of Time-Histories”. Available online: www.seismosoft.com (accessed on 29 May 2022).
- Baqersad, J.; Poozesh, P.; Niezrecki, C.; Avitabile, P. Photogrammetry and optical methods in structural dynamics—A review. Mech. Syst. Signal Process. 2017, 86, 17–34. [Google Scholar] [CrossRef]
- De Canio, G.; Mongelli, M.; Roselli, I.; Tatì, A. Elaborazione di dati di spostamento da sistema di motion capture 3D per prove su tavola vibrante. In Proceedings of the XV Convegno ANIDIS, Padua, Italy, 30 June–4 July 2013. [Google Scholar]
- Sorrentino, L.; Al Shawa, O.; Decanini, L.D. The relevance of energy damping in unreinforced masonry rocking mechanisms. Experimental and analytic investigations. Bull. Earthq. Eng. 2011, 9, 1617–1642. [Google Scholar] [CrossRef]
- Spanos, P.D.; Koh, A.S. Rocking of rigid blocks due to harmonic shaking. J. Eng. Mech. 1984, 110, 1627–1642. [Google Scholar] [CrossRef]
- Makris, N.; Roussos, Y.S. Rocking response of rigid blocks under near-source ground motions. Géotechnique 2000, 50, 243–262. [Google Scholar] [CrossRef]
- Cocuzza Avellino, G.; Caliò, I.; Cannizzaro, F.; Caddemi, S.; Impollonia, N. Response spectra of rigid blocks with uncertain behavior. In Proceedings of the COMPDYN 2019 7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete, Greece, 24–26 June 2019; Papadrakakis, M., Fragiadakis, M., Eds.; [Google Scholar] [CrossRef] [Green Version]






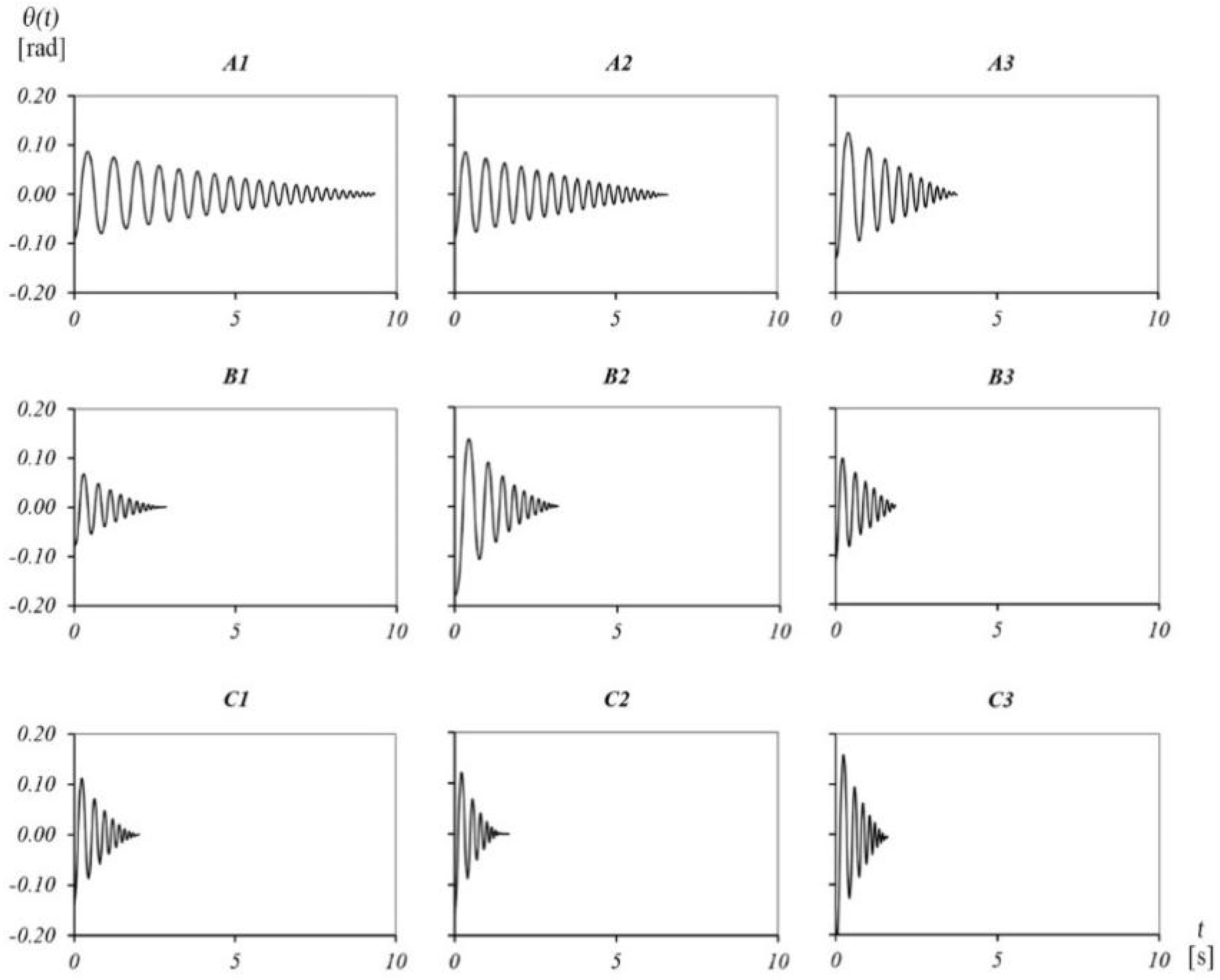

| A1 | A2 | A3 | B1 | B2 | B3 | C1 | C2 | C3 | |
|---|---|---|---|---|---|---|---|---|---|
| Aspect ratio | 5.2083 | 4.9883 | 5.0000 | 3.8927 | 3.7811 | 3.7772 | 2.5676 | 2.5133 | 2.6383 |
| Size factor | 1.0000 | 0.7124 | 0.4607 | 1.0000 | 0.7113 | 0.4642 | 1.0000 | 0.7138 | 0.4845 |
| m [kg] (1) | 1.286 | 0.435 | 0.113 | 0.995 | 0.300 | 0.084 | 0.641 | 0.201 | 0.059 |
| b [m] (1) | 0.0384 | 0.0285 | 0.0184 | 0.0385 | 0.0282 | 0.0184 | 0.0389 | 0.0283 | 0.0184 |
| h [m] (1) | 0.2000 | 0.1423 | 0.0920 | 0.1500 | 0.1065 | 0.0695 | 0.0998 | 0.0710 | 0.0485 |
| d [m] (2) | 0.2037 | 0.1451 | 0.0938 | 0.1549 | 0.1102 | 0.0719 | 0.1070 | 0.0764 | 0.0519 |
| δ [rad] (2) | 0.1897 | 0.1978 | 0.1974 | 0.2515 | 0.2586 | 0.2588 | 0.3714 | 0.3787 | 0.3623 |
| IG [kg m2] (2) | 0.017783 | 0.003049 | 0.000331 | 0.007956 | 0.001213 | 0.000143 | 0.002448 | 0.000390 | 0.000054 |
| IG + md2 [kg m2] (2) | 0.071119 | 0.012206 | 0.001326 | 0.031821 | 0.004854 | 0.000577 | 0.009794 | 0.001564 | 0.000213 |
| p [rad/s] (2) | 6.0105 | 7.1221 | 8.8572 | 6.8924 | 8.1728 | 10.1331 | 8.2905 | 9.8157 | 11.8824 |
| A1 | A2 | A3 | ||||||
|---|---|---|---|---|---|---|---|---|
| [g] | [g] | [-] | [g] | [g] | [-] | [g] | [g] | [-] |
| 0.192 | 0.120 | 0.625 | 0.200 | 0.140 | 0.700 | 0.200 | 0.130 | 0.650 |
| B1 | B2 | B3 | ||||||
| [g] | [g] | [-] | [g] | [g] | [-] | [g] | [g] | [-] |
| 0.257 | 0.190 | 0.739 | 0.264 | 0.240 | 0.909 | 0.265 | 0.150 | 0.566 |
| C1 | C2 | C3 | ||||||
| [g] | [g] | [-] | [g] | [g] | [-] | [g] | [g] | [-] |
| 0.389 | 0.290 | 0.745 | 0.398 | 0.350 | 0.879 | 0.379 | 0.280 | 0.739 |
| [s] | [rad] | [g] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00 | 0.0904 | 0.21 | 0.8593 | 0.9843 | - | 1 | 0.42 | 0.0864 | 0.63 | 0.8073 | 0.9718 | - |
| 2 | 0.83 | 0.0798 | 1.03 | 0.7969 | 0.9781 | 0.83 | 3 | 1.22 | 0.0752 | 1.43 | 0.7977 | 0.9746 | 0.80 |
| 4 | 1.61 | 0.0703 | 1.79 | 0.7540 | 0.9791 | 0.78 | 5 | 1.96 | 0.0666 | 2.14 | 0.7034 | 0.9706 | 0.74 |
| 6 | 2.30 | 0.0618 | 2.48 | 0.7434 | 0.9752 | 0.69 | 7 | 2.63 | 0.0581 | 2.79 | 0.6472 | 0.9791 | 0.67 |
| 8 | 2.94 | 0.0552 | 3.10 | 0.6395 | 0.9698 | 0.64 | 9 | 3.25 | 0.0513 | 3.40 | 0.6135 | 0.9764 | 0.62 |
| 10 | 3.54 | 0.0485 | 3.69 | 0.6480 | 0.9812 | 0.60 | 11 | 3.82 | 0.0464 | 3.97 | 0.6147 | - | 0.57 |
| [s] | [rad] | [g] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.0877 | 0.16 | 1.0013 | 0.9905 | - | 1 | 0.33 | 0.0854 | 0.52 | 0.9407 | 0.9618 | - |
| 2 | 0.67 | 0.0769 | 0.82 | 0.9035 | 0.9802 | 0.67 | 3 | 0.98 | 0.073 | 1.13 | 0.9272 | 0.9645 | 0.65 |
| 4 | 1.26 | 0.0666 | 1.41 | 0.8737 | 0.9823 | 0.59 | 5 | 1.54 | 0.0637 | 1.69 | 0.8787 | 0.9698 | 0.56 |
| 6 | 1.81 | 0.0591 | 1.94 | 0.855 | 0.9779 | 0.55 | 7 | 2.07 | 0.056 | 2.2 | 0.8219 | 0.9700 | 0.53 |
| 8 | 2.32 | 0.0521 | 2.44 | 0.7587 | 0.9716 | 0.51 | 9 | 2.55 | 0.0487 | 2.68 | 0.7263 | 0.9802 | 0.48 |
| 10 | 2.79 | 0.0465 | 2.89 | 0.7332 | 0.9674 | 0.47 | 11 | 3 | 0.0431 | 3.12 | 0.7188 | - | 0.45 |
| [s] | [rad] | [g] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.1325 | 0.19 | 1.4367 | 0.9846 | - | 1 | 0.39 | 0.1248 | 0.58 | 1.353 | 0.9185 | - |
| 2 | 0.73 | 0.0948 | 0.88 | 1.2427 | 0.9989 | 0.73 | 3 | 1.02 | 0.0945 | 1.18 | 1.2003 | 0.9182 | 0.63 |
| 4 | 1.29 | 0.0748 | 1.42 | 1.1268 | 0.9827 | 0.56 | 5 | 1.53 | 0.0715 | 1.66 | 1.0353 | 0.9198 | 0.51 |
| 6 | 1.75 | 0.0581 | 1.87 | 0.9569 | 0.9811 | 0.46 | 7 | 1.96 | 0.0555 | 2.07 | 0.9276 | 0.9212 | 0.43 |
| 8 | 2.15 | 0.0458 | 2.24 | 0.8976 | 0.9638 | 0.40 | 9 | 2.33 | 0.0421 | 2.42 | 0.8002 | 0.9184 | 0.37 |
| 10 | 2.49 | 0.0348 | 2.57 | 0.7635 | 0.9708 | 0.34 | 11 | 2.64 | 0.0326 | 2.73 | 0.6714 | - | 0.31 |
| [s] | [rad] | [g] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.0784 | 0.15 | 0.9835 | 0.9407 | - | 1 | 0.29 | 0.0677 | 0.41 | 0.9124 | 0.9105 | - |
| 2 | 0.53 | 0.0545 | 0.63 | 0.7944 | 0.9443 | 0.53 | 3 | 0.74 | 0.0479 | 0.83 | 0.7117 | 0.9142 | 0.45 |
| 4 | 0.94 | 0.0393 | 1.02 | 0.6841 | 0.9518 | 0.41 | 5 | 1.12 | 0.0353 | 1.19 | 0.5982 | 0.9124 | 0.38 |
| 6 | 1.28 | 0.029 | 1.35 | 0.5775 | 0.9481 | 0.34 | 7 | 1.43 | 0.0259 | 1.5 | 0.5203 | 0.9173 | 0.31 |
| 8 | 1.58 | 0.0216 | 1.63 | 0.4678 | 0.9211 | 0.30 | 9 | 1.71 | 0.0182 | 1.76 | 0.4059 | 0.8959 | 0.28 |
| 10 | 1.83 | 0.0145 | 1.87 | 0.3112 | 0.9231 | 0.25 | 11 | 1.94 | 0.0123 | 1.98 | 0.2843 | - | 0.23 |
| [s] | [rad] | [g] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.1798 | 0.26 | 1.6884 | 0.9237 | - | 1 | 0.44 | 0.1358 | 0.62 | 1.5231 | 0.9193 | - |
| 2 | 0.76 | 0.1067 | 0.91 | 1.3955 | 0.9309 | 0.76 | 3 | 1.03 | 0.0886 | 1.17 | 1.29 | 0.9158 | 0.59 |
| 4 | 1.27 | 0.0715 | 1.38 | 1.0935 | 0.9323 | 0.51 | 5 | 1.48 | 0.0607 | 1.58 | 1.0196 | 0.9205 | 0.45 |
| 6 | 1.67 | 0.0503 | 1.76 | 0.9833 | 0.9336 | 0.40 | 7 | 1.84 | 0.0432 | 1.93 | 0.8717 | 0.9101 | 0.36 |
| 8 | 1.99 | 0.0352 | 2.07 | 0.8054 | 0.9425 | 0.32 | 9 | 2.14 | 0.031 | 2.2 | 0.727 | 0.8878 | 0.30 |
| 10 | 2.26 | 0.0241 | 2.33 | 0.6323 | 0.9448 | 0.27 | 11 | 2.38 | 0.0214 | 2.33 | 0.6323 | - | 0.24 |
| [s] | [rad] | [g] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.1151 | 0.11 | 1.7023 | 0.9423 | - | 1 | 0.22 | 0.0981 | 0.33 | 1.5776 | 0.9310 | - |
| 2 | 0.42 | 0.0819 | 0.52 | 1.4691 | 0.9300 | 0.42 | 3 | 0.61 | 0.0688 | 0.69 | 1.3539 | 0.9283 | 0.39 |
| 4 | 0.78 | 0.0579 | 0.85 | 1.1843 | 0.9388 | 0.36 | 5 | 0.92 | 0.0502 | 1 | 1.0812 | 0.9345 | 0.31 |
| 6 | 1.06 | 0.0432 | 1.13 | 1.0629 | 0.9232 | 0.28 | 7 | 1.18 | 0.0363 | 1.25 | 0.8996 | 0.9178 | 0.26 |
| 8 | 1.3 | 0.0302 | 1.36 | 0.7679 | 0.8396 | 0.24 | 9 | 1.41 | 0.0209 | 1.46 | 0.6776 | 0.9861 | 0.23 |
| 10 | 1.5 | 0.0203 | 1.56 | 0.5753 | 0.7907 | 0.20 | 11 | 1.59 | 0.0125 | 1.63 | 0.4624 | - | 0.18 |
| [s] | [rad] | [g] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.1376 | 0.12 | 1.8976 | 0.9209 | - | 1 | 0.23 | 0.1121 | 0.35 | 1.7481 | 0.8965 | - |
| 2 | 0.44 | 0.0867 | 0.54 | 1.5214 | 0.9171 | 0.44 | 3 | 0.63 | 0.0713 | 0.73 | 1.3545 | 0.9098 | 0.40 |
| 4 | 0.79 | 0.0579 | 0.88 | 1.1829 | 0.9114 | 0.35 | 5 | 0.94 | 0.0474 | 1.02 | 1.0753 | 0.9023 | 0.31 |
| 6 | 1.08 | 0.0381 | 1.14 | 0.9543 | 0.9092 | 0.29 | 7 | 1.19 | 0.0312 | 1.25 | 0.8049 | 0.8971 | 0.25 |
| 8 | 1.3 | 0.0249 | 1.36 | 0.7168 | 0.9013 | 0.22 | 9 | 1.4 | 0.0201 | 1.45 | 0.6131 | 0.8780 | 0.21 |
| 10 | 1.48 | 0.0154 | 1.53 | 0.5138 | 0.8847 | 0.18 | 11 | 1.57 | 0.012 | 1.61 | 0.4376 | - | 0.17 |
| [s] | [rad] | [g] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.1602 | 0.12 | 2.3119 | 0.8971 | - | 1 | 0.21 | 0.1212 | 0.32 | 1.9921 | 0.8712 | - |
| 2 | 0.4 | 0.0875 | 0.48 | 1.7293 | 0.8986 | 0.40 | 3 | 0.55 | 0.0688 | 0.63 | 1.4585 | 0.8668 | 0.34 |
| 4 | 0.68 | 0.0504 | 0.75 | 1.2917 | 0.9108 | 0.28 | 5 | 0.8 | 0.0413 | 0.86 | 1.1194 | 0.8601 | 0.25 |
| 6 | 0.9 | 0.0301 | 0.96 | 0.9424 | 0.9073 | 0.22 | 7 | 0.99 | 0.0246 | 1.04 | 0.7669 | 0.8354 | 0.19 |
| 8 | 1.08 | 0.017 | 1.12 | 0.6512 | 0.8931 | 0.18 | 9 | 1.14 | 0.0135 | 1.18 | 0.4985 | 0.7773 | 0.15 |
| 10 | 1.21 | 0.0081 | 1.24 | 0.408 | 0.9368 | 0.13 | 11 | 1.26 | 0.0071 | 1.29 | 0.3222 | - | 0.12 |
| [s] | [rad] | [g] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.2376 | 0.14 | 3.2204 | 0.8800 | - | 1 | 0.23 | 0.1587 | 0.35 | 2.8293 | 0.9210 | - |
| 2 | 0.43 | 0.1278 | 0.52 | 2.4848 | 0.8833 | 0.43 | 3 | 0.58 | 0.0946 | 0.66 | 2.2565 | 0.9539 | 0.35 |
| 4 | 0.73 | 0.0848 | 0.79 | 2.0405 | 0.8684 | 0.30 | 5 | 0.84 | 0.0618 | 0.9 | 1.8067 | 0.9798 | 0.26 |
| 6 | 0.95 | 0.0591 | 1.01 | 1.5097 | 0.8079 | 0.22 | 7 | 1.04 | 0.0374 | 1.09 | 1.4107 | 0.9743 | 0.20 |
| 8 | 1.13 | 0.0354 | 1.18 | 1.1972 | 0.8096 | 0.18 | 9 | 1.21 | 0.0228 | 1.25 | 1.0137 | 0.9475 | 0.17 |
| 10 | 1.28 | 0.0204 | 1.33 | 0.7943 | 0.7120 | 0.15 | 11 | 1.34 | 0.0102 | 1.37 | 0.5898 | - | 0.13 |
| Outcome | Color |
|---|---|
| Experimental test not executed | |
| No motion | |
| Rolling | |
| Rocking | |
| Rocking followed by overturning (in the negative side) | |
| Rocking followed by overturning (in the positive side) | |
| Immediate overturning (negative side) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cocuzza Avellino, G.; Cannizzaro, F.; Impollonia, N. Shaking Table Seismic Experimental Investigation of Lightweight Rigid Bodies. Buildings 2022, 12, 915. https://doi.org/10.3390/buildings12070915
Cocuzza Avellino G, Cannizzaro F, Impollonia N. Shaking Table Seismic Experimental Investigation of Lightweight Rigid Bodies. Buildings. 2022; 12(7):915. https://doi.org/10.3390/buildings12070915
Chicago/Turabian StyleCocuzza Avellino, Giuseppe, Francesco Cannizzaro, and Nicola Impollonia. 2022. "Shaking Table Seismic Experimental Investigation of Lightweight Rigid Bodies" Buildings 12, no. 7: 915. https://doi.org/10.3390/buildings12070915
APA StyleCocuzza Avellino, G., Cannizzaro, F., & Impollonia, N. (2022). Shaking Table Seismic Experimental Investigation of Lightweight Rigid Bodies. Buildings, 12(7), 915. https://doi.org/10.3390/buildings12070915







