Identifying Key Information on Life Cycle of Engineering Data by Graph Convolutional Networks and Data Mining

Abstract

Engineering data, including product data-conversion networks and software dependency networks, are very important for the long-term preservation of product information. With the explosive growth of data in recent years, product information has become increasingly diversified and complex, which poses new challenges to the long-term preservation of product data. A better understanding of the functions of complex networks can help us take more effective measures to maintain and control such complex systems, and then adopt more effective methods to achieve life cycle management. It is currently difficult for traditional heuristic methods to deal with such large-scale complex systems. In recent years, however, the use of graph neural networks to identify key nodes attracted widespread attention, but this requires a large amount of training data. It is difficult to obtain large-scale relational data and establish identification models in engineering fields. Combining a graph convolution network with a data-mining method, a key node identification method in a graph convolution network based on data mining is proposed. The method first determines the type of complex network according to the power-law distribution and centrality of the network and then uses the corresponding evolutionary model to generate a large-scale synthetic network to effectively train the model. The experimental results from two real networks show that this method improves the identification performance of key nodes by using synthetic data with the same characteristics as the real network, and provides a new perspective for product life cycle management.

1. Introduction

Novel digital technology and ubiquitous computing bring much convenience to traditional engineering technology. Product data formats and tools are widely used to exchange product information between CAD models and the BIM (Building Information Modeling) system. The explosive growth of data and the diversification of product formats in recent years present an important challenge for the long-term preservation of engineering information, including product data conversion networks and software dependency networks [1]. Previous research on data migration was mainly achieved by manual and ad-hoc procedures; these depend on the selection of targets that researchers are implicitly expected to have and the results could be subjective [2]. It is unfeasible to manually translate all file formats. The diversity of data formats facilitates the recording and dissemination of information, which needs corresponding software to process different file formats. However, data formats and software tools used to maintain digital content may be superseded by newer versions, which may no longer be supported by vendors and software platforms. The rapid evolution and proliferation of various formats evolved into a major factor endangering the long-term preservation of digital information [3].

In recent years, a dramatic growth to identify and classify networks was witnessed in a wide variety of fields, including protein–protein interaction networks in BIM [4], biology, scientific collaboration, movie actor collaboration networks in sociology [5], and production networks in engineering [6]. Rather different from regular networks or simple random networks, it was discovered that these real-world networks share scale-free or small-world qualities. These properties greatly promoted the study of complex networks, which provides a novel perspective to understanding how the structures of complex systems remain robust and adaptable as they evolve [7].

The cohesiveness and connectivity of complex systems are significantly involved with a small part of nodes. Hence, identifying key nodes is a challenging but essential task that includes stopping the spreading of infections on scale-free networks, identifying essential proteins within the protein interaction network, assessing network vulnerability on critical links and nodes, maximizing the spread of influence by viral marketing and discovering a scientist’s standing in research communities [8,9].

The problem of finding critical nodes is known as an NP-hard problem [10]. Previous works identify key nodes from either centrality-based analysis methods or feature-based machine learning methods. These methods separately exploit network structures or node-level features. The development of machine learning and deep learning, computer vision (CV) [11,12], and natural language processing (NLP) enabled [13] to gradually make great breakthroughs; their research subjects, such as images and texts, were simple sequences or grids of structured data. However, applying deep learning to the unstructured graph data is a non-trivial task due to the non-Euclidean data of complex networks.

The graph convolutional network (GCN) [14] is a feature extractor that treats neighbor nodes of a node as the perceptual field. The field becomes larger as the number of network layers increases, which enables GCN to incorporate more features from more nodes. GCN is a graph neural network that uses the Laplacian matrix to obtain an easy-to-compute convolution kernel on the graph network. It combines the advances in deep learning techniques and graph representation. This feature allows for a wide range of purposes, such as node classification, link prediction, embedding [15], and identifying key nodes with complex structures and heterogeneous data [16].

The success of GCN benefits from massive training data. However, the application of complex networks to fields, such as product data-exchange networks, is still relatively limited. It suffers from the difficulty of obtaining and abstracting large-scale engineering information relationships for establishing corresponding networks. Complicated relationships can exist in large numbers and as scattered engineering information, such as migration, transformation, and reliability [2].

To identify key nodes in data-limited scenarios, in this paper, we propose a data-mining-based graph convolutional model (DMGCN). DMGCN first collects real data to solve the problem of data scarcity, then classifies a network by the characteristics of the system. It helps to train a better model with synthetic graphs generated from the corresponding evolving method of a complex network. Finally, we use the trained model to identify key nodes in real systems. The data-mining-based method not only provides training data for the inductive graph representation learning, but also ensures the consistency of characteristics between synthetic networks and the real system, thereby improving the performance of the key nodes identification method.

The remainder of this paper is structured as follows. Section 2 provides helpful background and works involved in GCN and key node identification. We present the proposed data-mining-based GCN framework in Section 3. Section 3 then presents two cases, including a production data-exchange network and a software packages dependency network, which suffer from the problem of data scarcity. Section 4 describes extensive experiments for node identification. Finally, Section 5 concludes this paper and directs future work.

2. Related Works

2.1. Graph Neural Networks

Recent decades witnessed an explosion in advances in feature extraction, learning, and representation methods that emerged as promising and effective approaches to understanding graphs. The traditional GCN aggregates the information of neighbors connected to the node that is being updated; however, it is transductive and has poor scalability.

Instead of training a separate embedding for all neighbors, GraphSAGE [17] is designed to learn a node representation by fixed-size sampling and aggregating features from local neighbors. GraphSAGE is an inductive framework that uses local information, thus efficiently generating embedding vectors for unseen nodes.

To solve the problem with the fixed adjacent matrix, GAT [18] adds an attention factor to GCN. The essence of such an approach is a different aggregation function with attention to the features of neighbors. GAT places importance on the edge between nodes to help the model learn structural information. Similar to the GCN, the graph attention layer creates a message for each node using a linear matrix.

2.2. Key Nodes Identification

There were several attempts to identify key nodes in complex networks [19]. The deep reinforcement learning framework FINDER [10] first performs offline learning in simulated graphs with a small number of nodes and then decides which nodes to remove based on the current network in real scenarios. In this paper, we use the same loss function for training models as FINDER. The difference with FINDER is that it uses the data generated from a fixed complex network model. If the features of the real-world data are different from the selected model, the performance of FINDER will decrease.

InfGCN [16] first transforms the evaluation of node importance into a classification task and then feeds the representations of nodes into the task-learning neural layers. To train a network identifying the most key nodes, InfGCN uses the ground truth derived from Susceptible Infected Recovered (SIR) simulation experiments. This data generation method is similar to the data mining section of DMGCN.

By counting the percentage of all four connections in the 3-node graph, 4-node graphs, and 5-node graphs, Bonato et al. [20] obtained a statistical distribution of the connectivity. They then used classifiers, including SVM (Support Vector Machine), random forest, and a boost decision tree to determine the network topology and identify the network type. This method utilizes the motif of complex networks, where all the small sub-networks from a large network with a given number of nodes can be extracted.

To design a system that can automatically model complex systems by looking at data, Zhang et al. [21] proposed a deep-learning-based method for reconstructing network structure and dynamics. This method can infer the connection structure of a network by only observing evolution data only. When relationships between nodes are unknown, the method further predicts accurate states of nodes by modeling the dynamics laws of interactions, using neural networks (NN).

2.3. The Life Cycle of Engineering Data

Engineering information is complex and discrete because of design methods and manufacturing processes; consequently, its long-term retention presents a great challenge. In the long-term preservation of engineering information, in order to make the formats of such information compatible with each other, conversion between engineering software and data formats can be utilized [22]. To deal with the data transfer problem between the CAD model and rapid prototyping systems, Zhang et al. [23] proposed a simple and programming-friendly AM (Additive Manufacturing) data format with backward compatibility and the formal specification of product data to migrate old STL file data. The entire life cycle of engineering data is accompanied by numerous highly dedicated software packages. The interoperability of the tools in use by engineers is an important prerequisite. To maintain the strong heterogeneity of existing data standards, Sandra et al. [24] presented a data-exchange format to replace the manual steps involved when migrating from one engineering software to another.

3. Model

In this section, we will first propose a key node identification method called DMGCN. We will then analyze two real-world complex systems based on the data-mining method.

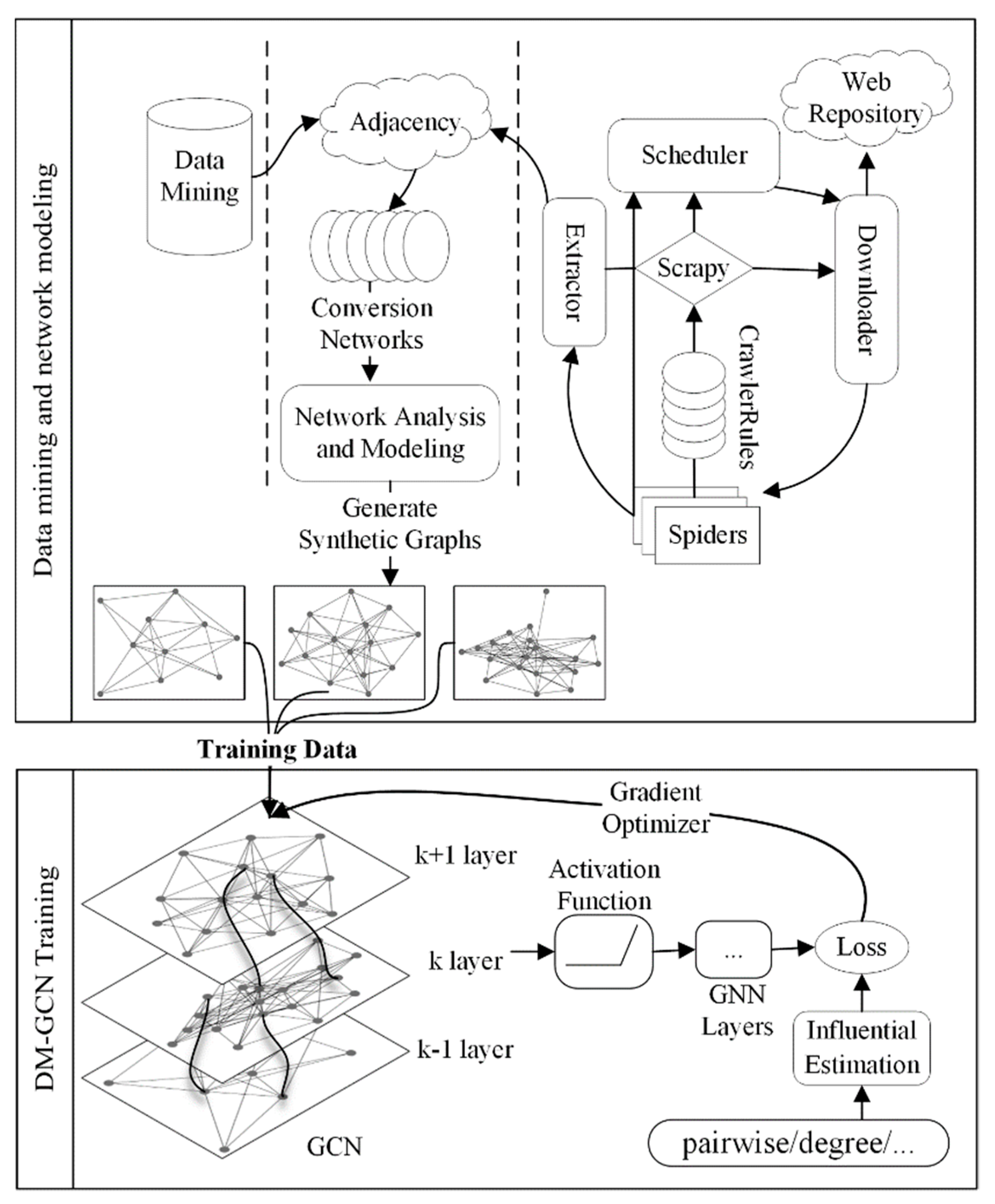
3.1. A Data-Mining-Based Graph Convolutional Model

As shown in Figure 1, the whole framework of DMGCN consists of two parts.

Table 1. The list of notations used in this paper.

Symbol	Description
$G$	A graph
$V$	vertices of $G$
$E$	edges of $G$
$v$	a vertex or node
$h_v^k$	The k-th layer embedding of the node $v$
$\sigma$	functions such as non-linearity neural layers
$AGGREGATE$	a differentiable aggregator function such as $sum$
$R$	ANC (Accumulated Normalized Connectivity)
$C_i$	the i-th connected subcomponents in G
$\sigma \left(G\right)$	the initial connectivity of $G$.
$d\left(v_i\right)$	The degree of a node $v_i$
$C$	The clustering coefficient of $G$
$p\left(x\right)$	the probability distribution function

provides the list of notations used in this paper. The first part includes data mining and training data generation. To address the lack of training data, we first collected the training data automatically by data mining and then generated synthetic networks with the same statistical properties as the original data. The great success of deep learning algorithms benefits from the diverse training data sets available; for example, ImageNet in CV, LFW in face recognition, and SquAD [25] in NLP. The analysis of engineering data, however, always encounters the problem of data scarcity. It is often infeasible to generate massive data by hand as in other fields and the direct use of the collected dataset for training is prone to model overfitting.

Real-world complex systems often share topological and statistical properties, such as being small-world, scale-free, and highly clustering, with generative rules and evolutionary models. DMGCN first detects the type of network by complex network and centralities analysis and then generates numerous synthetic networks with the same characteristics by the corresponding evolution model. Since the evolution model of complex networks is generally simple, we can efficiently generate synthetic networks of different scales to provide sufficient training data for the next step of GCN training.

In the second step of the DMGCN, we trained an identification model of the key nodes from the generated data. Taking the training efficiency and identification accuracy into consideration, we chose GraphSAGE [17] as the backbone framework. To learn how the information of a node is aggregated by the features of its neighbors, we obtained a representation of a node by combining the features and neighbor relationships of each node. For transductive methods, such as GCN, a unique embedding is learned for each node. In contrast, GraphSAGE generates the node embedding according to its neighbors. GraphSAGE further extends the aggregation method by LSTM (Long Short-Term Memory), Pooling, and other aggregation methods, besides simply averaging. It has the following features: (i) solving the problem of memory explosion by fixed-size neighbor sampling, suitable for large-scale graphs; (ii) transforming transductive learning into inductive learning; and (iii) avoiding retraining the features of nodes each iteration. With incremental features, GraphSAGE can effectively prevent training overfitting and enhance the generalization ability of trained models.

The complex network can be represented through a graph $G=\left(V,E\right)$ which is comprises a set of vertices or nodes $V$ and edges $E$ between them. The vertices or nodes may represent actors, co-authors, or data format, while the edges or the links may represent co-starring, co-authorship, or data translation. In addition to the structure of the graph, each vertex has its characteristics $h_i$ which is usually a high-dimensional vector. The embedding of the central node $v$ in $V$ can be described as:

$$h_v^k=\sigma (W^k.CONCAT\left(h_v^{k-1},AGGREGAT{E}_k\left(\left\{h_u^{k-1},\forall u\in N\left(v\right)\right\}\right)\right)$$

(1)

where $AGGREGATE$ denotes a differentiable aggregator function, such as $sum$, $mean,$ and $max$; $\sigma$ denotes functions, such as non-linearity neural layers; and $N$ denotes a neighborhood function. To keep the number of neighbors the same, we filtered neighbors of a node according to the betweenness centrality and discarded neighbors with smaller betweenness [16]. Embedding features of the graph with lower-dimensional data enables better results to be obtained in tasks of graph analysis. By replacing the data of the original graph with graph embedding, the topology of the graph and the correlation among nodes can be preserved. In the GraphSAGE model, the $k$-layer representation of a node is related to the $k-1$ layer representation of its neighbors, and this local feature results in the $k$-layer representation of a node only related to its $k-1$ network.

To obtain the feature representation of nodes, DMGCN first concatenates transformed self-connections and features of sampled neighbor nodes linearly and then performs ReLU linear transformation. In addition, the neighbors of a node also aggregate the information of their neighbors. Hence, in the $k$-layer aggregation, the node receives the $k$-order information of its neighbors. For graph embedding, we do not take a large recursion and only extend to the second-order neighbors ($k$ = 2). This is reasonable in real life, where friends and family belong to the first-order neighbors. For example, we may hear stories relating colleagues and friends, which have a certain impact on us; these people belong to the second-order neighbors, but further third-order neighbors may not have any influence on us.

Once completing the encoding of a graph, we will evaluate the change of the graph based on the connectivity measurement. We adopted ANC (Accumulated Normalized Connectivity) [10] as the loss function, defined as follows:

$$R\left(v_1,v_2,\dots ,v_N\right)=\frac{1}{N}{\displaystyle \sum }_{\left\{k=1\right\}}^N\frac{\sigma \left(G\backslash \left\{v_1,v_2,\dots ,v_N\right\}\right)}{\sigma \left(G\right)}$$

(2)

$$\sigma \left(G\right)={\displaystyle \sum }_{\left\{C_{i\in G}\right\}}\frac{{\delta }_i\left({\delta }_i-1\right)}{2}$$

(3)

where $N$ is the number of nodes in a graph $G$, $v_i$ denotes the $i$-th node in $G$. $\sigma \left(G\backslash \left\{v_1,v_2,\dots ,v_N\right\}\right)$ denotes the connectivity of the residual graph after removing the node-set $\left\{v_1,v_2,\dots ,v_N\right\}$ from $G$. $\sigma \left(G\right)$ is the initial connectivity of $G$. Any well-defined connectedness measure that translates a graph into a non-negative number may be handled by ANC. Appraisal of the location of nodes in the network is a problem of node centralities. It is an effective measure to evaluate the performance of individuals, groups, or entire networks. As shown in Equation (2), we use the pairwise connectivity $\sigma \left(G\right)$ to measure the critical node, where $C_i$ is the $i$-th connected subcomponents in G and ${\delta }_i$ is the size of $C_i$. If the $v_i$ is removed from $G$, the ANC of $G$ reduces fastest. We will think that $v_i$ is the current most important node in $G$.

The training process of the DMGCN may be slow or even difficult to converge. To alleviate the problem of the non-stationary distribution of training data, previous states can be randomly sampled by using the empirical playback mechanism, so that the training becomes smoother. This technology gathers many rounds into one playback memory. In the inner loop of the algorithm, small-batch updates are applied to the empirical samples randomly sampled from the stored sample pool. Compared with the standard training process, each historical step may be used in multiple weight updates. Secondly, because of the strong correlation between samples, it is easy to over-fit if a batch of quadruplets is taken as the training set directly in sequence. To solve this problem, we can simply randomly select a small number of quadruplets from the experience pool as a batch, which not only ensures that training samples are independent and identically distributed, but also makes the sample size of each batch small, thus speeding up the training speed.

The parameters of this model were tuned by backpropagation and gradient descent methods, commonly used in deep learning. As training proceeded, we gradually obtained a network capable of generating an accurate adjacency matrix and modeling the rules of inter-node connectedness. Finally, we combined it with a graph convolutional network for key node identification.

3.2. Complex Network Measures

To generate synthetic networks with corresponding structural features as real-world networks, a matching evolution model must be selected. The type of networks can be determined based on complexity measures, including the degree distribution, clustering coefficient, and so on. These measures are important parameters for the correlation between real networks and synthetic networks [26].

There are a variety of centrality measures to evaluate the influence of nodes on importance and effectiveness. The degree of centrality is the simplest way to identify centrality. The degree of a node $v_i$ is denoted by the number of all other nodes connected directly to the $v_i$ and is given by:

$$d\left(v_i\right)={\displaystyle \sum }_{i=1}^{n}a\left(v_j,v_i\right)$$

(4)

where $n$ is the number of nodes in $G$ and $a\left(v_j,v_i\right)$ is a binary function, whose value is 1 if $v_j$ and $v_i$ are connected, otherwise its value is 0. Degree portrays the central nodes in a network analysis by the most direct measurement. In scale-free networks, some nodes have very high degrees of connectivity, while most have small degrees.

Evidence shows that in most practical networks and social networks, nodes have a strong tendency to form groups. The clustering coefficient is another measure on a graph tending to gather together. The local clustering coefficient gives a single measure of how close its neighbors are to its full connectivity. Given ${\lambda }_G\left(v_i\right)$ is the number of all closed triplets (3 edges and 3 vertices), including vertex $v_i$ in graph $G$, and ${\tau }_G\left(v_i\right)$ is the number of all open triplets (2 edges and 3 vertices), including $v_i$, the clustering coefficient can be defined as:

$$\overline{C}=\frac{1}{n}{\displaystyle \sum }_i^{n}C\left(i\right)=\frac{1}{n}{\displaystyle \sum }_{i=1}^n({\lambda }_G\left(v_i\right)/\left({\tau }_G\left(v_i\right)+{\lambda }_G\left(v_i\right)\right))$$

(5)

A graph $G$ is called a small-world network, if it is much larger than the average clustering coefficient of a structure on the same set of vertices of random graphs, and its average path length stays the same as that of the random graph at the same time. In a random network, that is, $\overline{C}~1/n$.

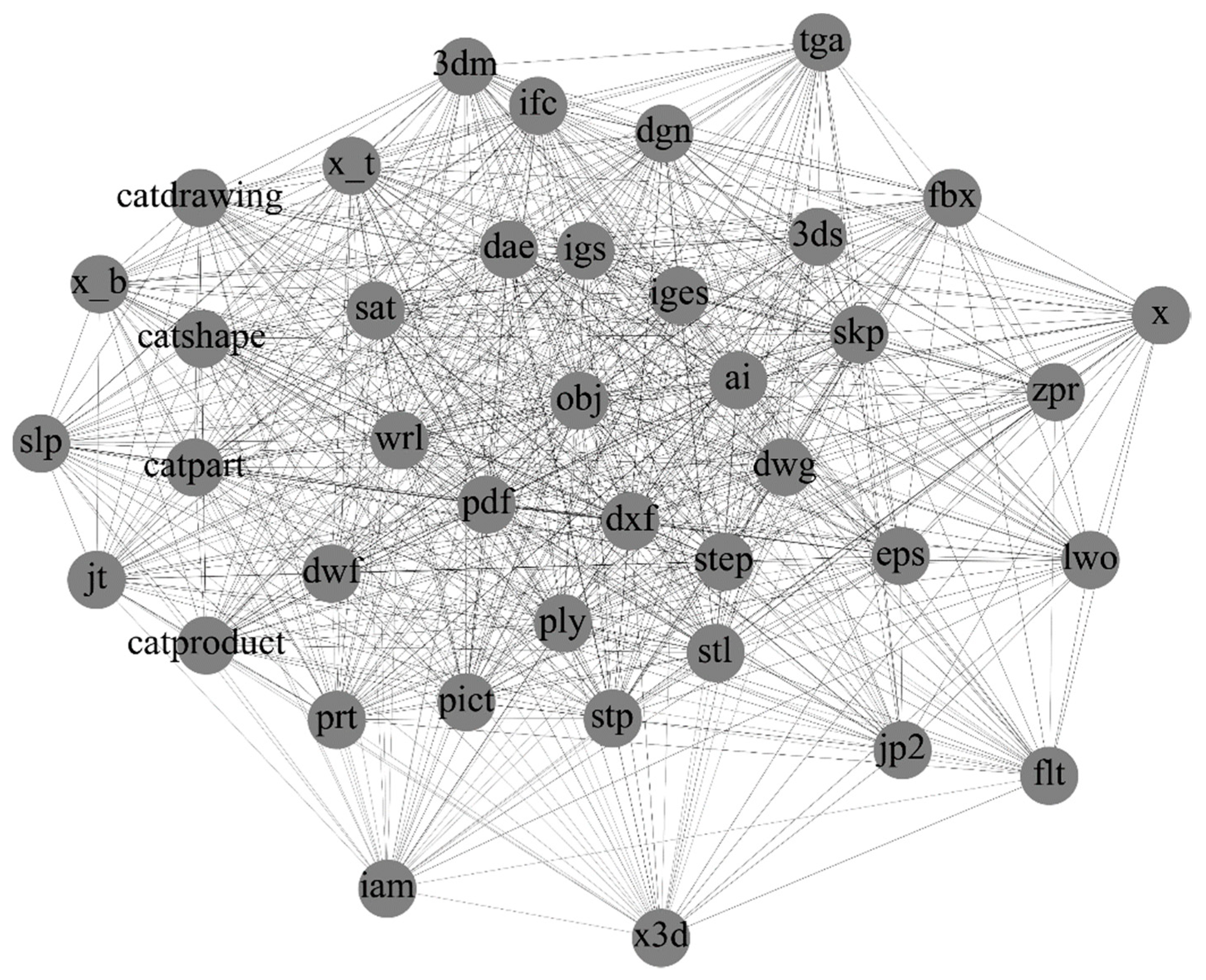
3.3. Case 1: Production Data-Exchange Networks

File formats are commonly used to represent the medium arrangement and layout of electronic documents. With the rapid development of computer and network technologies, an increasing number of documents are being produced and preserved in digital form. In particular, the number of computer-aided design (CAD) file formats remains uncontrolled. Many file formats, such as IGES, STEP, STL, and DXF are considered de facto standards, while new file formats, such as AMF and 3MF, are often created to replace them to adopt emerging technologies, e.g., AM (Additive Manufacturing).

To reduce the laborious work involved in data collection and formulation, automated build of the format exchange network is now a necessary step to ensure product data migration. Web crawlers are used to effectively collect formats and exchange data. Online file formats and software catalogs, such as like AlternativeTo [27] and File-Extensions [28], provide rich information about thousands of file types and their associated applications. We used AlternativeTo to collect CAD software tools. The cad and 3d-modeling tags were selected to find related software. To limit the scale of the exchange network and maintain data fidelity of migration, only exchange tools that exchange vector data were included. In general, less attention is given to software so it sometimes lacks sufficient information for product data migration, thus only software with more than 10 export or import formats were candidates for exchange formats. The File-Extensions site is the world’s largest computer file extension library, with a detailed explanation of each file type and links to associated software programs; this makes it appropriate for the collection of product data exchange information.

To extract information from sites that do not provide an open API, we adopted the crawler framework, Scrapy. Once the webpage is completely downloaded, Downloader sends the response content to Spiders, which transfers the response to an HTML Filter for further processing. Filter is the key for data mining and extracts the CAD software information from AlternativeTo and feeds them to the File-Extensions site for retrieval of open-and-save and import-and-export format information that the software supports. Due to the asynchronous network, the dependency is first saved in an intermediate file for each CAD system. The process repeats until there are no more requests from Scheduler. We applied RandomUserAgentMiddleware to prevent the crawler from being identified and blocked by web servers because of the default user-agent. When extracting product data information, it was found that the AlternativeTo Service Internet connection was unstable, so ProxyMiddleware was used to process requests using the proxy server.

After all the conversion relationships had been collected, they were converted to a GraphML file for graph construction and to calculate the measures of the exchange networks. After the extension names of file formats were cleansed, data for about 1673 nodes (data formats) and 10,123 edges (exchange relationships) were finally available for the network. Figure 2 shows the subgraph consisting of 40 nodes with the largest degree of data formats in CAD. It can be seen that popular formats, such as iges, dxf, and stl, have numerous edges and links. Although we cannot guarantee the accuracy of the collected results, the data scale is sufficient to guarantee the reliability of the analysis results.

The metrics of the production data-exchange network are shown in

Table 2. Metrics of the production data-exchange network.

Average Degree	6.15
Network Diameter	3
Average Path length	1.92
Average Betweenness Centrality	247.35
Average Closeness Centrality	0.00032
Clustering Coefficient	0.15

. Besides the degree and clustering coefficient, we also measured the Betweenness and Closeness centralities in the production data-exchange network. Betweenness is the number of the shortest paths through a node and describes the bridge importance of a node. Closeness is the reciprocal of the average shortest-path distance to a node. These measures help to determine the importance of a node in a network.

The average degree of the network was about 6.15. The number of edges was 2,797,256 in a complete graph with the same number of nodes, which is more than 276 times greater. Hence, the exchange network is sparse, which is similar to other complex networks. The network diameter was 3, that is, any file format in the network can be converted to another through two translation tools. The result reveals that the population of translation tools for CAD data is very small in terms of the number of data formats.

The clustering coefficient is defined for undirected graphs, so it was necessary to transform our directed graph into undirected. The clustering coefficient of the exchange network was about 0.150, which can be compared with the value coming from network models. For the corresponding Barabasi–Albert (BA) model with the same number of nodes and m = 6, a network with 10,017 edges was obtained, where $m$ is the number of new edges in each step. The clustering coefficient of the BA network was 0.306, which is in the same order of magnitude as that of the exchange network. Considering its average path length was 1.92, it could be said that the exchange network is a small-world network, which provides further evidence that complex networks are widespread in the real world.

3.4. Case 2: Operating System Package Dependency Networks

Software systems represent another important field where complex network theory may provide a valuable research method to manage functional complexity and high evolvability. Software systems are the core of the information-based world and hold a position of great importance in modern society. Software comprises many interacting units and subsystems. owever, it is still relatively new and not well-studied in complex networks. A reason for this is that collecting and analyzing data is forbidden or impossible because source code is inaccessible in commercial software. However, the rapid development in the open-source software (OSS) domain now allows researchers to access some software systems and collect data easily. We carried out an empirical network analysis on the package dependency network of the open-source operating systems by modeling packages as nodes, and dependencies among them as edges.

As a software-running environment, the operating system occupies a special place in the open-source software framework. Most Linux distributors now use a program, or set of programs, called a “pre-built package” to install software easily on release. A package is necessary to compile or run an application-bundle-related component. Packages typically include a series of commands to achieve all documents necessary. Since resource reuse is a pillar of the OSS, a package often depends on other packages, which may be toolkits, such as vim, find, and third-party tools, and resource packages, such as images, to work properly. Package dependencies often span across the whole project development group.

To offer a meaningful understanding of evolutionary processes, we analyzed a specific version of the Ubuntu (16.04 LTS) operating system. First, the package data were extracted from the x86_64 branch by the python-apt package. Each vertex is represented by the name of the package. Among a range of dependencies, only depend and pre-depend relations were dealt with to represent edges since that is the default behavior of the package management system. The dependency graph was then created through the Python module igraph [29]. While another Python complex network package, NetworkX [29], is popular and trivial to use, its performance becomes unacceptable when the graph size increases to tens of thousands of vertices or edges. Last, 20,233 packages that did not exist in the deb packages database were removed. In the deb database, multiple versions of the same package may be specified in the dependency, so 3877 duplicate edges were removed. After the above processing, 47,063 packages and 174,819 directed edges were finally available.

The graph measures are summarized in

Table 3. Metrics of the package dependency network.

Average Degree	3.72
Network Diameter	15
Average Path length	3.84
Average Betweenness Centrality	163.80
Average Closeness Centrality	0.00024
Clustering Coefficient	0.15

. Each package depends on about four other packages on average. The clustering coefficient of the dependency network was 0.15. A random network with as many nodes as the package dependency network can obtain a clustering coefficient of 7.89 × 10⁻⁵. That is, the clustering coefficient of the Ubuntu network is about 1951 times higher than that of the random graph. For the corresponding BA model with the parameters $N=\mathrm{47,063}$, $m=4$, we obtained a network with 188,921 edges. The clustering coefficient of the network was 0.0032. The parameters of the two models give a clustering coefficient two orders of magnitude smaller than that of the package dependency network, which is far lower than the random network. It can, therefore, be concluded that the package dependency network is a scale-free network.

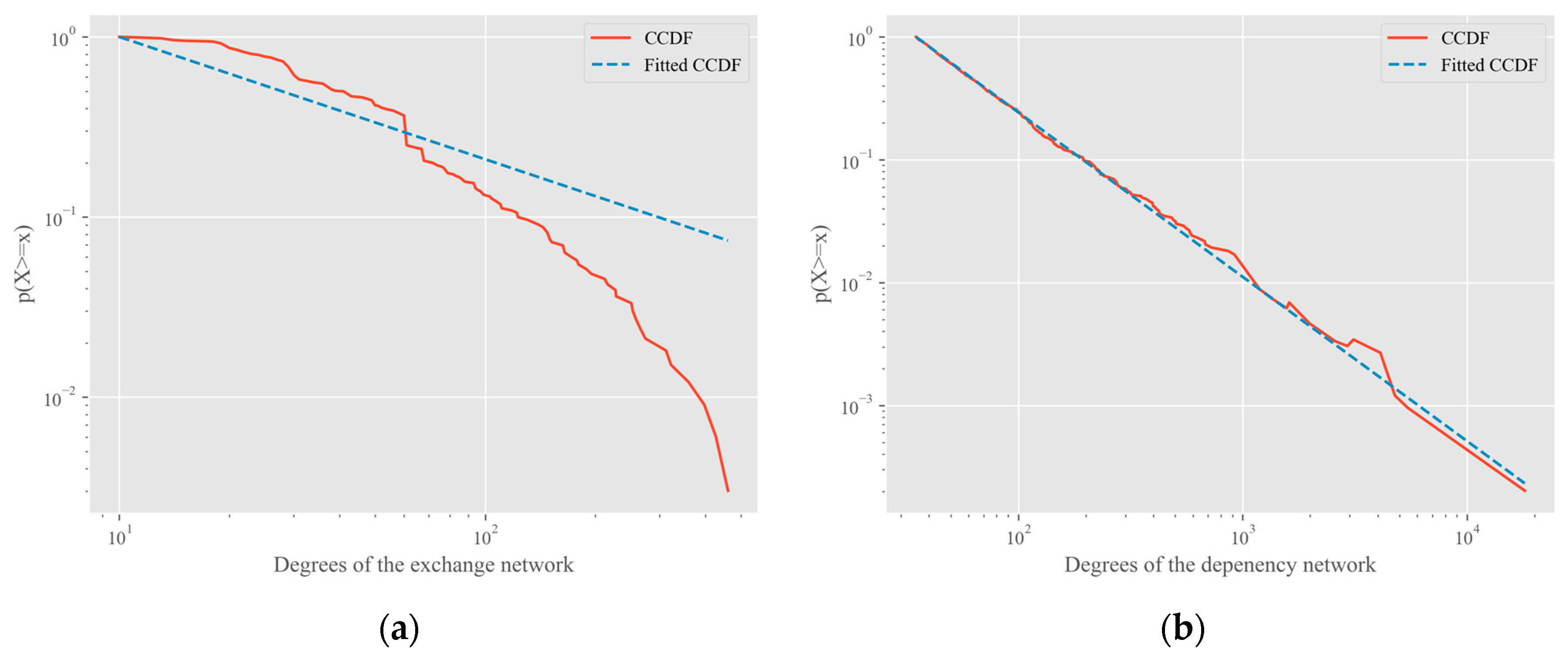
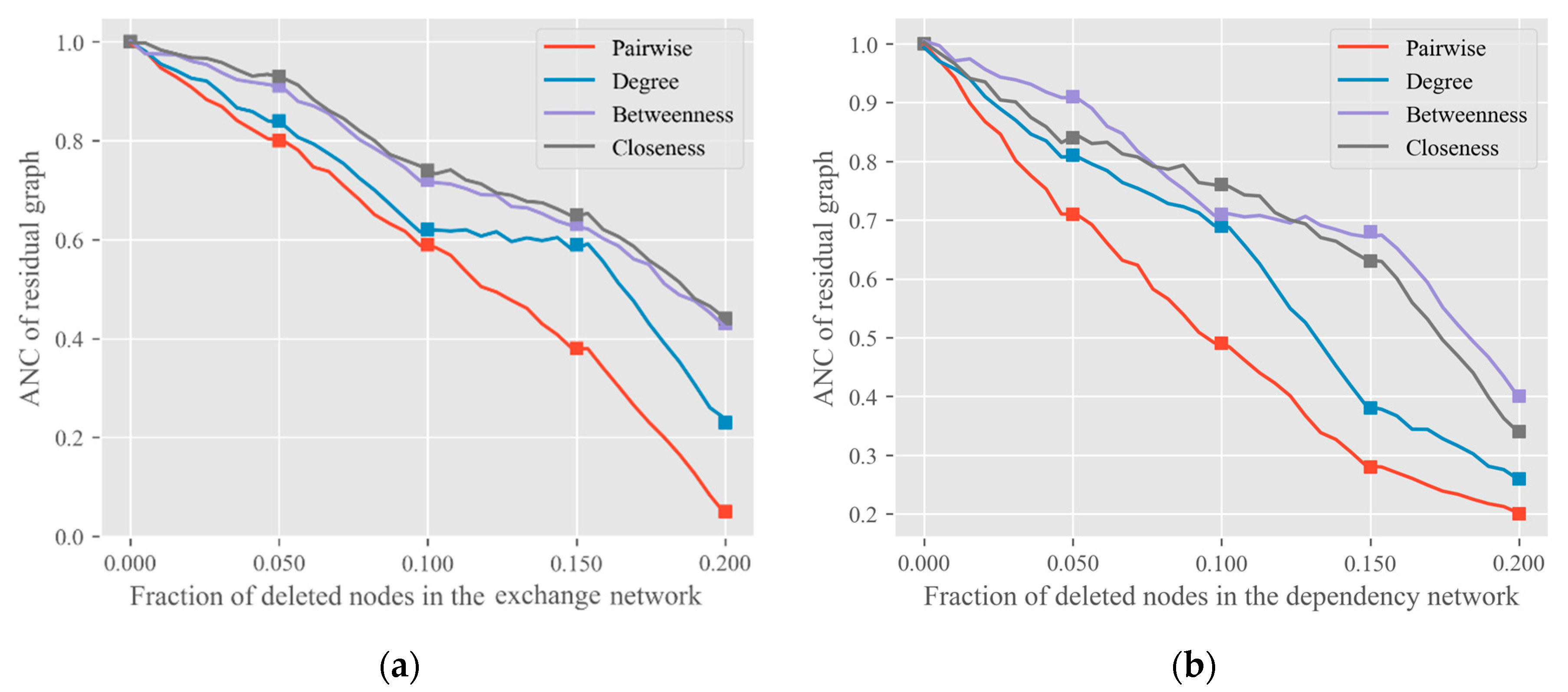
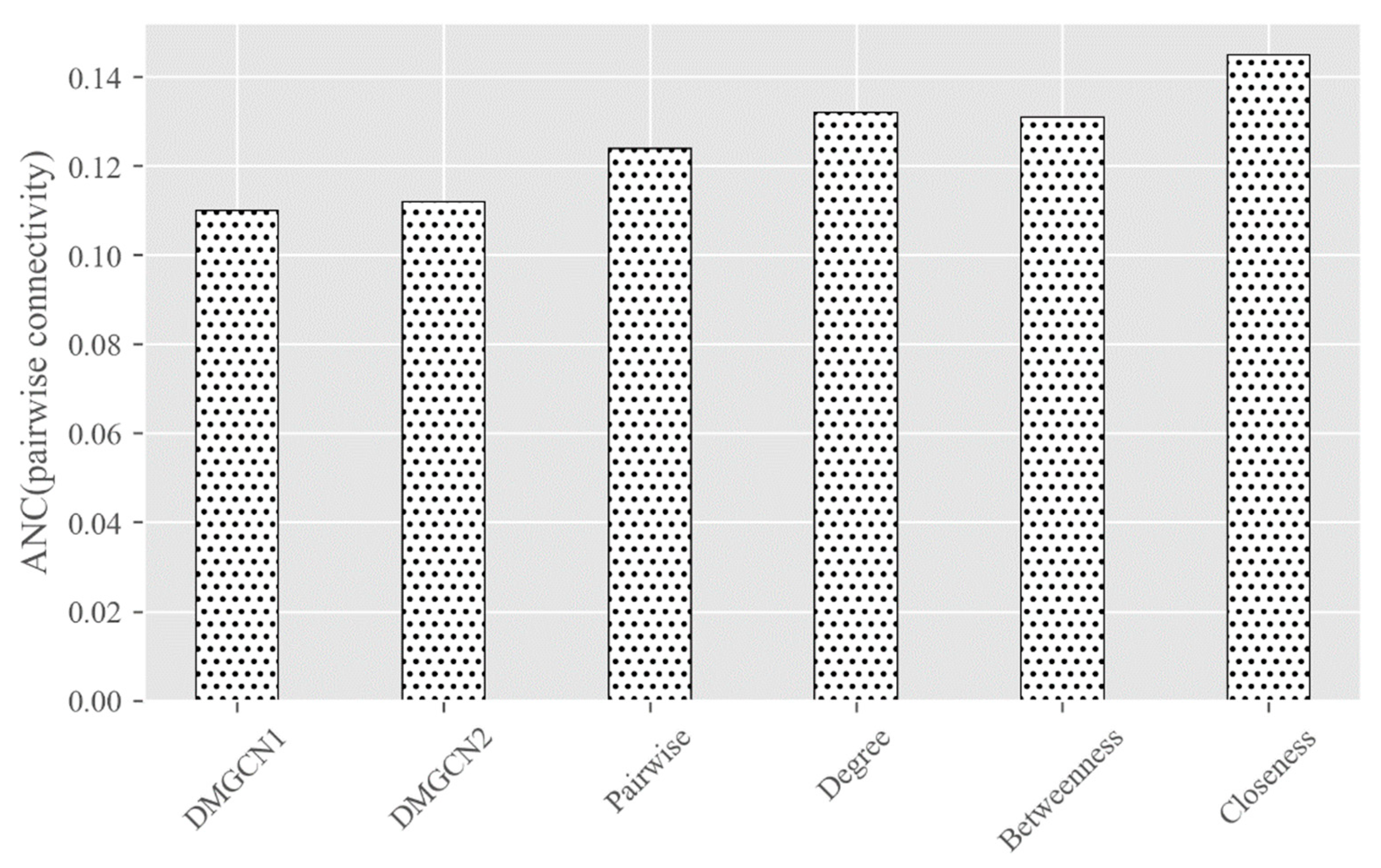
4. Experiments and Discussion

To generate training data, we first used the power-law [30] distribution to identify a scale-free network. Let $p\left(x\right)$ be the probability distribution function, if its histogram is a straight line on log–log, that is, $p\left(x\right)=-alnx+c,$ where $a$ and $c$ are constants. With the maximum likelihood method, the exponent $a$ of the degree distribution can be calculated as $a=1+n[{{\displaystyle \sum }}_{i=1}^{n}In\left(x_i/x_{min}\right)]$, where $x_{min}$ is the minimum value above which power-law only follows in real-world networks. The exponent of a network can be obtained from a set of n values $x_i$. It can be said that the scale-free networks follow power-law distribution and regular networks follow the $\delta$ distribution, while random networks and small-world networks follow the Poisson distribution. Figure 3 shows the complementary cumulative distribution function (CCDF) of degree for the exchange network and dependency network. It can be seen that the exchange network shows a poor power-law fit, and the dependency network also shows a poor fit.

Preferential attachment is an example of a positive feedback cycle where one node initially having more links or having started accumulating links earlier than another is automatically reinforced, thus obtaining more links. In the simplest cases, these are added to objects in proportion to the number that the object already has. We can reproduce the model by the following simple rule:

• Begin with a small graph containing $m_0$ nodes. Each step adds a new node.
• Construct $m$ ($m\le m_0$) edges by connecting this new node to the original $m$ nodes.
• When creating new edges, if a node refers to the degree of $k_i$ in the original network, the probability of new nodes connecting to it is $p_i=k_i/{{\displaystyle \sum }}_j{k}_j$.
• After step t, the process produces a graph with $N=t+m_0$ nodes and $m\times t$ edges.

After detecting the type of a network, we can generate synthetic networks by corresponding evolution rules for the Watts–Strogatz network, BA network, and ER random network. One of the most distinctive features of complex networks is to extract simple rules from complex manifestations and then reproduce the complexity observed [31]. Instead of fixed models, we used different evolutionary models for the empirical data in Section 4. For the production data-exchange network, we trained the DMGCN over 50,000 randomly generated Watts–Strogatz synthetic graphs with 30-500 nodes. The rewriting probability of graphs ranged from 0.2 to 0.6 and the number of nearest neighbors ranged from 2 to 4. For the package dependency network, we trained the GMGCN over 50,000 Barabasi–Albert graphs with 30–500 nodes. The number of edges to attach from a new node to existing nodes ranged from 4 to 8.

We used the PyTorch-Geometric [32] library for generalizing the convolution operator to irregular domains by the message passing scheme; after completing the training, we evaluated DMGCN on real systems described above. We deleted a batch of nodes at each adaptive step. The experimental results are shown in Figure 4. In contrast with the FINDER [10], which always has the same evolving model to generate all the training models, we first analyzed the characteristics of the real-world networks and took specific generation rules to generate synthetic networks. It can be seen that the DMGCN archives the best results. The reason our model can automatically evaluate important nodes is that we used GCN to model the relation between importance and the structure of a graph. As a type of neural network, GCN has a powerful function-fitting ability, so our method can work on real-world networks with different characteristics and scales of node-set size.

The WS model has a significant community structure, while the BA model has a less distinctive community structure feature. The clear community structure of the network is one of the important reasons for the small-world phenomenon. Because the small-world network and scale-free network share some common features, the performance of the key nodes identification model is better than the completely random ER network. Hence, we can infer that the predefined synthetic networks generated by data mining produce better results for finding key nodes.

It is reasonable to expect that some packages will be more visible than others, hence some package dependency will grow disproportionately larger than expected under random growth. In the development process of the operating system, its first version was released in 1991 with only tens of thousands of lines of code; developers then enhanced the operating system based on the existing functions, packages, or modules; the initial package was, therefore, more successful. Although developers have a choice of developing new packages with similar functions, their stability and functionality are not as good as those of the original package, which results in fewer references. This phenomenon which is called the Matthew effect, or rich-get-richer process, is widespread in real networks. In random networks, such as the Erdos–Renyi (ER) model, most of the nodes are concentrated in the vicinity of a particular value. The probability distribution from this specific value decreases exponentially. The probability of considerably greater than or less than that value is negligible. In a dependency network, some nodes have very high degrees, corresponding to some popular packages, on which much software development is based. In contrast, in an exchange network, vendors tend to use proprietary data formats to avoid copyright protection, and the available candidate data formats are not sufficiently diverse, which limits the growth of preferential attachment.

Figure 5 shows a comparison between the ANC results of DMGCN and real-world networks where centralities are pairwise, degree, betweenness, and closeness, respectively. It can be seen that the pairwise connectivity outperforms the other centralities. Nodes with larger degrees have more nodes connected; however, in the network with aggregation characteristics, if a node is located at the edge of the two sub-communities but at their intersection, although the degree may be small, the change of the network after removal is greater. We can infer that the importance of a node comes from its position in the network rather than centralities. It also can be observed that although the definition of degree is simple, it outperforms other centrality metrics in assessing the importance of nodes.

To further evaluate the effectiveness of DMGCN, we performed tests on the 9/11 criminal network as shown in Figure 6. The smaller the ANC, the more important the node deleted by this method, and the more destructive it is to the network. It can be seen that regardless of complex network used for training, the model that was trained based on DMGCN is better than other heuristic methods. Because the criminal network is more in line with the characteristics of a small-world network, DMGCN1 performs better in identifying key nodes. This experiment shows the effectiveness of GCN in identifying key nodes. At the same time, it also shows that the selection of appropriate training data sets is crucial to the prediction performance of the network.

5. Conclusions

The derivation of data formats and tools has facilitated the dissemination of product information, while a wide variety of formats and tools have posed new challenges to the long-term preservation of product data. This paper investigated two types of complex networks closely related to the life cycle of product data, that is, the product data-exchange network and package dependency network through the GCN method. Compared with traditional heuristic central measures, the proposed DMGCN method achieves superior performance for finding key players in engineering data. This provides a new perspective for the long-term preservation of engineering data in a complex environment.

Key nodes play an important role in understanding and controlling the structures and properties of a network. Previous methods either considered node centrality only or used a fixed evolution model, which limits the performance of identification models. In this work, we propose a graph convolutional network, named DMGCN, for key network analysis. The scale and quality of datasets are key factors in the success of deep learning methods. To solve the scarcity of training data, we utilized a data-mining-based method to construct synthetic networks with the same statistical properties as real networks. The case studies show the process of building a real network and provide targeted evolution models to generate sufficient synthetic networks for training the identification model. The experimental results show that DMGCN outperforms the existing method which uses fixed evolution models for identifying key nodes in a complex network. The results also show that the importance of a node comes from its position in the network rather than centralities.

Actual networks are generally sparse and complex in structure, and may have small-world phenomena, scale-free properties, and distinct community structures; in contrast, current network models, including ER, BA, and WS models, do not have these features. In future, first, we will work on more powerful evolution models to reflect the characteristics of real networks. Second, to provide an alternative to human intervention in network classification, we will develop a more flexible method of network classification and dataset generation to fully automate the identification of the key nodes.