Two Novel Vlasov Models for Bending Analysis of Finite-Length Beams Embedded in Elastic Foundations

Abstract

The issue of soil–structure interaction (SSI) is essentially to analyze the influence of complex media on the mechanical behavior of supported structures. With the development of underground space, geological structures and space constraints put forward higher requirements for foundations and buildings. In this paper, the effects of soil heterogeneity and embedment depth on the bending of finite-length beams embedded in two novel Vlasov elastic foundations are investigated. Firstly, the constitutive relations of subsoil are simulated by Gibson and transversely isotropic soils, and the type of elastic foundation is described by the modified Vlasov model. Then, based on variational principles, the governing differential equations for the deformation and attenuation parameters of beams embedded in elastic foundations are derived by taking the variation of the minimum potential energy of the system, and the characteristic coefficient related to the embedment depth is introduced. Finally, the mechanical performance of the beam and foundation is obtained by an iterative technique and the Fourier series method, and an extensive parametric study is performed to examine influence of some basic parameters on the deformation and internal forces of the system. The results show that the mathematical expressions of two refined elastic models are in good agreement with those of the traditional Vlasov foundation after degradation. The iterative technique based on the principles of solid mechanics can be employed to obtain more reliable model parameters. More importantly, with the increase in the embedment depth, the mechanical responses of the beam and subgrade forces decrease. The main reason is that the restraint effect of the soil media around structures, which leads to the reduction of the characteristic coefficient affecting the displacement of beams. Moreover, the heterogeneity of soil, including Gibson characteristics and transverse isotropy, should be considered according to specific working conditions in civil engineering.

1. Introduction

With the progress of technology and the development of economy, building engineering and underground structures are increasing day by day, and the adoption of deep foundation has also become popular. The research and utilization of underground space is an important topic in the construction of modern cities, such as lifeline project pipelines and subway building structures. A foundation is located below the ground and belongs to concealed works. Therefore, the survey of foundations, the design of structures, and the quality of construction will directly affect the safety of the structural system. The mechanical behavior of structures embedded in elastic soils is of great significance for structural engineering and geotechnical engineering, especially under complex geological conditions and extreme environmental loads. From the mechanical point of view, the bending problem of deep foundation structures is normally abstracted as beams and plates embedded in elastic foundations [1,2].

The analysis of the interaction between complex media and structures is one of the hot research directions of the dynamics of deformed solid, and is also one of the important research branches of contact problems in solid mechanics. The aim of soil–structure interaction (SSI) is mainly to study the mathematical models, mechanical mechanism, coupling effects, interface characteristics, and calculation methods of the system interaction between soils and structures. This discipline can deal with the static and dynamic coupling problems of various media, and also provide theoretical models and research methods for the analysis and design of geotechnical, structural, underground and protection engineering. Gu et al. [3] extended the direct differential method framework to realistic complicated soil–foundation–structure interaction models by developing the response gradients for different materials, elements and constraints involved. Bildik and Laman [4] investigated the stress behavior of buried pipes in cohesionless soils experimentally, and found that bearing capacities increased significantly with the increased of embedment ratio of pipes. Bao and Liu [5] reported a comprehensive study including numerical, theoretical, and experimental analyses to evaluate the performance of two predominant SSI models. Bucinskas and Andersen [6] proposed a numerical model to examine a coupled vehicle–bridge–soil system using lumped-parameter models for the soil–foundation system. Bolisetti and Whittaker [7] investigated the influence of structure–soil–structure interaction in low- to medium-rise buildings, and the numerical simulations agreed with experimental observations. Franza et al. [8] investigated the response of piled structures and pile groups to vertical and tunnelling-induced loads, and they used a two-stage model. Regarding other recent work, Aksoy et al. [9] proposed a new design chart for estimating the friction angle between soil and pile materials. Moayedi et al. [10] presented the modelling of a single thin steel pile to simulate the relationship between soil pressure reaction and lateral deflection. Moayedi et al. [11] predicted the load-settlement of square footing on layered soils using a new combined technique called ICA-MLP. Due to the importance of accurate analysis of bearing capacity, Gör [12] studied the efficiency of two novel metaheuristic-based models. The concept of SSI has been a convenient tool to obtain solutions for many engineering problems.

Various theoretical systems for structures on elastic foundations have been developed. The foundation models include the Winkler model, lumped parameter model and elastic half-space model, each of which has its characteristics in accordance with the corresponding hypotheses. The advantages and disadvantages of the different physical models are listed in

Table 1. A comparison of characteristics of different foundation models.

Foundation Models	Advantages	Disadvantages
Winkler model	Easy and uses closely spaced linear springs	Behavioral inconsistency
Half-space model	Accurate and represents soil continuum	Mathematically complex
Lumped parameter model	Simple and has perfect theory	Determination of parameters

. The Winkler model has been shown to be inconsistent to represent a continuous medium. The elastic half-space foundation model compensates for the defects of the Winkler foundation model, but it is more complex mathematically. Lumped parameter models have all of the advantages of a continuum approach as well as the simplicity of the coupled spring model. In a word, the advantages of lumped parameter foundation models have been proved by previous researchers [1,2]. Therefore, lumped parameter foundation models are adopted in this study, which is the first step to analyze SSI.

As is known, the Vlasov elastic foundation is one of various lumped parameter models. The Vlasov foundation model considers the elastic foundation as a single-layer or double-layer model whose physical properties are described by two or more generalized elastic characteristics. Aydoǧan et al. [13] investigated container structures which have a flat or shallow spherical shell bottom on a Vlasov foundation, and the variation of the soil’s elastic modulus was assumed exponential along the depth. Celik and Omurtag [14] determined the Vlasov soil parameters for quadratically varying modulus of elasticity of the compressible soil continuum and the foundation was simulated by displacement type elements. Teodoru and Musat [15] gave a unified framework and applied the modified Vlasov foundation model to static analysis of beams lying on elastic foundations. Ozgan et al. [16] carried out a parametric study to demonstrate the behavior of thick plates on modified Vlasov type elastic foundations with variable soil depth. Hizal and Catal [17] investigated the dynamic response of the axially loaded Timoshenko beams on modified Vlasov foundations by using the separation of variables method. Karakas et al. [18] explored the seismic response of a hyperbolic cooling tower resting on elastic foundations represented by a three-parameter Vlasov model. However, the drawback of the Vlasov model is that it introduced an attenuation parameter, whose value must be estimated. For this reason, an iterative procedure is proposed to solve the problem of beams embedded in Vlasov elastic foundations in the paper.

The traditional foundation models are based on the assumption that the elastic layer is usually homogeneous and isotropic. In fact, the characteristics of soils are quite complex, which are reflected in different constitutive relations. A large number of studies have been devoted to this subject. On the one hand, for structural analysis based on Gibson elastic foundations, Rajapakse [19] analyzed the response of an axially loaded elastic pile in Gibson soils. Guo [20] developed rigorous closed-form solutions to account for the nonhomogeneity of the soil profile using a load transfer method. Doherty and Deeks [21] proposed an axisymmetric formulation of the scaled boundary finite-element approach and incorporated non-homogeneous elasticity into the method. Chiou and Tsai [22] presented assessment formulas for the displacement ductility capacity of a pile in Gibson cohesionless soils based on an ideal model. Medina et al. [23] estimated the flexible-base fundamental period of structures supported on various pile configurations embedded in several Gibson soils. Efthymiou and Gazetas [24] conducted a finite-element study for the linear-elastic behavior of rigid suction caisson foundations installed in a Gibson soil stratum. On the other hand, regarding the analysis of structures on transversely isotropic foundations, Gharahi et al. [25] proposed a mathematical treatment approach for the boundary value problem of a flexible cylindrical pile embedded in a transversely isotropic half-space. Ai et al. [26] presented a coupled method of the finite element and the analytical layer-element to study vertically and laterally loaded piles. Shahbodagh et al. [27] proposed a hybrid analytical-numerical approach for the dynamic analysis of piles embedded in semi-infinite transversely isotropic media. Ba and Gao [28] analyzed SSI in transversely isotropic layered media subjected to incident plane SH waves by using the indirect boundary element method. Ai et al. [29] examined the static interaction between layered transversely isotropic soils and an eccentrically loaded rectangular rigid foundation. Han et al. [30] proposed a semi-analytical method for solving the dynamic response of a flexible foundation embedded in a transversely isotropic and multilayered half-space. Hence, Gibson soils and transversely isotropic soils are respectively used to reflect the heterogeneity of foundation soils, which is one of the main contributions of the article.

To sum up, there are some imperfections in the previous research works on the structures embedded in elastic foundations. In the practice of underground structures and deep foundation engineering, it is necessary to discuss the influence of embedment depth. For the mechanical analysis of structures embedded in elastic soils, it is generally simplified as a beam on elastic foundations for calculation. However, for such underground structures with a certain embedment depth, it is difficult to consider the influence of embedment depth by using the traditional model of a beam resting on elastic foundations. In addition, soil is a complex and heterogeneous discrete system with obvious anisotropy and heterogeneity. The static and dynamic interaction between heterogeneous soils and various structures cannot be solved perfectly by the classical Vlasov elastic theory.

Therefore, the main purpose of this study is to investigate the static bending of finite-length beams embedded in two novel Vlasov foundations, considering the non-homogeneity of foundation soils. For this purpose, Gibson-type and transversely anisotropic type soils are adopted, respectively, and the modified Vlasov model is employed to describe the elastic foundation. By taking the variation of the minimum potential energy of the foundation–beam system, the deformation governing differential equations for foundation beams are derived, and the equation for the attenuation function is also obtained. Combined with specific boundary conditions, the mechanical response of beams and foundations is solved using the iterative technique and the Fourier series method. The parametric analysis is carried out through numerical examples. The influence of foundation non-homogeneity and embedment depth on the deformation and internal forces of foundation beams is discussed in detail.

The present paper has six main objectives and highlights. (1) Two novel Vlasov models are adopted to simulate the mechanical response of elastic foundations. (2) Based on the variational principles, the governing equations for finite-length beams embedded in two modified elastic foundations are derived. (3) A comparative analysis between two modified Vlasov foundations and the traditional Vlasov model is carried out. (4) Using an iterative technique, the consistent value of an attenuation parameter is calculated. (5) The heterogeneity of foundation soils, including the Gibson elastic soil and the transversely isotropic soil, has a certain effect on the deformations and internal forces of beams and foundations. (6) The effects of embedment depth on the mechanical response of the beam embedded in elastic foundations are also investigated.

2. Mathematical Model

2.1. Deformation Assumption Considering Embedment Depth Effect

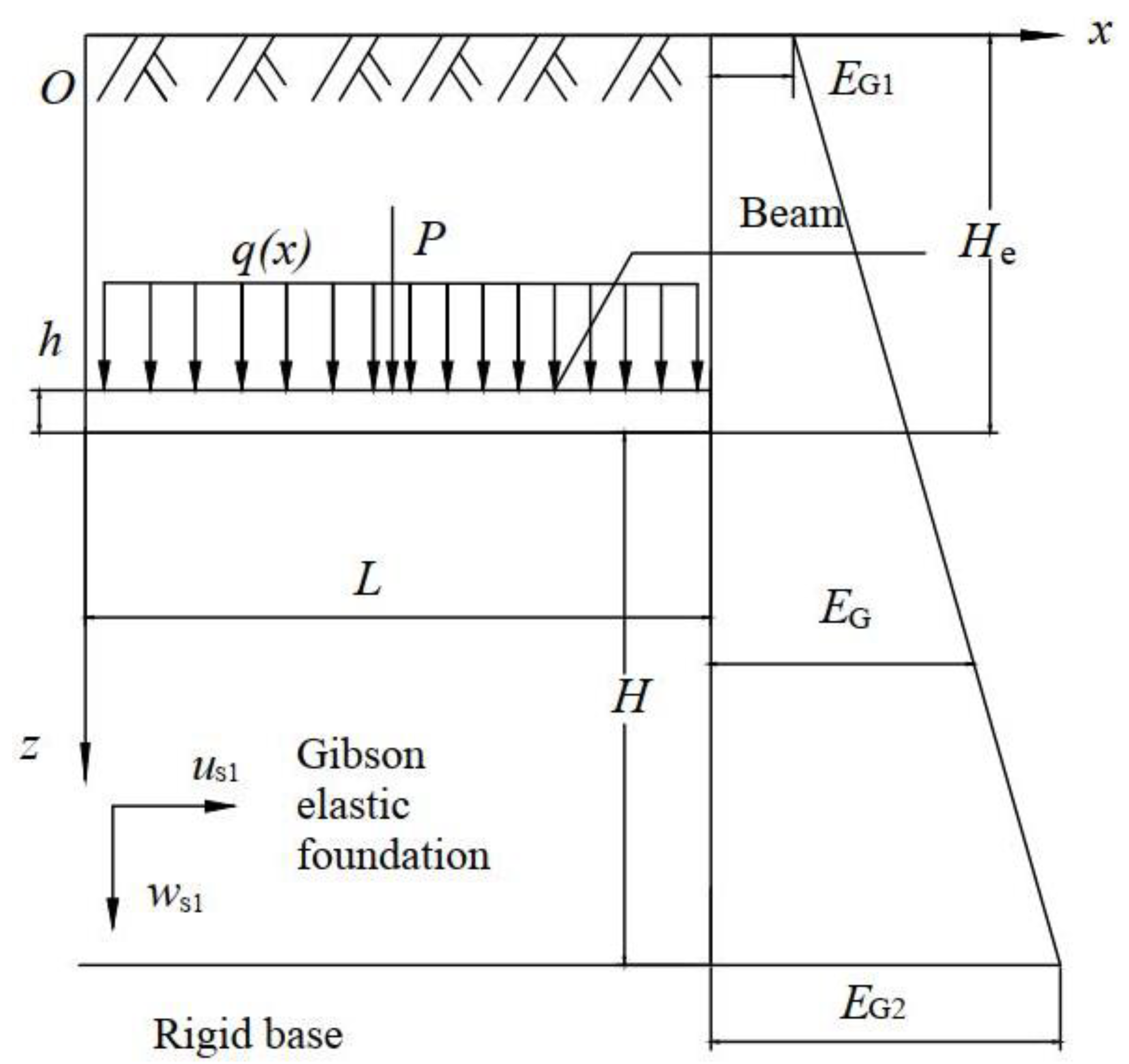
The beam structure utilized in the present study is embedded in elastic soil layers over a rigid base. The complex structural phenomena of the actual soils significantly affect the strength and stability of soils and the mechanical states of the foundation–structure system. The assumption of isotropy and homogeneity cannot reflect the real states of foundation soils. Considering the non-homogeneity of soils, the mechanism problems such as force transfer and foundation stability can be more accurately studied. As shown in Figure 1 and Figure 2, a finite-length beam is embedded in two novel Vlasov foundations whose concept is widely encountered in engineering practice. The length of the beam structure is $L$, the height is $h$, and the embedment depth is $H_e$. The width $b$ of the beam is assumed to be equal to 1 m, and the distance from the lower surface of the structure to the rigid base layer is $H$. The foundations are regarded as Gibson elastic soil and transversely isotropic elastic soil, respectively. It is generally assumed that the friction between the beams and foundation soils can be ignored. The uniformly distributed load acting on the elastic beam is $q\left(x\right)$, and the concentrated load on the beam in the midspan is $P$.

For the Gibson foundation in Figure 1, a dimensionless parameter $\eta$ is introduced to represent the ratio of the modulus of elasticity $E_{G1}$ of the top layer to the modulus of elasticity $E_{G2}$ of the bottom layer, and ${\mu }_G$ denotes Poisson’s ratio. Then, the modulus $E_G$ of elasticity at the depth $z$ is calculated by:

$$E_G=E_{G2}\left[\eta +\left(1-\eta \right)\frac{z}{H}\right]$$

(1)

For the transversely isotropic foundation in Figure 2, $E_{T1}$, ${\mu }_{T1}$ and $E_{T2}$, ${\mu }_{T2}$ are the modulus of elasticity and Poisson’s ratio in the isotropic direction and in the direction perpendicular to the isotropic direction, respectively. In addition, $G_T$ denotes the shear modulus. The relationship between stress $\sigma$ and strain $\epsilon$ for transversely isotropic elastic foundation can be written as:

$${\sigma }_x=C_{11}{\epsilon }_x+C_{12}{\epsilon }_y+C_{13}{\epsilon }_z\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}{\tau }_{xy}=C_{66}{\gamma }_{xy}$$

(2)

$${\sigma }_y=C_{12}{\epsilon }_x+C_{11}{\epsilon }_y+C_{13}{\epsilon }_z\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}{\tau }_{yz}=C_{44}{\gamma }_{yz}$$

(3)

$${\sigma }_z=C_{13}{\epsilon }_x+C_{13}{\epsilon }_y+C_{33}{\epsilon }_z\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}{\tau }_{zx}=C_{44}{\gamma }_{zx}$$

(4)

where $C_{11}$, $C_{12}$ … $C_{st}$ … $C_{66}$ are the physical property constants of foundation soils. When the five independent engineering elastic constants ($E_{T1}$, ${\mu }_{T1}$, $E_{T2}$, ${\mu }_{T2}$, $G_T$) of transversely isotropic bodies are determined, the value of $C_{st}$ can also be obtained. The conversion relationship between these elastic constants commonly used in practical engineering can be found in the relevant literature [25,26,27,28,29,30,31].

When the foundation–beam system is deformed due to external forces, the vertical deformation component is the main concern for the soil displacement field. Compatibility of vertical deformation at the foundation–structure interface alone is assumed to be important. Therefore, the horizontal deformation component $u_{si}$ and vertical deflection $w_{si}$ in the soil are assumed to be:

$$u_{si}\left(x,z\right)=0$$

(5)

$$w_{si}\left(x,z\right)={\overline{w}}_{si}\left(x\right){\varphi }_i\left(z\right)\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left(i=1,\hspace{0.33em}2\right)$$

(6)

where: ${\overline{w}}_{si}\left(x\right)$ is the vertical deflection of the modified Vlasov foundation surface. It is noted that when $i=1$, ${\overline{w}}_{s1}\left(x\right)$ denotes the deformation of the Gibson elastic foundation; when $i=2$, ${\overline{w}}_{s2}\left(x\right)$ represents the deformation of a transversely isotropic elastic foundation. In the following, unless otherwise specified, the symbols with subscript 1 denote the physical quantities of structures embedded in Gibson elastic foundations, while the symbols with subscript 2 represent the corresponding physical quantities of structures embedded in transversely isotropic soils.

In addition, the attenuation function is written as ${\varphi }_i\left(z\right)$ and is used to describe the variation of the vertical deflection $w_{si}\left(x,z\right)$ with the depth, and the corresponding boundary conditions are as follows:

$${\varphi }_i\left(0\right)=1\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{\varphi }_i\left(H_e+H\right)=0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left(i=1,\hspace{0.33em}2\right)$$

(7)

Then, the vertical deflection $w_{bi}$ of the beam structure at the embedment depth $H_e$ is expressed by the characteristic coefficient ${\varphi }_i\left(H_e\right)$:

$$w_{bi}={\overline{w}}_{si}\left(x\right){\varphi }_i\left(H_e\right)\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left(i=1,\hspace{0.33em}2\right)$$

(8)

In addition, the embedment depth ratio ($\lambda =H_e/H$) is used to express the ratio of the embedment depth $H_e$ of the beam to the distance $H$ from the lower surface of the structure to the rigid base. The classification is discussed as follows: if $\lambda =0$, the finite-length beam is lying on the foundation surface; if $\lambda =1$, the beam is embedded in the middle of the soil; if $\lambda \to \infty$, the beam is resting directly on the rigid base layer. The mechanical responses of structures embedded in shallow soils are the main physical quantities concerned by engineers, that is, when $\lambda \le 1$.

2.2. Theoretical Analysis Based on Variational Principles

Two novel Vlasov models are applied to the static bending analysis of finite-length beams embedded in elastic foundations. From the perspective of energy, the total deformation potential energy of the foundation–beam system is given by:

$$\begin{array}{l}{V}_i=V_b+V_{si}+V_q\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}=\frac{1}{2}{\displaystyle {\int }_0^{L}EI{\left(\frac{d^2{w}_{bi}}{d{x}^2}\right)}^2}dx+\frac{b}{2}{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_0^{H_e+H}\left\{\sigma \right\}}\left\{\epsilon \right\}dzdx}-{\displaystyle {\int }_0^{L}q\left(x\right)w_{bi}dx}\end{array}$$

(9)

where $V_b=$ strain energy in the finite-length beam, $V_{s1}=$ strain energy in the Gibson elastic foundation, $V_{s2}=$ strain energy in the transverse isotropic foundation, and $V_q=$ the external potential energy. $E$ is the modulus of elasticity of the beam, and $I$ is the moment of inertia of the beam. $\left\{\sigma \right\}$ and $\left\{\epsilon \right\}$ are the stress component and strain component in elastic soils, respectively, $q\left(x\right)$ denotes the external load, and $EI$ represents the flexural stiffness of the beam. The specific expression of the deformation potential energy and strain energy can be found in the literature [32,33,34,35,36]. After sorting out the complex mathematical formulas, the total potential energy of the beams embedded in two refined Vlasov foundations can be obtained as follows:

$$V_i\hspace{0.33em}=\frac{1}{2}{\displaystyle {\int }_0^{L}EI{\left(\frac{d^2{w}_{bi}}{d{x}^2}\right)}^2}dx+\frac{1}{2}{\displaystyle {\int }_{-\infty }^{+\infty }\left\{k_i{\overline{w}}_{si}{}^2+G_{pi}{(\frac{d{\overline{w}}_{si}}{dx})}^2\right\}}dx-{\displaystyle {\int }_0^{L}q\left(x\right)w_{bi}dx}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\left(i=1,2\right)$$

(10)

The reaction coefficient $k_i$ and shear coefficient $G_{pi}$ of two novel Vlasov elastic foundation are expressed as:

$$k_1={\displaystyle {\int }_0^{H_e+H}\frac{E_{G2}b\left(1-{\mu }_G\right)}{\left(1+{\mu }_G\right)\left(1-2{\mu }_G\right)}\left[\eta +\left(1-\eta \right)\frac{z}{H}\right]}{\left(\frac{d{\varphi }_1}{dz}\right)}^{2}dz$$

(11)

$$G_{p1}={\displaystyle {\int }_0^{H_e+H}\frac{E_{G2}b}{2\left(1+{\mu }_G\right)}\left[\eta +\left(1-\eta \right)\frac{z}{H}\right]}{\varphi }_1{}^{2}dz$$

(12)

$$k_2={\displaystyle {\int }_0^{H_e+H}{C}_{33}b{\left(\frac{d{\varphi }_2}{dz}\right)}^{2}dz}$$

(13)

$$G_{p2}={\displaystyle {\int }_0^{H_e+H}{C}_{44}b{\varphi }_2{}^{2}dz}$$

(14)

By taking variations of the total potential energy with respect to $\delta {\overline{w}}_{si}$, the governing differential equations for the foundation beam considering the embedment depth effect are derived as follows:

$$EI{\varphi }_i^2\left(H_e\right)\frac{d^4{\overline{w}}_{si}}{d{x}^4}-G_{pi}\frac{d^2{\overline{w}}_{si}}{d{x}^2}+k_i{\overline{w}}_{si}=q\left(x\right){\varphi }_i\left(H_e\right)\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left(i=1,\hspace{0.33em}2\right)$$

(15)

In addition, the foundation soils can be divided into the part under the beam and the part outside the domain of the beam, and the governing equation and corresponding boundary conditions for the foundation part outside the domain of the beam can also be obtained.

2.3. Attenuation Function and Iterative Solution

Similarly, collecting the coefficients of $\delta {\varphi }_i$ in the variational expression, the governing equation for the attenuation function ${\varphi }_i$ of the two novel Vlasov foundation models is also obtained as:

$$\frac{d^2{\varphi }_i}{d{z}^2}-{\left(\frac{{\gamma }_i}{H_e+H}\right)}^2{\varphi }_i=0\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left(i=1,2\right)$$

(16)

where the attenuation parameter of the elastic foundations is ${\gamma }_i$, which characterizes the distribution of displacements in the vertical direction in elastic foundations. Moreover, the value of ${\gamma }_i$ is determined as a function of the characteristics of beams and elastic foundations using an iterative technique. Other related expressions and additional parameters ($m_i$, $n_i$) are as follows:

$${\left(\frac{{\gamma }_i}{H_e+H}\right)}^2=\frac{n_i}{m_i}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left(i=1,2\right)$$

(17)

$$m_1={\displaystyle {\int }_{-\infty }^{+\infty }\frac{E_{G2}b\left(1-{\mu }_G\right)}{\left(1+{\mu }_G\right)\left(1-2{\mu }_G\right)}\left[\eta +\left(1-\eta \right)\frac{z}{H}\right]}{\overline{w}}_{s1}{}^{2}dx$$

(18)

$$n_1={\displaystyle {\int }_{-\infty }^{+\infty }\frac{E_{G2}b}{2\left(1+{\mu }_G\right)}}\left[\eta +\left(1-\eta \right)\frac{z}{H}\right]{\left(\frac{d{\overline{w}}_{s1}}{dx}\right)}^{2}dx$$

(19)

$$m_2={\displaystyle {\int }_{-\infty }^{+\infty }{C}_{33}b{\overline{w}}_{s2}{}^{2}dx}$$

(20)

$$n_2={\displaystyle {\int }_{-\infty }^{+\infty }{C}_{44}b{\left(\frac{d{\overline{w}}_{s2}}{dx}\right)}^{2}dx}$$

(21)

Minimizing the function $V_i$ with respect to ${\varphi }_i$ and applying the boundary conditions expressed in Equation (7), the attenuation function ${\varphi }_i\left(z\right)$ can be solved as:

$${\varphi }_i(z)=\frac{\sinh \left[{\gamma }_i\left(1-\frac{z}{H_e+H}\right)\right]}{\sinh ({\gamma }_i)}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left(i=1,2\right)$$

(22)

It can be seen that Equations (9)–(22) are similar in form to those in the literature [31,32,33,34,35,36]. However, after considering the embedment depth effect, the characteristic coefficient ${\varphi }_i\left(H_e\right)$ related to the embedment depth is added to these formulas. This indicates that the two refined foundation models proposed in this research are the extensions of the classical Vlasov model which take into account soil–structure interaction effects.

In order to obtain the solution to this problem, the analytical method, numerical method, semi-analytical semi-numerical method, and energy variational method are mainly used. Three-dimensional finite element modeling (FEM) is still quite cumbersome and cost-prohibitive. The Fourier series can be used to solve the bending differential equations for foundation beams embedded in elastic foundations. For example, the boundary condition of the finite-length beam is that both ends are free. The corresponding deflection expression is given as follows:

$${\overline{w}}_{si}={\displaystyle \sum _{m=1}^{\infty }{w}_m\sin \frac{m\pi x}{L}}+w_0\left(1-\frac{x}{L}\right)+w_L\frac{x}{L}$$

(23)

where $w_m$, $w_0$, and $w_L$ are unknown coefficients. The distributed load $q\left(x\right)$ is expanded as the following Fourier series:

$$q\left(x\right)={\displaystyle \sum _{n=1}^{\infty }{b}_n\sin \frac{n\pi }{L}}x$$

(24)

$$b_n=\frac{2}{L}{\displaystyle {\int }_0^{L}q\left(x\right)\sin \frac{n\pi }{L}}xdx\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}n=1,2,3,\dots$$

(25)

The concentrated load $P$ is represented by the Dirac Delta function which is expanded into the following Fourier series:

$$P^{*}=P\delta \left(x-x_0\right)$$

(26)

$$\delta \left(x-x_0\right)=\frac{2}{L}{\displaystyle \sum _{n=1}^{\infty }\sin \frac{n\pi x_0}{L}}\sin \frac{n\pi x}{L}$$

(27)

In order to compare coefficients, it is necessary to expand $x$, $x^2$, and $x^3$ into the Fourier series. By substituting the deflection function into the differential equations and corresponding boundary conditions, a series of equations can be obtained. It can be proved that the number of equations and the number of unknown coefficients is equal. With further algebraic simplification, the problem can be solved.

In the above formulas, the model coefficients ($k_i$, $G_{pi}$) and attenuation functions ${\varphi }_i$ are related to the attenuation parameter ${\gamma }_i$. Therefore, the iterative technique can be used to deal with this problem. The convergence rate of this process is fast, and the exact solution to the results can be derived. Figure 3 and Figure 4 show the iterative flowchart of the attenuation parameter ${\gamma }_1$ in a Gibson elastic foundation and the iterative flowchart of the attenuation parameter ${\gamma }_2$ in a transversely isotropic foundation, respectively [31,32,33,34,35,36,37]. Iteration is continued until the two values of ${\gamma }_i$ are approximately equal. That is, $\left|{\gamma }_i-{\gamma }_i^{*}\right|\le \delta$ and $\delta =0.001$.

More importantly, by substituting the vertical deflection ${\overline{w}}_{si}$ of the foundation surface into Formula (8), the deflection $w_{bi}$ of the finite-length beam considering the embedment depth effect can be obtained. Finally, other quantities in physics are derived from the deformation. According to the theories of material mechanics and elasticity, the mechanical responses such as the rotation angle ${\theta }_{bi}$, bending moment $M_{bi}$, and shear force $Q_{bi}$ can also be calculated, as shown in the following formulas:

$${\theta }_{bi}={\varphi }_i\left(H_e\right)\frac{d{\overline{w}}_{si}}{dx}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}{M}_{bi}=EI{\varphi }_i\left(H_e\right)\frac{d^2{\overline{w}}_{si}}{d{x}^2}$$

(28)

$$Q_{bi}=EI{\varphi }_i\left(H_e\right)\frac{d^3{\overline{w}}_{si}}{d{x}^3}-G_{pi}{\varphi }_i\left(H_e\right)\frac{d{\overline{w}}_{si}}{dx}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\left(i=1,\hspace{0.33em}2\right)$$

(29)

2.4. Advances in Two Novel Vlasov Models

Firstly, the two modified Vlasov foundations still use two independent coefficients ($k_i$, $G_{pi}$) to describe the compressive and shear properties of the physical models. If the soil of the two refined Vlasov foundations is assumed to be an isotropic and homogeneous medium, and the embedment depth effect is not considered ($H_e=0$), the results in the present study will degenerate to the case of the beam structure resting on a traditional Vlasov elastic foundation. Compared with equations for the traditional Vlasov model, the equations for the modified Vlasov foundations are not different in form. However, the relevant model coefficients will change, and this change mainly depends on the constitutive relation of the soil medium.

Secondly, geotechnical engineers usually encounter subsoil of finite depth and elastic properties are generally considered to remain constant. In the classical Vlasov two-parameter foundation model, the elastic layer was considered to be homogeneous and isotropic. However, soil is a relatively complex and multi-phase discrete medium. In many instances, elastic properties vary with depth and the elasticity modulus of Gibson soil is considered to change linearly with the depth of foundations. On the other hand, many tests show that many foundations are closer to transversely isotropic soils. In this study, the constitutive relations of Gibson soil and transversely isotropic soil are adopted, respectively.

Thirdly, in a previous analysis, the soil parameters in elastic foundation models were generally determined by specific tests or engineering experience. Moreover, the attenuation parameter ${\gamma }_i$ has been taken as a constant. In this paper, the model coefficients ($k_i$, $G_{pi}$, ${\gamma }_i$) of elastic foundation models can be calculated using an iterative technique, which shows that these model parameters determined by experience or tests are not accurate or reliable. Two novel models eliminate the need to determine experimentally or empirically the values of reaction coefficient or the shear coefficient, which provides for the shear interaction among adjacent points in the soil continuum.

Finally, the two-parameter model proposed by Vlasov for beams on elastic foundations represents the soil–structure interaction. In the present paper, the refined models proposed have deeper physical significance, and the theoretical system is more rigorous, and the mathematical calculation is simpler. The theoretical developments will gain more credibility when compared to standard numerical models such as Finite Element modelling (FEM). At the same time, the new models have a strong guiding significance for engineering practice, FEM, and the development of design and calculation software. The theories and methods herein further develop and enrich the Vlasov elastic foundation model.

3. Numerical Studies

Example 1. As a verification, the soil is assumed to be an isotropic and homogeneous medium, and the embedment depth $H_e$ is taken to be 0. Then, the two novel Vlasov models degenerate into the classical Vlasov elastic foundation, that is, a finite-length beam is lying on the traditional elastic foundation. The following data are taken in the numerical example: length of the beam $L=10\hspace{0.33em}\mathrm{m}$, width of the beam $b=1\hspace{0.33em}\mathrm{m}$, height of the beam $h=0.3\hspace{0.33em}\mathrm{m}$, elasticity modulus of the beam $E=2.0\times {10}^{10}\hspace{0.33em}{\mathrm{N}/\mathrm{m}}^2$, Poisson’s ratio of the beam $\mu =0.15$. The load $q=400\hspace{0.33em}\mathrm{N}/{\mathrm{m}}^2$ is the uniformly distributed load applied on the whole beam, and the concentrated force $P=400\hspace{0.33em}\mathrm{kN}$ is applied in the middle of the span. Depth of the foundation $H=2\hspace{0.33em}\mathrm{m}$, the elasticity modulus of the soil $E_s=2.6\times {10}^7\hspace{0.33em}{\mathrm{N}/\mathrm{m}}^2$, Poisson’s ratio of the foundation ${\mu }_s=0.32$.

This analysis has been caried out with the aid of a computer program (MATLAB software). The attenuation parameter $\gamma =0.39853$ is obtained by using an iterative technique. On this basis, the maximum deflection $w_b$ calculated by this method is $4.06\hspace{0.33em}\mathrm{mm}$, which is consistent with the displacement in the literature [38], and other results are also in good agreement with those in the literature. It is found that the mechanical responses of beams on elastic foundations are consistent with those in the literature, when the work conditions are the same. This verifies the effectiveness and correctness of the physical models and mathematical methods. Hence, the traditional Vlasov elastic foundation is a special case of the refined models proposed in this paper.

Example 2. The Gibson elastic foundation model is studied, and the bending problem of a finite-length beam embedded in a modified foundation is analyzed, as shown in Figure 1. The boundary condition is that both ends of the beam are free. The properties of the beam are as follows: height $h=0.3\hspace{0.33em}\mathrm{m}$, length $L=12\hspace{0.33em}\mathrm{m}$, width $b=1\hspace{0.33em}\mathrm{m}$, modulus of elasticity $E=2.0\times {10}^{10}\hspace{0.33em}{\mathrm{N}/\mathrm{m}}^2$, and Poisson’s ratio $\mu =0.15$. Load data include: uniformly distributed load $q=400\hspace{0.33em}\mathrm{N}/{\mathrm{m}}^2$ and concentrated load at the center $P=400\hspace{0.33em}\mathrm{kN}$. The properties of the Gibson foundation are: modulus of elasticity at the bottom of the soil $E_{G2}=2.8\times {10}^7\hspace{0.33em}{\mathrm{N}/\mathrm{m}}^2$, Poisson’s ratio ${\mu }_G=0.28$, and total thickness of the foundation layer $H+H_{e1}=3\hspace{0.33em}\mathrm{m}$. The non-homogeneity parameters of the Gibson elastic foundation are taken as ${\eta }_1=0.5$ and ${\eta }_2=2$, respectively, for comparison. The embedment depth is taken as $H_{e11}=0\hspace{0.33em}\mathrm{m}$, $H_{e12}=1\hspace{0.33em}\mathrm{m}$, and $H_{e13}=2\hspace{0.33em}\mathrm{m}$, respectively, while the total thickness of the foundation remains constant.

The mechanical behaviors of the elastic foundation beam under different working conditions are shown in Figure 5 and Figure 6. The displacement $w_{b1}$ and rotation angle ${\theta }_{b1}$ of the beams are given in Figure 5a,b and Figure 6a,b; the bending moment $M_{b1}$, shear force $Q_{b1}$ of beams, and subgrade force $T_{b1}$ are given in Figure 5c–e and Figure 6c–e, respectively. Figure 5a and Figure 6a shows that the inhomogeneity of Gibson foundation soil has a great influence on the displacement of the elastic layer around the load, but a little influence on the far position of the elastic layer ($H_{e1}=0\hspace{0.33em}\mathrm{m}$). The displacement of the finite-length beam embedded in the Gibson elastic foundation is mainly affected by the rigidity of the surface soil, but less by the deep part of the foundation. Therefore, in order to reduce the displacement of the foundation in engineering, physical properties of the foundation at a certain depth can be improved, such as increasing its strength; but to strengthen the deep part of the foundation, its effect will be limited. Figure 5c,d and Figure 6c,d satisfy the boundary condition that the bending moment and shear force of both ends are zero.

Furthermore, it can be seen from these figures that for different Gibson elastic foundations, the displacement, rotation angle, internal forces of the beam, and subgrade force decrease with the increase in the embedment depth. The main reasons are analyzed as follows: (1) the soil media near the beam have the characteristics of continuity and shear, which limits the settlement of the structure to some extent; (2) with the increase in the embedment depth, the characteristic coefficient related to the embedment depth decreases, resulting in the reduction of the vertical displacement of the beam structure.

The calculation results for different degrees of non-homogeneity are given in

Table 2. Results for a beam embedded in a Gibson elastic foundation (${\eta }_1=0.5$).

Depth He (m)	w (mm)	k (107 N/m3)	Gp (107 N/m)	${\mathit{\varphi }}_1$ (He)
0	6.1091	0.8804	0.6508	1.0000
1	2.7192	1.0215	0.7147	0.6461
2	0.6438	1.4450	0.9064	0.3170

and

Table 3. Results for a beam embedded in a Gibson elastic foundation (${\eta }_2=2$).

Depth He (m)	w (mm)	k (107 N/m3)	Gp (107 N/m)	${\mathit{\varphi }}_1$ (He)
0	3.0566	1.8276	1.8363	1.0000
1	1.6254	1.5453	1.7085	0.6461
2	0.7091	0.6983	1.3251	0.3170

, including the displacement $w$ at the center, reaction coefficient $k_1$, shear coefficient $G_{p1}$, and characteristic coefficient ${\varphi }_1\left(H_e\right)$. For the case $\eta =0.5$, the reaction coefficient and shear coefficient increase gradually with the increase in the embedment depth. However, for the case $\eta =2$, the reaction coefficient and shear coefficient decrease gradually with the increase in the embedment depth. This is mainly because the soft and hard conditions of Gibson soils depend on the specific value of the dimensionless parameter $\eta$.

Example 3. The bending problem of a finite-length beam embedded in a transversely isotropic elastic foundation is analyzed, as shown in Figure 2. Both ends of the beam are also free. The parameters of the foundation–beam system are as follows: the height of the beam $h=0.3\hspace{0.33em}\mathrm{m}$, the length of the beam $L=12\hspace{0.33em}\mathrm{m}$, the width of the beam $b=1\hspace{0.33em}\mathrm{m}$, modulus of elasticity $E=2.0\times {10}^{10}\hspace{0.33em}{\mathrm{N}/\mathrm{m}}^2$, and Poisson’s ratio $\mu =0.15$, uniformly distributed load $q=400\hspace{0.33em}\mathrm{N}/{\mathrm{m}}^2$ and concentrated load at center $P=400\hspace{0.33em}\mathrm{kN}$. The properties of the transversely isotropic foundation are: $E_{T1}=41.6\hspace{0.33em}\mathrm{MPa}$, ${\mu }_{T1}=0.3$, ${\mu }_{T2}=0.2$, $G_T=16\hspace{0.33em}\mathrm{MPa}$, and total thickness of the soil layer $H+H_{e2}=3\hspace{0.33em}\mathrm{m}$. Then, we take the values $E_{T2}$ of the elasticity modulus as $E_{T21}=28.8\hspace{0.33em}\mathrm{MPa}$ and $E_{T22}=57.6\hspace{0.33em}\mathrm{MPa}$,respectively, for comparison. The embedment depth is taken as $H_{e21}=0\hspace{0.33em}\mathrm{m}$, $H_{e22}=1\hspace{0.33em}\mathrm{m}$, and $H_{e23}=2\hspace{0.33em}\mathrm{m}$, respectively, while keeping the total thickness of the soil unchanged.

The mechanical responses ($w_{b2}$, ${\theta }_{b2}$, $M_{b2}$, $Q_{b2}$, $T_{b2}$) of the elastic foundation beam under different working conditions are shown in Figure 7 and Figure 8. The trend of these Figures is consistent with the reality. The bending moment and shear force meet the free boundary conditions at both ends as shown in Figure 7c,d and Figure 8c,d. It can be seen that when the modulus $E_{T2}$ of elasticity in the normal direction of the isotropic plane increases, the displacement, rotation angle, and bending moment of the finite-length beam decreases, while the shear force is almost constant and the subgrade force increases. Moreover, for different transversely isotropic foundations, the greater the embedment depth of the beam, the smaller the mechanical response of the structure, such as the displacement, rotation angle, bending moment, and so on. The reasons are similar to the factors of the beam embedded in Gibson foundations, including the restraining effect of foundation soils on the beam structure and the decrease of the characteristic coefficient affecting the beam displacement.

The calculation results for different cases are given in

Table 4. Results for a beam embedded in a transversely isotropic foundation ($E_{T21}=28.8\hspace{0.33em}\mathrm{MPa}$).

Depth He (m)	w (mm)	k (107 N/m3)	Gp (107 N/m)	${\mathit{\varphi }}_2$ (He)
0	4.0697	1.1561	1.4964	1.0000
1	1.8940	1.1561	1.4964	0.6360
2	0.5316	1.1561	1.4964	0.3090

and

Table 5. Results for a beam embedded in a transversely isotropic foundation ($E_{T22}=57.6\hspace{0.33em}\mathrm{MPa}$).

Depth He (m)	w (mm)	k (107 N/m3)	Gp (107 N/m)	${\mathit{\varphi }}_2$ (He)
0	3.0352	2.0964	1.5412	1.0000
1	1.4887	2.0964	1.5412	0.6494
2	0.4412	2.0964	1.5412	0.3196

, including the displacement $w$ at the center, reaction coefficient $k_2$, shear coefficient $G_{p2}$, and characteristic coefficient ${\varphi }_2\left(H_e\right)$. With the increase in the embedment depth, the displacement and characteristic coefficient decrease. However, as the embedment depth increases, the reaction coefficient and shear coefficient remain constant, which is different from the variation law of Gibson soils in Example 2. In addition, it can be seen from these tables that when the modulus $E_{T2}$ of elasticity in the normal direction of the isotropic plane increases, the two parameters (reaction coefficient and shear coefficient) become larger.

4. Conclusions

Analysis methods for soil structure interaction (SSI) with high efficiency and high accuracy are always required in geotechnical mechanics, disaster prevention and mitigation engineering, and seismic engineering. The beam structures embedded in elastic foundations have been widely used in engineering practice. Due to the importance of accurate analysis of SSI, this paper analyzes the bending problem of a finite-length beam embedded in two modified Vlasov foundations using variational principles for this objective. Gibson soils and transversely isotropic soils are used to reflect the non-homogeneity of elastic foundations. The governing differential equations are solved by combining the iterative technique and Fourier series method. The main conclusions are as follows:

(1) For two refined Vlasov foundation models, the influence of embedment depth on the mechanical performance of soil–beam system is similar. With the increase in the embedment depth, the mechanical behavior of the system decreases. That is to say, the vertical displacement and internal forces of the beam structure resting on the foundation surface are the largest. The main reasons are summarized as follows: (a) the mechanical response of the structure is constrained by the soil media due to the continuity and shear properties; (b) with the increase in the embedment depth, the characteristic coefficient ${\varphi }_i\left(H_e\right)$ related to the embedment depth decreases.

(2) The novel Vlasov foundation models can describe the continuity of foundation soils through the reaction coefficient $k_i$ and the shear coefficient $G_{pi}$. These model parameters ($k_i$, $G_{pi}$, ${\gamma }_i$) of the system are calculated iteratively using only the geometric and material properties of soils and beams to obtain more reliable results. It can be concluded that the iterative technique eliminates the necessity of field testing to determine model parameters.

(3) Gibson soils and transversely isotropic soils also significantly affect the mechanical response of the foundation–beam system. For example, when beams are resting on elastic foundations ($\lambda =0$), the rotation angle under the condition of ${\eta }_2=2$ is smaller than that under the condition of ${\eta }_1=0.5$. The mechanical behavior of the foundation beam is mainly determined by the characteristics of the shallow Gibson soils, rather than the deep part of foundations. For another example, when the embedment depth is the same, the displacement in the case of $E_{T22}=57.6\mathrm{MPa}$ is smaller than that in the case of $E_{T21}=28.8\mathrm{MPa}$. Because the number of constitutive parameters ($E_{T1}$, ${\mu }_{T1}$, $E_{T2}$, ${\mu }_{T2}$, $G_T$) of transversely isotropic soils is relatively large, the influence of the inhomogeneity on the mechanical behavior and model parameters ($k_i$, $G_{pi}$, ${\gamma }_i$) of foundation–beam system is complicated. Therefore, the non-homogeneity of foundation soils cannot be ignored in engineering. This requires further in-depth and comprehensive research.

It is hoped that the present study will contribute to the existing knowledge of classical theory of elastic foundation beams. The immediate interest is to extend two modified Vlasov models for bending analysis of beams embedded in elastic foundations. The limitations of this study include that the viscoelastic behavior of the soil has not been considered for the time being. In addition, this work needs more experimental results. Recommendations for future work are as follows. The static bending and steady-state response problems can still be solved iteratively for the unknown attenuation parameter. However, the problem of free vibration is quite different from that of static bending and steady-state response. There is scope for extensions to dynamic loads on structures embedded in different foundations, such as impact loads and seismic action.