Determining Cost and Time Performance Indexes for Diversified Investment Tasks
Abstract
:1. Introduction
1.1. Parameters of the Investment Process
1.2. Literature Review
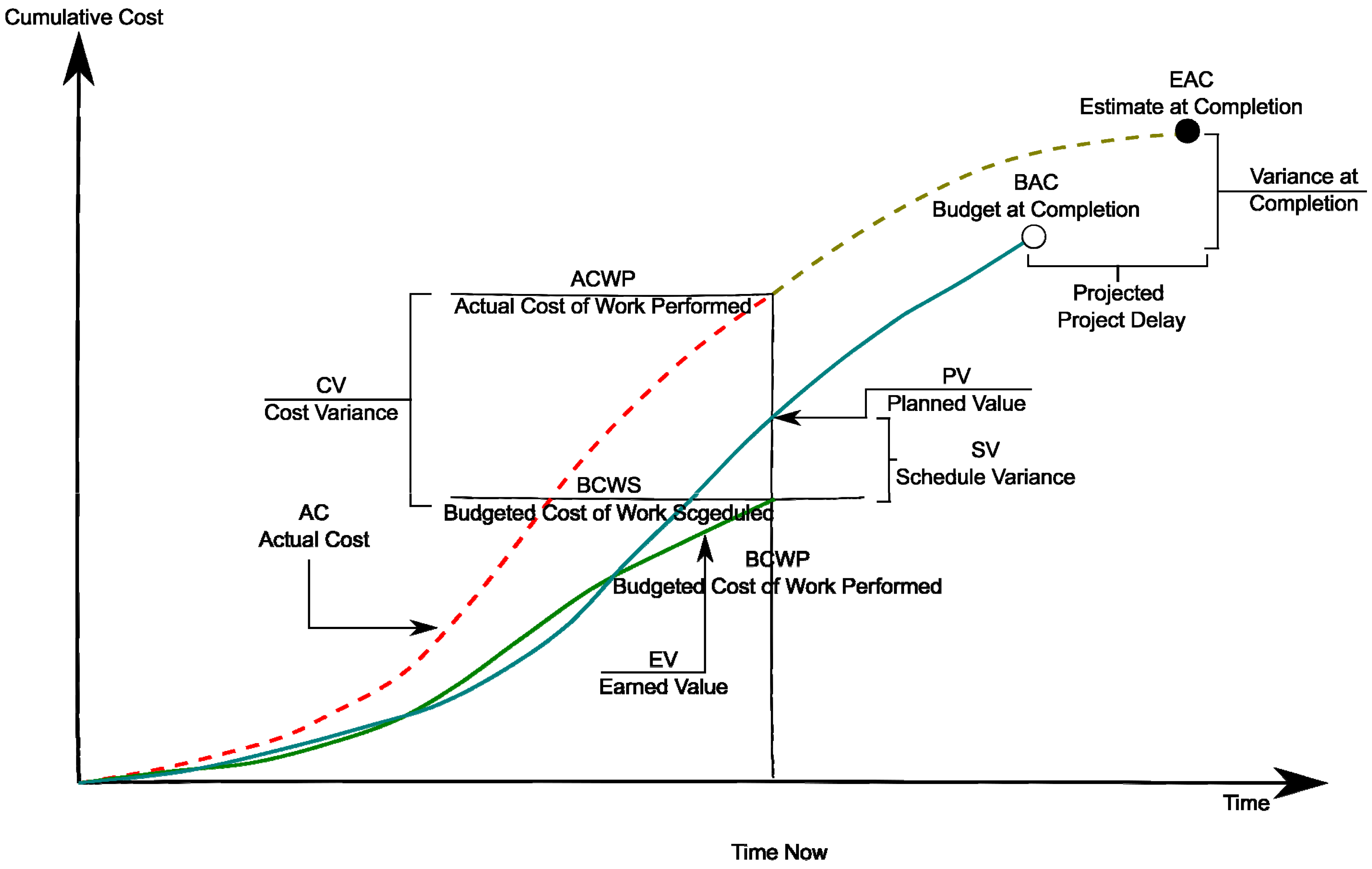
- planned value—PV, also known as the budgeted cost of work scheduled—BCWS;
- earned value—EV, also known as the budgeted cost of work performed—BCWP;
- actual cost—AC, also known as the actual cost of work performed—ACWP;
- schedule variance—SV;
- cost variance—CV;
- schedule performance index—SPI;
- cost performance index—CPI;
- estimation at completion—EAC;
- estimated time to complete—ETTC.
2. Methods and Models
2.1. Research Approach
2.2. Research Sample
2.3. Performance Indexes
- CPIj < 1—overrunning the budget. This means that the actual cost of work performed is higher than the budgeted cost of work performed, i.e., ACWPj > BCWPj;
- CPIj > 1—not using the budget (savings). This means that the actual cost of work performed is lower than the budgeted cost of work performed, i.e., ACWPj < BCWPj;
- CPIj = 1—the cost of works is as planned (according to the planned budget), which means that the actual cost of work performed is equal to the budgeted cost of work performed, i.e., ACWPj = BCWPj.
- SPIj < 1—delay in the schedule (progress of work is less than planned = work pace is slower than planned). This means that the budgeted cost of work scheduled is higher than the budgeted cost of work performed, i.e., BCWSj > BCWPj;
- SPIj > 1—ahead of schedule (work progress is greater than planned = work pace is faster than planned). This means that the budgeted cost of work scheduled is less than the budgeted cost of work performed, i.e., BCWSj < BCWPj;
- SPIj = 1—works are carried out in accordance with the schedule (progress of works is equal to the scheduled work = pace of work is in line with the planned pace). This means that the budgeted cost of work scheduled is equal to the budgeted cost of work performed, i.e., BCWSj = BCWPj.
3. Research Results
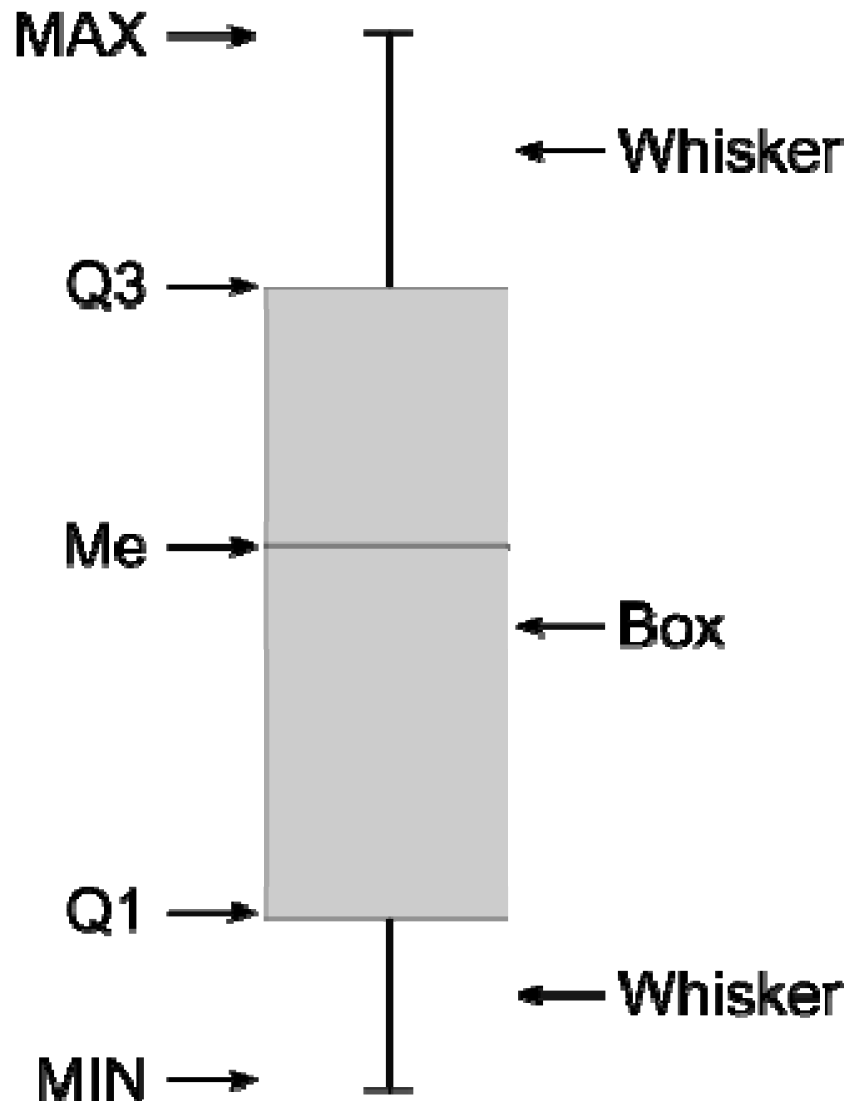
- maximum value—MAX;
- third quartile—Q3;
- median—Me (Q2);
- first quartile—Q1;
- minimum value—MIN.
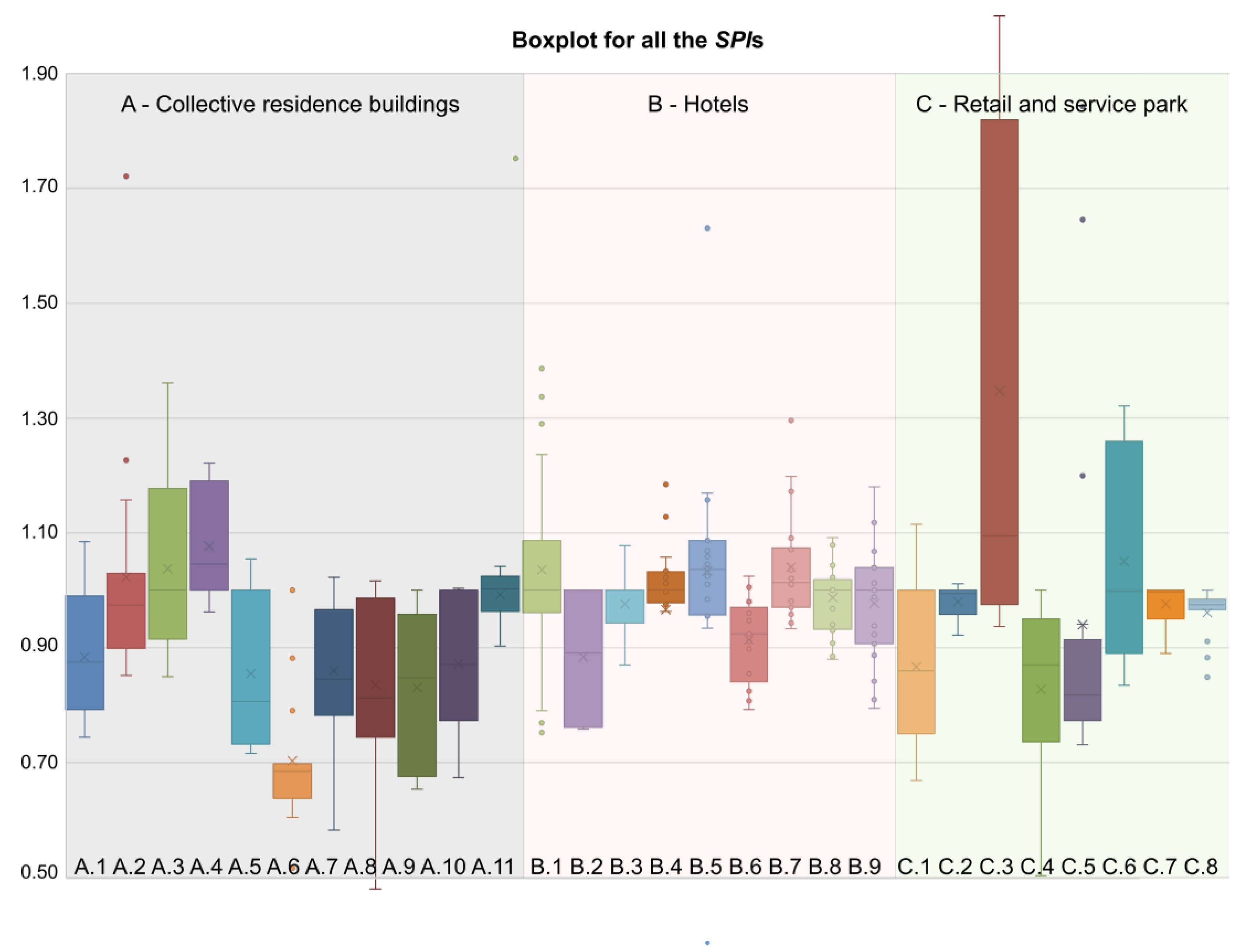
- Position: the position is indicated by the entire boxplot, e.g., the data range can be defined (Min, Max).
- Data dispersion: the longer the plot, the more dispersed the data, i.e., they can have a greater variety of values. Long whiskers are also evidence of distraction—i.e., there are extreme observations (very different from the box);.
- Shape: if the plot looks symmetrical to the median, it can be suspected that the graph is symmetrical. If the box is not evenly divided and/or the whiskers are of different lengths, there is an asymmetric distribution. Whether the asymmetry is right-handed or left-handed can be read from the Max and Min distance from the Median. If one of these distances is significantly greater than the other, there is a right-handed asymmetry (if the Max distance is significantly greater then Me) or a left-handed asymmetry (if the Min distance is greater than Me)
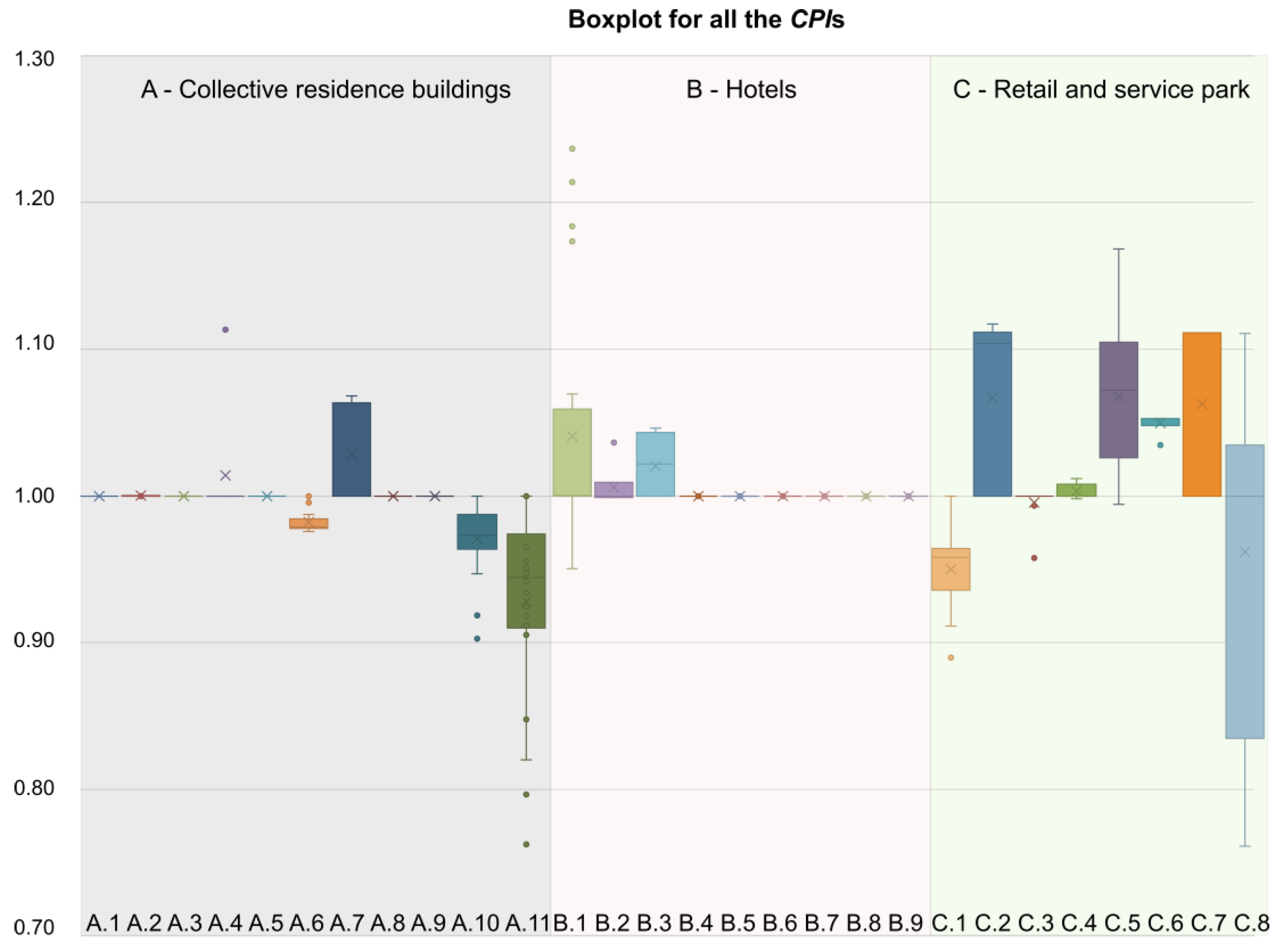
3.1. Cost Performance Index
3.2. Schedule Performance Index
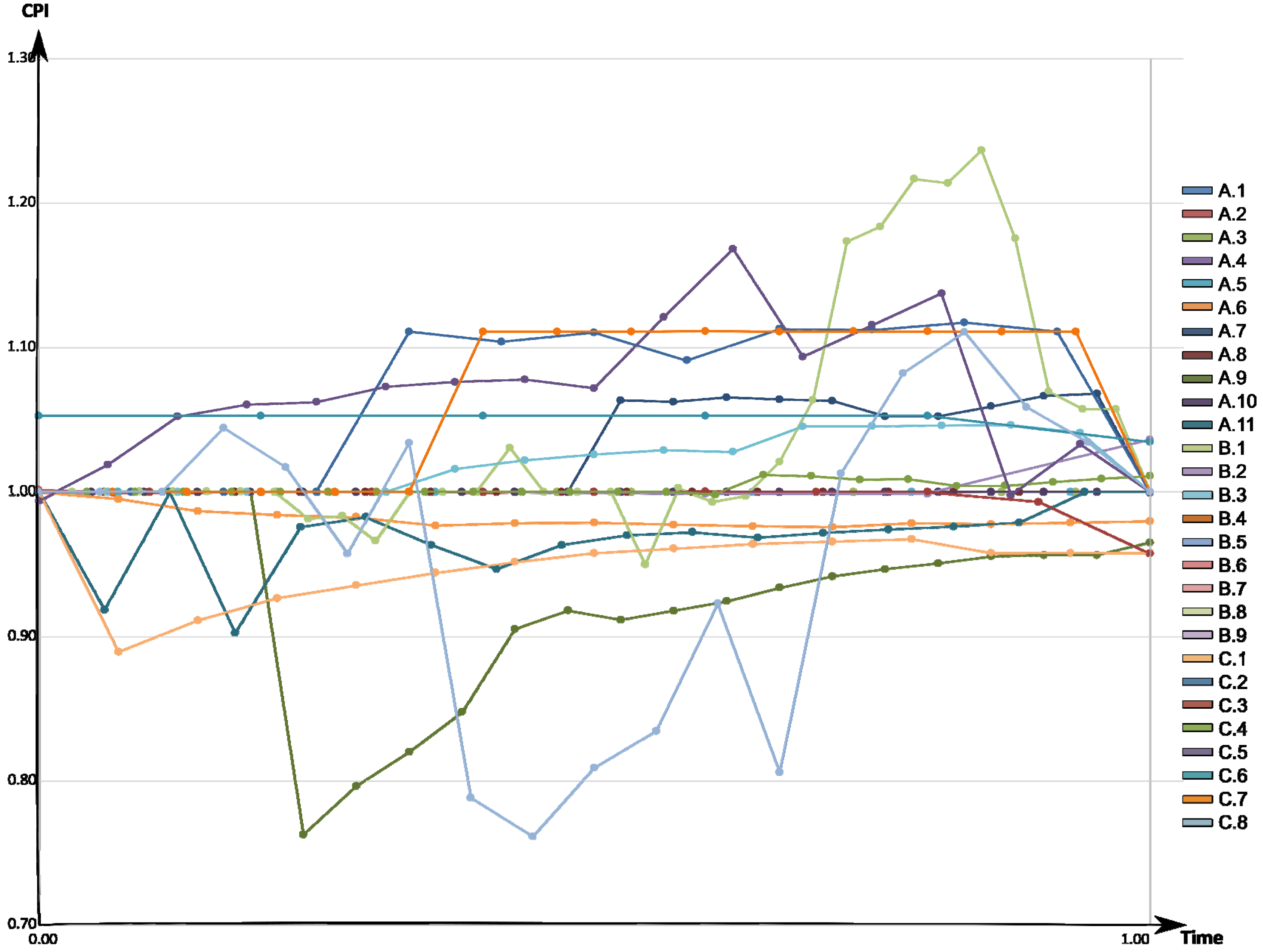
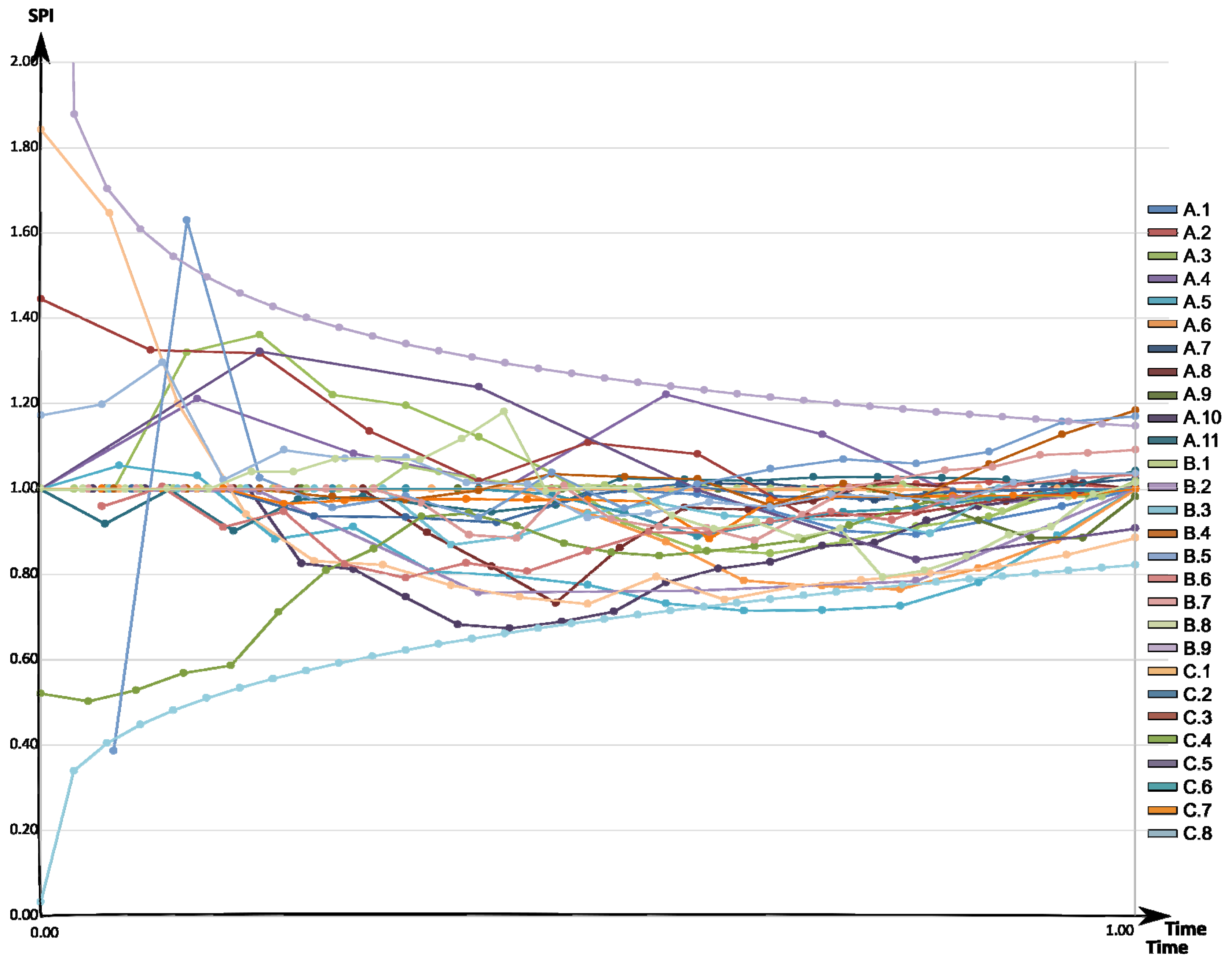
3.3. Simultaneous Assessment of Schedule and Cost Performance Indexes with Regards to Time
4. Discussion
5. Conclusions
- In the case of collective housing buildings (0.2 < t < 0.6; where t is the total duration of the project), the greatest progress was observed in the initial months of their construction. In the third month, there was 20–30% more work performed than was assumed in the case of approx. 40% of investment tasks, and from the 4th month there was a noticeable downward trend in all the curves of the indexes. In almost 50% of the assessed investments, there were negative deviations from the SV schedule, which indicate a delay in works. During one-sixth of the analyzed implementations, the work and expenditure schedules were updated in order to reflect the actual state of affairs.
- There was a very large convergence in cost and time deviation curves in the case of retail and service facilities, and therefore a budget loss of up to 5% over the entire implementation period can be assumed. In the course of implementation, between one-third and one-half of the time, savings of up to 25% can occur. Schedule deviations range from 10% (ahead of schedule) to approx. 30% (delays in the schedule).
- A share of 50% of housing facilities did not exceed their planned budget and completion time, or exceeded it minimally. The remaining 50% exceeded the costs by approx. PLN 2 million, and had delays with regards to implementing the assumed plan, which resulted in losses of approx. PLN 10 million.
- The cost deviation diagrams in all the analyzed groups of facilities show that in the first two quarters of the project duration, the costs were in line with the planned budget in approx. 90% of the analyzed investments. Only in 1/13 of the analyzed investment tasks were the costs significantly lower than assumed. The largest deviations occurred in the third and fourth quarter, where the costs that were incurred in 3/13 tasks were below the investment budget; in the other 3/13, they exceeded this budget. The most financial losses occurred in the fourth quarter and oscillated between PLN 2 and 10 million. The largest number of investments (with a budget oscillating below the planned budget ) occurred in the third quarter, and their value ranged between PLN 1 and 42 million.
- The most time deviations occurred in the third and fourth quarters of all the analyzed groups of objects. Due to the overrunning of time, the analyzed construction investments resulted in delays mostly at the end of the project. Projects that were ahead of schedule from the start of works were below the investment budget, or were within the planned costs without major problems, despite the fact that they had a slight excess of budget in the second phase of the task.
- The above conclusions can be generalized and synthesized in the following form:
- There is a need for reliable verification of achieved values of EVM indexes due to their high sensitivity to entered data.
- The correctness of defining the causes of fluctuations allows for appropriate remedial actions to be taken when there is a risk of exceeding cost and time.
- On the basis of a few simple parameters (EV, PV, AC), and the resulting indexes (CPI, SPI, EAC, ETTC), the actual progress of construction projects can be quickly assessed.
- The analysis of contingency curves allows for the tracking of changes in costs and implementation time, and also for the estimation of the risk of exceeding them (the probability of implementing the project within the planned budget and implementation time).
- The analysis of CV cost deviation and SV time deviation indexes allows for the proper management of investment projects. The obtained values enable the work and expenditure schedule to be properly planned in order to correctly estimate the actual costs and the deadline of investments.
- Exceeding the threshold of 0.7 of the CV index results in a high probability of exceeding the budget. It is similar in the case of the SV index—schedule deviations. However, both of these statements require confirmation using a larger number of studied cases.
- the conducted analyses for three groups of objects show a great similarity in the obtained parameters and indexes. Research indicates that the problem of exceeding the planned budget, and failure to meet the planned deadlines, is common, regardless of the type of investment.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IPMA. IPMA Individual Competence Baseline; IPMA: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Project Management Institute. A Guide to the Project Management Body of Knowledge (PMBOK Guide), 6th ed.; Project Management Institute (PMI): Newtown Square, PA, USA, 2017; ISBN 9781935589679. [Google Scholar]
- Kern, A.; Formoso, C. A model for integrating cost management and production planning and control in construction. J. Financ. Manag. Prop. Constr. 2006, 11, 75–90. [Google Scholar] [CrossRef]
- Hoła, B.; Sawicki, M.; Skibniewski, M. An IT model of a Knowledge Map which supports management in small and medium-sized companies using selected Polish construction enterprises as an example. J. Civ. Eng. Manag. 2015, 21, 1014–1026. [Google Scholar] [CrossRef]
- Mingus, N. Project Management; Alpha Publishing: Dubai, United Arab Emirates, 2001; ISBN 0028642236. [Google Scholar]
- Kerzner, H. Project Management: A Systems Approach to Planning, Scheduling, and Controlling; John Wiley & Sons, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Makesh, S.; Mathivanan, M. Analysis on causes of delay in building construction. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 335–341. [Google Scholar]
- Rachid, Z.; Toufik, B.; Mohammed, B. Causes of schedule delays in construction projects in Algeria. Int. J. Constr. Manag. 2019, 19, 371–381. [Google Scholar] [CrossRef]
- Kowalski, J.; Połoński, M.; Lendo-Siwicka, M.; Trach, R.; Wrzesiński, G. Method of assessing the risk of implementing railway investments in terms of the cost of their implementation. Sustainability 2021, 13, 13085. [Google Scholar] [CrossRef]
- Połoński, M. Management of Construction Investment Process; Wydawnictwo SGGW: Warszawa, Poland, 2018; ISBN 9788375830873. (In Polish) [Google Scholar]
- Miguel, A.; Madria, W.; Polancor, R. Project management model: Integrating Earned Schedule, quality, and risk in Earned Value Management. In Proceedings of the 6th IEEE International Conference on Industrial Engineering and Applications (ICIEA), Waseda, Tokyo, 12–15 April 2019; pp. 622–628. [Google Scholar]
- Guan, X.; Servranckx, T.; Vanhoucke, M. An analytical model for budget allocation in risk prevention and risk protection. Comput. Ind. Eng. 2021, 161, 107657. [Google Scholar] [CrossRef]
- Starczyk-Kołbyk, A.; Kruszka, L. Use of the EVM method for analysis of extending the construction project duration as a result of realization disturbances—Case study. Arch. Civ. Eng. 2021, 67, 373–393. [Google Scholar]
- Duarte-Vidal, l.; Herrera, R.; Atencio, E. Muñoz-La Rivera F. Interoperability of digital tools for the monitoring and control of construction projects. Appl. Sci. 2021, 11, 10370. [Google Scholar] [CrossRef]
- Wieczorek, D. Monitoring of Projects Costs Using Earned Value; Papers and Reports of the Faculty of Management of Gdansk University; Gdansk University: Sopot, Poland, 2006; Volume 1, pp. 551–560. (In Polish) [Google Scholar]
- Połoński, M. Kontrola kosztów realizacji obiektu budowlanego metodą Earned Value. In Inżynieria Przedsięwzięć Budowlanych: Rekomendowane Metody i Techniki; SGGW: Warszawa, Poland, 2015; Volume 1, pp. 23–46. (In Polish) [Google Scholar]
- Anysz, H.; Zawistowski, J. Cost-time control of the progress of construction works using the earned value method using MS Project (in Polish: Kontrola kosztowo-czasowa postępu robót budowlanych metodą wartości wypracowanej z wykorzystaniem programu MS Project). In Principles and Standards of Cost Estimation of Construction Works for Awarding Entities, Investors and Contractors (in Polish: Zasady i Standardy Kosztorysowania Robót Budowlanych Dla Zamawiających, Inwestorów i Wykonawców); Stowarzyszenie Kosztorysantów Budowlanych: Warsaw, Poland, 2017; pp. 71–88. [Google Scholar]
- Leśniak, A.; Kubek, D.; Plebankiewicz, E.; Zima, K.; Belniak, S. Fuzzy AHP Application for Supporting Contractors’ Bidding Decision. Symmetry 2018, 10, 642. [Google Scholar] [CrossRef]
- Jaśkowski, P.; Biruk, S.; Krzemiński, M. Planning repetitive construction processes to improve robustness of schedules in risk environment. Arch. Civ. Eng. 2020, 66, 643–657. [Google Scholar]
- Konior, J. Enterprise’s risk assessment of complex construction projects. Arch. Civ. Eng. 2015, 61, 63–74. [Google Scholar] [CrossRef]
- Lo, W.; Chen, Y. Optimization of Contractor’s S-Curve. In Proceedings of the 24th International Symposium on Automation & Robotics in Construction (ISARC 2007), Kochi, India, 19–21 September 2007; pp. 417–420. [Google Scholar]
- Leśniak, A.; Zima, K. Cost calculation of construction projects including sustainability factors using the case based reasoning (CBR) method. Sustainability 2018, 10, 1608. [Google Scholar] [CrossRef]
- Al-Jibouri, S. Monitoring systems and their effectiveness for project cost control in construction. Int. J. Proj. Manag. 2003, 21, 145–154. [Google Scholar] [CrossRef]
- Love, P.; Wang, X.; Sing, C.; Tiong, R. Determining the probability of project cost overruns. J. Constr. Eng. Manag. 2013, 139, 321–330. [Google Scholar] [CrossRef]
- De Marco, A.; Narbaev, T. Earned value-based performance monitoring of facility construction projects. J. Facil. Manag. 2013, 11, 69–80. [Google Scholar] [CrossRef]
- Abba, W. How earned value got to primetime: A short look back and glance ahead. In Project Management Institute Annual Seminars & Symposium; Project Management Institute (PMI): Houston, TX, USA, 2000. [Google Scholar]
- Zohoori, B.; Verbraeck, A.; Bagherpour, M.; Khakdaman, M. Monitoring production time and cost performance by combining earned value analysis and adaptive fuzzy control. Comput. Ind. Eng. 2019, 127, 805–821. [Google Scholar] [CrossRef]
- Chen, H.; Chen, W.; Lin, Y. Earned value project management: Improving the predictive power of planned value. Int. J. Proj. Manag. 2016, 34, 22–29. [Google Scholar] [CrossRef]
- Konior, J.; Szóstak, M. Methodology of planning the course of the cumulative cost curve in construction projects. Sustainability 2020, 12, 2347. [Google Scholar] [CrossRef]
- Waris, M.; Khamidi, M.; Idrus, A. The cost monitoring of construction projects through Earned Value Analysis. J. Constr. Eng. Proj. Manag. 2012, 2, 42–45. [Google Scholar]
- Bhosekar, M.; Vyas, G. Cost controlling using Earned Value Analysis in construction industries. Int. J. Eng. Innov. Technol. 2012, 1, 324–332. [Google Scholar]
- Khamidi, M.; Khan, W.; Idrus, A. The Cost Monitoring of Construction Projects Through Earned Value Analysis. In Proceedings of the International Conference on Economics and Finance Research (ICEFR 2011), Singapore, 26–28 February 2011; pp. 129–133. [Google Scholar]
- Klinowski, M. Analysis of the Current and Forecast of the Future Realization of the Project on the Basis of Earned Value Method; Research Papers of Wrocław University of Economics; Wrocław University of Economics: Wrocław, Poland, 2014; Volume 335, pp. 105–115. (In Polish) [Google Scholar]
- Sruthi, M.; Aravindan, A. Performance measurement of schedule and cost analysis by using earned value management for a residential building. Mater. Today Proc. 2020, 33, 524–532. [Google Scholar] [CrossRef]
- Chin-Keng, T.; Shahdan, N. The Application of Earned Value Management (EVM) in Construction Project Management. J. Technol. Manag. Bus. 2015, 2, 235–261. [Google Scholar]
- Vandevoorde, S.; Vanhoucke, M. A comparison of different project duration forecasting methods using earned value metrics. Int. J. Proj. Manag. 2006, 24, 289–302. [Google Scholar] [CrossRef]
- Kwon, O.; Kim, S.; Paek, J.; Eom, S. Application of Earned Value in the Korean Construction Industry. J. Asian Archit. Build. Eng. 2008, 7, 69–76. [Google Scholar] [CrossRef]
- Priyo, M. Earned Value Management System in Indonesian Construction Projects. Int. J. Integr. Eng. 2021, 13, 37–45. [Google Scholar] [CrossRef]
- Khamidi, M.; Ali, W.; Idrus, A. Application of Earned Value Management System on an Infrastructure Project: A Malaysian Case Study. Int. Conf. Manag. Sci. Eng. 2011, 8, 1–5. [Google Scholar]
- Połoński, M.; Komendarek, P. Earned value method for operational cost control of civil structure. Metody Ilościowe w Badaniach Ekonomicznych 2011, 12, 279–290. [Google Scholar]
- Przywara, D.; Rak, A. Monitoring of time and cost variances of schedule using simple Earned Value Method indicators. Appl. Sci. 2021, 11, 1357. [Google Scholar] [CrossRef]
- Czemplik, A. Application of earned value method to progress control of construction projects. Procedia Eng. 2014, 91, 424–428. [Google Scholar] [CrossRef]
- Wauters, M.; Vanhoucke, M. Study of the Stability of Earned Value Management Forecasting. J. Constr. Eng. Manag. 2014, 141, 04014086. [Google Scholar] [CrossRef]
- Babar, S.; Thaheem, M.; Ayub, B. Estimated Cost at Completion: Integrating Risk into Earned Value Management. J. Constr. Eng. Manag. 2016, 143, 04016104. [Google Scholar] [CrossRef]
- Przywara, D.; Rak, A. The time-cost analysis of schedule monitoring using the earned value method. Tech. Trans. 2017, 5, 57–66. [Google Scholar]
- Almeida, R.; Abrantes, R.; Romão, M.; Proença, I. The Impact of Uncertainty in the Measurement of Progress in Earned Value Analysis. Procedia Comput. Sci. 2021, 181, 457–467. [Google Scholar] [CrossRef]
- Starczyk-Kołbyk, A. Randomizowana Metoda Identyfikacji Stanu Zaawansowania Robót i Korekty Planu Budowy. Ph.D. Thesis, Wojskowa Akademia Techniczna, Warszawa, Poland, 2019. [Google Scholar]
- Kasprowicz, T.; Starczyk-Kołbyk, A.; Wójcik, R. The randomized method of estimating the net present value of construction projects efficiency. Int. J. Constr. Manag. 2022. [Google Scholar] [CrossRef]
- Dziadosz, A. Zmodyfikowana Metoda Kontroli Stanu Zaawansowania Robót i Oceny Ryzyka Realizacji Przedsięwzięcia Budowlanego. Ph.D. Thesis, Politechnika Poznańska, Poznań, Poland, 2017. [Google Scholar]
- Khamooshi, H.; Golafshani, H. EDM: Earned Duration Management, a New Approach to Schedule Performance Management and Measurement. Int. J. Proj. Manag. 2014, 32, 1019–1041. [Google Scholar] [CrossRef]
- de Andrade, P.; Martens, A.; Vanhoucke, M. Using real project schedule data to compare earned schedule and earned duration management project time forecasting capabilities. Autom. Constr. 2019, 99, 68–78. [Google Scholar] [CrossRef]
- Ballesteros-Pérez, P.; Sanz-Ablanedo, E.; Mora-Melià, D.; González-Cruz, M.; Fuentes-Bargues, J.; Pellicer, E. Earned Schedule min-max: Two new EVM metrics for monitoring and controlling projects. Autom. Constr. 2019, 103, 279–290. [Google Scholar] [CrossRef]
- Martens, A.; Vanhoucke, M. Integrating corrective actions in project time forecasting using exponential smoothing. J. Manag. Eng. Vol. 2020, 36, 423–471. [Google Scholar] [CrossRef]
- Vanhoucke, M.; Vandevoorde, S. A simulation and evaluation of earned value metrics to forecast the project duration. J. Oper. Res. Soc. 2007, 58, 1361–1374. [Google Scholar] [CrossRef]
- Khodabandehlou, A.; Parvishi, A.; Taghifam, R.; Lofti, M.; Taleii, A. Integrating Earned Value Management with risk management to control the time-cost of the project. Bus. Eng. 2017, 7, 114–119. [Google Scholar]
- Sackey, S.; Lee, D.; Kim, B. Duration Estimate at Completion: Improving Earned Value Management Forecasting Accuracy. J. Civ. Eng. 2020, 24, 693–702. [Google Scholar] [CrossRef]
- Ballesteros-Pérez, P.; Elamrousy, L. On the Limitations of the Earned Value Management Technique to Anticipate Project Delays; Abdul-Malak, M., Khoury, H., Singh, A., Yazdani, S., Eds.; Responsible Design and Delivery of the Constructed Project; ISEC Press: Fargo, North Dakota, 2018; ISBN 978-0-9960437-5-5. [Google Scholar]
- Ballesteros-Pérez, P.; Sanz-Ablanedo, E.; Soetanto, R.; González-Cruz, M.; Larsen, G.; Cerezo-Narváez, A. Duration and cost variability of construction activities: An empirical study. J. Constr. Eng. Manag. 2000, 146, 04019093. [Google Scholar] [CrossRef]
- Konior, J. Monitoring of construction projects feasibility by Bank Investment Supervision approach. Civ. Eng. Archit. 2019, 7, 31–35. [Google Scholar] [CrossRef]
- Konior, J.; Szóstak, M. The S-curve as a tool for planning and controlling of construction process-case study. Appl. Sci. 2020, 10, 2071. [Google Scholar] [CrossRef]
- Szóstak, M. Planning the time and cost of implementing construction projects using an example of residential buildings. Arch. Civ. Eng. 2021, 67, 243–259. [Google Scholar]
- Dziadosz, A.; Kapliński, O.; Rejment, M. Usefulness and fields of the application of the Earned Value Management in the implementation of construction projects. Bud. Archit. 2014, 13, 357–364. [Google Scholar] [CrossRef]
- Czarnigowska, A. Earned value method as a tool for project control. Bud. Archit. 2008, 3, 15–32. [Google Scholar] [CrossRef]
- Czarnigowska, A. Monitoring of project progress using the Earned Value. Przegląd Bud. 2009, 80, 50–55. [Google Scholar]
- Ziółkowska, A.; Połoński, M. Application of the EVM method and its extensions in the implementation of construction objects. Eng. Struct. Technol. 2015, 7, 189–196. [Google Scholar] [CrossRef]
- Bagherpour, M.; Khaje Zadeh, M.; Mahmoudi, A.; Deng, X. Interpretive structural modeling in Earned Value Management. J. Civ. Eng. Manag. 2020, 26, 524–533. [Google Scholar] [CrossRef]
- Howes, R. Improving the performance of Earned Value Analysis as a construction project management tool. Eng. Constr. Archit. Manag. 2000, 7, 399–411. [Google Scholar] [CrossRef]
- Lipke, W.; Zwikael, O.; Henderson, K.; Anbari, A. Prediction of project outcome. The application of statistical methods to earned value management and earned schedule performance indexes. Int. J. Proj. Manag. 2009, 27, 400–407. [Google Scholar] [CrossRef]
- Chen, Z.; Demeulemeester, R.; Bai, S.; Guo, Y. A Bayesian approach to set the tolerance limits for a statistical project control method. Int. J. Prod. Res. 2020, 58, 3150–3163. [Google Scholar] [CrossRef]
- Salari, M.; Bagherpour, M.; Reihani, M. A time-cost trade-off model by incorporating fuzzy earned value management: A statistical based approach. J. Intell. Fuzzy Syst. 2015, 28, 1909–1919. [Google Scholar] [CrossRef]
- Salari, M.; Khamooshi, H. A better project performance prediction model using fuzzy time series and data envelopment analysis. J. Oper. Res. Soc. 2016, 67, 1274–1287. [Google Scholar] [CrossRef]
- Hajali-Mohamad, M.; Mosavi, M.; Shahanaghi, L. Optimal estimating the project completion time and diagnosing the fault in the project. Dyna Rev. Fac. Nac. Minas 2016, 83, 121–127. [Google Scholar] [CrossRef]
- Yaseen, Z.; Ali, Z.; Salih, S.; Al-Ansari, N. Prediction of risk delay in construction projects using a hybrid artificial intelligence model. Sustainability 2020, 12, 1514. [Google Scholar] [CrossRef]
| Construction Group/Sector | Amount | Measurement Period | PR | MR | FR |
|---|---|---|---|---|---|
| A. Collective residential buildings | 14 | 2006–2020 | 14 | 169 | 6 |
| B. Office buildings | 4 | 2008–2020 | 4 | 55 | |
| C. Hotels | 9 | 2013–2020 | 9 | 93 | 8 |
| D. Retail and service parks | 8 | 2008–2018 | 8 | 97 | 8 |
| E. Logistics centers | 2 | 2017–2020 | 2 | 8 | 2 |
| F. Health centers | 1 | 2011–2012 | 1 | 10 | 1 |
| G. Airports | 1 | 2011–2015 | 1 | 35 | |
| H. Industrial plants | 1 | 2018–2019 | 1 | 4 | 1 |
| Total number of PR—MR—FR reports | 40 | 471 | 26 | ||
| Total number of all reports | 536 | ||||
| Cost Performance Index (CPIj) | ||||
| CPIj < 1 | CPIj = 1 | CPIj > 1 | ||
| Schedule performance index (SPIj) | SPIj < 1 |
Budget overrun (−) Schedule delay (−) | Compliance with the budget (0) Schedule delay (−) | Budget savings (+) Schedule delay (−) |
| SPIj = 1 | Budget overrun (−) Compliance with the schedule (0) | Compliance with the budget (0) Compliance with the schedule (0) | Budget savings (+) Compliance with the schedule (0) | |
| SPIj > 1 | Budget overrun (−) Ahead of schedule (+) | Compliance with the budget (0) Ahead of schedule (+) | Budget savings (+) Ahead of schedule (+) | |
| No | Investment Symbol | Scheduled Time | Actual Time | Actual Time/Scheduled Time | BCWS | ACWP | ACWP/BCWS |
|---|---|---|---|---|---|---|---|
| 1 | A.1 | 13 | 16 | 1.23 | 17,002,557.00 | 17,002,557.00 | 1.00 |
| 2 | A.2 | 14 | 16 | 1.14 | 12,580,200.00 | 12,580,200.00 | 1.00 |
| 3 | A.3 | 14 | 16 | 1.14 | 15,231,003.00 | 15,231,003.00 | 1.00 |
| 4 | A.4 | 7 | 8 | 1.14 | 1,093,948.99 | 1,093,949.02 | 1.00 |
| 5 | A.5 | 14 | 15 | 1.07 | 19,432,197.00 | 19,432,197.00 | 1.00 |
| 6 | A.6 | 13 | 15 | 1.15 | 14,389,720.00 | 14,684,668.35 | 1.02 |
| 7 | A.7 | 16 | 22 | 1.38 | 16,971,000.00 | 17,358,600.00 | 1.02 |
| 8 | A.8 | 18 | 18 | 1.00 | 8,517,838.00 | 8,517,838.00 | 1.00 |
| 9 | A.9 | 15 | 22 | 1.47 | 17,133,356.00 | 17,755,635.76 | 1.04 |
| 10 | A.10 | 17 | 22 | 1.29 | 9,846,580.14 | 9,882,087.53 | 1.00 |
| 11 | A.11 | 18 | 18 | 1.00 | 20,267,522.78 | 21,111,078.31 | 1.04 |
| 12 | B.1 | 22 | 34 | 1.55 | 42,313,695.00 | 58,646,384.15 | 1.39 |
| 13 | B.2 | 5 | 6 | 1.20 | 19,420,387.66 | 18,739,239.41 | 0.96 |
| 14 | B.3 | 15 | 17 | 1.13 | 14,670,506.00 | 15,811,877.84 | 1.08 |
| 15 | B.4 | 14 | 16 | 1.14 | 18,772,396.15 | 22,234,333.17 | 1.18 |
| 16 | B.5 | 13 | 16 | 1.23 | 19,397,717.04 | 22,687,867.32 | 1.17 |
| 17 | B.6 | 16 | 19 | 1.19 | 27,548,670.90 | 28,453,408.93 | 1.03 |
| 18 | B.7 | 19 | 19 | 1.00 | 48,739,724.74 | 50,467,311.37 | 1.04 |
| 19 | B.8 | 19 | 24 | 1.26 | 36,608,045.94 | 39,958,136.38 | 1.09 |
| 20 | B.9 | 27 | 27 | 1.00 | 42,023,393.72 | 42,549,046.61 | 1.01 |
| 21 | C.1 | 13 | 15 | 1.15 | 135,000,000.00 | 157,112,077.84 | 1.16 |
| 22 | C.2 | 10 | 13 | 1.30 | 65,000,000.00 | 65,000,000.00 | 1.00 |
| 23 | C.3 | 10 | 11 | 1.10 | 16,000,000.00 | 16,708,000.00 | 1.04 |
| 24 | C.4 | 20 | 24 | 1.20 | 186,518,999.02 | 184,491,999.00 | 0.99 |
| 25 | C.5 | 11 | 17 | 1.55 | 17,440,000.00 | 15,450,152.00 | 0.89 |
| 26 | C.6 | 6 | 6 | 1.00 | 1,230,000.00 | 1,079,890.40 | 0.88 |
| 27 | C.7 | 13 | 16 | 1.23 | 52,000,000.00 | 51,999,999.75 | 1.00 |
| 28 | C.8 | 17 | 19 | 1.12 | 39,409,285.00 | 35,880,604.91 | 0.91 |
| No | Investment Symbol | CPI | ACWP/BCWS | SPI | Actual Time/Scheduled Time |
|---|---|---|---|---|---|
| 1 | A.1 | 1.00 | 1.00 | 0.82 | 1.23 |
| 2 | A.2 | 1.00 | 1.00 | 0.90 | 1.14 |
| 3 | A.3 | 1.00 | 1.00 | 0.94 | 1.14 |
| 4 | A.4 | 1.00 | 1.00 | 0.96 | 1.14 |
| 5 | A.5 | 1.00 | 1.00 | 0.89 | 1.07 |
| 6 | A.6 | 0.98 | 1.02 | 0.79 | 1.15 |
| 7 | A.7 | 1.06 | 1.02 | 0.91 | 1.38 |
| 8 | A.8 | 1.00 | 1.00 | 1.00 | 1.00 |
| 9 | A.9 | 0.93 | 1.04 | 0.71 | 1.47 |
| 10 | A.10 | 1.00 | 1.00 | 0.87 | 1.29 |
| 11 | A.11 | 1.00 | 1.04 | 1.04 | 1.00 |
| 12 | B.1 | 1.00 | 1.39 | 0.75 | 1.55 |
| 13 | B.2 | 1.00 | 0.96 | 0.79 | 1.20 |
| 14 | B.3 | 1.05 | 1.08 | 1.03 | 1.13 |
| 15 | B.4 | 1.00 | 1.18 | 1.06 | 1.14 |
| 16 | B.5 | 1.00 | 1.17 | 1.06 | 1.23 |
| 17 | B.6 | 1.00 | 1.03 | 0.98 | 1.19 |
| 18 | B.7 | 1.00 | 1.04 | 1.04 | 1.00 |
| 19 | B.8 | 1.00 | 1.09 | 1.02 | 1.26 |
| 20 | B.9 | 1.00 | 1.01 | 1.01 | 1.00 |
| 21 | C.1 | 0.96 | 1.16 | 1.01 | 1.15 |
| 22 | C.2 | 1.11 | 1.00 | 0.98 | 1.30 |
| 23 | C.3 | 0.99 | 1.04 | 0.99 | 1.10 |
| 24 | C.4 | 1.00 | 0.99 | 0.98 | 1.20 |
| 25 | C.5 | 1.17 | 0.89 | 0.74 | 1.55 |
| 26 | C.6 | 1.03 | 0.88 | 0.91 | 1.00 |
| 27 | C.7 | 1.11 | 1.00 | 0.96 | 1.23 |
| 28 | C.8 | 1.06 | 0.91 | 0.85 | 1.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konior, J. Determining Cost and Time Performance Indexes for Diversified Investment Tasks. Buildings 2022, 12, 1198. https://doi.org/10.3390/buildings12081198
Konior J. Determining Cost and Time Performance Indexes for Diversified Investment Tasks. Buildings. 2022; 12(8):1198. https://doi.org/10.3390/buildings12081198
Chicago/Turabian StyleKonior, Jarosław. 2022. "Determining Cost and Time Performance Indexes for Diversified Investment Tasks" Buildings 12, no. 8: 1198. https://doi.org/10.3390/buildings12081198
APA StyleKonior, J. (2022). Determining Cost and Time Performance Indexes for Diversified Investment Tasks. Buildings, 12(8), 1198. https://doi.org/10.3390/buildings12081198






