Experimental Study on the Shear Behavior of Reinforced Highly Ductile Fiber-Reinforced Concrete Beams with Stirrups
Abstract
:1. Introduction
2. Experimental Programs
2.1. Material Properties
2.1.1. HDC
2.1.2. Concrete and Steel Reinforcement
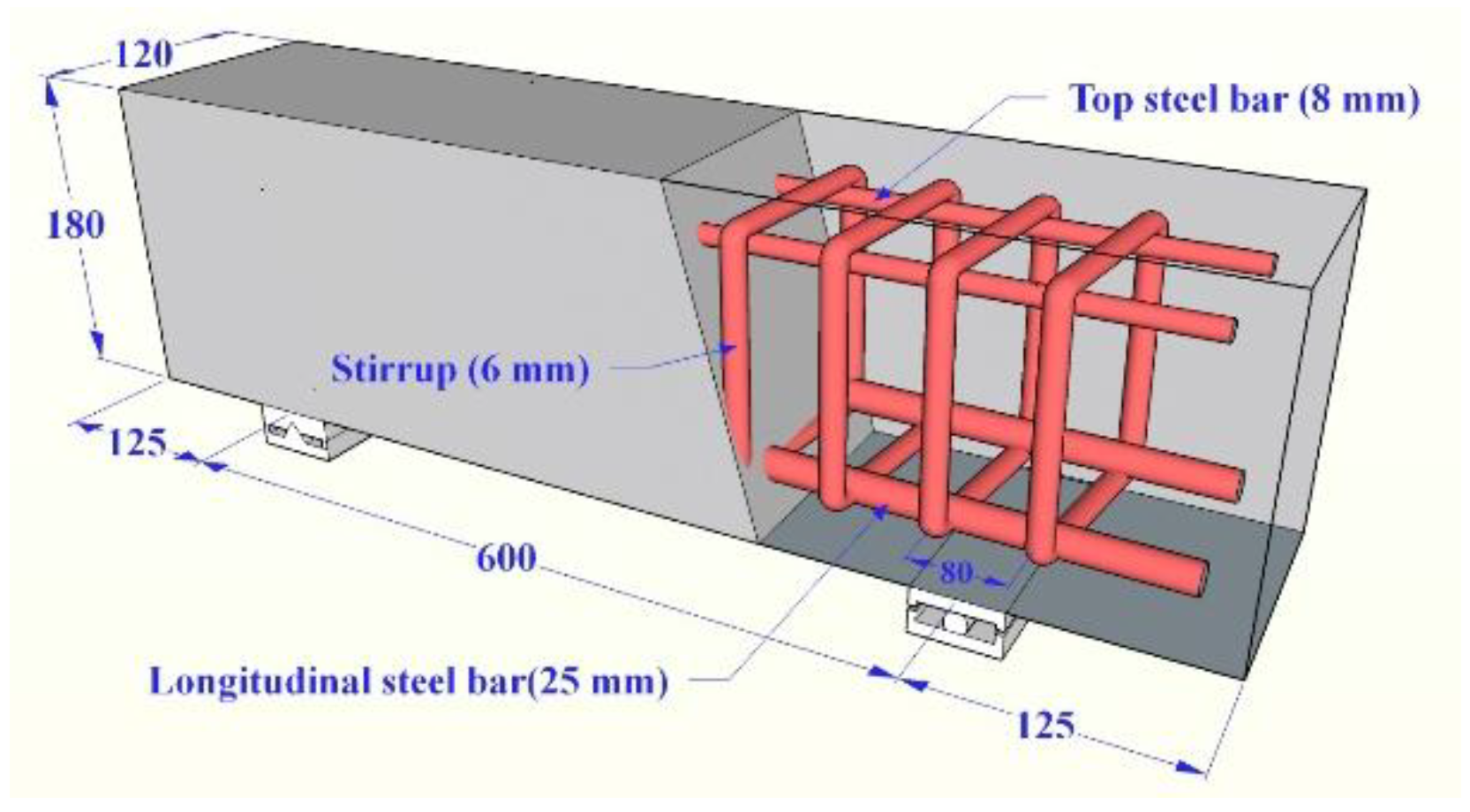
2.2. Beam Specimens
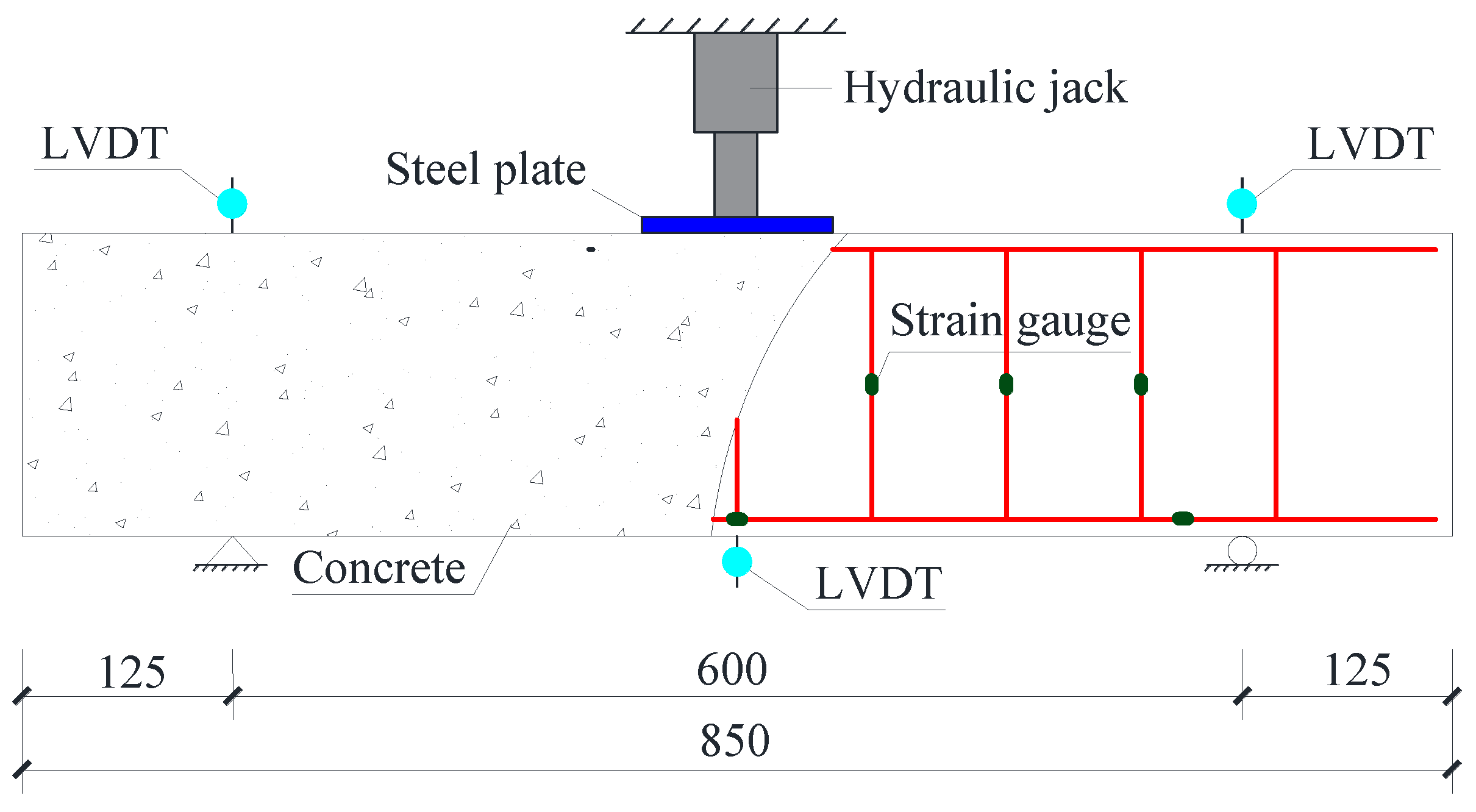
2.3. Test Apparatus
3. Test Results and Discussion
3.1. Crack Patterns and Failure Modes
3.1.1. RC Beam Specimens
- (1)
- Diagonal compression failure
- (2)
- Shear compression failure
3.1.2. RHDC Beam Specimens
- (1)
- Diagonal compression failure
- (2)
- Shear compression failure
- (3)
- Diagonal tension failure
- (4)
- Flexural shear failure
3.2. Discussion of Failure Modes
3.2.1. Diagonal Compression Failure
3.2.2. Shear-Compression Failure
3.2.3. Diagonal Tension Failure
3.2.4. Flexural Shear Failure
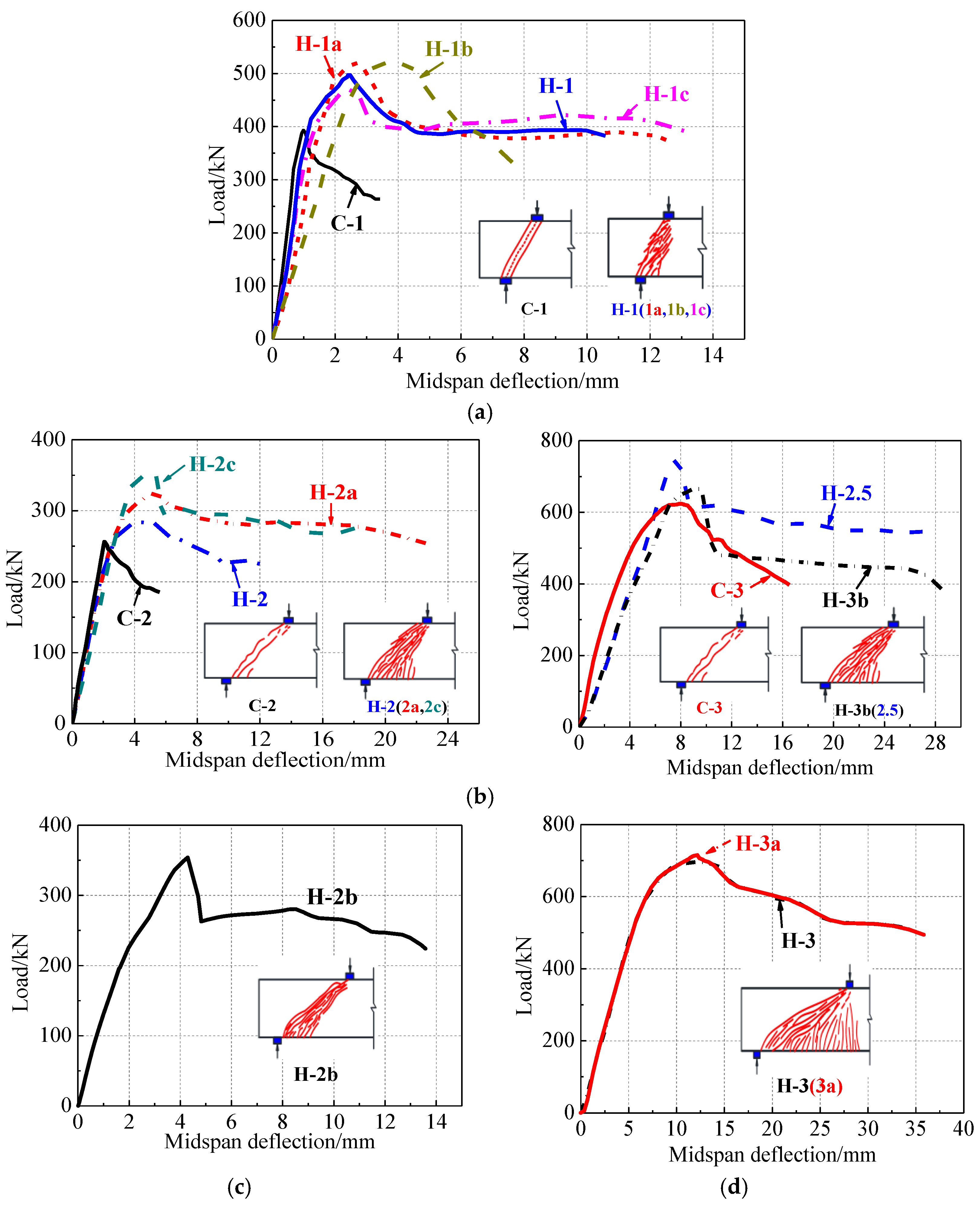
3.3. Load–Deflection Behavior
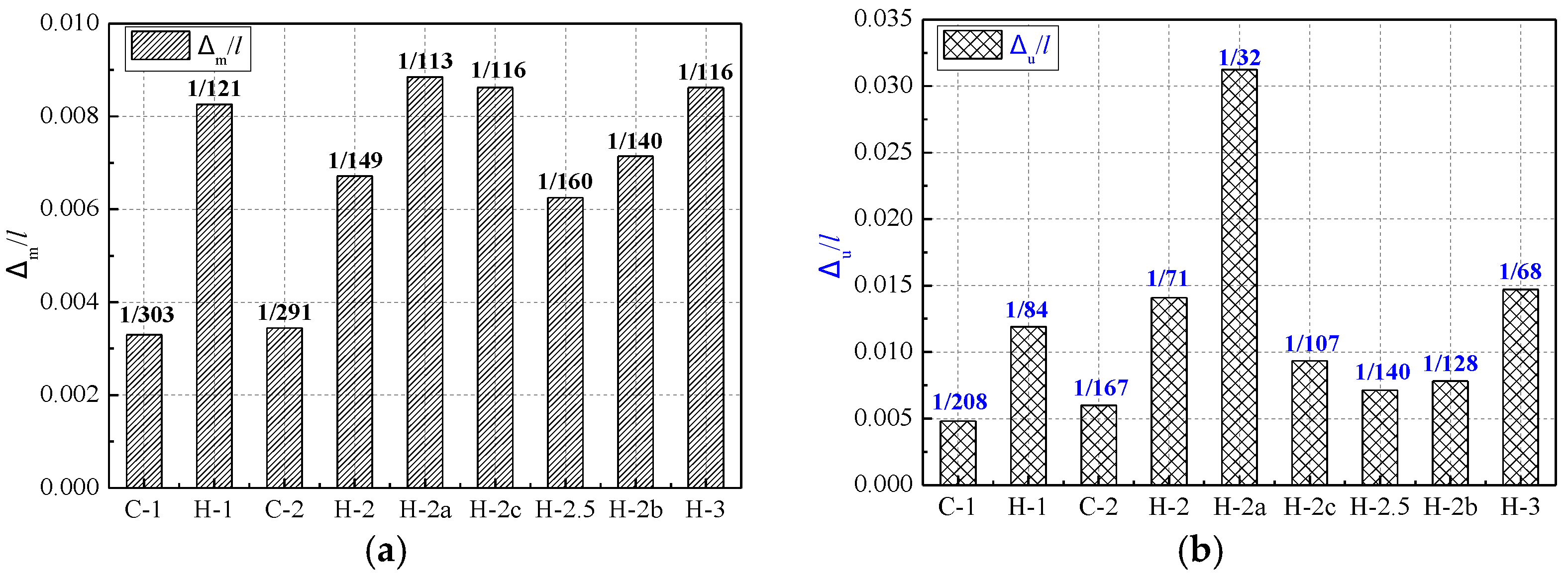
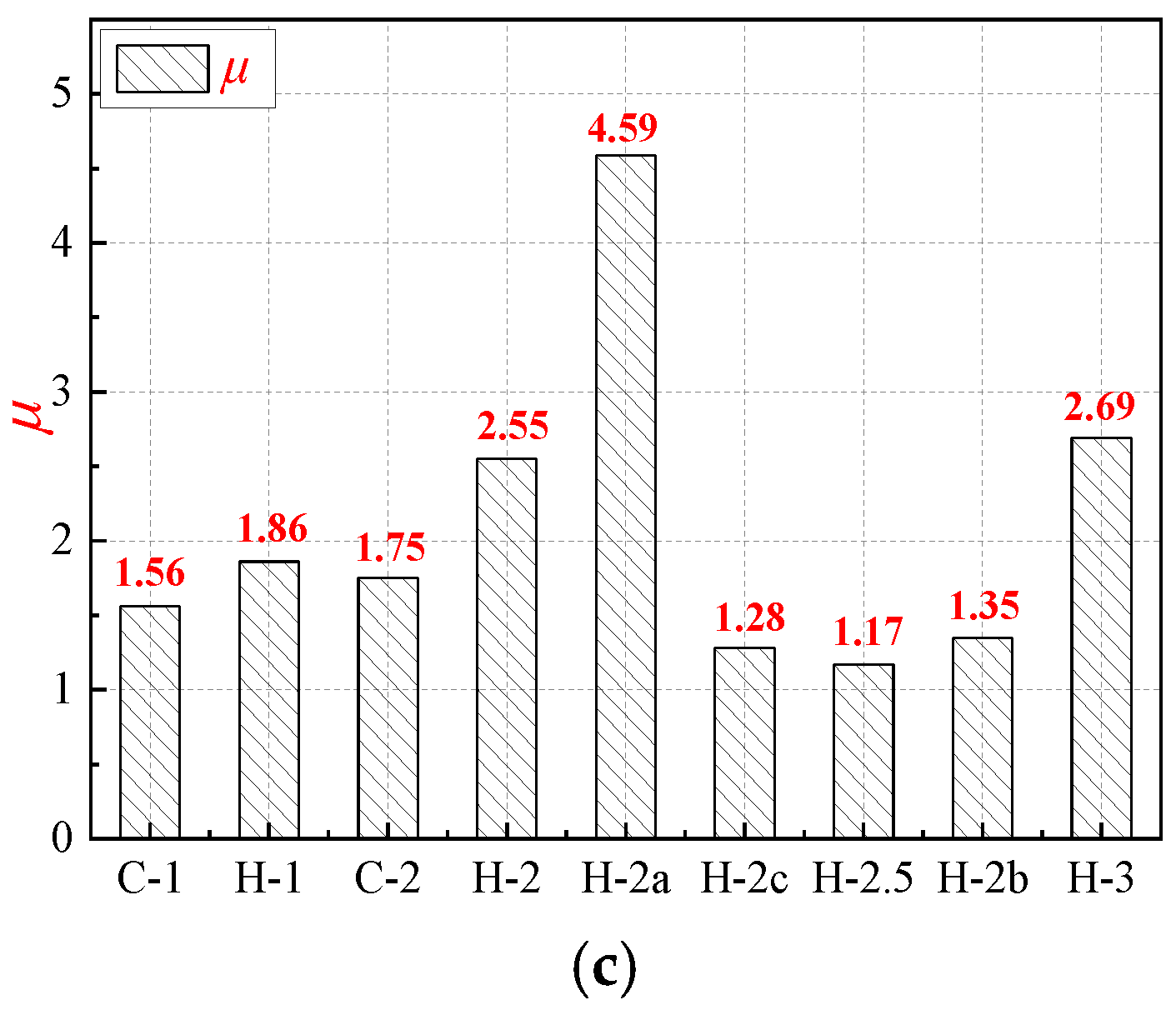
3.4. Deformation Capacity
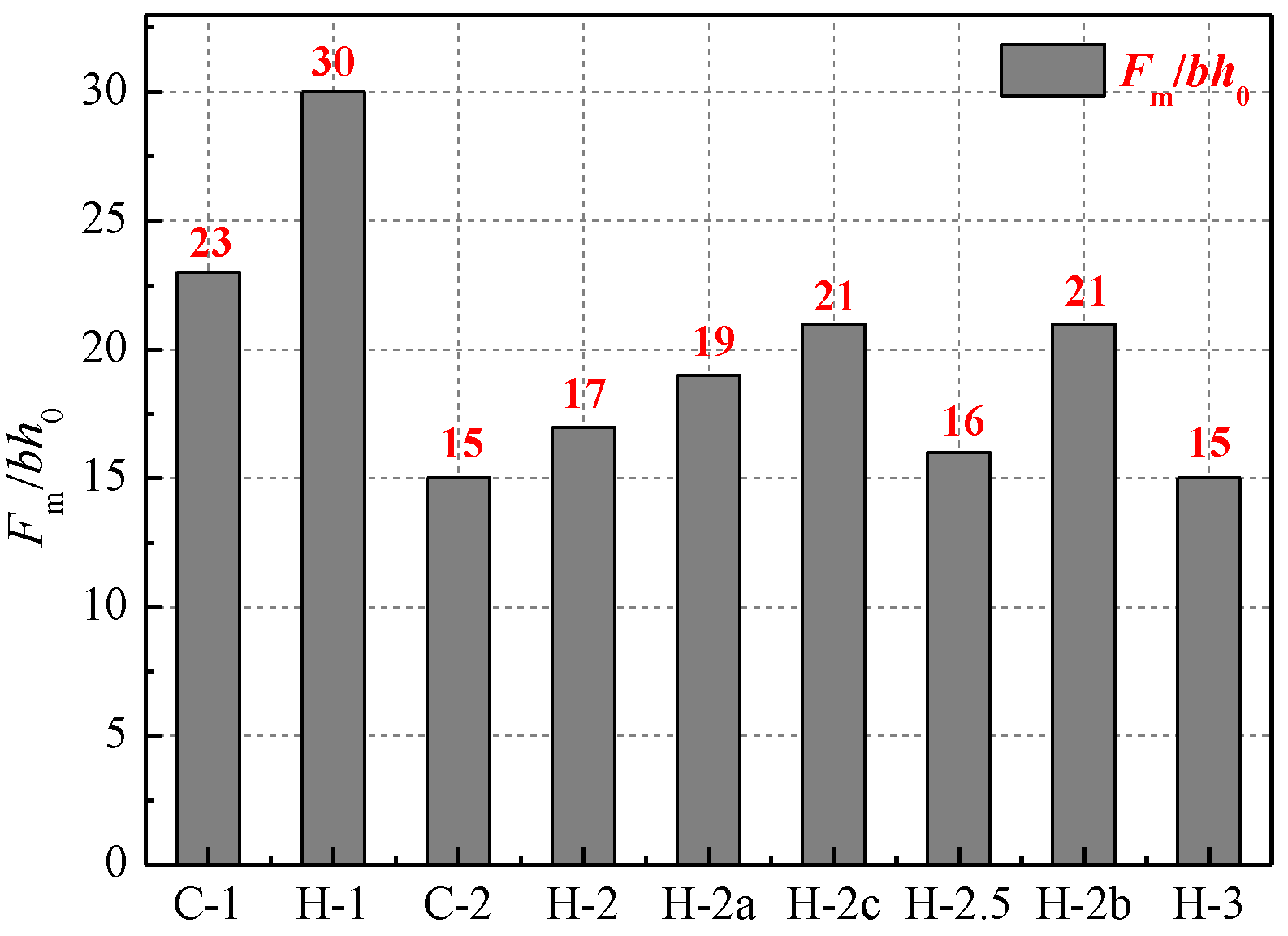
3.5. Shear Strength
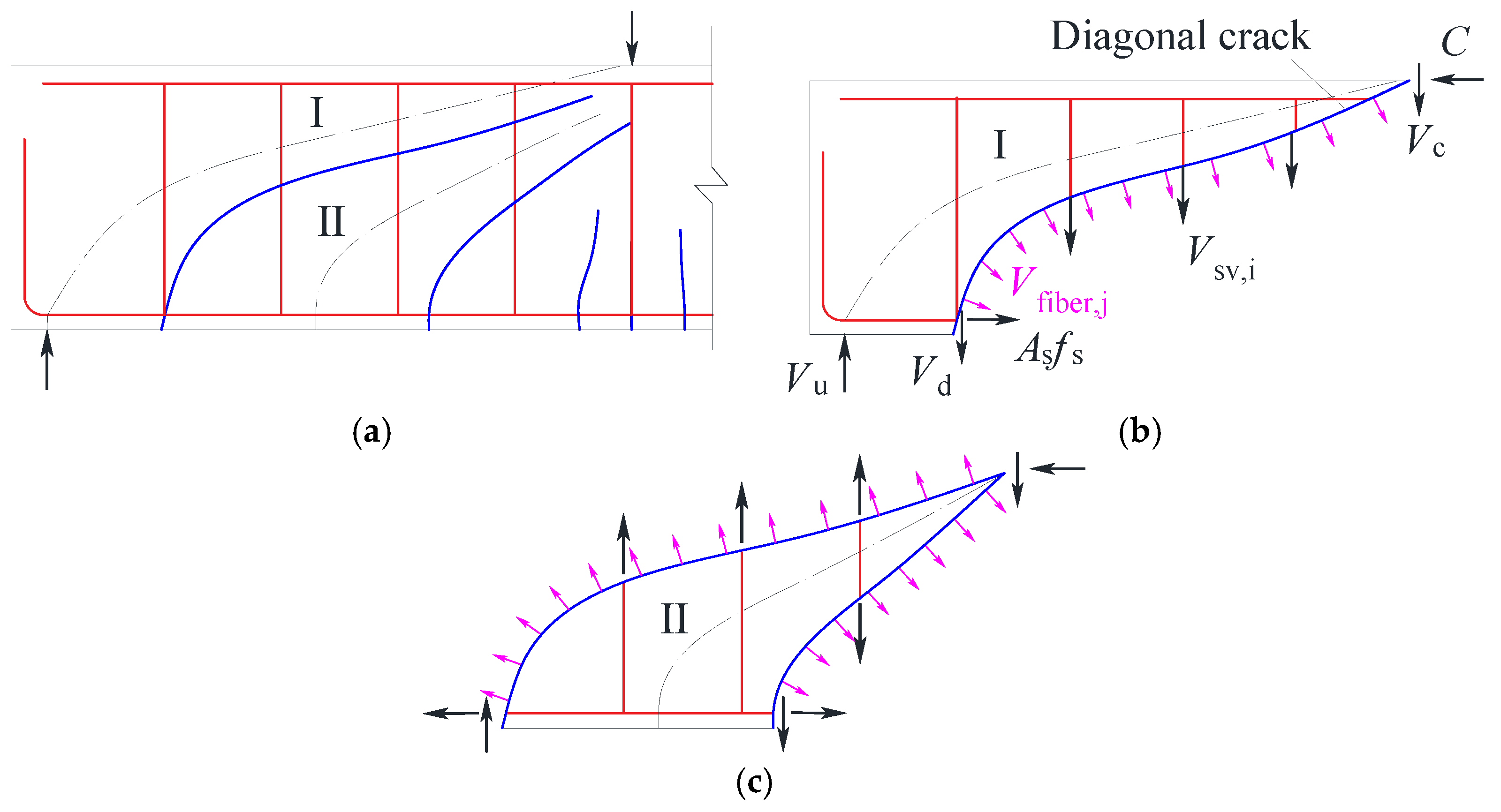
3.5.1. Shear Resistance Mechanisms
3.5.2. Analysis of Shear Strength
3.5.3. Prediction of Shear Strength According to the Code
4. Conclusions
- Unlike RC beams, RHDC beams failed in the shear mode with a gradual decrease in load-carrying capacity and higher residual strength. The modes of failure of RHDC beams included diagonal compression, shear-compression, flexural shear, and diagonal tension failures. When the shear span to effective depth ration was three, some RHDC beams failed in flexural shear mode with favorable ductility.
- Compared with RC beams, RHDC beams exhibited satisfactory integrity without the collapse and peeling-off of HDC. Stable crack propagation and multiple diagonal crack behavior were observed in RHDC beams, indicating that the fiber-bridging effect of HDC effectively restrained the development of shear cracks.
- Improvements in shear strength of RHDC beams ranged from 13.3% to 30.5% compared with RC beams; RHDC beams exhibited higher residual strength and deformation capacity, indicating that HDC significantly improved the brittle shear failure mode. Specimens H-1 and H-2 exhibited the largest improvement in shear strength and displacement ductility factor, respectively, compared with RC beams.
- The results proved that the shear span to effective depth ratio, stirrup ratio, and longitudinal reinforcement ratio of RHDC beams had a great influence on the shear failure modes. The shear strength of RHDC beams decreased as the shear span to effective depth ratio increased. For RHDC beams with the same shear span to effective depth ratio, the shear strength increased with the increase in longitudinal reinforcement ratio and stirrup ratio under shear compression failure.
- The calculated value of shear strength, according to GB 50010-2010, is conservative compared to the experimental values for shear strength of RHDC beams. The effect of material ductility on the shear strength of RHDC beams needs to be studied further, because shear failure modes and shear strength are closely related to the ultimate tensile strain and ultimate compressive strain of HDC.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deng, M.; Han, J.; Liu, H.; Qin, M.; Liang, X. Analysis of Compressive Toughness and Deformability of High Ductile Fiber Reinforced Concrete. Adv. Mater. Sci. Eng. 2015, 3, 1–7. [Google Scholar] [CrossRef]
- Li, V.C.; Wang, S.; Wu, C. Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite (PVA-ECC). ACI Mater. J. 2001, 98, 483–492. [Google Scholar]
- Li, V.C. Engineered cementitious composites (ECC)-a review of the material and its applications. J. Adv. Concr. Technol. 2003, 1, 215–230. [Google Scholar] [CrossRef]
- Mechtcherine, V.; de Andrade Silva, F.; Butler, M.; Zhu, D.; Mobasher, B.; Gao, S.-L.; Mäder, E. Behavior of strain-hardening cement based composites under high strain rates. J. Adv. Concr. Technol. 2011, 9, 51–62. [Google Scholar] [CrossRef]
- Naaman, A.E. High-Performance Construction Materials: Science and Applications; World Scientific Publishing: Singapore, 2008; pp. 91–153. [Google Scholar]
- Reinhardt, H.W.; Naaman, A.E. High Performance Fiber Reinforced Cement Composites (HPFRCC3); RILEM Publications: Mainz, Germany, 1999; pp. 371–385. [Google Scholar]
- Parramontesinos, G.J. High-performance fiber-reinforced cement composites: An alternative for seismic design of structures. ACI Struct. J. 2005, 102, 668–675. [Google Scholar]
- Kobayashi, K.; Ahn, D.L.; Rokugo, K. Effects of crack properties and water-cement ratio on the chloride proofing performance of cracked SHCC suffering from chloride attack. Cem. Concr. Compos. 2016, 69, 18–27. [Google Scholar] [CrossRef]
- Curosu, I.; Mechtcherine, V.; Forni, D.; Cadoni, E. Performance of various strain-hardening cement-based composites (SHCC) subject to uniaxial impact tensile loading. Cem. Concr. Res. 2017, 102, 16–28. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, J.; Leung, C.K.Y. Mechanical Behavior of Fiber-Reinforced Engineered Cementitious Composites in Uniaxial Compression. J. Mater. Civ. Eng. 2014, 17, 04014111. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Yang, J.-M. Effects of stirrup, steel fiber, and beam size on shear behavior of high-strength concrete beams. Cem. Concr. Compos. 2018, 87, 137–148. [Google Scholar] [CrossRef]
- Kachouh, N.; El-Maaddawy, T.; El-Hassan, H.; El-Ariss, B. Shear Behavior of Steel-Fiber-Reinforced Recycled Aggregate Concrete Deep Beams. Buildings 2021, 11, 423. [Google Scholar] [CrossRef]
- Yuan, F.; Pan, J.; Dong, L.; Leung, C.K.Y. Mechanical Behaviors of Steel Reinforced ECC or ECC/Concrete Composite Beams under Reversed Cyclic Loading. J. Mater. Civ. Eng. 2013, 26, 04014047. [Google Scholar] [CrossRef]
- Majdzadeh, F.; Soleimani, S.M.; Banthia, N. Shear strength of reinforced concrete beams with a fiber concrete matrix. Can. J. Civ. Eng. 2006, 33, 726–734. [Google Scholar] [CrossRef]
- Altoubat, S.; Yazdanbakhsh, A.; Rieder, K.-A. Shear behavior of macro-synthetic fiber-reinforced concrete beams without stirrups. ACI Mater. J. 2009, 106, 381–389. [Google Scholar]
- Choi, K.-K.; Park, H.-G.; Wight, J.K. Shear Strength of Steel Fiber-Reinforced Concrete Beams without Web Reinforcement. ACI Struct. J. 2007, 104, 12–21. [Google Scholar] [CrossRef]
- Xu, S.; Hou, L.-J.; Zhang, X.-F. Shear Behavior of Reinforced Ultrahigh Toughness Cementitious Composite Beams without Transverse Reinforcement. J. Mater. Civ. Eng. 2012, 24, 1283–1294. [Google Scholar] [CrossRef]
- Alrefaei, Y.; Rahal, K.; Maalej, M. Shear Strength of Beams Made Using Hybrid Fiber–Engineered Cementitious Composites. J. Struct. Eng. 2018, 144, 04017177. [Google Scholar] [CrossRef]
- Paegle, I.; Fischer, G. Phenomenological interpretation of the shear behavior of reinforced Engineered Cementitious Composite beams. Cem. Concr. Compos. 2016, 73, 213–225. [Google Scholar] [CrossRef]
- Hossain, K.M.A.; Hasib, S.; Manzur, T. Shear behavior of novel hybrid composite beams made of self-consolidating concrete and engineered cementitious composites. Eng. Struc. 2020, 202, 109856. [Google Scholar] [CrossRef]
- Hou, L.-J.; Xu, S.; Zhang, X.-F.; Chen, D. Shear Behaviors of Reinforced Ultrahigh Toughness Cementitious Composite Slender Beams with Stirrups. J. Mater. Civ. Eng. 2014, 26, 466–475. [Google Scholar] [CrossRef]
- Deng, M.; Dai, J.; Lu, H.; Liang, X. Shear Capacity and Failure Behavior of Steel-Reinforced High Ductile Concrete Beams. Adv. Mater. Sci. Eng. 2015, 2015, 1–8. [Google Scholar] [CrossRef]
- Deng, M.; Ma, F.; Ye, W.; Liang, X. Investigation of the shear strength of HDC deep beams based on a modified direct strut-and-tie model. Constr. Build. Mater. 2018, 172, 340–348. [Google Scholar] [CrossRef]
- Deng, M.; Ma, F.; Wang, X.; Lü, H. Investigation on the shear behavior of steel reinforced NC/HDC continuous deep beam. Structures 2019, 23, 20–25. [Google Scholar] [CrossRef]
- Deng, M.; Zhang, Y. Seismic Performance of High-Ductile Fiber-Reinforced Concrete Short Columns. Adv. Civ. Eng. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, M.; Dong, Z. Seismic response and shear mechanism of engineered cementitious composite (ECC) short columns. Eng. Struct. 2019, 192, 296–304. [Google Scholar] [CrossRef]
- Liang, X.; Lu, T. Seismic evaluation of engineered cementitious composites beam-column-slab subassemblies with various column-to-beam flexural strength ratios. Struct. Concr. 2017, 19, 735–746. [Google Scholar] [CrossRef]
- Deng, M.; Ma, F.; Song, S.; Lü, H.; Sun, H. Seismic performance of interior precast concrete beam-column connections with highly ductile fiber-reinforced concrete in the critical cast-in-place regions. Eng. Struct. 2020, 210, 110360. [Google Scholar] [CrossRef]
- Said, S.H.; Razak, H.A. Structural behavior of RC engineered cementitious composite (ECC) exterior beam–column joints under reversed cyclic loading. Constr. Build. Mater. 2016, 107, 226–234. [Google Scholar] [CrossRef]
- Xu, L.; Pan, J.; Lu, C.; Yin, W. Development mechanism of plastic hinge in reinforced engineered cementitious composite beams under monotonic loading. Struct. Concr. 2018, 20, 252–266. [Google Scholar] [CrossRef]
- Said, M.; Montaser, W.; Elgammal, A.S.; Zahir, A.H.; Shaaban, I.G. Shear strength of reinforced mortar beams containing pol-yvinyl alcohol fibre (PVA). Int. J. Civ. Eng. 2021, 19, 1155–1178. [Google Scholar] [CrossRef]
- Meng, D.; Lee, C.K.; Zhang, Y.X. Flexural and shear behaviours of plain and reinforced polyvinyl alcohol-engineered cementitious composite beams. Eng. Struct. 2017, 151, 261–272. [Google Scholar] [CrossRef]
- JGJ 55; Specification for Mix Proportion Design of Ordinary Concrete. Chinese Building Industry Press: Beijing, China, 2011. (In Chinese)
- GB 50010; Code for Design of Concrete Structures. Chinese Standard Press: Beijing, China, 2010. (In Chinese)
- GB/T 50152; Standard for Test Method of Concrete Structures. Chinese Architecture & Building Press: Beijing, China, 2012. (In Chinese)
- Mahin, S.A.; Bertero, V.V. An Evaluation of Inelastic Seismic Design Spectra. J. Struct. Div. 1981, 107, 1777–1795. [Google Scholar] [CrossRef]
- Hosen, A.; Althoey, F.; Jumaat, M.; Alengaram, U.; Sulong, N. Flexural Performance of RC Beams Strengthened with Externally-Side Bonded Reinforcement (E-SBR) Technique Using CFRP Composites. Materials 2021, 14, 2809. [Google Scholar] [CrossRef] [PubMed]
- DBJ61/T112; Technical Specification for Application of High Ductile Concrete. China Building Materials Press: Xi’an, China, 2016.
- JSCE. Recommendations for Design and Construction of High-Performance Fiber-Reinforced Cement Composites with Multiple Fine Cracks (HPFRCC); Japan Society of Civil Engineers: Tokyo, Japan, 2008. [Google Scholar]

| Fiber Type | Length/mm | Tensile Strength/MPa | Elastic Modulus/GPa | Elongation/% | |
|---|---|---|---|---|---|
| PVA | 12 | 39 | 1600 | 40 | 7 |
| Material | Cement | Fly Ash | Sand | Water | PVA Fibers |
|---|---|---|---|---|---|
| HDC | 593 | 593 | 427 | 344 | 26 |
| Chemical Composition | SiO2/% | Al2O3/% | Fe2O3/% | Sum/% | MgO/% | SO3/% | CaO/% |
|---|---|---|---|---|---|---|---|
| Cement | 19.56 | 5.79 | 3.60 | 28.95 | 0.97 | 2.43 | 64.22 |
| Fly ash | 64.59 | 19.92 | 3.49 | 88.00 | 1.31 | 0.40 | 3.83 |
| Type | Diameter (mm) | |||
|---|---|---|---|---|
| HPB300 | 6 | 392 | 581 | 1910 |
| 8 | 355 | 508 | 1775 | |
| HRB400 | 18 | 443 | 595 | 2215 |
| 20 | 423 | 585 | 2115 | |
| 22 | 445 | 613 | 2225 | |
| 25 | 437 | 605 | 2185 |
| Specimen | Mixture Proportions | Length/mm | Stirrups | Stirrup Ratio/% | Longitudinal Steel Bars | Longitudinal Steel Bars Ratio/% | ||
|---|---|---|---|---|---|---|---|---|
| H-1 | H2 | 1 | 120 × 180 | 550 | ϕ6 @ 80 ϕ | 0.59 | 2  20 20 | 2.91 |
| H-1a | H2 | 1 | 120 × 180 | 550 | ϕ6 @ 60 | 0.79 | 2 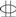 20 20 | 2.91 |
| H-1b | H2 | 1 | 120 × 180 | 550 | ϕ6 @ 120 | 0.40 | 2 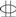 20 20 | 2.91 |
| H-1c | H2 | 1 | 120 × 180 | 550 | ϕ6 @ 80 | 0.59 | 2 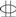 22 22 | 3.52 |
| C-1 | C | 1 | 120 × 180 | 550 | ϕ6 @ 80 | 0.59 | 2 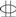 20 20 | 2.91 |
| H-2 | H2 | 2 | 120 × 180 | 850 | ϕ6 @ 80 | 0.59 | 2 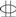 25 25 | 4.55 |
| H-2a | H2 | 2 | 120 × 180 | 850 | ϕ6 @ 60 | 0.79 | 2 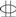 25 25 | 4.55 |
| H-2b | H2 | 2 | 120 × 180 | 850 | ϕ6 @ 120 | 0.40 | 2 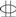 25 25 | 4.55 |
| H-2c | H2 | 2 | 120 × 180 | 850 | ϕ6 @ 80 | 0.59 | 2 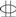 25 + 1 25 + 1 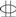 18 18 | 5.73 |
| C-2 | C | 2 | 120 × 180 | 850 | ϕ6 @ 80 | 0.59 | 2 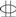 25 25 | 4.55 |
| H-2.5 | H2 | 2.5 | 200 × 300 | 1740 | ϕ8 @ 80 | 0.63 | 6 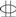 25 25 | 4.91 |
| H-3 | H2 | 3 | 200 × 300 | 1740 | ϕ8 @ 80 | 0.63 | 6 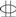 25 25 | 4.91 |
| H-3a | H2 | 3 | 200 × 300 | 1740 | ϕ8 @ 60 | 0.84 | 6  25 25 | 4.91 |
| H-3b | H2 | 3 | 200 × 300 | 1740 | ϕ8 @ 120 | 0.42 | 6  25 25 | 4.91 |
| C-3 | C | 3 | 200 × 300 | 1740 | ϕ8 @ 80 | 0.63 | 6  25 25 | 4.91 |
| Failure Modes | Crack Patterns | Failure Characteristic | Corresponding Beam Specimens |
|---|---|---|---|
| Diagonal compression failure | 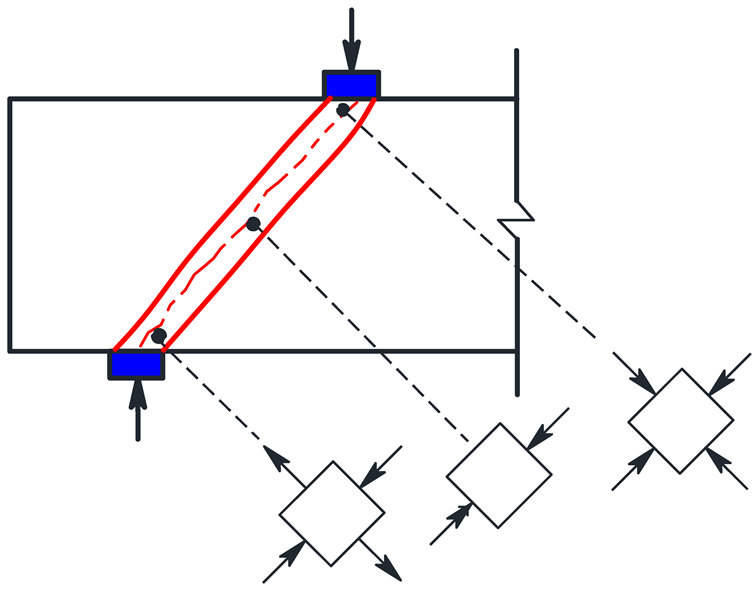 | The stirrups did not attain the yield strength. The shear strength depends mainly on the compressive load-carrying capacity of the diagonal concrete compression struts. The beam failed in shear because of brittle behavior. |  |
| Shear compression failure |  | The stirrups intersecting with diagonal cracks attained the yield strength. Shear strength depends mainly on the shear-compression composite strength of the concrete. The beam failed in brittle mode. |  |
| Failure Modes | Crack Patterns | Failure Characteristic | Corresponding Beam Specimens |
|---|---|---|---|
| Diagonal compression failure |  | The stirrups did not attain the yield strength. Shear strength depends mainly on the compressive load-carrying capacity of the diagonal HDC compression struts. The beam showed high residual strength. |  |
| Shear compression failure | 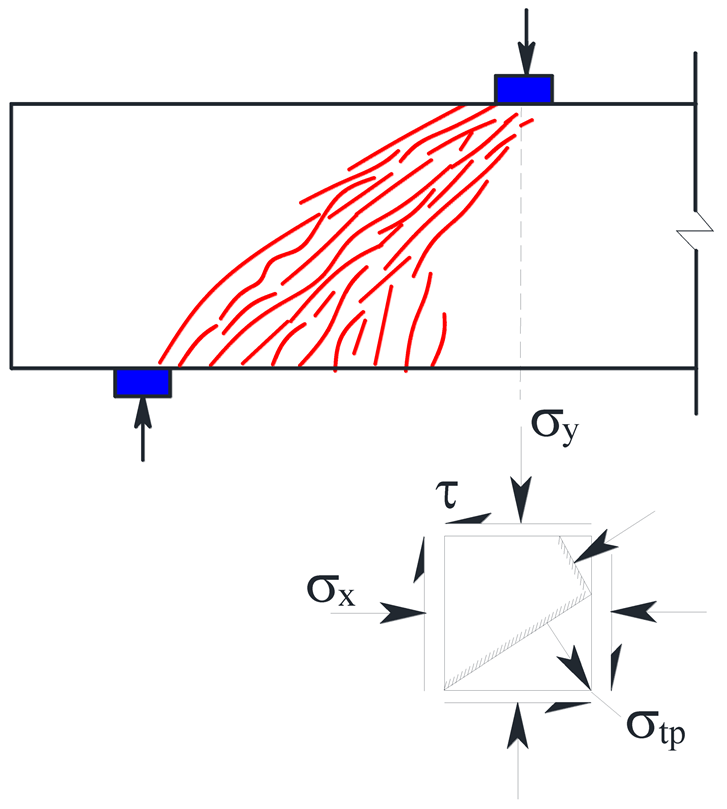 | The stirrups intersecting with the diagonal cracks attained the yield strength at a slower rate. Shear strength depends mainly on the shear-compression composite strength of HDC. The beam has high residual strength. |  |
| Diagonal tension failure |  | The stirrups attained the yield strength. The shear strength depends mainly on the tensile strength and ultimate tensile strain of HDC. |  |
| Flexural shear failure | 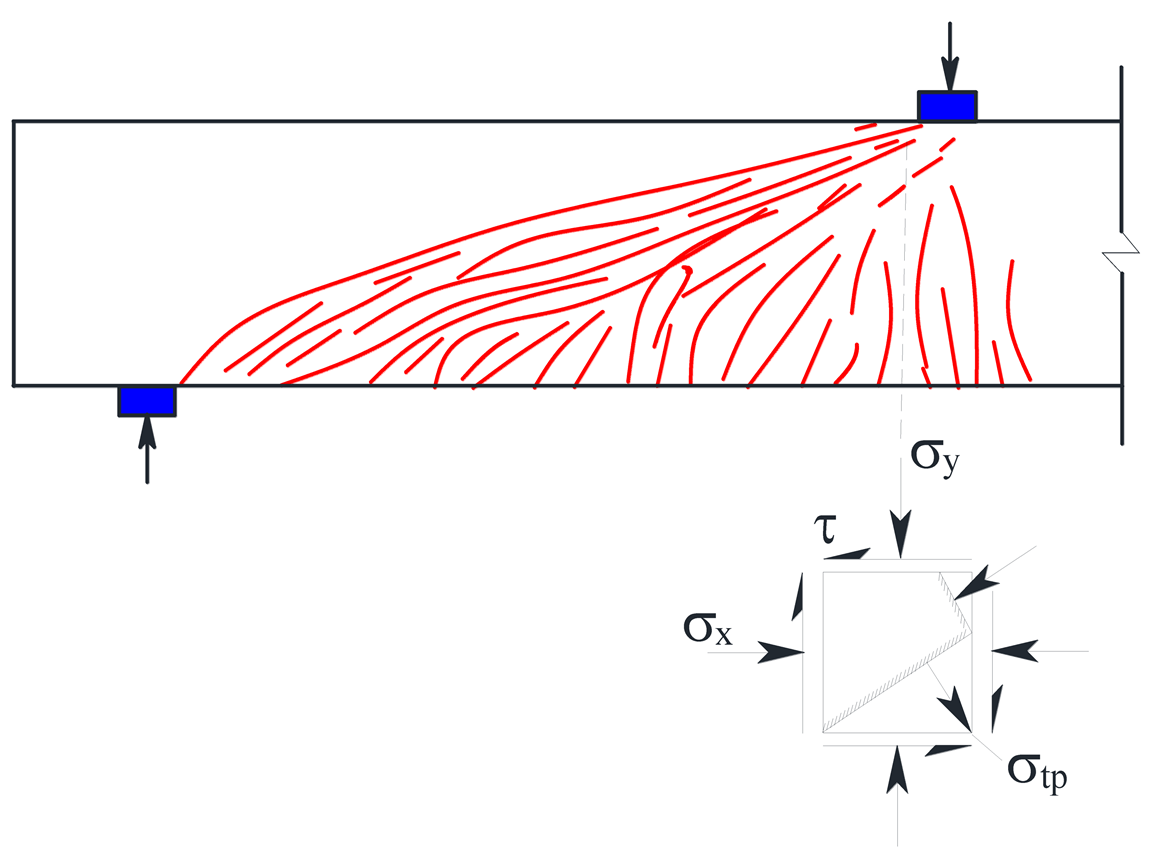 | The stirrup and longitudinal reinforcement yielded successively. The yield point depends on the flexural capacity. The final failure depends mainly on the composite strength of HDC in the shear-compression zone. The beam failed in ductile mode. |  |
| Specimen | Shear cracking | Yield | Major Diagonal Crack | Peak | /mm | Failure Mode | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| /kN | /mm | /kN | /mm | /kN | /mm | /kN | /mm | |||||||||||
| H-1 | 0.97 | 119 | 0.42 | 1/714 | 465 | 1.92 | 1/156 | 473 | 2.12 | 1/142 | 497 | 2.48 | 1/121 | 30 | 3.58 | 1/84 | 1.86 | A |
| H-1a | 0.97 | 140 | 0.66 | 1/455 | 496 | 2.12 | 1/142 | 476 | 3.21 | 1/94 | 520 | 2.7 | 1/111 | 31 | 3.48 | 1/86 | 1.64 | A |
| H-1b | 0.97 | 130 | 0.7 | 1/429 | 515 | 3.39 | 1/89 | 454 | 5.12 | 1/59 | 520 | 3.92 | 1/77 | 31 | 5.41 | 1/55 | 1.60 | A |
| H-1c | 0.98 | 165 | 0.53 | 1/567 | 462 | 2.2 | 1/136 | 434 | 2.86 | 1/105 | 471 | 2.38 | 1/126 | 28 | 3.60 | 1/83 | 1.64 | A |
| C-1 | 0.97 | 149 | 0.4 | 1/750 | 385 | 0.92 | 1/435 | 386 | 0.88 | 1/341 | 393 | 0.99 | 1/303 | 23 | 1.44 | 1/208 | 1.56 | A |
| H-2 | 1.98 | 131 | 1.18 | 1/254 | 275 | 3.3 | 1/182 | 227 | 9.53 | 1/63 | 285 | 4.02 | 1/149 | 17 | 8.43 | 1/71 | 2.55 | B |
| H-2a | 1.98 | 157 | 1.42 | 1/211 | 308 | 4.11 | 1/146 | 282 | 5.38 | 1/112 | 326 | 5.3 | 1/113 | 19 | 18.86 | 1/32 | 4.59 | B |
| H-2b | 1.98 | 91 | 0.66 | 1/455 | 320 | 3.47 | 1/173 | 260 | 10.9 | 1/55 | 354 | 4.29 | 1/140 | 21 | 4.69 | 1/128 | 1.35 | C |
| H-2c | 1.98 | 83 | 0.95 | 1/315 | 346 | 4.38 | 1/137 | 267 | 16.42 | 1/37 | 355 | 5.16 | 1/116 | 21 | 5.62 | 1/107 | 1.28 | B |
| C-2 | 1.98 | 89 | 0.70 | 1/429 | 256 | 2.06 | 1/291 | 192 | 4.61 | 1/131 | 256 | 2.06 | 1/291 | 15 | 3.61 | 1/167 | 1.75 | B |
| H-2.5 | 2.42 | 260 | 2.87 | 1/418 | 738 | 7.33 | 3/491 | 548 | 24.2 | 1/50 | 747 | 7.51 | 1/160 | 16 | 8.56 | 1/140 | 1.17 | B |
| H-3 | 2.90 | 201 | 2.2 | 1/655 | 633 | 7.83 | 1/184 | 564 | 23.91 | 1/60 | 696 | 12.38 | 1/116 | 15 | 21.08 | 1/68 | 2.69 | D |
| H-3a | 2.90 | 250 | 2.64 | 1/545 | 625 | 7.36 | 1/196 | 553 | 24.8 | 1/58 | 711 | 12.18 | 1/118 | 15 | 20.02 | 1/72 | 2.72 | D |
| H-3b | 2.90 | 221 | 2.44 | 1/590 | 635 | 7.5 | 1/192 | 454 | 19.76 | 1/73 | 666 | 9.23 | 1/156 | 14 | 9.91 | 1/145 | 1.32 | B |
| C-3 | 2.90 | 318 | 2.17 | 1/664 | 542 | 4.82 | 1/299 | 486 | 12.35 | 1/117 | 624 | 8.04 | 1/179 | 13 | 10.39 | 1/139 | 2.16 | B |
| Specimen | Failure Mode | |||
|---|---|---|---|---|
| H-1 | 248.500 | 107.120 | 2.320 | A |
| H-1a | 259.750 | 118.346 | 2.195 | A |
| H-1b | 259.900 | 95.902 | 2.710 | A |
| H-1c | 235.450 | 107.124 | 2.198 | A |
| C-1 | 196.500 | 77.766 | 2.527 | A |
| H-2 | 142.550 | 94.881 | 1.502 | B |
| H-2a | 162.800 | 106.103 | 1.534 | B |
| H-2b | 176.950 | 83.659 | 2.115 | C |
| H-2c | 177.500 | 94.881 | 1.871 | B |
| C-2 | 128.000 | 70.416 | 1.818 | B |
| H-2.5 | 373.480 | 235.365 | 1.587 | B |
| H-3 | 348.150 | 217.875 | 1.598 | D |
| H-3a | 357.480 | 249.690 | 1.432 | D |
| H-3b | 333.230 | 186.060 | 1.791 | B |
| C-3 | 312.000 | 168.945 | 1.847 | B |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Deng, M.; Yang, J.; Zhang, Y. Experimental Study on the Shear Behavior of Reinforced Highly Ductile Fiber-Reinforced Concrete Beams with Stirrups. Buildings 2022, 12, 1264. https://doi.org/10.3390/buildings12081264
Zhang M, Deng M, Yang J, Zhang Y. Experimental Study on the Shear Behavior of Reinforced Highly Ductile Fiber-Reinforced Concrete Beams with Stirrups. Buildings. 2022; 12(8):1264. https://doi.org/10.3390/buildings12081264
Chicago/Turabian StyleZhang, Min, Mingke Deng, Jiasheng Yang, and Yangxi Zhang. 2022. "Experimental Study on the Shear Behavior of Reinforced Highly Ductile Fiber-Reinforced Concrete Beams with Stirrups" Buildings 12, no. 8: 1264. https://doi.org/10.3390/buildings12081264
APA StyleZhang, M., Deng, M., Yang, J., & Zhang, Y. (2022). Experimental Study on the Shear Behavior of Reinforced Highly Ductile Fiber-Reinforced Concrete Beams with Stirrups. Buildings, 12(8), 1264. https://doi.org/10.3390/buildings12081264





