Damage Mechanism and Modeling of Concrete in Freeze–Thaw Cycles: A Review
Abstract
:1. Introduction
2. Damage Mechanism
2.1. Deterioration Theory
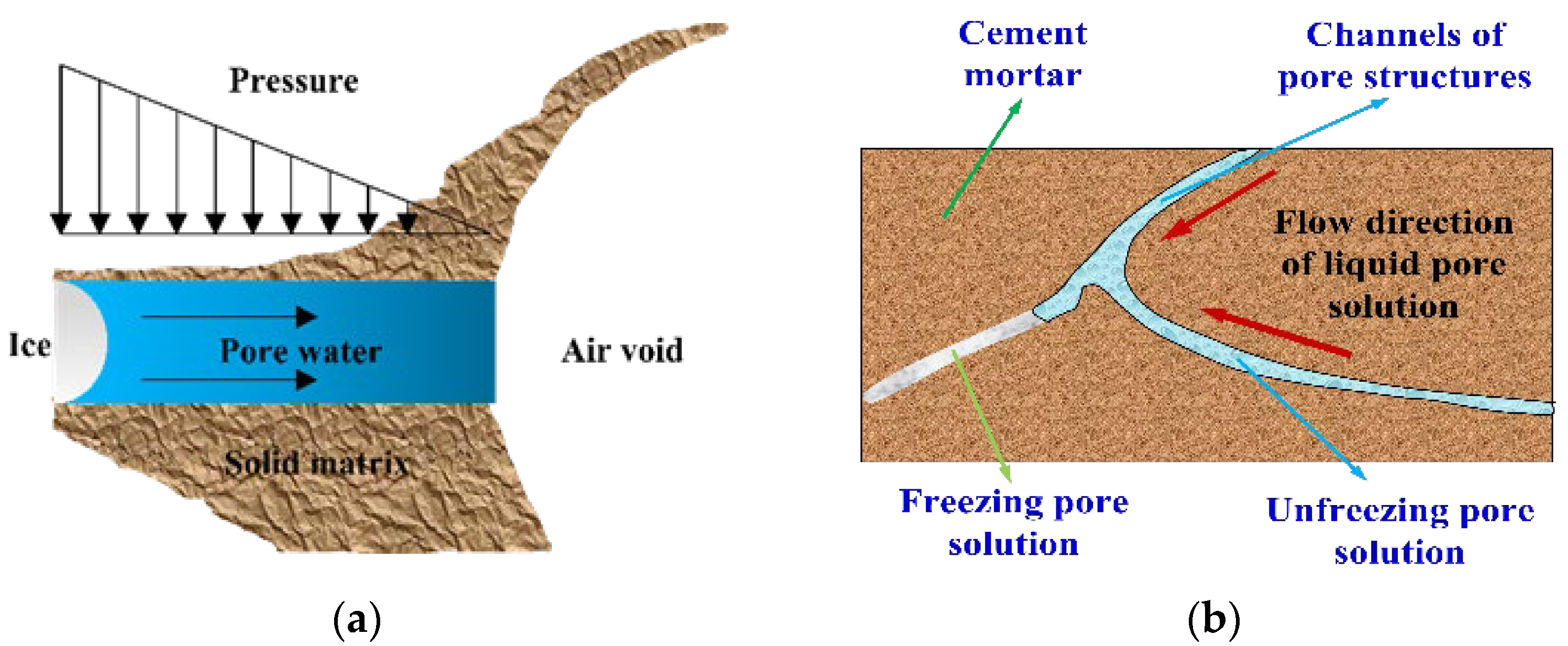
2.1.1. Hydraulic Pressure Theory and Osmotic Pressure Theory
2.1.2. Critical Saturation Theory
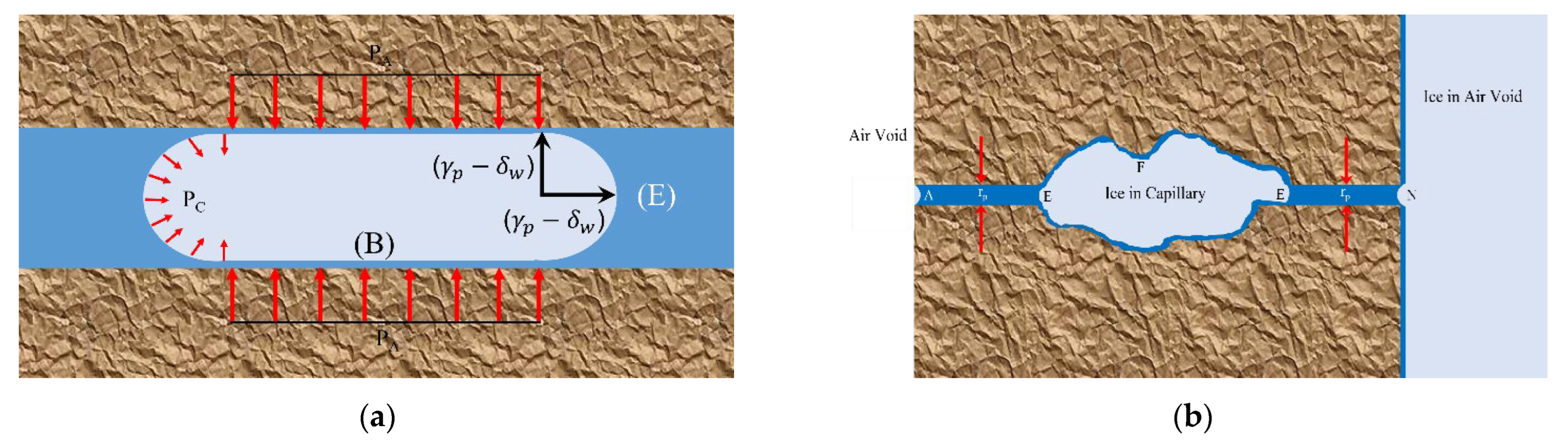
2.1.3. Crystallization Pressure Theory
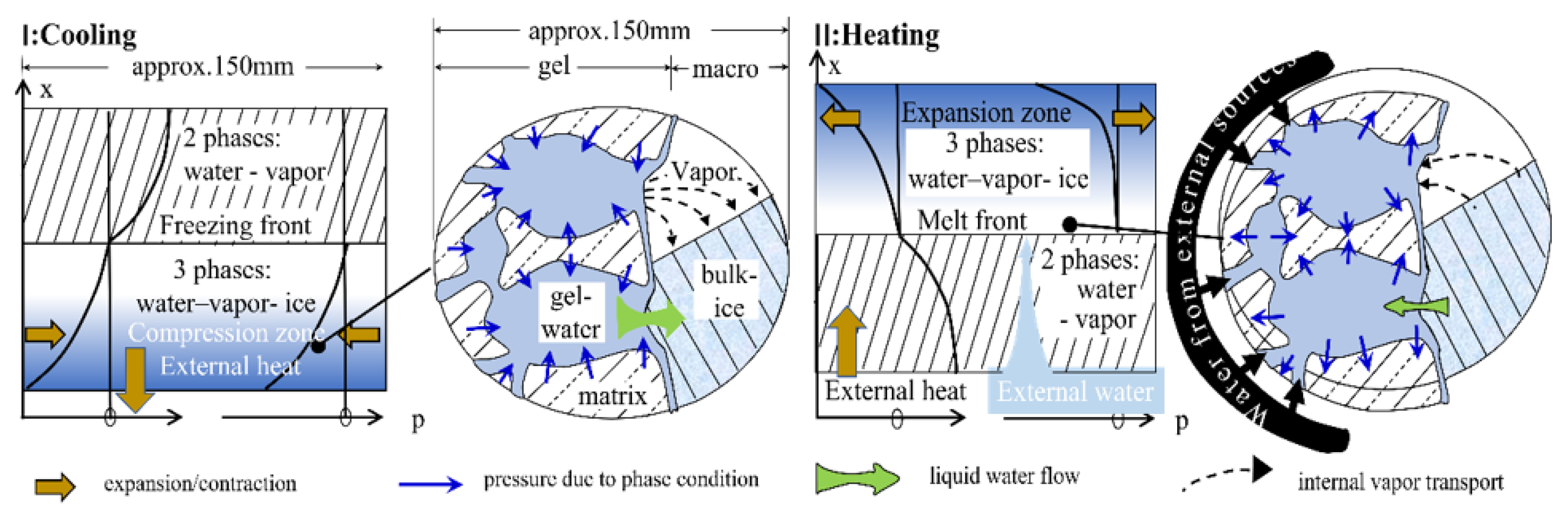
2.1.4. Micro-Ice Lens Theory
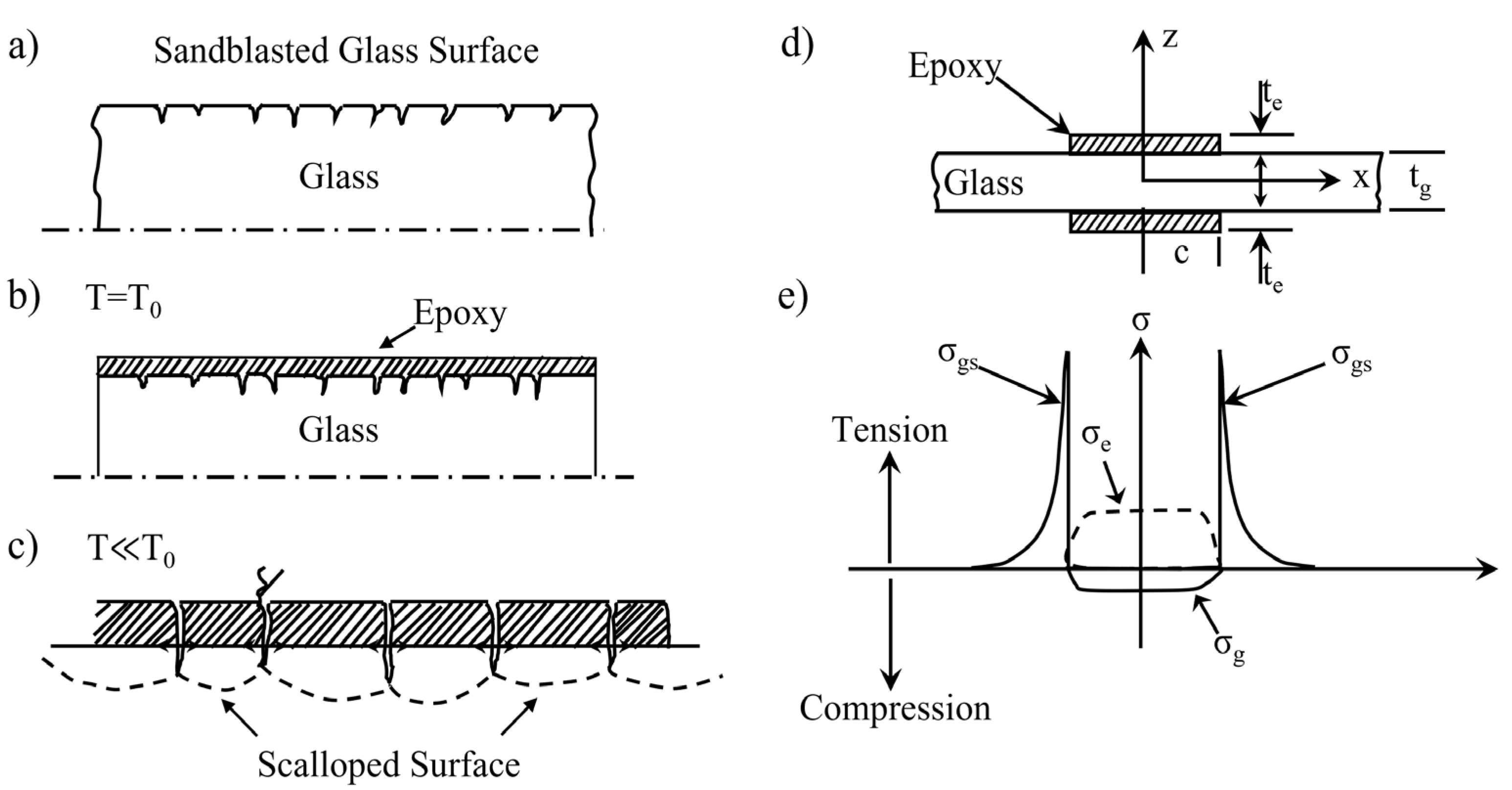
2.1.5. Glue Spall Theory
2.1.6. Theory of Unsaturated Porous Elasticity
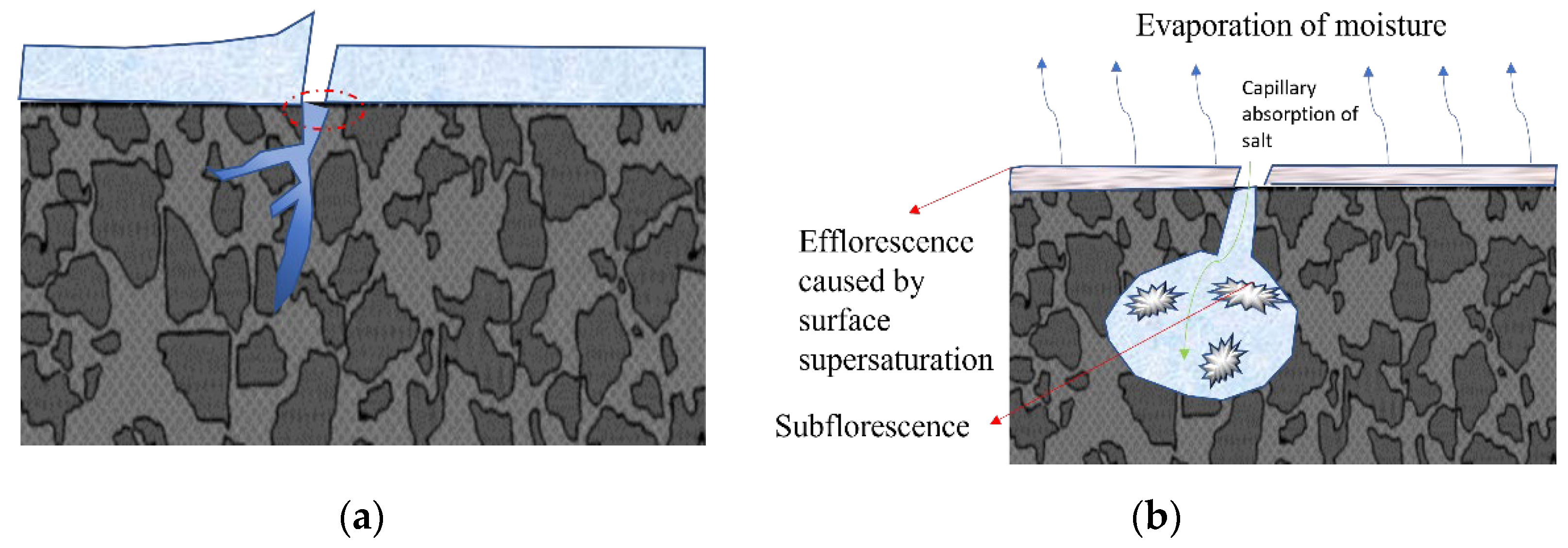
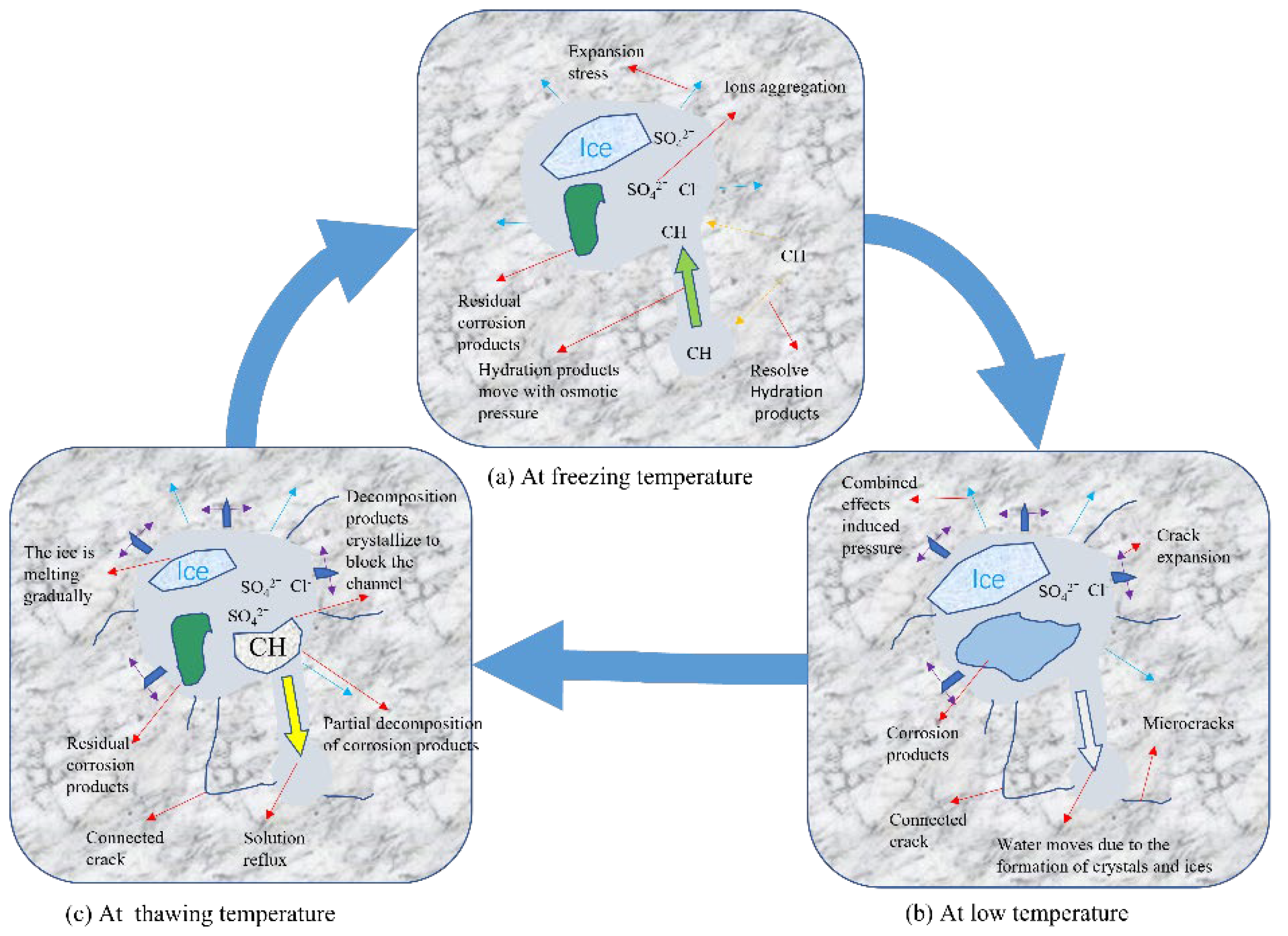
2.2. Salt-Freeze Coupling
2.2.1. Mechanism of Chloride-F–T Damage
2.2.2. Mechanism of Sulfate-F–T Damage
2.3. Microstructure Testing
2.3.1. SEM Observation
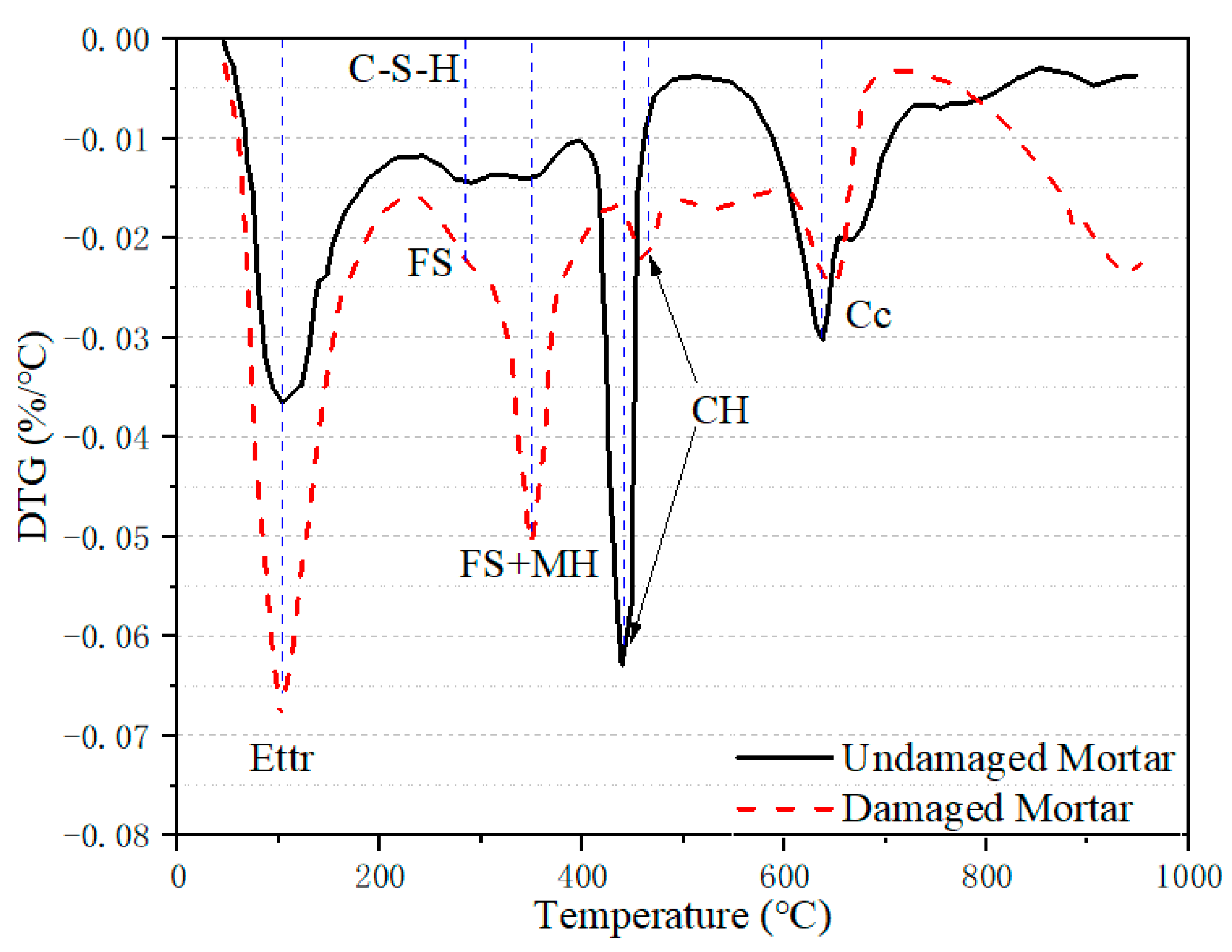
2.3.2. Composition
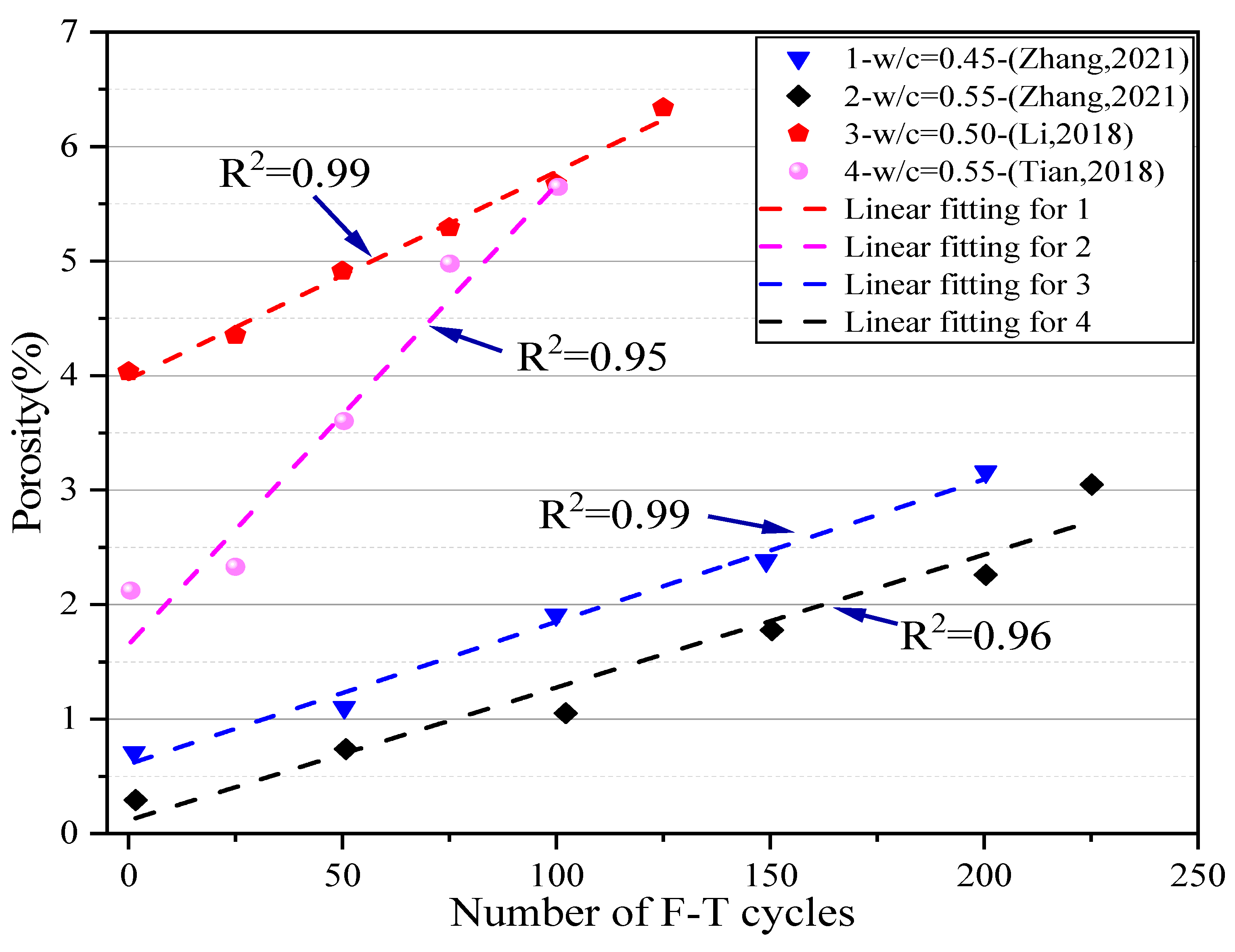
2.3.3. Pore Structure
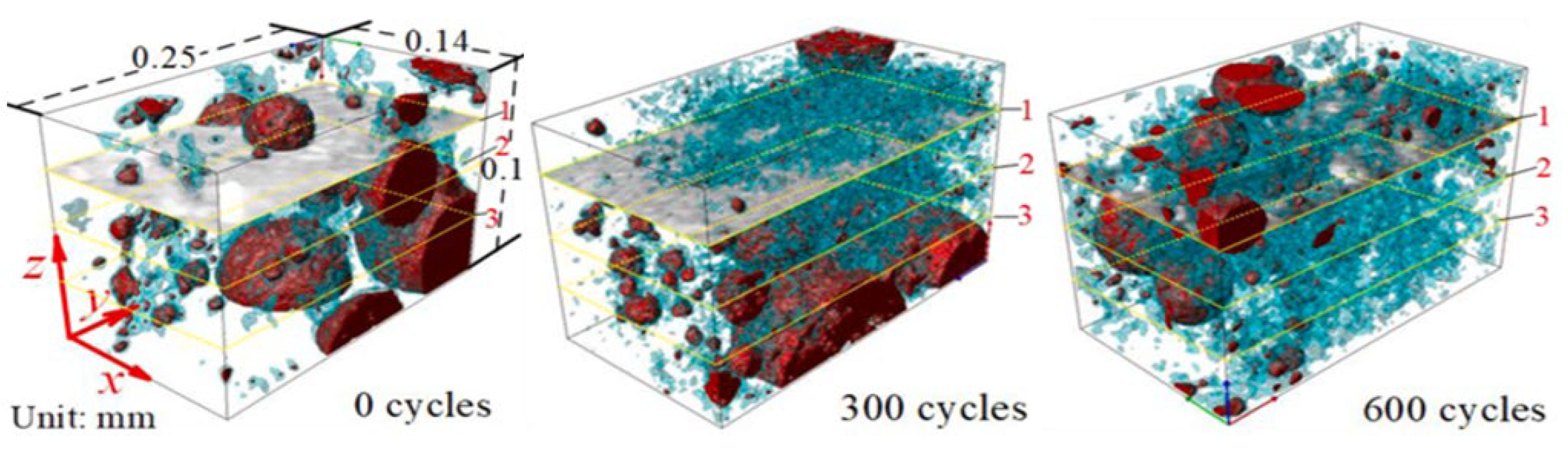
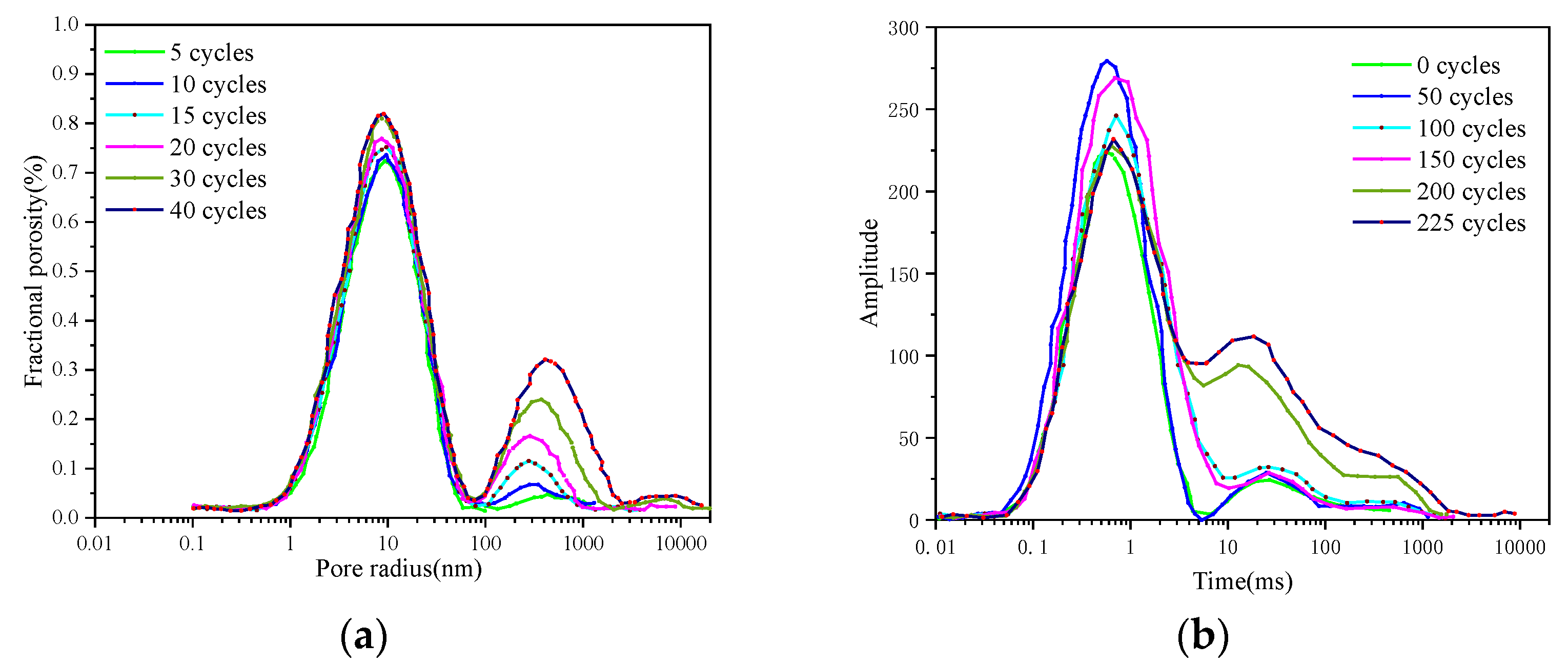
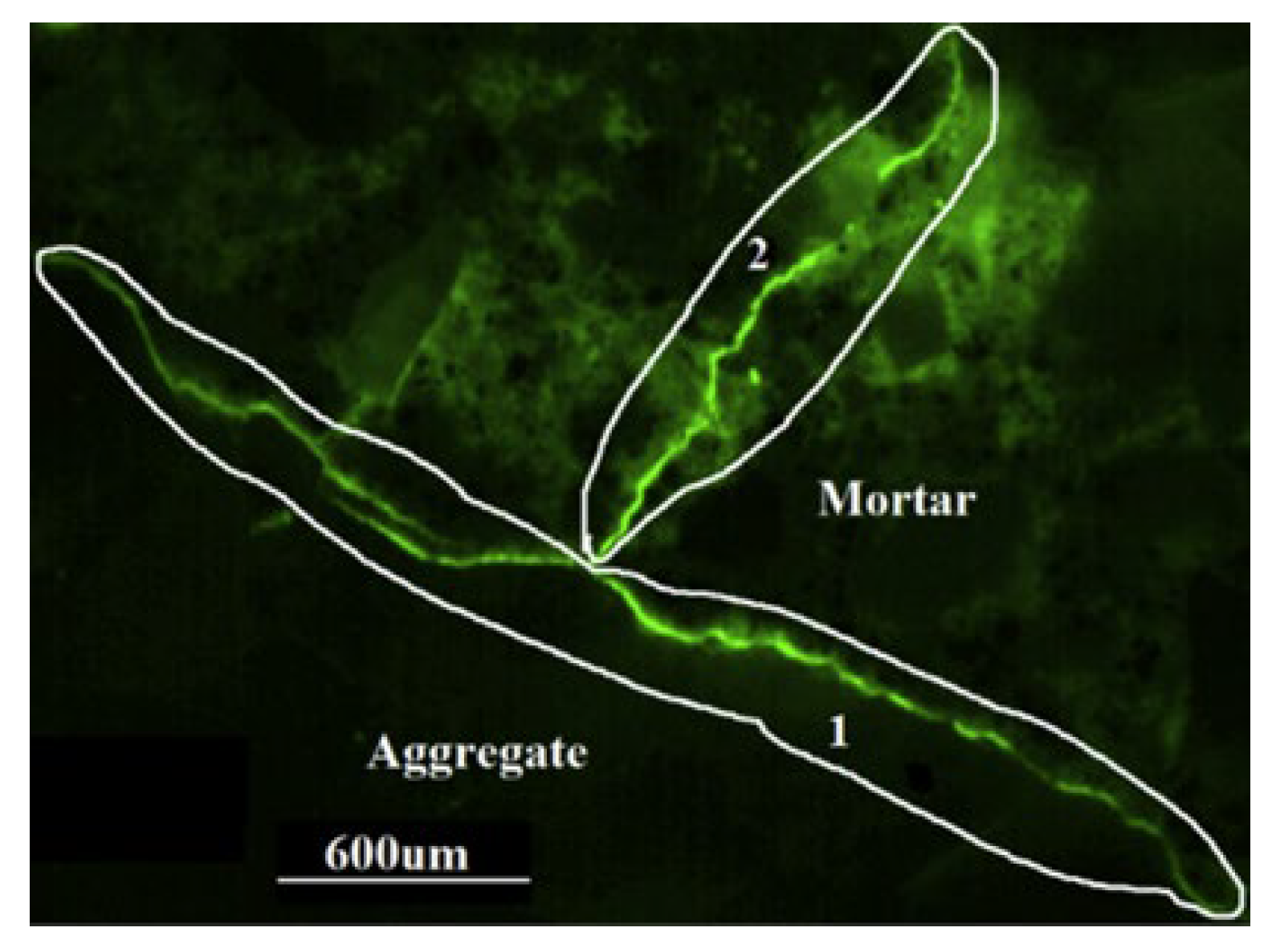
2.3.4. Microcracks
2.3.5. Interfacial Transition Zone
3. Modeling for Concrete in F–T Environments
3.1. Damage Model for RDEM
3.2. Damage Layer Thickness Model
3.3. Damage Model for Bulk Resistivity
3.4. Damage Model for Microstructure
4. Summary
- (1)
- From the concrete F–T deterioration theory, it can be revealed that the water phase transition during the F–T cycles is the main cause of concrete F–T damage;
- (2)
- Under the condition of a salt-freezing coupling environment, the F–T damage of concrete is accelerated by salt crystallization expansion and salt solution erosion. The effects of various salt solutions on concrete F–T cycle damage are different because of the inconsistent effects of salt solutions on the pores and hydration products;
- (3)
- During the F–T cycles, the deterioration of the concrete microstructure is a synthetic result. The microstructure test results show that the porosity increases, the microcracks expand, and the ITZ widens during the F–T cycles. The loss of hydration products and salt crystal expansion during salt freezing was determined by a phase analysis;
- (4)
- The damage model for the concrete microstructure in the F–T cycle essentially reveals the damage mechanism, and the deterioration model for the pore structure and the microcrack growth model were established to reflect the F–T damage process.
5. Recommendations for Future Research
- (1)
- The evolution of pore damage has always been the focus of the analysis of the concrete F–T cycle mechanism. However, the applicable conditions for different mechanisms are diverse, and the theoretical model of unified coordination among pore structure damage, water-phase transformation, matrix deformation, and damage variables need to be further explored.
- (2)
- Pore structure degradation and microcrack growth have been used to model F–T damage; however, the influence of erosion effects on hydration product components and the deterioration of the ITZ are not involved in the F–T damage model, and the response of the composition index and ITZ parameters in the damage model is novel and creative. Further research should be conducted in this area.
- (3)
- There are many detection techniques used to establish F–T damage models, but some are superficial for characterizing the F–T damage of concrete. In the wake of developments in science and technology, the emergence of advanced detection methods, such as acoustic emission and optical fiber monitoring, has provided a new field of vision for the study of concrete F–T damage. It is necessary to carry out related research to further understand freeze–thaw fatigue damage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mehta, P.K. Concrete durability-fifty years progress. In Proceedings of the 2nd International Conference on Concrete Durability, Montreal, QC, Canada, 1 September 1991; p. 132. [Google Scholar]
- Wenchen, M. Simulate Initiation and Formation of Cracks and Potholes. Master’s Thesis, Northeastern University, Boston, MA, USA, 2016. [Google Scholar]
- Qiu, J.S.; Zhou, Y.X.; Vatin, N.I.; Guan, X.; Sultanov, S.; Khemarak, K. Damage constitutive model of coal gangue concrete under freeze–thaw cycles. Constr. Build. Mater. 2020, 264, 120720. [Google Scholar] [CrossRef]
- Wang, B.; Wang, F.; Wang, Q. Damage constitutive models of concrete under the coupling action of freeze–thaw cycles and load based on Lemaitre assumption. Constr. Build. Mater. 2018, 173, 332–341. [Google Scholar] [CrossRef]
- Powers, T.C. A working hypothesis for further studies of frost resistance of concrete. J. Proc. 1945, 41, 245–272. [Google Scholar]
- Powers, T.C.; Helmuth, R.A. Theory of Volume Changes in Hardened Portland-Cement Paste During Freezing. In Proceedings of the Thirty-Second Annual Meeting of the Highway Research Board, Washington, DC, USA, 13–16 January 1953; pp. 285–297. [Google Scholar]
- Powers, T.C.; Willis, T.F. The Air Requirement of Frost Resistant Concrete. Highw. Res. Board Proc. 1950, 29, 184–211. [Google Scholar]
- Fagerlund, G. Critical Degrees of Saturation at Freezing of Porous and Brittle Materials, Report 34; Division of Building Technology, Lund Institute of Technology: Lund, Sweden, 1972; p. 408. [Google Scholar]
- Scherer, G.W. Crystallization in pores. Cement. Concr. Res. 1999, 29, 1347–1358. [Google Scholar] [CrossRef]
- Setzer, M.J. Micro-ice-lens formation in porous solid. J. Colloid. Interf. Sci. 2001, 243, 193–201. [Google Scholar] [CrossRef]
- Setzer, M.J. Mechanical stability criterion, triple-phase condition, and pressure differences of matter condensed in a porous matrix. J. Colloid. Interf. Sci. 2001, 235, 170–182. [Google Scholar] [CrossRef]
- Valenza, J.J.; Scherer, G.W. A review of salt scaling: I. Phenomenology. Cem. Concr. Res. 2007, 37, 1007–1021. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics of freezing materials. J. Mech. Phys. Solids 2005, 53, 1689–1718. [Google Scholar] [CrossRef]
- Liu, L.; Shen, D.; Chen, H.; Sun, W.; Qian, Z.; Zhao, H.; Jiang, J. Analysis of damage development in cement paste due to ice nucleation at different temperatures. Cem. Concr. Comp. 2014, 53, 1–9. [Google Scholar] [CrossRef]
- Gong, F.; Jacobsen, S. Modeling of water transport in highly saturated concrete with wet surface during freeze/thaw. Cem. Concr. Res. 2019, 115, 294–307. [Google Scholar] [CrossRef]
- Eriksson, D.; Wahlbom, D.; Malm, R.; Fridh, K. Hygro-thermo-mechanical modeling of partially saturated air-entrained concrete containing dissolved salt and exposed to freeze–thaw cycles. Cem. Concr. Res. 2021, 141, 106314. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.H.; Ueda, T.; Zhang, D.W.; Deng, J. Meso-scale mechanical deterioration of mortar subjected to freeze thaw cycles and sodium chloride attack. Cem. Concr. Comp. 2021, 117, 103906. [Google Scholar] [CrossRef]
- Mesbah, A.; Francois, M.; Cau-dit-Coumes, C.; Frizon, F.; Filinchuk, Y.; Leroux, F.; Ravaux, J.; Renaudin, G. Crystal structure of Kuzel’s salt 3CaO center dot Al2O3 center dot 1/2CaSO4center dot 1/2CaCl2center dot 11H(2)O determined by synchrotron powder diffraction. Cem. Concr. Res. 2011, 41, 504–509. [Google Scholar] [CrossRef]
- Wenchen, M. Behavior of Aged Reinforced Concrete Columns under High Sustained Concentric and Eccentric Loads. Ph.D. Thesis, University of Nevada, Las Vegas, NV, USA, 2021. [Google Scholar]
- Li, Y.; Li, Y.Q.; Guan, Z.Z.; Ding, Q.J. Elastic modulus damage model of cement mortar under salt freezing circumstance based on X-ray CT scanning. Constr. Build. Mater. 2018, 191, 1201–1209. [Google Scholar] [CrossRef]
- Gonzalez, D.C.; Mena, A.; Minguez, J.; Vicente, M.A. Influence of air-entraining agent and freeze–thaw action on pore structure in high-strength concrete by using CT-Scan technology. Cold Reg. Sci. Technol. 2021, 192, 103397. [Google Scholar] [CrossRef]
- Sokhansefat, G.; Moradian, M.; Finnell, M.; Behravan, A.; Ley, M.T.; Lucero, C.; Weiss, J. Using X-ray computed tomography to investigate mortar subjected to freeze–thaw cycles. Cem. Concr. Comp. 2020, 108, 103520. [Google Scholar] [CrossRef]
- Xu, F.; Yang, Z.Q.; Liu, W.Q.; Wang, S.G.; Zhang, H.G. Experimental investigation on the effect of sulfate attack on chloride diffusivity of cracked concrete subjected to composite solution. Constr. Build. Mater. 2020, 237, 117643. [Google Scholar] [CrossRef]
- Li, Y.; Wang, R.J.; Li, S.Y.; Zhao, Y.; Qin, Y. Resistance of recycled aggregate concrete containing low- and high-volume fly ash against the combined action of freeze–thaw cycles and sulfate attack. Constr. Build. Mater. 2018, 166, 23–34. [Google Scholar] [CrossRef]
- Jiang, L.; Niu, D.T.; Yuan, L.D.; Fei, Q.N. Durability of concrete under sulfate attack exposed to freeze–thaw cycles. Cold Reg. Sci. Technol. 2015, 112, 112–117. [Google Scholar] [CrossRef]
- Nili, M.; Ramezanianpour, A.A.; Sobhani, J. Evaluation of the effects of silica fume and air-entrainment on deicer salt scaling resistance of concrete pavements: Microstructural study and modeling. Constr. Build. Mater. 2021, 308, 124972. [Google Scholar] [CrossRef]
- Qiao, C.; Hosseinzadeh, N.; Suraneni, P.; Wei, S.; Rothstein, D. Petrographically quantifying the damage to field and lab-cast mortars subject to freeze–thaw cycles and deicer application. J. Infrastruct. Preserv. Resil. 2021, 2, 9. [Google Scholar] [CrossRef]
- Niu, D.T.; Jiang, L.; Fei, Q.N. Deterioration Mechanism of Sulfate Attack on Concrete under Freeze-thaw Cycles. J. Wuhan Univ. Technol. 2013, 28, 1172–1176. [Google Scholar] [CrossRef]
- Wang, D.Z.; Zhou, X.M.; Meng, Y.F.; Chen, Z. Durability of concrete containing fly ash and silica fume against combined freezing-thawing and sulfate attack. Constr. Build. Mater. 2017, 147, 398–406. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Liu, Z.; Fu, K.; Li, Q.M.; Wang, Y.C. Experimental studies on the chloride ion permeability of concrete considering the effect of freeze–thaw damage. Constr. Build. Mater. 2020, 236, 117556. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Zhang, J. Mechanical behavior and chloride penetration of high strength concrete under freeze–thaw attack. Cold Reg. Sci. Technol. 2017, 142, 17–24. [Google Scholar] [CrossRef]
- Hosseinzadeh, N.; Suraneni, P. Synergistic effects of air content and supplementary cementitious materials in reducing damage caused by calcium oxychloride formation in concrete. Cem. Concr. Comp. 2021, 122, 104170. [Google Scholar] [CrossRef]
- Jin, S.S.; Zheng, G.P.; Yu, J. A micro freeze–thaw damage model of concrete with fractal dimension. Constr. Build. Mater. 2020, 257, 119434. [Google Scholar] [CrossRef]
- Li, S.G.; Chen, G.X.; Ji, G.J.; Lu, Y.H. Quantitative damage evaluation of concrete suffered freezing-thawing by DIP technique. Constr. Build. Mater. 2014, 69, 177–185. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Li, Q.; Cao, Z.Y.; Tian, W.Y. The deterioration law of recycled concrete under the combined effects of freeze–thaw and sulfate attack. Constr. Build. Mater. 2019, 200, 344–355. [Google Scholar] [CrossRef]
- Yu, H.; Ma, H.; Yan, K. An equation for determining freeze–thaw fatigue damage in concrete and a model for predicting the service life. Constr. Build. Mater. 2017, 137, 104–116. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Cao, Z.Y.; Guan, X.; Li, Q.; Liu, X.L. Damage to recycled concrete with different aggregate substitution rates from the coupled action of freeze–thaw cycles and sulfate attack. Constr. Build. Mater. 2019, 221, 74–83. [Google Scholar] [CrossRef]
- Wang, B.X.; Pan, J.J.; Fang, R.C.; Wang, Q. Damage model of concrete subjected to coupling chemical attacks and freeze–thaw cycles in saline soil area. Constr. Build. Mater. 2020, 242, 118205. [Google Scholar] [CrossRef]
- Hang, M.; Cui, L.; Wu, J.; Sun, Z. Freezing-thawing damage characteristics and calculation models of aerated concrete. J. Build. Eng. 2020, 28, 101072. [Google Scholar] [CrossRef]
- Chen, F.L.; Qiao, P.Z. Probabilistic damage modeling and service-life prediction of concrete under freeze–thaw action. Mater. Struct. 2015, 48, 2697–2711. [Google Scholar] [CrossRef]
- Dahmani, L.; Khenane, A.; Kaci, S. Behavior of the reinforced concrete at cryogenic temperatures. Cryogenics 2007, 47, 517–525. [Google Scholar] [CrossRef]
- Jiang, Z.W.; He, B.; Zhu, X.P.; Ren, Q.; Zhang, Y. State-of-the-art review on properties evolution and deterioration mechanism of concrete at cryogenic temperature. Constr. Build. Mater. 2020, 257, 119456. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, K.; Fen-chong, T.; Dangla, P. In A study of the Behaviors of Cement-Based Materials Subject to Freezing. In Proceedings of the 2010 International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 26–28 June 2010; pp. 1611–1616. [Google Scholar]
- Liu, Z.; Zhang, Y.; Jiang, Q.; Zhang, W.; Wu, J. Solid Phases Percolation and Capillary Pores Depercolation in Hydrating Cement Pastes. J. Mater. Civil. Eng. 2014, 26, 04014090. [Google Scholar] [CrossRef]
- Sun, Z.; Scherer, G.W. Effect of air voids on salt scaling and internal freezing. Cem. Concr. Res. 2010, 40, 260–270. [Google Scholar] [CrossRef]
- Rønning, T.F. Freeze–Thaw Resistance of Concrete: Effect of: Curing Conditions, Moisture Exchange and Materials. Ph.D. Thesis, The Norwegian Institute of Technology, Trondheim, Norway, 2001. [Google Scholar]
- Washburn, E.W. The dynamics of capillary flow. Phys. Rev. 1921, 17, 273. [Google Scholar] [CrossRef]
- Sun, M.; Xin, D.B.; Zou, C.Y. Damage evolution and plasticity development of concrete materials subjected to freeze–thaw during the load process. Mech. Mater. 2019, 139, 103192. [Google Scholar] [CrossRef]
- Smith, S.H.; Qiao, C.Y.; Suraneni, P.; Kurtis, K.E.; Weiss, W.J. Service-life of concrete in freeze–thaw environments: Critical degree of saturation and calcium oxychloride formation. Cem. Concr. Res. 2019, 122, 93–106. [Google Scholar] [CrossRef]
- Fagerlund, G. The Long Time Water Absorption in the Air-Pore Structure of Concrete; Division of Building, Lund Institute of Technology: Lund, Sweden, 1993. [Google Scholar]
- Masoodi, R.; Pillai, K.M. Wicking in Porous Materials: Traditional and Modern Modeling Approaches; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Liu, L.; Qin, G.; Qin, S.N.; Tao, G.H. Simulation of the volumetric deformation and changes in the pore structure of unsaturated cement-based materials subjected to freezing/thawing. Constr. Build. Mater. 2020, 230, 116964. [Google Scholar] [CrossRef]
- Valenza, J.J.; Scherer, G.W. A review of salt scaling: II. Mechanisms. Cem. Concr. Res. 2007, 37, 1022–1034. [Google Scholar] [CrossRef]
- De Kock, T.; Boone, M.A.; De Schryver, T.; van Stappen, J.; Derluyn, H.; Masschaele, B.; De Schutter, G.; Cnudde, V. A Pore-Scale Study of Fracture Dynamics in Rock Using X-ray Micro-CT Under Ambient Freeze–Thaw Cycling. Environ. Sci. Technol. 2015, 49, 2867–2874. [Google Scholar] [CrossRef]
- Deprez, M.; De Kock, T.; De Schutter, G.; Cnudde, V. A review on freeze–thaw action and weathering of rocks. Earth Sci. Rev. 2020, 203, 103143. [Google Scholar] [CrossRef]
- Bluhm, J.; Setzer, M.J.; Kruschwitz, J. Modeling of ice formation in porous media. In IUTAM Symposium on Physicochemical and Electromechanical Interactions in Porous Media; Huyghe, J.M., Raats, P., Cowin, S.C., Eds.; Symposium on the Mechanics of Physicochemical and Electromechanical Interactions in Porous Media: New York, NY, USA, 2005; Volume 125, pp. 329–334. [Google Scholar]
- Rosenqvist, M.; Fridh, K.; Hassanzadeh, M. Macroscopic ice lens growth in hardened concrete. Cem. Concr. Res. 2016, 88, 114–125. [Google Scholar] [CrossRef]
- Valenza, J.J.; Scherer, G.W. Mechanism for salt scaling of a cementitious surface. Mater. Struct 2007, 40, 259–268. [Google Scholar] [CrossRef]
- Valenza, J.J.; Scherer, G.W. Mechanisms of salt scaling. Mater. Struct. 2005, 38, 479–488. [Google Scholar] [CrossRef]
- Valenza, J.J.; Scherer, G.W. Characterization of saturated porous bodies. Mater. Struct. 2004, 37, 21–30. [Google Scholar]
- Coussy, O.; Monteiro, P. Poroelastic model for concrete exposed to freezing temperatures. Cem. Concr. Res. 2008, 38, 40–48. [Google Scholar] [CrossRef]
- Dong, Y.J.; Su, C.; Qiao, P.Z.; Sun, L.Z. A thermal-hydraulic-mechanical coupling model for freezing process simulation of cementitious materials with entrained air voids. Constr. Build. Mater. 2020, 243, 118253. [Google Scholar] [CrossRef]
- Mayercsik, N.P.; Vandamme, M.; Kurtis, K.E. Assessing the efficiency of entrained air voids for freeze–thaw durability through modeling. Cem. Concr. Res. 2016, 88, 43–59. [Google Scholar] [CrossRef]
- Gou, Y.; Zhang, L.; Liu, C.; Zhang, H.; Wei, C.; Cai, X.; Yang, H.; Guan, Q.; Zhai, S.; Liu, L. Investigation of freeze–thaw mechanism for crumb rubber concrete by the online strain sensor. Measurement 2021, 174, 109080. [Google Scholar] [CrossRef]
- Qiao, C.; Chen, X.; Suraneni, P.; Weiss, W.J.; Rothstein, D. Petrographic analysis of in-service cementitious mortar subject to freeze–thaw cycles and deicers. Cem. Concr. Compos. 2021, 122, 104112. [Google Scholar] [CrossRef]
- Qiao, C.; Suraneni, P.; Weiss, J. Flexural strength reduction of cement pastes exposed to CaCl2 solutions. Cem. Concr. Compos. 2018, 86, 297–305. [Google Scholar] [CrossRef]
- Li, W.; Pour-Ghaz, M.; Castro, J.; Weiss, J. Water Absorption and Critical Degree of Saturation Relating to Freeze–Thaw Damage in Concrete Pavement Joints. J. Mater. Civ. Eng. 2012, 24, 299–307. [Google Scholar] [CrossRef]
- Song, Q.; Nie, J.; Wu, D.K.; Hu, Y.R.; Chen, Y.X. Effect of SO42−, Cl− and Mg2+ on the system of C-S-H and Ca(OH)2. Constr. Build. Mater. 2021, 285, 122955. [Google Scholar] [CrossRef]
- Birnin-Yauri, U.A.; Glasser, F.P. Friedel’s salt, Ca2Al(OH)6 center dot 2H2O: Its solid solutions and their role in chloride binding. Cem. Concr. Res. 1998, 28, 1713–1723. [Google Scholar] [CrossRef]
- Qiao, C.; Suraneni, P.; Weiss, J. Damage in cement pastes exposed to NaCl solutions. Constr. Build. Mater. 2018, 171, 120–127. [Google Scholar] [CrossRef]
- Farnam, Y.; Dick, S.; Wiese, A.; Davis, J.; Bentz, D.; Weiss, J. The influence of calcium chloride deicing salt on phase changes and damage development in cementitious materials. Cem. Concr. Compos. 2015, 64, 1–15. [Google Scholar] [CrossRef]
- Qiao, C.Y.; Suraneni, P.; Weiss, J. Phase Diagram and Volume Change of the Ca(OH)2 CaCl2 H2O System for Varying Ca(OH)2/CaCl2 Molar Ratios. J. Mater. Civil. Eng. 2018, 30, 04017281. [Google Scholar] [CrossRef]
- Xie, N.; Dang, Y.; Shi, X. New insights into how MgCl2 deteriorates Portland cement concrete. Cem. Concr. Res. 2019, 120, 244–255. [Google Scholar] [CrossRef]
- Sutter, L.; Peterson, K.; Touton, S.; Van Dam, T.; Johnston, D. Petrographic evidence of calcium oxychloride formation in mortars exposed to magnesium chloride solution. Cem. Concr. Res. 2006, 36, 1533–1541. [Google Scholar] [CrossRef]
- Ghazy, A.; Bassuoni, M. Resistance of concrete to different exposures with chloride-based salts. Cem. Concr. Res. 2017, 101, 144–158. [Google Scholar] [CrossRef]
- Nadelman, E.; Kurtis, K. Durability of Portland-limestone cement-based materials to physical salt attack. Cem. Concr. Res. 2019, 125, 105859. [Google Scholar] [CrossRef]
- Lee, B.Y.; Kurtis, K.E. Effect of pore structure on salt crystallization damage of cement-based materials: Consideration of w/b and nanoparticle use. Cem. Concr. Res. 2017, 98, 61–70. [Google Scholar] [CrossRef]
- Li, B.; Mao, J.; Nawa, T.; Liu, Z. Mesoscopic chloride ion diffusion model of marine concrete subjected to freeze–thaw cycles. Constr. Build. Mater. 2016, 125, 337–351. [Google Scholar] [CrossRef]
- Zhu, P.H.; Hao, Y.L.; Liu, H.; Wang, X.J.; Gu, L. Durability evaluation of recycled aggregate concrete in a complex environment. J. Clean Prod. 2020, 273, 122569. [Google Scholar] [CrossRef]
- Wang, D.Z.; Zhou, X.M.; Fu, B.; Zhang, L.R. Chloride ion penetration resistance of concrete containing fly ash and silica fume against combined freezing-thawing and chloride attack. Constr. Build. Mater. 2018, 169, 740–747. [Google Scholar] [CrossRef]
- Yazdchi, M.; Asl, A.F.; Talatahari, S.; Gandomi, A.H. Evaluation of the Mechanical Properties of Normal Concrete Containing Nano-MgO under Freeze–Thaw Conditions by Evolutionary Intelligence. Appl. Sci. 2021, 11, 2529. [Google Scholar] [CrossRef]
- Qiu, W.L.; Teng, F.; Pan, S.S. Damage constitutive model of concrete under repeated load after seawater freeze–thaw cycles. Constr. Build. Mater. 2020, 236, 117560. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Liu, Z.; Zhang, B.H.; Fu, K. A time-dependent diffusive model for the simulation of chloride penetration in concrete considering the effect of natural salt freeze–thaw cycles. Cold Reg. Sci. Technol. 2022, 201, 103622. [Google Scholar] [CrossRef]
- Hou, R.; Qi, Z.; Li, T.; Fu, Q.; Meng, F.; Liu, D.; Li, Q.; Zhao, H.; Yu, P. Mechanism of snowmelt infiltration coupled with salt transport in soil amended with carbon-based materials in seasonally frozen areas. Geoderma 2022, 420, 115882. [Google Scholar] [CrossRef]
- Luo, S.; Bai, T.; Guo, M.; Wei, Y.; Ma, W. Impact of Freeze–Thaw Cycles on the Long-Term Performance of Concrete Pavement and Related Improvement Measures: A Review. Materials 2022, 15, 4568. [Google Scholar] [CrossRef]
- Kunther, W.; Lothenbach, B.; Skibsted, J. Influence of the Ca/Si ratio of the C–S–H phase on the interaction with sulfate ions and its impact on the ettringite crystallization pressure. Cem. Concr. Res. 2015, 69, 37–49. [Google Scholar] [CrossRef]
- Kunther, W.; Lothenbach, B.; Scrivener, K. Influence of bicarbonate ions on the deterioration of mortar bars in sulfate solutions. Cem. Concr. Res. 2013, 44, 77–86. [Google Scholar] [CrossRef]
- Zhao, N.; Wang, S.; Wang, C.; Quan, X.; Yan, Q.; Li, B. Study on the durability of engineered cementitious composites (ECCs) containing high-volume fly ash and bentonite against the combined attack of sulfate and freezing-thawing (F–T). Constr. Build. Mater. 2019, 233, 117313. [Google Scholar] [CrossRef]
- Hime, W.G.; Mather, B. “Sulfate attack,” or is it? Cem. Concr. Res. 1999, 29, 789–791. [Google Scholar] [CrossRef]
- Li, C.; Jiang, Z.W.; Myers, R.J.; Chen, Q.; Wu, M.X.; Li, J.Q.; Monteiro, P. Understanding the sulfate attack of Portland cement-based materials exposed to applied electric fields: Mineralogical alteration and migration behavior of ionic species. Cem. Concr. Comp. 2020, 111, 103630. [Google Scholar] [CrossRef]
- Wang, K.; Guo, J.; Yang, L. Effect of dry–wet ratio on sulfate transport-reaction mechanism in concrete. Constr. Build. Mater. 2021, 302, 124418. [Google Scholar] [CrossRef]
- Bayraktar, O.Y.; Eshtewi, S.; Benli, A.; Kaplan, G.; Toklu, K.; Gunek, F. The impact of RCA and fly ash on the mechanical and durability properties of polypropylene fibre-reinforced concrete exposed to freeze–thaw cycles and MgSO4 with ANN modeling. Constr. Build. Mater. 2021, 313, 125508. [Google Scholar] [CrossRef]
- Tosun-Felekoğlu, K. The effect of C3A content on sulfate durability of Portland limestone cement mortars. Constr. Build. Mater. 2012, 36, 437–447. [Google Scholar] [CrossRef]
- Steiger, M.; Asmussen, S. Crystallization of sodium sulfate phases in porous materials: The phase diagram Na2SO4–H2O and the generation of stress. Geochim. Cosmochim. Acta 2008, 72, 4291–4306. [Google Scholar] [CrossRef]
- Al-Amoudi, O.S.B. Attack on plain and blended cements exposed to aggressive sulfate environments. Cem. Concr. Compos. 2002, 24, 305–316. [Google Scholar] [CrossRef]
- Bensted, J. Thaumasite—Background and nature in deterioration of cements, mortars and concretes. Cem. Concr. Comp. 1999, 21, 117–121. [Google Scholar] [CrossRef]
- Sotiriadis, K.; Hlobil, M.; Viani, A.; Mácová, P.; Vopálenský, M. Physical-chemical-mechanical quantitative assessment of the microstructural evolution in Portland-limestone cement pastes exposed to magnesium sulfate attack at low temperature. Cem. Concr. Res. 2021, 149, 106566. [Google Scholar] [CrossRef]
- Piasta, W.; Marczewska, J.; Jaworska, M. Durability of air entrained cement mortars under combined sulphate and freeze–thaw attack. In Proceedings of the 7th Scientific-Technical Conference Material Problems in Civil Engineering (MATBUD), Cracow University of Technology, Cracow, Poland, 22–24 June 2015; Tracz, T., Hager, I., Eds.; Volume 108, pp. 55–62. [Google Scholar]
- Ren, J.G.; Lai, Y.M. Study on the durability and failure mechanism of concrete modified with nanoparticles and polypropylene fiber under freeze–thaw cycles and sulfate attack. Cold Reg. Sci. Technol. 2021, 188, 103301. [Google Scholar] [CrossRef]
- Farnam, Y.; Bentz, D.; Sakulich, A.; Flynn, D.; Weiss, J. Measuring freeze and thaw damage in mortars containing deicing salt using a low-temperature longitudinal guarded comparative calorimeter and acoustic emission. Adv. Civ. Eng. Mater. 2014, 3, 316–337. [Google Scholar] [CrossRef]
- Sun, H.F.; Jiang, C.; Cao, K.; Yu, D.; Liu, W.; Zhang, X.G.; Xing, F.; Zhao, D.D. Monitoring of steel corrosion and cracking in cement paste exposed to combined sulfate-chloride attack with X-ray microtomography. Constr. Build. Mater. 2021, 302, 124345. [Google Scholar] [CrossRef]
- Wu, J.; Wei, J.; Huang, H.; Hu, J.; Yu, Q. Effect of multiple ions on the degradation in concrete subjected to sulfate attack. Constr. Build. Mater. 2020, 259, 119846. [Google Scholar] [CrossRef]
- Du, J.; Tang, Z.; Li, G.; Yang, H.; Li, L. Key inhibitory mechanism of external chloride ions on concrete sulfate attack. Constr. Build. Mater. 2019, 225, 611–619. [Google Scholar] [CrossRef]
- Chen, D.; Deng, Y.; Shen, J.; Sun, G.; Shi, J. Study on damage rules on concrete under corrosion of freeze–thaw and saline solution. Constr. Build. Mater. 2021, 304, 124617. [Google Scholar] [CrossRef]
- Qingli, D.; Ng, K. Transmission X-Ray Microscope Nanoscale Characterization and 3D Micromechanical Modeling of Internal Frost Damage in Cement Paste. J. Nanomech. Micromech. 2014, 4, A4013005–A4013010. [Google Scholar]
- Du, W.; Liu, Q.T.; Lin, R.S. Effects of toluene-di-isocyanate microcapsules on the frost resistance and self-repairing capability of concrete under freeze–thaw cycles. J. Build. Eng. 2021, 44, 102880. [Google Scholar] [CrossRef]
- Wen, Y.; Sun, H.; Hu, S.D.; Xu, G.M.; Wu, X.Z.; Song, C.C.; Liu, Z.; Li, Z.J. Microstructure and life prediction model of steel slag concrete under freezing-thawing environment. Nanotechnol. Rev. 2021, 10, 1776–1788. [Google Scholar] [CrossRef]
- Sakr, M.R.; Bassuoni, M.T. Silane and methyl-methacrylate based nanocomposites as coatings for concrete exposed to salt solutions and cyclic environments. Cem. Concr. Comp. 2021, 115, 103841. [Google Scholar] [CrossRef]
- Huang, X.; Wang, T.; Pang, J.; Song, F. Experimental Study on the Effect of Freeze–Thaw Cycles on the Apparent and Mechanical Properties of Rubber Concrete Under Chloride Environment. Arab. J. Sci. Eng. 2022, 47, 4133–4153. [Google Scholar] [CrossRef]
- Tian, W.; Gao, F.F. Damage and Degradation of Concrete under Coupling Action of Freeze–Thaw Cycle and Sulfate Attack. Adv. Mater. Sci. Eng. 2020, 2020, 8032849. [Google Scholar] [CrossRef]
- Wang, R.; Hu, Z.; Li, Y.; Wang, K.; Zhang, H. Review on the deterioration and approaches to enhance the durability of concrete in the freeze–thaw environment. Constr. Build. Mater. 2022, 321, 126371. [Google Scholar] [CrossRef]
- Jia, P.; Li, L.; Zhou, J.; Zhang, D.; Guan, Z.W.; Dong, J.F.; Wang, Q.Y. Performance Evolution of Recycled Aggregate Concrete under the Coupled Effect of Freeze–Thaw Cycles and Sulfate Attack. Appl. Sci. 2022, 12, 6950. [Google Scholar] [CrossRef]
- Divanedari, H.; Eskandari-Naddaf, H. Insights into surface crack propagation of cement mortar with different cement fineness subjected to freezing/thawing. Constr. Build. Mater. 2020, 233, 117207. [Google Scholar] [CrossRef]
- Xie, R.F.; Lu, L.J.; Qiao, P.Z.; Zhou, Z.D. Nanoindentation-based micromechanical characterisation of ultra-high-performance concrete exposed to freezing-thawing. Mag. Concr. Res. 2022, 74, 162–176. [Google Scholar] [CrossRef]
- Liu, M.X.; Liu, D.X.; Qiao, P.Z.; Sun, L.Z. Characterization of microstructural damage evolution of freeze–thawed shotcrete by an integrative micro-CT and nanoindentation statistical approach. Cem. Concr. Comp. 2021, 117, 103909. [Google Scholar] [CrossRef]
- Lyu, Z.; Shen, A.; Wang, W.; Lin, S.; Guo, Y.; Meng, W. Salt frost resistance and micro characteristics of polynary blended concrete using in frost areas. Cold Reg. Sci. Technol. 2021, 191, 103374. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Pang, J.; Lu, Y.; Bu, Y. Experimental Study on Damage Characteristics of Solidified Mud under Coupling Action of Freeze–Thaw Cycle and Chloride Salt. Geofluids 2022, 2022, 6050432. [Google Scholar] [CrossRef]
- Ji, R.; Li, T.; Yang, J.; Xu, J. Sulfate Freeze–Thaw Resistance of Magnesium Potassium Phosphate Cement Mortar according to Hydration Age. Materials 2022, 15, 4192. [Google Scholar] [CrossRef]
- Ebrahimi, K.; Daiezadeh, M.J.; Zakertabrizi, M.; Zahmatkesh, F.; Korayem, A.H. A review of the impact of micro- and nanoparticles on freeze–thaw durability of hardened concrete: Mechanism perspective. Constr. Build. Mater. 2018, 186, 1105–1113. [Google Scholar] [CrossRef]
- Wang, J.B.; Niu, D.T.; He, H. Frost durability and stress-strain relationship of lining shotcrete in cold environment. Constr. Build. Mater. 2019, 198, 58–69. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, S.H.; Niu, D.T.; Fu, Q. Quantitative evaluation of the characteristics of air voids and their relationship with the permeability and salt freeze–thaw resistance of hybrid steel-polypropylene fiber-reinforced concrete composites. Cem. Concr. Comp. 2022, 125, 104292. [Google Scholar] [CrossRef]
- Xu, F.; Wang, S.L.; Li, T.; Liu, B.; Zhao, N.; Liu, K.N. The mechanical properties and resistance against the coupled deterioration of sulfate attack and freeze–thaw cycles of tailing recycled aggregate concrete. Constr. Build. Mater. 2021, 269, 121273. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Q.B.; Niu, X.J.; Yang, L.; Hu, Y.; Zhang, J.L. Influence of a novel hydrophobic agent on freeze–thaw resistance and microstructure of concrete. Constr Build. Mater. 2021, 269, 121294. [Google Scholar] [CrossRef]
- Zhang, P.; Wittmann, F.H.; Vogel, M.; Muller, H.S.; Zhao, T.J. Influence of freeze–thaw cycles on capillary absorption and chloride penetration into concrete. Cem. Concr. Res. 2017, 100, 60–67. [Google Scholar] [CrossRef]
- Sun, M.; Zou, C.Y.; Xin, D.B. Pore structure evolution mechanism of cement mortar containing diatomite subjected to freeze–thaw cycles by multifractal analysis. Cem. Concr. Comp. 2020, 114, 103731. [Google Scholar] [CrossRef]
- Zheng, X.; Liu, F.; Luo, T.; Duan, Y.; Yi, Y.; Hua, C. Study on Durability and Pore Characteristics of Concrete under Salt Freezing Environment. Materials 2021, 14, 7228. [Google Scholar] [CrossRef]
- Tian, W.; Han, N. Pore characteristics (>0.1 mm) of non-air entrained concrete destroyed by freeze–thaw cycles based on CT scanning and 3D printing. Cold Reg. Sci. Technol. 2018, 151, 314–322. [Google Scholar] [CrossRef]
- Chen, J.; Deng, X.; Luo, Y.; He, L.; Liu, Q.; Qiao, X. Investigation of microstructural damage in shotcrete under a freeze–thaw environment. Constr. Build. Mater. 2015, 83, 275–282. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, W.; Ge, Y.; Liu, P.; Zhang, A. Analysis of freeze–thaw damage and pore structure deterioration of mortar by low-field NMR. Constr. Build. Mater. 2021, 319, 126097. [Google Scholar] [CrossRef]
- Jia, H.L.; Ding, S.; Zi, F.; Dong, Y.H.; Shen, Y.J. Evolution in sandstone pore structures with freeze–thaw cycling and interpretation of damage mechanisms in saturated porous rocks. Catena 2020, 195, 104915. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, C.; Zhou, K.; Tian, Y. Freeze-thaw cycling damage evolution of additive cement mortar. Eur. J. Environ. Civ. Eng. 2021, 25, 2089–2110. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, J.; Yin, Z. Experimental Study on Mechanical Properties and Pore Structure Deterioration of Concrete under Freeze–Thaw Cycles. Materials 2021, 14, 6568. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Wang, Y.; Wei, X.; Jia, H.; Yan, R. Investigation on meso-debonding process of the sandstone-concrete interface induced by freeze–thaw cycles using NMR technology. Constr. Build. Mater. 2020, 252, 118962. [Google Scholar] [CrossRef]
- Sypek, M.; Latawiec, R.; Lazniewska-Piekarczyk, B.; Pichor, W. Impact of Surfactant and Calcium Sulfate Type on Air-Entraining Effectiveness in Concrete. Materials 2022, 15, 985. [Google Scholar] [CrossRef] [PubMed]
- He, B.; Xie, M.; Jiang, Z.; Zhang, C.; Zhu, X. Temperature field distribution and microstructure of cement-based materials under cryogenic freeze–thaw cycles. Constr. Build Mater. 2020, 243, 118256. [Google Scholar] [CrossRef]
- Yao, H.; Xie, Z.; Huang, C.; Yuan, Q.; Yu, Z. Recent progress of hydrophobic cement-based materials: Preparation, characterization and properties. Constr. Build. Mater. 2021, 299, 124255. [Google Scholar] [CrossRef]
- Zeng, W.; Ding, Y.; Zhang, Y.; Dehn, F. Effect of steel fiber on the crack permeability evolution and crack surface topography of concrete subjected to freeze–thaw damage. Cement Concrete Res. 2020, 138, 106230. [Google Scholar] [CrossRef]
- Sanchez, L.F.M.; Drimalas, T.; Fournier, B.; Mitchell, D.; Bastien, J. Comprehensive damage assessment in concrete affected by different internal swelling reaction (ISR) mechanisms. Cem. Concr. Res. 2018, 107, 284–303. [Google Scholar] [CrossRef]
- Soroushian, P.; Elzafraney, M. Damage effects on concrete performance and microstructure. Cem. Concr. Comp. 2004, 26, 853–859. [Google Scholar] [CrossRef]
- Yang, X.L.; Shen, A.Q.; Guo, Y.C.; Zhou, S.B.; He, T.Q. Deterioration mechanism of interface transition zone of concrete pavement under fatigue load and freeze–thaw coupling in cold climatic areas. Constr. Build. Mater. 2018, 160, 588–597. [Google Scholar] [CrossRef]
- Liu, M.; Qiao, P.; Sun, L. Dependence of chloride ion diffusivity on evolution of pore-structures in freeze–thawed shotcrete: Multiscale characterization and modeling. Cem. Concr. Comp. 2021, 123, 104222. [Google Scholar] [CrossRef]
- Shields, Y.; Garboczi, E.; Weiss, J.; Farnam, Y. Freeze-thaw crack determination in cementitious materials using 3D X-ray computed tomography and acoustic emission. Cem. Concr. Comp. 2018, 89, 120–129. [Google Scholar] [CrossRef]
- Liu, M.X.; Qiao, P.Z.; Sun, L.Z. Multiscale modeling of damage and fracture in freeze–thawed shotcrete. Int. J. Damage Mech. 2022, 31, 142–162. [Google Scholar] [CrossRef]
- Dong, Y.; Su, C.; Qiao, P.; Sun, L.Z. Microstructural damage evolution and its effect on fracture behavior of concrete subjected to freeze–thaw cycles. Int. J. Damage Mech 2018, 27, 1272–1288. [Google Scholar] [CrossRef]
- Dong, Y.J.; Su, C.; Qiao, P.Z.; Sun, L.Z. Microstructural crack segmentation of three-dimensional concrete images based on deep convolutional neural networks. Constr. Build. Mater. 2020, 253, 119185. [Google Scholar] [CrossRef]
- Luo, Q.; Liu, D.X.; Qiao, P.Z.; Feng, Q.G.; Sun, L.Z. Microstructural damage characterization of concrete under freeze–thaw action. Int. J. Damage Mech. 2018, 27, 1551–1568. [Google Scholar] [CrossRef]
- Zou, D.J.; Wang, Z.Z.; Shen, M.M.; Liu, T.J.; Zhou, A. Improvement in freeze–thaw durability of recycled aggregate permeable concrete with silane modification. Constr. Build. Mater. 2021, 268, 121097. [Google Scholar] [CrossRef]
- Wu, K.; Han, H.; Li, H.; Dong, B.; Liu, T.; De Schutter, G. Experimental study on concurrent factors influencing the ITZ effect on mass transport in concrete. Cem. Concr. Compos. 2021, 123, 104215. [Google Scholar] [CrossRef]
- Wu, K.; Shi, H.; Xu, L.; Ye, G.; De Schutter, G. Microstructural characterization of ITZ in blended cement concretes and its relation to transport properties. Cem. Concr. Res. 2015, 79, 243–256. [Google Scholar] [CrossRef]
- Maruyama, I.; Sasano, H.; Lin, M. Impact of aggregate properties on the development of shrinkage-induced cracking in concrete under restraint conditions. Cem. Concr. Res. 2016, 85, 82–101. [Google Scholar] [CrossRef]
- Cwirzen, A.; Penttala, V. Aggregate-cement paste transition zone properties affecting the salt-frost damage of high-performance concretes. Cem. Concr. Res. 2005, 35, 671–679. [Google Scholar] [CrossRef]
- Lizarazo-Marriaga, J.; Higuera, C.; Claisse, P. Measuring the effect of the ITZ on the transport related properties of mortar using electrochemical impedance. Constr. Build. Mater. 2014, 52, 9–16. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, Y.; Zhang, S.; Xu, F.; Zhu, X.; Jiang, X.; Zhou, L.; Shen, Y.; Chen, Q.; Yan, Z.; et al. Research progress of the thermophysical and mechanical properties of concrete subjected to freeze–thaw cycles. Constr. Build. Mater. 2022, 330, 127254. [Google Scholar] [CrossRef]
- Hao, L.; Liu, Y.; Wang, W.; Zhang, J.; Zhang, Y. Effect of salty freeze–thaw cycles on durability of thermal insulation concrete with recycled aggregates. Constr. Build. Mater. 2018, 189, 478–486. [Google Scholar] [CrossRef]
- Zhou, Z.; Xie, R.; Qiao, P.; Lu, L. On the modeling of tensile behavior of ultra-high performance fiber-reinforced concrete with freezing-thawing actions. Compos. Part B Eng. 2019, 174, 106983. [Google Scholar] [CrossRef]
- Pang, B.; Zhou, Z.; Cheng, X.; Du, P.; Xu, H. ITZ properties of concrete with carbonated steel slag aggregate in salty freeze–thaw environment. Constr. Build. Mater. 2016, 114, 162–171. [Google Scholar] [CrossRef]
- Sicat, E.; Gong, F.; Ueda, T.; Zhang, D. Experimental investigation of the deformational behavior of the interfacial transition zone (ITZ) in concrete during freezing and thawing cycles. Constr. Build. Mater. 2014, 65, 122–131. [Google Scholar] [CrossRef]
- Siamardi, K.; Shabani, S. Evaluation the effect of micro-synthetic fiber on mechanical and freeze–thaw behavior of non-air-entrained roller compacted concrete pavement using response surface methodology. Constr. Build. Mater. 2021, 295, 123628. [Google Scholar] [CrossRef]
- Petersen, L.; Lohaus, L.; Polak, M.A. Influence of freezing-and-thawing damage on behavior of reinforced concrete elements. ACI Mater. J. 2007, 104, 369–378. [Google Scholar]
- Nili, M.; Azarioon, A.; Hosseinian, S.M. Novel Internal-Deterioration Model of Concrete Exposed to Freeze–Thaw Cycles. J. Mater. Civ. Eng. 2017, 29, 04017132. [Google Scholar] [CrossRef]
- Guan, X.; Chen, J.; Qiu, J.; Gao, Y.; Gao, J. Damage evaluation method based on ultrasound technique for gangue concrete under freezing-thawing cycles. Constr. Build. Mater. 2020, 246, 118437. [Google Scholar] [CrossRef]
- Guan, X.; Qiu, J.; Song, H.; Qin, Q.; Zhang, C. Stress–strain behaviour and acoustic emission characteristic of gangue concrete under axial compression in frost environment. Constr. Build. Mater. 2019, 220, 476–488. [Google Scholar] [CrossRef]
- Azarsa, P.; Gupta, R.; Biparva, A. Assessment of self-healing and durability parameters of concretes incorporating crystalline admixtures and Portland Limestone Cement. Cem. Concr. Compos. 2019, 99, 17–31. [Google Scholar] [CrossRef]
- Hasholt, M.T.; Christensen, K.U.; Pade, C. Frost resistance of concrete with high contents of fly ash—A study on how hollow fly ash particles distort the air void analysis. Cem. Concr. Res. 2019, 119, 102–112. [Google Scholar] [CrossRef]
- Xiao, Q.H.; Niu, D.T.; Zhu, W.P. Strength degradation model and durability service life prediction of concrete in freezing-thawing circumstance. Build. Struct. 2011, 41, 203–207. [Google Scholar]
- Yu, H.; Sun, W.; Ma, H.; Zhang, Y.; Miao, C.; Jin, Z.; Liu, J. Predicting method of concrete service life based on damage development equation. J. Archit. Civil. Eng. 2012, 29, 1–7. [Google Scholar]
- Mu, R. Durability and Service Life Prediction of Concrete Subjected to the Combined Action of Freezing-Thawing, Sustained External Flexural Stress and Salt Solution. Ph.D. Thesis, Southeast University, Nanjing, China, 2000. [Google Scholar]
- Zhang, F.; Li, S.; Li, S. Three-dimensional Random Damage Prediction Model of Concrete Caused by Freeze-thaw. J. Civil. Archit. Environ. Eng. 2011, 33, 31–35. [Google Scholar]
- Cho, T. Prediction of cyclic freeze–thaw damage in concrete structures based on response surface method. Constr. Build. Mater. 2007, 21, 2031–2040. [Google Scholar] [CrossRef]
- Li, B.; Mao, J.; Nawa, T.; Han, T. Mesoscopic damage model of concrete subjected to freeze–thaw cycles using mercury intrusion porosimetry and differential scanning calorimetry (MIP-DSC). Constr. Build. Mater. 2017, 147, 79–90. [Google Scholar] [CrossRef]
- Zhang, C.; Ma, W.; Liu, X.; Tian, Y.; Orton, S.L. Effects of high temperature on residual punching strength of slab-column connections after cooling and enhanced post-punching load resistance. Eng. Struct. 2019, 199, 109580. [Google Scholar] [CrossRef]
- Xu, W.-H.; Zhang, Q.-N.; Ma, W.-C.; Wang, E.-H. Response of Two Unequal-Diameter Flexible Cylinders in A Side-by-Side Arrangement: Characteristics of FIV. China Ocean Eng. 2020, 34, 475–487. [Google Scholar] [CrossRef]
- Chen, X.; Wang, D.Y.; Tang, J.B.; Ma, W.C.; Liu, Y. Geotechnical stability analysis considering strain softening using micro-polar continuum finite element method. J. Cent. South Univ. 2021, 28, 297–310. [Google Scholar] [CrossRef]
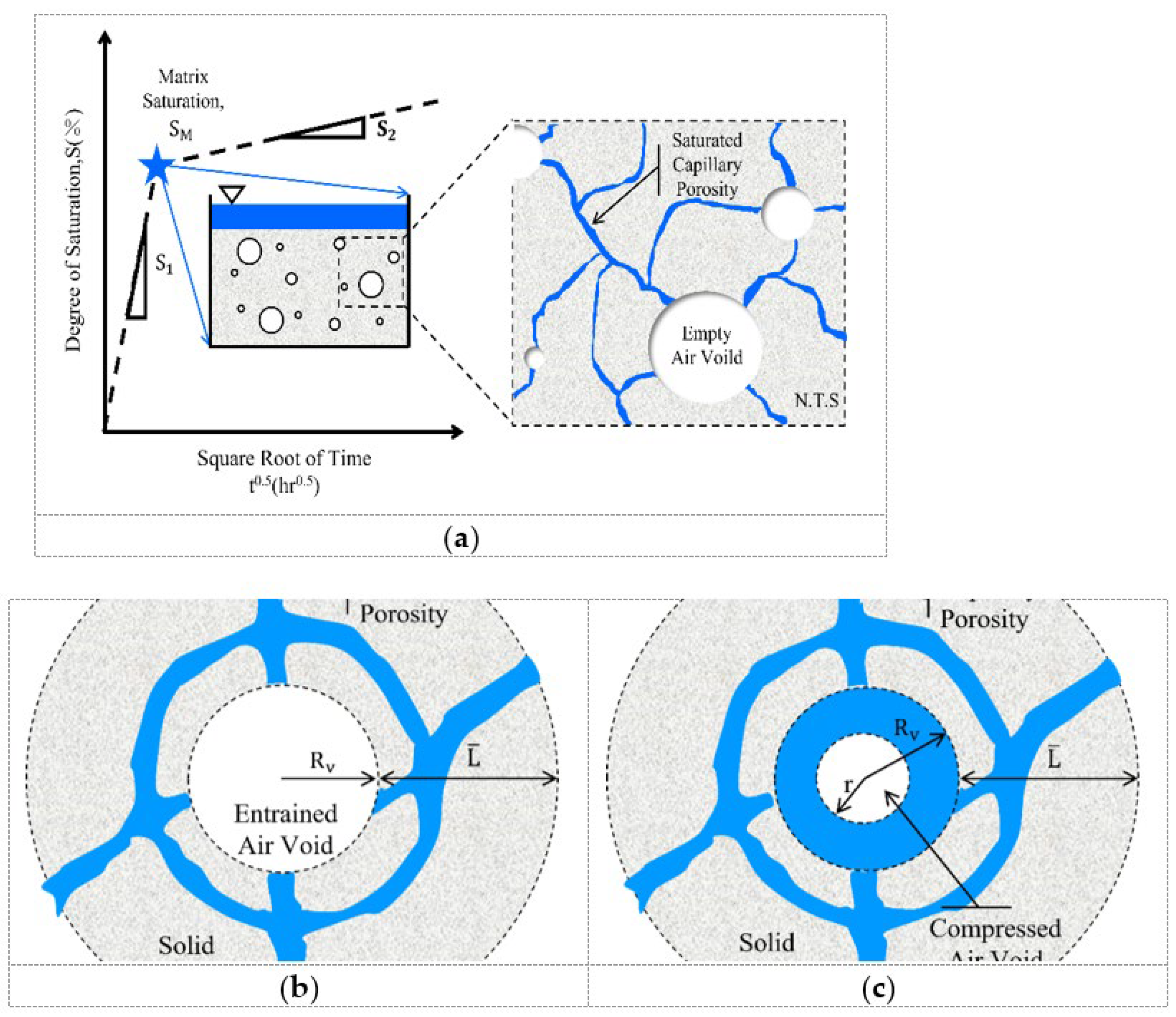



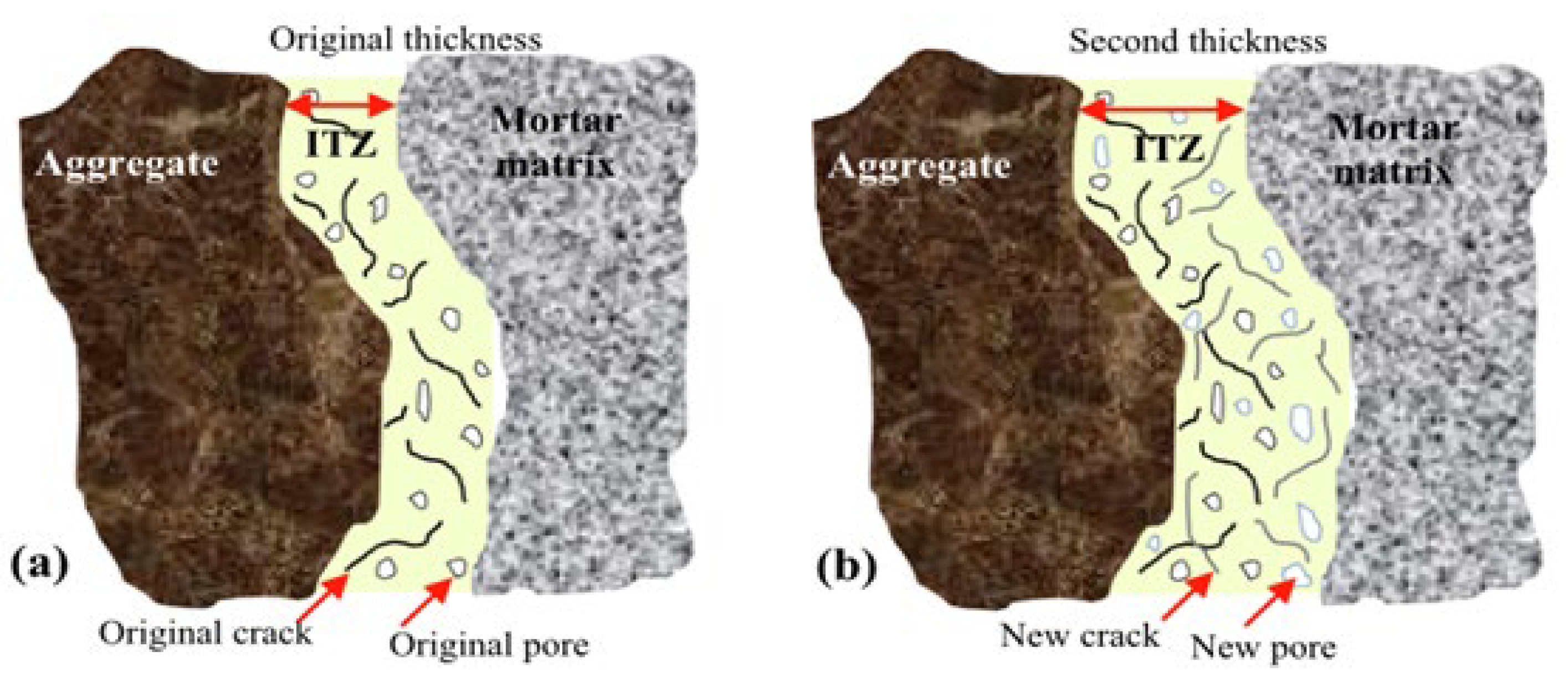
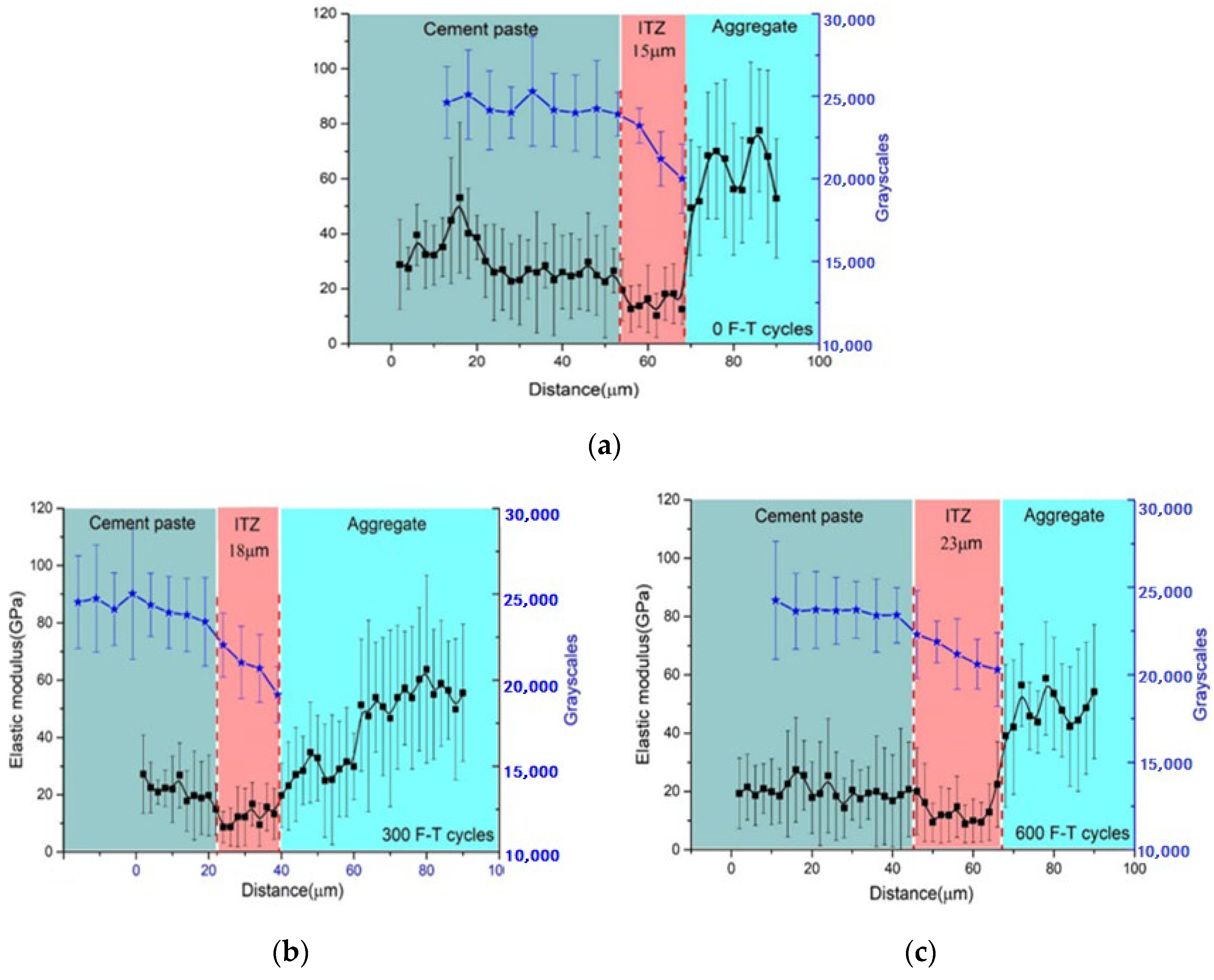
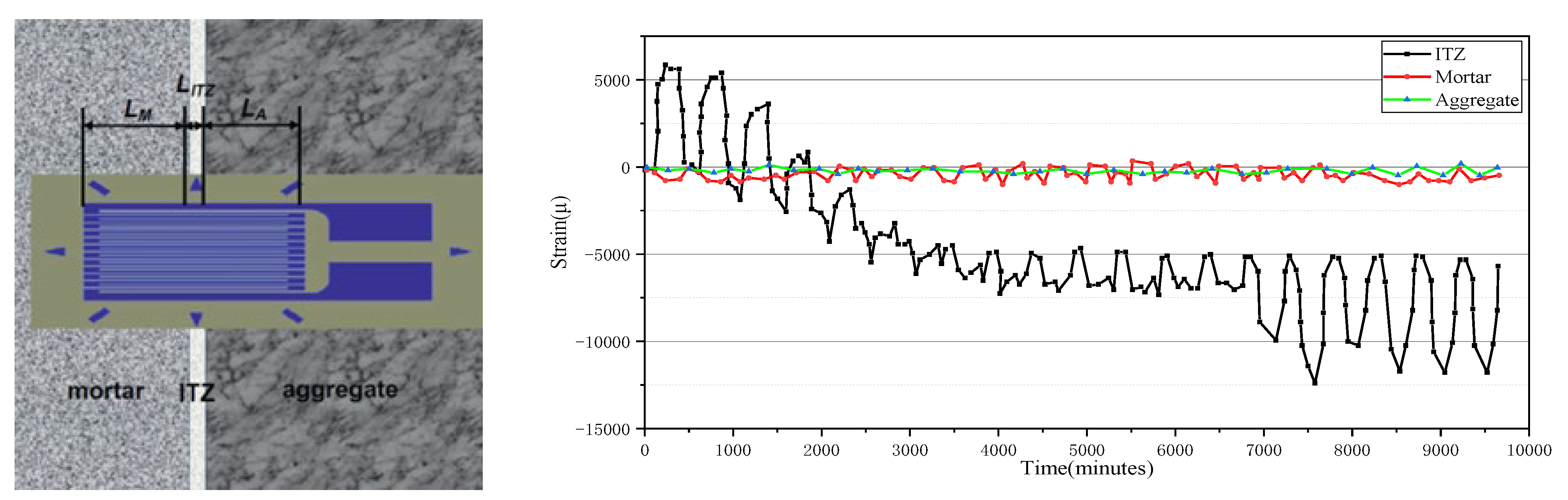

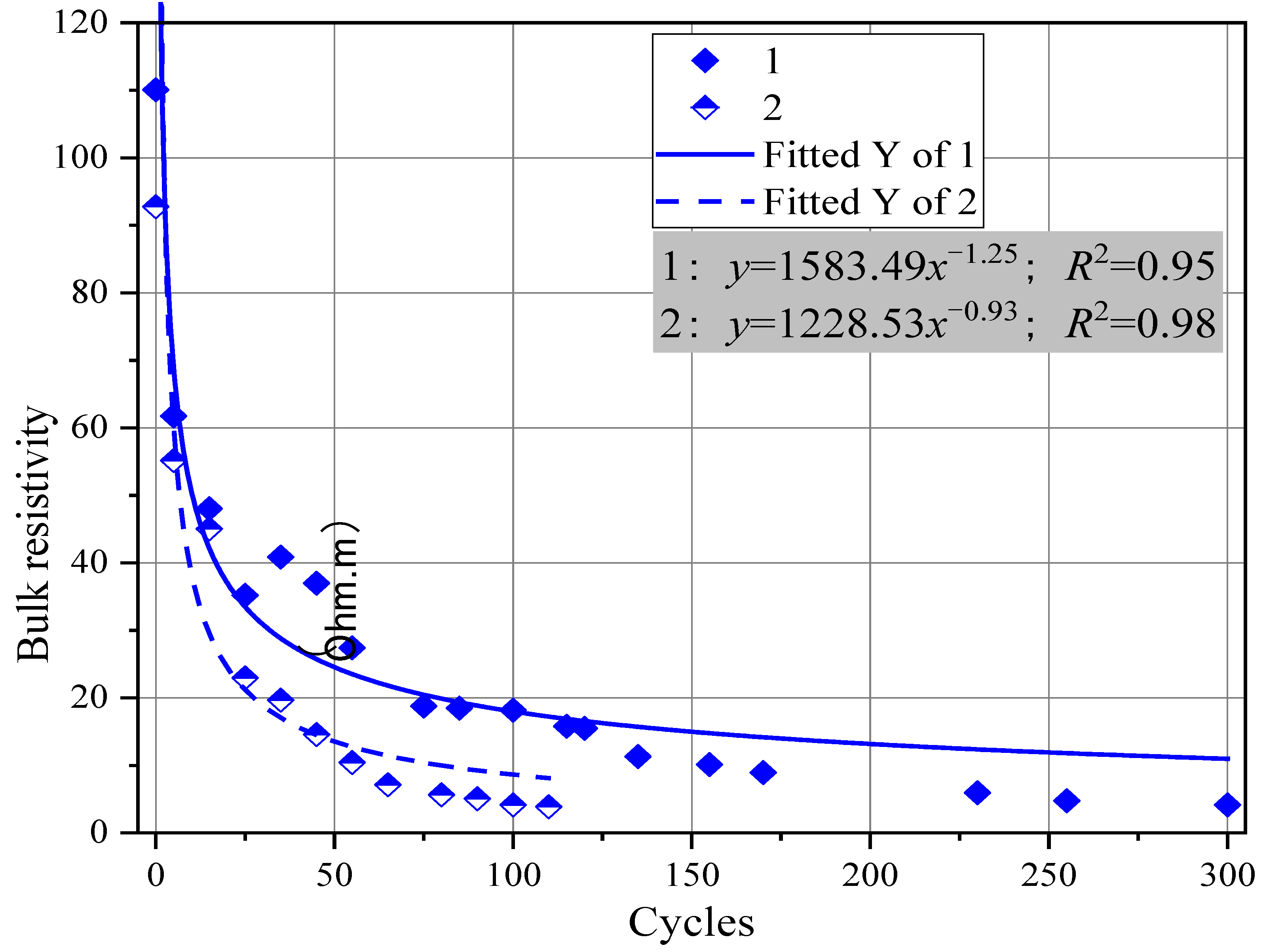
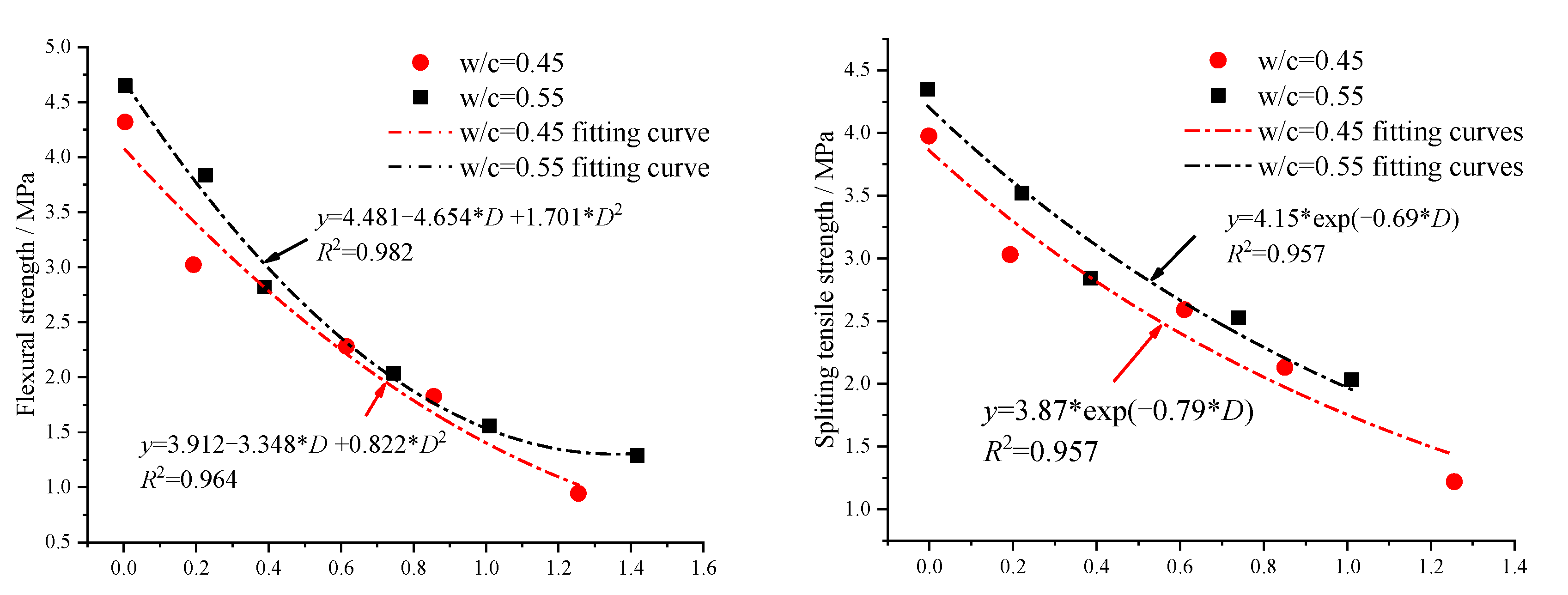
| Model | Pore Pressure Expression | Symbolic Meaning | Application/Limitation |
|---|---|---|---|
| Hydrostatic Pressure [5] | p: Hydraulic pressure k: Permeability coefficient n: Viscous resistance rE: Pose radius KE: Pose influence range | The function of air entraining agent and the phenomenon of freezing expansion of materials/Unable to explain the critical water content. | |
| Osmotic Pressure [6] | P0: Osmotic pressure difference V: Molar volume of solution R: Gas constant T: Temperature t: Icing temperature | Solute precipitation in salt solution accelerates F–T damage/The formation and release of pressure cannot be quantified. | |
| Critical saturation theory [49] | No definite formula | Effect of water saturation on concrete deterioration/Macro description, unable to explain the micro mechanism. | |
| Crystallization pressure theory [9] | : Crystal tail pressure : Pressure in the middle of the crystal : Surface energy of crystal and liquid : Small pore diameter : Radius of the crystal : Thickness of unfrozen water layer | Shrinkage of air-entraining concrete at low temperature/Extension of hydrostatic pressure theory. | |
| Micro-ice lens theory [10] | No definite formula | Explains the transport of water and the obvious increase of water absorption rate during F–T/There is no theoretical expression, which is essentially an extension of osmotic pressure theory. | |
| Glue spall theory [59] | : Stress on the ice T: Temperature b, n: Theoretical parameter : Coefficient of thermal expansion | Intuitively explains the spalling phenomenon of concrete surface after F–T/difficult to explain the internal damage. | |
| Theory of unsaturated porous elasticity [61] | : Density of water and ice : Relative volume fraction of water and ice : Bulk modulus of water and ice | Constructing the relationship between macroscopic damage and microscopic characterization of concrete during F–T/The theoretical basis is too complex to carry out numerical calculation. |
| Formula | Theoretical Basis | Applicable Scope | Provenance |
|---|---|---|---|
N: Standard F–T fatigue life, generally set at 300; n: Number of cycles. | Mechanical fatigue equation of material | F–T in pure water | Yu et al. [36] |
D1: Salt erosion factor; D2: F–T cycles factors; Dn: Coupling situation, n: Number of F–T cycles; x: Sulfate erosion days; α, β, γ, k, a, b c: Fitting parameters. | Macroscopic phenomenological damage mechanics | Salt-freeze coupling | Wang et al. [38] |
n: Number of F–T cycles. | Meso-statistical damage mechanics | 5% sodium sulfate F–T cycles | Xiao et al. [37] |
b: Fitting parameters; k: The general value is 1.25; nc: The number of cycles when RDEM is 0.8. | Low cycle fatigue theory & meso-statistical damage theory | F–T cycles of 0.4~0.5 water–cement ratio concrete | Nili et al. [160] |
a, b, c: Fitting parameters; n: Number of cycles. | Empirical formula | Steel slag concrete | Wen et al. [107] |
En/E0, Wn/W0: RDEM and relative mass loss after F–T cycles; a: Fitting parameters; n: Number of F–T cycles. | Empirical formula | Air entraining concrete. (considering quality loss) | Wang et al. [129] |
| Damage Model | Formula | Symbolic Meaning | Provenance |
|---|---|---|---|
| Compressive strength model | a: Fly ash content; b: Air contents; w: Water/binder ratio; n: Number of F–T cycles; f0: Initial strength. | Xiao et al. [165] | |
| Mass decay model | a, b, c: Fitting parameters; t0: Damage speed change point ; t: Mass denudation time. | Yu et al. [166] | |
| Mass decay model | n: Number of F–T cycles; a, b, c, d: Fitting parameters. | Mu et al. [167] | |
| Tensile strength model | ft0: Initial tensile strength; ftn: Tensile strength after F–T cycles; n: Number of F–T cycles. | Zhang et al. [168] | |
| Residual strain model | D(·): Limit state function; a: w/b ratio; b: gas drainage; n: Number of F–T cycles. | Cho et al. [169] | |
| Acoustic emission stress-strain model | a, b, c, d, e, f: Fitting parameters; : Peak strain; x: Normalized strain; : Compressive strain. | Qiu et al. [3] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Sun, W.; Xu, Y.; Lin, W.; Jing, W. Damage Mechanism and Modeling of Concrete in Freeze–Thaw Cycles: A Review. Buildings 2022, 12, 1317. https://doi.org/10.3390/buildings12091317
Guo J, Sun W, Xu Y, Lin W, Jing W. Damage Mechanism and Modeling of Concrete in Freeze–Thaw Cycles: A Review. Buildings. 2022; 12(9):1317. https://doi.org/10.3390/buildings12091317
Chicago/Turabian StyleGuo, Jinjun, Wenqi Sun, Yaoqun Xu, Weiqi Lin, and Weidong Jing. 2022. "Damage Mechanism and Modeling of Concrete in Freeze–Thaw Cycles: A Review" Buildings 12, no. 9: 1317. https://doi.org/10.3390/buildings12091317
APA StyleGuo, J., Sun, W., Xu, Y., Lin, W., & Jing, W. (2022). Damage Mechanism and Modeling of Concrete in Freeze–Thaw Cycles: A Review. Buildings, 12(9), 1317. https://doi.org/10.3390/buildings12091317