Investigating the Impact of Inclusions on the Behavior of 3D-Printed Composite Sandwich Beams
Abstract
:1. Introduction
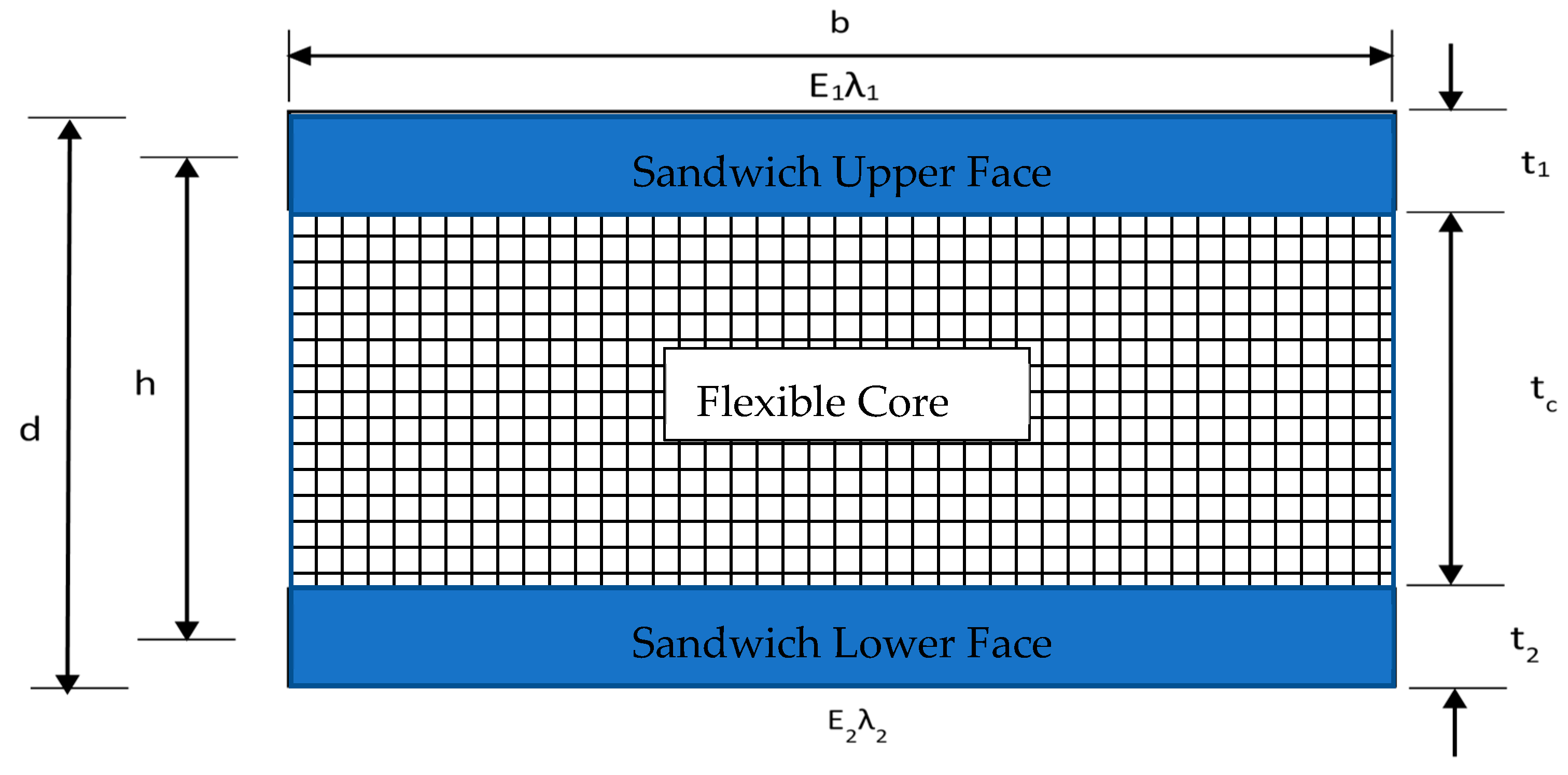
2. Material Properties and Experimental Setup
3. Research Methodology
4. FDM 3D Printing for the Manufacturing of Multilayered Bi-Materials
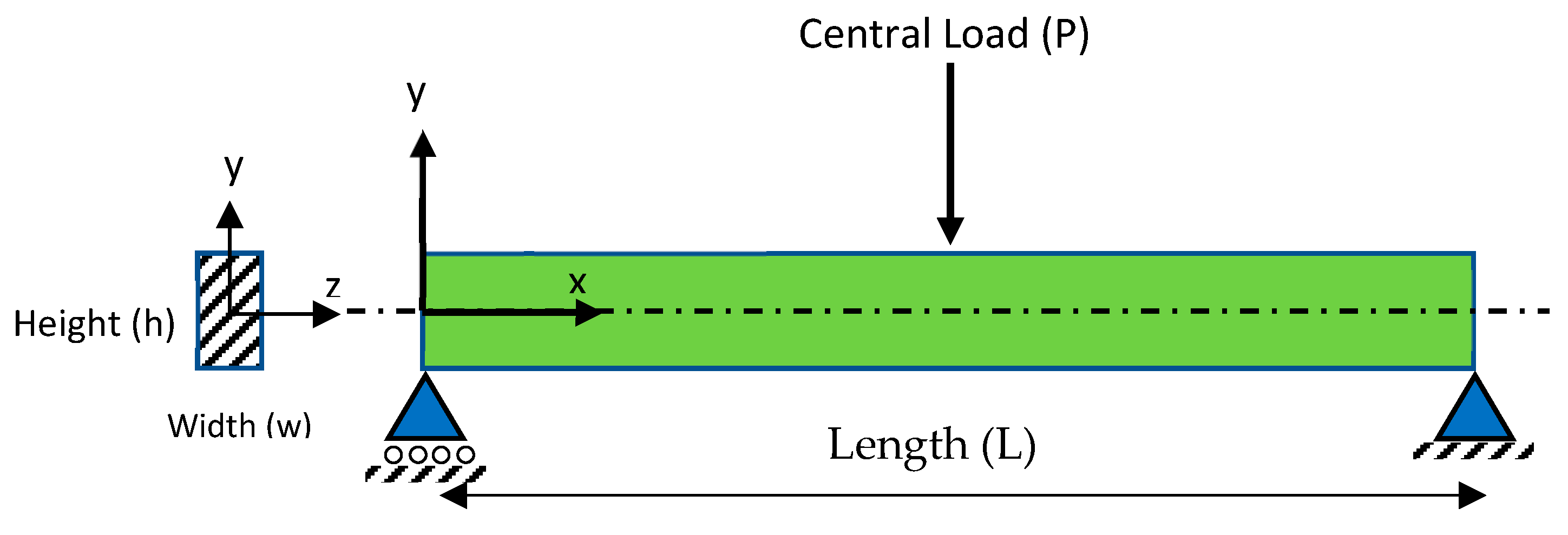
5. Analytics for a Beam under Bending Load
6. Results and Discussion
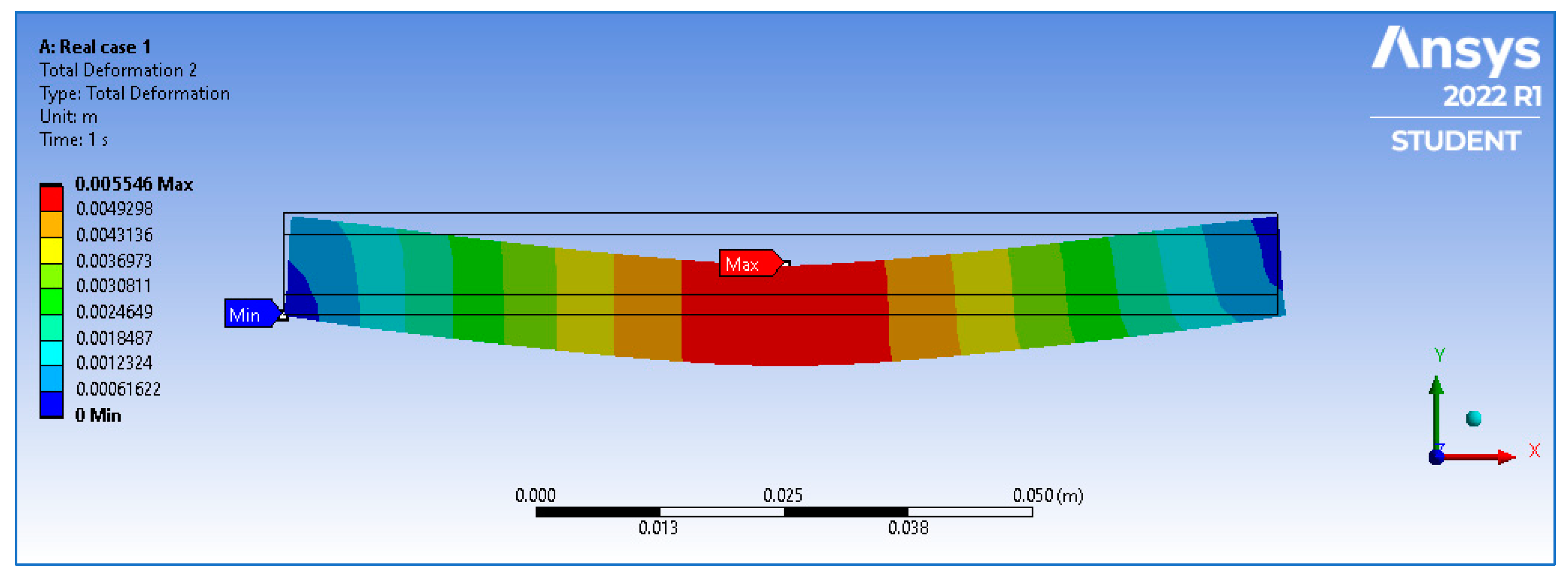
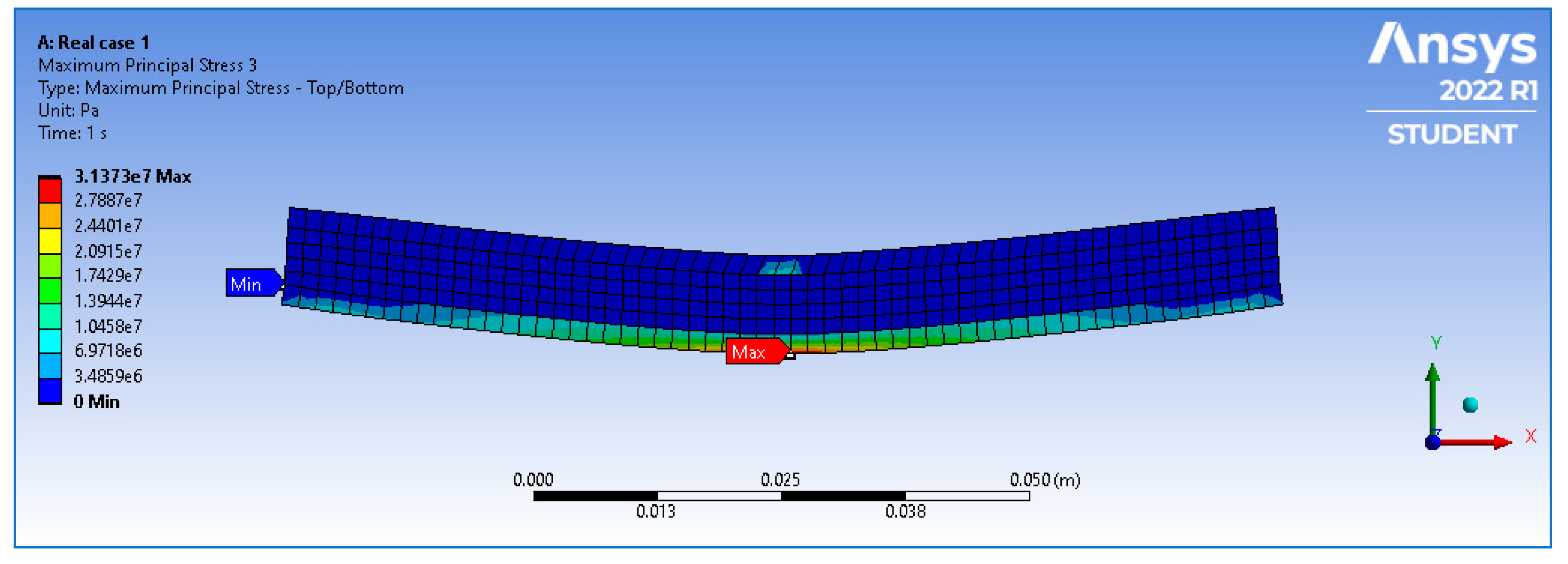
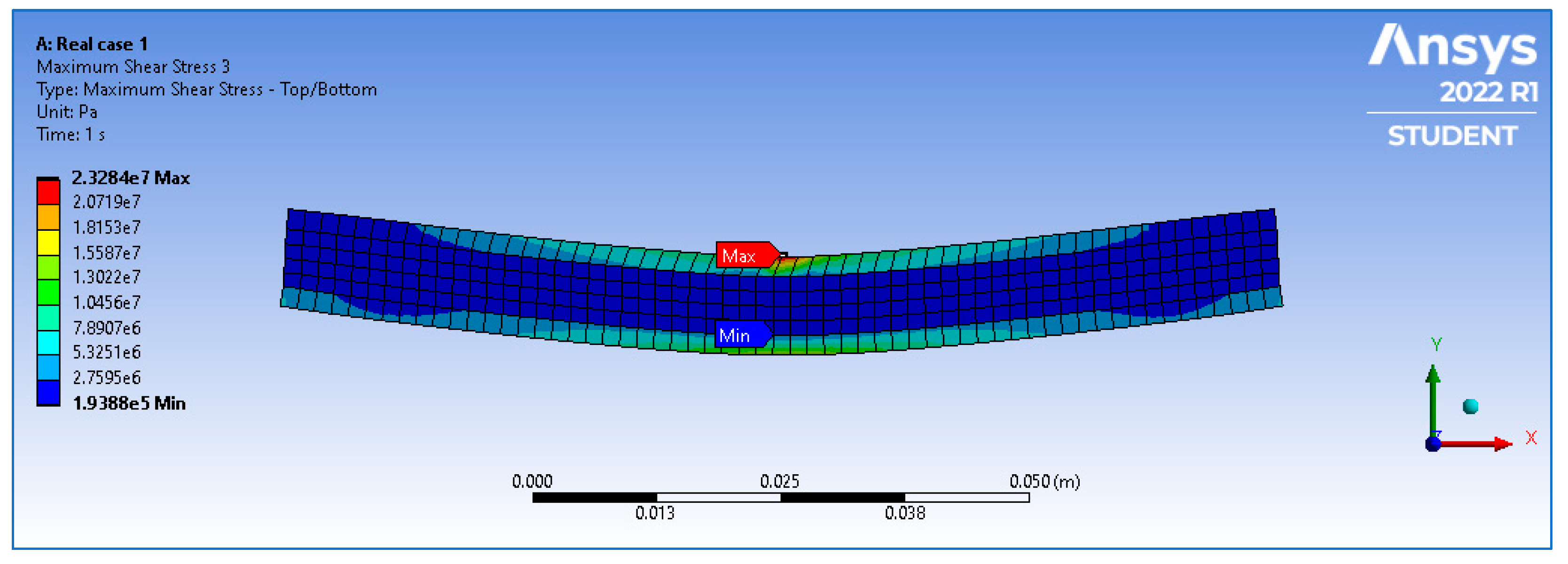
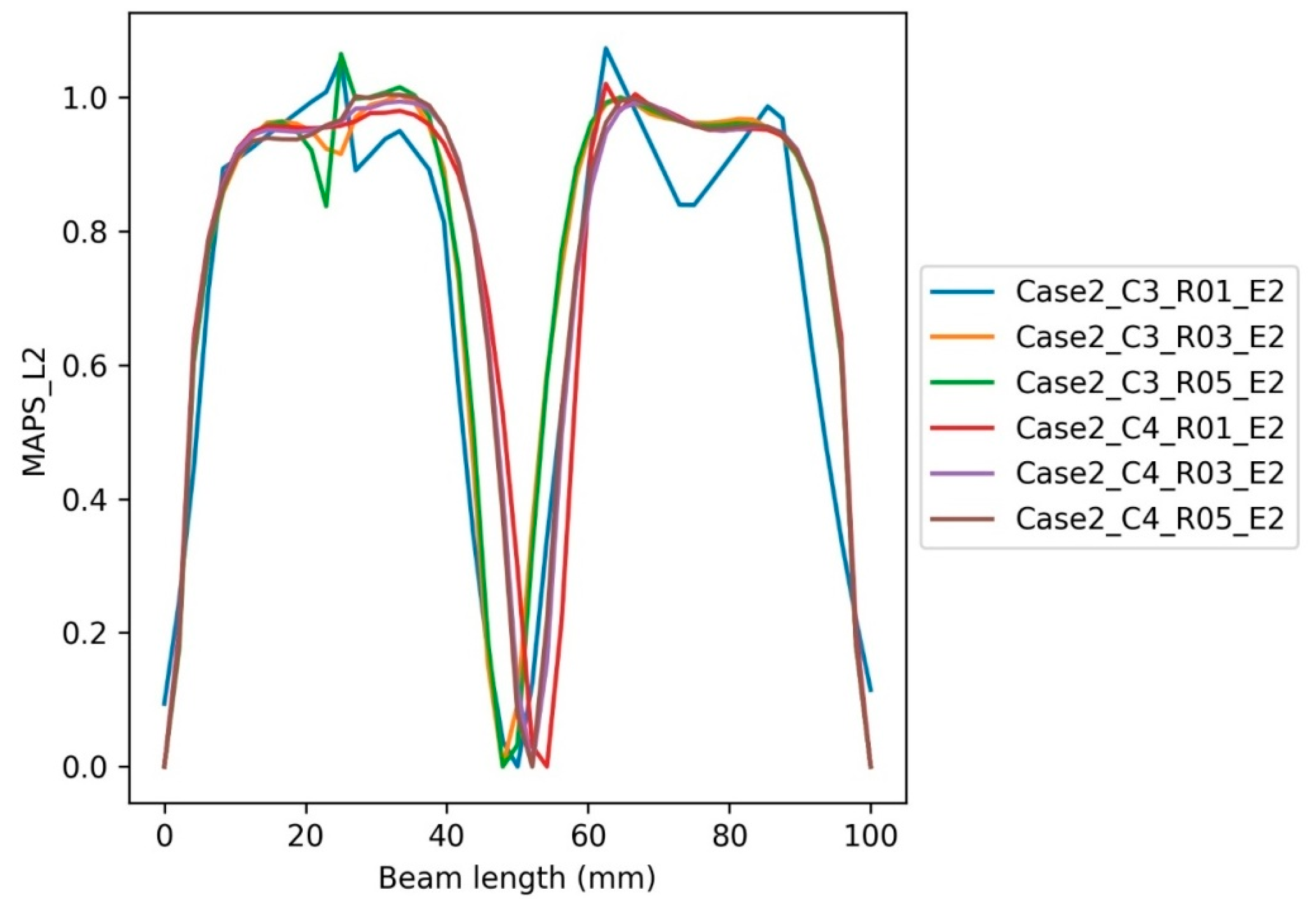
6.1. The Intact Case
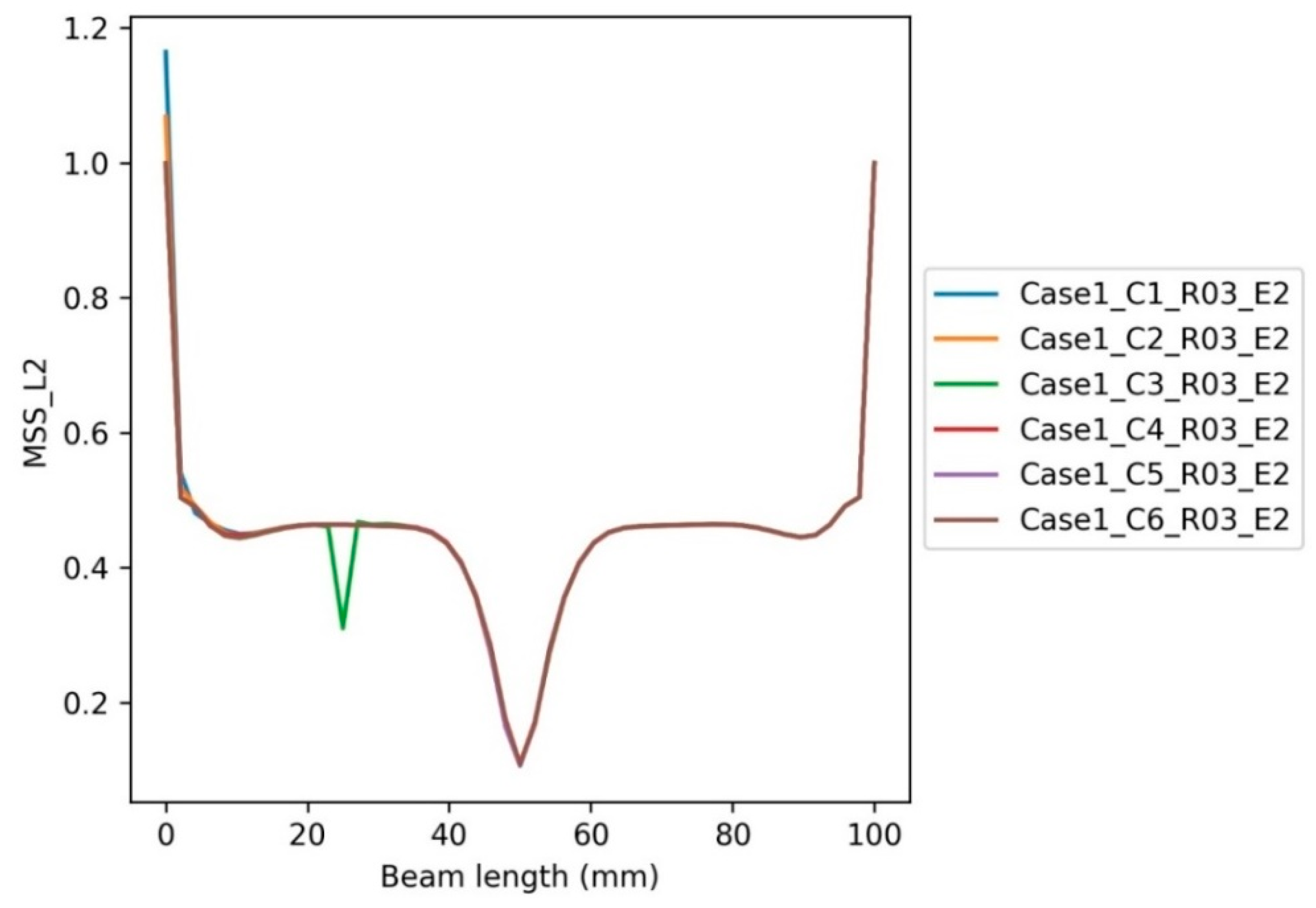
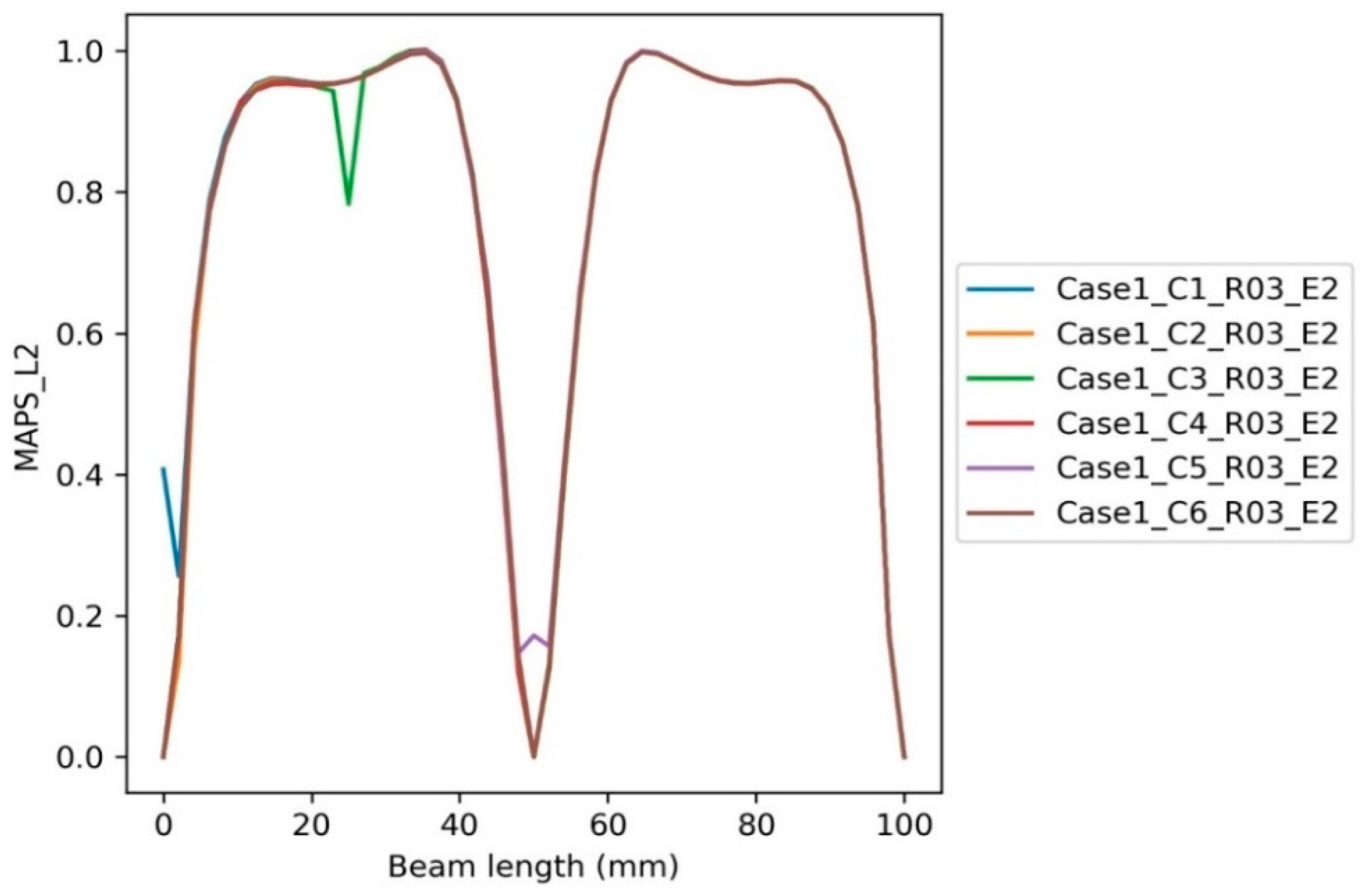
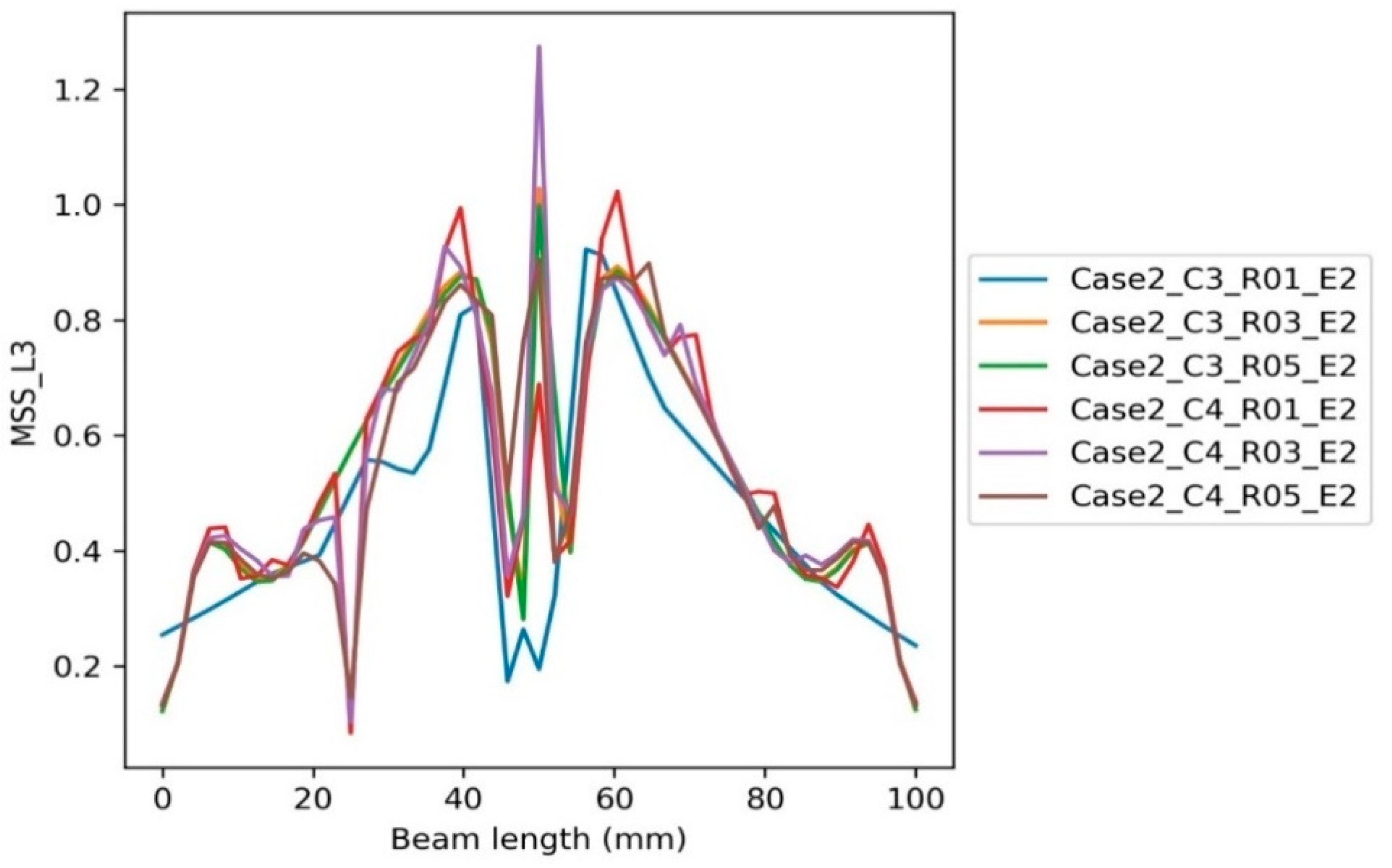
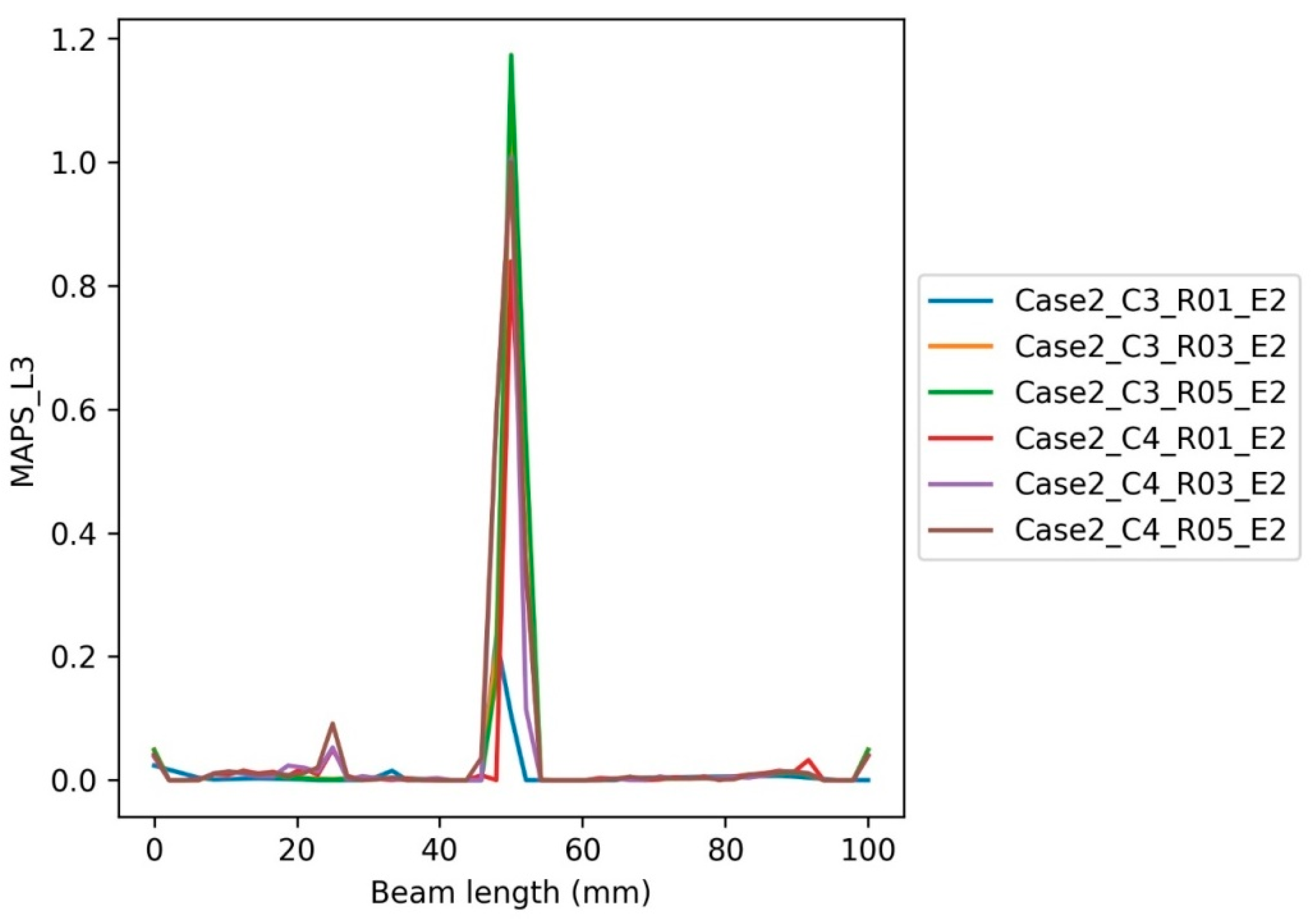
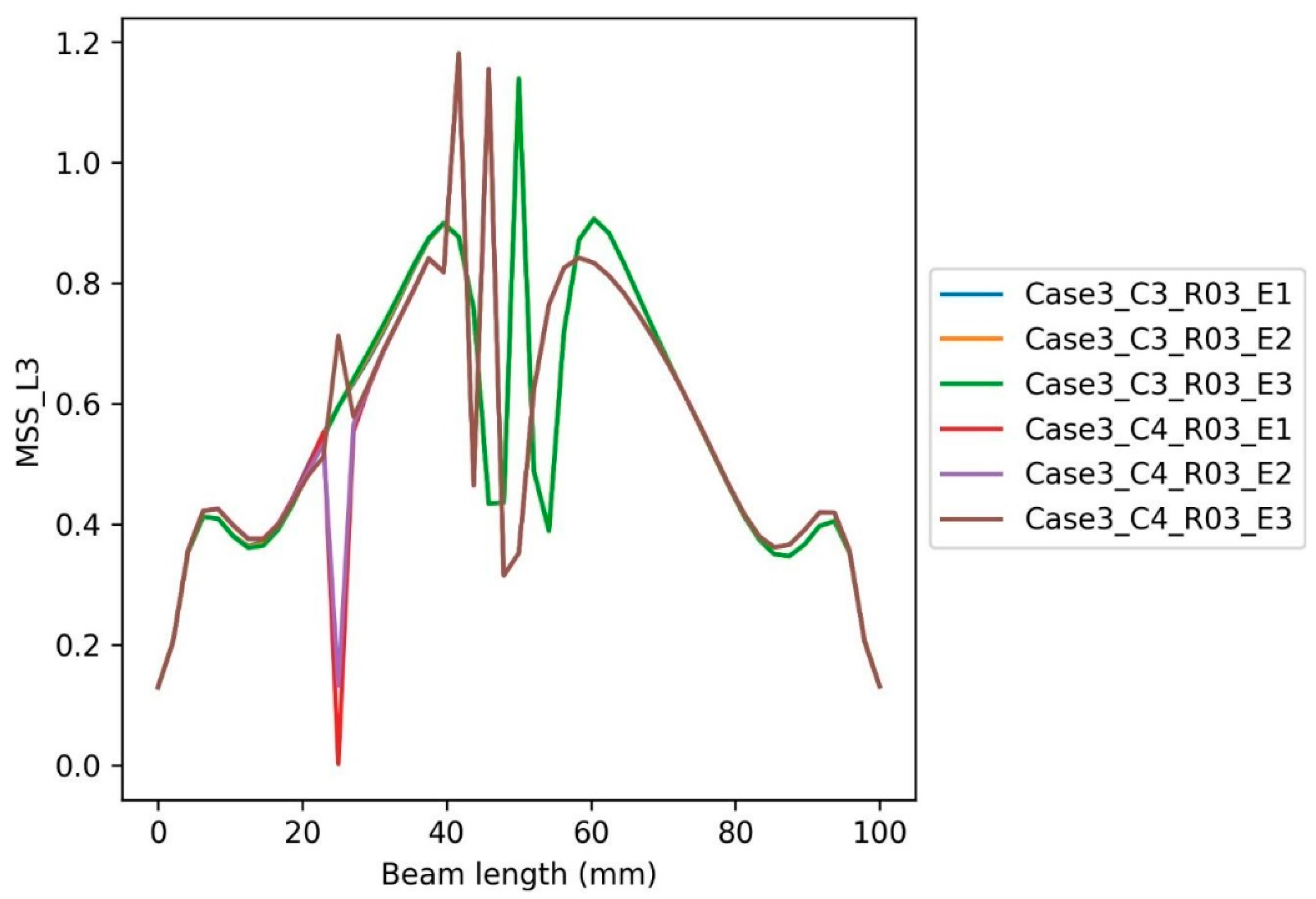
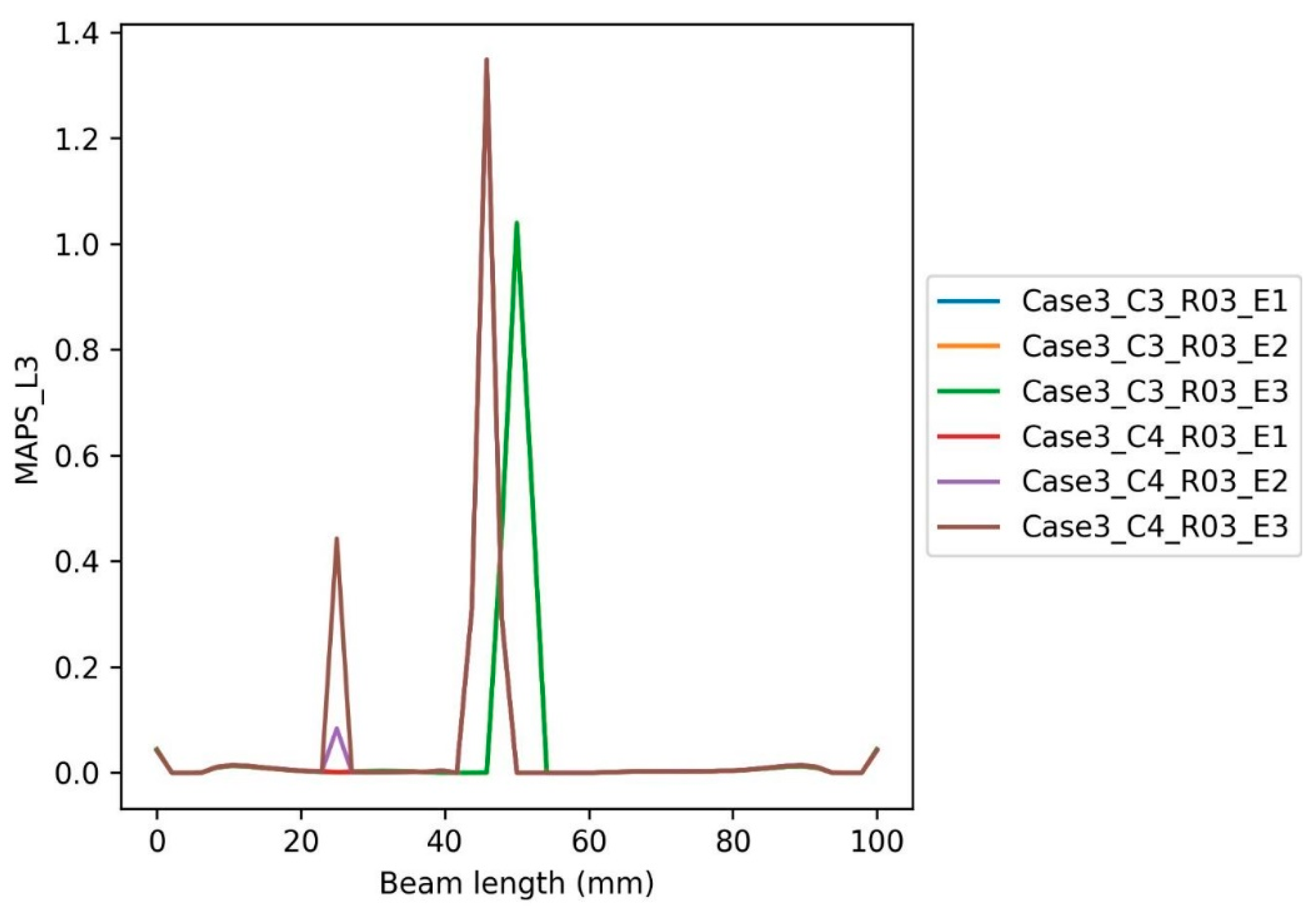
6.2. The Inclusion Cases
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Calignano, F.; Manfredi, D.; Ambrosio, E.P.; Biamino, S.; Lombardi, M.; Atzeni, E.; Salmi, A.; Minetola, P.; Iuliano, L.; Fino, P. Overview on additive manufacturing technologies. Proc. IEEE 2017, 105, 593–612. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar]
- Singh, S.; Ramakrishna, S.; Singh, R. Material issues in additive manufacturing: A review. J. Manuf. Process. 2017, 25, 185–200. [Google Scholar] [CrossRef]
- Stansbury, J.W.; Idacavage, M.J. 3D printing with polymers: Challenges among expanding options and opportunities. Dent. Mater. 2016, 32, 54–64. [Google Scholar] [CrossRef]
- Tofail, S.A.; Koumoulos, E.P.; Bandyopadhyay, A.; Bose, S.; O’Donoghue, L.; Charitidis, C. Additive manufacturing: Scientific and technological challenges, market uptake and opportunities. Mater. Today 2018, 21, 22–37. [Google Scholar] [CrossRef]
- Fateri, M.; Kaouk, A.; Cowley, A.; Siarov, S.; Palou, M.V.; González, F.G.; Marchant, R.; Cristoforetti, S.; Sperl, M. Feasibility study on additive manufacturing of recyclable objects for space applications. Addit. Manuf. 2018, 24, 400–404. [Google Scholar] [CrossRef]
- Gill, S.S.; Arora, H.; Sheth, V. On the development of Antenna feed array for space applications by additive manufacturing technique. Addit. Manuf. 2017, 17, 39–46. [Google Scholar] [CrossRef]
- Saltzman, D.; Bichnevicius, M.; Lynch, S.; Simpson, T.W.; Reutzel, E.W.; Dickman, C.; Martukanitz, R. Design and evaluation of an additively manufactured aircraft heat exchanger. Appl. Therm. Eng. 2018, 138, 254–263. [Google Scholar] [CrossRef]
- Huang, R.; Riddle, M.; Graziano, D.; Warren, J.; Das, S.; Nimbalkar, S.; Cresko, J.; Masanet, E. Energy and emissions saving potential of additive manufacturing: The case of lightweight aircraft components. J. Clean. Prod. 2016, 135, 1559–1570. [Google Scholar] [CrossRef]
- Zeltmann, S.E.; Gupta, N.; Tsoutsos, N.G.; Maniatakos, M.; Rajendran, J.; Karri, R. Manufacturing and security challenges in 3D printing. JOM 2016, 68, 1872–1881. [Google Scholar] [CrossRef]
- Schwarzer, E.; Holtzhausen, S.; Scheithauer, U.; Ortmann, C.; Oberbach, T.; Moritz, T.; Michaelis, A. Process development for additive manufacturing of functionally graded alumina toughened zirconia components intended for medical implant application. J. Eur. Ceram. Soc. 2019, 39, 522–530. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A. Additive manufacturing applications in medical cases: A literature based review. Alex. J. Med. 2018, 54, 411–422. [Google Scholar] [CrossRef]
- Rinaldi, M.; Ghidini, T.; Cecchini, F.; Brandao, A.; Nanni, F. Additive layer manufacturing of poly (ether ether ketone) via FDM. Compos. Part B Eng. 2018, 145, 162–172. [Google Scholar] [CrossRef]
- Turhan, D.; Celep, Z.; Zain-Edden, I.K. Transient wave propagation in layered media conducting heat. J. Sound Vib. 1991, 144, 247–261. [Google Scholar] [CrossRef]
- Ahmed, W.K.; Al-Rifaie, W.N. The impact of cracked microparticles on the mechanical and the fracture behavior of particulate composite. J. Nano- Electron. Phys. 2015, 7, 3008–3011. [Google Scholar]
- Sugiyama, K.; Matsuzaki, R.; Ueda, M.; Todoroki, A.; Hirano, Y. 3D printing of composite sandwich structures using continuous carbon fiber and fiber tension. Compos. Part A Appl. Sci. Manuf. 2018, 113, 114–121. [Google Scholar] [CrossRef]
- Carlsson, L.A.; Kardomateas, G.A. Structural and Failure Mechanics of Sandwich Composites; Springer Science & Business Media: Berlin, Germany, 2011; Volume 121. [Google Scholar]
- Emami, S. Development of Probabilistic Models for Long Term Reliability of Sandwich Composites in Saline Freeze/Thaw Environment for Civil Engineering Applications. Doctoral Dissertation, University of Dayton, Dayton, OH, USA, 2017. [Google Scholar]
- Ning, H.; Janowski, G.M.; Vaidya, U.K.; Husman, G. Thermoplastic sandwich structure design and manufacturing for the body panel of mass transit vehicle. Compos. Struct. 2007, 80, 82–91. [Google Scholar] [CrossRef]
- Karlsson, K.F.; TomasÅström, B. Manufacturing and applications of structural sandwich components. Compos. Part A Appl. Sci. Manuf. 1997, 28, 97–111. [Google Scholar] [CrossRef]
- Jakobsen, J.; Bozhevolnaya, E.; Thomsen, O.T. New peel stopper concept for sandwich structures. Compos. Sci. Technol. 2007, 67, 3378–3385. [Google Scholar] [CrossRef]
- Sypeck, D.J.; Wadley, H.N. Cellular metal truss core sandwich structures. Adv. Eng. Mater. 2002, 4, 759–764. [Google Scholar] [CrossRef]
- Dudek, P.F.D.M. FDM 3D printing technology in manufacturing composite elements. Arch. Metall. Mater. 2013, 58, 1415–1418. [Google Scholar] [CrossRef]
- Bates, S.R.; Farrow, I.R.; Trask, R.S. 3D printed polyurethane honeycombs for repeated tailored energy absorption. Mater. Des. 2016, 112, 172–183. [Google Scholar] [CrossRef] [Green Version]
- Yap, Y.L.; Yeong, W.Y. Shape recovery effect of 3D printed polymeric honeycomb: This paper studies the elastic behaviour of different honeycomb structures produced by PolyJet technology. Virtual Phys. Prototyp. 2015, 10, 91–99. [Google Scholar] [CrossRef]
- Chen, Y.; Li, T.; Jia, Z.; Scarpa, F.; Yao, C.W.; Wang, L. 3D printed hierarchical honeycombs with shape integrity under large compressive deformations. Mater. Des. 2018, 137, 226–234. [Google Scholar] [CrossRef]
- Sarvestani, H.Y.; Akbarzadeh, A.H.; Niknam, H.; Hermenean, K. 3D printed architected polymeric sandwich panels: Energy absorption and structural performance. Compos. Struct. 2018, 200, 886–909. [Google Scholar] [CrossRef]
- Sarvestani, H.Y.; Akbarzadeh, A.H.; Mirbolghasemi, A.; Hermenean, K. 3D printed meta-sandwich structures: Failure mechanism, energy absorption and multi-hit capability. Mater. Des. 2018, 160, 179–193. [Google Scholar] [CrossRef]
- Ang, K.C.; Leong, K.F.; Chua, C.K.; Chandrasekaran, M. Investigation of the mechanical properties and porosity relationships in fused deposition modelling-fabricated porous structures. Rapid Prototyp. J. 2006, 12, 100–105. [Google Scholar]
- Gebisa, A.W.; Lemu, H.G. Investigating effects of fused-deposition modeling (FDM) processing parameters on flexural properties of ULTEM 9085 using designed experiment. Materials 2018, 11, 500. [Google Scholar] [CrossRef]
- Calignano, F.; Lorusso, M.; Roppolo, I.; Minetola, P. Investigation of the mechanical properties of a carbon fibre-reinforced nylon filament for 3D printing. Machines 2020, 8, 52. [Google Scholar] [CrossRef]
- Hsueh, M.H.; Lai, C.J.; Liu, K.Y.; Chung, C.F.; Wang, S.H.; Pan, C.Y.; Huang, W.C.; Hsieh, C.H.; Zeng, Y.S. Effects of Printing Temperature and Filling Percentage on the Mechanical Behavior of Fused Deposition Molding Technology Components for 3D Printing. Polymers 2021, 13, 2910. [Google Scholar] [CrossRef]
- Heslehurst, R.B. Defects and Damage in Composite Materials and Structures; CRC Press: Boca Raton, FL, USA, 2014; Volume 19. [Google Scholar]
- Ahmed, W.; Alnajjar, F.; Zaneldin, E.; Al-Marzouqi, A.H.; Gochoo, M.; Khalid, S. Implementing FDM 3D Printing Strategies Using Natural Fibers to Produce Biomass Composite. Materials 2020, 13, 4065. [Google Scholar] [CrossRef] [PubMed]
- Yeon, Y.M.; Lee, W.; Hong, K.N. Finite Element Analysis of Reinforced Concrete Beams Prestressed by Fe-Based Shape Memory Alloy Bars. Appl. Sci. 2002, 12, 3255. [Google Scholar] [CrossRef]
- Ahmad, H.; Elnemr, A.; Ali, N.; Hussain, Q.; Chaiyasarn, K.; Joyklad, P. Finite element analysis of glass fiber-reinforced polymer-(Gfrp) reinforced continuous concrete beams. Polymers 2021, 13, 4468. [Google Scholar] [CrossRef] [PubMed]
- Pishro, A.A.; Zhang, Z.; Pishro, M.A.; Liu, W.; Zhang, L. Structural Performance of EB-FRP-Strengthened RC T-Beams Subjected to Combined Torsion and Shear Using ANN. Materials 2022, 15, 4852. [Google Scholar] [CrossRef] [PubMed]
- Ultimaker. Ultimaker TPU 95A Technical Datasheet. Available online: https://support.ultimaker.com/hc/en-us/articles/360012664440-Ultimaker-TPU-95A-TDS (accessed on 22 August 2022).
- FiberForce Italy. Nylforce Glass Fiber Data Sheet. Retrieved from 2019. Available online: http://www.fiberforce.it/wp-content/uploads/2019/07/TDS_NY-GLASS_REV-2.0.pdf (accessed on 22 August 2022).
- Stratford, T.; Cadei, J. Elastic analysis of adhesion stresses for the design of a strengthening plate bonded to a beam. Constr. Build. Mater. 2006, 20, 34–45. [Google Scholar] [CrossRef]
- Szeptyński, P. Comparison and experimental verification of simplified one-dimensional linear elastic models of multilayer sandwich beams. Compos. Struct. 2019, 241, 112088. [Google Scholar] [CrossRef]
- Stitic, A.; Nguyen, A.C.; Rezaei Rad, A.; Weinand, Y. Numerical Simulation of the Semi-Rigid Behaviour of Integrally Attached Timber Folded Surface Structures. Buildings 2019, 9, 55. [Google Scholar] [CrossRef]
- High Flexible Sandwich Panel Made of Glass Fibre Reinforced Nylon with Super Elastic Rubber Core Using Fused Filament Fabrication (FFF). Application Granted 2022-02-01; U.S. Patent US11235514B1. Available online: https://patents.google.com/patent/US11235514B1/en (accessed on 20 July 2022).
- Mostafaei, A.; Elliott, A.M.; Barnes, J.E.; Li, F.; Tan, W.; Cramer, C.L.; Nandwana, P.; Chmielus, M. Binder Jet 3D Printing–Process Parameters, Materials, Properties, and Challenges. Prog. Mater. Sci. 2020, 119, 100707. [Google Scholar] [CrossRef]
- Ahmed, W.; Alabdouli, H.; Alqaydi, H.; Mansour, A.; Al, K.H.; Al, J.H. Open Source 3D Printer: A Case Study. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Dubai, United Arab Emirates, 10–12 March 2020; pp. 2995–3004. [Google Scholar]
- Mansour, A.; Alabdouli, H.; Alqaydi, H.; Al, K.H.; Ahmed, W.; Al, J.H. Evaluating the 3D Printing Capabilities. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Dubai, United Arab Emirates, 10–12 March 2020; pp. 2618–2629. [Google Scholar]
- Ahmed, W.; Ahmed, S.; Alnajjar, F.; Zaneldin, E. Mechanical performance of three-dimensional printed sandwich composite with a high-flexible core. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2021, 235, 1382–1400. [Google Scholar] [CrossRef]
- Ahmed, W.; Zanledin, E.; Kabbani, S. Fracture Mechanics Performance of Through-Thickness Crack of Polymeric 3D Printed Components. Lect. Notes Mech. Eng. 2020, 12, 302. [Google Scholar]
- Waleed, A. Product and Method to Manufacture Multi-Layered, Multi-Material Composite Sandwich with Hyper Elasticity Rubber Like Core Made by Fusion Deposition Modelling. US10974444B1 United States Application granted 2021-04-13. Available online: https://patents.google.com/patent/US10974444B1/en (accessed on 20 July 2022).
- Gebrehiwot, S.Z.; Espinosa-Leal, L.; Eickhof, J.N.; Rechenberg, L. Correction to: The Influence of Stiffener Geometry on Flexural Properties of 3D-Printed Polylactic Acid (PLA) Beams. Prog. Addit. Manuf. 2020, 5, 421. [Google Scholar] [CrossRef]
- Gere, J.M.; Goodno, B.J. Mechanics of Materials; SI ed.; Cengage Learning: Boston, MA, USA, 2008. [Google Scholar]
- Barber, J.R. Introduction. In Elasticity; Barber, J.R., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 3–24. [Google Scholar]
- Practical Guide to Finite Elements—A Solid Mechanics Approach: By Steven M. Lepi–ScienceDirect. Available online: https://www-sciencedirect-com.uaeu.idm.oclc.org/science/article/pii/S0997753898905083?via%3Dihub (accessed on 25 November 2020).
- Barber, J.R. Calculation of Displacements. In Elasticity; Barber, J.R., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 123–134. [Google Scholar]
- ISO 178:2019-Plastics-Determination of Flexural Properties. Available online: https://standards.iteh.ai/catalog/standards/iso/6d9ee8ed-eaf6-49f6-b83b-bd615d3367df/iso-178-2019 (accessed on 25 November 2020).
- Barber, J.R. Application to Elasticity Problems. In Elasticity; Barber, J.R., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 293–317. [Google Scholar]
- Barber, J.R. Thermoelastic Displacement Potentials. In Elasticity; Barber, J.R., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 347–361. [Google Scholar]
- Bitzer, T.N. Honeycomb Technology: Materials, Design, Manufacturing, Applications and Testing; Springer: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Richard, H.; Sander, M.; Fulland, M.; Kullmer, G. Development of fatigue crack growth in real structures. Eng. Fract. Mech. 2008, 75, 331–340. [Google Scholar] [CrossRef]
- Fang, Q.; Chen, J.; Liu, Y.; Wen, P. Critical shear stress produced by interaction of edge dislocation with nanoscale inhomogeneity. Bull. Mater. Sci. 2010, 33, 123–127. [Google Scholar] [CrossRef]
- Xu, J.; Dong, C. Surface and interface stress effects on the interaction of nano-inclusions and nano-cracks in an infinite domain under anti-plane shear. Int. J. Mech. Sci. 2016, 111–112, 12–23. [Google Scholar] [CrossRef]
- Lin, P.; Lin, S.; Pan, J. Modeling of failure near spot welds in lap-shear specimens based on a plane stress rigid inclusion analysis. Eng. Fract. Mech. 2006, 73, 2229–2249. [Google Scholar] [CrossRef]
- Yan, A.; Nguyen-Dang, H. Multiple-cracked fatigue crack growth by BEM. Comput. Mech. 1995, 16, 273–280. [Google Scholar] [CrossRef]
- Thibodeau, W.E.; Wood, L.A. Photoelastic determination of stresses around a circular inclusion in rubber. J. Frankl. Inst. 1938, 225, 475–476. [Google Scholar] [CrossRef]
- Qi, D.; Hu, W.; Xin, K.; Zeng, Q.; Xi, L.; Tao, R.; Liao, H.; Deng, Y.; Liao, B.; Wu, W.; et al. In-situ synchrotron X-ray tomography investigation of micro lattice manufactured with the projection micro-stereolithography (PμSL) 3D printing technique: Defects characterization and in-situ shear test. Compos. Struct. 2020, 252, 112710. [Google Scholar] [CrossRef]
- Ma, C.; Zhang, G.; Wang, Y.; Zhang, Z.; Ren, Z. Effect of Non-metallic Inclusions on Subsurface Stress and Fatigue Life of High-speed Railway Bearings. IOP Conf. Ser. Earth Environ. Sci. 2021, 632, 052001. [Google Scholar] [CrossRef]
- Tam, K.; Mueller, C. Additive Manufacturing Along Principal Stress Lines. 3D Print. Addit. Manuf. 2017, 4, 63–81. [Google Scholar] [CrossRef]
- Wang, J.; Ren, L.; Xie, L.; Xie, H.; Ai, T. Maximum mean principal stress criterion for three-dimensional brittle fracture. Int. J. Solids Struct. 2016, 102–103, 142–154. [Google Scholar] [CrossRef]
- Blenkinsop, T. Relationships between faults, extension fractures and veins, and stress. J. Struct. Geol. 2008, 30, 622–632. [Google Scholar] [CrossRef]
- Fang, Q.; Liu, Y.; Huang, B.; Liu, Y.; Wen, P. Contribution to critical shear stress of nanocomposites produced by interaction of screw dislocation with nanoscale inclusion. Mater. Lett. 2008, 62, 3521–3523. [Google Scholar] [CrossRef]
- Lang, P.; Paluszny, A.; Nejati, M.; Zimmerman, R. Relationship Between the Orientation of Maximum Permeability and Intermediate Principal Stress in Fractured Rocks. Water Resour. Res. 2018, 54, 8734–8755. [Google Scholar] [CrossRef] [Green Version]
- Mori, T.; Hirayama, S. Fatigue Crack Propagation and Strength of Web-Gusset Welded Joints Under Varied Principal Stress Direction. J. JSCE 2015, 3, 128–139. [Google Scholar] [CrossRef]
- Ahmed, W.; Siraj, S.; Al-Marzouqi, A.H. 3D Printing PLA Waste to Produce Ceramic Based Particulate Reinforced Composite Using Abundant Silica-Sand: Mechanical Properties Characterization. Polymers 2020, 12, 2579. [Google Scholar] [CrossRef]
- Ahmed, W.; Siraj, S.; Al-Marzouqi, A.H. Comprehensive Characterization of Polymeric Composites Reinforced with Silica Microparticles Using Leftover Materials of Fused Filament Fabrication 3D Printing. Polymers 2021, 13, 2423. [Google Scholar] [CrossRef]
- Ahmed, W.; Siraj, S.; Al-Marzouqi, A.H. Embracing Additive Manufacturing Technology through Fused Filament Fabrication for Antimicrobial with Enhanced Formulated Materials. Polymers 2021, 13, 1523. [Google Scholar] [CrossRef]
- Al-Mazrouei, N.; Al-Marzouqi, A.H.; Ahmed, W. Characterization and Sustainability Potential of Recycling 3D-Printed Nylon Composite Wastes. Sustainability 2022, 14, 10458. [Google Scholar] [CrossRef]
- Almazrouei, N.; Siraj, S.; Al-Marzouqi, A.H.; Ahmed, W. Producing Particulate Composite Using 3D Printing Plastics Waste. In Proceedings of the 2022 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 21–24 February 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Al-Mazrouei, N.; Ismail, A.; Ahmed, W.; Al-Marzouqi, A.H. ABS/Silicon Dioxide Micro Particulate Composite from 3D Printing Polymeric Waste. Polymers 2022, 14, 509. [Google Scholar] [CrossRef]
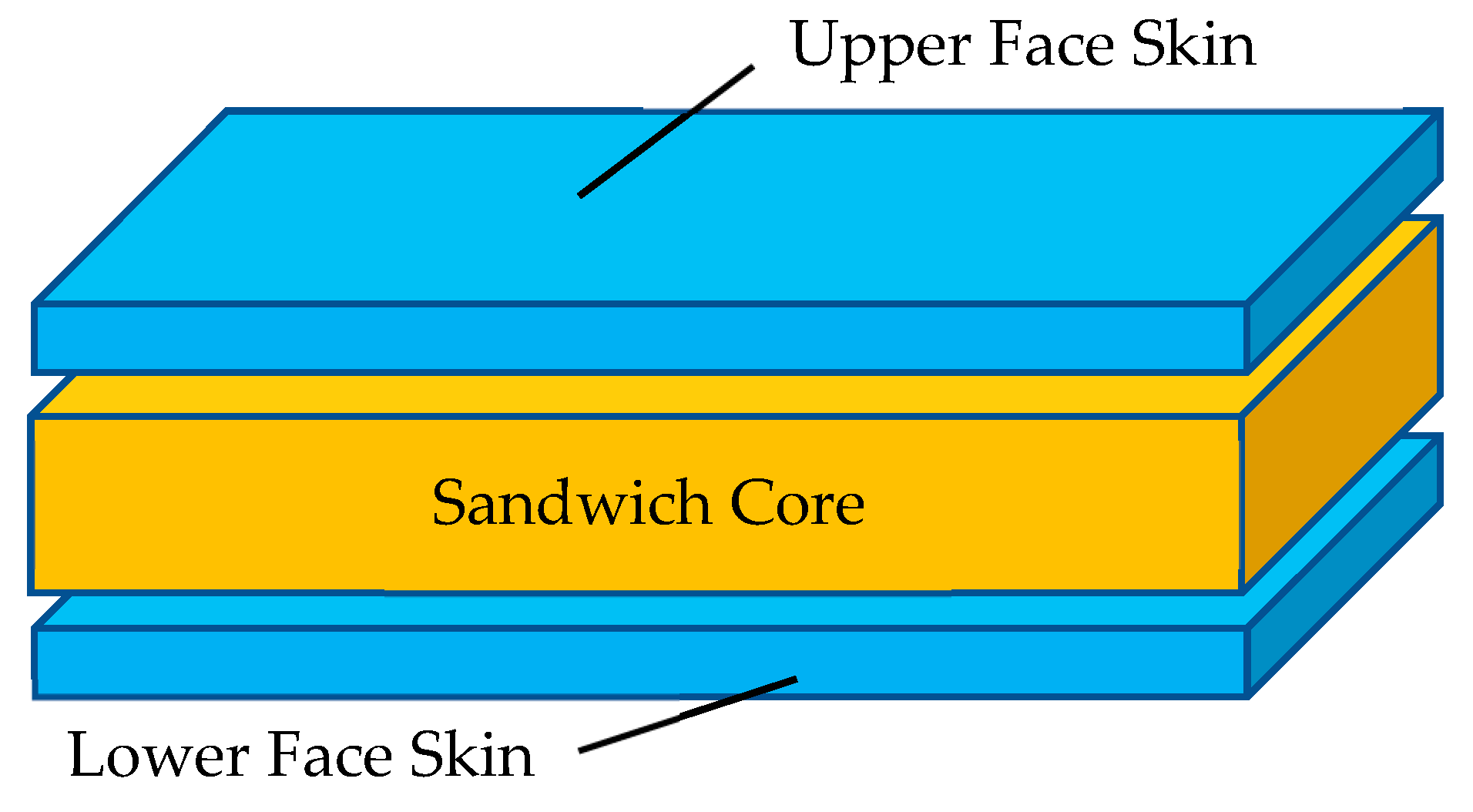
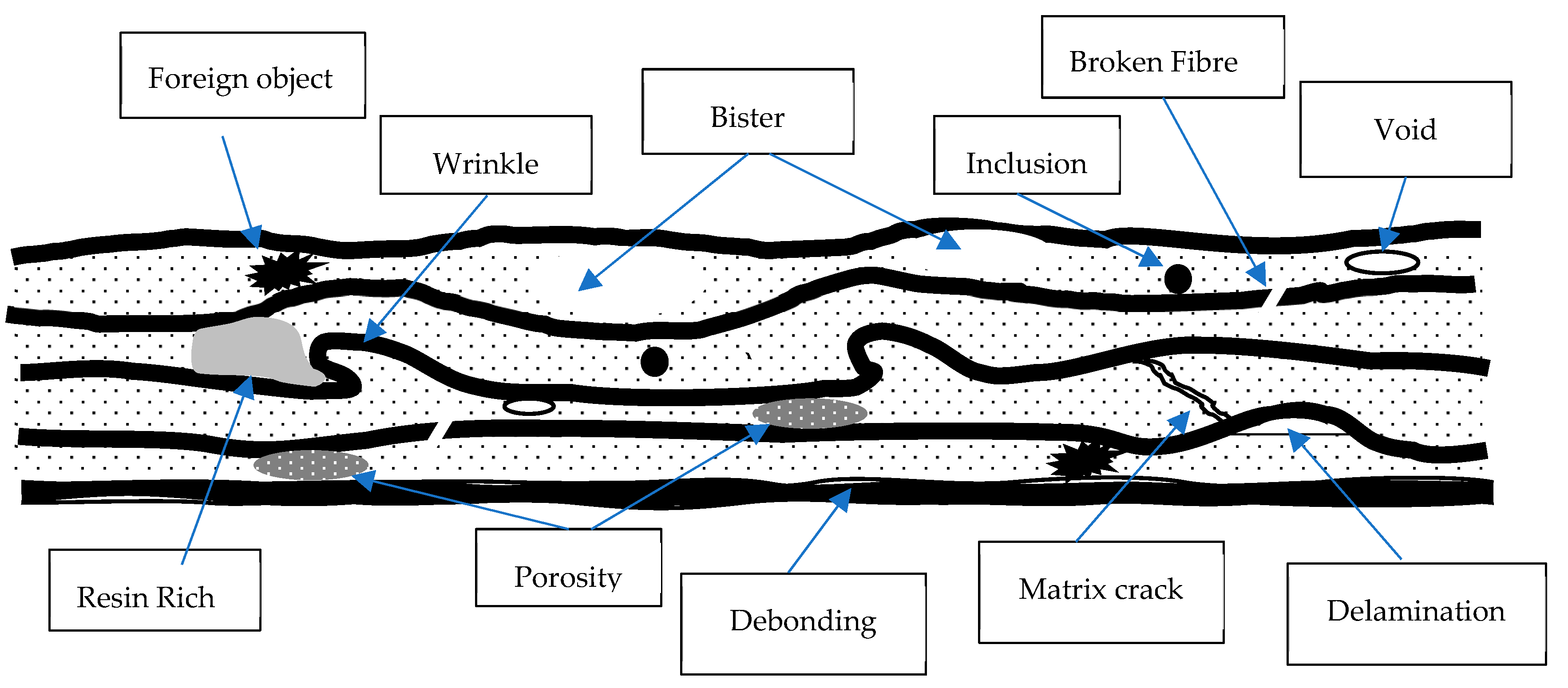
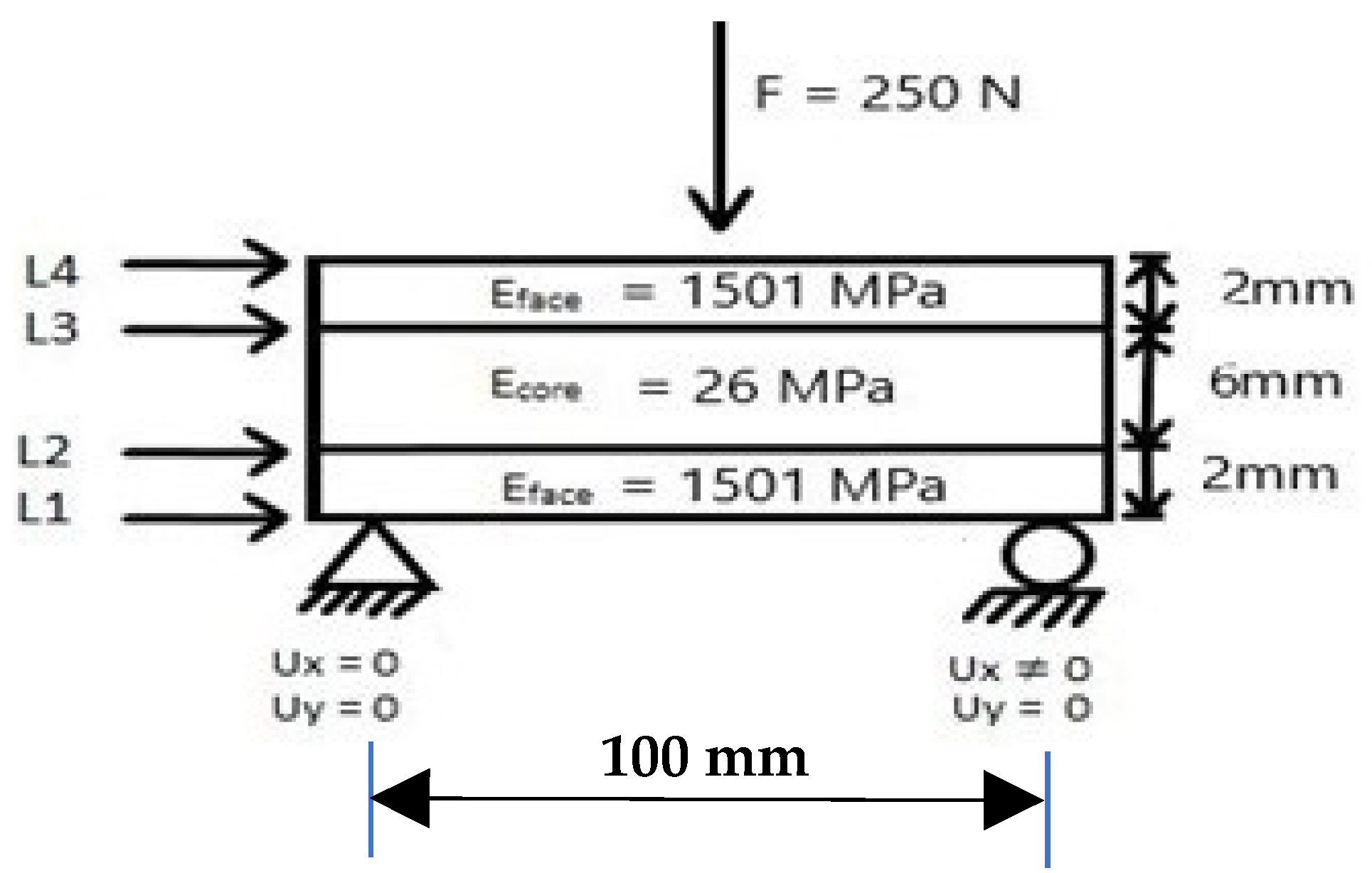
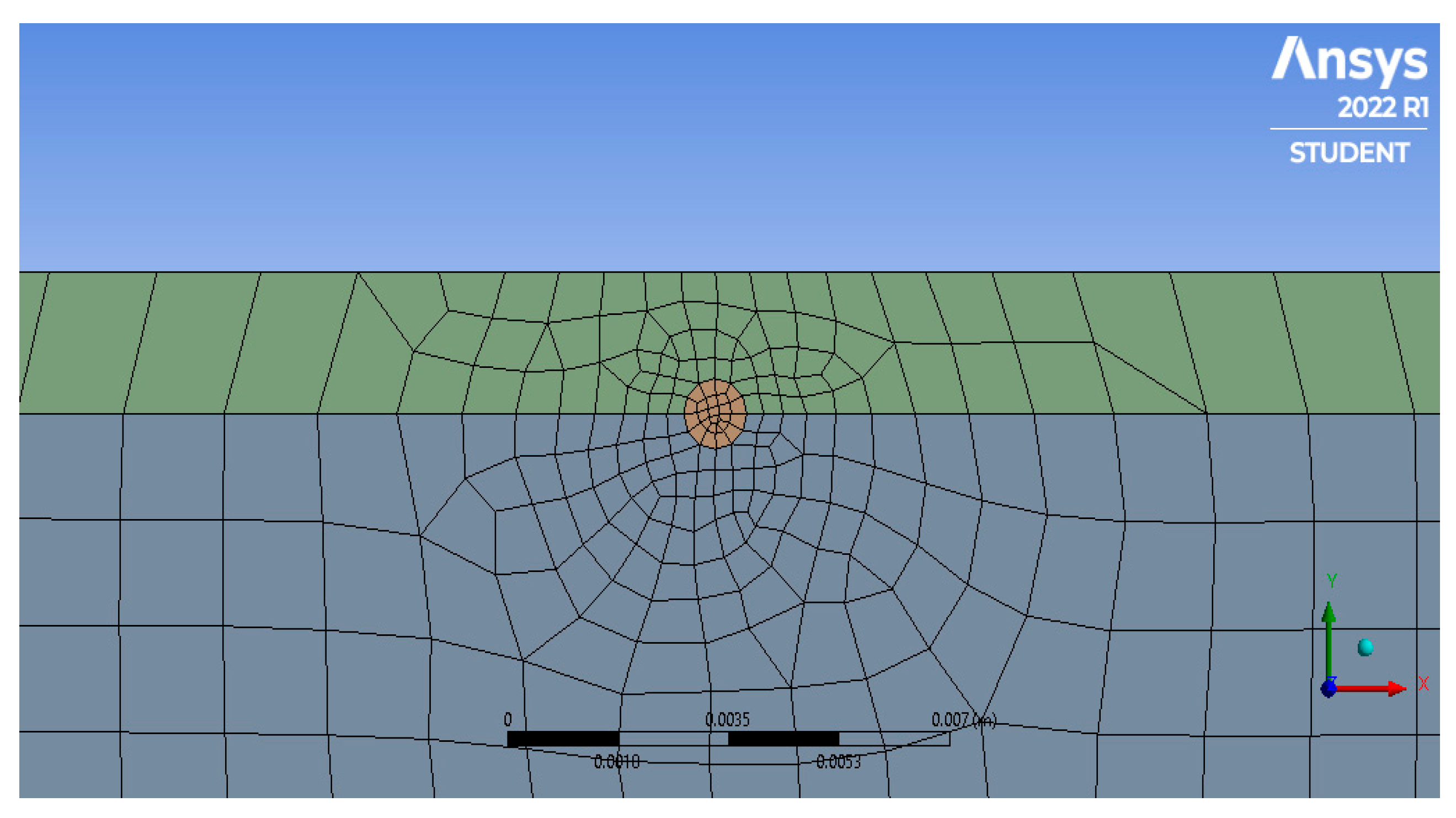











| Properties | Face Material | Core Material |
|---|---|---|
| Young’s Modulus | 1501 MPa | 26 MPa |
| Poison’s Ration | 0.3 | 0.3 |
| Bulk Modulus | 1250.8 MPa | 21.66 MPa |
| Shear Modulus | 577.31 MPa | 10 MPa |
| Varying Parameter | Range | Notation | Group | |||
|---|---|---|---|---|---|---|
| Group 1 | Group 2 | Group 3 | ||||
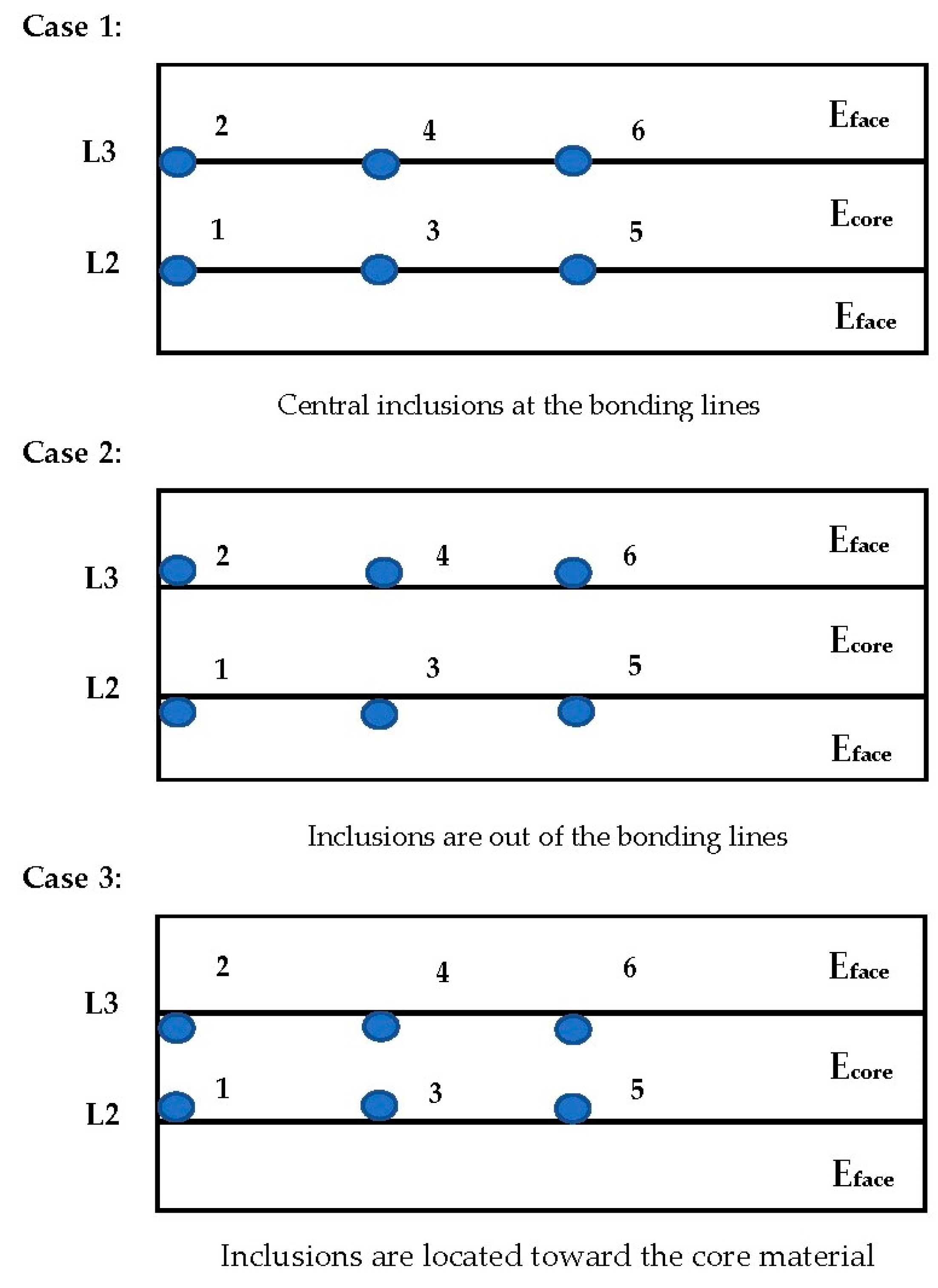
| Position of Inclusion | 0 mm | Along L2 | C1, C_ circle | Position of inclusion varies | Remains constant | Remains constant |
| 15 mm | C3 | |||||
| 50 | C5 | |||||
| 0 mm | Along L3 | C2 | ||||
| 15 mm | C4 | |||||
| 50 | C6 | |||||
| Geometry of Inclusion (Radius) | 0.1 mm | R01, R_ Radius | Radius is constant at R03 | Radius (R) of inclusion varies | Radius is constant at R03 | |
| 0.3 mm | R03 | |||||
| 0.5 mm | R05 | |||||
| Young’s modulus (E) of Inclusion | 0.26 MPa | E1, E_ Modulus | Modulus is constant at E2 | Modulus is constant at E2 | Young’s modulus of inclusion varies | |
| 26 MPa | E2 | |||||
| 1051 MPa | E3 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Hassan, A.; Ahmed, W.; Zaneldin, E. Investigating the Impact of Inclusions on the Behavior of 3D-Printed Composite Sandwich Beams. Buildings 2022, 12, 1448. https://doi.org/10.3390/buildings12091448
El Hassan A, Ahmed W, Zaneldin E. Investigating the Impact of Inclusions on the Behavior of 3D-Printed Composite Sandwich Beams. Buildings. 2022; 12(9):1448. https://doi.org/10.3390/buildings12091448
Chicago/Turabian StyleEl Hassan, Amged, Waleed Ahmed, and Essam Zaneldin. 2022. "Investigating the Impact of Inclusions on the Behavior of 3D-Printed Composite Sandwich Beams" Buildings 12, no. 9: 1448. https://doi.org/10.3390/buildings12091448
APA StyleEl Hassan, A., Ahmed, W., & Zaneldin, E. (2022). Investigating the Impact of Inclusions on the Behavior of 3D-Printed Composite Sandwich Beams. Buildings, 12(9), 1448. https://doi.org/10.3390/buildings12091448








