Research and Implementation of Three-Dimensional Spatial Information Characterization and Visualization of Fractures in Deteriorated Sandstone
Abstract
:1. Introduction
2. Specimen and Equipment
3. MATLAB-Based Visual Analysis
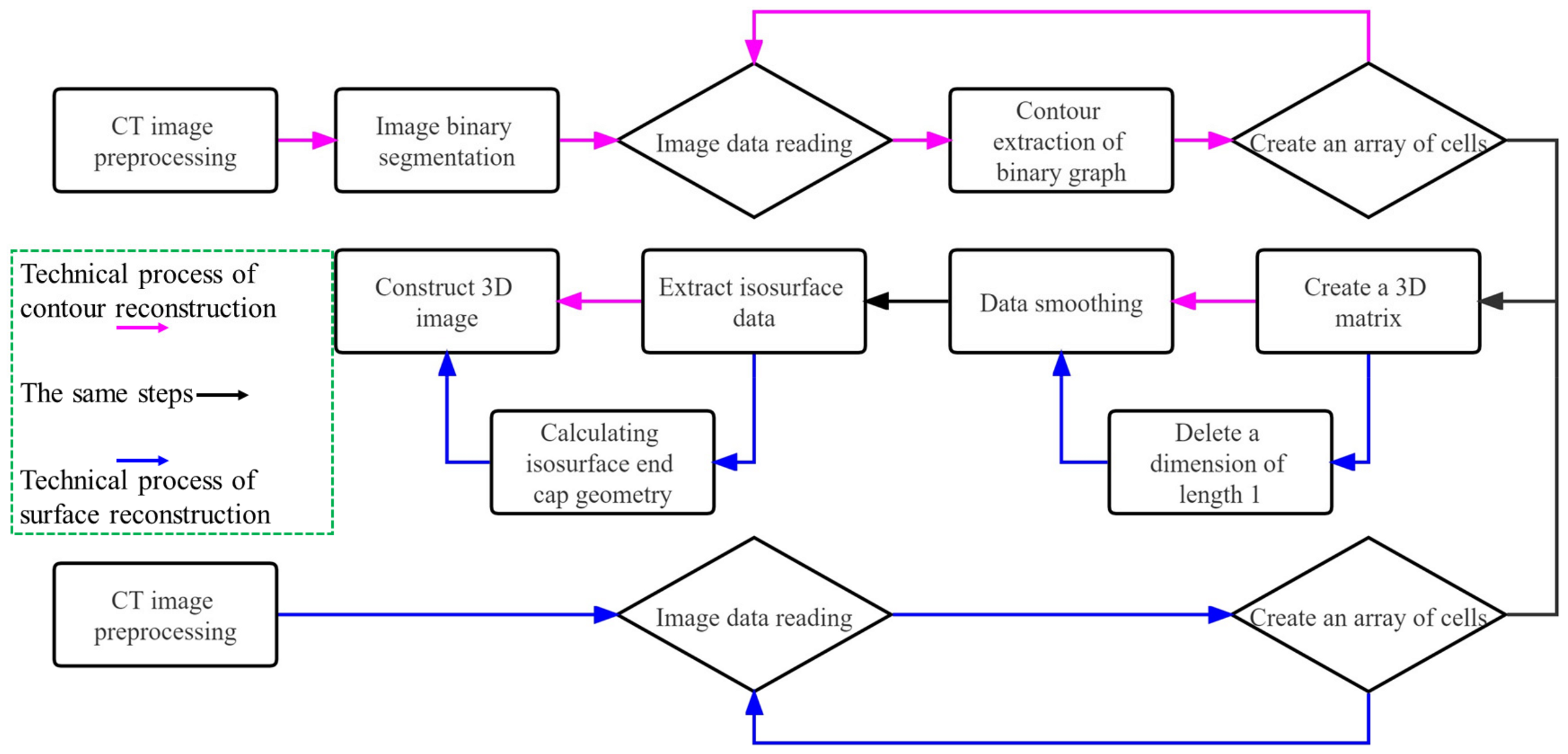
3.1. Three-Dimensional Reconstruction Technology Based on Object Cross-Section Information and Contour Information
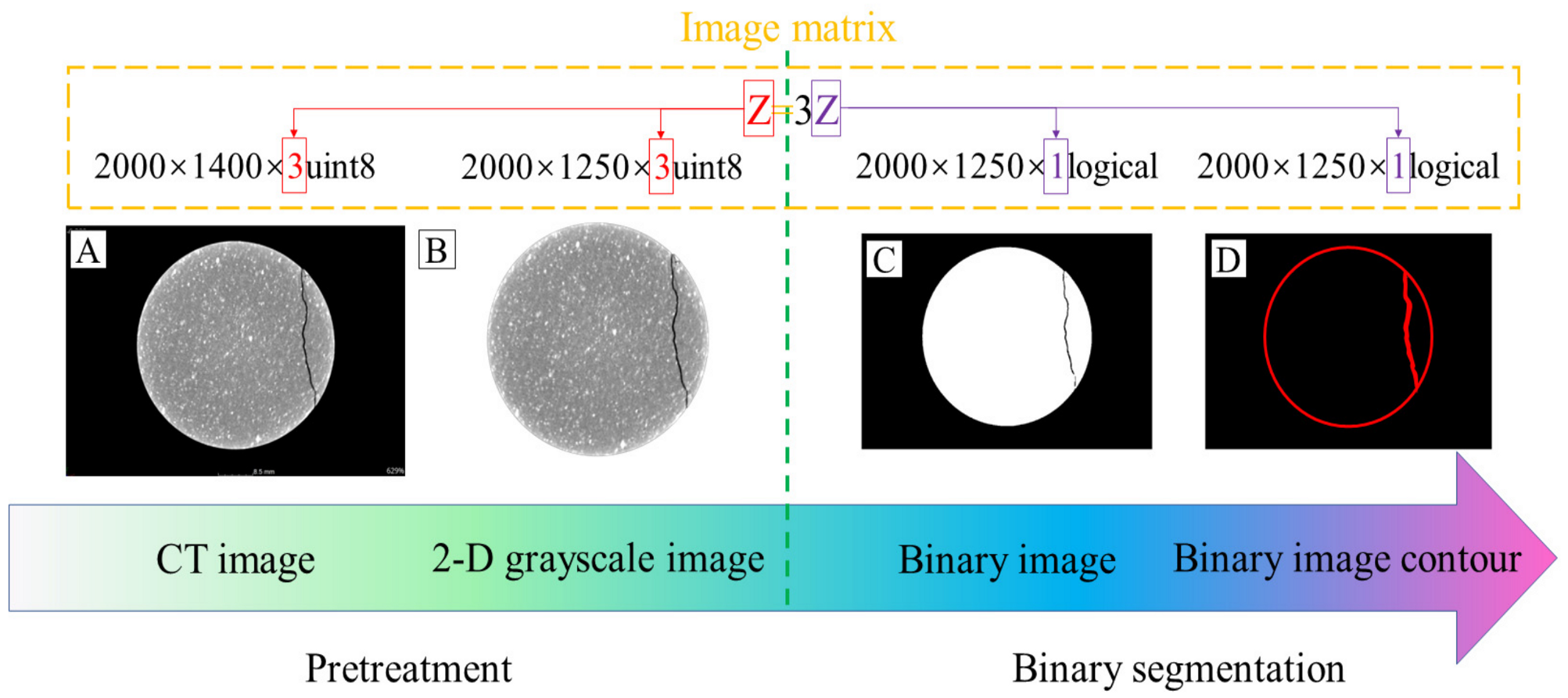
3.1.1. CT Image Preprocessing and Binary Graph Contour Representation
3.1.2. Analysis of 3D Reconstruction Results Based on Cross-Section Information and Contour Information
3.2. Three-Dimensional Reconstruction Technology for Extracting Point Cloud Data of Internal Cracks in Deteriorated Sandstone
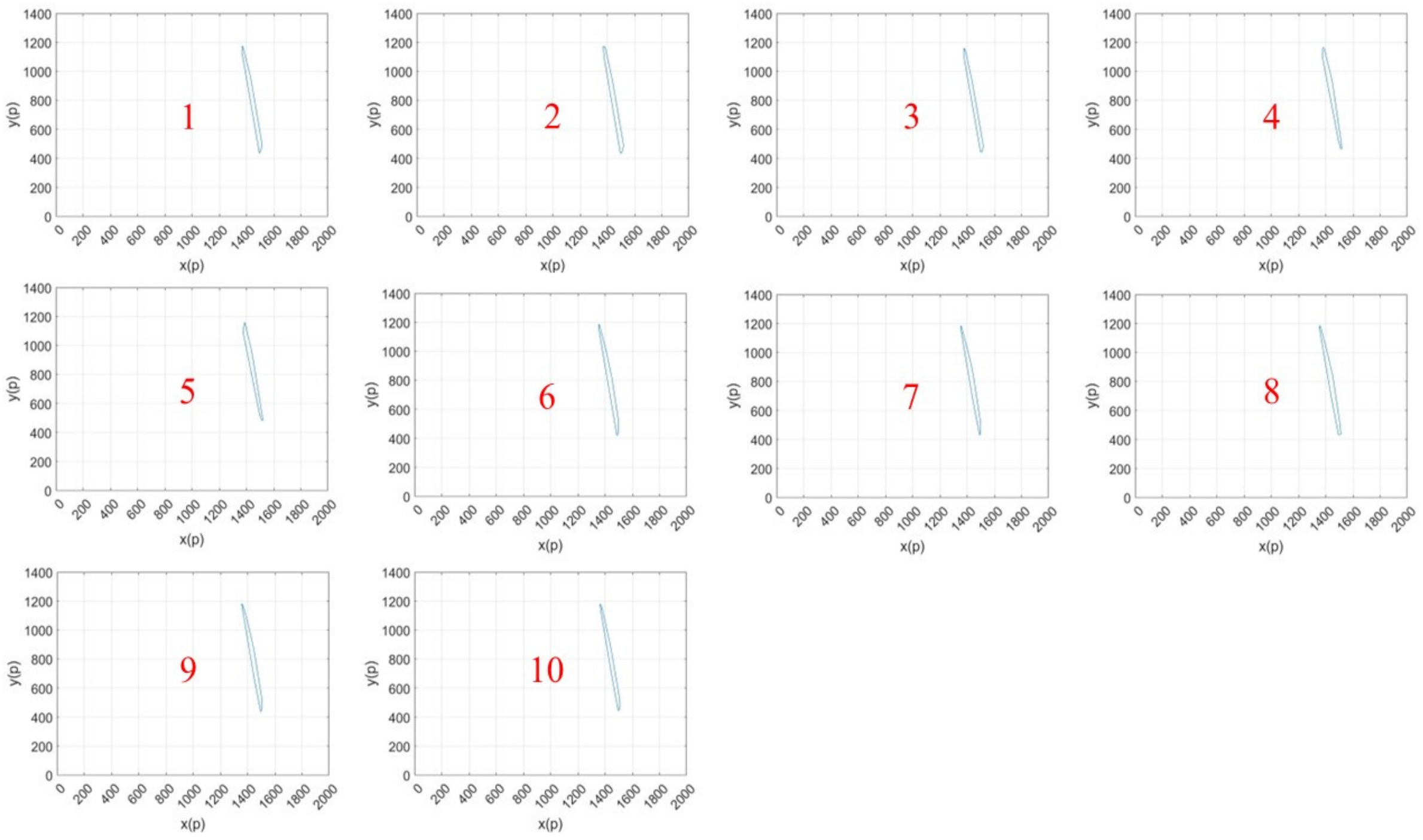
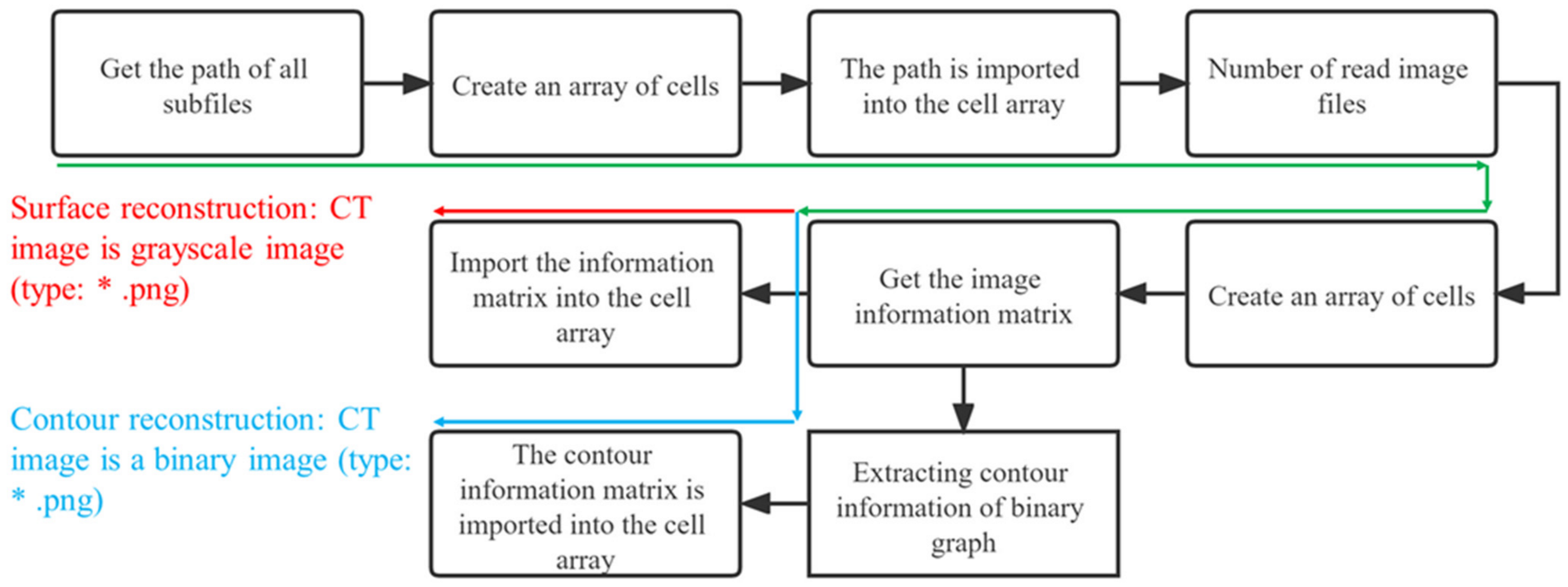
3.2.1. CT Scan Image Preprocessing and the Required Number of Images
3.2.2. Extracting Point Cloud Data and 3D Reconstruction
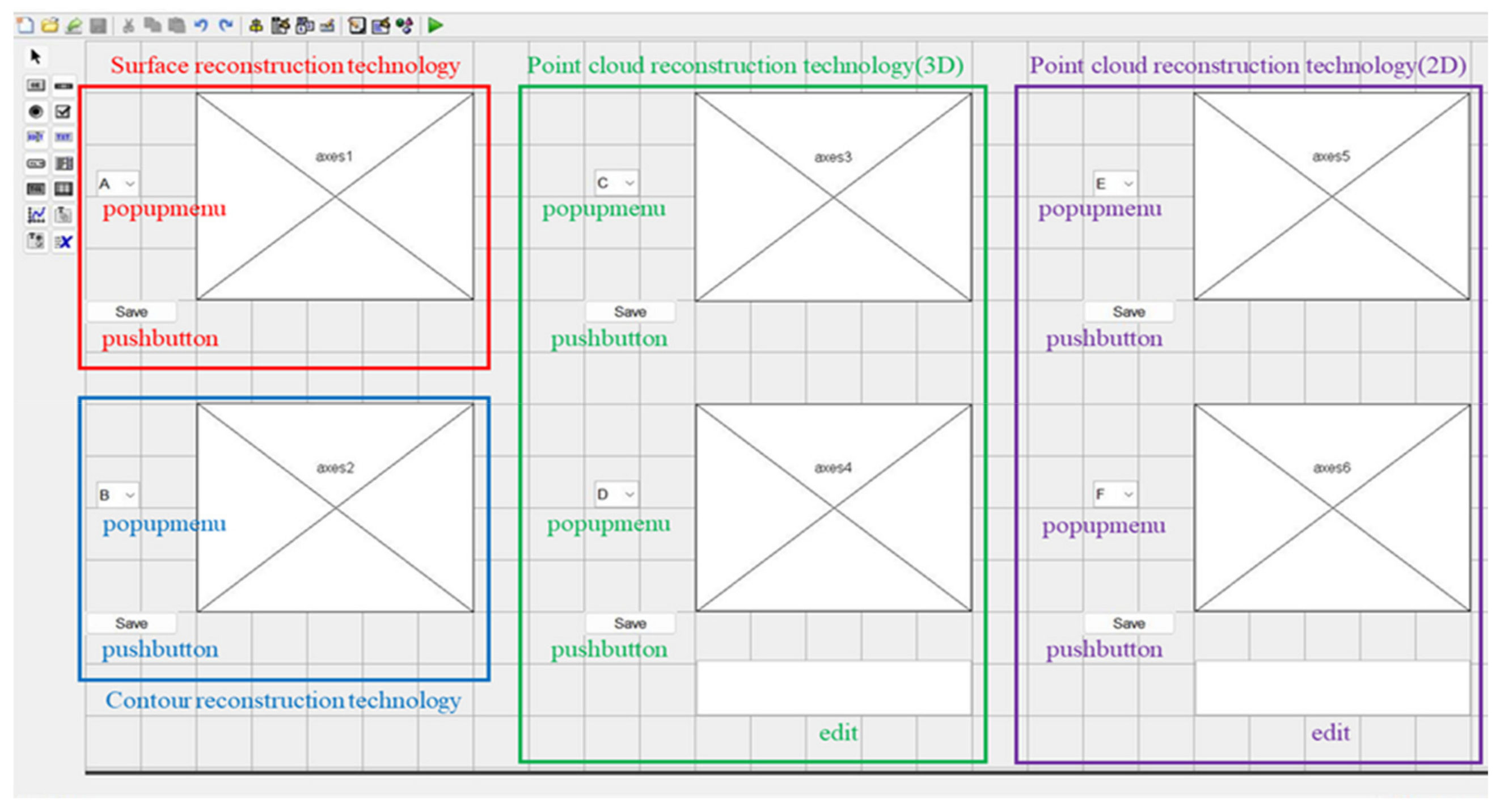
3.3. Visualization Analysis via GUI Control System
4. Conclusions
- (1)
- The combination of surface reconstruction technology and contour reconstruction technology can help better visualize the 3D data field of deteriorated sandstone, with which the location of the cracks in the deteriorated sandstone can be precisely marked on a 3D coordinate system, and their shape can be accurately described with a vector. The combination of the two technologies allows for the realization of visualization and quantitative characterization of the internal crack propagation laws. It offers a visualization model for exploring the developing laws of primary fractures.
- (2)
- We converted the internal cracks of deteriorated sandstone to 3D point cloud data and performed visualization analysis via point cloud reconstruction technology. At the same time, the crack cross-sectional area and crack space volume were obtained using the area and volume conversion formula. The average area of the point cloud reconstruction crack cross-section is 35.8022 mm2, and the average pixel area is 19,318p. The space volume of the point cloud reconstruction crack is 238.921 mm3, and the pixel volume is 2,148,600p. This method offered a model for the quantitative characterization of the influence of primary cracks on the stability of surrounding rock with only 10 CT scan images, considerably reducing the number of images that needed to be read and maximizing efficiency.
- (3)
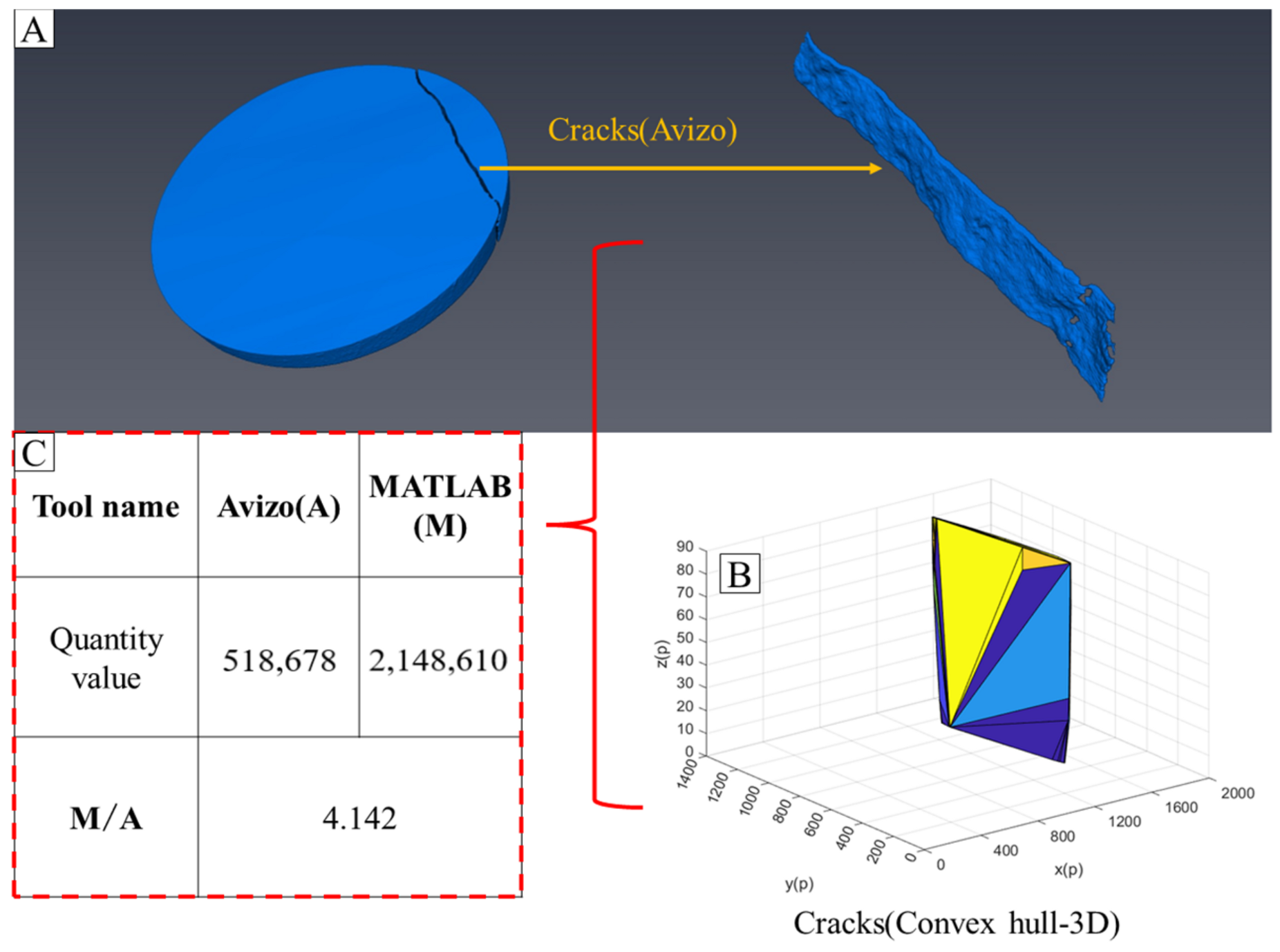
- The GUI control system is developed with MATLAB, and the GUI was also used to combine surface reconstruction technology, contour reconstruction technology, and point cloud reconstruction technology. Comparing the reconstruction results obtained using GUI with that of Avizo, the reconstruction effect of surface reconstruction technology and contour reconstruction technology is found to be very close to that of Avizo. The number of point clouds of 2D cracks counted via point cloud reconstruction technology is quite close to the calculated result of Avizo, which is 1.176 times that of Avizo. This shows that point cloud reconstruction technology has an excellent ability to identify cracks. The convex hull area of point cloud reconstruction technology is 3.293 times that of Avizo, and the convex hull volume is 4.142 times that of Avizo. The GUI control system integrates the strengths of the three 3D reconstruction technologies, which essentially promotes the 3D visualization of rock internal space.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.S.; Fei, T.; Zhang, L.Y.; Liu, X.P.; Zhang, J.Y. Improving Medical CT Image Blind Restoration Algorithm Based on Dictionary Learning by Alternating Direction Method of Multipliers. Autom. Control Comput. Sci. 2018, 52, 49–59. [Google Scholar] [CrossRef]
- Jin, Y. Quality of Service Aware Medical CT Image Transmission Anti-collision Mechanism Based on Big Data Autonomous Anti-collision Control. Curr. Bioinform. 2019, 14, 676–683. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.N. Research on 3D Reconstruction Algorithm of Medical CT Image Based on Parallel Contour. IEEE Sens. J. 2020, 20, 11828–11835. [Google Scholar] [CrossRef]
- Nie, Q.; Zou, Y.B.; Lin, J.C.W. Feature Extraction for Medical CT Images of Sports Tear Injury. Mob. Netw. Appl. 2021, 26, 404–414. [Google Scholar] [CrossRef]
- Ma, M.J.; Xia, H.Y.; Tan, Y.M.; Li, H.S.; Song, S.X. HT-Net: Hierarchical context-attention transformer network for medical ct image segmentation. Appl. Intell. 2022, 52, 10692–10705. [Google Scholar] [CrossRef]
- Cimen, S.; Gooya, A.; Grass, M.; Frangi, A.F. Reconstruction of coronary arteries from X-ray angiography: A review. Med. Image Anal. 2016, 32, 46–68. [Google Scholar] [CrossRef]
- Xu, Z.W.; Bartrina-Rapesta, J.; Blanes, I.; Sanchez, V.; Serra-Sagrista, J.; Garcia-Bach, M.; Munoz, J.F. Diagnostically lossless coding of X-ray angiography images based on background suppression. Comput. Electr. Eng. 2016, 53, 319–332. [Google Scholar] [CrossRef]
- Iyer, K.; Najarian, C.P.; Fattah, A.A.; Arthurs, C.J.; Soroushmehr, S.M.R.; Subban, V.; Sankardas, M.A.; Nadakuditi, R.R.; Nallamothu, B.K.; Figueroa, C.A. AngioNet: A convolutional neural network for vessel segmentation in X-ray angiography. Sci. Rep. 2021, 11, 18066. [Google Scholar] [CrossRef]
- Marcell, G.; Márton, B.; Csaba, C.N.; Dávid, S.; Viktor, Ó.I.; István, G.; János, K.P.; Veres, D.S.; Krisztián, S.; Szabolcs, O.; et al. Digital variance angiography allows about 70% decrease of DSA-related radiation exposure in lower limb X-ray angiography. Sci. Rep. 2021, 11, 21790. [Google Scholar]
- Kim, J.; Yoo, S.; Kim, J.; Kim, H.K. Towards subtraction angiography using a multi-layered X-ray detector. Phys. Med.-Eur. J. Med. Phys. 2022, 95, 32–40. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Verwaal, W.; van de Ven, M.F.C.; Molenaar, A.A.A.; Wu, S.P. Using high-resolution industrial CT scan to detect the distribution of rejuvenation products in porous asphalt concrete. Constr. Build. Mater. 2015, 100, 1–10. [Google Scholar] [CrossRef]
- Jiang, H.N. Defect Features Recognition in 3D Industrial CT Images. Inform.—J. Comput. Inform. 2018, 42, 477–482. [Google Scholar] [CrossRef]
- Tang, B.W.; Gao, S.; Wang, Y.G.; Liu, X.M.; Zhang, N. Pore structure analysis of electrolytic manganese residue based permeable brick by using industrial CT. Constr. Build. Mater. 2019, 208, 697–709. [Google Scholar] [CrossRef]
- Liang, C.Y.; Wang, Y.H.; Tan, G.J.; Zhang, L.D.; Zhang, Y.T.; Yu, Z.H. Analysis of Internal Structure of Cement-Stabilized Macadam Based on Industrial CT Scanning. Adv. Mater. Sci. Eng. 2020, 2020, 5265243. [Google Scholar] [CrossRef]
- Wang, D.K.; Zeng, F.C.; Wei, J.P.; Zhang, H.T.; Wu, Y.; Wei, Q. Quantitative analysis of fracture dynamic evolution in coal subjected to uniaxial and triaxial compression loads based on industrial CT and fractal theory. J. Pet. Sci. Eng. 2020, 196, 108051. [Google Scholar] [CrossRef]
- Jandejsek, I.; Jakubek, J.; Jakubek, M.; Prucha, P.; Krejci, F.; Soukup, P.; Turecek, D.; Vavrik, D.; Zemlicka, J. X-ray inspection of composite materials for aircraft structures using detectors of Medipix type. J. Instrum. 2014, 9, C05062. [Google Scholar] [CrossRef]
- Janeczek, K.; Arazna, A.; Futera, K.; Koziol, G. Failure analysis of epoxy molded IC packages. Microelectron. Int. 2016, 33, 94–101. [Google Scholar] [CrossRef]
- Kim, K.; Park, S.; Kim, G.; Cho, H.; Je, U.; Park, C.; Lim, H.; Lee, H.; Lee, D.; Park, Y.; et al. Industrial X-ray inspection system with improved image characterization using blind deblurring based on compressed-sensing scheme. Instrum. Sci. Technol. 2017, 45, 248–258. [Google Scholar] [CrossRef]
- Pfeifer, M.P.P.; Simerl, N.; Strahler, R.; Casburn, J.T.T.; Porter, J.; McNeil, W.J.J.; Bahadori, A.A.A. Methods for estimating X-ray machine output through measurement and simulation. Appl. Radiat. Isot. 2022, 183, 110125. [Google Scholar] [CrossRef]
- Valdiande, J.J.; Rodriguez-Cobo, L.; Cobo, A.; Lopez-Higuera, J.M.; Mirapeix, J. Spectroscopic Approach for the On-Line Monitoring of Welding of Tanker Trucks. Appl. Sci. 2022, 12, 5022. [Google Scholar] [CrossRef]
- Huang, C.Z.; Zhang, X.D.; Liu, S.; Li, N.Y.; Kang, J.; Xiong, G. Construction of pore structure and lithology of digital rock physics based on laboratory experiments. J. Pet. Explor. Prod. Technol. 2021, 11, 2113–2125. [Google Scholar] [CrossRef]
- Fang, H.H.; Xu, H.J.; Sang, S.X.; Liu, S.Q.; Song, S.L.; Liu, H.H. 3D reconstruction of coal pore network and its application in CO2-ECBM process simulation at laboratory scale. Front. Earth Sci. 2022, 16, 523–539. [Google Scholar] [CrossRef]
- Zhao, J.Y.; Wang, F.Y.; Cai, J.C. 3D tight sandstone digital rock reconstruction with deep learning. J. Pet. Sci. Eng. 2021, 207, 109020. [Google Scholar] [CrossRef]
- Zhou, X.P.; Xiao, N. A hierarchical-fractal approach for the rock reconstruction and numerical analysis. Int. J. Rock Mech. Min. Sci. 2018, 109, 68–83. [Google Scholar] [CrossRef]
- Lei, Y. Reconstruction and Analysis of Tight Sandstone Digital Rock Combined with X-Ray CT Scanning and Multiple-Point Geostatistics Algorithm. Math. Probl. Eng. 2020, 2020, 9476060. [Google Scholar] [CrossRef]
- Lin, W.; Li, X.; Yang, Z.; Manga, M.; Fu, X.; Xiong, S.; Gong, A.; Chen, G.; Li, H.; Pei, L.; et al. Multiscale Digital Porous Rock Reconstruction Using Template Matching. Water Resour. Res. 2019, 55, 6911–6922. [Google Scholar] [CrossRef]
- Gou, B.; Zhan, L.; Guo, J.C.; Zhang, R.; Zhou, C.L.; Wu, L.; Ye, J.X.; Zeng, J. Effect of different types of stimulation fluids on fracture propagation behavior in naturally fractured carbonate rock through CT scan. J. Pet. Sci. Eng. 2021, 201, 108529. [Google Scholar] [CrossRef]
- Sun, W.; Hou, K.P.; Yang, Z.Q.; Wen, Y.T. X-ray CT three-dimensional reconstruction and discrete element analysis of the cement paste backfill pore structure under uniaxial compression. Constr. Build. Mater. 2017, 138, 69–78. [Google Scholar] [CrossRef]
- Wang, Y.B.; Xiao, J.; Liu, L.P.; Wang, Y. Efficient Rock Mass Point Cloud Registration Based on Local Invariants. Remote Sens. 2021, 13, 1540. [Google Scholar] [CrossRef]
- Hu, L.; Xiao, J.; Wang, Y. An automatic 3D registration method for rock mass point clouds based on plane detection and polygon matching. Vis. Comput. 2020, 36, 669–681. [Google Scholar] [CrossRef]
- DiFrancesco, P.M.; Bonneau, D.A.; Hutchinson, D.J. Computational Geometry-Based Surface Reconstruction for Volume Estimation: A Case Study on Magnitude-Frequency Relations for a LiDAR-Derived Rockfall Inventory. ISPRS Int. J. Geo-Inf. 2021, 10, 157. [Google Scholar] [CrossRef]
- Engin, I.C.; Maerz, N.H.; Boyko, K.J.; Reals, R. Practical Measurement of Size Distribution of Blasted Rocks Using LiDAR Scan Data. Rock Mech. Rock Eng. 2020, 53, 4653–4671. [Google Scholar] [CrossRef]
- Voumard, J.; Abellan, A.; Nicolet, P.; Penna, I.; Chanut, M.A.; Derron, M.H.; Jaboyedoff, M. Using street view imagery for 3-D survey of rock slope failures. Nat. Hazards Earth Syst. Sci. 2017, 17, 2093–2107. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.; Yin, X.; Chen, J. Subarea Description and Breakage Constitutive Model of Rock Mass Based on CT Test. Buildings 2022, 12, 1232. [Google Scholar] [CrossRef]
- Yang, Z.; Linbing, W. Fractal Analysis of Tunnel Structural Damage Caused by High-Temperature and Explosion Impact. Buildings 2022, 12, 1410. [Google Scholar] [CrossRef]
- Wang, R.; Wu, H.; Zhao, M.; Liu, Y.; Chen, C. The Classification and Mechanism of Microcrack Homogenization Research in Cement Concrete Based on X-ray CT. Buildings 2022, 12, 1011. [Google Scholar] [CrossRef]
- Luo, C.; Zhang, Z.; Lin, D.; Tang, Z. Study of the Impact of Single-and Double-tube Tunnel Systems on Rockburst in Deep-buried Extra-long Tunnelling. Mod. Tunn. Technol. 2022, 59, 28–37. [Google Scholar]
- Zhong, W.; Zhang, X.; Li, T.; Yang, X.; Deng, W.; Shi, J. Study on Microscopic Characteristics of Spatial Distribution of Fractures in Deteriorated Sandstone. Geofluids 2022, 2022, 7895498. [Google Scholar] [CrossRef]







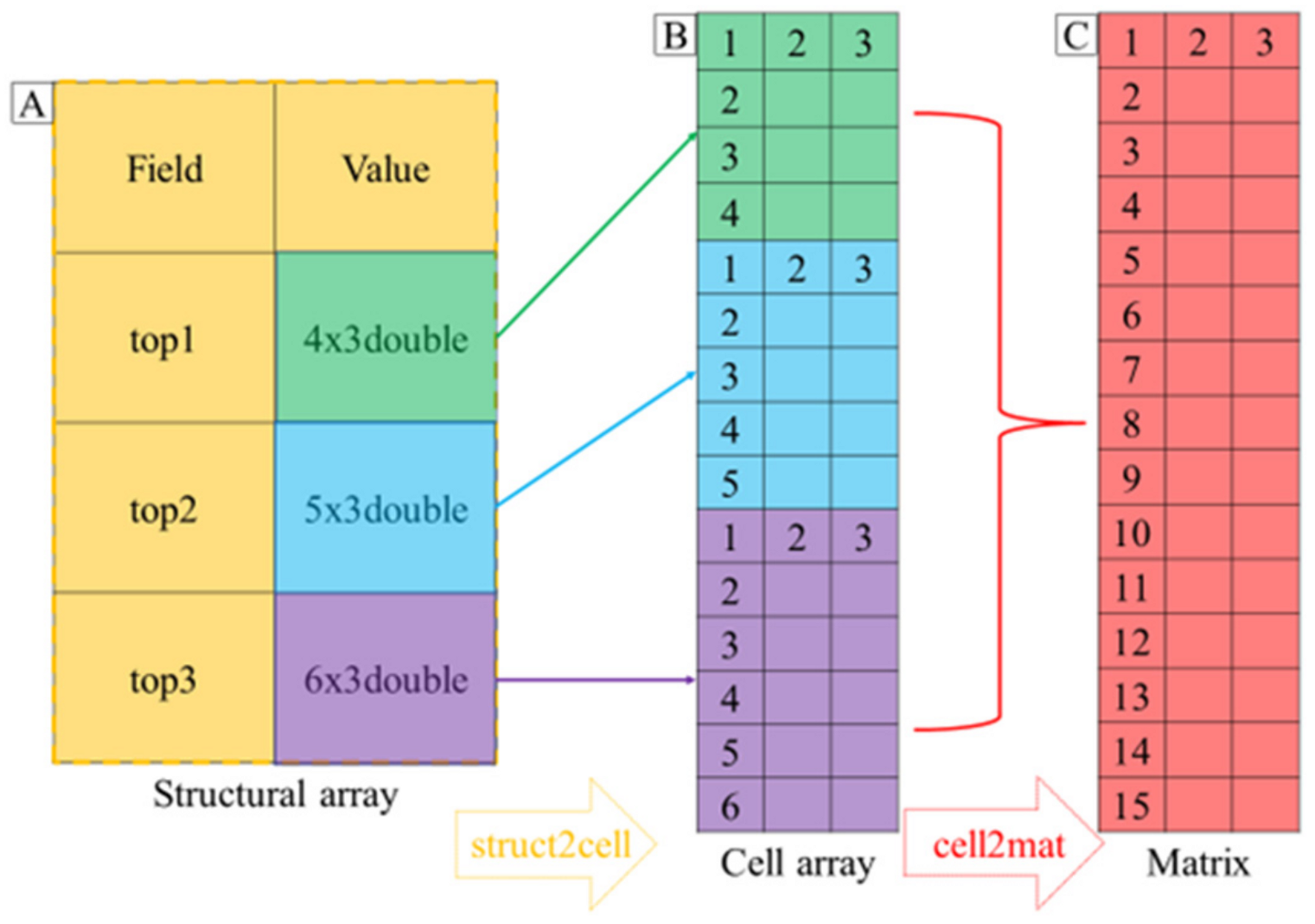


| A: Pixel Area of Sandstone Cross-Section (p) | : Area of Sandstone Cross-Section (mm2) |
|---|---|
| 1,059,456 | 1963.495 |
| Drawing Number | B: Crack Pixel Area (p) | : Crack Area (mm2) |
|---|---|---|
| 1 | 17,513.5 | 32.458 |
| 2 | 18,906.5 | 35.04 |
| 3 | 18,346.5 | 34.002 |
| 4 | 21,628.5 | 40.084 |
| 5 | 20,023 | 37.109 |
| 6 | 17,133.5 | 31.754 |
| 7 | 19,262 | 35.698 |
| 8 | 20,848 | 38.638 |
| 9 | 18,974 | 35.165 |
| 10 | 20,544 | 38.074 |
| Average value | 19,318 | 35.8022 |
| : Area of Sandstone Section (mm2) | A: Pixel Area of Sandstone Section (p) | : Pixel Volume of Crack (p) | |
|---|---|---|---|
| 1963.495 | 1,059,456 | 2,148,600 | 238.921 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Fei, Z.; Zhong, W.; Li, T.; Wang, Z.; Jiang, L. Research and Implementation of Three-Dimensional Spatial Information Characterization and Visualization of Fractures in Deteriorated Sandstone. Buildings 2023, 13, 2418. https://doi.org/10.3390/buildings13102418
Zhang X, Fei Z, Zhong W, Li T, Wang Z, Jiang L. Research and Implementation of Three-Dimensional Spatial Information Characterization and Visualization of Fractures in Deteriorated Sandstone. Buildings. 2023; 13(10):2418. https://doi.org/10.3390/buildings13102418
Chicago/Turabian StyleZhang, Xin, Zheng Fei, Wenwu Zhong, Tao Li, Zelin Wang, and Lijun Jiang. 2023. "Research and Implementation of Three-Dimensional Spatial Information Characterization and Visualization of Fractures in Deteriorated Sandstone" Buildings 13, no. 10: 2418. https://doi.org/10.3390/buildings13102418
APA StyleZhang, X., Fei, Z., Zhong, W., Li, T., Wang, Z., & Jiang, L. (2023). Research and Implementation of Three-Dimensional Spatial Information Characterization and Visualization of Fractures in Deteriorated Sandstone. Buildings, 13(10), 2418. https://doi.org/10.3390/buildings13102418






