Two-Way Time-Dependent Prestress Losses of Prestressed Concrete Containment with Bonded Prestressing Strands
Abstract
:1. Introduction
2. Three Conditions for Viscoelastic Analysis
2.1. Static Equilibrium Conditions
2.2. Physical Conditions
2.3. Deformation Compatibility Conditions
3. Calculation Method for Two-Way Prestress Losses of Prestressed Concrete Containment
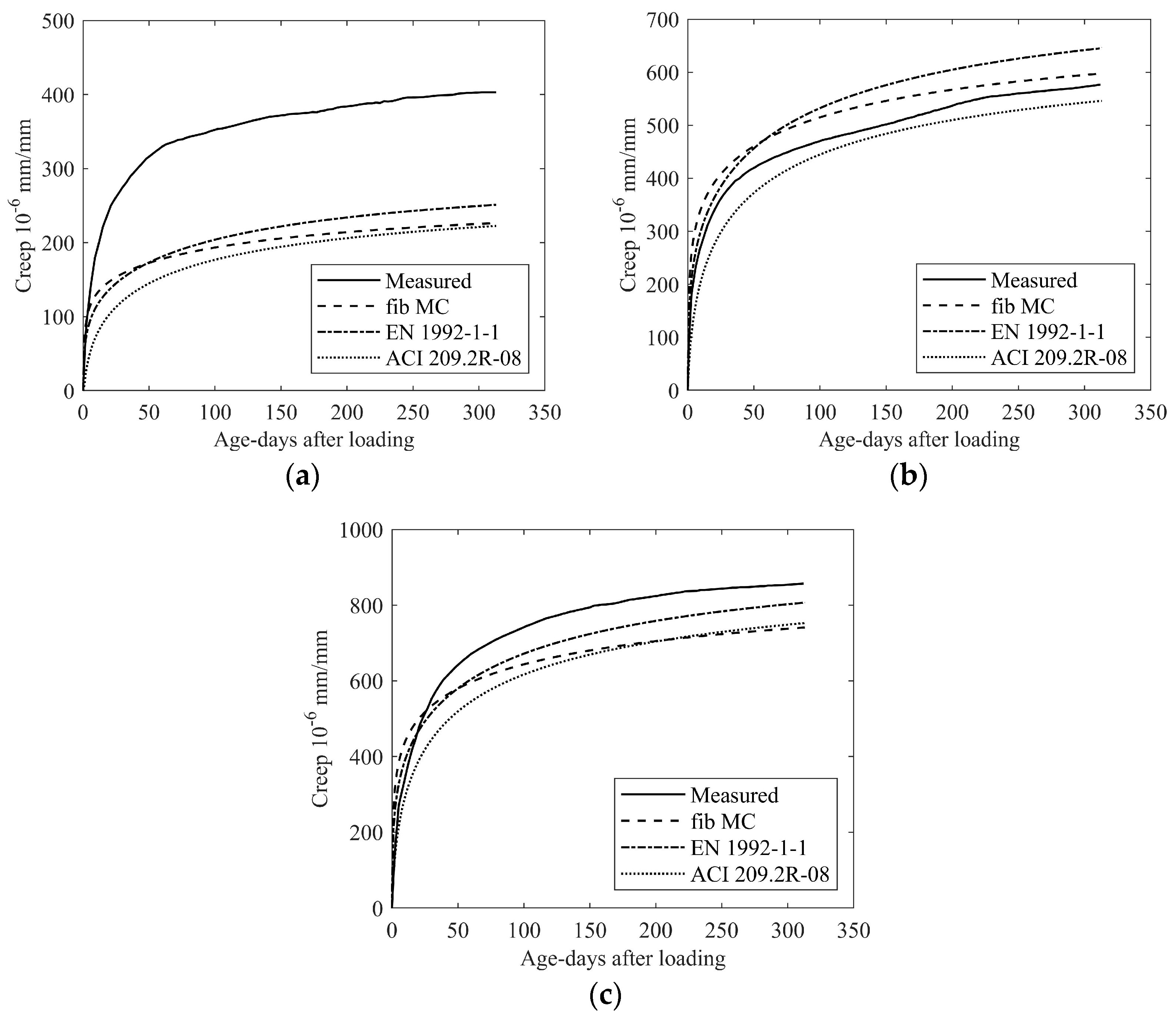
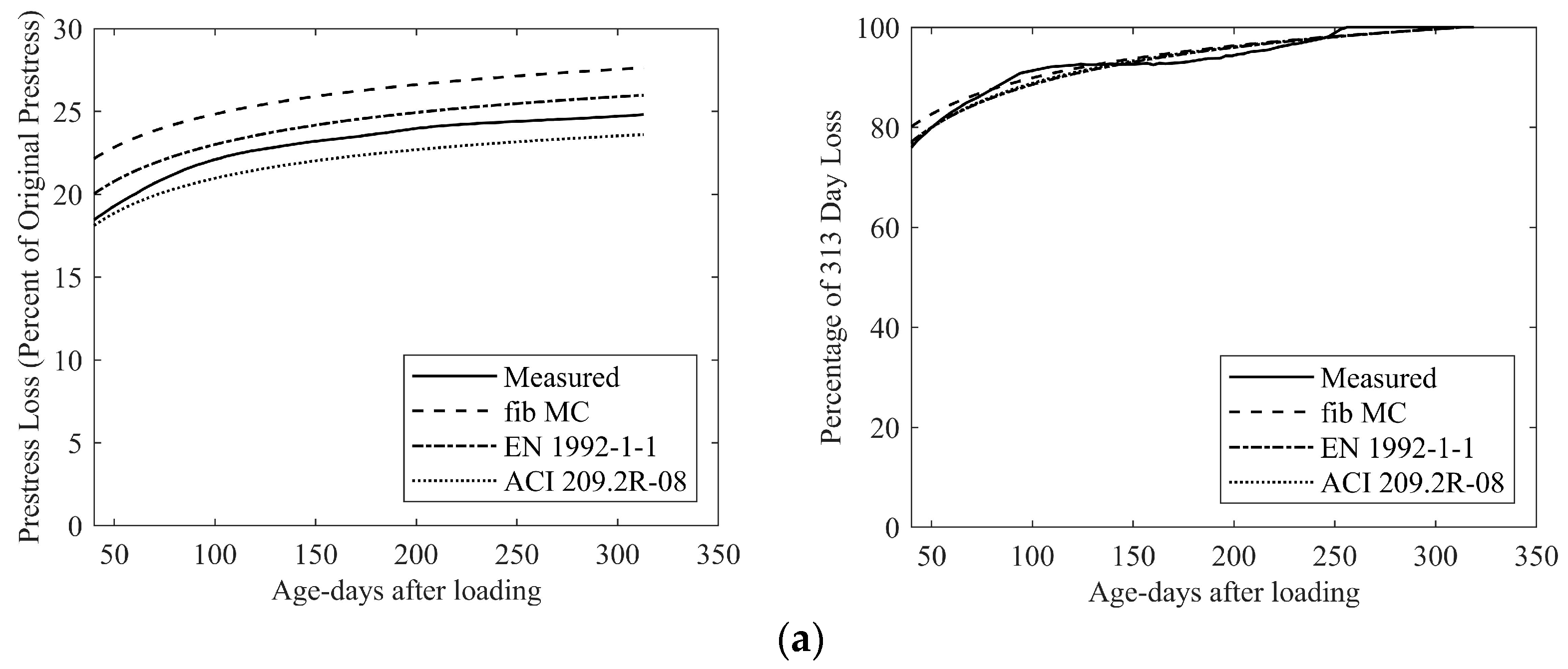
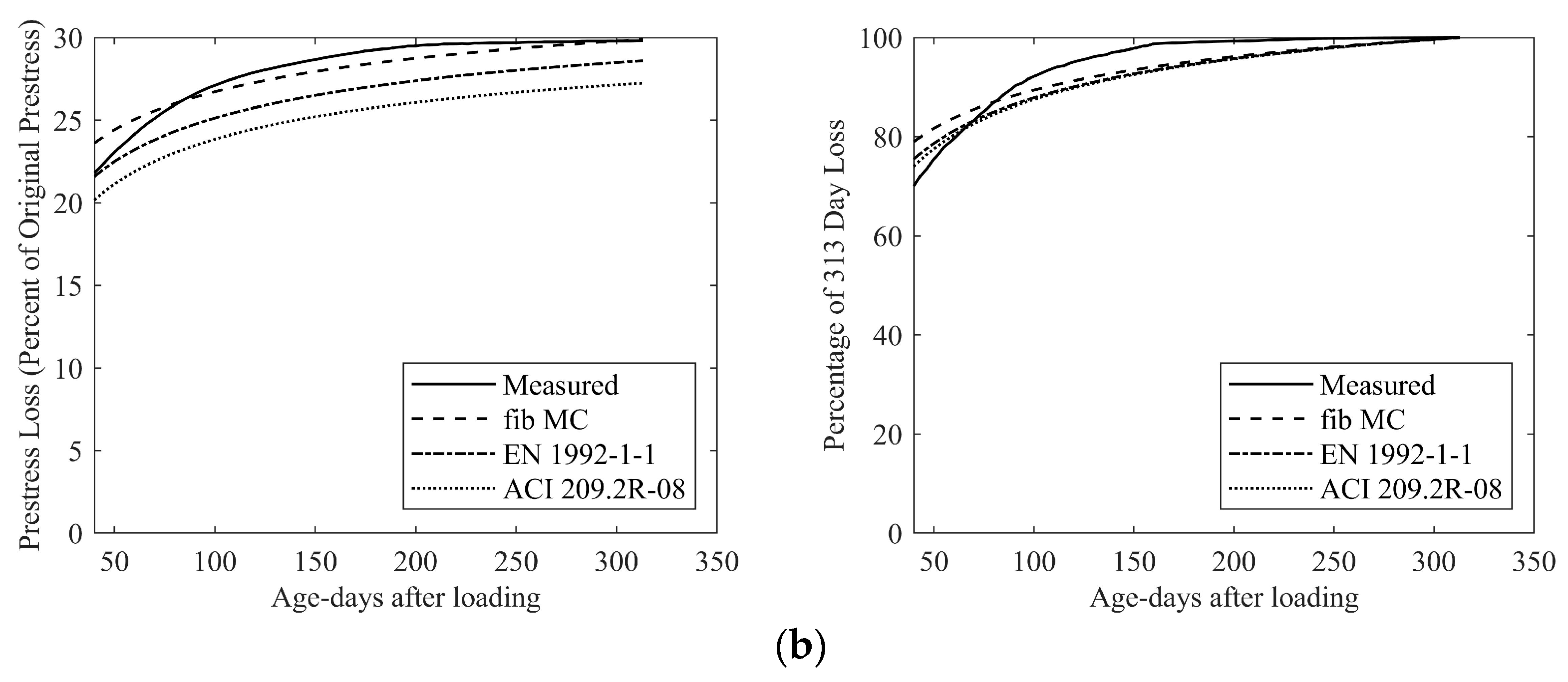
4. Comparison with Test Results
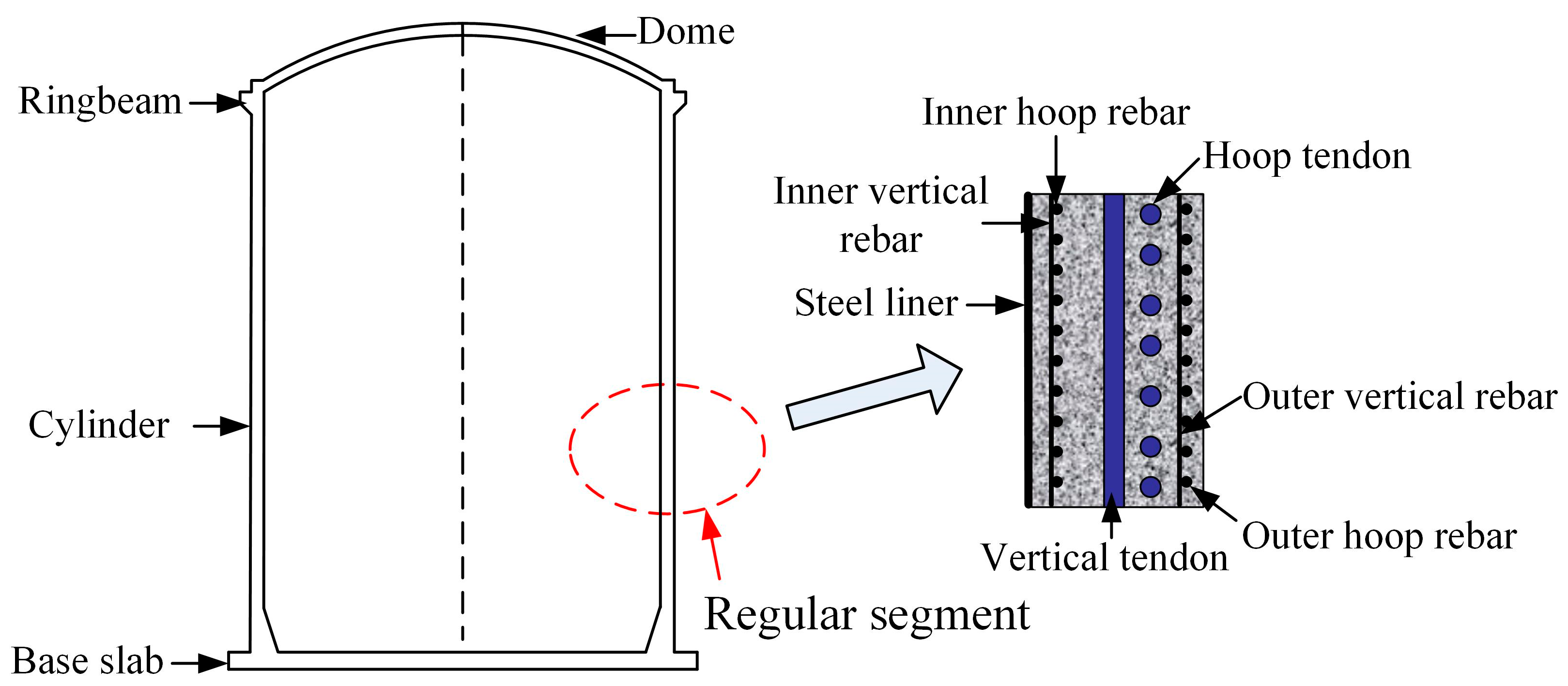
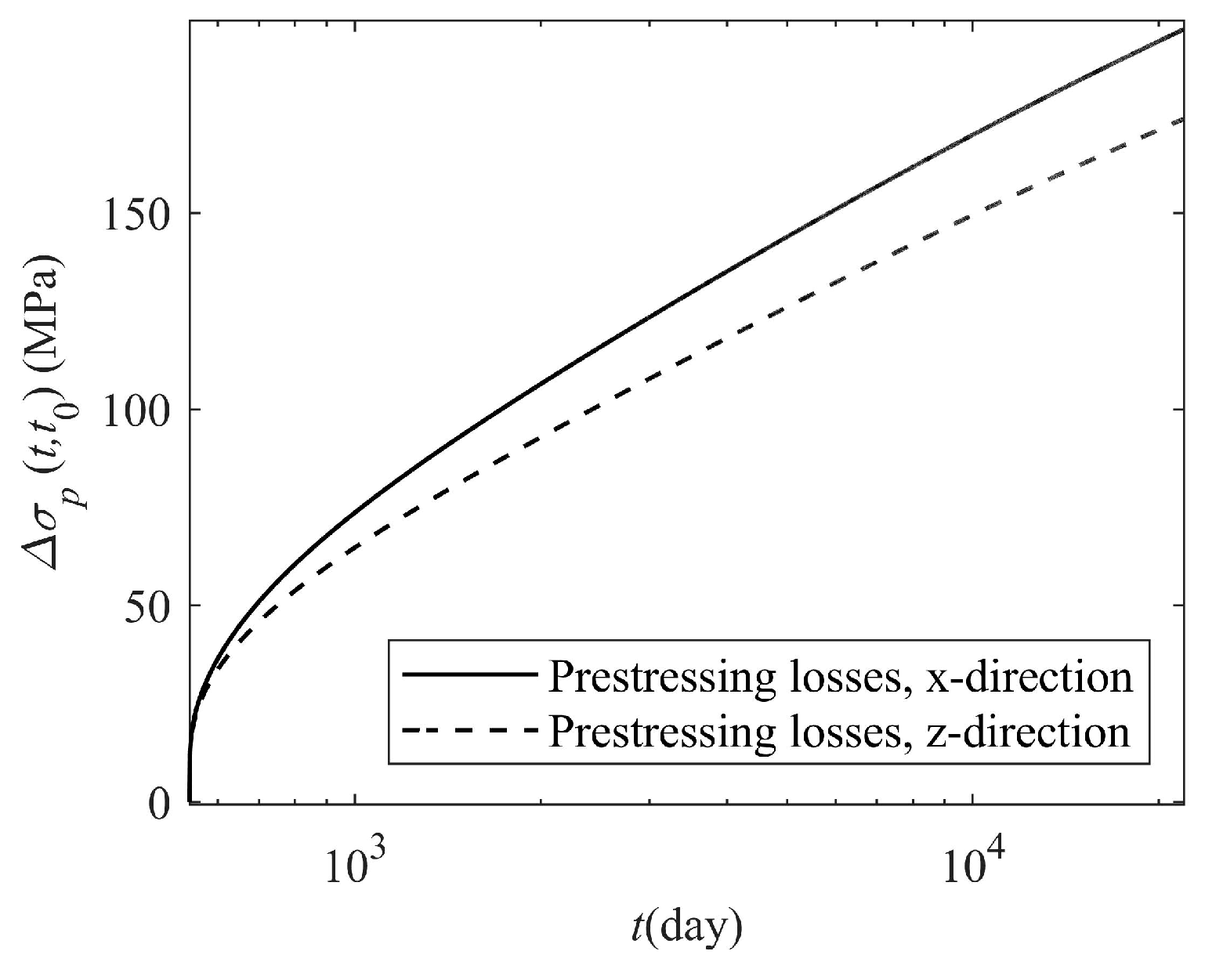
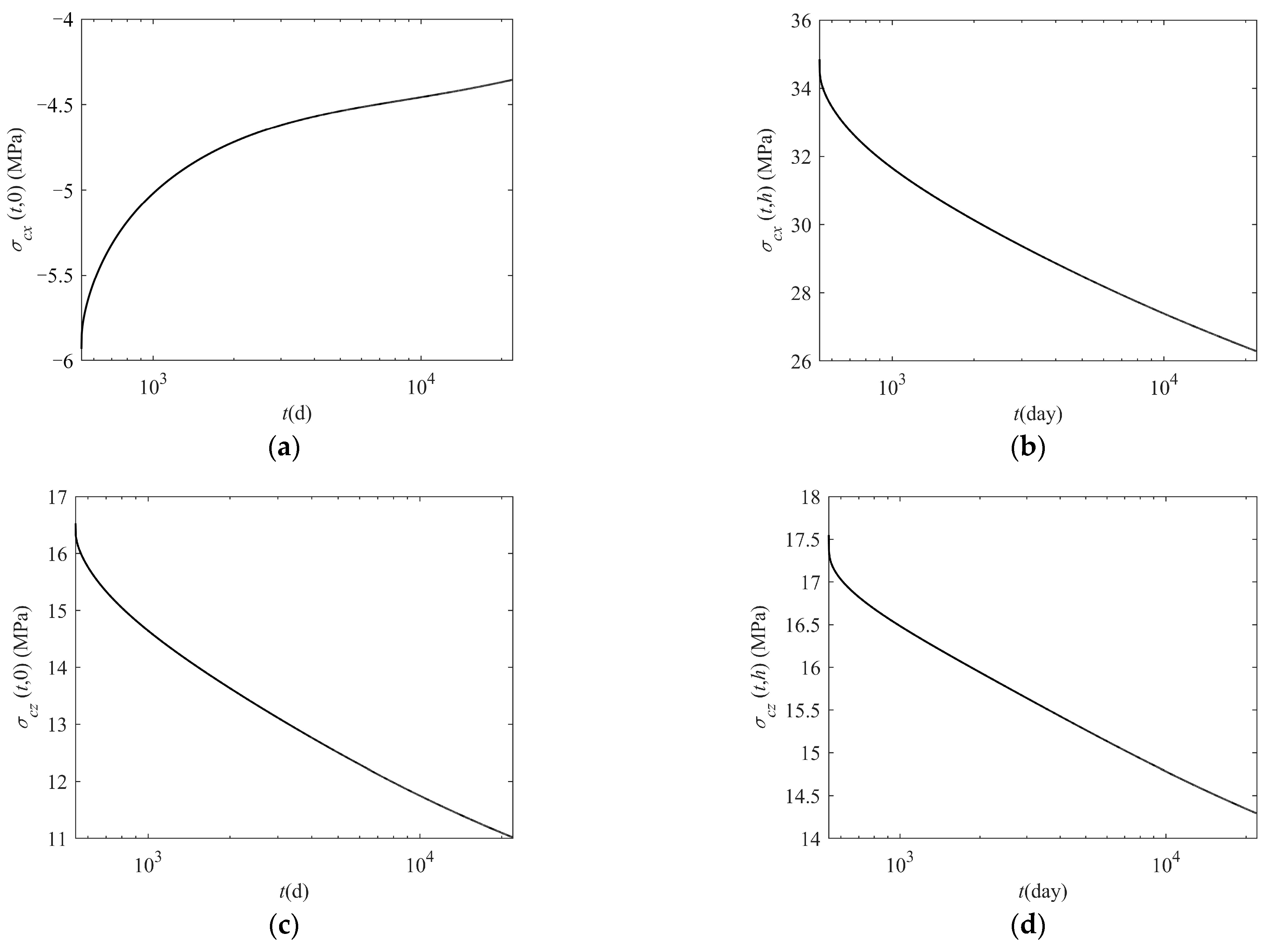
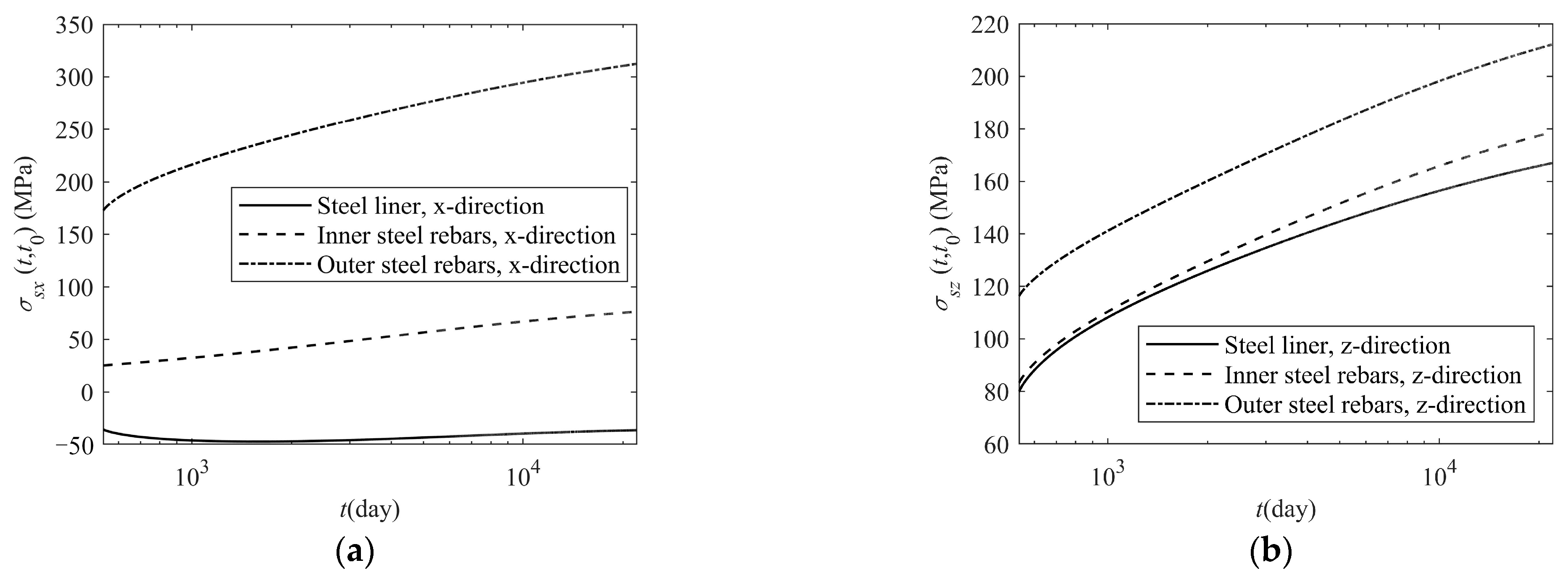
5. Case Study
5.1. Geometric Details
5.2. Calculation of Two-Way Prestress Losses
6. Conclusions
- The advantage of the proposed method is the consideration of the interaction of two-way prestress, mild steel rebars, and the steel liner in two directions. In the case of neglecting the interaction of two-way prestress and the influence of mild steel rebars and the steel liner in two directions, the equations derived in this study reduce to the ones in the design code such as Eurocode 2, which means that the equation for the prestress loss estimation in the design code is the degeneration of the one in this study.
- The consideration of the interaction of two-way prestress and the existence of mild steel rebars and the steel liner in two directions reduces the prestress loss of the prestressed concrete containment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of One-Way Prestress Loss Equation Based on the General Equations in this Study
References
- Li, X.; Gong, J. Effects of steel liner corrosion on the leak-tightness of prestressed concrete containment structure under severe accident loads. Ann. Nucl. Energy 2023, 180, 109487. [Google Scholar] [CrossRef]
- Guo, T.; Chen, Z.; Lu, S.; Yao, R. Monitoring and analysis of long-term prestress losses in post-tensioned concrete beams. Measurement 2018, 122, 573–581. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, H.; Mao, Y.; Wang, X. Prediction of Long-Term Prestress Loss and Crack Resistance Analysis of Corroded Prestressed Concrete Box-Girder Bridges. Adv. Civ. Eng. 2022, 2022, 1309936. [Google Scholar] [CrossRef]
- Breccolotti, M. On the evaluation of prestress loss in PRC beams by means of dynamic techniques. Int. J. Concr. Struct. Mater. 2018, 12, 1. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.C. Novel method for identifying residual prestress force in simply supported concrete girder-bridges. Adv. Struct. Eng. 2021, 24, 3238–3251. [Google Scholar] [CrossRef]
- Song, H.W.; Kim, S.H.; Byun, K.J.; Song, Y.C. Creep prediction of concrete for reactor containment structures. Nucl. Eng. Des. 2002, 217, 225–236. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Panula, L. Practical prediction of time-dependent deformation of concrete, part III and IV. Mater. Struct. 1978, 11, 415–434. [Google Scholar]
- Cai, D.; Wang, Y.; Zhang, J.; Yang, L.; Rong, H.; Li, J.; Wu, Z. Prestressed time-limited aging analyses of concrete containment structure. In Proceedings of the 2017 25th International Conference on Nuclear Engineering ICONE25, Shanghai, China, 2–6 July 2017. [Google Scholar]
- Lundqvist, P.; Nilsson, L.O. Evaluation of prestress losses in nuclear reactor containments. Nucl. Eng. Des. 2011, 241, 168–176. [Google Scholar] [CrossRef]
- Bílý, P.; Kohoutková, A.; Holan, J. Time-dependent strains of prestressed concrete containment vessels: Validation of analytical model by real-world data. Eng. Struct. 2022, 262, 114403. [Google Scholar] [CrossRef]
- Anderson, P. Thirty years of measured prestress at Swedish nuclear reactor containments. Nucl. Eng. Des. 2005, 235, 2323–2336. [Google Scholar] [CrossRef]
- Yang, Q.; Yao, D.; Yan, J.; Liu, M.; Fan, F.; Fu, Z. Analysis of time-varying mechanical properties of prestressed concrete containment during the tensioning process and service considering the influence of creep. Int. J. Press. Vessel. Pip. 2023, 204, 104962. [Google Scholar] [CrossRef]
- Zhang, H.; Guo, Q.Q.; Xu, L.Y. Prediction of long-term prestress loss for prestressed concrete cylinder structures using machine learning. Eng. Struct. 2023, 279, 115577. [Google Scholar] [CrossRef]
- Hu, H.T.; Lin, J.X. Ultimate analysis of PWR prestressed concrete containment under long-term prestressing loss. Ann. Nucl. Energy 2016, 87, 500–510. [Google Scholar] [CrossRef]
- Kjolsing, E.; James, R.; Kubischta, K.; Dan, P. Assessing prestress losses in a nuclear containment structure for license renewal. In Proceedings of the ASME 2019 Power Conference POWER2019, Salt Lake City, UT, USA, 15–18 July 2019. [Google Scholar]
- Ramaswamy, A. Uncertainty based model averaging for prediction of long-time prestress losses in concrete structures. Constr. Build. Mater. 2017, 153, 469–480. [Google Scholar]
- Berveiller, M.; Pape, Y.L.; Sudret, B.; Perrin, F. Updating the long-term creep strains in concrete containment vessels by using Markov chain Monte Carlo simulation and polynomial chaos expansions. Struct. Infrastruct. Eng. 2012, 8, 425–440. [Google Scholar] [CrossRef]
- Balomenos, G.P.; Pandey, M.D. Probabilistic finite element investigation of prestressing loss in nuclear containment wall segments. Nucl. Eng. Des. 2017, 311, 50–59. [Google Scholar] [CrossRef]
- AFCEN. RCC-CW 2015; Rules for Design and Construction of PWR Nuclear Civil Works. French Association for Design, Construction and In-Service Inspection Rules for Nuclear Island Components: Paris, France, 2015.
- ACI 359-13; Rules for Construction Nuclear Facility Components III, Code for Concrete Containments Division 2. The American Society of Mechanical Engineering: New York, NY, USA, 2013.
- Wang, W.; Gong, J.; Wu, X.; Wang, X. A general equation for estimation of time-dependent prestress losses in prestressed concrete members. Structures 2023, 55, 278–293. [Google Scholar] [CrossRef]
- Li, X.; Gong, J. Probabilistic evaluation of the leak-tightness function of the nuclear containment structure subjected to internal pressure. Reliab. Eng. Syst. Saf. 2024, 241, 109684. [Google Scholar] [CrossRef]
- Evans, R.H.; Wood, R.H. Transverse elasticity of building materials. Engineering 1937, 143, 161–163. [Google Scholar]
- Kordina, K. Experiments on the influence of the mineralogical character of aggregates on the creep of concrete. RILEM Bull. 1960, 6, 7–22. [Google Scholar]
- Gvozdev, A.A. Creep of concrete. Mekhanika Tverd. Tela 1966, 137–152. [Google Scholar]
- Charpin, L.; Pape, Y.L.; Coustabeau, É.; Toppani, É.; Heinfling, G.; Bellego, C.L.; Masson, B.; Montalvo, J.; Courtois, A.; Sanahuja, J. A 12year EDF study of concrete creep under uniaxial and biaxial loading. Cem. Concr. Res. 2018, 103, 140–159. [Google Scholar] [CrossRef]
- Pprrott, L.J. Lateral strains in hardened cement paste under short- and long-term loading. Mag. Concr. Res. 1974, 26, 198–202. [Google Scholar] [CrossRef]
- Jordaan, I.J.; Illston, J.M. Time-dependent strains in sealed concrete under systems of variable multiaxial stress. Mag. Concr. Res. 1971, 23, 79–88. [Google Scholar] [CrossRef]
- Gopalakrishnan, K.S.; Neville, A.M.; Ghali, A. Creep Poisson’s ratio of concrete under multiaxial compression. J. Proc. 1969, 66, 1008–1019. [Google Scholar]
- Meyer, H.G. On the influence of water content and of drying conditions on lateral creep of plain concrete. Matériaux Et Constr. 1969, 2, 125–131. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Jirásek, M. Creep and Hygrothermal Effects in Concrete Structures. In Solid Mechanics and its Applications; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Yang, M. Refined Calculation of Long-Term Deformation of Simply Supported Post-Tensioned Prestressed Concrete Bridges. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2021. [Google Scholar]
- fib Model Code. fib Model Code for Concrete Structures; Thomas Telford Ltd.: London, UK, 2010; p. 2013. [Google Scholar]
- Bílý, P.; Kohoutková, A. A numerical analysis of the stress-strain behavior of anchorage elements and steel liner of a prestressed concrete containment wall. Structures 2017, 12, 24–39. [Google Scholar] [CrossRef]
- EN 1992-1-1:2004; Eurocode 2: Design of Concrete Structures–Part 1–1. General Rules and Rules for Buildings. European Commission: Brussels, Belgium, 2004.
- Furr, H.L. Creep Tests of Two-Way Prestressed Concrete. ACI J. 1967, 64, 288–294. [Google Scholar]
- ACI 209.2R-08; Guide for Modeling and Calculating Shrinkage and Creep in Hardened Concrete. American Concrete Institute (ACI): Farmington Hills, MI, USA, 2008.

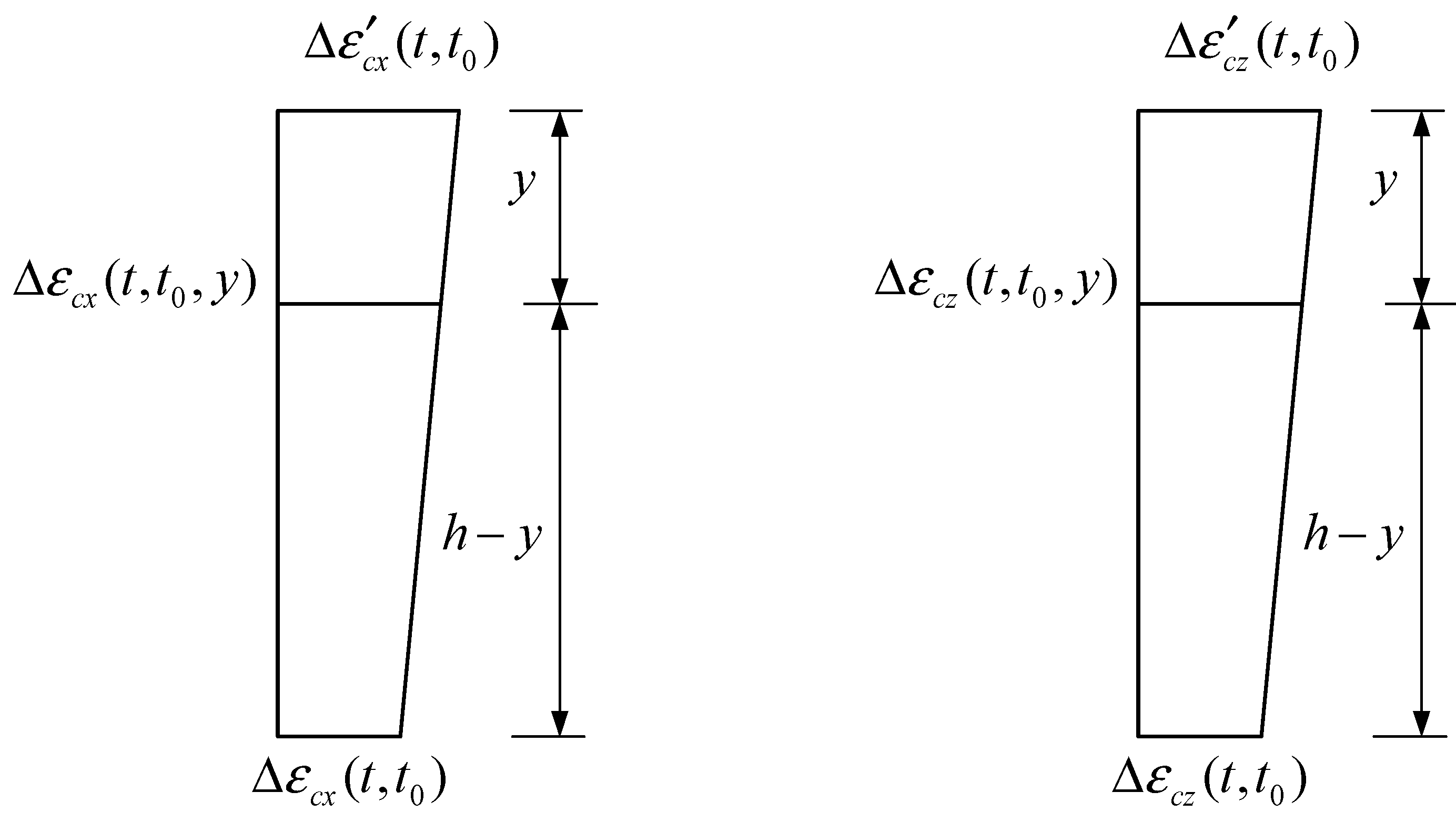



| Designation | Type | Size (mm × mm × mm) | Initial Stress | |
|---|---|---|---|---|
| C-1P | two-way prestress | 610 × 610 × 64 | 6.89 MPa, two-way | 33.1649 MPa |
| C-2P | two-way prestress | 610 × 610 × 64 | 13.79 MPa, two-way | 31.5791 MPa |
| C-3P | two-way prestress | 610 × 610 × 64 | 20.68 MPa, two-way | 35.0266 MPa |
| S-1P | C-1P control | 610 × 610 × 64 | None | 33.1649 MPa |
| S-2P | C-2P control | 610 × 610 × 64 | None | 31.5791 MPa |
| S-3P | C-3P control | 610 × 610 × 64 | None | 35.0266 MPa |
| Direction | Area of Section Concrete (mm2) | Distance from Innermost Fiber to Centroid (mm) | Moment of Inertia (mm4) | |||
|---|---|---|---|---|---|---|
| x | 1,980,000 | 600 | 2.3760 × 1011 | |||
| z | 540,000 | 600 | 6.4800 × 1010 | |||
| Member | Area (mm2) | Reinforcement Ratio (%) | Distance (mm) | Eccentricity (mm) | ) | ) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Steel liner, x-direction | 9900 | 0.50 | 0 | −600 | 4.00 | −2.00 | ||||||
| Steel liner, z-direction | 2700 | 0.50 | 0 | −600 | 4.00 | −2.00 | ||||||
| Inner steel rebars, x-direction | 11,259 | 0.57 | 226 | −374 | 2.87 | −0.87 | ||||||
| Outer steel rebars, x-direction | 11,259 | 0.57 | 1099 | 499 | −1.495 | 3.495 | ||||||
| Inner steel rebars, x-direction | 3770 | 0.70 | 190 | −410 | 3.05 | −1.05 | ||||||
| Outer steel rebars, z-direction | 3770 | 0.70 | 1063 | 463 | −1.315 | 3.315 | ||||||
| Prestressing tendons, x-direction | 24,300 | 1.23 | 900 | 300 | −0.50 | 2.50 | ||||||
| Prestressing tendons, z-direction | 8100 | 1.50 | 600 | 0 | 1 | 1 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Wang, X.; Li, X.; Gong, J. Two-Way Time-Dependent Prestress Losses of Prestressed Concrete Containment with Bonded Prestressing Strands. Buildings 2023, 13, 2513. https://doi.org/10.3390/buildings13102513
Wu X, Wang X, Li X, Gong J. Two-Way Time-Dependent Prestress Losses of Prestressed Concrete Containment with Bonded Prestressing Strands. Buildings. 2023; 13(10):2513. https://doi.org/10.3390/buildings13102513
Chicago/Turabian StyleWu, Xingyi, Xingchao Wang, Xinbo Li, and Jinxin Gong. 2023. "Two-Way Time-Dependent Prestress Losses of Prestressed Concrete Containment with Bonded Prestressing Strands" Buildings 13, no. 10: 2513. https://doi.org/10.3390/buildings13102513
APA StyleWu, X., Wang, X., Li, X., & Gong, J. (2023). Two-Way Time-Dependent Prestress Losses of Prestressed Concrete Containment with Bonded Prestressing Strands. Buildings, 13(10), 2513. https://doi.org/10.3390/buildings13102513





