Thermoelastic Behaviors of Temperature-Dependent Multilayer Arches under Thermomechanical Loadings
Abstract
:1. Introduction
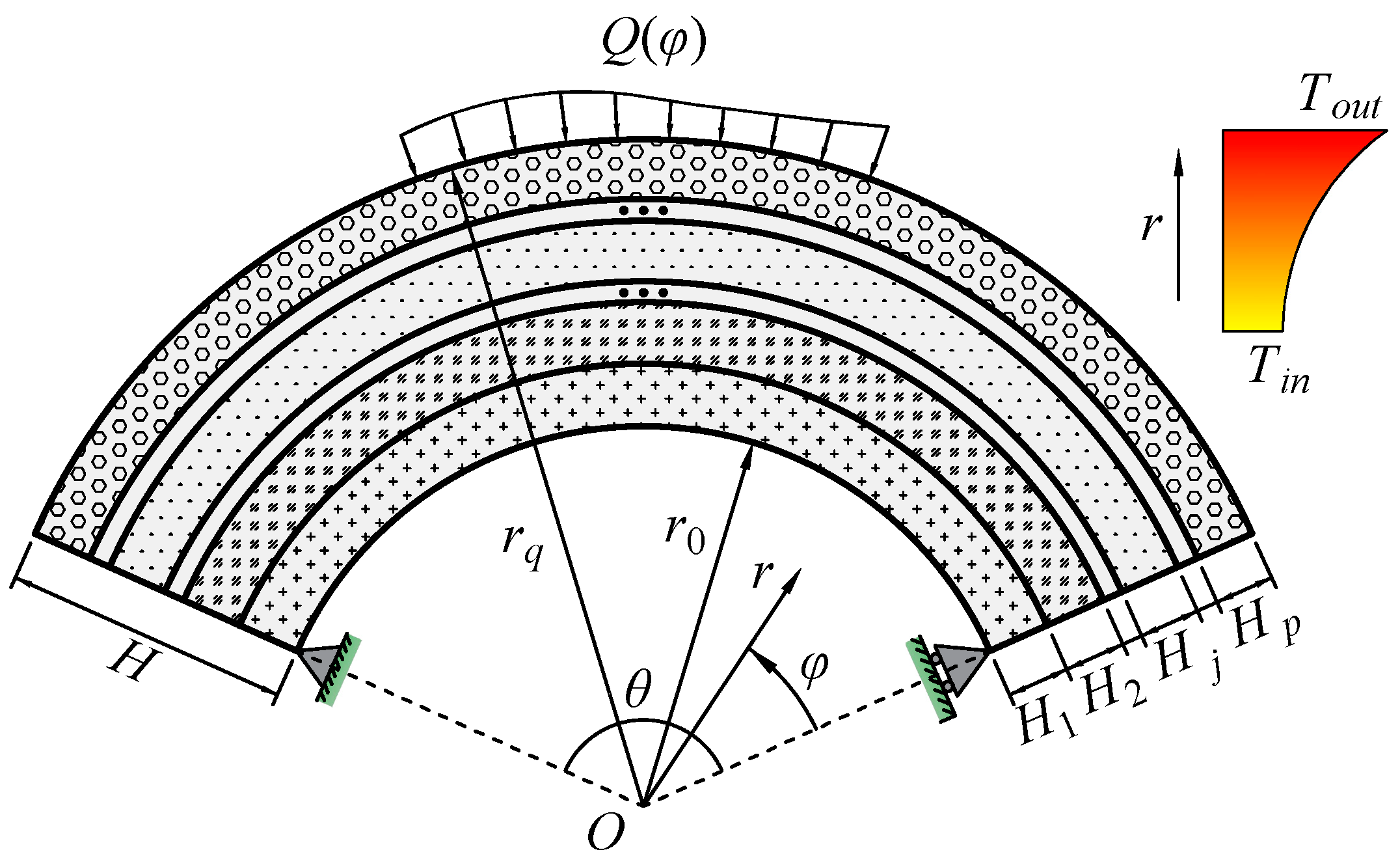
2. Problem Statement and Arched-Slice Model
2.1. Basic Assumptions
- i.
- The inside and outside surface temperatures are uniformly distributed on the surfaces and the two lateral surfaces are adiabatic;
- ii.
- Each layer is made of a homogenous isotropic material with uniform thickness;
- iii.
- Each layer is perfectly bonded with the adjacent layer;
- iv.
- The analysis is within the framework of linear elasticity and small strains.
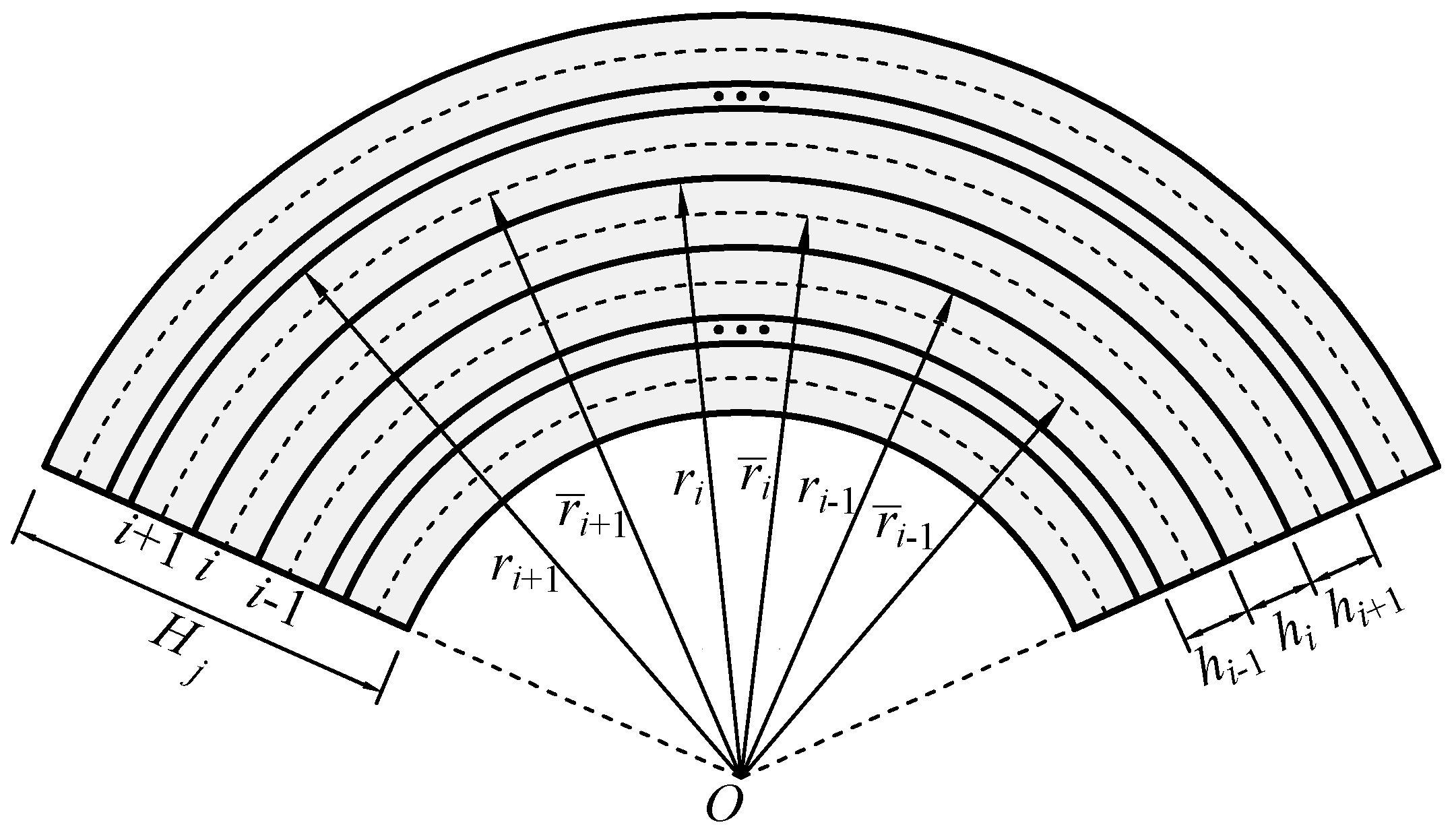
2.2. Arched-Slice Model
3. Temperature Solution
3.1. Temperature Solution for the TI Case
3.2. Temperature Solution for the TD Case
4. Displacement and Stress Solutions
4.1. Basic Equations
4.2. General Solution to the Thermoelasticity Equations
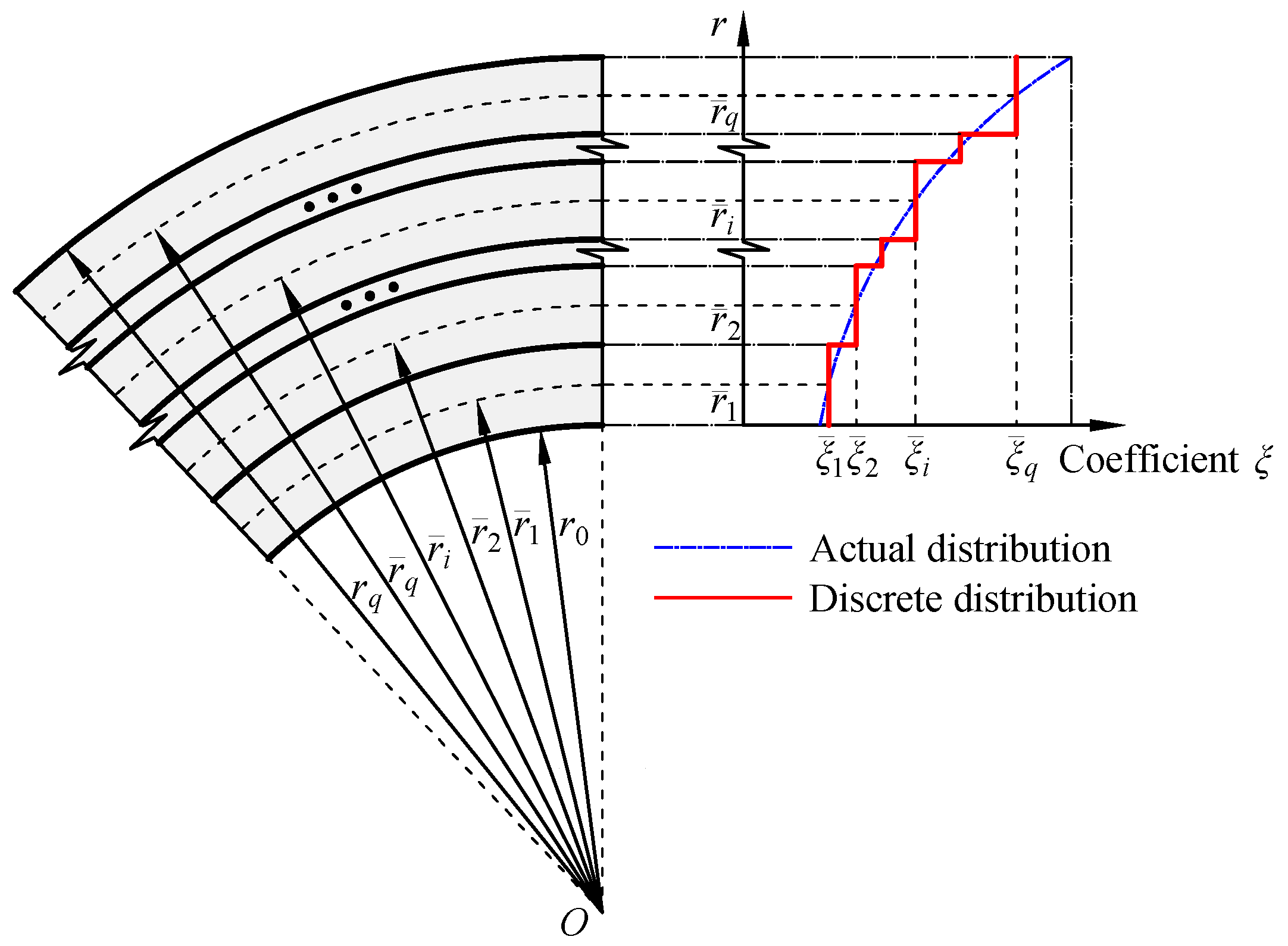
4.3. Transfer-Matrix Approach
5. Numerical Results and Discussion
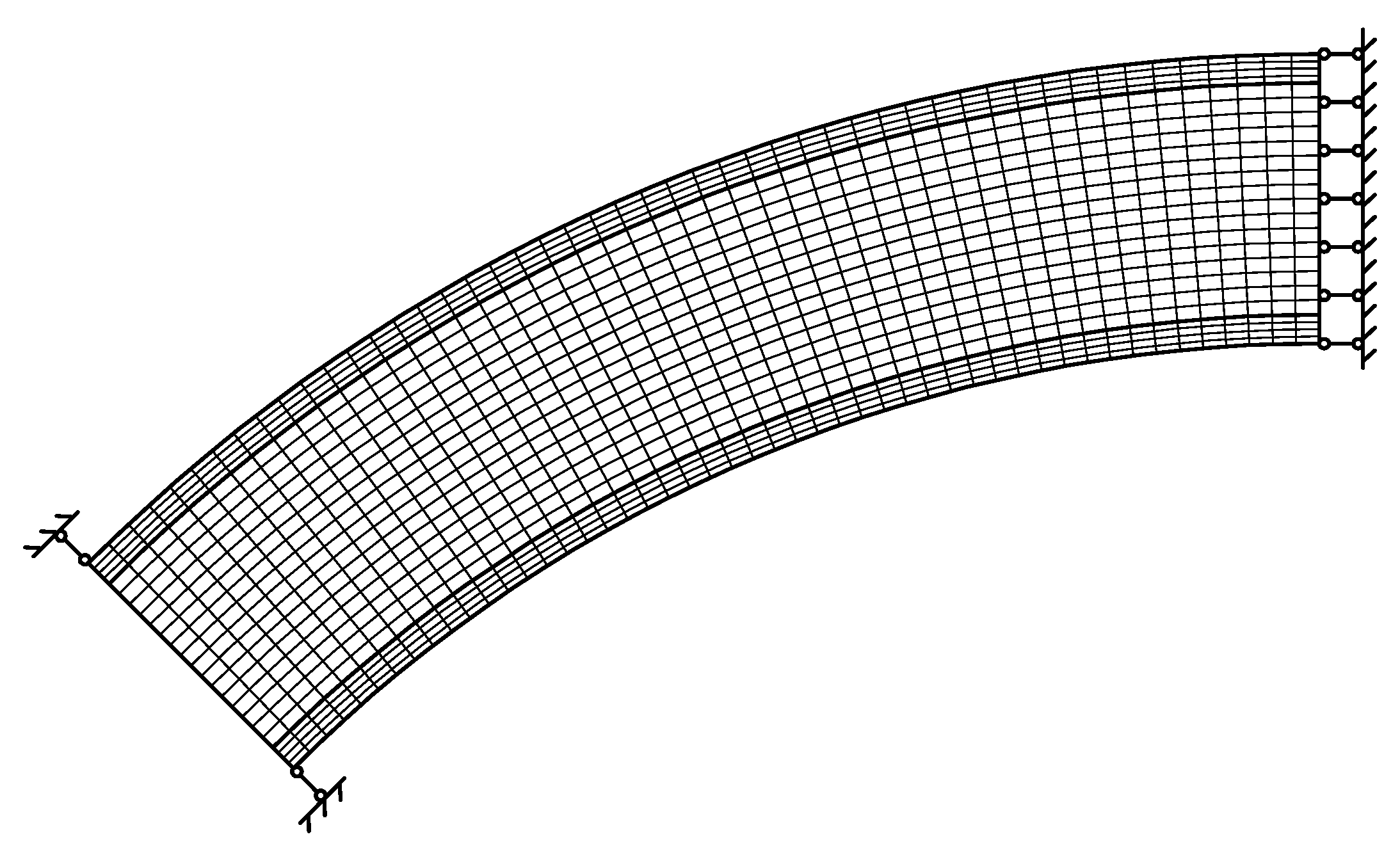
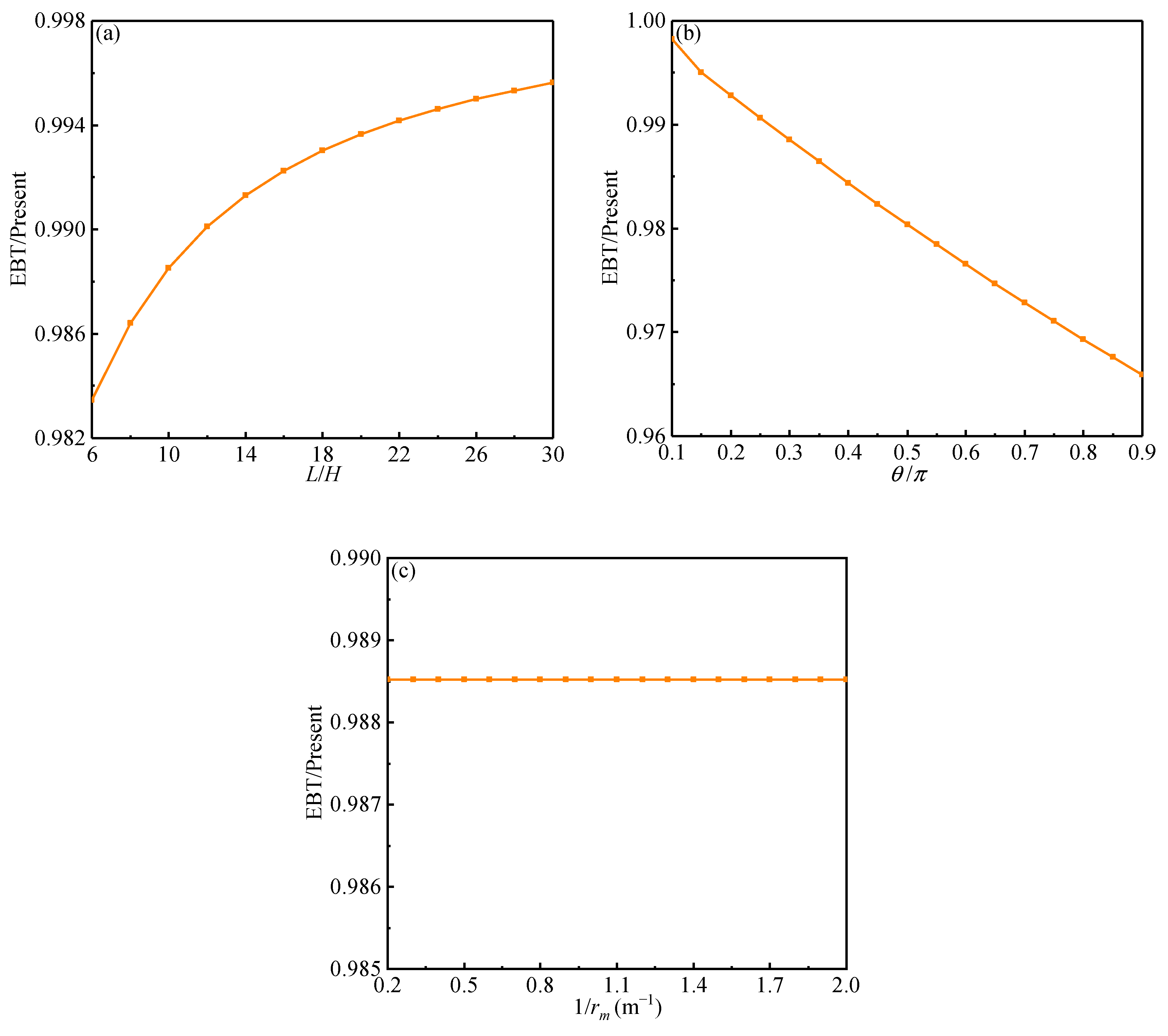
5.1. Validation of the Solutions
5.2. Parametric Study
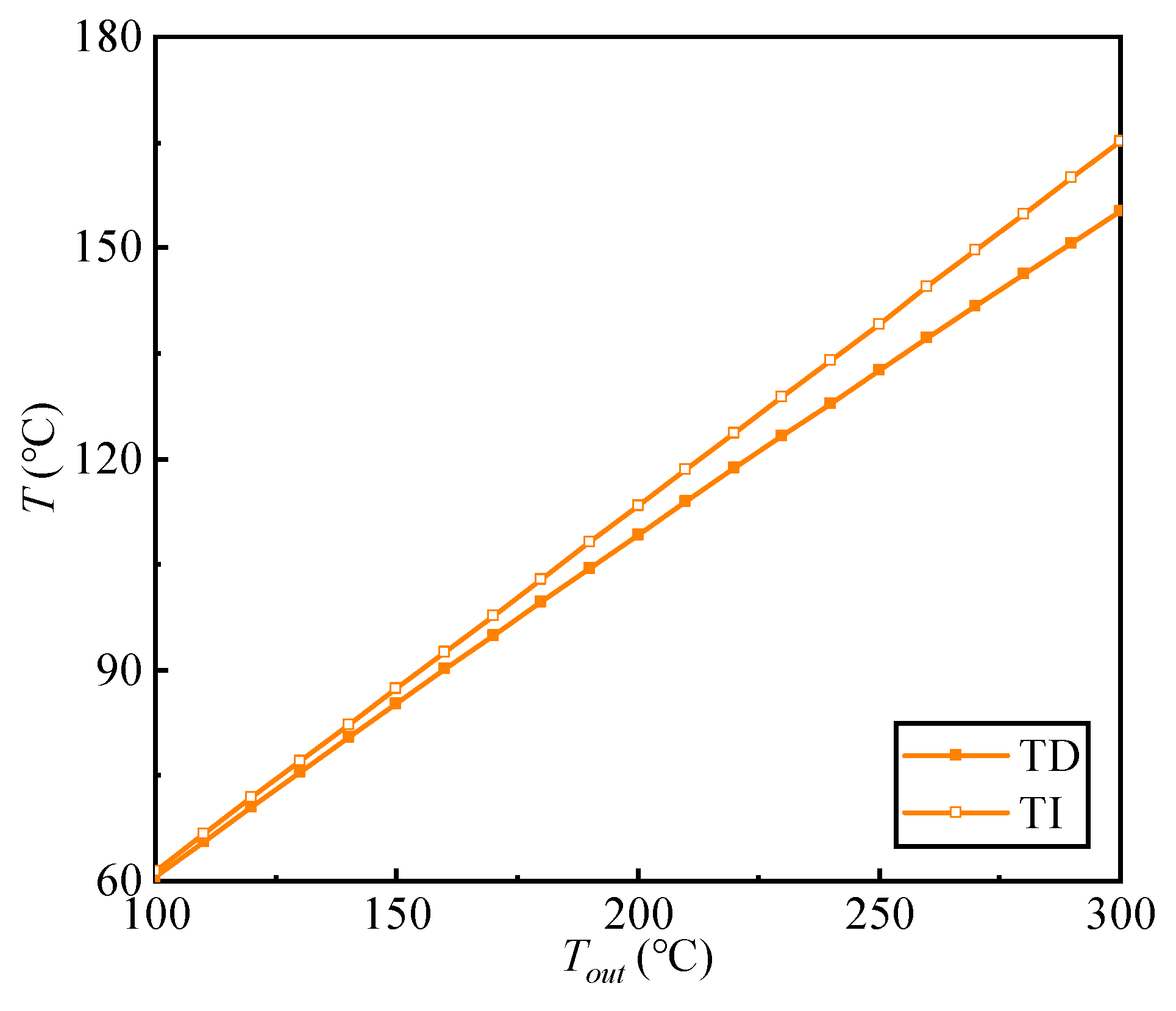
5.2.1. Temperature Distribution
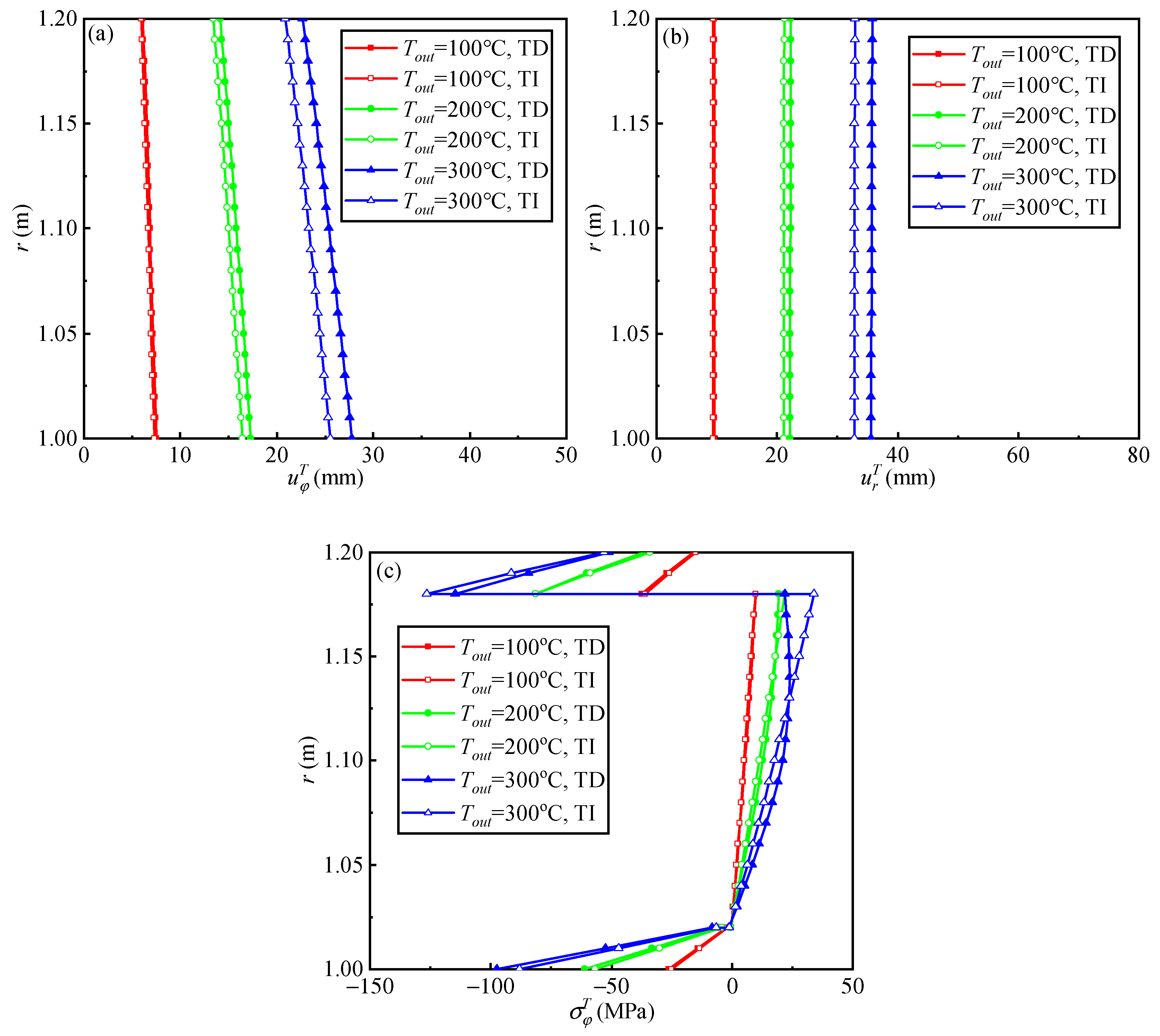
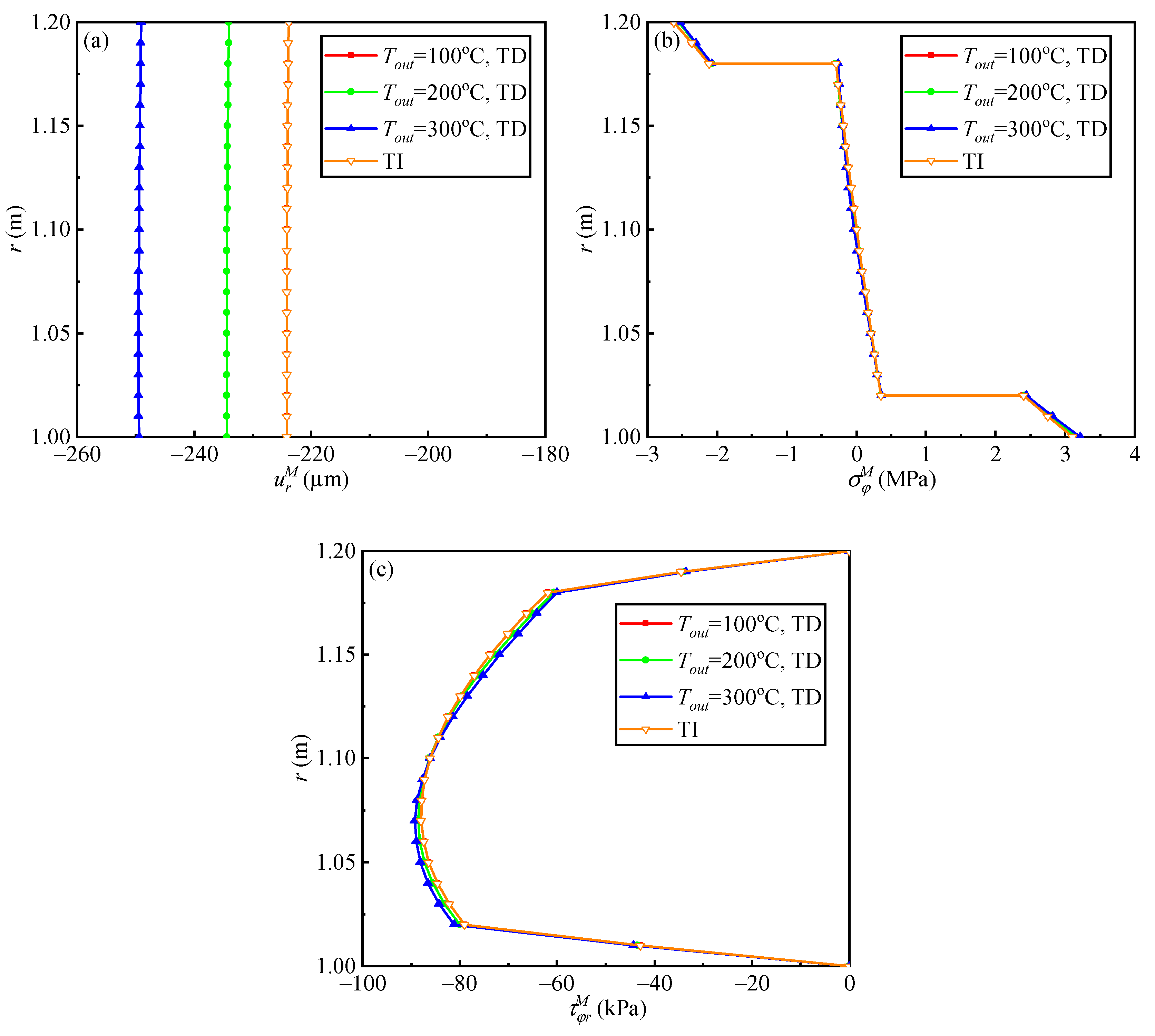
5.2.2. Displacement and Stress Distributions
6. Conclusions
- i.
- The present solutions converge quickly with high accuracy. By comparing the present solutions with those predicted by the EBT, it was found that for thin and shallow arches, the deflection predicted by the EBT agrees well with that predicted by the present thermoelasticity theory. However, the error of the EBT increases when the angle θ increases or the length-to-thickness ratio L/H decreases.
- ii.
- The temperature, displacement, and stress distributions nonlinearly change with the surface temperature in the TD case, but linearly change in the TI case.
- iii.
- By separately studying the mechanical responses of the arch induced by thermal loading and mechanical loading, two main effects of temperature can be revealed, directly inducing thermal stresses and deformations and affecting the responses induced by mechanical loading.
- iv.
- When the arch is subjected to thermal loading, the temperature dependence of thermomechanical properties has a much greater impact on the stress solution than on the temperature and displacement solutions.
- v.
- Regardless of whether the arch is subjected to thermal loading or mechanical loading, the induced deformations in the TD case are always greater than those in the TI case.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| thickness of the jth layer | |
| , , , | temperature-dependent thermomechanical properties of concrete |
| , , , | temperature-dependent thermomechanical properties of steel |
| , , , | assumed uniform thermal conductivity, thermal expansion coefficient, Young’s modulus, and Poisson’s ratio of the ith slice |
| m | number of half-waves along the φ direction |
| p, q | layer number and slice number |
| Q(φ) | radial load |
| , , , H, L, θ | inside radius, mean radius, outside radius, thickness, mean length, and angle of arch |
| , , | outer radius, mean radius, and thickness of the ith slice |
| s | iterative step |
| T | temperature |
| , , | reference temperature, inside surface temperature, and outside surface temperature |
| assumed uniform temperature of the ith slice | |
| , | displacement components |
| , , | strain components |
| , , | stress components |
| φ, r | polar coordinates |
References
- Zhou, M.; Zhuang, H.; An, L. Xuhong Bridge: A long span wooden arch bridge with glued laminated timber. Struct. Eng. Int. 2021, 31, 60–64. [Google Scholar] [CrossRef]
- Gao, Y.; Yu, F.; Wu, P. Exact analytical solutions for bending creep behavior of viscoelastic laminated arches with interlayers. Thin-Walled Struct. 2022, 174, 109128. [Google Scholar] [CrossRef]
- Xie, H.; Shen, C.; Fang, H.; Han, J.; Cai, W. Flexural property evaluation of web reinforced GFRP-PET foam sandwich panel: Experimental study and numerical simulation. Compos. Part B Eng. 2022, 234, 109725. [Google Scholar] [CrossRef]
- Yan, J.B.; Liew, J.Y.R.; Zhang, M.H.; Sohel, K.M.A. Experimental and analytical study on ultimate strength behavior of steel–concrete–steel sandwich composite beam structures. Mater. Struct. 2015, 48, 1523–1544. [Google Scholar] [CrossRef]
- Jeon, S.-J.; Jin, B.-M.; Kim, Y.-J.; Chung, C.-H. Consistent thermal analysis procedure of LNG storage tank. Struct. Eng. Mech. 2007, 25, 445–466. [Google Scholar] [CrossRef]
- Dai, T.; Li, B.; Tao, C.; He, Z.; Huang, J. Thermo-mechanical analysis of a multilayer hollow cylindrical thermal protection structure with functionally graded ultrahigh-temperature ceramic to be heat resistant layer. Aerosp. Sci. Technol. 2022, 124, 107532. [Google Scholar] [CrossRef]
- Shafigh, P.; Hafez, M.A.; Che Muda, Z.; Beddu, S.; Zakaria, A.; Almkahal, Z. Influence of different ambient temperatures on the thermal properties of fiber-reinforced structural lightweight aggregate concrete. Buildings 2022, 12, 771. [Google Scholar] [CrossRef]
- Špilák, D.; Majlingová, A.; Kačíková, D.; Tischler, P. Determining the charred layer of wooden beams with finite element analysis based on enthalpy approach. Buildings 2022, 12, 875. [Google Scholar] [CrossRef]
- Hajianmaleki, M.; Qatu, M.S. Vibrations of straight and curved composite beams: A review. Compos. Struct. 2013, 100, 218–232. [Google Scholar] [CrossRef]
- Auciello, N.M.; De Rosa, M.A. Free vibrations of circular arches: A review. J. Sound Vib. 1994, 176, 433–458. [Google Scholar] [CrossRef]
- Abrate, S.; Di Sciuva, M. Equivalent single layer theories for composite and sandwich structures: A review. Compos. Struct. 2017, 179, 482–494. [Google Scholar] [CrossRef]
- Hetnarski, R.B.; Eslami, M.R. Thermal Stresses—Advanced Theory and Applications; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Rafiee, M.; Nitzsche, F.; Labrosse, M. Dynamics, vibration and control of rotating composite beams and blades: A critical review. Thin-Walled Struct. 2017, 119, 795–819. [Google Scholar] [CrossRef]
- Reddy, J.N. Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 2007, 45, 288–307. [Google Scholar] [CrossRef]
- Keibolahi, A.; Kiani, Y.; Eslami, M.R. Dynamic snap-through of shallow arches under thermal shock. Aerosp. Sci. Technol. 2018, 77, 545–554. [Google Scholar] [CrossRef]
- Keibolahi, A.; Kiani, Y.; Eslami, M.R. Nonlinear rapid heating of shallow arches. J. Therm. Stress. 2018, 41, 1244–1258. [Google Scholar] [CrossRef]
- Khalili, M.M.; Keibolahi, A.; Kiani, Y.; Eslami, M.R. Application of Ritz method to large amplitude rapid surface heating of FGM shallow arches. Arch. Appl. Mech. 2022, 92, 1287–1301. [Google Scholar] [CrossRef]
- Keibolahi, A.; Heidari, M.; Kiani, Y.; Eslami, M.R. Nonlinear analysis of pin-ended deep arches under instantaneous heating. J. Therm. Stress. 2022, 45, 918–936. [Google Scholar] [CrossRef]
- Khdeir, A.A. Thermally induced vibration of cross-ply laminated shallow arches. J. Therm. Stress. 2001, 24, 1085–1096. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Rajabzadeh-Safaei, N.; Hozhabrossadati, S.M. Three-dimensional deformations of a curved circular beam subjected to thermo-mechanical loading using green’s function method. Int. J. Mech. Sci. 2018, 142–143, 163–175. [Google Scholar] [CrossRef]
- Vargas, G.; Arrese, A.; Carbajal, N.; Mujika, F. Analysis of in-plane and out-of-plane thermo-mechanical stresses in un-symmetric cross-ply curved laminated strips. J. Compos. Mater. 2009, 43, 3157–3184. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Daman, M. Nonlocal thermo-electro-mechanical vibration analysis of smart curved FG piezoelectric Timoshenko nanobeam. Smart Struct. Syst. 2017, 20, 351–368. [Google Scholar] [CrossRef]
- Bahranifard, F.; Golbahar Haghighi, M.R.; Malekzadeh, P. In-plane responses of multilayer FG-GPLRC curved beams in thermal environment under moving load. Acta Mech. 2020, 231, 2679–2696. [Google Scholar] [CrossRef]
- Babaei, H.; Eslami, M.R. Thermally induced large deflection of FGM shallow micro-arches with integrated surface piezoelectric layers based on modified couple stress theory. Acta Mech. 2019, 230, 2363–2384. [Google Scholar] [CrossRef]
- Sobhy, M. Differential quadrature method for magneto-hygrothermal bending of functionally graded graphene/Al sandwich-curved beams with honeycomb core via a new higher-order theory. J. Sandw. Struct. Mater. 2021, 23, 1662–1700. [Google Scholar] [CrossRef]
- Sayyad, A.S.; Ghugal, Y.M. A sinusoidal beam theory for functionally graded sandwich curved beams. Compos. Struct. 2019, 226, 111246. [Google Scholar] [CrossRef]
- Sayyad, A.S.; Avhad, P.V. Higher-order model for the thermal analysis of laminated composite, sandwich, and functionally graded curved beams. J. Therm. Stress. 2022, 45, 382–400. [Google Scholar] [CrossRef]
- Ghugal, Y.M.; Kulkarni, S.K.; Borate, R.D. Flexural response of cross ply laminated beams subjected to combined thermal and transverse mechanical loads. Acta Mech. 2023, 234, 3725–3735. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, Y.; Xiang, Z.; Qian, W.; Shao, X. Transient thermoelastic analysis of rectangular plates with time-dependent convection and radiation boundaries. Buildings 2023, 13, 2174. [Google Scholar] [CrossRef]
- Yu, Y.; Deng, W.; Yue, K.; Wu, P. Viscoelastic solutions and investigation for creep behavior of composite pipes under sustained compression. Buildings 2022, 13, 61. [Google Scholar] [CrossRef]
- Qian, H.; Zhou, D.; Liu, W.; Fang, H.; Lu, W. Elasticity solutions of simply supported laminated cylindrical arches subjected to thermo-loads. Compos. Struct. 2015, 131, 273–281. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, D.; Lim, Y.M.; Fang, H.; Huo, R. Analytical solutions for multilayered pipes with temperature-dependent properties under non-uniform pressure and thermal load. Appl. Math. Model. 2022, 106, 369–389. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, D.; Zhang, J.; Fang, H.; Han, H. Transient analysis of layered beams subjected to steady heat supply and mechanical load. Steel Compos. Struct. 2021, 40, 87–100. [Google Scholar] [CrossRef]
- Ren, Y.; Huo, R.; Zhou, D. Thermo-mechanical buckling analysis of non-uniformly heated rectangular plates with temperature-dependent material properties. Thin-Walled Struct. 2023, 186, 110653. [Google Scholar] [CrossRef]
- Ren, Y.; Huo, R.; Zhou, D. Buckling and post-buckling analysis of restrained non-uniform columns in fire. Eng. Struct. 2022, 272, 114947. [Google Scholar] [CrossRef]
- Asgari, H.; Bateni, M.; Kiani, Y.; Eslami, M.R. Non-linear thermo-elastic and buckling analysis of FGM shallow arches. Compos. Struct. 2014, 109, 75–85. [Google Scholar] [CrossRef]
- Hosseini, S.A.H.; Rahmani, O. Thermomechanical vibration of curved functionally graded nanobeam based on nonlocal elasticity. J. Therm. Stress. 2016, 39, 1252–1267. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, J.; Zhang, Z.; He, H. Nonlinear stability and buckling analysis of composite functionally graded arches subjected to external pressure and temperature loading. Eng. Struct. 2019, 199, 109606. [Google Scholar] [CrossRef]
- Pi, Y.L.; Bradford, M.A. In-plane thermoelastic behaviour and buckling of pin-ended and fixed circular arches. Eng. Struct. 2010, 32, 250–260. [Google Scholar] [CrossRef]
- Khalili, M.M.; Keibolahi, A.; Kiani, Y.; Eslami, M.R. Dynamic snap-through of functionally graded shallow arches under rapid surface heating. Thin-Walled Struct. 2022, 178, 109541. [Google Scholar] [CrossRef]
- Javani, M.; Kiani, Y.; Eslami, M.R. Geometrically nonlinear rapid surface heating of temperature-dependent FGM arches. Aerosp. Sci. Technol. 2019, 90, 264–274. [Google Scholar] [CrossRef]
- Babaei, H.; Kiani, Y.; Eslami, M.R. Large amplitude free vibration analysis of shear deformable FGM shallow arches on nonlinear elastic foundation. Thin-Walled Struct. 2019, 144, 106237. [Google Scholar] [CrossRef]
- Babaei, H.; Kiani, Y.; Eslami, M.R. Geometrically nonlinear analysis of shear deformable FGM shallow pinned arches on nonlinear elastic foundation under mechanical and thermal loads. Acta Mech. 2018, 229, 3123–3141. [Google Scholar] [CrossRef]
- Zhang, P.; Fu, Y. A higher-order beam model for tubes. Eur. J. Mech. A/Solids. 2013, 38, 12–19. [Google Scholar] [CrossRef]
- She, G.L.; Yuan, F.G.; Karami, B.; Ren, Y.R.; Xiao, W.S. On nonlinear bending behavior of FG porous curved nanotubes. Int. J. Eng. Sci. 2019, 135, 58–74. [Google Scholar] [CrossRef]
- Babaei, H.; Kiani, Y.; Eslami, M.R. Geometrically nonlinear analysis of functionally graded shallow curved tubes in thermal environment. Thin-Walled Struct. 2018, 132, 48–57. [Google Scholar] [CrossRef]
- Malekzadeh, P. Two-dimensional in-plane free vibrations of functionally graded circular arches with temperature-dependent properties. Compos. Struct. 2009, 91, 38–47. [Google Scholar] [CrossRef]
- Lim, C.W.; Yang, Q.; Lü, C.F. Two-dimensional elasticity solutions for temperature-dependent in-plane vibration of FGM circular arches. Compos. Struct. 2009, 90, 323–329. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, D. Two-dimensional thermoelastic analysis of beams with variable thickness subjected to thermo-mechanical loads. Appl. Math. Model. 2012, 36, 5818–5829. [Google Scholar] [CrossRef]
- CEN. Eurocode 2: Design of Concrete Structures—Part 1–2: General Rules—Structural Fire Design; European Committee for Standardization (CEN): Brussels, Belgium, 2004. [Google Scholar]
- CEN. Eurocode 3: Design of Steel Structures—Part 1–2: General Rules—Structural Fire Design; European Committee for Standardization (CEN): Brussels, Belgium, 2005. [Google Scholar]



| T (°C) | 20 | 100 | 150 | 200 | 300 | 400 | 500 | 600 | 700 |
|---|---|---|---|---|---|---|---|---|---|
| Es (GPa) | 210 | 210 | - | 189 | 168 | 147 | 126 | 65.1 | 27.3 |
| Ec (GPa) | 30 | 30 | 30 | - | - | - | - | - | 0 |
| P(T) | P2 | P1 | P0 |
|---|---|---|---|
| ks (W/m°C) | −3.33 × 10−2 | 0 | 54 |
| kc (W/m°C) | 5.7 × 10−7 | −3.36 × 10−3 | 1.36 |
| αs (°C−1) | 0 | 4 × 10−9 | 1.208 × 10−5 |
| αc (°C−1) | 1.4 × 10−11 | 2.8 × 10−10 | 6.0056 × 10−6 |
| μs | 0 | 0 | 0.3 |
| μc | 0 | 0 | 0.2 |
| Positions | FE Solutions | Present Solutions | ||||
|---|---|---|---|---|---|---|
| s = 1 | s = 2 | s = 3 | s = 4 | |||
| r = 1.05 m | 53.660 | q = 10 | 54.184 | 53.714 | 53.723 | 53.723 |
| q = 20 | 54.133 | 53.652 | 53.661 | 53.661 | ||
| q = 50 | 54.135 | 53.654 | 53.663 | 53.664 | ||
| q = 100 | 54.133 | 53.652 | 53.661 | 53.661 | ||
| q = 200 | 54.133 | 53.652 | 53.661 | 53.661 | ||
| r = 1.1 m | 109.212 | q = 10 | 110.006 | 109.214 | 109.214 | 109.214 |
| q = 20 | 110.006 | 109.214 | 109.214 | 109.214 | ||
| q = 50 | 110.006 | 109.214 | 109.214 | 109.214 | ||
| q = 100 | 110.006 | 109.214 | 109.214 | 109.214 | ||
| q = 200 | 110.006 | 109.214 | 109.214 | 109.214 | ||
| r = 1.15 m | 165.390 | q = 10 | 165.940 | 165.465 | 165.456 | 165.456 |
| q = 20 | 165.888 | 165.400 | 165.391 | 165.391 | ||
| q = 50 | 165.890 | 165.403 | 165.394 | 165.394 | ||
| q = 100 | 165.888 | 165.400 | 165.391 | 165.391 | ||
| q = 200 | 165.888 | 165.400 | 165.391 | 165.391 | ||
| Variables | FE Solutions | Present Solutions | |||||
|---|---|---|---|---|---|---|---|
| m = 5 | m = 25 | m = 45 | m = 65 | m = 85 | |||
| (mm) | 2.15 | q = 10 | 2.17 | 2.15 | 2.14 | 2.14 | 2.14 |
| q = 50 | 2.18 | 2.15 | 2.15 | 2.15 | 2.15 | ||
| q = 100 | 2.18 | 2.15 | 2.15 | 2.15 | 2.15 | ||
| q = 200 | 2.18 | 2.15 | 2.15 | 2.15 | 2.15 | ||
| q = 400 | 2.18 | 2.15 | 2.15 | 2.15 | 2.15 | ||
| q = 600 | 2.18 | 2.15 | 2.15 | 2.15 | 2.15 | ||
| (mm) | 5.68 | q = 10 | 5.68 | 5.67 | 5.67 | 5.67 | 5.67 |
| q = 50 | 5.69 | 5.68 | 5.68 | 5.68 | 5.68 | ||
| q = 100 | 5.69 | 5.68 | 5.68 | 5.68 | 5.68 | ||
| q = 200 | 5.69 | 5.68 | 5.68 | 5.68 | 5.68 | ||
| q = 400 | 5.69 | 5.68 | 5.68 | 5.68 | 5.68 | ||
| q = 600 | 5.69 | 5.68 | 5.68 | 5.68 | 5.68 | ||
| (MPa) | 12.7 | q = 10 | 10.3 | 10.2 | 10.2 | 10.2 | 10.2 |
| q = 50 | 12.5 | 12.2 | 12.3 | 12.3 | 12.3 | ||
| q = 100 | 12.8 | 12.5 | 12.5 | 12.5 | 12.5 | ||
| q = 200 | 12.9 | 12.6 | 12.6 | 12.6 | 12.6 | ||
| q = 400 | 13.0 | 12.7 | 12.7 | 12.7 | 12.7 | ||
| q = 600 | 13.0 | 12.7 | 12.7 | 12.7 | 12.7 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhao, W.; Sun, Y.; Gu, Z.; Qian, W.; Gong, H. Thermoelastic Behaviors of Temperature-Dependent Multilayer Arches under Thermomechanical Loadings. Buildings 2023, 13, 2607. https://doi.org/10.3390/buildings13102607
Zhang Z, Zhao W, Sun Y, Gu Z, Qian W, Gong H. Thermoelastic Behaviors of Temperature-Dependent Multilayer Arches under Thermomechanical Loadings. Buildings. 2023; 13(10):2607. https://doi.org/10.3390/buildings13102607
Chicago/Turabian StyleZhang, Zhong, Wenjie Zhao, Ying Sun, Zhenyuan Gu, Wangping Qian, and Hai Gong. 2023. "Thermoelastic Behaviors of Temperature-Dependent Multilayer Arches under Thermomechanical Loadings" Buildings 13, no. 10: 2607. https://doi.org/10.3390/buildings13102607






