Nonlinear Deformation Model for Analysis of Temperature Effects on Reinforced Concrete Beam Elements
Abstract
:1. Introduction
- To develop analytical expressions to evaluate the effect of temperature, time, and modes of loading and heating on the values of temperature-induced strain, characteristics of mechanical and rheological properties of concrete.
- To develop a system of equations to describe the equilibrium between external and internal forces for normal cross sections of reinforced concrete elements within the framework of a nonlinear strain model. The system of equations is to take into account principal factors triggered by temperature and loading effects, or heterogeneous characteristics of mechanical and rheological properties, temperature shrinkage and creep deformations of concrete, physical nonlinearity of concrete deformation and cracking.
- To verify the calculation model by comparing it with the data of experimental studies.
- To identify the effects of major factors on the SSS of reinforced concrete structures, given that these factors include the temperature difference, values of longitudinal forces, and bending moments in the general case of misalignment with the main axes of the cross section of elements.
2. Method
2.1. Mechanical Properties of Concrete under Exposure Conditions to High Temperatures
γtt = [1 − F2 + F5·Fbt(to,T)]
βb = [1 − F3 + F6·Fb(to,T)]
2.2. Thermal Shrinkage of Concrete
2.3. Time-Dependent Strains of Concrete at Elevated Temperatures
2.4. Nonlinear Deformation Model
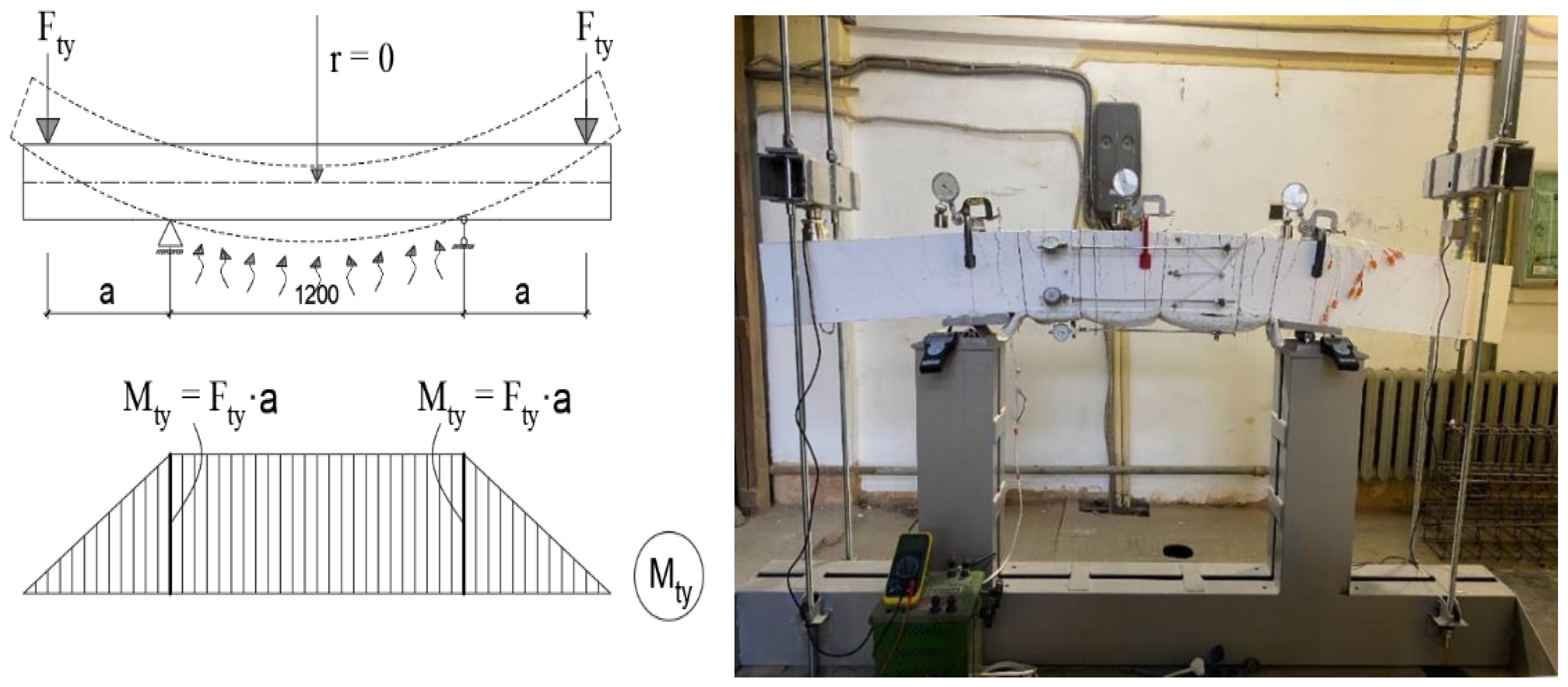
- A reinforced concrete beam element, featuring inhomogeneous physical–mechanical and rheological properties of concrete and rebars across the width and throughout the height of its section, loaded by a longitudinal compressive (tensile) force and bending moments in vertical and horizontal planes, is considered.
- A method of independent analysis of (a) long-term processes that are underway in concrete and (b) the phenomenon of physical nonlinearity of deformation is used.
- Bernoulli’s hypothesis is assumed to be true.
- Regularities that govern relations between stresses and strains in concrete and rebars are identified using analytical expressions for preset diagrams of deformation of materials, taking into account the effects of temperature, heating time, and long-term preloading.
- Temperature, shrinkage, and creep deformations of concrete are identified by using applicable methods and added to the deformations triggered by stresses in concrete and rebars (application of the superposition principle).
- The behavior of reinforced concrete with cracks in the tensile zone of an element is modeled using the averaged stress for sections with and without cracks. This is achieved by averaging the values of longitudinal stiffness of reinforcement bars.
- The nonuniform heating of the cross section of reinforced concrete beam elements is considered in case of the arbitrary orientation of the temperature plane relative to the main axes of the element cross section. It is assumed that the element is free to elongate along axes X and Y, or σx = 0 and σy = 0.
- The temperature distributions over the height and width of the section is assumed to be preset, with temperature being a function of the coordinates xji and yji. Initial mechanical characteristics of concrete and rebars are assumed to be functions of the temperature effect and its duration.
- The cross section of an inhomogeneous reinforced concrete element is represented as a system of hypothetically homogeneous small portions of concrete, having the dimensions dF = dx·dy and rebars with the cross-sectional area fs,k (Figure 1).
- Stresses arising within the boundaries of each dF section are assumed to be uniformly distributed according to the values of force-triggered deformations at the centers of gravity of the design sections. It is assumed that within the boundaries of each small element and at each stage of loading, mechanical and rheological properties, as well as stresses in concrete, σb,ji, and in rebars, σs,k, are constant and correspond to the temperature at the center of gravity of each design section.
- The inability of part of the concrete section to take load as a result of its failure in compression or cracking in tension is modeled by assigning the value of the modulus of deformation equal to E’b,ji = 0.
- The criteria of concrete strength inside layers are determined by the values of ultimate deformations.
3. Results and Discussion
3.1. Solving the Nonlinear Problems for Reinforced Concrete Elements That Have Inhomogeneous Properties
- –
- Identification of the SSS under the effect of regular temperature and load and taking into account the time factor;
- –
- Identification of the SSS under supplementary short-term loading, if the load value is increased to trigger the failure using methods of the theory of deformation of reinforced concrete with cracks.
3.2. Solution to the Problem under the Effect of Temperature and Short-Term Incremental Loading
4. Conclusions
- The nonlinear deformation model is improved by a system of equations applied to the inhomogeneous reinforced concrete beam elements in the general case of temperature and force effects, with different durations.
- The proposed system of equations allows for obtaining solutions in terms of deformations (elongations, curvatures), forces in design sections, stresses and deformations in small portions of the concrete cross section, and rebars for any moment during the temperature and load action. The general case of diagonal eccentric compression (tension) is considered in respect of an inhomogeneous beam element. This general case serves as the basis for special cases of diagonal and plane bending, plane eccentric compression, and tension.
- Independent analysis of the physical nonlinearity of deformation and long-term processes, which are underway in concrete, allows for modeling long-term operational temperature effects and a short-term increase in loading within the framework of analysis of structures.
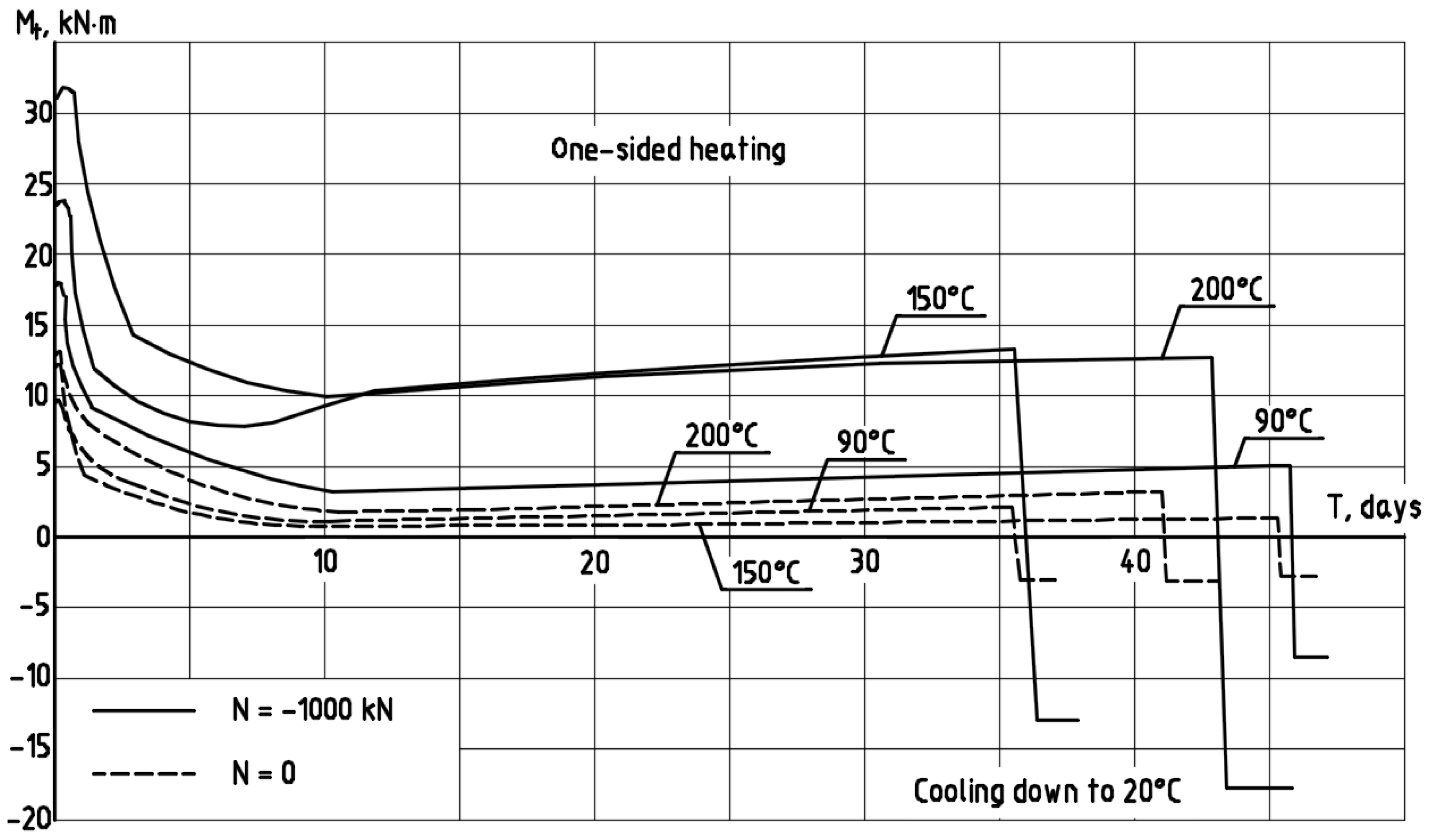
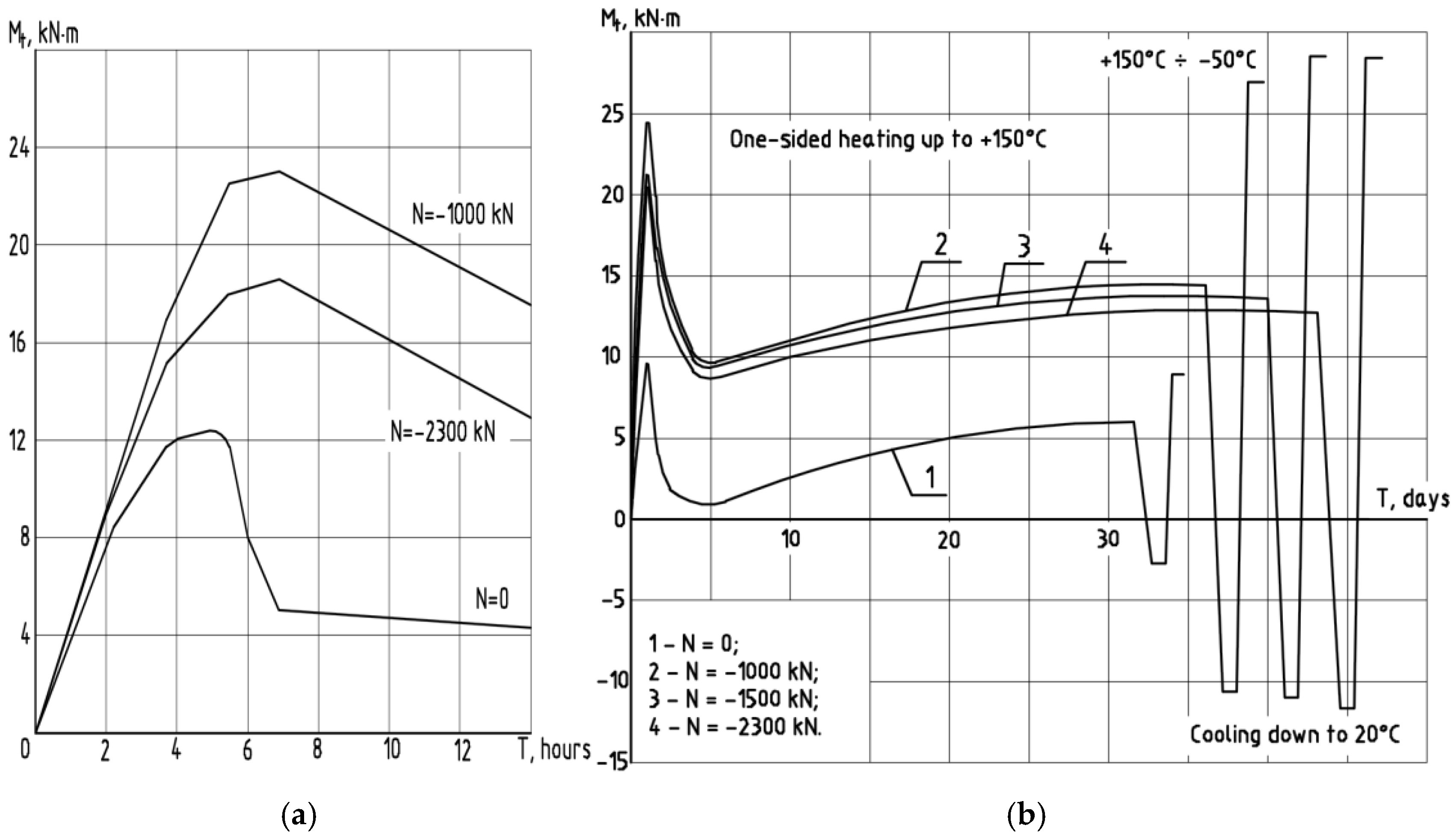
- The results of calculations made using the model are in good agreement with the experimental data on the characteristic modes of loading and nonuniform heating.
- The calculation model allows for identifying stresses, deformations, cracking in design elements of the inhomogeneous cross section of a structure, predicting changes in deformations, and temperature forces in statically indeterminate reinforced concrete structures as a result of time-dependent cracking and inhomogeneous development of long-term and short-term inelastic deformations of concrete along the height and width of the cross section.
- The most important factors affecting the stress–strain states of reinforced concrete structures under the combined effects of temperature gradients and loading are dependent, with respect to the deformation and strength properties of concrete, on the temperature and duration of its action, inhomogeneity of temperature shrinkage deformations, and creep of concrete, as well as cracking.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nekrasov, K.D.; Zhukov, V.V.; Gulyaeva, V.F. Heavy Concrete under Conditions of Elevated Temperatures; Stroyizdat: Moscow, Russia, 1972; 128p, Available online: https://search.rsl.ru/ru/record/01007183810 (accessed on 3 February 2021).
- Krichevskiy, A.P. Analysis of Temperature Effects on Reinforced Concrete Engineering Structures; Stroyizdat: Moscow, Russia, 1984; 148p. [Google Scholar]
- Korsun, V.I. Stress-Strain State of Reinforced Concrete Structures under Temperature Effects; DonGASA: Makeevka, Ukraine, 2003; 153p, Available online: https://www.academia.edu/12420694 (accessed on 4 August 2023).
- Krichevskiy, A.P.; Kardakov, V.V. Temperature Forces in Reinforced Concrete Engineering Structures; TsNIIEPSelstroy: Moscow, Russia, 1982; pp. 11–18. [Google Scholar]
- Krichevskiy, A.P.; Perederey, V.D. Determination of temperature forces in chimneys taking into account inhomogeneity of concrete properties. Concr. Reinf. Concr. 1978, 3, 16–18. [Google Scholar]
- Kirichevsky, A.P.; Perederey, V.D. Determination of temperature forces in chimneys accounting for changes in concrete properties Beton Zhelezobeton 1978, 16–18. Available online: https://jglobal.jst.go.jp/en/detail? JGLOBAL_ID=201002046940441563 (accessed on 10 October 2023).
- Wu, Y.; Li, J. Temperature and stress of RC T-beam under different heating curves. J. Build. Eng. 2022, 46, 103620. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Dwaikat, M.B.; Fike, R.S. An approach for evaluating the residual strength of fire-exposed RC beams. Mag. Concr. Res. 2010, 62, 479–488. [Google Scholar] [CrossRef]
- Ozbolt, J.; Bosnjak, J.; Periskic, G.; Sharma, A. 3D numerical analysis of reinforced concrete beams exposed to elevated temperature. Eng. Struct. 2014, 58, 166–174. [Google Scholar] [CrossRef]
- Xiao, J.; Hou, Y.; Huang, Z. Beam test on bond behavior between high-grade rebar and high-strength concrete after elevated temperatures. Fire Saf. J. 2014, 69, 23–35. [Google Scholar] [CrossRef]
- Choi, E.G.; Shin, Y.S. The structural behavior and simplified thermal analysis of normal-strength and high-strength concrete beams under fire. Eng. Struct. 2011, 33, 1123–1132. [Google Scholar] [CrossRef]
- Gao, W.Y.; Dai, J.-G.; Teng, J.G.; Chen, G.M. Finite element modeling of reinforced concrete beams exposed to fire. Eng. Struct. 2013, 52, 488–501. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Dwaikat, M. Performance-based fire safety design of reinforced concrete beams. Fire Prot. Eng. 2007, 17, 293–320. [Google Scholar] [CrossRef]
- Yuan, J.; Xu, F.; Du, H.; Yu, S.; Sun, G. Stressing state analysis of partially prestressed concrete beams with high strength reinforcement based on NSF method. Materials 2022, 15, 3377. [Google Scholar] [CrossRef]
- Alekseytsev, A.V. Mechanical Safety of Reinforced Concrete Frames under Complex Emergency Actions. Mag. Civ. Eng. 2021, 3, 10306. [Google Scholar] [CrossRef]
- Tamrazyan, A.G.; Avetisyan, L.A. Behavior of compressed reinforced concrete columns under thermodynamic influences taking into account increased concrete deformability. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 365, p. 052034. [Google Scholar]
- Tamrazyan, A.; Alekseytsev, A. Evolutionary optimization of reinforced concrete beams, taking into account design reliability, safety and risks during the emergency loss of supports. In Proceedings of the 22nd International Scientific Conference on Construction the Formation of Living Environment (FORM 2019), Moscow, Russia, 20–22 April 2019; p. 04005. [Google Scholar]
- Korsun, V.I.; Baranov, A.O. Mechanical properties of high-strength concrete after heating at temperatures up to 400 °C. In Proceedings of the EECE 2020: Energy, Environmental and Construction Engineering 3; Springer: Cham, Switzerland, 2021; Volume 150, pp. 454–463. [Google Scholar] [CrossRef]
- Korsun, V.I.; Korsun, A. The influence of precompression on strength and strain properties of concrete under the effect of elevated temperatures. Appl. Mech. Mater. 2015, 725–726, 469–474. [Google Scholar] [CrossRef]
- Korsun, V.I.; Baranov, A.; Khon, K.; Ha, Q. The influence of temperature and duration of heating on the properties of high-strength concrete modified by organo-mineral components. In Proceedings of the EECE 2020: Energy, Environmental and Construction Engineering 3; Springer: Cham, Switzerland, 2021; Volume 150, pp. 515–524. [Google Scholar] [CrossRef]
- Korsun, V.; Shvets, G. The calculation of creep deformation of high-strength concrete in relation to the conditions of exposure to elevated temperatures. IOP Conf. Ser. Mater. Sci. Eng. 2020, 896, 012039. [Google Scholar] [CrossRef]
- Vahid, A.; Susanto, T. Experiments on drying shrinkage and creep of high performance hybrid-fiber-reinforced concrete. Cem. Concr. Compos. 2020, 106, 103481. [Google Scholar] [CrossRef]
- Krishna, D.A.; Priyadarsini, R.S.; Narayanan, S. Effect of elevated temperatures on the mechanical properties of concrete. Procedia Struct. Integr. 2019, 14, 384–394. Available online: https://doi.org/10.1016/j.prostr.2019.05.047 (accessed on 3 August 2023). [CrossRef]
- Tufail, M.; Shahzada, K.; Gencturk, B.; Wei, J. Effect of elevated temperature on mechanical properties of limestone, quartzite and granite concrete. Int. J. Concr. Struct. Mater. 2017, 11, 17–28. [Google Scholar] [CrossRef]
- Kodur, V. Properties of concrete at elevated temperatures. ISRN Civ. Eng. 2014, 2014, 1–15. [Google Scholar] [CrossRef]
- Le, Q.X.; Dao, V.T.N.; Torero, J.L.; Maluk, C.; Bisby, L. Effects of temperature and temperature gradient on concrete performance at elevated temperatures. Adv. Struct. Eng. 2018, 21, 1223–1233. [Google Scholar] [CrossRef]
- Cheng, F.-P.; Kodur, V.K.R.; Wang, T.-C. Stress-strain curves for high strength concrete at elevated temperatures. J. Mater. Civ. Eng. 2004, 16, 84–90. [Google Scholar] [CrossRef]
- Saridemir, M.; Severcan, M.H.; Ciflikli, M.; Celikten, S.; Ozcan, F.; Atis, C.D. The influence of elevated temperature on strength and microstructure of high strength concrete containing ground pumice and metakaolin. Constr. Build. Mater. 2016, 124, 244–257. [Google Scholar] [CrossRef]
- Demirel, B.; Keleştemur, O. Effect of elevated temperature on the mechanical properties of concrete produced with finely ground pumice and silica fume. Fire Saf. J. 2010, 45, 385–391. [Google Scholar] [CrossRef]
- Nadeem, A.; Memon, S.A.; Lo, T.Y. The performance of Fly ash and Metakaolin concrete at elevated temperatures. Constr. Build. Mater. 2014, 62, 67–76. [Google Scholar] [CrossRef]
- Kim, G.Y.; Kim, Y.S.; Lee, T.G. Mechanical properties of high-strength concrete subjected to high temperature by stressed test. Trans. Nonferrous Met. Soc. China 2009, 19, 128–133. [Google Scholar] [CrossRef]
- Kirchhof, L.D.; Lima, R.C.A.D.; Santos Neto, A.B.D.; Quispe, A.C.; Silva Filho, L.C.P.D. Effect of moisture content on the behavior of high strength concrete at high temperatures. Rev. Mater. 2020, 25, e-12573. [Google Scholar] [CrossRef]
- Rehman, A.; Masood, A.; Akhtar, S.; Ibrahim, S.M.; Shariq, M. Experimental and numerical investigation into flexural bond strength of RC beams exposed to elevated temperature. Constr. Build. Mater. 2021, 282, 122630. [Google Scholar] [CrossRef]

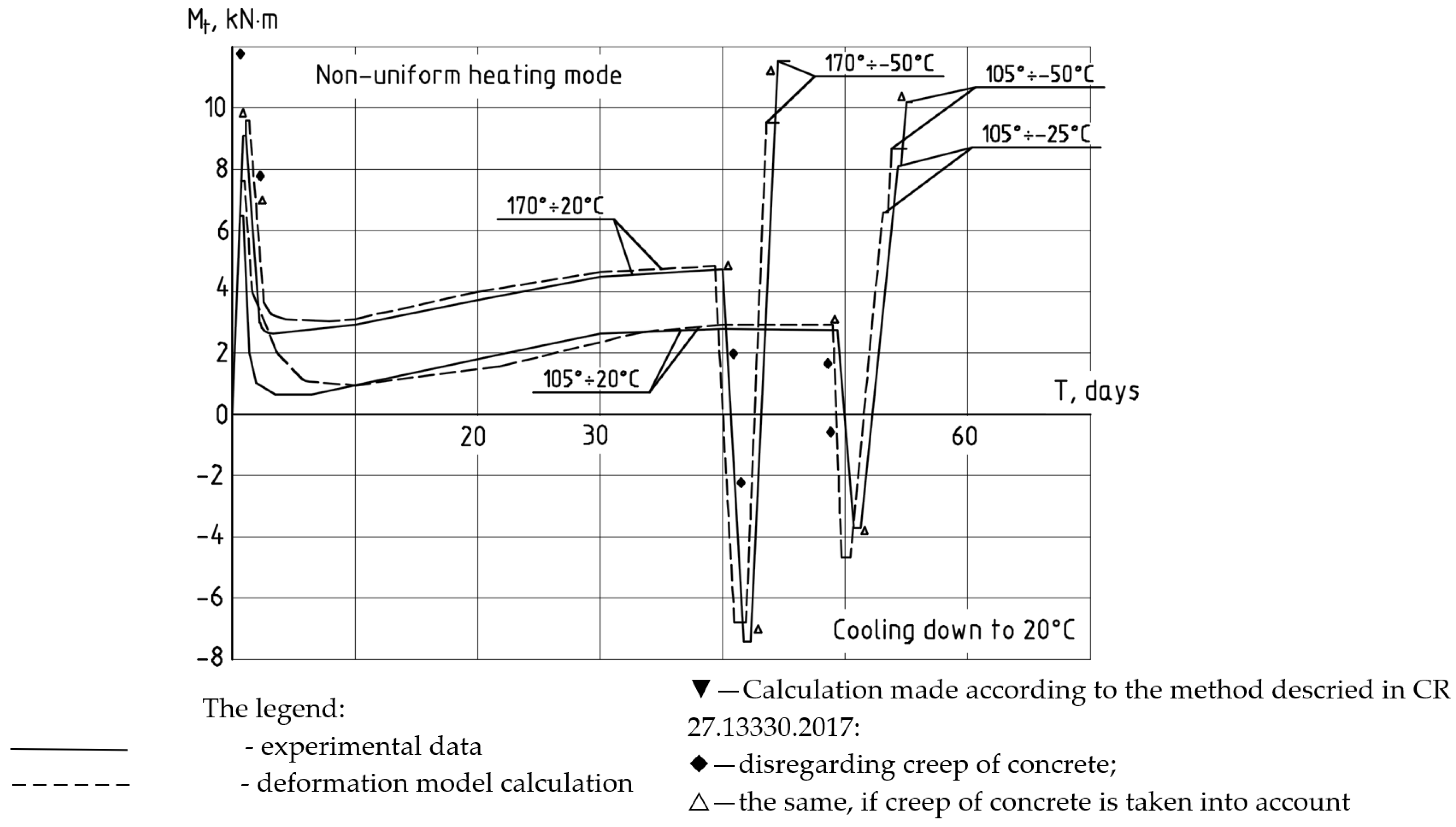
 —experimental data; – – – —calculation made using the deformation model.
—experimental data; – – – —calculation made using the deformation model.
 —experimental data; – – – —calculation made using the deformation model.
—experimental data; – – – —calculation made using the deformation model.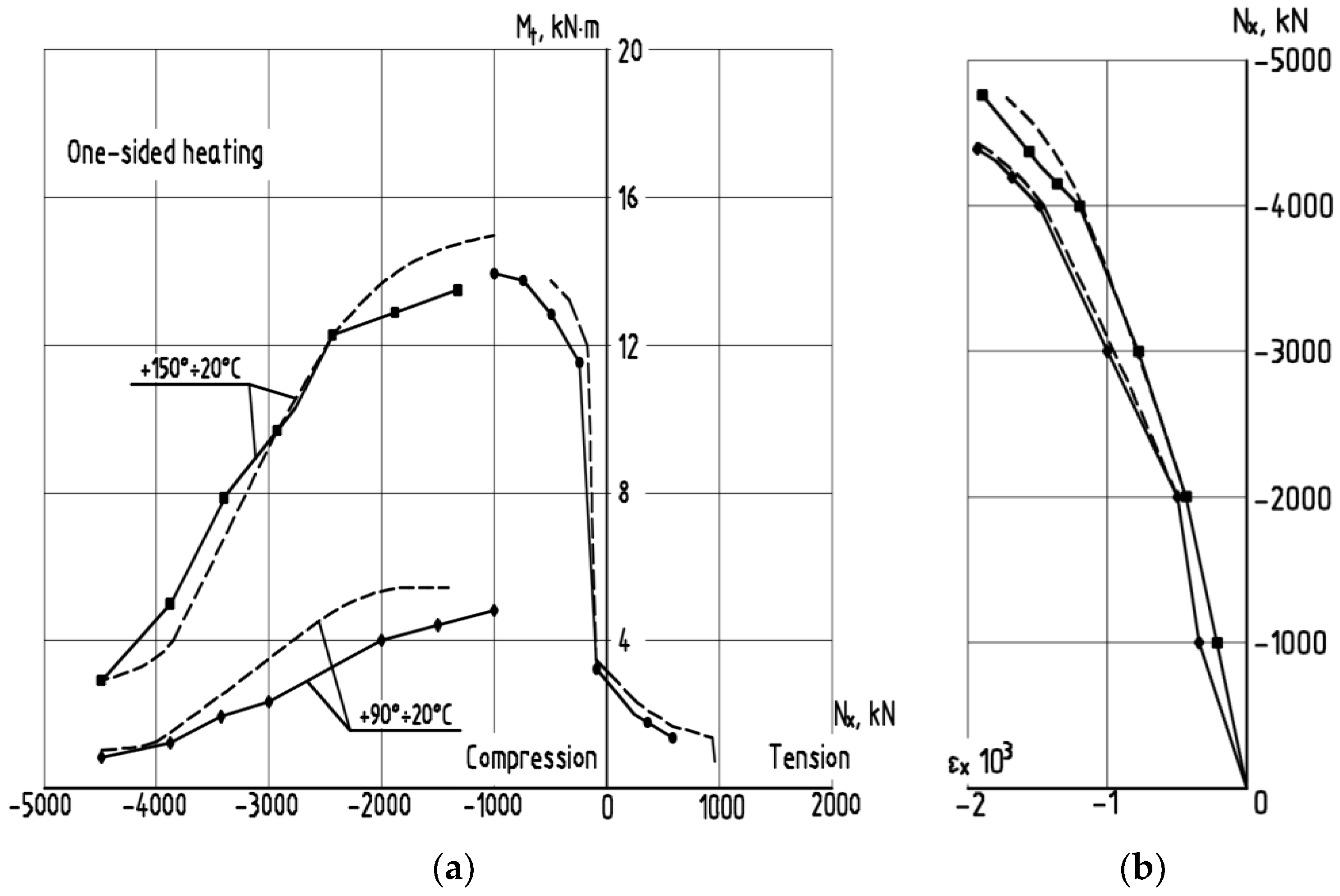

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korsun, V.I.; Morozov, V.I.; Tamrazyan, A.G.; Alekseytsev, A.V. Nonlinear Deformation Model for Analysis of Temperature Effects on Reinforced Concrete Beam Elements. Buildings 2023, 13, 2734. https://doi.org/10.3390/buildings13112734
Korsun VI, Morozov VI, Tamrazyan AG, Alekseytsev AV. Nonlinear Deformation Model for Analysis of Temperature Effects on Reinforced Concrete Beam Elements. Buildings. 2023; 13(11):2734. https://doi.org/10.3390/buildings13112734
Chicago/Turabian StyleKorsun, Vladimir I., Valeriy I. Morozov, Ashot G. Tamrazyan, and Anatoly V. Alekseytsev. 2023. "Nonlinear Deformation Model for Analysis of Temperature Effects on Reinforced Concrete Beam Elements" Buildings 13, no. 11: 2734. https://doi.org/10.3390/buildings13112734



