Experimental and Computational Research on the Shear Performance of Partially Filled Narrow-Width Steel Box-UHPC-Combined Girders under Negative Moment Action
Abstract
:1. Introduction
2. Experimental Method
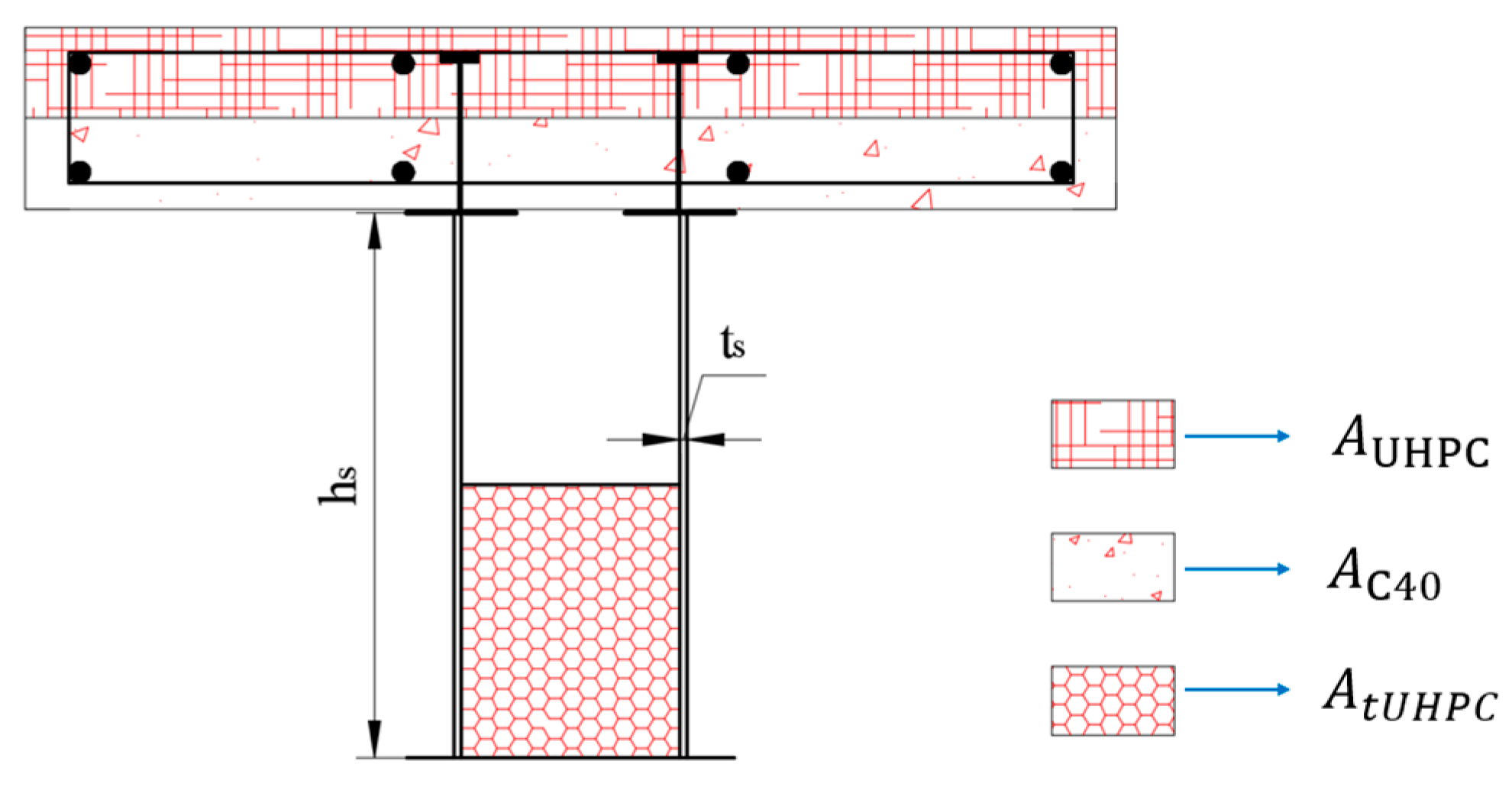
2.1. Experimental Beam Design
2.2. Material Properties
2.3. Experimental Loading and Testing System
3. Test Process and Phenomenon
3.1. Final Failure Mode of the Test Beams
3.2. Failure Phenomena and Analysis of the Test Beams
4. Processing and Analyzing the Test Results
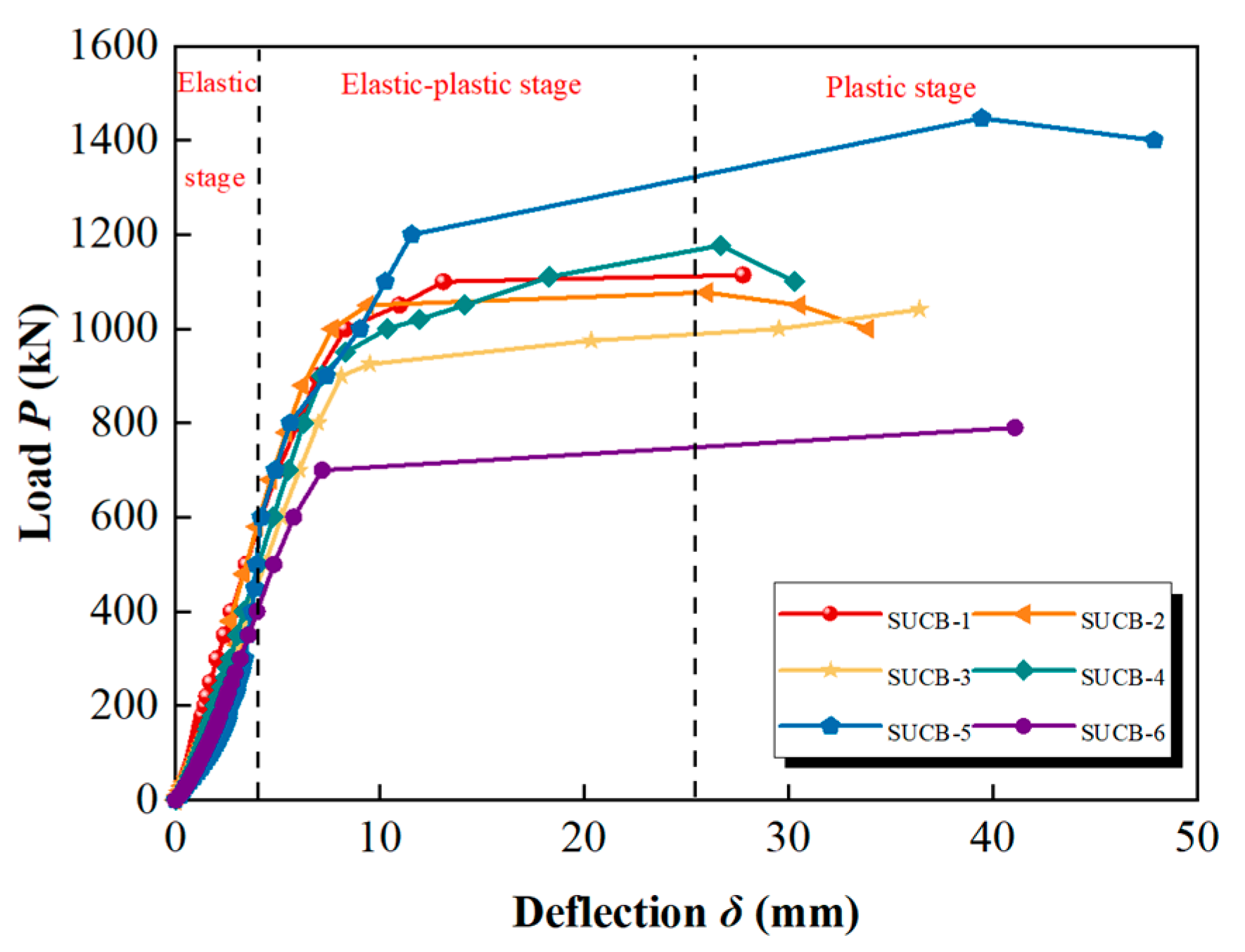
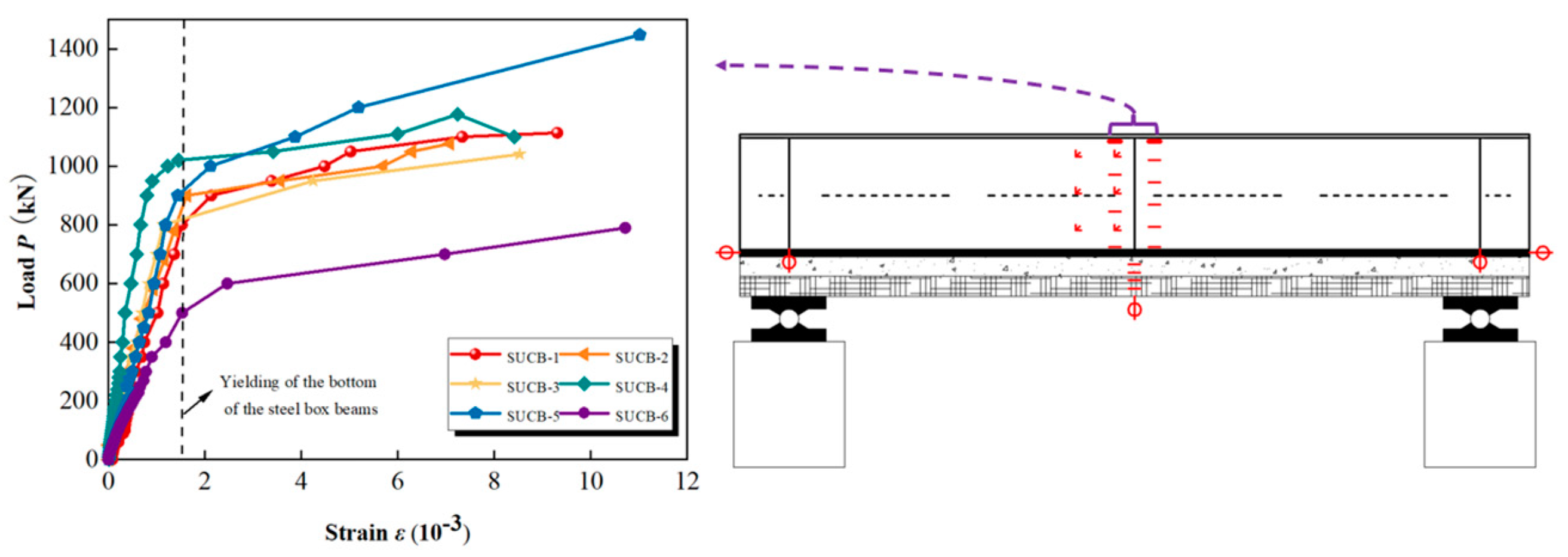
4.1. Curve Depicting the Relationship between Load and Deflection, As Well As the Relationship between Load and Strain
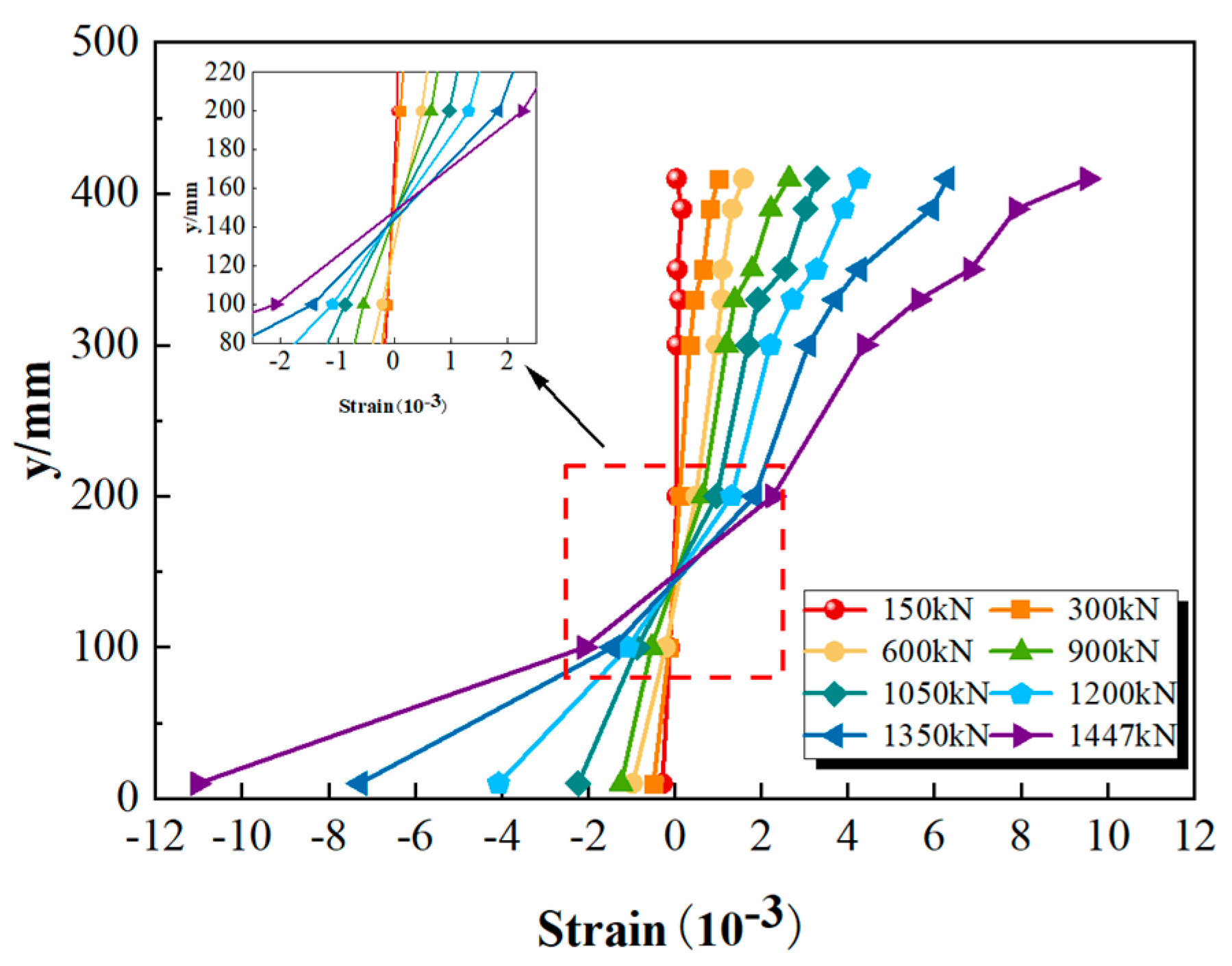
4.2. The Strain Distribution Curve at the Mid-Span Section along the Height of the Beam
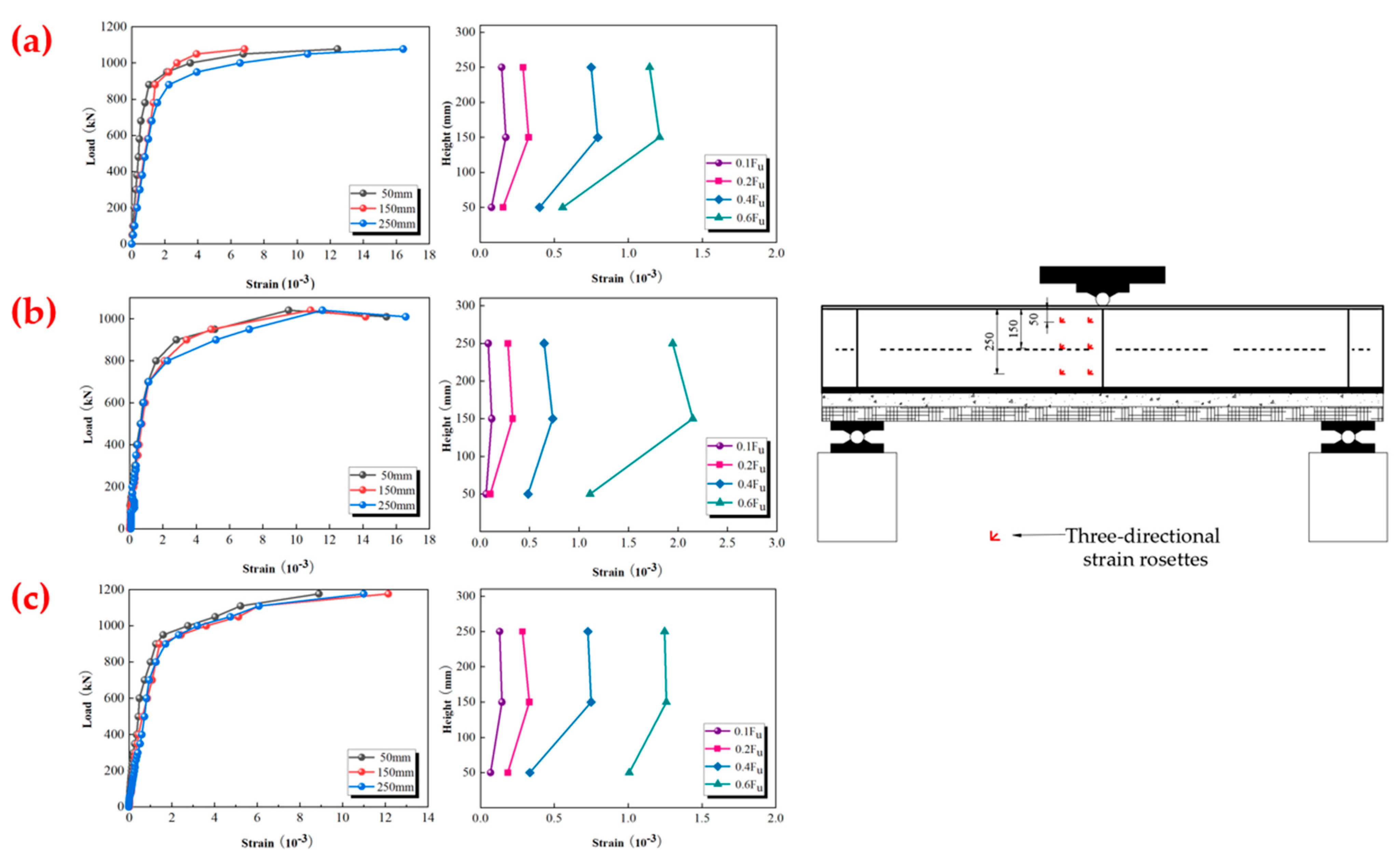
4.3. Distribution of Shear Strain in the Steel Box Web
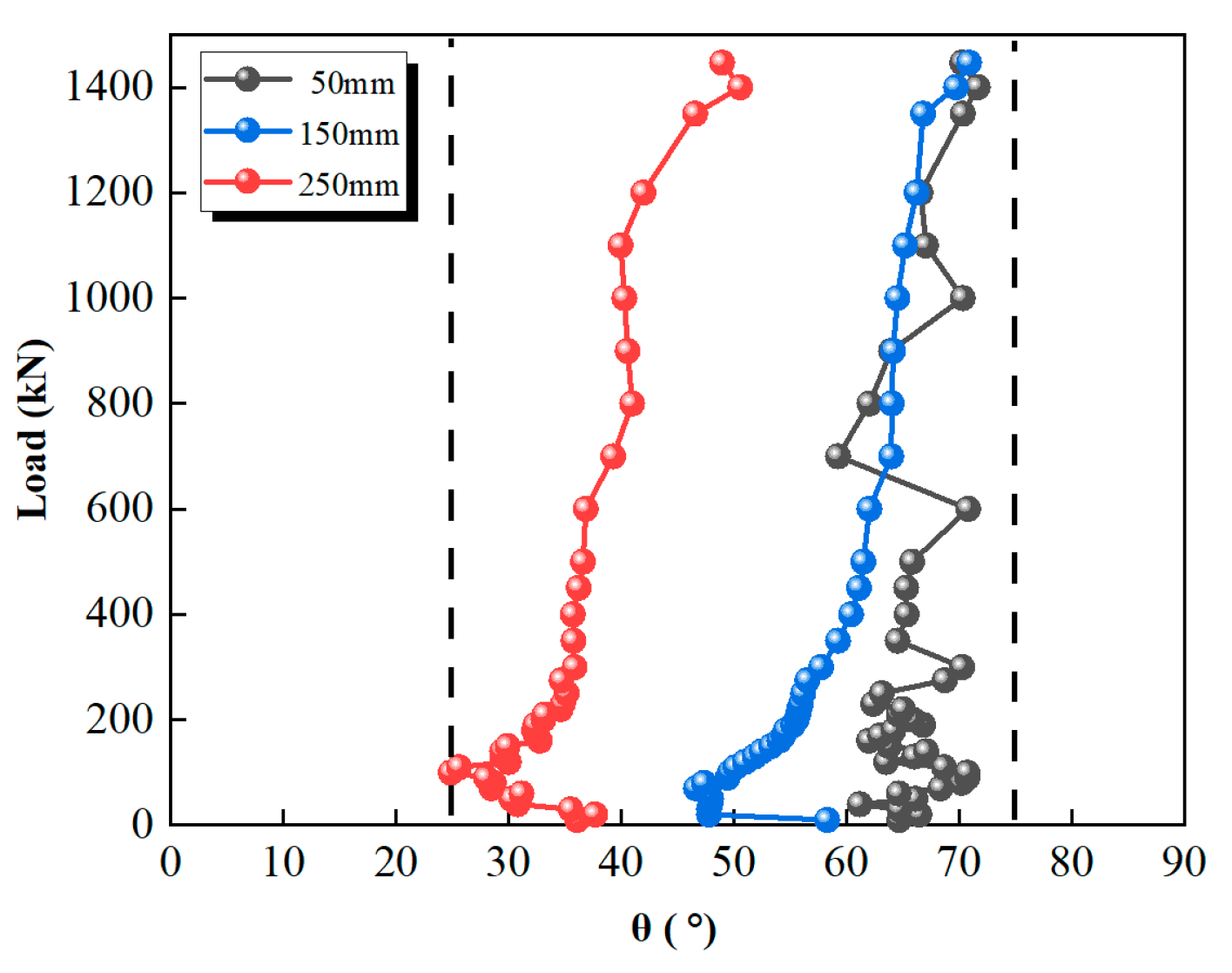
4.4. Angle of Inclination of the Steel Box Web’s Principal Compressive Strain
5. Shear Capacity Calculation of Composite Beam
6. Conclusions
- Typically, the composite beams experience three stages: elastic, elastic–plastic, and plastic, ultimately displaying the characteristic shear-bending failure.
- The ‘bridging effect’ of steel fibers within the UHPC material led to smaller and more concentrated crack widths observed in the UHPC flange, in contrast to a pure C40 flange. Moreover, the strain-hardening characteristics of UHPC greatly enhance the flexibility and ability to withstand the deformation of the composite beam. The impact of incorporating UHPC steel fibers on the cracking load, yield load, and ultimate load of the composite beam differs, with the cracking load showing the most significant enhancement. Furthermore, the incorporation of cast concrete into the steel container results in a substantial improvement in both shear resistance and the overall strength of the composite beam.
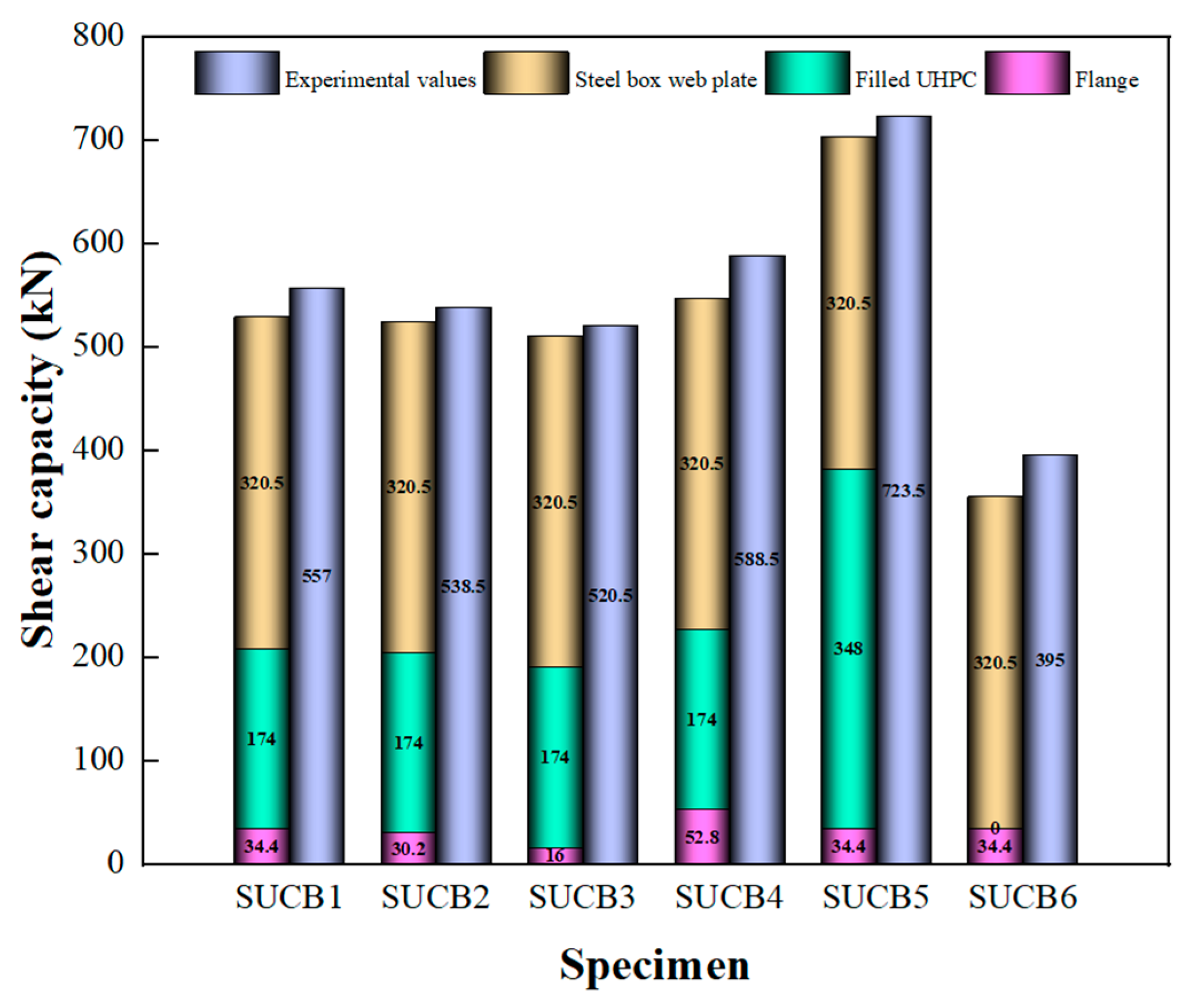
- This research demonstrated that the shear strain fluctuation pattern of narrow-width steel box-UHPC composite beams, which were partially filled, resembles that of regular composite beams. Additional assessments demonstrated that the concrete filling within the steel box can contribute up to 50% of the shear capacity of the composite beams. Fully filled concrete composite beams demonstrated a 33% higher shear capacity compared to partially filled concrete composite beams, leading to a 52% greater contribution to shear capacity. Additionally, during the later stages of loading, the steel container and its enclosed concrete contributed to over 90% of the composite beam’s shear capacity, whereas the concrete flange only made a negligible contribution to the shear capacity.
- The shear strength of the partially filled steel box-UHPC composite beams with narrow width, determined through the sub-assemblage method, shows a high degree of agreement with the experimental results, with an average precision of 95%. This suggests that the proposed calculation model in this research holds a certain degree of significance.
- Further investigation can be carried out to explore the impact of substituting the UHPC material in the steel box with C40 material on the shear behavior of partially filled narrow-width steel box-UHPC composite beams, given that the concrete inside the steel box primarily undergoes compression.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nie, J.G.; Tao, M.X.; Wu, L.L.; Nie, X.; Li, F.X.; Lei, F.L. Advances of research on steel-concrete composite bridges. China Civ. Eng. J. 2012, 45, 110–122. [Google Scholar]
- Zhu, J.W.; Wang, C.S.; Zhai, X.L. Experimental research on the mechanical properties of steel and concrete composite girders with circle tubular up-flange under negative bending. Eng. Mech. 2018, 35, 124–133. [Google Scholar]
- Chen, B.; Mu, T.; Chen, Y.; Huang, J. State-of-the-art of research and engineering application of steel-concrete composite bridges in China. J. Build. Struct. 2013, 34, 1–10. [Google Scholar]
- Tang, L.; Nie, J.G. Vertical shear strength of composite beams with compact steel sections. Part II: Composite beams subjected to hogging moment. China Civ. Eng. J. 2008, 41, 15–20. [Google Scholar]
- Xue, J.Y.; Cheng, G.; Zhao, H.T.; Fu, G. Experimental study on shear behavior of steel-concrete composite beams under negative moment. J. Build. Struct. (Suppl. Issue) 2008, 29 (Suppl. S1), 83–87. [Google Scholar]
- Cheng, G. Experimental Study on Shear Behavior of Steel-ConcreteComposite Beams under Negative Moment. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2007. [Google Scholar]
- Liao, W.Y.; Zhou, D.H.; Li, L.Q.; Han, C.X.; Yao, K.C. Experimental Study on Shear Behavior of Composite Beams with Web Opening Under Negative Moment. J. Sichuan Univ. (Eng. Sci. Ed.) 2014, 46, 46–52. [Google Scholar]
- Zhu, J.S.; Wang, Y.G.; Guo, X.Y.; Gao, C.E. Experimental Study on Shear Behaviors of Steel-UHPCComposite Beams with Waffle Slab. China J. Highw. Transp. 2020, 33, 169–181. [Google Scholar]
- Du, J.; Meng, W.; Khayat, K.H. New development of ultra-high-performance concrete (UHPC). Compos. Part B Eng. 2021, 224, 109220. [Google Scholar] [CrossRef]
- Abdal, S.; Mansour, W.; Agwa, I.; Nasr, M.; Abadel, A.; Onuralp Özkılıç, Y.; Akeed, M.H. Application of Ultra-High-Performance Concrete in Bridge Engineering: Current Status, Limitations, Challenges, and Future Prospects. Buildings 2023, 13, 185. [Google Scholar] [CrossRef]
- Bajaber, M.A.; Hakeem, I.Y. UHPC evolution, development, and utilization in construction: A review. J. Mater. Res. Technol. 2021, 10, 1058–1074. [Google Scholar] [CrossRef]
- Xue, J.; Briseghella, B.; Huang, F. Review of ultra-high performance concrete and its application in bridge engineering. Constr. Build. Mater. 2020, 260, 119844. [Google Scholar] [CrossRef]
- Abdul Sahib, M.Q.; Farzam, M.; Sukkar, K.A. Development and Performance Evaluation of UHPC and HPC Using Eco-Friendly Additions as Substitute Cementitious Materials with Low Cost. Buildings 2023, 13, 2078. [Google Scholar] [CrossRef]
- Shao, X.D.; Qiu, M.H.; Yan, B.F.; Luo, J. A Review on the Research and Application of Ultra-high Performance Concrete in Bridge Engineering Around the World. Mater. Rep. 2017, 31, 33–43. [Google Scholar]
- Zhao, Y. Review of UHPC Reinforcement Technology in Reinforcement Concrete Beams. In Proceedings of the 7th International Conference on Architecture, Materials and Construction: ICAMC 2021, Lisbon, Portugal, 27–29 October 2021; Springer International Publishing: Cham, Switzerland, 2022; pp. 204–212. [Google Scholar]
- Li, X.; Hu, Z. Cracking Resistance of UHPC-NC Structure in Negative Moment Zone of Prestressed Concrete Beam Bridges. Arab. J. Sci. Eng. 2023, 48, 4795–4804. [Google Scholar] [CrossRef]
- Zhu, J.S.; Wang, Y.G.; Yan, J.B. Shear behaviour of steel-UHPC composite beams in waffle bridge deck. Compos. Struct. 2020, 234, 111678. [Google Scholar] [CrossRef]
- Zhao, X.; Shao, X.; Cao, J. Experimental studies on shear behavior of steel-UHPC composite beam with hot rolled shape steel. Eng. Struct. 2023, 274, 115160. [Google Scholar] [CrossRef]
- Shao, X.; Zhao, X.; Liu, Q. Design and experimental study of hot rolled shape steel-ultrahigh performance concrete composite beam. Eng. Struct. 2022, 252, 113612. [Google Scholar] [CrossRef]
- GB/T 13239-2006; Metallic Materials—Tensile Testing at Low Temperature. China Standards Press: Beijing, China, 2006.
- GB/T 31387-2015; Reactive powder concreteStandardization Administration of the People’s Republic of China. China Standards Press: Beijing, China, 2015.
- GB 50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2012.
- GB/T 50107-2010; Standard for Evaluation of Concrete Compressive Strength. China Architecture & Building Press: Beijing, China, 2010.
- Qi, J.; Ma, Z.J.; Wang, J. Shear strength of UHPFRC beams: Mesoscale fiber-matrix discrete model. J. Struct. Eng. 2017, 143, 04016209. [Google Scholar] [CrossRef]
- Lin, Y.; Yan, J.; Cao, Z. Ultimate strength behaviour of S-UHPC-S and SCS sandwich beams under shear loads. J. Constr. Steel Res. 2018, 149, 195–206. [Google Scholar] [CrossRef]
- Zheng, H.; Fang, Z.; Liu, M. Experimental study on shear behavior of prestressed reactive powder concrete box girders. China Civ. Eng. J. 2015, 48, 51–63. [Google Scholar]
- Men, P.F. Study on Shear Performance and Shear Capacity Calculation Method of Steel-Concrete Composite Girders in Negative Moment Regions. Ph.D. Thesis, Chongqing University, Chongqing, China, 2021. [Google Scholar]
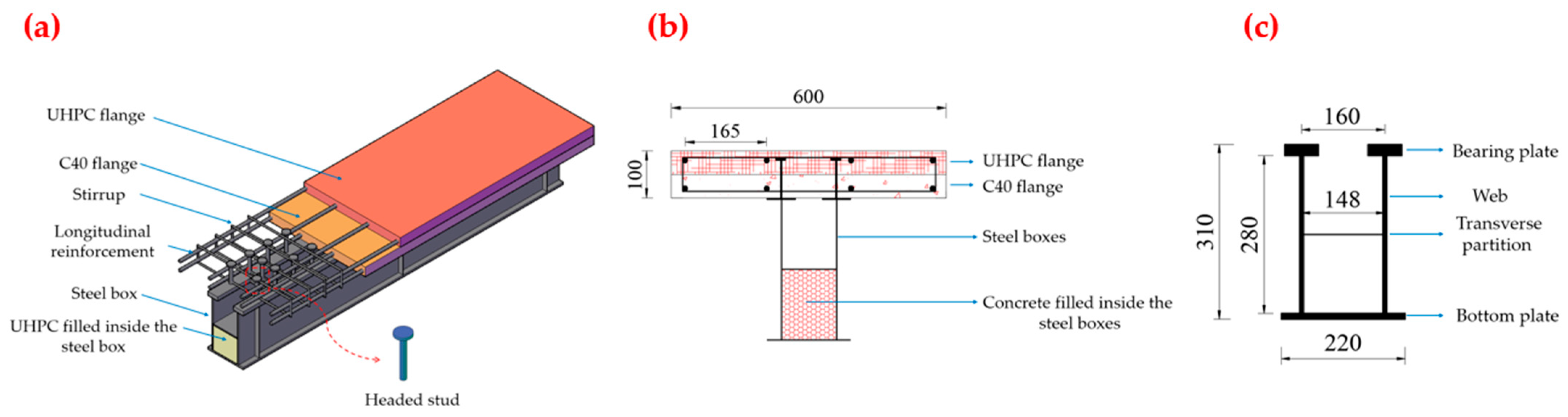
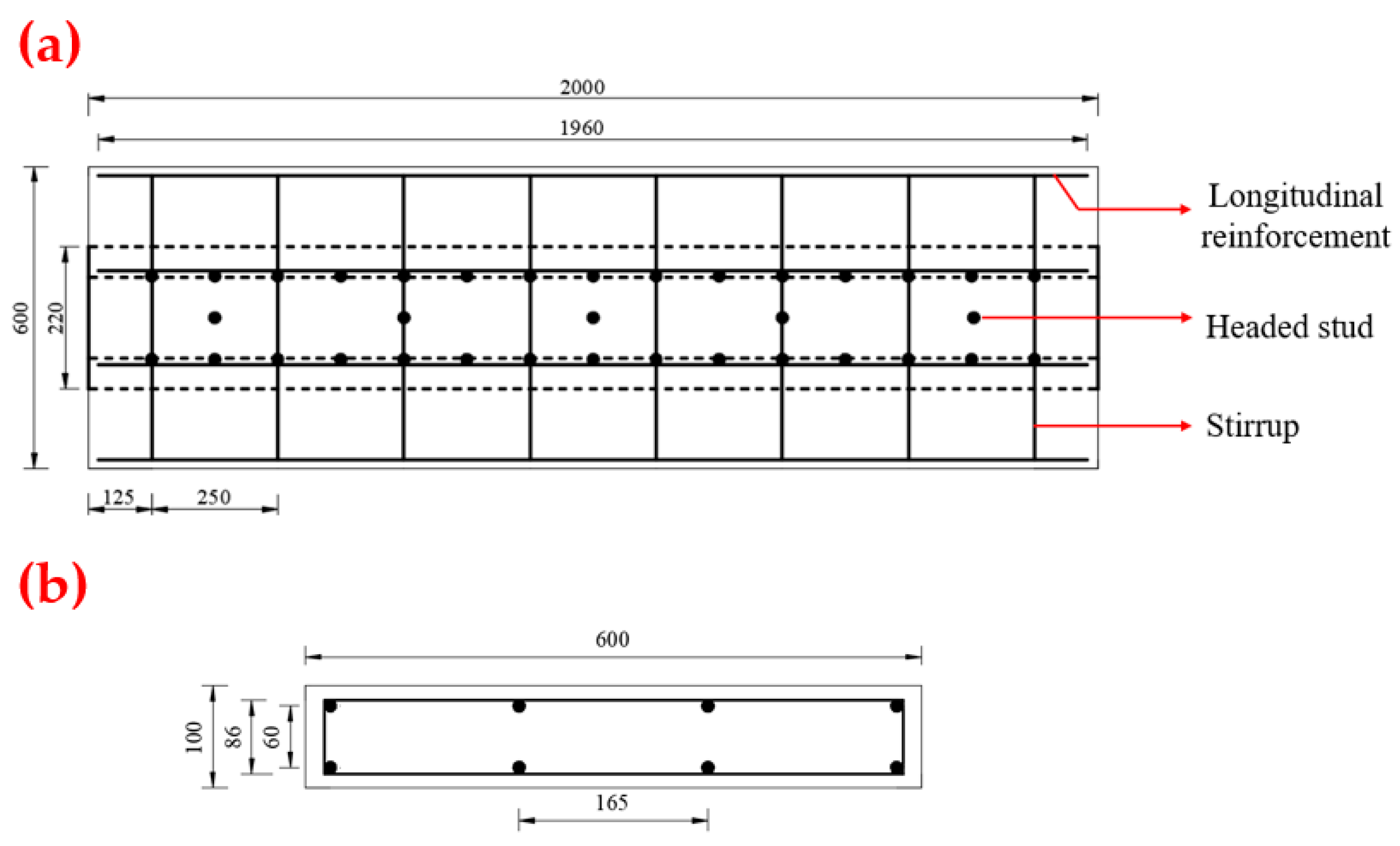
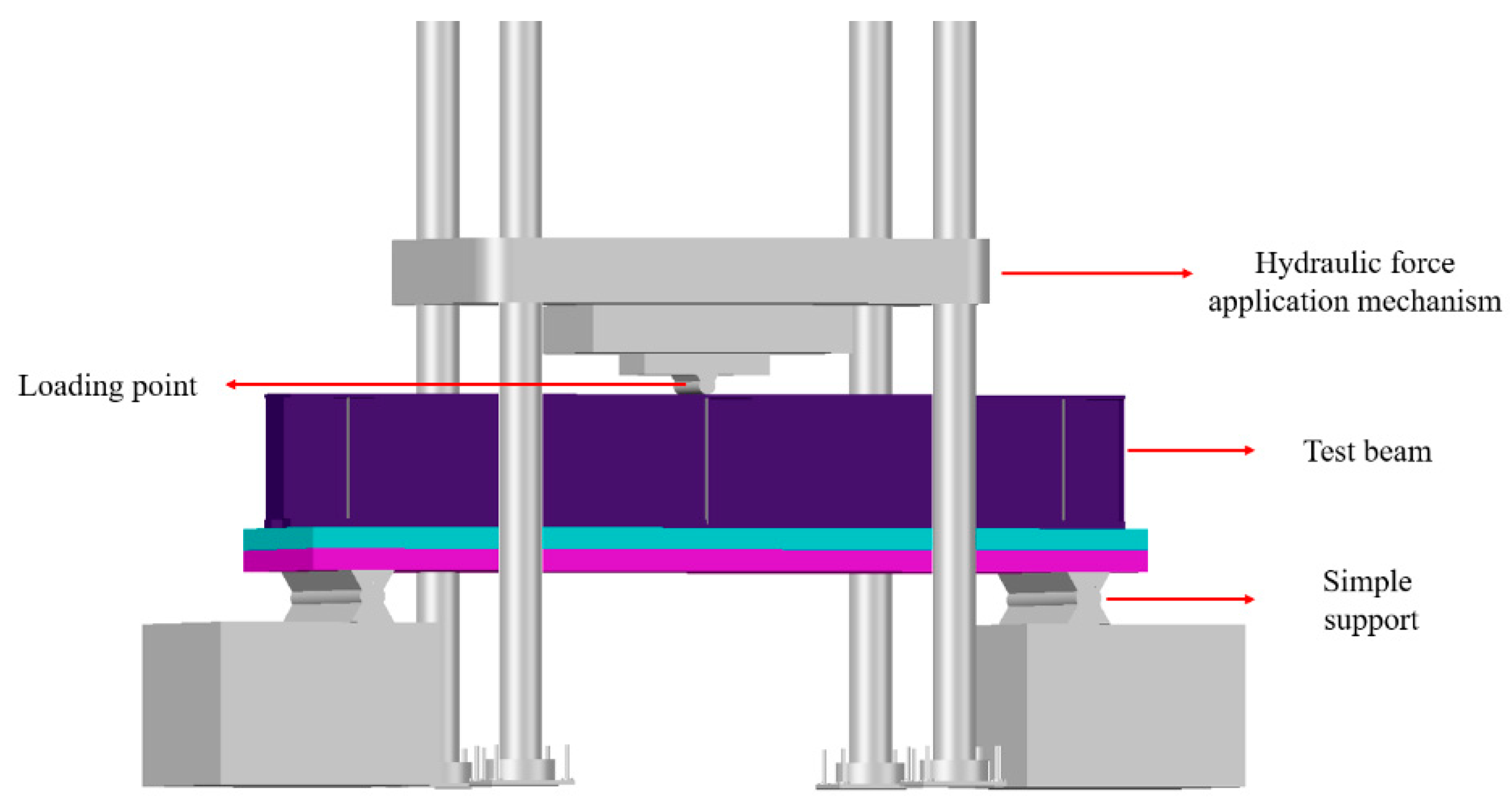
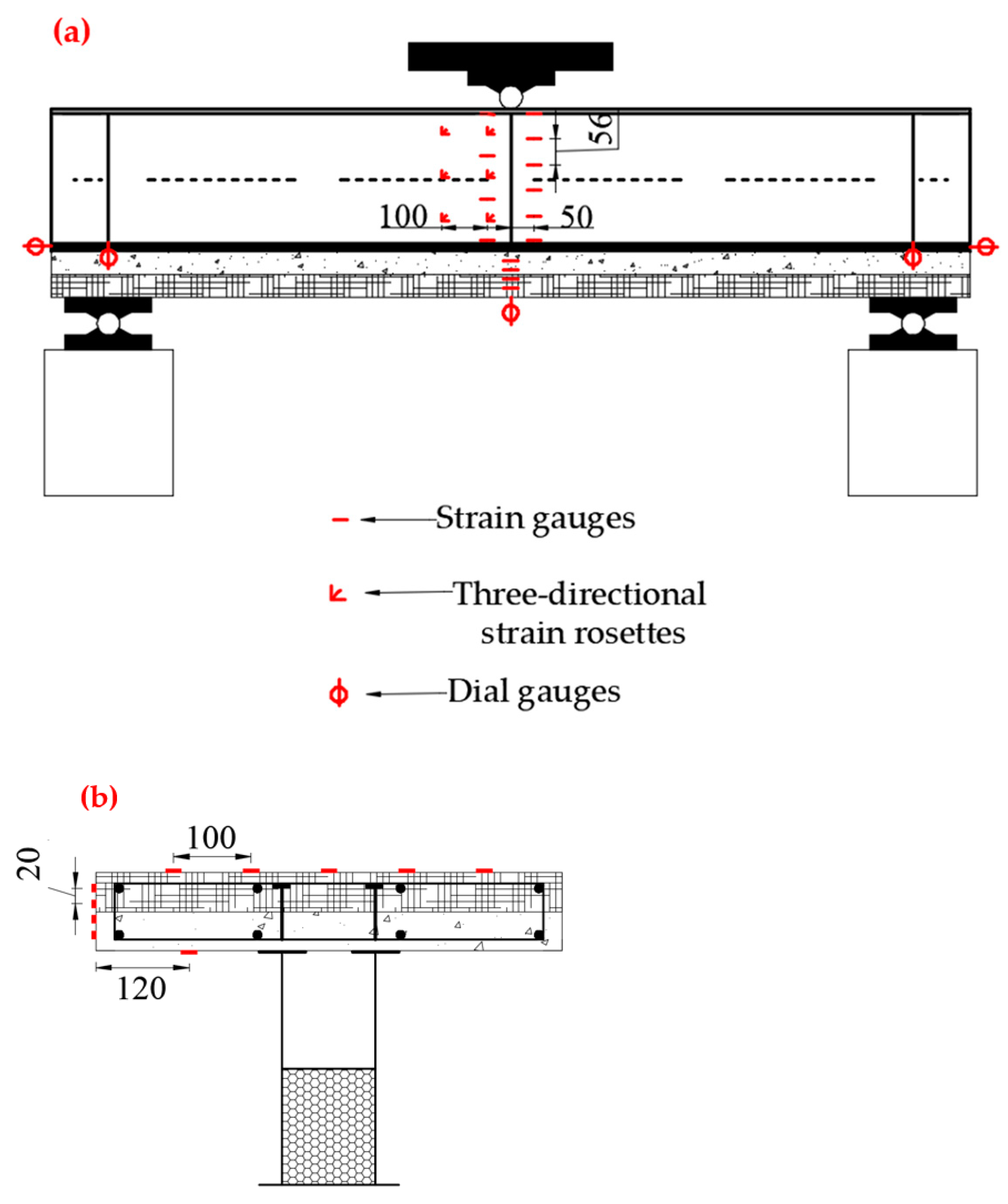




| Specimen | Reinforcement Ratio of Flanges (%) | Longitudinal Reinforcement Specifications (mm) | Reinforcement Specifications for Stirrups (mm) | Steel Fiber Content in UHPC (%) | Filling Concrete Height/Box Height | Relative Thickness of UHPC |
|---|---|---|---|---|---|---|
| SUCB-1 | 2.0 | 8 Φ14 | Φ6@250 | 2.0 | 0.5 | 0.5 |
| SUCB-2 | 2.0 | 8 Φ14 | Φ6@250 | 0.0 | 0.5 | 0.5 |
| SUCB-3 | 2.0 | 8 Φ14 | Φ6@250 | C40 | 0.5 | 0.0 |
| SUCB-4 | 2.0 | 8 Φ14 | Φ6@250 | 2.0 | 0.5 | 1.0 |
| SUCB-5 | 2.0 | 8 Φ14 | Φ6@250 | 2.0 | 1.0 | 0.5 |
| SUCB-6 | 2.0 | 8 Φ14 | Φ6@250 | 2.0 | 0.0 | 0.5 |
| Material | Type of Steel | t, r (mm) | (MPa) 1 | (MPa) 1 | (GPa) 1 |
|---|---|---|---|---|---|
| Longitudinal Reinforcement | HRB400 | 14 | 416 | 571 | 200 |
| Stirrup | HPB335 | 6 | 439 | 602 | 200 |
| Steel Plate (6 mm) | Q235 | 6 | 284 | 404 | 206 |
| Steel Plate (10 mm) | Q235 | 10 | 250 | 360 | 206 |
| Headed Studs | ML15 | 13 | 350 2 | 450 2 | 206 2 |
| Component | Coarse Sand | Medium Sand | Fine Sand | Silica Fume | Water Reducer | Cement | Water |
|---|---|---|---|---|---|---|---|
| Material Mass Ratio | 0.2 | 0.8 | 0.2 | 0.3 | 0.02 | 1 1 | 0.23 |
| Amount (kg/m3) | 210.9 | 843.6 | 210.9 | 316.4 | 21.1 | 1054.6 | 242.5 |
| D (mm) 1 | L (mm) 1 | L/D 1 | (MPa) 1 | (GPa) 1 |
|---|---|---|---|---|
| 0.18~0.22 | 13 | 59.09~72.22 | 2850 | 210 |
| Specimen Number | (MPa) 1 | (MPa) 1 | |||||
|---|---|---|---|---|---|---|---|
| C40 | 0% | 2% | UHPC Filled in Steel Box | C40 | 0% | 2% | |
| 1 | 40.3 | 84.9 | 127.6 | 82.0 | / | 6.9 | 7.8 |
| 2 | 42.7 | 88.3 | 118.9 | 87.5 | / | 7.7 | 8.2 |
| 3 | 41.8 | 80.3 | 125.8 | 88.2 | / | / | / |
| Average value | 41.6 | 84.5 | 124.1 | 85.9 | 2.39 | 7.3 | 8.0 |
| Standard deviation | 0.99 | 3.28 | 3.75 | 2.77 | / | 0.4 | 0.2 |
| Converted strength | 43.8 | / | / | / | / | / | / |
| Specimen | (kN) 1 | (kN) 1 | (mm) 1 | (kN) 1 | (mm) 1 | Failure Mode | |
|---|---|---|---|---|---|---|---|
| SUCB-1 | 140 | 548 | 4.19 | 1114 | 27.78 | 6.63 | Shear + bending |
| SUCB-2 | 120 | 532 | 3.99 | 1077 | 25.99 | 6.51 | Shear + bending |
| SUCB-3 | 90 | 467 | 4.01 | 1041 | 36.41 | 9.08 | Shear + bending |
| SUCB-4 | 150 | 573 | 4.20 | 1177 | 26.67 | 6.35 | Shear + bending |
| SUCB-5 | 170 | 607 | 4.23 | 1447 | 39.46 | 9.33 | Shear + bending |
| SUCB-6 | 130 | 405 | 4.08 | 790 | 41.07 | 10.07 | Shear + bending |
| Specimen | (kN) 1 | (kN) 1 | (kN) 1 | (kN) 1 | (kN) 1 | VG 1/V | ||
|---|---|---|---|---|---|---|---|---|
| SUCB-1 | 557.0 | 528.9 | 34.4 | 174 | 320.5 | 0.95 | 0.93 | 0.33 |
| SUCB-2 | 538.5 | 524.7 | 30.2 | 174 | 320.5 | 0.97 | 0.94 | 0.33 |
| SUCB-3 | 520.5 | 510.5 | 16 | 174 | 320.5 | 0.98 | 0.98 | 0.34 |
| SUCB-4 | 588.5 | 547.3 | 52.8 | 174 | 320.5 | 0.93 | 0.90 | 0.32 |
| SUCB-5 | 723.5 | 702.9 | 34.4 | 348 | 320.5 | 0.97 | 0.95 | 0.50 |
| SUCB-6 | 395.0 | 354.9 | 34.4 | 0 | 320.5 | 0.90 | 0.90 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Wang, B.; Zheng, Y.; Mo, S.; Zhang, Q.; Zhou, P. Experimental and Computational Research on the Shear Performance of Partially Filled Narrow-Width Steel Box-UHPC-Combined Girders under Negative Moment Action. Buildings 2023, 13, 2749. https://doi.org/10.3390/buildings13112749
Liu S, Wang B, Zheng Y, Mo S, Zhang Q, Zhou P. Experimental and Computational Research on the Shear Performance of Partially Filled Narrow-Width Steel Box-UHPC-Combined Girders under Negative Moment Action. Buildings. 2023; 13(11):2749. https://doi.org/10.3390/buildings13112749
Chicago/Turabian StyleLiu, Shuai, Bohan Wang, Yan Zheng, Shixu Mo, Qiyu Zhang, and Peixuan Zhou. 2023. "Experimental and Computational Research on the Shear Performance of Partially Filled Narrow-Width Steel Box-UHPC-Combined Girders under Negative Moment Action" Buildings 13, no. 11: 2749. https://doi.org/10.3390/buildings13112749
APA StyleLiu, S., Wang, B., Zheng, Y., Mo, S., Zhang, Q., & Zhou, P. (2023). Experimental and Computational Research on the Shear Performance of Partially Filled Narrow-Width Steel Box-UHPC-Combined Girders under Negative Moment Action. Buildings, 13(11), 2749. https://doi.org/10.3390/buildings13112749





