Dynamic Response and Optimal Design of Radio Telescope Structure under Wind Load Excitation
Abstract
:1. Introduction
2. Structure and Numerical Model
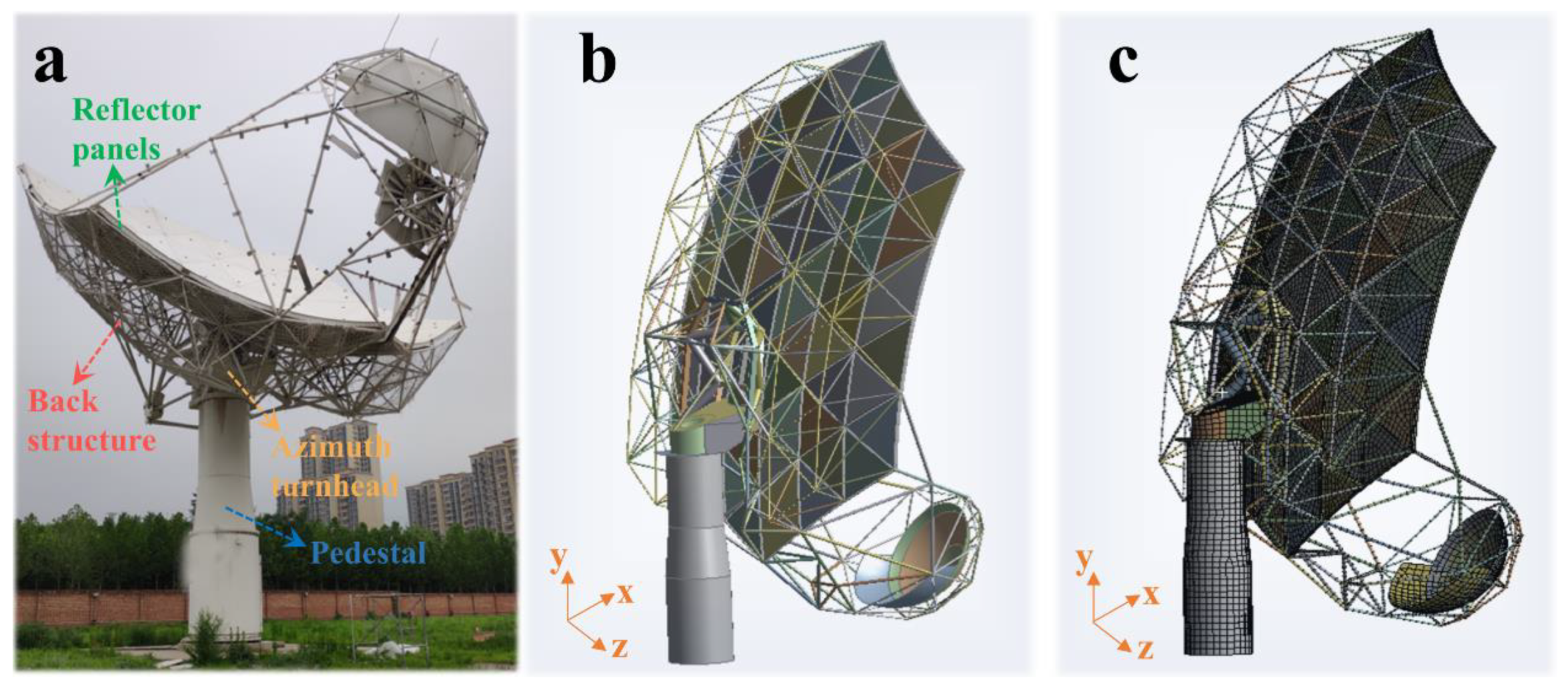
2.1. Description of the Structure
2.2. FE Model and Boundary Condition
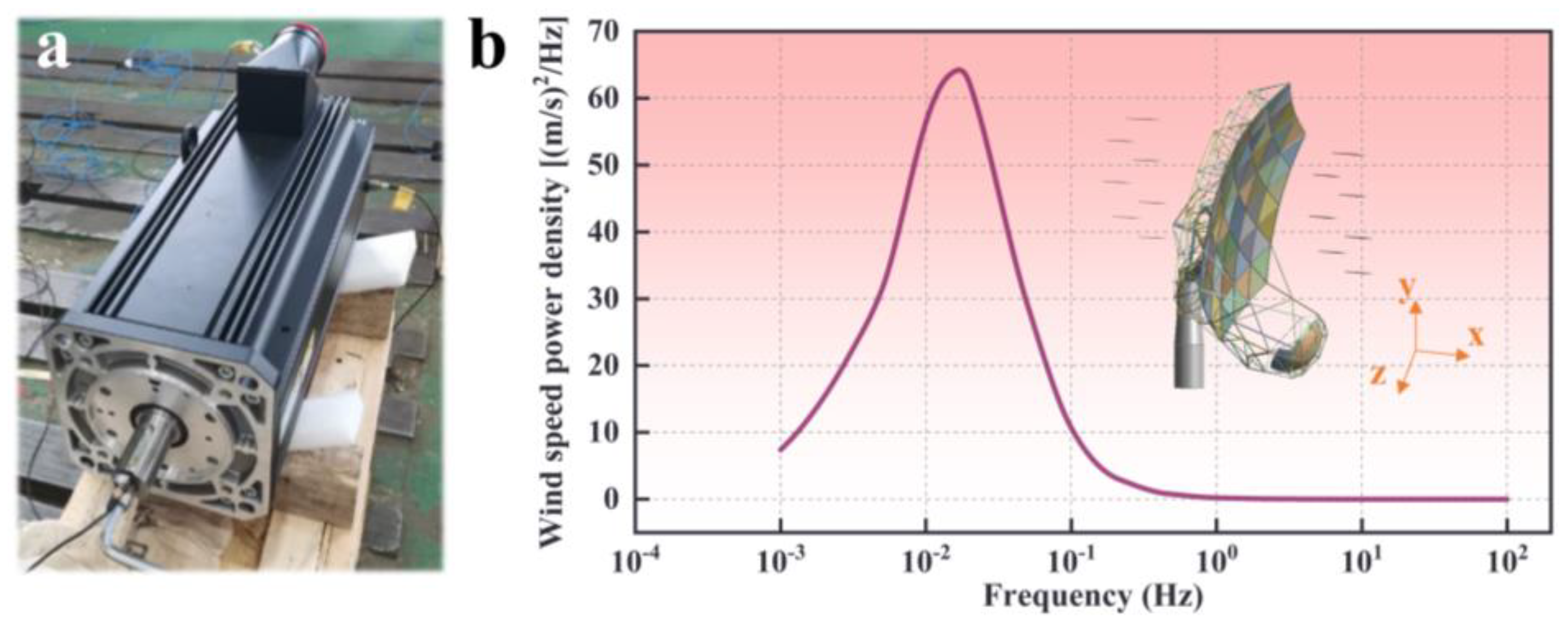
2.3. Modal Test
2.4. Wind Load Testing
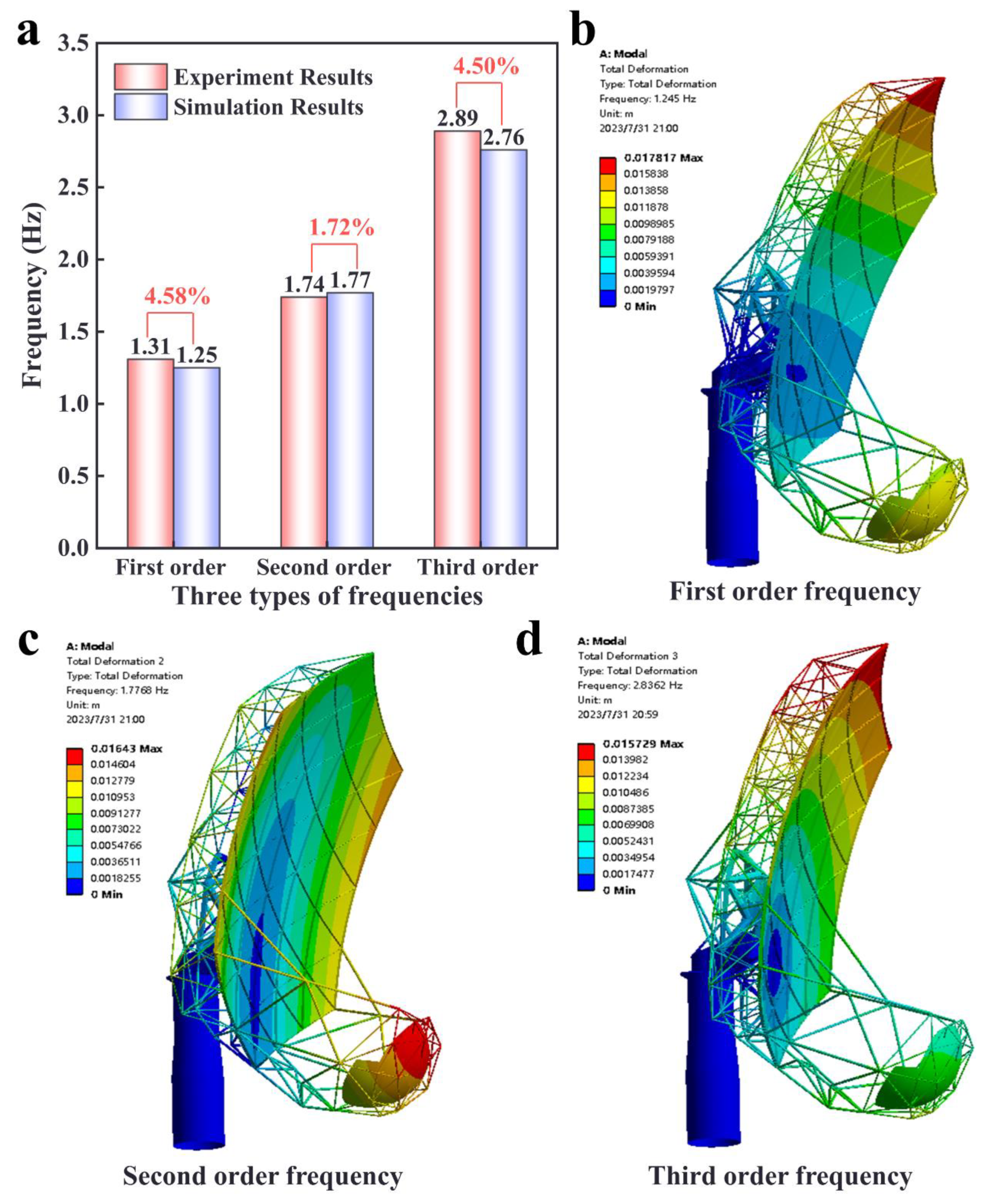
3. Finite Element Model Validation
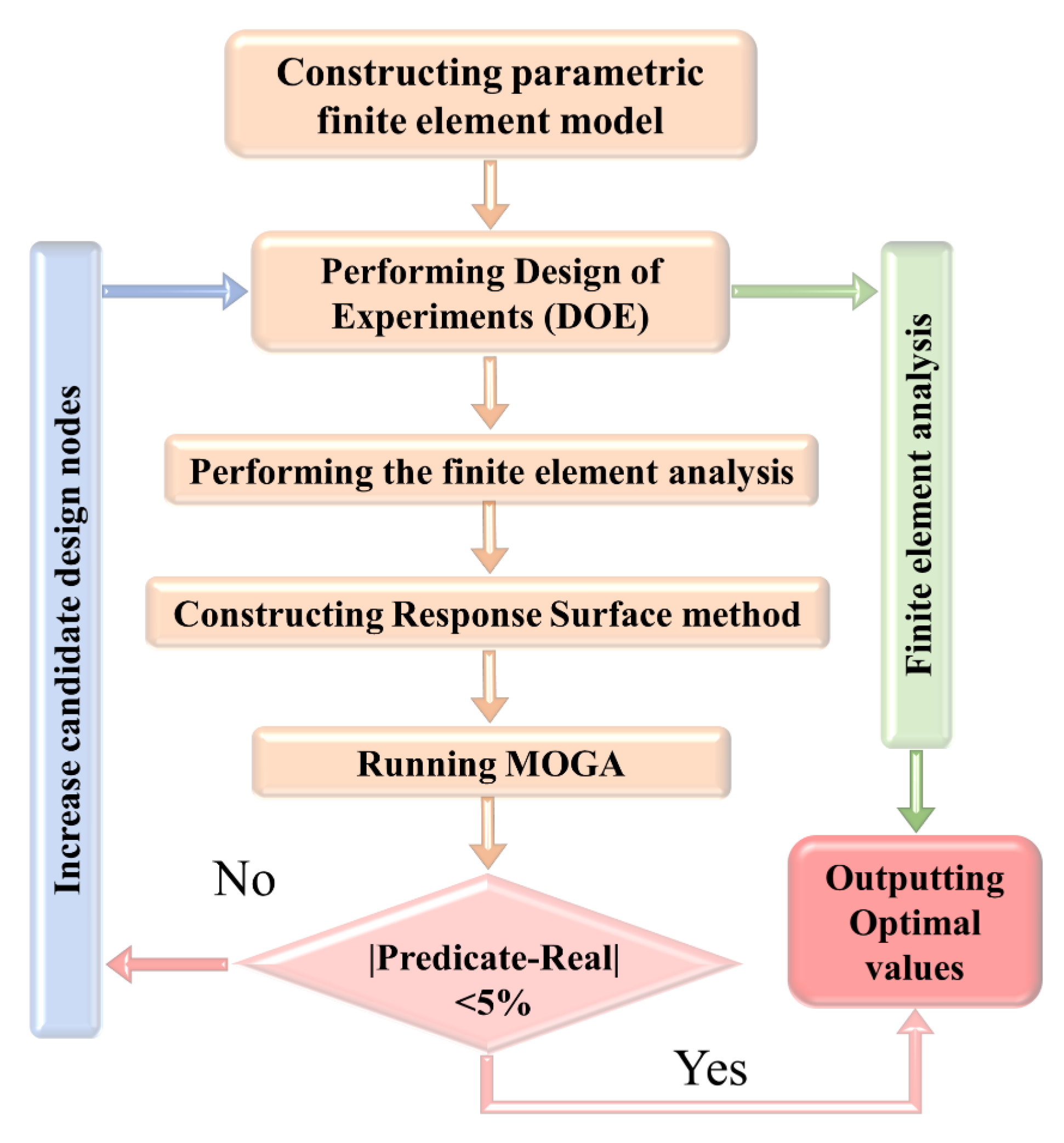
4. Structure Parameter Design Optimization
- (1)
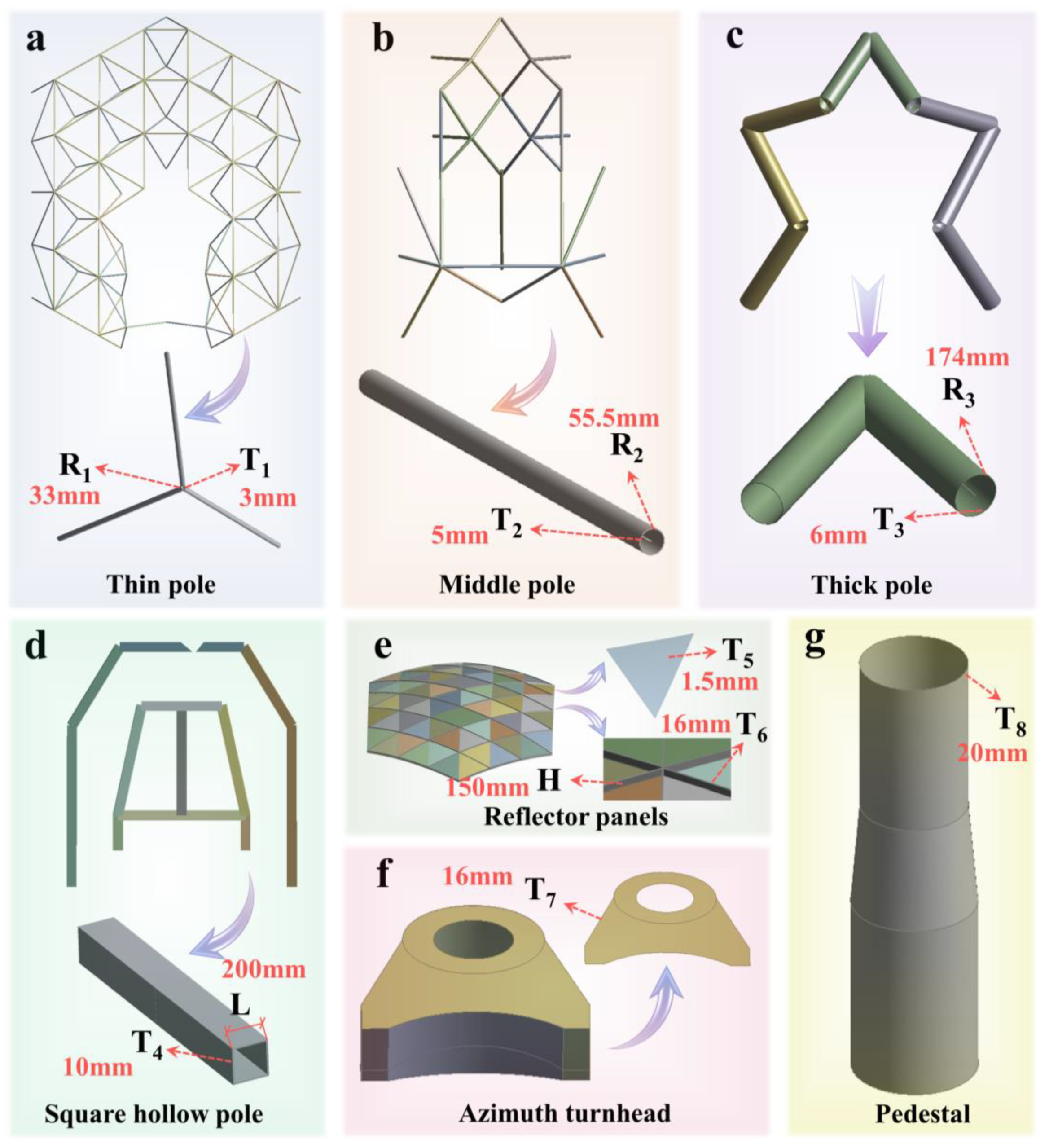
- Parametric finite element model construction: thirteen parametric variables, such as T1, T2, T3, L, T4, T5, H, T6, T7, and T8, were defined to carry out the evolution of structural dimensional parameters in different parts of the radio telescope. A parametric finite element model of the radio telescope, complete with fixed boundary conditions and loading specifications, was established in ANSYS.
- (2)
- Design of experiments (DOEs) execution: the design space, defined by Equation (2), was utilized to generate the dimensions for each structure. During this process, both the Latin hypercube sampling method [42] integrated into the ANSYS Workbench 2020R2 software and an improved Latin hypercube sampling method based on Ye et al. [43] were employed to execute DOE for the structural parameters. It is worth noting that the improved Latin hypercube sampling method is based on a principle of designing high-performance small-size base samples, determined by the maximum/minimum distance criterion from successive local enumeration, and then rapidly generating large-size test samples by “translating” the base samples. This approach effectively resolves the issues of time-consuming computations and low efficiency encountered in traditional optimal test design methods.
- (3)
- Finite element analysis: the radio telescope was analyzed in ANSYS, extracting key analyses like maximum deformation and self-oscillating frequency to evaluate performance at each design point.
- (4)
- Construction of response surface: a response surface model was built to correlate the 13 design parameters with the 4 target values reflecting the dynamic response of the radio telescope structure. This response surface was formed using the genetic aggregation algorithm integrated into the ANSYS Workbench software, considering the constraints provided in Equation (3). The genetic aggregation response surface, as illustrated in Equation (4), takes the form of an ensemble, represented as a weighted average of various metamodels.
- (5)
- MOGA parameter optimization: the optimization of the structural dimensional parameters of the radio telescope to minimize the dynamic response was carried out using the MOGA optimization function. The guidelines for this procedure were referenced from the DesignXplorer User’s Guide in ANSYS Workbench 2020R2 software [44].
- (6)
- Verification and output of optimal values: the optimization process was halted, and optimal values were recorded when the error between the predicted value and the actual calculated value fell below 5%. If the error exceeded this threshold, the process reverted to the second step for reevaluation.
5. Results and Discussion
5.1. Response Surface Validity Verification
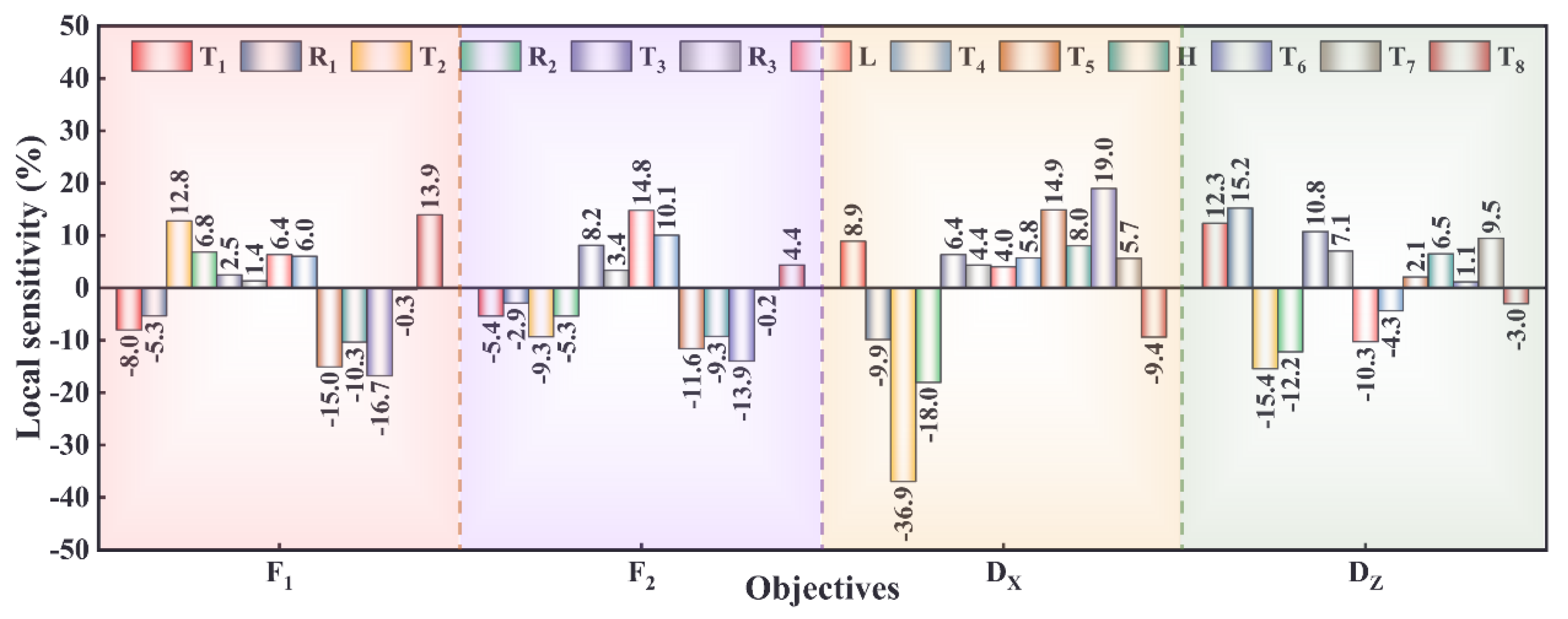
5.2. Parameter Sensitivity Analysis
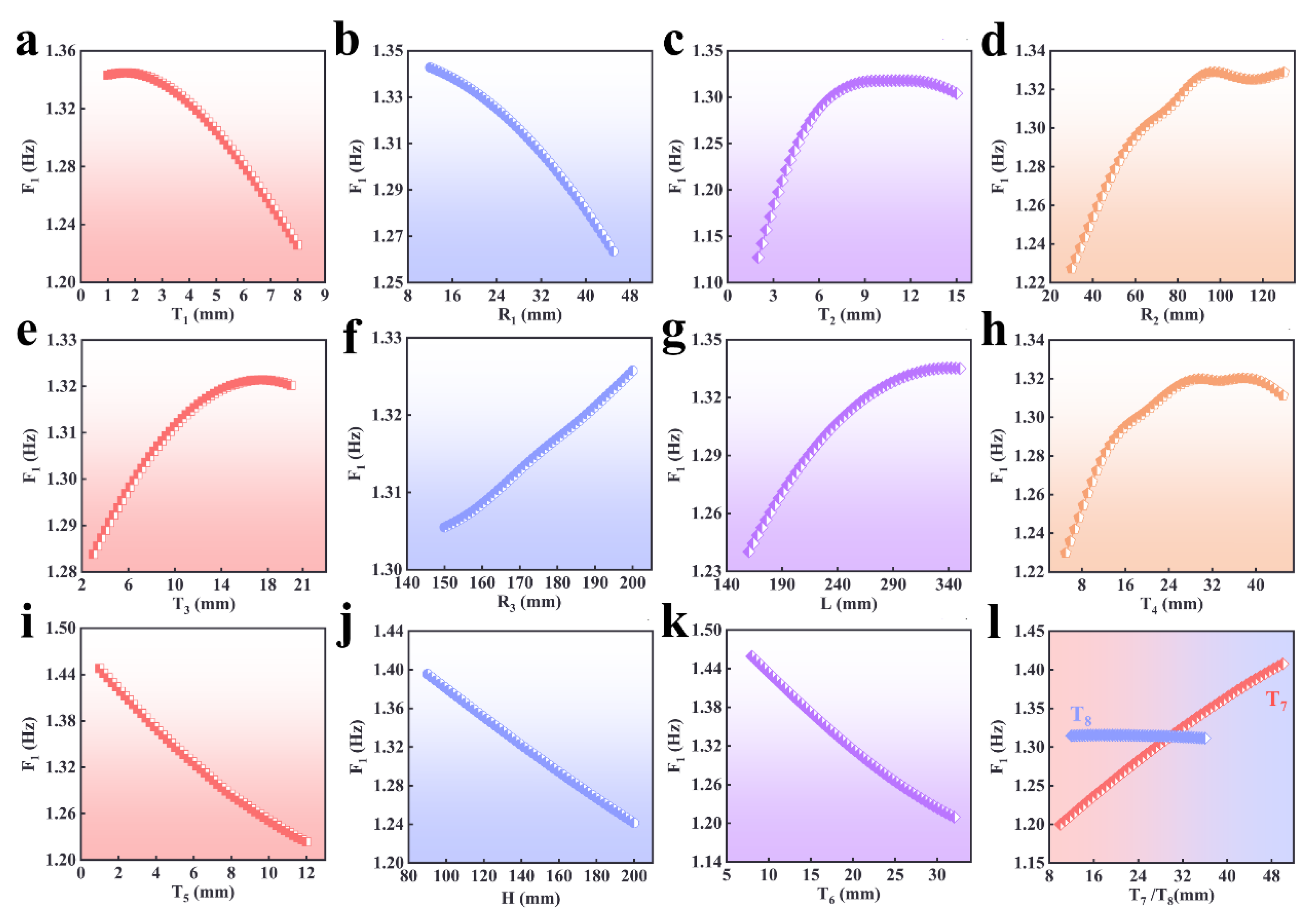
5.2.1. First-Order Frequency (F1)
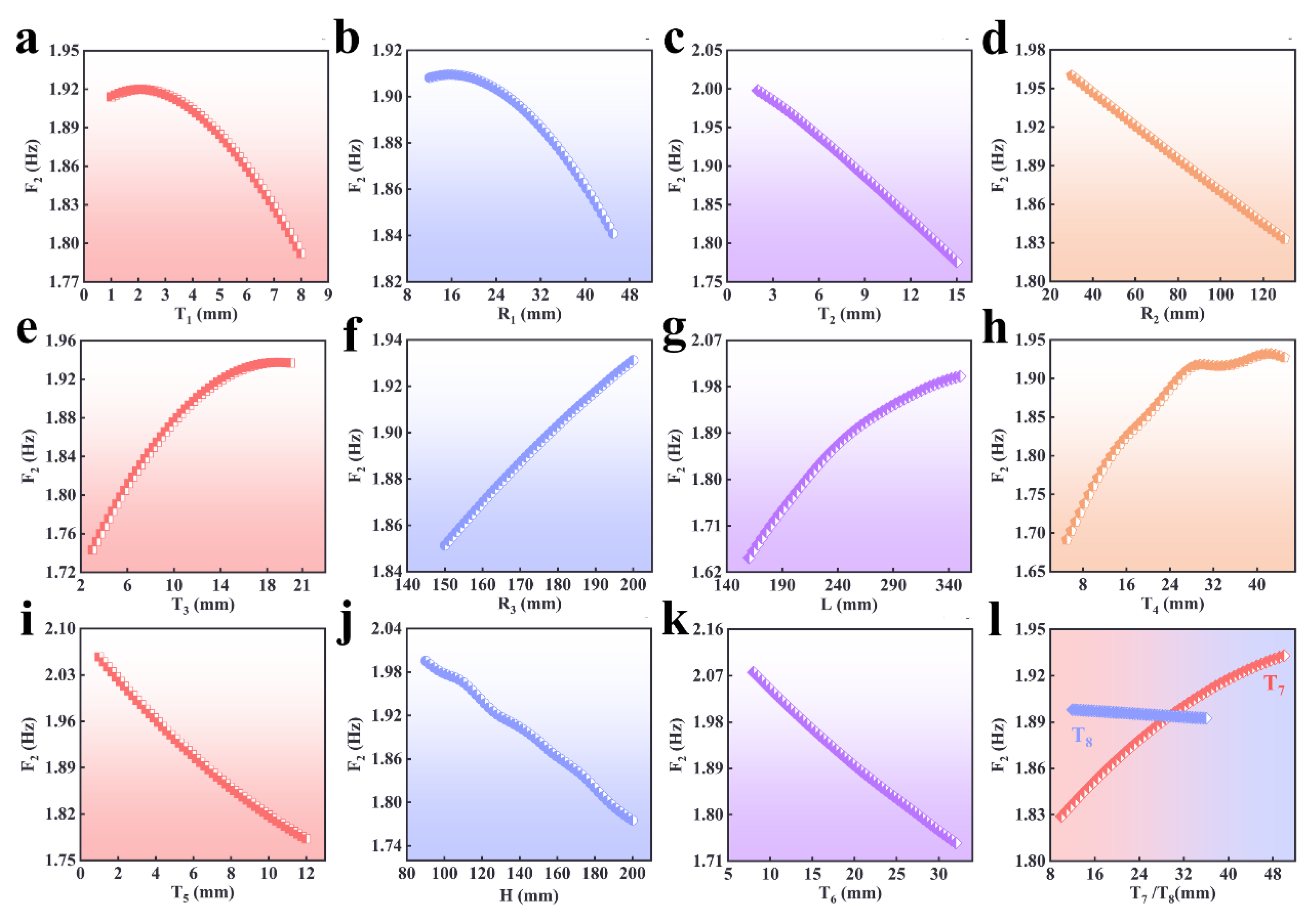
5.2.2. Second-Order Frequency (F2)
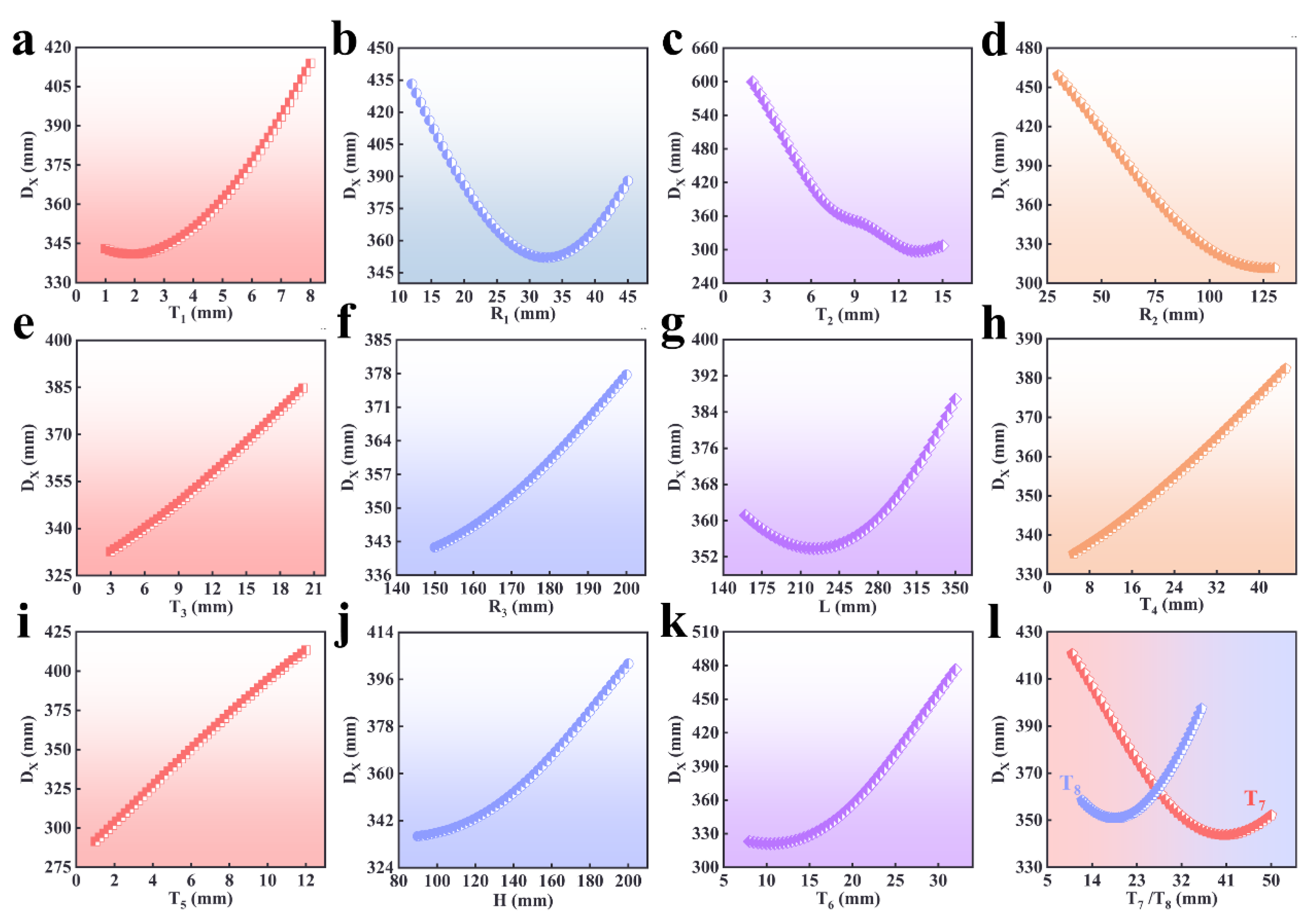
5.2.3. The Maximum Deformation in the X-Direction (DX)
5.2.4. The Maximum Deformation in the Z-Direction (DZ)
5.2.5. Sensitivity Analysis
- (1)
- To increase the F1 of the overall structure for the radio telescope to a greater extent by decreasing T1, R1, T5, H, and T6 and increasing T2, R2, L, T4, and T8.
- (2)
- To increase F2 of the overall structure for the radio telescope to a greater extent by decreasing T1, R1, T2, R2, T5, H, and T6 and increasing T3, R3, L, T4, and T8.
- (3)
- To reduce x-direction deformation of the overall structure for the radio telescope by decreasing T1, T3, R3, L, T4, T5, H, T6, and T7 and increasing R1, T2, R2, and T8.
- (4)
- To reduce z-direction deformation of the overall structure for the radio telescope to a greater extent by decreasing T1, R1, T3, R3, H, and T7 and increasing R2, T2, L, T4, and T8.
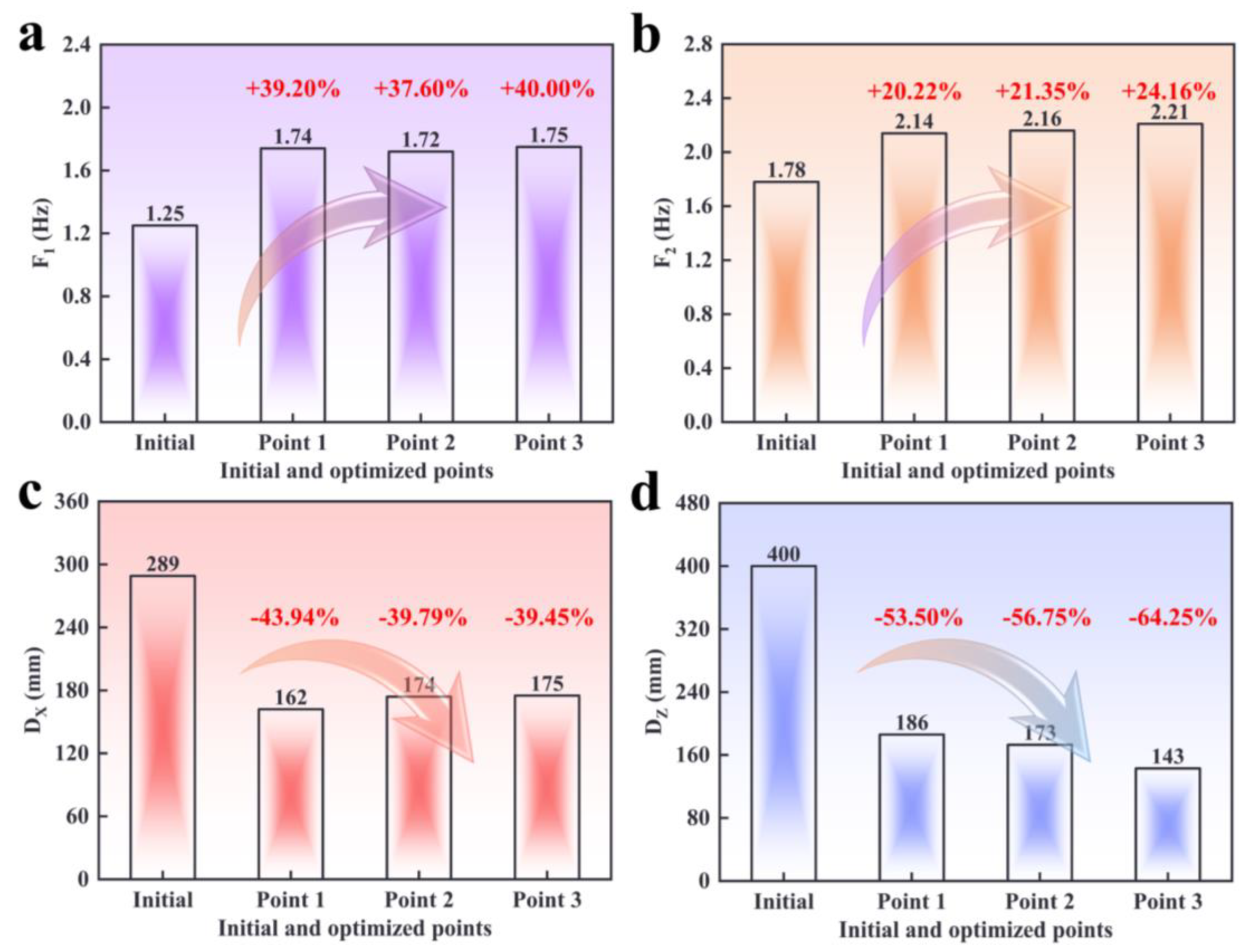
5.3. Optimization Results
6. Conclusions
- Errors between the finite element model simulation results and experimental test outcomes remained below 5% in each of the three modal tests. This attested to the precision of the simulation results, ensuring their reliability when subjected to subsequent wind-induced random vibrations.
- Employing the improved Latin hypercube sampling method in the DOE process across various structural components of radio telescopes of differing sizes not only enhanced the accuracy of the response surface model but also significantly economized computational resources associated with MOGA.
- Leveraging the response surface model, the study established a direct relationship between the 13 design variables and the respective objective values. Furthermore, the study derived the permissible parameter ranges for each design variable to achieve optimal objective values.
- Sensitivity analysis results unequivocally identified the structural parameters with the most substantial influence on the overall characteristics of the radio telescope, including F1, F2, DX, and DZ, pinpointing T6, L, T2, and R1 as the most impactful variables, respectively.
- The optimization of the radio telescope can increase F1 by 40.00% and F2 by 24.16% and decrease DX by 43.94% and DZ by 64.25%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Huang, J.; Qiu, L.; Song, R. Analysis of Reflector Vibration-Induced Pointing Errors for Large Antennas Subject to Wind Disturbance: Evaluating the pointing error caused by reflector deformation. IEEE Antennas Propag. Mag. 2015, 57, 46–61. [Google Scholar] [CrossRef]
- Attoli, A.; Stochino, F.; Buffa, F.; Poppi, S.; Serra, G.; Sanna, G.; Cazzani, A. Sardinia Radio Telescope structural behavior under solar thermal load. Structures 2022, 39, 901–916. [Google Scholar] [CrossRef]
- He, F.-L.; Xu, Q.; Wang, N.; Zhu, C.-h. Research on Wind Tower Position Optimization Method of Radio Telescope Site Based on Numerical Simulation. Chin. Astron. Astrophys. 2021, 45, 118–130. [Google Scholar]
- Hashimoto, I.; Chiba, M.; Okada, N.; Ogawa, H.; Kawabe, R.; Minamidani, T.; Tamura, Y.; Kimura, K. Wind- and Operation-Induced Vibration Measurements of the Main Reflector of the Nobeyama 45 m Radio Telescope. J. Vib. Eng. Technol. 2020, 8, 909–923. [Google Scholar] [CrossRef]
- He, F.-L.; Xu, Q.; Wang, N.; Zhu, C.-h. A method to obtain the wind field characteristics of super-large aperture radio telescope site based on single-point wind tower and numerical simulation. Res. Astron. Astrophys. 2020, 21, 157. [Google Scholar] [CrossRef]
- He, F.; Xu, Q.; Wang, N. Research on Wind Flow Control by Windbreak Fence for a Large Radio Telescope Site Based on Numerical Simulations. Adv. Astron. 2023, 2023, 5257749. [Google Scholar] [CrossRef]
- Liu, Y.; Qian, H.-L.; Fan, F. Reflector wind load characteristics of the large all-movable antenna and its effect on reflector surface precision. Adv. Steel Constr. 2017, 13, 1–29. [Google Scholar]
- Wei, S.-X.; Kong, D.-Q.; Wang, Q.-M. Effect of the alidade thermal behavior on the pointing accuracy of a large radio telescope. Res. Astron. Astrophys. 2021, 21, 137. [Google Scholar] [CrossRef]
- Dong, J.; Fu, L.; Liu, Q.; Shen, Z. Measuring and analyzing thermal deformations of the primary reflector of the Tianma radio telescope. Exp. Astron. 2018, 45, 397–410. [Google Scholar] [CrossRef]
- Li, N.; Wu, J.; Duan, B.-Y.; Wang, C.-S. Effect of the rail unevenness on the pointing accuracy of large radio telescope. Acta Astronaut. 2017, 132, 13–18. [Google Scholar] [CrossRef]
- Fu, L.; Wang, J.; Jiang, Y.; Yu, L.; Zhao, R.; Ling, Q.; Yang, B.; Liu, Q.; Shen, Z. Improvement of the pointing precision of the Tianma radio telescope with an inclinometer measurement system. Exp. Astron. 2019, 48, 49–64. [Google Scholar] [CrossRef]
- Yan, L.-D.; Zheng, F.; Rui, X. New design of large fully-steerable radio telescope reflector based on homogenized mesh structure. Res. Astron. Astrophys. 2021, 21, 244. [Google Scholar] [CrossRef]
- Sun, Z.-X.; Wang, J.-Q.; Yu, L.-F.; Gou, W.; Wang, G.-L. Research on the panel adjustment method of an active main reflector for a large radio telescope. Res. Astron. Astrophys. 2021, 21, 38. [Google Scholar] [CrossRef]
- Le, T.-H.; Caracoglia, L. Wavelet-Galerkin analysis to study the coupled dynamic response of a tall building against transient wind loads. Eng. Struct. 2015, 100, 763–778. [Google Scholar] [CrossRef]
- Guo, S.; Li, Y.; Chen, W. Analysis on dynamic interaction between flexible bodies of large-sized wind turbine and its response to random wind loads. Renew. Energ. 2021, 163, 123–137. [Google Scholar] [CrossRef]
- Cao, A.S.; Stamatopoulos, H. A theoretical study of the dynamic response of planar timber frames with semi-rigid moment-resisting connections subjected to wind loads. Eng. Struct. 2021, 240, 112367. [Google Scholar] [CrossRef]
- Xie, B.; Luo, X.; Zhang, Q.; Ding, J. Dynamic response evaluation of the Shanghai Tower in along- and across-wind directions during super typhoon Lekima. J. Build. Eng. 2023, 65, 105808. [Google Scholar] [CrossRef]
- Zhou, Q.; Lu, W.; Peng, X.; Wang, G.; Zhang, P. Frequency calculation method and wind-induced dynamic response of cable net façades considering the façade stiffness. Structures 2023, 55, 718–726. [Google Scholar] [CrossRef]
- Alonso-Martinez, M.; Adam, J.M.; Alvarez-Rabanal, F.P.; Díaz, J.J.d.C. Wind turbine tower collapse due to flange failure: FEM and DOE analyses. Eng. Fail. Anal. 2019, 104, 932–949. [Google Scholar] [CrossRef]
- Pournoury, M.; Kim, D. Optimized segmented cladding fiber for extreme large mode area using latin hypercube sampling. Opt. Commun. 2023, 542, 129593. [Google Scholar] [CrossRef]
- Li, Y.; Shi, C.; Liu, W.; Liu, Z. Structural parameter design of welded plate heat exchanger based on multi-objective optimization algorithm. Int. Commun. Heat Mass Transf. 2023, 146, 106900. [Google Scholar]
- Jin, F.; Chen, D.; Hu, L.; Huang, Y.; Bu, S. Optimization of zigzag parameters in printed circuit heat exchanger for supercritical CO2 Brayton cycle based on multi-objective genetic algorithm. Energy Convers. Manag. 2022, 270, 116243. [Google Scholar] [CrossRef]
- Sanaye, S.; Hajabdollahi, H. Multi-objective optimization of shell and tube heat exchangers. Appl. Therm. Eng. 2010, 30, 1937–1945. [Google Scholar] [CrossRef]
- Gu, X.; Wang, T.; Chen, W.; Luo, Y.; Tao, Z. Multi-objective optimization on structural parameters of torsional flow heat exchanger. Appl. Therm. Eng. 2019, 161, 113831. [Google Scholar] [CrossRef]
- Daneshparvar, M.R.; Beigzadeh, R. Multi-objective optimization of helical baffles in the shell-and-tube heat exchanger by computational fluid dynamics and genetic algorithm. Energy Rep. 2022, 8, 11064–11077. [Google Scholar] [CrossRef]
- Ni, X.; Han, S.; Ge, J.; Sun, J. Optimization of the gravity support in CFETR vacuum vessel. Fusion Eng. Des. 2021, 172, 112921. [Google Scholar] [CrossRef]
- Shi, C.; Guo, H.; Cheng, Y.; Liu, R.; Deng, Z. Design and multi-objective comprehensive optimization of cable-strut tensioned antenna mechanism. Acta Astronaut. 2021, 178, 406–422. [Google Scholar] [CrossRef]
- Liu, M.; Shi, C.; Guo, H.; Ma, X.; Liu, R.; Hu, F. Innovative design and optimization of the modular high deployment ratio two-dimensional planar antenna mechanism. Mech. Mach. Theory 2022, 174, 104928. [Google Scholar] [CrossRef]
- Chen, Z.; Shi, C.; Guo, H.; Liu, R.; Deng, Z. Design and optimization of new space modular planar antenna. Aerosp. Sci. Technol. 2022, 123, 107442. [Google Scholar] [CrossRef]
- Rasekh, S.; Aliabadi, S.K. Toward improving the performance of a variable pitch vertical axis wind turbine (VP-VAWT), Part 2: Multi-objective optimization using NSGA-II with CFD in the loop. Ocean Eng. 2023, 278, 114308. [Google Scholar] [CrossRef]
- Zhang, P.; Li, Y.; Tang, Y.; Zhang, R.; Li, H.; Gu, J. Multi-objective optimization and dynamic response predictions of an articulated offshore wind turbine. Ocean Eng. 2023, 273, 114017. [Google Scholar] [CrossRef]
- Lara, M.; Garrido, J.; Ruz, M.L.; Vázquez, F. Multi-objective optimization for simultaneously designing active control of tower vibrations and power control in wind turbines. Energy Rep. 2023, 9, 1637–1650. [Google Scholar] [CrossRef]
- Gonzalez-Delgado, D.; Jaen-Sola, P.; Oterkus, E. Design and optimization of multi-MW offshore direct-drive wind turbine electrical generator structures using generative design techniques. Ocean Eng. 2023, 280, 114417. [Google Scholar] [CrossRef]
- Annan, A.M.; Lackner, M.A.; Manwell, J.F. Multi-objective optimization for an autonomous unmoored offshore wind energy system substructure. Appl. Energy 2023, 344, 121264. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, W.; Sun, S. Parametric Optimisation Analysis of Micro/Nano-Satellite Flywheels Based on the NSGA-II Optimisation Algorithm. Aerospace 2022, 9, 386. [Google Scholar] [CrossRef]
- Shi, M.; Bai, Y.; Liu, G.; Wu, Y.; Liu, S. Structural Modelling and System Simulation Analysis of SKA Radio Telescope Dish. Radio Commun. Technol. 2019, 45, 431–436. [Google Scholar]
- Avendaño-Valencia, L.D.; Fassois, S.D. Stationary and non-stationary random vibration modelling and analysis for an operating wind turbine. Mech. Syst. Signal Process 2014, 47, 263–285. [Google Scholar] [CrossRef]
- Davenport, A.G. The spectrum of horizontal gustiness near the ground in high winds. Q. J. Royal Met. Soc. 1961, 87, 194–211. [Google Scholar] [CrossRef]
- GB50009-2012; Load Code for the Design of Building Structures. China Architecture and Building Press: Beijing, China, 2012. (In Chinese)
- Wang, X.; Cui, J. Formula of Coefficient K in Expression of Davenport Spectrum and Its Engineering Application. J. Tongji Univ. 2002, 30, 849–852. [Google Scholar]
- GB55006-2021; General Code for Steel Structures. China Architecture and Building Press: Beijing, China, 2021. (In Chinses)
- Navid, A.; Khalilarya, S.; Abbasi, M. Diesel engine optimization with multi-objective performance characteristics by non-evolutionary Nelder-Mead algorithm: Sobol sequence and Latin hypercube sampling methods comparison in DoE process. Fuel 2018, 228, 349–367. [Google Scholar] [CrossRef]
- Ye, P.; Pan, G.; Gao, S. Sampling Design Method of Fast Optimal Latin Hypercube. J. Northwest. Polytech. Univ. 2019, 37, 714–723. [Google Scholar] [CrossRef]
- ANSYS, Inc. Design Exploration User’s Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- McCall, J. Genetic algorithms for modelling and optimisation. J. Comput. Appl. Math. 2005, 184, 205–222. [Google Scholar] [CrossRef]


| Mesh Size | Model Mesh Diagrams | First-Order Modal Results | Second-Order Modal Results |
|---|---|---|---|
| 0.15 m |  | 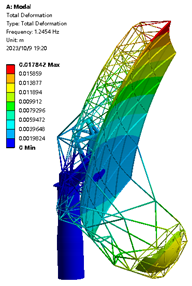 1.245 Hz | 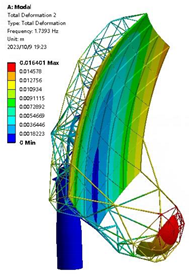 1.739 Hz |
| 0.21 m |  | 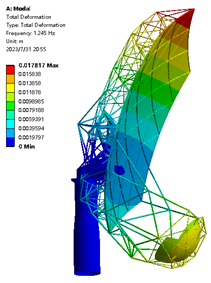 1.245 Hz | 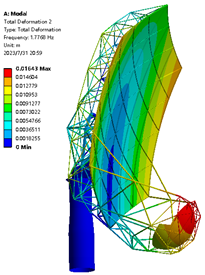 1.777 Hz |
| 0.25 m |  |  1.251 Hz | 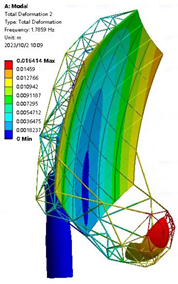 1.786 Hz |
| 0.4 m |  | 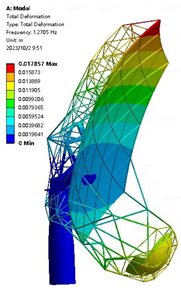 1.271 Hz | 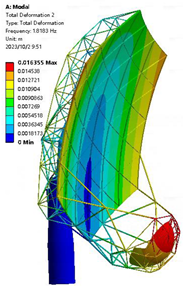 1.818 Hz |
| 0.8 m | 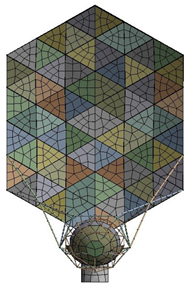 | 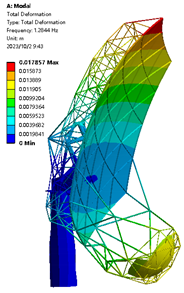 1.284 Hz | 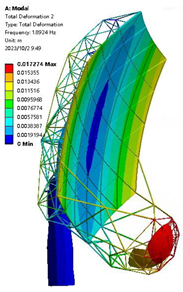 1.892 Hz |
| Design Node | T1 (mm) | R1 (mm) | T2 (mm) | R2 (mm) | T3 (mm) | R3 (mm) | L (mm) | T4 (mm) | T5 (mm) | H (mm) | T6 (mm) | T7 (mm) | T8 (mm) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Initial | 3 | 33 | 5 | 55.5 | 6 | 174 | 200 | 10 | 1.5 | 150 | 16 | 16 | 20 |
| Optimized point 1 | 1.98 | 34.89 | 7.94 | 107.02 | 4.92 | 158.51 | 260.55 | 16.33 | 1.32 | 105.15 | 9.24 | 47.84 | 15.14 |
| Optimized point 2 | 2.42 | 34.79 | 7.68 | 109.71 | 6.95 | 165.25 | 256.87 | 15.28 | 1.98 | 101.29 | 9.92 | 48.68 | 14.12 |
| Optimized point 3 | 2.65 | 31.64 | 7.98 | 103.24 | 5.40 | 180.26 | 254.62 | 20.13 | 1.74 | 114.34 | 8.51 | 49.87 | 17.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Zhang, L.; Yang, F.; Yang, J.; Wu, Y.; Cao, P. Dynamic Response and Optimal Design of Radio Telescope Structure under Wind Load Excitation. Buildings 2023, 13, 2764. https://doi.org/10.3390/buildings13112764
Wang D, Zhang L, Yang F, Yang J, Wu Y, Cao P. Dynamic Response and Optimal Design of Radio Telescope Structure under Wind Load Excitation. Buildings. 2023; 13(11):2764. https://doi.org/10.3390/buildings13112764
Chicago/Turabian StyleWang, Dawei, Lei Zhang, Fengfu Yang, Jinrong Yang, Yang Wu, and Peng Cao. 2023. "Dynamic Response and Optimal Design of Radio Telescope Structure under Wind Load Excitation" Buildings 13, no. 11: 2764. https://doi.org/10.3390/buildings13112764
APA StyleWang, D., Zhang, L., Yang, F., Yang, J., Wu, Y., & Cao, P. (2023). Dynamic Response and Optimal Design of Radio Telescope Structure under Wind Load Excitation. Buildings, 13(11), 2764. https://doi.org/10.3390/buildings13112764







