Numerical Analysis of Reinforced Concrete Corbels Using Concrete Damage Plasticity: Sensitivity to Material Parameters and Comparison with Analytical Models
Abstract
:1. Introduction
2. CDP Model (Concrete Damage Plasticity) on ABAQUS
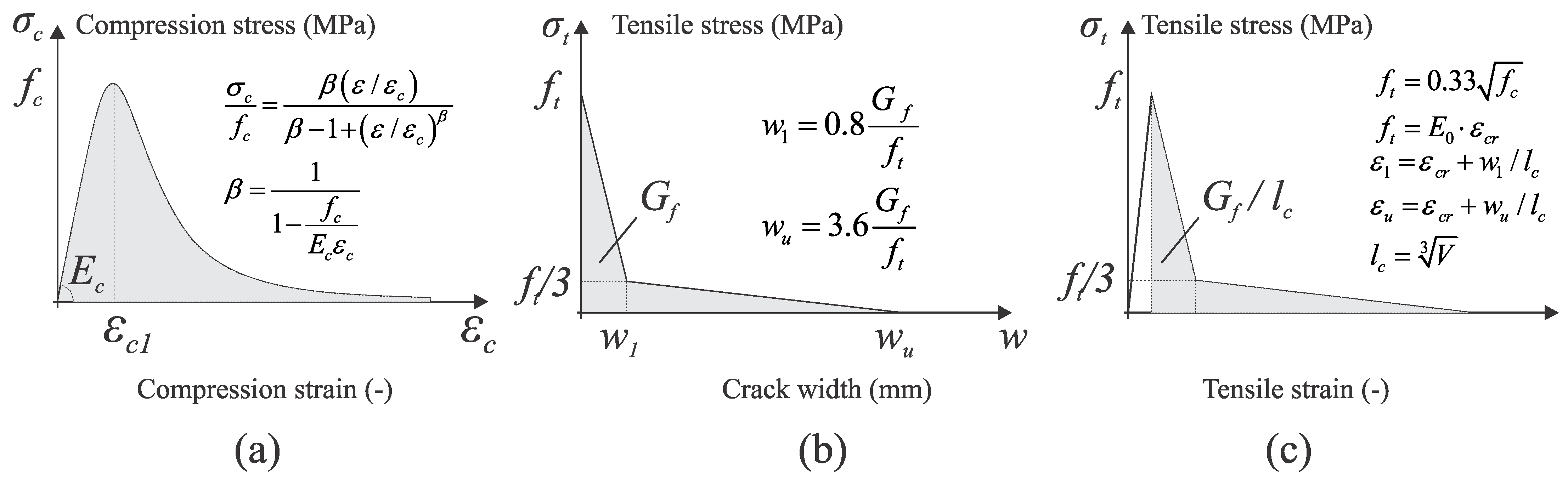
2.1. Stress–Strain Relationship
2.2. Hardening Variables
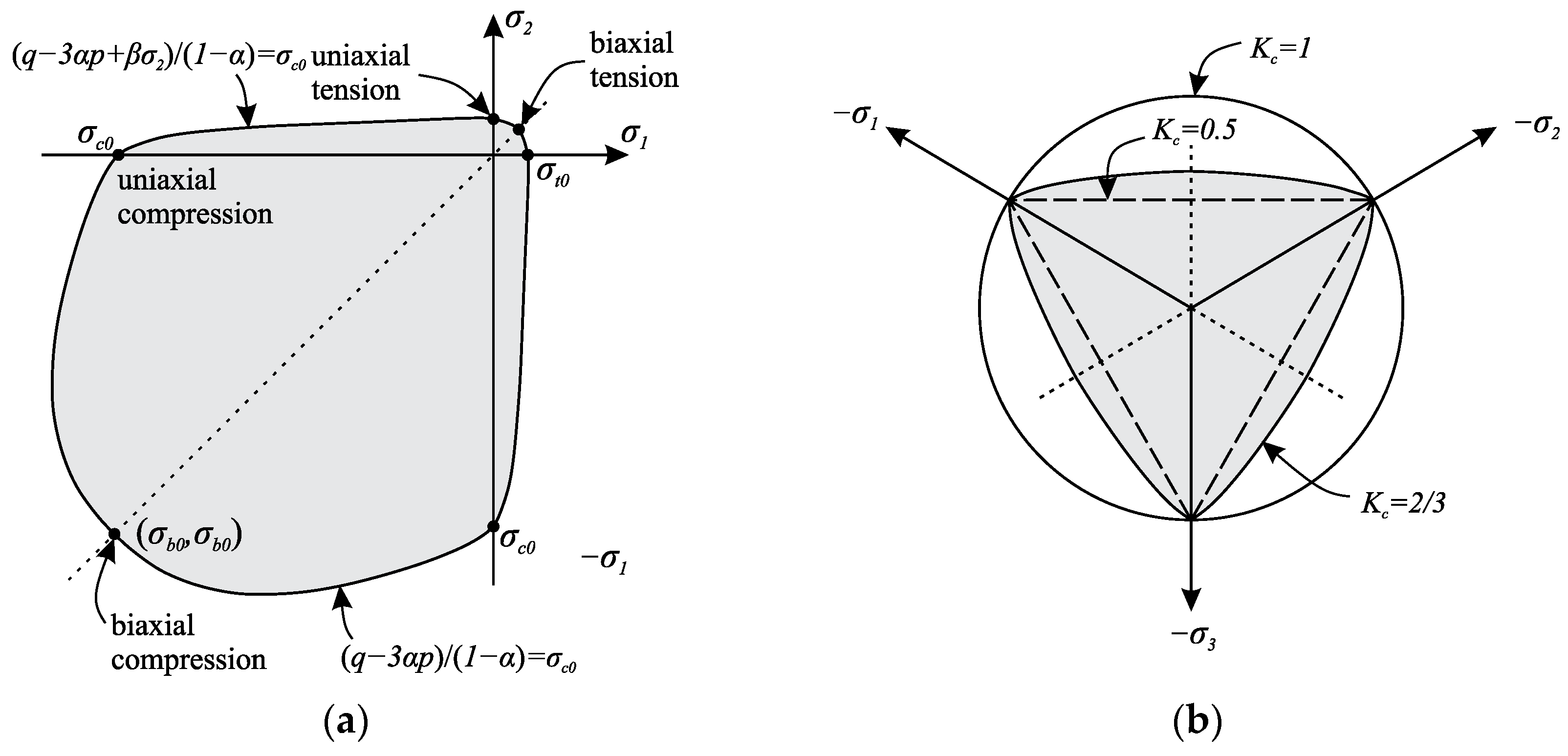
2.3. Yield Criteria
2.4. Flow Rule
2.5. Viscoplastic Regularization
3. Experimental Models
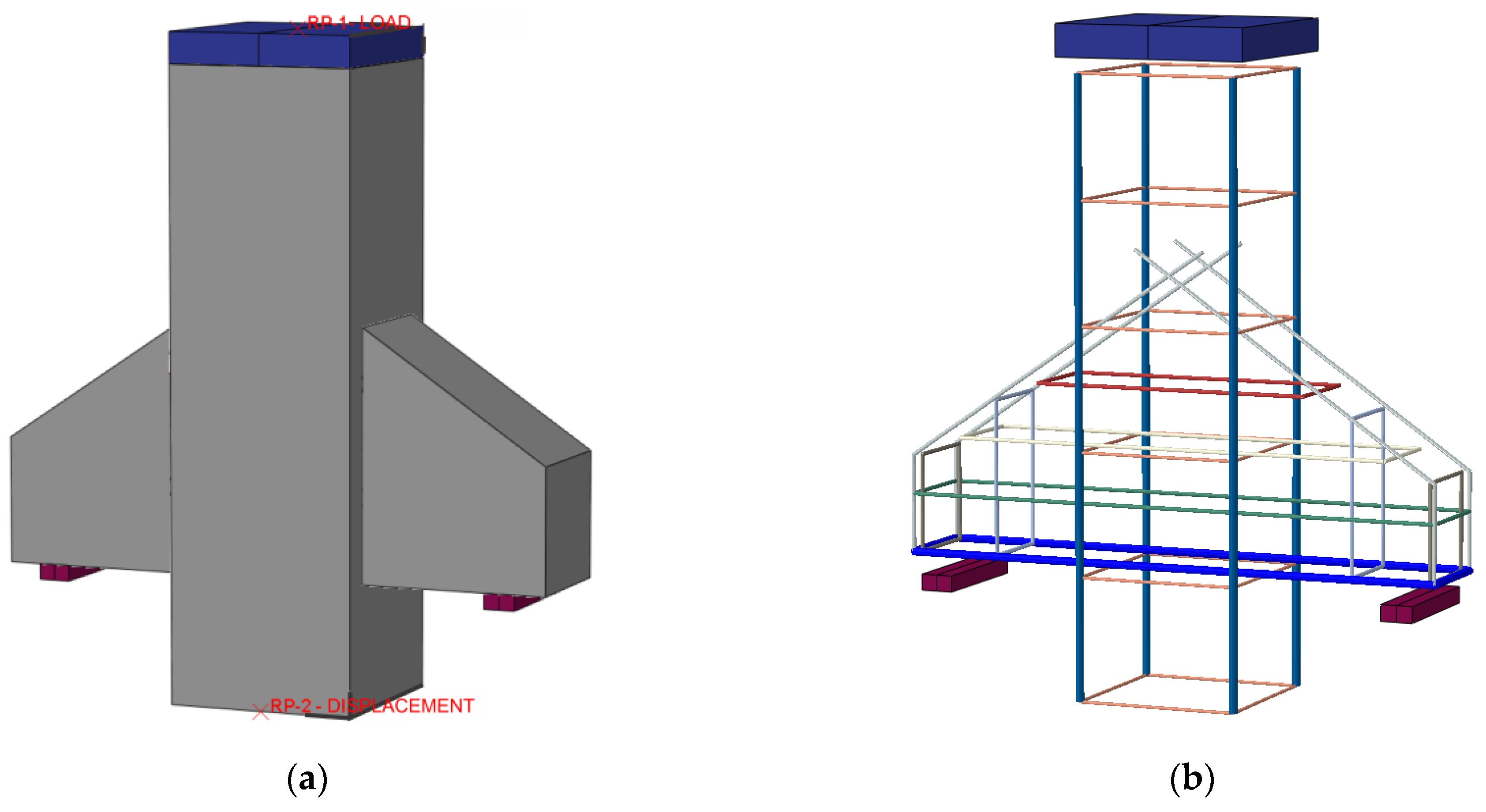
4. Computational Model
4.1. Steel Constitutive Model
4.2. Concrete Constitutive Model
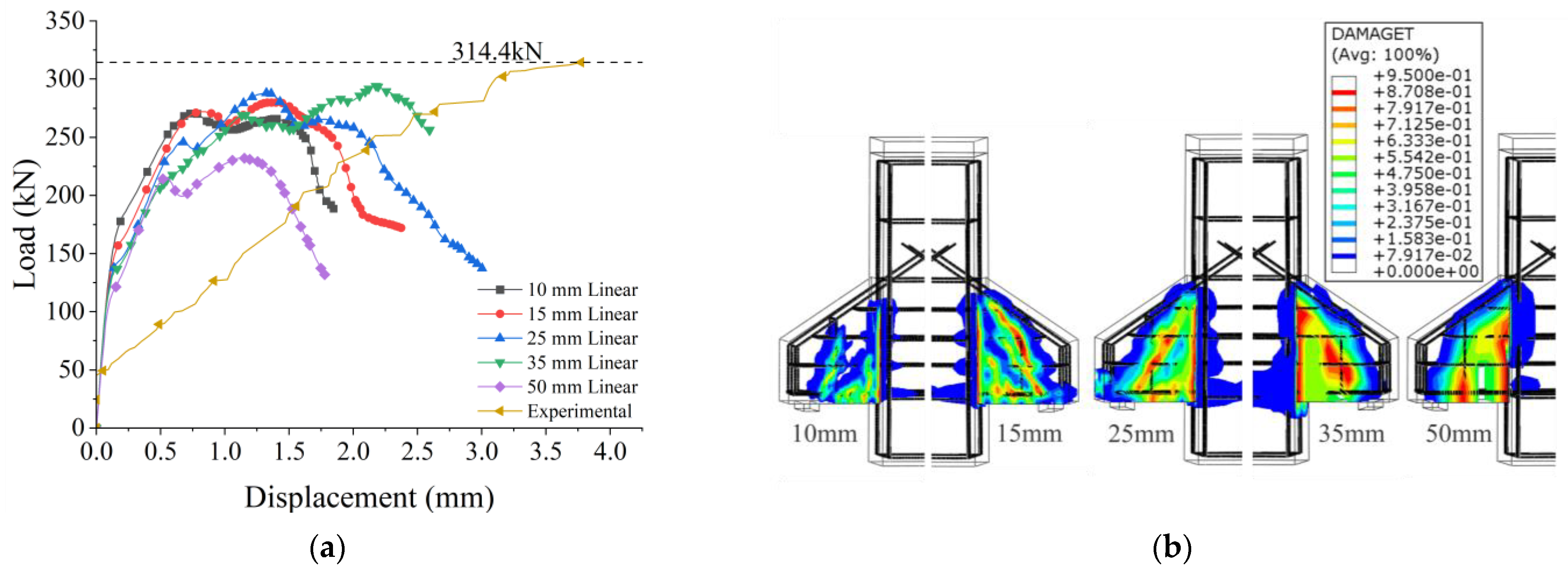
5. Mesh Refinement
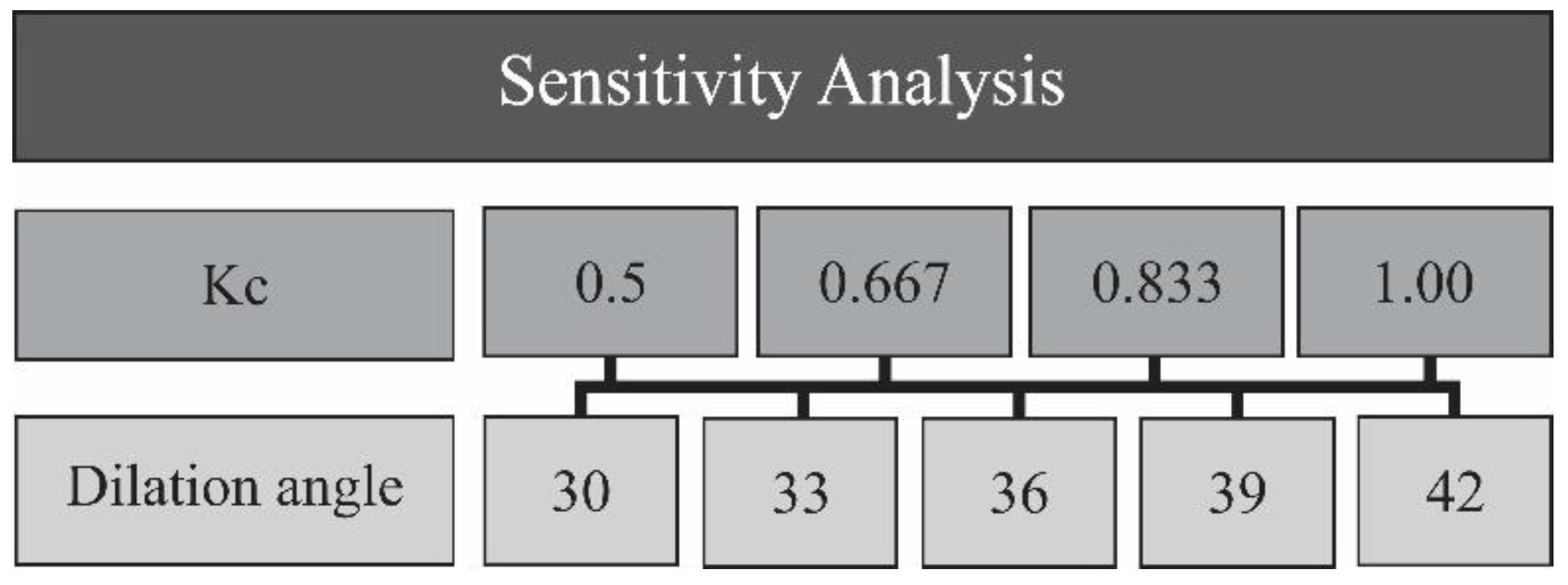
6. Sensitivity Analysis
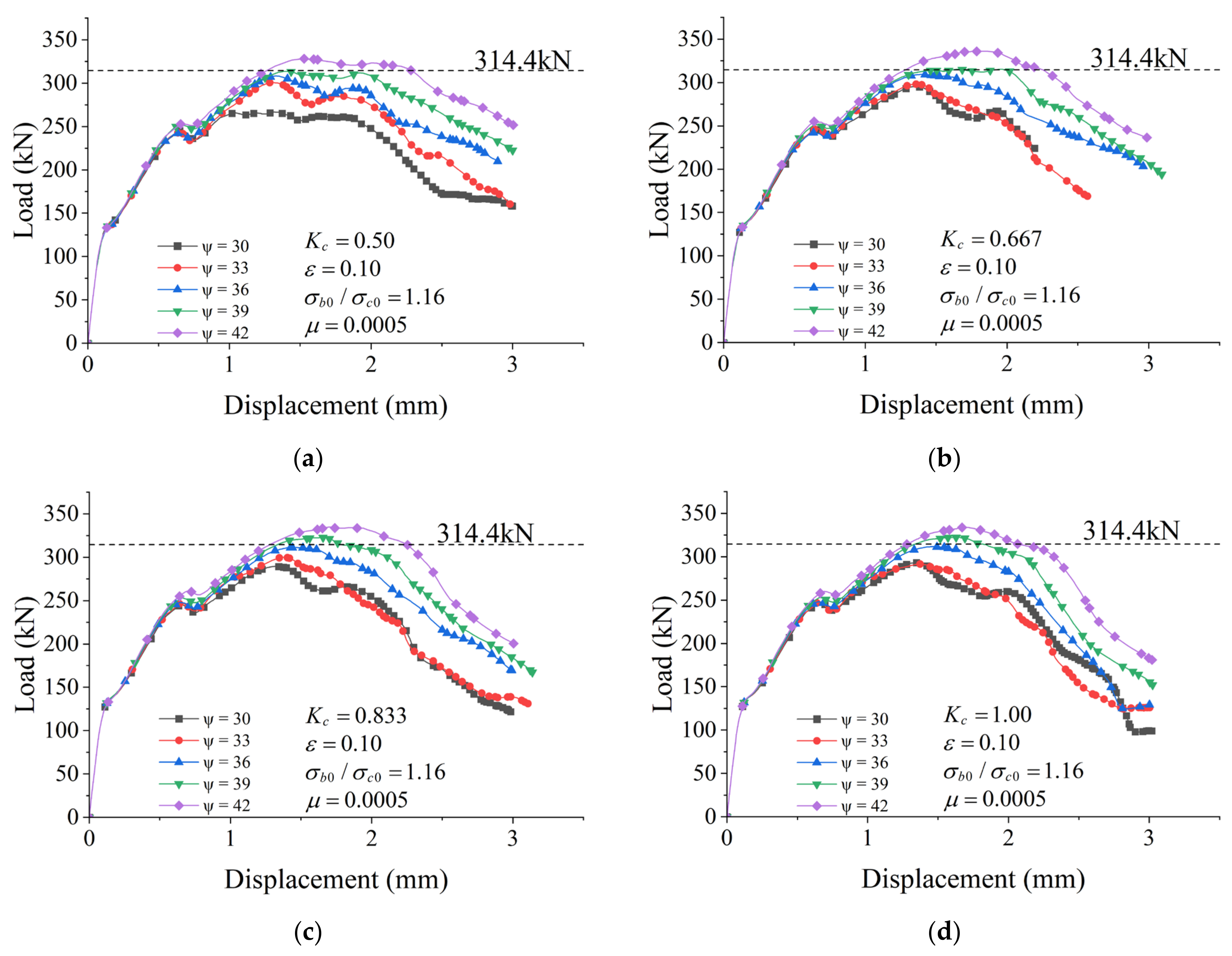
7. Sensitivity Analysis Results
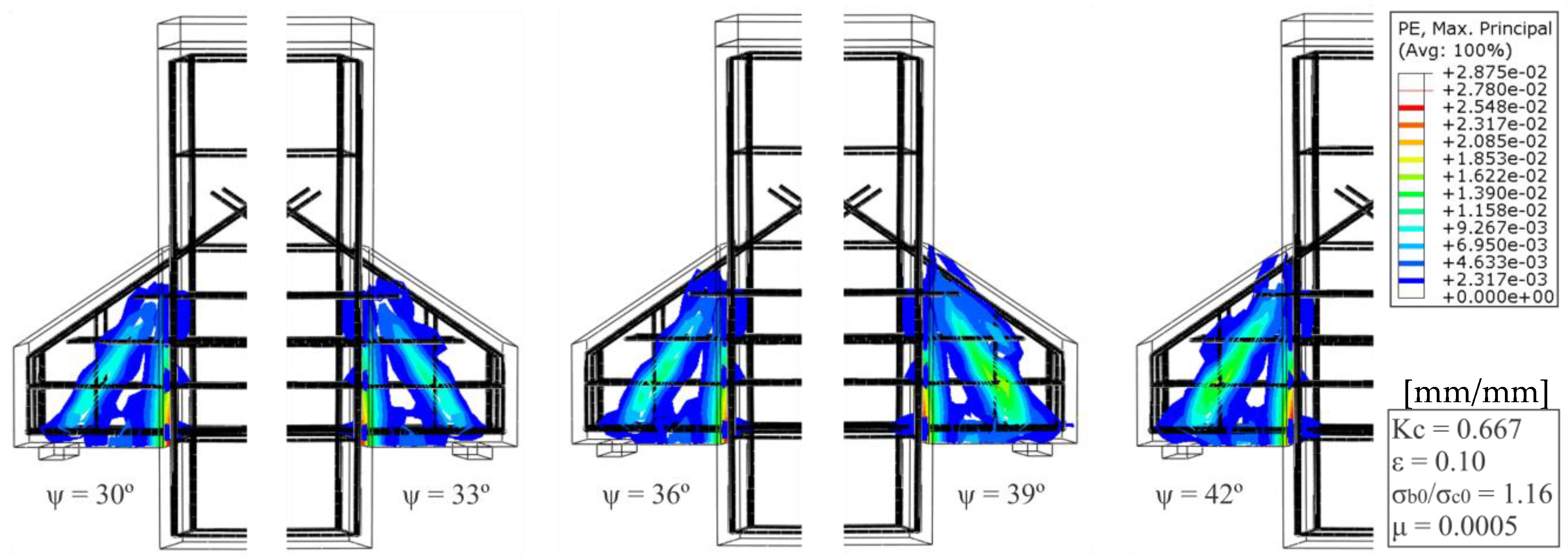
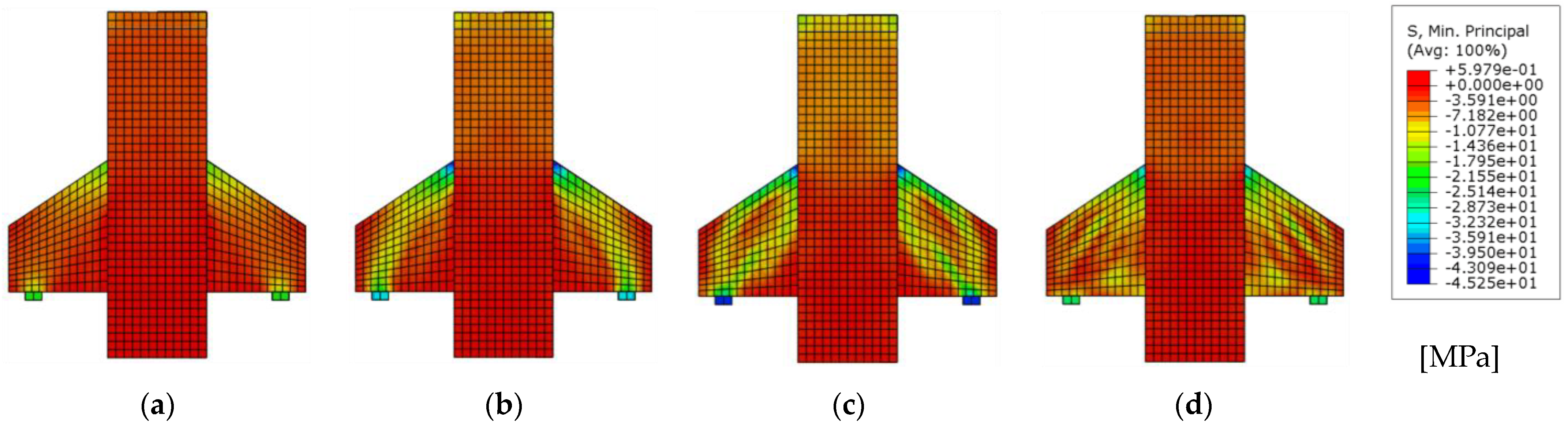
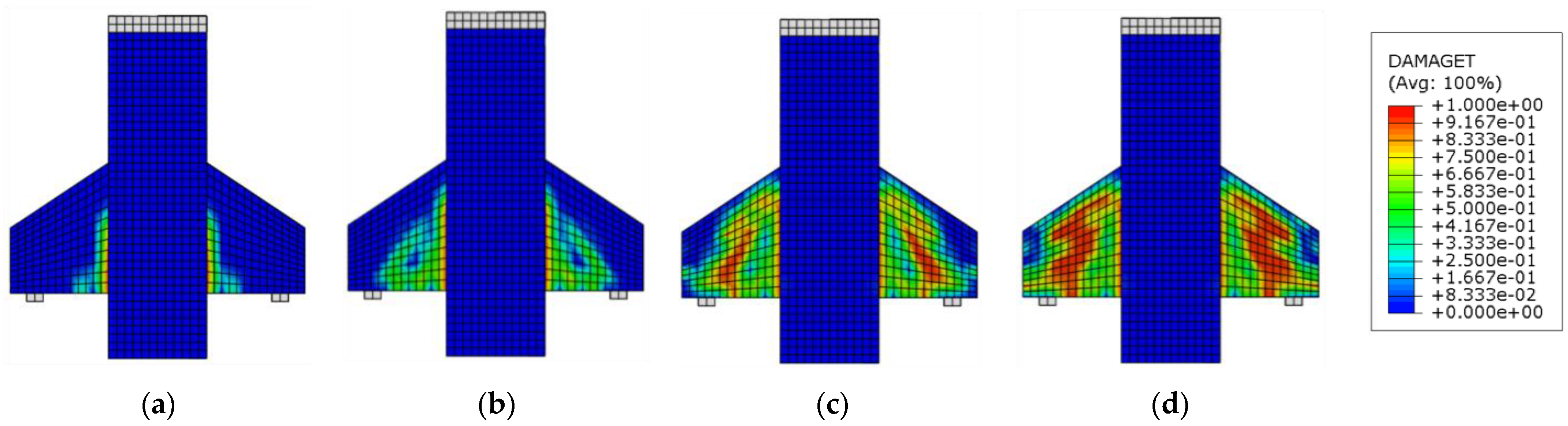
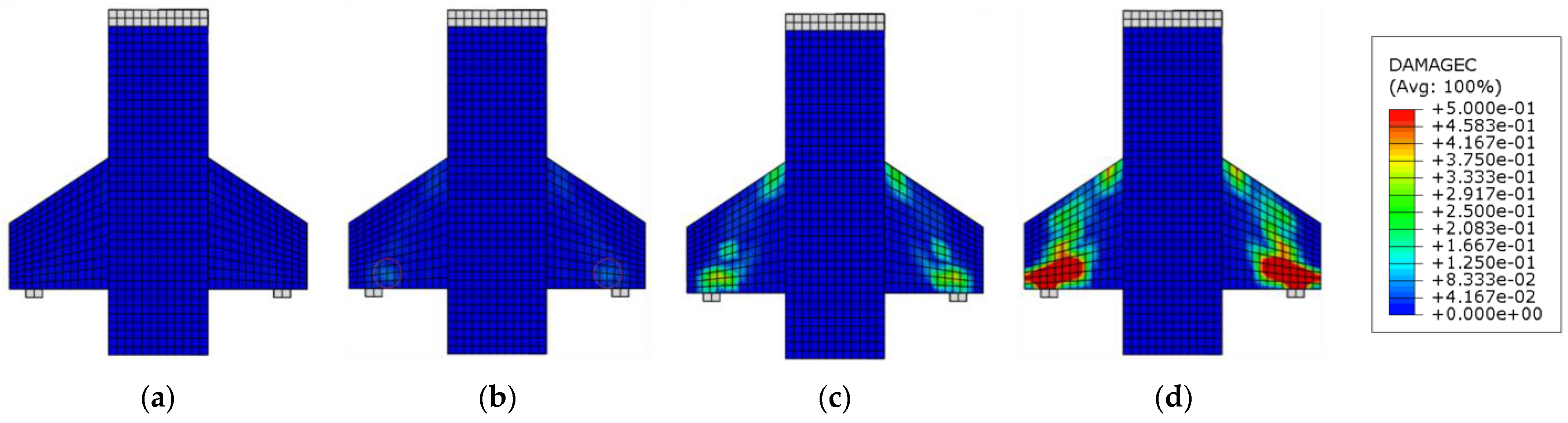
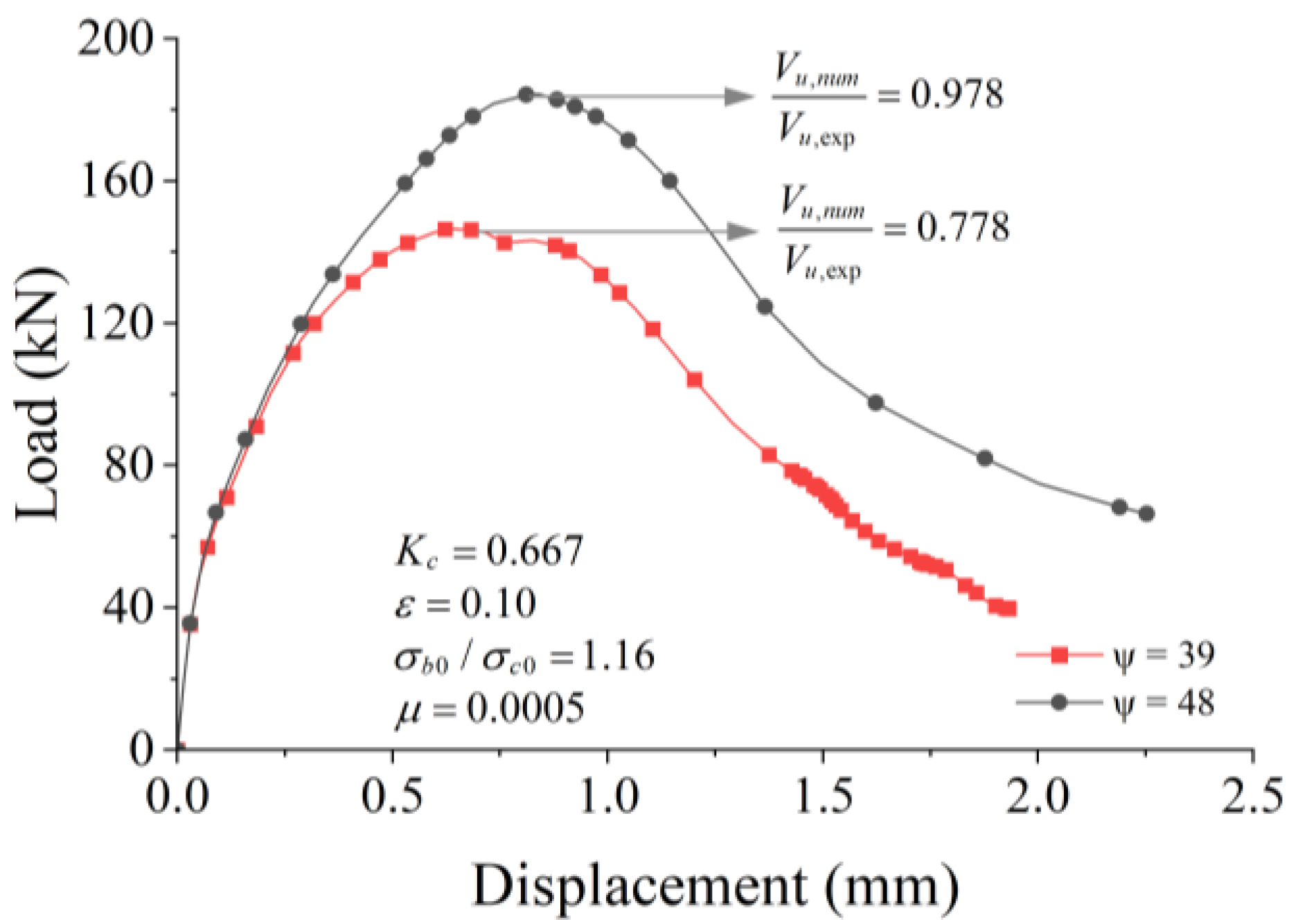
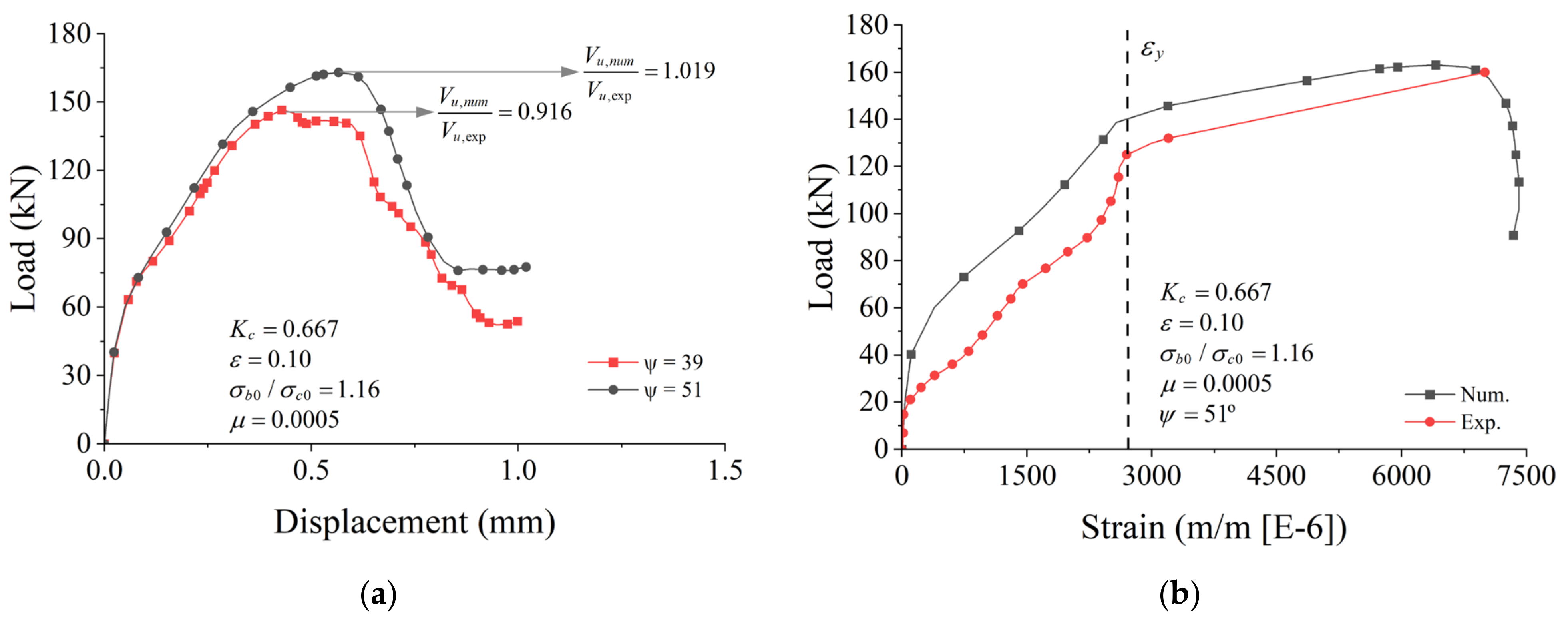
7.1. Evaluation of the Dilation Angle (ψ) with Constant (Kc)
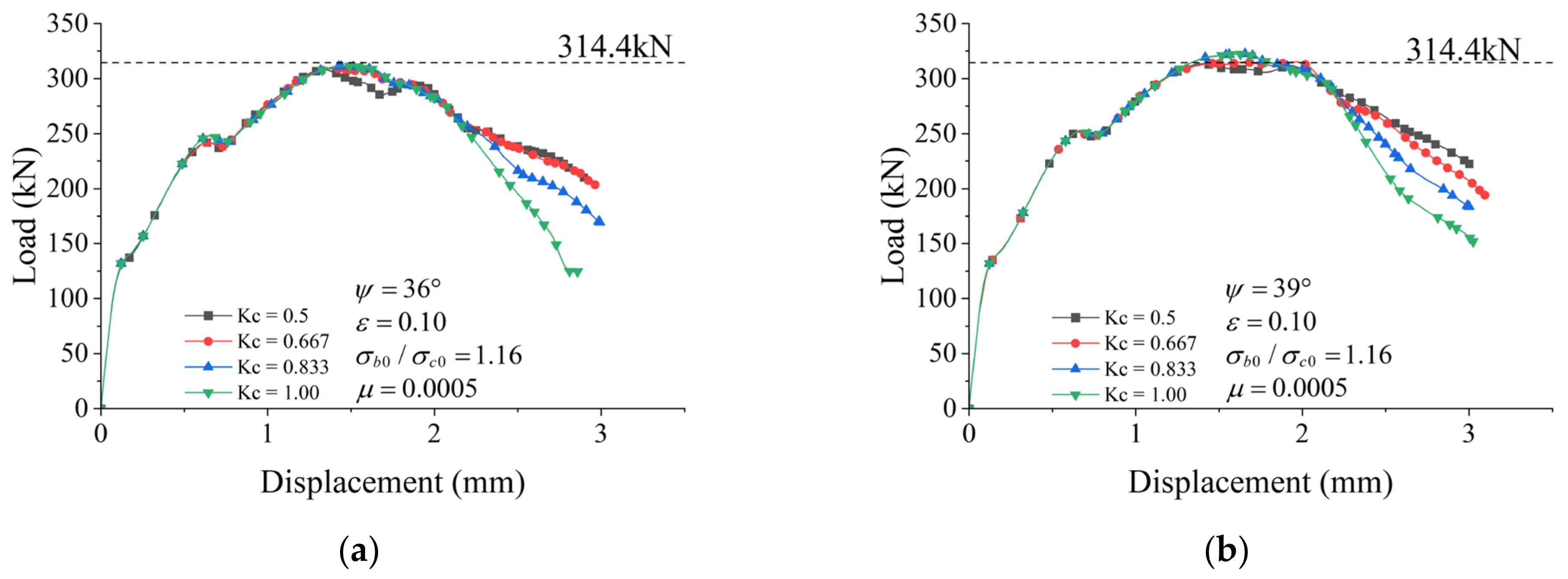
7.2. Variation of Plane Shape Factor (Kc) with Constant Dilation Angle (ψ)
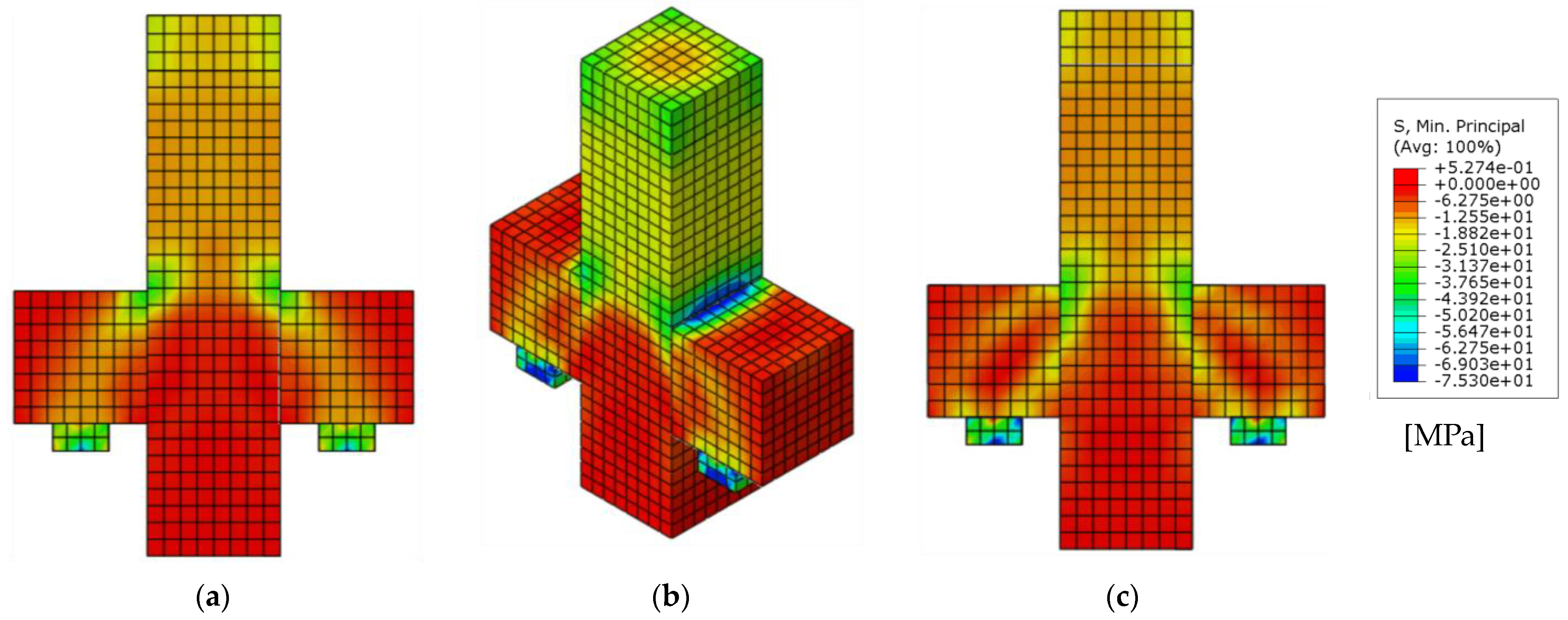
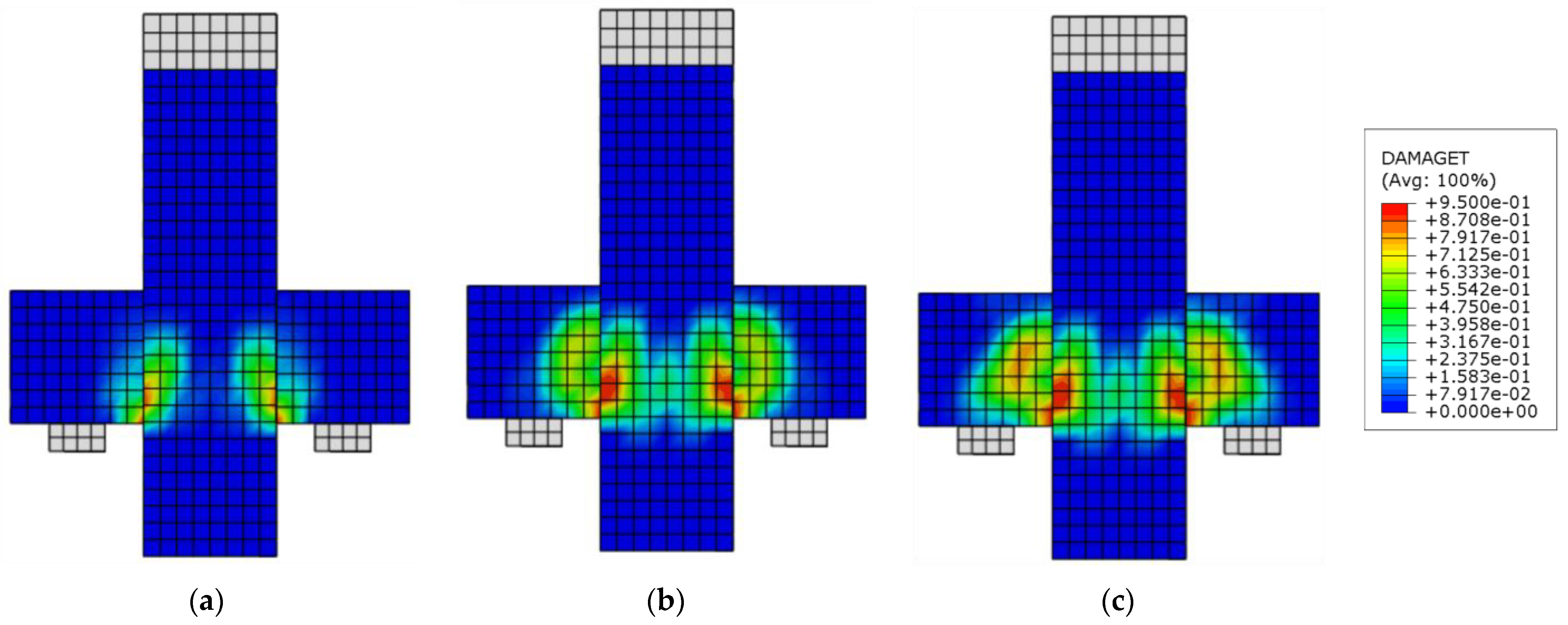
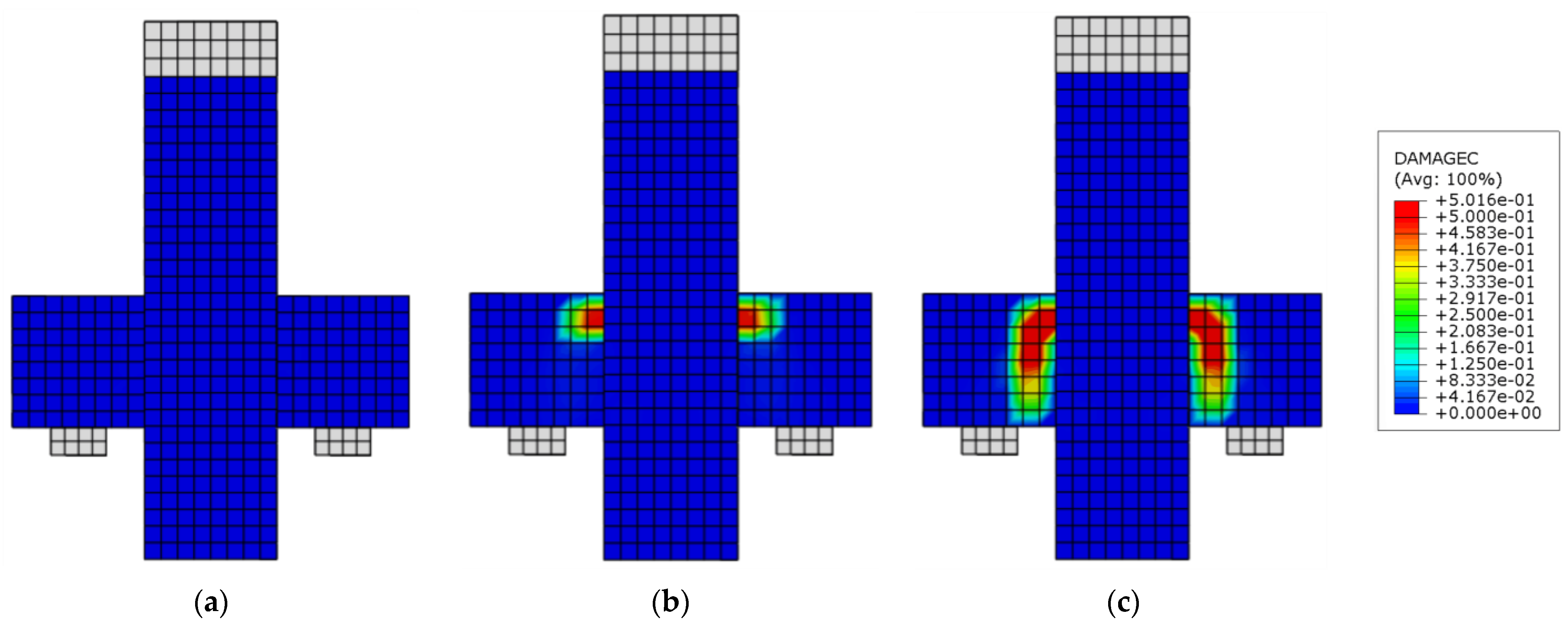
8. Evaluation of Numerical Results
8.1. Modeling of the M3-MONO-A Corbel
8.2. Corbel FA-T8 Modeling
8.3. Corbel FE-CS6-4A Modeling
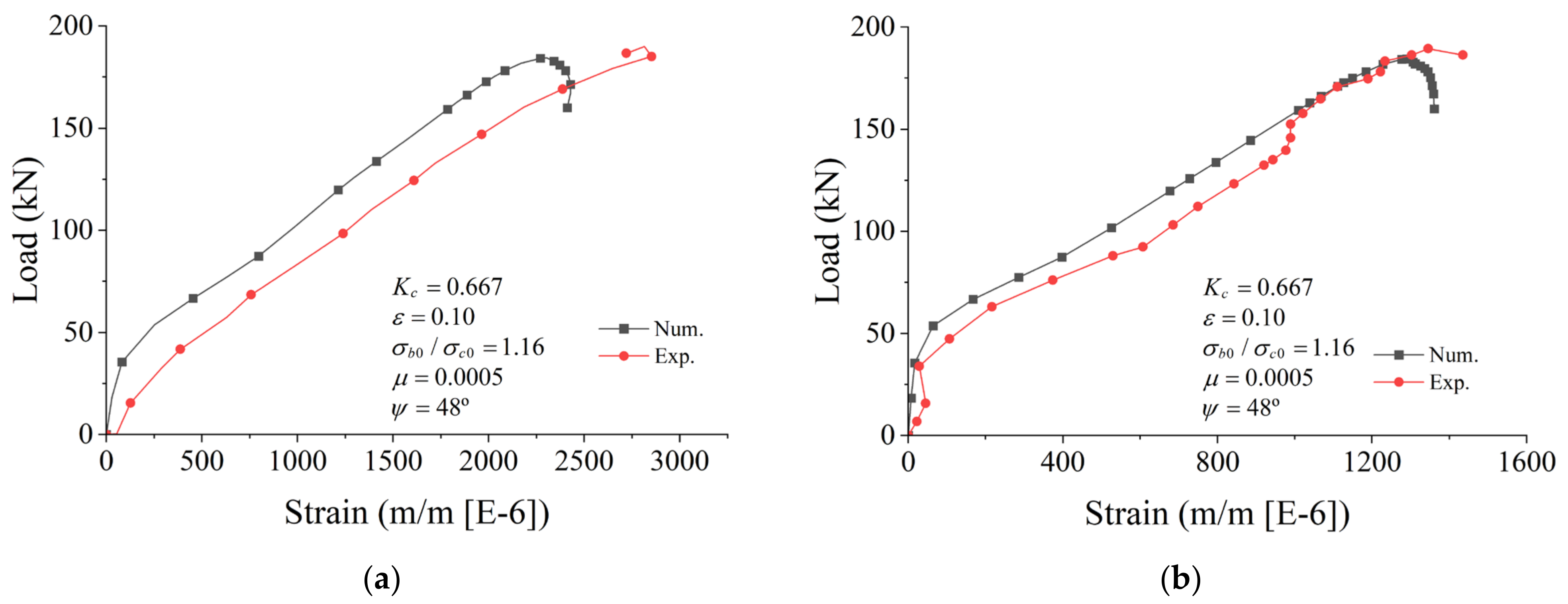
9. Comparison of Calibrations with Different Dilatancy Angles
10. Analytical Models Comparison
11. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ABNT NBR 9062; Projeto e Execução de Estruturas de Concreto Pré-Moldado. Associação Brasileira de Normas Técnicas—ABNT: Rio de Janeiro, Brazil, 2017.
- PCI. PCI Design Handbook, 7th ed.; PCI—Precast/Prestressed Concrete Institute: Chicago, IL, USA, 2010. [Google Scholar]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. CEN—Comité Européen de Normalisation: Brussels, Belgium, 2004.
- Foster, S.J.; Powell, R.E.; Selim, H.S. Performance of High-Strength Concrete Corbels. ACI Struct. J. 1996, 93, 555–563. [Google Scholar] [CrossRef]
- Campione, G.; La Mendola, L.; Papia, M. Flexural Behaviour of Concrete Corbels Containing Steel Fibers or Wrapped with FRP Sheets. Mater. Struct. Constr. 2005, 38, 617–625. [Google Scholar] [CrossRef]
- Campione, G.; La Mendola, L.; Mangiavillano, M.L. Steel Fiber-Reinforced Concrete Corbels: Experimental Behavior and Shear Strength Prediction. ACI Struct. J. 2007, 104, 570–579. [Google Scholar] [CrossRef]
- Campione, G. Flexural Response of FRC Corbels. Cem. Concr. Compos. 2009, 31, 204–210. [Google Scholar] [CrossRef]
- Yong, Y.-K.; Balaguru, P. Behavior of Reinforced High-Strength-Concrete Corbels. J. Struct. Eng 1994, 120, 1182–1201. [Google Scholar] [CrossRef]
- Fernandes, G.B. Behavior of Reinforced High-Strength Concrete Corbels-Experimental Investigation and Design Model. Am. Concr. Inst. ACI Spec. Publ. 1999, SP186, 445–462. [Google Scholar] [CrossRef]
- Araújo, D.D.L.; Oliveira, E.M.D.; Silva, E.M.O.; Coelho, S.A.; El Debs, M.K. Experimental Analysis of a Modified Two-Step Corbel for Precast Concrete System. Eng. Struct. 2021, 242, 112585. [Google Scholar] [CrossRef]
- Fattuhi, N.I.; Hughes, B.P. Ductility of Reinforced Concrete Corbels Containing Either Steel Fibers or Stirrups. Struct. J. 1989, 8, 644–651. [Google Scholar]
- Fattuhi, N.I. Column-Load Effect on Reinforced Concrete Corbels. J. Struct. Eng. 1990, 116, 188–197. [Google Scholar] [CrossRef]
- Fattuhi, N.I. Reinforced Corbels Made with High-Strength Concrete and Various Secondary Reinforcements. ACI Struct. J. 1994, 91, 376–383. [Google Scholar] [CrossRef]
- Araújo, D.L.; Silva Neto, A.P.; Lobo, F.A.; El Debs, M.K. Comparative Analysis of Design Models for Concrete Corbels. Rev. IBRACON Estrut. Mater. 2016, 9, 435–470. [Google Scholar] [CrossRef]
- Michał, S.; Andrzej, W. Analysis of “d” Regions of RC Structures Based on Example of Frame Corners. AIP Conf. Proc. 2018, 1922, 130002. [Google Scholar] [CrossRef]
- Beshara, F.B.A.; Mustafa, T.S.; Mahmoud, A.A.; Khalil, M.M.A. Constitutive Models for Nonlinear Analysis of SFRC Corbels. J. Build. Eng. 2020, 28, 101092. [Google Scholar] [CrossRef]
- Syroka, E.; Bobiński, J.; Tejchman, J. FE Analysis of Reinforced Concrete Corbels with Enhanced Continuum Models. Finite Elem. Anal. Des. 2011, 47, 1066–1078. [Google Scholar] [CrossRef]
- Canha, R.M.F.; Kuchma, D.A.; El Debs, M.K.; Souza, R.A. de Numerical Analysis of Reinforced High Strength Concrete Corbels. Eng. Struct. 2014, 74, 130–144. [Google Scholar] [CrossRef]
- Araújo, D.D.L.; Coelho, S.A.; Almeida, S.R.M.; El Debs, M.K. Computational Modelling and Analytical Model for Two-Step Corbel for Precast Concrete System. Eng. Struct. 2021, 244, 112699. [Google Scholar] [CrossRef]
- Neuberger, Y.M.; de Lima Araújo, D. An Improved Analytical Model for Two-Step Corbels in a Precast Concrete System. Eng. Struct. 2023, 284, 115947. [Google Scholar] [CrossRef]
- Simulia Abaqus 6.11 Theory Manual; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2017; Volume IV, p. 1172.
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A Plastic-Damage Model for Concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Jeeho, L.; Gregory, L.F. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar]
- Behnam, H.; Kuang, J.S.; Samali, B. Parametric Finite Element Analysis of RC Wide Beam-Column Connections. Comput. Struct. 2018, 205, 28–44. [Google Scholar] [CrossRef]
- Panahi, H.; Genikomsou, A.S. Comparative Evaluation of Concrete Constitutive Models in Non-Linear Finite Element Simulations of Slabs with Different Flexural Reinforcement Ratios. Eng. Struct. 2022, 252, 113617. [Google Scholar] [CrossRef]
- Chen, R.P.; Ma, Q.L.; Zhang, Y.; Wu, H.N.; Liu, Y.; Lu, L. Experimental Study on the Mechanical Behaviour of Eccentric Compression Short Column Strengthened by Ultra-High-Performance Fibre-Reinforced Concrete. Structures 2021, 33, 508–522. [Google Scholar] [CrossRef]
- Hany, N.F.; Hantouche, E.G.; Harajli, M.H. Finite Element Modeling of FRP-Confined Concrete Using Modified Concrete Damaged Plasticity. Eng. Struct. 2016, 125, 1–14. [Google Scholar] [CrossRef]
- Zhao, W.S.; Chen, W.Z. Effect of Near-Fault Ground Motions with Long-Period Pulses on the Tunnel. J. Vibroeng. 2015, 17, 841–858. [Google Scholar]
- Genikomsou, A.S.; Polak, M.A. Finite Element Analysis of Punching Shear of Concrete Slabs Using Damaged Plasticity Model in ABAQUS. Eng. Struct. 2015, 98, 38–48. [Google Scholar] [CrossRef]
- Reginato, L.; de Sousa, A.M.D.; Santos, J.V.C.; El Debs, M.K. NLFEA of Reinforced Concrete Corbels: Proposed Framework, Sensibility Study, and Precision Level. Buildings 2023, 13, 1874. [Google Scholar] [CrossRef]
- de Sousa, A.M.D.; Lantsoght, E.O.L.; Genikomsou, A.S.; Prado, L.P.; El Debs, M.K. NLFEA of One-Way Slabs in Transition between Shear and Punching: Recommendations for Modeling. Eng. Struct. 2023, 293, 116617. [Google Scholar] [CrossRef]
- Hegemier, G.A.; Nunn, R.O.; Arya, S.K. Behavior of Concrete Masonry Under Biaxial Stresses. In Proceedings of the North American Masonry Conference, Denver, CO, USA, 14–16 August 1978; pp. 656–666. [Google Scholar]
- Kupfer, H.B.; Hilsdorf, H.K.; Rusch, H. Behavior of Concrete Under Biaxial Stresses. ACI J. Proc. 1969, 66, 656–666. [Google Scholar] [CrossRef]
- Kupfer, H.B.; Gerstle, K.H. Behavior of Concrete under Biaxial Stresses. J. Eng. Mech. Div. 1973, 99, 853–866. [Google Scholar] [CrossRef]
- Poliotti, M.; Bairán, J.M. A New Concrete Plastic-Damage Model with an Evolutive Dilatancy Parameter. Eng. Struct. 2019, 189, 541–549. [Google Scholar] [CrossRef]
- Cheng, H.; Paz, C.M.; Pinheiro, B.C.; Estefen, S.F. Experimentally Based Parameters Applied to Concrete Damage Plasticity Model for Strain Hardening Cementitious Composite in Sandwich Pipes. Mater. Struct. Constr. 2020, 53, 78. [Google Scholar] [CrossRef]
- Carreira, D.J.; Chu, K.H. Stress-Strain Relatonship for Reinforced Concrete in Compression. ACI Struct. J. 1985, 83, 21–28. [Google Scholar]
- Yu, T.; Teng, J.G.; Wong, Y.L.; Dong, S.L. Finite Element Modeling of Confined Concrete-II: Plastic-Damage Model. Eng. Struct. 2010, 32, 680–691. [Google Scholar] [CrossRef]
- Comité Euro-International du Béton. CEB-FIB-Model Code 1990: Design Code; Thomas Telford: London, UK, 1993. [Google Scholar]
- Chi, Y.; Yu, M.; Huang, L.; Xu, L. Finite Element Modeling of Steel-Polypropylene Hybrid Fiber Reinforced Concrete Using Modified Concrete Damaged Plasticity. Eng. Struct. 2017, 148, 23–35. [Google Scholar] [CrossRef]
- Henriques, J.; Simões da Silva, L.; Valente, I.B. Numerical Modeling of Composite Beam to Reinforced Concrete Wall Joints. Part II: Global Behavior. Eng. Struct. 2013, 52, 734–746. [Google Scholar] [CrossRef]
- Kyriakopoulos, P.; Peltonen, S.; Vayas, I.; Spyrakos, C.; Leskela, M.V. Experimental and Numerical Investigation of the Flexural Behavior of Shallow Floor Composite Beams. Eng. Struct. 2021, 231, 111734. [Google Scholar] [CrossRef]
- Willam, K.J.; Warnke, E.P. Constitutive Model for the Triaxial Behaviour of Concrete. Semin. Concr. Struct. Subj. Triaxial Stress. 1974, 19, 30. [Google Scholar]
- Petersson, P. Crack Growth and Development of Fracture Zones in Plain Concrete and Similar Materials. Div. Build. Mater. 1981, 1–174. [Google Scholar]




| Reference | Corbels | Vy,exp (kN) | Vu,exp (kN) | Geometry | |||||
|---|---|---|---|---|---|---|---|---|---|
| a/d | a (mm) | h (mm) | b (mm) | d (mm) | d′ (mm) | ||||
| Fernandes [9] | FE-CS6-4A | 120 | 160 | 0.57 | 60 | 120 | 120 | 105 | 15 |
| Araújo et al. [10] | M3-MONO-A | 248 | 314.4 | 0.63 | 225 | 400 | 200 | 360 | 40 |
| Fattuhi e Hugles [11] | FA-T8 | 188.4 | 188.4 | 0.68 | 89 | 150 | 150 | 130 | 20 |
| fc (MPa) | Tie reinforcement | Seam reinforcement | |||||||
| ϕl (mm) | As (mm2) | fy (MPa) | ϕt (mm) | Asf2 (mm2) | fys (MPa) | wp (mm) | |||
| Fernandes [9] | FE-CS6-4A | 75.3 | 6.3 | 125 | 525 | 4.2 | 55 | 750 | 50 |
| Araújo et al. [10] | M3-MONO-A | 43.09 | 12.5 | 245 | 670 | 6.3 | 187 | 615 | 50 |
| Fattuhi e Hugles [11] | FA-T8 | 44.62 | 12 | 226 | 491 | 10 | 314 | 558 | 50 |
| Material Elastic Properties | |
| Modulus of elasticity (Ec): | a |
| Poisson coefficient (v): | v = 0.2 a |
| CDP Parameters | |
| Dilation angle (ψ): | 30 |
| Eccentricity (e): | 0.1 b |
| Relation between bi-axial and uniaxial stress (σb0/σc0): | 1.16 b |
| Shape factor (Kc): | 0.667 b |
| Viscosity (μ): | 0.0005 c |
| Stress–Strain Curves | |
| Compression | Carreira e Chu [37] |
| Tension | Genikomsou e Polak [29] |
| Damage Evolution Law | |
| Compression | Yu et al. [38]: (dc = 1 − σc/fc) |
| Tension | Yu et al. [38]: (dt = 1 − σct/fct) |
| Test | Interpolation Order | Average Element Size [mm] | Hexaedric Solid Element | Linear Element | Processing Time [min] | |
|---|---|---|---|---|---|---|
| 1 | Linear | 10 | C3D8R | T3D2 | 658 | 0.86 |
| 2 | Linear | 15 | C3D8R | T3D2 | 228 | 0.89 |
| 3 | Linear | 25 | C3D8R | T3D2 | 21 | 0.92 |
| 4 | Linear | 35 | C3D8R | T3D2 | 14 | 0.94 |
| 5 | Linear | 50 | C3D8R | T3D2 | 5 | 0.87 |
| Experimental | Numerical ψ = 39° | Numerical ψ = 48° | Numerical ψ = 51° | ||||
|---|---|---|---|---|---|---|---|
| Corbel | Vu,exp | Vu,num | Vu, num | Vu,num | |||
| M3-MONO-A | 314.42 | 315.32 * | 1.00 * | 367.65 | 1.17 | 374.99 | 1.19 |
| FA-T8 | 188.40 | 146.53 | 0.78 | 184.35 * | 0.98 * | 198.63 | 1.05 |
| FE SC6-4A | 160.00 | 146.60 | 0.92 | 154.74 | 0.97 | 163.07 * | 1.02 * |
| Mean value | 0.90 | 1.04 | 1.09 | ||||
| Standard deviation | 0.114 | 0.114 | 0.092 | ||||
| COV (%) | 12.63 | 10.94 | 8.42 | ||||
| Experimental | Numerical ψ = 48° | NBR 9062 | PCI | EN 1992-1-1 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Corbel | Vu,exp | Vu,num | Vu,num/Vu,exp | Vu,ana | Vu,ana/Vu,exp | Vu,ana | Vu,ana/Vu,exp | Vu,ana | Vu,ana/Vu,exp |
| M3-MONO-A | 314.42 | 367.65 | 1.17 | 421.98 | 1.34 | 735.5 | 2.34 | 691.52 | 2.20 |
| FA-T8 | 188.40 | 184.35 | 0.98 | 395.9 | 2.10 | 200.6 | 1.06 | 181.60 | 0.96 |
| FE CS6-4A | 160.00 | 154.74 | 0.97 | 371.3 | 2.32 | 230.8 | 1.44 | 290.90 | 1.82 |
| Mean values | 1.04 | 1.92 | 1.62 | 1.66 | |||||
| Standard deviation | 0.114 | 0.514 | 0.655 | 0.633 | |||||
| COV (%) | 10.94 | 26.73 | 40.52 | 38.10 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neuberger, Y.M.; Andrade, M.V.; de Sousa, A.M.D.; Bandieira, M.; da Silva Júnior, E.P.; dos Santos, H.F.; Catoia, B.; Bolandim, E.A.; de Moura Aquino, V.B.; Christoforo, A.L.; et al. Numerical Analysis of Reinforced Concrete Corbels Using Concrete Damage Plasticity: Sensitivity to Material Parameters and Comparison with Analytical Models. Buildings 2023, 13, 2781. https://doi.org/10.3390/buildings13112781
Neuberger YM, Andrade MV, de Sousa AMD, Bandieira M, da Silva Júnior EP, dos Santos HF, Catoia B, Bolandim EA, de Moura Aquino VB, Christoforo AL, et al. Numerical Analysis of Reinforced Concrete Corbels Using Concrete Damage Plasticity: Sensitivity to Material Parameters and Comparison with Analytical Models. Buildings. 2023; 13(11):2781. https://doi.org/10.3390/buildings13112781
Chicago/Turabian StyleNeuberger, Ygor Moriel, Maykon Vinicius Andrade, Alex Micael Dantas de Sousa, Mariana Bandieira, Edivaldo Pereira da Silva Júnior, Herisson Ferreira dos Santos, Bruna Catoia, Emerson Alexandro Bolandim, Vinicius Borges de Moura Aquino, André Luis Christoforo, and et al. 2023. "Numerical Analysis of Reinforced Concrete Corbels Using Concrete Damage Plasticity: Sensitivity to Material Parameters and Comparison with Analytical Models" Buildings 13, no. 11: 2781. https://doi.org/10.3390/buildings13112781
APA StyleNeuberger, Y. M., Andrade, M. V., de Sousa, A. M. D., Bandieira, M., da Silva Júnior, E. P., dos Santos, H. F., Catoia, B., Bolandim, E. A., de Moura Aquino, V. B., Christoforo, A. L., & de Araújo Ferreira, M. (2023). Numerical Analysis of Reinforced Concrete Corbels Using Concrete Damage Plasticity: Sensitivity to Material Parameters and Comparison with Analytical Models. Buildings, 13(11), 2781. https://doi.org/10.3390/buildings13112781






