Study of Damping of Bare and Encased Steel I-Beams Using the Thermoelastic Model
Abstract
:1. Introduction
2. Materials and Methods
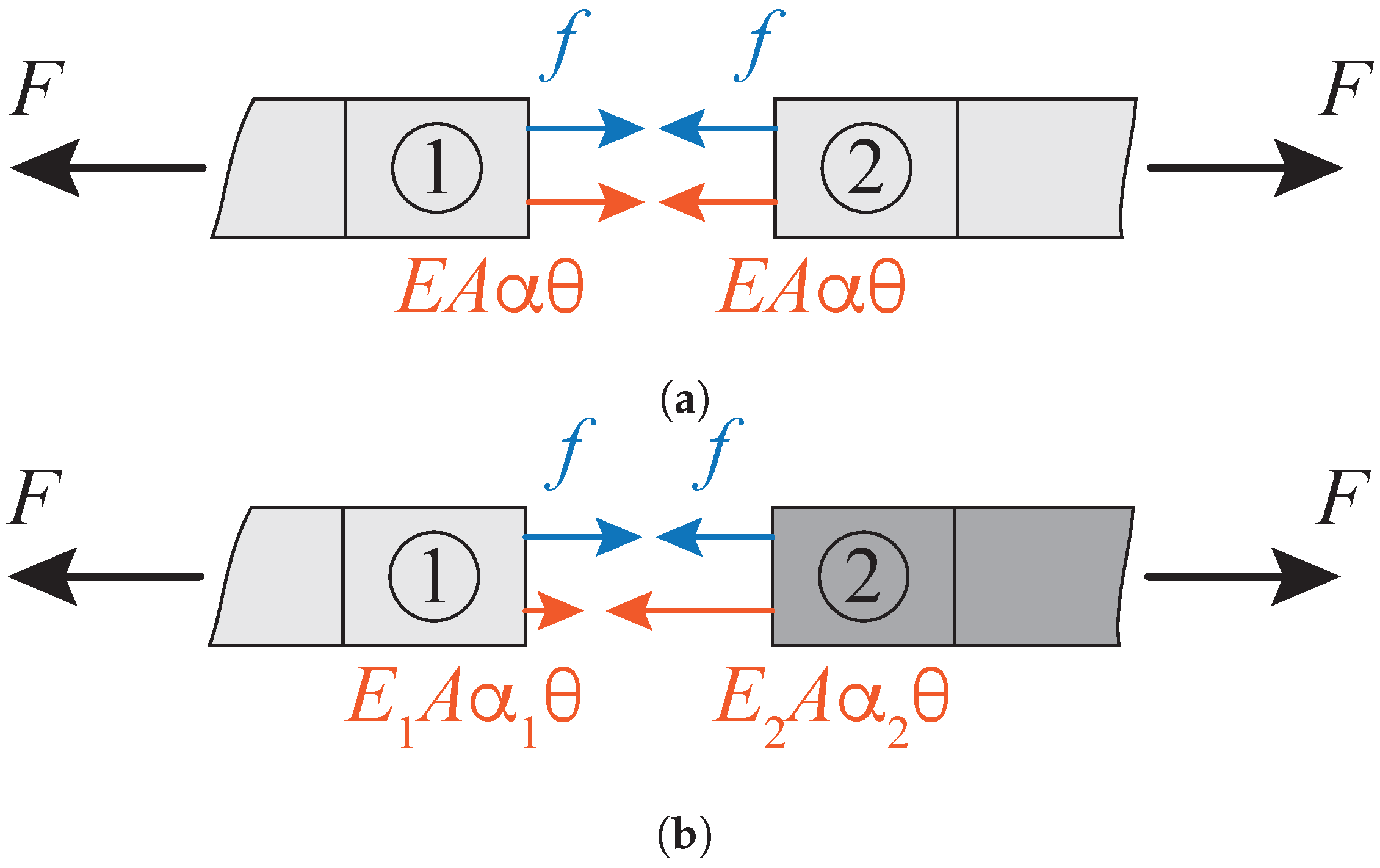
2.1. The Thermoelastic Model
2.2. Energy Flow and Balance in the Thermoelastic Model
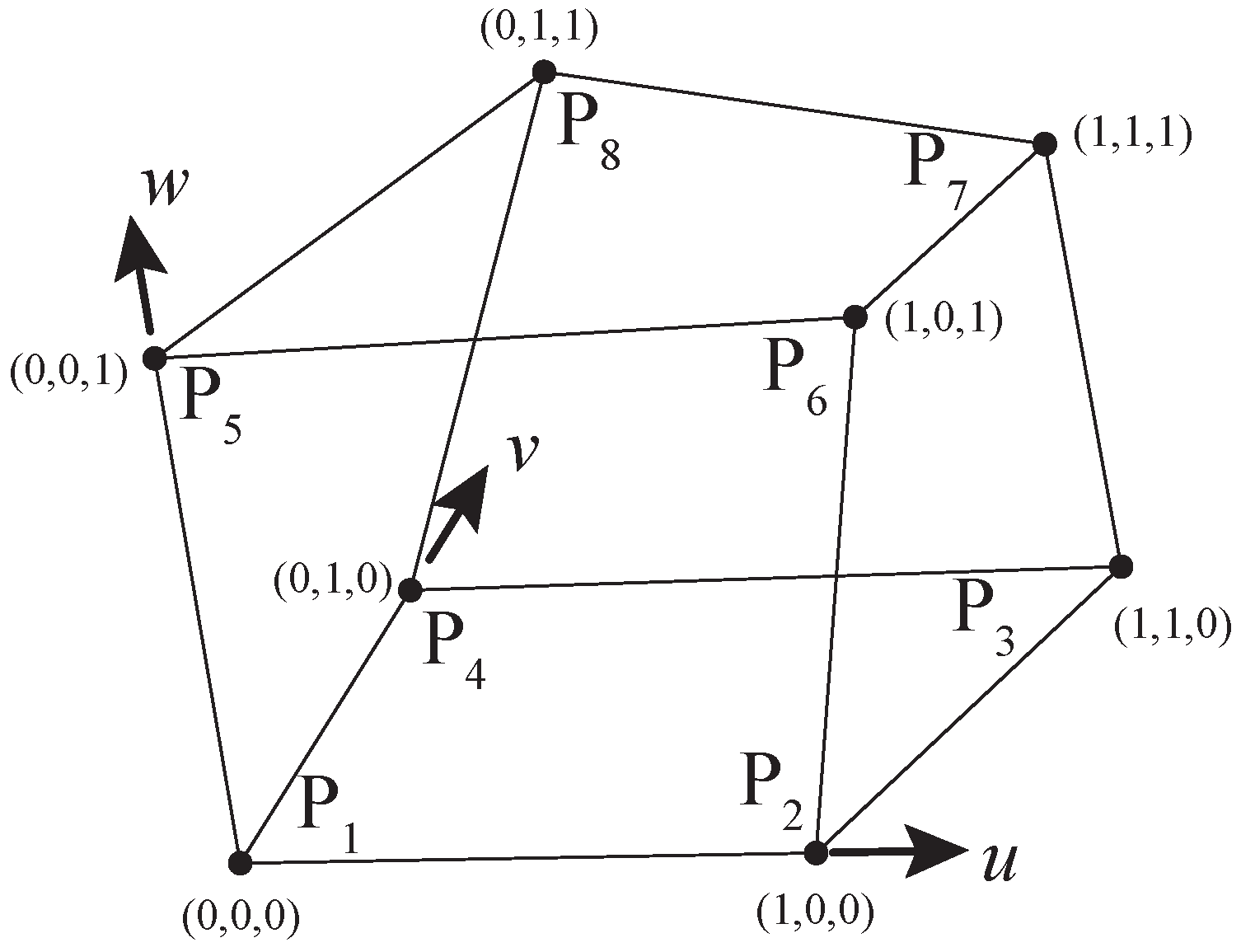
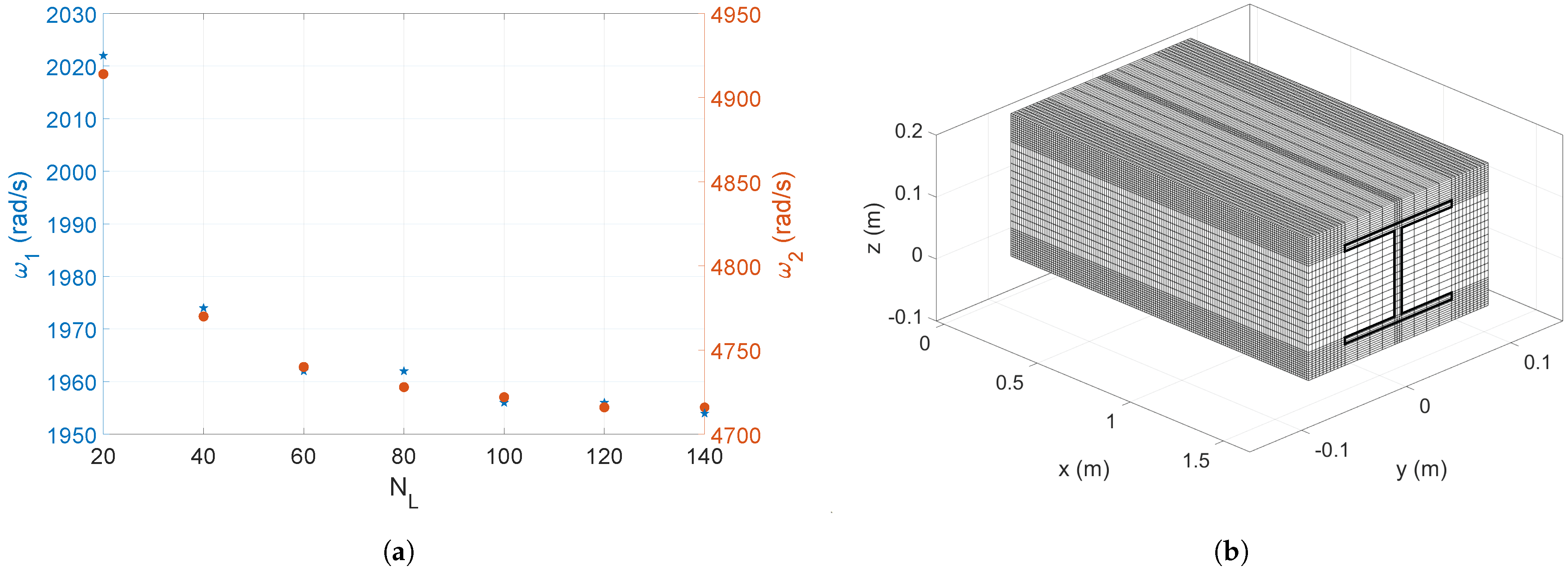
2.3. Finite Element Model
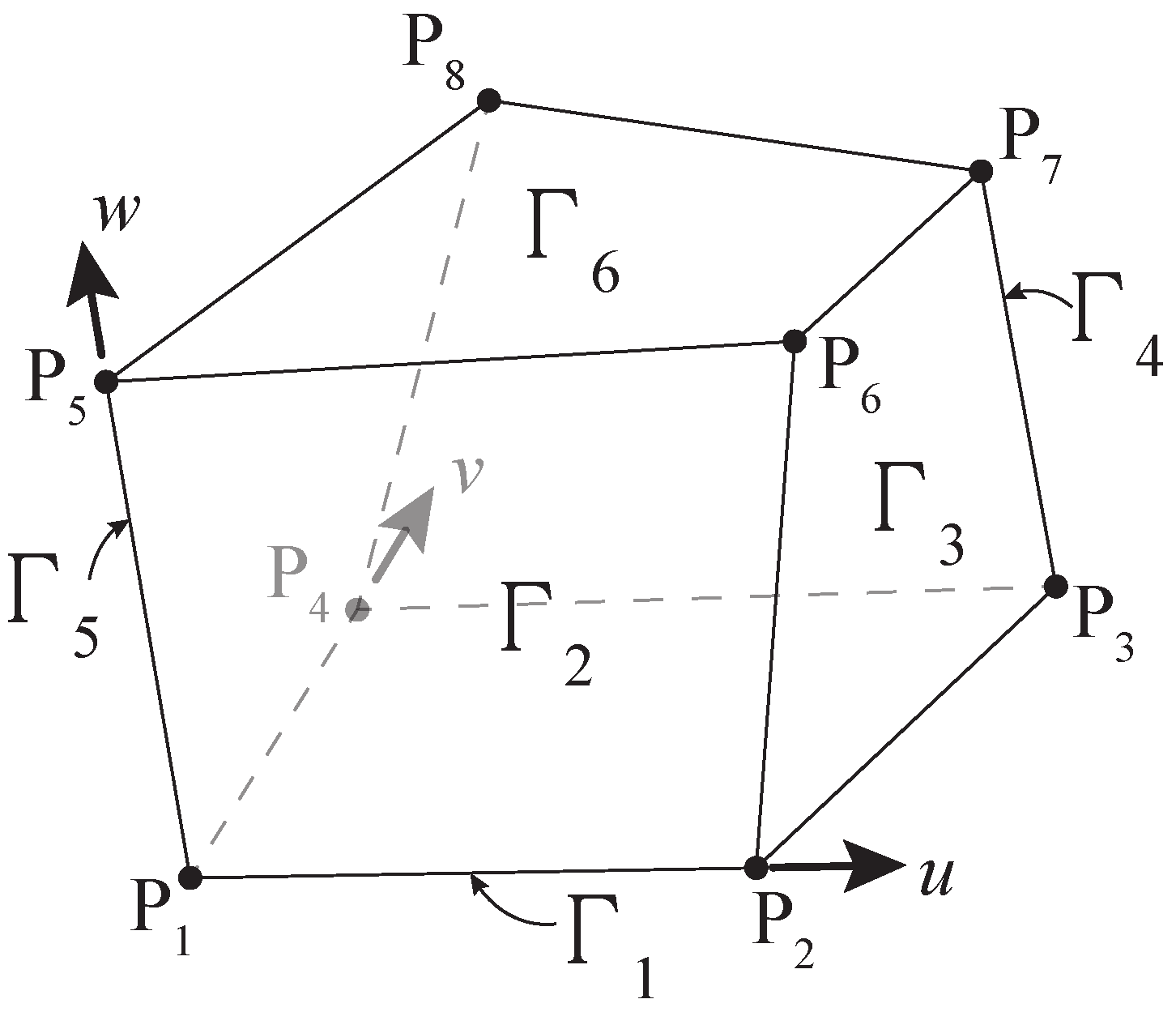
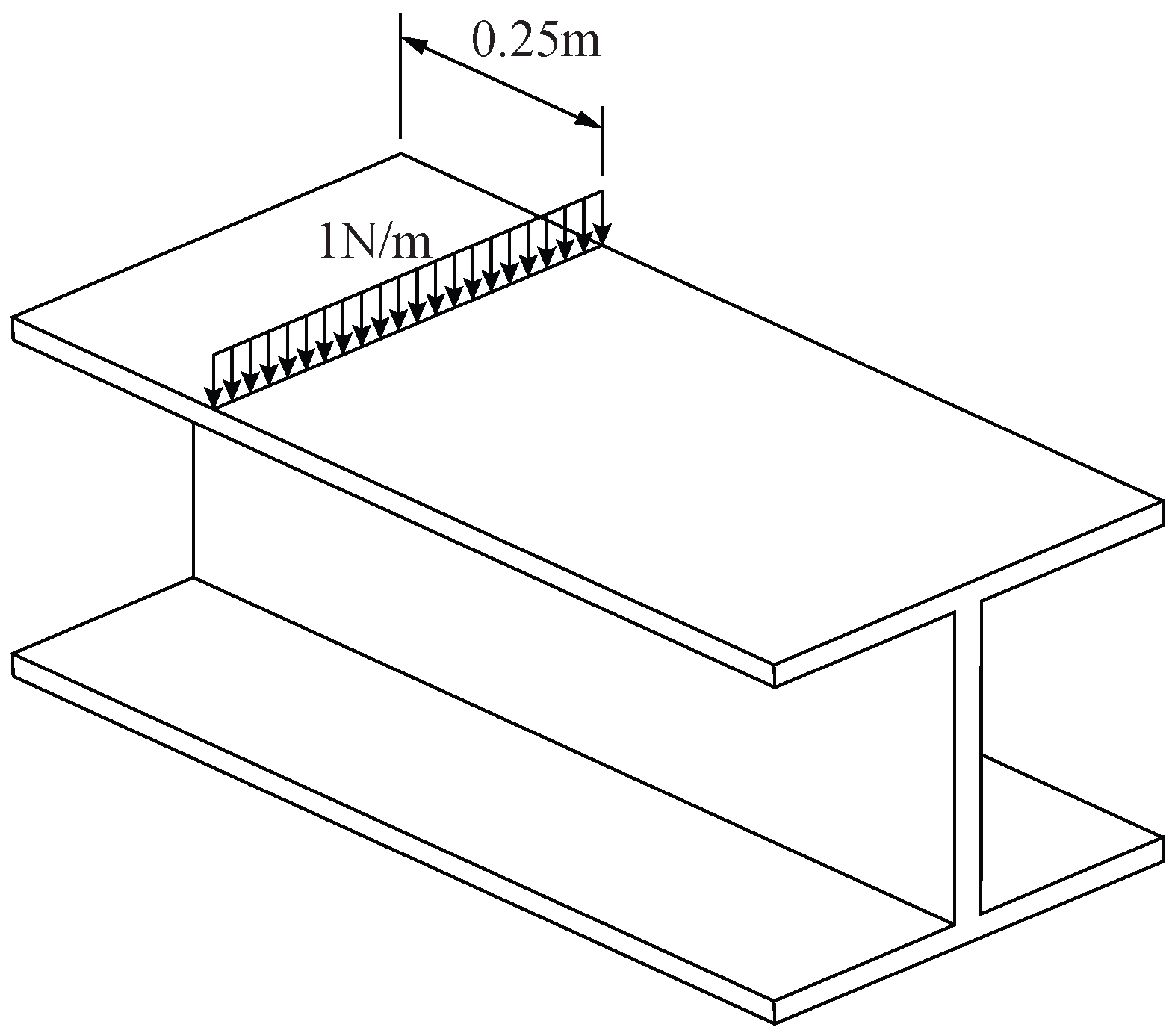
2.4. Boundary Conditions
- When a body is stretched, it cools down, and when compressed, it heats up.
- When heated, a body expands, and when cooled, it shrinks.
Implementation of the Boundary Conditions
2.5. Harmonic Solution
2.6. Energy Computation in the Finite Element Model
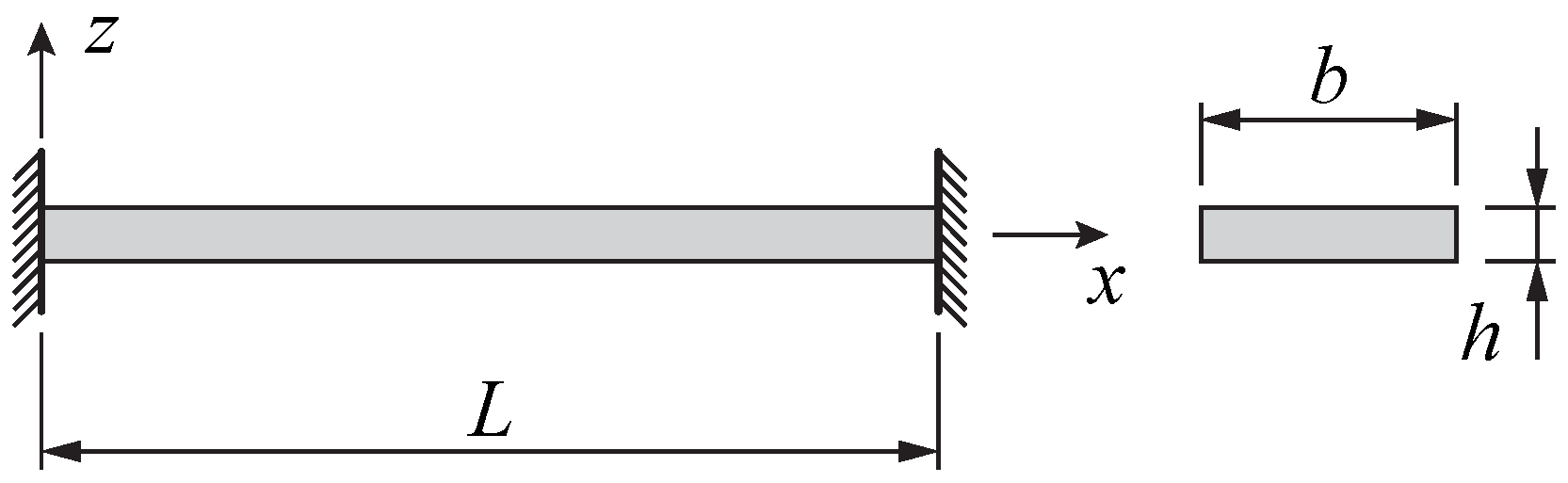
2.7. Geometries and Materials
3. Results and Discussion
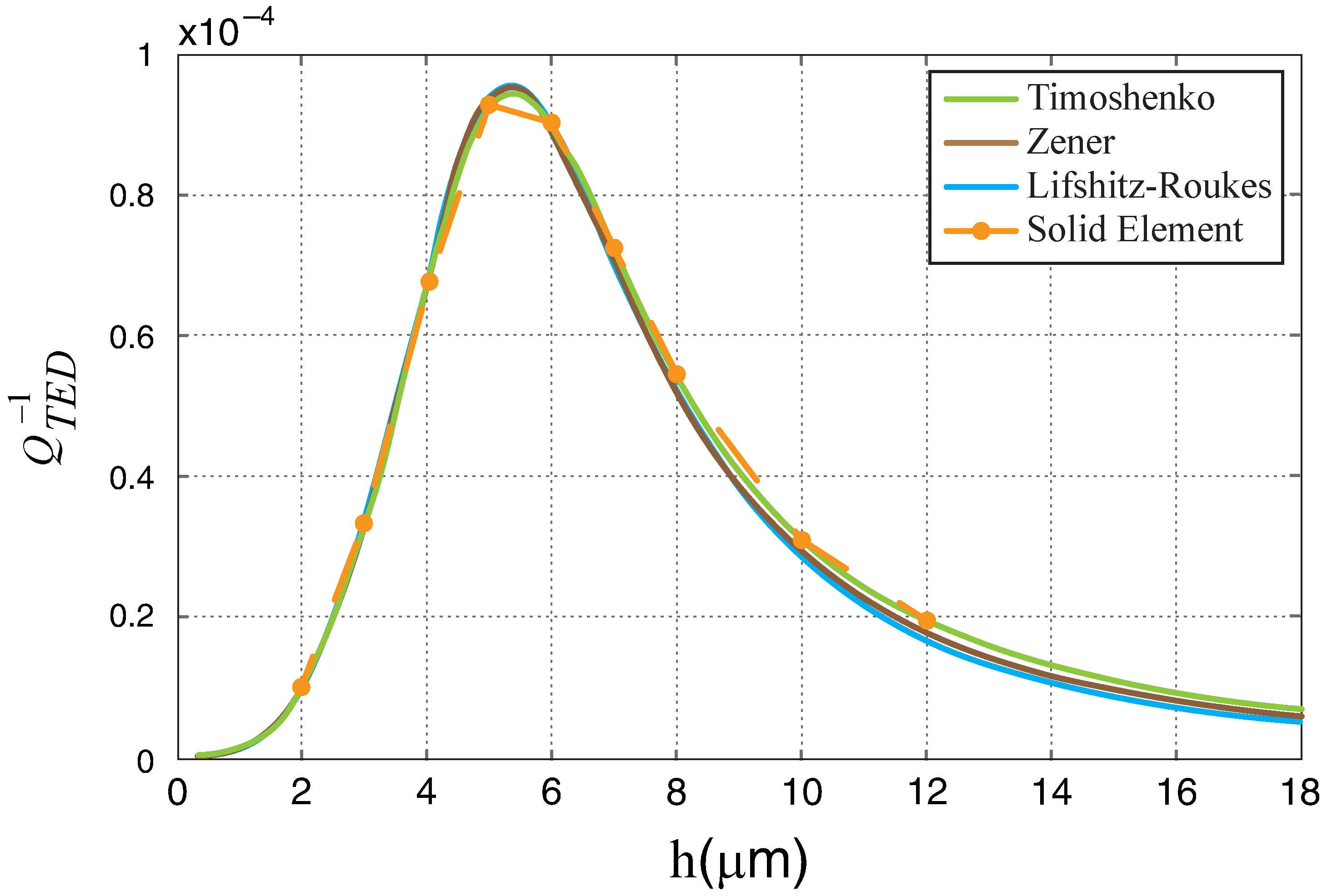
3.1. Validation Study
3.2. Mesh Convergence
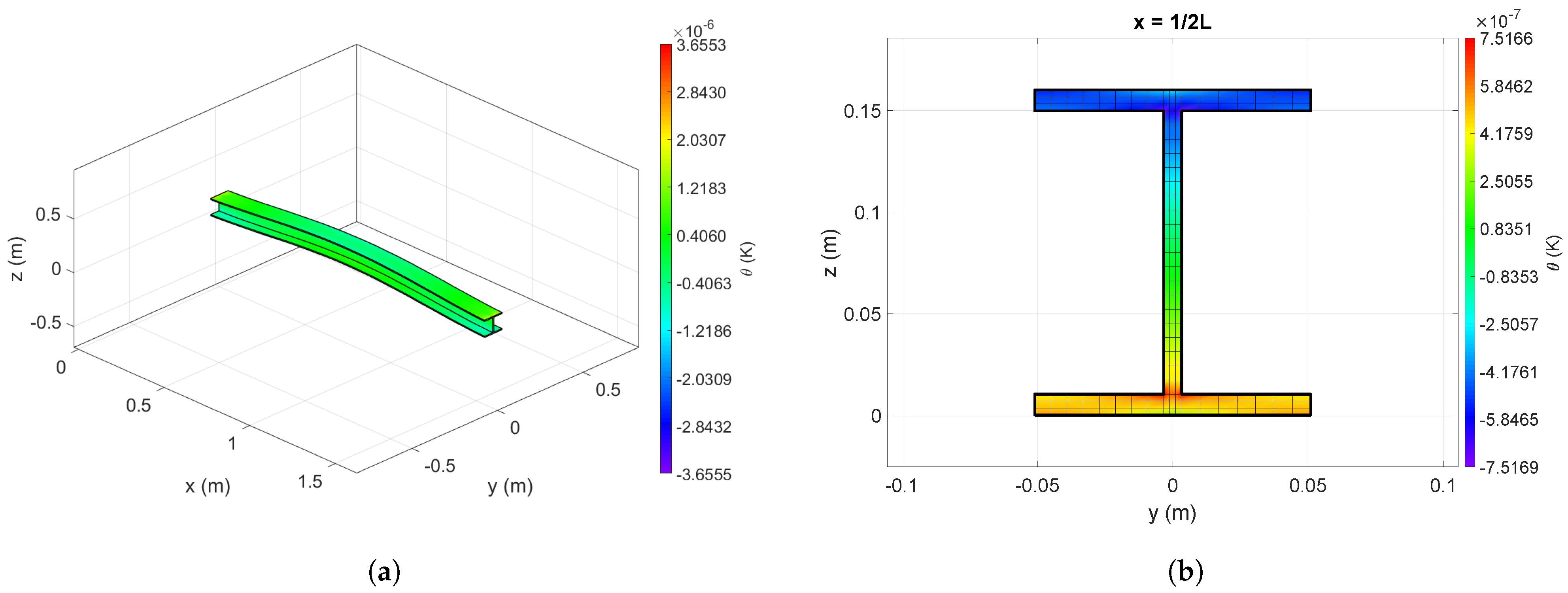
3.3. Case Studies
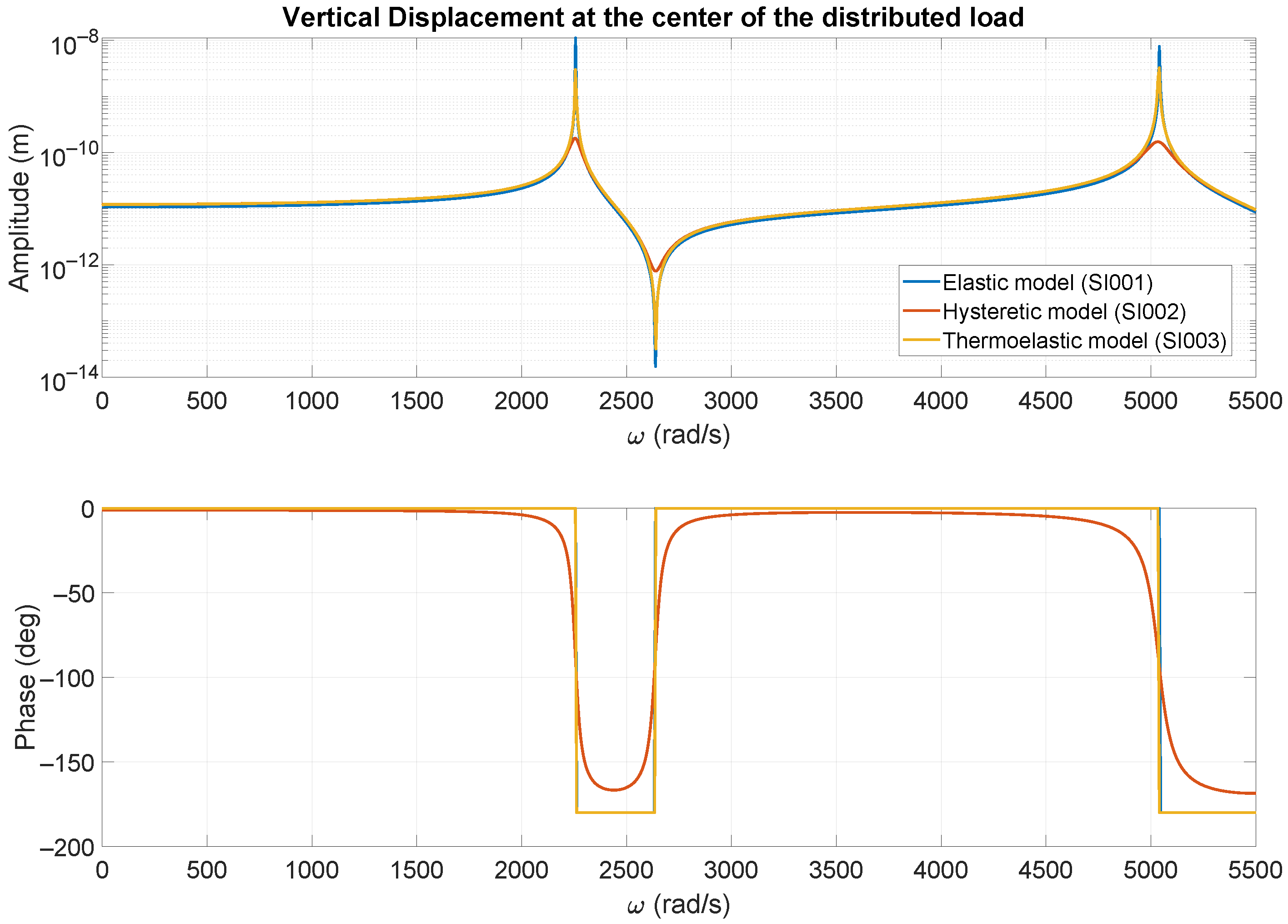
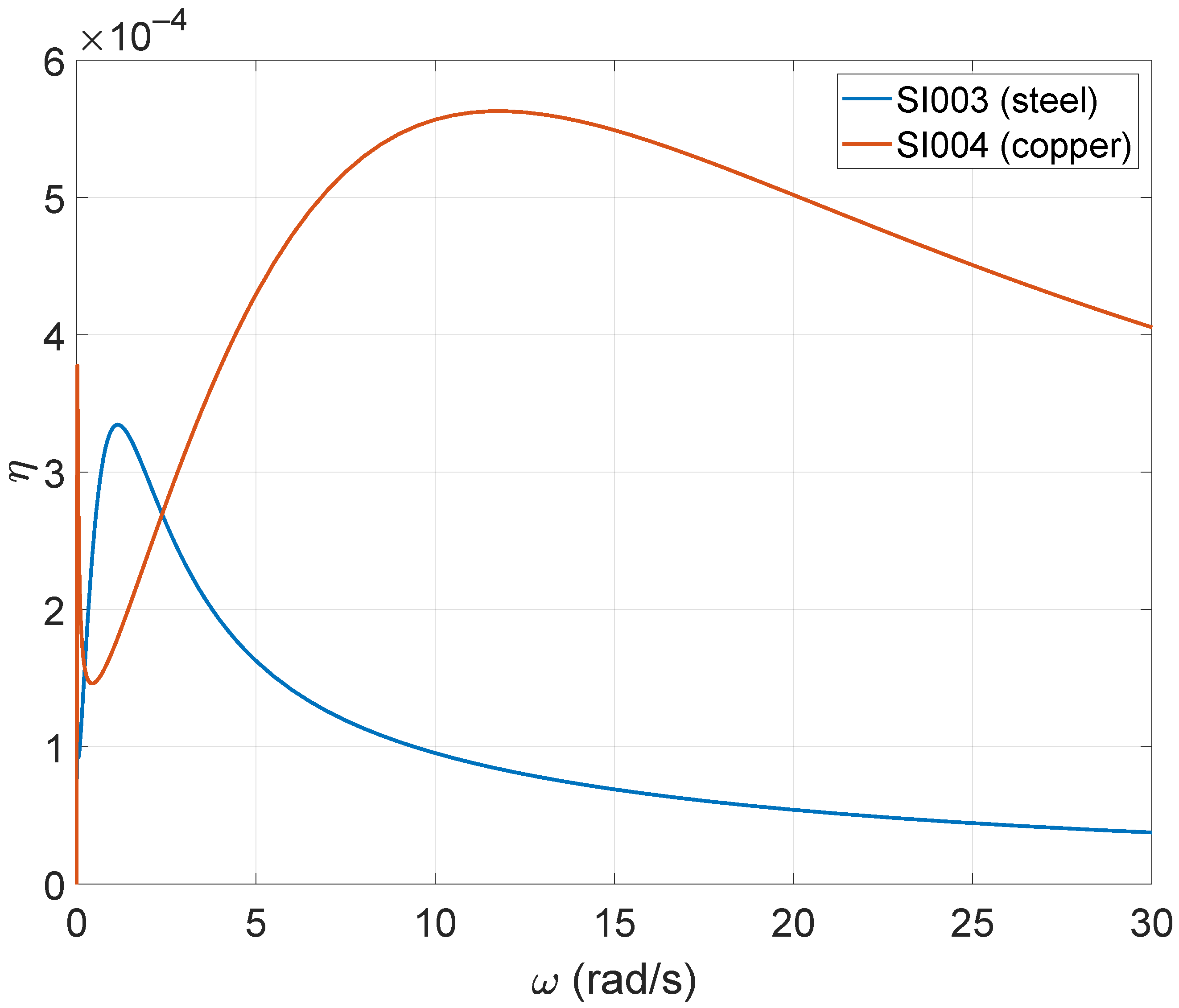
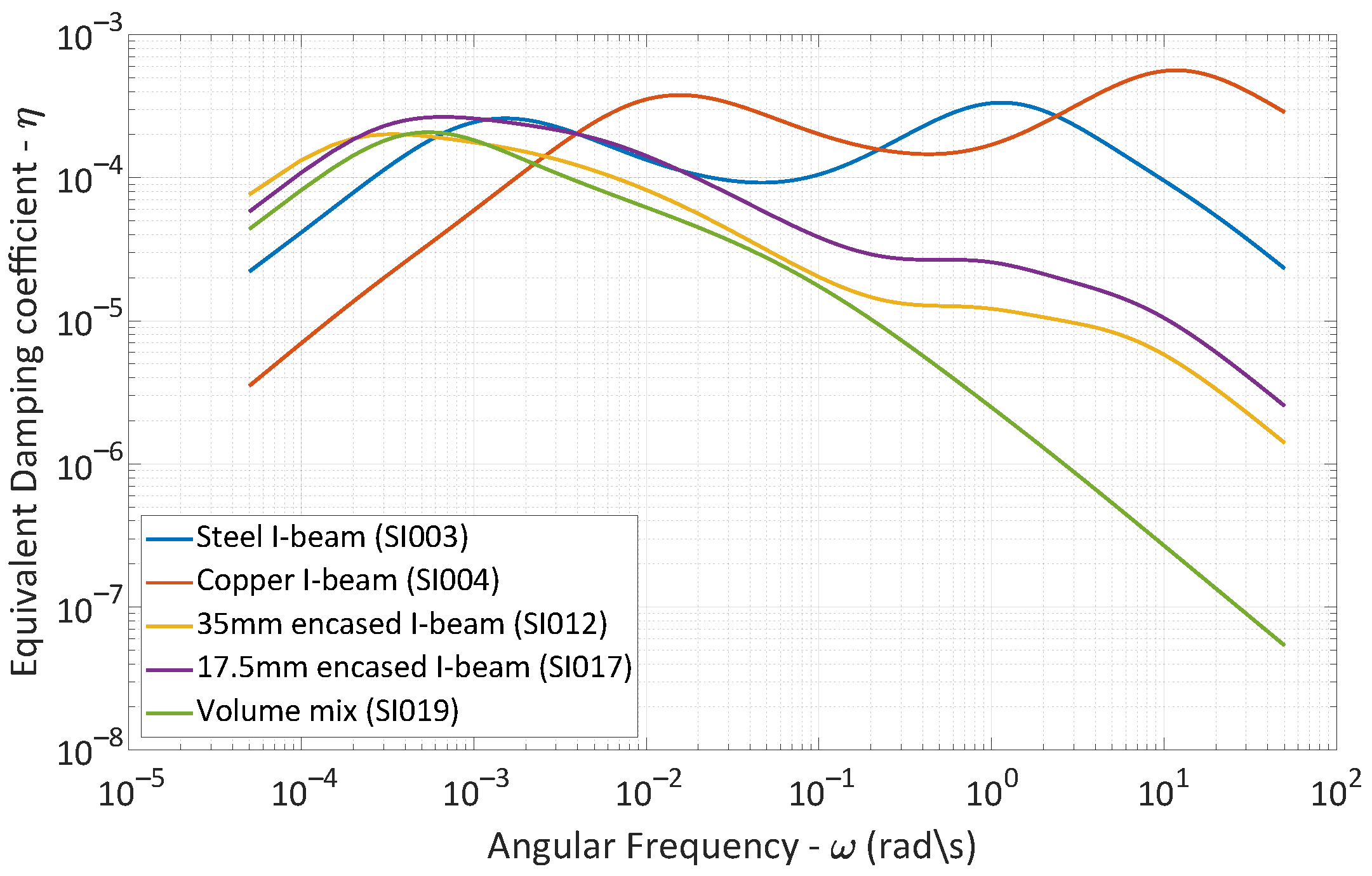
3.4. Harmonic Behavior of I-Beams
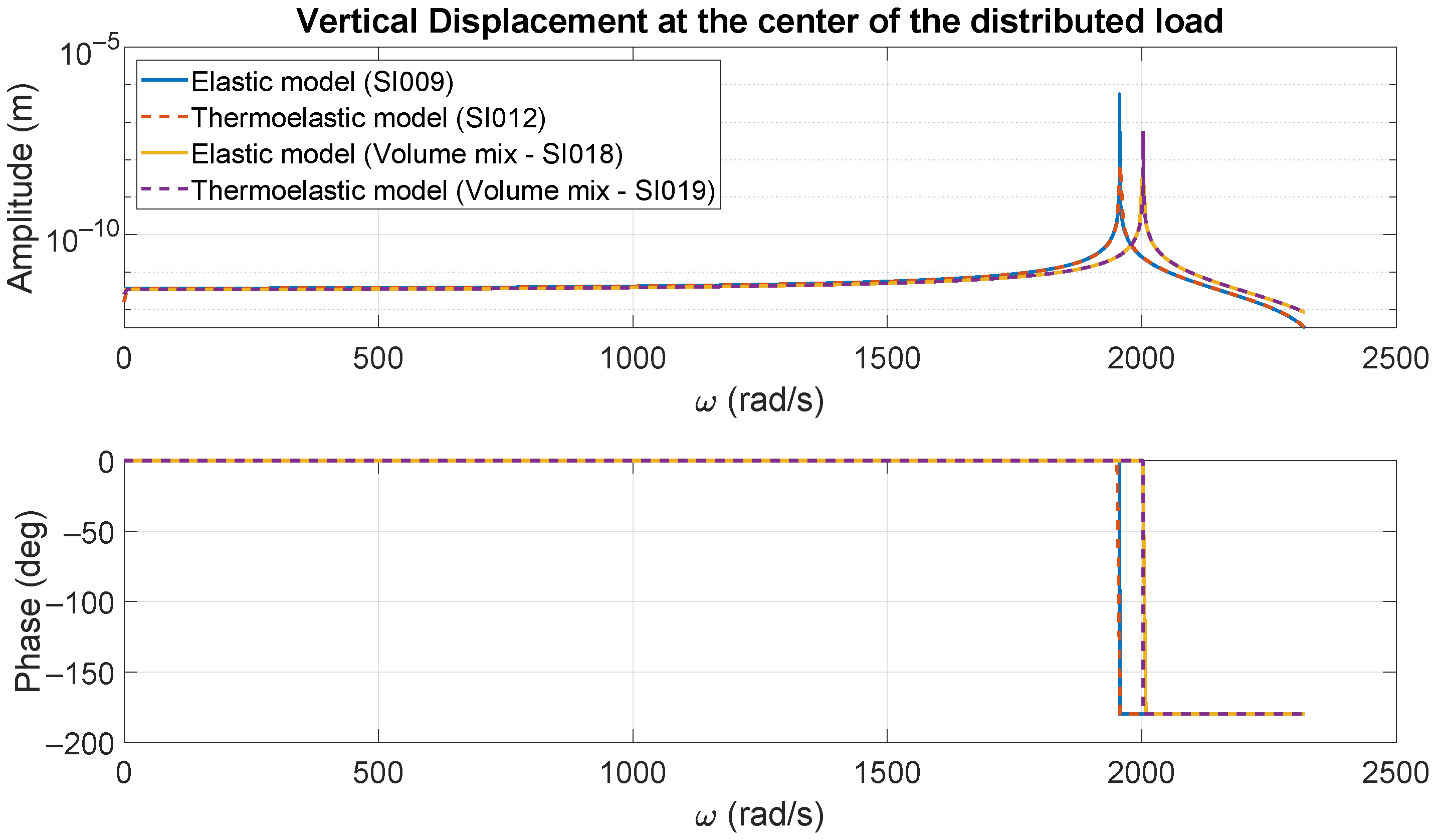
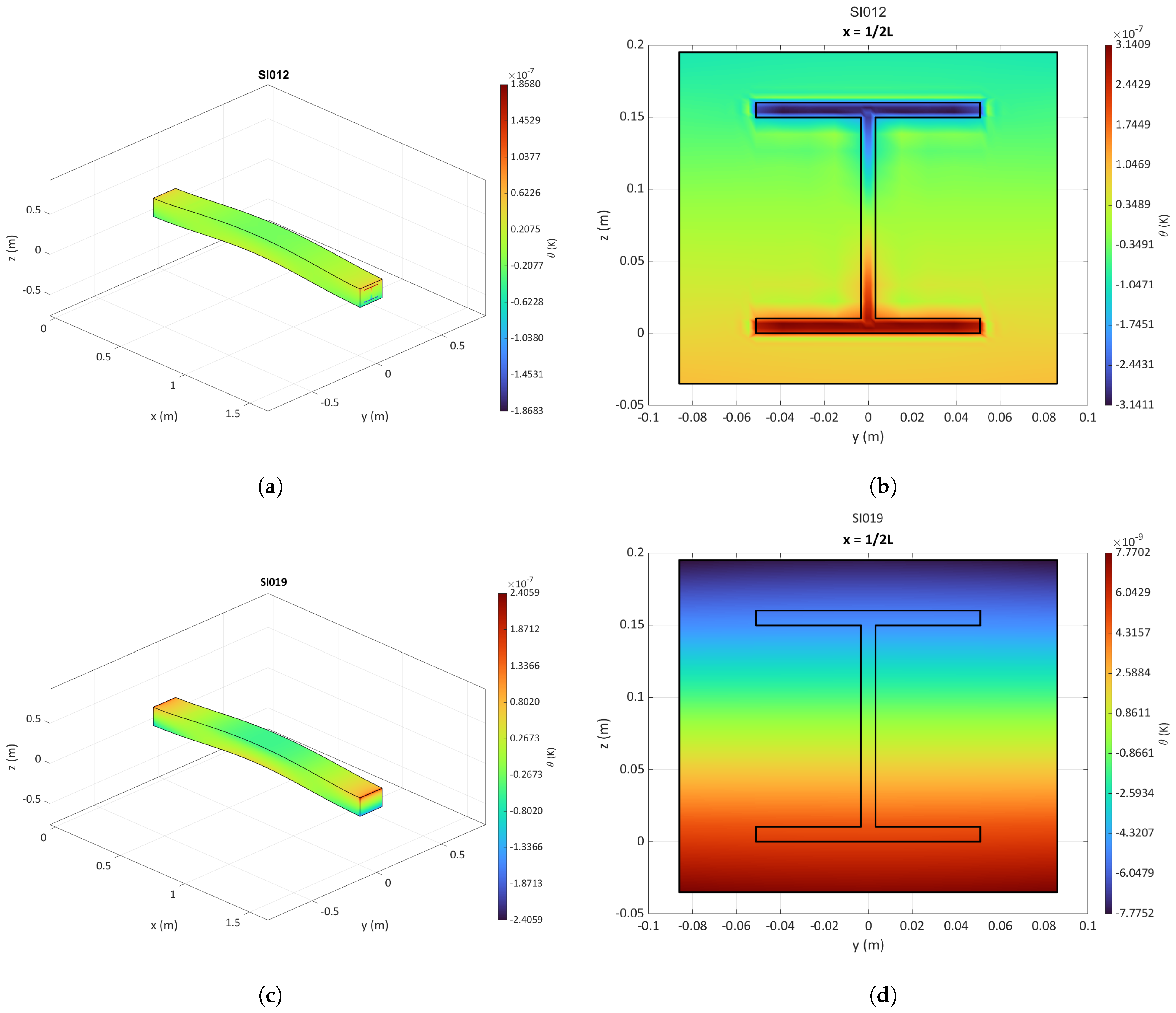
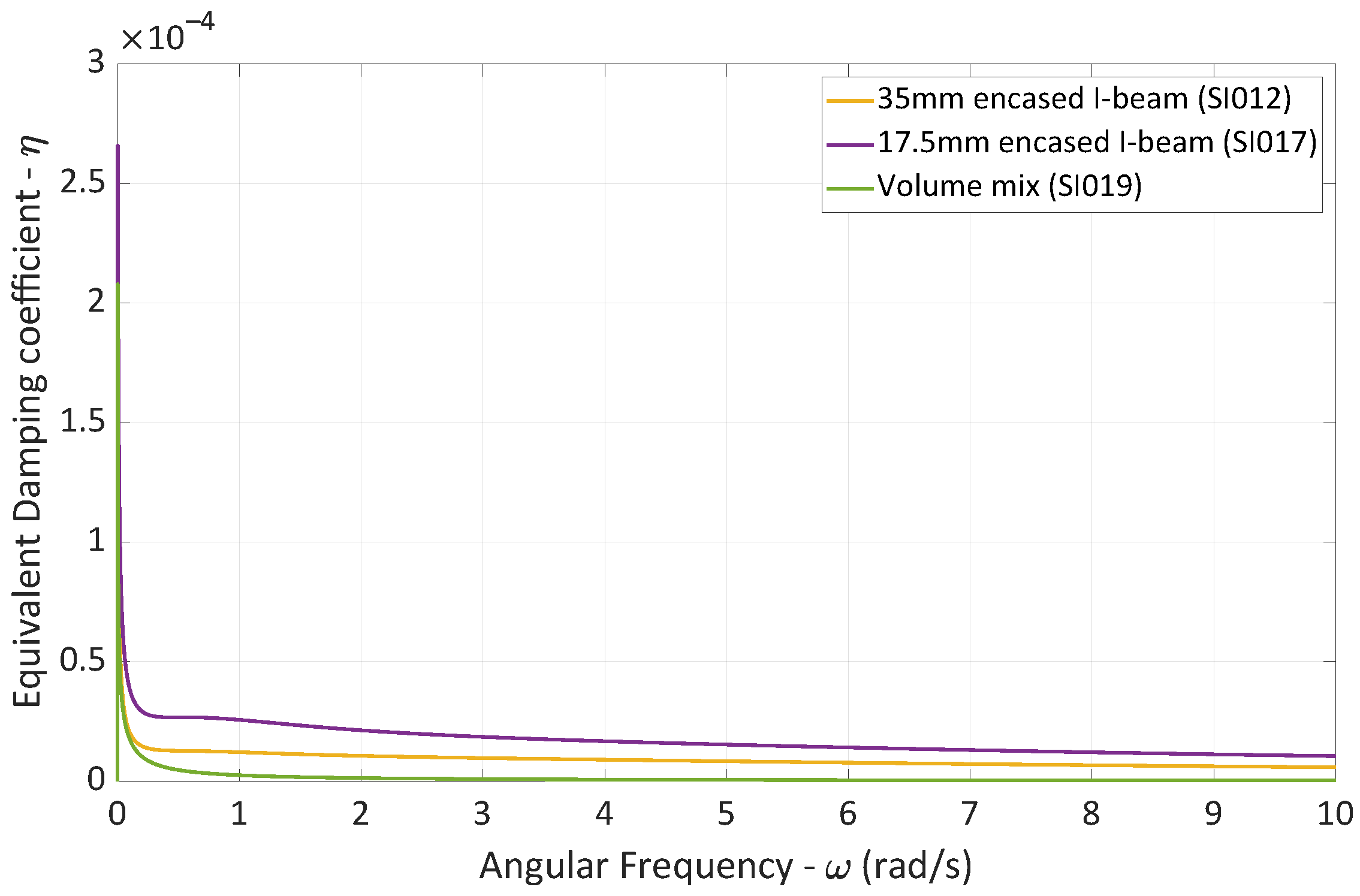
3.5. Harmonic Behavior of Encased I-Beams
4. Conclusions
- The thermoelastic model predicts an increase in the resonant frequencies, potentially attributable to the absence of “thermal inertia” in Fourier’s Law.
- A steel I-beam exhibits a maximum damping coefficient of , and due to the cross-section geometry of the beam, the damping evolution with frequency demonstrates two local maxima.
- The addition of a concrete casing to the I-beam reduces the maximum damping coefficient (approximately ), indicating that the beam dissipates less energy due to thermoelasticity compared to the bare configuration.
- While the added layer protects the beam, the decreased damping value results in less energy dissipation and a slower reduction in vibration amplitude.
- Given the distinct behavioral differences across the beam cross-section between the two material phases in case study SI012, traditional one-dimensional beam elements should not be employed, as they would oversimplify the problem.
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations and List of Symbols
| The following abbreviations are used in this manuscript: | |
| DoF | Degree of Freedom |
| BC | Boundary Condition |
| The following symbols are used in this manuscript (in order of appearance): | |
| Density | |
| Displacement vector | |
| Second Lamé constant | |
| First Lamé constant | |
| Thermoelastic coupling coefficient | |
| Temperature variation | |
| f | Volumetric load |
| Specific heat capacity | |
| k | Thermal conductivity |
| Base temperature | |
| q | Volumetric heat flux |
| Poisson coefficient | |
| E | Young modulus |
| Thermal expansion coefficient | |
| Thermal strain | |
| Kronecker Delta | |
| Total strain | |
| Mechanical strain | |
| s | Specific Entropy |
| Potential energy | |
| Kinetic energy | |
| Exergy | |
| Domain | |
| V | Volume |
| Work lost to irreversible entropy | |
| W | Work |
| Heat | |
| Variation of the internal energy | |
| Variation of the internal energy in a cycle | |
| Work lost to irreversible entropy in a cycle | |
| Work done in a cycle | |
| Heat generated in a cycle | |
| Dynamic modulus | |
| Storage modulus | |
| Loss modulus | |
| Loss angle | |
| Damping coefficient | |
| Angular frequency | |
| Shape function | |
| Mass matrix | |
| Velocity matrix | |
| Stiffness matrix | |
| Boundary terms | |
| Direct shape function matrix | |
| Gradient shape function matrix | |
| Cross shape function matrix | |
| P | Boundary load |
| A | Area |
| Boundary domain | |
| Boundary normal | |
| m | Direct shape function boundary matrix |
| Direct shape function boundary matrix with normal | |
| Thermoelastic Robin Boundary matrix | |
Appendix A
References
- Kaul, M.K. Stochastic characterization of earthquakes through their response spectrum. Earthq. Eng. Struct. Dyn. 1978, 6, 497–509. [Google Scholar] [CrossRef]
- Atkinson, G.M.; Silva, W. An empirical study of earthquake source spectra for California earthquakes. Bull. Seismol. Soc. Am. 1997, 87, 97–113. [Google Scholar] [CrossRef]
- Cacciola, P. A stochastic approach for generating spectrum compatible fully nonstationary earthquakes. Comput. Struct. 2010, 88, 889–901. [Google Scholar] [CrossRef]
- Chen, J.; Wen, L.; Bi, C.; Liu, Z.; Liu, X.; Yin, L.; Zheng, W. Multifractal analysis of temporal and spatial characteristics of earthquakes in Eurasian seismic belt. Open Geosci. 2023, 15, 20220482. [Google Scholar] [CrossRef]
- Feng, S.; Tagawa, H.; Chen, X. Seismic performance of steel structures with seesaw-twisting system using cylindrical steel slit damper. Structures 2023, 58, 105422. [Google Scholar] [CrossRef]
- Hegeir, O.A.; Stamatopoulos, H. Experimental investigation on axially-loaded threaded rods inserted perpendicular to grain into cross laminated timber. Constr. Build. Mater. 2023, 408, 133740. [Google Scholar] [CrossRef]
- Kong, S.; Zhao, G.; Ma, Y.; Cai, X.; Yang, Z.; Liu, W.; Xie, L. A novel response-amplified shape memory alloy-based damper: Theory, experiment and numerical simulation. Soil Dyn. Earthq. Eng. 2024, 176, 108291. [Google Scholar] [CrossRef]
- Tian, L.; Li, M.; Li, L.; Li, D.; Bai, C. Novel joint for improving the collapse resistance of steel frame structures in column-loss scenarios. Thin-Walled Struct. 2023, 182, 110219. [Google Scholar] [CrossRef]
- Yao, Y.; Huang, H.; Zhang, W.; Ye, Y.; Xin, L.; Liu, Y. Seismic performance of steel-PEC spliced frame beam. J. Constr. Steel Res. 2022, 197, 107456. [Google Scholar] [CrossRef]
- Hu, G.; Ying, S.; Qi, H.; Yu, L.; Li, G. Design, analysis and optimization of a hybrid fluid flow magnetorheological damper based on multiphysics coupling model. Mech. Syst. Signal Process 2023, 205, 110877. [Google Scholar] [CrossRef]
- Yan, L.; Li, Y.; Chang, W.S.; Huang, H. Seismic control of cross laminated timber (CLT) structure with shape memory alloy-based semi-active tuned mass damper (SMA-STMD). Structures 2023, 57, 105093. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Li, C.; Cao, J. Optimum Arrangement of TADAS Dampers for Seismic Drift Control of Buildings Using Accelerated Iterative Methods. Buildings 2023, 13, 2720. [Google Scholar] [CrossRef]
- Lazan, B. Damping of Materials and Members in Structural Mechanics; Pergamon Press: Oxford, UK, 1968. [Google Scholar]
- Hickey, J.; Moore, H.; Broderick, B.; Fitzgerald, B. Structural damping estimation from live monitoring of a tall modular building. Struct. Des. Tall Spec. Build. 2023, e2067. [Google Scholar] [CrossRef]
- Mogi, Y.; Nakamura, N.; Nabeshima, K.; Ota, A. Performance of inherent damping models in inelastic seismic analysis for tall building subject to simultaneous horizontal and vertical seismic motion. Earthq. Eng. Struct. Dyn. 2023, 52, 3746–3764. [Google Scholar] [CrossRef]
- Nakamura, N. Practical causal hysteretic damping. Earthq. Eng. Struct. Dyn. 2007, 36, 597–617. [Google Scholar] [CrossRef]
- Caughey, T. Vibration of dynamic systems with linear hysteretic damping. Proc. Natl. Congr. Appl. Mech. 1962, 1, 87–97. [Google Scholar]
- Cortés, F.; Elejabarrieta, M.J. Forced response of a viscoelastically damped rod using the superposition of modal contribution functions. J. Sound Vib. 2008, 315, 58–64. [Google Scholar] [CrossRef]
- Maia, N.M.M.; Silva, J.M.M.; Ribeiro, A.M.R. On a General Model for Damping. J. Sound Vib. 1998, 5, 749–767. [Google Scholar] [CrossRef]
- Crandall, S. The role of damping in vibration theory. J. Sound Vib. 1970, 11, 3–18. [Google Scholar] [CrossRef]
- Crandall, S.H. A new hysteretic damping model? Mech. Res. Commun. 1995, 22, 201–202. [Google Scholar] [CrossRef]
- Gaul, L. The influence of damping on waves and vibrations. Mech. Syst. Signal Process 1999, 13, 1–30. [Google Scholar] [CrossRef]
- Gaul, L.; Bohlen, S.; Kempfle, S. Transient and forced oscillations of systems with constant hysteretic damping. Mech. Res. Commun. 1985, 12, 187–201. [Google Scholar] [CrossRef]
- de Veubeke, B.M.F. Influence of internal damping on aircraft resonance. Agard Man. Aeroelasticity 1960. [Google Scholar]
- Holm, S.; Näsholm, S.P. Comparison of fractional wave equations for power law attenuation in ultrasound elastography. Ultrasound Med. Biol. 2014, 40, 695–703. [Google Scholar] [CrossRef] [PubMed]
- Maia, N.M.M.; Silva, J.M.M.; Ribeiro, A.M.R.; Leitão, J.J.A.A. On the Possible Application of Fractional Derivatives to Modal Analysis. In Proceedings of the 1996 IMAC XIV—14th International Modal Analysis Conference, Dearborn, Michigan, 12–15 February 1996. [Google Scholar]
- Näsholm, S.P.; Holm, S. On a Fractional Zener Elastic Wave Equation. Fract. Calc. Appl. Anal. 2013, 16, 26–50. [Google Scholar] [CrossRef]
- Caputo, M. Linear Model of dissipation whose Q is almost frequency independent-II. Geophys. J. R. Astron. Soc. 1967, 135, 529–539. [Google Scholar] [CrossRef]
- Biot, M.A. Thermoelasticity and Irreversible Thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Boley, B.A.; Barber, A.D. Dynamic Response of Beams and Plates to Rapid Heating. J. Appl. Mech. 1957, 24, 413–416. [Google Scholar] [CrossRef]
- Serra, E.; Bonaldi, M. A finite element formulation for thermoelastic damping analysis. Int. J. Numer. Methods Eng. 2009, 78, 671–691. [Google Scholar] [CrossRef]
- Bishop, J.; Kinra, V. Thermoelastic Damping of a Laminated Beam in Flexure and Extension. J. Reinf. Plast. Compos. 1993, 12, 210–226. [Google Scholar] [CrossRef]
- Solomou, A.G.; Machairas, T.T.; Saravanos, D.A. A coupled thermomechanical beam finite element for the simulation of shape memory alloy actuators. J. Intell. Mater. Syst. Struct. 2014, 25, 890–907. [Google Scholar] [CrossRef]
- Kinra, V.K.; Milligan, K.B. A Second-Law Analysis of Thermoelastic Damping. J. Appl. Mech. 1994, 61, 71–76. [Google Scholar] [CrossRef]
- Carvalho, A. Study of the Influence of Convection Boundary Condition on the Damping Factor in a Thermoelastic Beam Using Solid Elements. In Proceedings of the 6th International Conference on Numerical and Symbolic Computation, Evora, Portugal, 30–31 March 2023; pp. 151–168. [Google Scholar]
- Kazemnia Kakhki, E.; Hosseini, S.M.; Tahani, M. An analytical solution for thermoelastic damping in a micro-beam based on generalized theory of thermoelasticity and modified couple stress theory. Appl. Math. Model. 2016, 40, 3164–3174. [Google Scholar] [CrossRef]
- Guo, F.; Wang, G.; Rogerson, G. Analysis of thermoelastic damping in micro- and nanomechanical resonators based on dual-phase-lagging generalized thermoelasticity theory. Int. J. Eng. Sci. 2012, 60, 59–65. [Google Scholar] [CrossRef]
- Guha, S.; Singh, A.K. Frequency shifts and thermoelastic damping in different types of Nano-/Micro-scale beams with sandiness and voids under three thermoelasticity theories. J. Sound Vib. 2021, 510, 116301. [Google Scholar] [CrossRef]
- Sun, Y.; Fang, D.; Soh, A.K. Thermoelastic damping in micro-beam resonators. Int. J. Solids Struct. 2006, 43, 3213–3229. [Google Scholar] [CrossRef]
- Parayil, D.V.; Kulkarni, S.S.; Pawaskar, D.N. Analytical and numerical solutions for thick beams with thermoelastic damping. Int. J. Mech. Sci. 2015, 94–95, 10–19. [Google Scholar] [CrossRef]
- Zuo, W.; Li, P.; Du, J.; Tse, Z.T.H. Thermoelastic damping in anisotropic piezoelectric microbeam resonators. Int. J. Heat Mass Transf. 2022, 199, 123493. [Google Scholar] [CrossRef]
- Resmi, R.; Suresh Babu, V.; Baiju, M. Thermoelastic Damping Limited Quality Factor Enhancement and Energy Dissipation Analysis of Rectangular Plate Resonators Using Nonclassical Elasticity Theory. Adv. Mater. Sci. Eng. 2022, 2022, 6759093. [Google Scholar] [CrossRef]
- Zener, C. Internal Friction in Solids. I. Theory of Internal Friction in Reeds. Phys. Rev. 1937, 52, 230–235. [Google Scholar] [CrossRef]
- Lifshitz, R.; Roukes, M.L. Thermoelastic damping in micro- and nanomechanical systems. Phys. Rev. B 2000, 61, 5600–5609. [Google Scholar] [CrossRef]
- Ashley, H. On passive damping mechanisms in large space structures. J. Spacecr. Rocket. 1984, 21, 448–455. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K.A. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- López Molina, J.A.; Rivera, M.J.; Berjano, E. Fourier, hyperbolic and relativistic heat transfer equations: A comparative analytical study. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20140547. [Google Scholar] [CrossRef]
- Quintanilla, R. Moore–Gibson–Thompson thermoelasticity. Math. Mech. Solids 2019, 24, 4020–4031. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Ersoy, H.; Civalek, Ö. Solution of Moore–Gibson–Thompson Equation of an Unbounded Medium with a Cylindrical Hole. Mathematics 2021, 9, 1536. [Google Scholar] [CrossRef]



| Dimension | Value |
|---|---|
| 6.6 | |
| 139.4 | |
| 102 | |
| 10.3 | |
| 102 | |
| 10.3 | |
| h | 160 |
| Property | Unit | Steel | Copper | Portland Cement Concrete |
|---|---|---|---|---|
| Young modulus | 200 | 120 | 34.5 | |
| Poisson coefficient | - | 0.3 | 0.355 | 0.2 |
| Density | 7800 | 8960 | 2400 | |
| Thermal expansion coefficient | ||||
| Conductivity | 45 | 401 | 0.5 | |
| Specific heat capacity | 470 | 385 | 880 |
| Property | Value |
|---|---|
| Young Modulus | |
| Poisson coefficient | 0.2 |
| Density | |
| Conductivity | |
| Specific heat capacity | |
| Thermal expansion coefficient |
| No. DoF | Rel. var. | Rel. var. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 3 | 3 | 6 | 3 | 4704 | 2376 | – | 378.15 | 5418 | – | 862.30 |
| 40 | 3 | 4 | 8 | 3 | 9184 | 2298 | 365.74 | 5172 | 823.15 | ||
| 60 | 3 | 6 | 10 | 3 | 17,568 | 2274 | 361.92 | 5106 | 812.65 | ||
| 80 | 3 | 8 | 13 | 3 | 29,808 | 2268 | 360.96 | 5076 | 807.87 | ||
| 100 | 3 | 10 | 15 | 3 | 43,632 | 2262 | 360.01 | 5058 | 805.01 | ||
| 120 | 3 | 12 | 18 | 3 | 60,016 | 2262 | 360.01 | 5046 | 803.10 | ||
| 140 | 3 | 14 | 20 | 3 | 78,960 | 2256 | 359.05 | 5040 | 802.14 | ||
| 160 | 3 | 16 | 23 | 3 | 103,040 | 2256 | 359.05 | 5034 | 801.19 | ||
| 180 | 3 | 18 | 25 | 3 | 127,424 | 2256 | 359.05 | 5034 | 801.19 | ||
| 200 | 3 | 20 | 28 | 3 | 154,368 | 2256 | 359.05 | 5028 | 800.23 | ||
| 220 | 3 | 22 | 31 | 3 | 190,944 | 2256 | 359.05 | 5028 | 800.23 | ||
| 240 | 3 | 24 | 33 | 3 | 219,792 | 2256 | 359.05 | 5028 | 800.23 |
| No. DoF | Rel. var. | Rel. var. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | 3 | 3 | 6 | 3 | 10 | 65,520 | 2022 | – | 321.81 | 4914 | – | 782.09 |
| 40 | 3 | 4 | 6 | 3 | 10 | 127,920 | 1974 | 314.17 | 4770 | 759.17 | ||
| 60 | 3 | 6 | 6 | 3 | 10 | 210,816 | 1962 | 312.26 | 4740 | 754.39 | ||
| 80 | 3 | 8 | 8 | 3 | 10 | 310,068 | 1962 | 312.26 | 4728 | 752.48 | ||
| 100 | 3 | 10 | 9 | 3 | 10 | 424,200 | 1956 | 311.31 | 4722 | 751.53 | ||
| 120 | 3 | 12 | 10 | 3 | 10 | 555,148 | 1956 | 311.31 | 4716 | 750.57 | ||
| 140 | 3 | 14 | 11 | 3 | 10 | 703,872 | 1954.59 | 311.08 | 4716.15 | 750.60 |
| ID | Section | Case Thickness | Length Ratio | No. Elements | Analysis | Material | Thermal BC |
|---|---|---|---|---|---|---|---|
| SI001 | I-beam | - | 10 H | 240 | Elastic | Steel | - |
| SI002 | I-beam | - | 10 H | 240 | Hysteretic | Steel | - |
| SI003 | I-beam | - | 10 H | 240 | Thermoelastic | Steel | Adiabatic |
| SI004 | I-beam | - | 10 H | 240 | Thermoelastic | Copper | Adiabatic |
| SI009 | Encased | 10 H | 140 | Elastic | Steel/Concrete | - | |
| SI012 | Encased | 10 H | 140 | Thermoelastic | Steel/Concrete | Adiabatic | |
| SI017 | Encased | 10 H | 140 | Thermoelastic | Steel/Concrete | Adiabatic | |
| SI018 | Encased | 10 H | 140 | Elastic | Volume mix | - | |
| SI019 | Encased | 10 H | 140 | Thermoelastic | Volume mix | Adiabatic |
| Frequency | Elastic Model | Hysteretic Model | Thermoelastic Model |
|---|---|---|---|
| First | |||
| Second |
| Case-Study | Frequency |
|---|---|
| Elastic Model (SI009) | 1954 |
| Thermoelastic Model (SI012) | 1957 |
| Elastic Model (Volume mix—SI018) | |
| Thermoelastic Model (Volume mix—SI019) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, A. Study of Damping of Bare and Encased Steel I-Beams Using the Thermoelastic Model. Buildings 2023, 13, 2964. https://doi.org/10.3390/buildings13122964
Carvalho A. Study of Damping of Bare and Encased Steel I-Beams Using the Thermoelastic Model. Buildings. 2023; 13(12):2964. https://doi.org/10.3390/buildings13122964
Chicago/Turabian StyleCarvalho, André. 2023. "Study of Damping of Bare and Encased Steel I-Beams Using the Thermoelastic Model" Buildings 13, no. 12: 2964. https://doi.org/10.3390/buildings13122964






