Wooden Beams Modal Damage Identification Parameters Based on Strain
Abstract
:1. Introduction
2. Theory of Damage Identification
2.1. The Strain Mode Vibration Pattern’s Derivation
2.2. Mutual Correspondence of Strain Modes with Displacement and Curvature Modes
2.3. Modal Differences by Strain
2.4. The Difference in Strain Mode Curvature
3. Simulations with Numbers
3.1. Simply Supported Wooden Beam Modeling
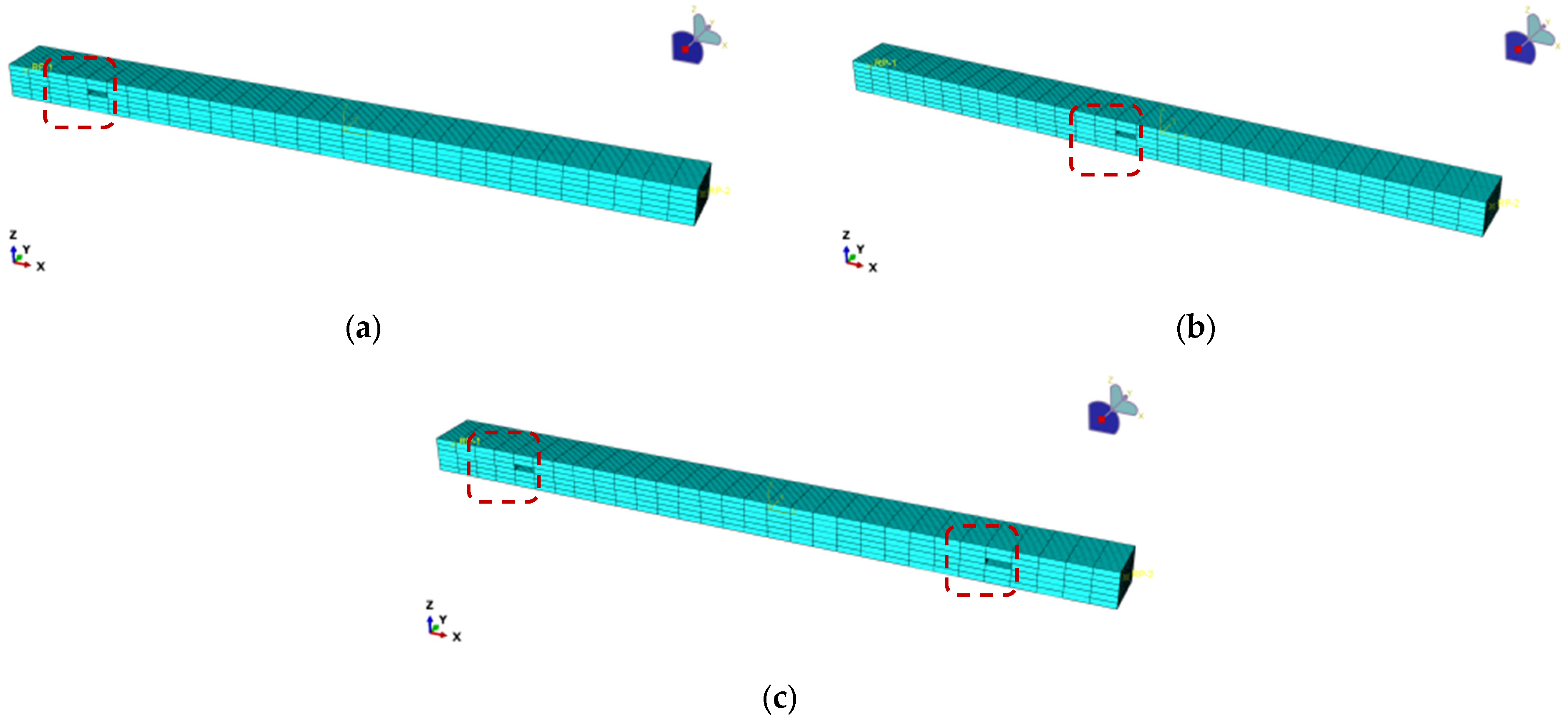
3.2. Damage Condition
3.3. Analysis of Modes
3.3.1. Modal Frequency
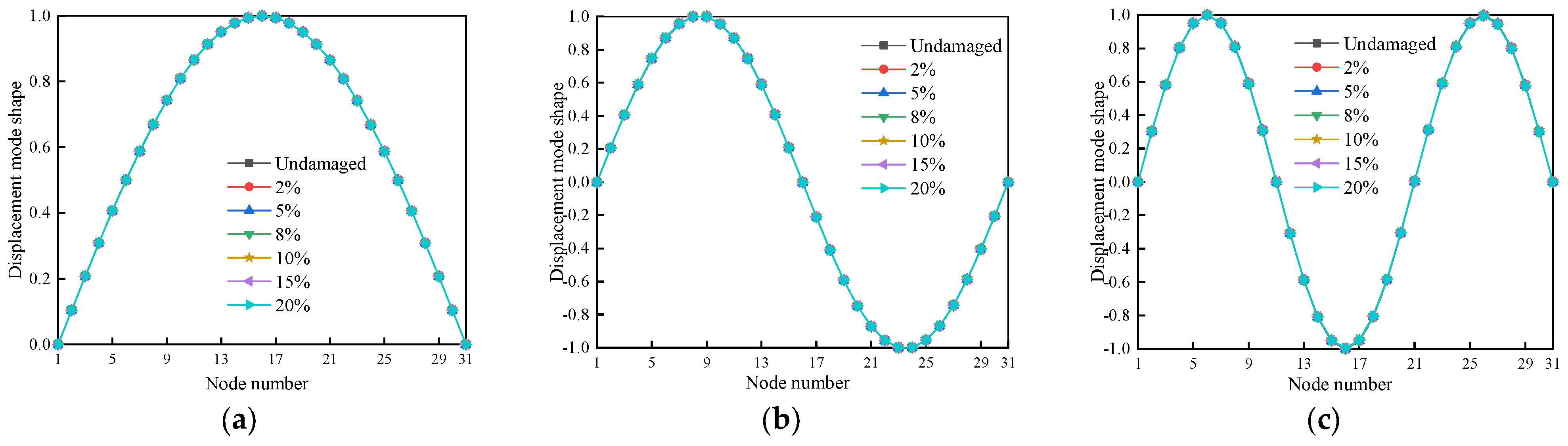
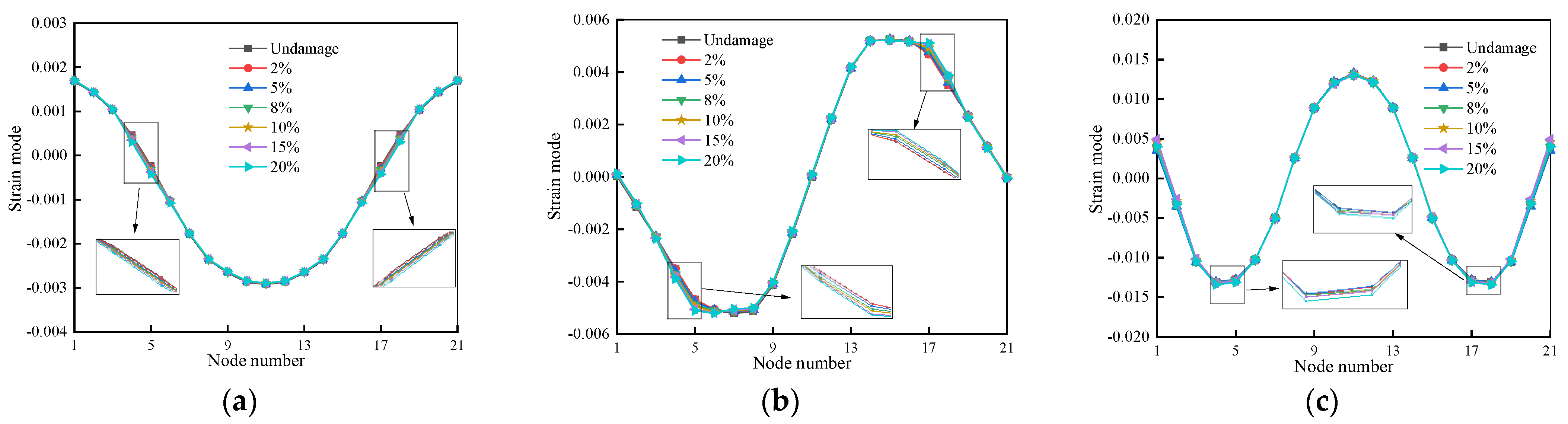
3.3.2. Displacement Mode Shapes
3.4. Identification of Damage Using Strain Modal Parameters
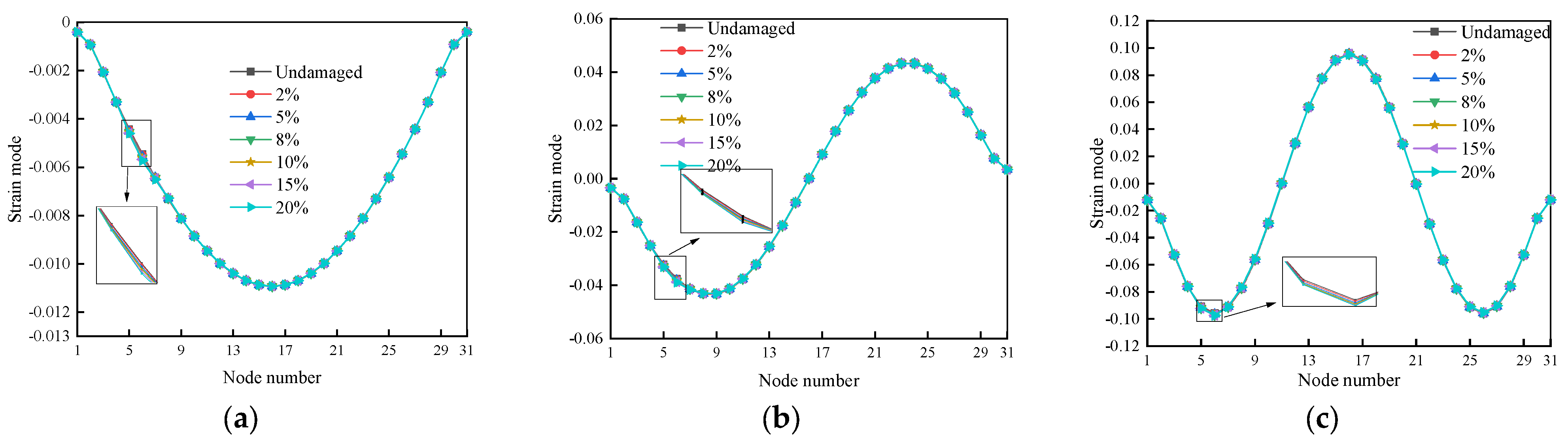
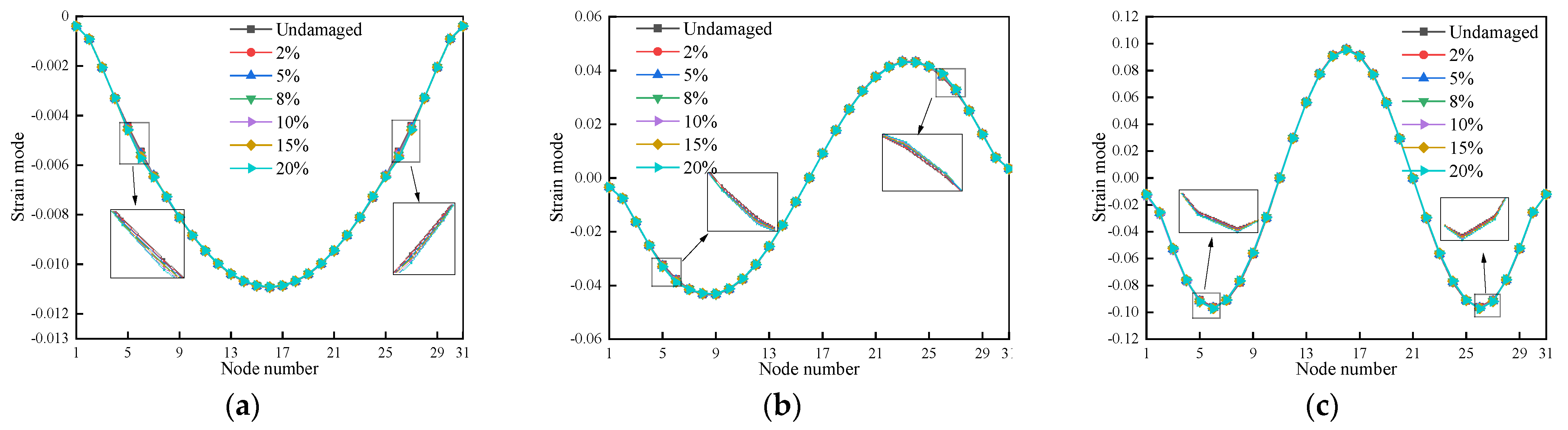
3.4.1. Modal Damage Identification Metrics Based on Strain
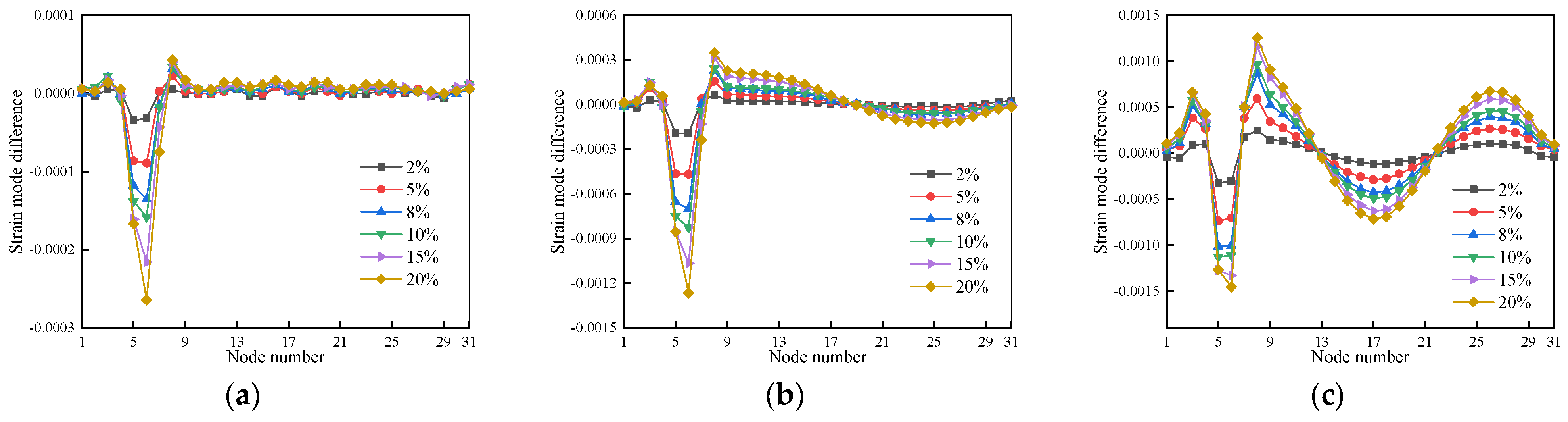
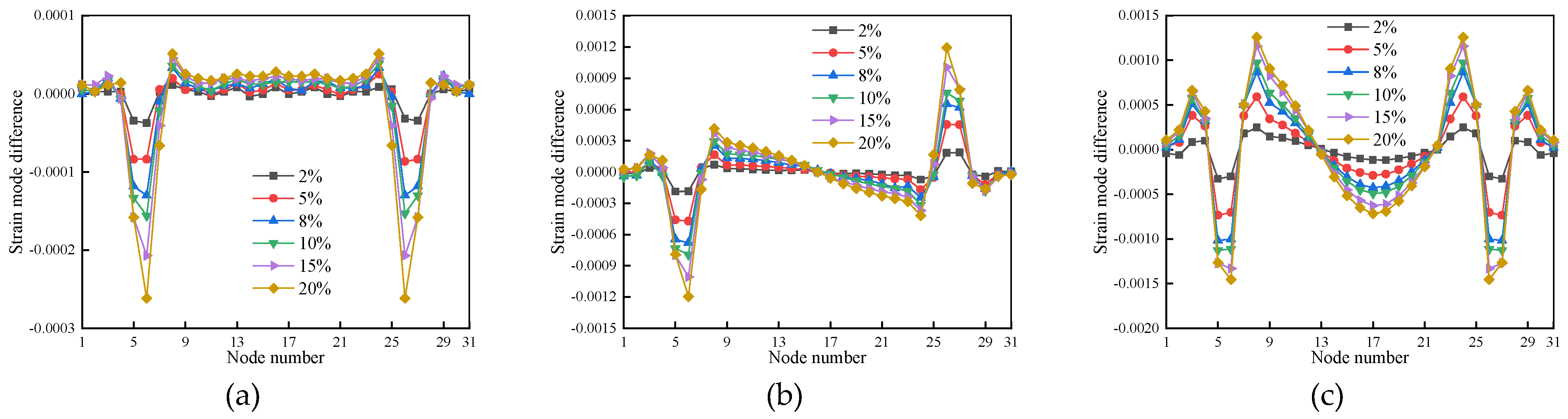
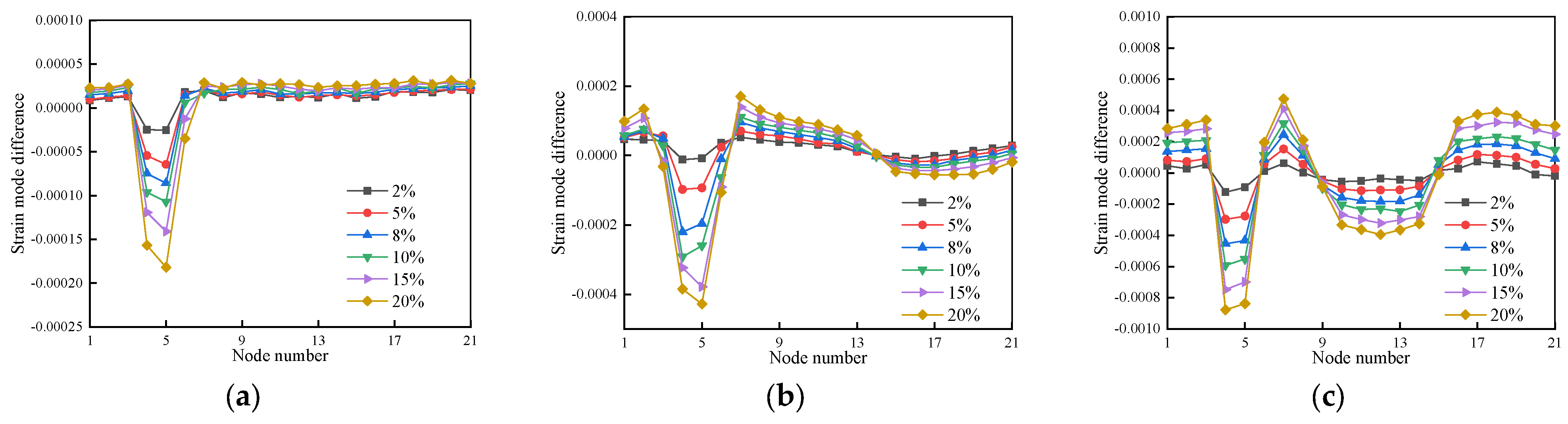
3.4.2. Strain Modal Difference Damage Recognition Indicator-Based
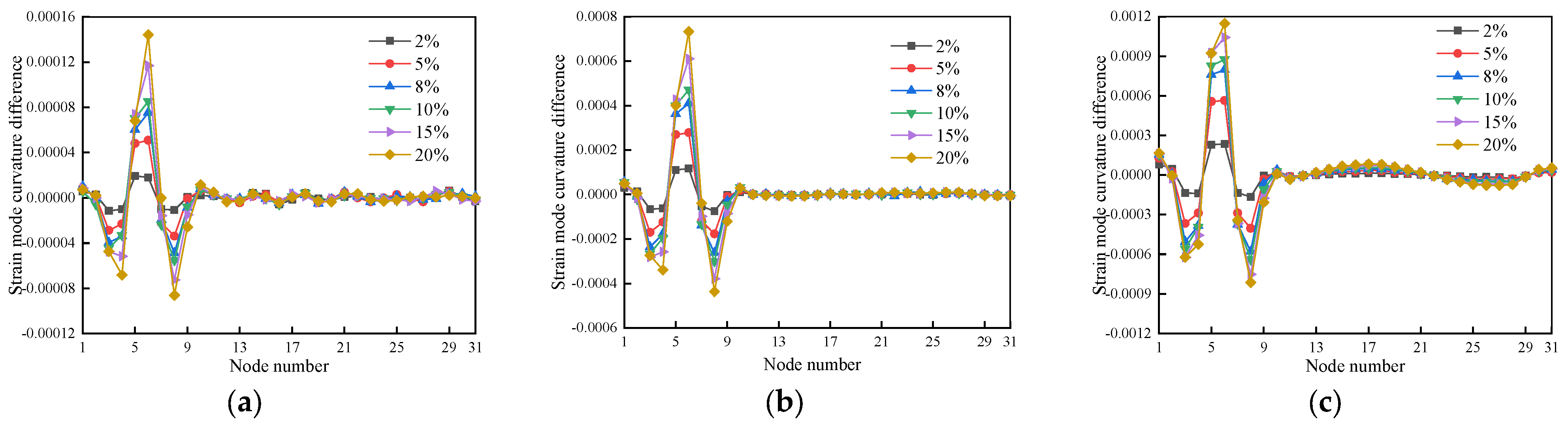
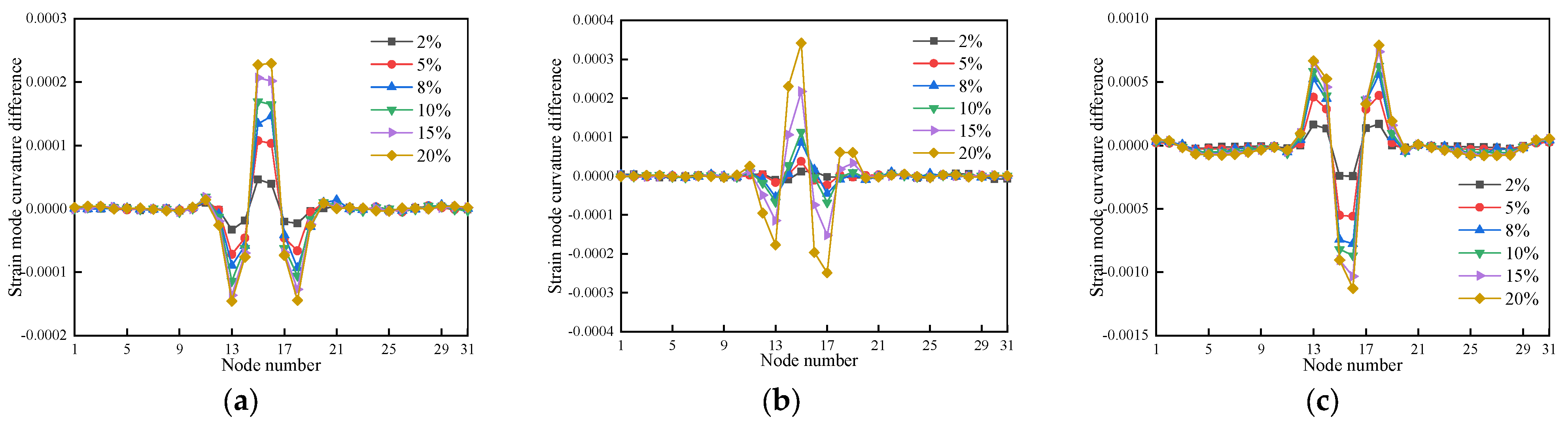
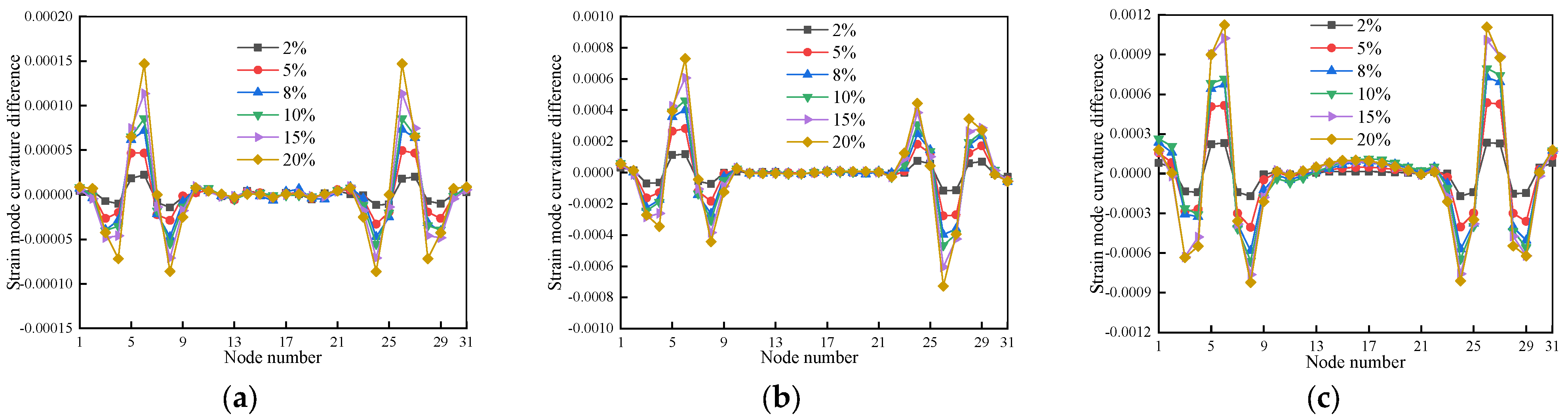
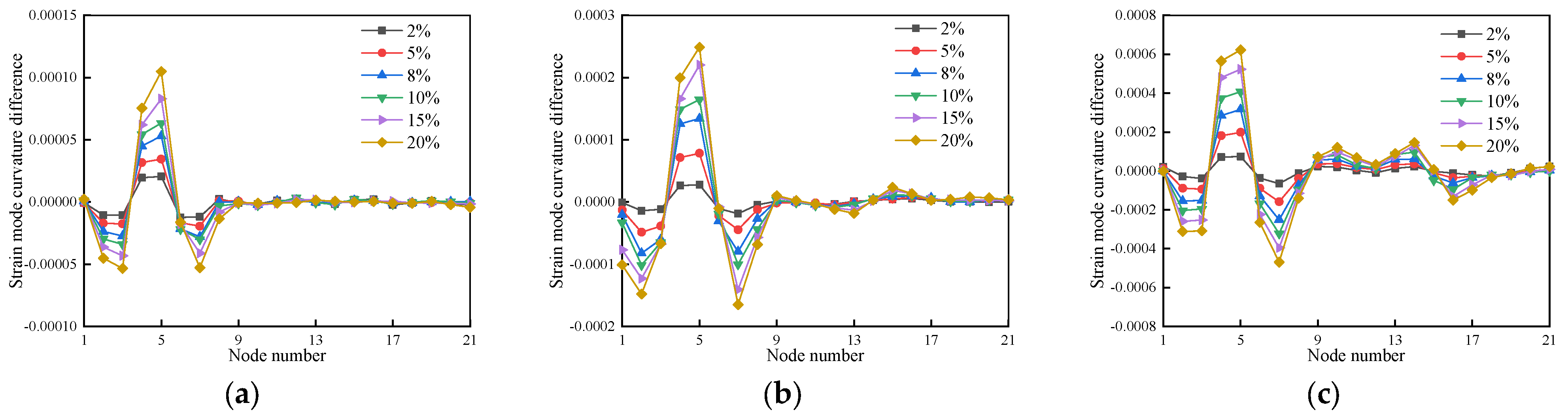
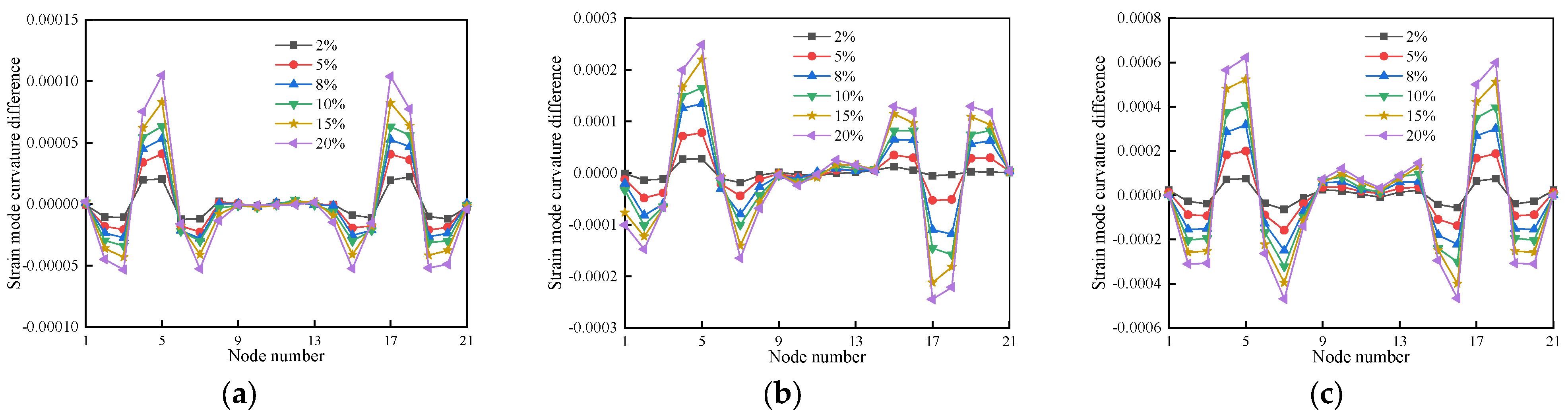
3.4.3. Strain Modal Curvature Difference Damage Recognition Indicator-Based
4. Experimental Validation
4.1. Experimental Program Design
4.2. Analysis of Test Results
4.3. Identification of Damage Using Strain Modal Parameters
4.3.1. Modal Damage Identification Metrics Based on Strain
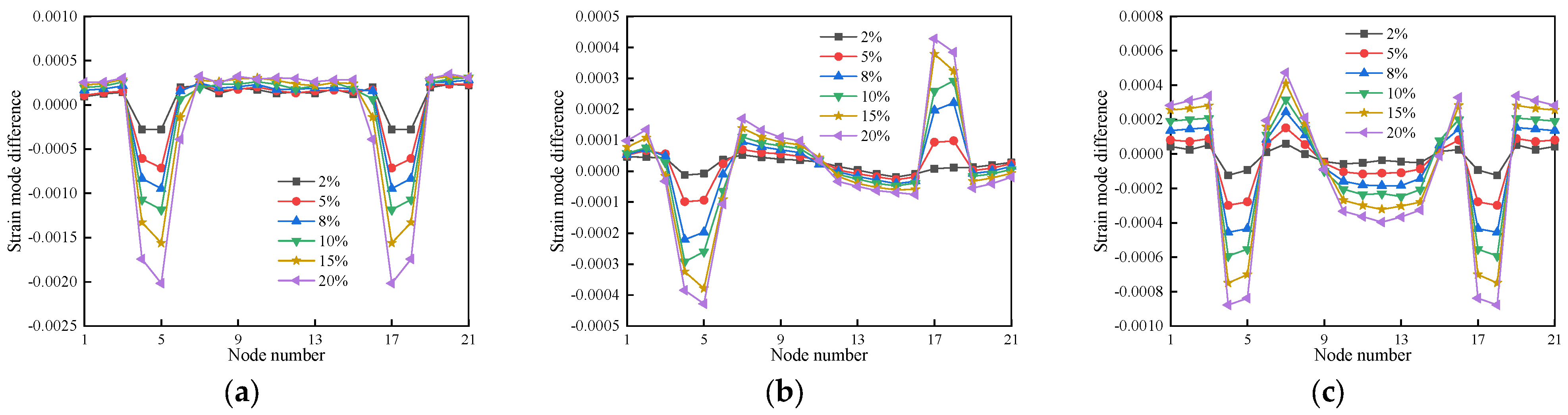
4.3.2. Strain Modal Difference Damage Recognition Indicator-Based
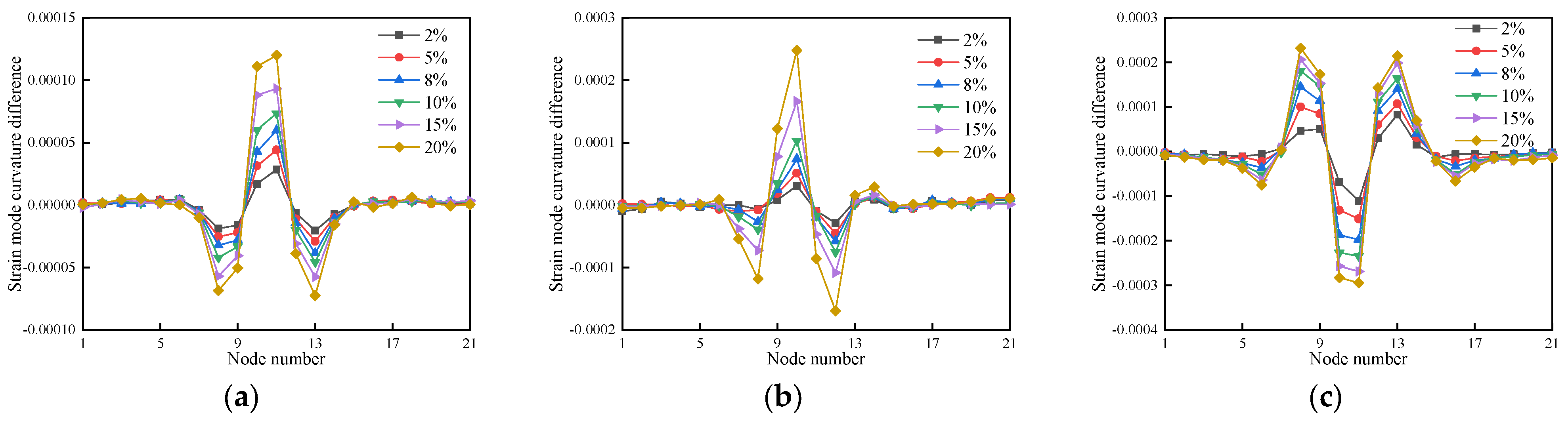
4.3.3. Strain Modal Curvature Difference Damage Recognition Indicator-Based
5. Conclusions
- We find that the relative error between the measured and simulated intrinsic frequencies is less than 8% by comparing the modal analysis results of the test and numerical simulation of wooden beams under various working conditions. This confirms that the simulated wooden beam model can more accurately reflect the modal parameters of the actual wooden beams and provides a basis for the structural damage analysis that follows.
- The results of the numerical simulation agree with the findings of the three damage identification indexes on the damage localization identification of the test data. The preliminary evidence for the viability and validity of the damage identification indexes based on the strain mode, strain mode difference, and strain mode curvature difference on the damage localization identification of the timber beams is provided by the identification effect of the three damage identification indexes, which is strain mode curvature difference > strain mode difference > strain mode.
- By slotting on wooden beams, this specimen simulates damage that differs from the real condition, such as fractures, decay, insect infestation, etc. More study is required to adjust the findings of the current studies to reflect the real circumstances.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Du, X.; Qi, X. Strain prediction for historical timber buildings with a hybrid prophet-XGBoost model. Mech. Syst. Signal. Process. 2022, 179, 109316. [Google Scholar] [CrossRef]
- Li, D.; Wang, J.; Shi, K. Research on the investigation and value evaluation of historic building resources in Xi’an city. Buildings 2023, 13, 2244. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, Y.P.; Guo, W.J. Features and prevention of common damages in ancient timber structures. Chin. J. Wood Sci. Technol. 2021, 35, 54–59. [Google Scholar] [CrossRef]
- Wu, C.W.; Xue, J.Y.; Zhou, S.Q.; Zhang, F.L. Seismic performance evaluation for a traditional chinese timber-frame structure. Int. J. Archit. Herit. 2020, 15, 1842–1856. [Google Scholar] [CrossRef]
- Qin, S.J.; Yang, N.; Cao, B.Z.; Dong, J.S. Damage analysis and protection of timber structure of tongdao hall in the imperial palace. J. Civ. Environ. Eng. 2022, 44, 119–128. [Google Scholar] [CrossRef]
- Wang, X.; Meng, Z.B.; Zhang, X.C. Study on the damage diagnosis of ancient wood structure in tianshui under traffic excitation. Adv. Civ. Eng. 2022, 1, 1040926. [Google Scholar] [CrossRef]
- Zielińska, M.; Rucka, M. Assessment of wooden beams from historical buildings using ultrasonic transmission tomography. Int. J. Archit. Herit. 2023, 17, 249–261. [Google Scholar] [CrossRef]
- Hacıefendioğlu, K.; Ayas, S.; Başağa, H.B.; Toğan, V.; Mostofi, F.; Can, A. Wood construction damage detection and localization using deep convolutional neural network with transfer learning. Eur. J. Wood. Prod. 2022, 80, 791–804. [Google Scholar] [CrossRef]
- Kai-Uwe, D.; Dirk, S. Adaptive modeling of reliability properties for control and supervision purposes. Int. J. Appl. Math. Comput. Sci. 2011, 21, 479–486. [Google Scholar] [CrossRef]
- Xiong, H.B.; Long, Y.W.; Chen, L.; Ding, Y.W. Review on research and application of nondestructive testing technology for timber structures. Struct. Eng. 2023, 39, 191–201. [Google Scholar] [CrossRef]
- Hou, R.R.; Xia, Y. Review on the new development of vibration-based damage identification for civil engineering structures: 2010–2019. J. Sound Vib. 2021, 491, 115741. [Google Scholar] [CrossRef]
- Li, H.N.; Gao, D.W.; Yi, Y.H. Advances in structural health monitoring systems in civil engineering. Adv. Mech. 2008, 38, 151–166. [Google Scholar] [CrossRef]
- Chinka, S.S.B.; Putti, S.R.; Adavi, B.K. Modal testing and evaluation of cracks on cantilever beam using mode shape curvatures and natural frequencies. Structures 2021, 32, 1386–1397. [Google Scholar] [CrossRef]
- Zhou, H.P.; Bo, H.E.; Chen, X.Q. Detection of structural damage through changes in frequency. J. Nat. Sci. Wuhan Univ. 2005, 10, 1069–1073. [Google Scholar] [CrossRef]
- Huynh, D.; He, J.; Tran, D. Damage location vector: A non-destructive structural damage detection technique. Comput. Struct. 2005, 83, 2353–2367. [Google Scholar] [CrossRef]
- Meng, Z.B.; Ren, X.C.; Chai, S.Q.; Wang, X.; Zhao, T.F.; Gao, F.F.; Wang, S.; Liu, Y. Wood beam damage identification based on the curvature mode and wavelet transform. Adv. Civ. Eng. 2023, 1, 2238021. [Google Scholar] [CrossRef]
- Pandey, A.K.; Biswas, M.; Samman, M.M. Damage detection from changes in curvature mode shapes. J. Sound Vib. 1991, 145, 321–332. [Google Scholar] [CrossRef]
- He, M.H.; Yang, T.; Du, Y. Nondestructive identification of composite beams damage based on the curvature mode difference. Compos. Struct. 2017, 176, 178–186. [Google Scholar] [CrossRef]
- Xiang, C.S.; Li, L.Y.; Zhou, Y.; Yuan, Z. Damage identification method of beam structure based on modal curvature utility information entropy. Adv. Civ. Eng. 2020, 2020, 8892686. [Google Scholar] [CrossRef]
- Dawari, V.B.; Vesmawala, G.R. Modal curvature and modal flexibility methods for honeycomb damage identification in reinforced concrete beams. Procedia Eng. 2013, 51, 119–124. [Google Scholar] [CrossRef]
- Yao, G.C.; Chang, K.C.; Lee, G.C. Damage diagnosis of steel frames using vibrational signature analysis. J. Eng. Mech. 1992, 118, 1949–1961. [Google Scholar] [CrossRef]
- Xu, Z.D.; Zeng, X.; Li, S. Damage detection strategy using strain-mode residual trends for long-span bridges. J. Comput. Civil. Eng. 2015, 29, 04014064. [Google Scholar] [CrossRef]
- Wang, T.; Celik, O.; Catbas, F.N. Damage detection of a bridge model based on operational dynamic strain measurements. Adv. Struct. Eng. 2016, 19, 1379–1389. [Google Scholar] [CrossRef]
- Cui, H.Y.; Xu, X.; Peng, W.Q.; Zhou, Z.H.; Hong, M. A damage detection method based on strain modes for structures under ambient excitation. Measurement 2018, 125, 438–446. [Google Scholar] [CrossRef]
- Li, Z.X.; Chan, T.H.T.; Zhang, R. Statistical analysis of online strain response and its application in fatigue assessment of a long-span steel bridge. Eng. Struct. 2003, 25, 1731–1741. [Google Scholar] [CrossRef]
- Li, Z.X.; Chan, T.H.T.; Ko, J.M. Fatigue analysis and life prediction of bridges with structural health monitoring data—Part I: Methodology and strategy. Int. J. Fatigue 2001, 23, 45–53. [Google Scholar] [CrossRef]
- Chan, T.H.T.; Li, Z.X.; Ko, J.M. Fatigue analysis and life prediction of bridges with structural health monitoring data—Part II: Application. Int. J. Fatigue 2001, 23, 55–64. [Google Scholar] [CrossRef]
- Zhang, X.D.; Liang, Q.H. A study on crack and motor-void identification of ballastless track slab using strain modal. J. Vib. Shock. 2020, 39, 179–184. [Google Scholar] [CrossRef]
- Li, L.J.; Han, J.; Li, D. Crack detection for the cantilever beam based on the difference of the strain mode. Sci. Tech. Eng. 2018, 18, 81–86. [Google Scholar] [CrossRef]
- Zhang, H.; Shi, F.Q. Research on damage identification method of continuous beams based on strain mode difference and application. J. Zhejiang Univ. Tech. 2019, 47, 280–285. [Google Scholar]
- Chen, J.; Yu, S.; Wei, W.; Ma, Y. Matrix-based method for solving decision domains of neighbourhood multigranulation decision-theoretic rough sets. CAAI Trans. Intell. Technol. 2022, 7, 313–327. [Google Scholar] [CrossRef]
- Hu, X.; Kuang, Q.; Cai, Q.; Xue, Y.; Zhou, W.; Li, Y. A coherent pattern mining algorithm based on all contiguous column bicluster. J. Artif. Intell. Technol. 2022, 2, 80–92. [Google Scholar] [CrossRef]
- Du, H.; Du, S.; Li, W. Probabilistic time series forecasting with deep non-linear state space models. CAAI Trans. Intell. Technol. 2023, 8, 3–13. [Google Scholar] [CrossRef]
- Zhang, Z.; Luca, G.D.; Archambault, B.; Mchavez, J.; Rice, A.B. Traffic dataset and dynamic routing algorithm in traffic simulation. J. Artif. Intell. Technol. 2022, 2, 111–122. [Google Scholar] [CrossRef]
- Zhao, H.; Ma, L. Several rough set models in quotient space. CAAI Trans. Intell. Technol. 2022, 7, 69–80. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, W.; Zhang, J.; Li, H. Contact high-temperature strain automatic calibration and precision compensation research. J. Artif. Intell. Technol. 2022, 2, 69–76. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to machine learning and deep learning applications. Mech. Syst. Signal. Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Nguyen, T.Q. Damage detection in beam structures using bayesian deep learning and balancing composite motion optimization. Structures 2022, 39, 98–114. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Kiani, K. Nonlocal-integro-surface energy-vibro analysis of twist in coaxially composite wire-like nanostructures with internal and interfacial defects via a meshless technique. Eng. Anal. Bound. Elem. 2022, 135, 217–232. [Google Scholar] [CrossRef]
- Kiani, K.; Żur, K.K. Vibrations of double-nanorod-systems with defects using nonlocal-integral-surface energy-based formulations. Compos. Struct. 2020, 256, 113028. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, K.; Kiani, K. Torsional vibration of nonprismatically nonhomogeneous nanowires with multiple defects: Surface energy-nonlocal-integro-based formulations. Appl. Math. Model. 2020, 82, 17–44. [Google Scholar] [CrossRef]
- Kiani, K.; Żur, K.K. Dynamic behavior of magnetically affected rod-like nanostructures with multiple defects via nonlocal-integral/differential-based models. Nanomaterials 2020, 10, 2306. [Google Scholar] [CrossRef]
- Simsek, M.; Kocatürk, T. Free and forced vibration of a functionally graded beam subjected to a concentrated moving harmonic load. Compos. Struct. 2009, 90, 465–473. [Google Scholar] [CrossRef]
- Han, H.F.; Zhou, S.P.; Hao, Z.F.; Zhang, L.Z. Study on identification of pipe damage based on strain modal difference. J. Vib. Measurem. Diagn. 2013, 33 (Suppl. S1), 210–213 + 232. [Google Scholar] [CrossRef]
- Cui, H.Y.; Peng, W.Q.; Xu, X.; Hong, M. A damage identification method for a thin plate structure based on PVDF sensors and strain mode. Proc. Inst. Mech. Eng. J. Mech. Eng. Sci. 2019, 233, 4881–4895. [Google Scholar] [CrossRef]
- Yam, L.Y.; Leung, T.P.; Li, D.B.; Xue, K.Z. Theoretical and experimental study of modal strain analysis. J. Sound Vib. 1996, 191, 251–260. [Google Scholar] [CrossRef]
- Wu, J.Q.; Li, H.Y.; Ye, F.; Ma, K. Damage identification of bridge structure based on frequency domain decomposition and strain mode. J. Vibroeng. 2019, 21, 2096–2105. [Google Scholar] [CrossRef]












| Elastic Modulus [MPa] | Poisson’s Ratio | Modulus of Shear [MPa] | Densities [kg/m3] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| EL | ER | ET | μLR | μLT | μRT | GLR | GLT | GRT | 508 |
| 9752.17 | 2058.57 | 452.90 | 0.490 | 0.410 | 0.353 | 585.13 | 731.41 | 175.54 | |
| Status Number | Injury Types | Damage Unit | Damage Depth [mm] | Damage Degree |
|---|---|---|---|---|
| Case 0 | - | - | - | - |
| Case 1 | single damage | 5 | 3.6 | 2% |
| Case 2 | 5 | 9 | 5% | |
| Case 3 | 5 | 14.4 | 8% | |
| Case 4 | 5 | 18 | 10% | |
| Case 5 | 5 | 27 | 15% | |
| Case 6 | 5 | 36 | 20% | |
| Case 7 | 15 | 3.6 | 2% | |
| Case 8 | 15 | 9 | 5% | |
| Case 9 | 15 | 14.4 | 8% | |
| Case 10 | 15 | 18 | 10% | |
| Case 11 | 15 | 27 | 15% | |
| Case 12 | 15 | 36 | 20% | |
| Case 13 | two damages | 5, 26 | 3.6 | 2% |
| Case 14 | 5, 26 | 9 | 5% | |
| Case 15 | 5, 26 | 14.4 | 8% | |
| Case 16 | 5, 26 | 18 | 10% | |
| Case 17 | 5, 26 | 27 | 15% | |
| Case 18 | 5, 26 | 36 | 20% |
| Working Condition | 1st Order | 2nd Order | 3rd Order | |||
|---|---|---|---|---|---|---|
| Frequency [Hz] | The Absolute Difference in Value | Frequency [Hz] | The Absolute Difference in Value | Frequency [Hz] | The Absolute Difference in Value | |
| 0 | 57.79 | - | 206.34 | - | 401.82 | - |
| 1 | 57.79 | 0.00 | 206.31 | 0.03 | 401.71 | 0.11 |
| 2 | 57.78 | 0.01 | 206.27 | 0.07 | 401.65 | 0.17 |
| 3 | 57.78 | 0.01 | 206.22 | 0.12 | 401.55 | 0.27 |
| 4 | 57.77 | 0.02 | 206.20 | 0.14 | 401.51 | 0.31 |
| 5 | 57.77 | 0.02 | 206.15 | 0.19 | 401.43 | 0.39 |
| 6 | 57.76 | 0.03 | 206.12 | 0.22 | 401.60 | 0.22 |
| 7 | 57.77 | 0.02 | 206.34 | 0.00 | 401.73 | 0.09 |
| 8 | 57.75 | 0.04 | 206.34 | 0.00 | 401.65 | 0.17 |
| 9 | 57.72 | 0.07 | 206.34 | 0.00 | 401.55 | 0.27 |
| 10 | 57.71 | 0.08 | 206.34 | 0.00 | 401.51 | 0.31 |
| 11 | 57.68 | 0.11 | 206.33 | 0.01 | 401.44 | 0.38 |
| 12 | 57.66 | 0.13 | 206.32 | 0.02 | 401.41 | 0.41 |
| 13 | 57.78 | 0.01 | 206.28 | 0.06 | 401.64 | 0.18 |
| 14 | 57.77 | 0.02 | 206.18 | 0.16 | 401.34 | 0.48 |
| 15 | 57.76 | 0.03 | 206.06 | 0.28 | 400.90 | 0.92 |
| 16 | 57.75 | 0.04 | 205.98 | 0.36 | 400.60 | 1.22 |
| 17 | 57.74 | 0.05 | 205.96 | 0.38 | 401.05 | 0.77 |
| 18 | 57.74 | 0.05 | 205.90 | 0.44 | 400.99 | 0.83 |
| Status Number | Injury Types | Damage Unit | Damage Depth [mm] | Damage Degree |
|---|---|---|---|---|
| Case 0 | - | - | - | - |
| Case 1 | single damage | 4 | 3.6 | 2% |
| Case 2 | 4 | 9 | 5% | |
| Case 3 | 4 | 14.4 | 8% | |
| Case 4 | 4 | 18 | 10% | |
| Case 5 | 4 | 27 | 15% | |
| Case 6 | 4 | 36 | 20% | |
| Case 7 | 10 | 3.6 | 2% | |
| Case 8 | 10 | 9 | 5% | |
| Case 9 | 10 | 14.4 | 8% | |
| Case 10 | 10 | 18 | 10% | |
| Case 11 | 10 | 27 | 15% | |
| Case 12 | 10 | 36 | 20% | |
| Case 13 | two damages | 4, 17 | 3.6 | 2% |
| Case 14 | 4, 17 | 9 | 5% | |
| Case 15 | 4, 17 | 14.4 | 8% | |
| Case 16 | 4, 17 | 18 | 10% | |
| Case 17 | 4, 17 | 27 | 15% | |
| Case 18 | 4, 17 | 36 | 20% |
| Device Name | Model of the Device | Manufacturer | City | Country of Origin |
|---|---|---|---|---|
| Acceleration sensors | INV9822 | China Orient Institute of Noise & Vibration | Beijing | China |
| IEPE Hammer | INV9312 | |||
| Acquisition instrument | INV3065N2 |
| Mode Number | Calculated with the Finite Element Method (Hz) | Obtained from Experimentally Observed Data (Hz) | Error (%) |
|---|---|---|---|
| 1 | 57.79 | 59.89 | 3.51 |
| 2 | 206.34 | 201.32 | 2.49 |
| 3 | 401.82 | 372.9 | 7.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Meng, Z.; Gao, F.; Zhang, L.; Ren, X.; Jiang, H.; Hu, R. Wooden Beams Modal Damage Identification Parameters Based on Strain. Buildings 2023, 13, 3035. https://doi.org/10.3390/buildings13123035
Cao Y, Meng Z, Gao F, Zhang L, Ren X, Jiang H, Hu R. Wooden Beams Modal Damage Identification Parameters Based on Strain. Buildings. 2023; 13(12):3035. https://doi.org/10.3390/buildings13123035
Chicago/Turabian StyleCao, Yu, Zhaobo Meng, Feifei Gao, Liwei Zhang, Xiancai Ren, Huanzhi Jiang, and Rong Hu. 2023. "Wooden Beams Modal Damage Identification Parameters Based on Strain" Buildings 13, no. 12: 3035. https://doi.org/10.3390/buildings13123035
APA StyleCao, Y., Meng, Z., Gao, F., Zhang, L., Ren, X., Jiang, H., & Hu, R. (2023). Wooden Beams Modal Damage Identification Parameters Based on Strain. Buildings, 13(12), 3035. https://doi.org/10.3390/buildings13123035





