The Influence of Composition Ratio on the Thermal Performance Parameters of Eutectic Phase Change Materials: Experimental Research and Theoretical Prediction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Raw Materials
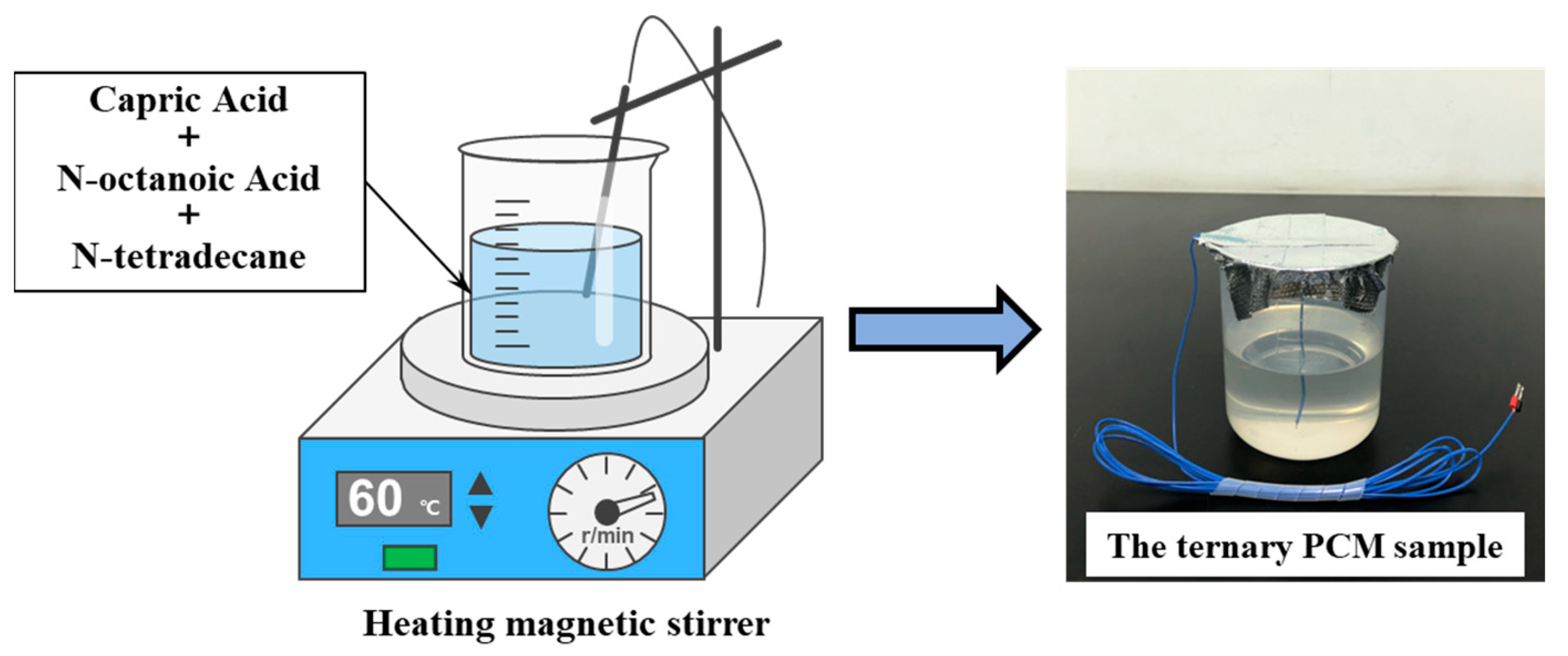
2.2. Preparation of EPCMs
2.2.1. Mix Proportions of EPCMs
2.2.2. Preparation Methods of EPCMs
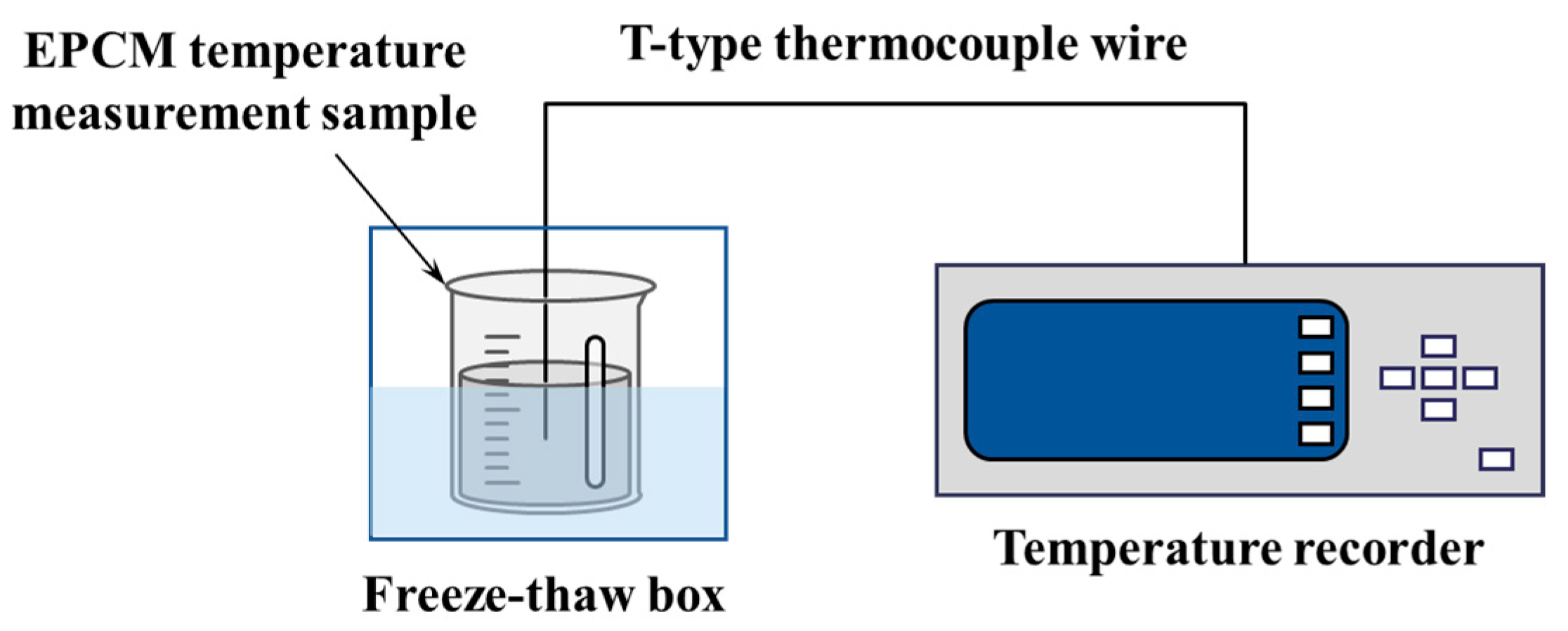
2.3. Experimental Methods
2.3.1. Cooling Curve Test
2.3.2. DSC Analysis
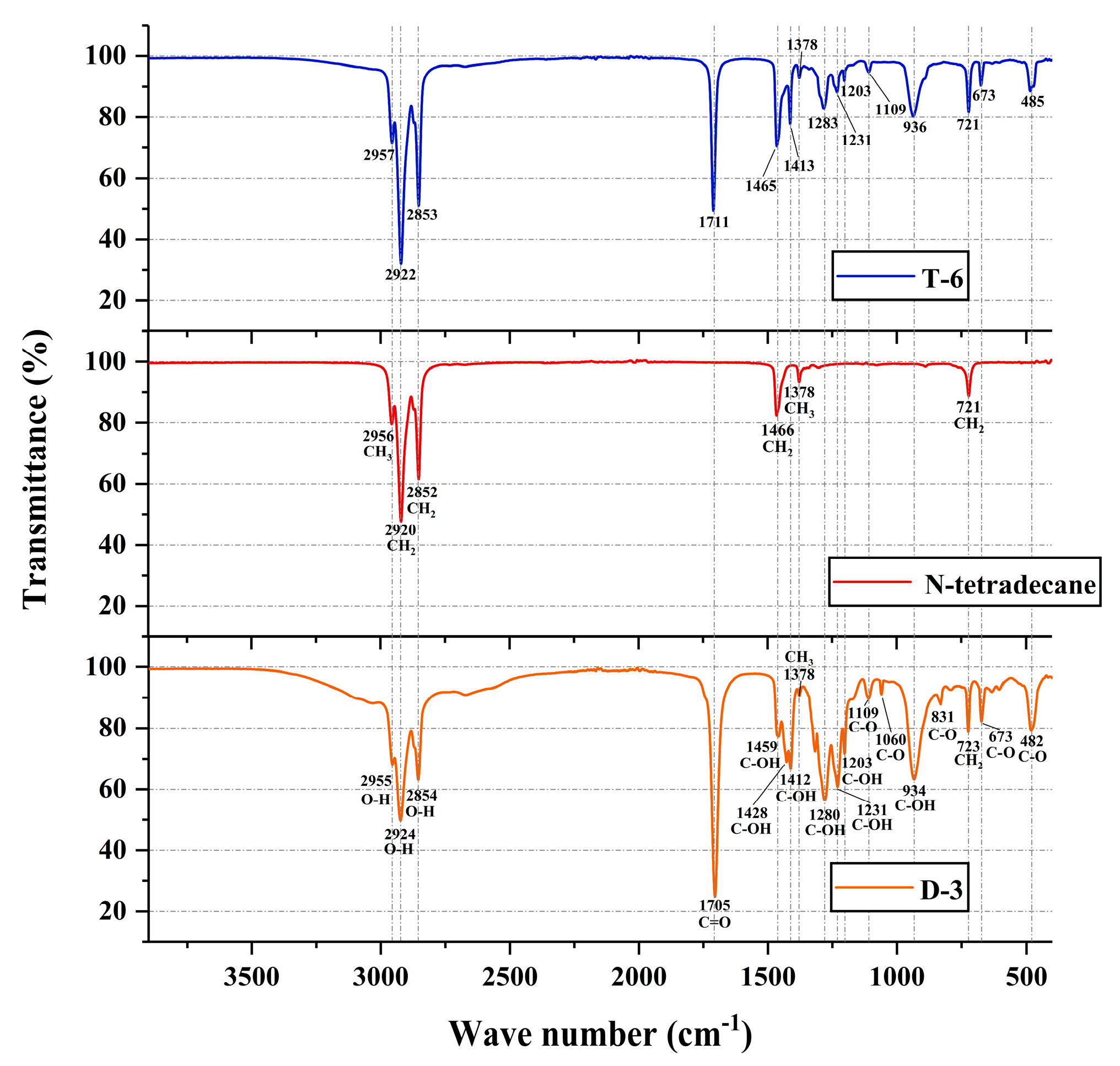
2.3.3. FTIR Analysis
2.3.4. Thermodynamic Model
- (1)
- Wilson Model
- (2)
- NRTL Model
- (3)
- UNIQUAC Model
- (4)
- Ideal Schrader Model
3. Results and Discussion
3.1. Thermal Properties of Binary PCM
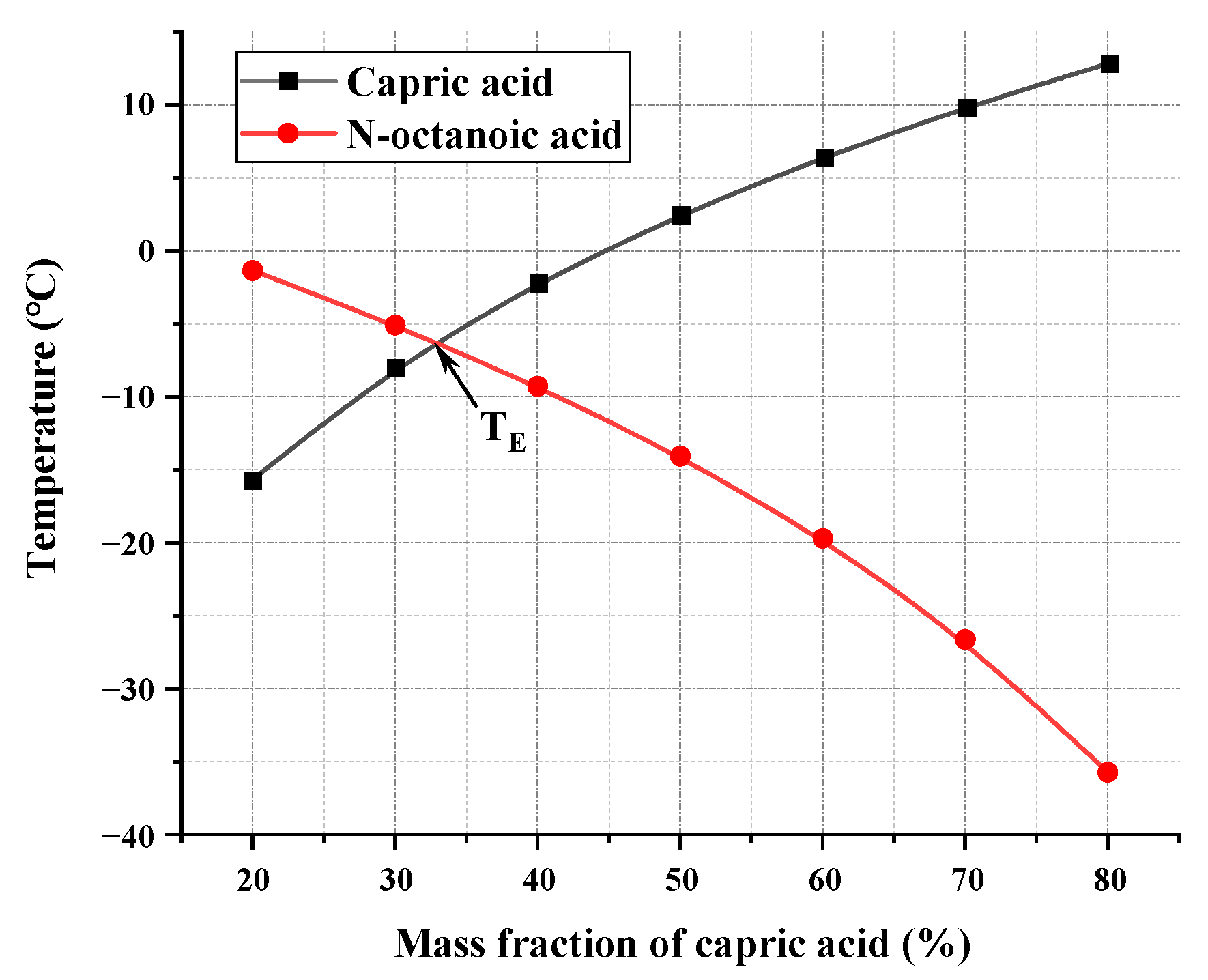
3.1.1. Cooling Curve Test
3.1.2. DSC Analysis
3.1.3. Thermodynamic Model Analysis
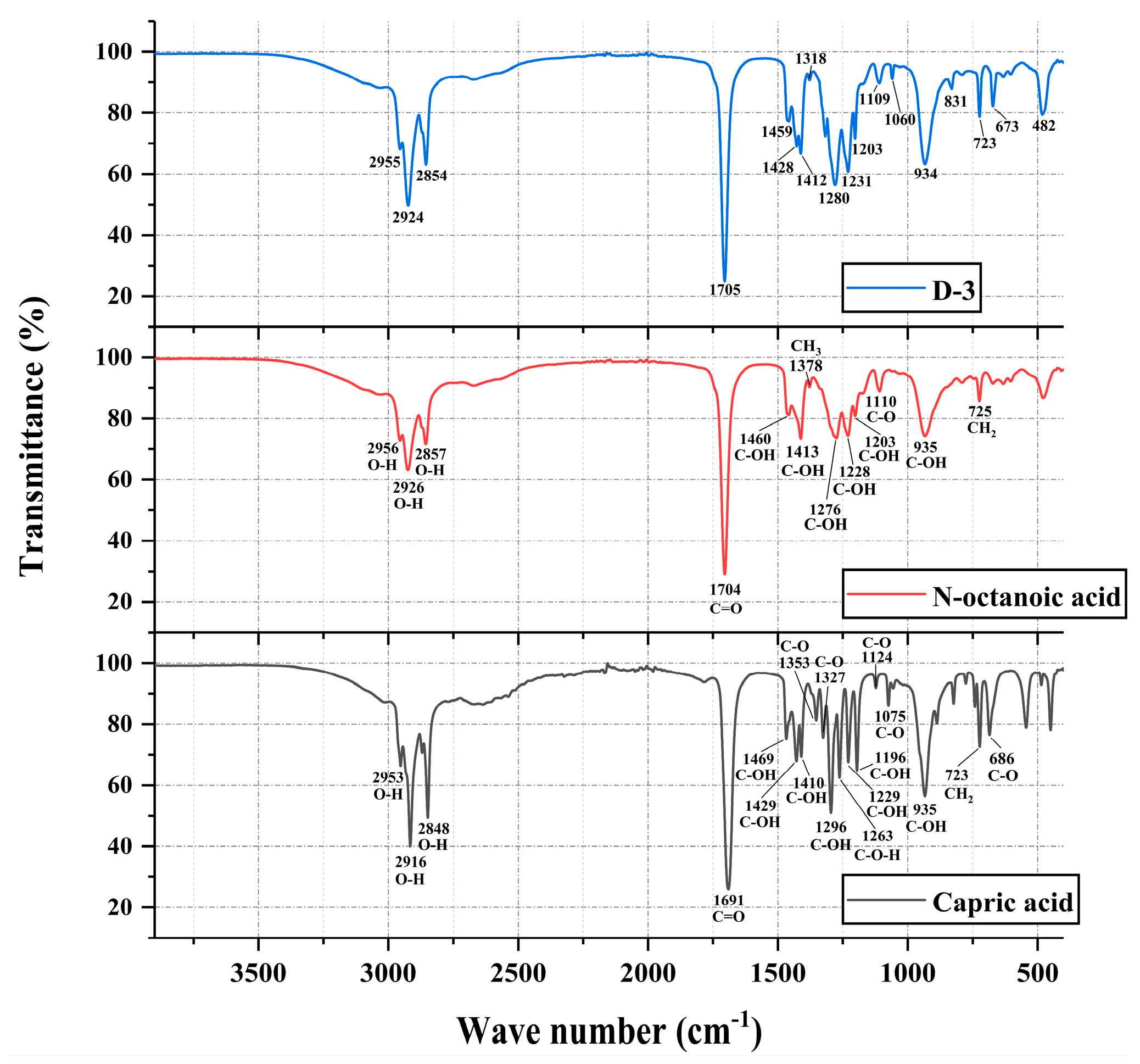
3.1.4. FTIR Analysis
3.2. Thermal Properties of Ternary PCM
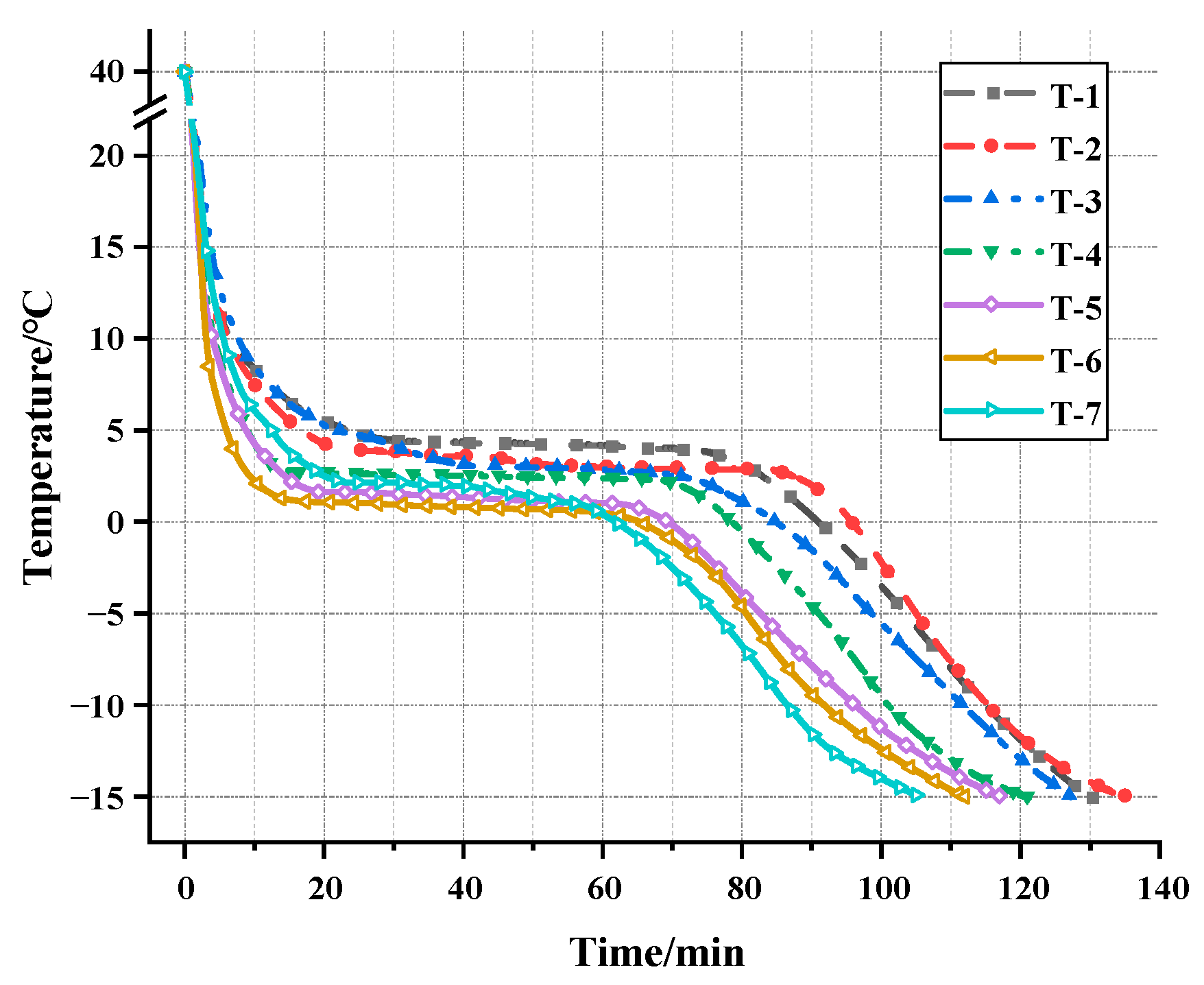
3.2.1. Cooling Curve Test
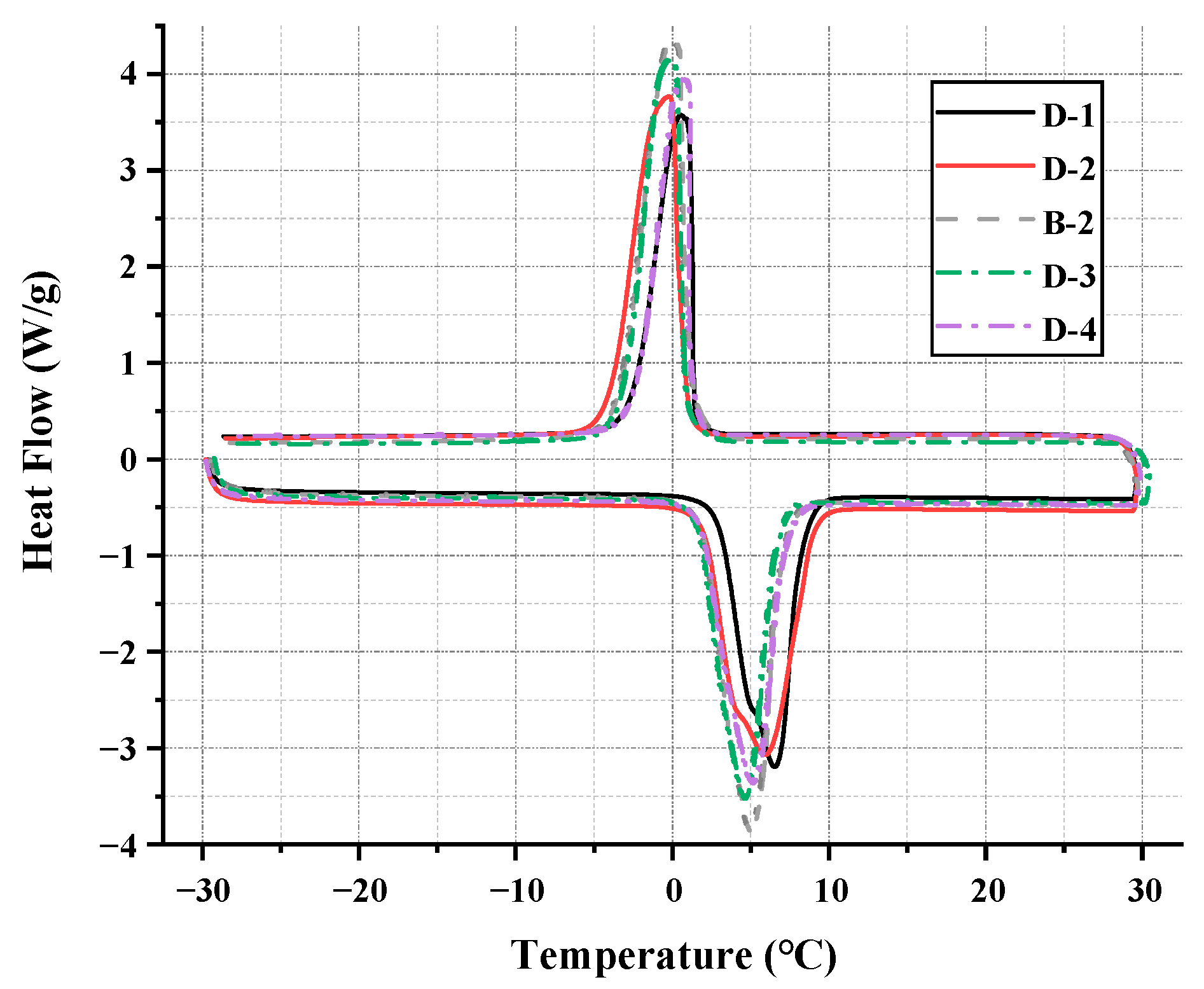
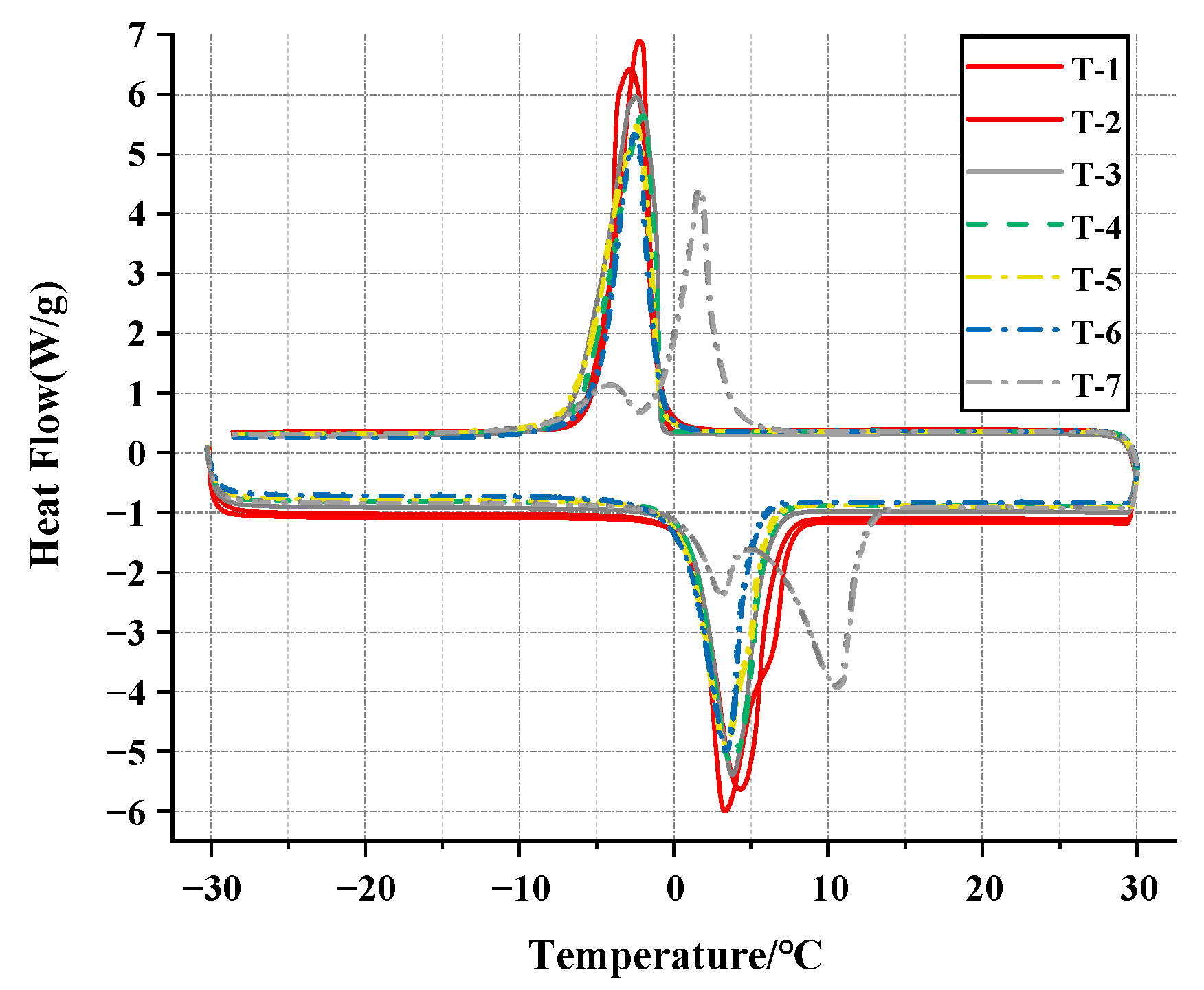
3.2.2. DSC Analysis
3.2.3. Thermodynamic Model Analysis
3.2.4. FTIR Analysis
4. Conclusions
- (1)
- The experimental results of the cooling curve and DSC show that the binary PCM reaches the minimum eutectic point of 1.42 °C at a mass ratio of 0.33:0.67 for capric acid to n-octanoic acid, while the ternary PCM reaches the minimum eutectic point of 0.34 °C at a mass ratio of 0.231:0.469:0.3 for capric acid, n-octanoic acid, and n-tetradecane. It can be seen that the melting point of EPCM prepared by mixing organic PCM, is lower than any of its components, and it can reach its lowest value un-der specific composition ratios. The phase change temperatures of the new binary and ternary PCM obtained in this study are both close to 0 °C, which are suitable for cooling work in practical engineering such as cold storage air conditioning and cold chain transportation. In addition, the latent heat of EPCM is between the lowest and highest values of the latent heat of the constituent components, and its value increases with the overall heat storage density of the material. At the composition ratio of reaching the lowest eutectic point, binary PCM and ternary PCM have melting latent heats of 126.1 J/g and 167.7 J/g, respectively. Therefore, when designing the mix proportion of EPCM, the final latent heat of the material can be changed by adjusting the composition proportion according to actual needs.
- (2)
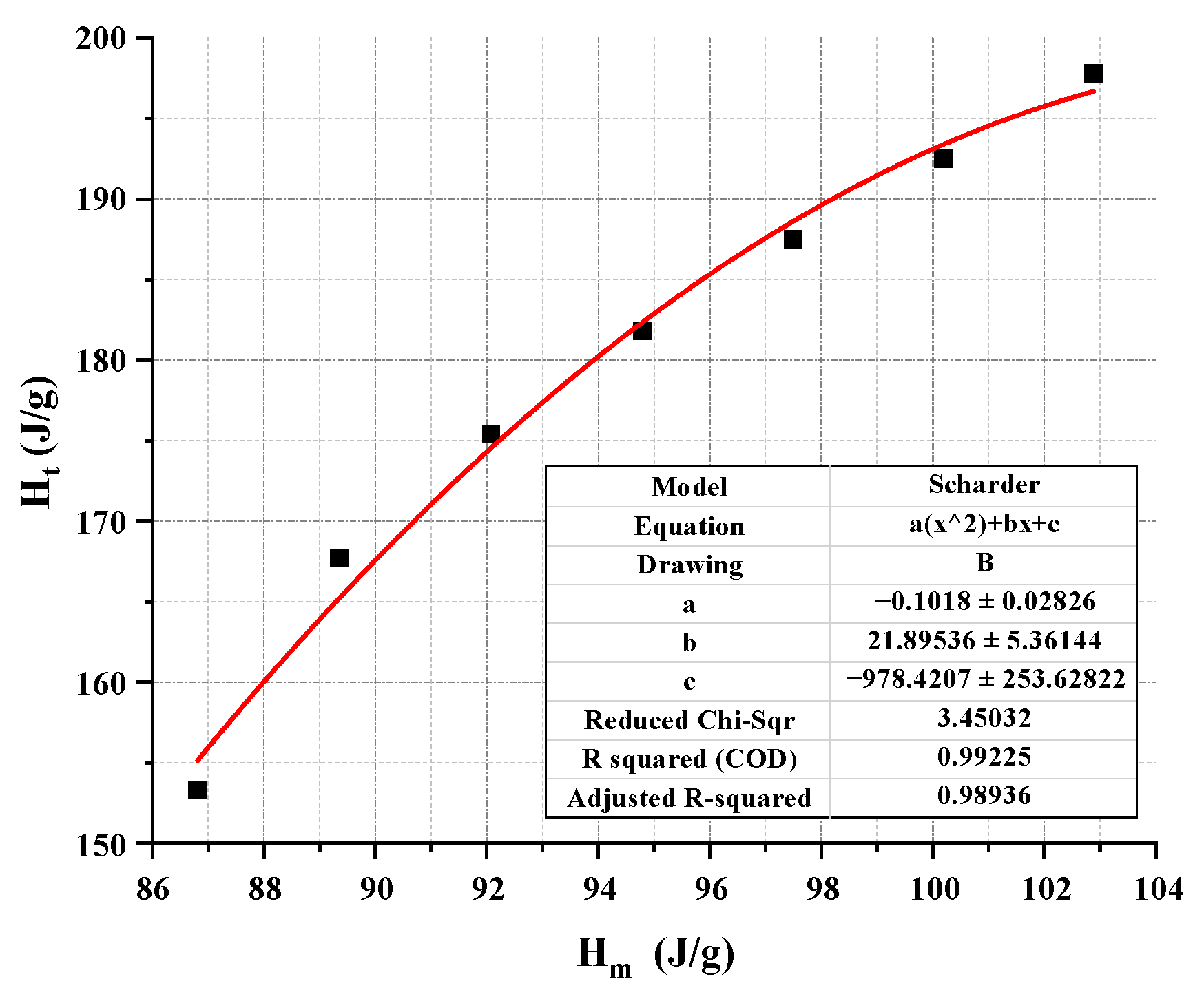
- The initial Schrader equation can accurately predict the composition ratio of the lowest eutectic point in EPCM, but the thermodynamic parameters calculated through it are far from the experimental values. Considering the simplicity and accuracy of the thermodynamic model, this study corrected the initial Schrader equation by quadratic fitting the thermodynamic parameters obtained from the initial Schrader equation. The results show that the modified thermodynamic model has a high fitting accuracy, with correlation coefficients R2 above 0.986, and the errors between the predicted and experimental values are also below 0.06. These conclusions indicate that the thermodynamic model composed of the modified Schrader equation can provide reliable theoretical support for the prediction of thermal parameters and composition ratio screening of organic eutectic phase change materials in practical engineering.
- (3)
- The chemical stability and eutectic effect of EPCM are tested and characterized by FTIR. The results indicate that capric acid, n-octanoic acid, and n-tetradecane can effectively co melt with each other. In the generation process of binary PCM and ternary PCM, there is only physical binding and no chemical reaction. Therefore, the chemical properties between each component are almost unaffected, and the thermal performance of the prepared EPCM is also enhanced. The above conclusion strongly proves that the method of preparing EPCM by melt blending organic PCM has good reliability and scientificity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Eanest, J.B.; Valan, A.A. Characterization and stability analysis of eutectic fatty acid as a low cost cold energy storage phase change material. J. Energy Storage 2020, 31, 101708. [Google Scholar]
- Veerakumar, C.; Sreekumar, A. Preparation, thermophysical studies, and corrosion analysis of a stable capric acid/cetyl alcohol binary eutectic phase change material for cold thermal energy storage. Energy Technol. 2018, 6, 397–405. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.; Xu, X.; Zhang, S. Development of composite phase change cold storage material and its application in vaccine cold storage equipment. J. Energy Storage 2020, 30, 101455. [Google Scholar] [CrossRef]
- Sana, B.S.; Hamida, M.B.B. Alternate PCM with air cavities in LED heat sink for transient thermal management. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4377–4393. [Google Scholar]
- Hamida, M.B.B.; Hajlaoui, K.; Almeshaal, M.A. A 3D numerical analysis using phase change material for cooling circular light emitting diode. Case Stud. Therm. Eng. 2023, 43, 102792. [Google Scholar] [CrossRef]
- Izadi, M.; Sheremet, M.; Hajjar, A.; Galal, A.M.; Mahariq, I.; Jarad, F.; Hamida, M.B.B. Numerical investigation of magne-to-thermal-convection impact on phase change phenomenon of Nano-PCM within a hexagonal shaped thermal energy storage. Appl. Therm. Eng. 2023, 223, 119984. [Google Scholar] [CrossRef]
- Izadi, M.; Fagehi, H.; Imanzadeh, A.; Altnji, S.; Ben Hamida, M.B.; Sheremet, M.A. Influence of finned charges on melting process performance in a thermal energy storage. Therm. Sci. Eng. Prog. 2023, 37, 101547. [Google Scholar] [CrossRef]
- Du, K.; Calautit, J.; Wang, Z.H.; Wu, Y.; Liu, H. A review of the applications of phase change materials in cooling, heating and power generation in different temperature ranges. Appl. Energy 2018, 220, 242–273. [Google Scholar] [CrossRef]
- Chandrasekaran, P.; Cheralathan, M.; Kumaresan, V.; Velraj, R. Enhanced heat transfer characteristics of water based copper oxide nanofluid PCM (phase change material) in a spherical capsule during solidification for energy efficient cool thermal storage system. Energy 2014, 72, 636–642. [Google Scholar] [CrossRef]
- Oró, E.; Miró, L.; Farid, M.M.; Martin, V.; Cabeza, L.F. Energy management and CO2 mitigation using phase change materials (PCM) for thermal energy storage (TES) in cold storage and transport. Int. J. Refrig. 2014, 42, 26–35. [Google Scholar] [CrossRef]
- Sha, Y.S.; Hua, W.S.; Cao, H.F.; Zhang, X. Properties and encapsulation forms of phase change material and various types of cold storage box for cold chain logistics: A review. J. Energy Storage 2022, 55, 105426. [Google Scholar] [CrossRef]
- Su, W.G.; Darkwa, J.; Kokogiannakis, G. Review of solid-liquid phase change materials and their encapsulation technologies. Renew. Sustain. Energy Rev. 2015, 48, 373–391. [Google Scholar] [CrossRef]
- Lin, Y.X.; Alva, G.; Fang, G.Y. Review on thermal performances and applications of thermal energy storage systems with inorganic phase change materials. Energy 2018, 165, 685–708. [Google Scholar] [CrossRef]
- Shamseldin, A.M.; Fahad, A.A.; Nasiru, I.I.; Zahir, M.H.; Al-Ahmed, A.; Saidur, R.; Sahin, A.Z. A review on current status and challenges of inorganic phase change materials for thermal energy storage systems. Renew. Sustain. Energy Rev. 2017, 70, 1072–1089. [Google Scholar]
- Xue, F.; Qi, X.D.; Huang, T.; Tang, C.Y.; Zhang, N.; Wang, Y. Preparation and application of three-dimensional filler network towards organic phase change materials with high performance and multi-functions. Chem. Eng. J. 2021, 419, 129620. [Google Scholar] [CrossRef]
- Nassima, R. A Comprehensive Review of Composite Phase Change Materials (cPCMs) for Thermal Management Applications, Including Manufacturing Processes, Performance, and Applications. Energies 2022, 15, 8271. [Google Scholar]
- Philip, N.; Dheep, G.R.; Sreekumar, A. Cold thermal energy storage with lauryl alcohol and cetyl alcohol eutectic mixture: Thermophysical studies and experimental investigation. J. Energy Storage 2020, 27, 101060. [Google Scholar] [CrossRef]
- Zhou, S.X.; Zhang, X.L.; Liu, S.; Li, Y.Y.; Xu, X.F. Performance study on expand graphite/organic composite phase change material for cold thermal energy storage. Energy Procedia 2019, 158, 5305–5310. [Google Scholar]
- Ke, H.Z. Phase diagrams, eutectic mass ratios and thermal energy storage properties of multiple fatty acid eutectics as novel solid-liquid phase change materials for storage and retrieval of thermal energy. Appl. Therm. Eng. 2017, 113, 1319–1331. [Google Scholar] [CrossRef]
- Kalidasan, B.; Pandey, A.K.; Saidur, R.; Mishra, Y.K. Experimental evaluation of binary and ternary eutectic phase change material for sustainable thermal energy storage. J. Energy Storage 2023, 68, 107707. [Google Scholar]
- Zuo, P.X.; Liu, Z.; Zhang, H.; Dai, D.; Fu, Z.; Corker, J.; Fan, M. Formulation and phase change mechanism of Capric acid/Octadecanol binary composite phase change materials. Energy 2023, 270, 126943. [Google Scholar] [CrossRef]
- Liu, L.; Niu, J.L.; Wu, J.Y. Development of highly stable paraffin wax/water phase change material nano-emulsions as potential coolants for thermal management. Sol. Energy Mater. Sol. Cells 2023, 252, 112184. [Google Scholar] [CrossRef]
- Teather, K.; Siddiqui, K. Non-invasive measurement of the temperature field of a phase change material (PCM) using thermal imaging. Exp. Therm. Fluid. Sci. 2023, 148, 110991. [Google Scholar] [CrossRef]
- ASTM D87-2009; Standard Test Method for Melting Point of Petroleum Wax (Cooling Curve). Annual Book of ASTM Standards: Philadelphia, PA, USA, 2009.
- Fatahi, H.; Claverie, J.P.; Poncet, S. Characterization by differential scanning calorimetry of thermal storage properties of organic PCMs with operating temperature of 150 °C. J. Chem. Thermodyn. 2023, 186, 107136. [Google Scholar] [CrossRef]
- Li, L.; Yu, H.; Wang, X.; Zheng, S. Thermal analysis of melting and freezing processes of phase change materials (PCMs) based on dynamic DSC test. Energy Build. 2016, 130, 388–396. [Google Scholar] [CrossRef]
- GB/T 28724-2012; Determination of Melting Temperature for Chemicals (Pharmaceuticals)—Differential Scanning Calorimetry. China Petroleum and Chemical Industry Federation: Beijing, China, 2012.
- Chelouche, S.; Trache, D.; Pinho, S.P.; Khimeche, K. Experimental and modeling studies of binary organic eutectic systems to be used as stabilizers for nitrate esters-based energetic materials. Fluid Phase Equilibria 2019, 498, 104–115. [Google Scholar] [CrossRef]
- Su, A.; Li, S.F. Measurement and correlation of solid–liquid phase equilibria for binary and ternary systems consisting of N-vinylpyrrolidone, 2-pyrrolidone and water. Chin. J. Chem. Eng. 2018, 24, 806–811. [Google Scholar] [CrossRef]
- Costa, M.C.; Boros, L.A.D.; Batista, M.L.S.; Coutinho, J.; Krähenbühl, M.; Meirelles, A.J. Phase diagrams of mixtures of ethyl palmitate with fatty acid ethyl esters. Fuel 2012, 91, 177–181. [Google Scholar] [CrossRef]
- Shen, T.; Peng, H.; Ling, X. Experimental Measurements and Thermodynamic Modeling of Melting Temperature of the Binary Systems n-C11H24-n-C14H30, n-C12H26-n-C13H28, n-C12H26-n-C14H30, and n-C13H28-n-C15H32 for Cryogenic Thermal Energy Storage. Ind. Eng. Chem. Res. 2019, 58, 15026–15035. [Google Scholar] [CrossRef]
- Sánchez, F.G.; Schwartzentruber, J.; Ammar, M.N.; Renon, H. Modeling of Multiphase Liquid Equilibria for Multicomponent Mixtures. Fluid Phase Equilibria 1996, 121, 207–225. [Google Scholar] [CrossRef]
- Wei, D.; Han, S.; Shen, X. Solid–liquid phase equilibria of (n-octadecane with myristic, and palmitic acid) binary mixtures used as phase change materials (PCMs). J. Chem. Thermodyn. 2016, 101, 7–11. [Google Scholar] [CrossRef]
- Lv, S.L.; Zhu, N.; Feng, G.H. Eutectic mixtures of capric acid and lauric acid applied in building wallboards for heat energy storage. Energy Build. 2006, 38, 708–711. [Google Scholar]
- Zhang, Y.P.; Su, Y.H.; Ge, X.S. Prediction of the melting temperature and the fusion heat of (quasi-) eutectic PCM. J. China Univ. Sci. Technol. 1995, 25, 474–478. [Google Scholar]
- Yuan, Y.P.; Tao, W.Q.; Cao, X.L.; Li, B. Theoretic prediction of melting temperature and latent heat for a fatty acid eutectic mixture. J. Chem. Eng. Data 2011, 56, 2889–2891. [Google Scholar]
- Zhao, P.; Yue, Q.; He, H.; Gao, B.; Wang, Y.; Li, Q. Study on phase diagram of fatty acids mixtures to determine eutectic temperatures and the corresponding mixing proportions. Appl. Energy 2014, 115, 483–490. [Google Scholar] [CrossRef]
- Singh, M.B.; Kumar, V.S.; Chaudhary, M.; Singh, P. A mini review on synthesis, properties and applications of deep eutectic solvents. J. Indian Chem. Soc. 2021, 98, 100210. [Google Scholar] [CrossRef]
- Karaman, S.; Karaipekli, A.; Sarı, A.; Bicer, A. Polyethylene glycol (PEG)/diatomite composite as a novel form-stable phase change material for thermal energy storage. Sol. Energy Mater. Sol. Cells 2011, 95, 1647–1653. [Google Scholar] [CrossRef]
- Huang, X.; Cui, Y.D.; Yin, G.Q.; Zhang, B.N.; Feng, G.Z. Kinetic study on solid-liquid transitions of fatty acids ternary mixtures phase change materials. New Chem. Mater. 2015, 43, 149–151. [Google Scholar]
- Nazir, H.; Batool, M.; Ali, M.; Kannan, A.M. Fatty acids based eutectic phase change system for thermal energy storage applications. Appl. Therm. Eng. 2018, 142, 466–475. [Google Scholar] [CrossRef]
- Shen, T.; Li, S.; Peng, H.; Ling, X. Experimental study and thermodynamic modeling of solid-liquid equilibrium of binary systems: Dodecane-tetradedcane and tridecane-pentadecane for cryogenic thermal energy storage. Fluid Phase Equilibria 2019, 493, 109–119. [Google Scholar] [CrossRef]
- Wang, Y.B.; Li, J.W.; Miao, M.W.J.; Su, Y.; He, X.; Strnadel, B. Preparation and characterizations of hydroxyapatite microcapsule phase change materials for potential building materials. Constr. Build. Mater. 2021, 297, 123576. [Google Scholar] [CrossRef]
- Cheng, W.L.; Zhang, R.M.; Xie, K.; Liu, N.; Wang, J. Heat conduction enhanced shape-stabilized paraffin/HDPE composite PCMs by graphite addition: Preparation and thermal properties. Sol. Energy Mater. Sol. Cells 2010, 94, 1636–1642. [Google Scholar] [CrossRef]





| Density (g/mL) | Molecular Weight | Melting Point (°C) | Latent Heat (J·g−1) | Flash Point (°C) | Water Solubility (g/L) | |
|---|---|---|---|---|---|---|
| Capric acid | 0.8858 | 172.26 | 31.5 | 172.8 | 121.8 | 0.15 |
| N-octanoic acid | 0.91 | 144.21 | 16.5 | 149.9 | 130 | 0.68 |
| N-tetradecane | 0.763 | 198.39 | 6 | 219.6 | 101 | 0 |
| B-1 | B-2 | B-3 | B-4 | B-5 | B-6 | B-7 | |
|---|---|---|---|---|---|---|---|
| Capric acid (wt%) | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| N-octanoic Acid (wt%) | 80 | 70 | 60 | 50 | 40 | 30 | 20 |
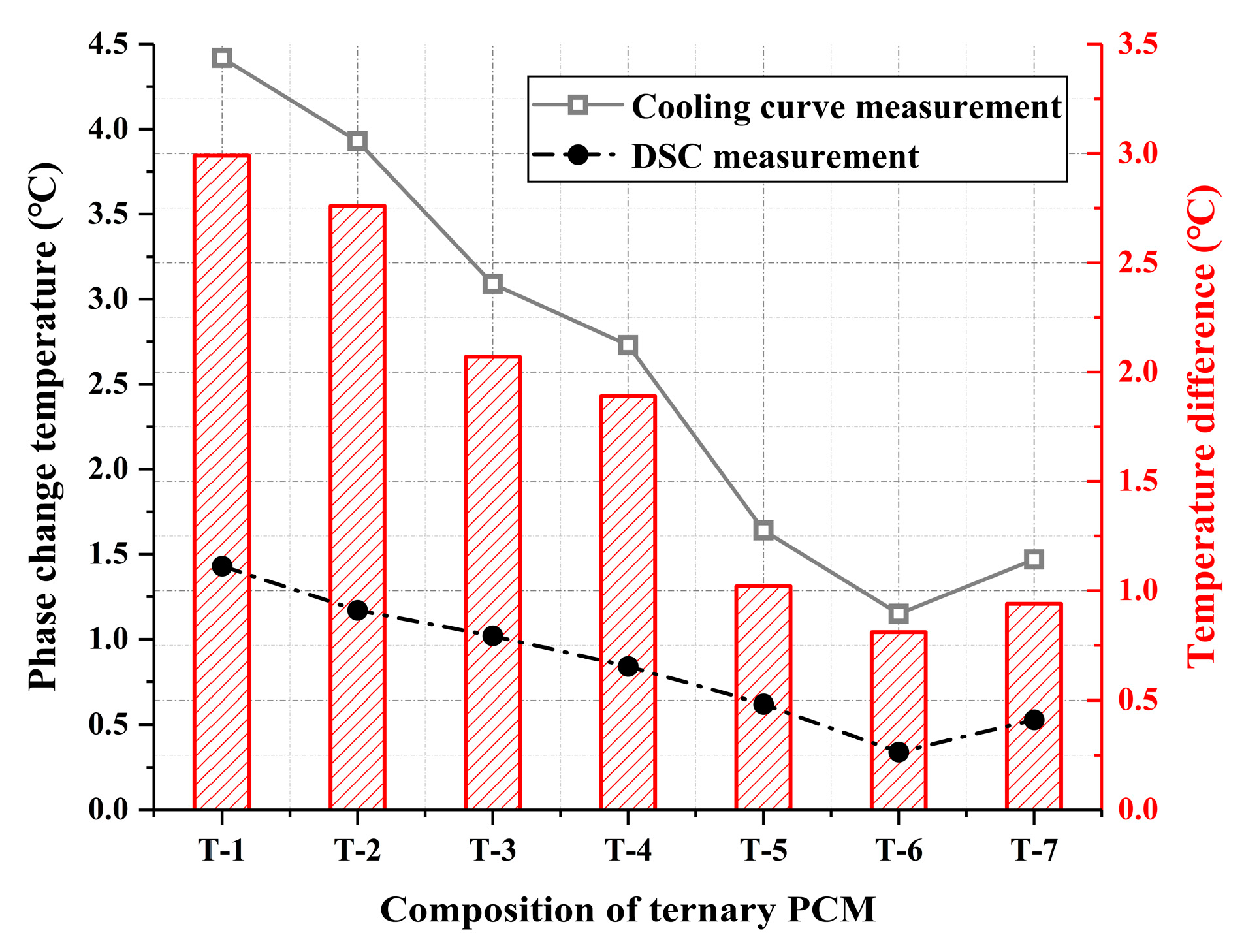
| T-1 | T-2 | T-3 | T-4 | T-5 | T-6 | T-7 | |
|---|---|---|---|---|---|---|---|
| Binary PCM (wt%) | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
| N-tetradecane (wt%) | 80 | 70 | 60 | 50 | 40 | 30 | 20 |
| B-1 | B-2 | B-3 | B-4 | B-5 | B-6 | B-7 | |
|---|---|---|---|---|---|---|---|
| Platform temperature (°C) | 3.51 | 1.85 | 4.02 | 5.63 | 7.72 | 10.28 | 12.58 |
| Cooling time (min) | 85 | 97 | 84 | 82 | 77 | 71 | 69 |
| D-1 | D-2 | B-2 | D-3 | D-4 | |
|---|---|---|---|---|---|
| Capric acid (wt%) | 24% | 27% | 30% | 33% | 36% |
| N-octanoic acid (wt%) | 76% | 73% | 70% | 67% | 64% |
| Sample | Melting Point (°C) | Crystallizing Point (°C) | Supercooling (°C) | Melting Enthalpy (J/g) |
|---|---|---|---|---|
| D-1 | 2.83 | 1.458 | 1.372 | 116.8 |
| D-2 | 1.96 | 1.121 | 0.839 | 119.6 |
| B-2 | 1.73 | 1.093 | 0.637 | 128.2 |
| D-3 | 1.42 | 0.889 | 0.531 | 126.1 |
| D-4 | 1.67 | 1.052 | 0.618 | 122.9 |
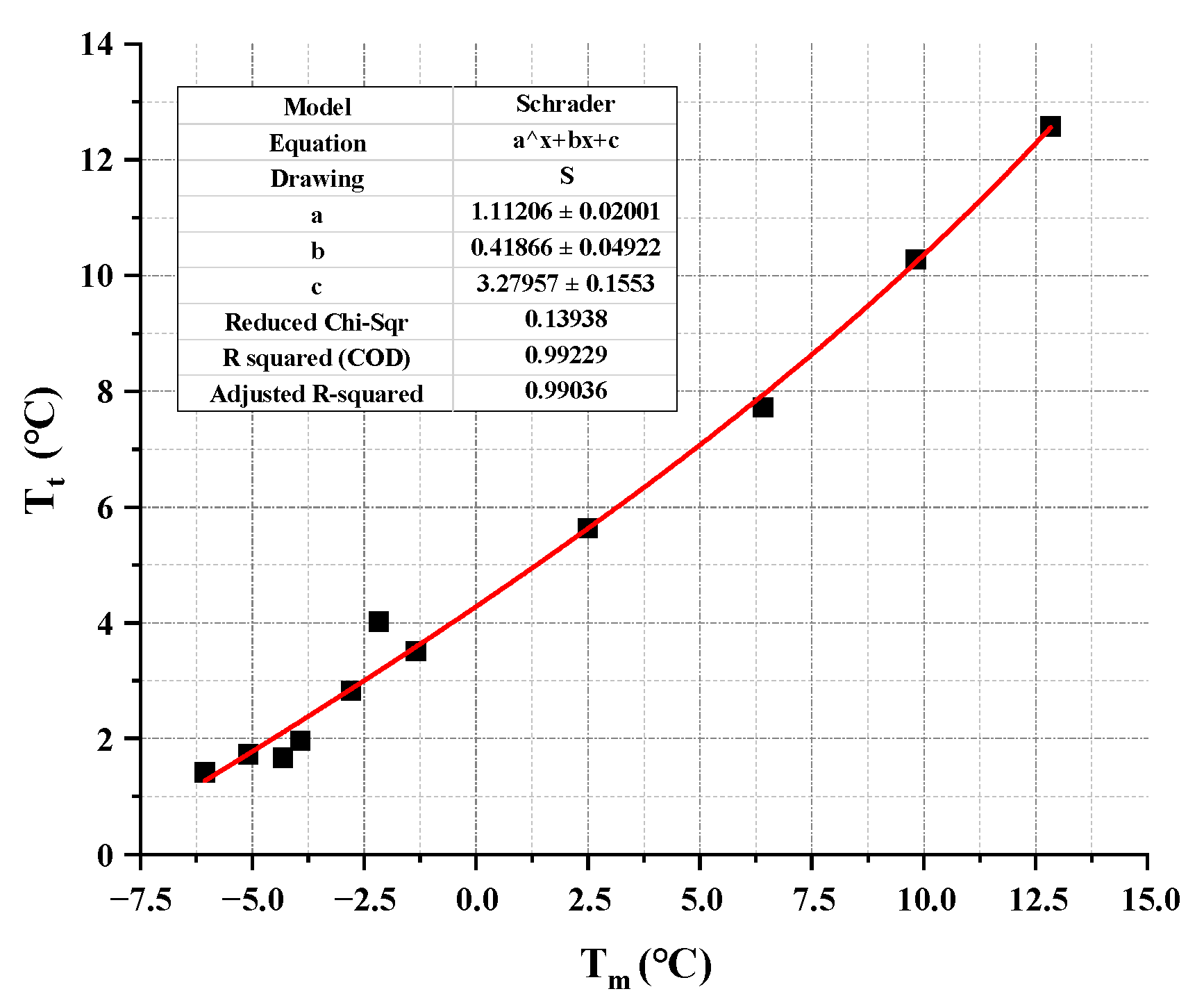
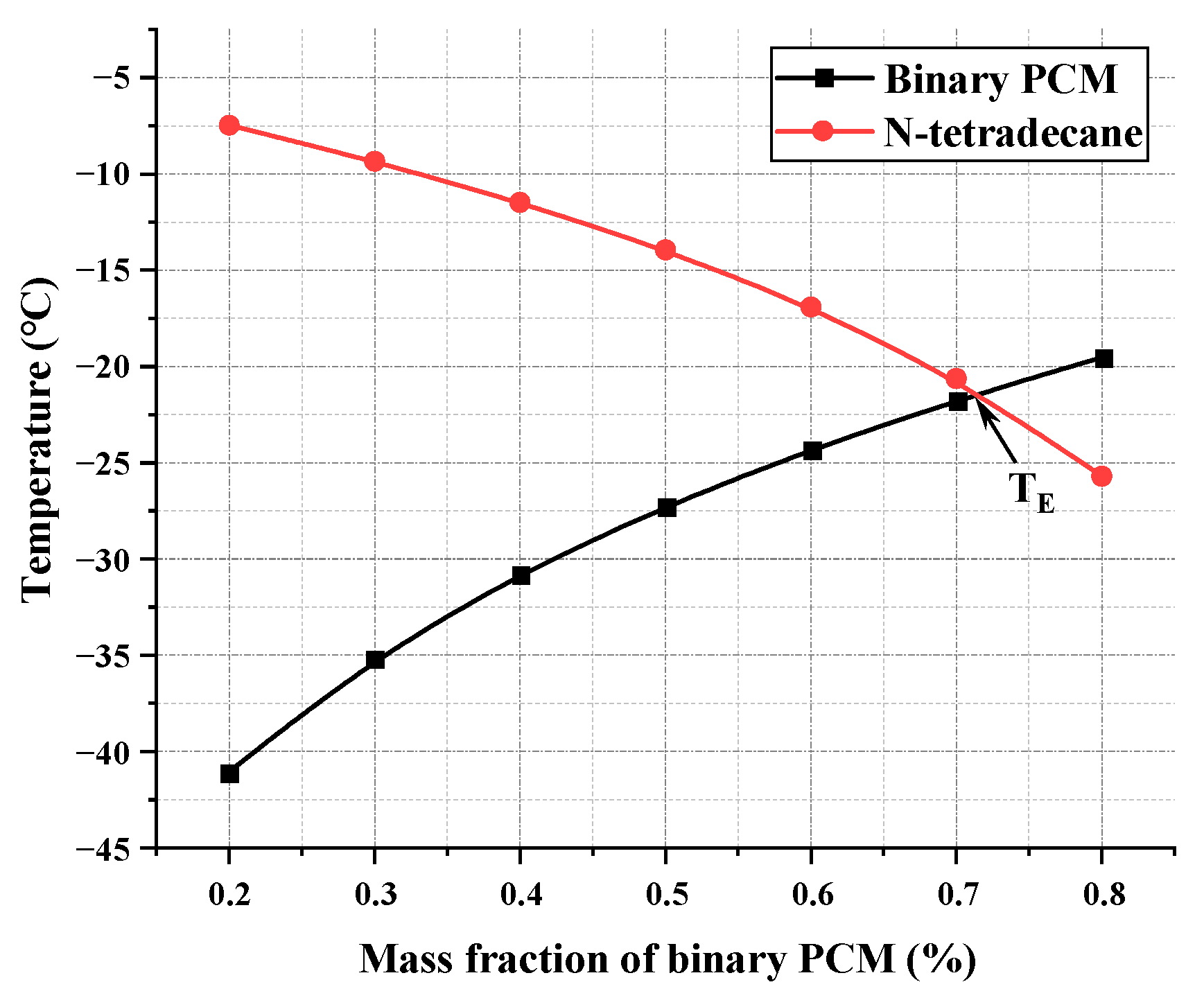
| Capric Acid (wt%) | Tc (°C) | Tt (°C) | bx |
|---|---|---|---|
| 20 | 3.554 | 3.51 | 0.003099 |
| 24 | 2.829 | 2.83 | 0.000052 |
| 27 | 2.287 | 1.96 | 0.038474 |
| 30 | 1.745 | 1.73 | 0.002095 |
| 33 | 1.305 | 1.42 | 0.021103 |
| 36 | 2.021 | 1.67 | 0.047592 |
| 40 | 3.237 | 3.98 | 0.053971 |
| 50 | 5.62 | 5.63 | 0.000446 |
| 60 | 7.991 | 7.72 | 0.008615 |
| 70 | 10.28 | 10.28 | 0.000011 |
| 80 | 12.506 | 12.58 | 0.001472 |
| T-1 | T-2 | T-3 | T-4 | T-5 | T-6 | T-7 | |
|---|---|---|---|---|---|---|---|
| Platform temperature (°C) | 4.42 | 3.93 | 3.09 | 2.73 | 1.64 | 1.15 | 2.06 |
| Cooling time (min) | 130 | 135 | 127 | 121 | 117 | 112 | 105 |
| Sample | Melting Point /°C | Crystallizing Point /°C | Supercooling /°C | Melting Enthalpy /J·g−1 |
|---|---|---|---|---|
| T-1 | 1.43 | −1.23 | 2.66 | 197.8 |
| T-2 | 1.17 | −1.12 | 2.29 | 192.5 |
| T-3 | 1.02 | −1.04 | 2.06 | 187.5 |
| T-4 | 0.84 | −1.01 | 1.85 | 181.8 |
| T-5 | 0.62 | −0.92 | 1.54 | 175.4 |
| T-6 | 0.34 | −0.98 | 1.32 | 167.7 |
| T-7 | 0.53 | 2.9 | 2.37 | 153.3 |
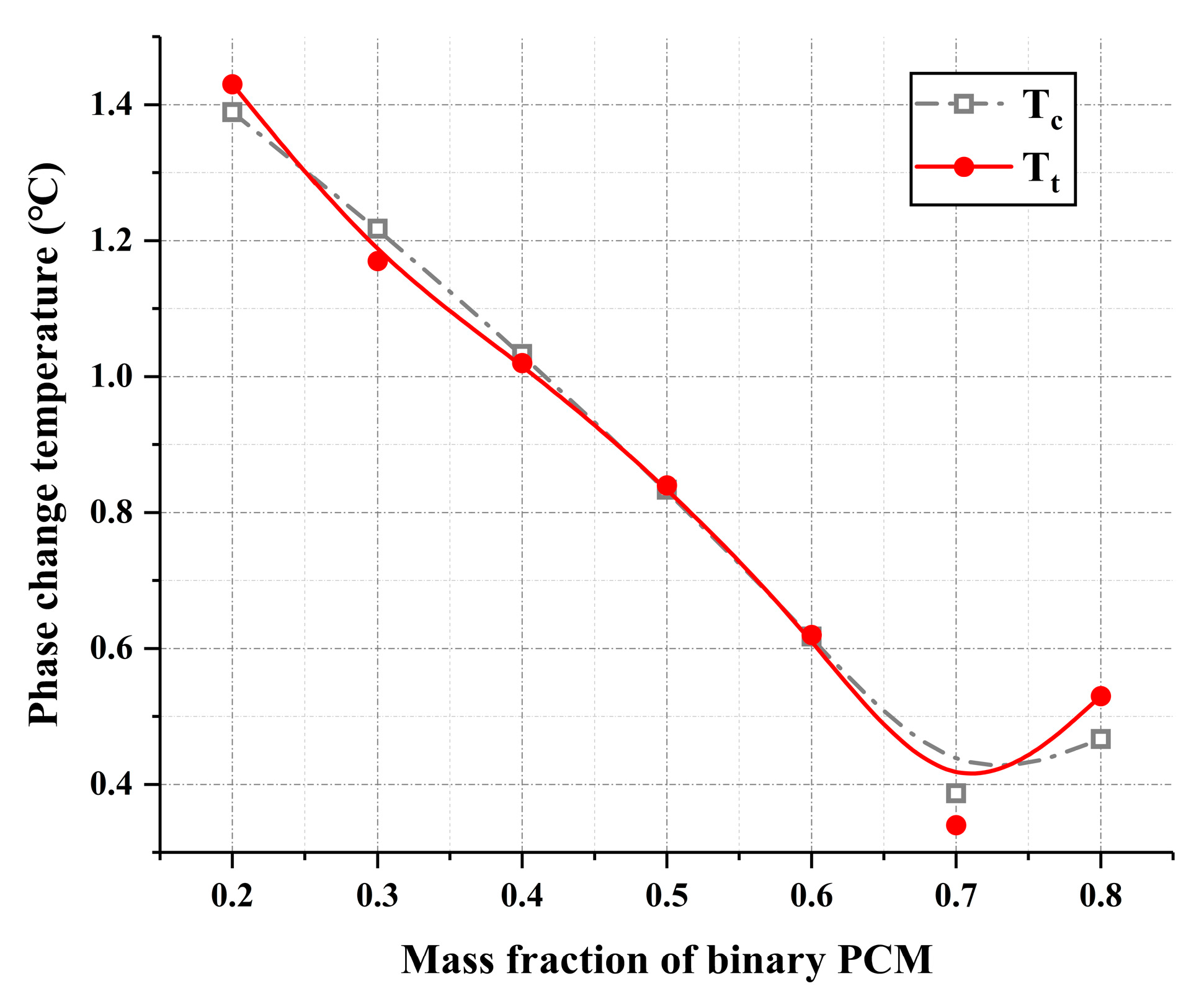
| Binary PCM (wt%) | Tc (°C) | Tt (°C) | bx |
|---|---|---|---|
| 20 | 1.389 | 1.43 | 0.007299 |
| 30 | 1.218 | 1.17 | 0.009963 |
| 40 | 1.033 | 1.02 | 0.003168 |
| 50 | 0.833 | 0.84 | 0.001979 |
| 60 | 0.617 | 0.62 | 0.001045 |
| 70 | 0.387 | 0.34 | 0.032241 |
| 80 | 0.467 | 0.53 | 0.031679 |
| Binary PCM (wt%) | Hc (J/g) | Ht (J/g) | bx |
|---|---|---|---|
| 20 | 196.7 | 197.8 | 0.001388 |
| 30 | 193.42 | 192.5 | 0.001187 |
| 40 | 188.64 | 187.5 | 0.001514 |
| 50 | 182.36 | 181.8 | 0.000771 |
| 60 | 174.57 | 175.4 | 0.001189 |
| 70 | 165.24 | 167.7 | 0.003692 |
| 80 | 155.15 | 153.3 | 0.002995 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Wang, S.; Jia, W.; Xie, J.; Lu, Z.; Ying, H.; Sun, Y. The Influence of Composition Ratio on the Thermal Performance Parameters of Eutectic Phase Change Materials: Experimental Research and Theoretical Prediction. Buildings 2023, 13, 3043. https://doi.org/10.3390/buildings13123043
Liu B, Wang S, Jia W, Xie J, Lu Z, Ying H, Sun Y. The Influence of Composition Ratio on the Thermal Performance Parameters of Eutectic Phase Change Materials: Experimental Research and Theoretical Prediction. Buildings. 2023; 13(12):3043. https://doi.org/10.3390/buildings13123043
Chicago/Turabian StyleLiu, Bo, Sheliang Wang, Wurong Jia, Jiangsheng Xie, Zhe Lu, Honghao Ying, and Yanwen Sun. 2023. "The Influence of Composition Ratio on the Thermal Performance Parameters of Eutectic Phase Change Materials: Experimental Research and Theoretical Prediction" Buildings 13, no. 12: 3043. https://doi.org/10.3390/buildings13123043
APA StyleLiu, B., Wang, S., Jia, W., Xie, J., Lu, Z., Ying, H., & Sun, Y. (2023). The Influence of Composition Ratio on the Thermal Performance Parameters of Eutectic Phase Change Materials: Experimental Research and Theoretical Prediction. Buildings, 13(12), 3043. https://doi.org/10.3390/buildings13123043







