Shear and Punching Capacity Predictions for One-Way Slabs under Concentrated Loads Considering the Transition between Failure Mechanisms
Abstract
1. Introduction
2. Literature Review
2.1. Background Calculations for One-Way Shear
2.2. Insights from the Literature for One-Way Shear
2.3. Background Calculations for Punching Capacity Predictions
2.4. Insights from the Literature for Punching Capacity Predictions
3. Proposed Approach
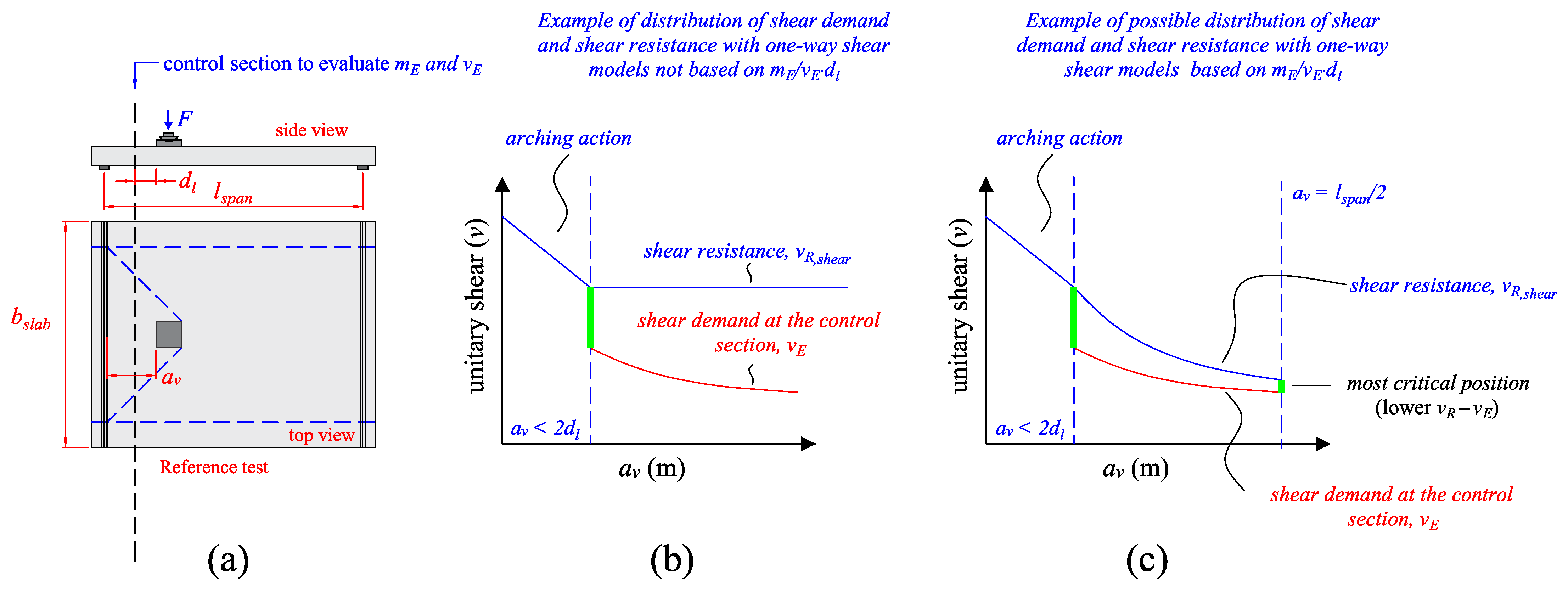
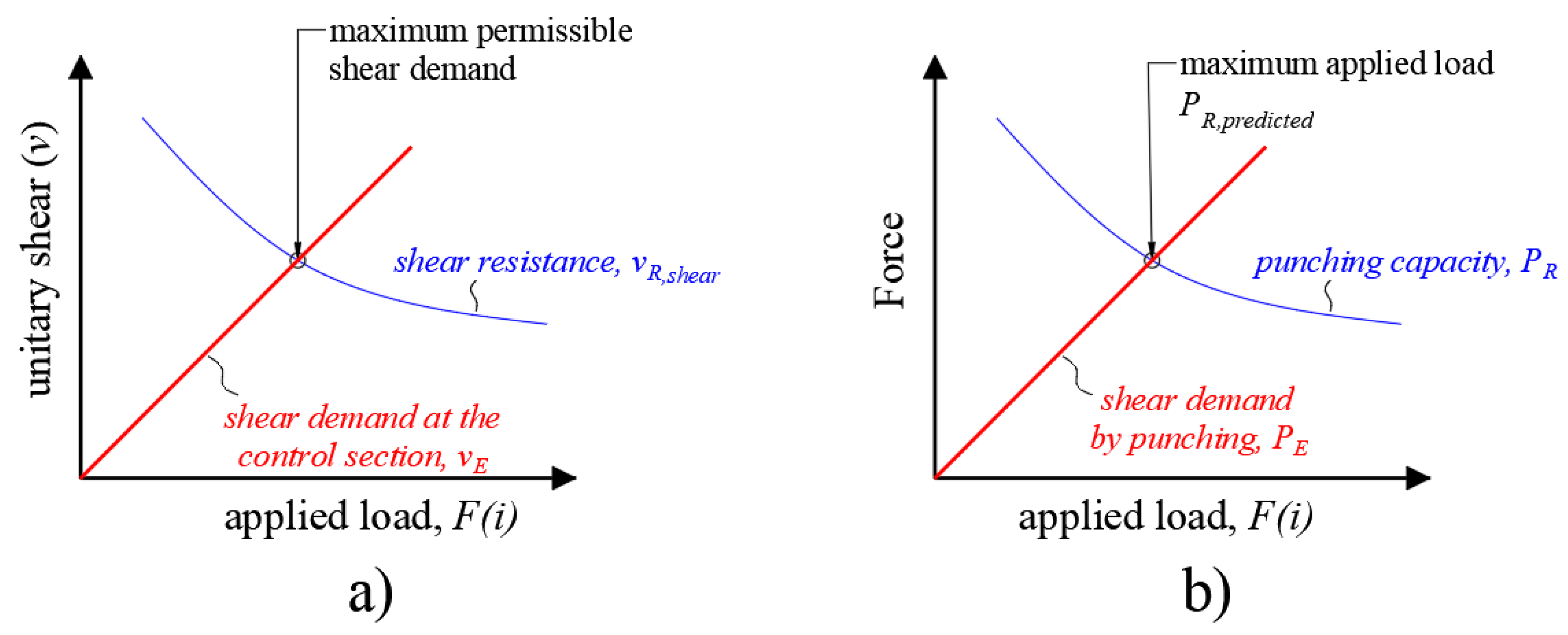
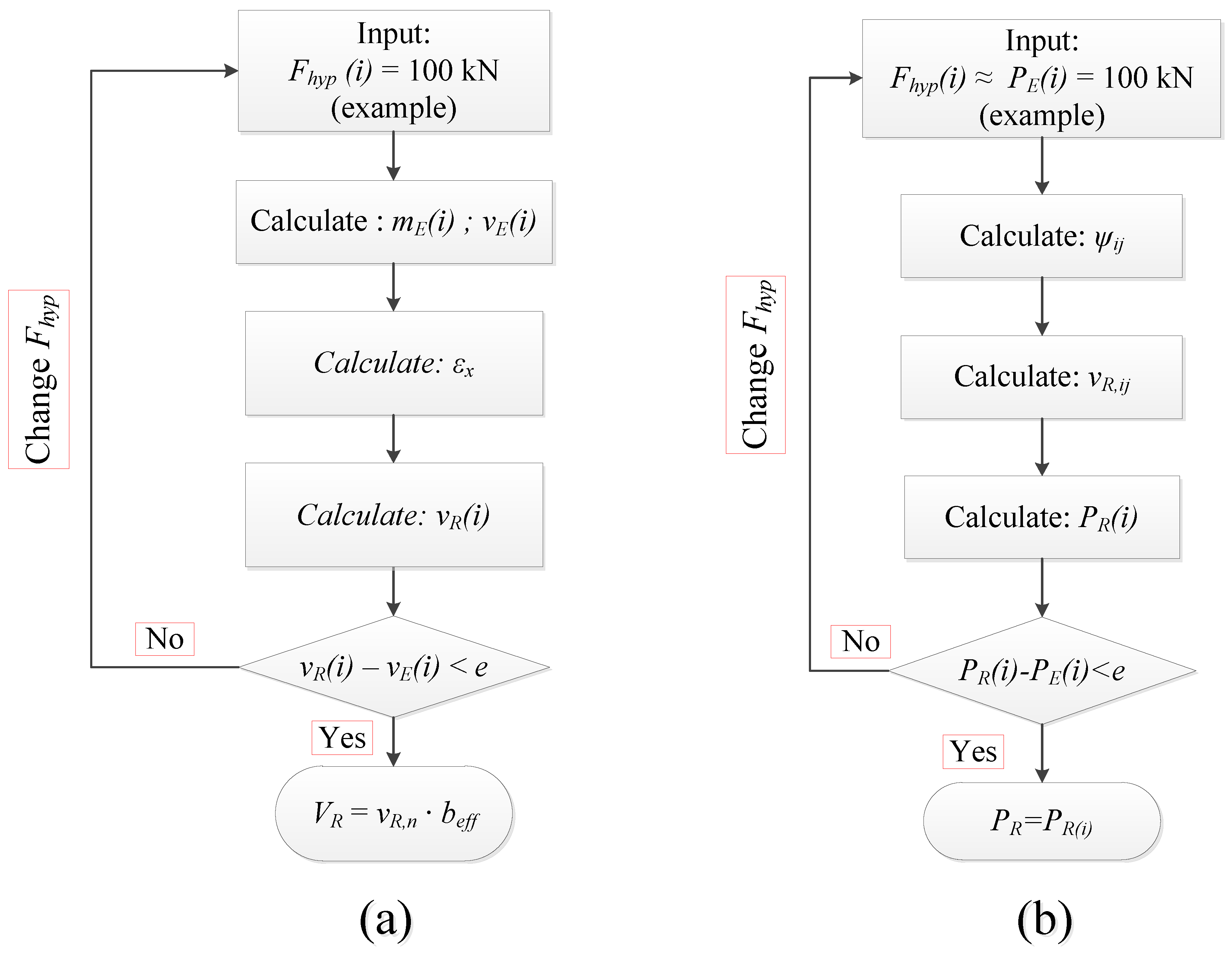
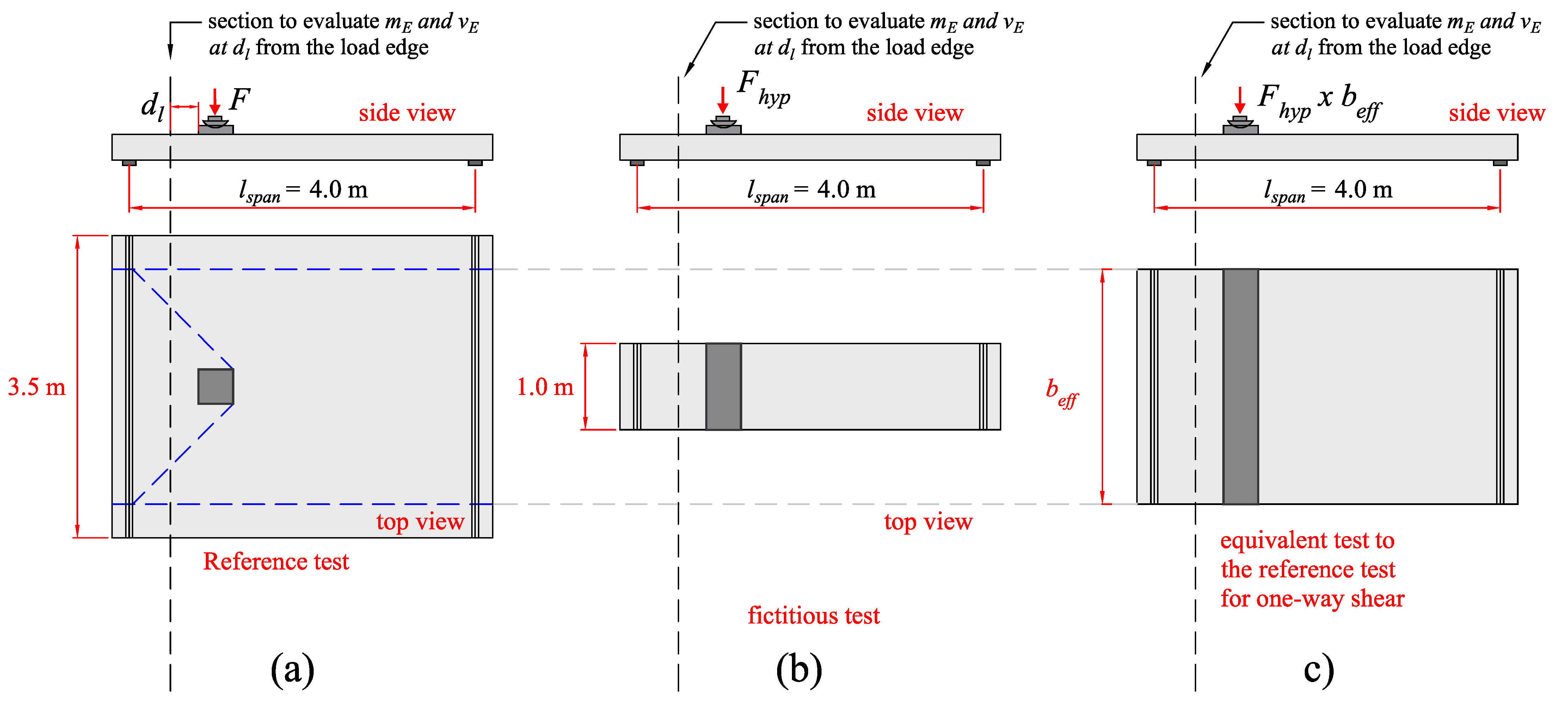
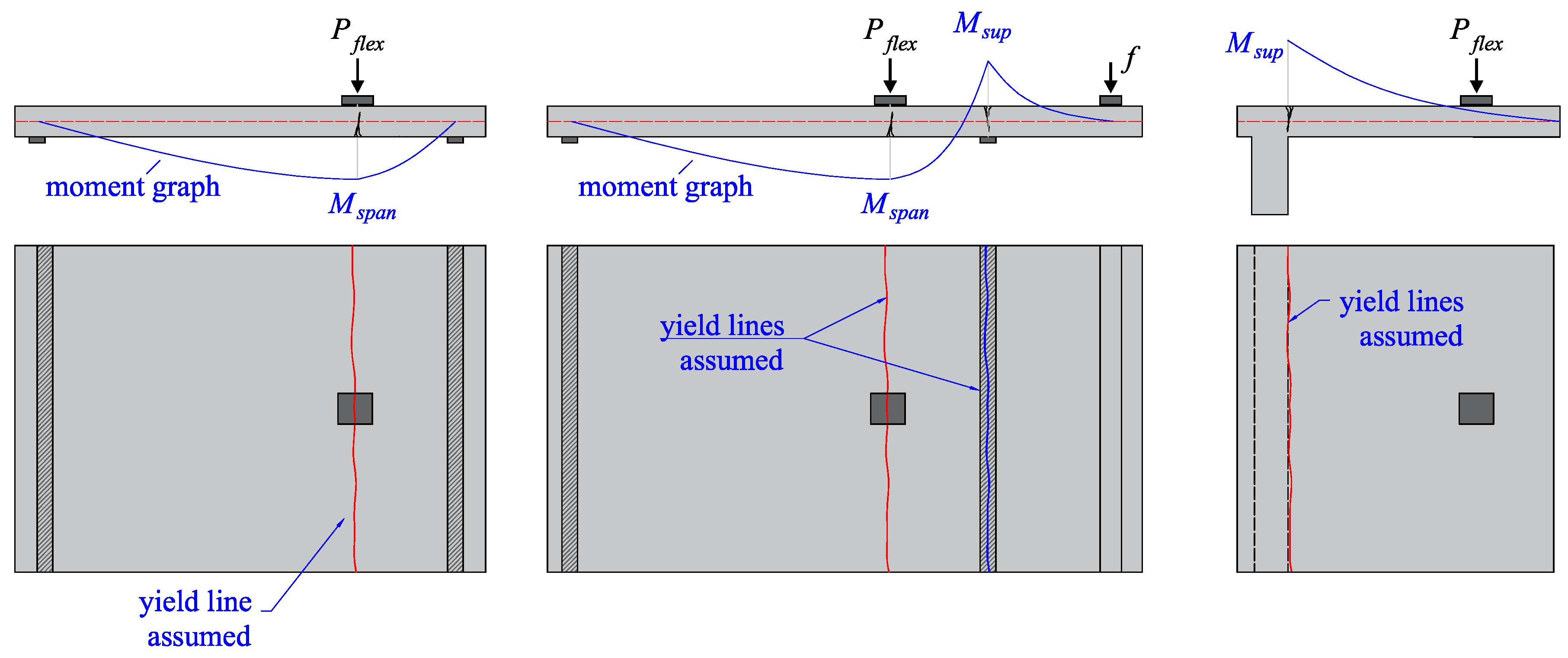
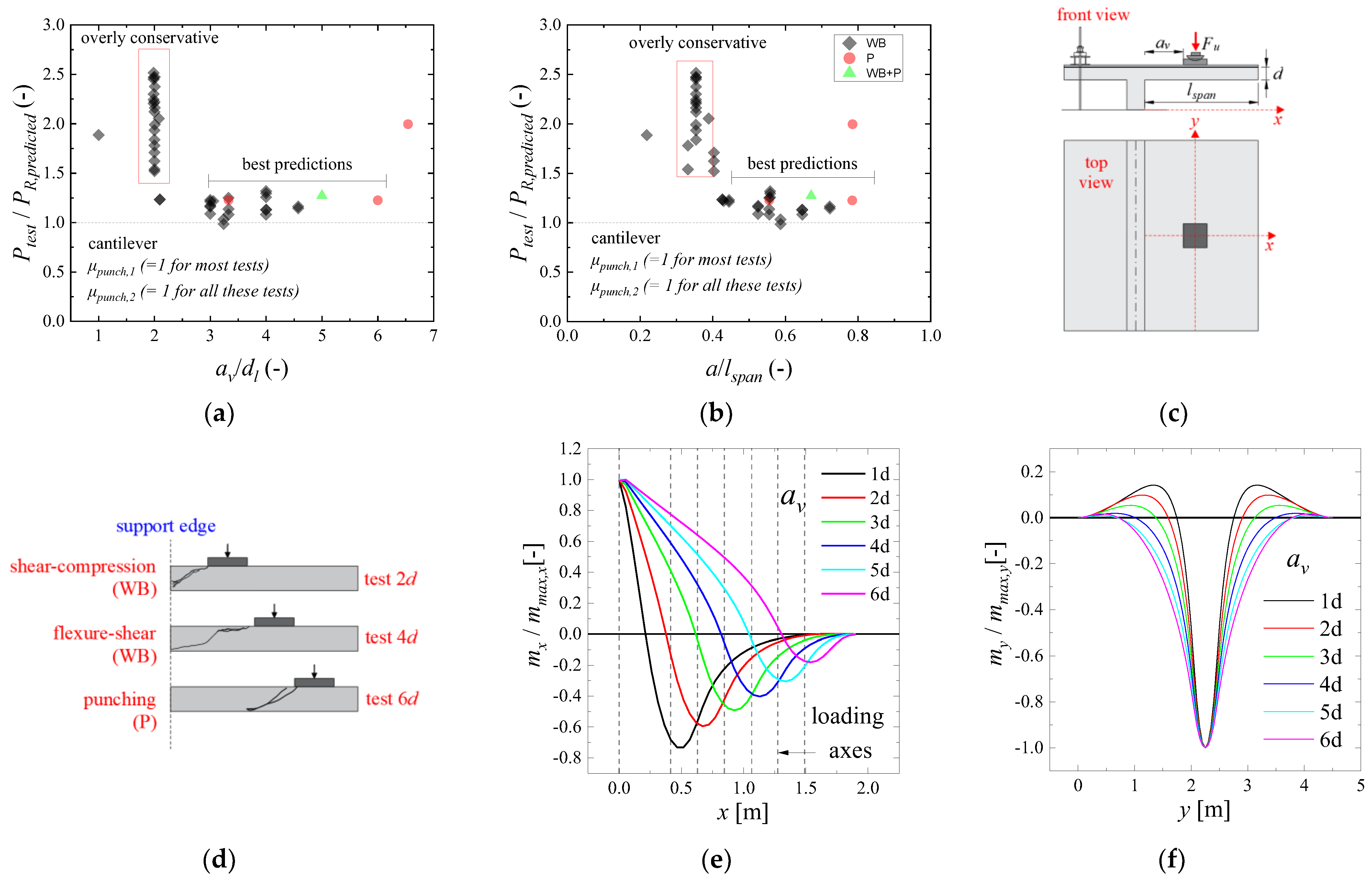
3.1. Proposed Approach for One-Way Shear
3.2. Proposed Approach for Punching Shear Capacity Predictions
4. Database
5. Results
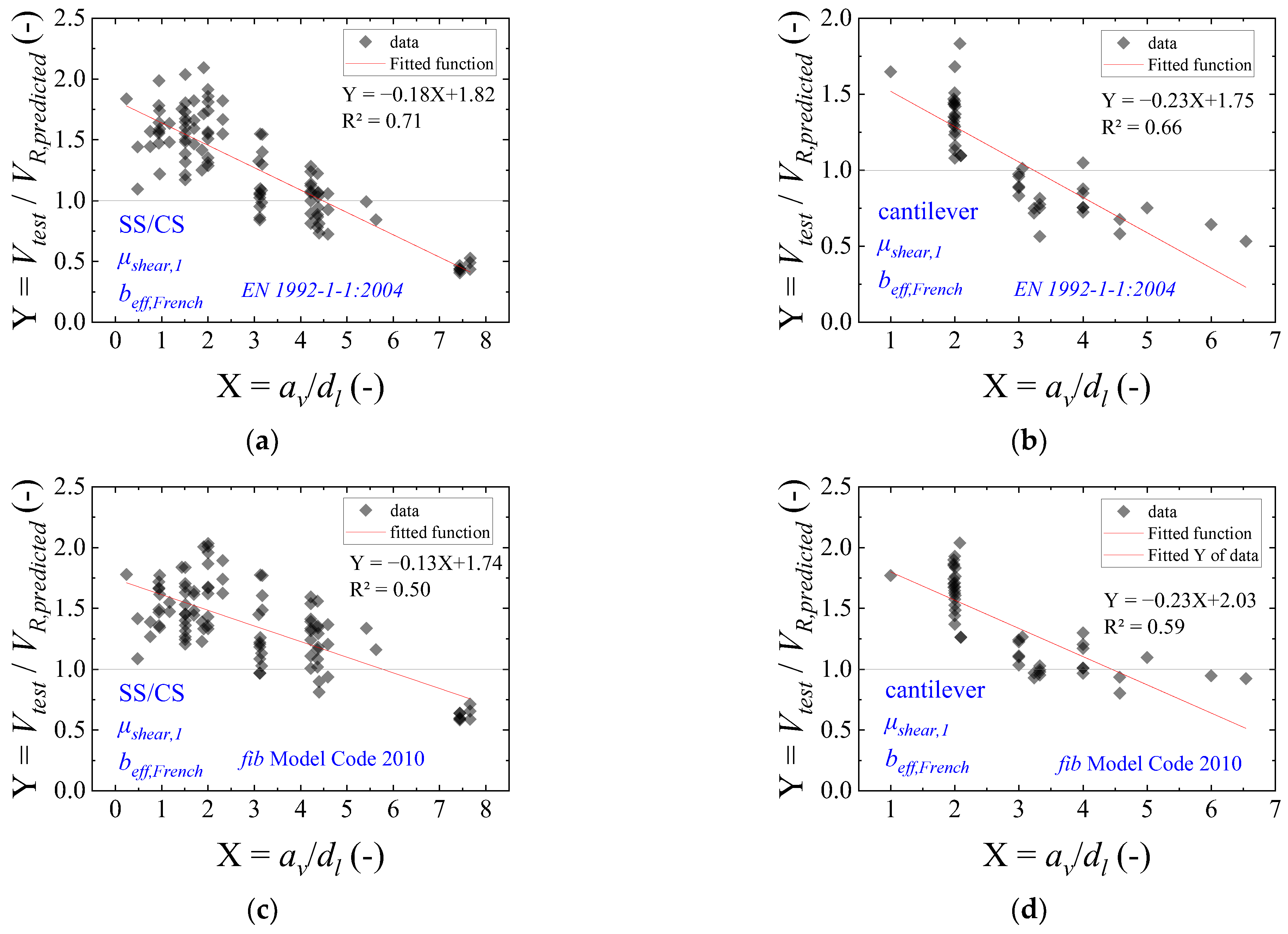
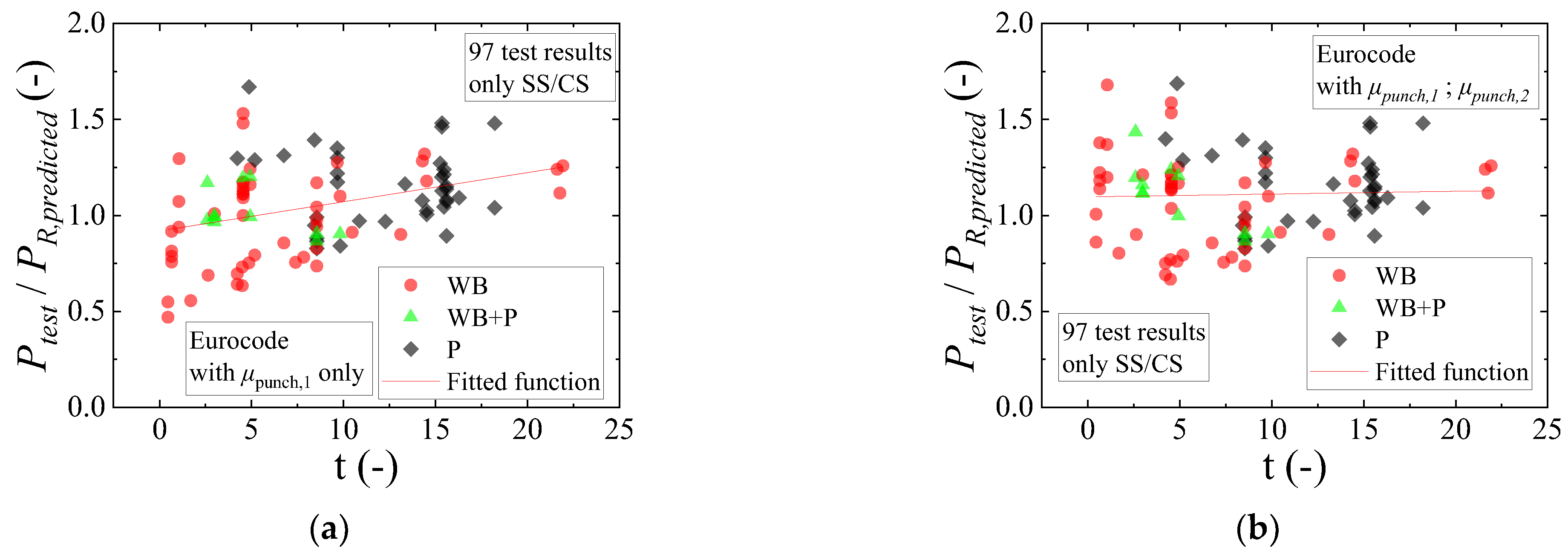
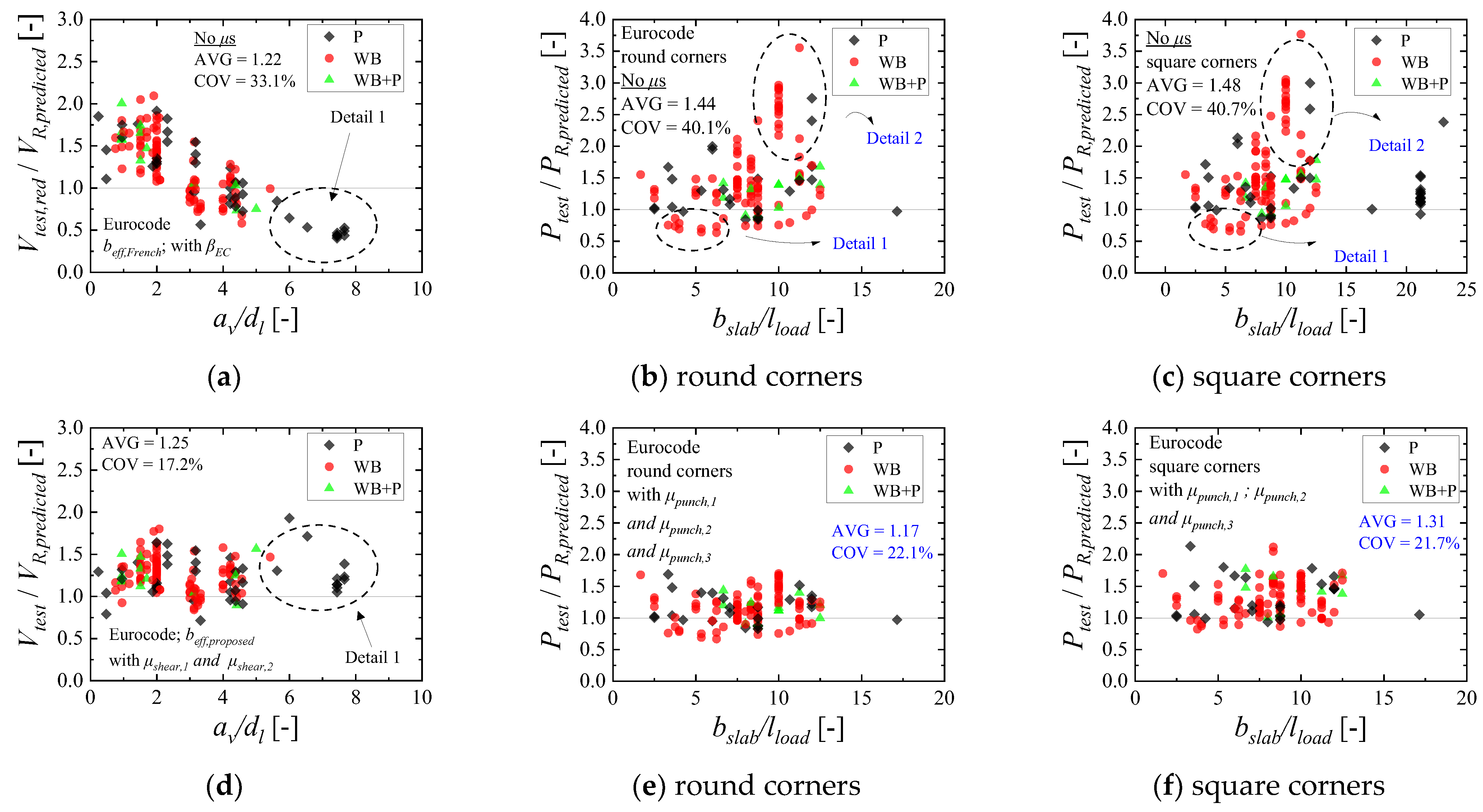
5.1. Results with the European Code Expressions
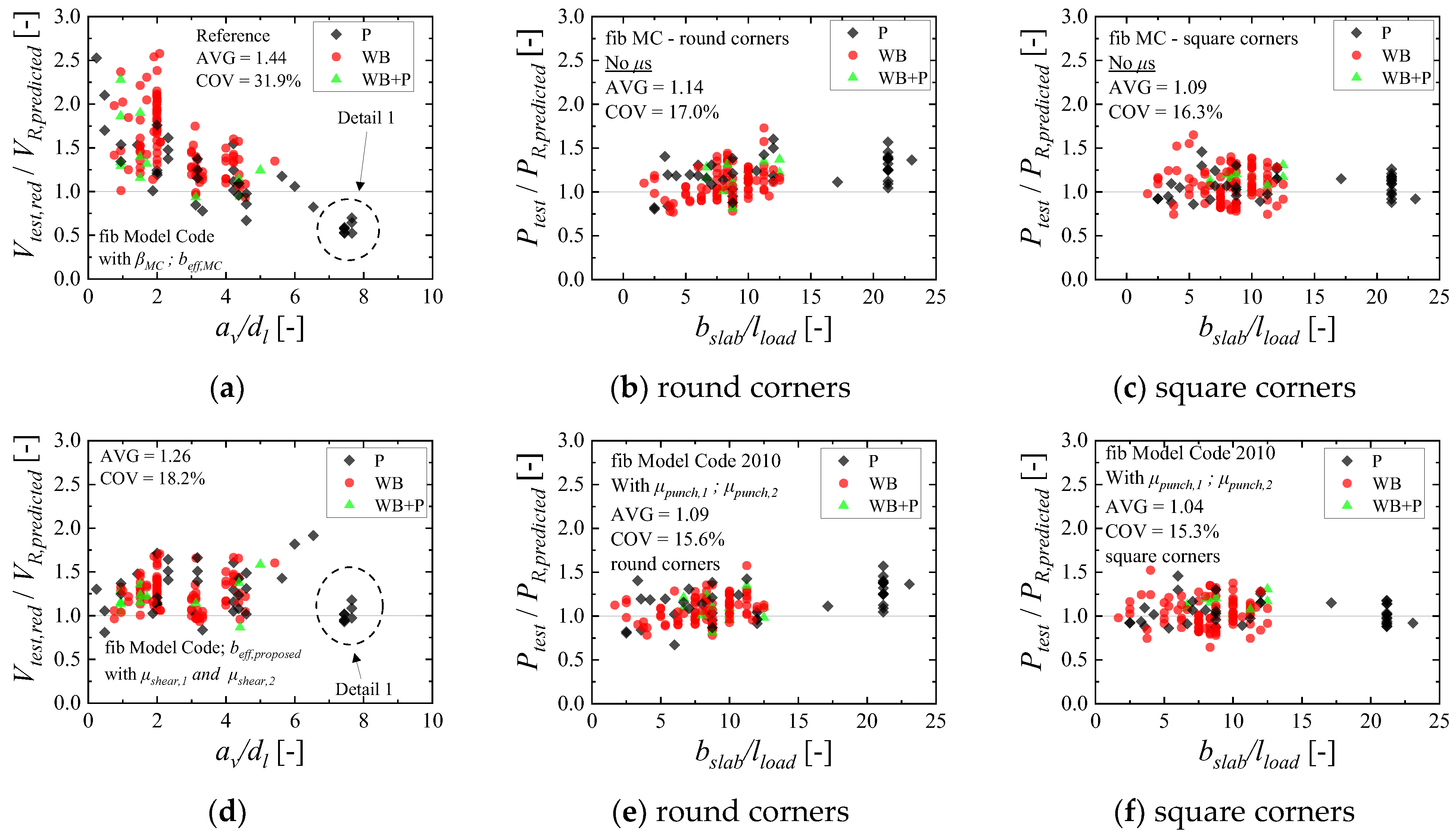
5.2. Results with the Fib Model Code 2010 Code Expressions
6. Discussion
7. Conclusions
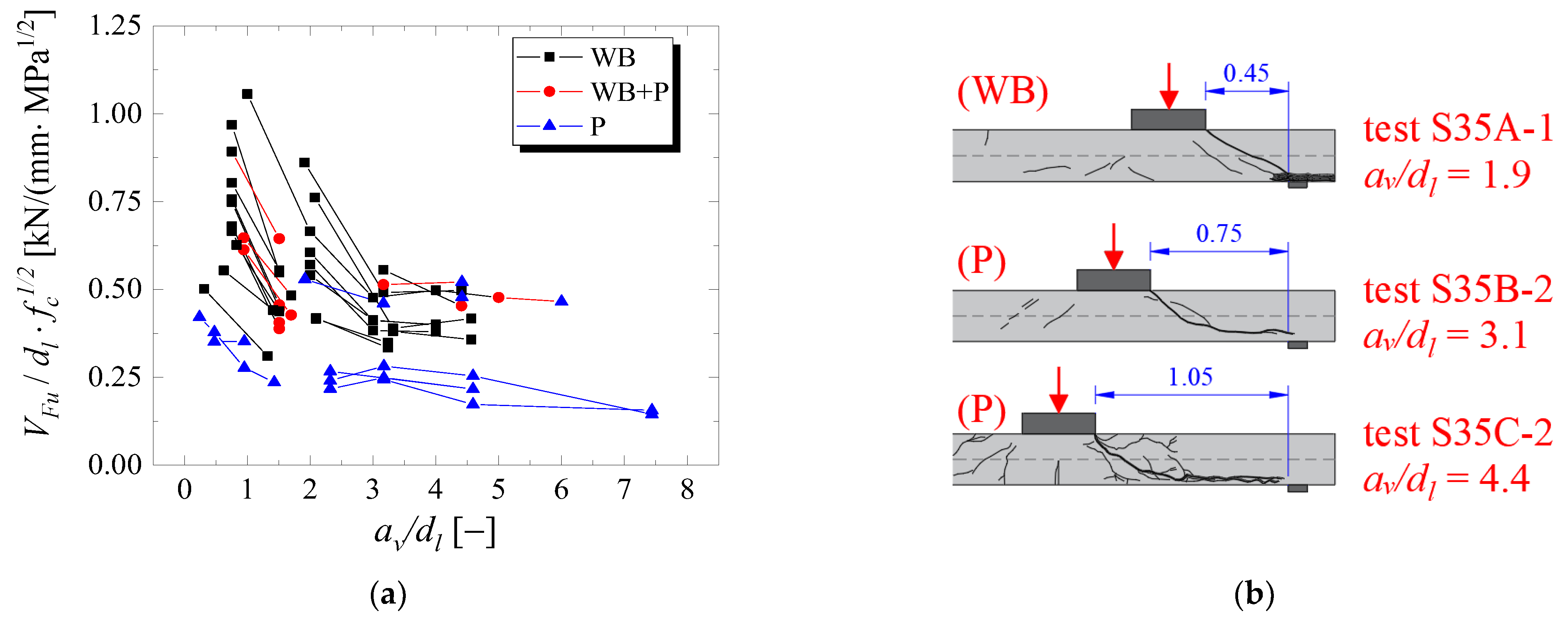
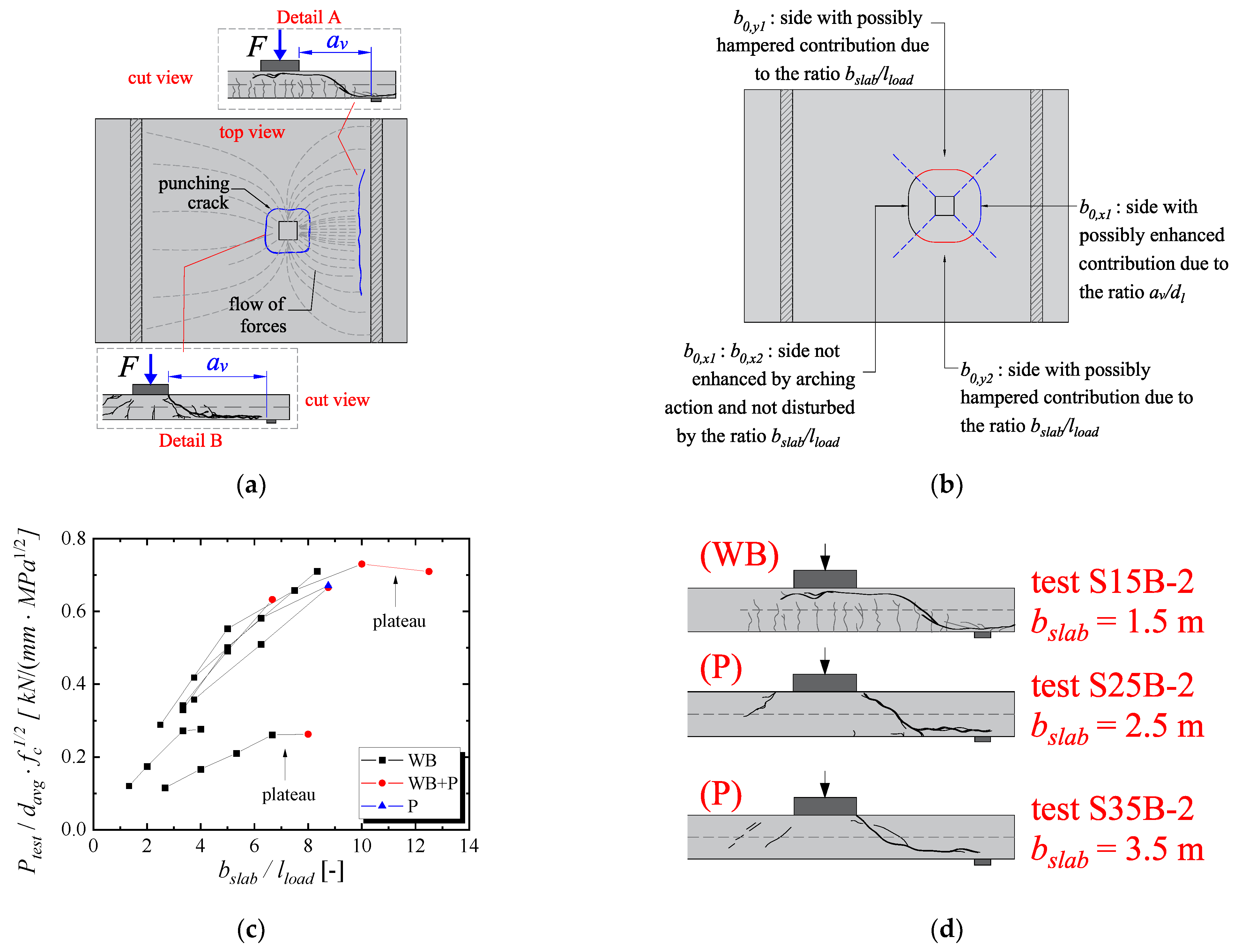
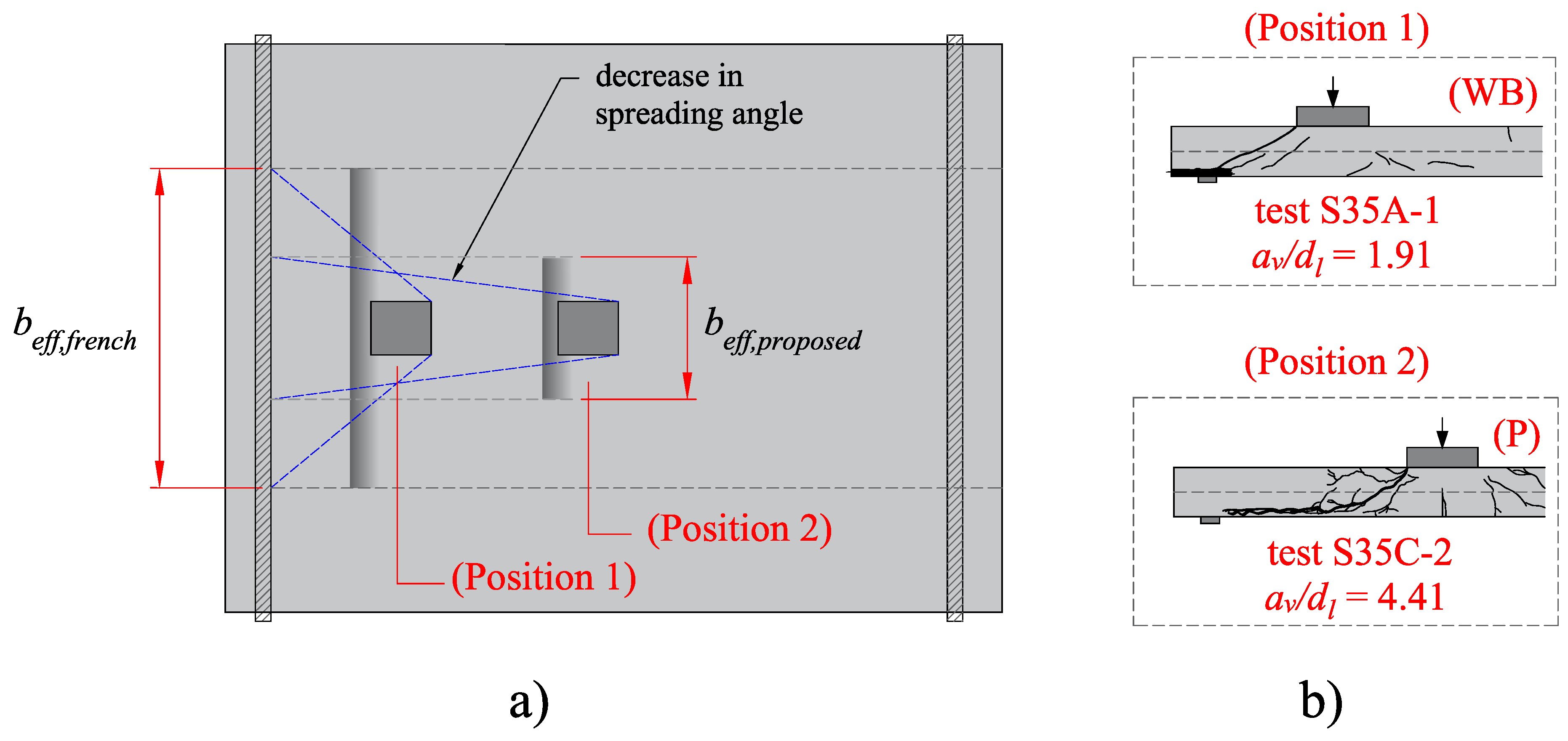
- The ultimate capacity of one-way slabs under concentrated loads increases significantly when the loads are placed close to the support at distances av/dl ≤ 2, due to arching action, regardless of the slabs failing in one-way shear as wide-beam (WB) or punching shear (P). In this study, the enhancement factor μshear,1 and μpunch,1 are applied for both one-way shear and punching shear expressions to consider this mechanism. Comparatively, the ultimate resistance of the slabs decreases significantly when the loads are placed at distances av/dl ≥ 3. At such positions, most slabs from the database failed by punching, which is a failure mechanism concentrated around the load. Therefore, a reduced effective shear width should be employed if the one-way shear resistance needs to be checked at such positions. In this study, the factor μshear,2 allows for decreasing the effective shear width for larger distances from the load to the support.
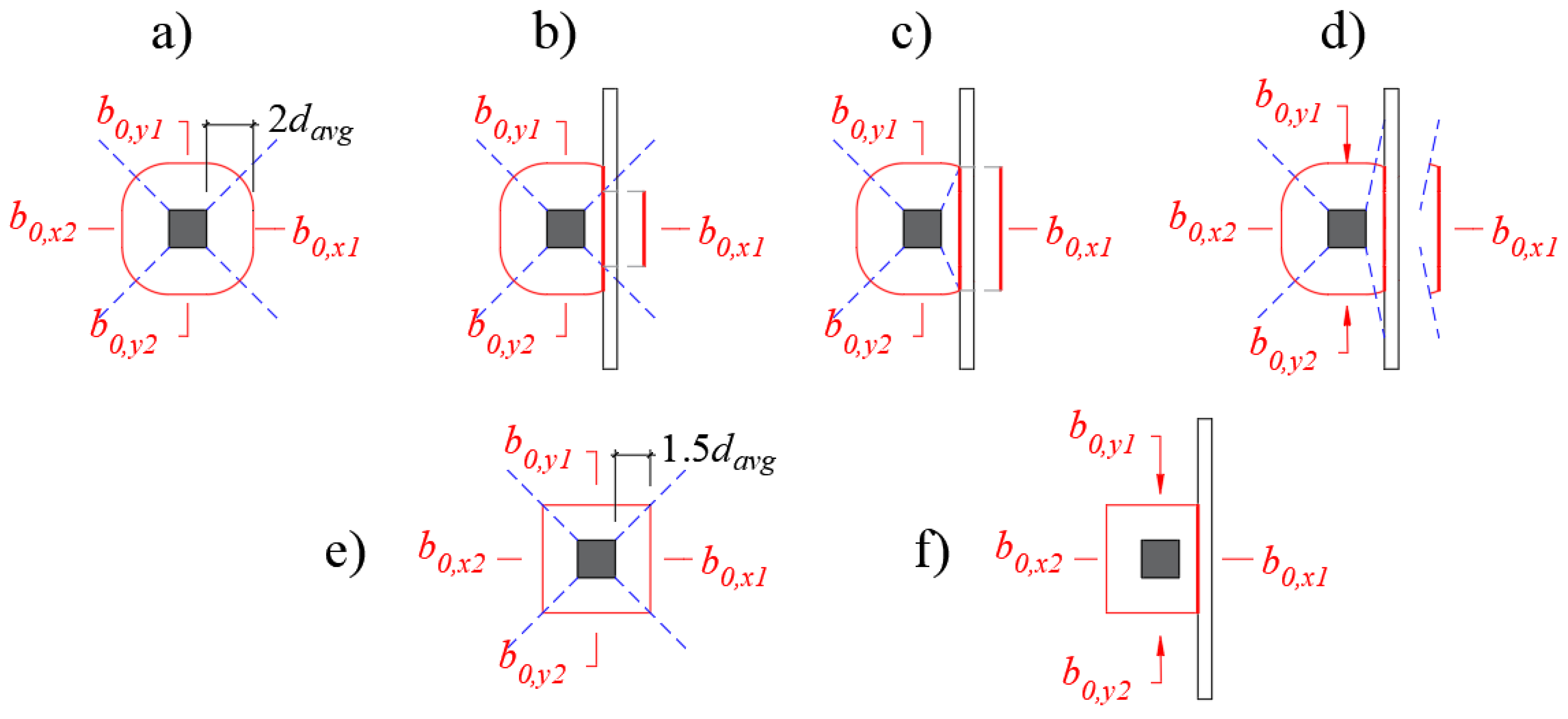
- In the punching shear resistance predictions, however, the slab width may also play a significant role. For slabs with a reduced slab width compared to the effective depth, for instance, t < 5 with t = (bslab − lload − 4davg)/davg, the contribution of the sides of the control perimeter parallel to the free edges is reduced due to the small shear flow going through these sides. In this study, it is proposed to multiply the contribution of these sides by μpunch,2 to consider this effect. In the case of cantilever slabs, and particularly with the Eurocode expressions, another aspect considerably influences the predictions of punching capacity. The punching capacity expressions use the bottom reinforcement of the slab in the calculations, and many of these slabs fail in one-way shear, presenting higher demand on the top reinforcement of the slabs. Consequently, the predictions of punching capacity can become overly conservative for loads placed at distances av/dl close to 2. Because of this, a third factor was needed to reach enhanced predictions for cantilever slabs using the Eurocode expressions.
- The one-way shear capacity predictions are significantly enhanced by considering the arching action for loads close to the support by a factor μshear,1. Furthermore, the transition from one-way shear failures as wide-beam (WB) to punching failures (P) by increasing the shear slenderness av/dl can be considered in a simplified way by multiplying the predicted effective shear width beff,french by the factor μshear,2. In this way, enhanced predictions of one-way shear capacity can be achieved for the tests, even when they fail by punching. In practice, these observations were valid for both codes (Eurocode and fib Model Code).
- The predictions of punching capacity with the Eurocode expressions are significantly enhanced considering the factors related to arching action and to the slab width in the proposed approach. In the case of the fib Model Code 2010 expression, these enhancements were less pronounced since the results without the proposed factors already led to relatively enhanced predictions. In other words, the proposed recommendations to calculate the slab rotations and respective shear capacity on each portion of the control perimeter (without the use of numerical models) have already led to good levels of accuracy.
- In general, the one-way shear and punching shear predictions led to similar levels of accuracy when using the proposed recommendations. In the case of the current Eurocode, the average ratio Vtest/VR,predicted was 1.25 with a coefficient of variation of 17.2%, while the average ratio Ptest/PR,predicted was 1.17 with a coefficient of variation of 22.1%. In the case of the fib Model Code 2010, the average ratio Vtest/VR,predicted was 1.26 with a coefficient of variation of 18.2% and the average ratio Ptest/PR,predicted was 1.09 with a coefficient of variation of 15.6%. Therefore, both one-way shear and punching shear predictions may lead to close estimations of the ultimate capacity, regardless of the governing failure mechanism of the slabs, when the parameters that influence the transition from one failure mechanism to another are embedded in the calculations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notation
| a | shear span: distance between the center of the support and the center of the load |
| av | clear shear span: distance between face of support and face of load |
| b0 | total length of the shear-resisting control perimeter |
| b0,x1 | side of the control perimeter in the spanning direction between the load and the closer support |
| b0,x2 | side of the control perimeter in the spanning direction between the load and the far support |
| b0,y1 | side of the control perimeter in the transverse direction close to the free edge 1 |
| b0,y2 | side of the control perimeter in the transverse direction close to the free edge 2 |
| beff | effective shear width |
| beff,proposed | proposed effective shear width |
| beff,french | French effective shear width |
| bslab | slab width |
| bload | size of the concentrated load in the slab width direction (transverse direction) |
| davg | average effective depth of the flexural reinforcement |
| dl | effective depth towards longitudinal steel |
| dt | effective depth towards transverse steel |
| dg | maximum aggregate size |
| dg0 | reference aggregate size (=16 mm in fib Model Code 2010) |
| ddg | parameter that considerers the crack roughness |
| fc | average compressive strength measured on cylinder specimens |
| fyi | steel yielding stress in the evaluated direction (x = longitudinal direction and y = transverse direction) |
| hslab | slab thickness |
| k | constant accounting for size effect in one-way shear for EN 1992-1-1:2004 |
| k1 | factor accounting for axial forces in one-way shear for EN 1992-1-1:2004 |
| kdg | coefficient for aggregate size (=32/(16 mm + dg) in fib Model Code 2010) |
| kv | factor accounting for strain effect and member size in fib Model Code 2010 |
| kψ | factor accounting for effect of crack widths and roughness of cracks on shear strength in fib Model Code 2010 |
| lspan | span length |
| lload | size of the concentrated load in the span direction |
| ls | is the length of the sides with one-way shear behavior |
| mR,i | yielding moment per unit length in the evaluated direction |
| mmax | maximum bending moment at the control section for a given applied load |
| ms,ij | averaged acting bending moment at the loading plate edge ij within the width bs |
| mEd | design bending moment at the control section |
| rs | distance between the center of the concentrated load and the line of contraflexure of moments (subscripts x, y refers to the direction considered) |
| rs,ij | distance between the center of the concentrated load and the point of contraflexure in the evaluated direction |
| v | shear force per unit length (nominal shear force) |
| vE | shear force at the control section |
| vEd | design shear force at the control section |
| vmin | minimum one-way shear resistance per unit length in EN 1992-1-1:2004 |
| vR,shear | unitary one-way shear resistance |
| vg | shear forcer per unit length in the control section placed at a/2 due to the self-weight |
| wcr | width of the critical shear crack |
| z | effective shear depth in fib Model Code 2010 |
| As | cross-sectional area of flexural reinforcement |
| CR,c | calibration factor in the shear and punching expressions of EN 1992-1-1:2004 |
| Ec | modulus of elasticity of concrete |
| Es | steel modulus of elasticity |
| F | applied concentrated load |
| FEd | design concentrated load |
| Fpredicted | predicted load that causes a one-way shear failure or two-way shear failure |
| Fu | applied concentrated load at failure |
| Fhyp | arbitrary concentrated load |
| L | span length |
| Vcontrol | total shear force going through the evaluated direction along the slab width |
| VEd | design shear action |
| VFu | shear force due to the concentrated load Fu |
| Vtest | measured one-way shear force at failure in the tests for a section at a/2. |
| VR | one-way shear capacity |
| VR,predicted | predicted one-way shear resistance |
| VRd | design one-way shear capacity |
| VR,CSCT | predicted one-way shear resistance with the CSCT expressions |
| VR,ij | punching shear strength corresponding to b0,ij |
| Ptest | maximum applied concentrated load at failure |
| PEd | design concentrated loads |
| PRd | design punching capacities |
| Ppredicted | predicted punching resistance |
| Pflex | concentrated load associated with the slab flexural capacity |
| PR,punching | total shear force resisted by punching |
| βshear | enhancement factor to account for arching action |
| ρavg | average flexural reinforcement ratio considering both directions |
| ρl | flexural reinforcement ratios in longitudinal direction |
| ρt | flexural reinforcement ratio in transverse direction |
| ψ | rotations around the loaded area |
| ψij | rotations in each side of the control perimeter |
| εx | strain in the control depth for one-way shear analyses |
| εy | is the flexural reinforcement yield strain |
| γ | concrete specific weight (assumed = 24 kN/m3 in this study) |
| γc | partial safety factor of concrete |
| μshear,1 | factor accounting for arching action in one-way shear analyses |
| μshear,2 | factor accounting for reduced beff for loads far away from the support |
| μpunch,1 | factor accounting for arching action in punching shear analyses |
| μpunching,2 | factor accounting for the influence of the slab width in the effective contribution of the sides b0,y1 and b0,y2 to the punching capacity |
| μpunching,3 | correction factor related to the load position in cantilever slabs for punching capacity predictions |
| AVG | average |
| COV | coefficient of variation |
| P | observed failure mode is punching failure |
| SS | test was performed with the load closer to the simple support |
| CS | tests was performed with the concentrated loads close to a continuous support |
| CT | test was performed with the concentrated load applied on a cantilever slab |
| WB | observed failure mode is wide-beam shear failure |
| WB + P | the observed failure mode combines characteristics of WB and P |
References
- Lantsoght, E.O.L.; van der Veen, C.; Walraven, J.; de Boer, A. Recommendations for the Shear Assessment of Reinforced Concrete Slab Bridges from Experiments. Struct. Eng. Int. 2013, 23, 418–426. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; de Boer, A.; van der Veen, C. Levels of Approximation for the Shear Assessment of Reinforced Concrete Slab Bridges. Struct. Concr. 2017, 18, 143–152. [Google Scholar] [CrossRef]
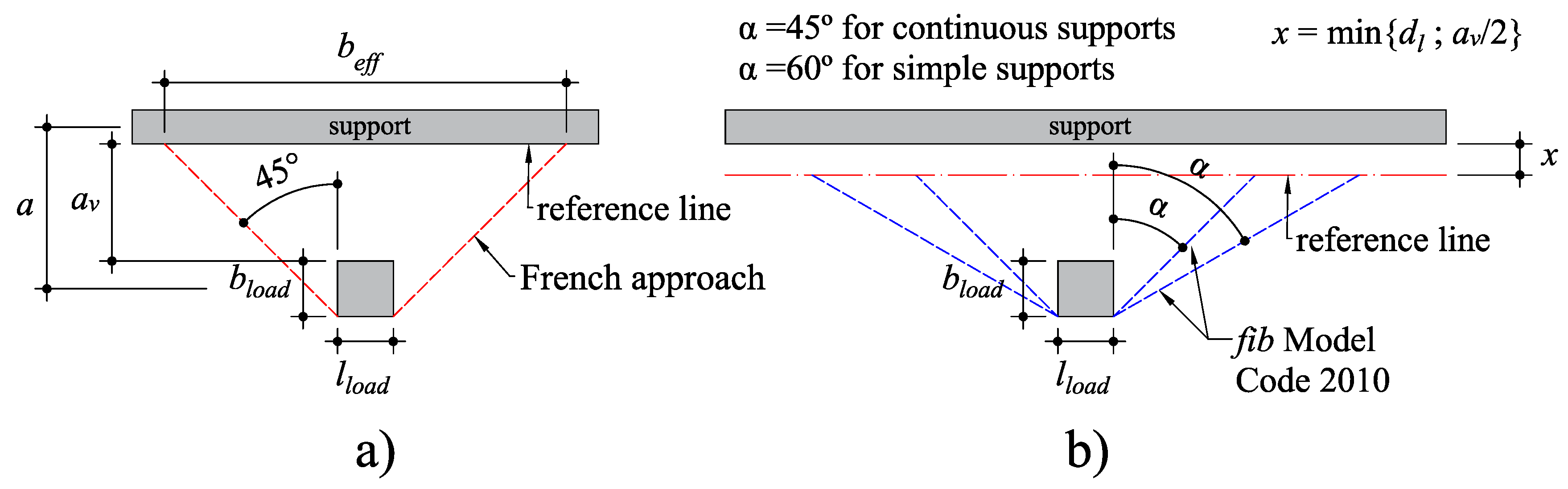
- Coin, A.; Thonier, H. Essais Sur Le Cisaillement Des Dalles En Beton Arme. In Annales du Batiment et des Travaux Publics; EIVP: Paris, France, 2007; pp. 7–16. [Google Scholar]
- FD P 18-717; Eurocode 2-Calcul des Structures en Béton-Guide D’application des Normes NF EN 1992. Association Française de Normalisation (AFNOR): Saint-Denis, France, 2013.
- Lantsoght, E.O.L.; van der Veen, C.; Walraven, J.C. Shear in One-Way Slabs under Concentrated Load Close to Support. ACI Struct. J. 2013, 110, 275–284. [Google Scholar] [CrossRef]
- Reiβen, K.; Classen, M.; Hegger, J. Shear in Reinforced Concrete Slabs-Experimental Investigations in the Effective Shear Width of One-Way Slabs under Concentrated Loads and with Different Degrees of Rotational Restraint. Struct. Concr. 2018, 19, 36–48. [Google Scholar] [CrossRef]
- Henze, L.; Rombach, G.A.; Harter, M. New Approach for Shear Design of Reinforced Concrete Slabs under Concentrated Loads Based on Tests and Statistical Analysis. Eng. Struct. 2020, 219, 110795. [Google Scholar] [CrossRef]
- Fernández, P.G.; Marí, A.; Oller, E. Theoretical Prediction of the Shear Strength of Reinforced Concrete Slabs under Concentrated Loads Close to Linear Supports. Struct. Infrastruct. Eng. 2021, 1–14. [Google Scholar] [CrossRef]
- Fernández, P.G.; Marí, A.; Oller, E. Experimental Investigation of the Shear Strength of One-Way Reinforced Concrete (RC) Slabs Subjected to Concentrated Loads and in-Plane Transverse Axial Tension. Struct. Concr. 2021, 22, 3661–3676. [Google Scholar] [CrossRef]
- Halvonik, J.; Vidaković, A.; Vida, R. Shear Capacity of Clamped Deck Slabs Subjected to a Concentrated Load. J. Bridge Eng. 2020, 25, 04020037. [Google Scholar] [CrossRef]
- Natário, F.; Fernández Ruiz, M.; Muttoni, A. Shear Strength of RC Slabs under Concentrated Loads near Clamped Linear Supports. Eng. Struct. 2014, 76, 10–23. [Google Scholar] [CrossRef]
- Sousa, A.M.D.; el Debs, M.K. Shear Strength Analysis of Slabs without Transverse Reinforcement under Concentrated Loads According to ABNT NBR 6118:2014. IBRACON Struct. Mater. J. 2019, 12, 658–693. [Google Scholar] [CrossRef]
- de Sousa, A.M.D.; Lantsoght, E.O.L.; Yang, Y.; el Debs, M.K. Extended CSDT Model for Shear Capacity Assessments of Bridge Deck Slabs. Eng. Struct. 2021, 234, 111897. [Google Scholar] [CrossRef]
- Reißen, K. Zum Querkrafttragverhalten von Einachsig Gespannten Stahlbe-Tonplatten Ohne Querkraftbewehrung Unter Einzellasten. Ph.D. Thesis, Faculty of Civil Engineering, RWTH Aachen University, Aachen, Germany, 2016. [Google Scholar]
- de Sousa, A.M.D.; Lantsoght, E.O.L.; el Debs, M.K. One-Way Shear Strength of Wide Reinforced Concrete Members without Stirrups. Struct. Concr. 2020, 968–992. [Google Scholar] [CrossRef]
- Yang, Y.; den Uijl, J.; Walraven, J.C. Critical Shear Displacement Theory: On the Way to Extending the Scope of Shear Design and Assessment for Members without Shear Reinforcement. Struct. Concr. 2016, 17, 790–798. [Google Scholar] [CrossRef]
- Muttoni, A.; Fernandez Ruiz, M. Shear Strength of Members without Transverse Reinforcement as Function of Critical Shear Crack Width. ACI Struct. J. 2008, 105, 163–172. [Google Scholar] [CrossRef]
- Regan, P.E.; Rezai-Jorabi, H. Shear Resistance of One-Way Slabs Under Concentrated Loads. ACI Struct. J. 1988, 85, 150–157. [Google Scholar] [CrossRef]
- Regan, P.E. Shear Resistance of Concrete Slabs at Concentrated Loads Close to Supports; Polytechnic of Central: London, UK, 1982. [Google Scholar]
- Vaz Rodrigues, R.; Fernández Ruiz, M.; Muttoni, A. Shear Strength of R/C Bridge Cantilever Slabs. Eng. Struct. 2008, 30, 3024–3033. [Google Scholar] [CrossRef]
- Fédération Internationale du Béton (FIB). Fib Model Code for Concrete Structures 2010. In Ernst & Sohn-Fédération Internationale du Béton; Bulletin 65: Lausanne, Switzerland, 2012; Volumes 1–2. [Google Scholar]
- NEN-EN 1992-1-1; Eurocode 2: Design of Concrete Structures-Part 1-1: General Rules and Rules for Buildings. Comité Européen de Normalisation: Brussels, Belgium, 2005.
- de Sousa, A.M.D.; Lantsoght, E.O.L.; Setiawan, A.; el Debs, M.K. Transition from One-Way to Two-Way Shear by Coupling LEFEA and the CSCT Models. In Proceedings of the fib Symposium 2021, Concrete Structures: New Trends for Eco-Efficiency and Performance, Lisbon, Portugal, 14–16 June 2021. [Google Scholar]
- de Sousa, A.M.D.; Lantsoght, E.O.L.; el Debs, M.K. Transition between Shear and Punching in RC Slabs: Review and Predictions with ACI Code Expressions. ACI Struct. J. 2023, 120. [Google Scholar] [CrossRef]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures-Part 1-1: General Rules and Rules for Buildings. Comité Européen de Normalisation: Brussels, Belgium, 2004.
- Lantsoght, E.O.L.; van der Veen, C.; Walraven, J.C.; de Boer, A. Database of Wide Concrete Members Failing in Shear. Mag. Concr. Res. 2015, 67, 33–52. [Google Scholar] [CrossRef]
- Pastore, M.V.F.; Vollum, R.L. Shear Enhancement in RC Beams with Stirrups Simultaneously Loaded within 2d and at 3d from Supports. Eng. Struct. 2022, 264, 114408. [Google Scholar] [CrossRef]
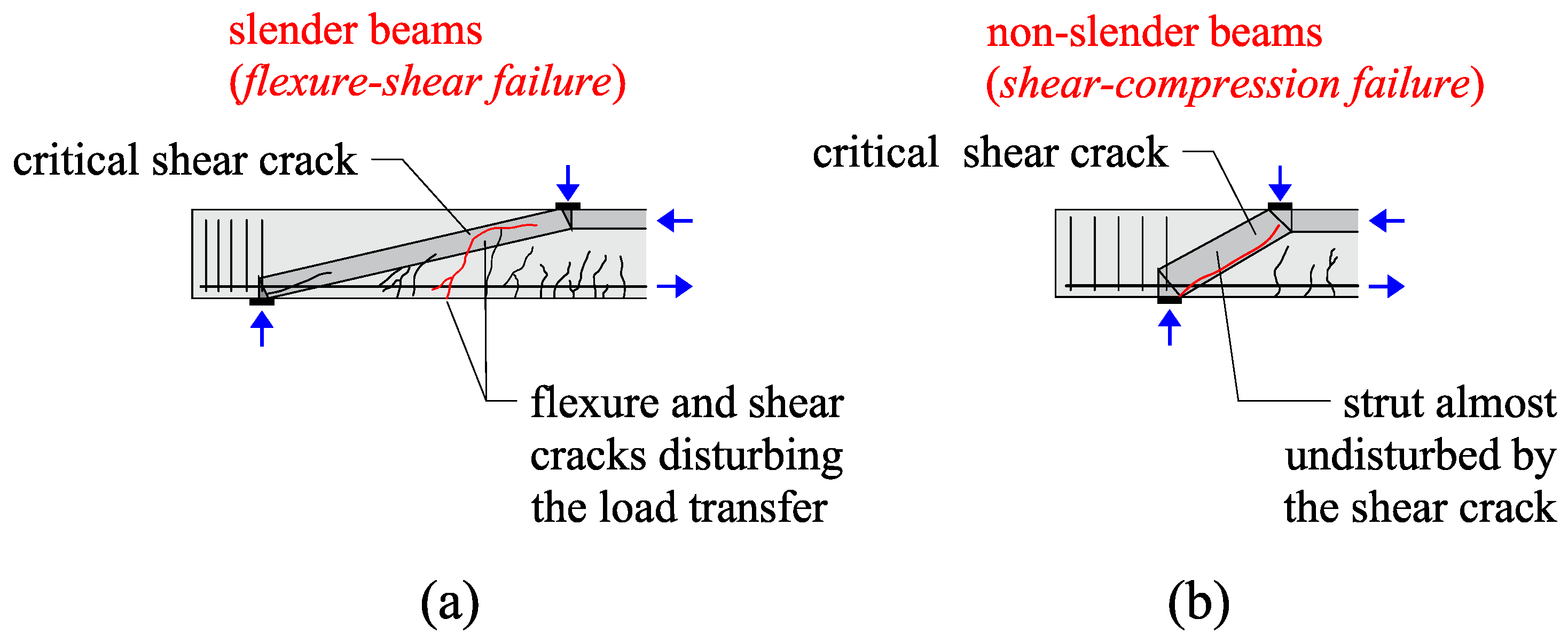
- Bairán, J.M.; Menduiña, R.; Marí, A.; Cladera, A. Shear Strength of Non-Slender Reinforced Concrete Beams. ACI Struct. J. 2020, 117, 277–290. [Google Scholar] [CrossRef]
- de Sousa, A.M.D.; Lantsoght, E.O.L.; el Debs, M.K. Databases of One-Way Slabs under Concentrated Loads: Parameter Analyses and Validation of the Proposed Approach; Zenodo: Geneva, Switzerland, 2022; Available online: https://zenodo.org/record/5911469 (accessed on 24 November 2022).
- Bui, T.T.; Limam, A.; Nana, W.-S.-A.; Ferrier, E.; Bost, M.; Bui, Q.-B. Evaluation of One-Way Shear Behaviour of Reinforced Concrete Slabs: Experimental and Numerical Analysis. Eur. J. Environ. Civ. Eng. 2017, 24, 190–216. [Google Scholar] [CrossRef]
- Carvalho, A.S. De Análise Experimental de Lajes Lisas de Concreto Armado de Alta Resistência Com Metacaulim Apoiadas Em Pilares Retangulares e Armadas à Punção. Master’s Thesis, Departamento de Engenharia Civil, Universidade Federal do Pará, Belém, Brazil, 2006. [Google Scholar]
- Damasceno, L.S.R. Experimental Analysis of One-Way Reinforced Concrete Flat Slabs in Punching Shear with Rectangular Columns (In Portuguese: Análise Experimental de Lajes Lisas Unidirecionais de Concreto Armado Com Pilares Retangulares Ao Puncionamento). Masters’ Thesis, Departamento de Engenharia Civil, Universidade Federal do Pará, Belém, Brazil, 2007. [Google Scholar]
- de P. Ferreira, M. Experimental Analysis of One-Way Reinforced Concrete Flat Slabs in Axis or Non-Axis-Symmetric Punching Shear (in Portuguese: Análise Experimental de Lajes Lisas Unidirecionais de Concreto Armado Ao Puncionamento Simétrico Ou Assimétrico). Master’s Thesis, Universidade Federal do Pará, Belém, Brazil, 2006. [Google Scholar]
- Lantsoght, E.O.L. Shear in Reinforced Concrete Slabs under Concentrated Loads Close to Supports. Ph.D. Thesis, Faculty of Civil Engineering and Geosciences, Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Natário, F.; Fernández Ruiz, M.; Muttoni, A. Experimental Investigation on Fatigue of Concrete Cantilever Bridge Deck Slabs Subjected to Concentrated Loads. Eng. Struct. 2015, 89, 191–203. [Google Scholar] [CrossRef]
- Rombach, G.A.; Latte, S. Shear Resistance of Bridge Decks without Shear Reinforcement. In Proceedings of the International Fib Symposium, Amsterdam, The Netherlands, 19–21 May 2008; pp. 519–525. [Google Scholar]
- Rombach, G.; Latte, S. Querkrafttragfähigkeit Von Fahrbahnplatten Ohne Querkraftbewehrung. Beton-Und Stahlbetonbau 2009, 104, 642–656. [Google Scholar] [CrossRef]
- Rombach, G.; Henze, L. Querkrafttragfähigkeit von Stahlbetonplatten Ohne Querkraftbewehrung Unter Konzentrierten Einzellasten. Beton- Und Stahlbetonbau 2017, 112, 568–578. [Google Scholar] [CrossRef]
- Vaz Rodrigues, R. LE JOUR DE L’ESSAI A L’ L’IS-BETON. In Essai d’un Porte-à-Faux de Pont Sous Charge Concentrée; ENAC: Lausanne, Switzerland, 2002; p. 88. [Google Scholar]
- Vida, R.; Halvonik, J. Experimentálne Overovanie Šmykovej Odolnosti Mostovkových Dosiek (Experimental Verification of Shear Resistance of Bridge Deck Slabs). Inžinierske Stavby/InženýrskÉ Stavby 2018, 4, 2–6. [Google Scholar]
- Lantsoght, E.O.L.; van der Veen, C.; de Boer, A.; Walraven, J.C. Transverse Load Redistribution and Effective Shear Width in Reinforced Concrete Slabs. Heron 2015, 60, 145–179. [Google Scholar]
- Lantsoght, E.O.L.; de Boer, A.; van der Veen, C.; Walraven, J.C. Effective Shear Width of Concrete Slab Bridges. Proc. Inst. Civ. Eng. -Bridge Eng. 2015, 168, 287–298. [Google Scholar] [CrossRef]
- Muttoni, A.; Fernandez Ruiz, M. Shear in Slabs and Beams: Should They Be Treated in the Same Way? In Proceedings of the FIB Bulletin 57: Shear and Punching shear in RC and FRC Elements, Salò, Italy, 15–16 October 2010; pp. 105–128. [Google Scholar]
- Marí, A.; Cladera, A.; Oller, E.; Bairán, J.M. A Punching Shear Mechanical Model for Reinforced Concrete Flat Slabs with and without Shear Reinforcement. Eng. Struct. 2018, 166, 413–426. [Google Scholar] [CrossRef]
- Shu, J.; Honfi, D.; Plos, M.; Zandi, K.; Magnusson, J. Assessment of a Cantilever Bridge Deck Slab Using Multi-Level Assessment Strategy and Decision Support Framework. Eng. Struct. 2019, 200, 109666. [Google Scholar] [CrossRef]
- de Sousa, A.M.D.; Lantsoght, E.O.L.; Genikomsou, A.S.; Krahl, P.A.; el Debs, M.K. Behavior and Punching Capacity of Flat Slabs with the Rational Use of UHPFRC: NLFEA and Analytical Predictions. Eng. Struct. 2021, 244, 112774. [Google Scholar] [CrossRef]


| Code | |
|---|---|
| EN 1992-1-1:2004 [25] | (11) |
| fib Model Code 2010 [21] | (12) |
| Code | Sup. Cond. | Factors |
|---|---|---|
| EN 1992-1-1:2004 [25] | SS, CS | (34) |
| EN 1992-1-1:2004 [25] | CT | (35) |
| fib Model Code 2010 [21] | SS, CS | (36) |
| fib Model Code 2010 [21] | CT | (37) |
| Code | Parameter | Factor μpunch,2 |
|---|---|---|
| Eurocode EN 1992-1-1:2004 | (40) | |
| fib Model Code 2010 | (41) |
| Code | Factor μpunch,2 |
|---|---|
| Eurocode EN 1992-1-1:2004 | (42) |
| fib Model Code 2010 | (43) |
| Parameter | Minimum | Maximum |
|---|---|---|
| h (m) | 0.10 | 0.30 |
| bslab (m) | 0.60 | 4.50 |
| t = (bslab − lload − 4davg)/davg | 0.45 | 27.21 |
| lspan (m) | 0.90 | 4.00 |
| bslab/lload (-) | 1.67 | 23.08 |
| bslab/dl (-) | 5.66 | 29.41 |
| av/dl (-) | 0.24 | 7.66 |
| fc (MPa) | 19.20 | 77.74 |
| ρl (%) | 0.602 | 2.150 |
| ρt (%) | 0.132 | 1.526 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Sousa, A.M.D.; Lantsoght, E.O.L.; El Debs, M.K. Shear and Punching Capacity Predictions for One-Way Slabs under Concentrated Loads Considering the Transition between Failure Mechanisms. Buildings 2023, 13, 434. https://doi.org/10.3390/buildings13020434
de Sousa AMD, Lantsoght EOL, El Debs MK. Shear and Punching Capacity Predictions for One-Way Slabs under Concentrated Loads Considering the Transition between Failure Mechanisms. Buildings. 2023; 13(2):434. https://doi.org/10.3390/buildings13020434
Chicago/Turabian Stylede Sousa, Alex Micael Dantas, Eva Olivia Leontien Lantsoght, and Mounir Khalil El Debs. 2023. "Shear and Punching Capacity Predictions for One-Way Slabs under Concentrated Loads Considering the Transition between Failure Mechanisms" Buildings 13, no. 2: 434. https://doi.org/10.3390/buildings13020434
APA Stylede Sousa, A. M. D., Lantsoght, E. O. L., & El Debs, M. K. (2023). Shear and Punching Capacity Predictions for One-Way Slabs under Concentrated Loads Considering the Transition between Failure Mechanisms. Buildings, 13(2), 434. https://doi.org/10.3390/buildings13020434







