A Numerical Study on the Exergy Performance of a Hybrid Radiant Cooling System in an Office Building: Comparative Case Study and Analysis
Abstract
:1. Introduction
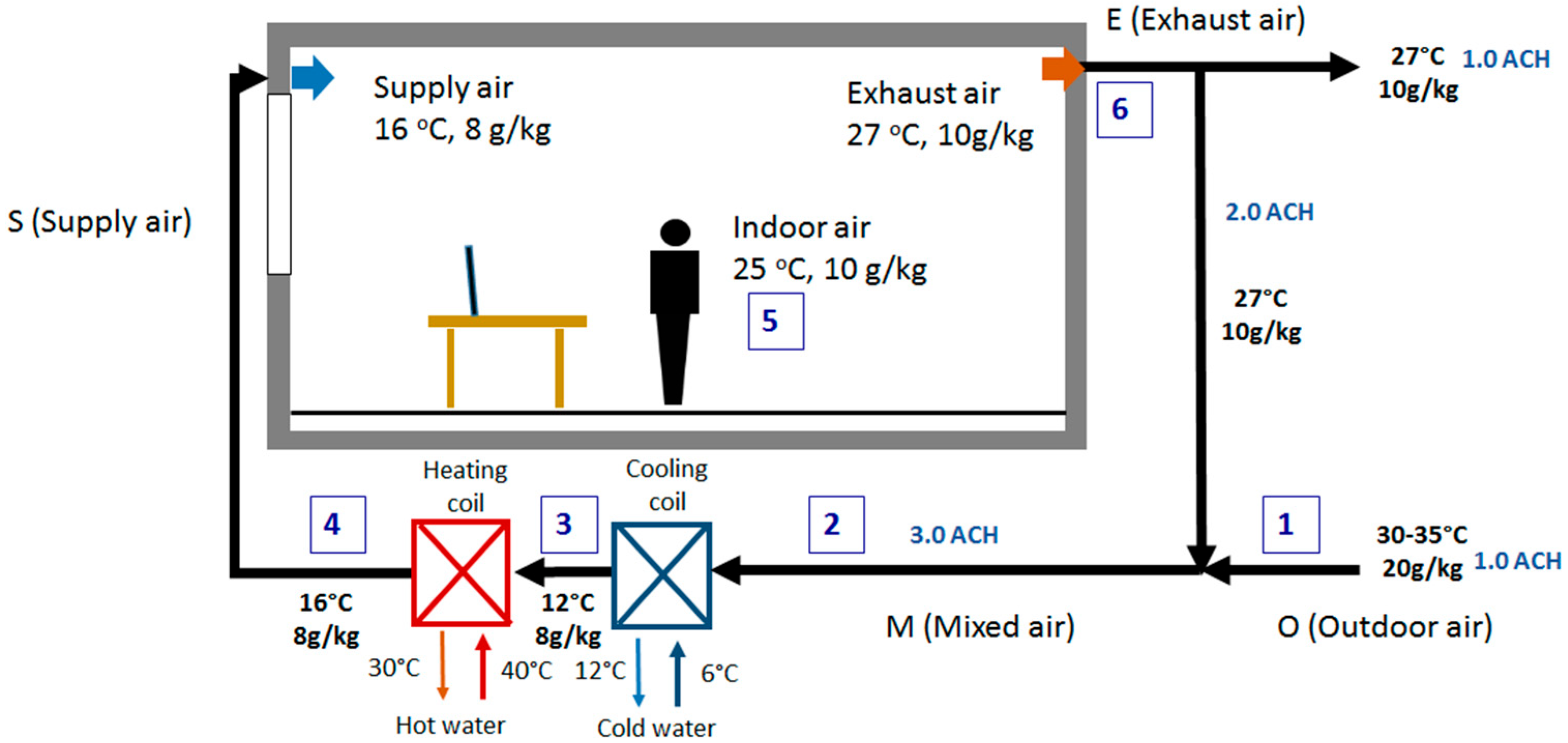
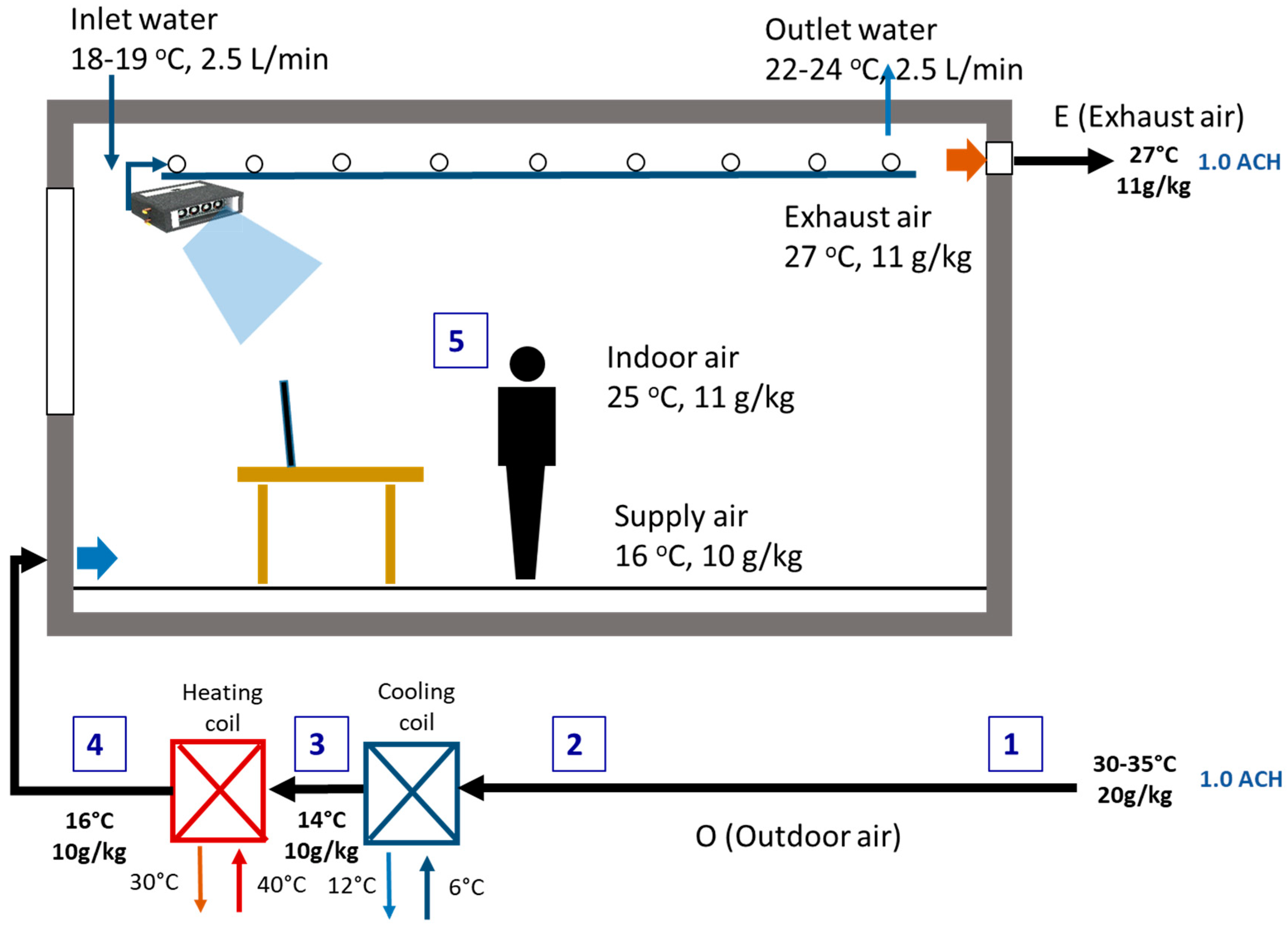
2. System Description and Methods
2.1. Cooling Systems in a Building
2.2. Weather and Building Characteristics as Case Studies in China
2.3. Energy and Exergy Performance of the Systems
2.3.1. Energy Load Calculation
2.3.2. Exergy Load Calculation
2.3.3. Exergy Efficiencies
3. Results
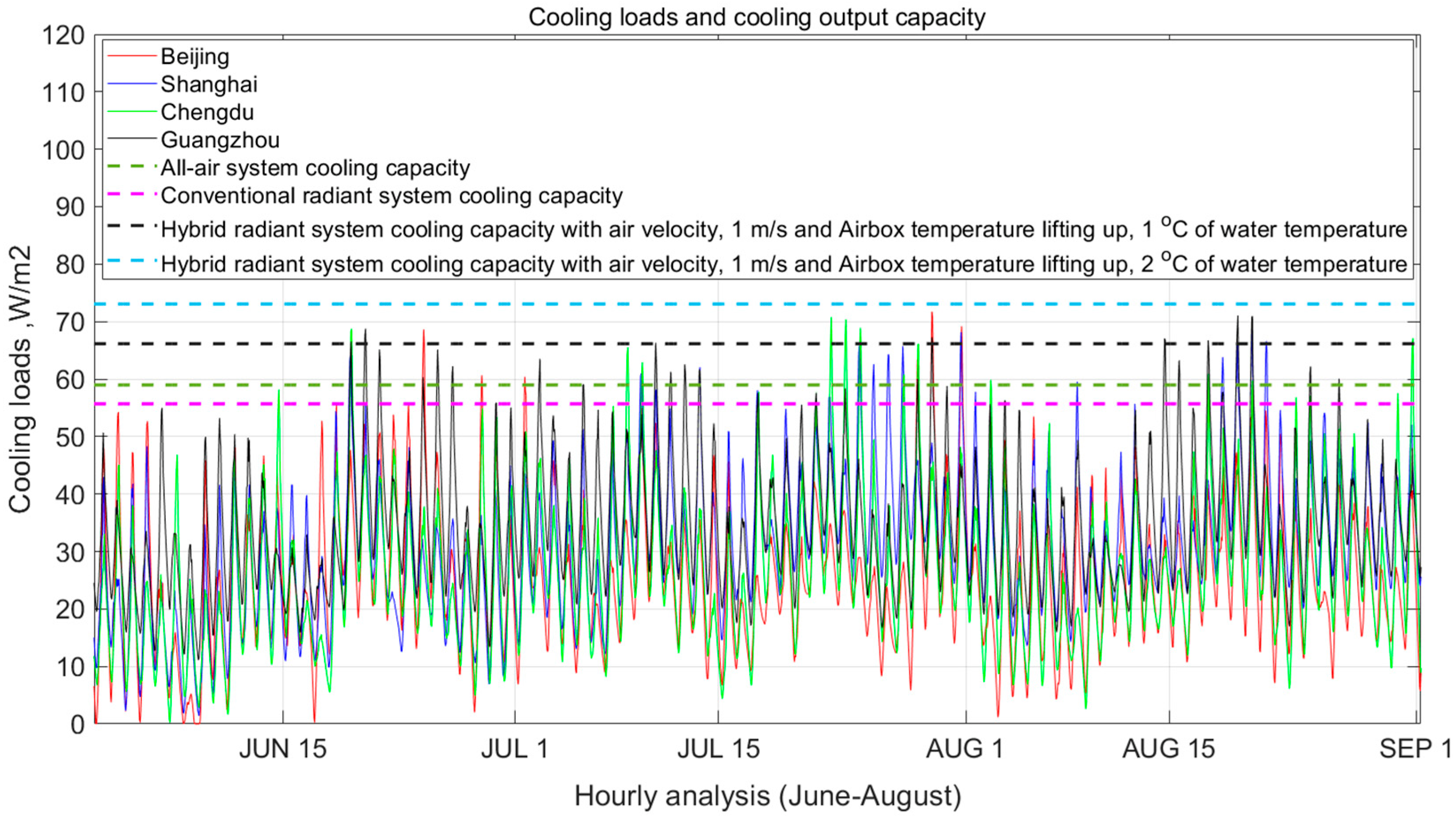
3.1. Energy Performance of Systems
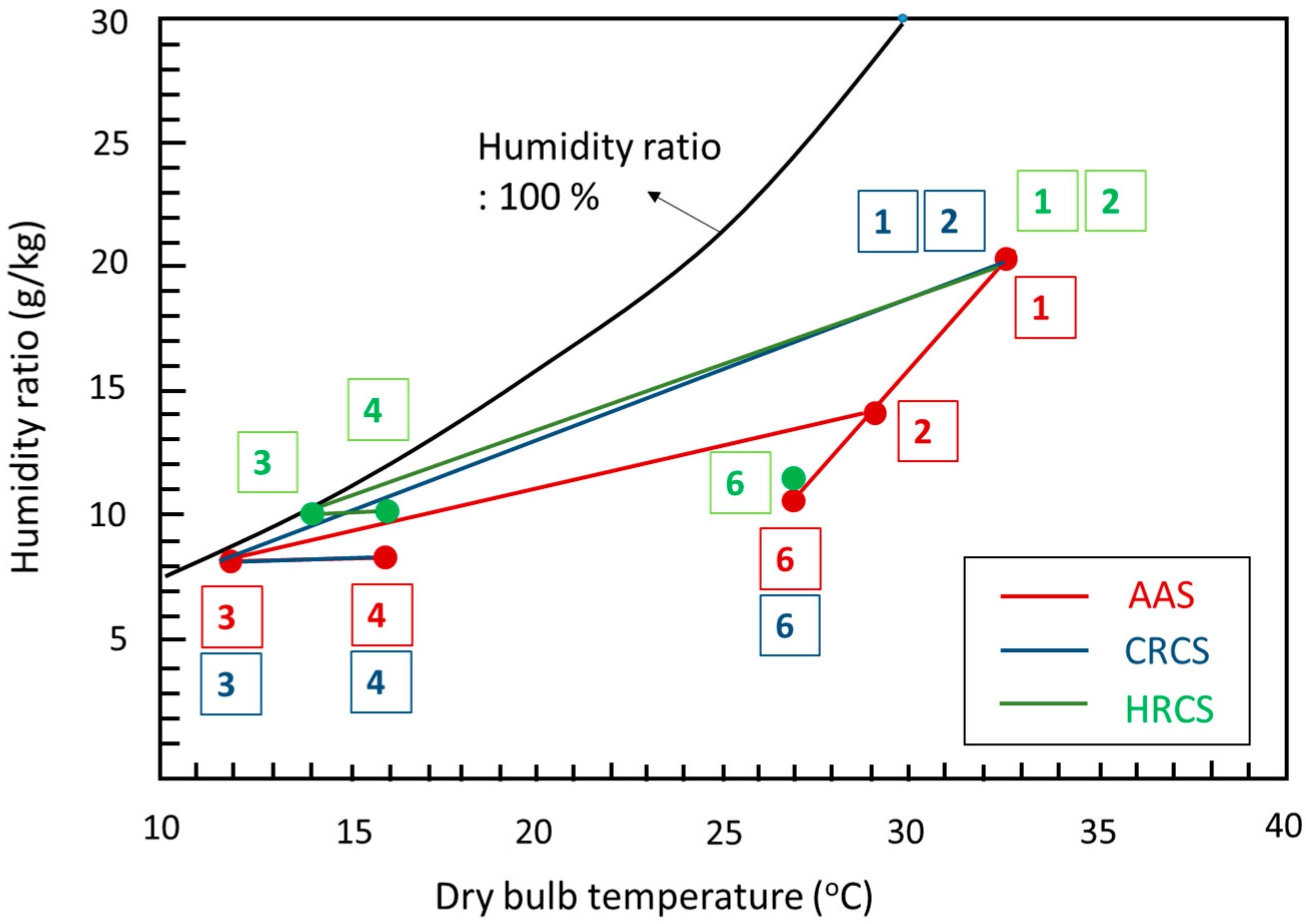
3.2. Exergy Analysis
4. Conclusions
- In the hot and humid summer season, the HRCS was the most efficient cooling strategy due to the extra cooling output provided by the compact convector and the relatively low exergy destruction in the cooling and dehumidification process with higher-temperature cooling sources.
- The HRCS released an additional 20–30% of cooling output, and it could adapt well in extreme hot and humid weather conditions.
- The comparison analysis using the four different weather datasets showed simple and rational exergy efficiency; as a result, the ambient condition, temperature, and humidity ratio significantly impacted the exergy efficiency ratio.
- The overall CIR of the HRCS with an airbox convector was approximately 185% higher than that of the AAS and 8.5% higher than that of the CRCS.
- The HRCS presented the most efficient characteristic in reducing the environmental impact and increasing the benefits compared with the AAS and CRCS in hot and humid summer conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| cp.air | specific heat capacity value of air, kJ/(kg⸱K) |
| cp.water | specific heat capacity of water, kJ/(kg⸱K) |
| cp.vapor | specific heat capacity of water vapor, kJ/(kg⸱K) |
| h | enthalpy, kJ/kg |
| hfg | specific enthalpy value of the vaporization of water, kJ/kg |
| mass flow rate, kg/h | |
| mass flow rate of air, kg/h | |
| mass flow rate of water, kg/h | |
| p | pressure, Pa |
| outdoor air pressure, Pa | |
| saturated water vapor pressure, Pa | |
| Pairbox | airbox energy load, kJ/h |
| Pfan | fan electricity, kJ/h |
| Ppump | pump electricity, kJ/h |
| cooling load, kJ/h | |
| lateral cooling energy load, kJ/h | |
| sensible cooling energy load, kJ/h | |
| total cooling energy load, kJ/h | |
| Rair | specific ideal gas constant, J/(kg⸱K) |
| T | temperature, K |
| indoor air temperature at the time of τ, K | |
| air or water volumetric flow rate, m3/h | |
| Greek letters | |
| Δ | difference or change in the specific parameter |
| ηpump | pump efficiency, % |
| ηfan | fan efficiency, % |
| τ | time |
| specific volume for liquid water, m3/kg | |
| relative humidity, % | |
| simple or universal exergy efficiency, % | |
| rational and functional exergy efficiency, % | |
| ω | humidity ratio, kg/kg |
| ῶ | mole fraction ratio |
| Abbreviation | |
| AAS | all-air system |
| ACH | air change per hour, h−1 |
| AHU | air handling unit |
| An | anergy, kJ/h |
| CIR | cooling impact ratio, % |
| COP | coefficient of performance |
| CRCS | conventional radiant cooling system |
| ex | specific exergy, kJ/kg |
| extot | total specific exergy, kJ/kg |
| exphys | physical exergy, kJ/kg |
| exchem | chemical exergy, kJ/kg |
| HRCS | hybrid radiant cooling system |
| HVAC | heating, ventilation, and air-conditioning |
| Subscripts | |
| 1, 2, 3, 4 | process number presented in the Figure 1, Figure 2 and Figure 3 |
| 1a, 2a, 3a | air mass flow in the process number presented in the Figure 1, Figure 2 and Figure 3 |
| a(ir) | air |
| c | cooling |
| acc | actual cooling capacity |
| cc | cooling coil |
| ceil | ceiling |
| ceil.re | ceiling return |
| ceil.sup | ceiling supply |
| chc | chilled ceiling |
| cool | cooling |
| cool.re | cooling return |
| cool.sup | cooling supply |
| cooling and dehum | cooling and dehumidification process for the systems |
| cw | condensed water |
| chem | chemical |
| desired.out | desired outdoor air |
| e.c. | energy consumption |
| hc | heating coil |
| hot.sup | hot water supply |
| hot.re | hot water return |
| in | inlet |
| input | exergy or anergy input |
| lat | latent cooling load |
| max | maximum |
| mix.air | mixed air |
| o | outdoor |
| out | outlet |
| p | pressure |
| phys | physical |
| rat | rational ratio |
| re | return |
| rec | re-circulated |
| reheat | reheated air |
| sat | saturated |
| sen | sensible cooling load |
| sim | simple |
| sup | supply |
| sup.air | supply air |
| sup.water | supply water |
| tot | total |
| w | water |
References
- De Ia Rue du Can, S.; Price, L. Sectoral trends in global energy use and greenhouse gas emissions. Energy Policy 2008, 36, 1386–1403. [Google Scholar] [CrossRef]
- Andrić, I.; Koc, M.; Al-Ghamdi, S.G. A review of climate change implications for built environment: Impacts, mitigation measures and associated challenges in developed and developing countries. J. Clean. Prod. 2019, 211, 83–102. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, J.; Zhu, X.; Wang, X.; Du, Y.; Miao, J. Experimental Study on Operating Characteristic of a Combined Radiant Floor and Fan Coil Cooling System in a High Humidity Environment. Buildings 2022, 12, 499. [Google Scholar] [CrossRef]
- Liu, J.; Ren, J.; Zhang, L.; Xie, X.; Kim, M.K.; Zhang, L. Optimization of Control Strategies for the Radiant Floor Cooling System Combined with Displacement Ventilation: A Case Study of an Office Building in Jinan, China. Int. J. Archit. Eng. Technol. 2019, 6, 33–48. [Google Scholar]
- Bejan, A. Entropy Generation Minimization, Exergy Analysis, and the Constructal Law. Arab. J. Sci. Eng. 2013, 38, 329–340. [Google Scholar] [CrossRef]
- Liu, J.; Xie, X.; Qin, F.; Song, S.; Lv, D. A case study of ground source direct cooling system integrated with water storage tank system. Build. Simul. 2016, 9, 659–668. [Google Scholar] [CrossRef]
- Lohani, S.P.; Schmidt, D. Comparison of energy and exergy analysis of fossil plant, ground and air source heat pump building heating system. Renew. Energy 2010, 35, 1275–1282. [Google Scholar] [CrossRef]
- Kazanci, O.B.; Shukuya, M. A theoretical study of the effects of different heating loads on the exergy performance of water-based and air-based space heating systems in buildings. Energy 2022, 238, 122009. [Google Scholar] [CrossRef]
- Shukuya, M. Exergetic approach to the understanding of built environment—State-of-the-art review. Jpn. Archit. Rev. 2019, 2, 143–152. [Google Scholar] [CrossRef]
- Shukuya, M. Exergy concept and its application to the built environment. Build. Environ. 2009, 44, 1545–1550. [Google Scholar] [CrossRef]
- Kim, M.K.; Leibundgut, H.; Choi, J.H. Energy and exergy analyses of advanced decentralized ventilation system compared with centralized cooling and air ventilation systems in the hot and humid climate. Energy Build. 2014, 79, 212–222. [Google Scholar] [CrossRef]
- Pires, L.; Silva, P.D.; Castro Gomes, J.P. Experimental study of an innovative element for passive cooling of buildings. Sustain. Energy Tech. 2013, 4, 29–35. [Google Scholar] [CrossRef]
- Ren, J.; Liu, J.; Zhou, S.; Kim, M.K.; Song, S. Experimental study on control strategies of radiant floor cooling system with direct-ground cooling source and displacement ventilation system: A case study in an office building. Energy 2022, 239, 122410. [Google Scholar] [CrossRef]
- Kim, M.K.; Leibundgut, H. A case study on feasible performance of a system combining an airbox convector with a radiant panel for tropical climates. Build. Environ. 2014, 82, 687–692. [Google Scholar] [CrossRef]
- Manjunath, K.; Kaushik, S.C. Second law thermodynamic study of heat exchangers: A review. Renew. Sustain. Energy Rev. 2014, 40, 348–374. [Google Scholar] [CrossRef]
- Yucer, C.T.; Hepbasli, A. Thermodynamic analysis of a building using exergy analysis method. Energy Build. 2011, 43, 536–542. [Google Scholar] [CrossRef]
- Hürdoǧan, E.; Buyükalaca, O.; Hepbasli, A.; Yilmaz, T. Exergetic modeling and experimental performance assessment of a novel desiccant cooling system. Energy Build. 2011, 43, 1489–1498. [Google Scholar] [CrossRef]
- Torio, H.; Schmidt, D. Development of system concepts for improving the performance of a waste heat district heating network with exergy analysis. Energy Build. 2010, 42, 1601–1609. [Google Scholar] [CrossRef]
- Meggers, F.; Ritter, V.; Goffin, P.; Baetschmann, M.; Leibundgut, H. Low exergy building systems implementation. Energy 2012, 41, 48–55. [Google Scholar] [CrossRef]
- Meggers, F.; Pantelic, J.; Baldini, L.; Saber, E.; Kim, M.K. Evaluating and adapting low exergy systems with decentralized ventilation for tropical climates. Energy Build. 2013, 67, 559–567. [Google Scholar] [CrossRef]
- Schmidt, D. Low exergy systems for high-performance buildings and communities. Energy Build. 2009, 41, 331–336. [Google Scholar] [CrossRef]
- Torio, H.; Angelotti, A.; Schmidt, D. Exergy analysis of renewable energy-based climatisation systems for buildings: A critical view. Energy Build. 2009, 41, 248–271. [Google Scholar] [CrossRef]
- Zhang, L.; Fang, H.; Wang, W.; Liu, J. Energy-saving analysis of ground source heat pump combined with floor radiant air conditioning system. Procedia Eng. 2017, 205, 4067–4073. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, X.; Tang, H.; Liu, J.; Jiang, Y. Exergy and entransy analyses in air-conditioning system part 1—Similarity and distinction. Energy Build. 2016, 128, 876–885. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, X.; Jiang, Y. Application of entransy in the analysis of HVAC systems in buildings. Energy 2013, 53, 332–342. [Google Scholar] [CrossRef]
- Mosa, M.; Labat, M.; Lorente, S. Role of flow architectures on the design of radiant cooling panels, a constructal approach. Appl. Therm. Eng. 2019, 150, 1345–1352. [Google Scholar] [CrossRef]
- Liu, J.; Li, Z.; Kim, M.K.; Zhu, S.; Zhang, L.; Srebric, J. A comparison of the thermal comfort performances of a radiation floor cooling system when combined with a range of ventilation systems. Indoor Built Environ. 2019, 29, 527–542. [Google Scholar] [CrossRef]
- Niu, J.L.; Zhang, L.Z.; Zuo, H.G. Energy savings potential of chilled-ceiling combined with desiccant cooling in hot and humid climates. Energy Build. 2002, 34, 487–495. [Google Scholar] [CrossRef]
- Jeong, J.-W.; Mumma, S.A. Ceiling radiant cooling panel capacity enhanced by mixed convection in mechanically ventilated spaces. Appl. Therm. Eng. 2003, 23, 2293–2306. [Google Scholar] [CrossRef]
- Novoselac, A.; Srebric, J. A critical review on the performance and design of combined cooled ceiling and displacement ventilation systems. Energy Build. 2002, 34, 497–509. [Google Scholar] [CrossRef]
- Jeong, J.W.; Mumma, S.A. Practical cooling capacity estimation model for a suspended metal ceiling radiant cooling panel. Build. Environ. 2007, 42, 3176–3185. [Google Scholar] [CrossRef]
- Baldini, L.; Kim, M.K.; Leibundgut, H. Decentralized cooling and dehumidification with a 3 stage LowEx heat exchanger for free reheating. Energy Build. 2014, 76, 270–277. [Google Scholar] [CrossRef]
- Su, M.; Liu, J.; Kim, M.K.; Wu, X. Predicting moisture condensation risk on the radiant cooling floor of an office using integration of a genetic algorithm-back-propagation neural network with sensitivity analysis. Energy Built Environ. 2022, in press. [CrossRef]
- Su, M.; Liu, J.; Zhou, S.; Miao, J.; Kim, M.K. Dynamic prediction of the pre-dehumidification of a radiant floor cooling and displacement ventilation system based on computational fluid dynamics and a back-propagation neural network: A case study of an office room. Indoor Built Environ. 2022, 31, 2386–2410. [Google Scholar] [CrossRef]
- Hu, R.; Niu, J.L. A review of the application of radiant cooling & heating systems in Mainland China. Energy Build. 2012, 52, 11–19. [Google Scholar]
- Rhee, K.N.; Olesen, B.W.; Kim, K.W. Ten questions about radiant heating and cooling systems. Build. Environ. 2017, 112, 367–381. [Google Scholar] [CrossRef]
- Liu, J.Y.; Kim, M.K.; Srebric, J. Numerical analysis of cooling potential and indoor thermal comfort with a novel hybrid radiant cooling system in hot and humid climates. Indoor Built Environ. 2022, 31, 929–943. [Google Scholar] [CrossRef]
- Yuan, Y.L.; Zhou, X.; Zhang, X. Numerical and experimental study on the characteristics of radiant ceiling systems. Build. Res. Inf. 2019, 47, 912–927. [Google Scholar] [CrossRef]
- Liu, J.; Dalgo, D.A.; Zhu, S.; Li, H.; Zhang, L.; Srebric, J. Performance analysis of a ductless personalized ventilation combined with radiant floor cooling system and displacement ventilation. Build. Simul. 2019, 12, 905–919. [Google Scholar] [CrossRef]
- Kim, M.K.; Liu, J.Y.; Cao, S.J. Energy analysis of a hybrid radiant cooling system under hot and humid climates: A case study at Shanghai in China. Build. Environ. 2018, 137, 208–214. [Google Scholar] [CrossRef]
- Lim, H.; Kang, Y.-K.; Jeong, J.-W. Thermoelectric radiant cooling panel design: Numerical simulation and experimental validation. Appl. Therm. Eng. 2018, 144, 248–261. [Google Scholar] [CrossRef]
- Krajčík, M.; Šikula, O. The possibilities and limitations of using radiant wall cooling in new and retrofitted existing buildings. Appl. Therm. Eng. 2020, 164, 114490. [Google Scholar] [CrossRef]
- Kim, M.K.; Leibundgut, H. Advanced Airbox cooling and dehumidification system connected with a chilled ceiling panel in series adapted to hot and humid climates. Energy Build. 2014, 85, 72–78. [Google Scholar] [CrossRef]
- Kim, M.K.; Leibundgut, H. Evaluation of the humidity performance of a novel radiant cooling system connected with an Airbox convector as a low exergy system adapted to hot and humid climates. Energy Build. 2014, 84, 224–232. [Google Scholar] [CrossRef]
- TRNSYS. TRNSYS Transient System Simulation Tool; Thermal Energy System Specialists, LLC: Madison, WI, USA, 2018. [Google Scholar]
- Fang, H.; Wang, W.; Liu, J.; Zhang, L. Operation Analysis of a Compound Air Conditioning System using Measurement and Simulation. Procedia Eng. 2017, 205, 1454–1460. [Google Scholar] [CrossRef]
- BS EN 1264-5:2008; Water Based Surface Embedded Heating and Cooling Systems. Heating and Cooling Surfaces Embedded in Floors, Ceilings and Walls. Determination of the Thermal Output European Committee for Standardization: Brussels, Belgium, 2008.
- ISO 11855-6:2012; Building Environment Design—Design, Dimensioning, Installation and Control of Embedded Radiant Heating and Cooling Systems. International Organization for Standardization: Geneva, Switzerland, 2012.
- ASHRAE 62.1 2013; Ventilation for Acceptable Indoor Air Quality. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2013.
- Jeong, J.W.; Mumma, S.A. Impact of mixed convection on ceiling radiant cooling panel capacity. Hvac. R. Res. 2003, 9, 251–257. [Google Scholar] [CrossRef]
- Zhang, L.Z.; Niu, J.L. Indoor humidity behaviors associated with decoupled cooling in hot and humid climates. Build. Environ. 2003, 38, 99–107. [Google Scholar] [CrossRef]
- Moran, M.J.; Shapiro, H.N. Fundamentals of Engineering Thermodynamics, 6th ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Bejan, A. Advanced Engineering Thermodynamics, 4th ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Shukuya, M. Exergy: Theory and Applications in the Built Environment; Springer: London, UK, 2013. [Google Scholar]
- Alpuche, M.G.; Heard, C.; Best, R.; Rojas, J. Exergy analysis of air cooling systems in buildings in hot humid climates. Appl. Therm. Eng. 2005, 25, 507–517. [Google Scholar] [CrossRef]
- Shukuya, M.; Hammache, A. Introduction to the Concept of Exergy—For a Better Understanding of Low-Temperature-Heating and High-Temperature-Cooling Systems; VTT Technical Research Centre of Finland: Espoo, Finland, 2002. [Google Scholar]
- Leoncini, L.; Baldi, M.G. Building Thermal Exergy Analysis. In Mediterranean Green Buildings & Renewable Energy; Sayigh, A., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 541–551. [Google Scholar]
- Tsatsaronis, G. Thermoeconomic Analysis and Optimization of Energy-Systems. Prog. Energy Combust. 1993, 19, 227–257. [Google Scholar] [CrossRef]
- Cornelissen, R. Thermodynamics and Sustainable Development. In The Use of Exergy Analysis and the Reduction of Irreversibility; University of Twente: Enschede, The Netherlands, 1997. [Google Scholar]
- Morosuk, T.; Tsatsaronis, G. A new approach to the exergy analysis of absorption refrigeration machines. Energy 2008, 33, 890–907. [Google Scholar] [CrossRef]
- Cui, M.; Liu, J.; Kim, M.K.; Wu, X. Application potential analysis of different control strategies for radiant floor cooling systems in office buildings in different climate zones of China. Energy Build. 2023, 282, 112772. [Google Scholar] [CrossRef]
- Ren, J.; Liu, J.; Zhou, S.; Kim, M.K.; Miao, J. Developing a collaborative control strategy of a combined radiant floor cooling and ventilation system: A PMV-based model. J. Build. Eng. 2022, 54, 104648. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, X.; Kim, M.K.; Cui, P.; Zhu, S.; Kosonen, R. A Transient Two-dimensional CFD Evaluation of Indoor Thermal Comfort with an Intermittently-operated Radiant Floor Heating System in an Office Building. Int. J. Archit. Eng. Technol. 2020, 7, 62–87. [Google Scholar]



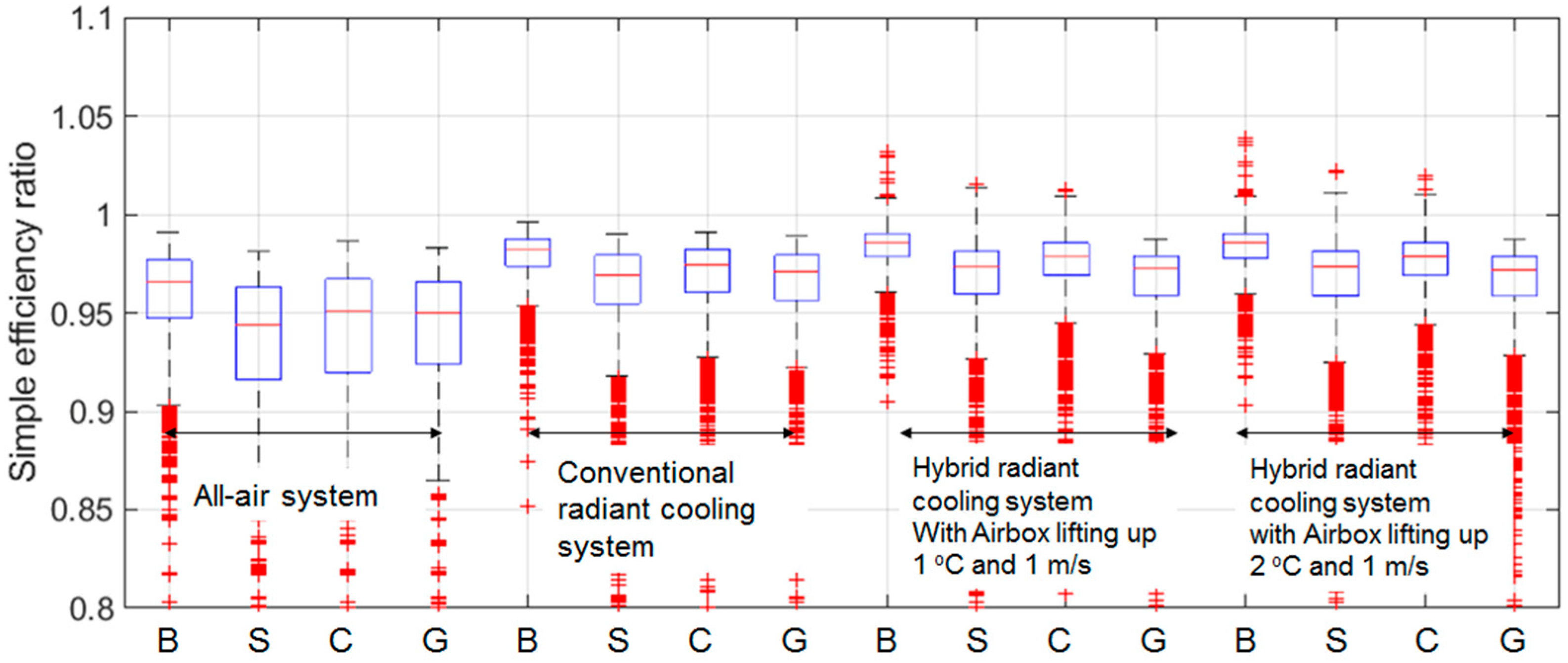

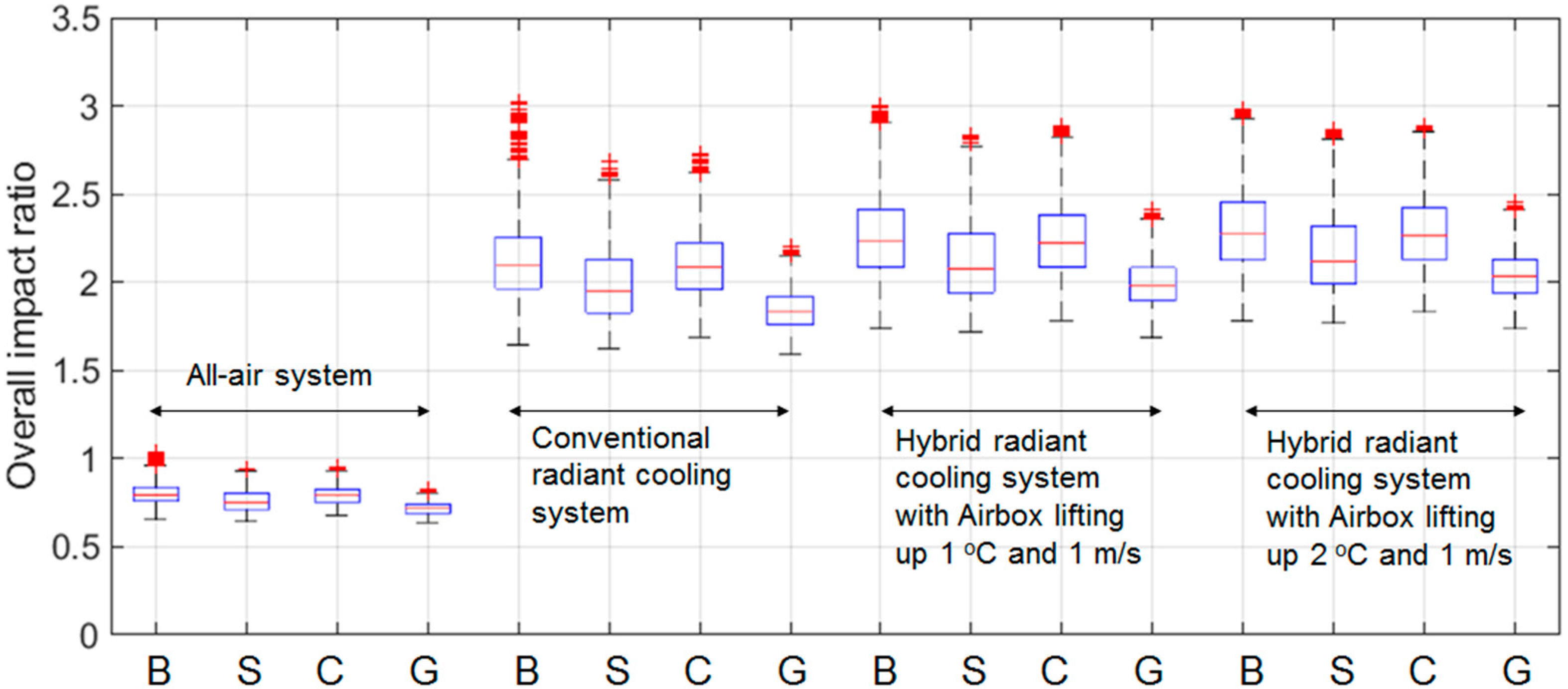

| Settings | Values |
|---|---|
| Volume flow rate (m3/h) | 43 |
| Net floor area (m2) | 15 |
| Indoor air temperature (°C) | 25 |
| Ventilation rate (h−1) | 1.0 |
| Infiltration rate (h−1) | 0.1 |
| Occupant (W) | 150 × 2 |
| Computer (W) | 100 × 2 |
| Lighting (W) | 10 × 2 |
| Structure | U-Values, W/(m2⸱K) |
|---|---|
| Ceiling | 0.215 |
| Long wall | 0.215 |
| Short wall | 0.215 |
| Ground | 0.151 |
| Window | 1.432 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Su, M.; Fu, N.; Kim, M.K. A Numerical Study on the Exergy Performance of a Hybrid Radiant Cooling System in an Office Building: Comparative Case Study and Analysis. Buildings 2023, 13, 465. https://doi.org/10.3390/buildings13020465
Liu J, Su M, Fu N, Kim MK. A Numerical Study on the Exergy Performance of a Hybrid Radiant Cooling System in an Office Building: Comparative Case Study and Analysis. Buildings. 2023; 13(2):465. https://doi.org/10.3390/buildings13020465
Chicago/Turabian StyleLiu, Jiying, Meng Su, Nuodi Fu, and Moon Keun Kim. 2023. "A Numerical Study on the Exergy Performance of a Hybrid Radiant Cooling System in an Office Building: Comparative Case Study and Analysis" Buildings 13, no. 2: 465. https://doi.org/10.3390/buildings13020465
APA StyleLiu, J., Su, M., Fu, N., & Kim, M. K. (2023). A Numerical Study on the Exergy Performance of a Hybrid Radiant Cooling System in an Office Building: Comparative Case Study and Analysis. Buildings, 13(2), 465. https://doi.org/10.3390/buildings13020465








