Damage Analysis of Box Girder Based on a Vehicle–Bridge Interaction System
Abstract
:1. Introduction
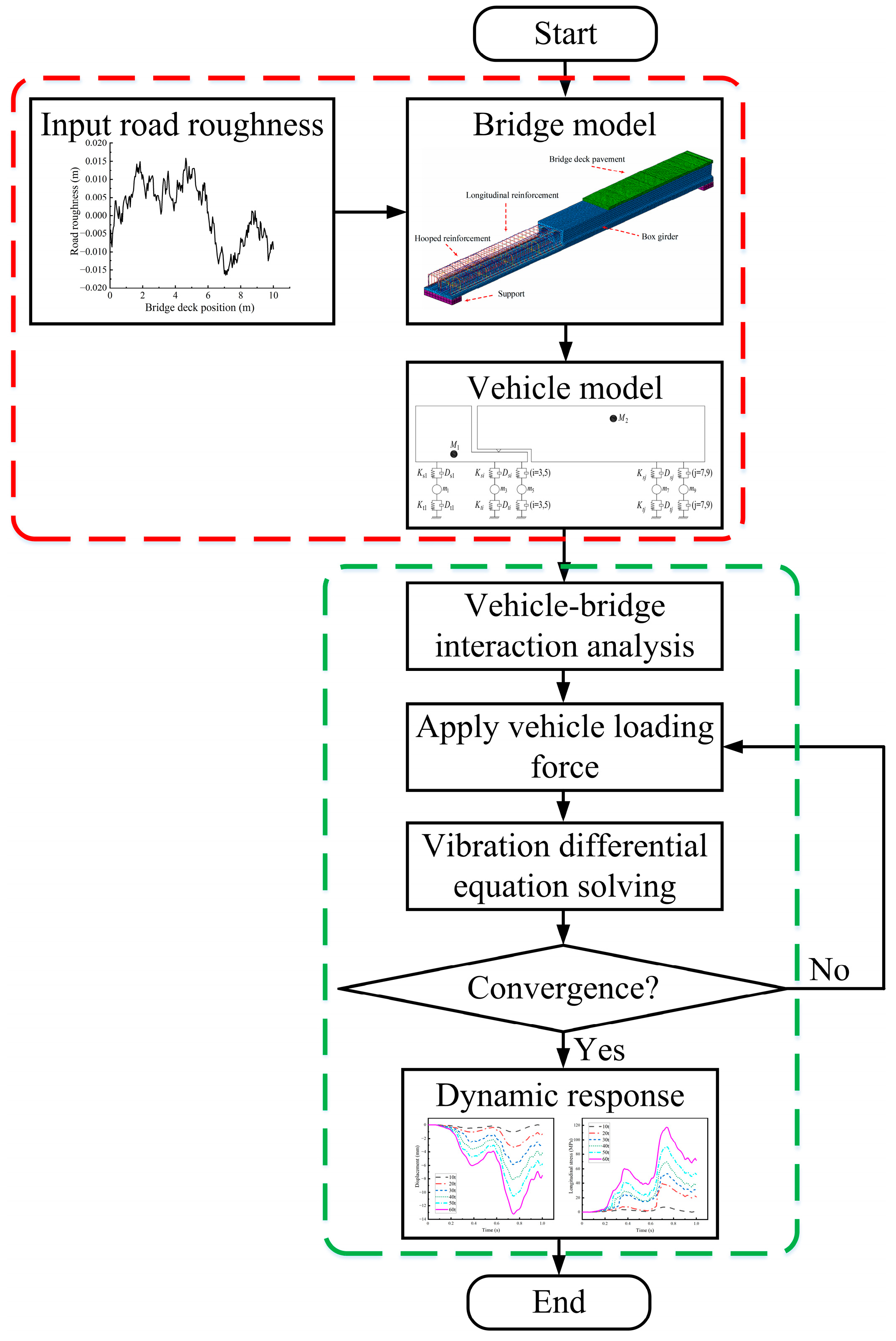
2. Vehicle–Bridge Interaction Dynamic Response Analysis Method
2.1. Newmark Algorithm
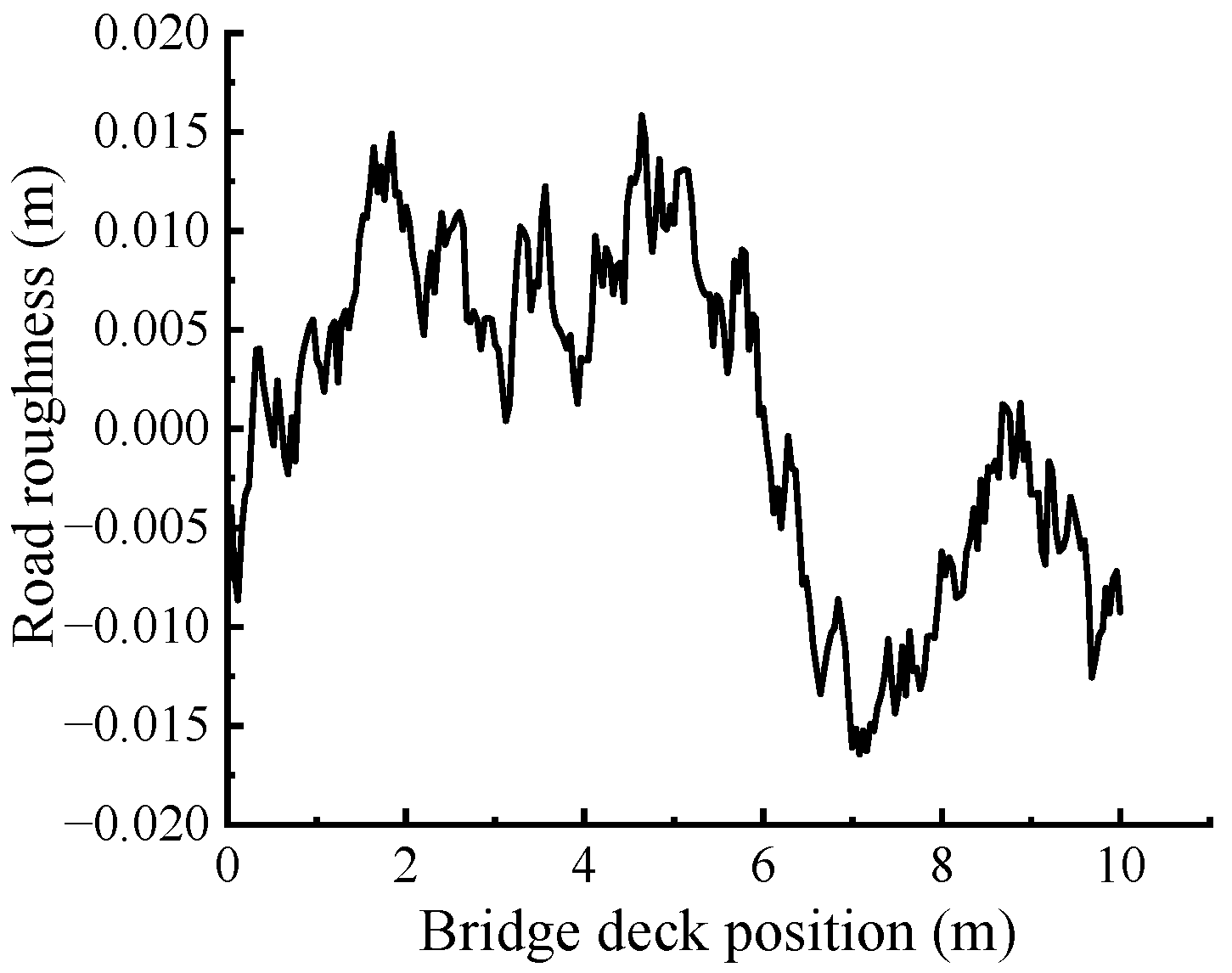
2.2. Road Roughness
3. Finite Element Modal Verification
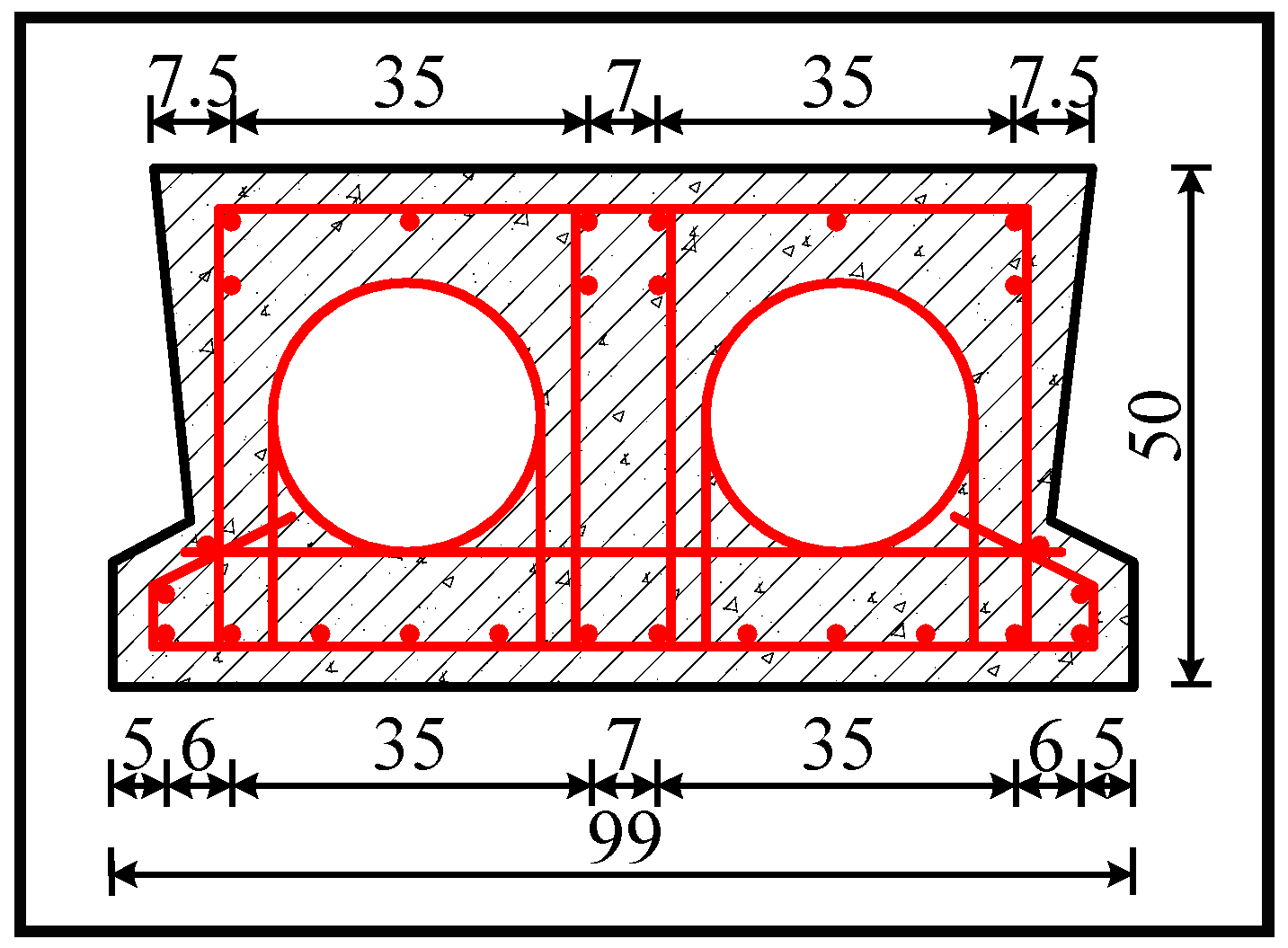
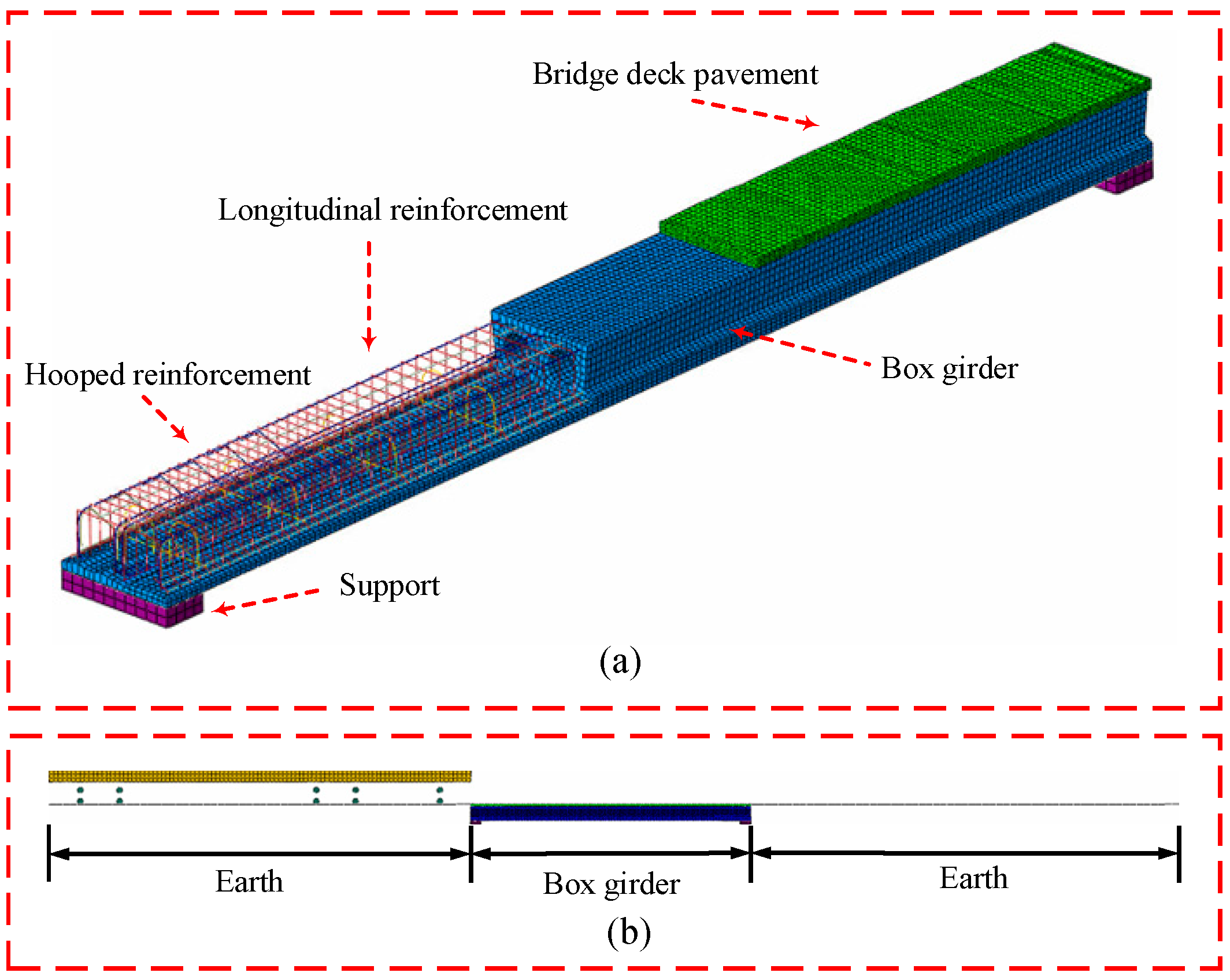
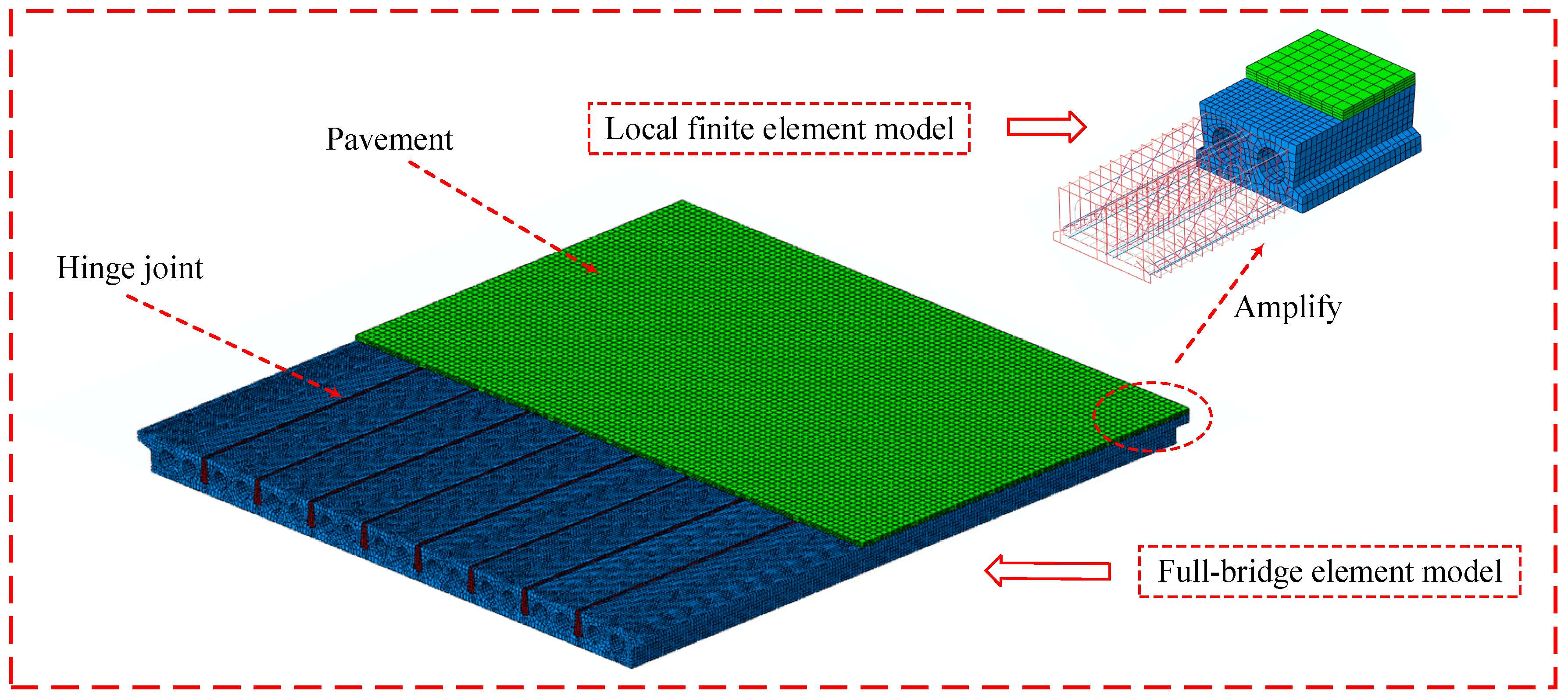
3.1. Finite Element Model
3.2. Material Model
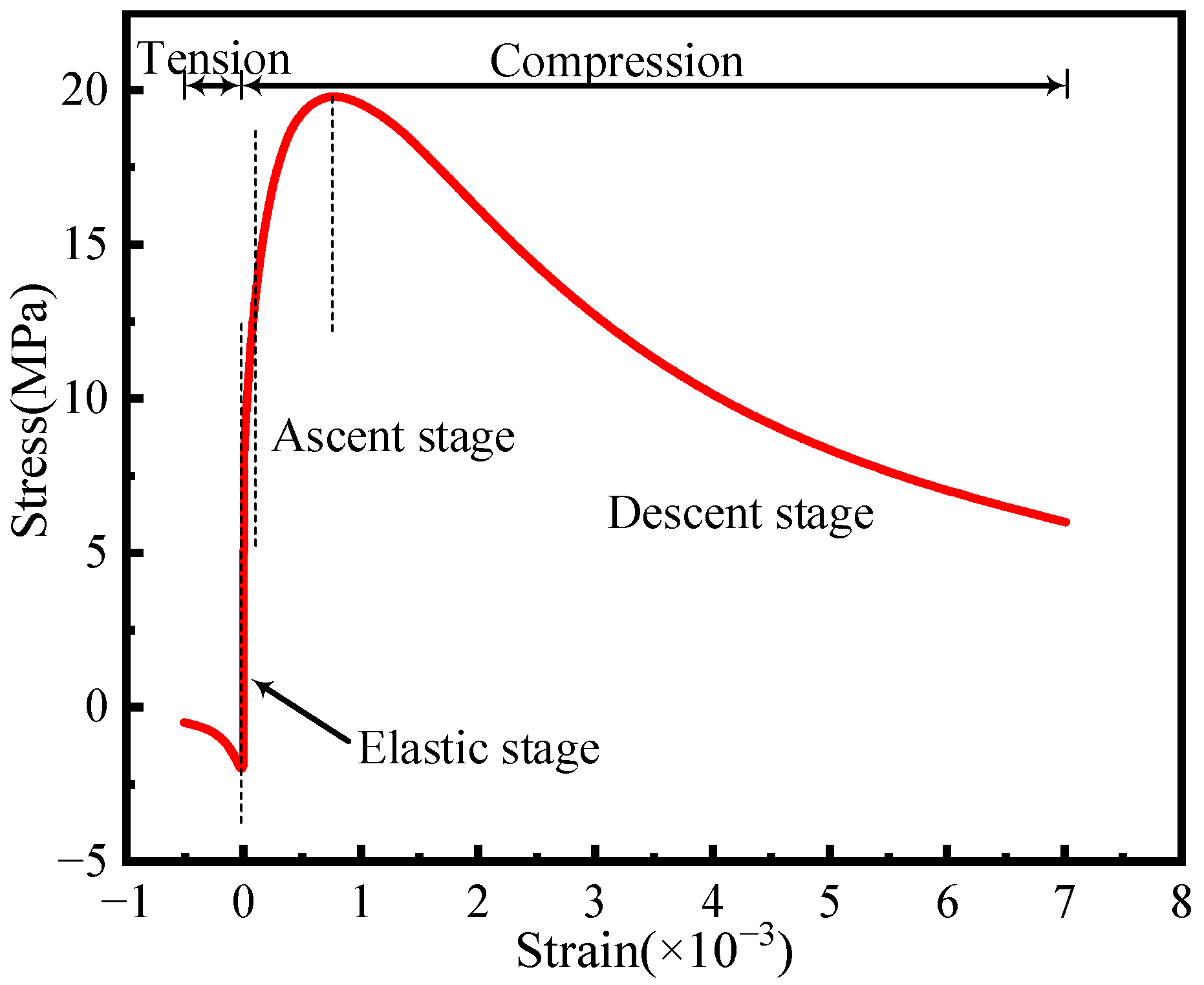
3.2.1. Constitutive Model of Concrete
3.2.2. Constitutive Model of Steel
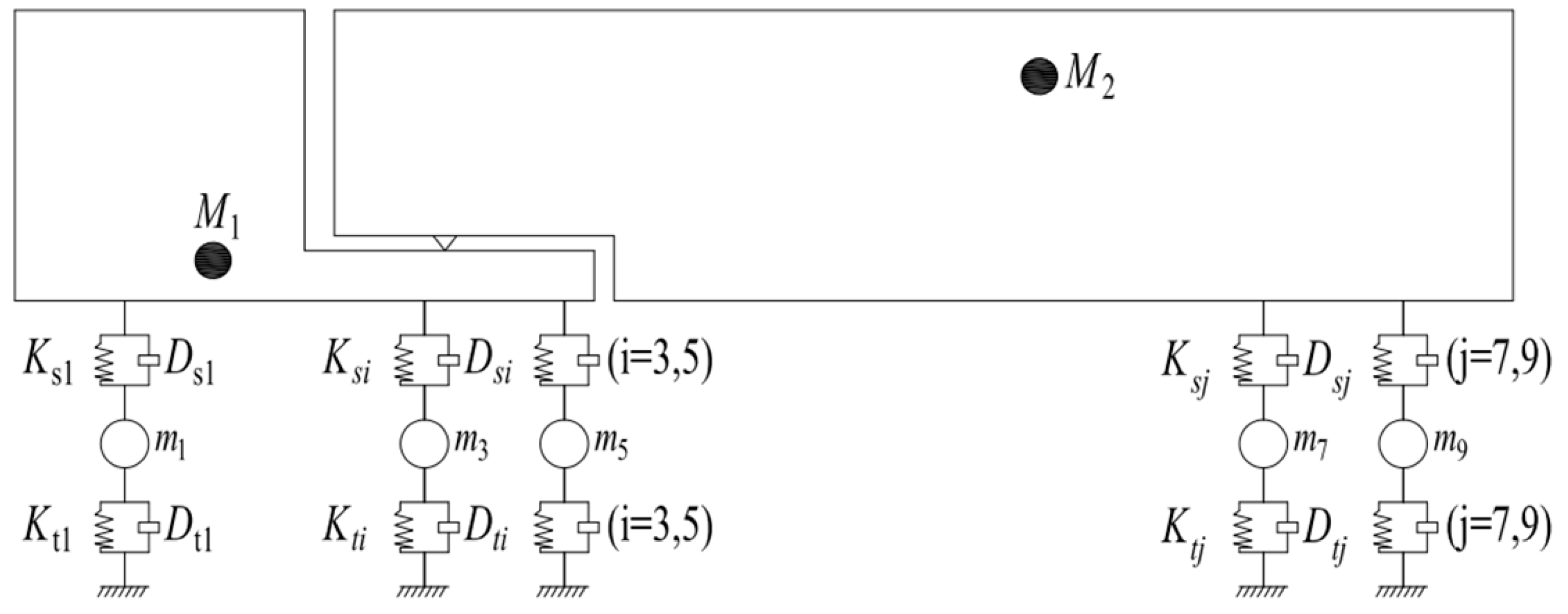
3.3. Vehicle Model
3.4. Vehicle–Bridge Interaction Model
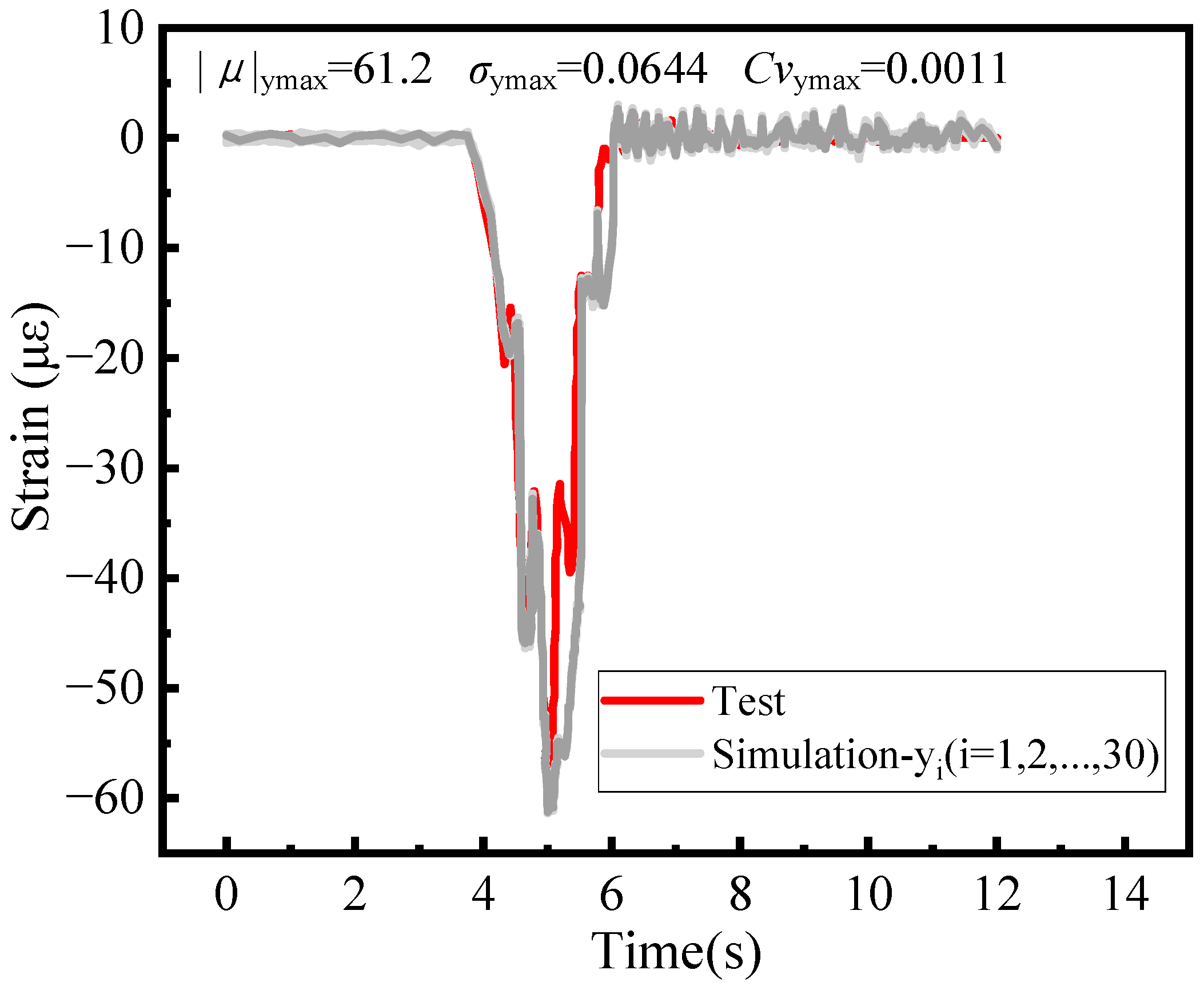
3.5. Model Verification
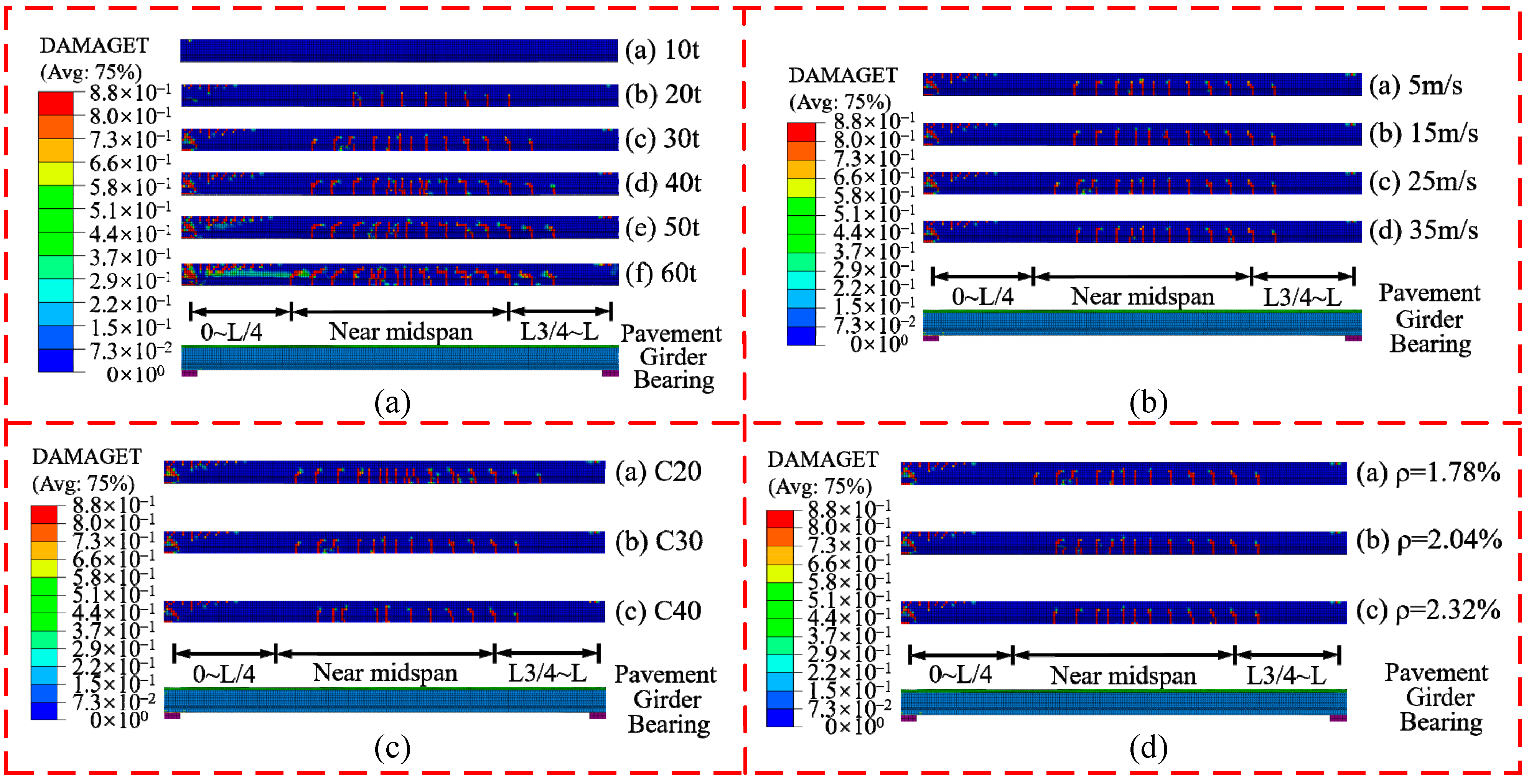
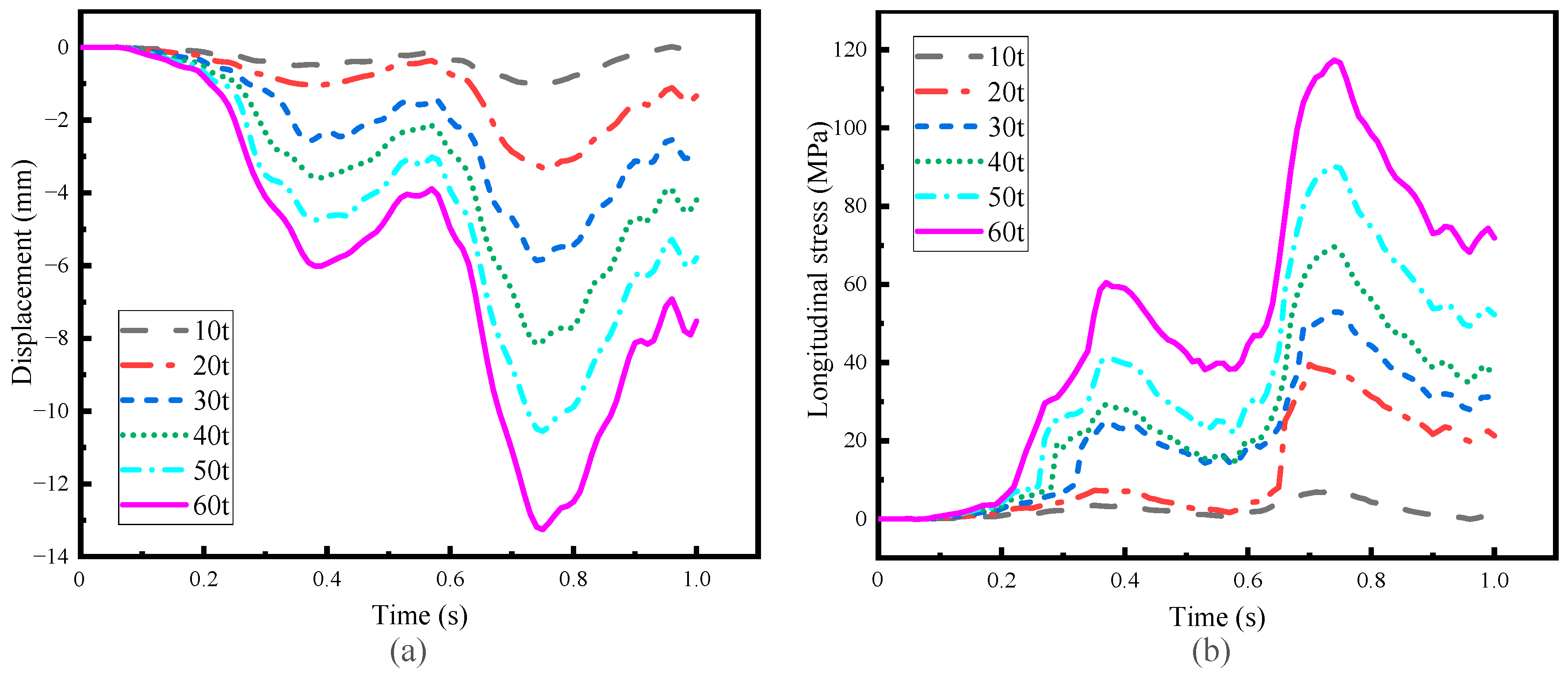
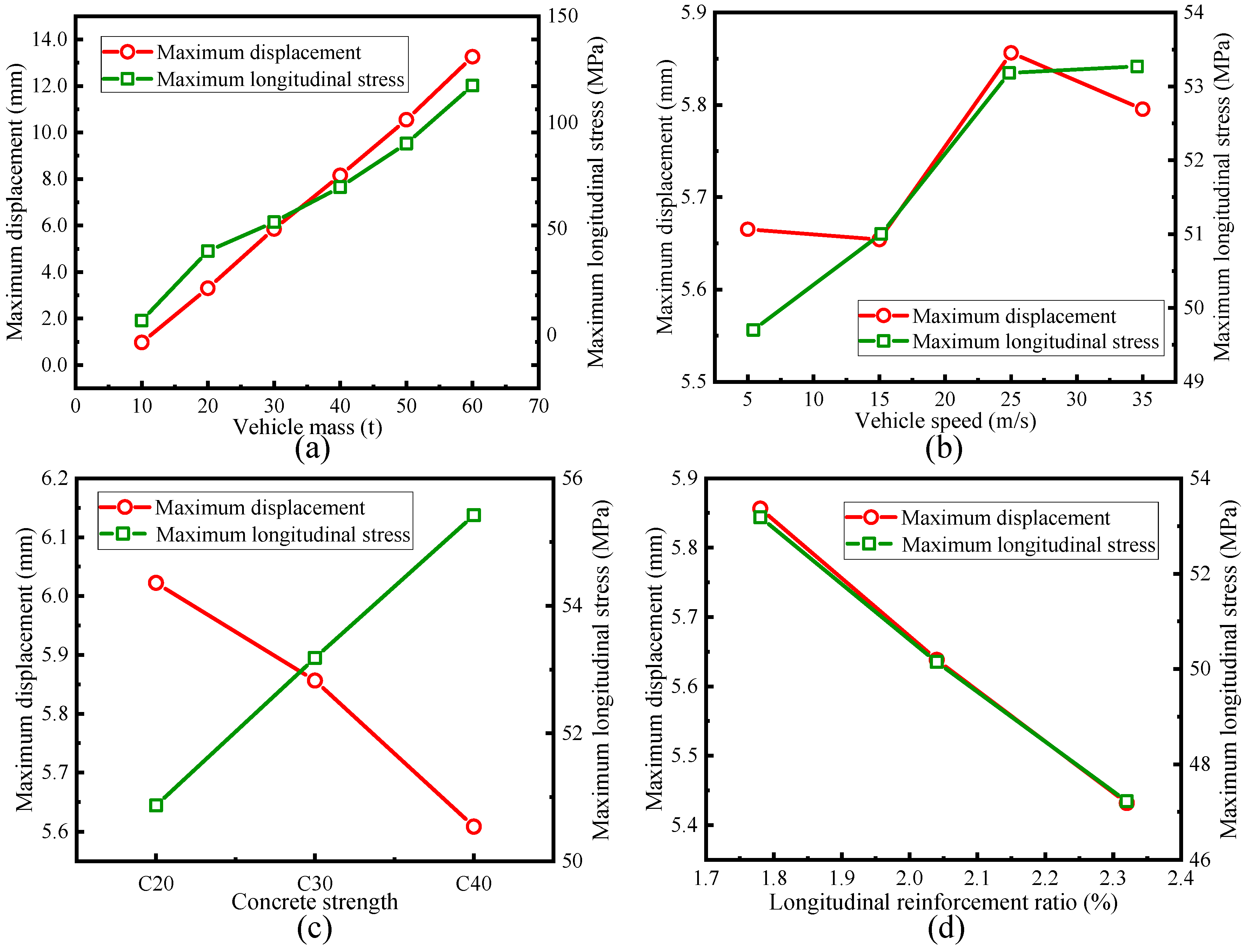
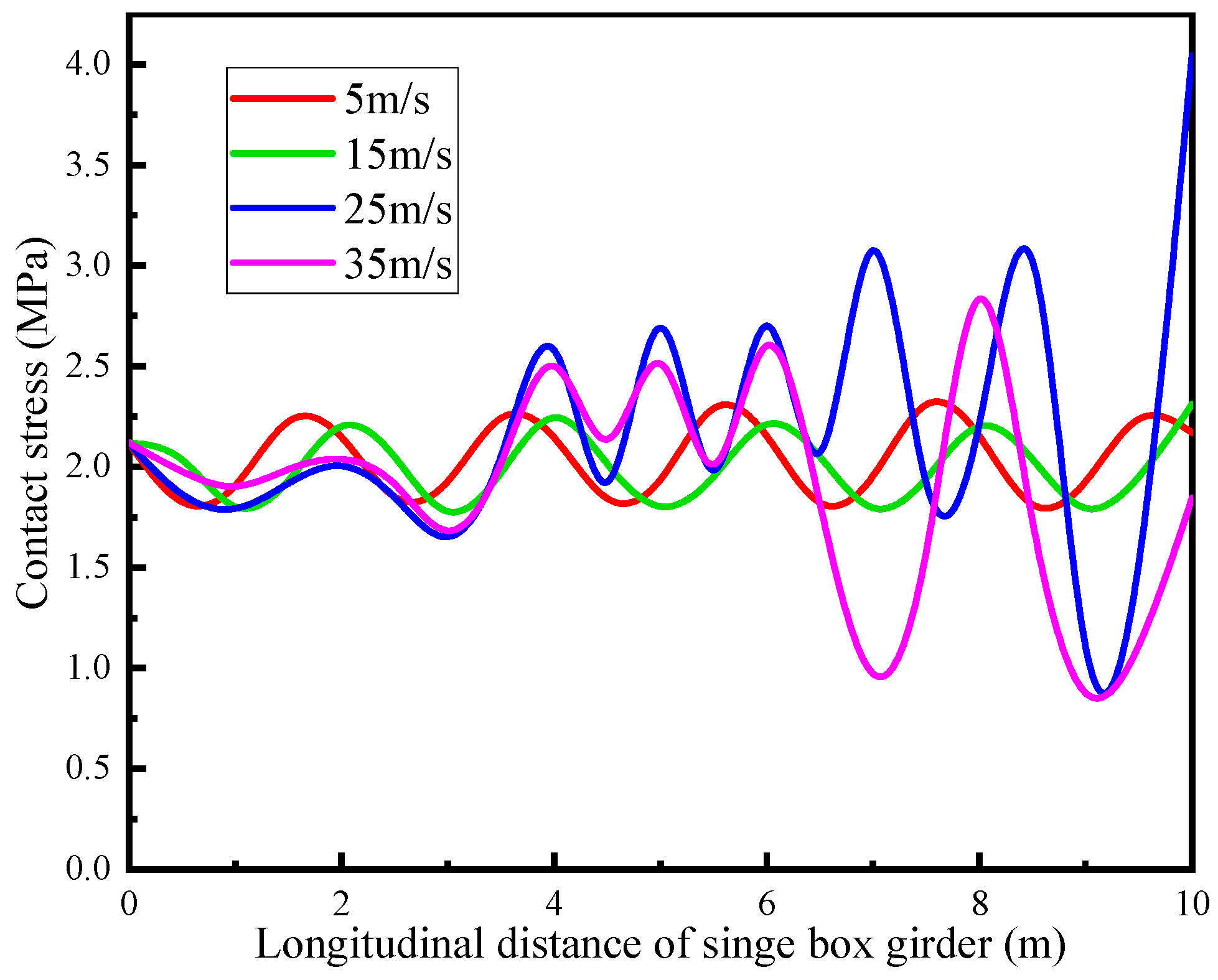
4. Damage Description of Single Box Girder
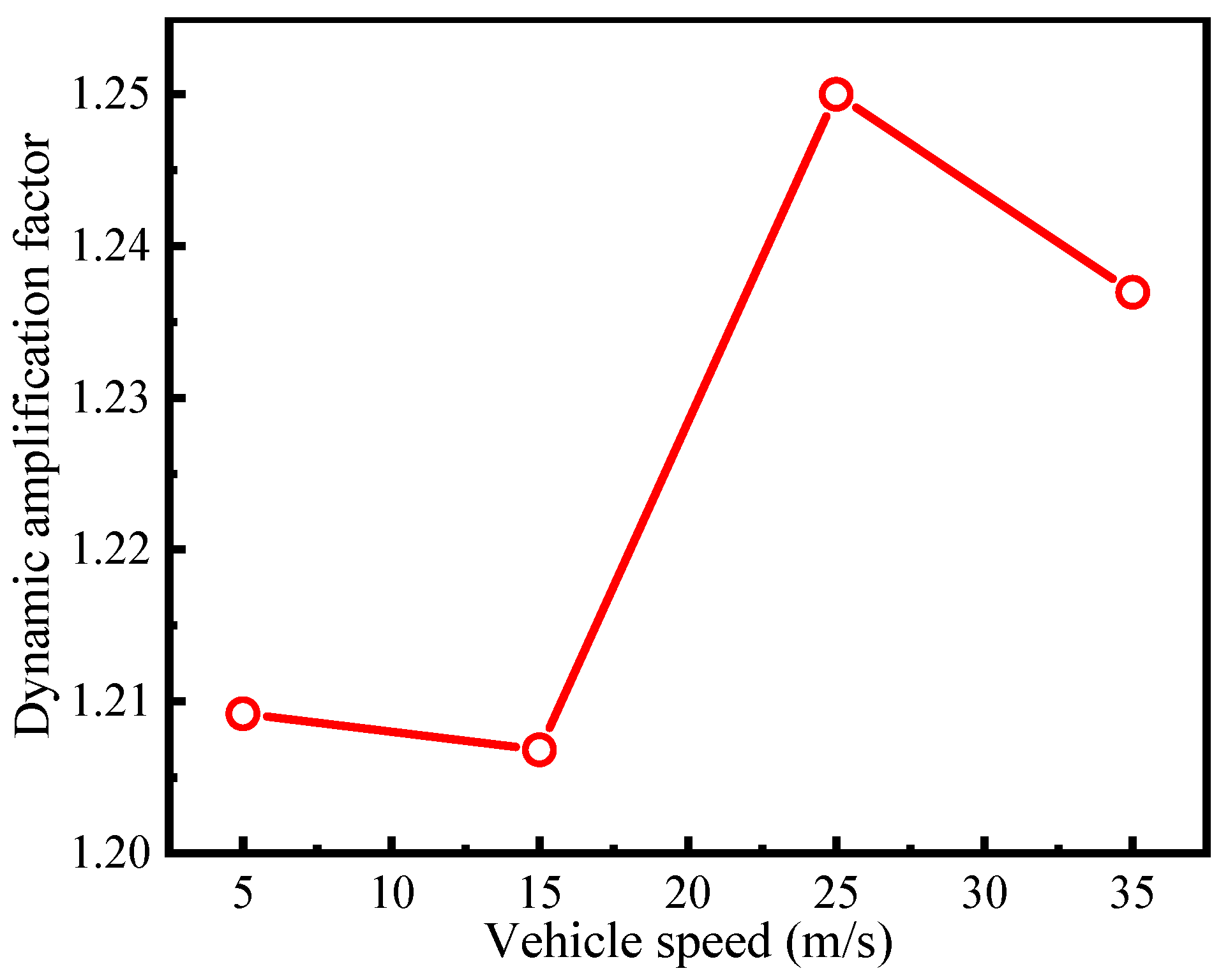
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hussein, H.H.; Sargand, S.M.; Khoury, I.; Al-Jhayyish, A.K. Environment induced behavior of transverse tie bars in adjacent prestressed box-girder bridges with partial depth shear keys. J. Perform. Constr. Fac. 2017, 31, 04017074. [Google Scholar] [CrossRef]
- Hhha, B.; Sms, A.; Ftar, A.; Eps, A. Experimental validation of optimized ultra-high-performance concrete shear key shape for precast pre-stressed adjacent box girder bridges. Constr. Build. Mater. 2018, 190, 178–190. [Google Scholar]
- Lucie, K.; Janda, T.; Jan, S.; Michal, S.; Guido, M. Experimental and numerical investigation of the response of GLT beams exposed to fire. Constr. Build. Mater. 2021, 299, 123846. [Google Scholar]
- Huang, Y.; Han, B.; Yin, W.M. Reinforced Concrete Corbels Shear Test: The Triangular-Truss Method Evaluation. Buildings 2022, 12, 1619. [Google Scholar] [CrossRef]
- Au, A.; Lam, C.; Au, J.; Tharmabala, B. Eliminating Deck joints using debonded link slabs: Research and field tests in Ontario. J. Bridge Eng. 2013, 18, 768–778. [Google Scholar] [CrossRef]
- Semendary, A.A.; Walsh, K.K.; Steinberg, E.P. Early-Age Behavior of an Adjacent Prestressed Concrete Box-Beam Bridge Containing UHPC Shear Keys with Transverse Dowels. J. Bridge Eng. 2017, 22, 01017007. [Google Scholar] [CrossRef]
- Hussein, H.H.; Sargand, S.M.; Steinberg, E.P. Shape Optimization of UHPC Shear Keys for Precast, Prestressed, Adjacent Box-Girder Bridges. J. Bridge Eng. 2018, 23, 04018009. [Google Scholar] [CrossRef]
- Leng, Y.L.; Zhang, J.Q.; Cheng, S.S.; Hai, F. Numerical analysis on single plate loading effect of precast hollow plate girder bridge. J. Highw. Transp. Res. Dev. 2013, 30, 63–73. [Google Scholar]
- Zhang, J.F.; Kong, L.Y.; Han, W.S.; Li, X.Z. Damage Mechanism and Post collision Bearing Capacity of Prestressed Concrete Hollow Slab Bridge Under Overheight-vehicle Collision. China J. Highw. Transp. 2021, 34, 177–187. [Google Scholar]
- Al-Saidy, A.H.; Klaiber, F.W.; Wipf, T.J.; Al-Jabri, K.S.; Al-Nuaimi, A.S. Parametric study on the behavior of short span composite bridge girders strengthened with carbon fiber reinforced polymer plates. Constr. Build. Mater. 2008, 22, 729–737. [Google Scholar] [CrossRef]
- Yang, D.H.; Yi, T.H.; Li, H.N. Coupled fatigue-corrosion failure analysis and performance assessment of RC bridge deck slabs. J. Bridge Eng. 2017, 20, 04017077. [Google Scholar] [CrossRef]
- Ma, Y.L.; Wang, D.W.; Li, G.H. Evaluation of load-bearing capacity of pre-stressed concrete hollow slab based on single slab load bearing. J. Highw. Transp. Res. Dev. 2013, 30, 45–55. [Google Scholar]
- Su, X.; Yin, S.P.; Yang, Y.H.; Feng, J.; Li, L.T. Comparative analysis of flexural performance of old full-scale hollow slab beams reinforced with fiber composites. Constr. Build. Mater. 2022, 338, 127657. [Google Scholar]
- Jin, H.; Xu, Y.; Zheng, Q.C.; Shao, G.T. Application of shaped steel and concrete composite reinforcement technique to hollow slab bridge. Bridge Constr. 2017, 47, 114–118. [Google Scholar]
- Deng, L.; Chen, Y.X.; Han, W.S.; Wang, W. Studying impact factors for short and medium-span simply supported concrete highway bridge and its suggested values. China J. Highw. Transp. 2020, 33, 69–78. [Google Scholar]
- Deng, L.; He, W.; Wang, F. Dynamic impact factors for simply supported bridges with different cross-section types. J. Vib. Shock 2015, 34, 70–75. [Google Scholar]
- Deng, L.; Duan, L.L.; Zou, Q.L. Comparison of dynamic amplification factors calculated from bridge strain and deflection. Eng. Mech. 2018, 35, 126–135. [Google Scholar]
- Gao, Q.F.; Wang, Z.L.; Koh, C.G.; Chen, C. Dynamic Load Allowances Corresponding to Different Responses in Various Sections of Highway Bridges to Moving Vehicular Loads. Adv. Struct. Eng. 2015, 18, 1685–1702. [Google Scholar] [CrossRef]
- Bu, J.Q.; Lou, G.C.; Luo, S.X. Analysis of impact effects of moving vehicles on a continuous bridge. J. Vib. Shock. 2007, 26, 52–55+64. [Google Scholar]
- Aloisio, A.; Rosso, M.M.; Alaggio, R. Experimental and analytical investigation into the effect of ballasted track on the dynamic response of railway bridges under moving loads. J. Bridge Eng. 2022, 27, 04022085. [Google Scholar] [CrossRef]
- Li, H.; Wang, T.Y.; Wu, G. A Bayesian deep learning approach for random vibration analysis of bridges subjected to vehicle dynamic interaction. Mech. Syst. Signal Pr. 2022, 170, 108799. [Google Scholar] [CrossRef]
- Jian, X.D.; Xia, Y.; Sun, L.M. Indirect identification of bridge frequencies using a four-wheel vehicle: Theory and three-dimensional simulation. Mech. Syst. Signal Pr. 2022, 177, 109155. [Google Scholar] [CrossRef]
- Zhao, L.W. The Analysis of Vehicle-bridge Coupling Vibration of CFST. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2017. [Google Scholar]
- Vehicle Vibration-Describing Method for Road Surface Irregularity (GB/T7031-86); China National Standard. China Standards Press: Beijing, China, 1986.
- Zhang, J.; Wang, Q.Y.; Hu, S.Y. Parameters verification of concrete damaged plastic model of ABAQUS. Build. Struct. 2008, 38, 127–130. [Google Scholar]
- Nie, J.G.; Wang, Y.H. Comparison study of constitutive model of concrete in ABAQUS for static analysis of structure. Eng. Mech. 2013, 30, 59–82. [Google Scholar]
- Kupfer, H.B.; Geretle, K.H. Behavior of conc-rete under biaxial stresses. J. Eng. Mech. Div. 1973, 99, 853–866. [Google Scholar] [CrossRef]
- Kachanov, L.M. Rupture time under creep conditions. Int. J. Fract. 1999, 97, 11–18. [Google Scholar] [CrossRef]
- Code for Design of Concrete Structrues (GB 50010); China National Standard. China Architecture & Building Press: Beijing, China, 2010.
- Deng, L.; Duan, L.L.; He, W.; Ji, W. Study on vehicle model for bridge coupling vibration of highway bridges in China. China J. Highw. Transp. 2018, 31, 92–100. [Google Scholar]




| Material | εs,y (10−3) | σs,y (MPa) | εs,u (10−3) | σs,u (MPa) |
|---|---|---|---|---|
| R235 | 1.119 | 235 | 0.100 | 370 |
| HRB335 | 1.675 | 335 | 0.075 | 455 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Suspension stiffness Ks1, Ks2 | 300 kN·m−1 | M1 | 2276.5 kg |
| Suspension stiffness Ks3~Ks6 | 500 kN·m−1 | M2 | 45,246 kg |
| Suspension stiffness Ks7~Ks10 | 1250 kN·m−1 | m1 | 700 kg |
| Tire stiffness Kt1, Kt2 | 1500 kN·m−1 | m3 | 1000 kg |
| Tire stiffness Kt3~Kt10 | 3000 kN·m−1 | m5 | 1000 kg |
| Suspension damping Ds1, Ds2 | 10 kN·s·m−1 | m7 | 800 kg |
| Suspension damping Ds3~Ds10 | 53 kN·s·m−1 | m9 | 800 kg |
| Suspension damping Dt1~Dt10 | 3 kN·s·m−1 |
| Parameter | Value |
|---|---|
| Mass of truck body | 59,860 kg |
| Mass of the front axle | 11,932 kg |
| Mass of the middle axle | 23,964 kg |
| Mass of the rear axle | 23,964 kg |
| Distance between the front and middle axle | 3.6 m |
| Distance between the middle and rear axle | 1.4 m |
| Distance of transverse axial | 1.8 m |
| Vehicle Speed (km/h) | Test Value (με) | Simulation Value (με) | Relative Error (%) |
|---|---|---|---|
| 30 | 39.6 | 41.6 | 5.05 |
| 40 | 38.5 | 41.0 | 6.49 |
| 50 | 57.8 | 61.3 | 6.05 |
| Measured Order | Test Value (Hz) | Simulation Value (Hz) | Relative Error (%) |
|---|---|---|---|
| 1 | 13.0 | 12.5 | 3.85 |
| 2 | 16.5 | 15.1 | 8.48 |
| 3 | 34.3 | 33.4 | 2.62 |
| Scheme | L a (t) | S a (m/s) | C a (MPa) | Ρ a (%) | Damage Description |
|---|---|---|---|---|---|
| 1 | 10 | 25 | C30 | 1.78 | No damage |
| 2 | 20 | 25 | C30 | 1.78 | Flexural damage in box girder |
| 3 | 30 | 25 | C30 | 1.78 | Flexural-shear damage in box girder and concrete shear damage near support |
| 4 | 40 | 25 | C30 | 1.78 | Flexural-shear damage in box girder and concrete shear damage near support |
| 5 | 50 | 25 | C30 | 1.78 | Flexural-shear damage in box girder and concrete shear damage near support |
| 6 | 60 | 25 | C30 | 1.78 | Flexural-shear damage in box girder and severe shear damage near support |
| 7 | 30 | 5 | C30 | 1.78 | Flexural damage in box girder and concrete shear damage near support |
| 8 | 30 | 15 | C30 | 1.78 | Flexural damage in box girder and concrete shear damage near support |
| 9 | 30 | 35 | C30 | 1.78 | Flexural damage in box girder and concrete shear damage near support |
| 10 | 30 | 25 | C20 | 1.78 | Flexural-shear damage in box girder and concrete shear damage near support |
| 11 | 30 | 25 | C40 | 1.78 | Flexural damage in box girder and concrete shear damage near support |
| 12 | 30 | 25 | C30 | 2.04 | Flexural damage in box girder and concrete shear damage near support |
| 13 | 30 | 25 | C30 | 2.32 | Flexural damage in box girder and concrete shear damage near support |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, B.; Hui, Y.; Zheng, X. Damage Analysis of Box Girder Based on a Vehicle–Bridge Interaction System. Buildings 2023, 13, 547. https://doi.org/10.3390/buildings13020547
Zhou B, Hui Y, Zheng X. Damage Analysis of Box Girder Based on a Vehicle–Bridge Interaction System. Buildings. 2023; 13(2):547. https://doi.org/10.3390/buildings13020547
Chicago/Turabian StyleZhou, Bin, Yingxin Hui, and Xiaobo Zheng. 2023. "Damage Analysis of Box Girder Based on a Vehicle–Bridge Interaction System" Buildings 13, no. 2: 547. https://doi.org/10.3390/buildings13020547
APA StyleZhou, B., Hui, Y., & Zheng, X. (2023). Damage Analysis of Box Girder Based on a Vehicle–Bridge Interaction System. Buildings, 13(2), 547. https://doi.org/10.3390/buildings13020547








