A Method for Computing Slip-Line Fields with Stress Discontinuity in Cohesionless Backfills

Abstract

A method for computing slip-line fields in the case of cohesionless backfills with stress discontinuity was proposed. The potential failure zone is divided into the Rankine zone and the transition zone, and the Rankine zone is rigorously determined using the theory of plastic mechanics. The potential failure zone and the Rankine zone are then further divided into a series of triangular slices. On the basis of the force and moment equilibrium conditions of a typical triangular slice, the recurrence equation of the lateral force is established. Furthermore, the relationship between the failure surface inclination angle and the interslice force inclination angle is established by satisfying the Mohr–Coulomb criterion. An iterative procedure for calculating the lateral force of the triangular slices by changing the failure surface inclination in the transition zone is performed until the interslice force satisfies the stress condition of the transition zone boundary, resulting in a stress discontinuity line if the Rankine zone and the transition zone intersect and the intersection line satisfies the stress characteristics of stress discontinuity. Example studies are performed to verify the present method, which shows that the soil–wall interface friction has the most significant effect on stress discontinuity, and the location of the stress discontinuity line gradually approaches the backfill surface with an increase in retaining wall inclination.

1. Introduction

The slip-line field method is a classic theory for calculating earth pressure [1]. Other methods are the limit equilibrium method [2], limit analysis [3], and numerical method [4,5]. The limit equilibrium method calculates earth pressure by assuming the shape of a sliding surface [6,7]. The limit analysis method is used to obtain the upper and lower bound solutions of earth pressure by constructing a displacement field with mobility permission and a statically permissible stress field [8,9,10,11]. Among other methods, the slip-line field method is a relatively rigorous method to obtain earth pressure as well as slip-line fields [12]. Xiong and Wang (2020) [13] proposed an approach to solve axisymmetric active earth pressure problems by using a rigorous characteristic line theory. Chen et al. (2022) [14] proposed a slip-line solution to earth pressure of narrow backfill. However, in some cases, stress discontinuity may occur in a slip-line field. How to determine the position of stress discontinuity is crucial to the computation of slip-line fields. Lee et al. (1972) [15] proposed a theoretical solution for the lateral pressure of a rigid retaining wall considering stress discontinuity, and a cycling process of stress discontinuity line was proposed. Zhu et al. (2001) [16] proposed the limit condition for the occurrence of stress discontinuity by using the relationship between the wall inclination, the soil–wall interface friction, the backfill surface inclination, and the backfill internal friction for weightless soil. Peng et al. (2002) [17] found that a folding phenomenon occurs in slip-line fields if the parameters in the retaining wall system meet a certain condition, and they explained that it is the only virtual solution for the boundary value problem in the mathematical sense. Based on the stress discontinuity judgment method proposed by Sokolovskii, Kumar and Chitikela (2002) [18] studied a method to calculate seismic passive earth pressure coefficients. Liu and Wang (2008) [19] put forward the occurrence conditions of stress discontinuity and proposed two calculation procedures of active earth pressure for a circular retaining wall. The existence of stress discontinuity was also considered in Keshavarz and Ebrahimi (2017) [20]’s study, which mainly proposed a method of solving axisymmetric active earth pressure using the method of stress characteristics. Liu et al. (2018) [21] proposed the conditions of concave failure surface, convex failure surface, and plane failure surface and used the logarithmic spiral method to calculate passive earth pressure; the result for the concave failure surface indicates that there is stress discontinuity in the slip-line field. There was a similar phenomenon in Zhu et al. (2000) [22] ’s study, which calculated the critical slip field of earth pressure based on the triangular slice method. In addition, Li and Jiang (2022) [23] proposed a solution to solve the ultimate bearing capacity of strip footings by considering stress discontinuity in slip-line fields. Smith and Gilbert (2022) [24] established the stress function basis of the upper bound theorem of plasticity by considering a discontinuous slip line. In the author’s previous study, a new method for computing earth pressure slip-line fields was proposed [25], which did not take stress discontinuity into account.

Therefore, a numerical method for computing slip-line fields with stress discontinuity was proposed in the present study. Based on the triangular slice method, the force and moment equilibrium equations for a typical slice are established. The relationship between the inclination of the interslice force and the inclination of the failure surface is established by considering the Mohr–Coulomb criterion. An iterative procedure for calculating the lateral force of the triangular slices by changing the failure surface inclination in the transition zone is performed until the interslice force satisfies the stress condition of the transition zone boundary, resulting in a stress discontinuity line if the Rankine zone and the transition zone intersect. It should be noted that the equations derived for the presented active case are also applicable to passive cases if the signs of the soil–wall interface friction angle and the backfill internal friction angle are changed, that is δ₀ = −δ₀ and φ = −φ.

2. Fundamentals

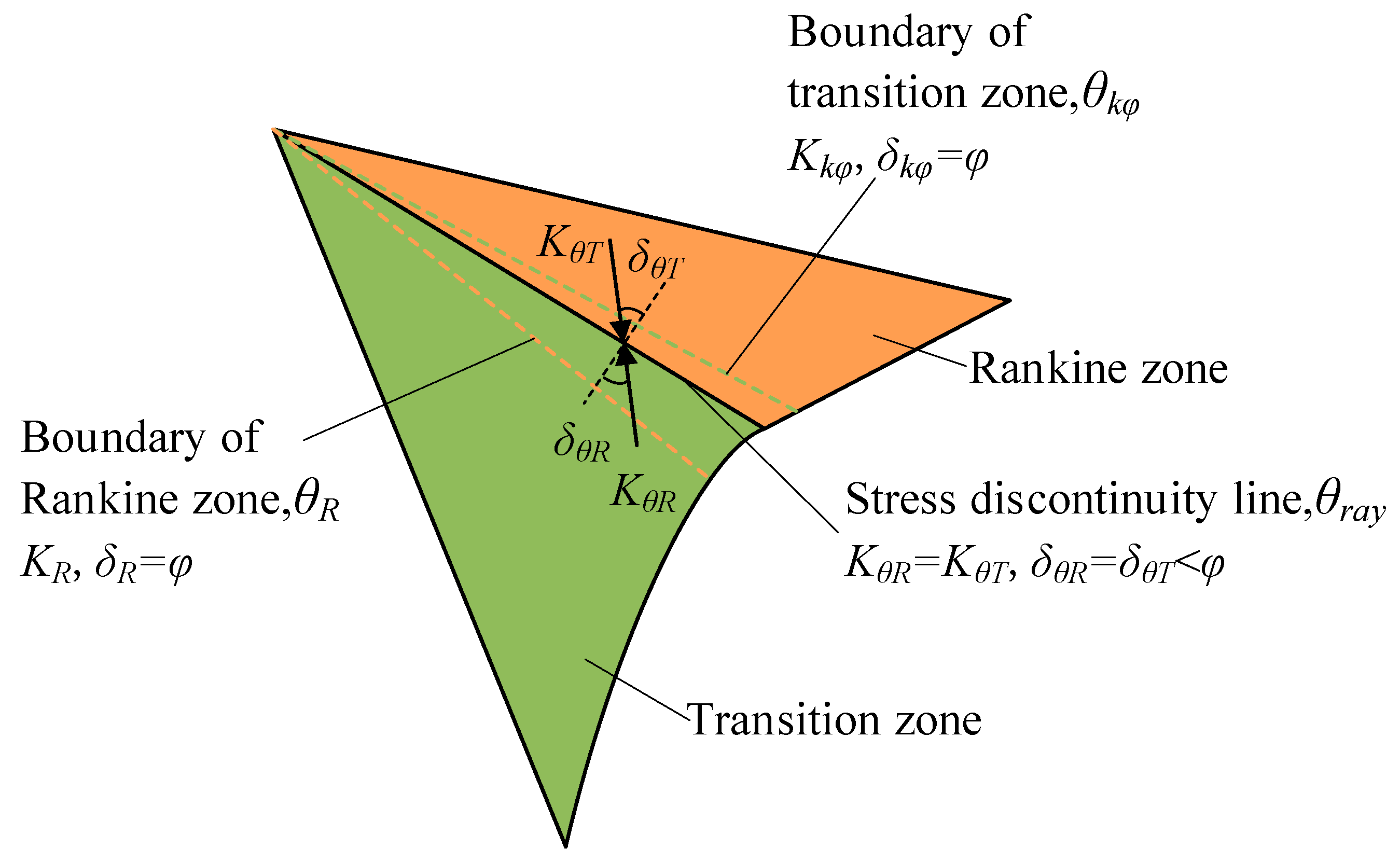
Figure 1 shows a typical stress system of a retaining wall in an active case. The potential failure zone can be divided into the Rankine zone and the transition zone according to the soil plasticity theory. If there is no stress discontinuity, the line OA is the transition ray between the two zones, and it is a slip line, as shown in Figure 1a. Otherwise, the Rankine zone and the transition zone will intersect, as shown in Figure 1b, where the line OD is the intersection line of the two zones, and the line OA is the boundary of the Rankine zone. The inclination of the line OA, i.e., θ_R, and the inclination of the Rankine zone failure surface, i.e., α_R, are drawn from Zhu et al. (2001) [16], as shown in Equations (1) and (2). Additionally, the two conjugate slip lines within the Rankine zone intersect each other at an angle of 90° − φ/2.

According to the theory of plasticity, the normal stress and the shear stress in the normal direction along both sides of the stress discontinuity line are equivalent (Equations (3) and (4)). Meanwhile, the stress along the tangential direction of the stress discontinuity line is discontinuous, and the stress discontinuity line must not be a stress slip line, as shown in Figure 2. Thus, if the stress characteristics along both sides of the intersection line OD are consistent with the stress discontinuity line, the intersection line is the stress discontinuity line.

$${\alpha }_R=\frac{\pi }{4}+\frac{\phi +\beta }{2}-\frac{1}{2}\arcsin (\frac{\sin \beta }{\sin \phi })$$

(1)

$${\theta }_R=\frac{\pi }{4}+\frac{\phi -\beta }{2}+\frac{1}{2}\arcsin (\frac{\sin \beta }{\sin \phi })$$

(2)

In a retaining wall system, H is the wall height; ε is the wall back inclination from a vertical line (ε is positive when the wall back inclines to the backfill, as shown in Figure 1); β is the inclination of the backfill (β is positive when the slope is higher than the horizontal plane, as shown in Figure 1); δ₀ is the friction angle of the soil-wall interface, which is positive when the wall is far away from the backfill, as shown in Figure 1; γ is the unit weight of the backfill; φ is the internal friction angle of the backfill; and P_a is the active earth pressure. Since the backfill is cohesionless and free of surcharge, the earth pressure is proportional to the wall height in a triangular distribution, with an acting point of resultant force located at one third of the wall toe. Therefore, the shapes of slip lines at different heights are similar.

$${\sigma }_{n1}={\sigma }_{n2}$$

(3)

$${\tau }_{n1}={\tau }_{n2}$$

(4)

3. Theoretical Derivations

3.1. Stresses within the Rankine Zone

The Rankine zone can be divided into m triangular slices, including m + 1 triangular slice lines. Since the failure surface of the Rankine zone is a plane, the lateral force of the triangular slices and its inclination angle can be calculated directly in accordance with the force equilibrium condition. To ensure the accuracy and simplicity of the calculation, the zone enclosed by each triangular slice line, slope surface, and failure surface is taken as a calculation zone. For example, in order to calculate the interslice force and its inclination on the ith slice line (OA_i), as shown in Figure 3a, the zone of OBA_i is the selected calculation zone. θ_Ri is the inclination of the ith slice line within the Rankine zone. When the ith slice line extends in the positive direction along the x-axis, its inclination θ_Ri = 0°, and θ_Ri is positive when the triangular slice line rotates clockwise around the x-axis. OA_i, P_Ri, and δ_Ri are the length, the interslice force, and the interslice force inclination angle of the ith slice line within the Rankine zone, respectively. R_Ri is the force acting on the failure surface of the calculation zone corresponding to the ith slice line, at an angle φ to the normal of the failure surface. θ_R is the inclination of the transition ray (line OA), P_R is the interslice force acting on the transition ray within the Rankine zone, and R_R is the force acting on the failure surface of the whole Rankine zone. Since θ_Ri = θ_R, it follows that OA_i = OA, P_Ri = P_R, δ_Ri = φ, R_Ri = R_R, and the inclination of the failure surface is α_R. From Figure 3b, the following geometric relationship can be obtained:

$$\overline{O^{\prime }D}=\sin \omega •\overline{O^{\prime }A}$$

(5)

$$\overline{O^{\prime }D}=\frac{\sin {\delta }_{Ri}}{\sin \phi }\overline{O^{\prime }{S}_2}$$

(6)

Thus, combining Equations (5) and (6) leads to

$$\omega =\arcsin (\frac{\sin {\delta }_{Ri}}{\sin \phi })$$

(7)

From Figure 3b, it follows that

$$2{\mathsf{\Phi }}_2=\frac{3\pi }{2}-\phi -{\delta }_{Ri}-\omega$$

(8)

Substituting Equation (7) into Equation (8) leads to

$${\mathsf{\Phi }}_2=\frac{3\pi }{4}-\frac{\phi +{\delta }_{Ri}}{2}-\frac{1}{2}\arcsin (\frac{\sin {\delta }_{Ri}}{\sin \phi })$$

(9)

From Figure 3a, it follows that

$${\alpha }_R=\pi -{\theta }_{Ri}-{\mathsf{\Phi }}_2$$

(10)

When substituting Equation (9) into Equation (10), the relationship between the interslice force inclination, i.e., δ_Ri, and the failure surface inclination, i.e., α_R, can be obtained as follows:

$${\alpha }_R=\frac{\pi }{4}-{\theta }_{Ri}+\frac{\phi +{\delta }_{Ri}}{2}+\frac{1}{2}\arcsin (\frac{\sin {\delta }_{Ri}}{\sin \phi })$$

(11)

Note that it satisfies the boundary condition of δ_Ri = φ when θ_Ri = θ_R.

In addition, according to the force equilibrium condition of the calculated zone OA_iB in Figure 3a,

$$\begin{array}{l}{P}_{Ri}\cos (\frac{\pi }{2}-{\theta }_{Ri}+{\delta }_{Ri})=R_{Ri}\cos (\frac{\pi }{2}-{\alpha }_R+\phi )\\ P_{Ri}\sin (\frac{\pi }{2}-{\theta }_{Ri}+{\delta }_{Ri})+R_{Ri}\sin (\frac{\pi }{2}-{\alpha }_R+\phi )=W_{Ri}\end{array}$$

(12)

With the weight of the calculated area OA_iB, W_Ri can be expressed as follows:

$$W_{Ri}=\frac{1}{2}\gamma {\overline{O{A}_i}}^2\frac{\sin ({\alpha }_R+{\theta }_{Ri})\sin ({\theta }_{Ri}+\beta )}{\sin ({\alpha }_R-\beta )}$$

(13)

Substituting Equation (13) into Equation (12) leads to

$$P_{Ri}=\frac{1}{2}\gamma {\overline{O{A}_i}}^2\frac{\sin ({\alpha }_R+{\theta }_{Ri})\sin ({\theta }_{Ri}+\beta )\sin ({\alpha }_R-\phi )}{\sin ({\alpha }_R-\beta )\sin ({\alpha }_R-\phi +{\theta }_{Ri}-{\delta }_{Ri})}$$

(14)

Additionally,

$$P_{Ri}=\frac{1}{2}\gamma {\overline{O{A}_i}}^2{K}_{Ri}$$

(15)

where K_Ri is the lateral pressure coefficient of the ith triangular slice line, which can be obtained by combining Equations (14) and (15).

Hence,

$$K_{Ri}=\frac{\sin ({\alpha }_R+{\theta }_{Ri})\sin ({\theta }_{Ri}+\beta )\sin ({\alpha }_R-\phi )}{\sin ({\alpha }_R-\beta )\sin ({\alpha }_R-\phi +{\theta }_{Ri}-{\delta }_{Ri})}$$

(16)

3.2. Stresses within the Transition Zone

When stress discontinuity occurs in slip-line fields, the boundary of the transition zone will exceed the transition ray OA of the Rankine zone, as shown in Figure 1b. Due to the fact that the location of stress discontinuity is unknown in advance, the whole potential failure zone is considered a transition zone and is divided into n triangular slices, as shown in Figure 4a. The actual boundary line of the transition zone is determined according to the calculated boundary conditions. The inclination angles of the triangular slice lines are denoted as θ₀ (θ₀ = π/2 − ε), θ₁, θ₂, …, θ_k, …, θ_n. The corresponding interslice forces are denoted as P₀ (the lateral force on the wall), P₁, P₂, …, P_k, …, P_n, at angles δ₀ (the friction angle of the soil–wall interface), δ₁, δ₂, …, δ_k, …, δ_n to the normal of the interslice surfaces, respectively. Additionally, the corresponding lateral pressure coefficients are denoted as K₀, K₁, K₂, …, K_k, …, K_n. The force acting on the failure surface of the triangular slices are denoted as R₀, R₁, R₂, …, R_k, …, R_n, at an angle φ to the normal of the failure surface. Figure 4b is the diagram of the force acting on the kth slice, and the corresponding stress Mohr diagram is shown in Figure 4c.

From the geometric relationship in Figure 4c, it can be concluded that

$$\overline{O{O}^{\prime }}=\frac{\overline{O^{\prime }{S}_2}}{\sin \phi }$$

(17)

$$\overline{OB}=\overline{O^{\prime }{S}_1}\frac{\sin {\omega }^{\prime }}{\tan {{\delta }_k}^{\prime }}$$

(18)

$$\overline{B{O}^{\prime }}=\overline{O^{\prime }{S}_1}\cos {\omega }^{\prime }$$

(19)

It is obvious that ω′ can be derived by combining Equations (17)–(19) as follows:

$${\omega }^{\prime }=\arcsin (\frac{\sin {{\delta }_k}^{\prime }}{\sin \phi })-{{\delta }_k}^{\prime }$$

(20)

where δ_k′ is the inclination angle of the interslice force acting on the kth slice central ray, δ_k′ = (δ_k + δ_k−1)/2.

Since $2{\mathsf{\Phi }}_k=\frac{\pi }{2}-\phi +{\omega }^{\prime }$, then it follows that

$${\mathsf{\Phi }}_k=\frac{\pi }{4}-\frac{\phi +{{\delta }_k}^{\prime }}{2}+\frac{1}{2}\arcsin (\frac{\sin {{\delta }_k}^{\prime }}{\sin \phi })$$

(21)

From ${\alpha }_k=\pi -{\theta }_k-{\mathsf{\Phi }}_k$,

$${\alpha }_k=\frac{3\pi }{4}-{{\theta }_k}^{\prime }+\frac{\phi +{{\delta }_k}^{\prime }}{2}-\frac{1}{2}\arcsin (\frac{\sin {{\delta }_k}^{\prime }}{\sin \phi })$$

(22)

where α_k is the failure surface inclination of the kth slice.

Moreover, from Figure 4b, by establishing the force and moment equilibrium equations of the kth slice, the recurrence equation of the interslice force can be obtained.

$$P_k=\frac{\sin ({\alpha }_k+{\theta }_{k-1}-\phi -{\delta }_{k-1})}{\sin ({\alpha }_k+{\theta }_k-\phi -{\delta }_k)}{P}_{k-1}-\frac{W_k\sin ({\alpha }_k-\phi )}{\sin ({\alpha }_k+{\theta }_k-\phi -{\delta }_k)}$$

(23)

$$R_k=\frac{\sin ({\delta }_k-{\theta }_k+{\theta }_{k-1}-{\delta }_{k-1})}{\sin ({\alpha }_k+{\theta }_k-\phi -{\delta }_k)}{P}_{k-1}+\frac{W_k\sin ({\theta }_k-{\delta }_k)}{\sin ({\alpha }_k+{\theta }_k-\phi -{\delta }_k)}$$

(24)

$$\begin{array}{ll}{M}_k& =P_k[\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.L_k\cos {\delta }_k-h_k\cos ({\alpha }_k+{\theta }_k-\phi -{\delta }_k)\cos ({{\theta }_k}^{\prime }+{\alpha }_k-\phi )]\\ & -P_{k-1}[\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.L_{k-1}\cos {\delta }_{k-1}-h_k\cos ({\alpha }_k+{\theta }_{k-1}-\phi -{\delta }_{k-1})\cos ({{\theta }_k}^{\prime }+{\alpha }_k-\phi )]\\ & -W_k[h_k\cos (\phi -{\alpha }_k)\cos ({{\theta }_k}^{\prime }+{\alpha }_k-\phi )+x_o-x_{wk}]\end{array}$$

(25)

The lateral pressure coefficient of the kth triangular slice is K_k, which is calculated as follows:

$$K_k=2P_k/(\gamma {\overline{OG}}^2)$$

(26)

where W_k is the weight of the kth triangular slice, and $W_k=\frac{1}{2}\overline{\mathrm{OC}}•\overline{OG}\sin ({\theta }_{k-1}-{\theta }_k)\gamma$; θ_k′ is the central ray inclination of the kth triangular slice; L_k−1 and L_k are the lengths of the k−1th slice line and the kth slice line, respectively; h_k is the central ray length of the kth triangular slice; and x₀ and x_wk are the x-coordinate of the origin and the barycentric coordinate of the kth triangular slice, respectively.

3.3. Determination of Stress Discontinuity

Whether there will be stress discontinuity in the slip-line fields can be determined by the relationship between the failure surface inclination angle α₀ at the retaining wall toe and the failure surface inclination angle α_R within the Rankine zone.

From Equation (22),

$${\alpha }_0=\frac{3\pi }{4}-{\theta }_0+\frac{\phi +{\delta }_0}{2}-\frac{1}{2}\arcsin (\frac{\sin {\delta }_0}{\sin \phi })$$

(27)

where θ₀ = π/2 − ε.

For $\Delta (\epsilon ,\beta ,\delta ,\phi )={\alpha }_R-{\alpha }_0$, that means

$$\Delta (\epsilon ,\beta ,\delta ,\phi )=\beta -\arcsin \left(\frac{\sin \beta }{\sin \phi }\right)-{\delta }_0+\arcsin (\frac{\sin {\delta }_0}{\sin \phi })-2\epsilon$$

(28)

If $\Delta (\epsilon ,\beta ,\delta ,\phi )<0$, stress discontinuity occurs in the slip-line fields, and the failure surface shows a concave curve; if $\Delta (\epsilon ,\beta ,\delta ,\phi )>0$, there is no stress discontinuity in the slip-line fields, and the failure surface shows a convex curve; and if $\Delta (\epsilon ,\beta ,\delta ,\phi )=0$, there is no stress discontinuity in the slip-line fields, and the two conjugate slip lines in the slip-line fields are straight lines, which is consistent with the Coulomb theory. The types of failure surface are shown in Figure 5.

According to the derivations in Section 3.1 and Section 3.2, if there is no stress discontinuity in the slip-line fields, the transition ray is the dividing line between the Rankine zone and the transition zone. The lateral pressure coefficient and the interslice force inclination angle of the transition ray calculated by Equation (16) and Equation (11) within the Rankine zone are equal to those calculated by Equation (26) and Equation (22) within the transition zone, that is K_R = K_k (θ_k = θ_R) and δ_R = δ_k (θ_k = θ_R); this satisfies the boundary condition of δ_R = φ, and the conclusion has been proved by the authors in a previous study [25]. If stress discontinuity occurs in the slip-line fields, the boundary line of the transition zone will exceed the transition ray OA of the Rankine zone. Thus, there is an intersection line between the Rankine zone and the transition zone. For the convenience of distinction, the lateral pressure coefficient and the interslice force inclination angle on the intersection line of the Rankine zone and the transition zone are, respectively, denoted as K_θR, δ_θR, K_θT, and δ_θT. Two conditions should be satisfied to ensure the intersection line is a stress discontinuity line: (i) The lateral pressure coefficient and the interslice force inclination angle of the intersection line calculated by Equation (26) and Equation (22) within the transition zone are equal to those calculated by Equation (16) and Equation (11) within the Rankine zone, that is, K_θT = K_θR and δ_θT = δ_θR, as shown in Figure 6. (ii) The interslice force inclination angle is less than the internal friction angle of soil, that is, δ_θT = δ_θR < φ.

4. Numerical Procedure

For a typical retaining wall, the value of the wall inclination, ε, the friction angle of the soil–wall interface, δ₀, the internal friction angle of the backfills, φ, the unit weight of the backfills, γ, and the backfills’ surface inclination angle, β, can be determined in advance. Firstly, for a retaining wall with a wall height of H, whether there will be stress discontinuity needs to be determined according to Equation (28). If there is no stress discontinuity, the slip-line fields can be obtained according to the previous study [25]. To computing slip-line fields with stress discontinuity, the potential failure zone is divided into the Rankine zone and the transition zone; the Rankine zone can be determined strictly based on the theory of plastic mechanics; and the boundary of the transition zone needs to be determined using an iterative procedure. The lateral pressure coefficient and the interslice force inclination angle of the slice lines within the Rankine zone and the transition zone can be calculated by using an iterative procedure, and then we can determine the location of the stress discontinuity line. Finally, the earth pressure and the slip-line fields with stress discontinuity can be obtained. The main calculation process are as follows:

(1) Divide the Rankine zone into m triangular slices, and the included angle of each slice is Δ_θ. According to Equations (11) and (16), the corresponding interslice force inclination angle of each slice line, i.e., δ_Ri, and the lateral pressure coefficient, i.e., K_Ri, can be calculated.

(2) Divide the potential zone into n triangular slices, and the included angle of each slice is Δ_θ. Assuming that the earth pressure coefficient K_a^(j=1) in the first calculation process is the Coulomb earth pressure coefficient, begin with the wall back and calculate the lateral pressure coefficient, i.e., K_k, and the interslice force inclination angle, i.e., δ_k, of each slice line successively according to the recursive equation (Equations (23)~(26)); for the iterative process of δ_k,, refer to the authors’ previous study [25]. If the inclination angle of the interslice force on the kth slice line is equal to the internal friction angle, that is, δ_k = φ, stop the calculation, and the inclination angle of the kth slice line is θ_kφ. Then, the following judgment needs to be made immediately:

(a) If θ_kφ^(j=1) = θ_R, and the lateral pressure coefficient and its inclination of the kth slice line within the Rankine zone are equal to those within the transition zone, that is, K_k = K_{R (}θ_kφ = θ_R) and δ_k = δ_R = φ ₍θ_kφ = θ_R), K_a^(j=1) is the active earth pressure coefficient K_a, α_{k(k=1,2,…,k)}, α_R is the inclination of the failure surface within the transition zone and the Rankine zone. The kth slice line is the transition ray between the Rankine zone and the transition zone, and it is a slip line. It indicates that there is no stress discontinuity in the slip-line field.

(b) If θ_kφ^(j=1) < θ_R, and the transition zone intersects the Rankine zone, it is necessary to judge whether there is an intersection line satisfying the features of stress discontinuity, that is, the lateral pressure coefficient and its inclination angle on the intersection line calculated by the Rankine zone equation (Equations (11) and (16)) are equal to those calculated by the transition zone equation (Equations (23)~(26)). (If Δ ≤ 10⁻³, and $\Delta =\sqrt{{(\frac{\Delta \delta }{\overline{{\delta }_{\theta }}})}^2+{(\frac{\Delta K}{\overline{K_{\theta }}})}^2}$, it is considered to satisfy the condition of equality, where Δδ is the difference of the interslice force inclination angle of the intersection line calculated by the Rankine zone equation and the transition zone equation, and $\stackrel{-}{{\delta }_{\theta }}$ is the average value. ΔK is the difference of the lateral pressure coefficient value of the intersection line calculated by the Rankine zone equation and the transition zone equation, and $\stackrel{-}{K_{\theta }}$ is the average value.). If there is an intersection line satisfying the conditions, that is, Δ ≤ 10⁻³, the intersection line is the stress discontinuity line, which inclination angle is denoted by θ_ray; α_{k(k=1,2,…,k)} is the inclination of the failure surface in the transition zone; and the value of K_a^(j=1) is the active earth pressure coefficient K_a. If Δ > 10⁻³, change the earth pressure coefficient, K_a^(j), and repeat step (2) until the stress features of the intersection line in step 2(a) or step 2(b) is satisfied.

(c) If θ_kφ^(j=1) > θ_R, there is no intersection line between the transition zone and the Rankine zone. Hence, it is necessary to change the earth pressure coefficient, K_a^(j=1) (increase the earth pressure coefficient value in an active case), so that K_a = K_a^(j=2), repeat step (2) until θ_kφ ≥ θ_R, and perform the judgment of step 2(a) or step 2(b).

(3) Take the calculated transition ray or stress discontinuity line as the boundary line, and plot the failure lines within the Rankine zone and the transition zone, respectively. Another conjugate slip line can be constructed according to the condition that the two slip lines intersect each other at an angle of π/2 − φ, and, thus, slip-line fields with stress discontinuity can be obtained.

5. Example studies

5.1. Example 1

This example considers an active case of a vertical and smooth retaining wall with a horizontal backfill surface, which conforms to the assumptions of Rankine’s earth pressure theory. Based on the Rankine theory, the active earth pressure coefficient of the retaining wall, K_a, is equal to 0.333. Additionally, based on the method proposed in this paper, the active earth pressure coefficient, K_a, is also equal to 0.333. As shown in Figure 7a, the inclination of the intersection line between the Rankine zone and the transition zone is 60°. The results of the lateral pressure coefficient and its inclination angle on the intersection line calculated by the Rankine zone equation are K_θR = 0.500 and δ_θR = 30°, and the results calculated by the transition zone equation are K_θT = 0.500 and δ_θT = 29.999°. Since it is normal to have small errors in iterative calculation, Δ = 3.3 × 10⁻⁵, and the calculation results meet the condition of K_θR = K_θT and δ_θR = δ_θT = φ. Thus, the intersection line of θ_ray = 60° is a slip line, and there is no stress discontinuity in the slip-line fields of this example, which is consistent with the conclusion of the Rankine theory. From Figure 7b, we can clearly see that the boundary of the Rankine zone coincides with the boundary of the transition zone. Additionally, Figure 7c is the slip-line fields of example 1, and the two slip lines are straight lines with an intersection angle of π/2 − φ.

5.2. Example 2

This example considers an active case of an inclined retaining wall with an inclined surface, and the relevant parameters are ε = 20°, β = −10°, φ = 30°, and δ₀ = −φ/2. The K_a calculated by the Coulomb theory is equal to 0.532, and the value computed by the present method is equal to 0.552. In general, the value of the active earth pressure coefficient calculated by the Coulomb theory is smaller than the actual situation due to the assumption of a planar failure surface [8]. The inclination of the intersection line between the Rankine zone and the transition zone is 49.3°, as shown in Figure 8a. Since K_θR = 0.419, δ_θR = 29.446°, K_θT = 0.419, δ_θT = 29.445°, and Δ = 3.4 × 10⁻⁵, it satisfies the condition of K_θR = K_θT and δ_θR = δ_θT ≠ φ; thus, the intersection line, i.e., θ_ray =49.3°, is the stress discontinuity line. Figure 8b shows that the location relationship of the Rankine zone boundary line, the transition zone boundary line, and the stress discontinuity line; it is obvious that the Rankine zone overlaps with the transition zone, and the inclination angle of the stress discontinuity line is smaller than the inclination of the Rankine zone boundary line. The slip-line field deflects sharply at the stress discontinuity line, as shown in Figure 8c.

5.3. Example 3

This example considers an inclined retaining wall with the same parameters of example 2, except for the wall inclination angle; the relevant parameters are ε = −2.93°, β = −10°, φ = 30°, and δ₀ = −φ/2, which satisfies the relationship of $\Delta (\epsilon ,\beta ,\delta ,\phi )=0$. The value of K_a calculated by the present method is consistent with the result of the Coulomb theory, with K_a = 0.368. The inclination of the intersection line between the Rankine zone and the transition zone is 54.8° (Figure 9a). Since K_θR = 0.420, δ_θR = 30°, K_θT = 0.420, δ_θT = 29.99°, and Δ = 9.3 × 10⁻⁵, the results meet the condition of K_θR = K_θT and δ_θR = δ_θT = φ; thus, there is no stress discontinuity in the slip-line field. From Figure 9b, we can clearly see that the boundary of the Rankine zone coincides with the boundary of the transition zone, and the slip-line field is formed by two families of straight lines, as shown in Figure 9c.

5.4. Example 4

This example considers a passive case of an inclined and smooth retaining wall with a horizontal backfill surface, and the relevant parameters are ε = 30°, β = 0°, φ = 30°, and δ₀ = 0°. The value of the passive earth pressure coefficient, K_p, computed by the present method is equal to 2.032, which is compared to existing solutions, as shown in

Table 1. Comparisons of value of K_p (ε = 30°, β = 0°, φ = 30°, δ₀ = 0°).

The Present Method	Coulomb Theory	Kumar and Chitikela (2002) [18]	Patki et al. (2015) [26]	Liu et al. (2018) [21]
2.032	2.154	1.91	2.05	2.06

. It can be seen that the result obtained by the present method is greater than that obtained by Kumar and Chitikela (2002) [18], and it is in a rough agreement with that of Patki et al. (2015) [26] and Liu et al. (2018) [21]; all of the above results are less than that calculated by the Coulomb theory. A consensus can be reached that the result obtained by the Coulomb theory is far from the actual earth pressure when the friction angle of the soil–wall interface is equal to the internal friction angle of the backfills [22,25].

The inclination of the intersection line between the Rankine zone and the transition zone is 25.9°, as shown in Figure 10a. Since K_θR = 0.694, δ_θR = 29.631°, K_θT = 0.694, δ_θT = 29.641°, and Δ = 3.4 × 10⁻⁴, the results meet the condition of K_θR = K_θT and δ_θR = δ_θT ≠ φ; thus, the intersection line, i.e., θ_ray =25.9°, is the stress discontinuity line. Figure 10b shows that the location relationship of the Rankine zone boundary line, the transition zone boundary line, and the stress discontinuity line; it is obvious that the Rankine zone overlaps with the transition zone, and the inclination angle of the stress discontinuity line is smaller than the inclination of the Rankine zone boundary line. The slip-line field deflects sharply at the stress discontinuity line, as shown in Figure 10c, and the failure surface is concave, which is consistent with that reported by Liu et al. (2018) [21] and Santhoshkumar et al. (2018) [27].

5.5. Example 5

This example considers a passive case of an inclined and rough retaining wall with an inclined backfill surface, and the relevant parameters are ε = 30°, β = 10°, φ = 30°, and δ₀ = −φ/2°. The passive earth pressure coefficient, K_p, calculated by the present method is equal to 1.784. The inclination of the intersection line between the Rankine zone and the transition zone is 8.9°, as shown in Figure 11a. Since K_θR = 0.479, δ_θR = 29.236°, K_θT = 0.479, δ_θT = 29.245°, and Δ = 3.1 × 10⁻⁴, the results meet the condition of K_θR = K_θT and δ_θR = δ_θT ≠ φ; thus, the intersection line, i.e., θ_ray = 8.9°, is the stress discontinuity line. The location of the Rankine zone boundary line, the transition zone boundary line, and the stress discontinuity line is shown in Figure 11b. The slip-line field with stress discontinuity is shown in Figure 11c.

6. Discussion

There is an ultimate inclination of a retaining wall, which refers to the maximum inclination of a retaining wall when there is no stress discontinuity in the slip-line field; that is, if the inclination of the retaining wall is greater than the ultimate inclination, stress discontinuity will occur in the slip-line field. Figure 12 indicates that the ultimate inclination decreases with an increase in internal friction angle, in other words, the greater the internal friction angle, the easier stress discontinuity will appear in the slip-line fields. From Figure 13, it can be seen that the ultimate inclination of a retaining wall increases with an increase in the soil–wall interface friction angle. If the soil–wall interface friction angle is less than 25°, the ultimate inclination is basically consistent with the slope of the increase in the soil–wall interface friction angle. When the soil–wall interface friction angle is greater than 25°, the ultimate inclination of the wall back increases significantly, and the slope is much larger than the small soil–wall interface friction angle; this feature can also be seen in Figure 12. It can be seen from Figure 14 that with an increase in the backfills’ inclination, the ultimate inclination of a retaining wall gradually decreases. Moreover, it can be clearly seen that when the soil–wall interface friction angle is equal to the internal friction angle, the ultimate inclination increases significantly. Finally, we can draw the conclusion that the soil–wall interface friction angle has a great impact on stress discontinuity.

Table 2. The active earth pressure coefficients and the position of stress discontinuity lines with φ = 30° and 40°, β = 0°, and δ₀ = 0°.

φ	ε	Ka (The Present Study)	Ka (Coulomb Theory)	Inclination of Intersection Line between the Rankine Zone and the Transition Zone, θ	Stress Discontinuity Line
30°	−10°	0.274	0.270	60°	No
	0°	0.333	0.333	60°	No
	5°	0.369	0.368	59.5°	Yes
	10°	0.411	0.407	59.1°	Yes
	15°	0.459	0.449	57.6°	Yes
	20°	0.517	0.498	55.2°	Yes
40°	−10°	0.162	0.158	65°	No
	0°	0.217	0.217	65°	No
	5°	0.252	0.251	64.9°	Yes
	10°	0.292	0.287	63.9°	Yes
	15°	0.341	0.329	61.8°	Yes
	20°	0.399	0.375	58.95°	Yes

shows the calculation results of active earth pressure coefficients and position of stress discontinuity with a smooth retaining wall, δ₀ = 0°, and a horizontal backfill surface, β = 0°. The wall inclination angle and the backfill internal friction angle are variable. It can be seen that there is no stress discontinuity in the slip-line field when the wall is vertical or inclined to a free position, that is, ε ≤ 0°. With an increase in the wall inclination, the slip-line field appears to have stress discontinuity, and the location of the stress discontinuity line gradually moves to the backfill surface with the increase in the wall inclination.

Table 3. The active earth pressure coefficients and the position of stress discontinuity lines with φ = 30°, ε = 10°, and β = 10°.

δ0	Ka (The Present Study)	Ka (Coulomb Theory)	Inclination of Intersection Line between the Rankine Zone and the Transition Zone, θ	Stress Discontinuity Line
−φ/2	0.579	0.542	60.3°	Yes
0	0.473	0.461	62.9°	Yes
φ/6	0.456	0.448	63.6°	Yes
φ/3	0.445	0.440	64.2°	Yes
φ/2	0.439	0.437	64.7°	Yes
φ	0.454	0.452	65.2°	No

shows the calculation results of active earth pressure coefficients and location of stress discontinuity with ε = 10°, β = 10°, and φ = 30°. It is obvious that with a decrease in the soil–wall interface friction angle, the slip-line field gradually shows stress discontinuity, and the smaller the soil–wall interface friction angle, the smaller the inclination angle of the stress discontinuity line, that is, the closer to the backfill surface.

7. Conclusions

In this paper, a numerical method is presented for computing slip-line fields with stress discontinuity lines in cohesionless backfills, and the corresponding earth pressure coefficients. The position of the stress discontinuity line can be accurately calculated. By dividing the potential failure zone into the Rankine zone and the transition zone, the position of the Rankine zone can be strictly determined by using the plasticity theory, and the transition zone is determined by using the numerical method presented in this paper. The potential failure zone is divided into a series of triangular slices, each of which satisfies the force and moment equilibrium conditions and the Mohr–Coulomb criterion. An iterative procedure is proposed for adjusting the inclination of the failure surface to ensure that the stress boundary conditions of the transition zone are satisfied. If the stress discontinuity line occurs in the slip-line field, there is an intersection line between the Rankine zone and the transition zone. The stress characteristics on both sides of the intersection line satisfy two conditions: (i) the lateral pressure coefficient on both sides of the intersection line is equal, and (ii) the interslice force inclination angle on both sides of the intersection line is equal, but not equal to the internal friction angle. Additionally, the two sides of the intersection line refer to the Rankine zone and the transition zone. Since the stress discontinuity line and the first family of slip lines have been obtained, the inclination of the second family of slip lines can be calculated according to the relationship that two conjugate slip lines intersect at an angle of π/2 − φ in an active case.

The method for computing slip-line fields with stress discontinuity presented herein is applicable to a retaining wall with an inclined cohesionless backfill surface without surcharge. Several examples are provided to demonstrate slip-line fields with stress discontinuity, and the earth pressure coefficients are in fair agreement with those of other numerical methods. In addition, the effects of retaining wall inclination, the soil–wall interface friction angle, the backfill friction angle, and the backfill inclination on stress discontinuity are discussed. The results indicate that the soil–wall interface friction angle has the most obvious effect on stress discontinuity. Since the shape of the failure surface and the interslice force inclination angle are not assumed, the results calculated by the present method are strictly approximate to the solution obtained based on the theory of plastic mechanics. If the internal friction angle, φ, and the friction angle of the soil–wall interface, δ₀, are replaced by −φ and −δ₀, the equations derived in this paper are also applicable to a passive case.