Abstract
Bridges are geometrically complex infrastructures, and their designs usually exhibit significant geometric variations between different structural solutions. The modelling complexity implies a low degree of model reuse in comparable projects; moreover, with the development of new technologies and design ways, the AEC industry often requires computational cost reduction, less time for model developments and analysis, and little-to-zero material waste in the face of the environmental emergency. The present document proposes a generative approach to enhance the bridge design process, increasing efficiency by reducing computational costs and modelling efforts, tackling the aforementioned objectives. The following methodology relies on a workflow to create flexible geometric models, introducing parameters and numerical relationships between all the design variables. Therefore, from a generative development, different geometric solutions of a bridge’s family are created by modifying the parameter settings within the same model. Then, the present work aims to define a modelling and analysis strategy for a multi-girder composite bridge project based on parametric development, structural analysis, and optimization. The results integrate building information modeling (BIM) to explore and create high-potential designs with complex geometries and find cost-effective solutions.
1. Introduction
Nowadays, architectural design tools have expanded the possibilities for innovative geometries and impressive structural details in the architectural and civil engineering fields. Nevertheless, as the infrastructure industry is embracing digitalization to increase productivity and be in compliance with new technologies and innovations, there is a framework for cost increases, sustainability issues, and short deadlines. As a result of these constraints, more operators in the AEC industry are exploring parametric design and BIM-based workflows.
The creative process and managing of building data over a structure’s life cycle refers to a method denominated as building information modelling (BIM). The BIM is a process supported by various tools, technologies, and contracts, which involves the generation and management of digital representations of physical and functional characteristics of places and structures [1]. As a result, CAD–BIM systems produce a data-rich, object-based, typically three-dimensional model. The system incorporates all available construction-related data, including architectural design (building element geometry, spatial relationships, connectivity); structural design (project design documentation, structural scheme); and information on the building’s construction and maintenance processes [2].
With the BIM design systems, parametric and generative modelling systems are becoming part of the ordinary design of buildings and infrastructures. The parametric modelling enhances the design process, increasing efficiency by reducing time and effort. The strategy relies on creating flexible models by introducing parameters and numerical relationships between the design variables. The implementation of geometry in parametric modelling is conducted through different programming languages, and most of the cases of parametric modelling revolve around visual scripting [3].
In a parametric model, the user acts directly on a single variable that creates the structural components, since they are not predefined as in direct modelling [4]. A parametric model is, thus, an ideal model able to provide several solutions according to the values imposed for each parameter or variable [5]. The association of building information modeling (BIM) with parametric modelling delivers a set of powerful tools for a complete workflow, comprehending the conceptual design until the construction and maintenance phase, enabling data reuse and decreasing costs. Through direct connections between BIM software and visual programming tools such as Grasshopper—a pre-installed add-on for Rhinoceros 3D (a computer graphics and computer-aided design application)—the AEC operators can implement a parametric workflow without prior programming experience [6].
Bridges are geometrically complex civil engineering structures, and regarding the case of curved bridges, the design complexity is increasing due to the numerous dependencies between the geometric entities and the complex 3D curved surfaces [7]. Bridge projects usually exhibit significant geometric variations between the different families of structures; additionally, the geometric dependencies between the design variables are difficult to control using conventional direct modelling. Furthermore, there is a low degree of reuse of the models in similar projects and updating the initial drawings and models implies a significant time waste.
The architectural and structural design aims to pursue solutions enabling the structures to perform their purpose with the least resources and effort. To create a better layout, the designers face an iterative process involving trial-and-error methods, changing the geometry and analyzing the results until the structural response is valid according to building regulations. The process often relies on the designer’s judgement and experience [8,9].
The workflow studied in this document aims to overcome all the limitations described by applying tools present in the Grasshopper environment—an add-on for Rhinoceros 3D employing visual script. For this purpose, parametric elements are generated to assemble projects in BIM environments and are further connected to create a single structural organism. The entire process can be performed thanks to the Grasshopper-Tekla Structures live link. Finally, preliminary structural analysis and verification are presented in Karamba3D, with the optimization strategy to reduce material waste and achieve an efficient design.
This work presents a powerful tool to accomplish the structural design of complex bridges. The present workflow allows engineers and architects to explore and create high-potential designs by replacing manual works, thanks to the introduction of logical rules and relationships describing the model and relying on design automation by changing design variables. The employed tools in this work show significant advantages to help improve the design process and guarantee high-quality results, increasing productivity and flexibility. The user can test and analyze different alternatives efficiently, permitting the discovery of innovative, cost-effective solutions. Hereby, complex composite bridges can be designed and verified from simple ordered geometrical operations and be automatically modified to create resource-efficient solutions to satisfy society’s demands.
2. Methodology and Model Development
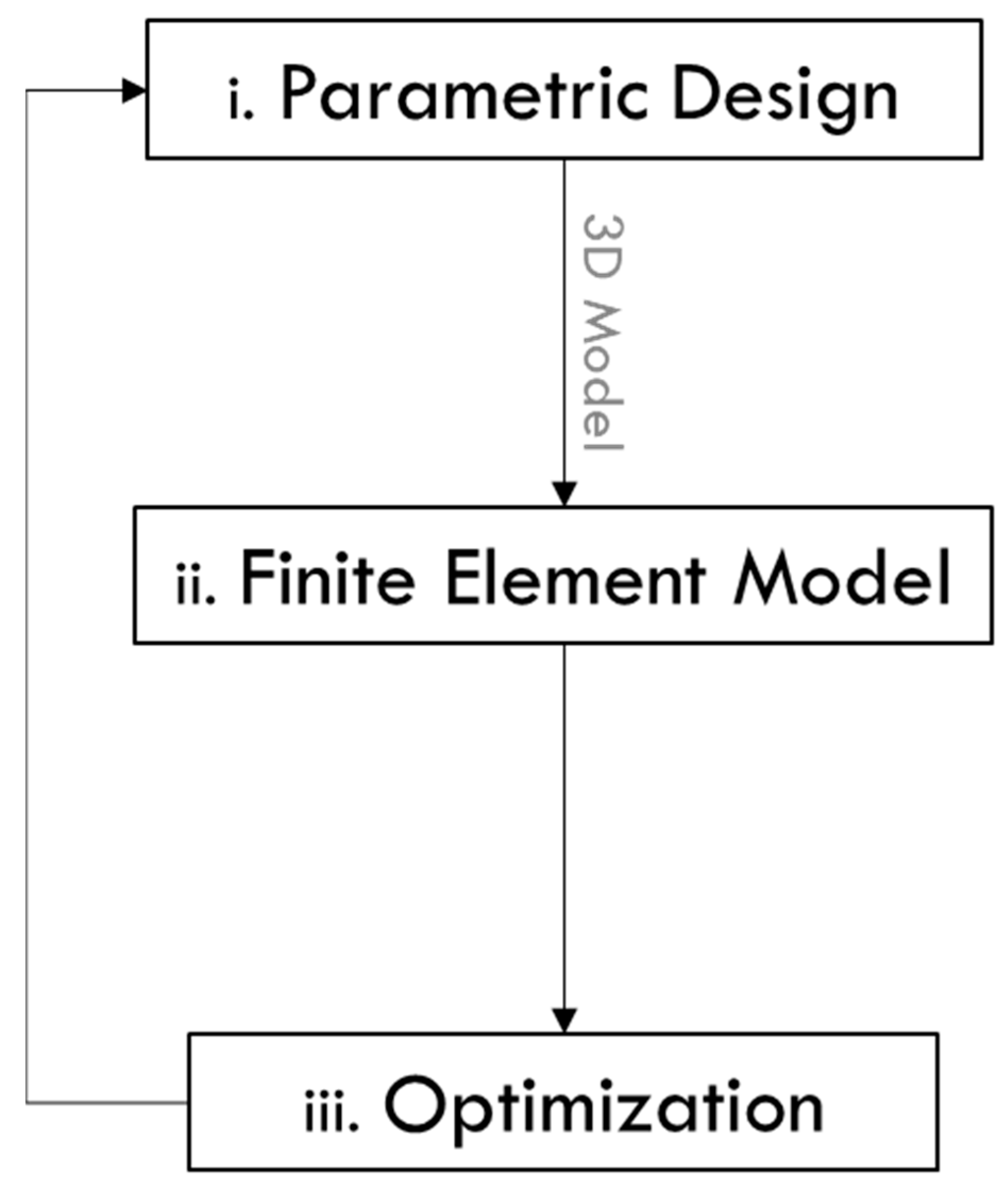
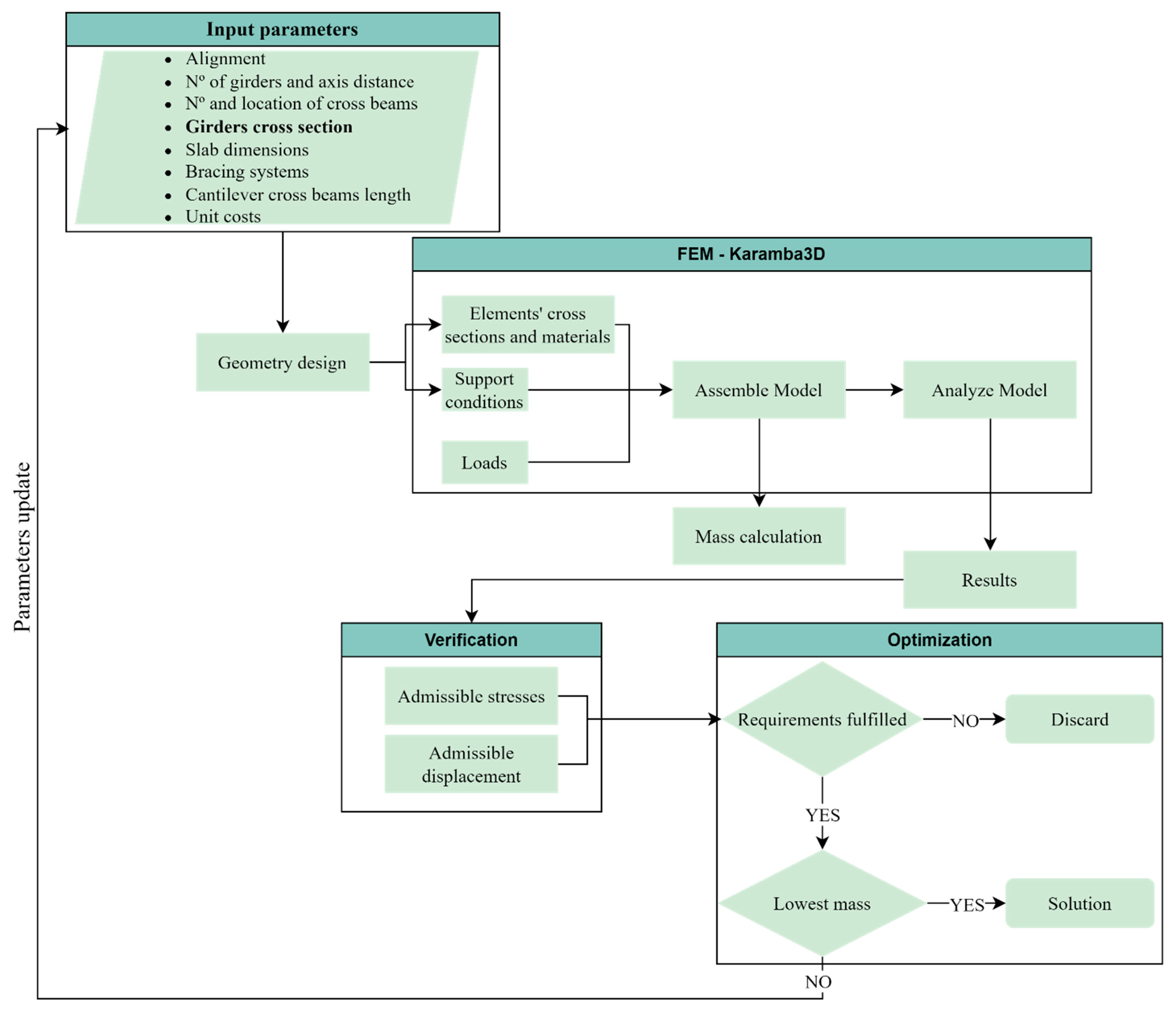
The main aim of the present work is to foster the design and analysis of bridge projects by developing a generative file to produce geometric alterations, avoiding the remodelling needed for the variation of the design variables. The study encompasses the bridge superstructure and substructure, extendable to auxiliary systems. The accomplishment of the goal is guided by different stages represented in Figure 1 [10].
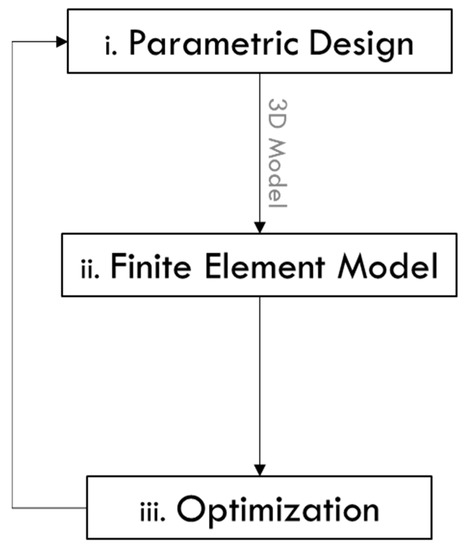
Figure 1.
Workflow development of the modelling and optimization strategy [10].
The first stage focuses on the parametric modelling design, strictly related to geometry development (i). The design variables are selected to perform geometrical and mathematical operations, aiming to generate the bridge cross-sections. The second stage encompasses the creation of the visual algorithm of the 3D model in Tekla. This step involves the definition of profiles, materials, and positions, as the design and details of the connections (ii). The third stage is the creation of the finite element model by defining and assembling the element’s cross-sections and materials, loads, and boundary conditions using Karamba3D plug-in in Grasshopper (visual programming language and environment that runs within the Rhinoceros 3D—CAD). After that, the resulting model is compared with a secondary software (Midas Civil), verifying the results. Finally, an optimization algorithm (evolutionary algorithm—EAs) is applied to determine the most cost-efficient girders’ cross-sections (iii).
2.1. Parametric Design: Geometry Development
The first workflow steps define the principal design variables to allow the creation of an adaptive bridge plan. The selection is based on engineering criteria to create a cluster of objects resulting in a single model composed of multiple design variables. The variables considered are:
- Bridge alignment;
- Number of girders and axis distance;
- Number and location of cross-beams;
- Girder cross-section;
- Slab dimensions;
- Bracing systems, axis distance, and vertical position;
- Cantilever cross-beams length.
This study considers the bridge longitudinal and transversal alignment as the central axis and guideline. The description of the bridge alignment is given by the quadratic equation as follows:
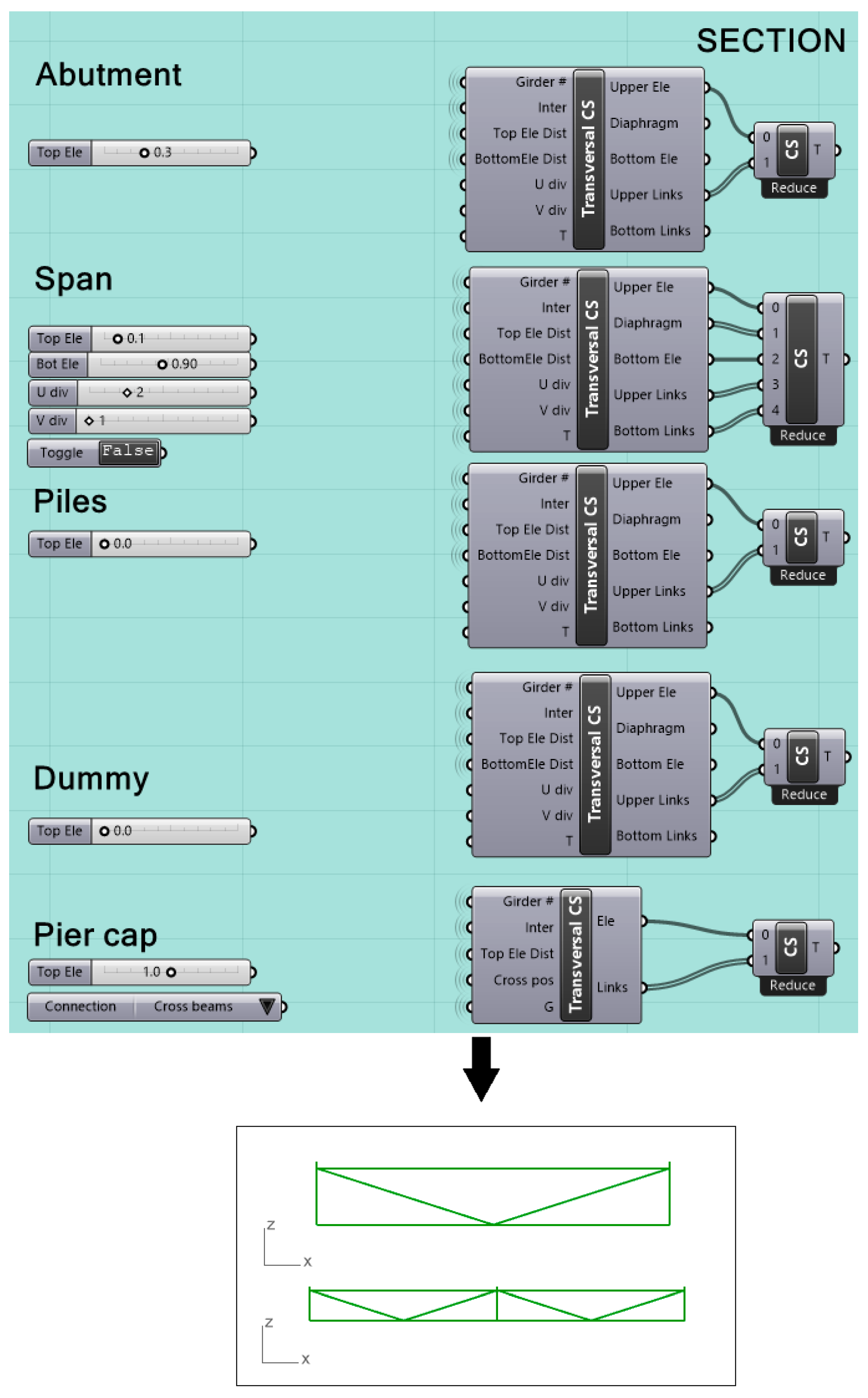
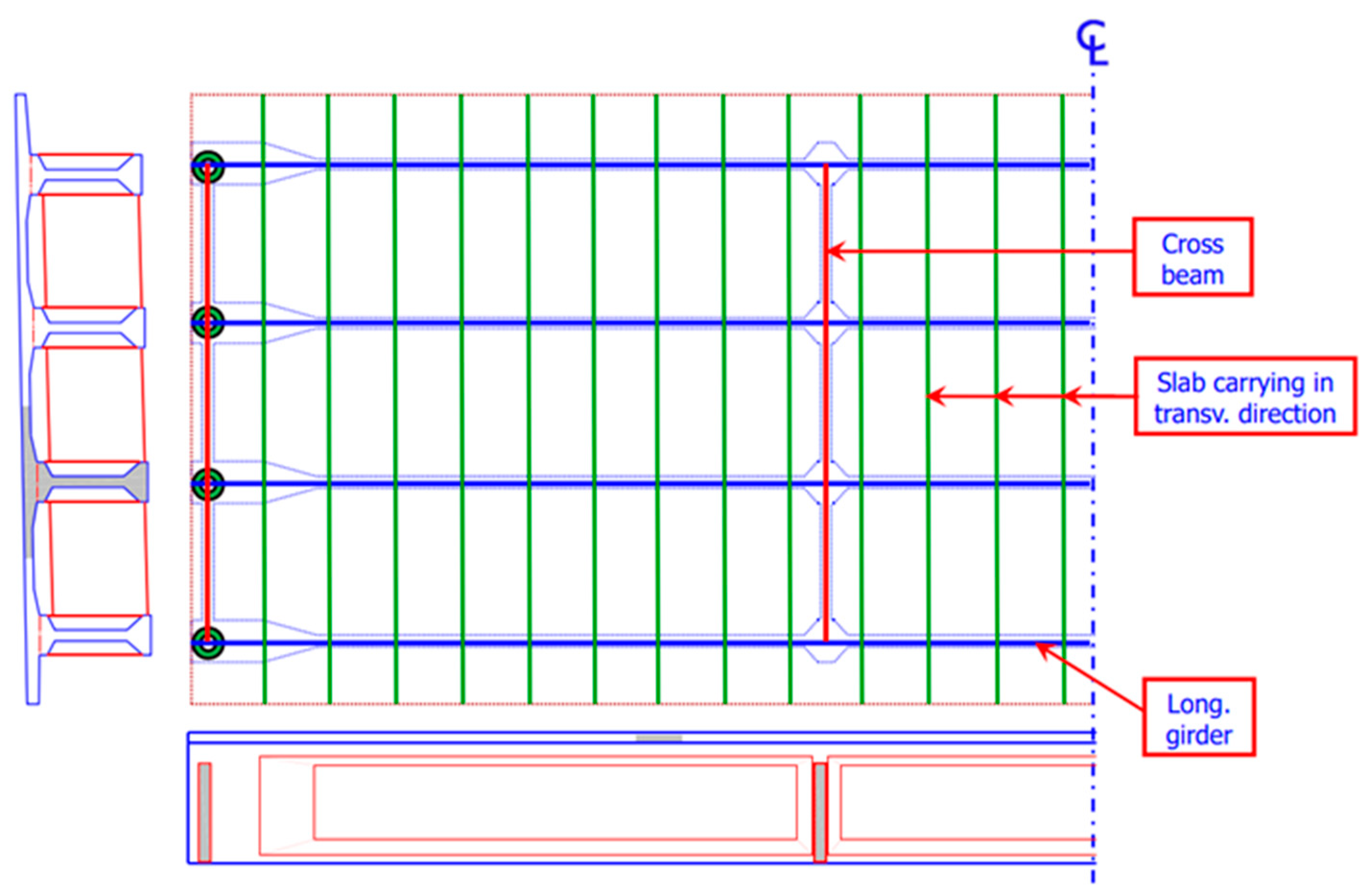
To define the bridge’s guideline in the grasshopper environment as described in Equation (1), the user can provide three points (start-, mid-, and end-point coordinates) or directly retrieve the curve from the bridge axis by reparametrizing the geometry obtained through the direct modelling using the curve component ⇒ set one curve. The later steps encompass the definition of the bridge transversal section elements through a cluster (group of Grasshopper components) to create different elements: cross-beams, diaphragms, and dummy transversal elements. The clustering of several Grasshopper functions allows the development of beam elements and rigid links needed for the structural analysis. Figure 2 illustrates the reiteration of clusters to generate all the bridge’s elements, showing two examples of diaphragm elements.
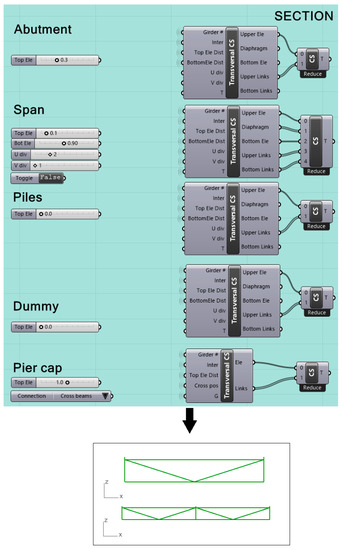
Figure 2.
Cluster of Grasshopper tools to create variable transversal elements.
The transversal elements represented in Figure 2 are placed along the bridge alignment through the following expression (Equation (2)):
Equation (2) describes the location of the bridge transversal elements in which f(x) represents the total evaluated length of the bridge, d is the distance between the members under consideration, and ni is the total number of transversal elements obtained.
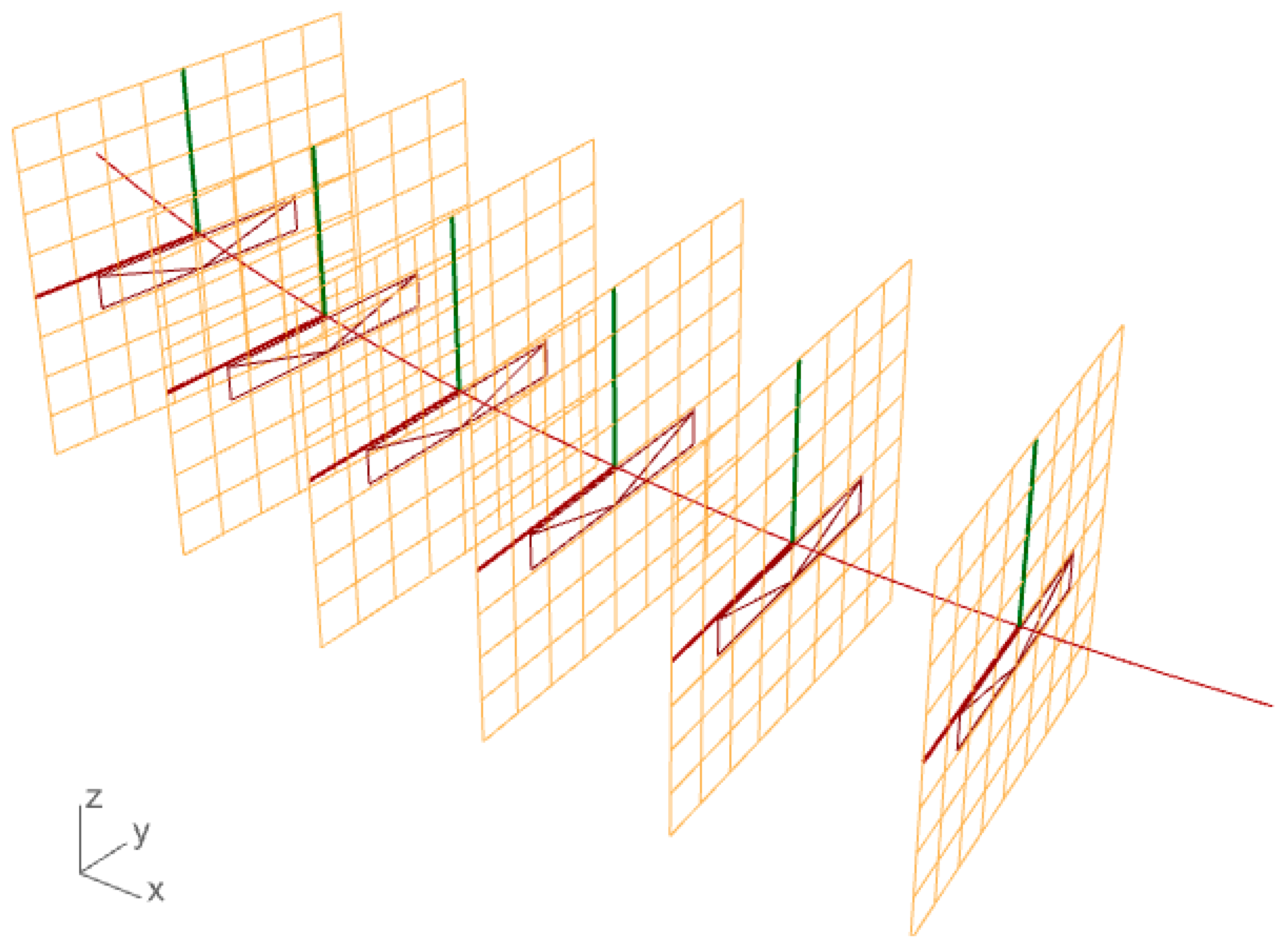
Following this, another cluster is designed to locate the elements along the bridge axis described by Equation (1). For this purpose, the curve is shattered into segments to define the elements’ positions. Additionally, the transversal members can be placed on the axis with equal or different lengths between them, depending on the case study. After creating all the points for positioning the transversal elements in the 3D space, perpendicular planes to the principal axis are generated (described by Equation (1)) in correspondence with the points. Finally, a cross-section remapping is performed to relocate the transversal elements considering the point’s position and the plane inclinations on the axis (Figure 3). The user can select to orient the planes aligned to the global z-axis or perpendicular to the longitudinal slope, as shown in Figure 3.
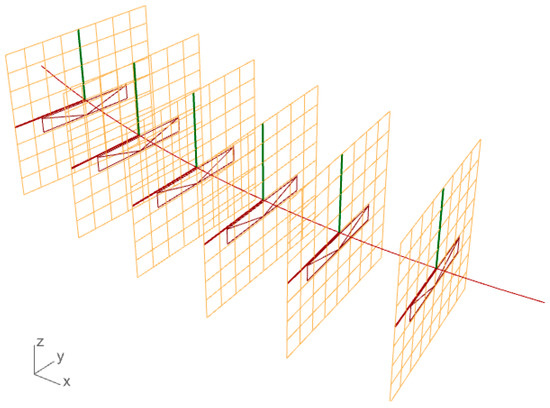
Figure 3.
Cross-sections alignment and rotation according to the bridge axis (Equation (1)).
The girders are created with polylines connecting the rigid links and dummy elements. Then, the girders’ division takes place according to the joint locations or beam length settings. For the structural model, it is possible to evaluate the points where the properties of the girders change, such as the effective width of the concrete elements or, in the case of a continuous bridge, cracked cross-section properties.
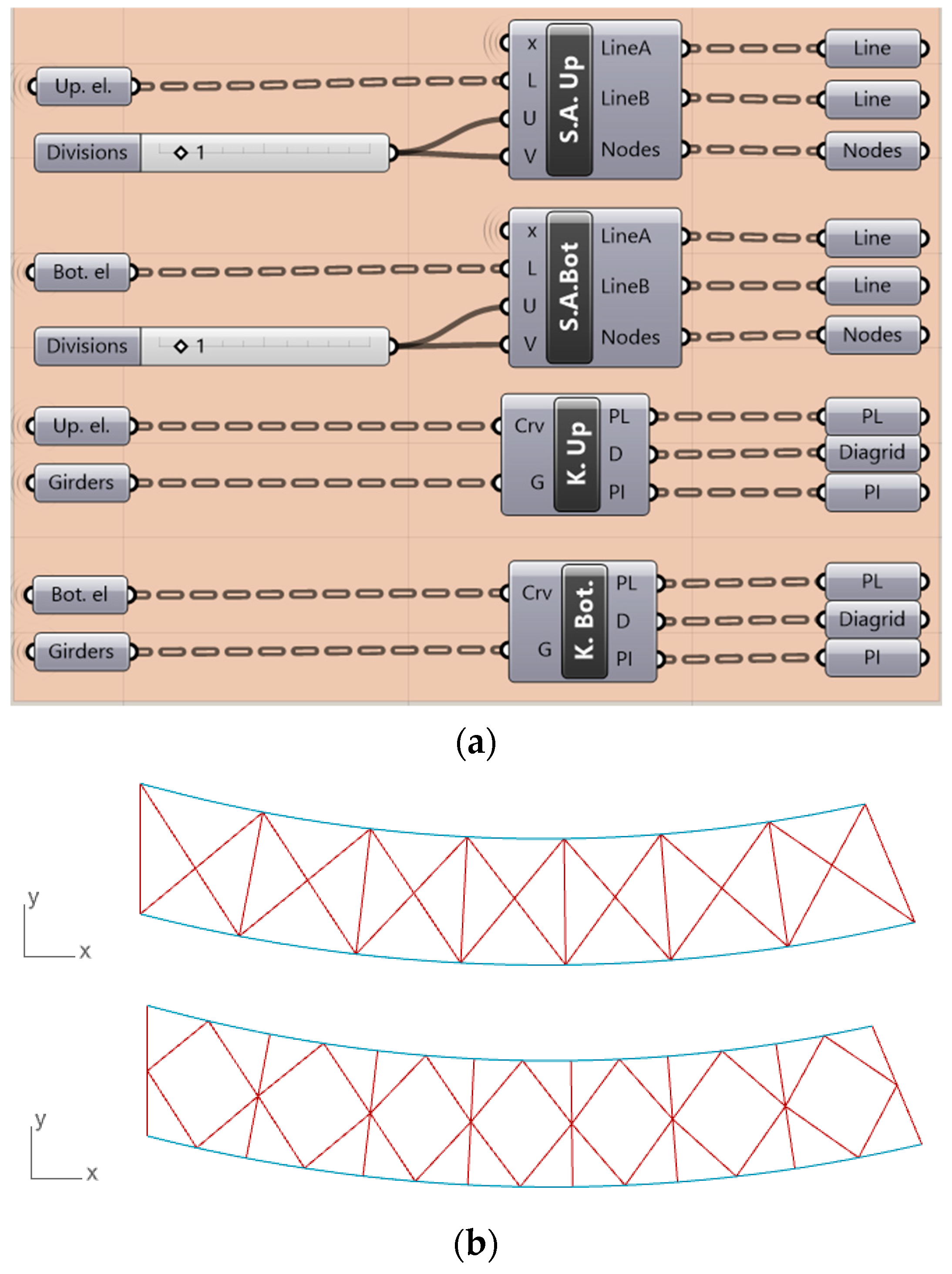
Finally, the design configurations of the upper and bottom horizontal bracing systems are obtained (Figure 4).
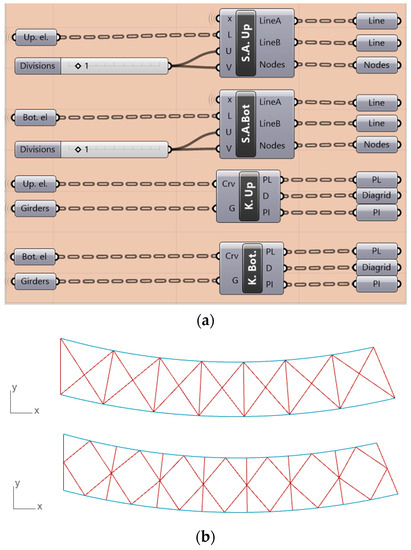
Figure 4.
(a) Bracing system and girders definitions algorithm in Grasshopper environment; (b) bracing systems visualization.
For the supports’ definition, it is possible to consider the bridge substructure and to create the piers with variable lengths; the script allows the generation of the pier caps and the connection to the main girders or crossbeams. In the case of modelling only the superstructure, the supports can be located at the girders or cross-beams, according to the profile characteristics. The geometry development involves multiple iterations to verify the adaptivity to the variations in parameters’ values and conditions.
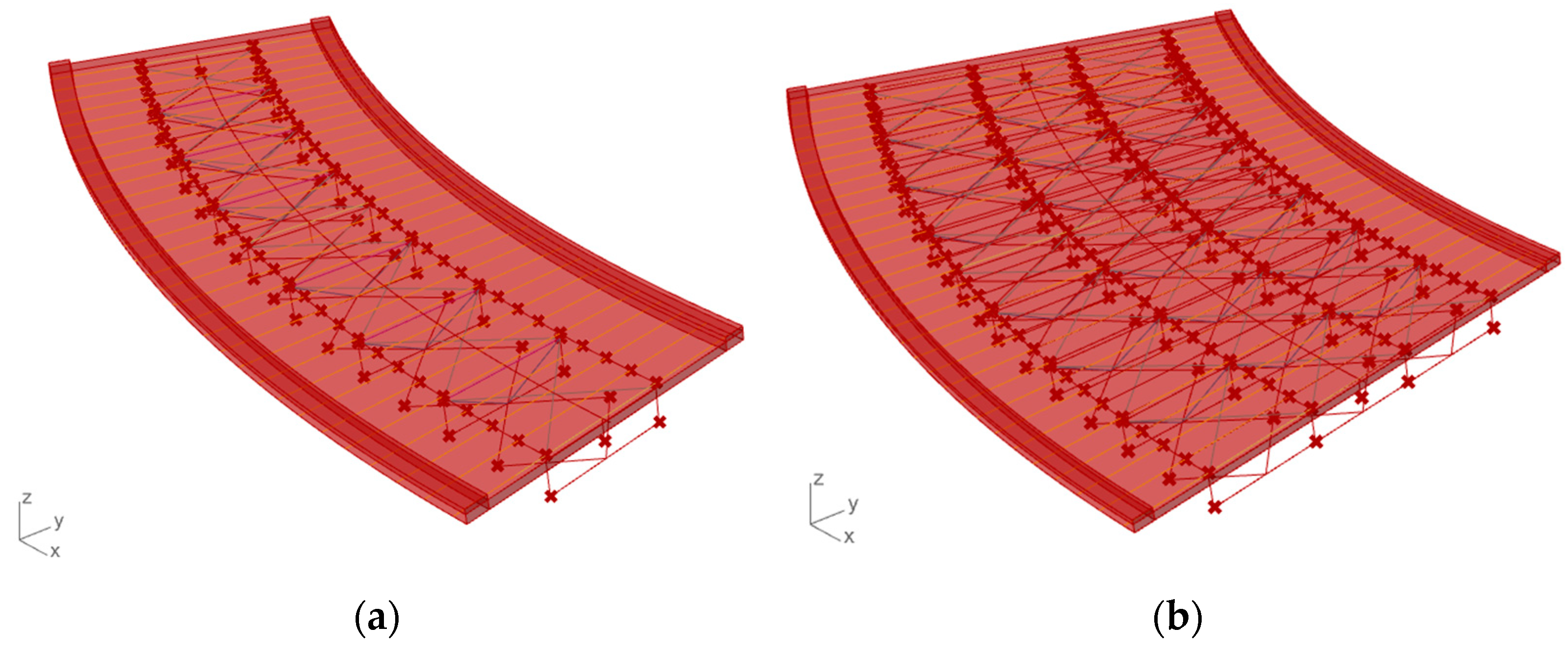
Figure 5 illustrates the resulting model and how it changes when modifying the parameter connected to the number of girders.
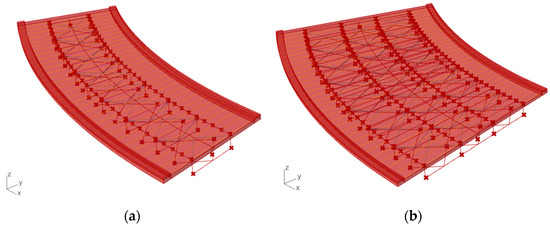
Figure 5.
Girder parametric variations: (a) double girder geometrical model; (b) four-girder bridge model.
2.2. Three-Dimensional Modelling for FEA Development
The stages following the parametric model development consist of creating the 3D model employing the pre-programmed tools provided by the Grasshopper-Tekla Structures live link. The tools allow automatic and live information transfer from Rhinoceros 3D to Tekla Structures. The live connection permits the modification of design variables in the Grasshopper environment with a real-time update in Tekla without it being necessary to export files from software to software. The direct link means risk reduction of information loss between different software, using, in a few words, the same principles of the BIM.
In this case, beams and slabs are defined from curves, points, and surfaces. For this purpose, the beam (for line-to-beam definition) and item (for slab definition from B-REP element) components of Tekla Structures are used. The generic model represents the superstructure of a short two-girder bridge; all the elements can be visualized and controlled. Additionally, the Tekla elements are converted to B-REP (boundary-REPresentation), allowing direct visualization in Rhinoceros.
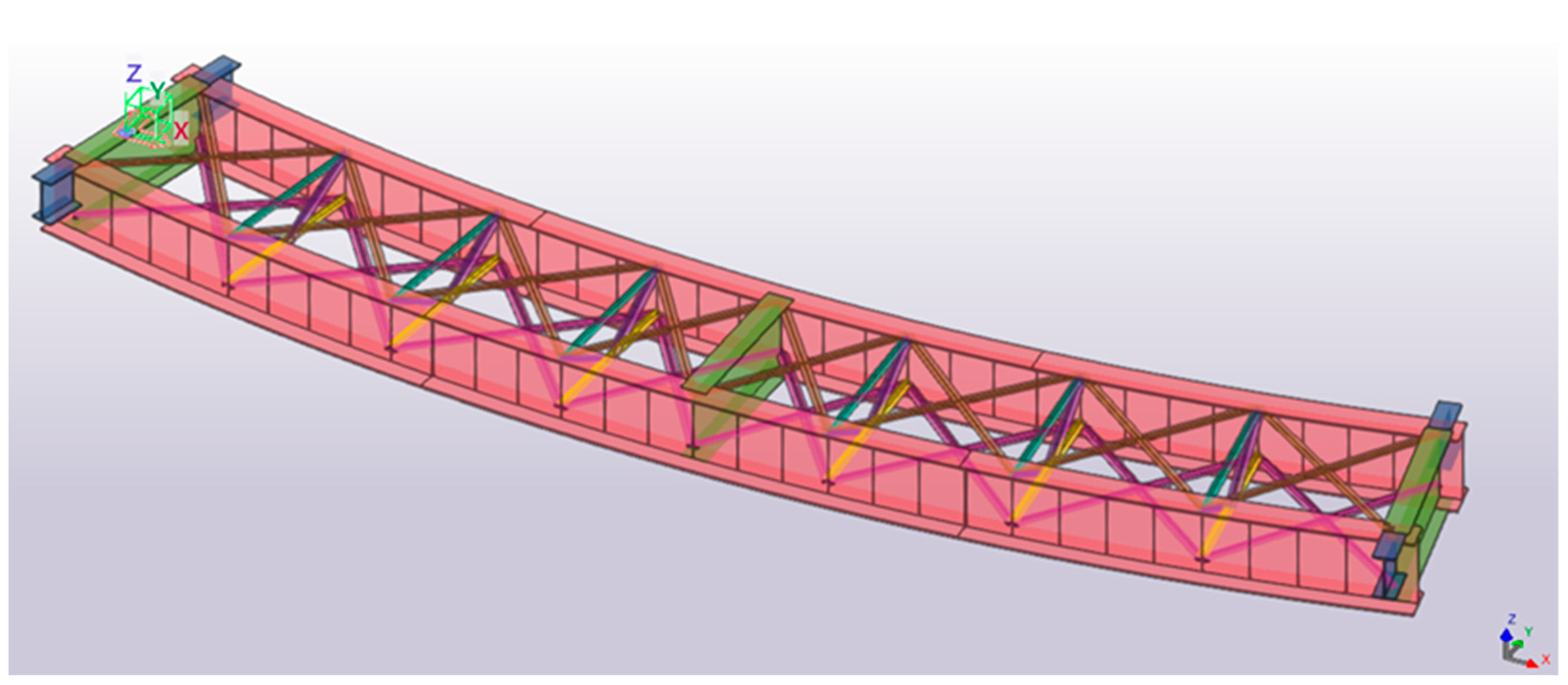
Figure 6 shows the bridge visualization in Tekla Structures after creating girders, cross-beams, bracing systems, and diaphragm elements.
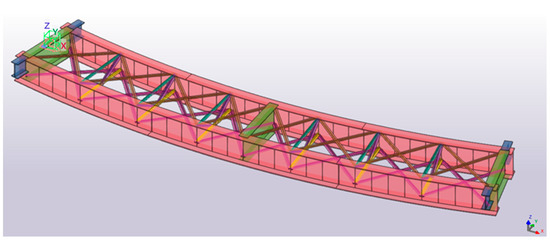
Figure 6.
Elements transfer from Rhinoceros 3D to Tekla Structures. Girders, cross-beams, and bracing systems development.
Following this, the connections and details are designed. Vertical stiffeners, bracing connections, girders connections, and studs are details parametrically created to assign variable properties. The algorithm of each component is generally divided into two parts: (i) organization and selection of geometric inputs for connection and details; and (ii) variable selection for property modification of each structural member.
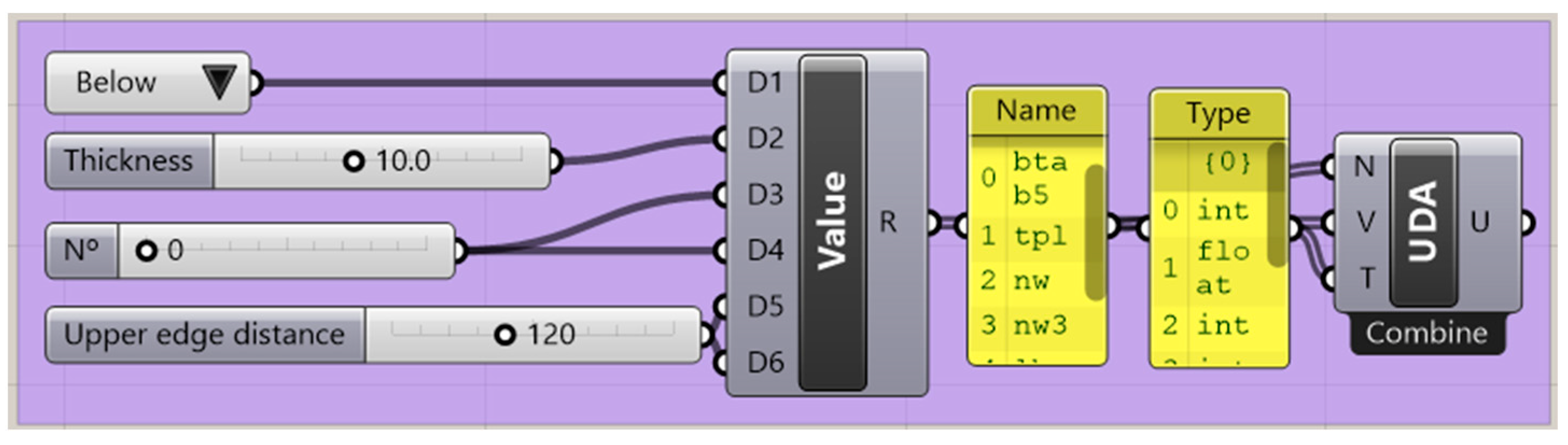
The parameters selected are components and attributes organized thanks to the construct UDA component. The tool allows the creation of a string representing one or several user-defined attributes. The inputs are user-defined values retrieved from number slider, the object’s name, and the type (auto, string, int, float, or date). An example of the definition of the attributes is presented in Figure 7, while Figure 8 illustrates a typical algorithm for a connection design.
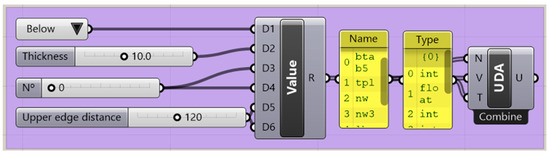
Figure 7.
Attributes organization with user-defined attributes component.
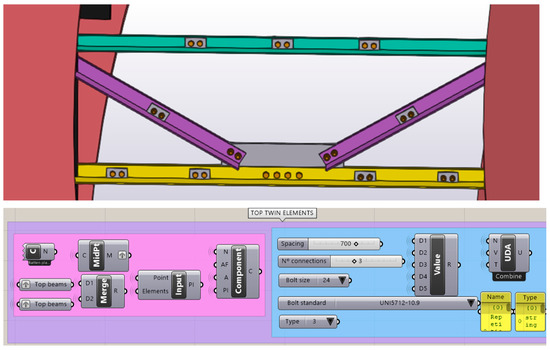
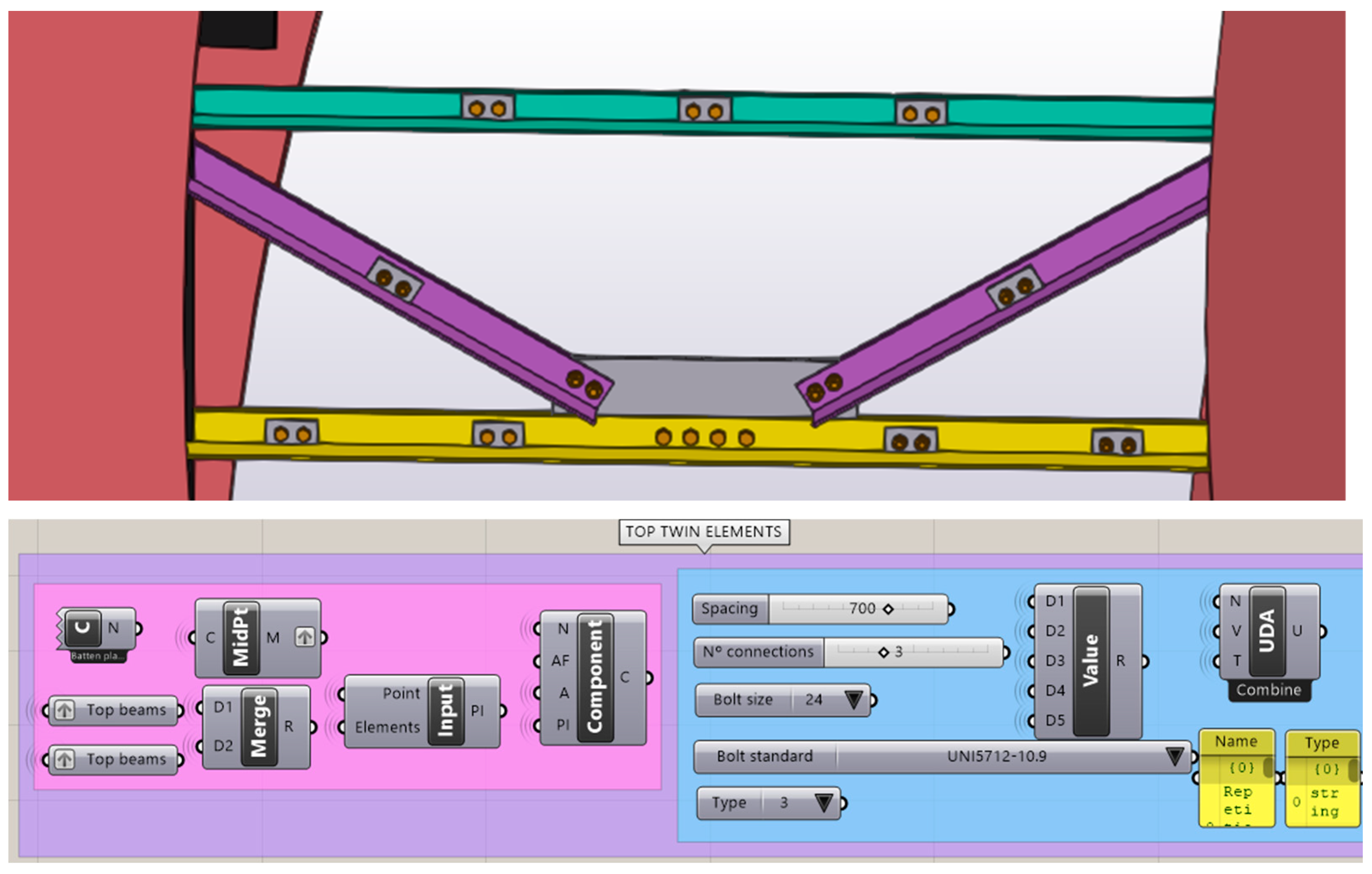
Figure 8.
Twin elements connection—visual script example for live model transfers from Grasshopper to Tekla Structures.
2.3. Structural Model: Finite Element Analysis Development
Nowadays, in bridge design, finite-element-based analysis (FEA) of bridge deck structures is a common practice. The deck representation can be determined in multiple ways, from a simple single-element spine model to a sophisticated full 3D solid/shell representation [11]. The deck modelling options can be summarized as the beam model, grid model, shell with eccentric beam model, full shell model, and solid model. In the present project, the grid model is considered for the evaluation (Figure 9) [12].
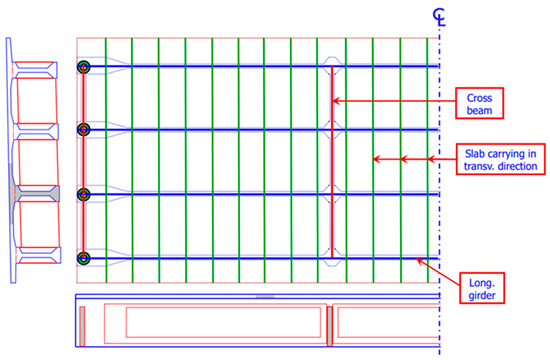
Figure 9.
Grid model representation [12].
A network of beam elements living in the same plane contains all the bridge structure’s longitudinal and transverse stiffness characteristics; the slab is modelled in strips as beam elements, such as girders and cross-beams. The properties of the longitudinal elements are calculated about the composite transformed section, considering the different elastic modulus of the main beams and slab. Concrete cracking in hogging areas should be considered while designing statically indeterminate structures, as the stiffness decreases and the distribution of the internal action varies. Additionally, the torsional constant (J) is placed equal to the sum of the girder torsional constant (Jg) and half of slab one (Js) as follow [12]:
The structural model development starts from the points and curves predefined for the geometrical model. By applying Karamba3D components (Grasshopper plug-in), it allows the definition and the analysis of a finite element model. For this study, the algorithm describes a simply-supported curved bridge; however, it is extendable to continuous bridges by changing the supporting system.
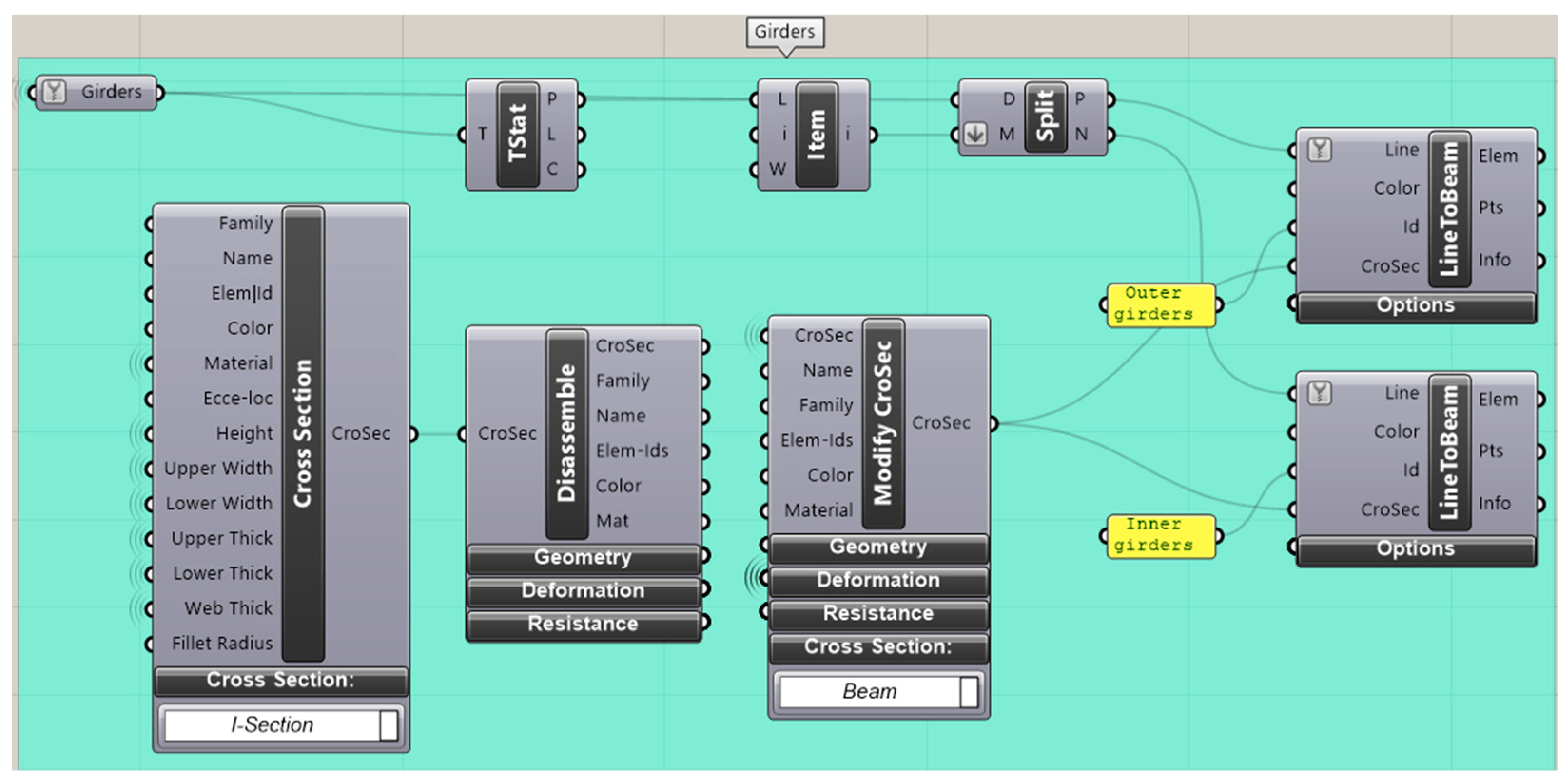
The model elements definition is possible by applying the component LineToBeam in the Grasshopper Canvas. It takes, as inputs, the line, the cross-section, and the ID (name) of the beam, to identify multiple cross-sections defined by the users. Figure 10 shows, as an example, the algorithm employed for the girder’s creation. In the case of a multi-girder bridge, the inner girders are separated from the outer ones to make the load application easier.
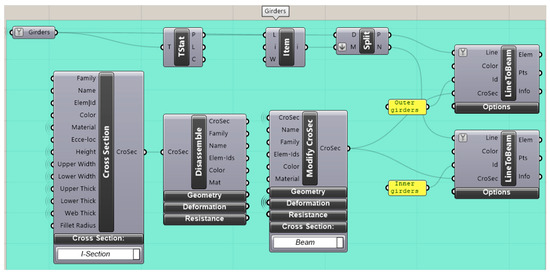
Figure 10.
Girders development using Karamba 3D in Grasshopper.
Karamba3D add-on provides different possibilities to define the cross-section in a generic model; the general definition is possible by manually setting the dimensions, selecting the properties from a library, or connecting a CSV file containing all the information related to the cross-sections to be applied. However, the catalogue distributed with the Karamba3D add-on does not enable selecting a composite cross-section.
For this study, the girders’ cross-sections are defined as I-beam employing the cross-section component; then, the algorithm considers the I-section steel properties and calculates the composite ones. The I cross-section is disassembled (through the disassemble component) and modified (ModifyCroSec component). Cross-beams, diaphragm elements, bracing systems, and dummy transversal elements are created using the same associative logic.
The materials definition is entrusted to the material selection component while establishing the supports with the corresponding tool (Karamba3D supports). The introduction of spring elements permits the connection of the girders with the supports, while setting different translational stiffness allows small displacements due to temperature changes, shrinkage, creep, and other factors. The rigid links allow the connection between the girders, diaphragm, and bracing elements axis. Since they are not in the same plane, beams with high stiffness and weightlessness are used. Finally, the cluster of components used to define the FEM converges in the analyze component, which calculates the deformation and stresses under external loads.
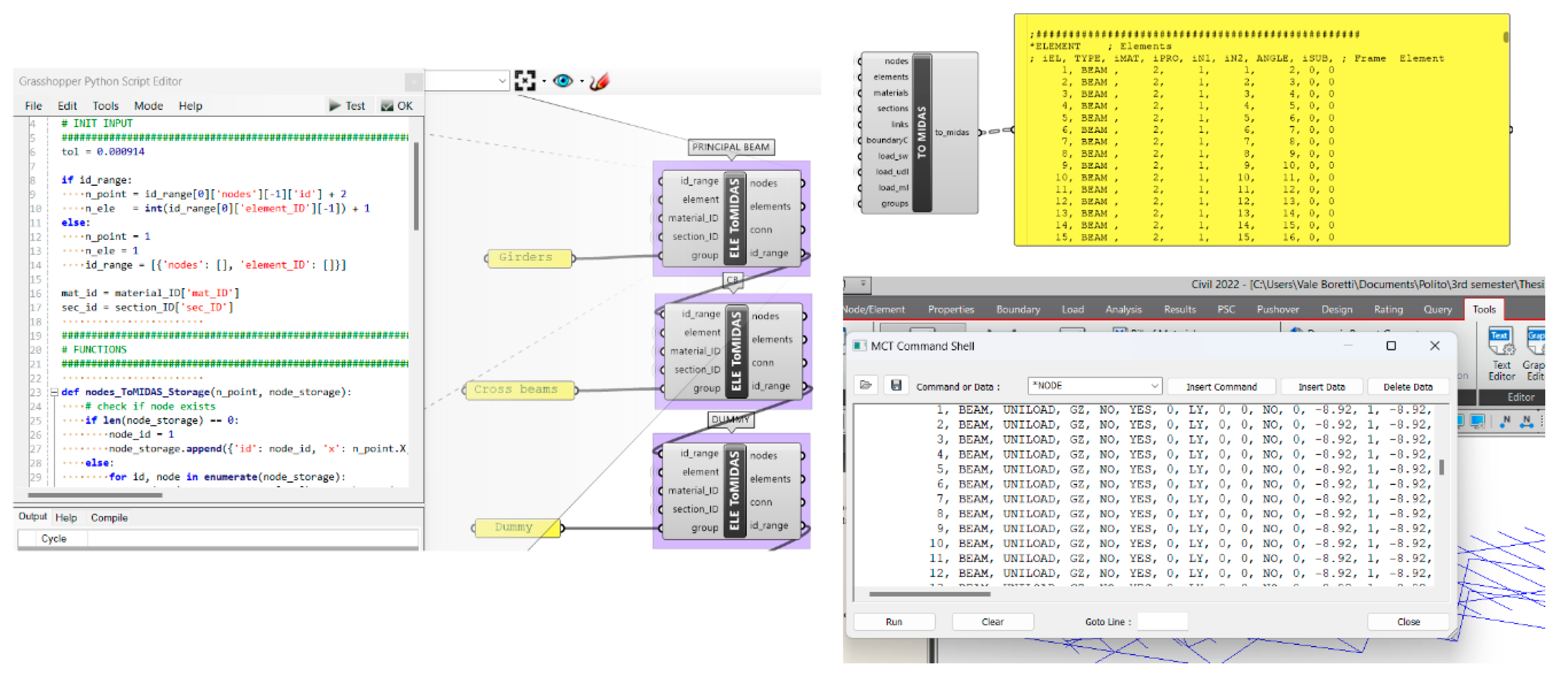
The structural response obtained with Karamba3D under permanent loads (self-weight) is validated by exporting the model to Midas Civil software and comparing the results. In this design step, the GHPython script component (IronPython) is employed to transmit the Midas Civil text file containing the modelling data, linking the Grasshopper geometry definition to Midas Civil software (output only). Finally, the model is automatically created using the MCT command shell, a Midas component (Figure 11).
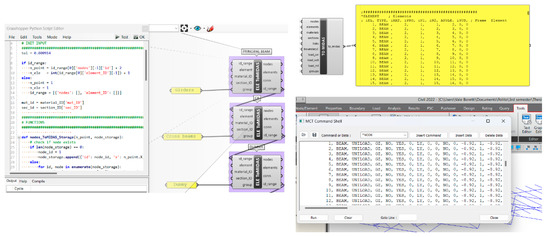
Figure 11.
MCT file for model data transmission from Grasshopper to Midas Civil.
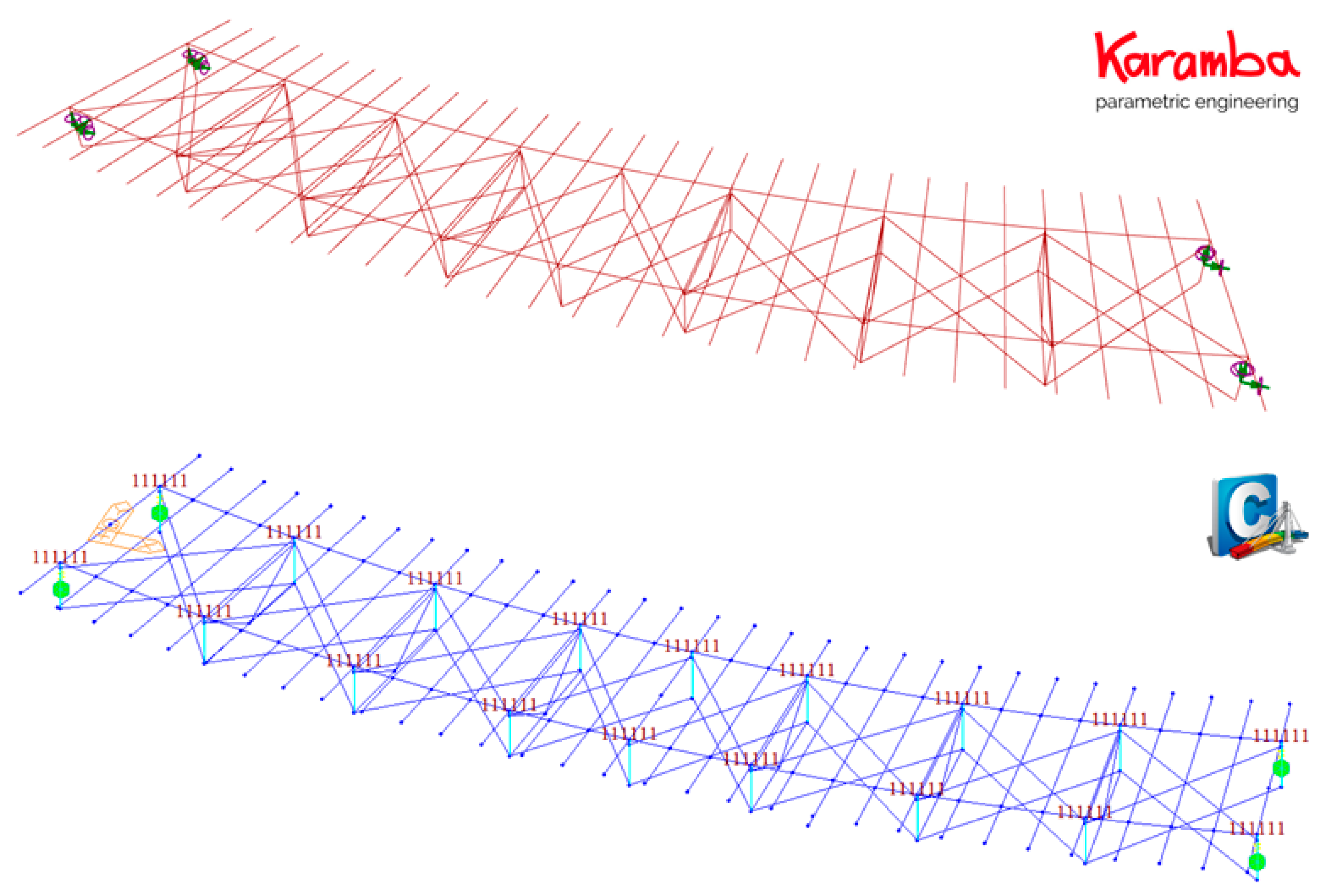
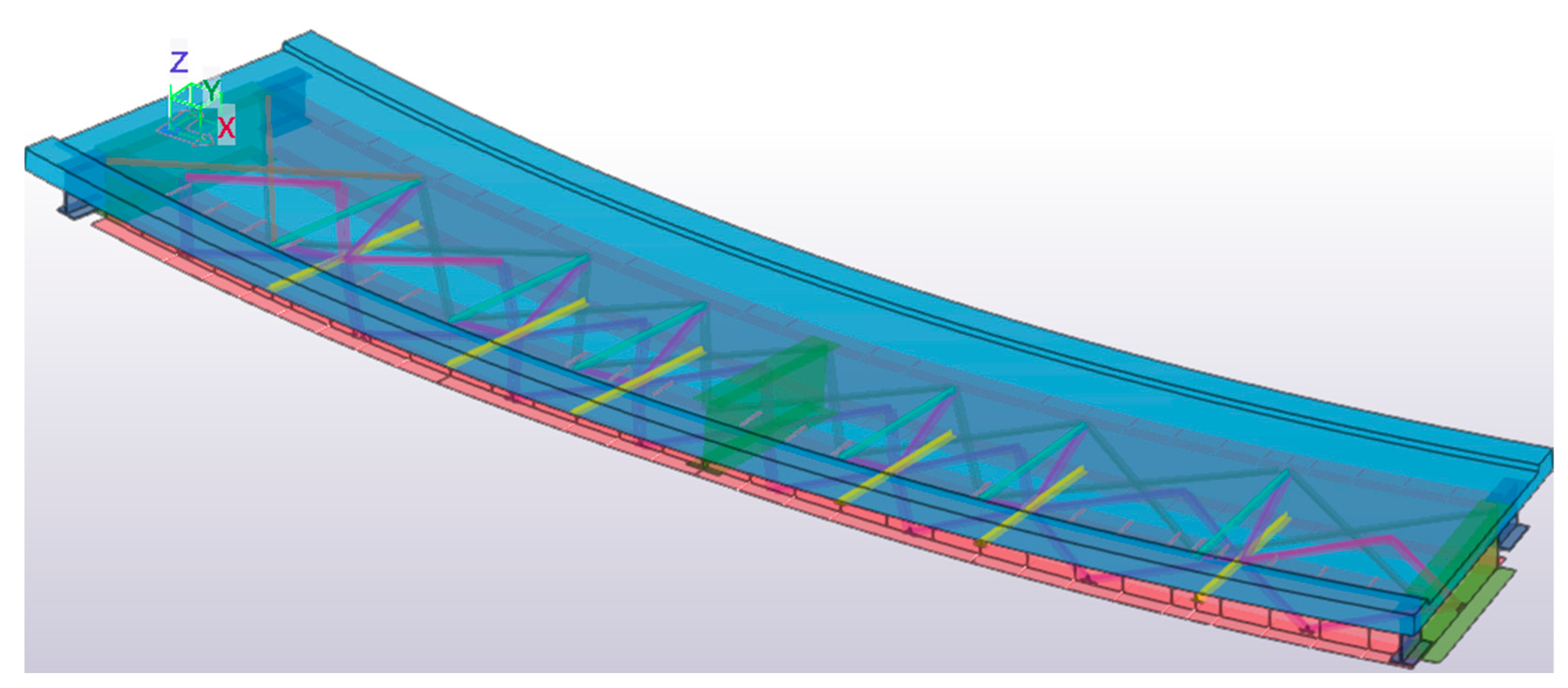
Figure 12 shows the resulting models in Karamba3D and Midas Civil.
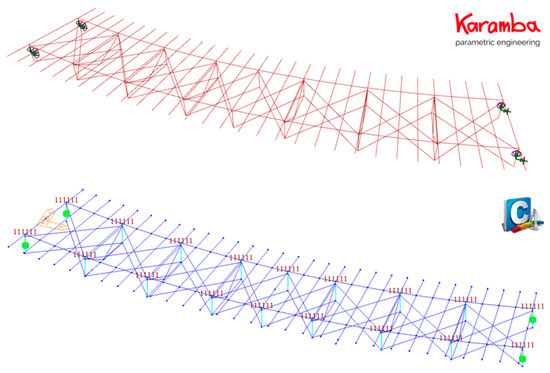
Figure 12.
Visualization of structural models in Karamba3D and Midas Civil.
In the following tables (Table 1 and Table 2), the FEA results show less than 5% of the percentage variation between the two software packages applied, validating the experimental analysis employing Karamba 3D add-on [13].

Table 1.
Maximum bridge displacement in nodes subject to higher stresses.

Table 2.
Girders forces.
In this phase of the work, different load conditions are defined. In addition to permanent loads, the model introduces the traffic loads employing the load model 1 (LM1), as it covers most of the effects of lorries and cars, and can be used for global and local verifications. Table 3 summarizes the load cases, while Table 4 describes the loads applied in the different notional lanes according to the LM1 [14].

Table 3.
Load cases.

Table 4.
LM1 loads.
The design of the visual algorithm makes the calculation of the carriageway width and notional lanes possible from the user’s inputs (axis distances, cantilevers, and curbs’ dimensions). Additionally, it allows the movement of the tandem systems with a slider, so the user can evaluate the structural response and select the best location to minimize or maximize the effect under study [15].
3. Optimization Strategy
The last stage of the present report presents a simplified methodology to find the optimal girder dimension to minimize material waste. The objective is to continue working in the parametric canvas provided by Grasshopper and develop a simple and efficient workflow, effective for the conceptual design phase, preliminary verifications, and decision-making [16]. Grasshopper allows applying evolutionary algorithms through Galapagos, an evolutionary solver that can be used on an extended range of problems by non-programmers. Evolutionary algorithms (EAs) are population-based metaheuristics. Historically, observations regarding natural evolution in biological populations served for designing the EAs [17].
For illustrative purposes, the study is conducted considering a simply-supported bridge of a span of 30 m; however, the application can be extended to any composite bridge project. The workflow representation is summarized in Figure 13.
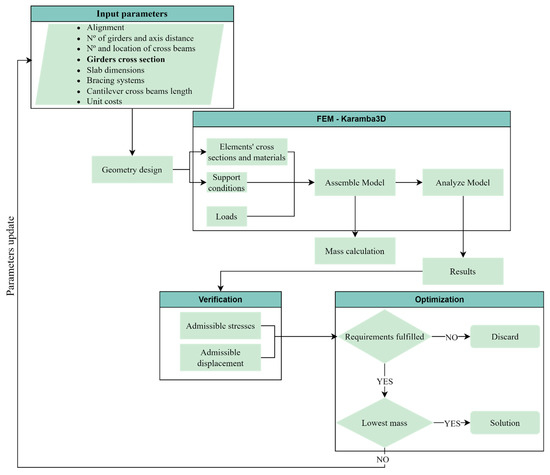
Figure 13.
Generative design and optimization process flowchart.
It is necessary to set an objective function to initialize the optimization process. For the purpose of this study, the goal is to minimize the total mass of the bridge structure, as shown in Equation (4) [18,19].
where x is the vector of design variables, and are the concrete density and volume, respectively, while and stand for the steel density and volume of the structure, respectively.
The design variables are the girder’s flanges dimensions, while the height and web thickness are considered fixed parameters. All the variables shown in Table 5 are discretized to create a discrete optimization problem to be solved.

Table 5.
Design variables and boundaries.
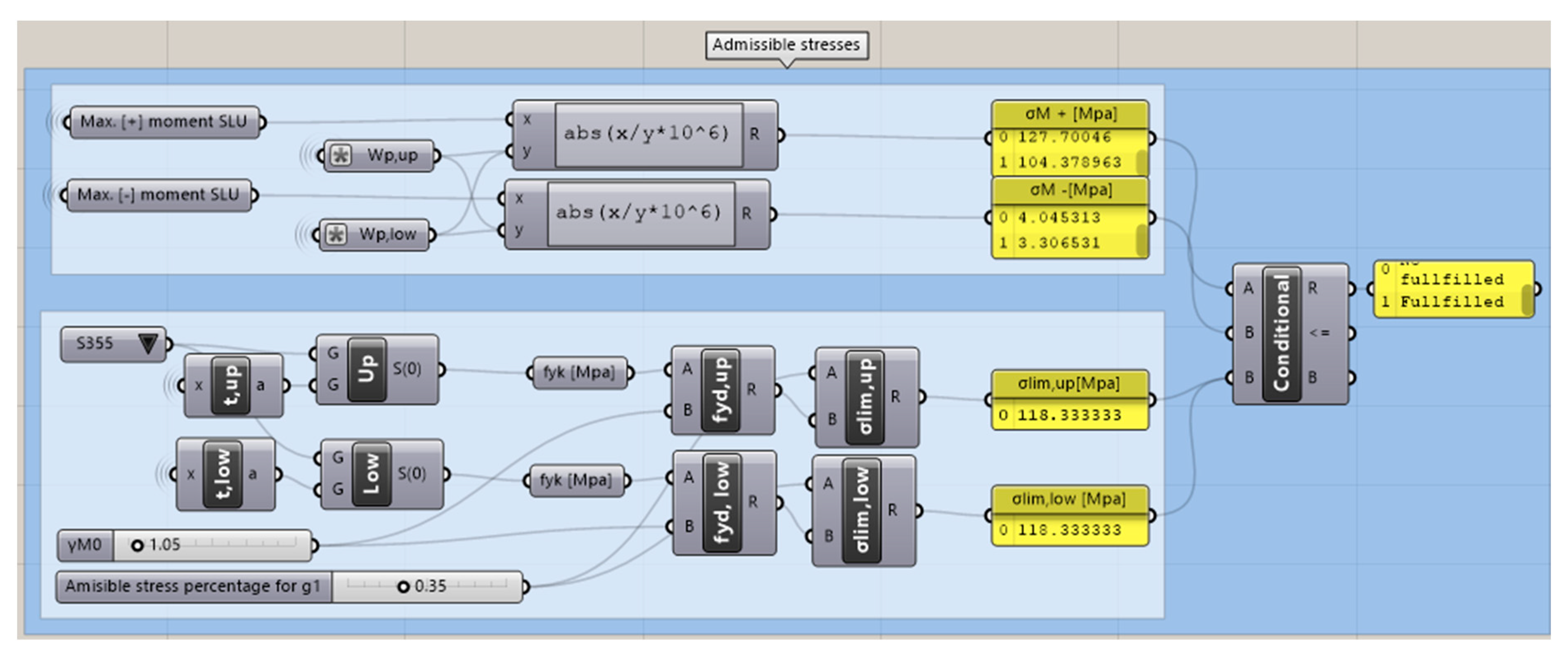
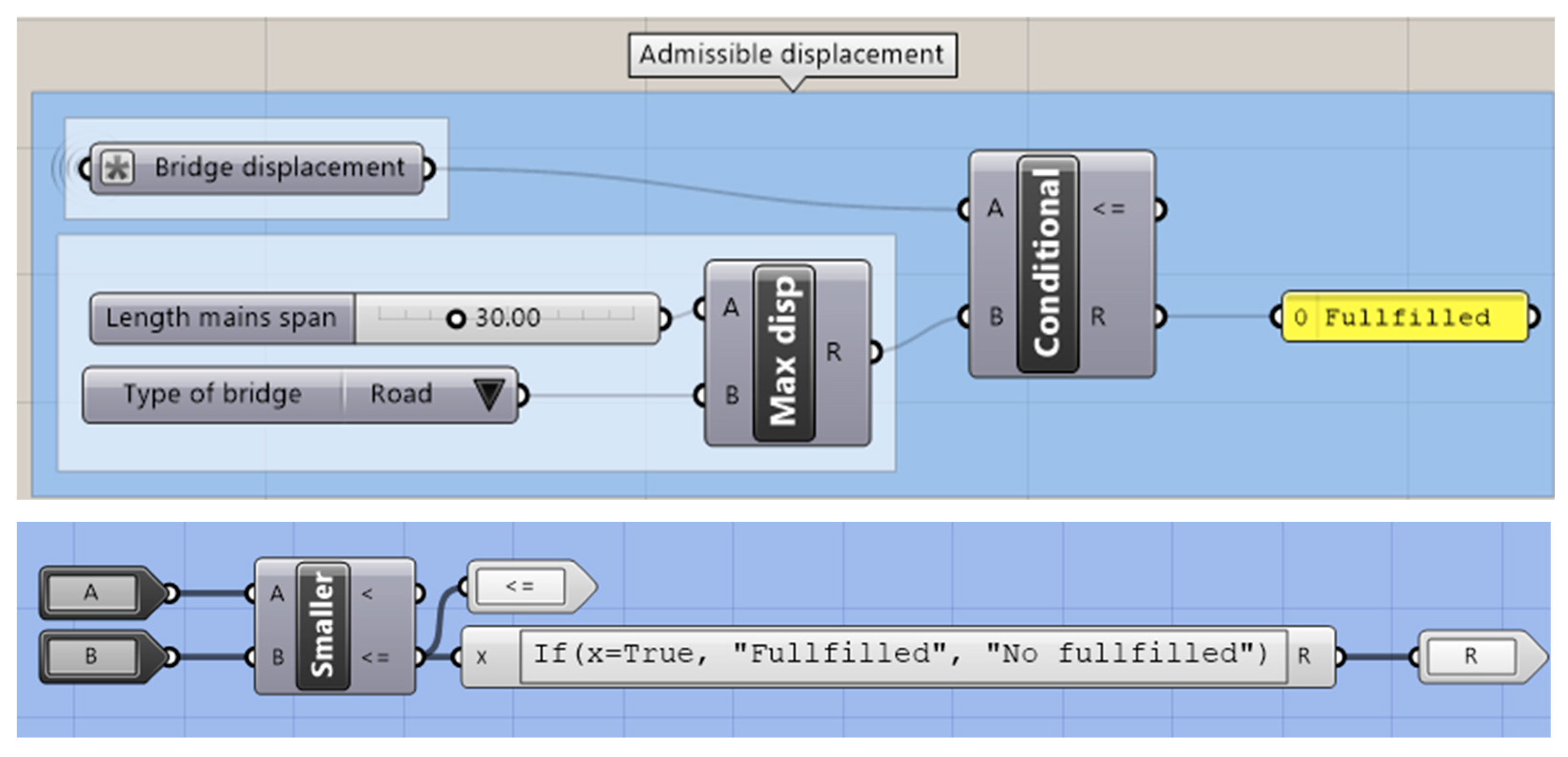
To carry on the optimization process using the Galapagos solver (EAs solver within the Grasshopper environment), the following constraints are imposed (Figure 14 and Figure 15):
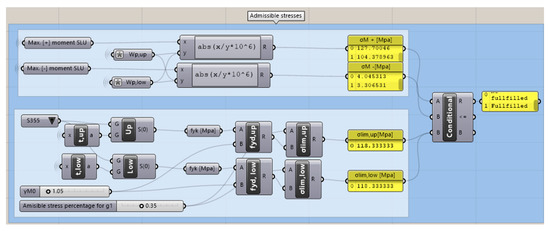
Figure 14.
Visual algorithm development in Grasshopper canvas of the admissible stresses’ constraint.
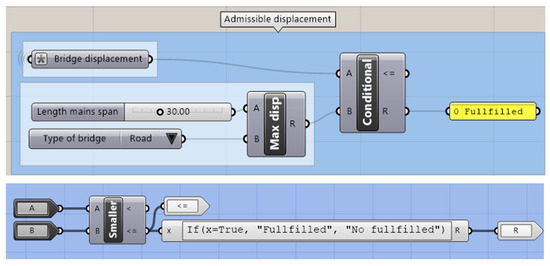
Figure 15.
Development of admissible maximum displacement constraint algorithm for road bridges in Grasshopper.
- Flanges’ admissible stress under permanent loads;
- Maximum displacement allowed.
Considering the mechanical properties of the steel, according to EC3 (Table 6), the imposed conditions are described by the following equations [20]:
where is the characteristic yield strength, the design yield strength, and is the safety coefficient for bending resistance.

Table 6.
Mechanical properties of structural steels produced to EN 10025, under EN 1998-1-1.
Then, the maximum deformation allowed under characteristic combination can be set as:
where is the bridge span. Equation (7) applies to road bridges, while Equation (8) corresponds to rail bridges.
Figure 15 shows the algorithm for applying the constraints in the Grasshopper environment. A road bridge is considered in the overall strategy to solve the optimization problem.
Finally, combining all the conditions, the mass is calculated by Karamba3D add-on using an if-statements (Boolean hard constraint with penalty function). While evaluating different combinations of design variables, if the structural response does not fulfil the requirements set in the constraint functions, the Boolean flag turns false—not fulfilled (Figure 15) and, consequently, applies a penalization of 200,000 kg on the objective (total mass), discarding the solution.
To solve the optimization problem (in Equation (4)), this phase of the work requires the application of a solver able to operate in the Grasshopper environment. For this purpose, the Galapagos© solver is introduced, which takes into account the design variables as inputs, as presented in Table 5. The variable parameters are set after several iterations and verification with the Goat© solver, which complements the Galapagos solver, relying on gradient-free optimization algorithms. The component pursues a mathematically rigorous approach to deliver fast and deterministic results [21,22].
The initial values for the girder cross-section are determined from a preliminary dimensioning according to generic engineering rules; the materials selected are (i) concrete C35/45, density = 25,000 kg/m3 (for the slab), and (ii) steel S355, density = 78,500 kg/m3 (for the main girders, diaphragm elements, and bracing systems).
The problem is simplified for experimental purposes, and the analysis considers only the self-weight of the structure. All the variable combinations generated by the Galapagos solver are recorded into a CVS file thanks to the Colibri© plug-in [23].
4. Optimal Results
The optimal solution that minimizes the mass of the bridge system is found after 155 generations. The obtained data are organized in a parallel coordinates plot through Design Explorer 2©, an online open-source tool (Figure 16) [24].

Figure 16.
Optimization results plot using Design Explorer 2©.
Figure 16 shows the trends plotted considering the Boolean hard constraint set in Equations (5)–(7), contemplating the penalty function applied to the objective functions in Equation (4).
Table 7 summarizes the optimization problem results with a 3.5% reduction in the total mass, showing the percentage variations of the design variables. Figure 17 presents the 3D model of the girder bridge after applying the optimization strategy.

Table 7.
Design variables and objectives before and after the optimization process.
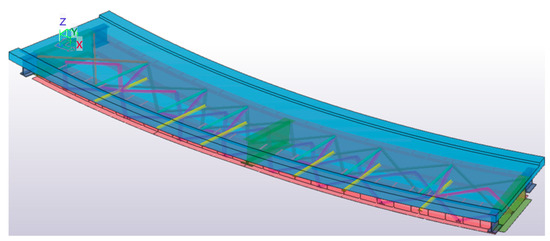
Figure 17.
Optimized 3D model in Tekla Structures.
5. Conclusions
In the present contribution, a parametric model for composite bridges is implemented through the Grasshopper add-on (visual programming language and environment) for Rhinoceros software while connecting a flexible generative model ready to be analyzed in Tekla Structures. The evaluation of the structural response is conducted with Karamba 3D© (FEA). The last step of the workflow is carried out by applying Galapagos©, an evolutionary solver in the Grasshopper environment, imposed in the script definition to find the optimal solution.
The workflow produced shows many advantages compared to traditional non-interoperable workflows concerning computational costs and resource-efficient design and analysis.
The model dataset allows the generation of multiple designs of composite bridges by changing the parameters’ values; therefore, the model flexibility highly increases the possibility of generating different configurations and analyses according to the objective.
The quality of the model is tested and verified, showing good accuracy for a conceptual design phase. Furthermore, the geometric development, the FE analysis and the optimization are performed in the same operational environment. The direct communication between all the design steps leads to a total decrease in the risk of data loss, errors, and discrepancies, while obtaining a quick structural response visualization thanks to the direct connection between all the software add-ons (Rhinceros© + Grasshopper© + Karamba3D© + Tekla©).
As shown from the results summarized in Table 7, the present workflow represents a ready-to-use script that permits speeding up the design process, achieving freedom in designing complex composite bridges efficiently and optimizing material consumptions and relative costs.
The presented visual script allows for centralizing the information in one file, generating an adaptive model for different projects, analyzing the structural response, and optimizing the design to find the most sustainable and effective solution.
Further development of the implemented visual script can lead to the insertion of an extensive set of parameters for modelling more bridge types, considering different geometries, constructive technologies, and materials, covering a broad range of design alternatives.
In this specific contribution, the imposition of the objective function (in Equation (4)) leads to the minimization of the total mass. However, the entire optimization process and strategy can be enhanced by introducing multi-objective algorithms (MOEAs) in the workflow while applying several constraints (structural and geometric) to obtain results strictly linked to objectives and needs.
Author Contributions
Conceptualization, L.S. and L.A.B.G.; methodology, L.S. and L.A.B.G.; software, V.B., L.S. and L.A.B.G.; validation, L.S., M.D. and L.A.B.G.; formal analysis, V.B., L.S. and L.A.B.G.; investigation, L.S. and V.B.; data curation, L.S. and V.B.; writing—original draft preparation, V.B.; writing—review and editing, L.S.; visualization, V.B. and L.S.; supervision, M.D. and G.C.M.; project administration, M.D., D.M. and G.C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The algorithmic workflow is produced by the Politecnico di Torino Research Unit. All the information about the visual script is under the domain of Masera Engineering Group Ltd., Turin, Italy.
Acknowledgments
This research was supported by the ADDOPTML project: “ADDitively Manufactured OPTimized Structures by means of Machine Learning” (No: 101007595) belonging to the Marie Skłodowska-Curie Actions (MSCA) Research and Innovation Staff Exchange (RISE) H2020-MSCA-RISE-2020.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Azhar, S.; Nadeem, A.; Mok, J.Y.; Leung, B.H. Building Information Modeling (BIM): A new paradigm for visual interactive modeling and simulation for construction projects. In Proceedings of the First International Conference on Construction in Developing Countries, Loughborough, UK, 14–16 May 2008; pp. 435–446. [Google Scholar]
- Svoboda, L.; Novák, J.; Kurilla, L.; Zeman, J. A framework for integrated design of algorithmic architectural forms. Adv. Eng. Softw. 2014, 72, 109–118. [Google Scholar] [CrossRef]
- Sardone, L.; Greco, R.; Fiore, A.; Moccia, C.; De Tommasi, D.; Lagaros, N.D. A preliminary study on a variable section beam through Algorithm-Aided Design: A way to connect architectural shape and structural optimization. Procedia Manuf. 2020, 44, 497–504. [Google Scholar] [CrossRef]
- Frangedaki, E.; Sardone, L.; Marano, G.C.; Lagaros, N.D. Optimisation-driven design in the architectural, engineering and construction industry. Proc. ICE Struct. Build. 2023, 0, 1–12. [Google Scholar] [CrossRef]
- Girardet, A.; Boton, C. A parametric BIM approach to foster bridge project design and analysis. Autom. Constr. 2021, 126, 103679. [Google Scholar] [CrossRef]
- Konia Company Ltd. Overcoming Complexity and Driving Efficiency in Bridge Design with Parametric Design. Available online: Storekonia.com (accessed on 21 November 2022).
- Ji, Y.; Beetz, J.; Bonsma, P.; Nisbet, N.; Katz, C.; Borrmann, A. Integration of Parametric Geometry into IFC-Bridge. In Proceedings of the 23rd European Conference Forum Bauinformatik, Cork, Ireland, 12–14 September 2011. [Google Scholar]
- Havelia, P.A. Ground Structure Method to Optimize Topology and Sizing of Steel Frame Structures to Minimize Material, Fabrication and Erection Cost. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2016. [Google Scholar]
- Sardone, L.; Fiore, A.; Manuello, A.; Greco, R. Performative Structural Design Optimization: Generative Algorithm for a Preliminary Study of a Voided Beam. Appl. Sci. 2022, 12, 8663. [Google Scholar] [CrossRef]
- Frangedaki, E.; Sardone, L.; Lagaros, N.D. Design Optimization of Tree-Shaped Structural Systems and Sustainable Architecture Using Bamboo and Earthen Materials. J. Archit. Eng. 2021, 27, 04021033. [Google Scholar] [CrossRef]
- Anwar, N. The Impact and Future Role of Computations and Software in Bridge Modeling, Analysis and Design. In Proceedings of the China Bridge Congress Chongqing, Chongqing, China, 29 March 2007. [Google Scholar]
- Giordano, L. Girder bridges, Bridge construction and design. PowerPoint slides for PoliTo Courses, DISEG. 2021. Available online: https://file.didattica.polito.it/download/MATDID/33329945 (accessed on 10 January 2023).
- Sardone, L.; Fiore, A.; Greco, R.; Moccia, C.; Lagaros, N.D.; De Tommasi, D. Algorithm-aided structural-optimization strategies for the design of variable cross-section beams. In Proceedings of the Fib Symposium, Attisholz, Switzerland, 16–18 September 2021; pp. 485–492. [Google Scholar] [CrossRef]
- Giordano, L.; Gino, D. Actions on road bridges, Bridge construction and design, PowerPoint slides for PoliTo Courses, DISEG. 2021. Available online: https://file.didattica.polito.it/download/MATDID/33335856 (accessed on 10 January 2023).
- Sotiropoulos, S.; Lagaros, N.D. A two-stage structural optimization-based design procedure of structural systems. Struct. Des. Tall Spec. Build. 2021, 31, e1909. [Google Scholar] [CrossRef]
- Preisinger, C. Linking Structure and Parametric Geometry. Archit. Des. 2013, 83, 110–113. [Google Scholar] [CrossRef]
- Corne, D.W.; Lones, A. Evolutionary Algorithms. In Handbook of Heuristics; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 1–22. [Google Scholar]
- Sotiropoulos, S.; Lagaros, N.D. Optimum topological bracing design of tall steel frames subjected to dynamic loading. Comput. Struct. 2022, 259, 106705. [Google Scholar] [CrossRef]
- Stromberg, L.L.; Beghini, A.; Baker, W.F.; Paulino, G.H. Topology optimization for braced frames: Combining continuum and beam/column elements. Eng. Struct. 2012, 37, 106–124. [Google Scholar] [CrossRef]
- EN 1993-1-1; Eurocode 3: Design of Steel Structures—Part 1-1: General Rules and Rules for Buildings. Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC. BSI: London, UK, 2005. (In English)
- Flöry, S. Goat. Free Optimization Solver Component for Rhino’s Grasshopper. Available online: https://www.rechenraum.com/en/goat.html (accessed on 3 January 2023).
- Rutten, D. Galapagos: On the Logic and Limitations of Generic Solvers. J. Archit. Des. 2013, 83, 132–135. [Google Scholar] [CrossRef]
- Tomasetti, T.; Dambron, O.; Peng, M.; Sun, H.; Colibri. A Design Space Exporter for Grasshopper. Published on GitHub Library under MIT License. 2017. Available online: https://github.com/bhowes-tt/colibri.grasshopper (accessed on 9 January 2023).
- Tomasetti, T. Design Explorer 2. Published Open Source under Thornton Tomasetti CORE Studio License. 2019. Available online: http://tt-acm.github.io/DesignExplorer/?GFOLDER=0B8secD5h7wUFanYtbEFWSjBLWFk (accessed on 9 January 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).