Effect of Clamp Deletion on Static Behavior and Dynamic Characteristics of Loop-Free Cable Net Structures
School of Civil Engineering, Yantai University, Yantai 264005, China
*
Author to whom correspondence should be addressed.
Buildings 2023, 13(4), 881; https://doi.org/10.3390/buildings13040881
Submission received: 17 February 2023
/
Revised: 13 March 2023
/
Accepted: 24 March 2023
/
Published: 28 March 2023
(This article belongs to the Section Building Structures)
Abstract
:The loop-free single-layer hyperbolic cable net structure (LSHCS) is a new tensile cable structure for buildings, and it can overcome the disadvantages of key elements and the high tension in tensile cable structures with loop cables. The imperfection of the LSHCS is that cable clamps near the inside boundary are redundant. In this paper, the static behavior and dynamic characteristics of thirty-one schemes in five levels of deleting cable clamps are carried out with ANSYS software and Midas/Gen software. The results show that SE1/1, SE2/1, SE3/1, and SE4/1 are the best cable clamp deleting schemes for their respective levels. Displacements are the most sensitive to deleting cable clamps, the natural vibration period comes in second, and tensions are not sensitive with the growth rates of 6.09%, 5.11%, 15.97%, and 19.28% in the best scheme of each level. It is concluded that schemes involving the virtual rings of cable clamps closest to the inside boundary cause the smallest effect on static behavior and dynamic characteristics. Deleting the cable clamps affects the structural stiffness significantly, but the bearing capacity is not seriously affected. It turns out that removing redundant cable clamps in the dense part of the LSHCS is feasible.
1. Introduction
Tensile structures are made up of tension-carrying components with neither compression nor bending, and they are classified as tensile cable structures and tensile membrane structures [1]. Tensile cable structures are widely used in modern buildings as well as bridges [2]. Tensile cable structures used in bridges have a long history of more than two thousand years [2], but it is widely believed that the first modern tensile cable structure used in a building is the hyperbolic cable net roof of the Dorton Arena [3] (also called the Raleigh Arena [4]) built in 1953. Since then, tensile cable structures for buildings have quickly progressed, included various structural forms, and have been applied to many famous buildings. Tensile cable structures are usually composed of tensile steel strands, high-strength tie rods, CFRP cables, or other tensile components [5]. The tensile cable structures make full use of the high-strength tensile properties of the materials, and these structures exhibit the advantages of being light in weight and having a large span. Currently, the structural forms of tensile cable structures include cable dome structures [6], space cable-truss structures [7], wheel-spoke cable structures [8], single-layer hyperbolic cable net structures [9], suspen-dome structures [10], etc.
In recent years, tensile cable structures with loop cables have been studied. Loop cables, which generate radial elements, are commonly used in gymnasiums and football stadiums to achieve a large-span structure [11]. Despite its advantages, current studies find that loop cables are key components of the structure [12], and they are subjected to high tensions [13]. The failure of a segment of a loop cable results in the slacking of the entire loop cable, and the radial components also fail due to the generated slack; moreover, it could cause a progressive collapse of the roof structure. The loop cables bear high tensions due to the adverse angle relationship between the loop cable and the radial component. The loop cables use a large amount of material because of high tensions. With the aim to make improvements, loop-free cable structures have been proposed. Xue et al. [14] summarized four forms, including the annular crossed cable-truss structure [15], loop-free single-layer hyperbolic cable net structure (LSHCS) [16], loop-free suspen-dome structure [17], and loop-free cable-supported shell with a large central opening [14]. The loop-free cable structures overcome the loop cable’s disadvantages with respect to its key elements and high tensions, and they provide alternative schemes for tensile cable structures with loop cables.
Among current loop-free cable structures, the LSHCS is composed of a loop-free hyperbolic cable net and a compression ring beam to form a self-balancing system (Figure 1). The LSHCS discards loop cables by arranging the cables along the chords of the ring beam. Cables are fixed to the ring beam, and they do not break at intersections of the cable net. Cables are integrated by cable clamps at the crossing points to prevent cable sliding. With this method, cables are relatively independent so the damage to the roof structure could be proportionate if some cables are ruptured [18]. The cables are straight on the plane projection and hyperbolically curved in the vertical direction. The force-transmitting paths in the LSHCS are much more direct than those of tensile cable structures with loop cables. As a result, tensions of the LSHCS are likely to be reduced. The mechanical properties and design methods of the LSHCS have been studied. Due to the progress, the LSHCS has been considered in engineering applications [13,18]. Xue et al. [19] studied the effect of cable rupture on the structure, verified the progressive collapse resistance, and analyzed the static performance of the LSHCS. Liu et al. [18] studied the cable arrangements and form-finding method on the LSHCS. It was found that the LSHCS can ensure structural stiffness and overall stability, significantly reduce the amount of material used, and reduce the difficulty of the construction. In addition, the tensions of different cables are much more uniform than the structure with loop cables. However, it can be observed in Figure 1 that intersections of the LSHCS become denser from the outside to the inside. Since cable clamps are set at intersections, cable clamps near the inside are quite redundant, which could cause unnecessary costs and difficulties during construction. Hence, redundant cable clamps should be properly deleted to achieve a better LSHCS.
In order to determine reasonable cable clamp deletion schemes, the influence of cable clamp deletion on the static behavior and dynamic characteristics of the LSHCS is studied in this paper. Firstly, a large-span LSHCS at the background of a stadium is designed according to the requirements of relevant specifications. Then, twenty-one cable clamp deletion schemes of five levels are considered. The static behavior of all schemes, including adverse displacements under the serviceability limit state and adverse cable tensions under the ultimate limit state, is analyzed with ANSYS software. The analysis of dynamic characteristics including mode shapes and self-vibration frequencies of all schemes is conducted with Midas/Gen software. In the end, based on the comparison between the original structure and each cable clamp deletion scheme, acceptable and reasonable cable clamp schemes are discussed, and advice for cable clamp deletion is provided.
2. Analysis Models and Methods
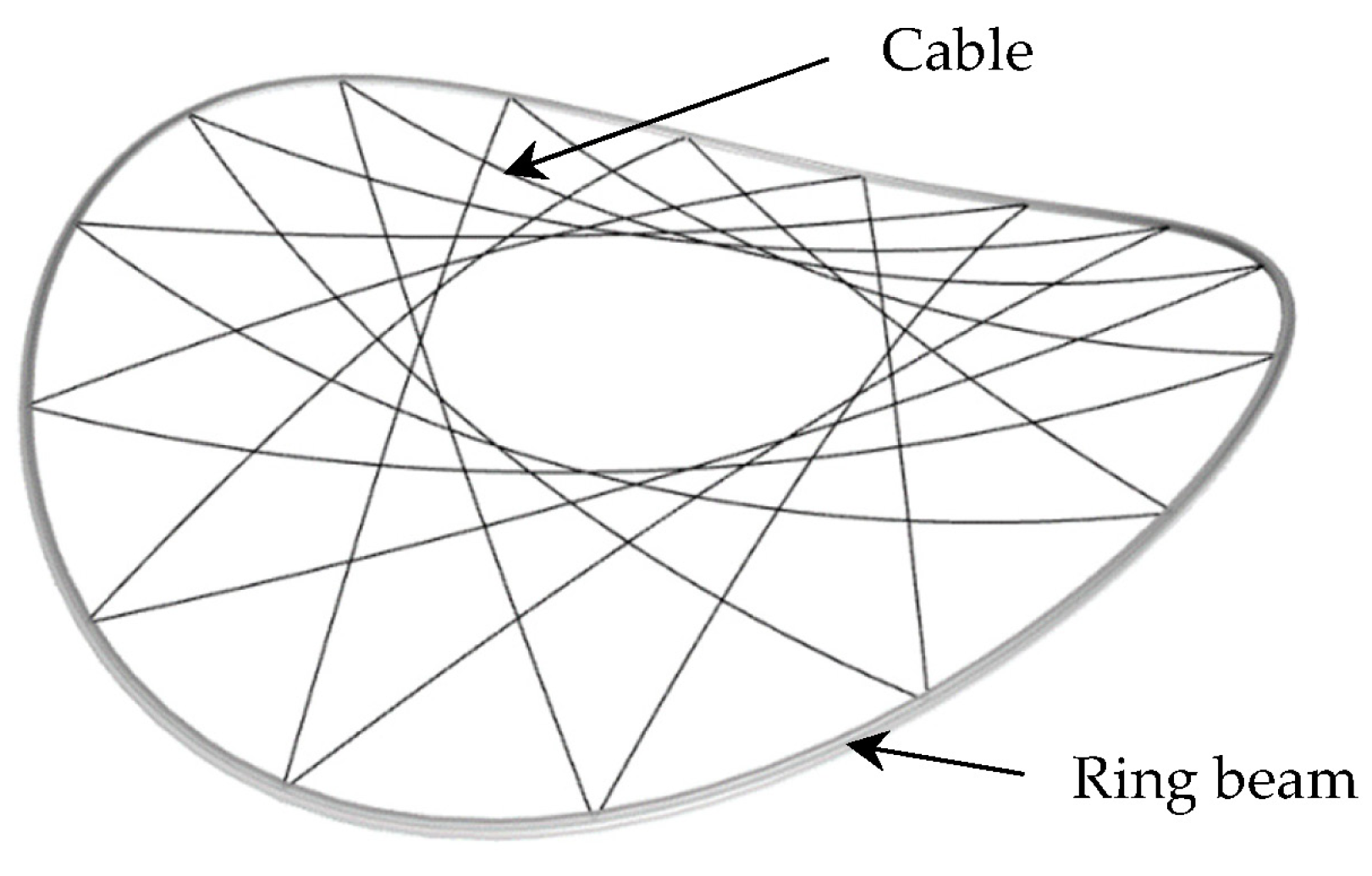
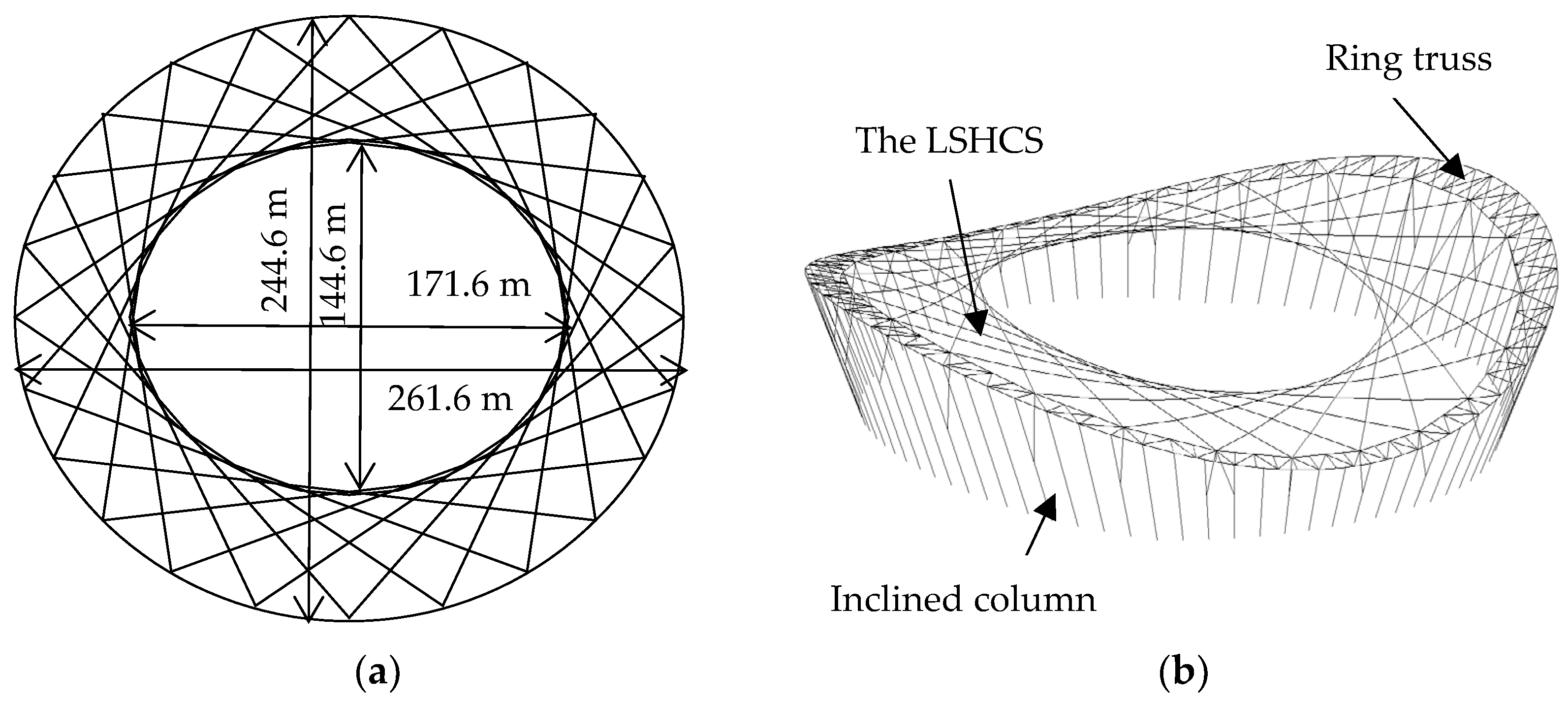
2.1. Engineering Background
The hyperbolic cable net roof structure of the Linyi Olympic stadium in China is taken as the study case. Figure 2a shows that the plane projection dimensions of the cable net are 261.6 m × 244.6 m with respect to the outside boundary and 171.6 m × 144.6 m with respect to the inside boundary. The vertical distance between the highest point and the lowest point of the hyperbolic cable net is 26.2 m. Figure 2b shows that the hyperbolic cable net is supported by a ring truss and inclined columns. The cable net is covered by an enclosure system composed of membrane and steel arches. The dead load (D) includes the weight of structural components, the weight of hanging equipment on the inside boundary (2.0 kN/m), the weight of the enclosure system (0.15 kN/m2), and the weight of a cable clamp (0.5 kN). The live load (L) includes the distributed live load on the roof (0.3 kN/m2) and the maintenance load on the gantry (1.0 kN/m). Wind load (W) is determined according to GB 50009-2012 [20]. The basic wind pressure is 0.45 kN/m2, and the ground roughness category is Class B. The wind load shape coefficient is determined by the wind tunnel test. Referring to design experience, the wind vibration coefficient is 1.2. The basic snow pressure of the snow load (S) is 0.4 kN/m2. Pretension is of vital importance for the LSHCS. The pretension (P) distribution coefficient of the cable net is obtained by form-finding analysis, and the pretension value is determined by optimization analyses.
2.2. Structural Design of the Model
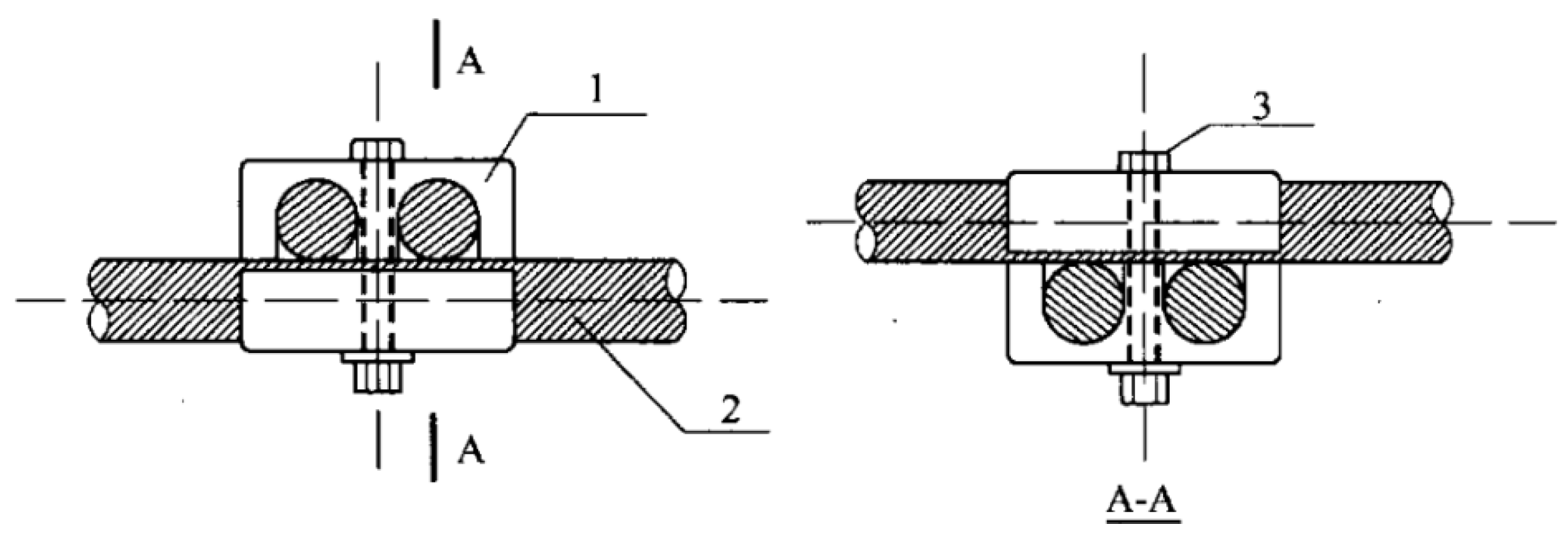
2.2.1. Materials and Components
The ring truss is welded with circular pipes made of Q390 D steel. The elastic modulus and characteristic yield strength of Q390 D are 2.06 × 105 N/mm2 and 390 N/mm2, respectively. The inclined support columns are welded by using a rectangular pipe made of Q390 D. The cables adopt spiral strands with an ultimate tensile strength of 1570 N/mm2 and elastic modulus of 1.6 × 105 N/mm2. According to the JGJ 257-2012 specification [21], the partial coefficient of the spiral-strands cable is 2.0. This means that the design tensile strength of the cable is 835 N/mm2. The stress ratio, which is the reaction stress divided by the design tensile strength, is limited to within 0.8. Figure 3 shows the cable clamp style of the LSHCS and the cable section, which is composed of two parallel cables. Due to the difference in tensions, there are two cable sections with nominal diameter spiral strands of 100 mm or 85 mm, respectively.
2.2.2. Load Combinations
According to GB50068-2018 [22] and GB50009-2010 [20], load combinations under the serviceability limit state and ultimate limit state are considered in the preliminary structural analysis (see Table 1), where combinations from LCB1 to LCB4 are of the serviceability limit state, and combinations from LCB5 to LCB8 are of the ultimate limit state.
2.2.3. Validation of the Model
Since the LSHCS is a flexible system, form finding, in which the geometric shape and pretension in the initial pre-stressed state, must be carried out before the structural analysis. At present, the form-finding methods of the cable net structure mainly include the force density method [23], the dynamic relaxation method [24], and nonlinear finite element method [25]. For a roof structure integrated by cable net, ring truss, and steel columns, the nonlinear finite element method is often used due to the convenience of modeling. In this paper, ANSYS software is used for form finding with the nonlinear finite element method. The Link180 element is adopted for cables [26], and the Beam188 element is used for ring truss members and inclined columns [27]. After form finding is completed, static analysis is carried out in Midas/Gen software with the Newton–Raphson Method, and every load combination list in Table 1 is subjected to the LSHCS. The adverse displacements under load combinations of the serviceability limit state and the adverse cable tensions under the ultimate limit state are studied.
Figure 4a shows that the maximum value of the envelope’s vertical downward displacements is −0.932 m, and the adverse value is located at the inside boundary. The uplift displacements are caused by wind lift effects. Figure 4b shows that the maximum value of the envelope’s vertical upward displacements is 0.318 m, and the adverse value is obtained from the location in the middle of the wider part of the roof. Hence, the deflection of the structure is within the deflection limit, which is 1/50 of the cantilever span of the cable net [21]. Figure 5a shows that the peak value of the maximum cable tensions is 1.14 × 104 kN. It indicates that the stress of cables does not exceed the design value of the tensile strength. Figure 5b shows that the minimum value of the minimum cable tensions is 3.56 × 103 kN. With this value, the stress of cables is more than 30 N/mm2, which avoids cable slack. Hence, cable tensions meet the requirement of the specification [21].
The dynamic characteristics of the LSHCS are analyzed in Midas/Gen, and the Lanczos method [28] is used for the eigenvalue analysis. Loadings of D + 0.5 L are considered the representative value of gravity. The mode shape and natural vibration period (T) of the first mode are concerned. Based on the mode shape, the local stiffness of the cable net can be evaluated and the accidental modeling mistake can be identified [29]. With the T value, the potential resonance of the cable net encountering wind or earthquakes can be evaluated [29]. Figure 6 shows that the shape of the first mode is the overall vertical motion of the cable net. It is logical that the motion amplitude of the wider side of the cable net is larger than the narrow side due to the cantilever span. It indicates that the local stiffness of the wider side is lower than that of the narrow side. The T value of the first mode is 1.8 s, which can keep the cable net away from the potential resonance that experiences wind or earthquakes, and it has been verified in the feasibility study of the project.
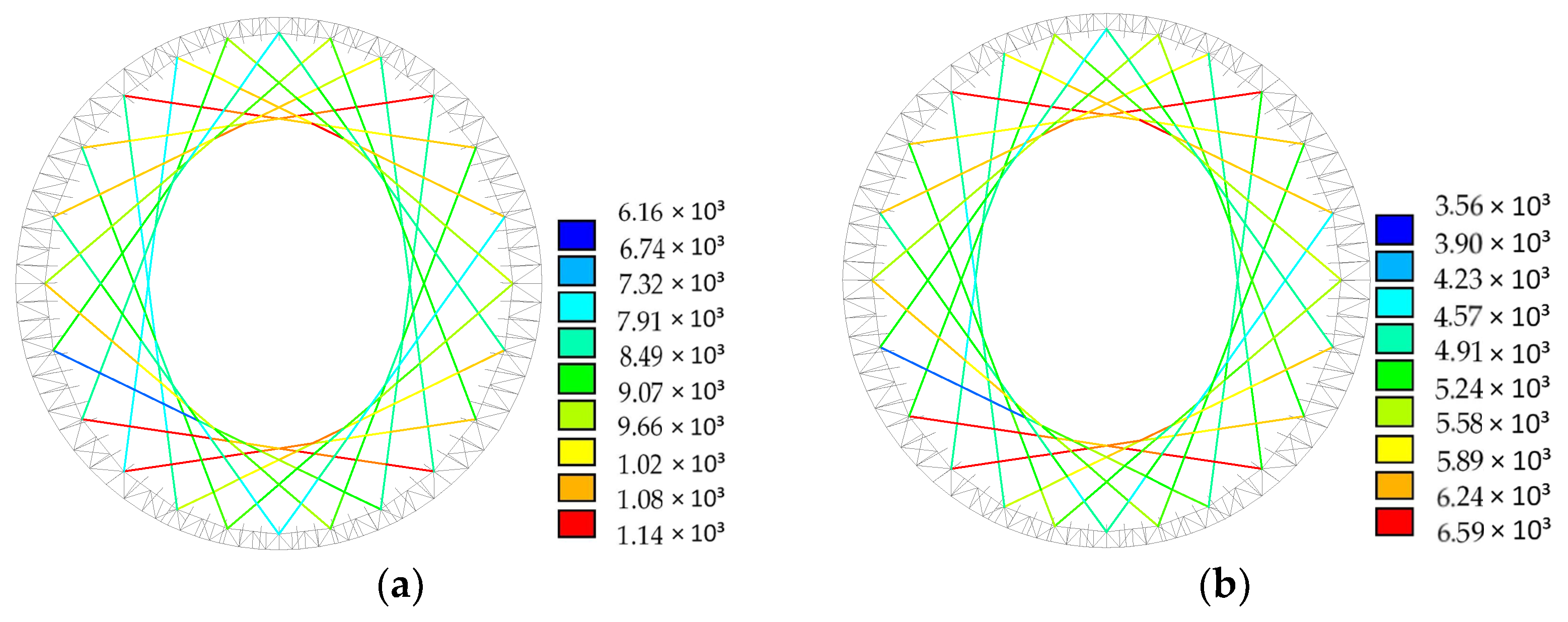
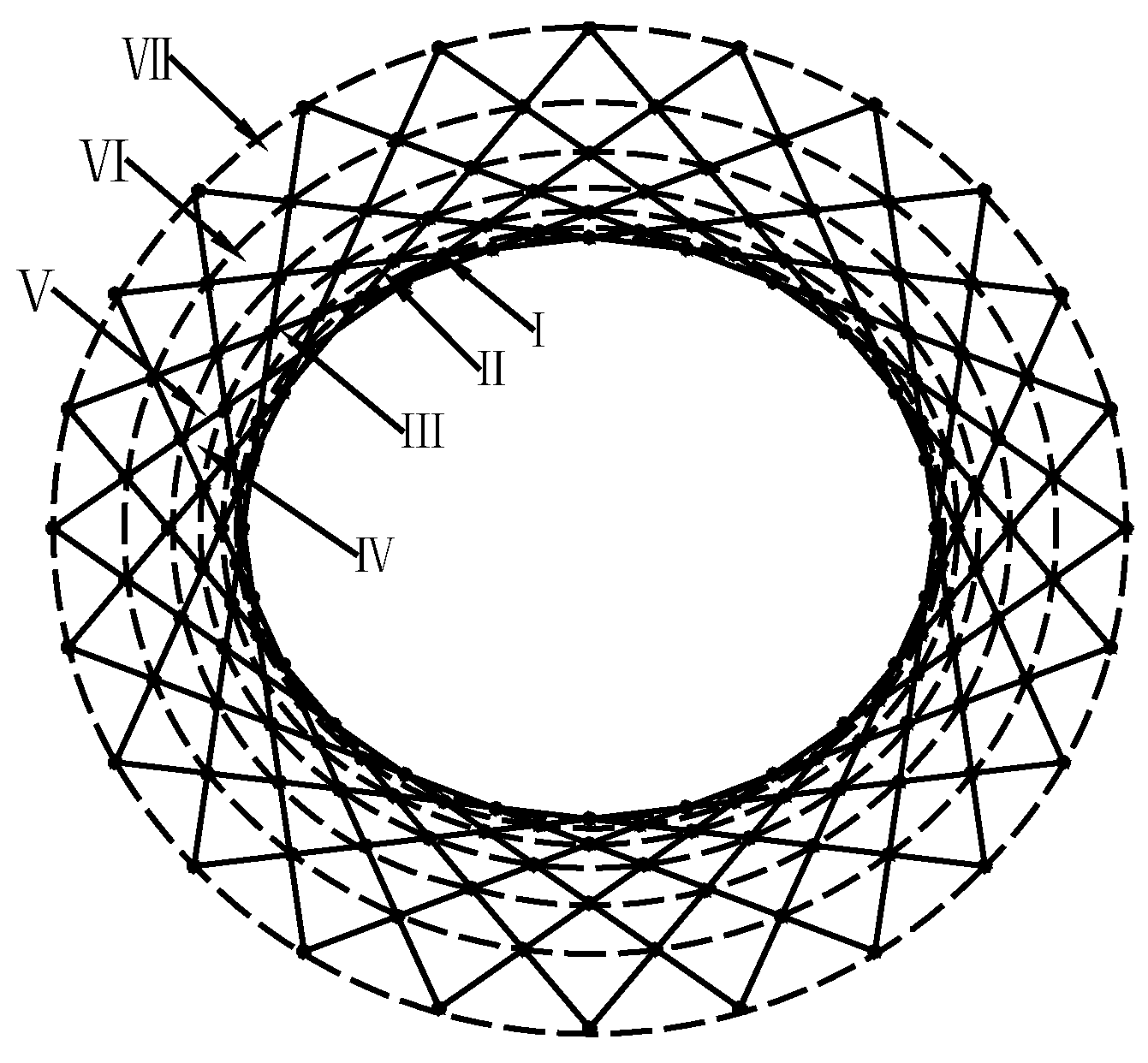
2.3. Cable Clamp Deletion Schemes
Virtual rings are used for classifying cable clamps, as shown in Figure 7. Each virtual ring includes twenty-four cable clamps, and the number of virtual rings increases from the inside to the outside. The cable clamps on virtual ring VII anchor the cable net to the ring truss, and the cable clamps on virtual ring I are used for fixing equipment, such as the lighting system and gantry system, so that cable clamps on the two virtual rings are not considered in the deletion schemes. Table 2 shows that thirty-one deletion schemes on five levels, including deleting one, two, three, four, or five virtual rings, are considered. If a virtual ring is involved in a deletion scheme, all cable clamps on this ring are deleted. After the deletion, a repeated form-finding step with respect to the cable net is carried out using the same initial strain as the original structure (SE0). The node displacements and cable tensions of cable clamp deletion schemes are analyzed under load combinations in Table 1. The dynamic characteristics including mode shape and natural vibration frequency are also emphasized. Based on a comparison and analysis of the results, the best deletion scheme for different levels is identified.
3. Results
3.1. Deleting One Virtual Ring
Table 3 shows the results of SE0 and the schemes of deleting one virtual ring. It is shown that SE1/4 exhibited the smallest increase in DP compared with SE0, with a growth of 36.48%, followed by an SE1/1 of 42.70%. The largest growth in DP is 64.32% in SE1/3. This indicates that when deleting cable clamps on one virtual ring, deleting ring V causes the smallest effect on displacements, and deleting ring II causes the second smallest effect. It is shown that SE1/1 has the smallest growth in MT by 6.09%, and SE1/4 causes growth by up to 13.14%. This indicates that deleting ring II has the smallest effect on MT, and SE1/4 causes the worst effect. Table 3 also shows that all schemes induce an increase in T, indicating that the overall structural stiffness becomes weaker. SE1/2 has the smallest growth in T by 11.18%, while SE1/4 causes the worst effect by 28.40%. Figure 8 shows that the mode shapes of schemes comprise the overall motion of the cable net, and abnormal motion on the local part does not happen. However, a slight difference from SE0 is that the modes of SE1/1, SE1/2, SE1/3, and SE1/4 comprise antisymmetric motions.
From the analysis above, it was found that displacements are the most sensitive to deleting cable clamps, the natural vibration period comes in second, and the tension is not sensitive. The reason is that the initial structural stiffness changes the most. However, since schemes causing the smallest or the worst effect on PD, MT, and T are different, identifying the best scheme or the worst scheme directly is difficult. SE1/1 causes the least amount of growth in MT, the growth in DP comes in second, and the growth in T comes in third. SE1/1 in which the virtual ring II is involved is selected as the best scheme among the deletion of one virtual ring, while the relative outer virtual ring caused the worse effect. In addition, this conclusion verifies the possibility of removing redundant cable clamps in the densest part of the LSHCS.
3.2. Deleting Two Virtual Rings
Table 4 shows the results of deleting two virtual rings. It is shown that SE2/1 has the smallest increase in DP compared with SE0, with a growth of 56.82%, and the largest growth in DP is 124.68% in SE2/9. This indicates that when deleting cable clamps on two virtual rings, deleting the first two rings near the inside boundary of the LSHCS causes the smallest effect on displacements. It is shown that SE2/1 has the smallest growth in MT by 5.11%, and SE2/10 causes growth by up to 22.71%. This indicates that deleting the first two rings near the inside boundary has the smallest effect on MT, and deleting the two rings near the outside boundary causes the worst effect. Table 4 also shows that SE2/1 has the smallest growth in T by 11.17%, while SE2/10 causes the worst effect by 27.45%. Figure 9 shows that the mode shapes of schemes comprise the overall motion of the cable net, and abnormal motion on the local part does not happen. A slight difference from SE0 is that the modes of some schemes comprise antisymmetric motions.
From the analysis above, similar steps with respect to deleting one virtual ring result in displacements that are the most sensitive to deleting cable clamps; the natural vibration period comes in second, and the tension is not sensitive. Since the scheme causing the smallest or the worst effect on PD, MT, and T is the same, it is easy to identify the best scheme: SE2/1. It is concluded that when deleting cable clamps on two virtual rings, deleting the first two rings near the inside boundary of the LSHCS causes the smallest effect.
3.3. Deleting Three Virtual Rings
Table 5 shows the results of the schemes that delete three virtual rings. It is shown that all schemes induce an increase in DP, and SE3/1 has the smallest increase in DP compared with SE0, with a growth of 88.13%. In contrast, the largest increase is 311.34% in SE3/10. It is shown that all schemes induce an increase in MT, SE3/1 has the smallest growth in MT by 15.97%, and SE3/10 causes the largest growth by up to 38.07%. Table 5 also shows that all schemes induce an increase in T, indicating that the overall structural stiffness becomes weaker. SE3/2 has the smallest growth in T by 19.31%, followed by SE3/1 with a growth of 21.64%, while SE3/10 causes the worst effect by 60.59%. Figure 10 shows that mode shapes of some schemes including SE3/9 and SE3/10 are the apparent local motion of the cable net, indicating that local structural stiffness is significantly weakened, which is usually unacceptable. The mode shapes of other schemes comprise the overall motion or a slight local motion in the cable net.
From the analysis above, it was found that when deleting three virtual rings, displacements are the most sensitive to deleting cable clamps, the natural vibration period comes in second, and the tension is not sensitive. Since SE3/1 causes the least growth in MT and DP and growth in T comes in second, SE3/1 in which virtual rings II, III, and IV are involved is selected as the best scheme among the deletion of three virtual rings. It was found that when deleting cable clamps on three virtual rings, deleting the first three rings near the inside boundary of the LSHCS causes the smallest effect.
3.4. Deleting Four or Five Virtual Rings
Table 6 shows the results of the schemes of deleting four or five virtual rings. It is shown that all schemes induced an increase in DP, SE4/1 had the smallest increase in DP compared with SE0, with a growth of 180.50%, while the largest growth was 603.10% in SE5/1. It is shown that all schemes induce an increase in MT, SE4/1 has the smallest growth in MT by 19.28%, and SE4/5 causes the largest growth by up to 92.70%. Table 6 also shows that all schemes induce an increase in T, indicating that the overall structural stiffness becomes weaker. SE4/2 has the smallest growth in T by 39.89%, followed by SE4/1 with a growth of 42.14%, while SE5/1 caused the worst effect by 131.30%. Figure 11 shows that the mode shapes of some schemes including SE4/5 and SE5/1 comprise the apparent local motion of the cable net, and the two schemes are not acceptable. The mode shapes of other schemes comprise the overall motion or the slight local motion of the cable net.
From the analysis above, it was found that when deleting four virtual rings, displacements are the most sensitive to deleting cable clamps, the natural vibration period comes in second, and the tension is not sensitive. Since SE4/1 causes the least growth in MT and DP and growth in T comes in second, SE4/1 in which virtual rings II, III, IV, and V are involved is selected as the best scheme when deleting four virtual rings. It was found that when deleting cable clamps on four virtual rings, deleting the first four rings near the inside boundary of the LSHCS causes the smallest effect.
4. Conclusions
The loop-free single-layer hyperbolic cable net structure is a new type of tensile cable structure for buildings, and it can overcome the disadvantages of key elements and the high tension in loop cables. The imperfection of the LSHCS is that cable clamps near the inside boundary are redundant. The static behavior and dynamic characteristics of the designed schemes for deleting cable clamps are carried out in this paper. The possibility of deleting some redundant cable clamps is verified, and the guidelines for deleting cable clamps are explored. The conclusions are as follows.
Firstly, results show that SE1/1, SE2/1, SE3/1, and SE4/1 are the best cable clamp deletion schemes for their respective levels. It is concluded that for all levels of deleting cable clamps, schemes involving the virtual rings of cable clamps closest to the inside boundary of the cable net cause the smallest effect on static behavior and dynamic characteristics.
Secondly, the results show that displacements are the most sensitive to deleting cable clamps, the natural vibration period comes in second, and the tension is not sensitive with growth rates of 6.09%, 5.11%, 15.97%, and 19.28% in the best schemes of each level. It is concluded that deleting cable clamps affects the structural stiffness significantly, but the bearing capacity is not seriously affected.
In the end, although structural stiffness decreases due to the deletion of cable clamps, the LSHCS is a stable and stiffened structure. Its structural stiffness can be easily improved by increasing pretension, or the cross-section area of cables can be improved to meet the requirement of design specifications. Since deleting cable clamps near the inside boundary causes the smallest effect, removing redundant cable clamps in the dense part of the cable net is feasible.
Author Contributions
Conceptualization, R.L. and G.W.; methodology, J.C.; software, G.W.; validation, J.C.; dynamic analysis, J.C.; investigation, J.C.; writing—original draft preparation, R.L.; writing—review and editing, G.W.; visualization, J.C.; supervision, G.W.; project administration, G.W.; funding acquisition, R.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Shandong, grant number (ZR201911030049).
Data Availability Statement
All data are shown in the paper, with no additional data available apart from those reported in the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xue, S.D. Tension structures in China. J. Int. Assoc. Shell Spat. Struct. 2006, 47, 125–134. [Google Scholar]
- Krishna, P. Tension roofs and bridges. J. Constr. Steel Res. 2001, 57, 1123–1140. [Google Scholar] [CrossRef]
- Yu, Y.J.; Wu, J.Z.; Chen, Z.H. The beginning of modern tension-hung roofs: Dorton Arena. Spat. Struct. 2016, 22, 50–58. [Google Scholar] [CrossRef]
- Quelle, I.G. Cable roofs. Evolution, Classification and Future Trends. In Proceedings of the IASS Symposium, Universidad Politecnica de Valencia, Valencia, Spain, 28 September–2 October 2009. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical Specification for Cable Structures; JGJ 257-2012; China Architecture and Building Press: Beijing, China, 2012. [Google Scholar]
- Krishnan, S. Structural design and behavior of prestressed cable domes. Eng. Struct. 2020, 209, 110294. [Google Scholar] [CrossRef]
- Liu, R.J.; Li, X.Y.; Xue, S.D.; Mollaert, M.; Ye, J.H. Numerical and experimental research on annular crossed cable-truss structure under cable rupture. Earthq. Eng. Eng. Vib. 2017, 16, 557–569. [Google Scholar] [CrossRef]
- Boom, I. Tensile-Compression Ring: A Study for Football Roof Structures. Master Thesis, University of Technology Delft, Rotterdam, The Netherlands, 2012. [Google Scholar]
- Ma, S.; Lu, K.; Chen, M.H.; Skelton, R.E. Design and control analysis of a deployable clustered hyperbolic paraboloid cable net. Eng. Struct. 2023, 279, 115569. [Google Scholar] [CrossRef]
- Liu, R.J.; Zou, Y.; Wang, G.Y.; Xue, S.D. On the collapse resistance of the levy type and the loop-free suspen-dome structures after accidental failure of cables. Int. J. Steel Struct. 2022, 22, 585–596. [Google Scholar] [CrossRef]
- Liu, R.J.; Xue, S.D.; Sun, G.J.; Li, X.Y. Formulas for the derivation of node coordinates of annular crossed cable-truss structure in a pre-stressed state. J. Int. Assoc. Shell Spat. Struct. 2014, 55, 223–228. [Google Scholar]
- Liu, R.J.; Xue, S.D.; Li, X.Y.; Mollaert, M.; Sun, G.J. Preventing disproportionate displacements in an annular crossed cable-truss structure. Int. J. Spat. Struct. 2017, 32, 3–10. [Google Scholar] [CrossRef]
- Liu, R.J.; Li, M.Q.; Cheng, T.C. Discussion on cable-strut systems of the suspen-dome structures. Int. J. Spat. Struct. 2022, 38, 20–29. [Google Scholar] [CrossRef]
- Xue, S.D.; Liu, R.J.; Li, X.Y.; Zou, Y.; Liu, Y. Innovation of non-loops cable-supported structures. Spat. Struct. 2020, 26, 15–22. [Google Scholar] [CrossRef]
- Liu, R.J.; Xue, S.D.; Li, X.Y. Static behavior analysis for annular crossed cable-truss structures. Spat. Struct. 2014, 20, 89–96. [Google Scholar] [CrossRef]
- Xue, S.D.; Tian, X.S.; Liu, Y.; Li, X.Y.; Liu, R.J. Mechanical behavior of single-layer saddle-shape crossed cable net without inner-ring. J. Build. Struct. 2021, 42, 30–38. [Google Scholar] [CrossRef]
- Liu, R.J.; Wang, C.; Xue, S.D.; Zou, Y. Analysis on the collapse resistance of the loop-free suspen-dome subjected to cable or strut failure. J. Int. Assoc. Shell Spat. Struct. 2022, 63, 5–15. [Google Scholar] [CrossRef]
- Liu, R.J.; Xue, S.D.; Cao, J.J.; Li, X.Y.; Liu, Y. Analysis on single-layer hyperbolic cable net structure schemes of stadium roof. J. Build. Struct. 2022, 43, 269–276. [Google Scholar] [CrossRef]
- Lu, J.; Xue, S.D.; Li, X.Y. Analysis on mechanical performance of ellipse cable-net structure without inner ring cables. J. Southeast Univ. (Nat. Sci. Ed.) 2021, 51, 783–789. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Load Code for the Design of Building Structures; GB 50009-2012; China Architecture and Building Press: Beijing, China, 2012. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. The Technical Regulations for Cable Structures; JGJ 257-2012; China Architecture and Building Press: Beijing, China, 2012. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Unified Standard for Reliability Design of Building Structures; GB50068-2018; China Architecture and Building Press: Beijing, China, 2018. [Google Scholar]
- Schek, H.J. The force density method for form finding and computation of general networks. Comput. Methods Appl. Mech. Eng. 1974, 3, 115–134. [Google Scholar] [CrossRef]
- Barnes, M.R. Form finding and analysis of tension structures by dynamic relaxation. Int. J. Space Struct. 1999, 14, 89–104. [Google Scholar] [CrossRef]
- Argyris, J.H.; Angelopoulos, T.; Bichat, B. A general method for the shape finding of lightweight tension structures. Comput. Methods Appl. Mech. Eng. 1974, 3, 135–149. [Google Scholar] [CrossRef]
- Xiang, Y.; Luo, Y.F.; Guo, X.N.; Xiong, Z.; Shen, Z.Y. A linearized approach for the seismic response analysis of flexible cable net structures. Soil Dynam. Earthq. Eng. 2016, 88, 92–108. [Google Scholar] [CrossRef] [Green Version]
- Singhal, D.; Narayanamurthy, V. Large and small deflection analysis of a cantilever beam. J. Inst. Eng. (India) Series A 2019, 100, 83–96. [Google Scholar] [CrossRef]
- Nour-Omid, B. Applications of the Lanczos method. Comput. Phys. Commun. 1989, 53, 157–168. [Google Scholar] [CrossRef]
- Zhu, M.L.; Luo, B.; Guo, Z.X. Analysis and Construction of Cable Net Structure of Suzhou Olympic Sports Center; China Architecture and Building Press: Beijing, China, 2018; pp. 106–111. [Google Scholar]
Figure 1.
Diagram of the loop-free single-layer hyperbolic cable net structure.
Figure 2.
The original structure scheme of the LSHCS: (a) plane projection and (b) 3-D drawing.
Figure 3.
The joint for the LSHCS: 1. cable clamp, 2. spiral strand cable, and 3. fastening bolt [21].
Figure 3.
The joint for the LSHCS: 1. cable clamp, 2. spiral strand cable, and 3. fastening bolt [21].
Figure 4.
Contours of envelope displacements: (a) vertical downward displacements/m and (b) vertical uplift displacements/m.
Figure 4.
Contours of envelope displacements: (a) vertical downward displacements/m and (b) vertical uplift displacements/m.
Figure 5.
Contours of envelope cable tensions: (a) maximum cable tensions/kN and (b) minimum cable tensions/kN.
Figure 5.
Contours of envelope cable tensions: (a) maximum cable tensions/kN and (b) minimum cable tensions/kN.
Figure 6.
The first vibration mode (T = 1.8 s).
Figure 7.
The number of virtual rings.
Figure 8.
Vibration modes of schemes deleting one virtual ring. (a) SE1/1; (b) SE1/2; (c) SE1/3; (d) SE1/4; (e) SE1/5.
Figure 8.
Vibration modes of schemes deleting one virtual ring. (a) SE1/1; (b) SE1/2; (c) SE1/3; (d) SE1/4; (e) SE1/5.
Figure 9.
Vibration modes of schemes deleting two virtual rings. (a) SE2/1; (b) SE2/2; (c) SE2/3; (d) SE2/4; (e) SE2/5; (f) SE2/6; (g) SE2/7; (h) SE2/8; (i) SE2/9; (j) SE2/10.
Figure 9.
Vibration modes of schemes deleting two virtual rings. (a) SE2/1; (b) SE2/2; (c) SE2/3; (d) SE2/4; (e) SE2/5; (f) SE2/6; (g) SE2/7; (h) SE2/8; (i) SE2/9; (j) SE2/10.
Figure 10.
Vibration modes of schemes deleting three virtual rings. (a) SE3/1; (b) SE3/2; (c) SE3/3; (d) SE3/4; (e) SE3/5; (f) SE3/6; (g) SE3/7; (h) SE3/8; (i) SE3/9; (j) SE3/10.
Figure 10.
Vibration modes of schemes deleting three virtual rings. (a) SE3/1; (b) SE3/2; (c) SE3/3; (d) SE3/4; (e) SE3/5; (f) SE3/6; (g) SE3/7; (h) SE3/8; (i) SE3/9; (j) SE3/10.
Figure 11.
Vibration modes of schemes when deleting four or five virtual rings. (a) SE4/1; (b) SE4/2; (c) SE4/3; (d) SE4/4; (e) SE4/5; (f) SE5/1.
Figure 11.
Vibration modes of schemes when deleting four or five virtual rings. (a) SE4/1; (b) SE4/2; (c) SE4/3; (d) SE4/4; (e) SE4/5; (f) SE5/1.
Table 1.
Load combinations.
| Numbers | Load Combination Expressions |
|---|---|
| LCB1 | D + P + S |
| LCB2 | D + P + W |
| LCB3 | D + P+S+0.6 W |
| LCB4 | D + P + 0.7 S + 1.0 W |
| LCB5 | 1.3 D + 1.3 P + 1.5 S |
| LCB6 | 1.3 D + 1.3 P + 1.5 W |
| LCB7 | 1.3 D + 1.3 P + 1.5 W + (1.5 × 0.7) S |
| LCB8 | 1.3 D + 1.3 P + 1.5 S + (1.5 × 0.6) W |
Table 2.
Cable clamp deletion schemes.
| No. | Virtual Ring | No. | Virtual Rings | No. | Virtual Rings | No. | Virtual Rings |
|---|---|---|---|---|---|---|---|
| SE1/1 | II | SE2/4 | II, VI | SE3/2 | II, III, V | SE3/10 | IV, V, VI |
| SE1/2 | III | SE2/5 | III, IV | SE3/3 | II, III, VI | SE4/1 | II, III, IV, V |
| SE1/3 | IV | SE2/6 | III, V | SE3/4 | II, IV, V | SE4/2 | II, III, IV, VI |
| SE1/4 | V | SE2/7 | III, VI | SE3/5 | II, IV, VI | SE4/3 | II, III, V, VI |
| SE1/5 | VI | SE2/8 | IV, V | SE3/6 | II, V, VI | SE4/4 | II, IV, V, VI |
| SE2/1 | II, III | SE2/9 | IV, VI | SE3/7 | III, IV, V | SE4/5 | III, IV, V, VI |
| SE2/2 | II, IV | SE2/10 | V, VI | SE3/8 | III, IV, VI | SE5/1 | II, III, IV, V, VI |
| SE2/3 | II, V | SE3/1 | II, III, IV | SE3/9 | III, V, VI |
Table 3.
Results of schemes that delete one virtual ring.
| Scheme | DP1/m | PDP2/% | MT3/kN | PMT4/% | T/s | PT5/% |
|---|---|---|---|---|---|---|
| SE0 | −0.932 | -- | 1.14 × 104 | -- | 1.866 | -- |
| SE1/1 | −1.330 | 42.70 | 1.21 × 104 | 6.09 | 2.152 | 15.33 |
| SE1/2 | −1.472 | 57.85 | 1.25 × 104 | 9.87 | 2.075 | 11.18 |
| SE1/3 | −1.532 | 64.32 | 1.26 × 104 | 10.23 | 2.096 | 12.35 |
| SE1/4 | −1.273 | 36.48 | 1.29 × 104 | 13.14 | 2.396 | 28.40 |
| SE1/5 | −1.362 | 46.11 | 1.26 × 104 | 10.39 | 2.244 | 20.24 |
1.DP represents the maximum vertical displacement of the cable net. 2.PDP is the DP growth rate of the deletion schemes compared with the original structure. 3.MT is the maximum tension. 4.PMT is the MT growth rate. 5.PT is the T growth rate.
Table 4.
Results of deleting two virtual rings.
| Scheme | DP/m | PDP/% | MT/kN | PMT/% | T/s | PT/% |
|---|---|---|---|---|---|---|
| SE2/1 | −1.462 | 56.82 | 1.20 × 104 | 5.11 | 2.074 | 11.17 |
| SE2/2 | −1.639 | 75.78 | 1.26 × 104 | 10.60 | 2.080 | 11.48 |
| SE2/3 | −1.854 | 98.85 | 1.36 × 104 | 19.12 | 2.222 | 19.07 |
| SE2/4 | −1.659 | 77.95 | 1.30 × 104 | 14.07 | 2.178 | 16.69 |
| SE2/5 | −1.968 | 111.14 | 1.28 × 104 | 12.03 | 2.206 | 18.24 |
| SE2/6 | −1.675 | 79.73 | 1.31 × 104 | 14.80 | 2.151 | 15.29 |
| SE2/7 | −1.682 | 80.41 | 1.32 × 104 | 16.00 | 2.217 | 18.83 |
| SE2/8 | −1.920 | 105.91 | 1.34 × 104 | 17.89 | 2.285 | 22.43 |
| SE2/9 | −2.095 | 124.68 | 1.37 × 104 | 20.53 | 2.332 | 24.99 |
| SE2/10 | −1.888 | 102.52 | 1.40 × 104 | 22.71 | 2.378 | 27.45 |
Table 5.
Results of deleting three virtual rings.
| Scheme | DP/m | PDP/% | MT/kN | PMT/% | T/s | PT/% |
|---|---|---|---|---|---|---|
| SE3/1 | −1.754 | 88.13 | 1.32 × 104 | 15.97 | 2.270 | 21.64 |
| SE3/2 | −2.000 | 114.53 | 1.33 × 104 | 16.26 | 2.226 | 19.31 |
| SE3/3 | −2.384 | 155.75 | 1.37 × 104 | 20.17 | 2.402 | 28.72 |
| SE3/4 | −2.309 | 147.72 | 1.46 × 104 | 27.98 | 2.410 | 29.15 |
| SE3/5 | −2.045 | 119.36 | 1.35 × 104 | 18.45 | 2.324 | 24.57 |
| SE3/6 | −2.896 | 210.68 | 1.49 × 104 | 30.59 | 2.616 | 40.17 |
| SE3/7 | −2.622 | 181.27 | 1.40 × 104 | 22.53 | 2.538 | 36.01 |
| SE3/8 | −2.393 | 156.68 | 1.34 × 104 | 17.83 | 2.3639 | 26.68 |
| SE3/9 | −2.146 | 130.18 | 1.44 × 104 | 26.69 | 2.469 | 32.30 |
| SE3/10 | −3.835 | 311.34 | 1.57 × 104 | 38.07 | 2.9956 | 60.54 |
Table 6.
Results of deleting four or five virtual rings.
| Scheme | DP/m | PDP/% | MT/kN | PMT/% | T/s | PT/% |
|---|---|---|---|---|---|---|
| SE4/1 | −2.615 | 180.50 | 1.36 × 104 | 19.28 | 2.652 | 42.14 |
| SE4/2 | −3.171 | 240.09 | 1.45 × 104 | 27.10 | 2.610 | 39.89 |
| SE4/3 | −3.835 | 311.34 | 1.57 × 104 | 38.07 | 2.945 | 57.82 |
| SE4/4 | −4.306 | 361.83 | 1.77 × 104 | 55.59 | 3.083 | 65.20 |
| SE4/5 | −6.111 | 555.40 | 2.20 × 104 | 92.70 | 3.999 | 114.33 |
| SE5/1 | −6.556 | 603.10 | 1.74 × 104 | 52.75 | 4.316 | 131.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Liu, R.; Cao, J.; Wang, G. Effect of Clamp Deletion on Static Behavior and Dynamic Characteristics of Loop-Free Cable Net Structures. Buildings 2023, 13, 881. https://doi.org/10.3390/buildings13040881
AMA Style
Liu R, Cao J, Wang G. Effect of Clamp Deletion on Static Behavior and Dynamic Characteristics of Loop-Free Cable Net Structures. Buildings. 2023; 13(4):881. https://doi.org/10.3390/buildings13040881
Chicago/Turabian StyleLiu, Renjie, Jiajia Cao, and Guangyong Wang. 2023. "Effect of Clamp Deletion on Static Behavior and Dynamic Characteristics of Loop-Free Cable Net Structures" Buildings 13, no. 4: 881. https://doi.org/10.3390/buildings13040881
APA StyleLiu, R., Cao, J., & Wang, G. (2023). Effect of Clamp Deletion on Static Behavior and Dynamic Characteristics of Loop-Free Cable Net Structures. Buildings, 13(4), 881. https://doi.org/10.3390/buildings13040881
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.
