A Simple Approach for the Dynamic Analysis of a Circular Tapered Pile under Axial Harmonic Vibration

Abstract

The tapered pile offers sustainable use of construction materials due to its higher axial and lateral capacity and better performance owing to its geometry. This paper develops a semi-analytical solution of the vertical dynamic impedance of the tapered pile based on the dynamic Winkler theory and transfer matrix method. The accuracy and reliability of the proposed approach are verified by comparing the impedance functions of cylindrical and tapered piles obtained from the analytical solution and finite element analysis. A parametric study is performed to investigate the influence of the taper angle on the vertical dynamic impedance and resonant frequency. The results reveal that the taper angle has a significant influence on the vertical dynamic impedance, while it does not affect the oscillation period of the dynamic impedance and the resonant frequency. Besides, the vibration performance of the tapered pile is better than that of a cylindrical pile with the same volume. For a fixed-volume tapered pile, varying the pile length while keeping the pile tip diameter constant yields a better dynamic impedance than varying the pile tip diameter while keeping the pile length constant. Finally, the vertical displacement amplitude of the tapered pile decreases as the taper angle increases, especially for high-frequency excitation.

1. Introduction

Tapered pile geometry is characterized by a linear variation of a cross section along its axis with a large diameter at its head and a small diameter at its toe. This configuration results in a larger axial and lateral load carrying capacity and improved performance under both vertical and lateral static loads. Many studies have reported that the vertical load capacity of the tapered pile increases by 50 to 250% over cylindrical piles with the same volume [1,2,3,4], and its lateral load capacity is higher by 60 to 80% [5,6,7,8]. Due to its advantages over conventional cylindrical pile configurations, it has been adopted in building foundations, slope retaining projects, support of high-speed railways, and highway weak-foundation treatment projects [9]. However, it has not yet been widely used in applications involving dynamic loading due to the limited knowledge of its dynamic pile−soil interaction mechanism. Most previous studies focused on the static bearing characteristics of the tapered pile using both experimental tests and finite element analysis [10,11,12,13,14,15]. The cyclic response of axially loaded tapered piles has also been investigated, and the taper angle was demonstrated to improve the cyclic performance of piles [16,17,18].

While the tapered piles bear the vertical loads from high-speed trains and their installation improves the surrounding soil and hence reduces the foundation settlement, the tapered pile foundation will be affected by enduring dynamic loads and can play an important role in the mitigation of ground-borne vibration due to high-speed train traffic. Therefore, the vertical vibration characteristics of tapered piles subjected to dynamic traffic load are important considerations, and effective analysis methods are desired to evaluate their dynamic characteristics. However, limited experimental and numerical investigations have been conducted to evaluate the vertical response of tapered piles under dynamic loading conditions. Tavasoli and Ghazavi [19] conducted field tests to evaluate the taper effect on pile driving performance, which showed that the tapered and semi-tapered pile geometry could offer better drivability with reduced cumulative hammer blow counts and efficient driving operations. Ghazavi [20] conducted a series of finite element analyses to characterize the dynamic response of tapered piles under vertical harmonic vibration, which illustrated that the dynamic performance of the tapered piles is superior to that of cylindrical piles with the same length and volume.

Compared to field tests and finite element analyses, analytical solutions are more efficient and should be easier to utilize in evaluating the dynamic response of the tapered pile foundation. Many studies have proposed theoretical analysis methods for the vertical dynamic response of tapered piles [21,22,23,24,25]. In addition, several studies examined the effects of fixed and free boundary conditions of the pile tip and taper angle on the vertical dynamic characteristics of tapered piles [26,27]. Dehghanpoor and Ghazavi [28] evaluated the seismic response of tapered piles and investigated the variation of their resonance amplitudes as a function of the taper angle. Wang et al. [29] and Guan et al. [30] analyzed the vertical and torsional dynamic impedance of tapered piles considering construction disturbance and demonstrated that the dynamic stiffness at the pile head increases with the degree of soil compaction due to pile installation, while the damping decreases with the increase of soil compaction. However, in all the above studies, tapered piles are idealized as a combination of multisegmented cylinders. Although these methods involve a simplified calculation procedure similar to conventional cylindrical piles [31,32,33], the accuracy of the results is highly dependent on the number of segments used to discretize the tapered pile, which reduces the efficiency of the analytical approach, and the computational time and cost can be high.

To effectively consider the interaction between the tapered pile and soil, this paper develops a dynamic Winkler model along the pile shaft incorporating distributed lateral and axial springs and dashpots, in addition to a concentrated axial spring and dashpot at the pile tip. The analytical expression for the vertical dynamic impedance is established in the frequency domain and is integrated with the transfer matrix method to yield the dynamic response of the tapered pile. The proposed method is validated by comparing its predictions with both the analytical solutions for cylindrical piles and the results from finite element analysis for tapered piles. The proposed approach is demonstrated to be accurate and efficient for analyzing and designing tapered piles subjected to dynamic loading. The influence of the taper angle and soil parameters on the vertical dynamic characteristics of the tapered pile is illustrated with an example.

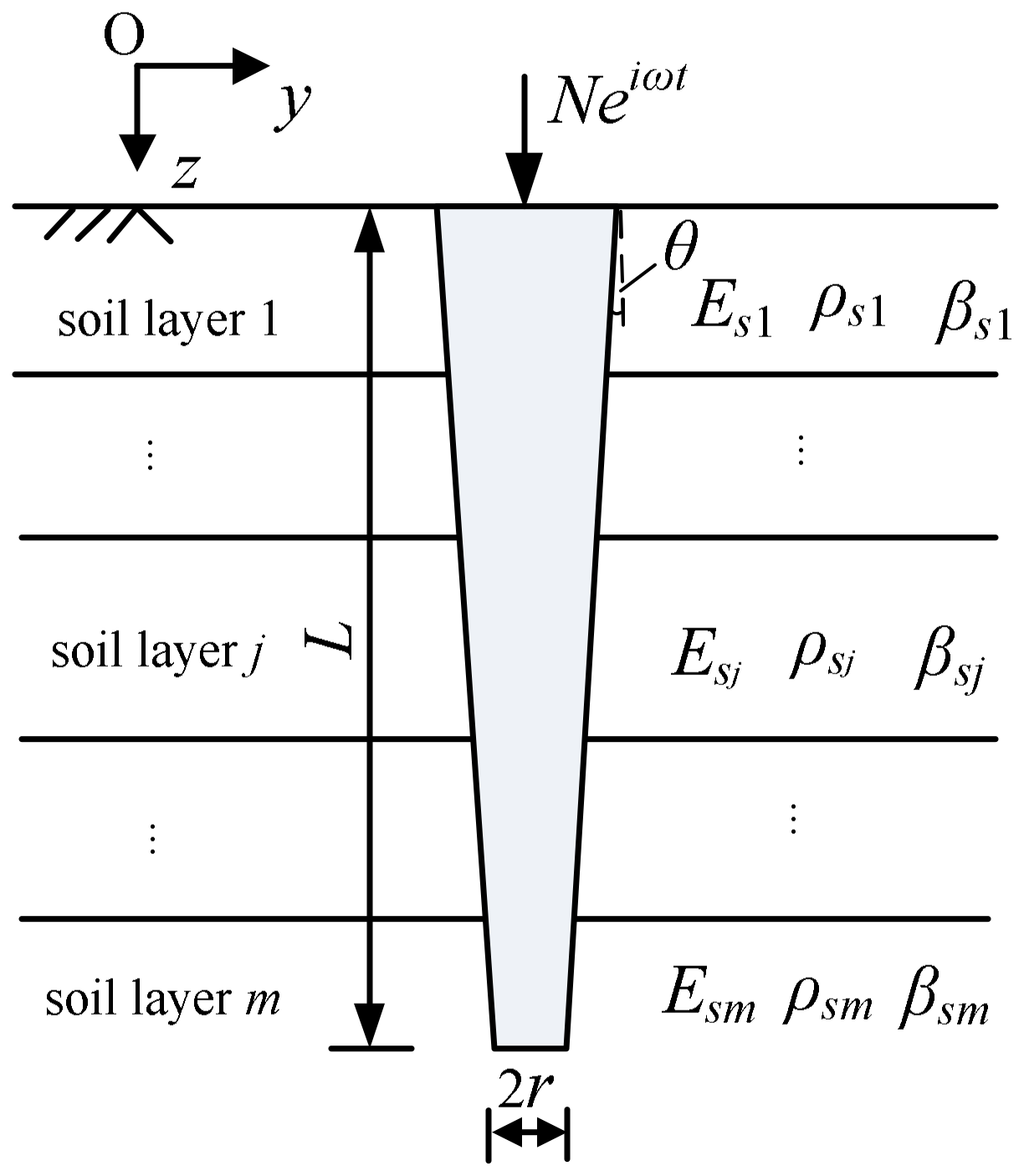
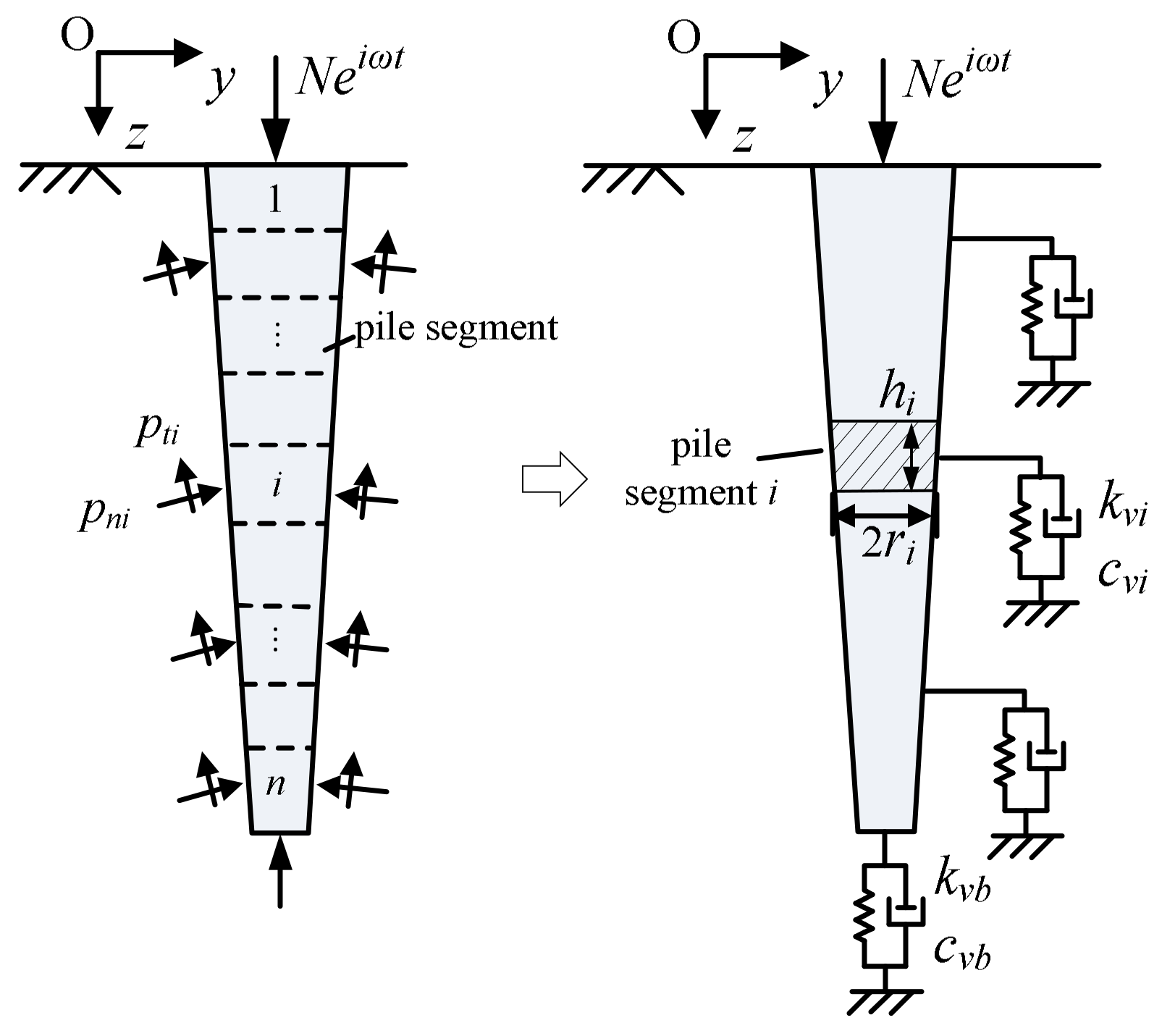
2. Physical Models

A tapered pile−soil system is shown in Figure 1. The analysis considers a tapered pile with pile length L and pile tip radius r_b embedded in layered soil. The following assumptions are adopted in developing the model:

(1)

The tapered pile is elastic and perfectly bonded to the soil. The pile has a circular cross-section and is tapered along its shaft with a constant taper angle of θ.

(2)

The soil has m layers, and each layer is isotropic and homogeneous. Young’s modulus, density, damping ratio, and shear wave velocity of each soil layer are E_si, ρ_si, β_si, and V_si for the i-th section, respectively, and soil nonlinearity is neglected. The ground surface is free of normal and shear forces.

(3)

The tapered pile is subjected to a steady-state harmonic excitation with an amplitude Ve^iωt with frequency ω. There is no force or deformation out of the plane Oyz.

In the following, a tapered pile divided into n frustum segments is considered. The tapered pile is subjected to a vertical harmonic load at the pile head and shear force p_ti and normal force p_ni (I = 1~n) along the tapered pile segment shaft, as shown in Figure 2. The thickness and radius of the i-th segment are assumed to be h_i and r_i, respectively. The tapered pile is divided into segments of the same thicknesses as the adjacent soil layers. The soil segment surrounding the pile is idealized as distributed complex springs to model its resistance to the pile. The frequency-dependent dynamic stiffness and damping of the complex springs, k_vi and c_vi, account for the soil stiffness and energy loss due to wave propagation and hysteretic dissipation. The vertical spring k_vb and dashpot c_vb are used to simulate soil resistance at the pile tip. A dynamic Winkler model is then developed, incorporating the distributed complex springs along the pile shaft and below the pile tip, as illustrated in Figure 2.

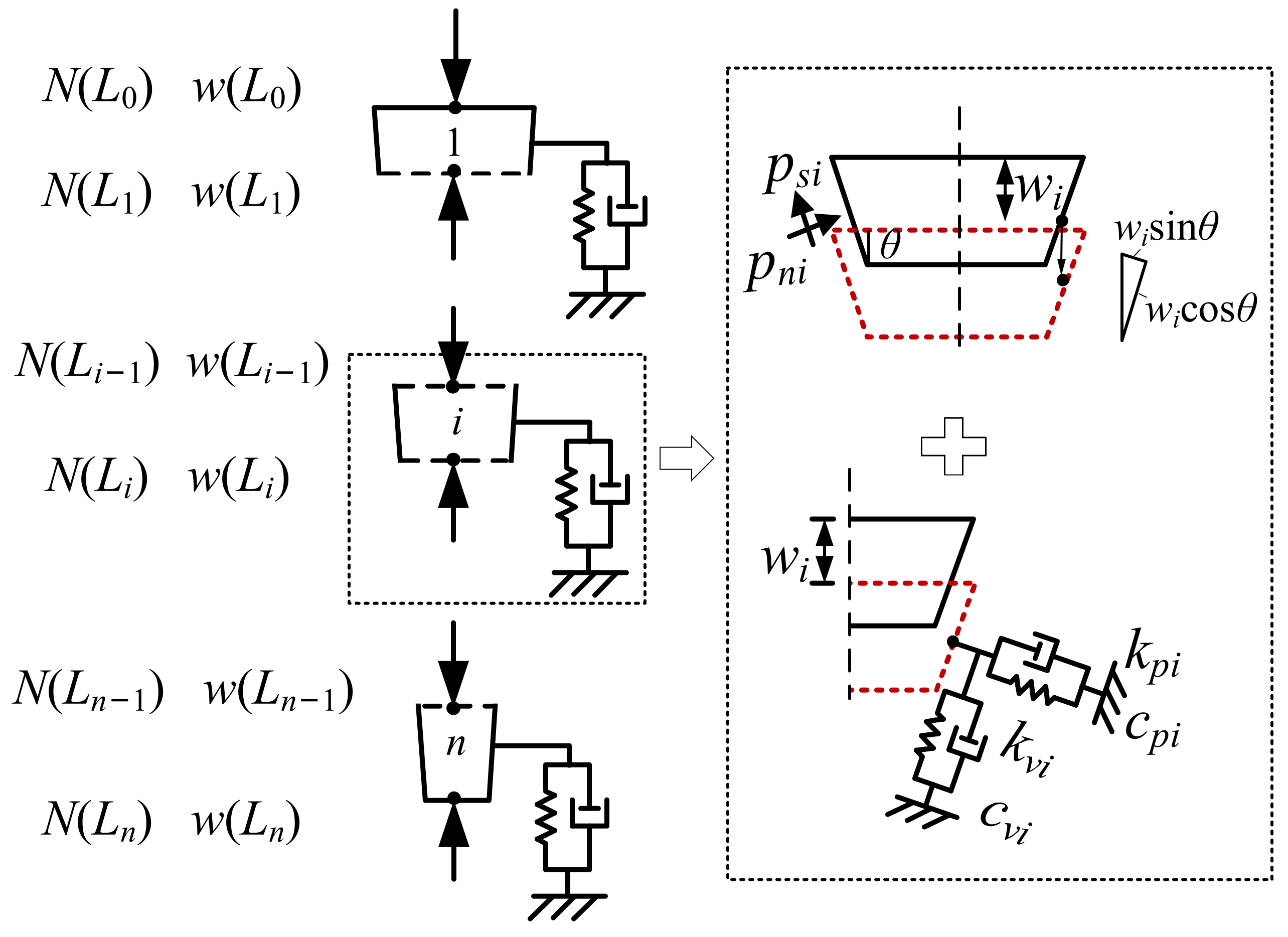
3. Formulation

The equilibrium of the i-th frustum segment of the tapered pile in the vertical direction is given by the following governing equation [27,34,35]

$${\rho }_p{A}_p\left(z\right)\frac{{\partial }^{2}w\left(z,t\right)}{\partial t^2}+p_i-E_p{A}_p\left(z\right)\frac{{\partial }^{2}w\left(z,t\right)}{\partial z^2}-E_p\frac{\partial A_p\left(z\right)}{\partial z}\frac{\partial w\left(z,t\right)}{\partial z}=0$$

(1)

where ρ_p is the density of the pile, E_p is Young’s modulus of the pile, A_p (z) is the cross-sectional area at depth z, w (z, t) is the displacement at depth z and time t, p_i is the soil resistance to the dynamic harmonic motion of the tapered pile, and ω is the circular frequency of the loading force. p_i can be decomposed into the shear force p_ti and normal force p_ni to the pile shaft as

$$p_i=p_{t_i}\cos \theta +p_{n_i}\sin \theta$$

(2)

Under vertical vibration, p_ti and p_ni are functions of the complex stiffness and displacement along the normal and tangential force directions and can be expressed based on the Winkler model assumption as

$$p_{t_i}=\left(k_{t_i}+i\omega c_{t_i}\right)w\left(z,t\right)\cos \theta$$

(3)

$$p_{n_i}=\left(k_{n_i}+i\omega c_{n_i}\right)w\left(z,t\right)\sin \theta$$

(4)

where k_ti and c_ti are the complex stiffness and damping coefficients parallel to the pile surface in plane Oyz, and k_ni and c_ni are the complex stiffness and damping coefficients perpendicular to the pile surface in plane Oyz, respectively.

Substituting Equations (3) and (4) into Equation (1) and considering the commonly adopted assumption that the vertical dynamic response is given by w (z,t) = w (z)e^iwt when the pile is under axial steady-state harmonic vibration [36,37,38], Equation (1) can be rewritten in the following form

$$E_p{A}_p\left(z\right)\frac{{\partial }^{2}w\left(z\right)}{\partial z^2}+E_p\frac{\partial A_p\left(z\right)}{\partial z}\frac{\partial w\left(z\right)}{\partial z}=\left[k_{vi}+i\omega c_{vi}-{\rho }_p{\omega }^2{A}_p\left(z\right)\right]w\left(z\right)$$

(5)

where k_vi and c_vi are the dynamic stiffness and damping constants of soil surrounding the pile shaft, which are defined as

$$k_{vi}=k_{ti}{\cos }^2\theta +k_{ni}{\sin }^2\theta$$

(6)

$$c_{vi}{=\mathrm{c}}_{ti}{\cos }^2\theta +c_{ni}{\sin }^2\theta$$

(7)

The nontrivial general solution of Equation (1) is

$$w\left(z\right)=C_1{J}_{\mu }\left(H\left(z\right)\right)+C_2{Y}_{\mu }\left(H\left(z\right)\right)$$

(8)

where C₁ and C₂ are complex constants that are determined by the boundary conditions; J_μ (H (z)) and Y_μ (H (z)) are the spherical Bessel functions of order μ of the first and second kinds, respectively. μ and H (z) are defined as

$$\mu =\frac{1}{2}\left(\sqrt{\frac{4k_{vi}+4i\omega c_{vi}}{\pi E_p{\tan }^2\theta }+1}-1\right)$$

(9)

$$H\left(z\right)=-\omega \sqrt{\frac{{\rho }_p}{E_p}}\frac{r_b+\left(L-z\right)\tan \theta }{\tan \theta }$$

(10)

With the differential relationship between the vertical displacement w (z) and axial force N (z), the axial force N (z) can be calculated from the pile displacement w (z) as

$$N\left(z\right)=-E_p{A}_p\left(z\right)\frac{dw\left(z\right)}{dz}=C_{1}F\left(H\left(z\right)\right)+C_{2}G\left(H\left(z\right)\right)$$

(11)

$$F\left(H\left(z\right)\right)=\frac{\omega }{2}\sqrt{\frac{{\rho }_p}{E_p}}\left[-\frac{J_{\mu }\left(H\left(z\right)\right)}{H\left(z\right)}+J_{\mu -1}\left(H\left(z\right)\right)-J_{\mu +1}\left(H\left(z\right)\right)\right]$$

(12)

$$G\left(H\left(z\right)\right)=\frac{\omega }{2}\sqrt{\frac{{\rho }_p}{E_p}}\left[-\frac{Y_{\mu }\left(H\left(z\right)\right)}{H\left(z\right)}+Y_{\mu -1}\left(H\left(z\right)\right)-Y_{\mu +1}\left(H\left(z\right)\right)\right]$$

(13)

For the i-th segment of the tapered pile embedded in a homogeneous soil, the relationship between the vertical displacement w (z) and the axial force N (z) at the ends of the section can be formulated as

$$\left\{\begin{array}{c}w\left(L_i\right)\\ N\left(L_i\right)\end{array}\right\}={\left[T\right]}_i\left\{\begin{array}{c}w\left(L_{i-1}\right)\\ N\left(L_{i-1}\right)\end{array}\right\}={\left[\begin{array}{cc}{T}_{11}& T_{12}\\ T_{21}& T_{22}\end{array}\right]}_i\left\{\begin{array}{c}w\left(L_{i-1}\right)\\ N\left(L_{i-1}\right)\end{array}\right\}$$

(14)

where {w (L_i−1), N (L_i−1)} and {w (L_i), N (L_i)} are the dynamic vertical displacement and axial force at the top and bottom ends of the i-th pile segment, respectively. The transfer matrix is then given as

$${\left[T\right]}_i=\left[\begin{array}{cc}{J}_{\mu }\left(H\left(L_i\right)\right)& Y_{\mu }\left(H\left(L_i\right)\right)\\ F\left(H\left(L_i\right)\right)& G\left(H\left(L_i\right)\right)\end{array}\right]{\left[\begin{array}{cc}{J}_{\mu }\left(H\left(L_{i-1}\right)\right)& Y_{\mu }\left(H\left(L_{i-1}\right)\right)\\ F\left(H\left(L_{i-1}\right)\right)& G\left(H\left(L_{i-1}\right)\right)\end{array}\right]}^{-1}\odot \left[\begin{array}{cc}1& -1/E_{p}A\left(L_{i-1}\right)\\ -E_{p}A\left(L_i\right)& A\left(L_i\right)/A\left(L_{i-1}\right)\end{array}\right]$$

(15)

where A (L_i−1) and A (L_i) are the cross-sectional areas of the top and bottom of the i-th pile segment, and ⊙ is the Hadamard product operator. The vertical displacement and axial force at any depth in a pile can be determined by the transfer matrix method with the continuity condition (see Figure 3) as

$$\left\{\begin{array}{c}w\left(L_n\right)\\ N\left(L_n\right)\end{array}\right\}=\left[T^w\right]\left\{\begin{array}{c}w\left(L_0\right)\\ N\left(L_0\right)\end{array}\right\}$$

(16)

$$\left[T^w\right]={\left[T\right]}_n{\left[T\right]}_{n-1}\cdots {\left[T\right]}_2{\left[T\right]}_1=\left[\begin{array}{cc}{T}_{11}^w& T_{11}^w\\ T_{21}^w& T_{22}^w\end{array}\right]$$

(17)

To obtain the transfer matrix [T^w], the stiffness k_v and damping c_v constants of soil around the i-th conical frustum pile segment should be determined first. The complex stiffness and damping coefficients of the springs along the pile can be approximated by the following empirical equations [34,39,40]

$$k_{ti}=0.6E_{si}\left(1+\frac{1}{2}\sqrt{a_{0i}}\right)$$

(18)

$$c_{ti}\approx 2{\beta }_{si}\frac{k_{vi}}{\omega }+\pi {\rho }_{si}{V}_{si}{d}_i{a}_{0i}^{-\frac{1}{4}}$$

(19)

$$k_{ni}\approx 1.2E_{si}$$

(20)

$$c_{ni}\approx 2{\beta }_{si}\frac{k_{ni}}{\omega }+6{\rho }_{si}{V}_{si}{d}_i{a}_{0i}^{-\frac{1}{4}}$$

(21)

where E_si, β_si, ρ_si and V_si are the elastic modulus, damping ratio, soil density, and shear wave velocity of the soil surrounding the i-th pile segment, respectively; a_0i is the dimensionless frequency, and d_i is the average diameter of the i-th conical frustum.

The vertical displacement w (L_n) and axial force N (L_n) at the pile tip can be determined based on the solution of rigid circular footing with vertical vibration in an elastic half-space given by Lysmer and Richart [41]:

$$N\left(L_n\right)=\left(k_{vb}+i\omega c_{vb}\right)w\left(L_n\right)$$

(22)

$$k_{vb}=\frac{4G_b{r}_b}{1-v_b}$$

(23)

$$c_{vb}=\frac{3.4r_b\sqrt{G_b{\rho }_b}}{1-v_b}$$

(24)

where k_vb and c_vb are the dynamic stiffness and damping coefficients at the pile tip, respectively, and G_b, ρ_b, and v_b are the shear modulus, mass density, and Poisson’s ratio of the soil at the pile tip, respectively.

Substituting Equation (22) into Equation (14), the vertical dynamic impedance Γ_v of the tapered pile can be obtained as

$${\Gamma }_v=\frac{N\left(L_0\right)}{w\left(L_0\right)}=-\frac{T_{11}^w\left(k_{vb}+i\omega c_{vb}\right)+T_{21}^w}{T_{12}^w\left(k_{vb}+i\omega c_{vb}\right)+T_{22}^w}=K_v+i{C}_v$$

(25)

where K_v and C_v are the vertical dynamic stiffness and damping constants of the tapered pile, respectively.

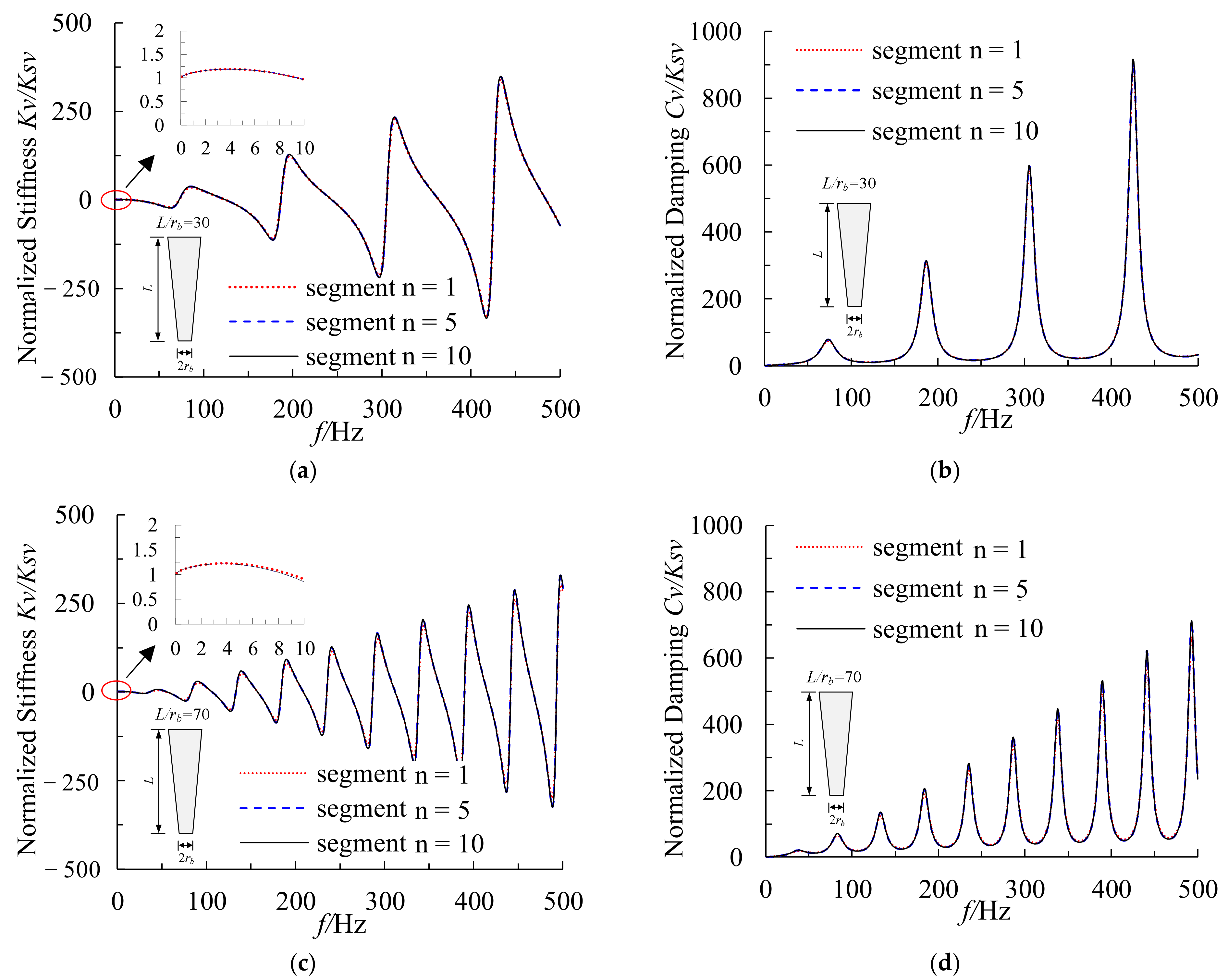
4. Validation and Convergence Studies

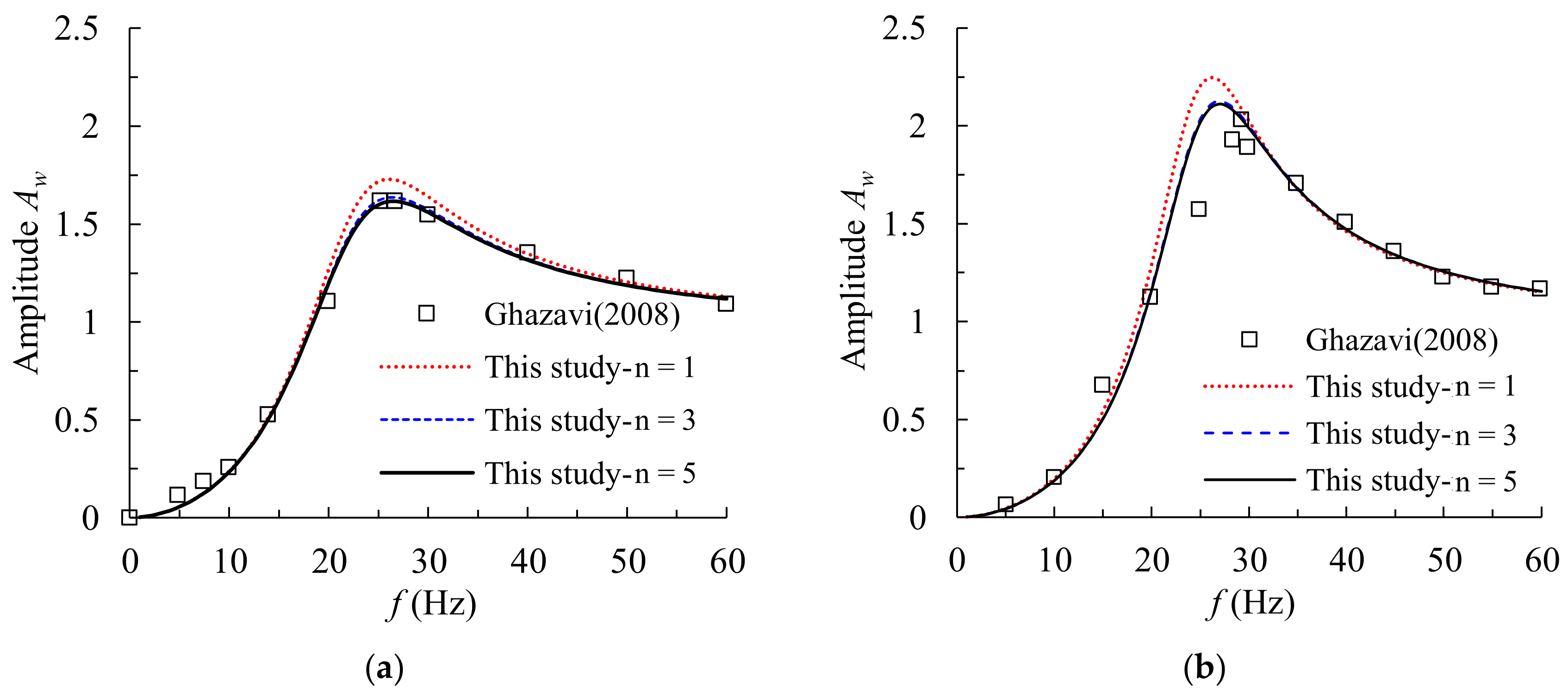
4.1. Validation on Small Taper Angle Solution

With the proposed dynamic Winkler model, the semi-analytical solution of the vertical dynamic impedance of the tapered pile can be obtained by the transfer matrix method. It should be noted that the proposed method does not apply to cylindrical piles. The degeneration to cylindrical pile case is difficult to achieve, if not impossible because the suitable asymptotic expansion of the spherical Bessel function of the first and second kinds can hardly be found as θ goes to 0. To verify the small taper angle result, the vertical dynamic response of the cylindrical pile is approximated by letting θ to be a small value in a heuristic manner. The normalized vertical dynamic impedance of the cylindrical pile based on the proposed method, cylindrical pile analytical solution [42], and boundary element numerical solution [27] are compared in Figure 4. The pile slenderness ratio L/d is 15, where d is pile diameter. The ratio between the pile elastic modulus and soil elastic modulus Ep/Es is 1000, and the soil-to-pile mass density ratio ρ_s/ρ_p is 0.7. The soil damping ratio β is 5%. The comparison shows that the proposed method agrees well with the solutions for cylindrical piles.

4.2. Validation on Medium Taper Angle Solution

The proposed semi-analytical model for vertical dynamics of the tapered pile with a medium taper angle is validated by comparing its predictions with the FEM results [20]. The tapered pile is embedded in homogeneous soil and is subjected to a vertical harmonic load with varying frequencies from 0 to 60 Hz. The properties of tapered pile and soil considered in the analysis are listed in

Table 1. Properties of the tapered pile and soil.

	Material Property	Value
Pile	Equivalent radius req	0.1 m
	Pile length L	5 m
	Taper angle θ	1.5°
	Elastic modulus Ep	20 GPa
	Density ρp	2400 kg/m3
Soil	Elastic modulus Es	30.6 MPa
	Density ρs	1800 kg/m3
	Shear wave velocity Vs	82.5m/s
	Poisson’s ratio νs	0.25

.

The equivalent radius r_eq is defined as the radius of cylindrical pile of the same volume and length as the tapered pile:

$$r_{eq}^2=\frac{1}{3}\left(r_0^2+r_0{r}_b+r_b^2\right)$$

(26)

where r₀ and r_b are the radii of the head and tip of the pile, respectively.

Both floating and end bearing tapered piles are investigated by adjusting the soil properties at the pile tip. The shear wave velocities of the soil at the pile tip are set to 82.5 m/s and 82,500 m/s for the floating and end bearing conditions, respectively. A mass block of 5000 kg is applied at the pile head, and the dimensionless dynamic displacement amplitude of the tapered pile is calculated by the dynamic impedance as

$$A_w=\frac{{\omega }^2}{\sqrt{{\left(\frac{K_v}{M}-{\omega }^2\right)}^2+{\left(\frac{\omega C_v}{M}\right)}^2}}$$

(27)

where K_v and C_v are the vertical dynamic stiffness and damping of the tapered pile, M is the pile head mass, and ω is the circular frequency.

Figure 5 illustrates the dimensionless displacement amplitude A_w at the top of the tapered pile as a function of the excitation frequency based on the proposed approach and the finite element analysis. Noting that the complex stiffness and damping coefficients are evaluated at the middle of each pile segment, the accuracy of the transfer matrix method would depend on the number of segments for the pile and surrounding soil. Therefore, the sensitivity of the solution to the segment size is also investigated. Figure 5 demonstrates the good agreement between the calculated dimensionless amplitudes from both the proposed method and the finite element analysis for both floating and end bearing tapered piles. Figure 5 also shows that the accuracy increases with the increase of the number of pile segments n; even with a limited number of segments, the difference between the two sets of results is still insignificant.

5. Results and Discussion

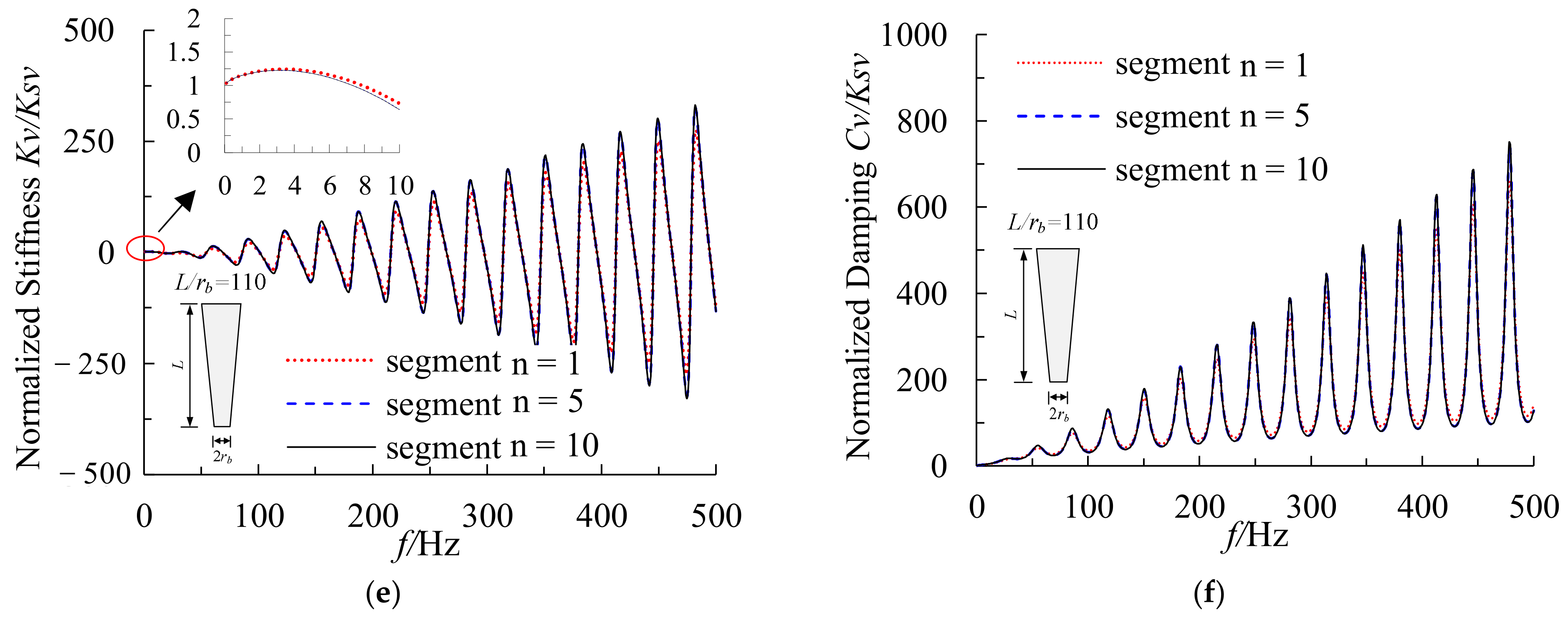
5.1. Effect of Pile Slenderness Ratio

The pile slenderness ratio is a decisive factor in determining the number of pile segments. In the following analysis, the pile tip radius r_b = 0.5 m is used along with slenderness ratios L/r_b = 30, 70, and 110, which covers the common range of pile slenderness ratios in engineering practice. To illuminate the effect of the tapered pile parameters on its dynamic characteristics, the soil surrounding the pile is assumed to be homogeneous with elastic modulus and mass density of 30 MPa and 1600 kg/m³, respectively. The same physical parameters used in Kaynia [42] are adopted in the analysis: the pile-to-soil elastic modulus ratio Ep/Es = 1000, soil-to-pile mass density ρ_s/ρ_p = 0.7, and soil damping ratio β = 5%, taper angle θ = 1°. Figure 6 displays the variation of calculated normalized vertical stiffness K_v and damping C_vin Equation (25) with loading frequency. In Figure 6, K_sv is the static stiffness of the tapered pile. To better employ tapered piles for improving the performance of high-speed railway subgrades, the range of frequency of ground-borne vibration from 20 to 300 Hz is of concern [43]. Therefore, the dynamic response of the tapered pile is calculated within that frequency range (0–400 Hz).

A clear oscillatory characteristic for both the stiffness and damping of the tapered pile is observed in Figure 6, and the oscillation is more obvious as the pile length increases. This phenomenon is the same as the longitudinal vibration response of the cylindrical rod [44]. Hence, the results from the proposed approach can be compared to the natural frequencies of the longitudinal vibration of a fixed-free cylindrical rod given by Thomson [44] as

$$f_i=\frac{2i-1}{4L_r}\sqrt{\frac{E_r}{{\rho }_r}},\begin{array}{c}\end{array}i=1,2,3\cdots$$

(28)

where f_i is the i-th natural frequency of the fixed-free rod, L_r is the length of the rod, E_r is the elastic modulus of the rod, and ρ_r is the density of the rod. Equation (28) clearly shows that the natural frequencies of the rod are closely related to its length.

For a pile with a slenderness ratio L/r_b of 30, the 0–400 Hz frequency range covers three natural frequencies of the cylindrical rod according to Equation (28), which is equal to the number of oscillation periods of the tapered pile in Figure 6a. The number of oscillation periods in the 0–400 Hz frequency range for the slenderness ratio L/r_b = 70 and 110 is about 2.3 and 3.7 times the number of natural frequencies for L/r_b = 30. Figure 6 also shows that only 10 segments are sufficient to produce accurate results for piles with different slenderness ratios, while the alternative analysis procedure that uses a stepping structure requires more than 100 pile segments for accurate results [26,45].

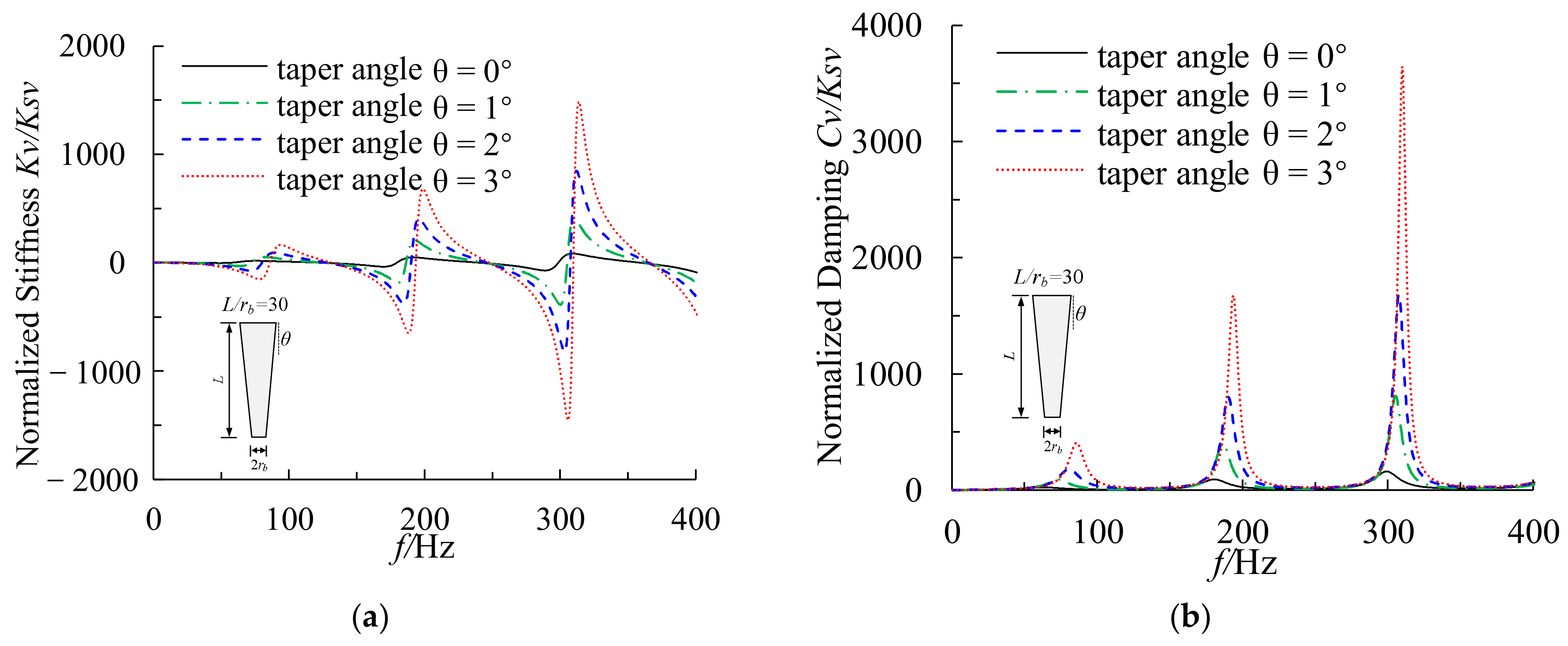
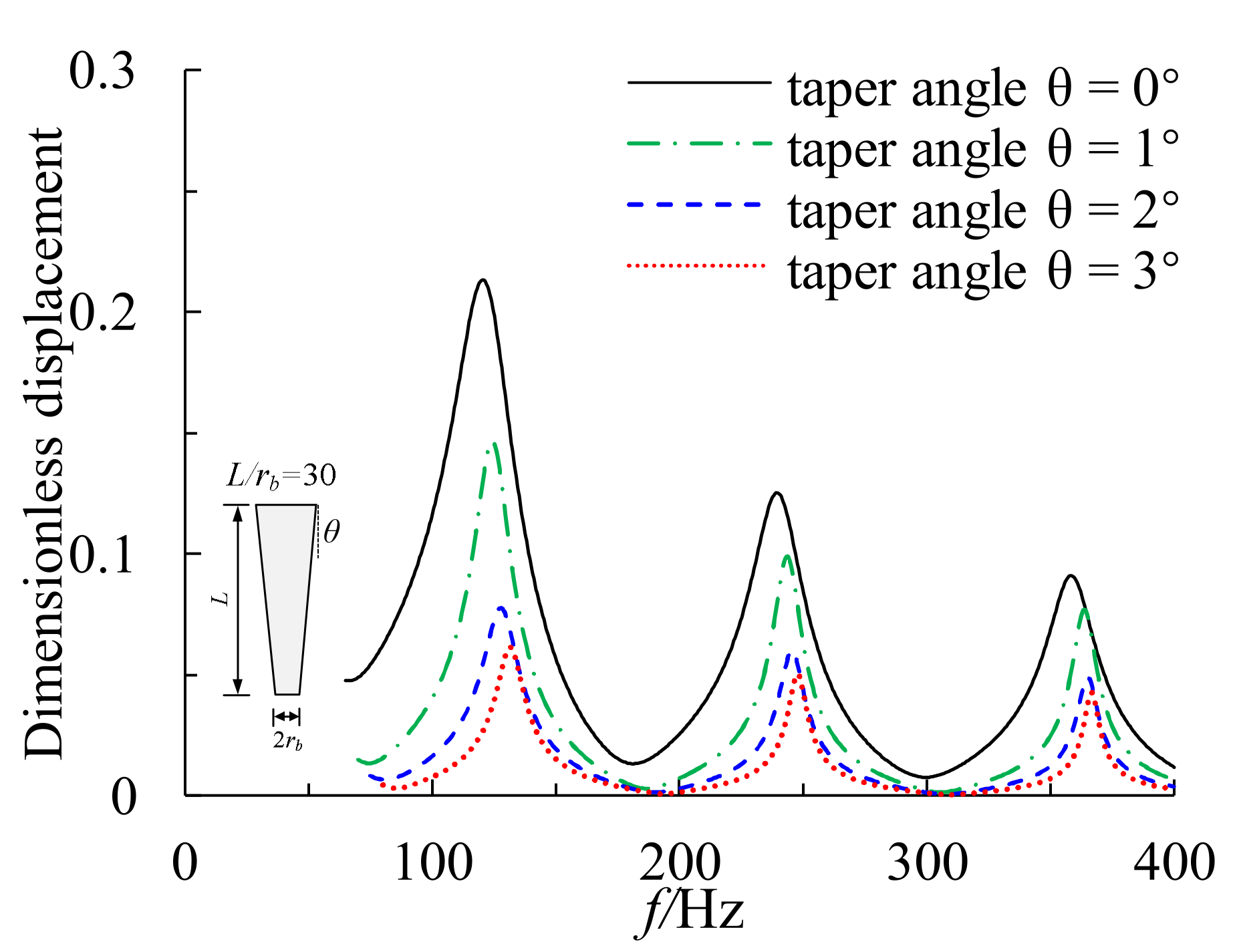
5.2. Effect of Taper Angle

The vertical dynamic response of the tapered pile is also significantly influenced by the taper angle [45,46]. In engineering practice, the taper angle is usually less than 5° for construction convenience. To illustrate the taper angle effect on the dynamic characteristics of tapered piles, four different taper angles θ = 0°, 1°, 2°, and 3° are considered in this section. The pile slenderness ratio L/r_b = 30 is used in this analysis, and K_sv is the tapered pile static stiffness for slenderness ratio L/r_b = 30 and taper angle θ = 1°. Other parameters, such as pile length and pile tip diameter, are chosen to be the same as in Section 5.1.

Figure 7 presents the vertical dynamic impedance of the tapered pile for the different taper angles. Figure 7 shows that the dynamic pile stiffness and damping increase as the taper angle increases, especially for high loading frequency. This observation is consistent with the results of Cai et al. [26]. Comparing the vertical dynamic impedance of the cylindrical pile (i.e., θ = 0°) and tapered pile with taper angle θ = 3°, the stiffness and damping increase about 15 times and 20 times, respectively, at f = 300 Hz, which indicates the potentially significant vibration isolation performance of the tapered pile near the loading frequency 300 Hz compared to the cylindrical pile. This large increase is attributed to two reasons. First, for a tapered pile with the same pile length and pile tip diameter, the diameter of the pile at the same depth increases as the taper angle increases (larger average diameter and pile volume). Second, the shear force p_t and normal force p_n along the pile shaft under unit displacement increase as the taper angle increases.

The natural foundation frequency is a main concern in engineering practice as resonance can increase the dynamic response significantly. To investigate the resonant frequency of the tapered pile, the dimensionless vertical dynamic displacement responses of piles with different taper angles are presented in Figure 8. The vertical dynamic displacements are normalized by the static vertical displacement of the cylindrical pile (i.e., θ = 0°) with the same pile volume. Figure 8 reveals that the vertical displacement response of the tapered pile is significantly reduced as the taper angle increases. Figure 8 also shows that the resonant frequency gradually increases as the taper angle increases. Although the dynamic impedance of the tapered pile increases significantly as the taper angle increase (as shown in Figure 7), the increase in resonant frequency is not remarkable, which is consistent with the effect of the taper angle on the oscillation period of the dynamic impedance of the taper pile. This is because the overall mass involved in the vertical vibration of the tapered pile increases simultaneously with the increase in the taper angle.

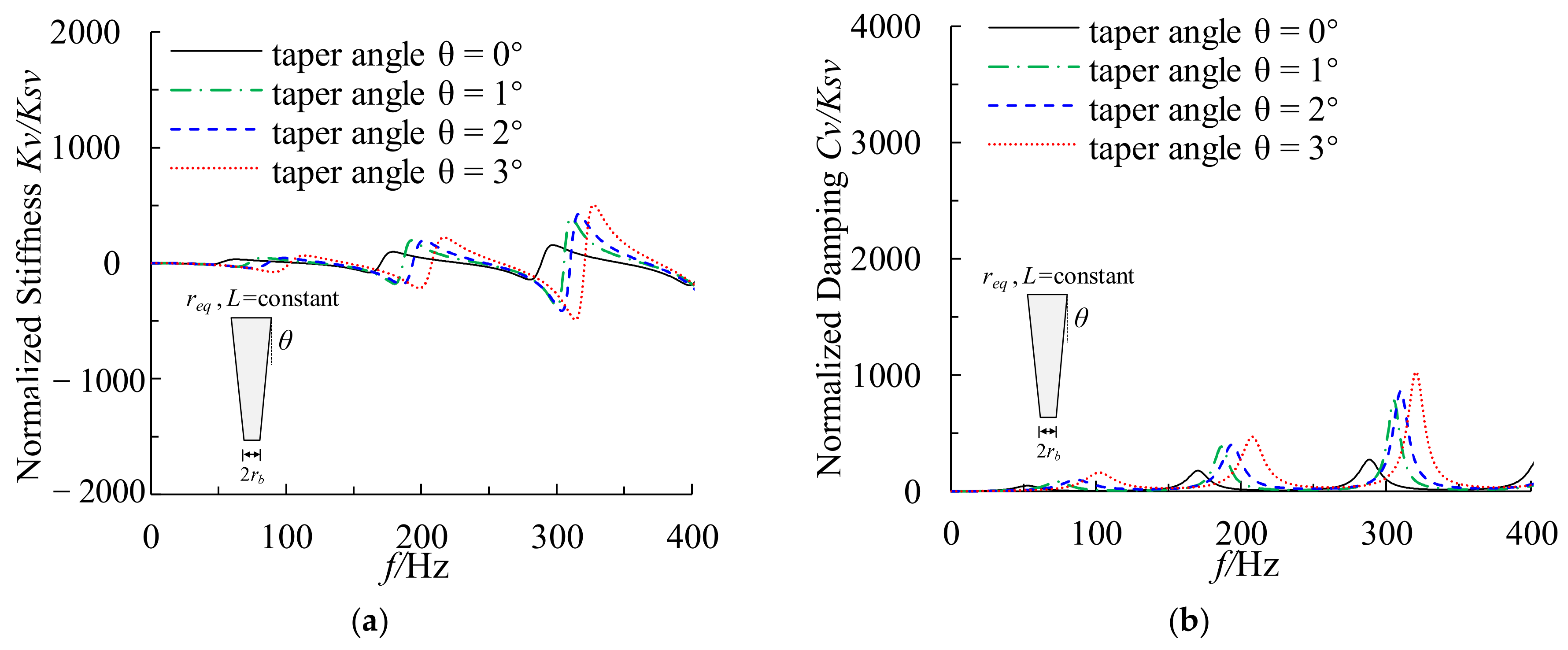
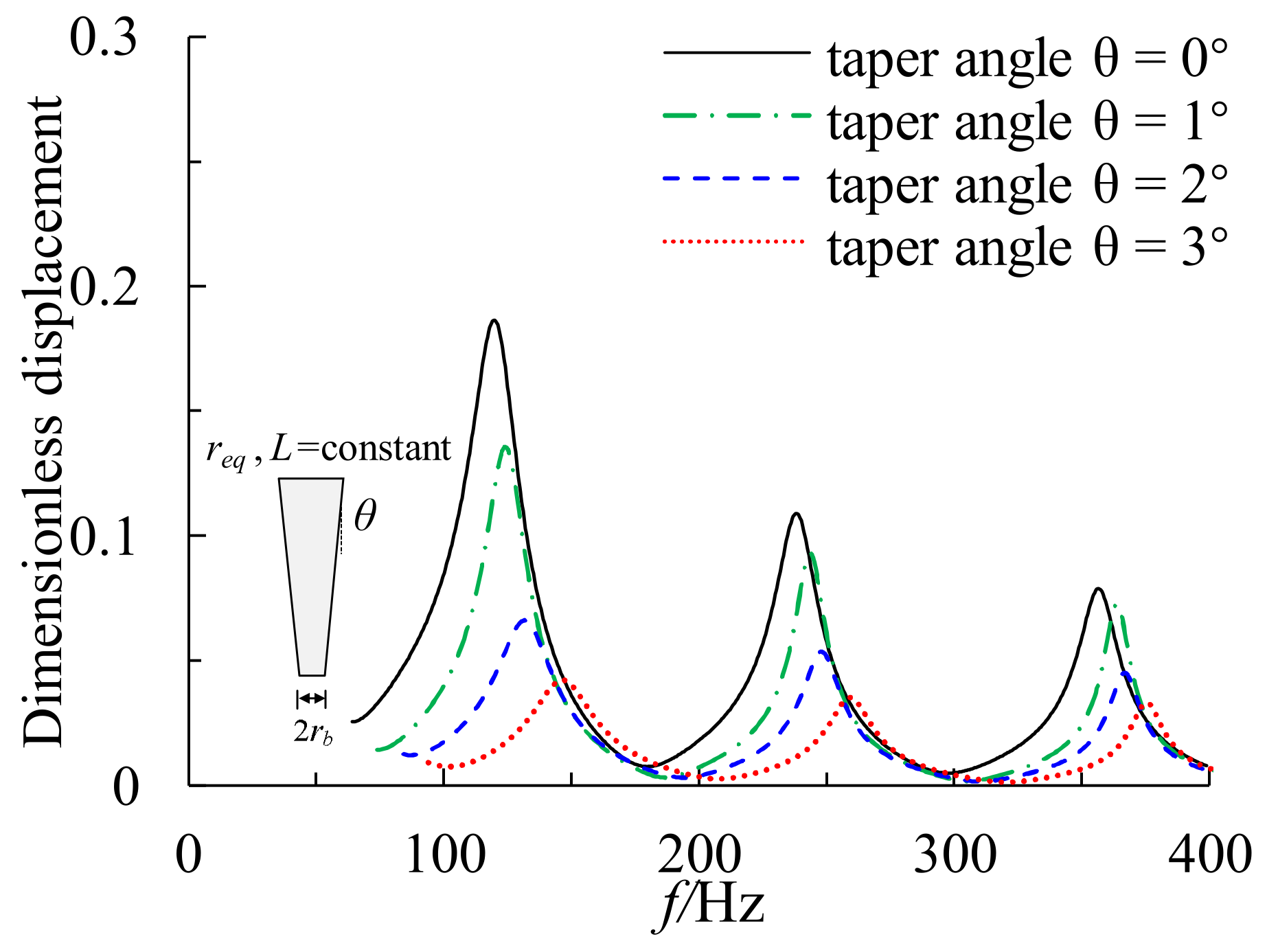
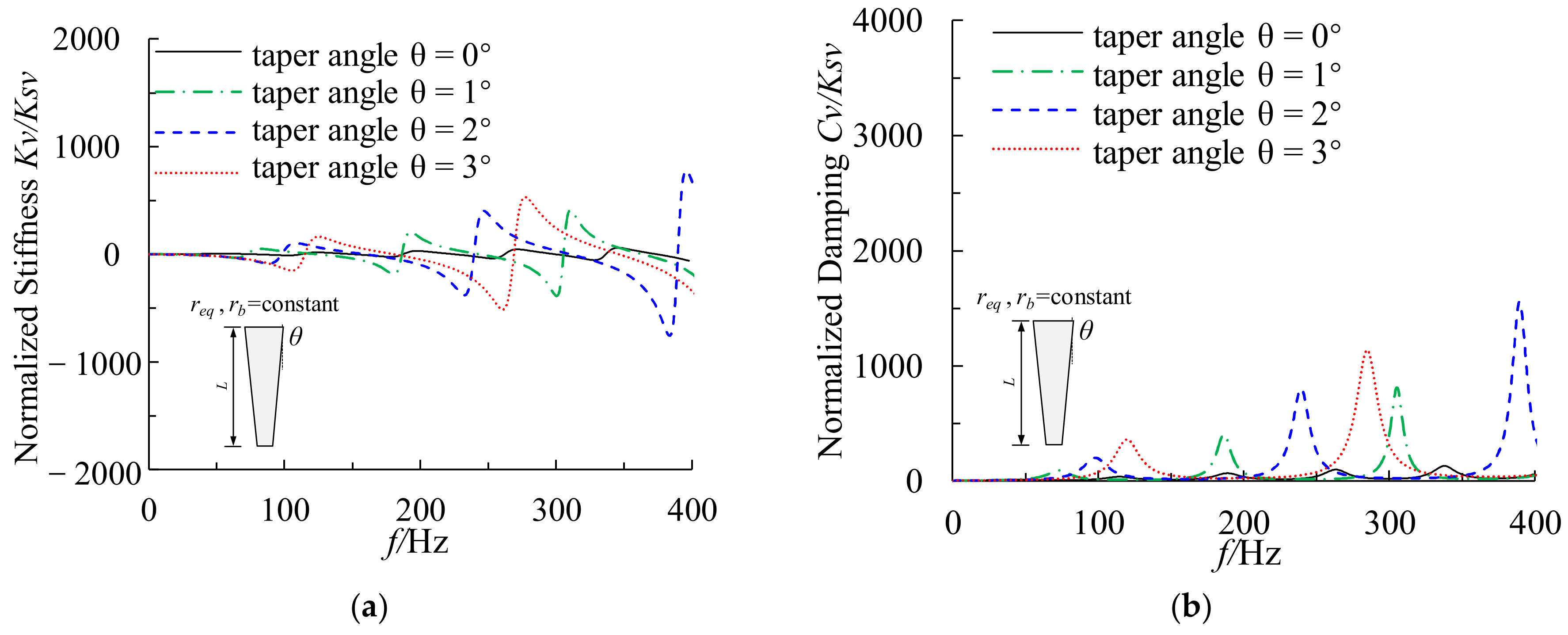
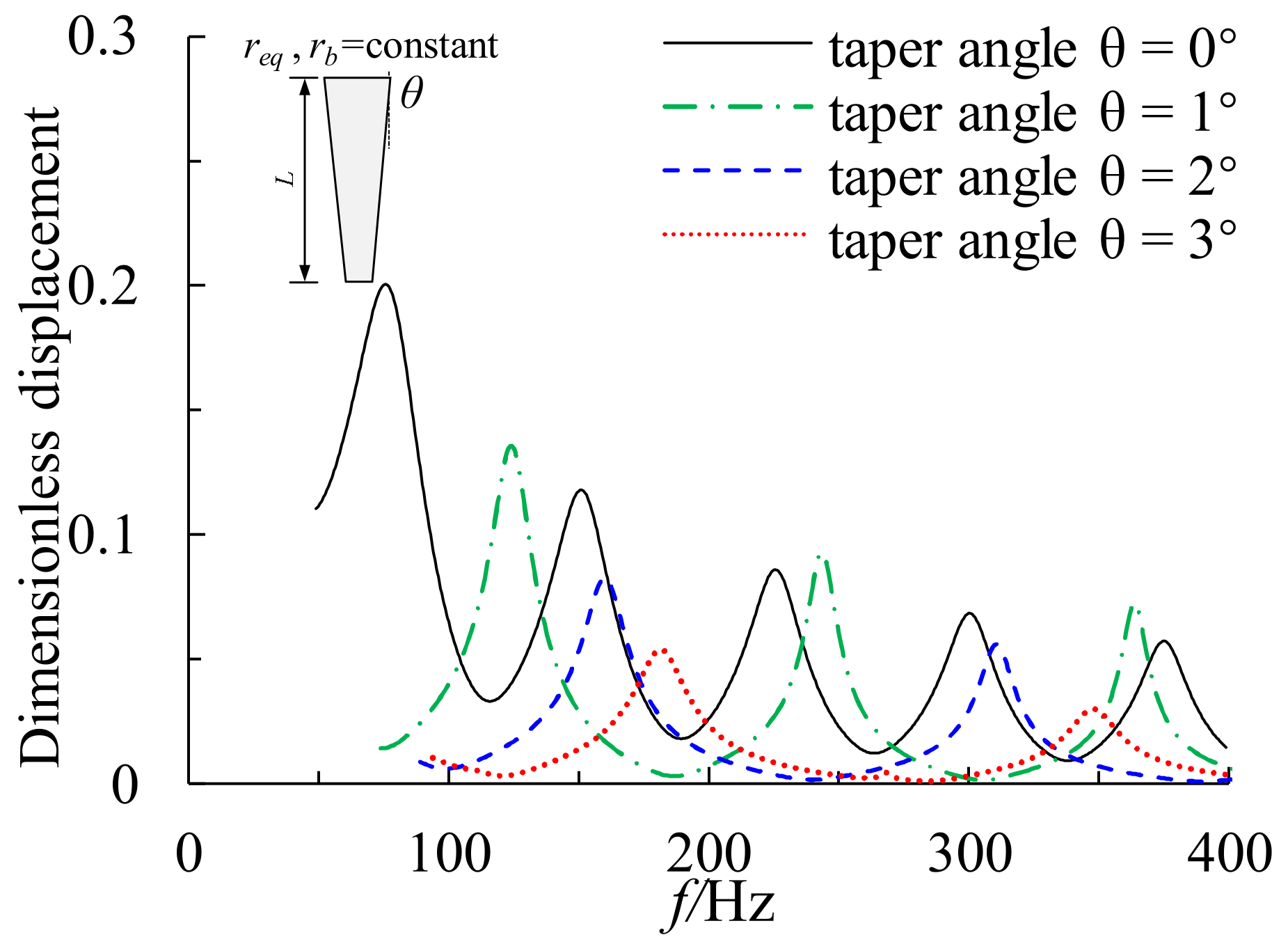
5.3. Discussion on Dynamic Impedance of Constant Volume Tapered Pile

From an economic point of view, the dynamic characteristics of different tapered piles of the same volume (i.e., same material quantity) are of interest. There are two ways to preserve a constant volume of taper pile: varying the pile tip diameter while keeping its length constant or varying the pile length while keeping its tip diameter constant. In the following, the vertical dynamic response of constant volume tapered pile with different pile lengths and pile tip diameters is investigated for a typical slenderness ratio L/r_b = 30. The soil and pile parameters are the same as in Section 5.1 if not specified otherwise.

5.3.1. Varying Pile Tip Diameter with Constant Pile Length

In this section, the dimensions of different piles with taper angles θ = 0°, 1°, 2°, and 3°, are calculated employing Equation (26) considering a constant pile length, and their dynamic impedances are shown in Figure 9. It is evident from Figure 9 that the dynamic stiffness and damping of the different tapered piles are improved compared with the cylindrical pile (i.e., θ = 0°); for example, the increases in peak dynamic stiffness and peak damping are 170% and 200%, respectively, for θ = 1° around f = 300 Hz. However, the increases in peak dynamic stiffness of piles with θ = 2° and 3° are only 10% and 28% to that of the tapered pile with θ = 1°.

Figure 10 displays the dimensionless dynamic response of the tapered pile with constant volume and the same length but different tip diameters. The vertical dynamic displacements are normalized by the static vertical displacement of the cylindrical pile. The results demonstrate that the dynamic response of the tapered pile is significantly lower than that of the cylindrical pile, and the reduction in displacement amplitude is more significant as the taper angle increases, especially in the low-frequency range. Figure 10 also shows that the resonant frequency of the tapered pile increases compared to the cylindrical pile with the same volume. This is because the overall dynamic impedance increases while the mass of the pile foundation remains constant due to the constant volume.

5.3.2. Varying Pile Tip Diameter with a Constant Pile Length

The dimensions of a constant volume tapered pile with constant tip diameter but different lengths are determined using Equation (26). The dynamic impedances of constant volume tapered piles of the same tip diameter, but different pile lengths are shown in Figure 11. Both the vertical dynamic stiffness and damping increase as the taper angle increases. The number of oscillation periods of the dynamic impedance also increases as the taper angle increases, which is the same as in the constant pile length scenario. This is because the pile length decreases as the taper angle increases, and the number of oscillation periods decreases in the concerned frequency range. Figure 12 displays the dimensionless dynamic response of the tapered pile with constant tip diameter but varying length. The results exhibit the same pattern for the case of constant length but varying tip diameter, i.e., the dynamic response decreases as the taper angle increases. However, as the taper angle increases, the increase in resonant frequency is more significant for the constant pile length case than for the constant pile tip diameter case.

The results obtained collectively indicate that the dynamic performance of tapered piles is superior to that of the cylindrical with the same volume at medium- and high-frequency ranges. This is particularly advantageous for the performance requirements of the high-speed railway subgrades. In addition, comparing the results in Figure 10 and Figure 12 demonstrates that considering a constant pile tip diameter strategy yields a better vibration improvement than the constant pile length strategy when choosing the design taper angle for the concerned frequency range. Given that the settlement of a high-speed railway subgrade is usually strictly controlled due to the high velocity of vehicles, lengthening the pile foundation is commonly used as an effective measure to reduce settlement in a high-speed rail subgrade. Therefore, the taper angle should be designed considering a combination of the vibration and settlement requirements to achieve the best performance.

6. Conclusions

This paper proposed a simple method for evaluating the vertical dynamic response of tapered piles based on the dynamic Winkler model and transfer matrix method. The method is easily extended to the dynamic analysis of tapered piles in layered soil. The effects of the pile slenderness ratio and taper angle on its vertical dynamic characteristics are assessed, and the following conclusions can be drawn:

(1)

The proposed method retains high accuracy for calculating the vertical impedance function and dynamic response of tapered piles with different taper angles and slenderness ratios, while reducing the computational time and cost significantly.

(2)

The dynamic stiffness and damping of the tapered pile are significantly improved compared to the cylindrical pile with the same pile length and pile tip diameter, especially in the high-frequency range. In addition, the tapered pile exhibits better vibration performance than a cylindrical pile of the same volume.

(3)

The vertical dynamic impedance of the constant volume and constant length tapered pile increases as the taper angle increases. However, the increases in dynamic stiffness and damping are limited for taper angles larger than 1°. Meanwhile, the resonant amplitude decreases, and the resonant frequency increases for tapered piles with constant volume and length as the taper angle increases.

(4)

The vertical dynamic impedance and its oscillation period of a tapered pile with constant volume and constant tip diameter tapered pile increase significantly as the taper angle increases. The resonant frequency increases and the resonance amplitude decreases significantly as the taper angle increases. In addition, as the taper angle increases, the number of response resonant peaks within the concerned frequency range for high-speed railway subgrades decreases.

(5)

For fixed-volume tapered piles, keeping the tip diameter constant while varying pile length for different taper angles yields better vertical dynamic impedance than varying the tip diameter and keeping the pile length constant. However, the selected tapered pile length should also satisfy the subgrade settlement requirements. Since the method can be easily implemented, it presents an attractive and efficient tool to analyze and design tapered piles subjected to dynamic loading.