Stability Analysis of the Foundation Pit and the Twin Shield Tunnels during Adjacent Construction
Abstract
:1. Introduction
2. Problem Statement
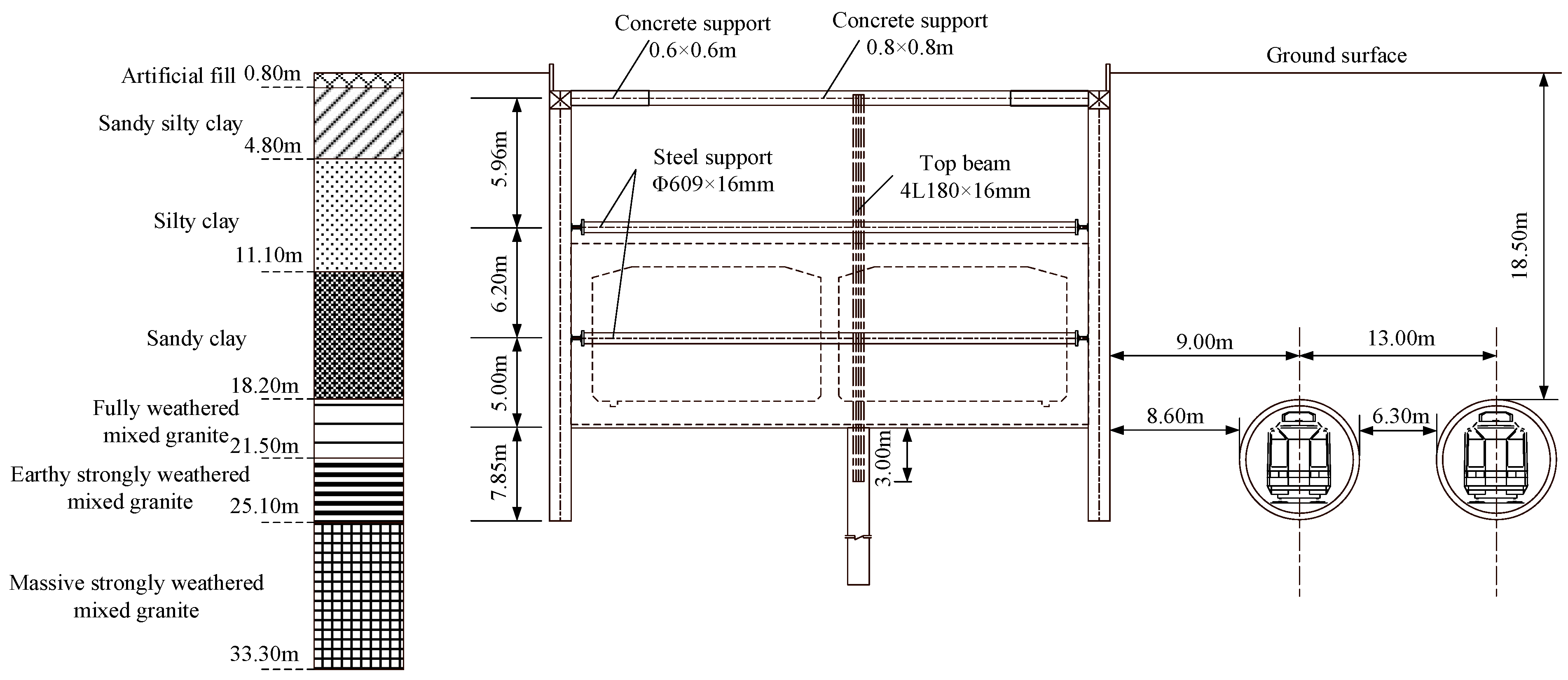
2.1. Engineering Background
2.2. Finite Element Limit Analysis
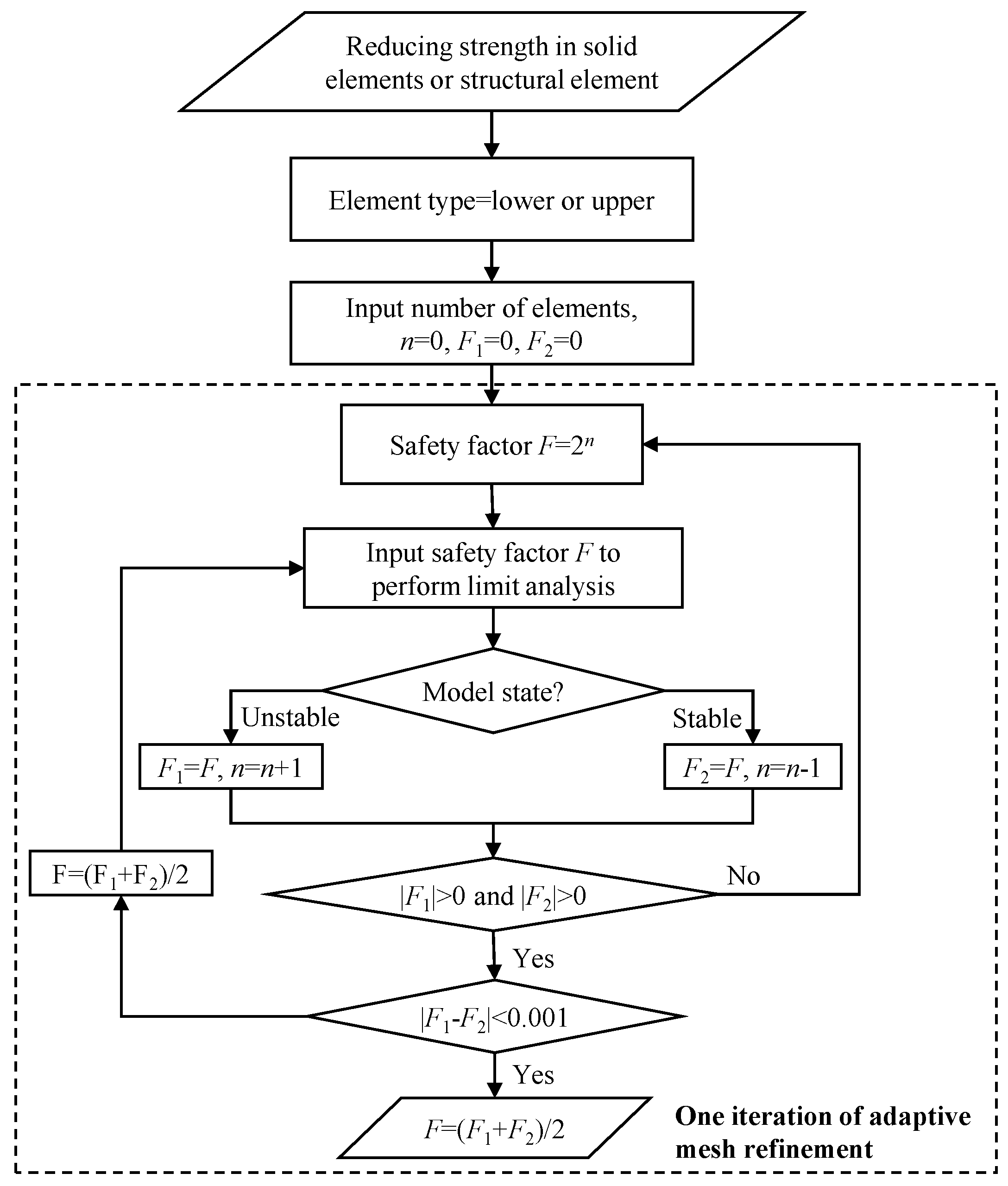
2.3. Strength Reduction Analysis
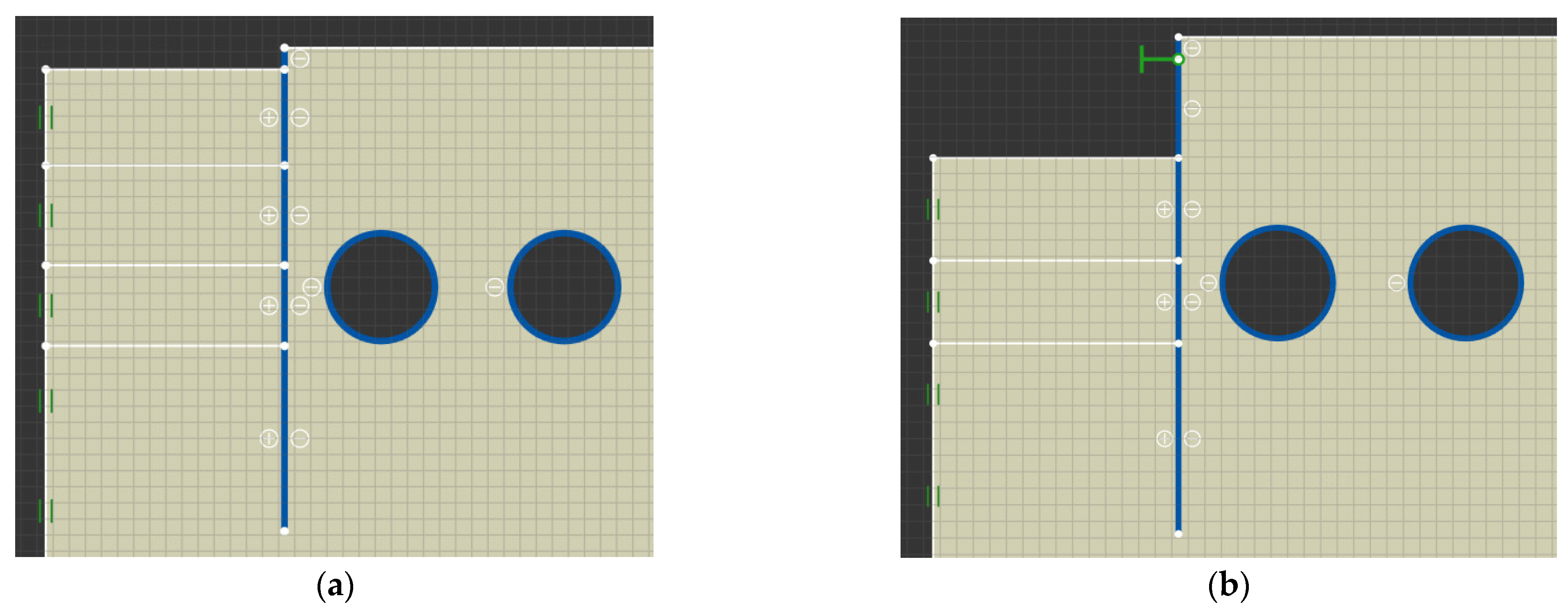
2.4. Numerical Model
3. Stability Analysis of the Adjacent Construction of Foundation Pit and Twin Shield Tunnels
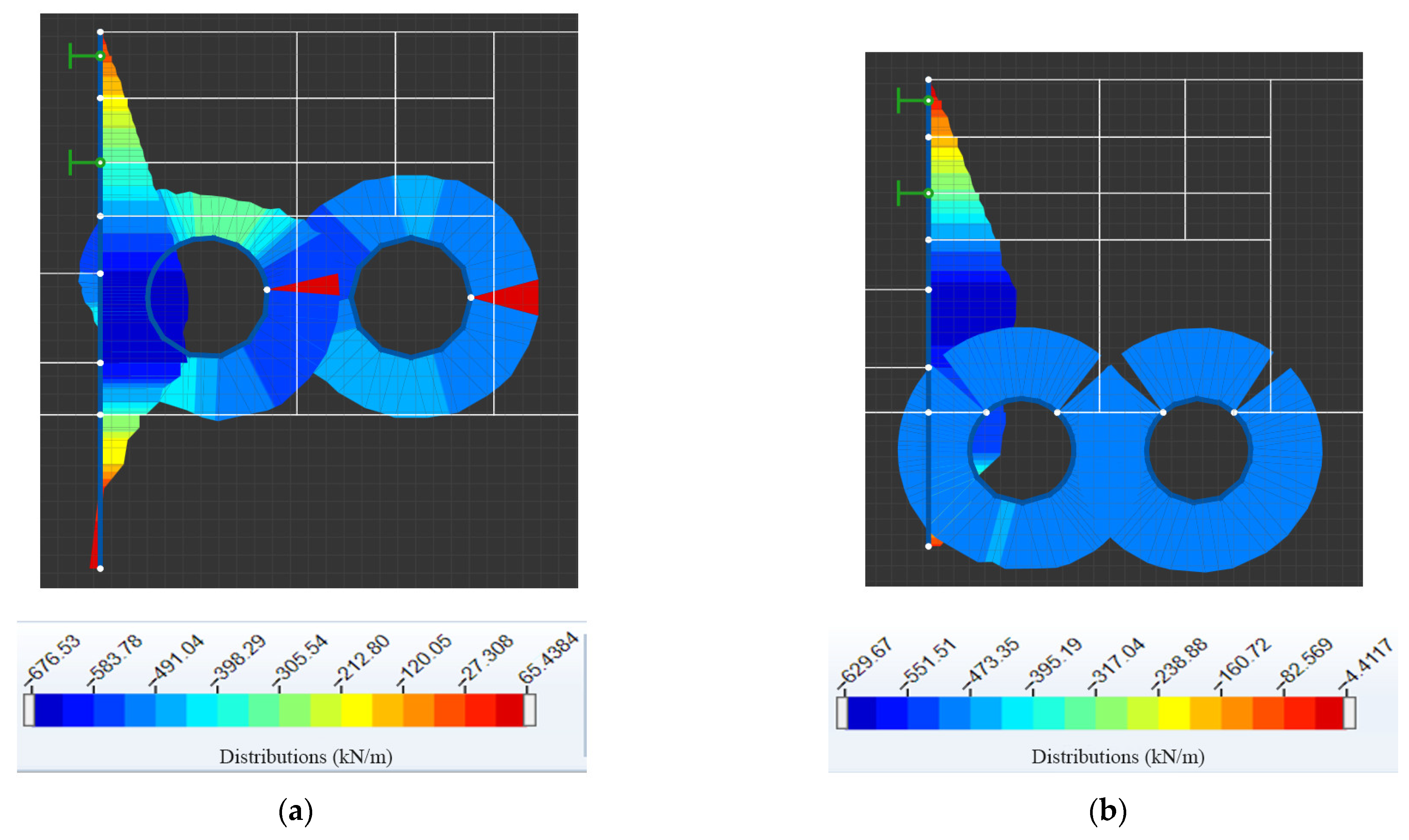
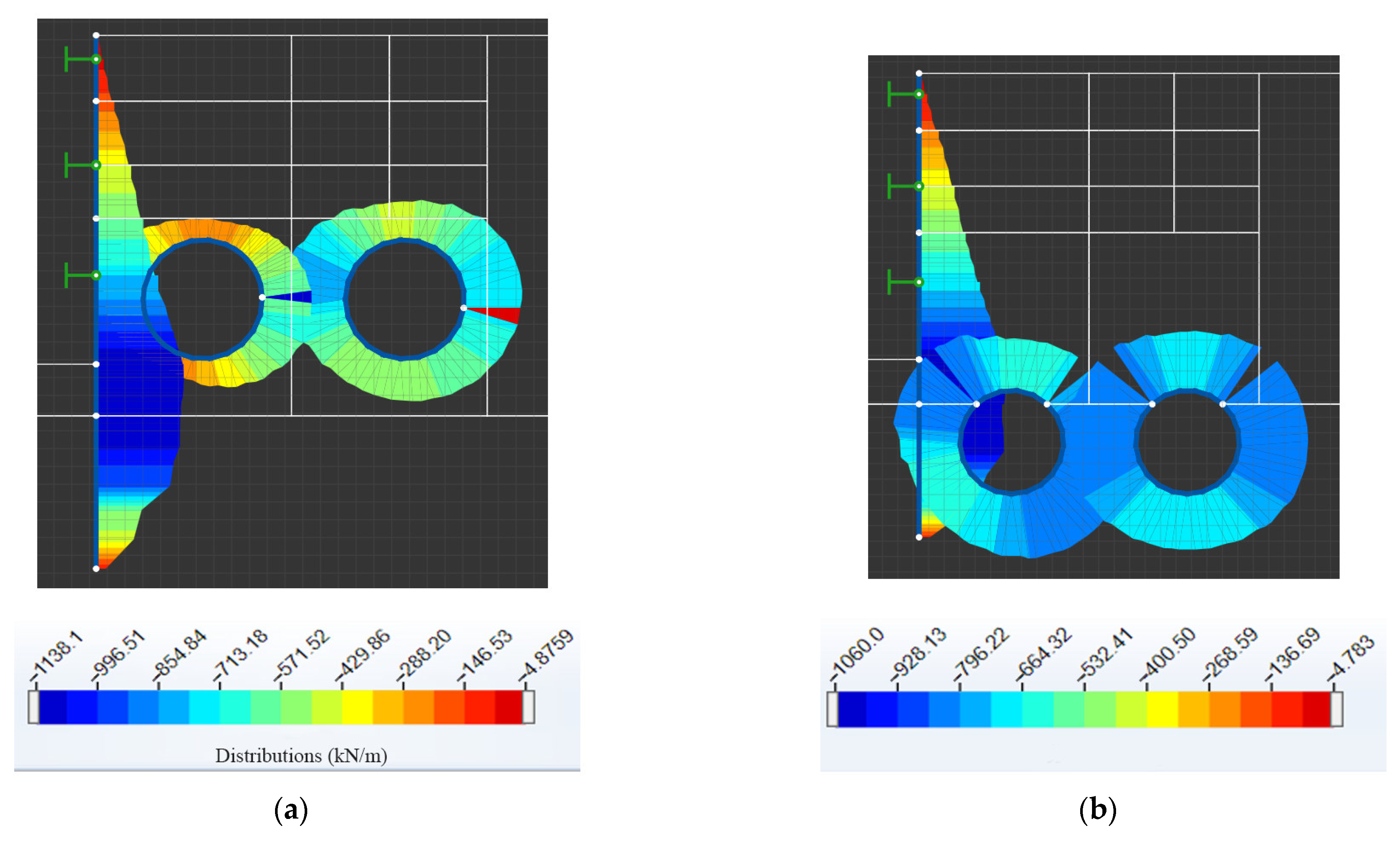
3.1. Interaction between Twin Tunnels Structure and Foundation Pit Structure
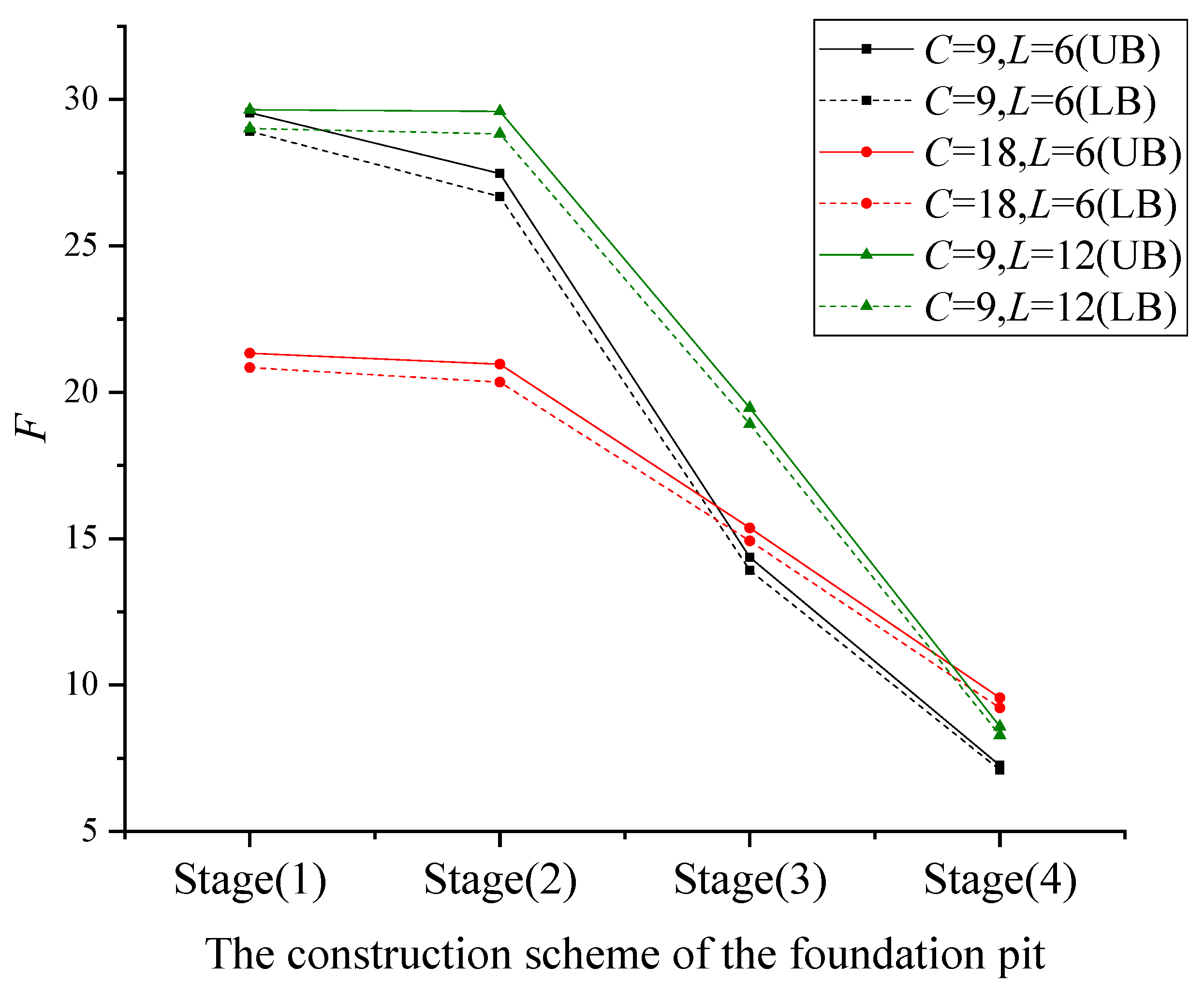
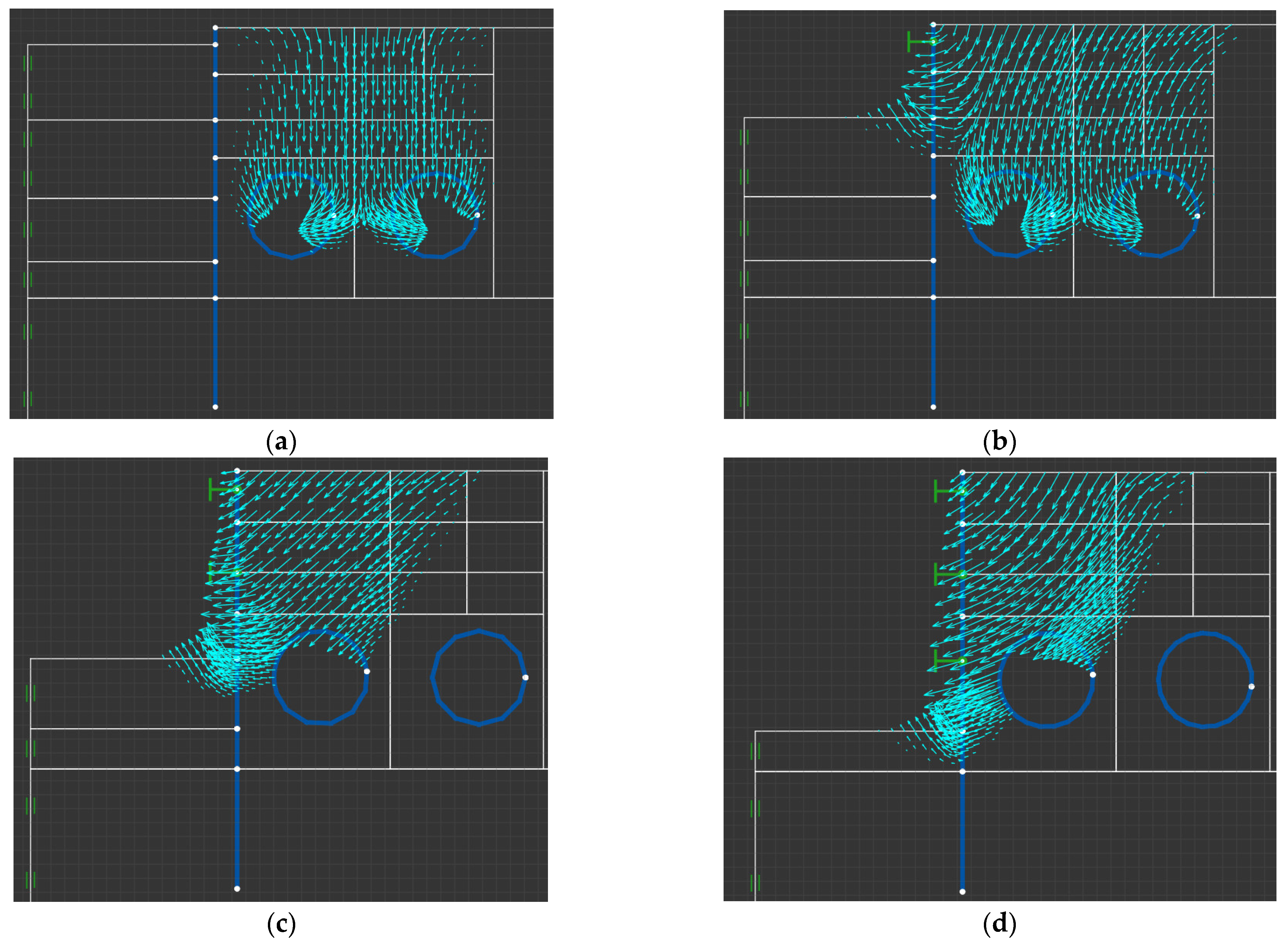
3.1.1. Influence of the Construction Scheme of the Foundation Pit
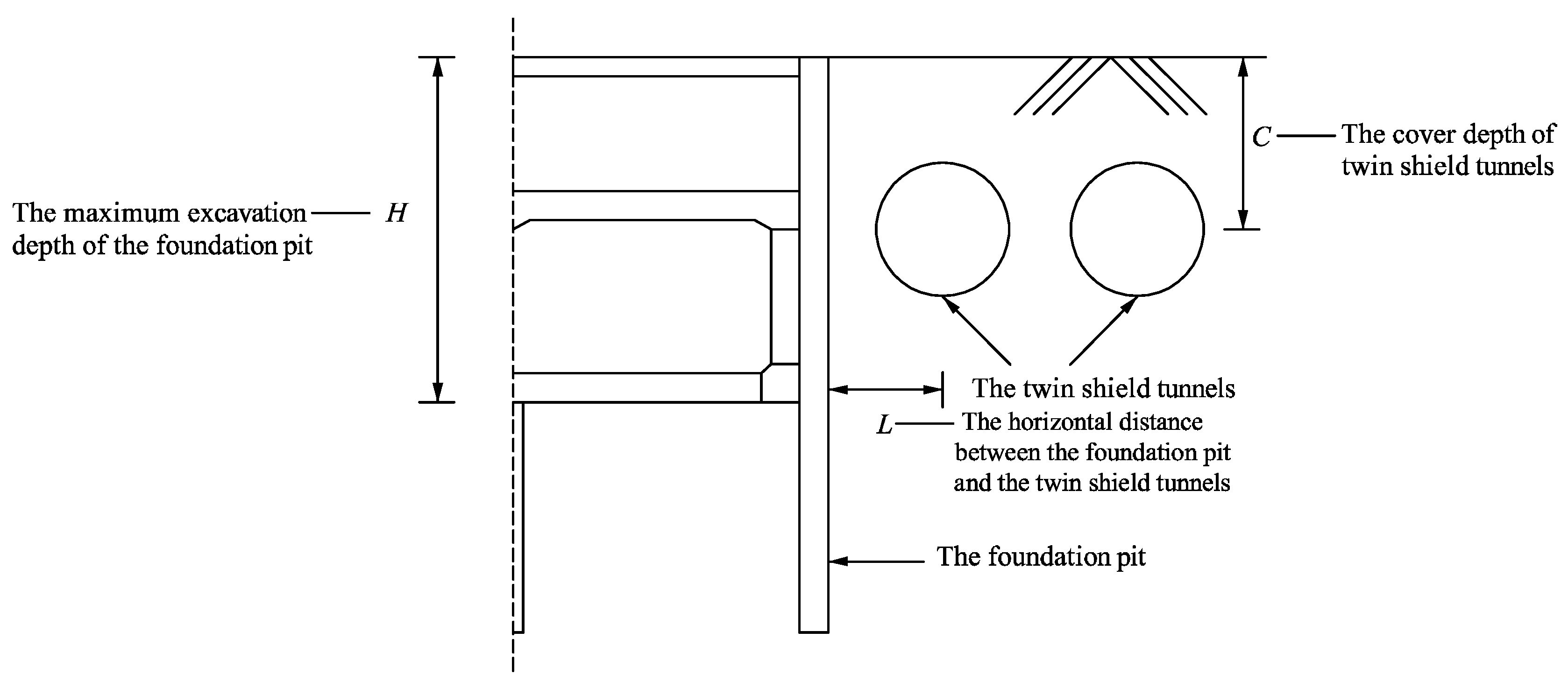
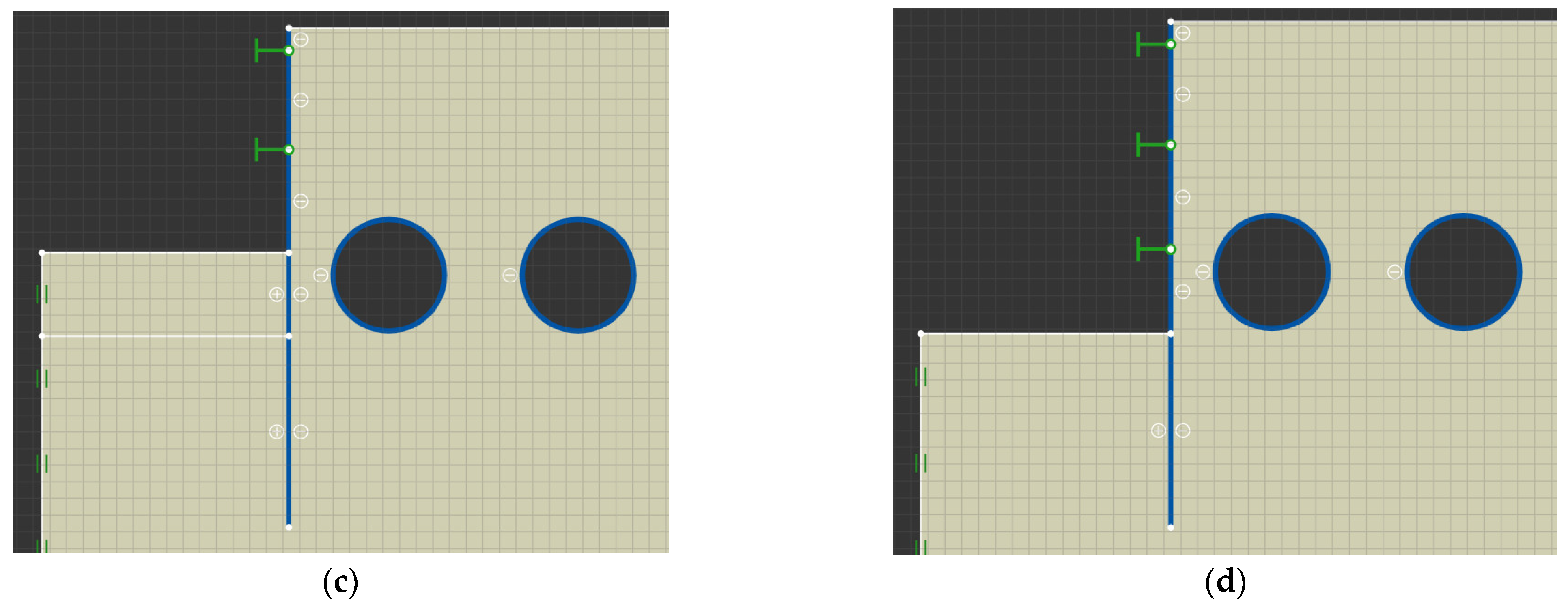
3.1.2. Influence of Relative Position between Twin Tunnels and Foundation Pit
Influence of Horizontal Distance L on Global Stability
Influence of Cover Depth C of Twin Shield Tunnels on the Global Stability
3.2. Stability Analysis of the Foundation Pit
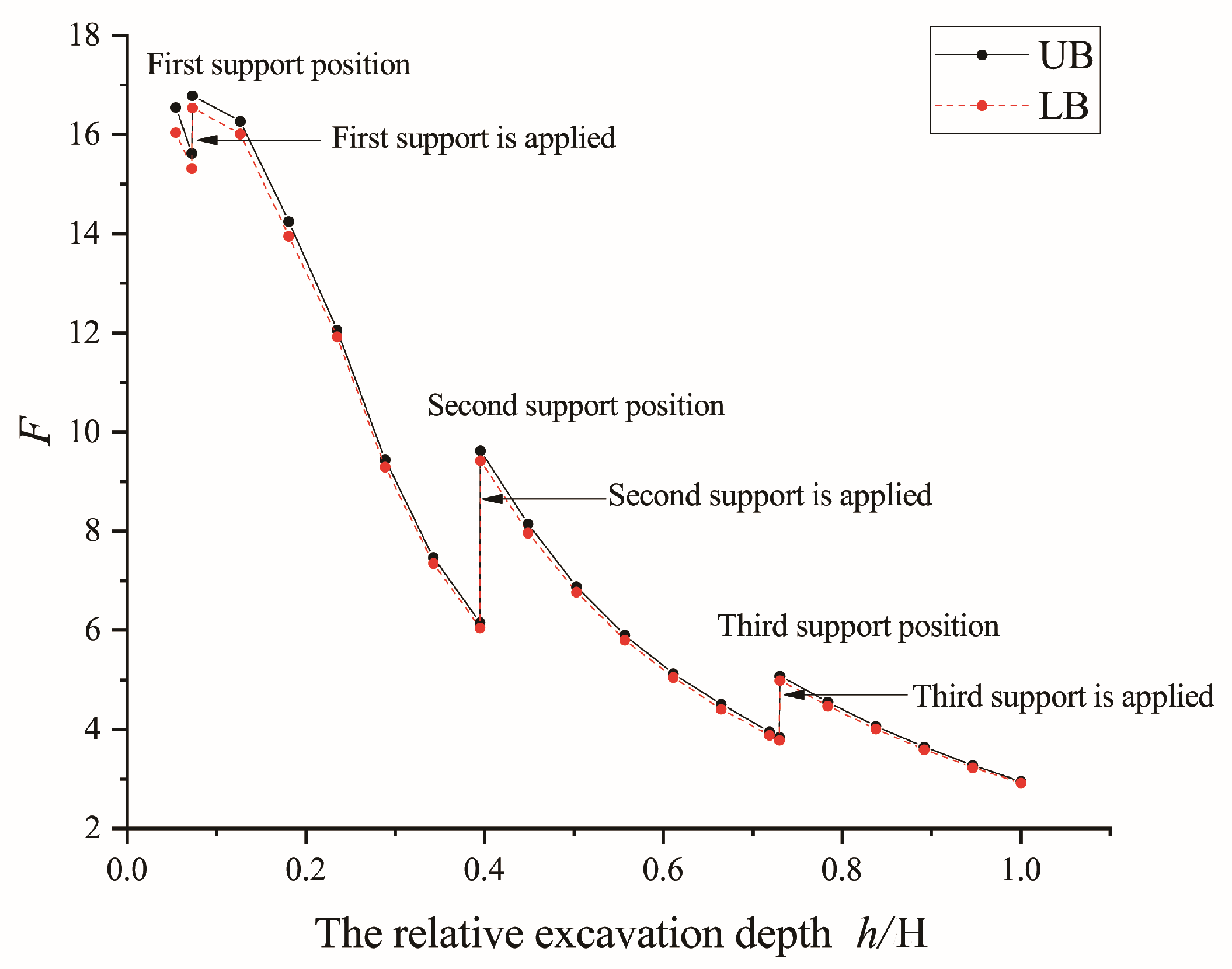
3.2.1. Safety Factor of Foundation Pit
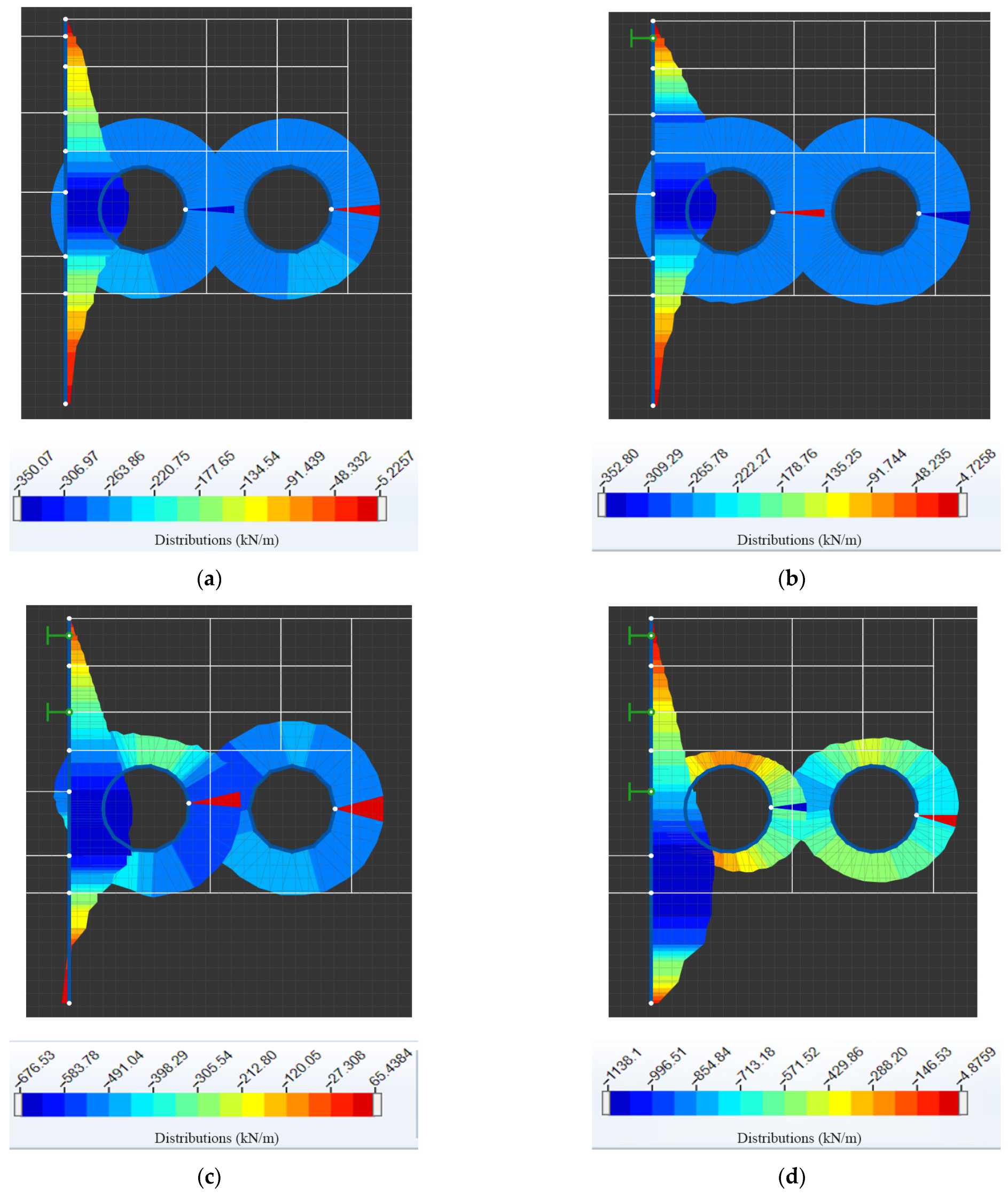
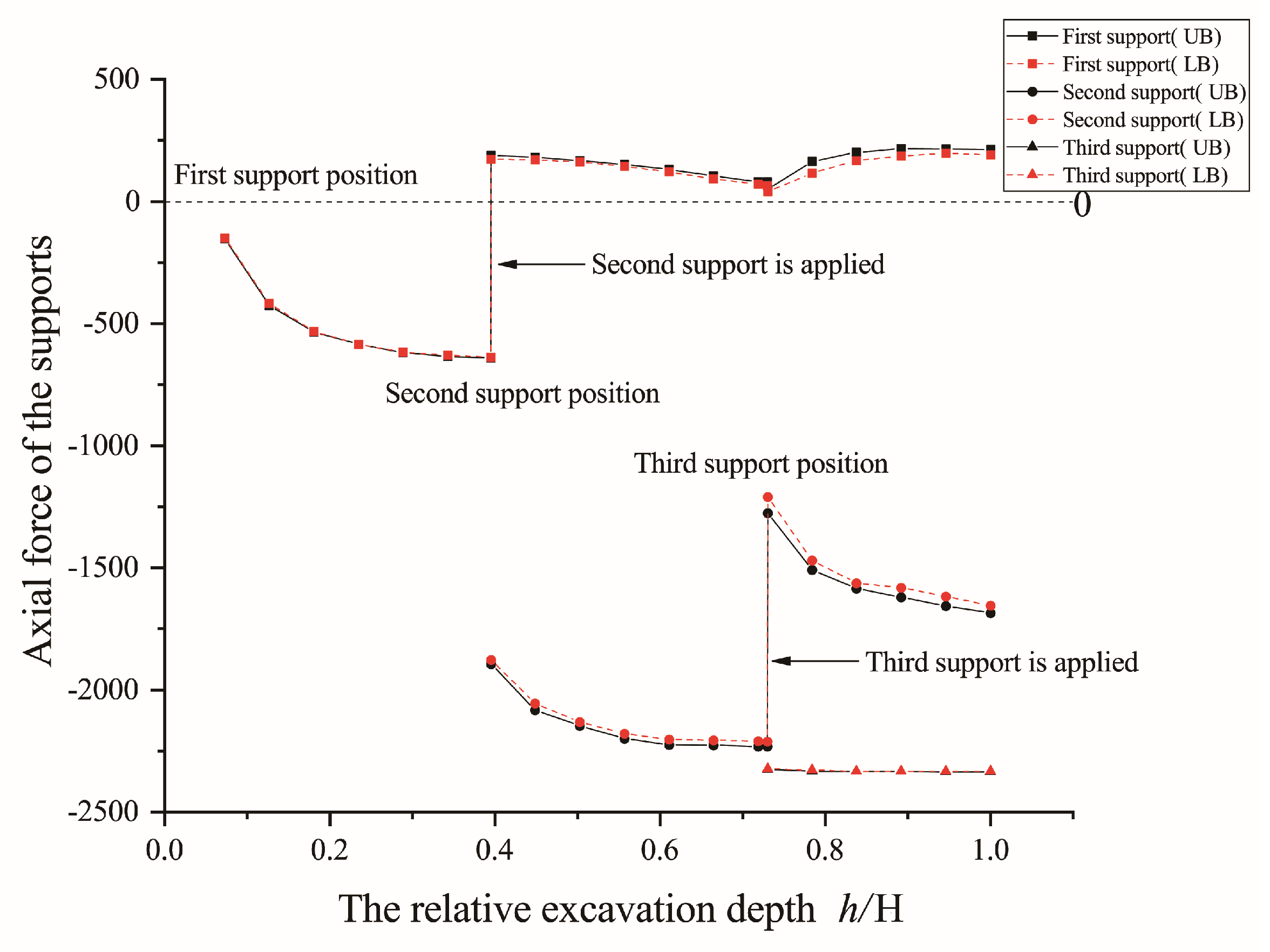
3.2.2. Axial Force of the Supports of the Foundation Pit
4. Adjacent Influential Partition
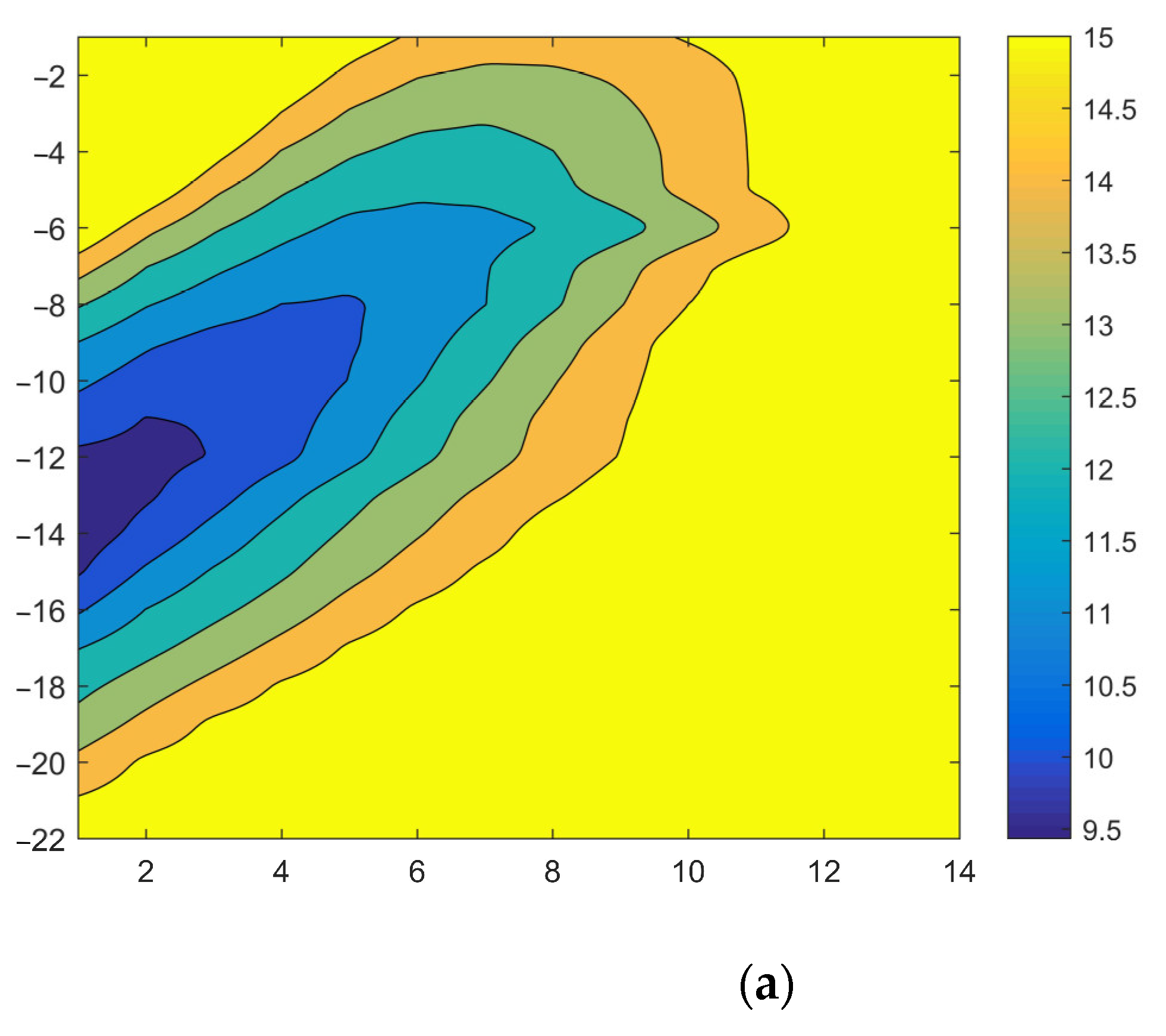
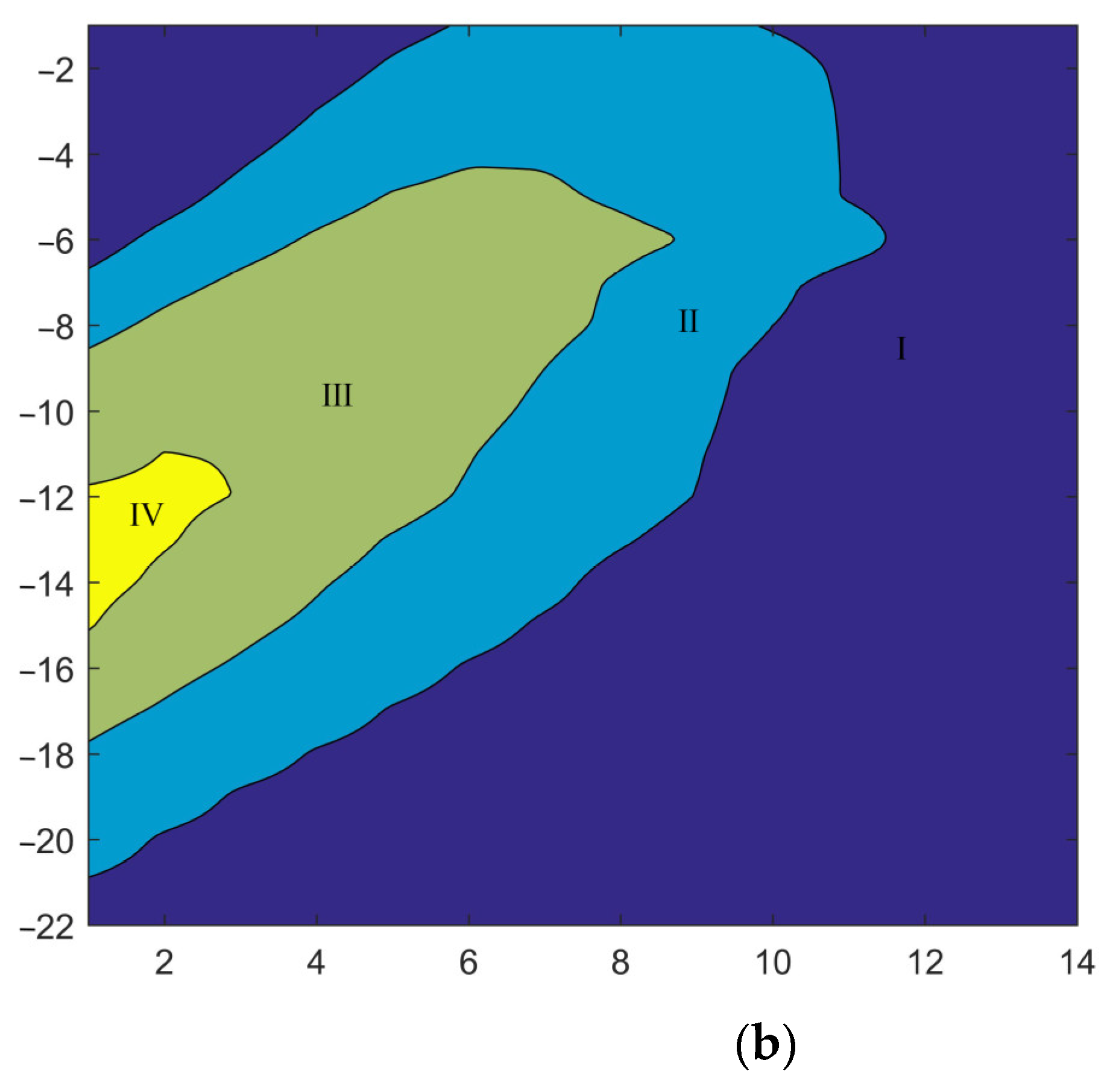
4.1. Adjacent Influential Partition Based on Safety Factor
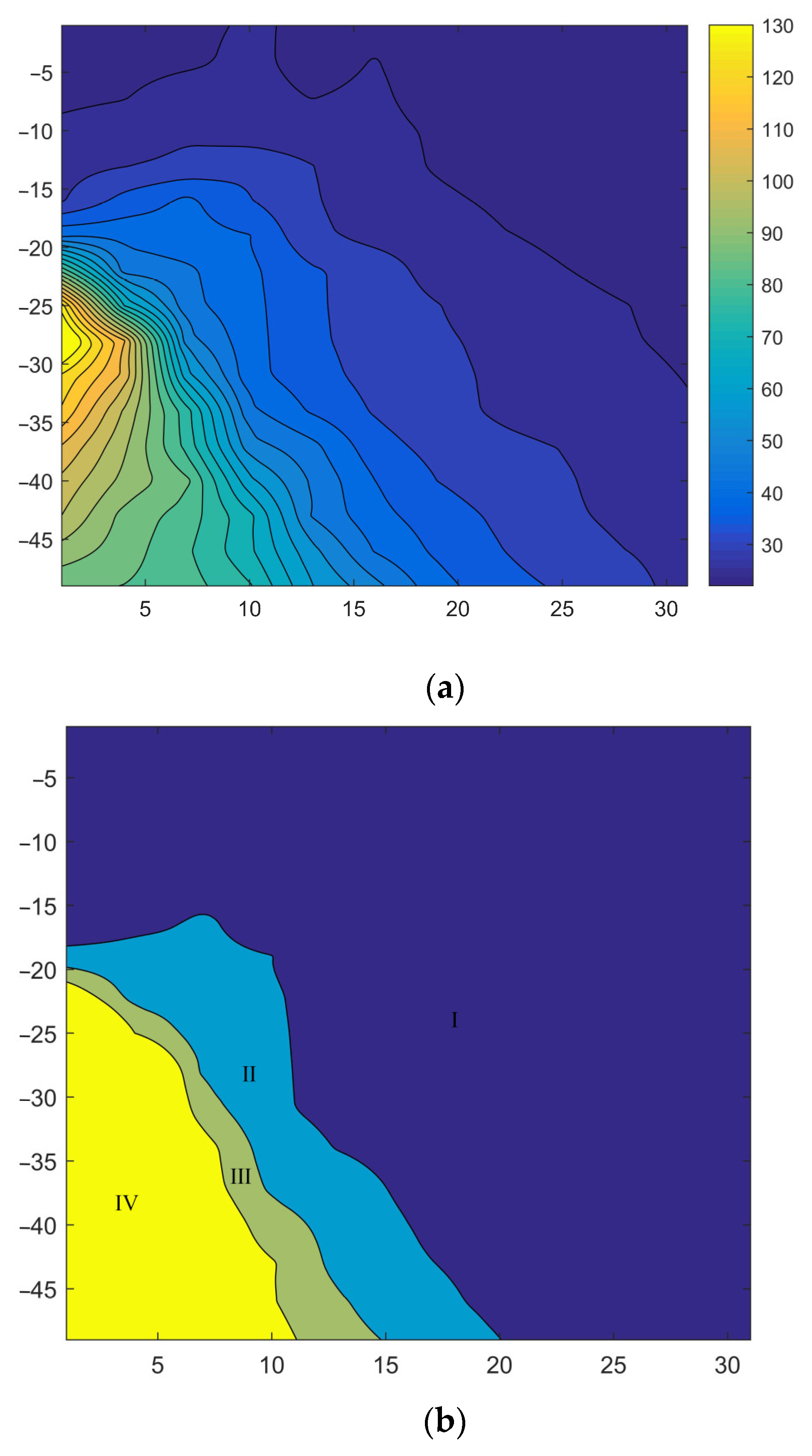
4.2. Adjacent Influential Partition Based on Displacement Data
4.3. Safety Risk Analysis of Adjacent Construction of Twin Tunnels and Foundation Pit
5. Design Equation for Safety Factor of Adjacent Construction
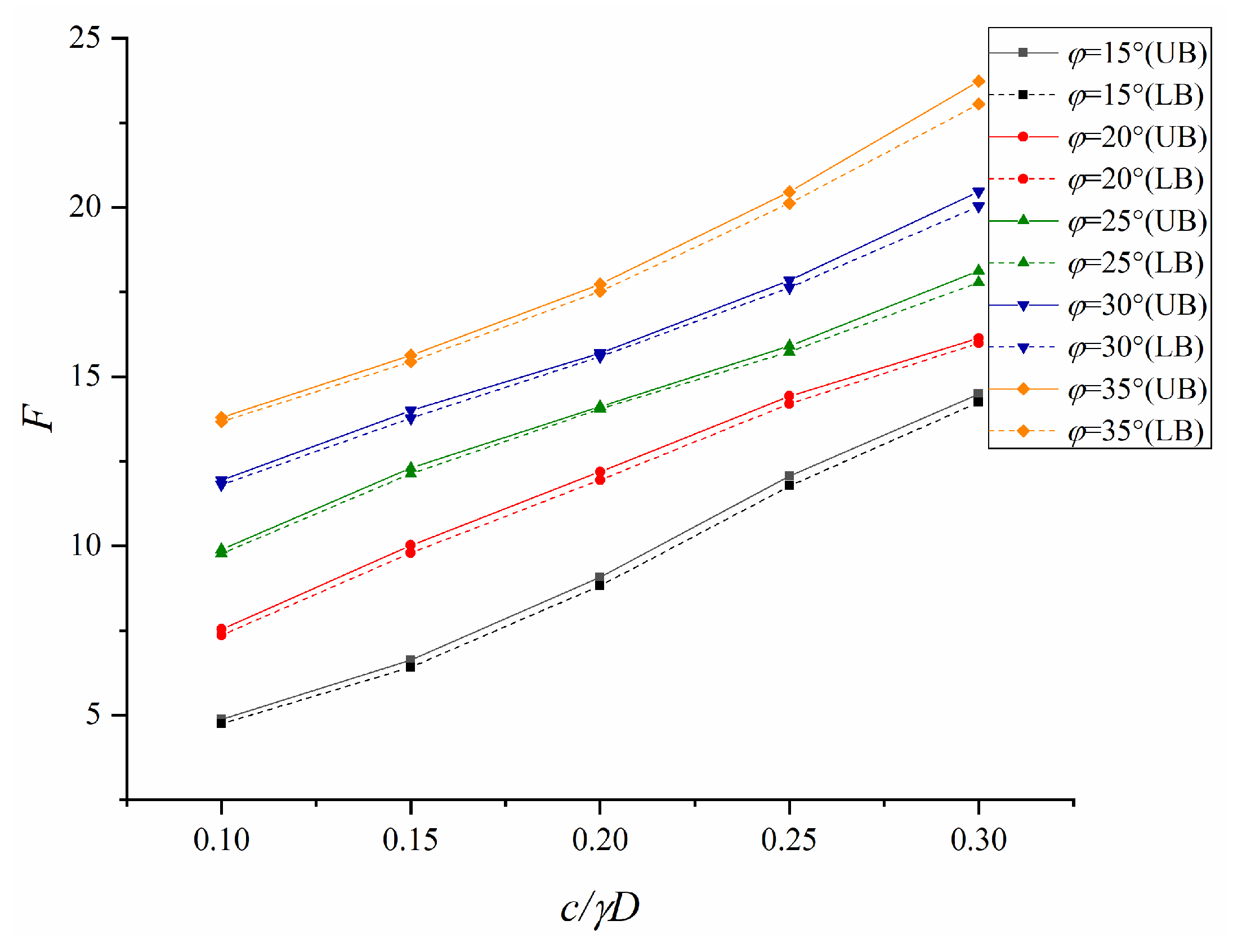
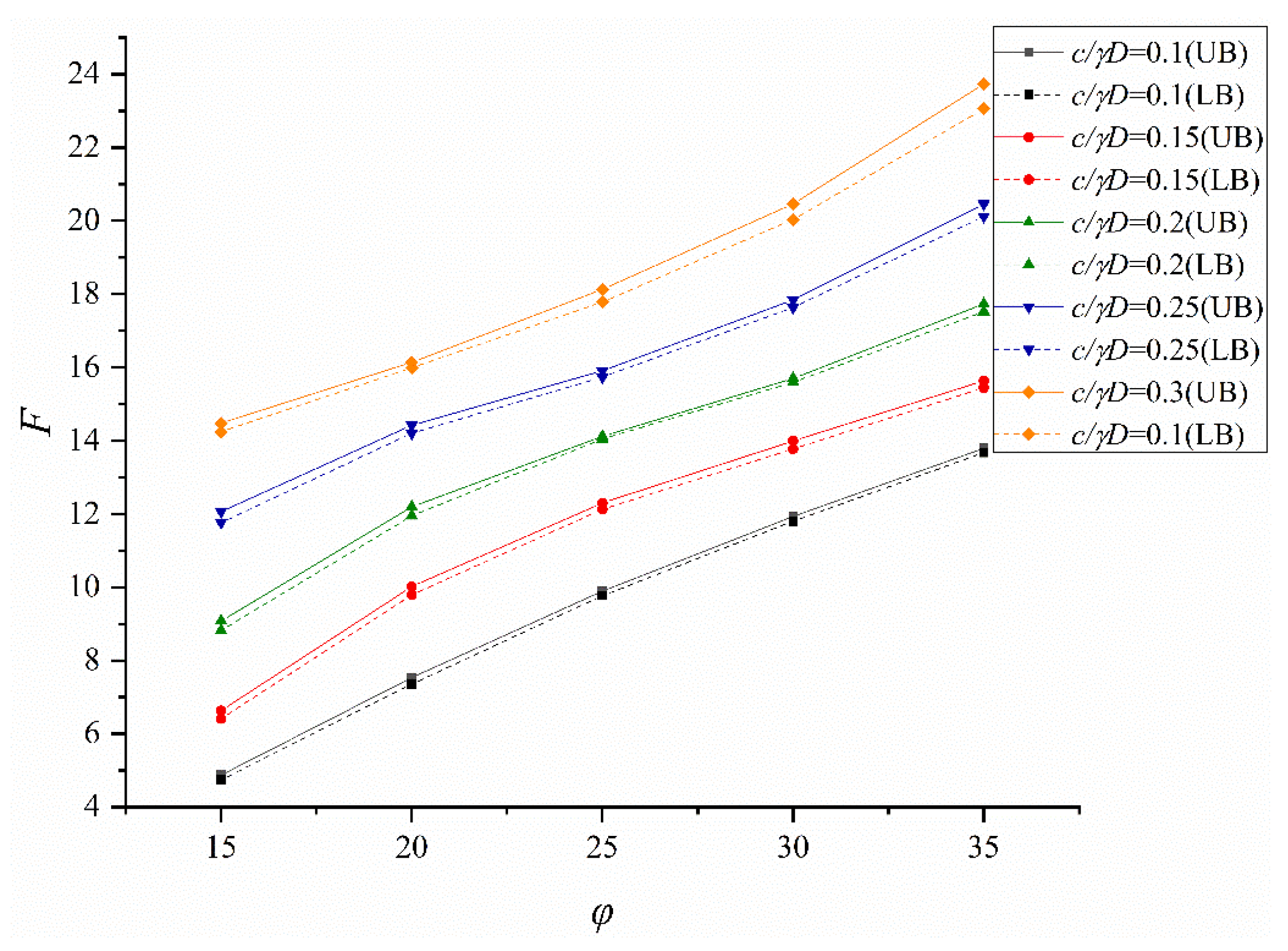
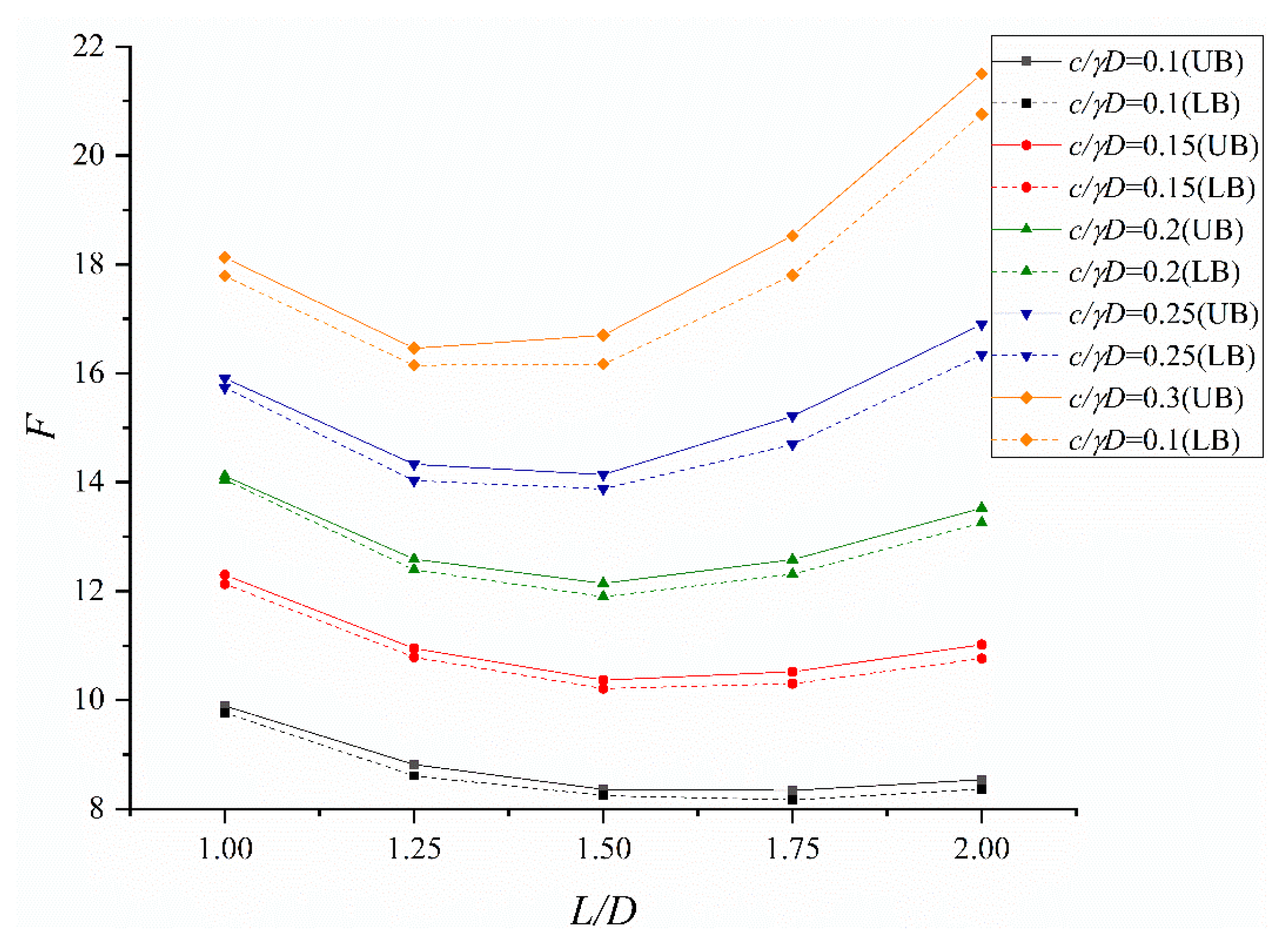
5.1. Influence of Input Parameter on the Global Stability of Adjacent Construction
5.2. Design Equation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zucca, M.; Valente, M. On the limitations of decoupled approach for the seismic behaviour evaluation of shallow multi-propped underground structures embedded in granular soils. Eng. Struct. 2020, 211, 110497. [Google Scholar] [CrossRef]
- Jancsecz, S.; Steiner, W. Face support for a large mix-shield in heterogeneous ground conditions. In Proceedings of the 7th International Symposium on Tunnelling ’94, London, UK, 5–7 July 1994; p. 531. [Google Scholar]
- Anagnostou, G. The contribution of horizontal arching to tunnel face stability. Geotechnik 2012, 35, 34–44. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Liu, C.; Huang, X. Numerical analysis of volume loss caused by tunnel face instability in soft soils. Environ. Earth Sci. 2017, 76, 563. [Google Scholar] [CrossRef]
- Terzaghi, K. Arching in Ideal Soils. In Theoretical Soil Mechanics; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1943; pp. 66–76. [Google Scholar]
- Bjerrum, L.; Eide, O. Stability of strutted excavations in clay. Géotechnique 1956, 6, 32–47. [Google Scholar] [CrossRef]
- Davis, E.H.; Gunn, M.J.; Mair, R.J.; Seneviratine, H.N. The stability of shallow tunnels and underground openings in cohesive material. Géotechnique 1980, 30, 397–416. [Google Scholar] [CrossRef]
- Leca, E.; Dormieux, L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material. Géotechnique 1990, 40, 581–606. [Google Scholar] [CrossRef] [Green Version]
- Soubra, A.-H.; Dias, D.; Emeriault, F.; Kastner, R. Three-dimensional face stability analysis of circular tunnels by a kinematical approach. In Proceedings of the GeoCongress 2008: Characterization, Monitoring, and Modeling of GeoSystems, New Orleans, LA, USA, 9–12 March 2008; pp. 894–901. [Google Scholar]
- Mollon, G.; Dias, D.; Soubra, A.-H. Face Stability Analysis of Circular Tunnels Driven by a Pressurized Shield. J. Geotech. Geoenvironmental Eng. 2010, 136, 215–229. [Google Scholar] [CrossRef] [Green Version]
- Mollon, G.; Dias, D.; Soubra, A.-H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 1363–1388. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Han, K.; Zhang, D. Face stability analysis of shallow circular tunnels in cohesive-frictional soils. Tunn. Undergr. Space Technol. 2015, 50, 345–357. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C. Face Stability Analysis for a Shield Tunnel in Anisotropic Sands. Int. J. Geomech. 2020, 20, 04020043. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.; Zhang, X. Stability analysis of the tunnel face in the cohesive-frictional soils considering the arch effect and rotational mechanism. J. Chin. Inst. Eng. 2018, 41, 697–709. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.; Zhu, W.; Zhang, D. Upper-bound solutions for the face stability of a non-circular NATM tunnel in clays with a linearly increasing undrained shear strength with depth. Comput. Geotech. 2019, 114, 103136. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.; Tan, Z.; Ma, M. Effect of the seepage flow on the face stability of a shield tunnel. Tunn. Undergr. Space Technol. 2021, 112, 103900. [Google Scholar] [CrossRef]
- Zhang, C.; Li, W.; Zhu, W.; Tan, Z. Face stability analysis of a shallow horseshoe-shaped shield tunnel in clay with a linearly increasing shear strength with depth. Tunn. Undergr. Space Technol. 2020, 97, 103291. [Google Scholar] [CrossRef]
- Tu, S.; Li, W.; Zhang, C.; Chen, W. Effect of inclined layered soils on face stability in shield tunneling based on limit analysis. Tunn. Undergr. Space Technol. 2023, 131, 104773. [Google Scholar] [CrossRef]
- Su, S.F.; Liao, H.J.; Lin, Y.H. Base stability of deep excavation in anisotropic soft clay. J. Geotech. Geoenvironmental Eng. 1998, 124, 809–819. [Google Scholar] [CrossRef]
- Chang, M.-F. Basal Stability Analysis of Braced Cuts in Clay. J. Geotech. Geoenvironmental Eng. 2000, 126, 276–279. [Google Scholar] [CrossRef]
- Zou, G.-D. Analysis of stability against upheaval of deep excavation by an upper limit method. Yantu Lixue Rock Soil Mech. 2004, 25, 1873–1878. [Google Scholar]
- Chen, R.P.; Tang, L.J.; Ling, D.S.; Chen, Y.M. Face stability analysis of shallow shield tunnels in dry sandy ground using the discrete element method. Comput. Geotech. 2011, 38, 187–195. [Google Scholar] [CrossRef]
- Chen, R.-p.; Li, J.; Kong, L.-g.; Tang, L.-j. Experimental study on face instability of shield tunnel in sand. Tunn. Undergr. Space Technol. 2013, 33, 12–21. [Google Scholar] [CrossRef]
- Ukritchon, B.; Yingchaloenkitkhajorn, K.; Keawsawasvong, S. Three-dimensional undrained tunnel face stability in clay with a linearly increasing shear strength with depth. Comput. Geotech. 2017, 88, 146–151. [Google Scholar] [CrossRef]
- Goh, A.T.C. Assessment of basal stability for braced excavation systems using the finite element method. Comput. Geotech. 1990, 10, 325–338. [Google Scholar] [CrossRef]
- Sloan, S.W. Lower bound limit analysis using finite elements and linear programming. Int. J. Numer. Anal. Methods Geomech. 1988, 12, 61–77. [Google Scholar] [CrossRef]
- Sloan, S.W. Upper bound limit analysis using finite elements and linear programming. Int. J. Numer. Anal. Methods Geomech. 1989, 13, 263–282. [Google Scholar] [CrossRef]
- Graettinger, A.J.; Lee, J.; Reeves, H.W. Upper bound limit analysis using linear finite elements and non-linear programming. Int. J. Numer. Anal. Methods Geomech. 2002, 26, 181–216. [Google Scholar] [CrossRef]
- Lyamin, A.V.; Sloan, S.W. Lower bound limit analysis using non-linear programming. Int. J. Numer. Methods Eng. 2002, 55, 573–611. [Google Scholar] [CrossRef]
- Krabbenhoft, K.; Lyamin, A.V.; Hjiaj, M.; Sloan, S.W. A new discontinuous upper bound limit analysis formulation. Int. J. Numer. Methods Eng. 2005, 63, 1069–1088. [Google Scholar] [CrossRef]
- Krabbenhøft, K.; Lyamin, A.V.; Sloan, S.W. Formulation and solution of some plasticity problems as conic programs. Int. J. Solids Struct. 2007, 44, 1533–1549. [Google Scholar] [CrossRef] [Green Version]
- Ukritchon, B.; Keawsawasvong, S. A new design equation for drained stability of conical slopes in cohesive-frictional soils. J. Rock Mech. Geotech. Eng. 2018, 10, 358–366. [Google Scholar] [CrossRef]
- Ukritchon, B.; Keawsawasvong, S. Stability of unlined square tunnels in Hoek-Brown rock masses based on lower bound analysis. Comput. Geotech. 2019, 105, 249–264. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Ukritchon, B. Stability of unsupported conical excavations in non-homogeneous clays. Comput. Geotech. 2017, 81, 125–136. [Google Scholar] [CrossRef]
- Keawsawasvong, S.; Ukritchon, B. Undrained basal stability of braced circular excavations in non-homogeneous clays with linear increase of strength with depth. Comput. Geotech. 2019, 115, 103180. [Google Scholar] [CrossRef]
- Shiau, J.; Al-Asadi, F. Revisiting Broms and Bennermarks’ original stability number for tunnel headings. Géotechnique Lett. 2018, 8, 310–315. [Google Scholar] [CrossRef] [Green Version]
- Shiau, J.; Al-Asadi, F. Two-dimensional tunnel heading stability factors Fc, Fs and F. Tunn. Undergr. Space Technol. 2020, 97, 103293. [Google Scholar] [CrossRef]
- Shiau, J.; Al-Asadi, F. Three-Dimensional Analysis of Circular Tunnel Headings Using Broms and Bennermark’s Original Stability Number. Int. J. Geomech. 2020, 20, 06020015. [Google Scholar] [CrossRef]
- Liang, R.; Xia, T.; Huang, M.; Lin, C. Simplified analytical method for evaluating the effects of adjacent excavation on shield tunnel considering the shearing effect. Comput. Geotech. 2017, 81, 167–187. [Google Scholar] [CrossRef]
- Liang, R.; Wu, W.; Yu, F.; Jiang, G.; Liu, J. Simplified method for evaluating shield tunnel deformation due to adjacent excavation. Tunn. Undergr. Space Technol. 2018, 71, 94–105. [Google Scholar] [CrossRef]
- Sun, H.; Chen, Y.; Zhang, J.; Kuang, T. Analytical investigation of tunnel deformation caused by circular foundation pit excavation. Comput. Geotech. 2019, 106, 193–198. [Google Scholar] [CrossRef]
- Wei, G.; Zhang, X.-H.; Lin, X.-B.; Hua, X.-X. Variations of transverse forces on nearby shield tunnel caused by foundation pits excavation. Yantu Lixue Rock Soil Mech. 2020, 41, 635–644 and 654. [Google Scholar] [CrossRef]
- Zhang, Z.-G.; Zhang, M.-X.; Wang, W.-D. Two-stage method for analyzing effects on adjacent metro tunnels due to foundation pit excavation. Yantu Lixue Rock Soil Mech. 2011, 32, 2085–2092. [Google Scholar]
- Zhou, Z.-L.; Chen, S.-G.; Chen, L.; Tu, P. Analysis of uplift deflection of subway tunnel due to adjacent pit excavation. Yantu Gongcheng Xuebao Chin. J. Geotech. Eng. 2015, 37, 2224–2234. [Google Scholar] [CrossRef]
- Zong, X. Study of longitudinal deformation of existing tunnel due to above excavation unloading. Yantu Lixue Rock Soil Mech. 2016, 37, 571–577 and 596. [Google Scholar] [CrossRef]
- Chen, R.; Meng, F.; Li, Z.; Ye, Y.; Ye, J. Investigation of response of metro tunnels due to adjacent large excavation and protective measures in soft soils. Tunn. Undergr. Space Technol. 2016, 58, 224–235. [Google Scholar] [CrossRef] [Green Version]
- Yanhua, H.; Wenhai, Y.; Qifen, W. Reserch on the influence of new shield tunnel to adjacent existing tunnel. In Proceedings of the 2012 International Conference on Sustainable Energy and Environmental Engineering, ICSEEE 2012, Guangzhou, China, 29–30 December 2012; pp. 2985–2989. [Google Scholar]
- Huang, H.; Huang, X.; Helmut, S.F. Numerical analysis of the influence of deep excavation on underneath existing road tunnel. Tumu Gongcheng Xuebao China Civ. Eng. J. 2012, 45, 182–189. [Google Scholar]
- Mahajan, S.; Ayothiraman, R.; Sharma, K.G. A Parametric Study on Effects of Basement Excavation and Foundation Loading on Underground Metro Tunnel in Soil. Indian Geotech. J. 2019, 49, 667–686. [Google Scholar] [CrossRef]
- Zheng, G.; Liu, Q.-C.; Deng, X. Numerical analysis of effect of excavation on underlying existing metro tunnel and deformation control. Yantu Lixue Rock Soil Mech. 2013, 34, 1459–1468+1477. [Google Scholar]
- SLOAN, S.W. Geotechnical stability analysis. Géotechnique 2013, 63, 531–571. [Google Scholar] [CrossRef] [Green Version]
- Drucker, D.C.; Prager, W.; Greenberg, H.J. Extended Limit Design Theorems for Continuous Media. Q. Appl. Math. 1952, 9, 381–389. [Google Scholar] [CrossRef] [Green Version]












| Material | Unit Weight γ (kg/m3) | Cohesion c (kPa) | Friction Angle φ (°) | Elasticity Modulus E (MPa) | Poisson’s Ratio v |
|---|---|---|---|---|---|
| Mohr–Coulomb | 1900 | 22 | 20 | 22 | 0.3 |
| Name | Material | Unit Weight γ (kg/m3) | Elasticity Modulus E (GPa) | Poisson’s Ratio v | Area (m2) |
|---|---|---|---|---|---|
| Supporting | C30 | 2500 | 30 | 0.3 | 0.8 |
| Lining | C50 | 2500 | 34.5 | 0.2 | 0.35 |
| Name | Material | Elasticity Modulus E (GPa) | Area (m2) | Interval (m) |
|---|---|---|---|---|
| Steel support | Q235 | 200 | 0.0298 | 3 |
| Concrete support | C30 | 30 | 0.64 | 9 |
| The Horizontal Distance between the Foundation Pit and the Twin Tunnels L (m) | The Cover Depth of the Twin Shield Tunnels C(m) | |||
|---|---|---|---|---|
| C = 9 | C = 18 | C = 27 | C = 36 | |
| L = 6 | (C = 9, L = 6) | (C = 18, L = 6) | (C = 27, L = 6) | (C = 36, L = 6) |
| L = 9 | (C = 9, L = 9) | (C = 18, L = 9) | (C = 27, L = 9) | (C = 36, L = 9) |
| L = 12 | (C = 9, L = 12) | (C = 18, L = 12) | (C = 27, L = 12) | (C = 36, L = 12) |
| L = 18 | (C = 9, L = 18) | (C = 18, L = 18) | (C = 27, L = 18) | (C = 36, L = 18) |
| L = 24 | (C = 9, L = 24) | (C = 18, L = 24) | (C = 27, L = 24) | (C = 36, L = 24) |
| L = 36 | (C = 9, L = 36) | (C = 18, L = 36) | (C = 27, L = 36) | (C = 36, L = 36) |
| Zone | Safety Factor |
|---|---|
| Ⅳ | >15 |
| Ⅲ | 12.5~15 |
| Ⅱ | 10~12.5 |
| Ⅰ | <10 |
| Zone | Surface Settlement (mm) | Horizontal Displacement of the Concrete Supporting (mm) |
|---|---|---|
| Ⅳ | >70 | >70 |
| Ⅲ | 55~70 | 55~70 |
| Ⅱ | 40~55 | 40~55 |
| Ⅰ | <40 | <40 |
| Buried Depth of Twin Tunnels | Zone Ⅰ (Very Safe) | Zone Ⅱ (Safe) | Zone Ⅲ (Dangerous) | Zone Ⅳ (Very Dangerous) |
|---|---|---|---|---|
| 1–2 m | 1 m–31 m | - | - | - |
| 3 m | 1 m–8 m, 11 m–31 m | 9 m–10 m | - | - |
| 4 m | 1 m–7 m, 11 m–31 m | 8 m–10 m | - | - |
| 5 m | 1 m–2 m, 11 m–31 m | 3 m–10 m | - | - |
| 6 m | 12 m–14 m, 18 m–31 m | 1 m–11 m, 15 m–17 m | - | - |
| 7 m–10 m | 19 m–31 m | 1 m–18 m | - | - |
| 11 m–12 m | 19 m–31 m | 3 m–18 m | 1 m–2 m | - |
| 13 m | 25 m–31 m | 3 m–24 m | 1 m–2 m | - |
| 14 m–17 m | - | 3 m–31 m | 1 m–2 m | - |
| 18 m–22 m | - | 4 m–31 m | 1 m–3 m | - |
| 23 m | - | 5 m–31 m | 1 m–4 m | - |
| 24 m–25 m | - | 6 m–31 m | 1 m–5 m | - |
| 26 m–28 m | - | 7 m–31 m | 1 m–6 m | - |
| 29 m–30 m | - | 8 m–31 m | 1 m–7 m | - |
| 31 m–33 m | - | 9 m–31 m | 1 m–8 m | - |
| 34 m–40 m | - | 10 m–31 m | 1 m–9 m | - |
| 41 m | - | 11 m–31 m | 1 m–10 m | - |
| 42 m | - | 12 m–31 m | 1 m–11 m | - |
| 43 m | 30 m–31 m | 12 m–29 m | 1 m–11 m | - |
| 44 m | 29 m–31 m | 12 m–28 m | 1 m–11 m | - |
| 45 m | 24 m–31 m | 12 m–23 m | 1 m–11 m | - |
| 46 m–49 m | 22 m–31 m | 12 m–21 m | 1 m–11 m | 46 m–49 m |
| Case | G1 | G2 | G3 | G4 | G5 | G6 | R2 |
|---|---|---|---|---|---|---|---|
| C/D = 1 | |||||||
| L/D = 1 | −7.092 | 38.11 | 0.5931 | 20.2 | −0.07628 | −0.002984 | 0.9914 |
| L/D = 1.25 | 2.575 | 5.915 | −0.07412 | 38.29 | 0.8374 | 0.00751 | 0.9898 |
| L/D = 1.5 | 12.27 | −38.4 | −0.74 | 81.26 | 2.152 | 0.01872 | 0.9884 |
| L/D = 1.75 | 26.33 | −109.8 | −1.639 | 165.5 | 4.238 | 0.03322 | 0.9789 |
| L/D = 2 | 27.59 | −159.1 | −1.494 | 249.6 | 5.383 | 0.02817 | 0.9822 |
| C/D = 1.5 | |||||||
| L/D = 1 | −1.681 | 23.75 | 0.2223 | 19.63 | 0.1061 | 0.002044 | 0.9937 |
| L/D = 1.25 | 6.567 | −9.775 | −0.3683 | 45.33 | 1.179 | 0.01193 | 0.9938 |
| L/D = 1.5 | 16.57 | −58 | −1.074 | 95.1 | 2.748 | 0.02438 | 0.9918 |
| L/D = 1.75 | 28.19 | −115.2 | −1.829 | 164.3 | 4.472 | 0.03697 | 0.9837 |
| L/D = 2 | 25.89 | −162.6 | −1.354 | 257.9 | 5.418 | 0.02566 | 0.985 |
| C/D = 2 | |||||||
| L/D = 1 | 5.269 | −8.658 | −0.2652 | 41.01 | 0.9975 | 0.009547 | 0.9977 |
| L/D = 1.25 | 10.44 | −35.73 | −0.6765 | 67.68 | 2.016 | 0.01764 | 0.9984 |
| L/D = 1.5 | 21.45 | −91.72 | −1.391 | 139.3 | 3.677 | 0.03007 | 0.9872 |
| L/D = 1.75 | 28.42 | −156.6 | −1.634 | 235.3 | 5.394 | 0.03147 | 0.9807 |
| L/D = 2 | 23.23 | −160.2 | −1.148 | 265.3 | 5.282 | 0.02202 | 0.9849 |
| C/D = 2.5 | |||||||
| L/D = 1 | 7.646 | −33.05 | −0.4807 | 69.93 | 1.835 | 0.0145 | 0.9983 |
| L/D = 1.25 | 22.47 | −98.93 | −1.469 | 147 | 3.94 | 0.03138 | 0.9842 |
| L/D = 1.5 | 27.11 | −154.8 | −1.543 | 233.9 | 5.356 | 0.02991 | 0.9804 |
| L/D = 1.75 | 22.72 | −157.8 | −1.124 | 260.1 | 5.264 | 0.02166 | 0.984 |
| L/D = 2 | 22.33 | −152.6 | −1.114 | 265.7 | 5.048 | 0.0219 | 0.9834 |
| C/D = 3 | |||||||
| L/D = 1 | 27.76 | −131.6 | −1.769 | 180.6 | 5.075 | 0.03532 | 0.9783 |
| L/D = 1.25 | 25.24 | −136.3 | −1.494 | 184.2 | 5.351 | 0.02894 | 0.9699 |
| L/D = 1.5 | 22.16 | −147.8 | −1.134 | 236.6 | 5.204 | 0.02191 | 0.9821 |
| L/D = 1.75 | 22.09 | −147.9 | −1.121 | 247.1 | 5.12 | 0.02176 | 0.9824 |
| L/D = 2 | 22.81 | −149.5 | −1.171 | 262.1 | 5.01 | 0.02302 | 0.9825 |
| Gi | ai | bi | ci | di | ei | fi |
|---|---|---|---|---|---|---|
| G1 | −125.1 | 120.2 | 35.04 | −19.81 | −20.76 | 0.4592 |
| G2 | 524.9 | −422.2 | −150.4 | 34.89 | 88.45 | −7.31 |
| G3 | 9.081 | −8.883 | −2.58 | 1.653 | 1.465 | 0.01583 |
| G4 | −338.2 | 238.2 | 94.75 | 31.27 | −64.89 | 15.7 |
| G5 | −15.87 | 14.93 | 4.139 | −1.812 | −2.842 | 0.3708 |
| G6 | −0.1486 | 0.1548 | 0.04369 | −0.03064 | −0.02454 | −0.0006089 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, L.; Ma, M.; Li, W.; Wang, Y. Stability Analysis of the Foundation Pit and the Twin Shield Tunnels during Adjacent Construction. Buildings 2023, 13, 1000. https://doi.org/10.3390/buildings13041000
Zhang X, Wang L, Ma M, Li W, Wang Y. Stability Analysis of the Foundation Pit and the Twin Shield Tunnels during Adjacent Construction. Buildings. 2023; 13(4):1000. https://doi.org/10.3390/buildings13041000
Chicago/Turabian StyleZhang, Xuan, Libin Wang, Mengshuo Ma, Wei Li, and Yuzheng Wang. 2023. "Stability Analysis of the Foundation Pit and the Twin Shield Tunnels during Adjacent Construction" Buildings 13, no. 4: 1000. https://doi.org/10.3390/buildings13041000
APA StyleZhang, X., Wang, L., Ma, M., Li, W., & Wang, Y. (2023). Stability Analysis of the Foundation Pit and the Twin Shield Tunnels during Adjacent Construction. Buildings, 13(4), 1000. https://doi.org/10.3390/buildings13041000






