Non-Destructive Damage Detection of Structural Joint by Coaxial Correlation Method in 6D Space
Abstract
:1. Introduction
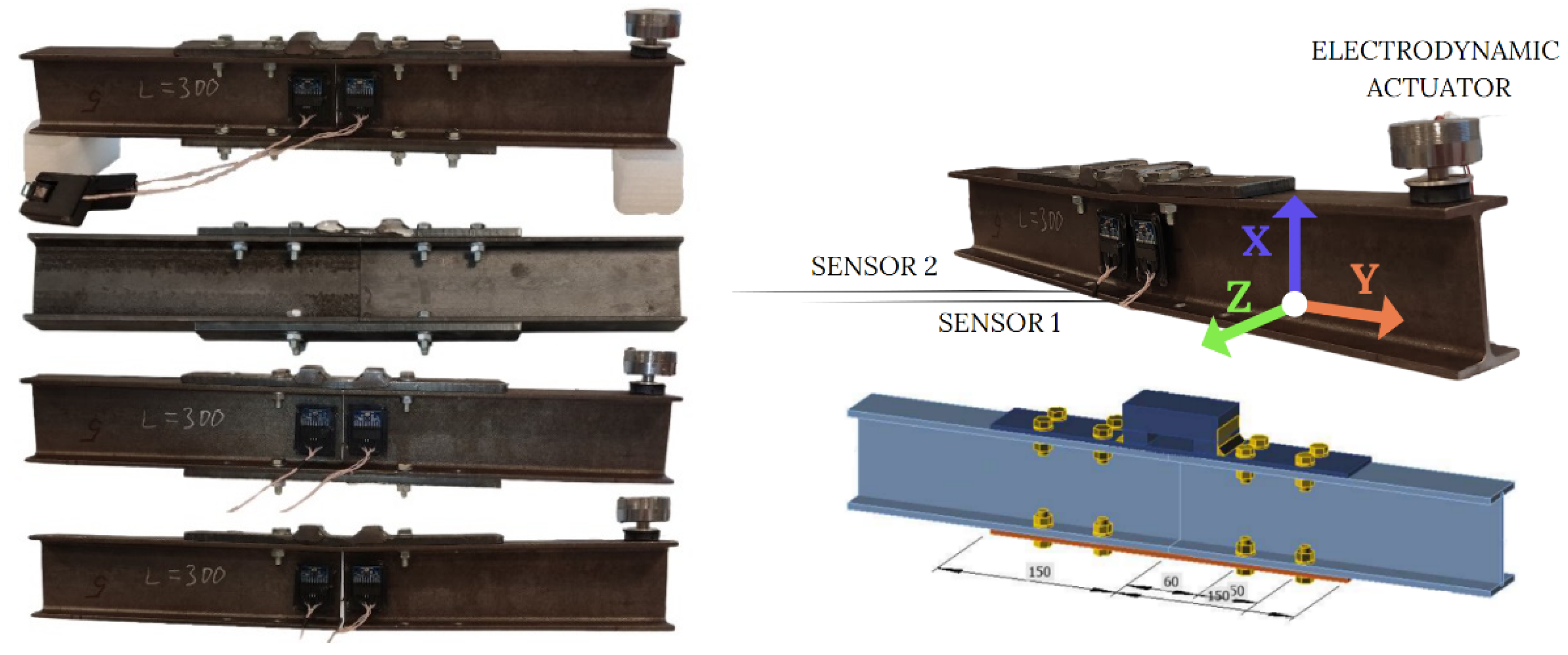
2. Materials and Methods
2.1. Improved Coaxial Correlations Method for Structural Joints Quality Evaluation
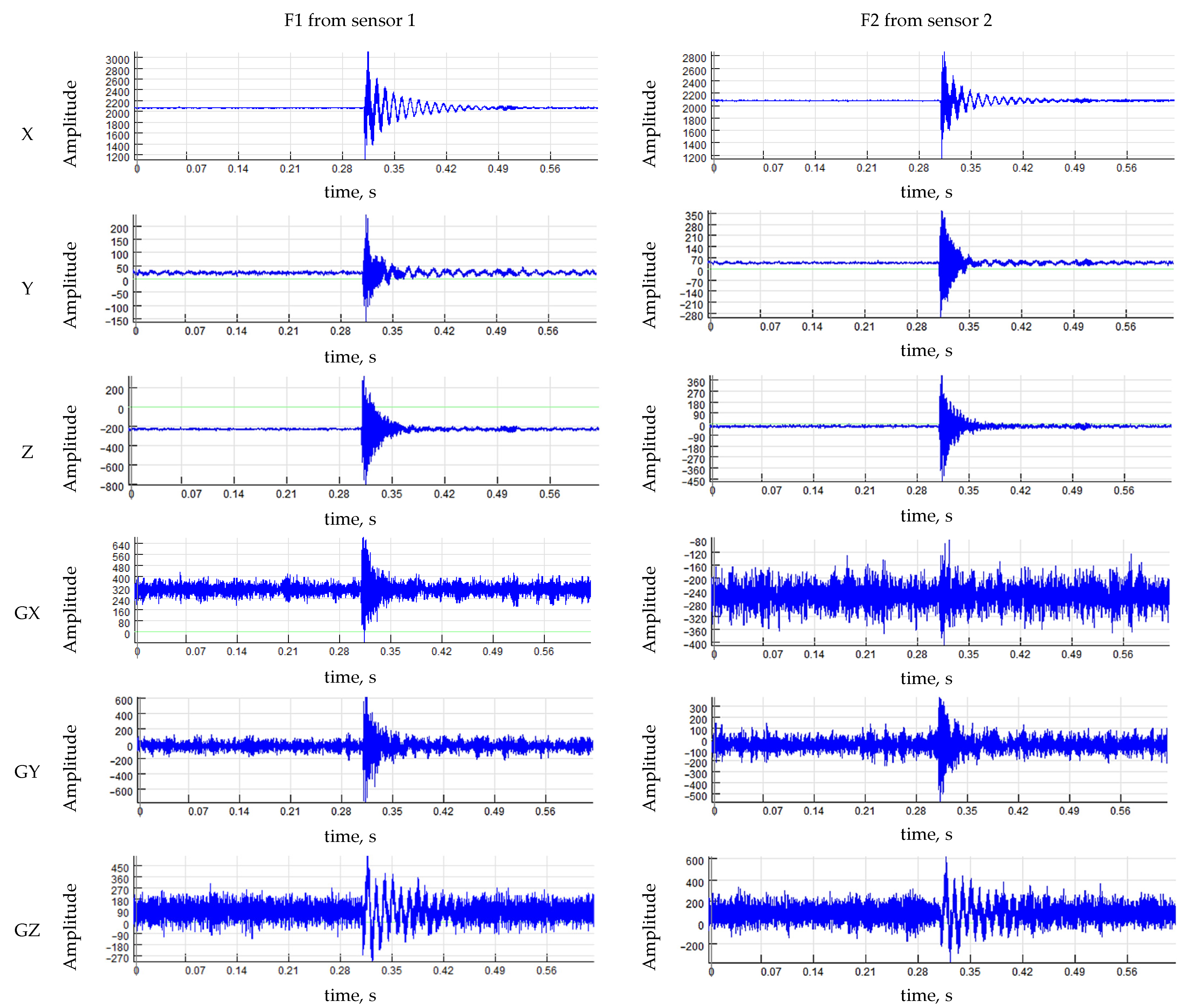
- Remove the constant offset from F1 and F2 by subtracting the signal’s mean value from all the amplitude values. The result is a signal with a mean equal to zero;
- Make the normalisation of concatenated pairs of responses F1 and F2 to ensure a mutual comparison of the obtained data under the conditions of the experiment with artificial degradation of the connection;
- Choose the frequency range in which the object’s behaviour under study will be observed based on the spectrum analysis;
- Split the filtered concatenated signal into two signals, F1* and F2*;
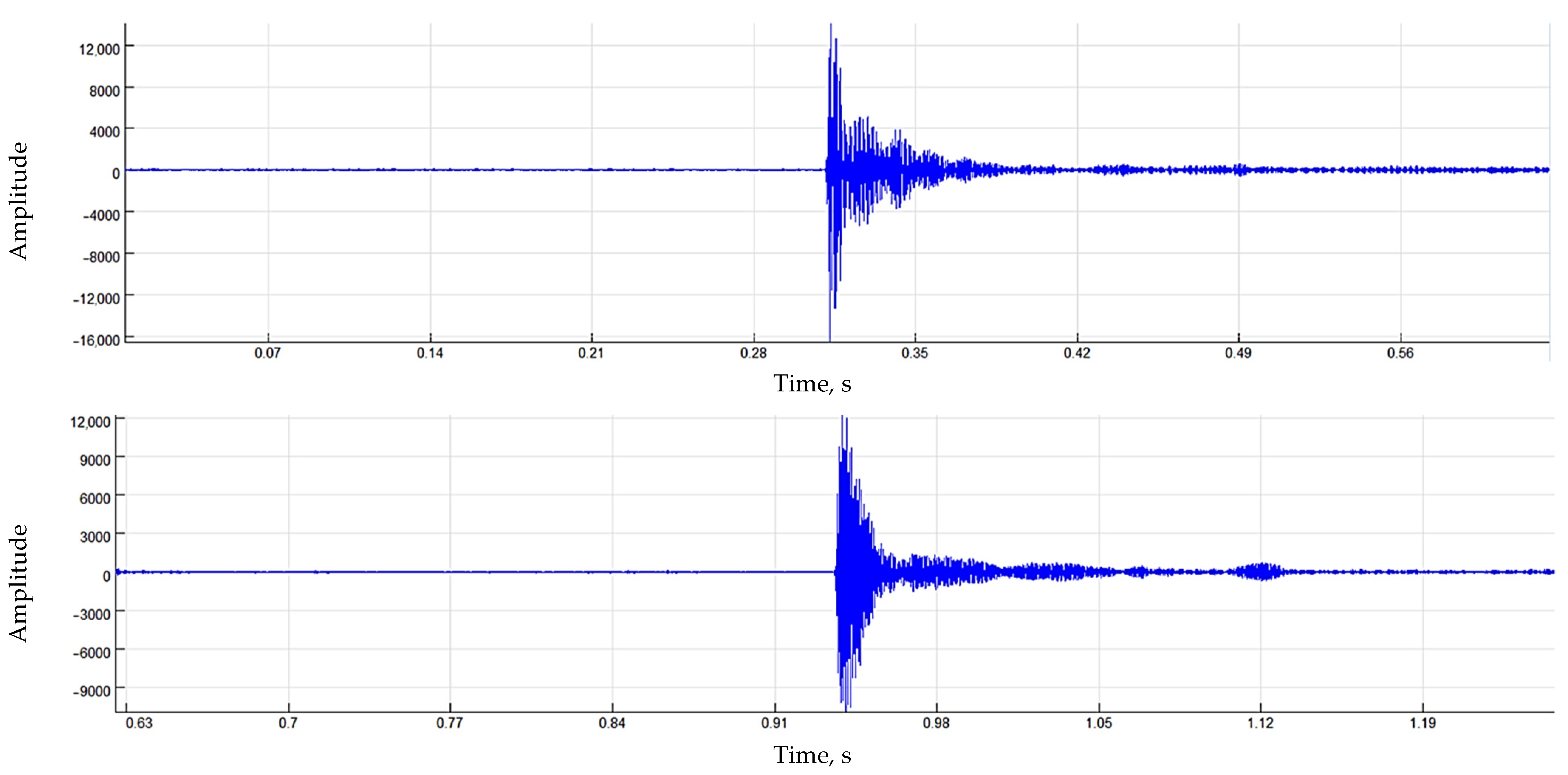
- Convolve the obtained normalised pairs of signals F1* and F2* from both sensors to characterise the degree of similarity between the two signals.;
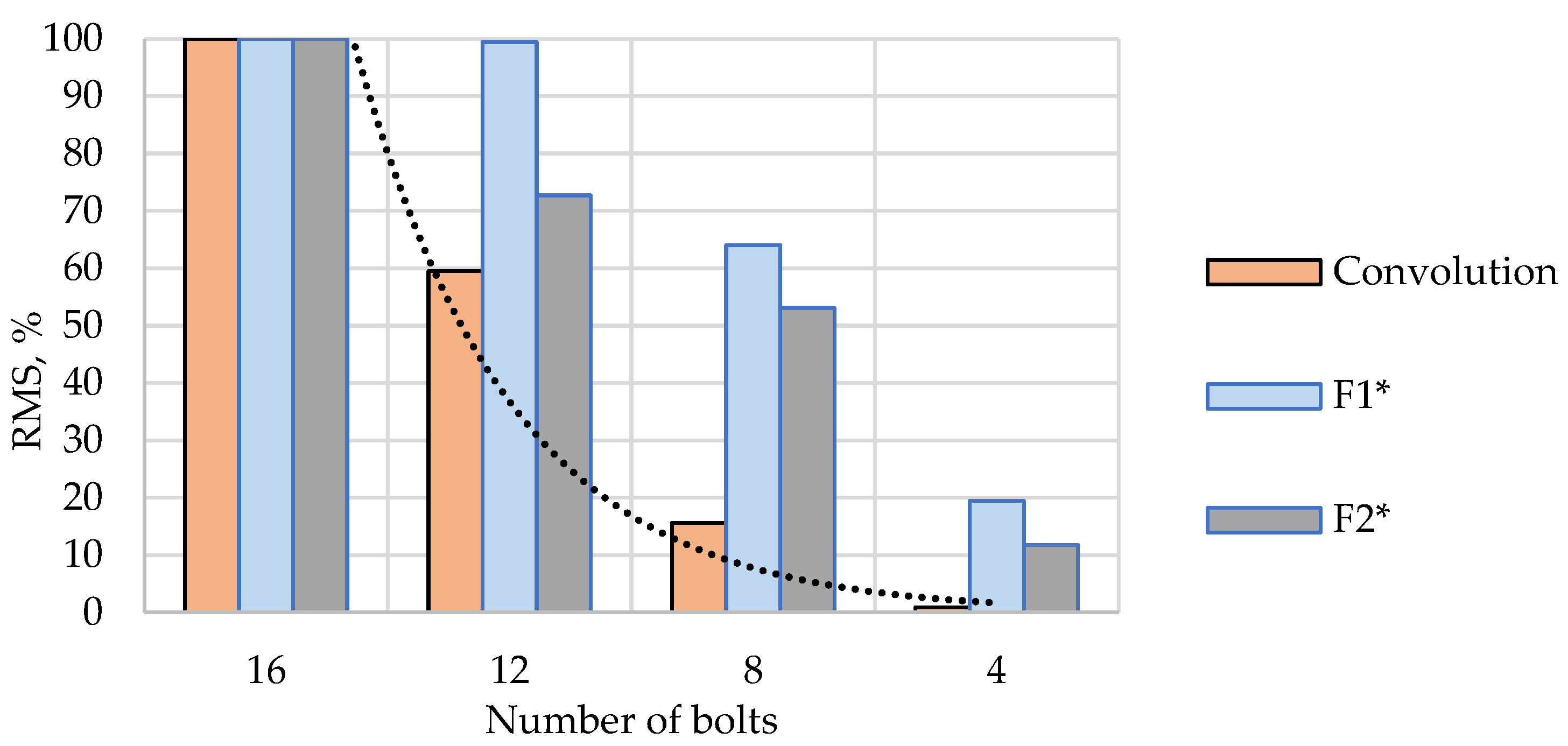
- Determine the root mean square (RMS) value from the obtained signals convolution as a measure of the similarity between two signals.
2.2. Verification Approach
3. Results and Discussion
4. Conclusions
- Determining linear accelerations and angular velocities, thus providing a measurement option in 6D space;
- Analysing at frequencies higher than 500 Hz, which is essential to ensure the possibility of studying the prototype of the structural joint in laboratory conditions;
- Processing data in the time domain thanks to synchronisation between the input signal and system responses;
- Using even weak input signal thanks to averaging system response.
Author Contributions
Funding

Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korkmaz, H.H.; Dere, Y.; Özkılıç, Y.O.; Bozkurt, M.B.; Ecemiş, A.S.; Özdoner, N. Excessive Snow Induced Steel Roof Failures in Turkey. Eng. Fail. Anal. 2022, 141, 106661. [Google Scholar] [CrossRef]
- Korkmaz, H.H.; Yakut, A.; Bayraktar, A. Analysis of a Multi-Story Reinforced Concrete Residential Building Damaged under Its Self-Weight. Eng. Fail. Anal. 2019, 98, 38–48. [Google Scholar] [CrossRef]
- Krentowski, J.R.; Knyziak, P.; Mackiewicz, M. Durability of Interlayer Connections in External Walls in Precast Residential Buildings. Eng. Fail. Anal. 2021, 121, 105059. [Google Scholar] [CrossRef]
- Šabatka, L.; Kolaja, D.; Vild, M.; Wald, F.; Kuříková, M.; Kabeláč, J. Influence of Joint Stiffness on Design of Steel Members. In Advances and Trends in Engineering Sciences and Technologies III; CRC Press: Boca Raton, FL, USA, 2019; ISBN 978-0-429-02159-6. [Google Scholar]
- Ngo, T.; Pham, T.; Hao, H. Ductile and Dry Exterior Joints Using CFRP Bolts for Moment-Resisting Frames. Structures 2020, 28, 668–684. [Google Scholar] [CrossRef]
- Özkılıç, Y.O. Cyclic and Monotonic Performance of Unstiffened Extended End-Plate Connections Having Thin End-Plates and Large-Bolts. Eng. Struct. 2023, 281, 115794. [Google Scholar] [CrossRef]
- Mashaly, E.; El-Heweity, M.; Abou-Elfath, H.; Osman, M. Behavior of Four-Bolt Extended End-Plate Connection Subjected to Lateral Loading. Alex. Eng. J. 2011, 50, 79–90. [Google Scholar] [CrossRef]
- Steneker, P.; Wiebe, L.; Filiatrault, A. Steel Moment Resisting Frames with Sliding Hinge Joint Connections: Seismic Evaluation Using Various Response Indices. In Proceedings of the 12th Canadian Conference on Earthquake Engineering (12CCEE), Quebec City, QC, Canada, 17–20 June 2019; Available online: https://research.iusspavia.it/handle/20.500.12076/5694 (accessed on 12 April 2023).
- Lemonis, M. Steel Moment Resisting Frames with Both Joint and Beam Dissipation Zones. J. Constr. Steel Res. 2018, 147, 224–235. [Google Scholar] [CrossRef]
- An Overview of the Connection Classification Index; The Hong Kong Institute of Steel Construction: Honolulu, HI, USA, 2019.
- Boscato, G.; Fragonara, L.Z.; Cecchi, A.; Reccia, E.; Baraldi, D. Structural Health Monitoring through Vibration-Based Approaches. Shock Vib. 2019, 2019, 2380616. [Google Scholar] [CrossRef]
- Opazo-Vega, A.; Benedetti, F.; Nuñez-Decap, M.; Maureira-Carsalade, N.; Oyarzo-Vera, C. Non-Destructive Assessment of the Elastic Properties of Low-Grade CLT Panels. Forests 2021, 12, 1734. [Google Scholar] [CrossRef]
- Gaile, L.; Ratnika, L.; Pakrastins, L. RC Medium-Rise Building Damage Sensitivity with SSI Effect. Materials 2022, 15, 1653. [Google Scholar] [CrossRef]
- Park, H.S.; Oh, B.K. Real-Time Structural Health Monitoring of a Supertall Building under Construction Based on Visual Modal Identification Strategy. Autom. Constr. 2018, 85, 273–289. [Google Scholar] [CrossRef]
- Varanis, M.; Silva, A.L.; Mereles, A.G. On Mechanical Vibration Analysis of a Multi Degree of Freedom System Based on Arduino and MEMS Accelerometers. Rev. Bras. Ensino Física 2017, 40, e1304. [Google Scholar] [CrossRef]
- Li, W.; Guo, S.; Liu, Y.; Shen, Z.; Xiong, Y.; Gao, F.; Hughes, D.J.; Lin, J. Structure Health Monitoring of Composites Joint Reinforced by Acoustic Emission Based Smart Composite Fasteners. Compos. Commun. 2022, 33, 101213. [Google Scholar] [CrossRef]
- Zhu, L.; Fu, Y.; Chow, R.; Spencer, B.F.; Park, J.W.; Mechitov, K. Development of a High-Sensitivity Wireless Accelerometer for Structural Health Monitoring. Sensors 2018, 18, 262. [Google Scholar] [CrossRef]
- Wu, T.; Liu, G.; Fu, S.; Xing, F. Recent Progress of Fiber-Optic Sensors for the Structural Health Monitoring of Civil Infrastructure. Sensors 2020, 20, 4517. [Google Scholar] [CrossRef]
- Muttillo, M.; Stornelli, V.; Alaggio, R.; Paolucci, R.; Di Battista, L.; de Rubeis, T.; Ferri, G. Structural Health Monitoring: An IoT Sensor System for Structural Damage Indicator Evaluation. Sensors 2020, 20, 4908. [Google Scholar] [CrossRef]
- Sulaiman, M.S.A.; Yunus, M.A.; Bahari, A.R.; Rani, M.N.A. Identification of Damage Based on Frequency Response Function (FRF) Data. MATEC Web Conf. 2017, 90, 01025. [Google Scholar] [CrossRef]
- Zhan, J.; Zhang, F.; Siahkouhi, M. A Step-by-Step Damage Identification Method Based on Frequency Response Function and Cross Signature Assurance Criterion. Sensors 2021, 21, 1029. [Google Scholar] [CrossRef]
- Buka-Vaivade, K.; Gaile, L.; Serdjuks, D.; Tatarinovs, A.; Pakrastins, L. Non-Destructive Quality Control of the Adhesive Rigid Timber-to-Concrete Connection in TCC Structures. Buildings 2022, 12, 2151. [Google Scholar] [CrossRef]
- Tol, Ş.; O¨zgu¨ven, H.N. Dynamic Characterization of Bolted Joints Using FRF Decoupling and Optimization. Mech. Syst. Signal Process. 2015, 54, 124–138. [Google Scholar] [CrossRef]
- Wang, X. Chapter 1—Analysis of a Single Degree of Freedom Spring-Mass-Dashpot System Using Transfer Function, Integration, State Space, and Frequency Response Methods. In Frequency Analysis of Vibration Energy Harvesting Systems; Wang, X., Ed.; Academic Press: Cambridge, MA, USA, 2016; pp. 1–13. ISBN 978-0-12-802321-1. [Google Scholar]
- Gomez-Cabrera, A.; Escamilla-Ambrosio, P.J. Review of Machine-Learning Techniques Applied to Structural Health Monitoring Systems for Building and Bridge Structures. Appl. Sci. 2022, 12, 10754. [Google Scholar] [CrossRef]
- Zajam, S.; Joshi, T.; Bhattacharya, B. Application of Wavelet Analysis and Machine Learning on Vibration Data from Gas Pipelines for Structural Health Monitoring. Procedia Struct. Integr. 2019, 14, 712–719. [Google Scholar] [CrossRef]
- Izham, M.H.N.; Sani, M.S.M.; Abdul Rani, M.N.; Yunus, M.A. Damage Assessment on Frame Structure with Bolted Joints Based on Experimental Modal Analysis. IOP Conf. Ser. Mater. Sci. Eng. 2019, 469, 012102. [Google Scholar] [CrossRef]
- Nguyen, K.-D.; Chan, T.H.; Thambiratnam, D.P.; Nguyen, A. Damage Identification in a Complex Truss Structure Using Modal Characteristics Correlation Method and Sensitivity-Weighted Search Space. Struct. Health Monit. 2019, 18, 49–65. [Google Scholar] [CrossRef]
- Nguyen, T.H.A. Vibration Testing for Dynamic Properties of Building Floors. IOP Conf. Ser. Mater. Sci. Eng. 2020, 869, 052005. [Google Scholar] [CrossRef]
- Knak, M.; Wojtczak, E.; Rucka, M. Non-Destructive Diagnostics of Concrete Beams Strengthened with Steel Plates Using Modal Analysis and Wavelet Transform. Materials 2021, 14, 3014. [Google Scholar] [CrossRef]
- Serdjuks, D.; Kurtenoks, V.; Tatarinovs, A.; Mironovs, V.; Lapkovskis, V.; Buka-Vaivade, K.; Macevics, A.; Topcijs, K.; Vilnitis, M. Method of Coaxial Accelerations Correlation for Quality Assessment of Structural Joints. Procedia Struct. Integr. 2022, 37, 547–554. [Google Scholar] [CrossRef]
- Serdjuks, D.; Kurtenoks, V.; Tatarinovs, A.; Buka-Vaivade, K.; Lapkovskis, V.; Mironovs, V.; Podkoritovs, A.; Topcijs, K. Non-Model Vibration Analysis Method for Health Monitoring of Structural Joints. Procedia Struct. Integr. 2022, 37, 555–562. [Google Scholar] [CrossRef]
- Ravanshad, N.; Rezaee-Dehsorkh, H. Chapter 12—Level-Crossing Sampling: Principles, Circuits, and Processing for Healthcare Applications. In Compressive Sensing in Healthcare; Khosravy, M., Dey, N., Duque, C.A., Eds.; Advances in Ubiquitous Sensing Applications for Healthcare; Academic Press: Cambridge, MA, USA, 2020; pp. 223–246. [Google Scholar]
- Mark, H.; Workman, J. Chapter 102—Calibration Transfer, Part 2: The Instrumentation Aspects. In Chemometrics in Spectroscopy, 2nd ed.; Mark, H., Workman, J., Eds.; Academic Press: Cambridge, MA, USA, 2018; pp. 751–764. ISBN 978-0-12-805309-6. [Google Scholar]
- Christ, R.D.; Wernli, R.L. Chapter 7—Power and Telemetry. In The ROV Manual, 2nd ed.; Christ, R.D., Wernli, R.L., Eds.; Butterworth-Heinemann: Oxford, UK, 2014; pp. 141–161. ISBN 978-0-08-098288-5. [Google Scholar]
- Ibrahim, D. Chapter 8—Advanced PIC32 Projects. In Designing Embedded Systems with 32-Bit PIC Microcontrollers and MikroC; Ibrahim, D., Ed.; Newnes: Oxford, UK, 2014; pp. 359–442. ISBN 978-0-08-097786-7. [Google Scholar]
- Pyeatt, L.D.; Ughetta, W. Chapter 11—Devices. In ARM 64-Bit Assembly Language; Pyeatt, L.D., Ughetta, W., Eds.; Newnes: Oxford, UK, 2020; pp. 405–444. ISBN 978-0-12-819221-4. [Google Scholar]






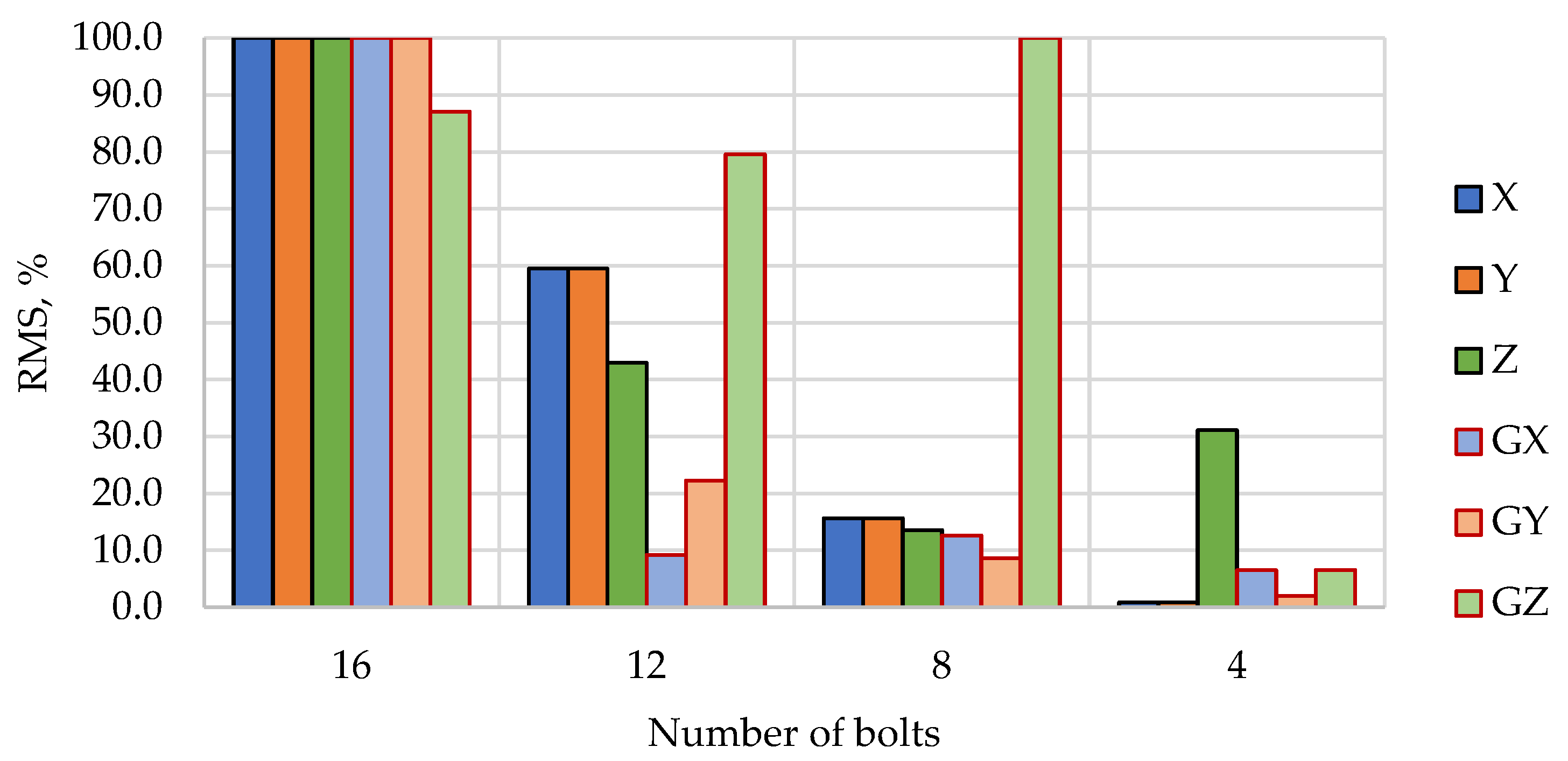
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buka-Vaivade, K.; Kurtenoks, V.; Serdjuks, D. Non-Destructive Damage Detection of Structural Joint by Coaxial Correlation Method in 6D Space. Buildings 2023, 13, 1151. https://doi.org/10.3390/buildings13051151
Buka-Vaivade K, Kurtenoks V, Serdjuks D. Non-Destructive Damage Detection of Structural Joint by Coaxial Correlation Method in 6D Space. Buildings. 2023; 13(5):1151. https://doi.org/10.3390/buildings13051151
Chicago/Turabian StyleBuka-Vaivade, Karina, Viktors Kurtenoks, and Dmitrijs Serdjuks. 2023. "Non-Destructive Damage Detection of Structural Joint by Coaxial Correlation Method in 6D Space" Buildings 13, no. 5: 1151. https://doi.org/10.3390/buildings13051151
APA StyleBuka-Vaivade, K., Kurtenoks, V., & Serdjuks, D. (2023). Non-Destructive Damage Detection of Structural Joint by Coaxial Correlation Method in 6D Space. Buildings, 13(5), 1151. https://doi.org/10.3390/buildings13051151







